第四讲 逻辑函数的公式化简法
合集下载
逻辑函数的公式化简
一、化简的意义
逻辑函数的公式化简
1.逻辑函数表达式的不同形式 2.逻辑函数化简的意义 用较少的门电路实现相同的逻辑功能，不仅可以降低成本，而且还可提高电路工作的可 靠性。
二、公式化简的方法
1.并项法 2.吸收法 3.消去法 4.配项法
谢谢！
每一个逻辑函数式都对应 着一个具体电路。在具体实现 电路时，往往根据现有的元器 件（集成门电路）选择相应的 逻辑表达式。
一、化简的意义
2.逻辑函数化简的意义
在数字电路中，是由逻辑门电路来实现一定的逻辑功能，逻辑函数的化简就意味着实现该 功能的电路简化，能用较少的门电路实现相同的逻辑功能，不仅可以降低成本，而且还可提高 电路工作的可靠性。
逻辑函数的公式化简
逻辑函数化简的意义是什么？ 逻辑函数公式化简的方法有哪些？
一、化简的意义
1.逻辑函数表达式的不同形式
异或门
Y AB AB A B
Y AB AB
与或表达式
AB AB AB AB (A B)(A B) AB AB AB AB
与或非-非表达式 与非-与非表达式 或与非表达式 与或非表达式 或非-或非表达式
AB
二、公式化简的方法
2.吸收法 利用公式A+AB＝A ，吸收多余项AB。
【例2】化简逻辑函数 Y AC ABCD 【解】 Y AC ABCD
AC（1 BD） AC
二、公式化简的方法
3.消去法
利用公式 A AB A B，消去 AB 项中的多余因子 A。 【例3】化简逻辑函数 Y AB AC BC 【解】Y AB AC BC
AB（A B）C AB（AB）C AB C
二、公式化简的方法
4.配项法
利用公式 A A 1 ，给适 【解】Y AB BC BC AB
第四讲 逻辑函数的公式化简法
化简逻辑函数： 例.6 化简逻辑函数：
L = AD + AD + AB + AC + BD + ABEF + BEF
解： = A + AB + AC + BD + A BEF + BEF （利用 L
利用A+AB=A） ） = A + AC + BD + BEF （利用
A+ A =1 ）
= A + C + BD + BEF
= AC+ BC + D(A + B)
= AC + BC + DAB
消项AB 消项AB
消因律
= AC+ BC + AB+ DAB
= AC+ BC + AB+ D
= AC+ BC + D
代数法化简函数
例4：简化函数 F=AB+AC+BC+BD+BD+BC+ADE(F+G) 利用反演律 解： F=AB+AC+BC+BD+BD+BC+ADE(F+G) 消因律 =A(B+C)+BC+BD+BD+BC+ADE(F+G) 吸收律 =ABC+BC+BD+BD+BC+ADE(F+G) =A+BC+BD+BD+BC+ADE(F+G) 配项A+A=1 配项A+A=1 =A+BC+BD+BD+BC =A+BC(D+D)+BD+BD (C+C) +BC F（或与式）求对偶式 F′（与或式）简化 F′ （或与式） ′ 与或式） ′ =A+BD+BC+CD 最简与或式） 或与式） （最简与或式）求对偶式 F（最简或与式） （最简或与式
L = AD + AD + AB + AC + BD + ABEF + BEF
解： = A + AB + AC + BD + A BEF + BEF （利用 L
利用A+AB=A） ） = A + AC + BD + BEF （利用
A+ A =1 ）
= A + C + BD + BEF
= AC+ BC + D(A + B)
= AC + BC + DAB
消项AB 消项AB
消因律
= AC+ BC + AB+ DAB
= AC+ BC + AB+ D
= AC+ BC + D
代数法化简函数
例4：简化函数 F=AB+AC+BC+BD+BD+BC+ADE(F+G) 利用反演律 解： F=AB+AC+BC+BD+BD+BC+ADE(F+G) 消因律 =A(B+C)+BC+BD+BD+BC+ADE(F+G) 吸收律 =ABC+BC+BD+BD+BC+ADE(F+G) =A+BC+BD+BD+BC+ADE(F+G) 配项A+A=1 配项A+A=1 =A+BC+BD+BD+BC =A+BC(D+D)+BD+BD (C+C) +BC F（或与式）求对偶式 F′（与或式）简化 F′ （或与式） ′ 与或式） ′ =A+BD+BC+CD 最简与或式） 或与式） （最简与或式）求对偶式 F（最简或与式） （最简或与式
逻辑函数的公式化简法
逻辑函数的公式化简法
公式化简法的原理就是反复使用规律代数的基本公式和常用公式消去函数式中多余的乘积项和多余的因式，以求得函数式的最简形式。
公式化简法没有固定的步骤。
现将常常使用的方法归纳如下：
一、并项法
二、汲取法
利用公式A+AB=A，汲取掉（即除去）多余的项。
A和B同样也可以是任何一个简单的规律式。
【例】试用汲取法化简下列规律函数：
三、消项法利用公式AB+ C+BC=AB+ C及AB+ C+BCD=AB+ C，将BC或BCD消去。
其中A、B、C、D都可以是任何简单的规律式。
【例】用消项法化简下列规律函数：
四、消因子法利用公式A+B=A+B，可消去多余的因子。
A、B均可以是任何简单的规律式。
【例】试用消因子法化简下列规律函数
五、配项法1、依据基本公式A+A=A可以在规律函数式中重复写入某一项，有时能获得更加简洁的化简结果。
2、依据基本公式A+=1，可以在函数式中乘以（A+ ），然后拆成两项分别与其他项合并，有时能得到更加简洁的化简结果。
在化简简单的规律函数时，往往需要敏捷、交替地运用上述方法，才能得到最终的化简结果。
【例】化简规律函数。
逻辑函数化简公式大全
逻辑函数化简公式大全逻辑函数化简是在布尔代数中常用的一种方法，它通过应用逻辑运算规则和布尔代数定律，将复杂的逻辑函数简化为更简洁的形式。
这种简化可以减少逻辑电路的复杂性，提高计算机系统的效率。
以下是一些常见的逻辑函数化简公式大全：1. 与运算的化简：- 与运算的恒等律：A∧1 = A，A∧0 = 0- 与运算的零律：A∧A' = 0，A∧A = A- 与运算的吸收律：A∧(A∨B) = A，A∧(A∧B) = A∧B- 与运算的分配律：A∧(B∨C) = (A∧B)∨(A∧C)- 与运算的交换律：A∧B = B∧A2. 或运算的化简：- 或运算的恒等律：A∨1 = 1，A∨0 = A- 或运算的零律：A∨A' = 1，A∨A = A- 或运算的吸收律：A∨(A∧B) = A，A∨(A∨B) = A∨B- 或运算的分配律：A∨(B∧C) = (A∨B)∧(A∨C)- 或运算的交换律：A∨B = B∨A3. 非运算的化简：- 非运算的双重否定律：(A) = A- 非运算的德摩根定律：(A∧B) = A∨B，(A∨B) = A∧B4. 异或运算的化简：- 异或运算的恒等律：A⊕0 = A，A⊕1 = A- 异或运算的自反律：A⊕A = 0- 异或运算的结合律：A⊕(B⊕C) = (A⊕B)⊕C- 异或运算的交换律：A⊕B = B⊕A5. 条件运算的化简：- 条件运算的恒等律：A→1 = 1，A→0 = A- 条件运算的零律：A→A' = 0，A→A = 1- 条件运算的反转律：A→B = A∨B- 条件运算的分配律：A→(B∧C) = (A→B)∧(A→C)这些公式是逻辑函数化简中常用的基本规则，通过灵活应用它们，可以将复杂的逻辑表达式简化为更简单的形式。
使用这些规则，我们可以提高逻辑电路的效率和简洁性，并降低硬件成本。
第四章：逻辑代数及其化简(4)
0 1 1 0
BC
F2
F = AB + C = AB + C = AB ⋅ C 1
F2 = BC + ABC = BC + ABC = BC ⋅ ABC 2、将 F1 和 F2 整体 化简(找公共项 找公共项） 找公共项
AB AB C 00 01 11 10 C 00 01 11 10 0 0 0 0 1 ABC 0 0 0 0 1 1 0 1 1 0 1 1 1 1 1 C
尾部代替因子 一个乘积项的尾部因子，可根据需要加以扩展，如果扩 展变量是属于头部内的变量，则该乘积项的值不变。扩展后 的因子，称为原乘积项尾部因子的代替因子。
Ei = abc = abac = abbc = ababc 头部因子可以随意放入尾部因子， 头部因子可以随意放入尾部因子，也可以从尾部因 子中取走。 子中取走。 即：尾部因子的反号可以任意伸长和缩短，伸长将头 部因子 放进去，缩短将头部因子取出来。
例： 证明： 证明： abc = abac = ab(a + c) = aba + abc = abc
abc = abbc = ab b + c = abc abc = ababc = ab a + b + c = abc
(
(
)
(a ⋅a = 0)
)
乘积项合并 如果两个或两个以上乘积项的头部完全相同，则这几个 乘机项可以合并为一个乘积项。 AB
例4:已知 F = ∑m(0,1,3,4,5)求F' 的最小项表达式。
F = B+ A C F' = B A + C = AB + BC
(
1 1 0 1 B = ABC + ABC + ABC A C = ∑m (0,1,5) F和F'号码数目相同，对应之和为7。 变量： F和F'之间的关系： 由此推广到 n 变量： ) F = ∑m (0,1,3,4,5) F( a, b, cL = ∑( i) 最小项编号
逻辑函数的公式法化简 数电课件
，X给某个X逻辑1函数表达式增加适当的多余项，
进而消去原来函数中的某些项，从而达到化简逻辑函数的目的。
例2.3.3 化简逻辑函数
F7 AB BC AB BC
方法1
F7 AB BC AB BC
AB BC AB C C A A BC
3. F3 AB ABC AC
ABC A B C
ABC ABC
A
2. 吸收法
利用吸收律Ⅰ
A A；B或吸收A律Ⅱ
例2.3.2 化简下列逻辑函数。
1. F4 AB AD BE A B AD BE AB
，A消去A多B余的A与项B或因子。
例2.3.4 化简逻辑函数
F8 AD AD AB AC BD ACE BE DE F8 AD AD AB AC BD ACE BE DE
A AB AC BD ACE BE DE A C BD BE DE A C BD BE
§2·3 逻辑函数的公式法化简
一个逻辑函数可以有不同形式的表达式。
Ⅰ. “与或”式 Ⅱ. “或与”式 Ⅲ. “与非—与非”式 Ⅳ. “与或非”式 Ⅴ. “或非—或非”式
F AgB AgC
F A Bg A C
F AgB g AgC F AgB AgC
F AB AC
其次，逻辑函数的最简“与或”式最优先。
二、逻辑函数的公式法化简
1. 合并项法
利用合并律
AB A，B将两 个A与项合并成一项，并消去多余的与项和变量。
例2.3.1 化简下列逻辑函数。
1. F1 ABC ABC AB
逻辑函数的化简
AB CD 00 01 11 10 00 1 0 0 1 01 1 0 0 1 11 × × × × 10 1 0 × ×
不利用随意项 的化简结果为：
Y AD AC D
利用随意项的化 简结果为：
Y D
3、变量互相排斥的逻辑函数的化简 在一组变量中，如果只要有一个变量取值为1，则其它变量 的值就一定为0，具有这种制约关系的变量叫做互相排斥的变量。 变量互相排斥的逻辑函数也是一种含有随意项的逻辑函数。
ＢＣ的公因子
3、卡诺图的性质 （1）任何两个（21个）标1的相邻最小项，可以合并为一项， 并消去一个变量（消去互为反变量的因子，保留公因子）。
AB C 0 1 00 1 0 01 0 1 11 0 1 10 1 0
A B C AB C BC
A BC ABC
AB CD 00 01 11 10 00 0 0 0 0 01 1 0 0 1 11 0 0 0 0
A BC A BC ABC ABC ( A C A C AC AC) B B
AB CD 00 01 11 10 00 0 1 0 0 01 1 1 1 1 11 0 1 1 0 10 0 1 0 0
CD
AB
AB CD 00 01 11 10 00 0 1 1 0 01 1 0 0 1 11 1 0 0 1 10 0 1 1 0
ＡＤ
ＢＤ
AB CD 00 01 11 10 00 1 0 0 1 01 0 1 1 0 11 0 1 1 0 10 1 0 0 1
ＢＤ
ＢＤ
（3）任何8个（23个）标1的相邻最小 项，可以合并为一项，并消去3个变量。
AB CD 00 01 11 10 00 0 1 1 0 01 0 1 1 0 11 0 1 1 0 10 0 1 1 0
不利用随意项 的化简结果为：
Y AD AC D
利用随意项的化 简结果为：
Y D
3、变量互相排斥的逻辑函数的化简 在一组变量中，如果只要有一个变量取值为1，则其它变量 的值就一定为0，具有这种制约关系的变量叫做互相排斥的变量。 变量互相排斥的逻辑函数也是一种含有随意项的逻辑函数。
ＢＣ的公因子
3、卡诺图的性质 （1）任何两个（21个）标1的相邻最小项，可以合并为一项， 并消去一个变量（消去互为反变量的因子，保留公因子）。
AB C 0 1 00 1 0 01 0 1 11 0 1 10 1 0
A B C AB C BC
A BC ABC
AB CD 00 01 11 10 00 0 0 0 0 01 1 0 0 1 11 0 0 0 0
A BC A BC ABC ABC ( A C A C AC AC) B B
AB CD 00 01 11 10 00 0 1 0 0 01 1 1 1 1 11 0 1 1 0 10 0 1 0 0
CD
AB
AB CD 00 01 11 10 00 0 1 1 0 01 1 0 0 1 11 1 0 0 1 10 0 1 1 0
ＡＤ
ＢＤ
AB CD 00 01 11 10 00 1 0 0 1 01 0 1 1 0 11 0 1 1 0 10 1 0 0 1
ＢＤ
ＢＤ
（3）任何8个（23个）标1的相邻最小 项，可以合并为一项，并消去3个变量。
AB CD 00 01 11 10 00 0 1 1 0 01 0 1 1 0 11 0 1 1 0 10 0 1 1 0
逻辑函数的化简方法
一、公式法化简：是利用逻辑代数的基本公式，对函数进行消项、消因子。
常用方法有：①并项法利用公式AB+AB’=A 将两个与项合并为一个，消去其中的一个变量。
②吸收法利用公式A+AB=A 吸收多余的与项。
③消因子法利用公式A+A’B=A+B 消去与项多余的因子④消项法利用公式AB+A’C=AB+A’C+BC 进行配项，以消去更多的与项。
⑤配项法利用公式A+A=A，A+A’=1配项，简化表达式。
二、卡诺图化简法逻辑函数的卡诺图表示法将n变量的全部最小项各用一个小方块表示，并使具有逻辑相邻性的最小项在几何位置上相邻排列，得到的图形叫做n变量最小项的卡诺图。
逻辑相邻项：仅有一个变量不同其余变量均相同的两个最小项，称为逻辑相邻项。
1.表示最小项的卡诺图将逻辑变量分成两组，分别在两个方向用循环码形式排列出各组变量的所有取值组合，构成一个有2n个方格的图形，每一个方格对应变量的一个取值组合。
具有逻辑相邻性的最小项在位置上也相邻地排列。
用卡诺图表示逻辑函数：方法一：1、把已知逻辑函数式化为最小项之和形式。
2、将函数式中包含的最小项在卡诺图对应的方格中填1，其余方格中填0。
方法二：根据函数式直接填卡诺图。
用卡诺图化简逻辑函数：化简依据：逻辑相邻性的最小项可以合并，并消去因子。
化简规则：能够合并在一起的最小项是2n个。
如何最简：圈数越少越简；圈内的最小项越多越简。
注意：卡诺图中所有的1 都必须圈到，不能合并的1 单独画圈。
说明，一逻辑函数的化简结果可能不唯一。
合并最小项的原则：1）任何两个相邻最小项，可以合并为一项，并消去一个变量。
2）任何4个相邻的最小项，可以合并为一项，并消去2个变量。
3）任何8个相邻最小项，可以合并为一项，并消去3个变量。
卡诺图化简法的步骤：画出函数的卡诺图;画圈（先圈孤立1格；再圈只有一个方向的最小项（1格）组合）；画圈的原则：合并个数为2n；圈尽可能大（乘积项中含因子数最少）；圈尽可能少（乘积项个数最少）；每个圈中至少有一个最小项仅被圈过一次，以免出现多余项。
[精品]1.3逻辑函数公式化简法
![[精品]1.3逻辑函数公式化简法](https://img.taocdn.com/s3/m/664f09561711cc7931b7168d.png)
逻辑函数的公式法化简
[例] 证明公式 A BC ( A B)( A C ) [解] 方法2：真值表法 A B 0 0 0 0 0 1 0 1 1 0 1 0 1 1 1 1 C B C A BC A B A C ( A B)( A C ) 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1
A ( BC B C ) A ( BC BC )
A B C A( B C ) A
逻辑函数的公式法化简
二、吸收法：
A AB A
[例 1] Y AB AD BE
A B AD BE A B
[例2] Y AB ACD BCD
) A
(3) A AB ( A A)( A B) A B (4) AB AC BC AB AC
(5) AB AB A B AB
逻辑函数的公式法化简
公式 (4) 证明：
AB AC BC AB AC
左 AB AC ( A A) BC A AB A
取反（即还原），最后用摩根定理去掉反号。
[例] 写出函数 Y AB AC 的最简或与式。
[ 解]
Y = ( A + B)( A + C) = AC + AB + BC
= AC + AB + BC
Y AB AC AB AC ( A B ) ( A C )
逻辑函数的公式法化简
相等
相等
逻辑函数的公式法化简
第四课时：逻辑函数的代数化简法
三 变 量 最 小 项 表
最小项编号 A B C ABC ABC ABC ABC ABC ABC ABC ABC 最小项 编号
最小项值
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
用摩根定律
解： Y A B ABC AC
A B AC A B C
应用 A AB A B
Y A B C ABC
1.7逻辑函数的卡诺图化简法
主要要求：
理解卡诺图的意义和构成原则。
掌握用卡诺图表示和化简逻辑函数的方法。
掌握无关项的含义及其在卡诺图化简法中 的应用。
1.7.1 逻辑函数的两种标准形式
1. 最小项的定义
在逻辑函数中，如果一个与项（乘积项）包含该逻辑函数的 全部变量，且每个变量或以原变量或以反变量只出现一次，则该 与项称为最小项。对于 n 个变量的逻辑函数共有 2n 个最小项。
三 变 量 最 小 项 表
最小项编号 A B C ABC ABC ABC ABC ABC ABC ABC ABC 最小项 编号
b. 卡诺图的组 成
卡诺图是最小项按一定 规则排列成的方格图。
将 n 个变量的 2n 个最小项用 2n 个小方格表示， 并且使相邻最小项在几何位置上也相邻且循环相邻，
这样排列得到的方格图称为 n 变量最小项卡诺图， 简称为 n 变量卡诺图。
B 二 变 A 量 0 卡 诺 1 图
0
1 m1 1 m3 3
ABCD+ABCD=ABD ABCD+ABCD +ABCD+ABCD
逻辑函数公式的化简
多外的另
运用摩根定律 余 一 因 外 如
的个子一果
。乘，个乘
Y2 A B CD ADB A BCD AD B ( A AD) (B BCD) A B
积则乘积 项这积项
（２）利用公式Ａ＋ＡＢ＝Ａ+Ｂ，消去多余的变量。
Y AB AC BC AB (A B )C AB ABC AB C
因项，量一两 子，则，个个
运用分配律
。并这而因乘 消两其子积
Y2 ABC AB AC ABC A(B C ) ABC ABC A(BC BC) A
去项他的项 互可因原中 为以子变分
反合都量别
运用摩根定律
2、吸收法
（１）利用公式Ａ＋ＡＢ＝Ａ，消去多余的项。
是另项是
Y1 AB ABCD(E F ) AB
４、消去冗余项法 利用冗余律ＡＢ＋ＡＣ＋ＢＣ＝ＡＢ＋ＡＣ， 将冗余项ＢＣ消去。
Y1 AB AC ADE CD AB (AC CD ADE) AB AC CD
Y2 AB BC AC(DE FG) AB BC
例：化简函数
Y (B D)(B D A G)(C E)(C G)(A E G)
Y AB BC BC AB AB BC (A A)BC AB(C C ) AB BC ABC ABC ABC ABC AB (1 C) BC (1 A) AC(B B) AB BC AC
（２）利用公式Ａ＋Ａ＝Ａ，为某项配上其所能合并的项。
Y ABC ABC ABC ABC ( ABC ABC ) ( ABC ABC) ( ABC ABC) AB AC BC
1.4.2 逻辑函数的公式化简法
逻辑函数的公式化简法就是运用逻辑代数的基本公式、定 理和规则来化简逻辑函数。
逻辑化简(公式)
核心
二、逻辑函数的最简表达式及相互转换 最简与或式
Y AB AC BC
最简 与非-与非式 最简或与非式 最简与或非式 最简或与式
AB AC
( A B)( A C )
AB A C
A B A C
最简或非-或式 最简或非-或非式
AB AC BC
( A B) ( A C )
ABC ABC ABC ABC
最小项
标准与或式就是最小项之和的形式
标准与 或式
1. 最小项的概念： 包括所有变量的乘积项，每个变量均以原变量或反变量的形式出现且仅出现一次。
Y F ( A ,B )
AB AB AB
( 2 变量共有 4 个最小项)
AB
( 3 变量共有 8 个最小项)
ABC ABC ABC ABC ABC ABC AB C ABC
1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1
Y ABC ABC ABC ABC ABC
4. 最小项的编号： 把与最小项对应的变量取值当成二进制数，与之相应的十进制数，就是该最小项的 编号，用 mi 表示。
对应规律：原变量 1
反变量 0
ABC ABC ABC ABC ABC ABC AB C ABC
000 0 m0 001 1 m1 010 2 m2 011 3 m3 100 4 m4 101 5 m5 110 6 m6 111 7 m7
E BC D AE BC D
数字逻辑第4讲
College of Computer Science, SWPU
卡诺图表示逻辑函数
A B C 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1
数字逻辑
F 1 0 0 1 0 1 1 0 C
AB 0 1 1 0 0 1
F = Σ(A,B,C)(0,3,5,6)
数字逻辑
College of Computer Science, SWPU
具有“无关”输入逻辑函数及其化 具有“无关” 简
约束
在分析某些具体的逻辑函数时， 在分析某些具体的逻辑函数时，经常会遇到 这样一种情况， 这样一种情况，即输入变量的取值不是任意 约束。 对输入变量取值所加的限制称为约束 的。对输入变量取值所加的限制称为约束
卡诺图、 卡诺图、用卡诺图化简函数
Computer Science
本讲最要内容
1、卡诺图 2、几个基本概念 3、用卡诺图化简逻辑函数 4、无关项在化简中的使用 5、多输出函数的最小化问题 6、组合电路的综合 7、组合电路的竞争、冒险及解决方法 组合电路的竞争、
数字逻辑
College of Computer Science, SWPU
数字逻辑
College of Computer Science, SWPU
卡诺图表示逻辑函数
X Y 0 1 XY Z 00 01 11 10 0 m0 m2 m6 m4 1 m1 m3 m7 m5
数字逻辑
College of Computer Science, SWPU
—— 真值表的图形表示
0 1 YZ 00 0 01 1 11 3 10 2 WX 00 01 11 10
A B C = 0, ABC = 0, ABC = 0, ABC = 0, ABC = 0
卡诺图表示逻辑函数
A B C 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1
数字逻辑
F 1 0 0 1 0 1 1 0 C
AB 0 1 1 0 0 1
F = Σ(A,B,C)(0,3,5,6)
数字逻辑
College of Computer Science, SWPU
具有“无关”输入逻辑函数及其化 具有“无关” 简
约束
在分析某些具体的逻辑函数时， 在分析某些具体的逻辑函数时，经常会遇到 这样一种情况， 这样一种情况，即输入变量的取值不是任意 约束。 对输入变量取值所加的限制称为约束 的。对输入变量取值所加的限制称为约束
卡诺图、 卡诺图、用卡诺图化简函数
Computer Science
本讲最要内容
1、卡诺图 2、几个基本概念 3、用卡诺图化简逻辑函数 4、无关项在化简中的使用 5、多输出函数的最小化问题 6、组合电路的综合 7、组合电路的竞争、冒险及解决方法 组合电路的竞争、
数字逻辑
College of Computer Science, SWPU
数字逻辑
College of Computer Science, SWPU
卡诺图表示逻辑函数
X Y 0 1 XY Z 00 01 11 10 0 m0 m2 m6 m4 1 m1 m3 m7 m5
数字逻辑
College of Computer Science, SWPU
—— 真值表的图形表示
0 1 YZ 00 0 01 1 11 3 10 2 WX 00 01 11 10
A B C = 0, ABC = 0, ABC = 0, ABC = 0, ABC = 0
4逻辑函数的化简方法
最简的标准 ◆最简的标准与实际应用中能够提供的逻 辑器件有关系，要根据实际而定； ◆常用的逻辑器件有与非门、或非门、与 或非门、异或门、非门等； ◆以使用的器件数目最少、成本最低为判 断最简的标准； ◆默认最简形式为最简与-或式，即用最少 的与门和或门来实现函数。 公式化简法√ 化简的方法 卡诺图化简法√ *Q-M 法
输入变量
逻辑相邻：相邻单 元输入变量的取值 只能有一位不同。
01 m1 m5 11 m3 m7 10
BC 00 A 0 m0
1 m4
m2 m6
注意：m2与m0逻辑相邻。
（13）
四变量卡诺图
CD 00 AB 00 01 m4 01 11 10
m0 m1 m3 m2 m5 m7 m6
11 m12 m13 m15 m14 10 m8
（18）
L m(15,13,10,6,0)
所以，L的卡诺图为：
CD 00 AB 00 01 01 11 10
0
1 1 1
1
1 0 1
1
1 0 1
1
0 1 0
11
10
（19）
二、 用卡诺图化简逻辑函数
• 原理：相邻的两个最小项可以化简消去 一对因子。
CD 00 AB 00
01 11 10
01
（21）
两个最小项相邻的情况
1 1 1 1 1 1
1
（22）
四个最小项相邻的情况
1 1 1 1 1 1 1 1 1 1 1 1
（23）
八个最小项相邻的情况
1 1 1 1
1 1 1 1
1
1 1 1 1
1
1 1
1 1 1 1
1 1 1 1
逻辑函数的化简逻辑函数的最简形式逻辑函数的公式化简法
AB BC
上页
11
下页
返回
2019/1/10
第五节 逻辑函数的化简
根据公式
A A 1
( A A) ，
可在逻辑函数式中的某一项乘
然后拆成两项分别与其他项合并。 [例2.5.13]： Y
BC AC AB
( A A)BC AC AB
ABC ABC AC AB
Y A( BC ) ABC [例2.5.3]： A(( BC ) BC ) A
上页
5
下页
返回
2019/1/10
第五节 逻辑函数的化简
[例2.5.4]：用并项法将
Y BCD BCD BCD BCD
化简为最简与-或表达式。 解： Y BCD BCD BCD BCD
AB AC
上页
12
下页
返回
2019/1/10
第五节 逻辑函数的化简
综合法
[例2.5.14]：
Y AC BC BD CD A( B C ) ABCD ABDE
AC BC BD CD A( BC ) ABCD ABDE AC ( BC A( BC )) BD (CD ABCD) ABDE
上页
10
下页
返回
2019/1/10
第五节 逻辑函数的化简
5.配项法 根据公式
A A A
可在逻辑函数式中重复写入某一项。 [例2.5.12]： Y
ABC ABC ABC
ABC ABC ABC ABC
AB(C C ) ( A A)BC
返回
逻辑函数的化简
逻辑相邻
根据逻辑相邻的定义,不难由图8-10看出, 几何相邻的两个方格的最小项满足逻辑相邻性. 而不直接相邻的方格,但以卡诺图中心轴对称 的方格对应的最小项也满足逻辑相邻,如图810c中m0与m2,m0与m8,m3与m11等,称这种相 邻叫对称相邻.所以卡诺图可看作是立体图. 这是卡诺图巧妙之所在 .
由图8-12中可以看出卡诺图覆盖过的变量以0 和1两种取值出现,则该变量被消去;只以0出 现,则该变量用反变量表示;只以1出现,则 以原变量出现.卡诺圈越大消去的变量越多, 能够合并相邻项的一个正确的卡诺圈必须符合 以下要求.
(1) 卡诺圈里的1方格数必须是2m个.m=0,1, 2,…. (2) 2m个1方格必须排列成方阵或矩阵. (3) 2m个1方格必须是方格相邻或对称相邻的.
二,公式化简
1.并项法 利用 A + A =1将两项合并成一 项并消去一个变量. 2.吸收法 3.消去法 F= = 利用A+AB=A,消去多余项. 利用A+AB=A+B,消去多余项.
AB + A B + A BD + ABD
AB + AB + D AB + A B
= AB + A B + D
4. 配项法
二,三,四个变量的函数的卡诺图
a.二变量函数的卡诺图 b.三变量函数的卡诺图. c.四变量函数的卡诺图
构造卡诺图时应遵循以下规则
① n变量函数有2n个最小项,则卡诺图有2n方 格,即方格与最小项一一对应. ② 2n个方格必须排列成方阵或矩阵. ③ 变量分成两组,行变量和列变量组,行变 量为高位组,列变量为低位组.如图8-10中C 中,为行变量,为列变量. ④ 变量取值遵守反射码的形成规则.
逻辑函数的公式化简法
分配律 吸收律 分配律 吸收律 并项 吸收律
逻辑函数的公式化简法
化简逻辑函数表达式的方法 ◇公式化简法
◆没有固定的步骤可以遵循 ◆依赖于对逻辑代数公式的熟练掌握 ◆需要一些化简技巧 ◆难以确定被化简过的逻辑函数是否最简 ◇卡诺图化简法 √简便、直观
= B (A+AC)+ AC + BCD = B (A+C)+ AC + BCD = AB + AC + BC (1 + D) = AB + AC + BC = AB + AC
化简逻辑函数表达式的方法 公式化简法 卡诺图化简法
逻辑函数的公式化简法
(1) 并项、配项 A + A = 1 ； 1 = A + A
逻辑函数的公式化简法
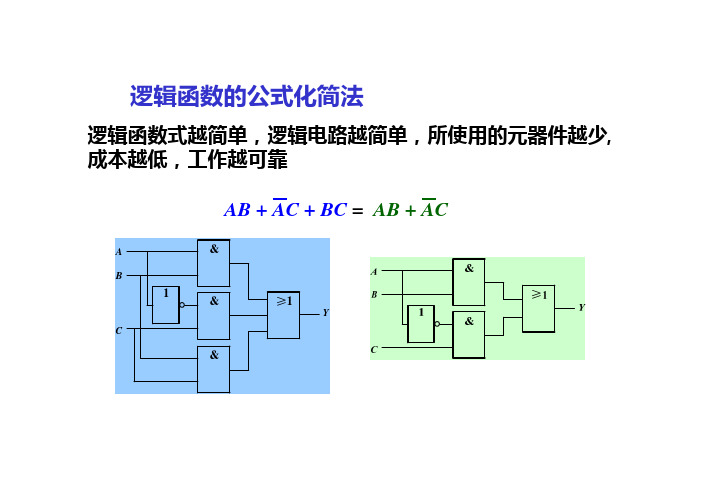
逻辑函数式越简单，逻辑电路越简单，所使用的元器件越少, 成本越低，工作越可靠
AB + AC + BC = AB + AC
A
&
B
1 &
C
&
1
Y
逻辑函数的公式化简法
☆最简与—或表达式 也最少
Y = AB + AC + BCD + ABC
分配律 吸收律
逻辑函数的公式化简法
Y = ABCD + ABD + BCD + ABC + BD + BC = ABC(D + 1)+ BD(A + 1)+ BCD + BC = ABC+ BD + BCD + BC = B(AC + C)+ B(D + CD) = B(A + C)+ B(D + C) = AB + BD + B(C + C) =B
第04讲逻辑函数的公式化简
第04讲逻辑函数的公式化简逻辑函数是由逻辑变量和逻辑运算符组成的表达式。
在实际应用中，对逻辑函数进行简化通常是非常重要的，因为简化后的逻辑函数更容易理解和分析。
本文将介绍逻辑函数的公式化简方法，包括代数化简、卡诺图方法和奎因-麦克拉斯基方法。
一、代数化简代数化简是一种通过应用逻辑等式和等价变换来简化逻辑函数的方法。
逻辑等式是逻辑函数之间的等式关系，可以用来表示逻辑函数的等价性。
常见的逻辑等式包括德摩根定律、分配律、吸收律等。
1.1德摩根定律德摩根定律包括两个等式：1)非(A和B)等于非A或非B：~(A∧B)=~A∨~B2)非(A或B)等于非A和非B：~(A∨B)=~A∧~B通过应用德摩根定律，可以将逻辑函数中的与或非运算转化为或与非的运算，从而简化逻辑函数。
1.2分配律分配律包括两个等式：1)A和(B或C)等于(A和B)或(A和C)：A∧(B∨C)=(A∧B)∨(A∧C)2)A或(B和C)等于(A或B)和(A或C)：A∨(B∧C)=(A∨B)∧(A∨C)通过应用分配律，可以将逻辑函数中的与或运算关系转化为或与运算关系，从而简化逻辑函数。
1.3吸收律吸收律包括两个等式：1)A或(A和B)等于A：A∨(A∧B)=A2)A和(A或B)等于A：A∧(A∨B)=A通过应用吸收律，可以将逻辑函数中的与或运算关系进行简化。
通过应用上述逻辑等式和等价变换，可以将逻辑函数进行代数化简。
例如，假设有一个逻辑函数F=A∧(B∨C)，我们可以应用分配律将其化简为F=(A∧B)∨(A∧C)。
二、卡诺图方法卡诺图是一种通过图形化表示逻辑函数的方法，可以帮助我们更好地理解和分析逻辑函数。
对于每个逻辑变量，卡诺图使用一个格子来表示该变量的取值，格子的数目等于变量的取值数。
逻辑函数的值则通过在卡诺图中填写格子来表示。
根据逻辑函数的真值表，我们可以绘制对应的卡诺图。
卡诺图的优势在于能够直观地观察逻辑函数的特点，并以此进行化简。
化简的原则是找出卡诺图中连续的1所对应的格子，并构建出尽可能简单的表达式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
逻辑函数的简化
函数的简化依据
降低成本 • 逻辑电路所用门的数量少 提高电路的工作 速度和可靠性 • 每个门的输入端个数少 • 逻辑电路构成级数少 • 逻辑电路保证能可靠地工作
一、逻辑函数的代数化简法
1．逻辑函数式的常见形式
一个逻辑函数的表达式不是唯一的，可以有多种形式， 一个逻辑函数的表达式不是唯一的，可以有多种形式， 并且能互相转换。例如： 并且能互相转换。例如：
异或门可以用4个与非门实现： 异或门可以用 个与非门实现： 个与非门实现
Y = A ⊕ B = A B + AB = A ⋅ A ⋅ B ⋅ B ⋅ A ⋅ B
&
A B
& &
&
Y
例9：化简为最简逻辑代数式 ：
Y = ABC + ABC + ABC + ABC + ABC
Y = ABC + ABC + ABC + ABC + ABC
• 或与表达式的简化
化简逻辑函数： 例5 化简逻辑函数：L = AB + BC + BC + AB 解法1： 解法 ：
解法2： 解法 ：
• 由上例可知，逻辑函数的化简结果不是唯一的。 由上例可知，逻辑函数的化简结果不是唯一的。
在化简逻辑函数时，要灵活运用上述方法， 在化简逻辑函数时，要灵活运用上述方法，才能将 逻辑函数化为最简。 逻辑函数化为最简。 再举几个例子： 再举几个例子：
§1.6 逻辑函数的化简
代数法化简函数 卡诺图化简函数 含有无关项函数 的化简
第四讲 逻辑函数的公式化简法 课题： 课题：逻辑函数的公式化简法 课时安排： 课时安排：2 重点： 重点：用公式和定理化简逻辑函数 难点：对公式、 难点：对公式、定理的掌握和灵活运用 教学目标：使同学掌握逻辑函数的公式化简法，掌握 教学目标：使同学掌握逻辑函数的公式化简法， 逻辑函数各种表达式间的相互转换 教学过程： 教学过程： 一、逻辑函数表达式的五种形式 1、逻辑函数表达式的五种形式 、 2、各种表达式间的相互转换 、 二、逻辑函数的公式化简法 1、与或式最简的标准 、 2、化简方法 （结合例题） 结合例题） 、 （1）并项法（2）吸收法（3）消元法 ）并项法（ ）吸收法（ ） （4） 消因子法（5）配项法 ） 消因子法（ ）
• 与或表达式的简化
• 实现电路的与门少 • 下级或门输入端个数少 最简式的标准 与门的输入端个数少 • 首先是式中乘积项最少 首先是式中乘积项最少 • 乘积项中含的变量少 乘积项中含的变量少
方法： 方法：
且消去一个变量
将两项并为一项， 并项： • 并项： 利用 AB + A B = A 将两项并为一项，
AA = 0
例： F = ABC + ABC • AB
F = ABC + ABC • AB
= ABC + ABC • AB + 0
= ABC + ABC • AB + AB • AB
= AB ( AB + C ) + ABC • AB
= AB( ABC ) + ABC • AB
= ABC
举例 最简与或式 乘积项的项数最少。 乘积项的项数最少。 项数最少 每个乘积项中变量个数最少。 每个乘积项中变量个数最少。 变量个数最少 例1： F = A BC + ABC + ABC ：
B
• 吸收： 利用A + AB = A消去多余的项 AB 吸收： 消元： • 消元：利用 A + AB = A + B消去多余变量 A 消项： • 消项：利用 AB+ AC + BC= AB+ AC 消去多余项 BC • 配项：利用 A+A=A,A+A=1,A*A=0 等先增添项， 配项： 等先增添项，
（3）消元法。 ）消元法。
例1. 例2.
Y2 = A + A CD + A BC = A + CD + BC
Y1 = B + ABC = B + AC
例3.
Y3 = AB C D + AB C
= D + AB C = A + B+C + D
例4.
Y4 = AC + A D + C D = AC + ( A + C ) D
再化简。 再化简。
用代数法化简逻辑函数
将两项合并为一项， （1）并项法。运用公式 A + A = 1 ，将两项合并为一项，消去一 ）并项法。 个变量。 个变量。如 例1.
Y1 = A B CD + AB CD = A( B CD + B CD ) = A
例2. Y2 = AB + ACD + A B + A CD
；A=A ;利用反演定理 ;利用公式A+AB=A+B
= A B + ( A + B)CD
= A B + A BCD
= ABC + AB(C + C) = ABC + AB = A(BC + B ) = A (C + B ) = AC + AB
提出AB 提出 =1
提出A 提出 反变量吸收
例2：F ：
= AB + A B ⋅ BC + B C
（ = AB + A B + (BC + B C) ） = AB + A B (C + C )
例３.
= ( A BC + A BC ) + ( A BC + ABC )
= AB + BC + A C Y3 = AB + AC + BCD = AB + AC + BCD( A + A) = AB + AC + ABCD + ABCD = AB + AC
（６）添项法。 添项法。 加入零因子
AA • f ( A, B, ⋯) = 0
; AB=A+B
= A ⋅A ⋅B + B⋅A ⋅B
; A= A
= A ⋅ (A + B) + B ⋅ (A + B)
= 0+ A ⋅B + B⋅A + 0
= A ⋅B + B⋅A
; A + B = A⋅ B
; 展开
= A⋅A + A⋅B + B⋅A + B⋅B
= 右边
结论：异或门可以用 个 结论：异或门可以用4个 与非门实现。 与非门实现。
= AC + AC D = AC + D
例5.
Y5 = A + AB + BE = A + B + BE = A + B + E
（４）消项法。运用公式AB+ AC + BC = AB+ AC ，将Ｂ 消项法。 消去。 Ｃ消去。如
例1.
Y1 = AC + AB + B + C
= AC + AB + B C
化简逻辑函数： 例.6 化简逻辑函数：
L = AD + AD + AB + AC + BD + ABEF + BEF
解： = A + AB + AC + BD + A BEF + BEF （利用 L
利用A+AB=A） ） = A + AC + BD + BEF （利用
A+ A =1 ）
= A + C + BD + BEF
（利用 A + AB = A + B ）
化简逻辑函数： 例7 化简逻辑函数： L = AB + AC + BC + C B + BD + DB + ADE ( F + G )
解：L = ABC + BC + CB + BD + DB + ADE( F + G) （利用反演律 ）
= A + BC + C B + BD + DB + ADE ( F + G )
= AC + B C
例2.
Y2 = AB CD + A E + BE + CD E
= AB CD + ( A + B ) E + CD E
= AB CD + AB E + CD E
= AB CD + AB E
（5）配项法。 ）配项法。
例1.
Y1 = A BC + A BC + ABC
= A B (C + C ) + ( A + A) BC = A B + BC 例2. Y2 = AB + A B + BC + B C = AB + A B (C + C ) + BC + B C ( A + A ) = AB + A BC + A BC + BC + AB C + A B C = ( AB + AB C ) + ( A BC + BC ) + ( A BC + A B C )
= AC+ BC + D(A + B)