现代信号处理-胡广书-清华
X ( jΩ)
=
1 2π
<
x(t), e jΩt
>
式中 < x, y > 表示信号 x 和 y 的内积。若 x ， y 都是连续的，则
（1.1.5）
< x, y >= ∫ x(t) y*(t)dt
若 x ， y 均是离散的，则
< x, y >= ∑ x(n) y*(n)
从时域波形还是从频域波形，我们都很难看出该信号的调制类型及其他特点。和图 1.1.1(c)
一样，图 1.1.2(c)也是 x(n) 的时－频分布表示，由该图可明显看出，该信号的频率与时间成
Line ar sca le
Real part
S ignal in time 1
0
-1 |S TF T|2, Lh=48 , Nf=1 92, lin. scale, co ntour, Thld =5%
gt,Ω (τ ) = g(t − τ )e jΩτ
（1.1.8）
来代替傅立叶变换中的基函数 e jΩt ，则
< x(τ ), gt,Ω (τ ) >=< x(τ ), g(t −τ )e jΩτ >
∫= x(τ )g*(t − τ )e− jΩτ dτ = STFTx (t, Ω)
(1.1.9)
该式称为 x(t) 的短时傅立叶变换（Short Time Fourier Transform, STFT）。式中 g(τ ) 是一窗函
愈多。但由傅立叶变换 X ( jΩ) 看不出在什么时刻发生了此种类型的突变。现举两个例子说
明这一概念。 例 1．1．1 设信号 x(n)由三个不同频率的正弦所组成，即
x(n) = ⎪⎨⎧ssiinn((ωω12nn)),, ⎪⎩sin(ω3n),
0 ≤ n ≤ N1 −1 N1 ≤ n ≤ N2 −1 N2 ≤ n ≤ N −1
信号是变化着的，变化着的信号构成了我们周围五彩斑斓的世界。此处所说的“变化”， 一是指信号的幅度随时间变化，二是指信号的频率内容随时间变化。幅度不变的信号是“直 流”信号，而频率内容不变的信号是由单频率信号，或多频率信号所组成的信号，如正弦波、 方波、三角波等。不论是“直流”信号还是正弦类信号都只携带着最简单的信息。
（ e jΩt = cos Ωt + j sin Ωt ），因此其在时域的持续时间是从 − ∞ ~ +∞ ，因此，在时域有着
最坏的分辨率。 我们在“数字信号处理”的课程中已熟知，一个宽度为无穷的矩形窗（即直流信号）的
傅立叶变换为一δ 函数，反之亦然。当矩形窗为有限宽时，其傅立叶变换为一 Sinc 函数，即
5
∫ X (
jΩ)
=
A
T −T
e− jΩt dt
=
2
A
sin ΩT Ω
（1.1.8）
式中 A 是窗函数的高度， T 是其单边宽度。 x(t) 和其频谱如图 1.1.3(a)和(b)所示。
x(t)
X(Ω) 2AT
A
-T
0
Tt
0
Ω
图 1.1.3 矩形窗及其频谱 (a) 时域矩形窗， （b）矩形窗的频谱
−∞
（1.1.1b）
式 中 Ω = 2πf ， 单 位 为 弧 度 / 秒 ， 将 X ( jΩ) 表 示 成 | X ( jΩ) | e jϕ (Ω) 的 形 式 ， 即 可 得 到
| X ( jΩ) | 和ϕ (Ω) 随 Ω 变化的曲线，我们分别称之为 x(t) 的幅频特性和相频特性。
如果我们想知道在某一个特定时间，如 t0 ，所对应的频率是多少，或对某一个特点的频
n
内积的概念将贯穿在本书的始终。
（1.1.6a） （1.1.6b）
（1.1.5）式说明信号 x(t) 的傅立叶变换等效于 x(t) 和基函数 e jΩt 作内积，由于 e jΩt 对不
同的 Ω 构成一族正交基，即
∫ < e , e jΩ1t jΩ2t >= e dt j(Ω1−Ω2 )t = 2πδ (Ω1 − Ω2 )
第 1 章 信号分析基础
1．1 信号的时－频联合分析
我们生活在一个信息社会里，而信息的载体就是我们本书要讨论的主题——信号。在我 们身边以及在我们身上，信号是无处不在的。如我们随时可听到的语音信号，随时可看到的 视频图像信号，伴随着我们生命始终的心电信号，脑电信号以及心音、脉搏、血压、呼吸等 众多的生理信号。
频率随时间变化的信号（如例 1.1.2 中的 x(n) ）称为时变信号。文献[13]称这一类信号为“非
平稳”信号，而把频率不随时间变化的信号称为“平稳”信号。此处的“平稳”和“不平稳” 和随机信号中的“平稳随机信号”及“非平稳随机信号”的意义不同。平稳随机信号是指该
4
类信号的一阶及二阶统计特征（均值与方差）不随时间变化，其自相关函数和观察的起点无 关，而非平稳信号的均值、方差及自相关函数均与时间有关，即是时变的。尽管这两类说法 的出发点不同，但非平稳信号的频率实质上也是时变的，因此，把频率随时间变化的信号统 称为“非平稳信号”并无大碍。但要说一个信号是“平稳信号”，则要具体说明所指的是频 率不随时间变化的信号还是平稳随机信号。
Energy spectral density
0.4 0.3 0.2 0.1
0 365 182 0
Frequency [Hz]
20
40
60
80
100 120
Time [s]
图 1.1.2 chirp 信号的时－频表示. （a）信号 x(n), (b) x(n)的频谱，(c) x(n)时 －频分布的二维表示，(d) x(n)时－频分布的三维表示，
数。（1.1.9）式的意义实际上是用 g(τ ) 沿着 t 轴滑动，因此可以不断地截取一段一段的信号，
然后对其作傅立叶变换，故得到的是 (t, Ω) 的二维函数。g(τ ) 的作用是保持在时域为有限长
（一般称作“有限支撑”），其宽度越小，则时域分辨率越好。在频域，由于 e jΩt 为一δ 函数，
因此仍可保持较好的频域分辨率。比较（1.1.9）式和（1.1.5）式可以看出，使用不同的基函 数可得到不同的分辨率效果。有关短时傅立叶变换的内容我们将在第二章详细讨论。
氏变换 X ( jΩ) 是信号 x(t) 在整个积分区间的时间范围内所具有的频率特征的平均表示。反
之，（1.1.1b）式也是如此，因此，傅立叶变换不具有时间和频率的“定位”功能。 前已述及，信号的幅度不但随时间变化，而且对现实物理世界中的大部分信号，其频率
也随时间变化。实际上，在时域中愈是在较短时间内发生幅度突变的信号，其包含的信息就
给定了信号 x(t) 的函数表达式，或 x 随 t 变化的曲线，我们可以由此得出在任一时刻处
该信号的幅值。如果想要了解该信号的频率成分，即“在××Hz 处频率分量的大小”，则可 通过傅立叶变换来实现，即
∫ X ( jΩ) = ∞ x(t)e− jΩtdt −∞
（1.1.1a）
∫ x(t)
=
1 2π
∞ X ( jΩ)e jΩtdΩ
对一个给定的信号，如 x(t) ，我们可以用众多的方法来描述它，如 x(t) 的函数表达式，
通过傅立叶变换所得到的 x(t) 的频谱，即 X ( jΩ) ，再如 x(t) 的相关函数，其能量谱或功率
谱等。在这些众多的描述方法中，有两个最基本的物理量，即时间和频率。显然，时间和频 率与我们的日常生活关系最为密切，我们时时可以感受到它们的存在。时间自不必说，对频 率，如夕阳西下时多变的彩霞，音乐会上那优美动听的旋律以及在一片寂静中突然冒出的一 声刺耳的尖叫等，这些都包含了丰富的频率内容。正因为如此，时间和频率也成了描述信号 行为的两个最重要的物理量。
6
总之，对给定的信号 x(t) ，人们希望能找到一个二维函数Wx (t, Ω) ，它应是我们最关心 的两个物理量 t 和 Ω 的联合分布函数，它可反映 x(t) 的能量随时间 t 和频率 Ω 变化的形态，
同时，又希望Wx (t, Ω) 既具有好的时间分辨率，同时又具有好的频率分辨率。
显然，矩形窗的宽度 T
和其频谱主瓣的宽度（ −
π T
~
π T
）成反比。由于矩形窗在信号处理中
起到了对信号截短的作用，因此，若信号在时域取得越短，即保持在时域有高的分辨率，那
么由于 X ( jΩ) 的主瓣变宽因此在频域的分辨率必然会下降。所有这些都体现了傅立叶变换
中在时域和频域分辨率方面所固有的矛盾。 如果我们用基函数
Energy spectral density
0 .4 0 .3 0 .2 0 .1
0 159517975 0
Frequency [Hz]
50 100 150 200 250 300 350 Time [s]
图 1.1.1 信号的时－频表示 （a）信号 x(n), (b) x(n)的频谱， (c) x(n)时－频分布的二维表示，(d) x(n)时－频分布的三维表示，
由上述两例可以看出，傅立叶变换反映不出信号频率随时间变化的行为，因此，它只适 合于平稳信号，而对频率随时间变化的非平稳信号，它只能给出一个总的平均效果。
现在，我们再从“分辨率”的角度来讨论傅立叶变换的不足。“分辨率”包含了信号的 时域和频域两个方面，它是指对信号所能作出辨别的时域或频域的最小间隔（又称最小分辨 细胞）。分辨能力的好坏一是取决于信号的特点，二是取决于所用的算法。对在时域具有瞬 变的信号，我们希望时域的分辨率要好（即时域的观察间隔尽量短），以保证能观察到该瞬 变信号发生的时刻及瞬变的形态。对在频域具有两个（或多个）靠得很近的谱峰的信号，我 们希望频域的分辨率要好（即频域的观察间隔尽量短，短到小于两个谱峰的距离），以保证 能观察这两个或多个谱峰。有关分辨率的讨论见文献[19]的第三章。
现代数字信号处理
无线信道的估计、均衡与信道分配
4/5G移动通信中的多用户检测和智能天线 软件无线电技术
加密、认证
网络信号处理
4.3 信号处理发展趋势
随机信号 处理
统计信号 处理
确定性信号处理 Deterministic Signal processing
Statistical SP
技术分类
统 计 过 程 分 析
3.2 主要方法 (2/4)
基于模型的方法 信号产生过程的参数模型 分析: 线性预测 参数谱估计 滤波: 最优线性滤波器 维纳滤波器，卡尔曼滤波器 自适应滤波器
3.3 主要方法 (3/4)
统计信号处理方法 信号统计模型 贝叶斯估计 分析: 参数估计 隐马尔科夫模型 滤波: MAP, ML, LS
现代信号处理
教材事项
教材：
① 《现代数字信号处理》 姚天任等编，华中科技大学出 版社 ② 《现代数字信号处理》王炳和 西安电子科技大学出版 社 参考书： ①张贤达，现代信号处理，北京：清华大学出版社， 2002年10月。 ②Mitra，数字信号处理，北京：清华大学出版社， 2001年9月（影印版）。 ③胡广书，现代信号处理教程，北京：清华大学出版社， 2004年11月。 ④皇甫堪等，现代数字信号处理，北京：电子工业出版 社，2004年6月。
4.1 信号处理与现代通信
新的信号处理方法：
高阶统计量方法 盲信号处理方法 小波变换 神经网络信号处理方法 量子信号处理方法
4.2 信号处理与现代通信
信号处理在现代通信中的应用： 接入网的宽带化－ADSL
CDMA 语音、图像和视频信息的压缩与传输，分发，转码
胡广书《现代信号处理教程》第一章
1. 傅里叶变换在时间、频率“定位”的不足
如果我们想求一个信号，如 x(t ) ，在某一个频 率，如 0 处的值，则
X ( j0 ) x(t )e j 0t d t
需要
t ~
；
反之，如果我们想求某一个时刻，如 t 0
处的值，需要 ~
1 x(t0 ) 2
a: 是尺度定标常数，决定频率中心及带宽; b: 是位移，决定分析位置； (t ) : 又称为基本小波或母小波。
方法四、信号的子带分解
将信号的频谱均匀或非均匀地分解成若干部分， 每一个部分都对应一个时间信号，我们称它们为 原信号的子带信号 。
H0 ( z)
x ( n)
x0 (n)
M
v0 (n)
“分辨率（resolution）”是信号处理中的基本概念， 能作出辨别的时域或频域的最小间隔（又称最小分辨
细胞）。频率分辨率是通过一个频域的窗函数来观察 频谱时所看到的频率的宽度，时间分辨率是通过一个 时域的窗函数来观察信号时所看到的时间的宽度。显 然，这样的窗函数越窄，相应的分辨率就越好。分辨
能力的好坏一是取决于信号的特点，二是取决于信号
（二）多抽样率信号处理； （三）小波变换； （四）高阶统计量分析； （五）独立分量分析（ICA）； （六）压缩感知理论（CS）；
现代信号处理这十多年来的新进展
一、Hilbert－Huang变换 二、信号的稀疏表达 （sparse representations） －1998；
－1998；
三、压缩感知 （ compressed sensing，CS） －2006
g ( , ) 1 then
Cohen类分布变成Wigner-Ville分布
现代信号处理--清华胡广书讲义-第6章滤波器组基础
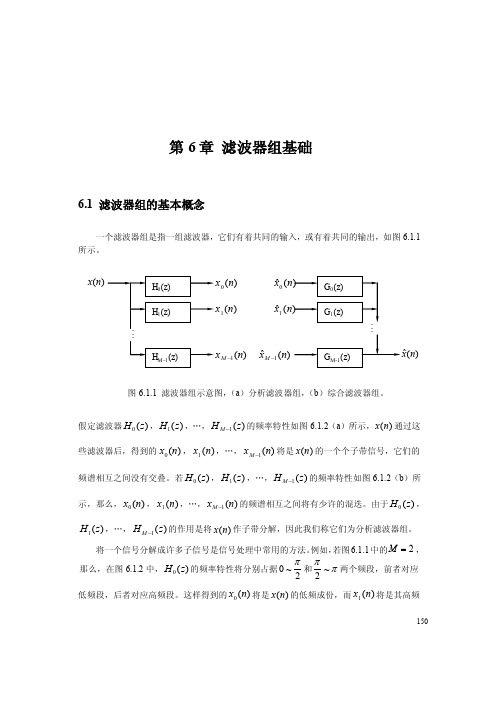
150第6章 滤波器组基础6.1 滤波器组的基本概念一个滤波器组是指一组滤波器，它们有着共同的输入，或有着共同的输出，如图6.1.1所示。
图6.1.1 滤波器组示意图，（a ）分析滤波器组，（b ）综合滤波器组。
假定滤波器)(0z H ，)(1z H ，…，)(1z H M -的频率特性如图6.1.2（a ）所示，)(n x 通过这些滤波器后，得到的)(0n x ，)(1n x ，…，)(1n x M -将是)(n x 的一个个子带信号，它们的频谱相互之间没有交叠。
若)(0z H ，)(1z H ，…，)(1z H M -的频率特性如图6.1.2（b ）所示，那么，)(0n x ，)(1n x ，…，)(1n x M -的频谱相互之间将有少许的混迭。
由于)(0z H ，)(1z H ，…，)(1z H M -的作用是将)(n x 作子带分解，因此我们称它们为分析滤波器组。
将一个信号分解成许多子信号是信号处理中常用的方法。
例如，若图6.1.1中的2=M ，那么，在图6.1.2中，)(0z H 的频率特性将分别占据2~0π和ππ~2两个频段，前者对应低频段，后者对应高频段。
这样得到的)(0n x 将是)(n x 的低频成份，而)(1n x 将是其高频)(0n x )(1n x )(1n x M -)(n x(ˆ0x (ˆ1x)(ˆ1n xM -)(ˆn x151成份。
我们可依据实际工作的需要对)(0n x 和)(1n x 作出不同的处理。
例如，若我们希望对)(n x 编码，设)(n x 的抽样频率为20KHz ，若每个数据点用16bit ，那么每秒钟需要的码图6.1.2 分析滤波器组的频率响应，（a ）无混迭，（b ）稍有混迭流为320Kbit 。
若)(n x 是一低频信号，也即)(n x 的有效成份（或有用成份）大都集中在)(0n x 内，)(1n x 内含有很少的信号能量。
这样，我们可对)(0n x 仍用16bit ，对)(1n x 则用8bit ，甚至是4bit ，由于)(0n x 和)(1n x 的带宽分别比)(n x 减少了一倍，所以，)(0n x 和)(1n x 的抽样频率可降低一倍。
现代信号处理教程 - 胡广书(清华)
- 230 -第8章 M 通道滤波器组8．1 M 通道滤波器组的基本关系图8.1.1是一个标准的M 通道滤波器组。
图8.1.1 M 通道滤波器组由第五章~第七章的讨论，我们不难得到图中各处信号之间的如下相互关系： ()()()k k X z X z H z = (8.1.1)1101111()()1 ()() (8.1.2)M lMk kM l M l lMMMk M l V z XW z M X Wz H W z M-=-===∑∑及 101()()()() M l lMk k Mk M l U z V z X zWH zW M-===∑ (8.1.3)滤波器组的最后输出111ˆ()()()1()()() (8.1.4)M k kk M M llM k M k l k X z G z U z X zW H zW G z M-=--====∑∑∑. . . ˆ()z (X- 231 -令 101()()() (8.1.5)M ll kM k k A z HzW G z M-==∑则 10ˆ()()() (8.1.6)M l l Ml X z A z X zW -==∑ 这样，最后的输出ˆ()X z 是()lMX zW 的加权和。
由于 (2/)()()j lj l M M z e X zW X e ωωπ-== (8.1.7)在0l ≠时是()j X e ω的移位，因此，ˆ()j Xe ω是()j X e ω及其移位的加权和。
由上一章的讨论可知，在0l ≠时，(2/)()j l M X e ωπ-是混迭分量，应想办法去除。
显然，若保证()0 1~1l A z l M ==- (8.1.8)则可以去除图8.1.1所示滤波器组中的混迭失真.再定义1001()()()()M kk k T z A z Hz G z M-==∑ (8.1.9)显然，()T z 是在去除混迭失真后整个系统的转移函数。
这时，ˆ()Xz 是否对()X z 产生幅度失真和相位失真就取决于()T z 的性能。
现代信号处理教程 - 胡广书(清华)
69第3章 Wigner 分布3.1 Wigner 分布的定义我们在第一章讨论了对非平稳信号作时－频联合分析的必要性，在第二章介绍了具有线性形式的时－频分布，如STFT 及Gabor 变换。
这一类形式的时－频分布还有小波变换，我们将在第九章以后详细讨论。
本章及下一章集中讨论具有双线性形式的时－频分布，主要是Wigner 分布及具有更一般形式的Cohen 类分布。
所谓双线性形式，是指所研究的信号在时－频分布的数学表达式中以相乘的形式出现两次。
在有的文献中又称为非线性时－频分布。
令信号()t x ，()t y 的傅立叶变换分别是()Ωj X ，()Ωj Y ，那么，()t x ，()t y 的联合Wigner分布定义为：()()(),,22j x y W t x t y t e d ττττ∞-Ω-∞Ω=+-⎰＊ （3.1.1）信号()t x 的自Wigner 定义为 ()()(),22j x W t x t x t e d ττττ∞-Ω-∞Ω=+-⎰＊ （3.1.2）Wigner 于1932年首先提出了Wigner 分布的概念［120］，并把它用于量子力学领域。
在之后的一段时间内并没有引起人们的重视。
直到1948年，首先由Ville 把它应用于信号分析。
因此，Wigner 分布又称Wigner －Ville 分布，简称为WVD 。
1973年，DE ．Bruijn 对WVD分布作了评述，并给出了把WVD 用于信号变换的新的数学基础［32］。
1966年，Cohen 给出了各种时－频分布的统一表示形式［46］，1980年，Classen 在Philips ．J ．Res ．上连续发表了三篇关于WVD 的文章［38,39,40］，对WVD 的定义、性质等作了全面的讨论。
由于这些工作，使得80年代后对WVD 的研究骤然引起了人们的兴趣，发表的论文很多，也取得了一些可喜的成果。
由下面的讨论可知，在已提出的各种时－频分布中，WVD 具有最简单的形式，并具有很好的性质。
清华大学《现代信号处理》课件
现代信号处理（离散随机信号处理）电子工程系本课程要讨论的主要问题：（1）对信号特性的了解随机信号（随机过程，时间序列––随机过程的一个实现）信号模型→参数估计→现代谱估计：参数化谱估计讨论信号模型及模型参数的估计问题，比较参数谱估计方法和周期图方法的优劣。
（2）对统计意义下最优滤波器设计的研究平稳条件下：Wiener滤波器理论非平稳条件下：Kalman滤波理论上的目标，实际算法可达到的最佳结果（3）对环境的自适应，具备“学习能力”的滤波算法自适应均衡、波束形成、线性自适应滤波器（4）更多信息的利用，挖掘（针对非高斯问题）线性系统、功率谱：二阶矩，高斯过程的完全刻划非线性、多谱：高阶量，循环平稳（5）对时间（空间）–––频率关系的适应性：全局特性与局域特性，小波变换，时频分析信号处理算法设计面向的几个主要因素n信噪比n先验知识n雷达n通信系统n电子对抗n对先验知识的利用：统计基础上的假设、学习过程n算法复杂性与性能要求的匹配性一些进展中的课题盲自适应信号处理序列贝叶斯估计、粒子滤波阵列信号处理等等与信号处理紧密关联的学科人工神经网络统计学习理论模式识别等等教材n张旭东，陆明泉：离散随机信号处理，2005年10月，清华大学出版社主要参考书①S. Haykin, Adaptive Filter theory, Third Edition, Prentice-Hall, 1996，//Fouth Edition 2001 (电子工业出版社均有影印本)①S.M. Kay, Modern Spectral Estimation: Theory & Application,Prentice-Hall, 1988①S.M. Kay, Fundamentals of Statistical Signal Processing: Estimation Theory, Prentice Hall PTR, 1993.①S. Mallat, A Wavelet Tour of Signal Processing, Academic press, 1998，Second Edition 1999①扬福生, 小波变换的工程分析与应用, 科学出版社, 2000.① D. G. Manolakis, et,al. Statistical and Adaptive Signal Processing, Mcgraw-Hall, 2000.①J. G. Proakis, et al. Algorithms for Statistical Signal Processing, Prentice hall, 2002①张贤达现代信号处理第2版清华大学出版社课程成绩n平时作业10％n2个Matlab作业40％（布置后2周内提交）n期末开卷考试50％1.1随机信号基础被噪声干扰的初相位是随机值的正弦波信号本质上均是随机的，但将信号作为随机信号处理，还是做为确定信号处理，与我们的应用目标和我们的先验知识有关，一般地，我们总是选择对应用有利的处理方式。
chapter04 清华大学《现代信号处理》讲义-胡广书
1.幅度是中心在（0，0）的高斯信号； 2.在 θ , τ 两个方向上是振荡的，振荡频率 由 Ω 0 , t0 决定 ；注意，Ω 0 , t0 并不影响
AF的中心位置； 3. AF是复函数。
例2
α 2 x(t ) = ∑ exp − α (t − t i ) 2 + jΩ i t i =1 π
结论：Cohen 类的任一成员都可由Wigner分布 得到。
（5）用广义模糊函数表示
M x (θ，τ ) = Ax (θ，τ )g(θ，τ )
Cx (t，Ω) = ∫∫ M x (θ，τ )e
− j (θt +Ωτ )
dτdθ
（6）用广义时间相关表示
− jtθ ′ 定义： g ( t，τ ) = ∫ g (θ，τ ) e dθ
上一例已求出，中心在 (θ , τ ) = (0, 0) 处；
互项：
1 2 α 2 1 Ax1 ,x2 (θ，τ ) = exp − (θ −Ωd ) + (τ − td ) exp j ( Ωuτ +θ tu +Ωd tu 2π 4 4α
1 2 α 2 1 Ax1 ,x2 (θ，τ ) = exp − (θ −Ωd ) + (τ − td ) exp j ( Ωuτ +θ tu +Ωd tu ) 2π 4 4α
Wx ( t，Ω ) = ∫ rx (t , τ )e − jΩτ dτ
WVD定义为瞬时自相关对 时间延迟 的傅里叶正变换
τ
rx ( t，τ ) = ∫ Ax (θ ，τ ) e − jθ t dθ
Wx ( t，Ω ) = ∫ rx (t , τ )e − jΩτ dτ = ∫∫ Ax (θ ，τ ) e
现代信号处理教程_-_胡广书(清华)
- 352 -
a1 (n)
a 0 ( n)
H0 (z-1)
′ ( n) a1
↑2
H0(z)
↓2
ˆ 0 ( n) a
d 1 2
H1(z)
↓2
图 12.1.1 双正交滤波器组
a1 ( n ) = a0 ( n ) ∗ h0 ( 2n )
= ∑ a0 ( k )h0 ( k − 2n ) = a0 ( k ), h0 ( k − 2n )
- 355 -
(12.1.14a)
ˆ 1 ( z ) = z − ( 2 l +1) H 0 ( − z −1 ) H
假定 l = 0 ，它们对应的时域关系是
(12.1.14b)
ˆ (1 − n ) h1 ( n ) = ( −1) n +1 h 0
ˆ ( n ) = ( −1) n +1 h (1 − n ) h 1 0
重建的充要条件是：
* ˆ 0 (ω ) + H 1* (ω + π ) H ˆ 1 (ω ) = 0 H 0 (ω + π ) H
(12.1.6a) (12.1.6b)
及
ˆ 0 (ω ) + H 1 (ω ) H ˆ 1 (ω ) = 2 H 0 (ω ) H
* *
证明：仿照(7.1.5)式的导出，有
ˆ ∗ (ω + π ) H 1 (ω ) = e − j ( 2 l +1)ω H 0 ˆ (ω ) = e − j ( 2 l +1)ω H ∗ (ω + π ) H 1 0
或
(12.1.13a) (12.1.13b)
ˆ 0 ( − z −1 ) H 1 ( z ) = z − ( 2 l +1) H
现代信号处理教程 - 胡广书(清华)-推荐下载
81 为了看清图3.3.4中交叉项的行为，我们将该图作了旋转，因此，水平方向为频率，垂直方向为时间。
图3.3.3 例3.3.3的WVD 图3.3.4 例3.3.4的WVD例3.3.5 令 ()2142t x t e ααπ-⎛⎫= ⎪⎝⎭（3.3.5）可求出其WVD 为 ()22,2exp[]x W t t ααΩ=--Ω（3.3.6）这是一个二维的高斯函数，，且是恒正的，如图3.3.5所示。
()Ω,t W x 由该图可以看出，该高斯信号的WVD 的中心在处，峰值为2。
参数控()()0,0,=Ωt α制了WVD 在时间和频率方向上的扩展。
越大，在时域扩展越小，而在频域扩展越大，反α之亦然。
其WVD 的等高线为一椭圆。
当WVD 由峰值降到时，该椭圆的面积。
1-e π=A 它反映了时－频平面上的分辨率。
如果令 ，，则的谱图()2142t h t e ααπ-⎛⎫=⎪⎝⎭()2142t x t eββπ-⎛⎫= ⎪⎝⎭()t x ()⎥⎦⎤⎢⎣⎡Ω+-+-+=Ω2221exp 2,βαβααββααβt t STFT x82（3.3.7）图3.3.5 例3.3.5的WVD,（a ）高斯信号，（b ）高斯信号的WVD它也是时－频平面上的高斯函数。
当其峰值降到时，椭圆面积。
这一结果说明，1-e π2=A WVD 比STFT 有着更好的时－频分辨率。
如果令 ()()tj et t x t x 001Ω-=（3.3.8）式中是（3.3.5）式的高斯函数。
是的时移加调制，其WVD 是：()t x ()t x 1()t x （3.3.9）()12200,2exp[()()/]x W t t t ααΩ=---Ω-Ω它将（3.3.6）式的由移至处。
其WVD 图形请读者()Ω,t W x ()()0,0,=Ωt ()()00,,Ω=Ωt t 自己画出。
83例3.3.6令 ()2201422j tt j t z t ee e αβαπΩ-⎛⎫=⎪⎝⎭（3.3.10）它是由（3.3.5）式的与()t x ()202j t j t y t Aee βΩ=（3.3.11）相乘而得到的（在（3.3.9）式中，A=1）。
现代信号处理教程 - 胡广书(清华)
98第4章 Cohen 类时－频分布4.1 前言除了Wigner 分布和谱图以外，近几十年来人们还提出了很多其它具有双线性行式的时－频分布。
1966年，Cohen 给出了时－频分布的更一般表示形式［44］： ()()()()() ，：，⎰⎰⎰-Ω+-*-+=Ωθττθττπθτθd dud eg 2u x 2u x 21g t C u t j x （4.1.1）该式中共有五个变量，即t ，Ω，τ，θ和u ，它们的含义我们将在下一节解释。
式中()τθ，g 称为时－频分布的核函数，也可以理解为是加在原Wigner 分布上的窗函数。
给出不同的()τθ，g ，就可以得到不同类型的时－频分布。
通过后面的讨论可知，目前已提出的绝大部分具有双线性形式的时－频分布都可以看作是Cohen 类的成员。
通过对Cohen 类分布的讨论有助于我们更全面地理解时－频分布，深入地了解它们的性质，并提出改进诸如交叉项这些不足之处的方法。
在Cohen 类时－频分布的讨论及抑制交叉项的方法中，在雷达信号处理中广泛应用的模糊函数（Ambiguity Function, AF ）起着重要的作用。
因此，本章首先给出模糊函数的定义及其与Wigner 分布的关系，然后讨论Cohen 类分布及其不同的成员。
在4.4节讨论为确保Cohen 类分布具有一系列好的性质而对()τθ，g 所提出的要求。
最后，在4.5节讨论核的设计问题。
文献[47]对非平稳信号的联合时－频分布给出了较为详细且是较为权威性的论述。
4.2 Wigner 分布与模糊函数令()t x 为一复信号，我们在第三章已定义()()()22τττ-+=*t x t x t r x ， （4.2.1）为()t x 的瞬时自相关函数，并定义()τ，t r x 相对τ的傅立叶变换 ()()⎰Ω-=Ωτττd t r t W j x x ，， （4.2.2）为()t x 的WVD 。
除去特别说明，该式及以下各式中的积分均是从∞+∞-～。