数字信号处理胡广书第6章_滤波器组(完整版)
例6.3.1 利用 Lagrange 插值法设计一半带滤波器
J=5(即N=19) H(z)共有18个零点，8个在右半平面共轭、镜像 对称，10个是在z=-1处的重零点，如图6.3.1a所 示。该滤波器的幅频响应如图6.3.1b所示，显然 该滤波器具有低通特性。
图6.3.1 19点lagrange半带滤波器的极零图与幅频响应
带内不“平”，而其相频特性不具有线性 相位所致；
• 3. 编码,量化，传输所产生的误差。此误差 来源于信号编码或处理算法，它和滤波器 组无关。
6.2 滤波器组的种类及有关的滤波器
6.2.1 最大均匀抽取滤波器组 6.2.2 正交镜像滤波器组 6.2.3 第M带滤波器 6.2.4 半带滤波器 6.2.5 互补型滤波器
M=8。由图可得，H0(z)是低通滤波器，H7(z)是 高通滤波器，而H1(z), ... ,H6(z)是带通滤波器，
并且它们具有相同的带宽，都是 /8 。
M 8
Hk (e j )
H0
H1
H2 H3
H4 H5
H6
H7
0
2
3 4 5 6
7
8
8
8
8
8
8
8
6.2.2 正交镜像滤波器组 （ Quadrature Mirror Filter Bank, QMFB)
半带滤波器既满足上式，又是正交镜像滤波器；而两 通道正交镜像滤波器不一定是半带滤波器。半带滤波 器在设计具有准确重建性能的滤波器组方面具有重要 的作用。
6.2.5 互补型滤波器
1.严格互补滤波器 （strictly complementary filter，scf）
M 1
H k (z) cz n0
的抽取，并且M=K，那么称该滤波器组为
最大均匀抽取滤波器组（maximally decimated
uniform filter bank），称这种情况为临界抽样
（critical subsampling）这是因为M=K是保证
实现准确重建的最大抽取数。
在实际工作中，由于要处理的信号一般都是
实信号，因此总希望滤波器组中的所有2M 个滤波器的系数也都是实的。得到实系数
也就是说综合滤波器组G0(z),G1(z),...,GM-1(z) 的作用：去除插值后的镜像；实现真正的
插值；重建原信号
Hk (e j ) k 0 k 1
k M 1 k 0
a.无混叠
0
2
M
Hk (e j ) k 0 k 1
2 (M 1)
2
M
k M 1 k 0
b.有混叠
0
2
M
2 (M 1) 2
k 0
假定利用H0(z), ... ,HM-1(z)把x(n)分成M个子带信号，然后再把这M 个子带信号相加，有
M 1
X (z)H0(z) X (z)HM 1(z) X (z) Hk (z) X (z)czn0 k 0
X (z)对cz应n0 的时域信号是cx(n-n0),它和x(n)仅差了一个延迟和常 数倍。显然，这样严格互补的滤波器对于信号的准确重建是 非常有用的。
M
图6.1.2 分析滤波器组的频率响应
H0 (z) x0 (n) M v0 (n) M u0 (z) G0 (z)
x(n)
H1(z) x1(n) M v1(n) M u1(z) G1(z)
xˆ(n)
H M 1(z) xM 1(n) M vM 1(n) M uM 1(z) GM 1(z)
第6章 滤波器组基础
6.1 滤波器组的基本概念 6.2 滤波器组的种类及有关的滤波器
6.2.1 最大均匀抽取滤波器组 6.2.2 正交镜像滤波器组 6.2.3 第M带滤波器 6.2.4 半带滤波器 6.2.5 互补型滤波器 6.3 半带滤波器设计 6.4 多抽样率系统的应用简介
6.1 滤波器组的基本概念
(
z)
H
(z)
X
(
z
M
)
c
M 1
(6.2z.5l E) l
l 1
(
z
M
)
X
(
z
M
)
该式意味着y(Mn)=cx(n)，这就是说，将x(n)作L=M倍的插
值后，再经一个Mth滤波器，x(n)中所有的值乘以c后变为
y在Mn处的值。若c=1，则y(Mn)=cx(n)，在n的非M整数 倍处，即是插值的结果。
定理6.2.1 H(z)若是一 M th滤波器，则
有线性相位的滤波器H(z)。
由图6.2.6，可以假定要设计的半带滤波器的截止频
率 wc 2 ，并令理想滤波器的频率特性为
H
d
(e
jw
)
1, 0
w 2
其他
于是可求出
即hd(n)是一个零相位的半带滤波器。将hd(n)截短并移位，得
式中，w(n)是选用的窗函数；h(n)即是所设计的半带滤波器， h(n)的长度是N=4J-1。
由定理6.2.1，Mth滤波器一定是scf。hbf是Mth滤波器的特例， 因此，hbf也是scf。然而，scf并不一定是Mth滤波器或hbf。
2. 功率互补滤波器（power complementary filter，PCF）
若M个滤波器的频率响应满足
M 1
| H kc(为e j常 )数|2 （6c.2.17）
这就是说，如果有一个M th滤波器h(n),那么将其依 次移位 2k 后M ，所得到的M个滤波器的频率响应
之和等于1.
（6.2.3）式的M th滤波器也可推广到更一般的情况。
6.2.4 半带滤波器(Half-Band Filter)
h(n)
c n
图6.2.5 某一半带滤波器的h(n)
以上均是半带滤波器，即半带滤波器可以是因果 的，也可以是非因果的；其系数可以是实的，也 可以是复的。但是，在实际工作中，限定所要讨 论的对象是实系数的、因果的且具有线性相位的 半带滤波器。
3.用单带滤波器来设计半带滤波器
欲设计一个半带滤波器H(z)，假定其长度为N，截止频率为
wp，阻带频率为ws。首先，用Chebyshew最佳一致逼近法设 计出一个“单带”滤波器G(z)，所谓“单带”，是令G(z)的
通带频率为2wp，阻带频率w为s ，从wp ~ 是其过渡带，因此， G(z)只是一个通带，没有阻带；然后，对g(n)作二倍的插值，
由定M理6.2.1，若假定c=1/2,则
H (z) H (z) 1
let
H (e j ) H (e j( ) ) 1
并假定H(z)具有线性相位，即
H0(z) H (z) H1(z) H (z)
H (e jw ) e j(N1)w 2Hg (w) 式H一图频中0(个6率z，.)2+全范.HH6通 围所1g((zw)系 内示的)是统 基。增w。 本可益的上H以在实0(等看z整函)，于出个数H1，频1，。(zH)带称及0(z内为H)+0等HH(z(1)于z(+)z的H)的11，(增z增)的相益益增当，在益于那整如是么个，
k 0
则称H0(z), ... ,HM-1(z)是功率互补的。该式又可表示成
M 1
Hk (z)H（k6(.z2).18c）
k 0
~
式中
H (z) H（*(z6.12).19）
表示将H(z)的系数取共轭，并用z-1代替z ，若H(z)系数是实
的，则
~
H (z) H (z 1)
下面的定理给出了pcf和Mth滤波器之间的关系。
图6.1.3 M通道滤波器组
H 0 (e jw ),
H k (e jw ) H 0 (ei(w2k / M ) )
图6.1.3的系统中，x(n)对 x(n) 的失真原因：
• 1. 混迭失真：分析滤波器组和综合滤波器 组的频带不能完全分开及
抽样频率不满足： fs 2Mfc • 2 .幅度及相位失真： 滤波器组的频带在通
证明:
M 1
H(zW k ) 1
k 0
el (n) h(Mn l)
Poisson 和公式
h(n) (n Mi l)
h(n)
1 M
M 1
e j 2 k (ln) / M
k 0
n ~
i 0,1,, M 1 l 0,1,, M 1
若令 H0(z) H(z) H k (z) H (zWMk ) k则H00,,1H, 1 , ,..M. ,HM1-1的 频率响应之和等于1，
定理6.2.2 给定一转移函数 H(z)，其多相表示为
M 1
H (z) z 1El (z M ) l0
再令
~
G(z) H(z)H(z)
当且仅当 G(z) 是一 Mth滤波器时，
E0 ( z),..., EM 1(z)
是功率互补的。
6.3半带滤波器设计
半带滤波器在两通道滤波器组的分析与实现中具有重要的作 用，本节讨论其设计方法。由6.2节所述，半带滤波器的单 位抽样响应h(n)除n=0以外的偶序号项皆为零，且其频率响 应有着(6.2.14)式的对称性。至今，人们已提出了多种半带 滤波器的设计方法，现择其主要讨论。 1.窗函数法 用窗函数法设计FIR滤波器是简单易行的方法。它包括： .令理想滤波器的频率响应为 H d (；e jw ) .对 Hd作(e j积w ) 分求出理想的单位抽样响应hd(n); .对hd(n)截短、移位等步骤，最后得到因果的、有限长且具
6.2.1 最大均匀抽取滤波器组
设HK某-1(一z) ,滤这波K个器滤组波有器K个有分关析系滤波器H0(z) , ... ,
即
Hk (z) H0 (zWKk )
H k (e j ) H 0 e j( 2
现代信号处理--清华胡广书讲义-第6章滤波器组基础
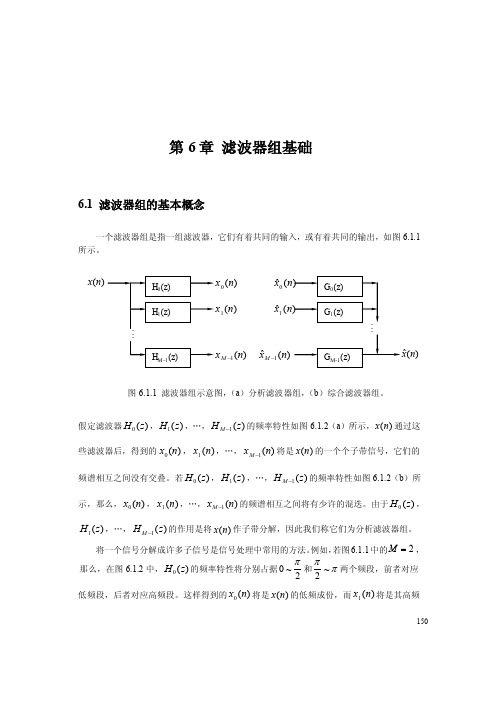
150第6章 滤波器组基础6.1 滤波器组的基本概念一个滤波器组是指一组滤波器，它们有着共同的输入，或有着共同的输出，如图6.1.1所示。
图6.1.1 滤波器组示意图，（a ）分析滤波器组，（b ）综合滤波器组。
假定滤波器)(0z H ，)(1z H ，…，)(1z H M -的频率特性如图6.1.2（a ）所示，)(n x 通过这些滤波器后，得到的)(0n x ，)(1n x ，…，)(1n x M -将是)(n x 的一个个子带信号，它们的频谱相互之间没有交叠。
若)(0z H ，)(1z H ，…，)(1z H M -的频率特性如图6.1.2（b ）所示，那么，)(0n x ，)(1n x ，…，)(1n x M -的频谱相互之间将有少许的混迭。
由于)(0z H ，)(1z H ，…，)(1z H M -的作用是将)(n x 作子带分解，因此我们称它们为分析滤波器组。
将一个信号分解成许多子信号是信号处理中常用的方法。
例如，若图6.1.1中的2=M ，那么，在图6.1.2中，)(0z H 的频率特性将分别占据2~0π和ππ~2两个频段，前者对应低频段，后者对应高频段。
这样得到的)(0n x 将是)(n x 的低频成份，而)(1n x 将是其高频)(0n x )(1n x )(1n x M -)(n x(ˆ0x (ˆ1x)(ˆ1n xM -)(ˆn x151成份。
我们可依据实际工作的需要对)(0n x 和)(1n x 作出不同的处理。
例如，若我们希望对)(n x 编码，设)(n x 的抽样频率为20KHz ，若每个数据点用16bit ，那么每秒钟需要的码图6.1.2 分析滤波器组的频率响应，（a ）无混迭，（b ）稍有混迭流为320Kbit 。
若)(n x 是一低频信号，也即)(n x 的有效成份（或有用成份）大都集中在)(0n x 内，)(1n x 内含有很少的信号能量。
这样，我们可对)(0n x 仍用16bit ，对)(1n x 则用8bit ，甚至是4bit ，由于)(0n x 和)(1n x 的带宽分别比)(n x 减少了一倍，所以，)(0n x 和)(1n x 的抽样频率可降低一倍。
数字信号处理第六、七章教案
教案（第23次课2学时）一、授课题目第六章无限脉冲响应数字滤波器的设计§6.4 用双线性变换法设计IIR数字低通滤波器§6.5 数字高通滤波器的设计二、教学目的和要求掌握用双线性变换法设计IIR数字低通滤波器；掌握利用低通滤波器设计数字高通滤波器的方法。
三、教学重点和难点用双线性变换法设计IIR数字低通滤波器；利用低通滤波器设计数字高通滤波器。
四、教学过程（包含教学内容、教学方法、辅助手段、板书、学时分配等）复习：本章主要介绍无限脉冲响应数字滤波器的设计。
无限脉冲响应数字滤波器的特点是单位脉冲响应是无限长的，这主要是由于它的系统函数中含有反馈，即差分方程中含y(n-i)项。
对于无限脉冲响应数字滤波器我们主要是利用技术已经非常成熟的模拟滤波器的设计进行的，由于我们这本书主要是讨论具有单调下降的幅频特性的滤波器的设计，所以我们介绍了具有单调下降特性的巴特沃斯模拟滤波器的设计。
掌握了它之后，利用模拟滤波器进行设计，只要找出频率以及系统函数之间的关系，就可以设计出需要的数字滤波器。
由于它是借助模拟滤波器进行的，所以他保留了一些典型模拟滤波器优良的幅度特性，但涉及种植考虑复读特性，没考虑相位特性，所设计的滤波器一般是某种确定的非线性相位特性。
我们一般用到的是脉冲响应不变法和双线性变换法来设计无限脉冲响应数字滤波器。
上节课中我们介绍了双线性变换法设计数字滤波器。
设计时我们只需要先利用频率之间的关系将我们要设计的数字滤波器的技术指标转换为对应的模拟滤波器的技术指标，之后利用我们之前讲的模拟滤波器的设计，求出模拟滤波器的系统函数，然后利用系统函数之间的关系得到数字滤波器的系统函数。
脉冲响应不变法进行设计时，模拟滤波器的系统函数Ha （s ）与数字滤波器的系统函数H(z)之间的关系是 若∑=-=N i ii s s A s H 1a )(，则对应的数字滤波器的系统函数为 ∑=--=N i T s i z A z H i 11e1)(，即H a(s )的极点si 映射到z 平面的极点为T s i e ，系数A i 不变。
《数字信号处理导论_第6章》
每一种又有模拟(AF)、数字(DF)两种滤波器.
对数字滤波器, 从实现方法上, 有IIR滤波器和
FIR滤波器之分, 转移函数分别为: FIR DF:
直接设计
IIR DF:
利用模拟滤 波器设计
3. 滤波器的技术要求
低通：
：通带允许的最大衰减；
：阻带内应达到的最小衰减
单位 (dB)
若幅度下降到 0.707, 则幅平方下降 0.5 （半 功率点）：
k 1,2,..., N
5）滤波器的设计步骤:
确定技术指标： p p s s
注： p c
根据技术指标求出滤波器阶数N及 ：
2 10
1
0.1 p
1
1 ch 100.1 s 1 N 1 s ch c
k 1, 2,..., N
c cr 1 rad / s
为归一化系统的系统函数 H an ( s) 去归一化，得 H ( s ) H ( s ) a an
cr s H an cr s s c c
4）滤波器的设计步骤：
确定技术指标： p p s s
由H a ( s)
s 0
H a ( j)
0
，得K0 4
4( s 2 25) 4s 2 100 H a (s) 2 ( s 7)( s 6) s 13s 42
2、Butterworth 低通逼近
幅度平方函数： H a ( j)
2
1 1 c
• 极点在s平面呈象限对称，分布在Buttterworth圆上，共2N点 • 极点间的角度间隔为 / N rad • 极点不落在虚轴上 • N为奇数，实轴上有极点，N为偶数，实轴上无极点
现代信号处理基础及应用6章-白化滤波器
内积空间：
设有 M 个两两正交的随机矢量 ε1, ε2, , εM ，满足
εi , εj 0, i j
令 Y=ε1, ε2,
εM , 是由这 M 个随机矢量张成的线
性子空间，那么随机矢量就是该内积空间的正交基底。
根据正交分解定理，对于任何随机矢量 x ， 相对于线性子空间 Y ，可唯一分解为两个互 相正交的部分，即
D(
z)
可能不是因果的，
D(z) G(z)
就不是因果的；
D(z) （3） G(z) 对应的是一个因果稳定的 IIR 滤波器，而所
设计的 H(z) 是一个 n 阶的 FIR 滤波器。
上述因素都会使滤波器的实际输出 y = g* h 不一定等
于期望输出 d 。
设 d l2 g l2 ，且 g 是因果的。则滤波器实际输出 y 与期望
lim n
δ-
gh
2
1
1 2
例 6.2 假设信道的传递函数为G(z) 1 z2 ，它是非最小相 4
设 x = x1 + x2 ，其中 x1 与 y 相关， x2 与 y 不相关，由 于 Rxy R[ xyT ] E[( x1 x2 ) yT ] Rx1y Rx2 y Rx1y
所以， xˆ Rxy Ry1 y Rx1y Ry1 y xˆ1，因此， xˆ 实际上就 是对 xˆ1的估计，即对 x 中与 y 相关部分的估计。所 以相关抵消器的输出中与 y 相关的部分 x1 得到了 尽可能大的抵消。
Yn ε1, ε2 , , εn y1, y2,
, yn
用符号 yˆn n1 来表示 yn 在子空间Yn1 上的正交投影即
n 1
1
yˆn n1 E yni E ii i
数字信号处理第六章
1）幅度函数特点：
H a ( j)
2
1 1 c
2
2N
0
c
H a ( j) 1 H a ( j) 1/ 2 1 3dB 3dB不变性
2
c 通带内有最大平坦的幅度特性，单调减小
c 过渡带及阻带内快速单调减小
3、逼近情况
1）
s平面虚轴
2）
z平面单位圆
s平面
左半平面
z平面 单位圆内 单位圆外 单位圆上
右半平面
虚轴
例7.4
已知模拟滤波器的传输函数为
1 H a ( s) 2 2s 3s 1
采用双线性变换法将其转换为数字滤波 器的系统函数，设T=2s 解 将s代入Ha(s)可得
H ( z ) H a ( s ) s 2 1 z 1 ,T 2
i 1,2,..., m
例6.4.1试分别用脉冲响应不变法和双 线性不变法将图6.4.4所示的RC低通滤波器 转换成数字滤波器。 解 首先按照图6.4.4写出该滤波器的传 输函数Ha(s)为 1
H a ( s)
s
,
RC
利用脉冲响应不变法转换，数字滤波器的系统函 数H1(z)为
低通
0 高通
0 带通 0
带阻
0
全通 0
通带
阻带 过渡带 平滑过渡
三、DF频响的三个参量 1、幅度平方响应
2、相位响应
3、群延迟
它是表示每个频率分量的延迟情况；当其为常 数时， 就是表示每个频率分量的延迟相同。 四、DF设计内容 1、按任务要求确定Filter的性能指标； 2、用因果稳定LSI的系统函数去逼近这一性 能要求； 3、选择适当的运算结构实现这个系统函数； 4、用软件还是用硬件实现。
数字信号处理 第六章
第六章数字滤波器结构6、1:级联得实现num = input('分子系数向量 = ');den = input('分母系数向量 = ');[z,p,k] = tf2zp(num,den);sos = zp2sos(z,p,k)Q6、1使用程序P6、1,生成如下有限冲激响应传输函数得一个级联实现:H1(z)=2+10z^(-1)+23z^(-2)+34z^(-3)+31z^(-4)+16 z^(-5)+4z^(-6)画出级联实现得框图。
H1(z)就是一个线性相位传输函数吗?答:运行结果:sos = zp2sos(z,p,k)Numerator coefficient vector = [2,10,23,34,31,16,4]Denominator coefficient vector = [1]sos =2、0000 6、0000 4、0000 1、0000 0 01、0000 1、00002、0000 1、0000 0 01、0000 1、0000 0、5000 1、0000 0 0级联框图:H1(z)不就是一个线性相位传输函数,因为系数不对称。
Q6、2使用程序P6、1,生成如下有限冲激响应传输函数得一个级联实现:H2(z)=6+31z^(-1)+74z^(-2)+102z^(-3)+74z^(-4)+31 z^(-5)+6z^(-6)画出级联实现得框图。
H2(z)就是一个线性相位传输函数吗?只用4个乘法器生成H2(z)得一级联实现。
显示新得级联结构得框图。
Numerator coefficient vector = [6,31,74,102,74,31,6]Denominator coefficient vector = [1]sos =6、0000 15、0000 6、0000 1、0000 0 01、00002、00003、0000 1、0000 0 01、0000 0、6667 0、3333 1、0000 0 0级联框图:H2(z)就是一个线性相位传输函数。
数字信号处理第六章 习题及参考答案
第六章 习题及参考答案一、习题1、已知一个由下列差分方程表示的系统，x(n)、y(n)分别表示该系统的输入、输出信号：)1(21)()2(61)1(65)(-+=-+--n x n x n y n y n y （1）画出该系统的直接型结构； （2）画出该系统的级联型结构； （3）画出该系统的并联型结构。
2、已知某系统的系统函数为：)6.09.01)(5.01()9.21)(1()(211211------++-+-+=z z z z z z z H 请画出该系统的级联型结构。
3、已知FIR 滤波器的单位脉冲响应为)(8.0)(5n R n h n =， （1）求该滤波器的系统函数； （2）画出该滤波器的直接型结构。
4、已知滤波器的系统函数为：3213218.09.09.018.04.16.01)(-------+-+--=zz z z z z z H 请画出该滤波器的直接型结构。
5、已知滤波器的系统函数为：)8.027.11)(5.01()44.11)(1(3)(211211------+--+--=z z z z z z z H 请画出该滤波器的级联型结构和并联型结构。
6、已知某因果系统的信号流图如下图所示：x(n)y(n)-25-3求该系统的系统函数和单位脉冲响应。
7、已知某系统的信号流图如下图所示：x(n)y(n)求该系统的系统函数和极点。
8、已知IIR 滤波器的系统函数为：4.035.04.046.16.14)(2323++++--=z z z z z z z H （1）画出级联型网络结构，要求利用MATLAB 分解H(z); （2）用MATLAB 验证所求的级联型结构是否正确。
9、已知IIR 滤波器的系统函数为：3213214.035.04.016.141.158.12.5)(-------++-++=zz z z z z z H （1）画出该系统的并联型网络结构，要求用MATLAB 分解； （2）用MATLAB 验证（1）中所求的并联型结构是否正确。
6-5数字信号处理
X
第14页
例 6.5.3 设 计 一 个 数 字 带 阻 滤 波 器 ， 通 带 下 限 频 率 ωl=0.19π,阻带下截止频率 s1=0.198π， 阻带上截止频 阻带下截止频率ω 阻带下截止频率 ， 率ωs2=0.202π，通带上限频率 u=0.21π，阻带最小衰减 ，通带上限频率ω ， αs=13dB，ωl和ωu处衰减 p=3dB。采用巴特沃斯型。 处衰减α ， 和 处衰减 。采用巴特沃斯型。 解 (1) 数字带阻滤波器技术指标： 数字带阻滤波器技术指标： ωl=0.19πrad, ωu=0.21πrad, αp=3dB ωs1=0.198πrad, ωs2=0.202πrad, αs=13dB
N= lg ksp lg λsp = 1.3043, N =2
X
第6页
查表6.2.1，得到归一化模拟低通传输函数G(p)为 ，得到归一化模拟低通传输函数 查表 为
1 G( p) = 2 p + 2p +1
去归一化， 去归一化，将p=s/
2 Ωc G( s) = 2 2 s + 2Ω c s + Ω c
p= sB 2 s +Ω0
2
(6) 将Ha(s)通过双线性变换，得到数字带阻滤波器 通过双线性变换， 通过双线性变换 得到数字带阻滤波器H(z)
sB p= 2 2 s + Ω0
1− z −1 1+ z −1
s =2
2(1 − z −2 ) B = 2 4(1 − z −1 ) 2 + Ω0 (1 + z −1 ) 2 0.969(1 − 619 z −1 + z −2 ) = 1 − 1.569 z −1 + 0.939 z −2
数字信号处理第六章chhy
6.1 数字滤波器的基本概念
(3) 从滤波器的实现网络结构或从单位脉冲响应分类 无限脉冲响应(IIR)数字滤波器
H ( z)
N 1
M
1 ak z k
r 0 N
br z r
N阶IIR滤 波器函数
r H ( z ) n 0 0N 有限脉冲响应(FIR)数字滤波器： 1 ak z k k 1
6.2
模拟滤波器的设计
模拟滤波器的理论和设计方法已发展得相当成熟，且有若干典型 的模拟滤波器 可供选择。 这些滤波器都有严格的设计公式、现成的曲线和图表供设计人员使用。 常用模拟原型滤波器及特点:
（1）巴特沃斯（Butterworth） 滤波器具有单调下降的幅频特性； （2）切比雪夫（Chebyshev）滤波器： 幅频特性在通带或阻带有波动，可提高选择性； （3）贝塞尔（Bessel）滤波器： 通带内较好的线性相位； HH(j(j Ω) a a Ω) （4）椭圆（Ellipse）滤波器： 通带、阻带等纹波，选择性相对于前三种是最好的。
k 0
N 1
k
)
只要知道滤波器的阶数N，可得归一 化的传输函数，去归一化p=jλ=s/ c , 可得到实际的传输函数Ha(s)
归一化极点pk=ej (½+(2k+1)/2N)，k=0,1,…,N-1。
6.2
模拟滤波器的设计
一、巴特沃斯滤波器的设计步骤：
a p 2N (1) 根据给出的技术指标P、S、1、S，求滤波器阶数N p( ) 10 p /10
过渡带
低通数字滤波器的幅频特性技术指标
通带
ωp ωC
阻带
ωS
6.1 数字滤波器的基本概念
数字信号处理胡广书第6章_滤波器组(完整版)
j
2
2
j ( )
频带
H1 ( e ) H 0 ( e
)
图6.2.2 两通道滤波器组 (a)系统框图；(b)镜像对称的幅频特性
6.2.3 第M(Mth)带滤波器
将分析滤波器组写成多相形式，如果其第0相， E0 (恒为一常数，即 zM ) 也即
M 1 k 0
| H k (e ) | c
j 2
M 1 k 0
c为常数 （6.2.17）
则称H0(z), ... ,HM-1(z)是功率互补的。该式又可表示成
H k ( z) H k ( z) c
H ( z ) H * ( z 1 )
~
（6.2.18）
式中 （6.2.19） 表示将H(z)的系数取共轭，并用z-1代替z ，若H(z)系数是实 ~ 的，则 1
• 1. 混迭失真：分析滤波器组和综合滤波器 组的频带不能完全分开及 抽样频率不满足：f s 2Mfc • 2 .幅度及相位失真： 滤波器组的频带在 通带内不“平”，而其相频特性不具有线 性相位所致； • 3. 编码,量化，传输所产生的误差。此误 差来源于信号编码或处理算法，它和滤波 器组无关。
第6章 滤波器组基础
6.1 滤波器组的基本概念 6.2 滤波器组的种类及有关的滤波器 6.2.1 最大均匀抽取滤波器组 6.2.2 正交镜像滤波器组 6.2.3 第M带滤波器 6.2.4 半带滤波器 6.2.5 互补型滤波器 6.3 半带滤波器设计 6.4 多抽样率系统的应用简介
6.1 滤波器组的基本概念
和常数倍。显然，这样严格互补的滤波器对于信号的准确重 建是非常有用的。 由定理6.2.1，Mth滤波器一定是scf。hbf是Mth滤波器的特例， 因此，hbf也是scf。然而，scf并不一定是Mth滤波器或hbf。