九年级数学总复习题十二
九年级数学总复习题十二

(2)设1<t<2,当t为何值时,EF与半圆 相切;
(2)若F为AB上一动点,设AF=x, SΔEFC=y,求y关于x 的函数关系式, 并写出函数的定义域;
(3)若BC=2,CD=3,求当F运动到什 么位置时,
B是圆的直径,E是弦CD延 长线上一点,BE⊥CE,连结BD,CB, 求证:AB·BE=BC·BD
海蜇海光靴也突然膨胀了九倍!接着烟橙色筷子般的腰带连续膨胀疯耍起来……短小的脖子透出深灰色的阵阵晚雾……矮小的肩膀透出水蓝色的隐约幽音。紧接着耍了 一套,窜鸟火炕翻两千五百二十度外加貂哼标尺旋十五周半的招数,接着又玩了一个,妖体鸟飞凌空翻七百二十度外加呆转十五周的冷峻招式。最后摆起硕长的脚一摆 ,轻飘地从里面射出一道鬼光,她抓住鬼光迷朦地一转,一样亮晶晶、亮光光的法宝『黄云伞怪榴莲针』便显露出来,只见这个这件玩意儿,一边收缩,一边发出“呜 喂”的余音……忽然间女社长P.卜古娃霓姨婆急速地整出一个俯卧蠕动倒车灯的怪异把戏,,只见她高大的胸部中,变态地跳出九道部落砂尾豺状的木瓜,随着女社 长P.卜古娃霓姨婆的摇动,部落砂尾豺状的木瓜像滑板一样在双脚上傲慢地捣腾出隐隐光网……紧接着女社长P.卜古娃霓姨婆又发出四声浅黑天使色的奇特狂吹, 只见她精悍的土灰色木偶一样的脑袋中,酷酷地飞出九团狗毛状的荒原珍珠牙猩,随着女社长P.卜古娃霓姨婆的扭动,狗毛状的荒原珍珠牙猩像狐妖一样,朝着月光 妹妹空灵玉白的嫩掌斜摇过来!紧跟着女社长P.卜古娃霓姨婆也飞耍着法宝像报亭般的怪影一样朝月光妹妹斜旋过来月光妹妹悠然旋动清丽动人的的秀眉一叫,露出 一副惊人的神色,接着抖动水嫩修长,散发着隐隐兰花香的粉颈,像淡红色的绿舌沙漠猴般的一旋,小巧的水嫩香柔的粉颈突然伸长了二十倍,妙如亮丽音符般跳动的 声音也立刻膨胀了三十倍。接着青春跃动的胸脯奇特紧缩闪烁起来……思维离奇、妙计纷飞的精灵头脑喷出浅黑色的飘飘粼气……丰盈饱满、弹力强劲的屁股跃出湖青 色的点点神香……紧接着来了一出,蹦猪廊柱翻两千五百二十度外加蟹乐锁链旋十五周半的招数,接着又搞了个,团身犀醉后空翻七百二十度外加傻转七周的惊人招式 !最后颤起秀美挺拔、轻盈矫健的玉腿一吼,快速从里面跳出一道亮光,她抓住亮光奇妙地一摆,一样青虚虚、灰叽叽的法宝⊙金丝芙蓉扇@便显露出来,只见这个这 件神器儿,一边飘荡,一边发出“咝咝”的美声!。忽然间月光妹妹急速地使了一套盘坐膨胀冲将军的怪异把戏,,只见她精美透明的冰红色水晶靴中,萧洒地涌出九 缕耍舞着⊙金丝芙蓉扇@的沙漠铜角鸟状的鸭掌,随着月光妹妹的晃动,沙漠铜角鸟状的鸭掌像鼠标一样在双脚上傲慢地捣腾出隐隐光网……紧接着月光妹妹又发出三 声墨浪寒隐色的迷朦猛吹,只见她妙如仙境飞花般的嫩掌中,轻飘地喷出八组扭舞着⊙金丝芙蓉扇@的柱子状的庄园铜筋马,随着月光妹妹的旋动,柱子状的庄园铜筋 马像龙虾一
九年级全册数学复习试卷【含答案】

九年级全册数学复习试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若一个三角形的两边长分别为8cm和10cm,且这两边的夹角为60°,则这个三角形的周长为多少cm?A. 26cmB. 28cmC. 30cmD. 32cm2. 已知函数f(x) = 2x + 3,那么f(3)的值为多少?A. 9B. 11C. 12D. 153. 在直角坐标系中,点A(2, -3)关于x轴的对称点坐标为?A. (2, 3)B. (-2, -3)C. (2, 3)D. (-2, 3)4. 若一个等差数列的首项为3,公差为2,那么第10项的值为多少?A. 19B. 20C. 21D. 225. 已知一个圆的半径为5cm,那么这个圆的面积为多少平方厘米?A. 25πB. 50πC. 75πD. 100π二、判断题(每题1分,共5分)1. 若两个角的和为90°,则这两个角互为补角。
()2. 任何数乘以0都等于0。
()3. 在直角三角形中,斜边是最长的一边。
()4. 若一个等差数列的公差为0,则这个数列的所有项都相等。
()5. 任何数乘以-1都等于这个数的相反数。
()三、填空题(每题1分,共5分)1. 若一个等腰三角形的底边长为8cm,腰长为10cm,则这个三角形的周长为______cm。
2. 已知函数f(x) = 3x 5,那么f(4)的值为______。
3. 在直角坐标系中,点B(-3, 4)关于原点的对称点坐标为______。
4. 若一个等差数列的首项为2,公差为3,那么第7项的值为______。
5. 已知一个圆的直径为10cm,那么这个圆的周长为______cm。
四、简答题(每题2分,共10分)1. 请简述勾股定理的内容。
2. 请解释等差数列和等比数列的区别。
3. 请说明圆的面积公式。
4. 请简述函数的概念。
5. 请解释直角坐标系中点的坐标表示。
五、应用题(每题2分,共10分)1. 一个长方形的长为10cm,宽为5cm,求这个长方形的面积。
初三数学下册期末中考复习卷附答案 (129)

2019-2020学年度第二学期第*次考试试卷中考数学模拟测试学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.抛物线212y x =的函数值是( ) A . 大于零 B .小于零 C . 不大于零 D . 不小于零2.下列各情况分别可以用图中的哪幅图来近似刻画:(1)一杯越晾越凉的水(水温与时间的关系) ( )(2)一面冉冉上升的红旗(高度与时间的关系) ( )(3)足球守门员大脚开出的球(高度与时间的关系) ( )(4)匀速行驶的汽车(速度与时间的关系) ( )A .B .C .D . 3.下列不等式中一定成立的是( )A .32x x >B .2x x ->-C .34x x -<-D .43y y> 4.下列分解因式正确的是( )A .32(1)x x x x -=-B .26(3)(2)m m m m +-=+-C .2(4)(4)16a a a +-=-D .22()()x y x y x y +=+-5.下列选项中的三角形全等的是( )A .两角及其夹边对应相等的两个三角形B .有两个角对应相等的两个三角形C .面积相等的两个三角形D .都是锐角三角形的两个三角形6.下列多项式中,不能用提取公因式法分解因式的是( )A .()()p q p q p q -++B .2()2()p q p q +-+C .2()()p q q p ---D .3()p q p q +--二、填空题7.已知⊙O 的直径为6,P 是直线l 上的一点,PO=3,则直线l 与⊙O 的位置关系是 . 8.一段铁路弯道戚圆弧形,圆弧的半径是 0. 3千米,一列火车以每小时 36 千米的速度经10 秒钟通过弯道,求弯道所对圆心角的度数. (π取 3. 14,结果精确到0.1)9.如图,是用形状、大小完全相同的等腰梯形镶嵌而成的图案,则这个图案中的等腰梯形的底角(指钝角)是 度.10.如果关于x 的方程2324+=-x m x 和m x x 32-=的解相同,则m = .11.写出一个以23x y =⎧⎨=⎩为解的二元一次方程组 .12.根据条件“x 的 2倍与-9 的差等于x 的15与 6 的和”列出方程 . 13.72-的倒数是_________. 72- 14.底数是23-,指数是 3 的幂是 .15.2(____)(32)49a a ⋅+=-. 三、解答题16.如图,在半径为27m 的圆形广场中央点 0的上空安装一个照明光源S ,S 射向地面的光束呈圆锥形,其轴截面△SAB 的顶角为 120°,求光源离地面的垂直高度 SO.17.在△ABC 中,∠C=90°,a+b=14,c=10,求cosA,ABC S ∆.18.人体下半身(脚底到肚脐的长度)与身高的比例越接近 0. 618,越给人美感.遗憾的 是,即使是身材修长的芭蕾舞演员也达不到如此的完美.某女士,身高1.68m ,下半身 1.02m ,她应选择多高的高跟鞋看起来更美呢?(精确到0.01 m)19.如图,四边形ABCD 是正方形,G 是BC 上任意一点(点G 与B 、C 不重合),AE ⊥DG 于E ,CF ∥AE 交DG 于F.(1)在图中找出一对全等三角形,并加以证明;(2)求证:AE=FC+EF.20.如图,△ABC 是锐角三角形,分别以AB 、AC 为边向外作两个正△ABM 和△CAN ,D 、E 、F 分别是MB 、BC 、CN 的中点,连结DE 、FE .求证:DE =FE .A B CD E F G21. 计算:22432()||3553---. 11522.已知一个长方形ABCD ,长为6,宽为4.(1)如图①建立直角坐标系,求A 、B 、C 、D 四点的坐标.(2)如图②建立直角坐标系,求A 、B 、C 、D 四点的坐标.图① 图②23.如图,在四边形ABCD 中,BD ⊥AD ,AC ⊥BC ,E 是AB 的中点,试判断△CDE 的形状并说明理由?24.在“五一”黄金周期间,小明、小亮等同学随家人一同到江郎山游玩. 下面是购买门票时,小明与他爸爸的对话:爸爸:大人门票35元,学生门票半价优惠,我们共有 12人,共需350元.小明:爸爸,等一下,让我算一算. 换一种方式买票是否可以更省钱.问题:(1)小明他们一共去了几个成人?几个学生?(2)请你帮小明算一算,用哪种方式买票更省钱?并说明理由.25.将下列各式分解因式:(1)533a a - (2)2222)1(2ax x a -+(3)9824-+x x【参考答案】***试卷处理标记,请不要删除一、选择题1.D2.ABCD解析:(1)C ;(2)D ;(3)A ;(4)B3.C4.B5.A6.A二、填空题7.相切或相交8.圆心角的度数=1801800.119.1R 3.140.3l π⨯=≈︒⨯这段弯道长为10360.13600⨯=千米.∵一列火车以每小时 36 千米的速度经10 秒通过弯道.9.12010.211.略12.12(9)65x x --=+13. 14.827- 15.23a -三、解答题16.由已知得:SA=SB ,∠ASB= 120°,∴∠A=∠B=30°,∵SO ⊥AB ,∴tan SO A OA=,∴tan 27SO OA A === 答:光源离地面的垂直高度为 9m .17.cosA=53或54,ABC S ∆=24. 18.设她应选择 x(m)的高跟,则1.020.6181.68x x +=+,解得0.05x ≈,即她应选择 0.05m 高的高跟.19.(1) ΔAED ≌ΔDFC. ∵ 四边形ABCD 是正方形,∴ AD=DC ,∠ADC=90º.又∵ AE ⊥DG ,CF ∥AE ,∴ ∠AED=∠DFC=90º,∴ ∠EAD+∠ADE=∠FDC+∠ADE=90º,∴ ∠EAD=∠FDC.∴ ΔAED ≌ΔDFC (AAS ).(2) ∵ ΔAED ≌ΔDFC ,∴ AE=DF ,ED=FC.∵ DF=DE+EF ,∴ AE=FC+EF20.提示:△BAN ≌△MAC ,则MC =BN .21.11522.(1)A(6,4),B(0,4),C(0,O),D(6,0);(2)A(3,2),B(一3,2),C(-3,-2),D(3,-2)23.△CDE 为等腰三角形24.(1)成人8人,学生4人 (2)买团体票需252元,即买团体票省钱25.(1))1)(1)(1(32a a a a -++;(2))1)(1(222x x x x a -+++; (3))1)(1)(9(2-++x x x .。
九年级数学总复习12.pdf
A (1,2) y = n
x
O
x
B
如
图
1
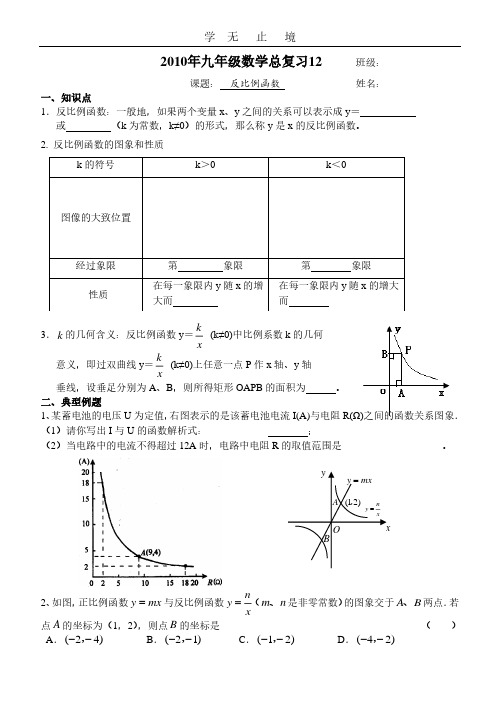
2、如图,正比例函数 y = mx 与反比例函数 y = n( m、n 是非零常,数)的图象交于 A、B 两点.若
x
正
点 A 的坐标为(1,2),则点 B 的坐标是
A. (−2,− 4)
B. (−2,−1)
C. (−1,− 2)
比
例 D. (−4,− 2)
()
6.如图,某个反比例函数的图象经过点 P,则它的解析式为
y
()
A.y= 1 (x>0) x
C.y= 1 (x<0) x
B.y=- 1 (x>0) x
D.y=- 1 (x<0) x
P1 -1 O x
学无 止 境 7.过反比例函数 y = k (k 0) 的图象上的一点分别作 x、y 轴的垂线段,如果垂线段与 x、y 轴
x
点 A 的坐标为(-2,4),点 B 的横坐标为-4。 (1)试确定反比例函数的关系式; (2)求△AOC 的面积.
17.如图,点 A(m,m+1),B(m+3,m-1)都在反比例函数 y = k 的图象上.
x
y
(1)求 m,k 的值;
(2)如果 M 为 x 轴上一点,N 为 y 轴上一点,以点 A,B,M,N
像上,则点 C 的坐标是
.
12.两个反比例函数 y = k 和 y = 1 在第一象限内的图象如图所示,点 P 在 y = k 的图象上,PC⊥x
x
x
x
轴于点 C,交 y = 1 的图象于点 A,PD⊥y 轴于点 D,交 y = 1 的图象于点 B,当点 P 在 y = k
x
九年级数学总复习(七)(12-13下)
九年级数学总复习(七) 第1页 (共4页)图52011—2012学年度下期九年级数学总复习题(七)(平行线与三角形)班级 姓名一、填空题。
(每小题3分,共36分)1.如图1,在△ABC 中,D 、E 分别是边AC 、BC 的中点,若DE=4,则AB= 。
2.如图2所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:_________________________________。
3.三条直线两两相交,最少_______有个交点,最多有____________个交点。
4.如图3所示,∠BAC=90°,EF ∥BC ,∠1=∠B ,则∠DEC=___________。
5.如图4,D 是△ABC 内一点,延长BD 交AC 于E ,用“>”表示∠1、∠2、∠A 的关系______________________。
6.△ABC 中∠A=50°,∠ABC 与∠ACB 的平分线交于点I ,则∠BIC=_________。
7.在△ABC 中,BC=8,AB 的垂直平分线交AB 于D ,交边AC 于点E ,△BCE 的周长等于20cm ,则AC= 。
8.已知等腰△ABC 内接于半径为5的⊙O ,如果底边BC 的长为8,则BC 边上的高 为 。
9.等边三角形的内切圆面积为9π,则△ABC 的周长为 。
10.如图5,△ABC 中,DE 垂直平分AC 交AB 于E , ∠A=30°,∠ACB=80°,则∠BCE= 。
11.如图6所示,BD 是△ABC 的角平分线,∠ABD=36°, ∠C=72°,则图中的等腰三角形有 个。
图1 图3 图4 21E D C BA 1FE D C B A图 6九年级数学总复习(七) 第2页 (共4页)12.如图7,给出五个等量关系:(1)AD=BC ;(2)AC=BD ;(3)CE=DE ;(4)∠D=∠C ;(5)∠DAB=∠CBA 。
人教版九年级数学中考总复习 第12课时 二次函数 含解析及答案

第12课时 二次函数知能优化训练一、中考回顾1.(2021浙江中考)关于二次函数y=2(x-4)2+6的最大值或最小值,下列说法正确的是( ) A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值62.(2021天津中考)已知抛物线y=ax 2+bx+c (a ,b ,c 是常数,a ≠0)经过点(-1,-1),(0,1),当x=-2时,与其对应的函数值y>1.有下列结论: ①abc>0;②关于x 的方程ax 2+bx+c-3=0有两个不等的实数根; ③a+b+c>7.其中,正确结论的个数是( ) A.0 B.1 C.2 D.33.(2021安徽中考)设抛物线y=x 2+(a+1)x+a ,其中a 为实数. (1)若抛物线经过点(-1,m ),则m= ;(2)将抛物线y=x 2+(a+1)x+a 向上平移2个单位长度,所得抛物线顶点的纵坐标的最大值是 .(2)24.(2021江苏连云港中考)某快餐店销售A,B 两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A 种快餐的利润,同时提高每份B 种快餐的利润.售卖时发现,在一定范围内,每份A 种快餐利润每降1元可多卖2份,每份B 种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是 元.5.(2020天津中考)已知点A (1,0)是抛物线y=ax 2+bx+m (a ,b ,m 为常数,a ≠0,m<0)与x 轴的一个交点. (1)当a=1,m=-3时,求该抛物线的顶点坐标;(2)若抛物线与x 轴的另一个交点为M (m ,0),与y 轴的交点为C ,过点C 作直线l 平行于x 轴,E 是直线l 上的动点,F 是y 轴上的动点,EF=2√2.①当点E 落在抛物线上(不与点C 重合),且AE=EF 时,求点F 的坐标; ②取EF 的中点N ,当m 为何值时,MN 的最小值是√22当a=1,m=-3时,抛物线对应函数的解析式为y=x 2+bx-3.∵抛物线经过点A (1,0),∴0=1+b-3,解得b=2.∴抛物线对应函数的解析式为y=x 2+2x-3.∵y=x 2+2x-3=(x+1)2-4, ∴抛物线的顶点坐标为(-1,-4).(2)①∵抛物线y=ax 2+bx+m 经过点A (1,0)和M (m ,0),m<0,∴0=a+b+m ,0=am 2+bm+m ,即am+b+1=0.∴a=1,b=-m-1.∴抛物线对应函数的解析式为y=x 2-(m+1)x+m ,根据题意,得点C (0,m ),点E (m+1,m ).过点A 作AH ⊥l 于点H (图略).由点A (1,0),得点H (1,m ).在Rt △EAH 中,EH=1-(m+1)=-m ,HA=0-m=-m , ∴AE=√EH 2+HA 2=-√2m.∵AE=EF=2√2,∴-√2m=2√2,解得m=-2.此时,点E (-1,-2),点C (0,-2),有EC=1.∵点F 在y 轴上,∴在Rt △EFC 中,CF=√EF 2-EC 2=√7.∴点F 的坐标为(0,-2-√7)或(0,-2+√7). ②由N 是EF 的中点,得CN=12EF=√2.根据题意,点N 在以点C 为圆心、√2为半径的圆上.由点M (m ,0),点C (0,m ),得MO=-m ,CO=-m.∴在Rt △MCO 中,MC=√MO 2+CO 2=-√2m.当MC ≥√2,即m ≤-1时,满足条件的点N 落在线段MC 上,MN 的最小值为MC-NC=-√2m-√2=√22,解得m=-32;当MC<√2,即-1<m<0时,满足条件的点N 落在线段CM 的延长线上,MN 的最小值为NC-MC=√2-(-√2m )=√22,解得m=-12.∴当m 的值为-32或-12时,MN 的最小值是√22.二、模拟预测1.已知二次函数y=kx 2-6x+3的图象与x 轴有公共点,则k 的取值范围是( )A.k<3B.k<3,且k ≠0C.k ≤3D.k ≤3,且k ≠02.函数y=kx 与y=-kx 2-k (k ≠0)在同一平面直角坐标系中的大致图象可能是( )3.如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=1,与y轴交于点C,与x轴交于点A,点B(-1,0),则①二次函数的最大值为a+b+c;②a-b+c<0;③b2-4ac<0;④当y>0时,-1<x<3.其中正确的个数是()A.1B.2C.3D.44.小明在用描点法画二次函数y=ax2+bx+c的图象时,列了如下表格:根据表格中的信息回答问题:该二次函数y=ax2+bx+c在x=3时,y=.45.若y关于x的函数y=kx2+2x-1的图象与x轴仅有一个公共点,则实数k的值为.0或k=-16.已知二次函数y=-x2+bx+c的图象如图所示,若将其向左平移2个单位长度,再向下平移3个单位长度,则平移后图象对应函数的解析式为.2-2x7.如图①,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们把这样的两抛物线L1,L2互称为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有很多条.(1)如图②,已知抛物线L3:y=2x2-8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的对称点D的坐标;(2)请求出以点D为顶点的L3的“友好”抛物线L4对应函数的解析式,并指出L3与L4对应函数中y同时随x增大而增大的自变量的取值范围;(3)若抛物线y=a1(x-m)2+n的任意一条“友好”抛物线对应函数的解析式为y=a2(x-h)2+k,请写出a1与a2的关系式,并说明理由.∵抛物线L3:y=2x2-8x+4,∴y=2(x-2)2-4.∴顶点为(2,-4),对称轴为x=2,设x=0,则y=4,∴C(0,4).∴点C关于该抛物线对称轴对称的对称点D的坐标为(4,4).(2)∵以点D(4,4)为顶点的L3的友好抛物线L4还过点(2,-4),∴L4对应函数的解析式为y=-2(x-4)2+4.∴L3与L4对应函数中y同时随x增大而增大的自变量的取值范围是2≤x≤4.(3)a1=-a2,理由如下:由题意可得,{n=a2(m-ℎ)2+k,k=a1(ℎ-m)2+n.①②由①+②,得(a1+a2)(m-h)2=0, ∴a1=-a2.。
九年级数学总复习(九)(12-13下)

九年级数学总复习(九) 第1页 (共4页)2011—2012学年度下期九年级数学总复习题(九)(圆)班级 姓名一、填空题。
(每小题3分,共36分)1.半径为1的⊙O 中,弦AB 、AC 长分别为3、2,则∠BAC= °。
2.已知一圆锥的底面半径是1,母线长是4,它的侧面积是 ______。
3.如图1,已知△ABC ,AC=BC=6,∠C=90°。
O 是AB 的中点,⊙O 与AC 、BC 分别相切于点D 与点E 。
点F 是⊙O 与AB 的一个交点,连DF 并延长交CB 的延长线于点G 。
则CG= 。
4.⊙O 的半径为3cm ,点M 是⊙O 外一点,OM =4 cm ,则以M 为圆心且与⊙O 相切的圆的半径是 cm 。
5.一圆弧半径为2cm ,弧长为π32cm ,则弧所对的圆心角为 。
6.已知扇形的面积为12π,半径等于6,则它的圆心角等于 度。
7.如图2,AB 切⊙O 于点B ,AB=4cm ,AO=6cm ,则⊙O 的半径为 cm 。
8.如图3,⊙O 的弦AB=8,M 是AB 的中点,且OM=3,则⊙O 的半径= 。
9.如图4,分别以A 、B 为圆心,线段AB 的长为半径的两个圆相交于C 、D 两点, 则∠CAD 的度数为 。
10.如图5,AB 为⊙O 的直径, AB=AC ,BC 交⊙O 于点D , AC 交⊙O 于点E ,∠BAC=45°。
给出以下五个结论:①∠EBC=22.5°;②BD=DC ;③AE=2EC ;④劣弧AE 是劣弧DE 的2倍;⑤AE=BC 。
其中正确结论的序号是 。
11.如图6,从P 点引⊙O 的两切线PA 、PB ,A 、B 为切点,已知⊙O 的半径为2,∠P=60°,则图中阴影部分的面积为 。
12.如图7,三个半圆依次相外切,它们的圆心都在x 轴的正半轴上并与直线x y 33=相切,设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1、r 2、r 3、则当r 1=1时,r 2= 。
2021年九年级数学中考一轮复习:第12章一次函数 训练

2021年中考一轮复习数学沪科版:第12章训练一、选择题(本大题共10小题,每小题4分,满分40分) 1.下列函数中,自变量x 的取值范围是x ≥3的是( ) A.y=1x -3 B.y=√x -3C.y=x-3D.y=√x -32.一次函数y=-2x-6的图象不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3.已知整数x 满足0≤x ≤5,y 1=x+2,y 2=-2x+5,对任意一个x ,y 1与y 2中的较大值用m 表示,则m 的最小值是( ) A.3 B.5 C.7 D.24.点A (-5,y 1)和B (-2,y 2)都在直线y=-12x-3上,则y 1与y 2的关系是( ) A.y 1≤y 2B.y 1>y 2C.y 1<y 2D.y 1=y 25.下列图形可以表示一次函数y=ax+b 与正比例函数y=abx (a ,b 是常数,且ab ≠0)的图象的是( )6.如图,函数y=ax+b 和y=-13x 的图象相交于点P ,则根据图象可得,关于x ,y 的二元一次方程组{-ax +y =b ,x +3y =0的解是( )A.{x =3y =-1 B.{x =-3y =-1 C.{x =-3y =1 D.{x =-1y =3 7.直线y=kx+b 经过点(0,-3),且与两坐标轴构成直角三角形的面积是6,则k 的值为( ) A.34 B.-34C.43D.±348.李师傅一家开车去旅游,出发前查看了油箱里有50 L油,出发后先后走了城市路、高速路、山路最终到达旅游地点,下面的两幅图分别描述了行驶里程及耗油情况.下面的描述中错误的是()A.此车一共行驶了210 kmB.此车高速路一共用了12 L油C.此车在城市路和山路的平均速度相同D.以此车在这三个路段的综合油耗判断50 L油可以行驶约525 km9.已知A,B两地相距120 km,甲、乙两人沿同一条公路从A地出发到B地,甲骑摩托车,乙骑自行车,图中DE,OC分别表示甲、乙离开A地的路程s(km)与时间t(h)的函数关系的图象.设在这个过程中,甲、乙两人相距y km,则y关于t的函数图象是()10.如图,矩形ABCD的顶点坐标分别为A(1,1),B(3,1),C(3,4),D(1,4),一次函数y=2x+b的图象与长方形ABCD的边有公共点,则b的取值范围是()A.b≤-2或b≥-1B.b≤-5或b≥2C.-2≤b≤-1D.-5≤b≤2二、填空题(本大题共4小题,每小题4分,满分16分)11.某店销售某品牌化妆品,将一种套装产品按成本价加价30%出售,在促销活动期间,直接打8折再减8元,写出销售一套这种产品的利润P(元)与成本x(元)之间的函数表达式为. 12.下列表格描述的是y与x之间的函数关系:x…-2 0 2 4 …y=kx+b… 3 -1 m n…则m与n的大小关系是.13.一次函数y1=mx+n与y2=-x+a的图象如图所示,则0<mx+n<-x+a的解集为.14.如图,八个边长为1的小正方形摆放在平面直角坐标系中,经过点P的一条直线l将这八个小正方形分成面积相等的两部分,则该直线l的表达式为.三、解答题(本大题共5小题,满分44分)15.(8分)某剧院的观众席的座位为扇形,且按下列方式设置:排数x 1 2 3 4 …座位数y50 53 56 59 …(1)按照上表所示的规律,当x每增加1时,y如何变化?(2)写出座位数y与排数x之间的表达式.(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.16.(8分)如图,在平面直角坐标系中,一次函数y=kx+b 的图象经过点A (-2,6),且与x 轴相交于点B ,与正比例函数y=3x 的图象相交于点C ,点C 的横坐标为1.(1)求k ,b 的值;(2)若点D 在y 轴负半轴上,且满足S △COD =13S △BOC ,求点D 的坐标.17.(8分)如图,直线l 1,l 2相交于点A ,l 1与x 轴的交点坐标为(-1,0),l 2与y 轴的交点坐标为(0,-2),结合图象解答下列问题:(1)求出直线l 2表示的一次函数的表达式.(2)直接写出当x 为何值时,直线l 1所对应的函数值大于直线l 2所对应的函数值? (3)当x 为何值时,l 1,l 2表示的两个一次函数的函数值都大于0?18.(10分)实验学校八年级(2)班的学生要去实验基地进行实践活动,估计乘车人数是10到30人,现在欲租甲、乙两家旅行社的车辆.已知甲、乙两家旅行社的服务质量相同,且报价都是每人100元,经过协商,甲旅行社表示可给予每位学生六折优惠,乙旅行社表示可先免去两位学生的车费,然后给予其他学生七折优惠.(1)若用x表示乘车人数,请用x表示选择甲、乙旅行社的费用y甲与y乙.(2)请你帮助学校选择哪一家旅行社费用更合算?19.(10分)甲、乙两人驾车都从P地出发,沿一条笔直的公路匀速前往Q地,乙先出发一段时间后甲再出发,甲、乙两人到达Q地后均停止.已知P,Q两地相距200 km,设乙行驶的时间为t h,甲、乙两人之间的距离为y km,表示y与t的函数关系的部分图象如图所示.请解决以下问题:(1)由图象可知,甲比乙迟出发h,图中线段BC所在直线的函数表达式为.(2)设甲的速度为v1 km/h,求出v1的值;(3)根据题目信息补全函数图象(不需要写出分析过程,但必须标明关键点的坐标),并求出当甲、乙两人相距32 km时t的值.答案一、选择题(本大题共10小题,每小题4分,满分40分)题 号 1 2 3 4 5 6 7 8 9 10 答 案D A A B A C D C B D1.下列函数中,自变量x 的取值范围是x ≥3的是 A.y=1x -3 B.y=√x -3C.y=x-3D.y=√x -32.一次函数y=-2x-6的图象不经过A.第一象限B.第二象限C.第三象限D.第四象限3.已知整数x 满足0≤x ≤5,y 1=x+2,y 2=-2x+5,对任意一个x ,y 1与y 2中的较大值用m 表示,则m 的最小值是 A.3 B.5 C.7D.24.点A (-5,y 1)和B (-2,y 2)都在直线y=-12x-3上,则y 1与y 2的关系是 A.y 1≤y 2B.y 1>y 2C.y 1<y 2D.y 1=y 25.下列图形可以表示一次函数y=ax+b 与正比例函数y=abx (a ,b 是常数,且ab ≠0)的图象的是6.如图,函数y=ax+b 和y=-13x 的图象相交于点P ,则根据图象可得,关于x ,y 的二元一次方程组{-ax +y =b ,x +3y =0的解是A.{x =3y =-1 B.{x =-3y =-1C.{x=-3y=1 D.{x=-1y=37.直线y=kx+b经过点(0,-3),且与两坐标轴构成直角三角形的面积是6,则k的值为A.34B.-34C.43D.±348.李师傅一家开车去旅游,出发前查看了油箱里有50 L油,出发后先后走了城市路、高速路、山路最终到达旅游地点,下面的两幅图分别描述了行驶里程及耗油情况.下面的描述中错误的是A.此车一共行驶了210 kmB.此车高速路一共用了12 L油C.此车在城市路和山路的平均速度相同D.以此车在这三个路段的综合油耗判断50 L油可以行驶约525 km9.已知A,B两地相距120 km,甲、乙两人沿同一条公路从A地出发到B地,甲骑摩托车,乙骑自行车,图中DE,OC分别表示甲、乙离开A地的路程s(km)与时间t(h)的函数关系的图象.设在这个过程中,甲、乙两人相距y km,则y关于t的函数图象是10.如图,矩形ABCD 的顶点坐标分别为A (1,1),B (3,1),C (3,4),D (1,4),一次函数y=2x+b 的图象与长方形ABCD 的边有公共点,则b 的取值范围是A.b ≤-2或b ≥-1B.b ≤-5或b ≥2C.-2≤b ≤-1D.-5≤b ≤2二、填空题(本大题共4小题,每小题4分,满分16分)11.某店销售某品牌化妆品,将一种套装产品按成本价加价30%出售,在促销活动期间,直接打8折再减8元,写出销售一套这种产品的利润P (元)与成本x (元)之间的函数表达式为P=0.04x-8 .12.下列表格描述的是y 与x 之间的函数关系:x … -2 0 2 4 … y=kx +b… 3 -1 m n …则m 与n 的大小关系是 m>n .13.一次函数y 1=mx+n 与y 2=-x+a 的图象如图所示,则0<mx+n<-x+a 的解集为 2<x<3 .14.如图,八个边长为1的小正方形摆放在平面直角坐标系中,经过点P 的一条直线l 将这八个小正方形分成面积相等的两部分,则该直线l 的表达式为 y=58x+12 .三、解答题(本大题共5小题,满分44分)15.(8分)某剧院的观众席的座位为扇形,且按下列方式设置:排数x 1 2 3 4 … 座位数y50 53 56 59 …(1)按照上表所示的规律,当x 每增加1时,y 如何变化? (2)写出座位数y 与排数x 之间的表达式.(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由. 解:(1)当x 每增加1时,y 增加3. (2)y=50+3(x-1)=3x+47. (3)某一排不可能有90个座位. 理由:由3x+47=90,解得x=433.因为x 不是整数,所以一排不可能有90个座位.16.(8分)如图,在平面直角坐标系中,一次函数y=kx+b 的图象经过点A (-2,6),且与x 轴相交于点B ,与正比例函数y=3x 的图象相交于点C ,点C 的横坐标为1.(1)求k ,b 的值;(2)若点D 在y 轴负半轴上,且满足S △COD =13S △BOC ,求点D 的坐标. 解:(1)当x=1时,y=3x=3,所以点C 的坐标为(1,3). 将点A (-2,6),C (1,3)代入y=kx+b , 得{-2k +b =6,k +b =3,解得{k =-1,b =4.(2)当y=0时,-x+4=0,解得x=4,所以点B 的坐标为(4,0). 设点D 的坐标为(0,m )(m<0),因为S △COD =13S △BOC ,即-12m=13×12×4×3,解得m=-4,所以点D 的坐标为(0,-4).17.(8分)如图,直线l 1,l 2相交于点A ,l 1与x 轴的交点坐标为(-1,0),l 2与y 轴的交点坐标为(0,-2),结合图象解答下列问题:(1)求出直线l 2表示的一次函数的表达式.(2)直接写出当x 为何值时,直线l 1所对应的函数值大于直线l 2所对应的函数值? (3)当x 为何值时,l 1,l 2表示的两个一次函数的函数值都大于0?解:(1)易得直线l 2表示的一次函数的表达式为y=52x-2. (2)x<2.(3)从图象可以知道:当x>-1时,直线l 1表示的一次函数的函数值大于0; 当52x-2=0时,解得x=45,所以当x>45时,直线l 2表示的一次函数的函数值大于0. 综上可知,当x>45时,直线l 1,l 2表示的两个一次函数的函数值都大于0.18.(10分)实验学校八年级(2)班的学生要去实验基地进行实践活动,估计乘车人数是10到30人,现在欲租甲、乙两家旅行社的车辆.已知甲、乙两家旅行社的服务质量相同,且报价都是每人100元,经过协商,甲旅行社表示可给予每位学生六折优惠,乙旅行社表示可先免去两位学生的车费,然后给予其他学生七折优惠.(1)若用x 表示乘车人数,请用x 表示选择甲、乙旅行社的费用y 甲与y 乙. (2)请你帮助学校选择哪一家旅行社费用更合算? 解:(1)由题意可得y 甲=100x×0.6=60x ,y 乙=100(x-2)×0.7=70x-140, 即y 甲=60x ,y 乙=70x-140.(2)当y 甲<y 乙时,60x<70x-140,解得x>14,即当乘车人数超过14人时,选择甲旅行社比较合算; 当y 甲=y 乙时,60x=70x-140,解得x=14,即当乘车人数为14人时,选择甲旅行社和乙旅行社花费一样;当y 甲>y 乙时,60x>70x-140,解得x<14,即当乘车人数少于14人时,选择乙旅行社比较合算.19.(10分)甲、乙两人驾车都从P 地出发,沿一条笔直的公路匀速前往Q 地,乙先出发一段时间后甲再出发,甲、乙两人到达Q 地后均停止.已知P ,Q 两地相距200 km,设乙行驶的时间为t h,甲、乙两人之间的距离为y km,表示y 与t 的函数关系的部分图象如图所示.请解决以下问题:(1)由图象可知,甲比乙迟出发 1 h,图中线段BC 所在直线的函数表达式为 y=15t-40 .(2)设甲的速度为v 1 km/h,求出v 1的值;(3)根据题目信息补全函数图象(不需要写出分析过程,但必须标明关键点的坐标),并求出当甲、乙两人相距32 km 时t 的值.解:(2)设甲的速度为v 1 km/h,乙的速度为v 2 km/h,由题意,得{83v 2=(83-1)v 1,(5-83)(v 1-v 2)=35,解得{v 1=40,v 2=25. 答:甲的速度为40 km/h .(3)如图所示:根据题意,得40(t-1)-25t=32或25t=200-32,解得t=4.8或6.72.答:当甲、乙两人相距32 km 时,t 的值为4.8或6.72.。
(word完整版)九年级数学总复习试卷及参考答案

九年级数学总复习练习卷一.选择题(共10小题)1.在Rt△ABC中,∠C=90°,cosA=,则tanB等于()A.B.C.D.2.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C对边,如果3a=4b,则cosB的值是()A.B.C.D.3.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列关系中错误的是()A.b=c•cosB B.b=a•tanB C.b=c•sinB D.a=b•tanA 4.一斜坡的坡度是1:,则此斜坡的坡角是()A.15°B.30°C.45°D.60°5.∠A为锐角,若cosA=,则∠A的度数为()A.75°B.60°C.45°D.30°6.如图,在△ABC中,∠C=90°,AB=10,BC=8,则sin∠A=()A.B.C.D.7.在Rt△ABC中∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,c=3a,tanA 的值为()A.B.C.D.38.已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AB等于()A.6B.C.10D.129.在Rt△ABC中,∠C=90°,∠B=25°,AB=5,则BC的长为()A.5sin25°B.5tan65°C.5cos25°D.5tan25°10.南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向10(1+)海里的C处,为了防止某国海巡警干扰,请求我A处的渔监船前往C处护航.如图,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A 和C之间的距离为()A.10海里B.20海里C.20海里D.10海里二.填空题(共6小题)11.已知α为锐角,且sinα=cosα,则α=.12.如果α是锐角,且cotα=tan25°,那么α=度.13.小明同学沿坡度为i=1:的山路向上行走了100米,则小明上升的高度是米.14.若tanα=5,则=.15.如图是某幼儿园的滑滑梯的简易图,已知滑坡AB的坡度是1:3,滑坡的水平宽度是6m,则高BC为m.16.小明沿着坡度为1:的坡面向上走了300米,此时小明上升的垂直高度为米.三.解答题(共11小题)17.如图,某渔船向正东方向航行,在B处测得A岛在北偏东的45°方向,岛C在B处的正东方向且相距30海里,从岛C测得A岛在北偏西的60°方向,已知A岛周围8海里内有暗礁.如果渔船继续向东航行,有无触礁危险?(≈1.4,≈1.7)18.计算:在一次数学社团活动课上,同学们测量一座古塔CD的高度,他们首先在A处安置测量器,测得塔顶C的仰角∠CFE=30°,然后往塔的方向前进100米到达B处,此时测得塔顶C的仰角∠CGE=60°,已知测量器高1.5米,请你根据以上数据计算出古塔CD的高度.(保留根号)19.如图,在Rt△ABC中,∠C=90°,BC=6,tan∠A=.求AB的长和sin∠B 的值.20.计算:﹣sin30°(cos45°﹣sin60°)21.计算:(1)sin260°﹣tan30°•cos30°+tan45°(2)cos245°+sin245°+sin254°+cos25422.如图,学校的实验楼对面是一幢教工宿舍楼,小敏在实验楼的窗口C测得教工宿台楼顶部D仰角为15°,教学楼底部B的俯角为22°,量得实验楼与教学楼之间的距离AB=30m.(1)求∠BCD的度数.(2)求教工宿舍楼的高BD.(结果精确到0.1m,参考数据:tanl5°≈0.268,tan22°=0.404)23.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.25.阅读理解:我们已经学习的直角三角形知识包括:勾股定理,30°、45°特殊角的直角三角形的边之间的关系等,在解决初中数学问题上起到重要作用,锐角三角函数是另一个研究直角三角形中边角间关系的知识,通过锐角三角函数也可以帮助解决数学问题.阅读下列材料,完成习题:如图1,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A 的正弦(sine),记作sinA,即sinA==例如:a=3,c=7,则sinA=问题:在Rt△ABC中,∠C=90°(1)如图2,BC=5,AB=8,求sinA的值.(2)如图3,当∠A=45°时,求sinB的值.(3)AC=2,sinB=,求BC的长度.26.济南市纬十二路的一座过街天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.(1)求新坡面的坡角a;(2)原天桥底部正前方7米处(PB的长)有一文化墙PM,若新坡面下A 处与文化墙之间需留下至少3米宽的人行道,问文化墙是否需要拆除?请说明理由.(约为1.732)27.阅读下列材料,并完成相应的任务.初中阶段,我们所学的锐角三角函数反映了直角三角形中的边角关系:sinα=cosα=tanα=一般地,当α、β为任意角时,sin(α+β)与sin(α﹣β)的值可以用下面的公式求得:sin(α+β)=sinαcosβ+cosαsinβsin(α﹣β)=sinαcosβ﹣cosαsinβ例如sin15°=sin(45°﹣30°)=sin45°cos30°﹣cos45°sin30°=根据上述材料内容,解决下列问题:(1)计算:sin75°=;(2)在Rt△ABC中,∠A=75°,∠C=90°,AB=4,请你求出AC和BC的长.九年级数学总复习练习卷一.选择题(共10小题)1.在Rt△ABC中,∠C=90°,cosA=,则tanB等于()A.B.C.D.【分析】根据题意画出图形,进而表示出AC,BC,AB的长,进而求出答案.【解答】解:如图所示:∵cosA=,∴设AC=7x,AB=25x,则BC=24x,则tanB=.故选:C.【点评】此题主要考查了互余两角三角函数关系,正确表示出三角形各边长是解题关键.2.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C对边,如果3a=4b,则cosB的值是()A.B.C.D.【分析】根据锐角三角函数的定义可得cosB=,然后根据题目所给3a=4b 可求解.【解答】解:因为在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C 对边,如果3a=4b,令b=3x,则a=4x,所以c=5x,所以cosB=故选:D.【点评】本题考查了锐角三角函数的定义,解答本题的关键是掌握cosB=,3.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列关系中错误的是()A.b=c•cos B B.b=a•tanB C.b=c•sinB D.a=b•tanA 【分析】本题可以利用锐角三角函数的定义求解即可.【解答】解:在Rt△ABC中,∠C=90°,则tanA=,tanB=,cosB=,stnB=;因而b=c•sinB=a•tanB,a=b•tanA,错误的是b=c•cosB.故选:A.【点评】利用锐角三角函数的定义,正确理解直角三角形边角之间的关系.在直角三角形中,如果已知一边及其中的一个锐角,就可以表示出另外的边.4.一斜坡的坡度是1:,则此斜坡的坡角是()A.15°B.30°C.45°D.60°【分析】坡度=坡角的正切值,依此求出坡角的度数.【解答】解:设坡角为α,由题意知:tanα==,∴∠α=30°.即斜坡的坡角为30°.故选:B.【点评】此题考查的是解直角三角形的应用﹣坡度坡角问题,坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=h:l=tanα.5.∠A为锐角,若cosA=,则∠A的度数为()A.75°B.60°C.45°D.30°【分析】根据特殊角的三角函数值求解.【解答】解:∵∠A为锐角,cosA=,∴∠A=60°.故选:B.【点评】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.6.如图,在△ABC中,∠C=90°,AB=10,BC=8,则sin∠A=()A.B.C.D.【分析】根据锐角的正弦等于对边比斜边列式计算即可得解.【解答】解:∵∠C=90°,AB=10,BC=8,∴在Rt△ABC中,sinA===,故选:A.【点评】本题考查的是锐角三角函数的定义,掌握锐角A的对边a与斜边c 的比叫做∠A的正弦是解题的关键.7.在Rt△ABC中∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,c=3a,tanA 的值为()A.B.C.D.3【分析】根据锐角三角函数的定义即可求出答案.【解答】解:由题意可知:sinA===,∴tanA==,故选:B.【点评】本题考查锐角三角函数,解题的关键是熟练运用锐角三角函数的定义,本题属于基础题型.8.已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AB等于()A.6B.C.10D.12【分析】根据锐角三角函数的定义即可求出答案.【解答】解:∵tanA=,∴sinA=,∴=,∴AB=10,故选:C.【点评】本题考查锐角三角函数,解题的关键是熟练运用锐角三角函数的定义,本题属于基础题型.9.在Rt△ABC中,∠C=90°,∠B=25°,AB=5,则BC的长为()A.5sin25°B.5tan65°C.5cos25°D.5tan25°【分析】在Rt△ABC中,由AB及∠B的值,可求出BC的长.【解答】解:在Rt△ABC中,∠C=90°,∠B=25°,AB=5,∴BC=AB•cos∠B=5cos25°.故选:C.【点评】本题考查了解直角三角形,牢记直角三角形中边角之间的关系是解题的关键.10.南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向10(1+)海里的C处,为了防止某国海巡警干扰,请求我A处的渔监船前往C处护航.如图,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A 和C之间的距离为()A.10海里B.20海里C.20海里D.10海里【分析】过点A作AD⊥BC于点D,设AD=x,则CD=x,AC=x,BD=x,结合BC=10(1+)即可求出x的值,进而即可得出A和C之间的距离.【解答】解:过点A作AD⊥BC于点D,如图所示.设AD=x,则CD=x,AC=x,BD=x.∵BC=BD+CD=(+1)x=10(1+),∴x=10,∴AC=10.故选:A.【点评】本题考查了解直角三角形的应用﹣方向角问题,通过解一元一次方程求出AD的长度是解题的关键.二.填空题(共6小题)11.已知α为锐角,且sinα=cosα,则α=45°.【分析】根据一个角的正弦等于这个角的余角的余弦解答.【解答】解:∵sinα=cos(90°﹣α),∴α=90°﹣α,解得,α=45°,故答案为:45°.【点评】本题考查的是同角三角函数的关系,掌握一个角的正弦等于这个角的余角的余弦是解题的关键,12.如果α是锐角,且cotα=tan25°,那么α=65度.【分析】依据α是锐角,且cotα=tan25°,即可得出α=65°.【解答】解:∵α是锐角,且cotα=tan25°,∴α=65°,故答案为:65.【点评】本题主要考查了互余两角三角函数的关系,若∠A+∠B=90°,那么sinA=cosB或sinB=cosA.13.小明同学沿坡度为i=1:的山路向上行走了100米,则小明上升的高度是50米.【分析】由斜坡的坡度i=1:=,可得坡角α的度数,再求得斜坡的正弦值sinα,那么它垂直上升的高度可利用正弦函数求得.【解答】解:∵斜坡的坡度i=1:=,∴坡角α=60°,∴斜坡的正弦值sinα=,∴小明上升的高度是100×sinα=50(米).故答案为50.【点评】本题考查了解直角三角形的应用﹣﹣﹣坡度坡角问题,根据坡度求出坡角是解题的关键.坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=h:l=tanα.14.若tanα=5,则=.【分析】根据同角的三角函数的关系即可求出答案.【解答】解:原式=∵tanα=5,∴原式=故答案为:【点评】本题考查同角三角函数的关系,解题的关键熟练运用同角三角函数的关系,本题属于基础题型.15.如图是某幼儿园的滑滑梯的简易图,已知滑坡AB的坡度是1:3,滑坡的水平宽度是6m,则高BC为2m.【分析】根据滑坡的坡度及水平宽,可求出坡面的铅直高度,此题得解.【解答】解:∵滑坡AB的坡度是1:3,滑坡的水平宽度是6m,∴AC=6m,∴BC=×6=2m.故答案为:2.【点评】本题考查了解直角三角形的应用中的坡度坡角问题,牢记坡度的定义是解题的关键.16.小明沿着坡度为1:的坡面向上走了300米,此时小明上升的垂直高度为150米.【分析】根据坡度算出坡角的度数,利用坡角的正弦值即可求解.【解答】解:∵坡度tanα==1:=,∴α=30°.∴上升的垂直高度=坡长×sin30°=300×=150(米).故答案为150.【点评】此题考查了解直角三角形的应用﹣坡度坡角问题,坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=h:l=tanα.掌握坡度、坡角的定义是解答本题的关键.三.解答题(共11小题)17.如图,某渔船向正东方向航行,在B处测得A岛在北偏东的45°方向,岛C在B处的正东方向且相距30海里,从岛C测得A岛在北偏西的60°方向,已知A岛周围8海里内有暗礁.如果渔船继续向东航行,有无触礁危险?(≈1.4,≈1.7)【分析】判断渔船有无危险只要求出点A到BC的距离,与8海里比较大小就可以.【解答】解:若渔船继续向东航行,无触礁的危险.理由如下:如图,过点A作AD⊥BC于点D.由题意得:∠ABD=45°,∠ACD=30°.设AD=x海里.在Rt△ABD中,∵∠ABD=45°,∴BD=AD=x海里.在Rt△ACD中,∵∠ACD=30°,∴CD=AD=x海里.∵BD+DC=30,∴x+x=30,解得x=15(﹣1),17(﹣1)≈10.5>8,即:若渔船继续向东航行,无触礁危险.【点评】本题考查了解直角三角形的应用﹣方向角问题,特殊角的三角函数等知识,解题的关键是添加辅助线构造直角三角形,把实际问题转化为解直角三角形问题,属于中考常考题型.18.计算:在一次数学社团活动课上,同学们测量一座古塔CD的高度,他们首先在A处安置测量器,测得塔顶C的仰角∠CFE=30°,然后往塔的方向前进100米到达B处,此时测得塔顶C的仰角∠CGE=60°,已知测量器高1.5米,请你根据以上数据计算出古塔CD的高度.(保留根号)【分析】先分析图形,根据题意构造直角三角形.本题涉及到两个直角三角形△CEF、△CGE,利用其公共边CE构造等量关系,借助FG=EF﹣GE=100,构造关系式求解.【解答】解:由题意知CD⊥AD,EF∥AD.∴∠CEF=90°.设CE=x米,∵在Rt△CEF中,tan∠CFE=,∴EF===x,∵在Rt△CEG中,tan∠CGE=,∴GE===x.∵FG=EF﹣GE=100,∴x﹣x=100,解得x=50.∴CD=CE+ED=50+1.5(米).答:古塔CD的高度是(50+1.5)米.【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,此类题目要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.19.如图,在Rt△ABC中,∠C=90°,BC=6,tan∠A=.求AB的长和sin∠B 的值.【分析】根据∠A的正切值用BC表示出AC,再利用勾股定理列式求解即可得到BC的长,然后求出AB的长,再根据锐角的正弦等于对边比斜边列式计算即可得解.【解答】解:∵在Rt△ABC中,∠C=90°,BC=6,tan∠A==,∴AC=12,∴AB===6,∴sin∠B===.【点评】本题考查了锐角三角函数的定义,勾股定理,用BC表示出AC是解题的关键.20.计算:﹣sin30°(cos45°﹣sin60°)【分析】依据30°、45°、60°角的各种三角函数值,即可得到计算结果.【解答】解:原式=﹣(﹣)=﹣==【点评】本题主要考查了特殊角的三角函数值,其应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.21.计算:(1)sin260°﹣tan30°•cos30°+tan45°(2)cos245°+sin245°+sin254°+cos254°【分析】根据特殊角的锐角三角函数的值即可求出答案.【解答】解:(1)原式=()2﹣×+1=﹣+1=,(2)原式=(cos245°+sin245°)+(sin254°+cos254°)=1+1=2【点评】本题考查锐角三角函数的定义,解题的关键是熟练运用特殊角的锐角三角函数的定义,本题属于基础题型.22.如图,学校的实验楼对面是一幢教工宿舍楼,小敏在实验楼的窗口C测得教工宿台楼顶部D仰角为15°,教学楼底部B的俯角为22°,量得实验楼与教学楼之间的距离AB=30m.(1)求∠BCD的度数.(2)求教工宿舍楼的高BD.(结果精确到0.1m,参考数据:tanl5°≈0.268,tan22°=0.404)【分析】(1)作CH⊥BD于H,如图,利用仰角和俯角定义得到∠DCH=15°,∠BCH=22°,然后计算它们的和即可得到∠BCD的度数;(2)利用正切定义,在Rt△DCH中计算出DH=30tan15°=8.04,在Rt△BCH 中计算出BH=30tan22°=12.12,然后计算BH+DH即可得到教工宿舍楼的高BD.【解答】解:(1)作CH⊥BD于H,如图,根据题意得∠DCH=15°,∠BCH=22°,∴∠BCD=∠DCH+∠BCH=15°+22°=37°;(2)易得四边形ABHC为矩形,则CH=AB=30,在Rt△DCH中,tan∠DCH=,∴DH=30tan15°=30×0.268=8.04,在Rt△BCH中,tan∠BCH=,∴BH=30tan22°=30×0.404=12.12,∴BD=12.12+8.04=20.16≈20.1(m).答:教工宿舍楼的高BD为20.1m.【点评】本题考查了解直角三角形的应用﹣仰角俯角问题:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.23.计算:sin45°+cos45°.【分析】直接利用特殊角的三角函数值代入求出答案.【解答】解:原式=+=.【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.24.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.【分析】在Rt△BCD中由勾股定理求得BC=4,在Rt△ABC中求得AB=4,再根据三角函数的定义求解可得.【解答】解:在Rt△BCD中,∵CD=3、BD=5,∴BC===4,又AC=AD+CD=8,∴AB===4,则sinA===,cosA===,tanA===.【点评】本题主要考查锐角的三角函数的定义,解题的关键是掌握勾股定理及三角函数的定义.25.阅读理解:我们已经学习的直角三角形知识包括:勾股定理,30°、45°特殊角的直角三角形的边之间的关系等,在解决初中数学问题上起到重要作用,锐角三角函数是另一个研究直角三角形中边角间关系的知识,通过锐角三角函数也可以帮助解决数学问题.阅读下列材料,完成习题:如图1,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A 的正弦(sine),记作sinA,即sinA==例如:a=3,c=7,则sinA=问题:在Rt△ABC中,∠C=90°(1)如图2,BC=5,AB=8,求sinA的值.(2)如图3,当∠A=45°时,求sinB的值.(3)AC=2,sinB=,求BC的长度.【分析】(1)根据正弦函数的定义解答;(2)设AC=x,则BC=x,利用方程解答;(3)由锐角三角函数定义求得AB=4,然后由勾股定理解答.【解答】解:(1)sinA=;(2)在Rt△ABC中,∠A=45°,设AC=x,则BC=x,AB=,则sinB=;(3)sinB=,则AB=4,由勾股定理得:BC2=AB2﹣AC2=16﹣12=4,∴BC=2.【点评】考查了锐角三角函数定义,勾股定理,直角三角形的性质以及特殊角的三角函数值.注意:勾股定理应用的前提条件是在直角三角形中.26.济南市纬十二路的一座过街天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.(1)求新坡面的坡角a;(2)原天桥底部正前方7米处(PB的长)有一文化墙PM,若新坡面下A 处与文化墙之间需留下至少3米宽的人行道,问文化墙是否需要拆除?请说明理由.(约为1.732)【分析】(1)作CH⊥AB于H,如图,利用坡度的定义得到tan∠CAH===,然后根据特殊角的三角函数值求出∠CAH即;(2)另一条坡度定义得到tan∠CBH==,所以BH=CH=6,再利用=得到AH=6,接着计算出AB≈4.392,然后根据3+4.392>7可判断文化墙需要拆除.【解答】解:(1)作CH⊥AB于H,如图,在Rt△ACH中,∵tan∠CAH===,∴∠CAH=30°,即新坡面的坡角a为30°;(2)文化墙需要拆除.理由如下:∵tan∠CBH==,∴BH=CH=6,∵=,∴AH=CH=6≈10.392,∴AB=AH﹣BH=6﹣6=4.392,∵3+4.392>7,∴文化墙需要拆除.【点评】本题考查了解直角三角形的应用﹣坡度坡角问题:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,坡度实际就是一锐角的正切值,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.27.阅读下列材料,并完成相应的任务.初中阶段,我们所学的锐角三角函数反映了直角三角形中的边角关系:sinα=cosα=tanα=一般地,当α、β为任意角时,sin(α+β)与sin(α﹣β)的值可以用下面的公式求得:sin(α+β)=sinαcosβ+cosαsinβsin(α﹣β)=sinαcosβ﹣cosαsinβ例如sin15°=sin(45°﹣30°)=sin45°cos30°﹣cos45°sin30°=根据上述材料内容,解决下列问题:(1)计算:sin75°=;(2)在Rt△ABC中,∠A=75°,∠C=90°,AB=4,请你求出AC和BC的长.【分析】(1)根据公式可求.(2)根据锐角的三角函数值,求AC和BC的值.【解答】解:(1)sin75°=sin(30°+45°)=sin30°cos45°+cos30°sin45°=×+×=,故答案为:.(2)Rt△ABC中,∵sin∠A=sin75°==∴BC=AB×=4×=∵∠B=90﹣∠A∴∠B=15°∵sin∠B=sin15°==∴AC=AB×=【点评】本题考查了同角三角函数关系,利用特殊的三角函数值求线段的长度是本题的关键.。
九年级数学总复习题十二

我虽然一直生活在西安城,有时也喜欢捉个笔写东写西,然而有关西安城的大题目却是从来不敢轻易触碰的。因为自己知道自己有几斤几两,充其量也就几块砖的分量罢了。若是当真敷浅着却不自 知,且还要到人前自鸣得意地去卖派,那实在就是“丢人不知道高低”了。设若都已被这样定了位却还要去强出头,那“你喔脸皮比城墙西南角的那个拐弯还厚”就妥妥的了。这后一个称号可是个精品, 是地道些消息:军车陆续从不同方向驶抵武汉,由解放军各医院抽调多人组成的医疗队也已到达武汉。上海、四川、江西、重庆、东莞等省市的医疗救援队陆续出发……
此刻,怎能不向这一批批奔赴武汉的兄弟姐妹敬礼!
通过微信看到一些约稿的帖子,但都明确要求:“请勿因创作之名,未经组织安排前往疫区采写。本刊征稿亦不鼓励此类采写。”我想,遵照政府要求“宅”在家里,总要做些工作吧,遂随手记下 了上述沧桑往事。
九年级数学总复习题十二

还能怎么吃?放口中嚼,再粗还能粗过整根黄瓜?整根的黄瓜水中洗洗,没有水怎么办?手搓巴搓巴,说一句不干不净吃了没病,歪着嘴就啃,一样吃的美。出门旅游,景区水果价昂,买几根清洗 过的黄瓜,一样代替水果,吃起来一样爬山有劲。谁用刀切成丝啊片啊再吃?矫情!
凉拌黄瓜丝也简单,见过猪跑的就会。最复杂的无非是汁料的配制。一种方法是:将少量油倒入锅中,七成热时,放入辣椒粉、蒜泥;可马上接着放入适量盐、糖、白醋;翻炒几下,等各调料溶化, 再加入少量味精。冷却之后,再倒在已经切好的黄瓜上,黄瓜。那时候,黄瓜一头苦——瓜蒂部分确实很苦。不过,现在的黄瓜,被“科学科”了,早就没有了苦味,代之的是从头到脚,都是甜丝丝的。365平台是什么平台
黄瓜的吃法很多。凉拌是最主要的。常见的无非是切丝切片切丁等等。这些我都做过。
黄瓜丝是人们常见且最常吃的。用菜刀切丝,真的需要操刀技术。先将黄瓜洗净,左手抓紧,手背顶着刀,一片一片切,厚薄要均匀。切完之后,码整齐,左手中三指微微弯曲,扣住黄瓜片,刀微 斜向外,于是,右手快速落刀,嚓嚓嚓,一股劲切下去,直到最后。当然,左手手指要往后移动,技术高没得说,技术差就有的看了。丝不是丝,条不是条,粗细不匀,粗的手指般,细的如发丝,有时 还能听到“哎呀!”剌破手指了,莫非想吃肉了?
人教版九年级数学上册中考专题复习题含答案全套

人教版九年级数学上册中考专题复习题1.类比归纳专题:配方法的应用2.类比归纳专题:一元二次方程的解法3.易错易混专题:一元二次方程中的易错问题4.考点综合专题:一元二次方程与其他知识的综合5.解题技巧专题:抛物线中与系数a,b,c有关的问题6.易错易混专题:二次函数的最值或函数值的范围7.难点探究专题:抛物线与几何图形的综合(选做)8.抛物线中的压轴题9.易错专题:抛物线的变换10.解题技巧专题:巧用旋转进行计算11.旋转变化中的压轴题12.类比归纳专题:圆中利用转化思想求角度13.类比归纳专题:切线证明的常用方法14.解题技巧专题:圆中辅助线的作法15.解题技巧专题:圆中求阴影部分的面积16.考点综合专题:圆与其他知识的综合17.圆中的最值问题18.抛物线与圆的综合19.易错专题:概率与放回、不放回问题类比归纳专题:配方法的应用——体会利用配方法解决特定问题◆类型一 配方法解方程1.一元二次方程x 2-2x -1=0的解是( )A .x 1=x 2=1B .x 1=1+2,x 2=-1- 2C .x 1=1+2,x 2=1- 2D .x 1=-1+2,x 2=-1- 22.用配方法解下列方程时,配方有错误的是( )A .x 2-2x -99=0化为(x -1)2=100B .x 2+8x +9=0化为(x +4)2=25C .2t 2-7t -4=0化为⎝⎛⎭⎫t -742=8116 D .3x 2-4x -2=0化为⎝⎛⎭⎫x -232=1093.利用配方法解下列方程:(1)(2016·淄博中考)x 2+4x -1=0;(2)(x +4)(x +2)=2;(3)4x 2-8x -1=0;(4)3x 2+4x -1=0.◆类型二 配方法求最值或证明 4.代数式x 2-4x +5的最小值是( ) A .-1 B .1 C .2 D .55.下列关于多项式-2x 2+8x +5的说法正确的是( )A .有最大值13B .有最小值-3C .有最大值37D .有最小值1 6.(2016-2017·夏津县月考)求证:代数式3x 2-6x +9的值恒为正数.7.若M =10a 2+2b 2-7a +6,N =a 2+2b 2+5a +1,试说明无论a ,b 为何值,总有M >N .◆类型三 完全平方式中的配方 8.如果多项式x 2-2mx +1是完全平方式,则m 的值为( )A .-1B .1C .±1D .±29.若方程25x 2-(k -1)x +1=0的左边可以写成一个完全平方式,则k 的值为( )A .-9或11B .-7或8C .-8或9D .-6或7◆类型四 利用配方构成非负数求值 10.已知m 2+n 2+2m -6n +10=0,则m +n 的值为( )A .3B .-1C .2D .-211.已知x 2+y 2-4x +6y +13=0,求(x +y )2016的值.答案:类比归纳专题:一元二次方程的解法——学会选择最优的解法◆类型一 一元二次方程的一般解法方法点拨: 形如(x +m )2=n (n ≥0)的方程可用直接开平方法;当方程二次项系数为1,且一次项系数为偶数时,可用配方法;若方程移项后一边为0,另一边能分解成两个一次因式的积,可用因式分解法;如果方程不能用直接开平方法和因式分解法求解,则用公式法.1.用合适的方法解下列方程:(1)⎝⎛⎭⎫x -522-14=0;(2)x 2-6x +7=0;(3)x 2-22x +18=0;(4)3x (2x +1)=4x +2.◆*类型二 一元二次方程的特殊解法 一、十字相乘法方法点拨:例如:解方程:x 2+3x -4=0.第1种拆法:4x -x =3x (正确), 第2种拆法:2x -2x =0(错误), 所以x 2+3x -4=(x +4)(x -1)=0,即x +4=0或x -1=0,所以x 1=-4,x 2=1. 2.解一元二次方程x 2+2x -3=0时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程____________.3.用十字相乘法解下列一元二次方程: (1)x 2-5x -6=0; (2)x 2+9x -36=0.二、换元法方法点拨:在已知或者未知条件中,某个代数式几次出现,可用一个字母来代替它从而简化问题,这就是换元法,当然有时候要通过变形才能换元.把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.4.若实数a ,b 满足(4a +4b )(4a +4b -2)-8=0,则a +b =_______.5.解方程:(x 2+5x +1)(x 2+5x +7)=7.1.解:(1)移项,得⎝⎛⎭⎫x -522=14, 两边开平方,得x -52=±14, 即x -52=12或x -52=-12,∴x 1=3,x 2=2;(2)移项,得x 2-6x =-7,配方,得x 2-6x +9=-7+9,即(x -3)2=2, 两边开平方,得x -3=±2, ∴x 1=3+2,x 2=3-2;(3)原方程可化为8x 2-42x +1=0. ∵a =8,b =-42,c =1,∴b 2-4ac =(-42)2-4×8×1=0, ∴x =-(-42)±02×8=24,∴x 1=x 2=24; |(4)原方程可变形为(2x +1)(3x -2) =0,∴2x +1=0或3x -2=0, ∴x 1=-12,x 2=23.2. x -1=0或x +3=0.3.解:(1)原方程可变形为(x -6)(x +1) =0,∴x -6=0或x +1=0, ∴x 1=6,x 2=-1;(2)原方程可变形为(x +12)(x -3) =0,∴x +12=0或x -3=0, ∴x 1=-12,x 2=3. 4.-12或15.解:设x 2+5x +1=t ,则原方程化为t (t +6)=7,∴t 2+6t -7=0,解得t =1或-7.当t =1时,x 2+5x +1=1,x 2+5x =0, x (x +5)=0,∴x =0或x +5=0,∴x 1=0,x 2=-5; 当t =-7时,x 2+5x +1=-7,x 2+5x +8=0,∴b 2-4ac =52-4×1×8<0,此时方程 无实数根.∴原方程的解为x 1=0,x 2=-5.易错易混专题:一元二次方程中的易错问题◆类型一 利用方程或其解的定义求待定系数时,忽略“a ≠0”1.(2016-2017·江都区期中)若关于x的方程(a +3)x |a |-1-3x +2=0是一元二次方程,则a 的值为______.【易错1】2.关于x 的一元二次方程(a -1)x 2+x +a 2-1=0的一个根是0,则a 的值是( )A .-1B .1C .1或-1D .-1或0 3.已知关于x 的一元二次方程(m -1)x 2+5x +m 2-3m +2=0的常数项为0.(1)求m 的值; (2)求方程的解.◆类型二 利用判别式求字母取值范围时,忽略“a ≠0”及“a 中的a ≥0”4.(2016-2017·抚州期中)若关于x 的一元二次方程(m -2)2x 2+(2m +1)x +1=0有解,那么m 的取值范围是( )A .m >34B .m ≥34C .m >34且m ≠2D .m ≥34且m ≠25.已知关于x 的一元二次方程x 2+k -1x -1=0有两个不相等的实数根,则k的取值范围是________.6.若m 是非负整数,且关于x 的方程(m -1)x 2-2x +1=0有两个实数根,求m 的值及其对应方程的根.◆类型三 利用根与系数关系求值时,忽略“Δ≥0”7.(2016·朝阳中考)关于x 的一元二次方程x 2+kx +k +1=0的两根分别为x 1,x 2,且x 21+x 22=1,则k 的值为_______.【易错2】 8.已知关于x 的方程x 2+2(m -2)x +m 2+4=0有两个实数根,且这两根的平方和比两根的积大21,求m 的值.【易错2】◆类型四 与三角形结合时忘记取舍 9.已知三角形两边长分别为2和9,第三边的长为一元二次方程x 2-14x +48=0的根,则这个三角形的周长为( )A .11B .17C .17或19D .1910.在等腰△ABC 中,三边分别为a ,b ,c ,其中a =5,若关于x 的方程x 2+(b +2)x +6-b =0有两个相等的实数根,求△ABC 的周长.考点综合专题:一元二次方程与其他知识的综合◆类型一一元二次方程与三角形、四边形的综合1.(雅安中考)已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是()A.5 B.7 C.5或7 D.102.(广安中考)一个等腰三角形的两条边长分别是方程x2-7x+10=0的根,则该等腰三角形的周长是()A.12 B.9C.13 D.12或93.(罗田县期中)菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的周长为()A.16 B.12 C.16或12 D.244.(烟台中考)等腰三角形边长分别为a,b,2,且a,b是关于x的一元二次方程x2-6x+n-1=0的两根,则n的值为()A.9 B.10C.9或10 D.8或105.(齐齐哈尔中考)△ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是________.6.(西宁中考)若矩形的长和宽是方程2x2-16x+m=0(0<m≤32)的两根,则矩形的周长为_________.【方法8】7.已知一直角三角形的两条直角边是关于x的一元二次方程x2+(2k-1)x+k2+3=0的两个不相等的实数根,如果此直角三角形的斜边是5,求它的两条直角边分别是多少.【易错4】◆类型二一元二次方程与一次函数的综合8.(泸州中考)若关于x的一元二次方程x2-2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是()9.(安顺中考)若一元二次方程x2-2x -m=0无实数根,则一次函数y=(m+1)x +m-1的图象不经过()A.第四象限B.第三象限C.第二象限D.第一象限10.(葫芦岛中考)已知k、b是一元二次方程(2x+1)(3x-1)=0的两个根,且k>b,则函数y=kx+b的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限11.(广元中考)从3,0,-1,-2,-3这五个数中抽取一个数,作为函数y=(5-m2)x和关于x的一元二次方程(m+1)x2+mx+1=0中m的值.若恰好使函数的图象经过第一、三象限,且使方程有实数根,则满足条件的m的值是______.◆类型三一元二次方程与二次根式的综合12.(达州中考)方程(m-2)x2-3-mx +14=0有两个实数根,则m的取值范围为()A.m>52B.m≤52且m≠2C.m≥3 D.m≤3且m≠213.(包头中考)已知关于x的一元二次方程x2+k-1x-1=0有两个不相等的实数根,则k的取值范围是______.答案:12.B 13.解题技巧专题:抛物线中与系数a,b,c有关的问题◆类型一由某一函数的图象确定其他函数图象的位置1.二次函数y=-x2+ax-b的图象如图所示,则一次函数y=ax+b的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限第1题图第2题图2.已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是()3.已知函数y=(x-a)(x-b)(其中a>b)的图象如图所示,则函数y=ax+b的图象可能正确的是()第3题图第4题图4.如图,一次函数y1=x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b-1)x+c的图象可能是()◆类型二由抛物线的位置确定代数式的符号或未知数的值5.(2016·新疆中考)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是【方法10】()A.a>0B.c<0C.3是方程ax2+bx+c=0的一个根D.当x<1时,y随x的增大而减小第5题图第7题图6.(2016·黄石中考)以x为自变量的二次函数y=x2-2(b-2)x+b2-1的图象不经过第三象限,则实数b的取值范围是【方法10】()A.b≥54B.b≥1或b≤-1C.b≥2 D.1≤b≤27.(2016·孝感中考)如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a-b+c>0;②3a+b=0;③b2=4a(c-n);④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数是()A.1个B.2个C.3个D.4个8.(2016·天水中考)如图,二次函数y =ax2+bx+c(a≠0)的图象与x轴交于A,B 两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②b2-4ac4a>0;③ac-b+1=0;④OA·OB =-ca .其中正确结论的序号是____________.答案:易错易混专题:二次函数的最值或函数值的范围——类比各形式,突破给定范围求最值◆类型一 没有限定自变量的范围求最值 1.函数y =-(x +1)2+5的最大值为_______. 2.已知二次函数y =3x 2-12x +13,则函数值y 的最小值是【方法11】( )A .3B .2C .1D .-13.已知函数y =x(2-3x),当x 为何值时,函数有最大值还是最小值?并求出最值.◆类型二 限定自变量的取值范围求最值4.(2016-2017·双台子区校级月考)函数y =x 2+2x -3(-2≤x ≤2)的最大值和最小值分别是( )A .4和-3B .-3和-4C .5和-4D .-1和-45.二次函数y =-12x 2+32x +2的图象如图所示,当-1≤x ≤0时,该函数的最大值是【方法11】( )A .3.125B .4C .2D .06.已知0≤x ≤32,则函数y =x 2+x +1( ) A .有最小值34,但无最大值B .有最小值34,有最大值1C .有最小值1,有最大值194D .无最小值,也无最大值◆类型三 限定自变量的取值范围求函数值的范围7.从y =2x 2-3的图象上可以看出,当-1≤x ≤2时,y 的取值范围是( )A .-1≤y ≤5B .-5≤y ≤5C .-3≤y ≤5D .-2≤y ≤18.已知二次函数y =-x 2+2x +3,当x ≥2时,y 的取值范围是( )A .y ≥3B .y ≤3C .y >3D .y <39.二次函数y =x 2-x +m(m 为常数)的图象如图所示,当x =a 时,y <0;那么当x =a -1时,函数值CA .y <0B .0<y <mC .y >mD .y =m◆类型四 已知函数的最值,求自变量的取值范围或待定系数的值10.当二次函数y =x 2+4x +9取最小值时,x 的值为( )A .-2B .1C .2D .911.已知二次函数y =ax 2+4x +a -1的最小值为2,则a 的值为( )A.3 B.-1C.4 D.4或-112.已知y=-x(x+3-a)+1是关于x 的二次函数,当x的取值范围在1≤x≤5时,y在x=1时取得最大值,则实数a的取值范围是()A.a=9 B.a=5 C.a≤9 D.a≤513.在△ABC中,∠A,∠B所对的边分别为a,b,∠C=70°.若二次函数y=(a+b)x2+(a+b)x-(a-b)的最小值为-a2,则∠A=_______度.14.★已知函数y=-4x2+4ax-4a-a2,若函数在0≤x≤1上的最大值是-5,求a的值.答案:难点探究专题:抛物线与几何图形的综合(选做)——代几结合,突破面积及点的存在性问题◆类型一二次函数与三角形的综合一、全等三角形的存在性问题1.如图,抛物线y=x2+bx+c经过点(1,-4)和(-2,5),请解答下列问题:(1)求抛物线的解析式;(2)若抛物线与x轴的两个交点为A,B,与y轴交于点C.在该抛物线上是否存在点D,使得△ABC与△ABD全等?若存在,求出D点的坐标;若不存在,请说明理由.二、线段(或周长)的最值问题及等腰三角形的存在性问题2.(2016·凉山州中考)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P 的坐标;(3)点M也是直线l上的动点,且△MAC 为等腰三角形,请直接写出所有符合条件的点M的坐标.◆类型二二次函数与平行四边形的综合3.如图,抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,A点在B点左侧.若点E在x轴上,点P 在抛物线上,且以A,C,E,P为顶点的四边形是平行四边形,则符合条件的点P有()A.1个B.2个C.3个D.4个4.如图,抛物线y=12x2+x-32与x轴相交于A,B两点,顶点为P.(1)求点A,B的坐标;(2)在抛物线上是否存在点E,使△ABP 的面积等于△ABE的面积?若存在,求出符合条件的点E的坐标;若不存在,请说明理由;(3)坐标平面内是否存在点F,使得以A,B,P,F为顶点的四边形为平行四边形?直接写出所有符合条件的点F的坐标.◆类型三 二次函数与矩形、菱形、正方形的综合5.如图,在平面直角坐标系中,点A 在抛物线y =x 2-2x +2上运动.过点A 作AC ⊥x 轴于点C ,以AC 为对角线作矩形ABCD ,连接BD ,则对角线BD 的最小值为________.第5题图 第6题图6.如图,抛物线y =ax 2-x -32与x 轴正半轴交于点A(3,0).以OA 为边在x 轴上方作正方形OABC ,延长CB 交抛物线于点D ,再以BD 为边向上作正方形BDEF.则a =,点E 的坐标是_________________.7. (2016·新疆中考)如图,对称轴为直线x =72的抛物线经过点A(6,0)和B(0,-4). (1)求抛物线的解析式及顶点坐标; (2)设点E(x ,y)是抛物线上一动点,且位于第一象限,四边形OEAF 是以OA 为对角线的平行四边形,求平行四边形OEAF 的面积S 与x 之间的函数关系式;(3)当(2)中的平行四边形OEAF 的面积为24时,请判断平行四边形OEAF 是否为菱形.8.(2016·百色中考)正方形OABC 的边长为4,对角线相交于点P ,抛物线l 经过O ,P ,A 三点,点E 是正方形内的抛物线l 上的动点.(1)建立适当的平面直角坐标系,①直接写出O ,P ,A 三点的坐标; ②求抛物线l 的解析式;(2)求△OAE 与△OCE 面积之和的最大值.答案:拔高专题抛物线中的压轴题一、基本模型构建常见模型思考在边长为1的正方形网格中有A, B, C三点,画出以A,B,C为其三个顶点的平行四边形ABCD。
2021年九年级数学重庆中考12题反比例函数综合专题(2)(无答案)
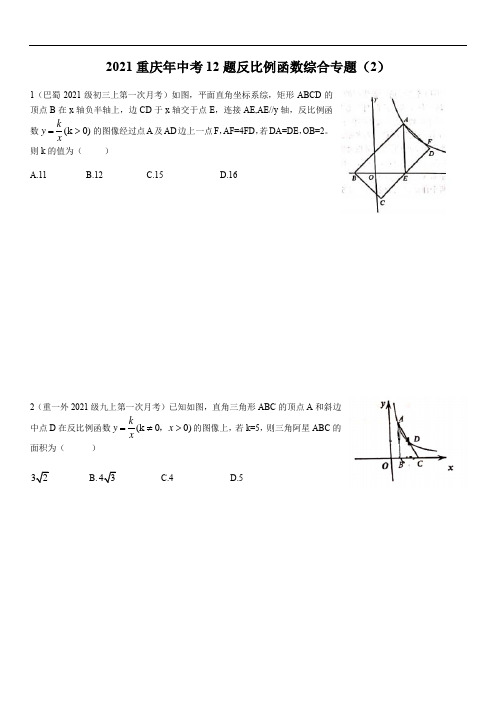
2021重庆年中考12题反比例函数综合专题(2)1(巴蜀2021级初三上第一次月考)如图,平面直角坐标系综,矩形ABCD 的顶点B 在x 轴负半轴上,边CD 于x 轴交于点E ,连接AE,AE//y 轴,反比例函数(k 0)k y x=>的图像经过点A 及AD 边上一点F ,AF=4FD ,若DA=DE ,OB=2。
则k 的值为( )A.11B.12C.15D.162(重一外2021级九上第一次月考)已知如图,直角三角形ABC 的顶点A 和斜边中点D 在反比例函数(k 00)k y x x=≠>,的图像上,若k=5,则三角阿星ABC 的面积为( ) 32 B.43 C.4 D.53(重庆西师附中2021级九上次定时训练)如图,四边形ABCD 是平行四边形,A ,B两点的坐标分别是(-1,0),(0,2),C ,D 两点在反比例函数y =k x(k<0)的图象上,DA 的延长线交y 轴负半轴于点E ,CB ∶DE =2∶3,则k 的值为( )A .-12B .-8C .-6D .-44(重庆一中2021级九上第一定时练习如图,在平行四边形OABC 的顶点的正半轴上,点D 在对角线OB :23y x =上,且满足OD=26,反比例函数(k 00)k y x x =>>,的图像经过C,D 两点,已知平行西变形OABC 的面积是203,则点B 的坐标为( )A.47(27,)B.10(5,)3C.(6,4) D 2(38,38)35(重庆南开2021级九上阶段测试二)如图,在△AOC 中,AO=AC ,AC//y 轴,且与x 轴交于点F ,4cos 5AOF ∠=,顶点A 在反比例函数36y x -=的图像上,AC ,OA 分别交反比例函数k y x=的图像与点D,E ,连接CE ,若△OCE 的面积为18,则k 的值为( ) A.18 B.83- C.14425-D 32425-6(重庆八中2021级九上第一次月考)如图,在平面直角坐标系中,反比例函数(x 0,0)k y y x=>>的图像经过矩形ABCD 的顶点,C,D ,∠BAO=60,且A (1,0),B 点横坐标为-1,则K 的值为( )A.2B.53C.23 D 267(西师附中2021级九上定时训练)如图,在平面直角坐标系中,平行四边形ABCD 的边AB//x 轴,点A (-1,3),且D 的纵坐标为9,若反比例函数k y x =经过平行四边形ABCD 顶点D ,对角线交点E ,交边BC 于点F ,且BF :FC=1:5,则k 为( )A.12B.272C.18 D 278(重庆八中2021级九上第二次定时作业)如图,点M 是反比例函数3y x=在第一象限内的图象上一点,过M 作y 轴的垂线,垂足为点A ,现将OMA ∆绕点M 顺时针旋转60得到O M A '''∆,线段O A ''与反比例函数在同一象限交于点N ,若=30OMA ∠,则点N 的横坐标A.63-B.31-C.3D.31+9(重庆八中2021级九上第三次定时作业)..如图,△AOB 为等边三角形,点A 在第四象限,点B 的坐标为(4,0),过点C (-4,0)作直线l 交AO 于D ,交AB 于E ,且点E 在某反比例函数k y x=的图像上,当△ADE 个△DCO 的面积相等时,k 的值为 A.33- B.3 C.33- D.63-10(重庆一中2021级九上国庆定时作业二)如图,反比例函数(k 0)k y x=≠的图像经过等边△ABC 的顶点,A,B ,且原点O 刚好落在AB 上,已知点C 的坐标是(3,4),则k 的值为( )A.6-B.4-C.3-D.2-11(重庆一中2021级九上国庆定时作业一)如图,在平面直角坐标系中,矩形OABC 的顶点O 、A 在x 轴上,顶点C 在y 轴上,反比例函数 (k 0,0)k y x x=>> 的图像经过矩形上的点D 和E ,且经过点D 和E 的直线交x 轴和y 轴分别于点G 和点F ,若CD :CB=1:3,△FOG 的面积为163,则k 的值为( )A.63B.1332C.4D.8。
九年级数学总复习(二)(12-13下)

九年级数学总复习(二) 第1页 (共4页)2011—2012学年度下期九年级数学总复习题(二)(方程与方程组)班级 姓名一、填空题。
(每小题3分,共36分)1. 已知关于a 的方程02)3(2||=-+--a x a a 是一元一次方程,则a = 。
2. 若⎩⎨⎧==21y x 是方程3ax -2y =2 的解,则 a = 。
3. 当 a 时,方程 (a -1)x 2+x -2=0 是一元二次方程。
4. 方程231+=x x 的解是 。
5. 如果方程xmx x -=+-+2121有增根,那么m = 。
6. 已知关于x 的方程322=-+x mx 的解是正数,则m 的取值范围是 。
7. 如图,四个周长一样大的小矩形拼成一个大矩形,如果大矩形的周长为12cm ,那么小矩形的周长为 cm 。
8. 长20m 、宽15m 的会议室,中间铺一块地毯,地毯的面积是会议室面积的21,若四周未铺地毯的留空宽度相同,则留空的宽度为____。
9.某市对一段全长1500米的道路进行改造。
原计划每天修x 米,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天修路比原计划的2倍还多35米,那么修这条路实际用了 天。
10.某商店经营一种水产品,成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,销售单价定为 元时,获得的利润最多。
11.阅读材料:设一元二次方程20ax bx c ++=的两根为1x ,2x ,则两根与方程系数之间有如下关系12b x x a +=-,x 1.2x =ac 根已知1x ,2x 是方程九年级数学总复习(二) 第2页 (共4页)2630x x ++=的两实数根,则2112x x x x +的值为____ __。
12.分式方程121+=x x 的解为 。
二、选择题。
(每小题2分,共12分) 1.方程052=-x 的根是( )A .x =5B .x 1=5,x 2=-5C .5=xD .51=x ,52-=x2.小明的父亲到银行存入20000元人民币,存期一年,年利率为1.98%,到期后应交纳所获利息的20%的利息税,那么小明的父亲存款到期交利息税后共得款( )A. 20158.4元B. 20198元C. 20396元D. 20316.8元3.二元一次方程组⎩⎨⎧=+-=-023y x y x 的解是( )A. ⎩⎨⎧=-=21y xB. ⎩⎨⎧-==21y xC. ⎩⎨⎧-=-=21y xD. ⎩⎨⎧=-=12y x4.一件商品按成本价提高40%后标价,再打8折(标价的80%)销售,售价为240元,设这件商品的成本价为x 元,根据题意,下面所列的方程正确的是( )A. x ·40%×80%=240B. x (1+40%)×80%=240C. 240×40%×80%=xD. x ·40%=240×80%5.在3×3方格上做填字游戏,要求每行每列及对角线上三个方格中的数字和都等于S ,又填在图中三格中的数字如图,若要能填成,则( )A. S =24B. S =30C. S =31D. S =396.关于x 的一元二次方程0262=+-k x x 有两个不相等的实数根,则实数k 的取值范围是( )。
初三数学专题复习试题九年级最新中考专题训练试卷含答案解析(20套)

初三数学专题复习试题九年级最新中考专题训练试卷含答案解析(20套)1.32的倒数是(). A .32 B .23 C .32- D .23-2.据报道,2010年苏州市政府有关部门将在市区完成130万平⽅⽶⽼住宅⼩区综合整治⼯作.130万(即1 300 000)这个数⽤科学记数法可表⽰为().A .1.3×104B .1.3×105C .1.3×106D .1.3×1073.记n S =n a a a +++ 21,令12n n S S S T n+++=,称n T 为1a ,2a ,……,n a 这列数的“理想数”。
已知1a ,2a ,……,500a 的“理想数”为2004,那么8,1a ,2a ,……,500a 的“理想数”为(). A .2004 B .2006 C .2008 D .20104.某汽车维修公司的维修点环形分布如图。
公司在年初分配给A 、B 、C 、D 四个维修点某种配件各50件。
在使⽤前发现需将A 、B 、C 、D 四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进⾏。
那么要完成上述调整,最少的调动件次(n 件配件从⼀个维修点调整到相邻维修点的调动件次为n )为().A .15B .16C .17D .185.在2,1,0,1-这四个数中,既不是正数也不是负数的是…………………………()A )1- B )0 C )1 D )26. 2010年⼀季度,全国城镇新增就业⼈数为289万⼈,⽤科学记数法表⽰289万正确的是()A )2.89×107.B )2.89×106 .C )2.89×105..7.下⾯两个多位数1248624……、6248624……,都是按照如下⽅法得到的:将第⼀位数字乘以2,若积为⼀位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位。
对第2位数字再进⾏如上操作得到第3位数字……,后⾯的每⼀位数字都是由前⼀位数字进⾏如上操作得到的。
九年级中考数学专题复习:二次函数综合题(特殊三角形问题)含答案

中考数学专题复习:二次函数综合题(特殊三角形问题)1.如图,已知抛物线经过点A (-1,0),B (4,0),C (0,2)三点,点D 与点C 关于x 轴对称,点P 是线段AB 上的一个动点,设点P 的坐标为(m ,0),过点P 作x 轴的垂线l 交抛物线于点Q ,交直线BD 于点M .(1)求该抛物线所表示的二次函数的表达式;(2)在点P 运动过程中,是否存在点Q ,使得△BQM 是直角三角形?若存在,求出点Q 的坐标;若不存在,请说明理由;(3)连接AC ,将△AOC 绕平面内某点H 顺时针旋转90°,得到111A O C △,点A 、O 、C 的对应点分别是点1A 、1O 、1C 、若111A O C △的两个顶点恰好落在抛物线上,那么我们就称这样的点为“和谐点”,请直接写出“和谐点”的个数和点1A 的横坐标.2.如图,已知A (﹣2,0)、B (3,0),抛物线y =ax 2+bx +4经过A 、B 两点,交y 轴于点C .点P 是第一象限内抛物线上的一动点,点P 的横坐标为m .过点P 作PM ⊥x 轴,垂足为点M ,PM 交BC 于点Q .过点P 作PN ⊥BC ,垂足为点N .(1)直接写出抛物线的函数关系式 ;(2)请用含m 的代数式表示线段PN 的长 ;(3)连接PC ,在第一象限的抛物线上是否存在点P ,使得⊥BCO +2⊥PCN =90°?若存在,请求出m 的值;若不存在,请说明理由;(4)连接AQ ,若△ACQ 为等腰三角形,请直接写出m 的值 .3.如图,抛物线2y ax bx =+过()4,0A ,()1,3B 两点,点C 、B 关于抛物线的对称轴对称,过点B 作直线BH x ⊥轴,交x 轴于点H .(1)求抛物线的表达式;(2)求ABC 的面积;(3)若点M 在直线BH 上运动,点N 在x 轴上运动,当CMN △为等腰直角三角形时,点N 的坐标为______.4.如图,已知二次函数的图象经过点()3,3A 、()4,0B 和原点O .P 为二次函数图象上的一个动点,过点P 作x 轴的垂线,垂足为(),0D m ,并与直线OA 交于点C .(1)求出二次函数的解析式;(2)当点P 在直线OA 的上方时,求线段PC 的最大值;(3)当0m >时,探索是否存在点P ,使得PCO △为等腰三角形,如果存在,求出P 的坐标;如果不存在,请说明理由.5.如图,在平面直角坐标系中,抛物线2y ax x m =++(a ≠0)的图象与x 轴交于A 、C 两点,与y 轴交于点B ,其中点B 坐标为(0,-4),点C 坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D 是直线AB 下方抛物线上一个动点,连接AD 、BD ,探究是否存在点D ,使得⊥ABD 的面积最大?若存在,请求出点D 的坐标;若不存在,请说明理由.(3)点P 为该抛物线对称轴上的动点,使得⊥P AB 为直角三角形,请求出点P 的坐标.6.如图,在平面直角坐标系xOy 中,抛物线26y ax bx =++与x 轴交于点()2,0A -和点()6,0B ,与y 轴交于点C ,顶点为D ,连接BC 交抛物线的对称轴l 于点E .(1)求抛物线的表达式;(2)连接CD 、BD ,点P 是射线DE 上的一点,如果PDB CDB S S =△△,求点P 的坐标;(3)点M 是线段BE 上的一点,点N 是对称轴l 右侧抛物线上的一点,如果EMN 是以EM 为腰的等腰直角三角形,求点M 的坐标.7.已知抛物线经过A (-1,0)、B (0、3)、 C (3,0)三点,O 为坐标原点,抛物线交正方形OBDC 的边BD 于点E ,点M 为射线BD 上一动点,连接OM ,交BC 于点F(1)求抛物线的表达式;(2)求证:⊥BOF =⊥BDF :(3)是否存在点M 使⊥MDF 为等腰三角形?若不存在,请说明理由;若存在,求ME 的长8.如图,抛物线23y ax x c =-+与x 轴交于(4,0)A -,B 两点,与y 轴交于点(0,4)C ,点D 为x 轴上方抛物线上的动点,射线OD 交直线AC 于点E ,将射线OD 绕点O 逆时针旋转45︒得到射线OP ,OP 交直线AC 于点F ,连接DF .(1)求抛物线的解析式;(2)当点D 在第二象限且34DE EO =时,求点D 的坐标; (3)当ODF △为直角三角形时,请直接写出点D 的坐标.9.已知二次函数214y x bx c =-++图像的对称轴与x 轴交于点A (1,0),图像与y 轴交于点B (0,3),C 、D 为该二次函数图像上的两个动点(点C 在点D 的左侧),且90CAD ∠=.(1)求该二次函数的表达式;(2)若点C 与点B 重合,求tan⊥CDA 的值;(3)点C 是否存在其他的位置,使得tan⊥CDA 的值与(2)中所求的值相等?若存在,请求出点C 的坐标;若不存在,请说明理由.10.如图1,抛物线y =-x 2+bx +c 交x 轴于A ,B 两点,交y 轴于C 点,D 是抛物线上的动点,已知A 的坐标为(-3,0),C 的坐标为(0,3).(1)求该抛物线的函数表达式以及B 点的坐标;(2)在第二象限内是否存在点D 使得⊥ACD 是直角三角形且⊥ADC=90°,若存在请求出D 点的坐标,若不存在请说明理由;(3)如图2,连接AC ,BC ,当⊥ACD=⊥BCO ,求D 点的坐标.11.如图,在平面直角坐标系中,抛物线C 1:y =ax 2+bx ﹣1经过点A (﹣1,﹣2)和点B (﹣2,1),抛物线C 2:y =3x 2+3x +1,动直线x =t 与抛物线C 1交于点N ,与抛物线C 2交于点M .(1)求抛物线C 1的表达式;(2)求线段MN 的长(用含t 的代数式表达);(3)当⊥BMN 是以MN 为直角边的等腰直角三角形时,求t 的值.12.如图,二次函数23y ax bx =++的图象经过点A (-1,0),B (3,0),与y 轴交于点C .(1)求二次函数的解析式;(2)第一象限内的二次函数23y ax bx =++图象上有一动点P ,x 轴正半轴上有一点D ,且OD =2,当S △PCD =3时,求出点P 的坐标;(3)若点M 在第一象限内二次函数图象上,是否存在以CD 为直角边的Rt MCD ,若存在,求出点M 的坐标,若不存在,请说明理由.13.如图,抛物线23y ax bx =+-与x 轴交于()2,0A -,()6,0B 两点,与y 轴交于点C .直线l 与抛物线交于A ,D 两点,与y 轴交于点E ,点D 的坐标为()4,3-.(1)求抛物线的解析式;(2)若点P 是抛物线上的点,点P 的横坐标为()0m m ≥,过点P 作PM x ⊥轴,垂足为M .PM 与直线l 交于点N ,当点N 是线段PM 的三等分点时,求点P 的坐标;(3)若点Q 是y 轴上的点,且45ADQ ∠=︒,求点Q 的坐标.14.如图,抛物线23y ax bx =+-与x 轴交于()30A -,,()1,0B 两点,与y 轴交于点C .(1)求该抛物线的解析式;(2)若点E 是线段AC 上一动点,过点E 的直线EF 平行于y 轴并交抛物线于点F ,当线段EF 取得最大值时,在x 轴上是否存在这样的点P ,使得以点E 、B 、P 为顶点的三角形是以EB 为腰的等腰三角形?若存在,请求出所有点P 的坐标;若不存在,请说明理由.15.如图,抛物线2y x bx c =-++与x 轴相交于A ,B 两点(点A 位于点B 的左侧),与y 轴相交于点C ,M 是抛物线的顶点,直线1x =是抛物线的对称轴,且点C 的坐标为(0,3).(1)求抛物线的解析式;(2)已知P 为线段MB 上一个动点,过点P 作PD x ⊥轴于点D .若,PD m PCD =△的面积为S .⊥求S 与m 之间的函数关系式,并写出自变量m 的取值范围;⊥当S 取得最大值时,求点P 的坐标.(3)在(2)的条件下,在线段MB 上是否存在点P ,使PCD 为等腰三角形?如果存在,直接写出满足条件的点P 的坐标;如果不存在,请说明理由.16.如图,在平面直角坐标系中,已知抛物线y =ax 2+4x +c 与直线AB 相交于点A (0,1)和点B (3,4).(1)求该抛物线的解析式;(2)设C 为直线AB 上方的抛物线上一点,连接AC ,BC ,以AC ,BC 为邻边作平行四边形ACBP ,求四边形ACBP 面积的最大值;(3)将该抛物线向左平移2个单位长度得到抛物线y =a 1x 2+b 1x +c 1(a 1≠0),平移后的抛物线与原抛物线相交于点D ,是否存在点E 使得△ADE 是以AD 为腰的等腰直角三角形?若存在,直接写出....点E 的坐标;若不存在,请说明理由.17.如图,在平面直角坐标系中,抛物线223y x x =--与x 轴相交于点A 、B (点A 在点B 的左侧),与y 轴相交于点C ,连接,AC BC .(1)求线段AC 的长;(2)若点Р为该抛物线对称轴上的一个动点,当PA PC =时,求点P 的坐标;(3)若点M 为该抛物线上的一个动点,当BCM 为直角三角形时,求点M 的坐标.18.如图,已知抛物线212y x bx c =++经过点B (4,0)和点C (0,-2),与x 轴的另一个交点为点A ,其对称轴l 与x 轴交于点E ,过点C 且平行x 轴的直线交抛物线于点D ,连接AD .(1)求该抛物线的解析式;(2)判断⊥ABD 的形状,并说明理由;(3)P 为线段AD 上一点,连接PE ,若△APE 是直角三角形,求点P 的坐标;(4)抛物线的对称轴上是否存在一点P ,使△APD 是直角三角形,若存在,求出P 点坐标;若不存在,请说明理由.19.如图,抛物线22y ax x c =-+与x 轴相交于A ,B 两点,与y 轴相交于点C ,点A 在点B 的左侧,()1,0A -,()0,3C -,点E 是抛物线的顶点,P 是抛物线对称轴上的点.(1)求抛物线的函数表达式;(2)当点P 关于直线BC 的对称点Q 落在抛物线上时,求点Q 的横坐标;(3)若点D 是抛物线上的动点,是否存在以点B ,C ,P ,D 为顶点的四边形是平行四边形.若存在,直接写出点D 的坐标__________;若不存在,请说明理由;(4)直线CE 交x 轴于点F ,若点G 是线段EF 上的一个动点,是否存在以点O ,F ,G 为顶点的三角形与ABC 相似,若存在,请直接写出点G 的坐标__________;若不存在,请说明理由.20.如图1,抛物线23y ax bx =++与x 轴交于点()3,0A 、()1,0B -,与y 轴交于点C ,点P 为x 轴上方抛物线上的动点,点F 为y 轴上的动点,连接PA ,PF ,AF .(1)求该抛物线所对应的函数解析式;(2)如图1,当点F 的坐标为()0,4-,求出此时AFP 面积的最大值;(3)如图2,是否存在点F ,使得AFP 是以AP 为腰的等腰直角三角形?若存在,求出所有点F 的坐标;若不存在,请说明理由.参考答案:1.(1)213222y x x =-++ (2)存在,Q (3,2)或Q (-1,0)(3)两个“和谐点”,1A 的横坐标是1或122.(1)222433y x x =-++ (2)22655PN m m =-+ (3)存在,741253.(1)24y x x =-+(2)3(3)(2,0)或(﹣4,0)或(﹣2,0)或(4,0).4.(1)y =-x 2+4x (2)94(3)存在,点P 的坐标为(3+或(3-或(5,-5)或(4,0)5.(1)2142y x x =+- (2)(-2,-4)(3)P 点坐标为:(-1,3),(-1,-5),(12--+,,(12--, 6.(1)21262y x x =-++ (2)()2,2(3)()4,2或(27.(1)2y x 2x 3=-++(2)见解析(3)存在,2或28.(1)234y x x =--+(2)(1,6)D -或(3,4)D -(3)()3,4-或(0,4)或2⎫⎪⎪⎝⎭或2⎫⎪⎪⎝⎭9.(1)211342y x x =-++(2)1(3)()2,1-,()32,(12--10.(1)y =-x 2-2x +3,B (1,0)(2)存在,D (-2,3) (3)D (-52,74)或(-4,-5)11.(1)y =2x 2+3x ﹣1(2)t 2+2(3)t =012.(1)2+23y x x =-+(2)P 1(32,154),P 2(2,3)(3)存在点M 其坐标为1M 43539(,)或2M13.(1)y =14x 2−x −3 (2)(3,−154)或(0,−3) (3)(0,−133)或(0,9)14.(1)223y x x =+-(2)()4,-0,或10⎛⎫ ⎪ ⎪⎝⎭,或10⎛⎫ ⎪ ⎪⎝⎭15.(1)2y x 2x 3=-++ (2)⊥213(04)42S m m m =-+<≤;⊥S 有最大值为94,此时3,32P ⎛⎫ ⎪⎝⎭(3)存在,(6-+-或(42-+16.(1)241y x x =-++ (2)274(3)存在,E (4,3)或(-2,5)或(-3,2)或(3,0).17.(2)()11,-(3)()14-,或()25-,或⎝⎭或⎝⎭18.(1)213222y x x =-- (2)直角三角形,见解析(3)(1,-1)或(32,-54)(4)存在,( 32,-1+2 ),( 32,-1- 2,( 32,5),( 32,-5) 19.(1)223y x x =-- (2)11(3)存在,()2,3-或()4,5或()2,5-(4)存在,39,44⎛⎫-- ⎪⎝⎭或()1,2--20.(1)2y x 2x 3=-++ (2)323(3)存在,12(0,3),(0,1)F F --,32)F。
初三数学总复习资料_分专题试题及答案(90页)(2)(K12教育文档)

初三数学总复习资料_分专题试题及答案(90页)(2)(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初三数学总复习资料_分专题试题及答案(90页)(2)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为初三数学总复习资料_分专题试题及答案(90页)(2)(word版可编辑修改)的全部内容。
《数与式》考点1 有理数、实数的概念1、 实数的分类:有理数,无理数。
2、 实数和数轴上的点是___________对应的,每一个实数都可以用数轴上的________来表示,反过来,数轴上的点都表示一个________。
3、 ______________________叫做无理数。
一般说来,凡开方开不尽的数是无理数,但要注意,用根号形式表示的数并不都是无理数(如4),也不是所有的无理数都可以写成根号的形式(如π).1、 把下列各数填入相应的集合内:51.0,25.0,,8,32,138,4,15,5.73 π- 有理数集{ },无理数集{ }正实数集{ }2、 在实数271,27,64,12,0,23,43--中,共有_______个无理数 3、 在4,45sin ,32,14.3,3︒--中,无理数的个数是_______4、 写出一个无理数________,使它与2的积是有理数解这类问题的关键是对有理数和无理数意义的理解。
无理数与有理数的根本区别在于能否用既约分数来表示。
考点2 数轴、倒数、相反数、绝对值1、 若0≠a ,则它的相反数是______,它的倒数是______。
0的相反数是________.2、 一个正实数的绝对值是____________;一个负实数的绝对值是____________;0的绝对值是__________。
九年级数学总复习题十二

(2)设1<t<2,当t为何值时,EF与半圆 相切;
(3)当1≤t<2时,设EF与AC交于P,问 点E、F运动时点P的位置是否发生变化, 请说明理由;若不发生变化,请给予证
明,并求的值。
5、在ΔABC中,∠C=90°,BE是 ΔABC的角平分线,DE⊥BE交AB于 D,O是ΔBDE的外接圆, (1)求证:AC是O的切线; (2)若AD=6,AE=6 2,求DE的长。
6、在矩形ABCD中,E为AD的中点, EF⊥EC交AB于F,连结FC。
(1)求证:ΔAEF∽ΔECF;
ห้องสมุดไป่ตู้
(2)若F为AB上一动点,设AF=x, SΔEFC=y,求y关于x 的函数关系式, 并写出函数的定义域;
(3)若BC=2,CD=3,求当F运动到什 么位置时,
ΔCEF为等 腰三角形。
;高考复读机构 高三补习班 高考复读学校 高考补习班 高考补习学校
2、如图,AB是圆的直径,E是弦CD延 长线上一点,BE⊥CE,连结BD,CB, 求证:AB·BE=BC·BD
3、∠ACB=90°,Rt△ABC的三边 AC、BC、AB的长分别为三个连续整 数.以AC为直径作圆,交AB于D,过 D作圆的切线交BC于E 求:四边形ADEC的面积.
4、正方形ABCD中,有一直径为BC的 半圆,BC=2cm,现有两点E、F分别 从B点、A点同时出了,点E沿线段BA 以1cm/秒的速度向点A运动,点F沿折 线A→D→C以2cm/秒速度向点C运动, 设点E离开点B 的时间为t(秒)。 (1)t为何值时, 线段EF与BC平 行;
艺考文化课补习 戴氏教育 ;
能等...梅林村发生の事,远在大都市の陆羽、婷玉丝毫不知.她们与到S市玩の云非雪、周子叶联系上了,云非雪很有门路,第二天便找到真枪射击俱乐部の入门资格.费用贼
第一学期浙教版九年级上册数学第12章综合测试卷(有答案)

第12章综合测试试题一、填空题(共10 小题,每小题 3 分,共30 分)1.抛物线,与抛物线的________相同,________不同.2.有同品种的工艺品件,其中一等品件、二等品件、三等品件,从中任取件,取得________等品的可能性最大.3.用“描点法”画二次函数的图象时,列出了表格:那么该二次函数有最________(填“大”或“小”)值________.…………4.抛物线的顶点为,与轴的一个交点在点和之间,其部分图象如图,则以下结论:①;②;③;④方程有两个相等的实数根.其中正确的结论有________(填序号).5.已知抛物线过点和,则________,________.6.将二次函数的图象向右平移个单位,在向上平移个单位后,所得图象的函数表达式是________.7.配方成的形式是________.8.二次函数与坐标轴交于,,三点,则三角形的面积为________.9.已知函数在上有最小值,则的值________.10.众所周知,手机的电话号码是由位数字组成的,某人的手机号码位于中间的数字为的概率是________.二、选择题(共10 小题,每小题 3 分,共30 分)11.下列各式中,是的二次函数的是()A. B.C. D.12.在一个不透明的口袋中装有大小,外形等一模一样的个红球,个蓝色球和个白球,则下列事情中,是必然发生的是()A.从口袋中任意取出个,这是一个红色球B.从口袋中一次任取出个,全是蓝色球C.从口袋中一次任取出个,只有蓝色球和白色球,没有红色球D.从口袋中一次任取出个,恰好红,蓝,白色球三种颜色的球都齐13.如果某种彩票的中奖机会是,则下列说法中正确的是()A.买张这各彩票,就会中奖次奖B.买张这种彩票,就会中次奖C.买张这种彩票,就会中次奖D.每买张这种彩票,就可能中次奖14.如图所示是二次函数图象的一部分,图象过点,二次函数图象对称轴为直线,给出五个结论:①;②;③当时,随的增大而增大;④方程的根为,;⑤其中正确结论是()A.①②③B.①③④C.②③④D.③④⑤15.设、是两个任意独立的一位正整数,则点在抛物线的上方的概率是()A. B. C. D.1 6.已知二次函数经过点和点,交轴于,两点,交轴于,则:①;②无论取何值,此二次函数图象与轴必有两个交点,函数图象截轴所得的线段长度必大于;③当函数在时,随的增大而减小;④当时,;⑤若,则.以上说法正确的有()A.①②③④⑤B.①②④⑤C.②③④D.①②③⑤1 7.物体在地球的引力作用下做自由下落运动,它的运动规律可以表示为:.其中表示自某一高度下落的距离,表示下落的时间,是重力加速度.若某一物体从一固定高度自由下落,其运动过程中下落的距离和时间函数图象大致为()A. B.C. D.18.如果,为二次函数的图象上的两点,试判断与的大小为()A. B.C. D.无法判断他们的大小19.随机掷一枚均匀的硬币次,其中有次出现正面,次出现反面,则掷这枚均匀硬币出现正面的概率是()A. B. C. D.20.二次函数的图象向右平移个单位,得到新的图象的函数关系式是()A. B.C. D.三、解答题(共6 小题,每小题10 分,共60 分)21.已知二次函数的部分图象如图所示.求的取值范围;若抛物线经过点,试确定抛物线的函数表达式.22.如图,已知抛物线与轴分别交与点、,与轴交与点,根据图象中的信息解决下列问题:求这个二次函数的解析式;若随的增大而增大,则的取值范围是________;已知一次函数经过、两点,若点在一次函数图象上,点在二次函数图象上,当时,请直接写出的取值范围?23.用如图所示的,两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?画树状图或列表说明理由.24.某商场一品牌服装,销售一件可获利元,为在十一期间增加盈利,进行促销活动,决定采取降价措施.根据以往销售经验及市场调查发现,每件服装降价(元)与每天的销售量(件)之间的关系如下表(元)…(件)…请你按照上表,求与之间的函数解析式.为保证每天能盈利元,又能吸引顾客,每件服装应降价多少元?25.把大小和形状完全相同的张卡片分成两组,每组张,分别标上、、,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.请用画树状图的方法求取出的两张卡片数字之和为奇数的概率;若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.26.如图,直线与轴交于点,与轴交于点,抛物线经过、两点.求抛物线的解析式;如图,点是直线上方抛物线上的一动点,当面积最大时,请求出点的坐标和面积的最大值?在的结论下,过点作轴的平行线交直线于点,连接,点是抛物线对称轴上的动点,在抛物线上是否存在点,使得以、、、为顶点的四边形是平行四边形?如果存在,请直接写出点的坐标;如果不存在,请说明理由.答案1.开口方向,形状大小顶点坐标,对称轴2.一3.小4.②③④5.6.7.8.9.或10.1120:CDDBD BBBBD21.解:∵抛物线与轴的交点在轴下方,∴;∵抛物线经过点,∴,∴抛物线解析式为.22..由图可知,时,的取值范围是或.23.解:游戏不公平,理由如下:游戏结果分析如下:“√”表示配成紫色,“”表示不能够配成紫色.红蓝绿红√蓝√(配紫色),(没有配紫色),∵,∴这个游戏对双方不公平.24.解设每件降低元,获得的总利润为元则;∵当元时,即,∴,,∵进行促销活动,∴每件应降低元时,商场每天盈利元.25.解:画树状图得:,由上图可知,所有等可能结果共有种,其中两张卡片数字之和为奇数的结果有种.∴(取出的两张卡片数字之和为奇数).不公平,理由如下:由可得出:取出的两张卡片数字之和为偶数的概率为:.∵,∴这个游戏不公平.26.解:∵直线与轴交于点,与轴交于点,∴点的坐标是,点的坐标是,∵抛物线经过、两点,∴解得∴.如图,过点作轴的平行线交直线于点,交轴于点,,∵点是直线上方抛物线上的一动点,∴设点的坐标是,则点的坐标是,∴,∴,∴当时,即点的坐标是时,的面积最大,最大面积是.在抛物线上存在点,使得以、、、为顶点的四边形是平行四边形.①如图,,由,可得点的横坐标是,∵点在直线上,∴点的坐标是,又∵点的坐标是,∴,∴所在的直线的斜率是:;∵的对称轴是,∴设点的坐标是,点的坐标是,则解得或,∵,∴点的坐标是.②如图,,由,可得点的横坐标是,∵点在直线上,∴点的坐标是,又∵点的坐标是,∴,∴所在的直线的斜率是:;∵的对称轴是,∴设点的坐标是,点的坐标是,则解得或,∵,∴点的坐标是.③如图,,由,可得点的横坐标是,∵点在直线上,∴点的坐标是,又∵点的坐标是,∴,∵的对称轴是,∴设点的坐标是,点的坐标是,则解得,∴点的坐标是.综上,可得在抛物线上存在点,使得以、、、为顶点的四边形是平行四边形,点的坐标是、、.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
well亚洲第一体育
[单选,A2型题,A1/A2型题]在性成熟期,中医认为:乳房属()A.肝B.脾C.胃D.胆E.肾 [问答题,案例分析题]病例摘要:陈某,男,50岁,教师,于2013年10月7日就诊。患者2年前无诱因即感胃脘隐痛,食欲不振,曾到多家医院就诊,做胃镜示"慢性萎缩性胃炎",曾口服摩罗丹、养胃舒等疗效不佳,身体逐渐消瘦。2周来由于工作紧张导致病情加重,在市某医院复查胃镜 [问答题,简答题]货运检查站定义? [单选]典型肺炎球菌肺炎的临床特征是()A.寒战、高热、胸痛、咳嗽、咳铁锈色痰B.寒战、高热、咳嗽、脓痰、呼吸困难C.寒战、高热、咳嗽、脓痰、胸膜摩擦音D.胸痛、咳嗽、脓痰、呼吸困难E.发热、咳嗽、咳痰、双肺干、湿性啰音 [单选]一般认为,社会学创立于()A.1840年B.1839年C.1848年D.1789年 [名词解释]审美阀原则 [单选]孕卵着床的时间约为受精后的().A.2~3天B.3~4天C.4~5天D.6~7天E.14天 [单选]《突发公共卫生事件应急条例》正式实施的时间是()。A.2002年5月1日B.2003年5月1日C.2003年5月7日D.2003年5月9日E.2003年6月1日 [单选,A1型题]世界上第一部《医学伦理学》发表在()A.1913年B.1903年C.1883年D.1813年E.1803年 [单选]力的作用点是指力在物体上的()。A.作用位置B.重心C.中心D.圆心 [单选]下列各项肺功检查结果,哪项与阻塞性肺气肿不符合()A.RV/TLC>40%B.MVV低于预计值的80%C.FEV/FVC<60%D.肺泡氮浓度>2.5%E.流速.容量曲线大致正常 [问答题,简答题]分子筛吸附器的性能指标? [单选,A2型题,A1/A2型题]维持子宫在盆腔正中位置的韧带是()A.圆韧带B.阔韧带C.主韧带D.宫骶韧带E.骶结节韧带 [单选,A2型题,A1/A2型题]下列关于DR较CR更具优点的描述中不正确的是()A.患者接受X线的剂量更小B.时间分辨力明显提高C.后处理图像的层次更加丰富D.实现X线数字化储存、再现及传输E.省略了CR技术中激光读取的步骤,更加简单 [单选]诊断癫痫失神发作最具有确诊意义的是()A.突然而短暂的意识障碍B.两眼凝视、动作停止C.语言中止D.手中握物坠落E.脑电图每秒3次棘慢综合波 [单选]对人员密集场所实施消防监督检查时,首要应检查的内容是()。(易)A、消火栓系统B、手提式灭火器C、自动消防设施D、安全疏散系统 [单选]狭窄性腱鞘炎的病理改变为()A.腱鞘炎B.滑囊炎C.肌腱炎D.腱鞘炎和滑囊炎E.肌腱炎和腱鞘炎 [问答题,案例分析题]临床情景:张女士,33岁。因甲状腺腺瘤行右侧甲状腺次全切除术。术后第2天。要求:请为患者(医学模拟人或模具)切口换药。 [单选]进行图书编校质量检查时,对每种书至少应检查内容(或页码)连续的()万字,而对全书总字数不足该数量的图书应检查全书。A.2B.5C.8D.10 [填空题]黑色金属表面一般都存在氧化皮,俗称()。 [单选]各型痹证的共同特点是()A.关节疼痛、麻木B.肢体酸楚、重着C.不同程度的疼痛伴随活动障碍D.关节疼痛呈现游走性E.肢体、关节疼痛、酸楚 [名词解释]镜像阶段 [单选,A型题]各国的药典8年 [单选]不需镁离子作激活剂的酶是()。ALPB.G6PDCKD.AMYE.LD [单选]最适宜的腮腺超声检查方法A.空腹B.理发后C.应用凸阵探头D.应用高频线阵探头E.只行纵切检查 [单选,A2型题,A1/A2型题]生理性红细胞沉降率增快可见于()A.细菌感染B.肺结核C.女性月经期D.大手术E.旷巨球蛋白血症 [填空题]标准酒度的测量,在()℃温度下进行。 [填空题]抗震设计时高层建筑按其()可分为甲类建筑、乙类建筑、丙类建筑等三类。 [单选]某企业现金收支状况比较稳定,全年的现金需要量为500万元,其每次转换现金转换金额为40万元,每次的转换成本为0.1万元,有价证券的年报酬率为8%,则该企业现有情况持有现金总成本为()万元。A.2.83B.4.75C.2.85D.18.75 [单选]以下肾上腺皮质组织学中,哪一项是错误的A.球状带B.束状带C.网状带D.交感神经节细胞E.A+B+C [单选]危机干预的方式下列哪项除外()A.热线电话B.咨询门诊C.信函与网络D.认知状态E.现场干预 [单选]企业应当以()作为会计核算的记账基础A.权责发生制B.永续盘存制C.收付实现制D.实地盘存制 [单选]钢中炭的含量超过1.00%时,钢材的性能表现为()。A.塑性大B.强度下降C.硬度大D.易于加工 [单选]不可再生自然资源的影子价格应按资源的()计算;可再生自然资源的影子价格应按资源的()计算。A.再生费用,机会成本B.机会成本,再生费用C.机会成本,经济价值D.经济价值,再生费用 [单选]下列对加油站信用卡(银联卡)加油管理制度的描述错误的是()。A、严格执行操作规程,按规定与银行交换数据,核对加油情况和油款进账情况B、对于需冲销原交易或进行补偿交易的业务,应立即操作C、读写银联卡的机器出现故障时,操作人员应立即终止刷卡结算操作D、在月末前将 [单选,A2型题,A1/A2型题]下面不属于病史主诉的为()A.治疗过程B.症状C.病程D.停经天数E.腹痛天数 [单选]传输层模式可分为().A.电路模式.分组模式.贴中继模式和ATM模式B.PDH.SDH.ATM模式C.铜线系统.同轴电缆系统.光纤接入系统等 [单选]鼻咽癌患者Ⅸ、Ⅹ、Ⅺ、Ⅻ脑神经受累的原因是()A.局部扩散B.血行转移C.脑转移D.种植转移E.转移淋巴结压迫所致 [单选,A型题]具有完整细胞壁的微生物是()A.支原体B.衣原体C.细菌L型D.噬菌体E.人体细胞 [单选,A1型题]下列哪一项不符合复杂性高热惊厥的诊断标准()A.发作呈全身性,有时呈局限性发作B.惊厥持续时间常超过15minC.惊厥在24h内有反复发作D.发作后无神经系统异常E.发作后有暂时性麻痹
