勾股定理证明题
勾股定理十六种证明方法
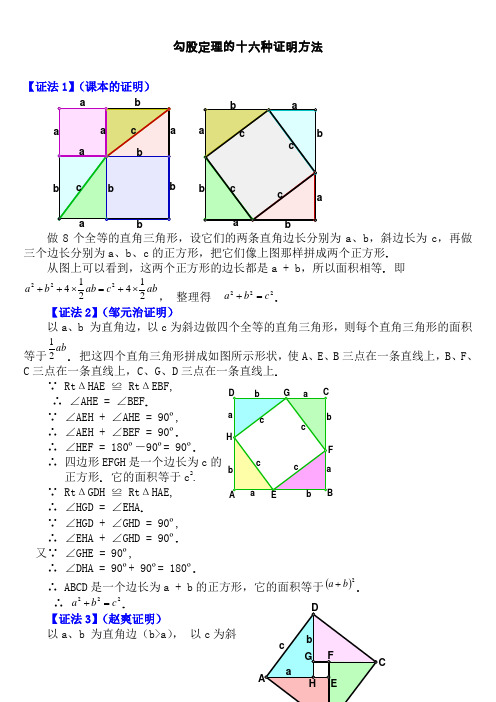
勾股定理的十六种证明方法【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21.把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴ 222c b a =+. 【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +. ∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P . 过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ ,∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明).【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD . 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点L . ∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD , ∵ ΔFAB 的面积等于221aΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a 同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º,∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB , 即 AB AD AC •=2.同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC •=2. ∴ ()222AB AB DB AD BC AC =•+=+,即 222c b a =+. 【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º,∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c , ∴ Rt ΔDHA ≌ Rt ΔBCA .∴ DH = BC = a ,AH = AC = b . 由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE . 又∵ ∠BTH = ∠BEA = 90º, BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a , ∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC •=2=()()BD AB BE AB -+=()()a c a c -+= 22a c -,即222a c b -=,∴ 222c b a =+.【证法12】在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=,∴ 222c b a =+.【证法13】(作直角三角形的内切圆证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC 21=∆,∴ ABC S ab ∆=42, 又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+.【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中,∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B , ∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a ba 2222++=+;把正方形ABCD划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图). 在EH = b 上截取ED = a ,连结DA 、则 AD = c .∵ EM = EH + HM = b + a , ED = a ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a , ∠AED = 90º, AE = b , ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º,D∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中,∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
勾股定理的证明(最全证明)

勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即ab c ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF ,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE , ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90º,∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE,∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE ,∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠D EC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD , ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD , ∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º.即 ∠CBD= 90º.又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ,交AC 于点P .过点B 作BM ⊥PQ ,垂足为M ;再过点F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明).【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD . 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点L .∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD , ∵ ΔFAB 的面积等于221a , ΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a . 同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积 = 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+.【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中, ∵ ∠ADC = ∠ACB = 90º, ∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB ,即 AB AD AC ∙=2. 同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC ∙=2.∴ ()222AB AB DB AD BC AC =∙+=+,即 222c b a =+.【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠P AC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c ,∴ Rt ΔDHA ≌ Rt ΔBCA .∴ DH = BC = a ,AH = AC = b . 由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a . ∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA .∴ Rt ΔDGT ≌ Rt ΔDHA . ∴ DH = DG = a ,∠GDT = ∠HDA .又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . T F ⊥AF ,TF = GT ―GF = b ―a . ∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为 543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+∙-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+=812SS b -- . ② 把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +. ∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º,BT = BE = b ,∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a , ∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =. 过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE . ∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a , ∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ,即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC ∙=2=()()BD AB BE AB -+ =()()a c a c -+= 22a c -,即222a c b -=, ∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB ∙+∙=∙, ∵ AB = DC = c ,AD = BC = a ,AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=,∴ 222c b a =+.【证法13】(作直角三角形的内切圆证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵abS ABC 21=∆, ∴ ABC S ab ∆=42,又∵ AOCBOC AOB ABC S S S S ∆∆∆∆++= = brar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+. 【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2,或者 BD AB BC ∙≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中, ∵ ∠A = ∠A , ∴ 若 AD :AC ≠AC :AB ,则 ∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B ,∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a ,连结DA 、DC ,则 AD = c .∵ EM = EH + HM = b + a , ED = a ,∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a , ∠AED = 90º, AE = b ,∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º, ∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º,∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE ,D∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中, ∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=, 76451S S S S S +===, ∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
勾股定理证明练习

图1CA B F D E 勾股定理证明习题1.已知:如图1,点A 、D 、B 、E 在同一条直线上,AD=BE,AC∥DF,BC∥EF. 求证:AC=DF.2.已知:如图2,BE⊥AC,DF⊥AC,垂足分别是E 、F,O 是BD 的中点. 求证:BE=DF.3.已知:如图3, AB=DE,BC=EF,AF=CD. 求证:AB∥DE, BC∥EF.4.已知:如图4, AB=AD,AC=AE, ∠BAD=∠CAE.求证:. ∠B=∠D.5.已知:如图5, AD=AE,点D 、E 在BC 上,BD=CE,∠ADE=∠AED. 求证: ⊿ABE≌⊿ACDA 图2C DB A E F图4E DC BA图3BA CE D F6.已知:如图6, 已知AC 、BD 相交于点O ,AB∥CD, OA=OC.求证: AB=CD7.已知:如图7, 已知AC∥DF,BC=EF ,∠C=∠F. 求证: ⊿ABC≌⊿DEF.8.已知:如图,四边形ABCD 中,AD ∥BC ,AD ⊥DC ,AB ⊥AC ,∠B=45°,CD=2cm. 求证:BC 的长.9.已知:如图,AD 是△ABC 的高,AB=10,AD=8,BC=12。
求证:△ABC 是等腰三角形。
10.已知:如图,在△ABC 中,∠C=90°,∠B=30°,AB 的垂直平分线交BC 于D ,垂足为E ,BD=4cm 。
求AC 的长。
图6O A BDC 图7AB C F E D11.在ABC ∆中,AC AB =,D 为BC 边上任一点,求证:DC BD AD AB ⋅=-2212.已知:如图,在ABC Rt ∆中,90=∠C ,D 是AC 的中点,AB ED ⊥于E求证:(1)22243BD BC AB =+(2)222BC AE BE =-13.如图,在ABC ∆中,90=∠C ,13=AB ,12=BC ,BC BD 21=(1)AD 的长.(2)ABD ∆的面积.14.如图,有一个直角三角形纸片,两直角边AC=6cm ,BC=8cm ,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗?BCADACBDEBC AD C B AD E15.若△ABC 的三边a 、b 、c 满足条件a 2+b 2+c 2+338=10a +24b +26c ,试判断△ABC 的形状.16.已知:如图, ABC 中,AB=AC=10,BC=16,点D 在BC 上,DA ⊥CA 于A 。
勾股定理9种证明(有图)
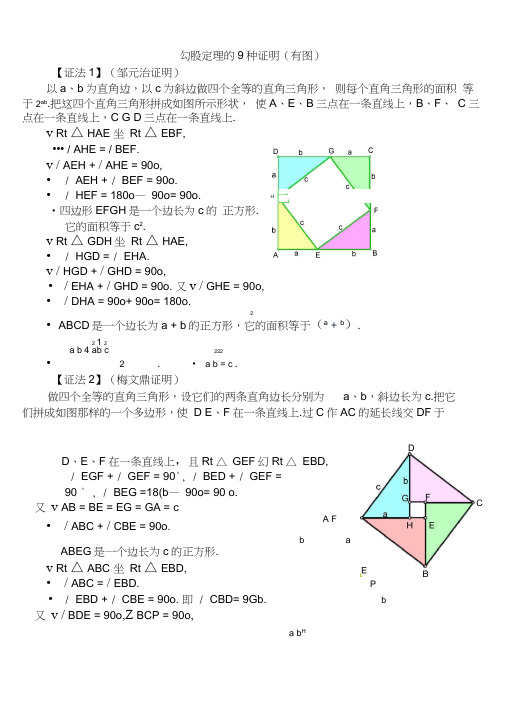
勾股定理的9种证明(有图)【证法1】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形, 则每个直角三角形的面积 等于2ab .把这四个直角三角形拼成如图所示形状, 使A 、E 、B 三点在一条直线上,B 、F 、 C 三点在一条直线上,C G D 三点在一条直线上.v Rt △ HAE 坐 Rt △ EBF, ••• / AHE = / BEF.v / AEH + / AHE = 90o, • / AEH + / BEF = 90o.• / HEF = 180o — 90o= 90o.•四边形EFGH 是一个边长为c 的 正方形.它的面积等于c 2.v Rt △ GDH 坐 Rt △ HAE, • / HGD = / EHA. v / HGD + / GHD = 90o,• / EHA + / GHD = 90o. 又v / GHE = 90o, • / DHA = 90o+ 90o= 180o.2• ABCD 是一个边长为a + b 的正方形,它的面积等于(a + b ).21 2a b 4 ab c222•2. • a b = c .【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为 a 、b ,斜边长为c.把它 们拼成如图那样的一个多边形,使 D E 、F 在一条直线上.过C 作AC 的延长线交DF 于/ EGF + / GEF = 90°, / BED + / GEF = 90 ° , / BEG =18(b — 90o= 90 o. 又 v AB = BE = EG = GA = c• / ABC + / CBE = 90o.v Rt △ ABC 坐 Rt △ EBD, • / ABC = / EBD.• / EBD + / CBE = 90o. 即 / CBD= 9Gb. 又 v / BDE = 90o ,Z BCP = 90o ,D 、E 、F 在一条直线上,且Rt △ GEF 幻Rt △ EBD, ABEG 是一个边长为c 的正方形.a b HH匕DA FbaP bCBC = BD = a.••• BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCB 的面积为S,则21 b S2 ab, 2 1=S 2 ab2 ,a 2 +b 2 =c 2【证法3】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为 a 、b (b>a )c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形,使 直线上. 过点Q 作QP// BC 交AC 于点P. 过点B 作BML PQ 垂足为M ;再过点 F 作FNL PQ 垂足为N.v / BCA = 90o , QP// BC • / MPC = 90o , v BM 丄 PQ• / BMP = 90o ,• BCPM 是一个矩形,即/ MBC = 90o.v / QBM + / MBA = / QBA = 90o , / ABC + / MBA = / MBC = 90o , • / QBM = / ABC又 v / BMP = 90o ,/ BCA = 90o , BQ = BA = c , • Rt △ BMQ 坐 Rt △ BCA.同理可证Rt △ QNF 幻Rt △ AEF.从而将问题转化为【证法4】(梅文鼎证明). 【证法4】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使 在一条直线上,连结BF CD.过 C 作 CL L DE 交AB 于点M 交DE 于点L.v AF = AC , AB = AD,/ FAB = / GAD• △ FAB 坐△ GADE 、A ,斜边长为C 三点在一条 H 、C B 三点 v △ FAB 的面积等于K△ GAD 的面积等于矩形ADLM 的面积的一半,二矩形ADLM 的面积二 同理可证,矩形 MLEE 的面积 v 正方形ADEB 勺面积 =矩形ADLM!勺面积+ /. c 2 a 2 b 2,即 a 2 -【证法5】(杨作玫证明) 做两个全等的直角三角形,设它们的两条直角边长分别为 a 、b (b>a ),斜边长为c. 再做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF 丄AC AF 交GT 于F , AF 交DT 于 R.过B 作BP 丄AF,垂足为 E , DE 交 AF 于 H. v / BAD = 90o ,Z PAC = 90o , ••• / DAH = / BAC. 又 v / DHA = 90o ,Z BCA = 90o , AD = AB = c ,• Rt △ DHA 坐 Rt △ BCA. • DH = BC = a , AH = AC = b. 由作法可知,PBCA 是一个矩形, 所以 Rt △ APB 坐 Rt △ BCA.即 PB = CA = b , AP= a ,从v Rt △ DGT 坐 RtRt △ DHA 坐 Rt• Rt △ DGT 坐 Rt • DH = DG = a , 又 v / DGT = 90o ,2 a . =b 2 矩形MLEB 勺面积 b 2 =c 2. PH = b — a. △ BCA , △ BCA. △ DHA . / GDT = / HDA . / DHF = 90o ,P.过D 作DE 与CB 的延长线垂直,垂足为 / GDH = / GDT + / TDH = / HDA+Z TDH = 90o ,• DGFH 是一个边长为a 的正方形.• GF = FH = a . TF 丄AF , TF = GT — GF = b — a .• TFPB 是一个直角梯形,上底 TF=b-a ,下底BP= b ,高FP=a + (b —a ).用数字表示面积的编号(如图),则以c 为边长的正方形的面积为 c 2 = Si S 2 S 3 S 4 S 51S 8 +S 3 +S 4 =- b + (b - a )】• a + (b -a /v2S5 - S 8' S 9丄21 .S 3S 4-b 2 ab・・ 2把②代入①,得c^S iS 2b 2 -S^S 8S 8S 9①b 2 -1 ab2 ,2=bS2S 9 = b 2 川 a 2【证法6】(李锐证明)设直角三角形两直角边的长分别为 a 、b (b>a ),斜边的长为c.做三个边长分别为a 、 b 、c 的正方形,把它们拼成如图所示形状,使 A 、E 、G 三点在一条直线上.用数字表示 面积的编号(如图).v / TBE = / ABH = 900, ••• / TBH = / ABE. 又 v / BTH = / BEA = 900,BT = BE = b , • Rt △ HBT 坐 Rt △ ABE. • HT = AE = a. • GH = GT — HT = b — a. 又 v / GHF + / BHT = 900,/ DBC + / BHT = / TBH + • / GHF = / DBC.v DB = EB — ED = b — a , / HGF = / BDC = 90o , • Rt △ HGF 坐 Rt △ BDC.即 S ^ S 2.过 Q 作 QM L AG 垂足是 M.由/ BAQ = / BEA = 90o ,可知 / ABE =/ QAM 而 AB = AQ = c ,所以 Rt △ ABE 幻 Rt △ QAM .又 Rt △ HBT 幻Rt △ ABE.所以 Rt △ HBT 幻 Rt △ QAM .即 S 8 二 S 5.由 Rt △ ABE 坐 Rt △ QAM 又得 QM = AE = a ,/ AQM = / BAE.v / AQM + / FQM = 90o ,Z BAE + / CAR = 90o ,Z AQM = / BAE • / FQM = / CAR.【证法7】(利用多列米定理证明)• Rt △ QMF 坐 Rt △ ARC.即 S 4 =S6.• • c 2 =S 1 S 2 S 3 S 4 S 5 a 2 S 6又v S 7 二 S 2 S g 二 S 5 S 4 二 S 6> > >• a 2 b 2 = S ! S 6 S 3 S 7 S 8=S iS 4 S 3 S 2 S 52=c ,即a 2 + b 2 =c 2.又 v / QMF = / ARC = 90o , QM = AR = a , b^ S 3 S 7 S 8R a A在Rt △ ABC 中,设直角边 BC= a , AC= b ,斜边AB = c (如图).过点A 作AD// CB, 过点B 作BD//CA 则ACBD 为矩形,矩形ACBD 内接于一个圆.根据多列米定理,圆内接 四边形对角线的乘积等于两对边乘积之和,有AB ・DC 二 AD ・BC AC *BD ,AB = DC = c , AD = BC = a , AC = BD = b ,AB 2 =BC 2 +AC 2,即 c 2 =a 2 +b 2 a 2 +b 2 =c 2【证法8】(利用反证法证明) 如图,在Rt △ ABC 中,设直角边 AG点C 作CDL AB 垂足是D.假设a 2 b 2=c 2,即假设AC 2 BC —AB 2,则由AB^AB *AB =AB AD BD =AB ・AD AB * BD可知 AC 2 式 AB ・AD ,或者 BC 2 式 AB ・BD .即 AD : AO AG AB 或者 BD : BO BC AB. 在厶ADC 和△ ACB 中, v / A = / A,.若 AD : AW AC AB 」 / AD 字/ ACB.在厶CDB 和△ ACB 中, v / B = / B ,.若 BD BW BC AB,贝S / CDB^Z ACB. 又v / ACB = 90o ,. / AD& 90o ,Z CD 字 90o. 这与作法CDLAB 矛盾.所以,/. a 2 b 2 = c 2.【证法9](辛卜松证明)设直角三角形两直角边的长分别为 a 、b,斜边的长为c.作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为 (a +bf =a +b +2ab ;把正方形ABCD 划分成上方右图所示的几个部分,则正方形 ABCD 勺21 2,.十.(a +b 『=4 乂一ab+c 2面积为 2= 2ab c .2 2 2.. a b 2ab 二 2ab c ,BC 的长度分别为a 、b ,斜边AB 的长为c ,过 AC 2 • BC 2 = AB 2的假设不能成立..a2+b2=c2.。
专题01 勾股定理的证明综合题(原卷版)

专题01 勾股定理的证明(综合题)知识点:勾股定理的证明方法一:将四个全等的直角三角形拼成如图(1)所示的正方形. 图(1)中,所以. 方法二:将四个全等的直角三角形拼成如图(2)所示的正方形. 图(2)中,所以.方法三:如图(3)所示,将两个直角三角形拼成直角梯形. ,所以.一.选择题1.(2022春•龙凤区期中)如图,在四边形ABDE 中,AB ∥DE ,AB ⊥BD ,点C 是边BD 上一点,BC =DE =a ,CD =AB =b ,AC =CE =c.下列结论:易错点拨易错题专训①△ABC≌△CDE;②∠ACE=90°;③四边形ABDE的面积是(a+b)2;④(a+b)2﹣c2=2×ab;⑤该图可以验证勾股定理.其中正确的结论个数是( )A.5B.4C.3D.22.(2022秋•杏花岭区校级月考)下面四幅图中,不能证明勾股定理的是( )A.B.C.D.3.(2022春•威县期末)课堂上,王老师要求学生设计图形来证明勾股定理,同学们经过讨论,给出两种图形,能证明勾股定理的是( )A.①行,②不行B.①不行,②行C.①,②都行D.①,②都不行4.(2022•大观区校级开学)如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形.若图中的直角三角形的一条直角边长为5,大正方形的边长为13,则中间小正方形的面积是( )A.144B.49C.64D.255.(2022春•交城县期中)勾股定理是一个古老的数学定理,它有很多种证明方法,如图所示四幅几何图形中,不能用于证明勾股定理的是( )A.B.C.D.6.(2022春•邕宁区期末)下面图形能够验证勾股定理的有( )A.4个B.3个C.2个D.1个7.(2022•邯郸三模)在证明勾股定理时,甲、乙两位同学分别设计了方案:甲:如图,用四个全等的直角三角形拼成,其中四边形ABDE和四边形CFGH均是正方形,通过用两种方法表示正方形ABDE的面积来进行证明;乙:两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C、D重合,通过用两种方法表示四边形ACBE的面积来进行证明.对于甲、乙两种方案,下列判断正确的是( )A.甲、乙均对B.甲对、乙不对C.甲不对,乙对D.甲、乙均不对8.(2021秋•无锡期末)如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=18,则S2的值是( )A.B.6C.5D.9.(2020春•海陵区期末)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=6,大正方形的面积为16,则小正方形的面积为( )A.8B.6C.4D.3二.填空题10.(2021秋•漳州期末)如图所示的四边形图案是用4个全等的直角三角形拼成的.已知四边形ABCD的面积为64,四边形EFGH的面积为9,若用x、y表示直角三角形的两直角边(x>y);下列四个结论:①x2+y2=64;②x﹣y=3;③x+y=;④2xy+9=64.其中正确的是 .(写出所有正确结论的序号)11.(2021秋•皇姑区期末)把图1中长和宽分别6和4的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2的正方形,则图2中小正方形ABCD的面积为 .12.(2021秋•迎泽区校级月考)“赵爽弦图”是由四个全等的直角三角形拼接而成.如图,若直角三角形的短直角边长为2,小正方形的面积为4,则大正方形边长为 .13.曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为 ,又可以表示为 .对比两种表示方法可得 .化简,可得a2+b2=c2.他的这个证明也就成了数学史上的一段佳话.三.解答题14.(2021秋•东坡区期末)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.将两个全等的直角三角形按如图所示摆放,使点A、E、D 在同一条直线上.利用此图的面积表示式证明勾股定理.15.(2021春•利辛县期中)如图,小明用4个图1中的矩形组成图2,其中四边形ABCD,EFGH,MNPQ都是正方形,证明:a2+b2=c2.16.(2021春•滑县期末)如图是用硬纸板做成的四个全等的直角三角形,两直角边的长分别为a和b,斜边长为c.请你开动脑筋,用它们拼出正方形图案,要求拼图时直角三角形纸片不能互相重叠.(1)请你画出拼成的这个图形的示意图;(2)利用(1)中画出的图形证明勾股定理.17.(2021秋•汝州市期中)用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形.它是美丽的弦图.其中四个直角三角形的直角边长分别为a,b(a<b),斜边长为c.(1)结合图①,求证:a2+b2=c2;(2)如图②,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH.若该图形的周长为24,OH=3,求该图形的面积;(3)如图③,将八个全等的直角三角形紧密地拼接成正方形PQMN,记正方形PQMN、正方形ABCD、正方形EFGH的面积分别为S1、S2、S3,若S1+S2+S3=18,则S2= .18.(2022春•大观区校级期末)如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△DAE,所以∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图形写出一种证明勾股定理的方法.19.(2021秋•武汉月考)2000多年来,人们对直角三角形三边之间的关系的探究颇感兴趣,古往今来,下至平民百姓,上至帝王总统都愿意探究它,研究它的证明,新的证法不断出现.下面给出几种探究方法(由若干个全等的直角三角形拼成如图图形),试用面积法选择其中一种推导直角三角形的三边a、b、c 之间的数量关系(1)三边a、b、c之间的数量关系为 ;(2)理由: .20.(2018•保定二模)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2证明:连接DB ,过点D 作BC 边上的高DF ,则DF =EC =b ﹣a∵S 四边形ADCB =S △ACD +S △ABC =b 2+ab .又∵S 四边形ADCB =S △ADB +S △DCB =c 2+a (b ﹣a )∴b 2+ab =c 2+a (b ﹣a )∴a 2+b 2=c 2请参照上述证法,利用图2完成下面的证明.将两个全等的直角三角形按图2所示摆放,其中∠DAB =90°.求证:a 2+b 2=c 2.。
勾股定理16种经典证明方法

ab c ab b a 214214222⨯+=⨯++【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º,∴ ∠EHA + ∠GHD = 90º.又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a ,∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+.【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明) 做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c , ∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a . ∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P . 过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N .∵ ∠BCA = 90º,QP ∥BC ,∴ ∠MPC = 90º,∵ BM ⊥PQ ,∴ ∠BMP = 90º,∴ BCPM 是一个矩形,即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º, ∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c ,∴ Rt ΔBMQ ≌ Rt ΔBCA . 同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明). 【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD . 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点 L .∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD ,∵ ΔFAB 的面积等于221a ,ΔGAD 的面积等于矩形ADLM的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB∴ 222b ac += ,即 222c b a =+【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º, ∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB . AD ∶AC = AC ∶AB ,即 AB AD AC •=2.同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC •=2.∴ ()222AB AB DB AD BC AC =•+=+,即 222c b a =+.【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形.把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC . 又∵ ∠DHA = 90º,∠BCA = 90º,AD = AB = c , ∴ Rt ΔDHA ≌ Rt ΔBCA . ∴ DH = BC = a ,AH = AC = b .由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a . ∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA .∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+=812SS b -- . ② 把②代入①,得98812212S S S S b S S c ++--++==922S S b ++ = 22a b +. ∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º, BT = BE = b ,∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a .∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º, ∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a , ∠HGF = ∠BDC = 90º, ∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27SS =. 过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE= ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58SS =. 由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=, 又∵27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ,即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC •=2=()()BD AB BE AB -+=()()a c a c -+ = 22a c -,即222a c b -=,∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = bAD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC ADDC AB •+•=•,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222ACBC AB +=,即 222b a c +=, ∴ 222c b a =+.【证法13】(作直角三角形的内切圆证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2. ∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ ab S ABC 21=∆,∴ABC S ab ∆=42, 又∵AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+.【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+• 可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中, ∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则 ∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B ,∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.D D∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a ,连结DA 、DC ,则 AD = c .∵ EM = EH + HM = b + a , ED = a , ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a ,∠AED = 90º, AE = b , ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中,∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=,732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++ =5432S S S S +++=2c∴ 222c b a =+.。
勾股定理16种证明方法

勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE,∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2.∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +. ∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c , ∴ ABEG 是一个边长为c 的正方形∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则abS c 2122⨯+=,∴ 222c b a =+. 【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P . 过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明). 【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD . 过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L . ∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD ,∵ ΔFAB 的面积等于221a ,ΔGAD 的面积等于矩形ADLM的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º,∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB , 即 AB AD AC •=2.同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC •=2. ∴ ()222AB AB DB AD BC AC =•+=+,即 222c b a =+. 【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c ,∴ Rt ΔDHA ≌ Rt ΔBCA . ∴ DH = BC = a ,AH = AC = b .由作法可知, PBCA 是一个矩形,所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a . ∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①,得= 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE . 又∵ ∠BTH = ∠BEA = 90º,BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a , ∠HGF = ∠BDC = 90º, ∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+. 【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得=()()BD AB BE AB -+ =()()a c a c -+= 22a c -,即222a cb -=, ∴ 222c b a =+. 【证法12】在Rt ΔABC 中,设直角边BC . 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=, ∴ 222c b a =+.【证法13】在Rt ΔABC 中,设直角边BC = a ,作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC 21=∆,∴ ABC S ab ∆=42, 又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+.【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中,∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B , ∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+. 【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+. 【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a ,连结DA 、DC , 则 AD = c .∵ EM = EH + HM = b + a , ED = a , ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a ,∠AED = 90º, AE = b , ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中,∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
专题01 勾股定理的证明(解析版)

专题01 勾股定理的证明1.做8个全等的直角三角形,设它们的两条直线边分别为a ,b ,斜边为c ,再做3个边长分别为a ,b ,c 的正方形,把它们按下图所示的方式拼成两个正方形.利用两个正方形的面积相等来证明勾股定理:a 2+b 2=c 2【答案】证明见解析【解析】【分析】根据不同图形拼成的两个正方形面积相等即可证明【详解】证明:①左图大正方形的边长为:a +b ,则面积为(a +b )2,分成了四个直角边为a ,b ,斜边为c 的全等的直角三角形和一个边长为c 的小正方形,()22142a b ab c \+=´+;②右图大正方形的边长为:a +b ,则面积为(a +b )2,分成了边长为a 的一个正方形,边长为b 的一个正方形,还有四个直角边为a ,b ,斜边为c 的全等的直角三角形,()222142a b a b ab \+=++´;综上所述:2142ab c ´+()222142a b a b ab =+=++´,即222+=a b c .【点睛】本题考查利用图形面积的关系证明勾股定理,解题关键是利用三角形和正方形边长的关系进行组合图形.2.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,也可以用面积法来证明勾股定理,请完成证明过程.(提示:BD 和AC 都可以分割四边形ABCD )【答案】证明见解析【解析】【详解】如图,连接DB,过点D作BC边上的高DF,根据S四边形ADCB=S△ACD+S△ABC=S△ADB+S△DCB 即可求解.【解答】证明:如图,连接DB,过点D作BC边上的高DF,则DF=EC=b﹣a.∵S四边形ADCB=S△ACD+S△ABC=12b2+12ab.又∵S四边形ADCB=S△ADB+S△DCB=12c2+12a(b﹣a)∴12b2+12ab=12c2+12a(b﹣a)∴a2+b2=c2.【点睛】本题考查了等面积法证明勾股定理.解题得关键在于利用等面积法进行证明.3.如图,四边形ACFD是一个边长为b的正方形,延长FC到B,使BC=a,连接AB,使AB=C;E是边DF上的点且DE=a.(1)判断△ABE的形状,并证明你的结论;(2)用含b的式子表示四边形ABFE的面积;(3)求证:a2+b2=c2.【答案】(1)△ABE 是等腰直角三角形,证明见解析;(2)b 2;(3)证明见解析.【解析】【分析】(1)由题意可以得到△ADE ≌△ACB ,从而得到△ABE 是等腰直角三角形;(2)由(1)可得四边形ABFE 的面积=正方形ACFD 的面积=b 2;(3)由(2)可得正方形ACFD 的面积=△ABE 的面积+△BEF 的面积,把a 、b 、c 代入上式即可整理得a 2+b 2=c 2.【详解】解:(1)△ABE 是等腰直角三角形,理由如下:∵四边形ACFD 是正方形,∴AC =AD ,∠D =∠DAC =∠ACB =90°,∵CB =a =DE ,∴△ADE ≌△ACB ,∴AB =AE ,∠BAC =∠EAD ,∴∠BAE =90°,∴△ABE 是等腰直角三角形.(2)∵△ADE ≌△ACB ,∴四边形ABFE 的面积=正方形ACFD 的面积=b 2.(3)证明:∵四边形ABFE 的面积=△ABE 的面积+△BEF 的面积,∴正方形ACFD 的面积=△ABE 的面积+△BEF 的面积,∴()()221122b c b a b a =++-,∴22222b c b a =+-,∴a 2+b 2=c 2.【点睛】本题考查正方形的综合应用,熟练掌握正方形的性质、三角形全等的判定与性质、等腰直角三角形的判定方法、三角形与四边形面积的灵活计算是解题关键 .4.如图,小明用6个图1中的矩形组成图2,其中四边形ABCD ,EFGH ,MNPQ 都是正方形,证明:222+=a b c .【答案】见解析【解析】【分析】根据4BEF ABCD EFGH S S S =+V 正方形正方形,列式计算即可求解.【详解】证明:由图得:4BEF ABCD EFGH S S S =+V 正方形正方形,∴()22142a b c ab +=+´,整理得:22222a ab b c ab ++=+,∴222a b c +=.【点睛】本题考查了勾股定理的证明,得到4BEF ABCD EFGH S S S =+V 正方形正方形是解题的关键.5.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt ABC V 中,90ACB Ð=°,若AC b =,BC a =,请你利用这个图形说明222+=a b c ;【答案】见解析【解析】【分析】根据题意,可在图中找出等量关系,由大正方形的面积等于中间的小正方形的面积加上四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式.【详解】解:∵大正方形面积为2c ,直角三角形面积为12ab ,小正方形面积为()2b a -,∴()222214222c ab b a ab b ab a =´+-=+-+,即222c a b =+.【点睛】本题考查了对勾股定理的证明,解决问题的关键是在图中找出等量关系.7.勾股定理被誉为“几何明珠”,在数学的发展历程中占有举足轻重的地位.它是初中数学中的重要知识点之一,也是初中学生以后解决数学问题和实际问题中常常运用到的重要知识,因此学好勾股定理非常重要.学习数学“不仅要知其然,更要知其所以然”,所以,我们要学会勾股定理的各种证明方法.请你利用如图图形证明勾股定理:已知:如图,四边形ABCD 中,BD ⊥CD ,AE ⊥BD 于点E ,且△ABE ≌△BCD .求证:AB 2=BE 2+AE 2.【答案】证明见解析【解析】【分析】连接AC ,根据四边形ABCD 面积的两种不同表示形式,结合全等三角形的性质即可求解.【详解】解:连接AC ,∵△ABE ≌△BCD ,∴AB =BC ,AE =BD ,BE =CD ,∠BAE =∠CBD ,∵∠ABE +∠BAE =90°,∴∠ABE +∠CBE =90°,∴∠ABC =90°,∴S 四边形ABCD =2111111222222ABD BDC S S BD AE BD CD AE AE BD BE AE BD BE D D +=×+×=×+×=+×,又∵S 四边形ABCD =2111111222222ABC ADC S S AB BC CD DE AB AB BE DE AB BE DE D D +=×+×=×+×=+×,2211112222AE BD BE AB BE DE +×=+×Q ,∴AB 2=AE 2+BD •BE -BE •DE ,∴AB 2=AE 2+(BD -DE )•BE ,即AB 2=BE 2+AE 2.【点睛】本题考查了勾股定理的证明,解题时,利用了全等三角形的对应边相等,对应角相等的性质.8.【经典回顾】梅文鼎是我国清初著名的数学家,他在《勾股举隅》中给出多种证明勾股定理的方法图1是其中一种方法的示意图及部分辅助线.在ABC V 中,90ACB Ð=°,四边形ADEB 、ACHI 和BFGC 分别是以Rt ABC V 的三边为一边的正方形.延长IH 和FG ,交于点L ,连接LC 并延长交DE 于点J ,交AB 于点K ,延长DA 交IL 于点M .(1)证明:AD LC =;(2)证明:正方形ACHI 的面积等于四边形ACLM 的面积;(3)请利用(2)中的结论证明勾股定理.(4)【迁移拓展】如图2,四边形ACHI 和BFGC 分别是以ABC V 的两边为一边的平行四边形,探索在AB 下方是否存在平行四边形ADEB ,使得该平行四边形的面积等于平行四边形ACHI 、BFGC 的面积之和.若存在,作出满足条件的平行四边形ADEB (保留适当的作图痕迹);若不存在,请说明理由.【答案】(1)见解析(2)见解析(3)见解析(4)存在,见解析【解析】【分析】(1)根据正方形的性质和SAS 证明△ACB ≌△HCG ,可得结论;(2)证明S △CHG =S △CHL ,所以S △AMI =S △CHL ,由此可得结论;(3)证明正方形ACHI 的面积+正方形BFGC 的面积=▱ADJK 的面积+▱KJEB 的面积=正方形ADEB,可得结论;(4)如图2,延长IH和FG交于点L,连接LC,以A为圆心CL为半径画弧交IH于一点,过这一点和A作直线,以A为圆心,AI为半径作弧交这直线于D,分别以A,B为圆心,以AB,AI为半径画弧交于E,连接AD,DE,BE,则四边形ADEB即为所求.(1)证明:如图1,连接HG,∵四边形ACHI,ABED和BCGF是正方形,∴AC=CH,BC=CG,∠ACH=∠BCG=90°,AB=AD,∵∠ACB=90°,∴∠GCH=360°﹣90°﹣90°﹣90°=90°,∴∠GCH=∠ACB,∴△ACB≌△HCG(SAS),∴GH=AB=AD,∵∠GCH=∠CHI=∠CGL=90°,∴四边形CGLH是矩形,∴CL=GH,∴AD=LC;(2)证明:∵∠CAI=∠BAM=90°,∴∠BAC=∠MAI,∵AC=AI,∠ACB=∠I=90°,∴△ABC ≌△AMI (ASA ),由(1)知:△ACB ≌△HCG ,∴△AMI ≌△HGC ,∵四边形CGLH 是矩形,∴S △CHG =S △CHL ,∴S △AMI =S △CHL ,∴正方形ACHI 的面积等于四边形ACLM 的面积;(3)证明:由正方形ADEB 可得AB DE ∥,又AD LC P ,所以四边形ADJK 是平行四边形,由(2)知,四边形ACLM 是平行四边形,由(1)知,AD LC =,所以ACHI ADJK ACLM S S S ==正方形平行四边形平行四边形,延长EB 交LG 于Q ,同理有BFGC KJEB CBQL S S S ==正方形平行四边形平行四边形,所以+ACHI BFGC ADEB ADJK KJEB S S S S S +==正方形正方形正方形平行四边形平行四边形.所以222AC BC AB +=.(4)解:如图为所求作的平行四边形ADEB .【点睛】本题是四边形的综合题,考查的是全等三角形的性质和判定,平行四边形的性质和判定,矩形的性质和判定,正方形的性质,勾股定理的证明等知识;熟练掌握正方形的性质和全等三角形的判定与性质,根据图形面积的关系证出勾股定理是解题的关键,属于中考常考题型.9.阅读理解下列材料,并解决相应的问题.材料一:对角线互相垂直的四边形的面积等于对角线乘积的一半.如图1,四边形ABCD 中,若AC BD ^,则12ABCD S AC BD =×四边形.材料二:人教版教材八年级下册介绍了几种利用全等直角三角形通过拼图证明勾股定理的方法.这些方法的共同特点:利用两种不同的方法计算同一个拼图的面积,然后建立等量关系,化简即可证明勾股定理.小文发现:把两块全等的直角三角板ACB 和直角三角板DEF 摆成图2的形状,点C 与点F 重合,并且点C ,E ,B 在同一条直线上,连接DA ,DB .利用这种摆放方式,也能证明勾股定理.问题:如图2,已知(),90,,,ABC CDE ACB DEC BC DE a AC CE b a b Ð=Ð=°====>△≌△AB CD c ==,AB ,CD 交于点O .求证:(1)AB CD ^;(2)222+=a b c .【答案】(1)见解析(2)见解析【解析】【分析】(1)根据全等三角形的性质得到∠CAB =∠DCE ,利用等角的余角相等得到结论(2)根据四边形的对角线垂直得到四边形的面积,再利用BDE ACBD ACED S S S =+V 四边形梯形得到四边形的面积,即可得到结论.(1)证明:∵△ABC ≌△CDE ,∴∠CAB =∠DCE ,∵∠DCE +∠ACO =90°,∴∠CAB +∠ACO =90°,∴∠AOC =90°,即AB ⊥CD ;(2)∵四边形ACBD 中,若AB ⊥CD ,∴21122ACBD S AB CD c =×=四边形.∵BDEACBD ACED S S S =+V 四边形梯形=()1122AC DE CE DE BE +×+×=()()1122b b a a a b ++-=221122b a +,∴222111222b ac +=,即222+=a b c .【点睛】此题考查了全等三角形的性质,应用题意的结论进行推论论证,正确理解题意并应用是解题的关键.10.数学王老师在探索乘法公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,我国三国时期的数学家赵爽创造了一幅“勾股圆方图”(也称“赵爽弦图”)证明了勾股定理.2002年在北京召开的国际数学家大会把“赵爽弦图”作为会徽(如图1),彰显了这一中国古代的重大成就.运用“赵爽弦图”证明勾股定理的基本思路如下:“赵爽弦图”是将四个完全相同的直角三角形(如图2,其中构成直角的两条边叫直角边,边长分别为a 和b ,且a b <;最长的那条边叫做斜边,边长为c )围成一个边长为c 的大正方形(如图3),中间空的部分是一个边长为b a -的小正方形.(1)验证过程:大正方形的面积可以表示为2S c =,又可用四个直角三角形和一个小正方形的和表示为214()2S ab b a =´+-,∴2214()2c ab b a =´+-.化简等号右边的式子可得∴2c =_______.即直角三角形两直角边的平方和等于斜边的平方.(2)爱动脑筋的小新把这四个相同的直角三角形拼成了另一个大的正方形(如图4),模仿上述过程也能验证这个结论,请你帮助小新完成验证的过程.【答案】(1)a 2+b 2;(2)见解析【解析】【分析】(1)化简等号右边的式子,即可得出答案;(2)利用以c为边的正方形和4个直角三角形的面积和等于以边为a+b的正方形的面积建立方程,即可得出结论.(1)解:(1)验证过程:大正方形的面积可以表示为S=c2,又可用四个直角三角形和一个小正方形的和ab+(b-a)2,表示为S=4×12ab+(b-a)2.∴c2=4×12化简等号右边的式子可得c2=a2+b2.即直角三角形两直角边的平方和等于斜边的平方.故答案为:a2+b2;(2)如图4,∵大的正方形的面积可以表示为(a+b)2,ab,大的正方形的面积又可以表示为c2+4×12∴c2+2ab=a2+b2+2ab,∴a2+b2=c2.【点睛】本题考查了勾股定理的证明.求面积时,利用了“分割法”.11.阅读理解:我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中,汉代数学家赵爽为了证明勾股定理,创制了一幅如图1所示的“弦图”,后人称之为“赵爽弦图”(边长为c的大正方形中放四个全等的直角三角形,两直角边长分别为a,b,斜边长为c).(1)请根据“赵爽弦图”写出勾股定理的推理过程;探索研究:(2)小亮将“弦图”中的2个三角形进行了运动变换,得到图2,请利用图2证明勾股定理;问题解决:(3)如图2,若6a =,8b =,此时空白部分的面积为__________;(4)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为24,3OC =,求该风车状图案的面积.【答案】(1)见详解;(2)见详解;(3)52;(4)24.【解析】【分析】(1)运用等面积法4S S S =+△小正方形大正方形计算即可;(2)连接大正方形一条对角线,运用等面积法2BDE ACDE S S S =+△△梯形化简计算即可;(3)先用勾股定理计算出c ,再利用2S S S =-△空白大正方形计算面积即可;(4)将风车周长表示出来4()24C c b a =+-=风车,其中a =OC =3,得到b 、c 的等量关系,再结合勾股定理求解出b ,最后计算面积即可.(1)证明:由图可知,每个直角三角形的面积为12S ab =△,空白小正方形的面积为2()S b a =-小正方形,整个围成的大正方形的面积为2S c =大正方形,∵4S S S =+△小正方形大正方形,即2222221()4222c b a ab b a ab ab b a =-+×=+-+=+,故222c b a =+;(2)如下图所示,连接大正方形一条对角线DE可知2BDE ACDE S S S =+△△梯形 ,其中,1()()2ACDE S a b a b =++梯形,212BDE S c =△,12S ab =△,代入可得,22111()2222a b ab c +=×+,即222+=a b c ;(3)由图2可知,2S S S =-△空白大正方形,∵6a =,8b =,∴10c ==,则2S c =大正方形=100,∴21210068522S c ab =-×=-×=空白,故空白部分的面积为52;(4)由题意可知,风车的周长为4()24C c b a =+-=风车 ,其中OC =a =3,代入上式可得c +b =9,则c =9-b ,且222+=a b c ,即2229c b a -==,将c =9-b 代入得,22(9)9b b --=,解得b =4,则1144342422S ab =×=×××=风车.【点睛】本题考查了勾股定理的证明与运用,灵活掌握等面积法在证明勾股定理中的作用是解题的关键.12.勾股定理在全世界有超过400种证法,下面介绍欧几里得的证法:(不得直接运用勾股定理结论进行证明)在Rt ABC V 中,90ACB Ð=°分别以AB ,BC ,AC 为边向Rt ABC V 外侧做正方形,求正方形,分别得到正方形ACDE ,正方形BCJK ,正方形ABGF .(1)如图1,连接CF ,BE ,试证明线段CF 和线段BE 的数量关系.(2)如图2,过点C 作直线l AB ^交正方形ABGF 中AB 边于点H ,FG 边于点I ,求证:ACDE AHIF S S =正方形长方形.(3)设BC a =,AC b =,AB c =,运用此图合勾股定理的学习经验证明结论:222+=a b c .(不得直接运用勾股定理结论证明)【答案】(1)EB =CF ,证明见解析(2)见解析(3)见解析【解析】【分析】(1)连接BE ,CF ,再证明EAB CAF SAS ()△≌△即可;(2)首先得出,·ACDE S EA AC =正方形,·AHIF S AF AH =长方形,再根据EAB CAF △≌△可得结论;(3)根据第第二问结论,可得出ACDE AHIF S S =正方形长方形,BCJK BGHI S S =正方形长方形即可证明.(1)解:如图,连接BE ,CF∵ACDE ,BCJK 为正方形∴AC =AE ,AB =AF ,∠EAC =90°,∠BAF =90°EAB CAF Ð=Ð∴EAB CAF SAS ()△≌△ ∴EB =CF .(2)证明:过B 作BR EA ^于点R ,·ACDE S EA AC =正方形.1·2EAB S EA BR =V .∵BR =AC ∴12ACDE S 正方形=EAB S V (同底等高三角形面积是长方形的一半)·AHIF S AF AH =长方形.1·2FAC S AF SC =V .∵AH =SC ∴12FAC AHIF S S =V 长方形又∵EAB CAF△≌△∴EAB FACS S =V V ∴ACDE AHIF S S =正方形长方形.(3)证明:如图,已知ACDE AHIFS S =正方形长方形同理可证BCJK BGHIS S =正方形长方形∴ACDE BCJK AHIF BGHI S S S S +=+正方形正方形长方形长方形.即ACDE BCJK ABGFS S S +=正方形正方形正方形又∵2ACDE S b =正方形,2BCJK S a =正方形,2ABGF S c=正方形∴222+=a b c .【点睛】本题考查了勾股定理的验证,理解题意根据图形,找出等量关系是解题的关键.13.(1)阅读理解我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.根据“赵爽弦图”写出勾股定理和推理过程;(2)问题解决勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形ACDE 的中心O ,作FG ⊥HP ,将它分成4份,所分成的四部分和以BC 为边的正方形恰好能拼成以AB 为边的正方形.若AC =12,BC =5,求EF 的值.【答案】(1)222+=a b c ,见解析;(2)EF 为172或72【解析】【分析】(1)根据大正方形的面积等于4个直角三角形的面积与小正方形的面积和证明;(2)分a >b 和a <b 两种情况求解.【详解】解:(1)222+=a b c (直角三角形两条直角边的平方和等于斜边的平方),证明如下:∵如图①,∵△ABE ≌△BCF ≌△CDG ≌△DAH ,∴AB =BC =CD =DA =c ,∴四边形ABCD 是菱形,∴∠BAE +∠HAD =90°,∴四边形ABCD 是正方形,同理可证,四边形EFGH 是正方形,且边长为(b ﹣a ),∵=4+ABE ABCD EFGHS S S △正方形正方形∴2211=4+()22c ab a b ´´´-,∴222+=a b c (2)由题意得:正方形ACDE 被分成4个全等的四边形,设EF =a ,FD =b ,分两种情况:①a >b 时,∴a +b =12,∵正方形ABIJ 是由正方形ACDE 被分成的4个全等的四边形和正方形CBLM 拼成,∴E 'F '=EF ,KF '=FD ,E 'K =BC =5,∵E 'F '﹣KF '=E 'K ,∴a ﹣b =5,∴=125a b a b +ìí-=î解得:a =172,∴EF =172;②a <b 时,同①得:=125a b b a +ìí-=î,解得:a =72,∴EF =72;综上所述,EF 为172或72.【点睛】本题考查了勾股定理的证明和应用,熟练掌握面积法证明勾股定理,并灵活运用是解题的关键.14.勾股定理是人类重大科学发现之一.我国古代数学书《周髀算经》记载,约公元前11世纪,我国古代劳动人民就知道“若勾三,股四,则弦五”,比西方早500多年.请你运用学到的知识、方法和思想探究以下问题.【探究一】我国汉代数学家赵爽创制了“赵爽弦图”,通过图形切割、拼接,巧妙地利用面积关系证明了勾股定理.古往今来,人们对勾股定理的证明一直保持着极大的热情.意大利著名画家达·芬奇用两张一样的纸片,拼出不一样的空洞,利用空洞面积相等也成功地证明了勾股定理(如图).请你写出这一证明过程(图中所有的四边形都是正方形,三角形都是直角三角形).【探究二】在学习勾股定理的过程中,我们获得了以下数学活动经验:分别以直角三角形的三边为边向外侧作正方形(如图2),它们的面积1S,2S,3S之间满足的等量关系是:__________.迁移应用:如图3,图中所有的四边形都是正方形,三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,3,2,则正方形E的面积是________.【探究三】如图4,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积1S,2S,3S之间满足的等量关系是________.迁移应用:如图5,直角三角形的两条直角边长分别为a ,b ,斜边长为c ,分别以三边为直径作半圆.若5a =,13c =,则图中阴影部分的面积等于________.【探究四】《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尺.问索长几何.译文:今有一竖立着的木柱,在木桩的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺.牵着绳索(绳索与地面接触)退行,在距木柱根部8尺处时绳索用尽.问绳索长多少?【答案】【探究一】:见解析;【探究二】:S 1+S 2=S 3;迁移应用:47;【探究三】S 1+S 2=S 3;迁移应用:30;【探究四】绳索长为736尺.【解析】【分析】【探究一】根据直角三角形以及正方形的面积公式计算即可解决问题.【探究二】由正方形面积公式以及勾股定理得S 1+S 2=S 3;迁移应用:根据正方形的面积公式,结合勾股定理,能够导出正方形A ,B ,C ,D 的面积和即为正方形E 的面积;【探究三】利用直角△ABC 的边长就可以表示出半圆S 1、S 2、S 3的大小;迁移应用:求出阴影部分的面积等于直角三角形的面积,然后列式计算即可得解;【探究四】设绳索长为x尺,根据勾股定理列出方程解答即可.【详解】解:【探究一】:由题意得:②的面积为a2+b2+212´ab=a2+b2+ab;图③的面积为c2+212´ab=c2+ab,∴a2+b2+ab=c2+ab,即a2+b2=c2;【探究二】S1+S2=S3.证明如下:∵S3=c2,S1=a2,S2=b2,∴S1+S2=a2+b2=c2=S3;故答案为:S1+S2=S3;迁移应用:根据勾股定理的几何意义,可知SE=SF+SG=SA+SB+SC+SD=32+52+32+22=47;故答案为:47;【探究三】S1+S2=S3.证明如下:∵S3=18πc2,S1=18πa2,S2=18πb2,∴S1+S2=18πa2+18πb2=18πc2=S3;故答案为:S1+S2=S3;迁移应用:阴影部分面积和=S1+S2+12ab-S3=12ab,∵a=5,c=13,∴b==12,∴阴影部分面积和=12×5×12=30,故答案为:30;【探究四】设绳索长为x尺,根据题意得:x2-(x-3)2=82,解得:x=736,答:绳索长为736尺.【点睛】本题考查了勾股定理的证明及应用,读懂题目材料的信息并用两种方法准确表示出同一个图形的面积是解题的关键.。
勾股定理16种证明方法

勾股定理的证明之邯郸勺丸创作【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长辨别为a 、b,斜边长为c,再做三个边长辨别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即ab c ab b a 214214222⨯+=⨯++,整理得222c b a =+. 【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21.把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵RtΔHAE ≌RtΔEBF,∴∠AHE = ∠BEF.∵∠AEH + ∠AHE = 90º,∴∠AEH + ∠BEF = 90º.∴∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c2.∵RtΔGDH ≌RtΔHAE,∴∠HGD = ∠EHA.∵∠HGD + ∠GHD = 90º,∴∠EHA + ∠GHD = 90º.又∵∠GHE = 90º,∴∠DHA = 90º+ 90º= 180º.∴ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴222c b a =+. 【证法3】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状.∵RtΔDAH ≌ RtΔABE,C∴∠HDA = ∠EAB.∵∠HAD + ∠HAD = 90º,∴∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c2.∵EF = FG =GH =HE = b―a ,∠HEF = 90º.∴EFGH 是一个边长为b―a 的正方形,它的面积等于()2a b -.∴()22214c a b ab =-+⨯.∴222c b a =+.【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵RtΔEAD ≌RtΔCBE,∴∠ADE = ∠BEC.∵∠AED + ∠ADE = 90º,∴∠AED + ∠BEC = 90º.∴∠DEC = 180º―90º= 90º.∴ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵∠DAE = 90º, ∠EBC = 90º,∴ AD∥BC.∴ABCD 是一个直角梯形,它的面积等于()221b a +.∴()222121221c ab b a +⨯=+.∴222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长辨别为a 、b ,斜边长为c. 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P.∵D、E 、F 在一条直线上,且RtΔGEF ≌RtΔEBD,∴∠EGF = ∠BED,∵∠EGF + ∠GEF = 90°,∴∠BED + ∠GEF = 90°,∴∠BEG =180º―90º= 90º.C 又∵AB = BE = EG = GA = c,∴ABEG是一个边长为c的正方形.∴∠ABC + ∠CBE = 90º.∵RtΔABC ≌RtΔEBD,∴∠ABC = ∠EBD.∴∠EBD + ∠CBE = 90º.即∠CBD= 90º.又∵∠BDE = 90º,∠BCP = 90º,BC = BD = a.∴BDPC是一个边长为a的正方形.同理,HPFG是一个边长为b的正方形.设多边形GHCBE的面积为S,则abSc2122⨯+=,∴222cba=+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长辨别为a、b(b>a) ,斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形,使E、A、C三点在一条直线上.过点Q作QP∥BC,交AC于点P.过点B作BM⊥PQ,垂足为M;再过点F作FN⊥PQ,垂足为N.∵∠BCA = 90º,QP∥BC,∴∠MPC = 90º,∵BM⊥PQ,∴∠BMP = 90º,∴BCPM是一个矩形,即∠MBC = 90º.∵∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º,∴∠QBM = ∠ABC,又∵∠BMP = 90º,∠BCA = 90º,BQ = BA = c,∴RtΔBMQ ≌RtΔBCA.同理可证RtΔQNF ≌RtΔAEF.从而将问题转化为【证法4】(梅文鼎证明).【证法7】(欧几里得证明)做三个边长辨别为a、b、c的正方形,把它们拼成如图所示形状,使H、C、B三点在一条直线上,连结BF、CD. 过C作CL⊥DE,交AB于点M,交DE于点L.∵AF = AC,AB = AD,∠FAB = ∠GAD,∴ΔFAB ≌ΔGAD,∵ΔFAB 的面积等于221a ,ΔGAD 的面积等于矩形ADLM的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积∴222b a c += ,即 222c b a =+.【证法8】(利用相似三角形性质证明)如图,在RtΔABC 中,设直角边AC 、BC 的长度辨别为a 、b,斜边AB 的长为c,过点C 作CD⊥AB,垂足是D.在ΔADC 和ΔACB 中,∵∠ADC = ∠ACB = 90º,∠CAD = ∠BAC,∴ΔADC ∽ΔACB.AD∶AC = AC ∶AB,即AB AD AC •=2.同理可证,ΔCDB ∽ΔACB,从而有AB BD BC •=2.∴()222AB AB DB AD BC AC =•+=+,即 222c b a =+.【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长辨别为a 、b (b>a ),斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF⊥AC,AF 交GT 于F,AF 交DT 于R. 过B 作BP⊥AF,垂足为P. 过D 作DE 与CB 的延长线垂直,垂足为E,DE 交AF 于H.∵∠BAD = 90º,∠PAC = 90º,∴∠DAH = ∠BAC.又∵∠DHA = 90º,∠BCA = 90º,AD = AB = c,∴RtΔDHA ≌RtΔBCA.∴DH = BC = a,AH = AC = b.由作法可知, PBCA 是一个矩形,所以 RtΔAPB ≌RtΔBCA. 即PB =CA = b,AP= a,从而PH = b―a.∵RtΔDGT ≌RtΔBCA ,RtΔDHA ≌RtΔBCA. ∴RtΔDGT ≌RtΔDHA .∴DH = DG = a,∠GDT = ∠HDA .又∵∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º,∴DGFH 是一个边长为a 的正方形.∴GF = FH = a . TF⊥AF,TF = GT―GF = b―a .∴ TFPB 是一个直角梯形,上底TF=b―a,下底BP= b,高FP=a +(b―a). 用数字暗示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++=①∵()[]()[]a b a a b b S S S -+•-+=++21438= ab b 212-, 985S S S +=,∴824321S ab b S S --=+= 812S S b --.② 把②代入①,得= 922S S b ++ = 22a b +.∴222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长辨别为a 、b (b>a ),斜边的长为c. 做三个边长辨别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字暗示面积的编号(如图).∵∠TBE = ∠ABH = 90º,∴∠TBH = ∠ABE.又∵∠BTH = ∠BEA = 90º,BT = BE = b,∴RtΔHBT ≌RtΔABE.∴HT = AE = a.∴GH = GT―HT = b―a.又∵∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º,∴∠GHF = ∠DBC.∵ DB = EB―ED = b―a,∠HGF = ∠BDC = 90º,∴RtΔHGF ≌RtΔBDC. 即27S S=.过Q 作QM⊥AG,垂足是M. 由∠BAQ = ∠BEA = 90º,可知∠ABE= ∠QAM,而AB = AQ = c,所以RtΔABE ≌RtΔQAM . 又RtΔHBT ≌ RtΔABE. 所以RtΔHBT ≌RtΔQAM .即58S S =.由RtΔABE ≌RtΔQAM,又得QM = AE = a,∠AQM = ∠BAE.∵∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE,∴∠FQM = ∠CAR.又∵∠QMF = ∠ARC = 90º,QM = AR = a,∴RtΔQMF ≌RtΔARC. 即64S S =.∵543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵27S S=,58S S =,64S S =,∴8736122S S S S S b a ++++=+=52341S S S S S ++++=2c ,即222c b a =+.【证法11】(利用切割线定理证明)在RtΔABC 中,设直角边BC = a,AC = b,斜边AB = c. 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线辨别于D 、E,则BD = BE = BC = a. 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得=()()BD AB BE AB -+=()()a c a c -+=22a c -,即222ac b -=,∴222c b a =+.【证法12】(利用多列米定理证明)在RtΔABC 中,设直角边BC = a,AC = b,斜边AB = c为矩形,矩形ACBD 内接于一个圆. 按照多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•,∵ AB = DC = c,AD = BC = a,AC = BD = b,∴222AC BC AB +=,即 222b a c +=,∴222c b a =+.【证法13】(作直角三角形的内切圆证明)在RtΔABC 中,设直角边BC = a,AC = b,斜边AB = c. 作RtΔABC ,设⊙O的半径为r.∵ AE = AF,BF = BD,CD = CE,∴()()()BF AF CD BD CE AE AB BC AC +-+++=-+=CD CE += r + r = 2r,即r c b a 2=-+, ∴c r b a +=+2.∴()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC21=∆,∴ABC S ab ∆=42,又∵AO C BO CAO B ABCS S S S∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2, ∴()ABC S rc r∆=+442,∴()ab rc r242=+,∴22222c ab ab b a +=++, ∴222c b a =+.【证法14】(利用反证法证明)如图,在RtΔABC 中,设直角边AC 、BC 的长度辨别为a 、b,斜边AB 的长为c,过点C 作CD⊥AB,垂足是D.假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC≠AC:AB,或者 BD :BC≠BC:AB.在ΔADC 和ΔACB 中,∵∠A = ∠A,∴若 AD :AC≠AC:AB,则∠ADC≠∠ACB.在ΔCDB 和ΔACB 中,∵∠B = ∠B,∴若BD :BC≠BC:AB,则∠CDB≠∠ACB.又∵∠ACB = 90º,∴∠ADC≠90º,∠CDB≠90º.这与作法CD⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不克不及成立.∴222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长辨别为a 、b,斜边的长为c. 作边长是a+b 的正方形ABCD. 把正方形ABCD 划分红上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分红上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.∴22222c ab ab b a +=++, ∴222c b a =+.【证法16】(陈杰证明)设直角三角形两直角边的长辨别为a 、b (b>a ),斜边的长为c. 做两个边长辨别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字暗示面积的编号(如图).在EH = b 上截取ED = a,连结DA 、DC,则 AD = c.∵EM = EH + HM = b + a , ED = a, ∴DM = EM―ED =()a b +―a = b.又∵∠CMD = 90º,CM = a,∠AED = 90º, AE = b,∴RtΔAED ≌RtΔDMC.∴∠EAD = ∠MDC,DC = AD = c.∵∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º,∴∠ADC = 90º.∴ 作AB∥DC,CB∥DA,则ABCD 是一个边长为c 的正方形.∵∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º,∴∠BAF=∠DAE.连结FB,在ΔABF 和ΔADE 中,∵AB =AD = c,AE = AF = b,∠BAF=∠DAE,∴ΔABF ≌ΔADE.∴∠AFB = ∠AED = 90º,BF = DE = a. ∴ 点B 、F 、G 、H 在一条直线上.在RtΔABF 和RtΔBCG 中,∵AB = BC = c,BF = CG = a,∴RtΔABF ≌RtΔBCG.∵54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+=()76132S S S S S ++++ =5432S S S S +++=2c∴222c b a =+.。
勾股定理16种证明方法
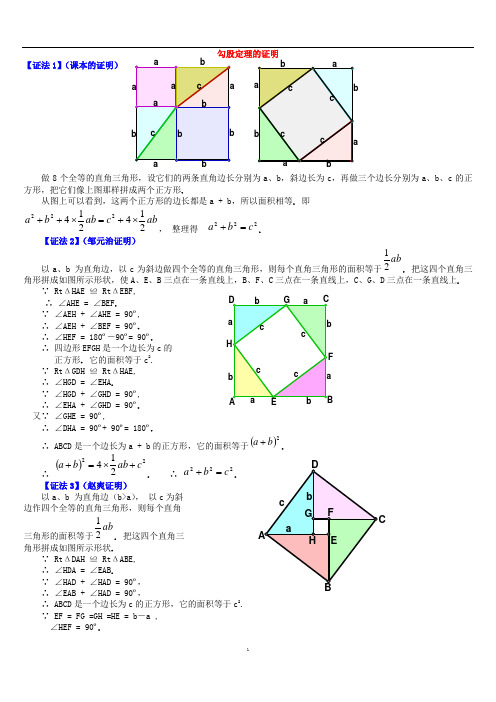
勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º,∴ ∠EHA + ∠GHD = 90º.又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴()22214cab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.EB A ∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴()22214ca b ab =-+⨯.∴ 222c b a =+.【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE,∴ ∠ADE = ∠BEC . ∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +.∴ ()222121221cab b a +⨯=+.∴ 222c b a =+. 【证法5】(梅文鼎证明) 做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形.∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD,∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º,∠BCP = 90º, BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+abS c2122⨯+=,∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P .过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º,∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c ,∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明). 【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD . 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点 L .∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD ,∵ ΔFAB 的面积等于221a,ΔGAD 的面积等于矩形ADLM的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB∴ 222b ac += ,即 222c b a =+【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D . 在ΔADC 和ΔACB 中, ∵ ∠ADC = ∠ACB = 90º, ∠CAD = ∠BAC ,∴ ΔADC ∽ ΔACB . AD ∶AC = AC ∶AB , 即 AB AD AC ∙=2.同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC∙=2.∴ ()222AB AB DB AD BCAC=∙+=+,即 222c b a =+.【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形.B把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c ,∴ Rt ΔDHA ≌ Rt ΔBCA . ∴ DH = BC = a ,AH = AC = b . 由作法可知, PBCA 是一个矩形,所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA .又∵ ∠DGT = 90º,∠DHF = 90º, ∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c++++= ①∵()[]()[]a b a a b b S S S -+∙-+=++21438 = abb 212-,985S S S +=,∴824321S ab b S S --=+=812S S b -- . ②把②代入①,得98812212S S S S b S S c++--++==922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º, BT = BE = b ,∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a .∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º, ∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ,∠HGF = ∠BDC = 90º, ∴ Rt ΔHGF ≌ Rt ΔBDC . 即27S S =.TE BQ过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =. ∵543212S S S S S c++++=,612S S a+=,8732S S S b++=,又∵ 27S S =,58S S =,64S S =, ∴8736122S S S S S ba ++++=+=52341S S S S S ++++ =2c ,即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC∙=2=()()BD AB BE AB -+=()()a c a c -+ = 22a c -, 即22a cb -=,∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BCAD DC AB ∙+∙=∙,∵ AB = DC = c ,AD = BC = a , AC = BD = b , ∴ 222AC BCAB+=,即 222b ac +=,∴ 222c b a =+.【证法13】(作直角三角形的内切圆证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE , ∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵abS ABC 21=∆,∴ ABC S ab ∆=42,又∵AOCBOC AOB ABC S S S S ∆∆∆∆++= = brar cr 212121++= ()rc b a ++21= ()rc c r ++221= rc r +2,∴ ()ABCS rc r∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+. 【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D . 假设222c b a ≠+,即假设 222AB BCAC≠+,则由AB AB AB∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2,或者 BD AB BC∙≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中, ∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则 ∠ADC ≠∠ACB .在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B ,∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BCAC≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214cab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++, ∴ 222c b a =+.【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a ,连结DA 、DC , 则 AD = c . ∵ EM = EH + HM = b + a , ED = a ,∴ DM = EM ―ED = ()a b +―a = b .又∵ ∠CMD = 90º,CM = a , ∠AED = 90º, AE = b , ∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC ,DC = AD = c .∵ ∠ADE + ∠ADC+ ∠MDC =180º, ∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中,∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c+++=, 6212S S S b++=,732S S a+=,76451S S S S S +===,∴6217322S S S S S ba ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c∴ 222c b a =+.A。
勾股定理9种证明

勾股定理的9 种证明(有图)【证法1】(邹元治证明)以a、b 为直角边,以 c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于.把这四个直角三角形拼成如图所示形状,使A E、B三点在一条直线上,B、F、C 三点在一条直线上,C G D三点在一条直线上.v Rt △HAE 坐Rt △EBF,• / AHE =/ BEF./ AEH + / AHE = 90o, /AEH + / BEF = 90o.• / HEF = 180o—90o= 90o.二四边形EFGH是一个边长为c的正方形. 它的面积等于c2.v Rt △GDH坐Rt △HAE,••• / HGD = / EHA.v / HGD + / GHD = 90o,•/ EHA + / GHD = 90o.又v / GHE = 90o,•/ DHA = 90o+ 90o= 180 o.•ABCD是一个边长为a + b的正方形,它的面积等于【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a、b ,斜边长为 c. 把它们拼成如图那样的一个多边形,使 D E、F在一条直线上.过C作AC的延长线交DF于点P.v D、E、F在一条直线上,且Rt △ GEF坐Rt △ EBD,•/ EGF = / BEDv / EGF + / GEF = 90°,•/ BED + / GEF = 90 ° ,•/ BEG =18(b—90o= 90 o.又v AB = BE = EG = GA = c ,•ABEG是一个边长为c的正方形.•/ ABC + / CBE = 90o.v Rt △ABC 幻Rt △EBD,•/ ABC = / EBD.•/ EBD + / CBE = 90o.即/ CBD= 9Gb.又v / BDE = 90o,Z BCP = 90o,BC = BD = a.• BDPC是一个边长为a的正方形. 同理,HPFG是一个边长为b的正方形. 设多边形GHCB的面积为S,则【证法3】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a),斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E、A、C 三点在一条直线上.过点Q作QP// BC交AC于点P. 过点B作BMiL PQ垂足为M;再过点F作FNL PQ垂足为N.v / BCA = 90o , QP// BC••• / MPC = 90o,v BM 丄PQ•/ BMP = 90o,•BCPM是一个矩形,即/ MBC = 90o.v / QBM + / MBA = / QBA = 90o,/ ABC + / MBA = / MBC = 90o,•/ QBM = / ABC又v / BMP = 90o,Z BCA = 90o, BQ = BA = c ,•Rt △ BMQ坐Rt △ BCA.同理可证Rt △ QNF幻Rt △ AEF.从而将问题转化为【证法4】(梅文鼎证明).【证法4】(欧几里得证明)做三个边长分别为a、b、c的正方形,把它们拼成如图所示形状,使H、C B三点在一条直线上,连结BF CD.过C作CL± DE交AB于点M交DE于点L.v AF = AC ,AB = AD,/ FAB = / GAD•△ FAB 坐△ GADv △ FAB的面积等于,△ GAD的面积等于矩形ADLM 的面积的一半,•矩形ADLM的面积=. 同理可证,矩形MLEE的面积二.v正方形ADEB勺面积=矩形ADLM勺面积+矩形MLEB勺面积•,即.【证法5】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a、b (b>a),斜边长为c.再做一个边长为c的正方形.把它们拼成如图所示的多边形.过A作AF丄AC AF交GT 于F, AF 交DT于R.过B作BP丄AF,垂足为P.过D作DE与CB的延长线垂直,垂足为E, DE交AF 于H.v / BAD = 90o,Z PAC = 90o,••• / DAH = / BAC.又v / DHA = 90o,Z BCA = 90o,AD = AB = c ,• Rt △ DHA坐Rt △ BCA.• DH = BC = a , AH = AC = b.由作法可知, PBCA 是一个矩形, 所以Rt △ APB 坐Rt △ BCA.即PB = CA = b , AP= a,从而PH = b —a.v Rt △DGT 坐Rt △BCA ,Rt △ DHA坐Rt △ BCA.• Rt △ DGT坐Rt △ DHA .•DH = DG = a,/ GDT = / HDA . 又v / DGT = 90o,Z DHF = 90o,/ GDH = / GDT + / TDH = / HDA+Z TDH = 90o,• DGFH是一个边长为a的正方形.• GF = FH = a . TF 丄AF, TF = GT—GF = b — a .• TFPB是一个直角梯形,上底TF=b-a,下底BP= b,高FP=a + (b—a).用数字表示面积的编号(如图),则以c为边长的正方形的面积为①v = ,• = . ②把②代入①,得【证法6】(李锐证明)设直角三角形两直角边的长分别为a、b(b>a),斜边的长为c.做三个边长分别为a、b、c的正方形,把它们拼成如图所示形状,使A、E、G三点在一条直线上.用数字表示面积的编号(如图).v / TBE = / ABH = 90o,•/ TBH = / ABE.又v / BTH = / BEA = 90o,BT = BE = b ,• Rt △ HBT 坐Rt △ ABE.••• HT = AE = a.••• GH = GT—HT = b —a.又T / GHF + / BHT = 90o,/ DBC + / BHT = / TBH + / BHT = 90o,•/ GHF = / DBC.T DB = EB—ED = b—a,/ HGF = / BDC = 90o,• Rt △ HGF坐Rt △ BDC.即.过Q作QM L AG 垂足是M.由/ BAQ = / BEA = 90o,可知 / ABE =/ QAM 而AB = AQ = c,所以Rt △ ABE 幻Rt △ QAM .又Rt △ HBT 幻Rt △ ABE.所以Rt △ HBT 幻Rt △ QAM .即.由Rt △ ABE 坐Rt △ QAM 又得QM = AE = a,/ AQM = / BAE.T / AQM + / FQM = 90o,Z BAE + / CAR = 90o,Z AQM = / BAE•/ FQM = / CAR.又T / QMF = / ARC = 90o, QM = AR = a ,• Rt △ QMF坐Rt △ ARC.即.T ,,,【证法7】(利用多列米定理证明)在Rt△ ABC中,设直角边BC= a, AC= b,斜边AB = c (如图).过点A作AD// CB, 过点B作BD//CA则ACBD为矩形,矩形ACBD^接于一个圆.根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有T AB = DC = c , AD = BC = a , AC = BD = b ,•,即,【证法8】(利用反证法证明)如图,在Rt△ ABC中,设直角边AC BC的长度分别为a、b,斜边AB的长为c,过点C 作CDL AB垂足是D.假设,即假设,则由可知,或者.即AD: AO AC AB或者BD: BO BC AB.在厶ADCF" ACB中,v / A = / A,•••若AD: AO AC AB」/ AD字/ ACB.在厶CDB^H A ACB中,v / B = / B,•若BD BO BC AB,贝S/ CDB^Z ACB.又v / ACB = 90o,• / AD& 90o,Z CD字90o.这与作法CD!AB矛盾.所以,的假设不能成立证法9】(辛卜松证明)设直角三角形两直角边的长分别为a、b,斜边的长为c.作边长是a+b的正方形ABCD. 把正方形ABC划分成上方左图所示的几个部分,则正方形ABC啲面积为;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD勺面积为=.。
勾股定理证明题试题及参考答案

勾股定理证明题试题及参考答案勾股定理是数学常见的定理,这些定理该怎么证明呢?证明的方法是怎样的呢?下面就是店铺给大家整理的勾股定理证明题内容,希望大家喜欢。
勾股定理证明题一已知△ABC中,∠ACB=90°,以△ABC的各边为长边在△ABC外作矩形,使每个矩形的宽为长的一半,S1、S2、S3分别表示这三个矩形的面积,则S1、S2、S3之间有什么关系?并证明你的结论。
(要详细解题过程)因为D是AB的中点,DE垂直于DF于D所以,∠EDF=90度,AC=2DF, BC=2DE又因为,∠ACB=90度,∠EDF=90度,所以DE//BC,DF//AC即,∠DFB=∠AED=90度根据勾股定理则有 AE^2=AD^2-DE^2-------(1)BF^2=BD^2-DF^2-------(2)又因为D是AB的中点,DE//BC,DF//AC。
所以EF//AB,且AD=BD=EF----------------(3)在Rt△EDF中, EF^2 =DE^2+DF^2 = 2AD^2-(AE^2+BF^2) 即 EF^2=AE^2+BF^2因为D是AB的中点,DE垂直于DF于D所以,∠EDF=90度,AC=2DF, BC=2DE又因为,∠ACB=90度,∠EDF=90度,所以DE//BC,DF//AC即,∠DFB=∠AED=90度根据勾股定理则有 AE^2=AD^2-DE^2-------(1)BF^2=BD^2-DF^2-------(2)又因为D是AB的中点,DE//BC,DF//AC。
所以EF//AB,且AD=BD=EF----------------(3)在Rt△EDF中, EF^2 =DE^2+DF^2 = 2AD^2-(AE^2+BF^2) 即 EF^2=AE^2+BF^2勾股定理证明题二设MD,ME,MF分别交AC,BC,AB于P,Q,R,连接MA.MB,MC由勾股定理MB^2=MP^2+BP^2=MR^2+BR^2 (1)BD^2=MP^2+PD^2=BF^2=BR^2+FR^2 (2)CM^2=CP^2++MP^2=CQ^2+MQ^2 (3)CD^2=PD^2+PC^2=CF^2=CQ^2+QF^2 (4)MA^2=MQ^2+AQ^2=AR^2+MR^2 (5)由(1)(2)(3)(4)(5)可得AQ^2+MQ^2=AR^2+FR^2即AE^2=AF^2AE=AF中学勾股定理课堂实录师:我们知道,数学是一门基础学科,它用概念、公式、定理演绎着数学的神奇和魅力,今天我们在一起继续学习一个古老而著名的数学定理。
勾股定理及经典例题

一、勾股定理1.勾股定理:直角三角形两直角边的平方和等于斜边的平方;即222a b c +=。
2.勾股定理的证明:用三个正方形的面积关系进行证明(两种方法)。
3.勾股定理逆定理:如果三角形的三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形。
满足222a b c +=的三个正整数称为勾股数。
练习题:1. 直角三角形的斜边比一直角边长2 cm ,另一直角边长为6 cm ,则它的斜边长(A )4 cm (B )8 cm (C )10 cm (D )12 cm2. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) (A )13 (B )8 (C )25 (D )643.如图,A B ⊥CD 于B ,△ABD 和△BCE 都是等腰直角三角形,如果CD=17,BE=5,那么AC 的长为( ).(A )12 (B )7 (C )5 (D )13几何A 级概念:(要求深刻理解、熟练运用、主要用于几何证明) 1.三角形的角平分线定义: 三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.(如图) A B CD 几何表达式举例: (1) ∵AD 平分∠BAC ∴∠BAD=∠CAD (2) ∵∠BAD=∠CAD∴AD 是角平分线2.三角形的中线定义: 在三角形中,连结一个顶点和它的对边的中点的线段叫做三角形的中线.(如图)A BC D 几何表达式举例: (1) ∵AD 是三角形的中线 ∴ BD = CD (2) ∵ BD = CD ∴AD 是三角形的中线E A B C D从三角形的一个顶点向它的对边画垂线,顶点和垂足间的线段叫做三角形的高线. (如图)ABC D(1) ∵AD 是ΔABC 的高 ∴∠ADB=90° (2) ∵∠ADB=90° ∴AD 是ΔABC 的高※4.三角形的三边关系定理: 三角形的两边之和大于第三边,三角形的两边之差小于第三边.(如图)AB C几何表达式举例: (1) ∵AB+BC >AC ∴……………(2) ∵ AB-BC <AC ∴……………5.等腰三角形的定义: 有两条边相等的三角形叫做等腰三角形. (如图) A B C几何表达式举例: (1) ∵ΔABC 是等腰三角形 ∴ AB = AC (2) ∵AB = AC∴ΔABC 是等腰三角形6.等边三角形的定义: 有三条边相等的三角形叫做等边三角形. (如图) A BC几何表达式举例:(1)∵ΔABC 是等边三角形∴AB=BC=AC (2) ∵AB=BC=AC∴ΔABC 是等边三角形 7.三角形的内角和定理及推论: (1)三角形的内角和180°;(如图) (2)直角三角形的两个锐角互余;(如图) (3)三角形的一个外角等于和它不相邻的两个内角的和;(如图) ※(4)三角形的一个外角大于任何一个和它不相邻的内角.(1) (2) (3)(4)几何表达式举例: (1) ∵∠A+∠B+∠C=180° ∴………………… (2) ∵∠C=90° ∴∠A+∠B=90°(3) ∵∠ACD=∠A+∠B ∴………………… (4) ∵∠ACD >∠A ∴………………… 8.直角三角形的定义: 有一个角是直角的三角形叫直角三角形.(如图)A B C几何表达式举例: (1) ∵∠C=90° ∴ΔABC 是直角三角形 (2) ∵ΔABC 是直角三角形∴∠C=90° D AB C A B C AB C两条直角边相等的直角三角形叫等腰直角三角形.(如图) AB C(1) ∵∠C=90° CA=CB ∴ΔABC 是等腰直角三角形 (2) ∵ΔABC 是等腰直角三角形∴∠C=90° CA=CB10.全等三角形的性质: (1)全等三角形的对应边相等;(如图) (2)全等三角形的对应角相等.(如图) 几何表达式举例: (1) ∵ΔABC ≌ΔEFG ∴ AB = EF ……… (2) ∵ΔABC ≌ΔEFG∴∠A=∠E ……… 11.全等三角形的判定: “SAS ”“ASA ”“AAS ”“SSS ”“HL ”. (如图) (1)(2) (3) 几何表达式举例: (1) ∵ AB = EF ∵ ∠B=∠F 又∵ BC = FG ∴ΔABC ≌ΔEFG(2) ………………(3)在Rt ΔABC 和Rt ΔEFG中 ∵ AB=EF又∵ AC = EG ∴Rt ΔABC ≌Rt ΔEFG12.角平分线的性质定理及逆定理: (1)在角平分线上的点到角的两边距离相等;(如图) (2)到角的两边距离相等的点在角平分线上.(如图)A O BC DE 几何表达式举例: (1)∵OC 平分∠AOB 又∵CD ⊥OA CE ⊥OB ∴ CD = CE (2) ∵CD ⊥OA CE ⊥OB又∵CD = CE∴OC 是角平分线 13.线段垂直平分线的定义: 垂直于一条线段且平分这条线段的直线,叫做这条线段的垂直平分线.(如图) A B E FO 几何表达式举例: (1) ∵EF 垂直平分AB ∴EF ⊥AB OA=OB (2) ∵EF ⊥AB OA=OB ∴EF 是AB 的垂直平分线A B C G EFA B C G E FA B C E F G14.线段垂直平分线的性质定理及逆定理:(1)线段垂直平分线上的点和这条线段的两个端点的距离相等;(如图)(2)和一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.(如图)A BCMNP几何表达式举例:(1) ∵MN是线段AB的垂直平分线∴PA = PB(2) ∵PA = PB∴点P在线段AB的垂直平分线上15.等腰三角形的性质定理及推论:(1)等腰三角形的两个底角相等;(即等边对等角)(如图)(2)等腰三角形的“顶角平分线、底边中线、底边上的高”三线合一;(如图)(3)等边三角形的各角都相等,并且都是60°.(如图)AB C(1)AB CD(2)AB C(3)几何表达式举例:(1) ∵AB = AC∴∠B=∠C(2) ∵AB = AC又∵∠BAD=∠CAD∴BD = CDAD⊥BC………………(3) ∵ΔABC是等边三角形∴∠A=∠B=∠C =60°16.等腰三角形的判定定理及推论:(1)如果一个三角形有两个角都相等,那么这两个角所对边也相等;(即等角对等边)(如图)(2)三个角都相等的三角形是等边三角形;(如图)(3)有一个角等于60°的等腰三角形是等边三角形;(如图)(4)在直角三角形中,如果有一个角等于30°,那么它所对的直角边是斜边的一半.(如图)AB C(1)AB C(2)(3)ABC(4)几何表达式举例:(1) ∵∠B=∠C∴AB = AC(2) ∵∠A=∠B=∠C∴ΔABC是等边三角形(3) ∵∠A=60°又∵AB = AC∴ΔABC是等边三角形(4) ∵∠C=90°∠B=30°∴AC =21AB17.关于轴对称的定理(1)关于某条直线对称的两个图形是全等形;(如图)(2)如果两个图形关于某条直线对称,那么对称轴是对应点连线的垂直平分线.(如图)几何表达式举例:(1) ∵ΔABC、ΔEGF关于MN轴对称∴ΔABC≌ΔEGF(2) ∵ΔABC、ΔEGF关于MN轴对称∴OA=OE MN⊥AEEFMOABCNG18.勾股定理及逆定理:(1)直角三角形的两直角边a 、b 的平方和等于斜边c 的平方,即a2+b2=c2;(如图) (2)如果三角形的三边长有下面关系: a2+b2=c2,那么这个三角形是直角三角形.(如图)ABC几何表达式举例:(1) ∵ΔABC 是直角三角形∴a2+b2=c2 (2) ∵a2+b2=c2∴ΔABC 是直角三角形19.Rt Δ斜边中线定理及逆定理: (1)直角三角形中,斜边上的中线是斜边的一半;(如图) (2)如果三角形一边上的中线是这边的一半,那么这个三角形是直角三角形.(如图)DA BC几何表达式举例:∵ΔABC 是直角三角形 ∵D 是AB 的中点∴CD = 21AB(2) ∵CD=AD=BD∴ΔABC 是直角三角形练习题:一、选择题1.下列命题中正确的是( )①全等三角形对应边相等; ②三个角对应相等的两个三角形全等; ③三边对应相等的两三角形全等;④有两边对应相等的两三角形全等。
勾股定理的十六种证明方法

勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF ,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE , ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE,∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE ,∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠D EC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD , ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD , ∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+abS c 2122⨯+=, ∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ,交AC 于点P .过点B 作BM ⊥PQ ,垂足为M ;再过点F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明).【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD . 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点L .∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD ,∵ ΔFAB 的面积等于221a , ΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a . 同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积 = 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+.【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中, ∵ ∠ADC = ∠ACB = 90º, ∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB ,即 AB AD AC •=2. 同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC •=2.∴ ()222AB AB DB AD BC AC =•+=+,即 222c b a =+.【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠P AC = 90º, ∴ ∠DAH = ∠BAC . 又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c ,∴ Rt ΔDHA ≌ Rt ΔBCA .∴ DH = BC = a ,AH = AC = b .由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA ,Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . T F ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为 543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+=812SS b -- . ② 把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +. ∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º,BT = BE = b ,∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ,∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE= ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a , ∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ,即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC •=2=()()BD AB BE AB -+ =()()a c a c -+= 22a c -,即222a c b -=, ∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•, ∵ AB = DC = c ,AD = BC = a ,AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=,∴ 222c b a =+.【证法13】(作直角三角形的内切圆证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ ab S ABC 21=∆,∴ ABC S ab ∆=42,又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+. 【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中, ∵ ∠A = ∠A , ∴ 若 AD :AC ≠AC :AB ,则 ∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B ,∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a ,连结DA 、DC ,则 AD = c .∵ EM = EH + HM = b + a , ED = a ,∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a , ∠AED = 90º, AE = b ,∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º, ∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º,∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中, ∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,D D76451S S S S S +===, ∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
