数字信号处理第三版习题答案
数字信号处理-(第三版)试题及答案

数字信号处理 试卷一、填空题:(本大题共10小题,每空2分,共28分)2、从奈奎斯特采样定理得出,要使实信号采样后能够不失真还原,采样频率f 与信号最高频率fs 关系为:f ≥2fs 。
3、已知一个长度为N 的序列x(n),它的傅立叶变换为X (ejw ),它的N 点离散傅立叶变换X (K )是关于X (ejw )的N 点等间隔抽样。
4、有限长序列x(n)的8点DFT 为X (K ),则X (K )=()70()nk N n X k x n W ==∑ 。
5、无限长单位冲激响应(IIR )滤波器的结构上有反馈,因此是递归型的。
6、若正弦序列x(n)=sin(30n π/120)是周期的,则周期是N= 8 。
7、已知因果序列x(n)的Z 变换为X(z)=eZ-1,则x(0)= 0 。
8、无限长单位冲激响应滤波器的基本结构有直接Ⅰ型,直接Ⅱ型,级联型 和 并联型 四种。
9、DFT 与DFS 有密切关系,因为有限长序列可以看成周期序列的主值序列,而周期序列可以看成有限长序列的 周期序列 。
10、对长度为N 的序列x(n)圆周移位m 位得到的序列用xm(n)表示,其数学表达式为xm(n)=x((n+m))N R N (n)。
二、选择填空题(本大题共6小题,每题2分,共12分) 1、δ(n)的z 变换是 ( A ) 。
A. 1B.δ(w)C. 2πδ(w)D. 2π 2、序列x1(n)的长度为4,序列x2(n)的长度为3,则它们线性卷积的长度是 ( B ) , 5点圆周卷积的长度是 。
A. 5, 5B. 6, 5C. 6, 6D. 7, 53、在N=32的时间抽取法FFT 运算流图中,从x(n)到X(k)需 ( B ) 级蝶形运算 过程。
A. 4B. 5C. 6D. 34、下面描述中最适合离散傅立叶变换DFT 的是( B ) A .时域为离散序列,频域也为离散序列B .时域为离散有限长序列,频域也为离散有限长序列C .时域为离散无限长序列,频域为连续周期信号D .时域为离散周期序列,频域也为离散周期序列5、设系统的单位抽样响应为h(n),则系统因果的充要条件为( C ) A .当n>0时,h(n)=0 B .当n>0时,h(n)≠0 C .当n<0时,h(n)=0 D .当n<0时,h(n)≠06、已知序列Z 变换的收敛域为|z |<1,则该序列为( C )。
数字信号处理-第3版-答案(PDF)

2.1 判断下列序列是否是周期序列。若是,请确定它的最小周期。 (1)x(n)=Acos( (2)x(n)= e (
j
π 5π n+ ) 8 6
n −π) 8 π 3π (3)x(n)=Asin( n+ ) 4 3
(1)对照正弦型序列的一般公式 x(n)=Acos( ωn + ϕ ),得出 ω =
k = −∞
∑ u (k ) a
∞
n−k
u (n − k ) =
k = −∞
∑a
∞
n−k
=
1 − a n +1 u(n) 1− a
2.3 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)= λ
n
u(n)*u(n)
解:(1)
y(n)=
k = −∞ ∞
∑ u(k )u(n − k )
π 2π (n-k)+ ]| 3 6 π 2π =|x(n)|| sin[ (n-k)+ ]| 3 6
≤M|sin[
π 2π (n- k)+ ]|≤M 3 6
故系统是稳定系统。 因 y(n)只取决于现在和过去的输入 x(n),不取决于未来的输入,故该系统是因果系统。 (3)设 y1(n)=
k = −∞
−n
u(-n),0<a<1 用直接计算线性卷积的方法,求
2.6 试证明线性卷积满足交换率、结合率和加法分配率。
证明
(1)交换律 X(n) * y(n) =
k = −∞
∑ x(k ) y (n − k )
∞
令 k=n-t,所以 t=n-k,又- ∞ <k< ∞ ,所以- ∞ <t< ∞ ,因此线性卷积公式变成
《数字信号处理》第三版课后答案

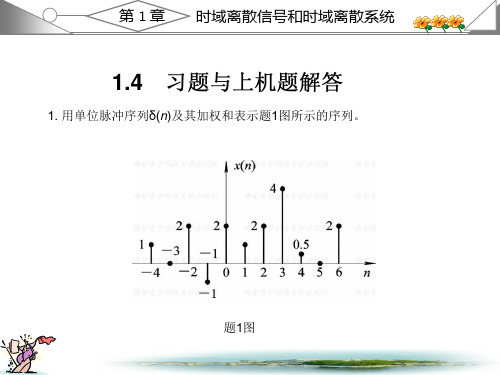
数字信号处理(西电科大第三版)课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值; (2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数; (2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; (2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理(第三版)-课后习题答案全-(原题+答案+图)
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
数字信号处理第三版课后答案

数字信号处理第三版课后答案西安电⼦(⾼西全丁美⽟第三版)数字信号处理课后答案1.2教材第⼀章习题解答1.⽤单位脉冲序列及其加权和表⽰题1图所⽰的序列。
解:2.给定信号:(1)画出序列的波形,标上各序列的值;(2)试⽤延迟单位脉冲序列及其加权和表⽰序列;(3)令,试画出波形;(4)令,试画出波形;(5)令,试画出波形。
解:(1)x(n)的波形如题2解图(⼀)所⽰。
(2)(3)的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(⼆)所⽰。
(4)的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所⽰。
(5)画时,先画x(-n)的波形,然后再右移2位,波形如题2解图(四)所⽰。
3.判断下⾯的序列是否是周期的,若是周期的,确定其周期。
(1),A是常数;(2)。
解:(1),这是有理数,因此是周期序列,周期是T=14;(2),这是⽆理数,因此是⾮周期序列。
5.设系统分别⽤下⾯的差分⽅程描述,与分别表⽰系统输⼊和输出,判断系统是否是线性⾮时变的。
(1);(3),为整常数;(5);(7)。
解:故该系统是时不变系统。
故该系统是线性系统。
(3)这是⼀个延时器,延时器是⼀个线性时不变系统,下⾯予以证明。
令输⼊为,输出为,因为故延时器是⼀个时不变系统。
⼜因为故延时器是线性系统。
(5)令:输⼊为,输出为,因为故系统是时不变系统。
⼜因为因此系统是⾮线性系统。
(7)令:输⼊为,输出为,因为故该系统是时变系统。
⼜因为故系统是线性系统。
6.给定下述系统的差分⽅程,试判断系统是否是因果稳定系统,并说明理由。
(1);(3);(5)。
(1)只要,该系统就是因果系统,因为输出只与n时刻的和n时刻以前的输⼊有关。
如果,则,因此系统是稳定系统。
(3)如果,,因此系统是稳定的。
系统是⾮因果的,因为输出还和x(n)的将来值有关.(5)系统是因果系统,因为系统的输出不取决于x(n)的未来值。
如果,则,因此系统是稳定的。
7.设线性时不变系统的单位脉冲响应和输⼊序列如题7图所⽰,要求画出输出输出的波形。
《数字信号处理》第三版课后答案

《数字信号处理》第三版课后答案1 数字信号处理(西电科大第三版)课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+- 2. 给定信号:25,41()6,040,n n x n n +-≤≤-??=≤≤其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列;(3)令1()2(2)x n x n =-,试画出1()x n 波形;(4)令2()2(2)x n x n =+,试画出2()x n 波形;(5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+- (3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n eπ-=。
解:。
数字信号处理(第三版)课后习题答案全

| z |
| z | 1 2
1 5 7 z n 1 F ( z ) X ( z ) z n 1 z (1 0.5 z 1 )(1 2 z 1 ) 5z 7 zn ( z 0.5)( z 2)
n≥0时, 因为c内无极点,x(n)=0; n≤-1时, c内有极点 0 , 但z=0是一个n阶极点, 改为求圆外极点留数, 圆外极点有z1=0.5, z2=2, 那么
0.5n 2 n
n<0时, c内有极点0.5、 2、 0, 但极点0是一个n阶极点,
改成求c外极点留数, 可是c外没有极
点, 因此 x(n)=0 最后得到
x(n)=(0.5n-2n)u(n)
第2章
时域离散信号和系统的频域分析
19. 用部分分式法求以下X(z)的反变换:
(1)
1 1 z 1 3 X ( z) , 1 2 5z 2 z 2
0
jn
令n′=n-n0, 即n=n′+n0, 则
FT[ x(n n0 )]
n
x(n)e
j ( n n0 )
e jn0 X (e j )
第2章
(2)
时域离散信号和系统的频域分析
FT[ x (n)]
(6) 因为
n
x ( n ) e jn
j 3 j n n n 3
n 0
3
e
jn
n 1
3
e
j n
n 0
3
e
jn
n 1
3
e j n
数字信号处理》第三版课后习题答案

数字信号处理课后答案教材第一章习题解答1.用单位脉冲序列()nδ及其加权和表示题1图所示的序列。
解:2.给定信号:25,41 ()6,040,n nx n n+-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n序列;(3)令1()2(2)x n x n=-,试画出1()x n波形;(4)令2()2(2)x n x n=+,试画出2()x n波形;(5)令3()2(2)x n x n=-,试画出3()x n波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)(3)1()x n的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n时,先画x(-n)的波形,然后再右移2位,3()x n波形如题2解图(四)所示。
3.判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14;(2)12,168w wππ==,这是无理数,因此是非周期序列。
5.设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)()()2(1)3(2)y n x n x n x n =+-+-; (3)0()()y n x n n =-,0n 为整常数; (5)2()()y n x n =; (7)0()()nm y n x m ==∑。
解:(1)令:输入为0()x n n -,输出为'000'0000()()2(1)3(2)()()2(1)3(2)()y n x n n x n n x n n y n n x n n x n n x n n y n =-+--+---=-+--+--=故该系统是时不变系统。
(完整版)数字信号处理(第三版)高西全丁玉美课后答案

西安电子(咼西全丁美玉第二版)数字信号处理课后答案1.2 教材第一章习题解答解:x(n)(n 4)2 (n 2)0.5 (n 4) 2 (n(n 1) 2 (n) (n 1) 2 (n 2) 4 (n 3) 6)2n 5, 4 n 12.给定信号 :x(n)6,0 n 4 0,其它(1) 画出x(n)序列的波形,标上各序列的值; (2)试用延迟单位脉冲序列及其加权和表示 x(n)序列;(3) 令X 1(n) 2x(n 2),试画出捲(n)波形; (4) 令 X 2(n) 2x(n 2),试画出 X 2(n)波形; (5) 令 x 3(n) 2x(2 n),试画出 X 3(n)波形。
解:(1) x(n)的波形如 题2解图(一)所示。
(2)x(n) 3 (n 4) (n 3) (n 2) 3 (n 1) 6 (n)6 (n 1) 6 (n 2) 6 (n 3) 6 (n 4)(5)画X 3(n)时,先画x(-n)的波形,然后再右移 2位,X 3(n)波形如题2解图(四)所示。
3.判断下面的序列是否是周期的,若是周期的,确定其周期。
3(1) x(n) Acos( n -),A 是常数;1j (7n)(2) x(n) e 8。
1.用单位脉冲序列(n)及其加权和表示 题1图所示的序列。
(3) x, n)的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4) X 2 (n)的波形是x(n)的波形左移 2位,在乘以2,画出图形如 题2解图(三)所示。
解:3 2 14(1)W , ,这是有理数,因此是周期序列,周期是T=14 ;7 w 31 2(2)w , 16 ,这是无理数,因此是非周期序列。
8 w5.设系统分别用下面的差分方程描述,x(n)与y(n)分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)y(n) x(n) 2x(n 1) 3x(n 2);(3)y(n) x(n n°),n o为整常数;(5)y(n) x2(n);(7)y(n) nx(m)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字信号处理第三版习题答案
数字信号处理(Digital Signal Processing,简称DSP)是一门研究如何对数字信号进行处理和分析的学科。
它在现代通信、音频处理、图像处理等领域有着广泛的应用。
为了更好地理解和掌握数字信号处理的知识,许多人选择了《数字信号处理(第三版)》这本经典教材。
本文将为大家提供一些《数字信号处理(第三版)》习题的答案,以帮助读者更好地学习和巩固所学知识。
第一章:离散时间信号和系统
1.1 习题答案:
a) 离散时间信号是在离散时间点上取值的信号,而连续时间信号是在连续时间上取值的信号。
b) 离散时间系统是对离散时间信号进行处理的系统,而连续时间系统是对连续时间信号进行处理的系统。
c) 离散时间信号可以通过采样连续时间信号得到。
1.2 习题答案:
a) 线性系统满足叠加性和齐次性。
b) 时不变系统的输出只与输入的时间延迟有关,与输入信号的具体形式无关。
c) 因果系统的输出只与当前和过去的输入有关,与未来的输入无关。
第二章:离散时间信号的时域分析
2.1 习题答案:
a) 离散时间信号的能量是信号幅值的平方和,而功率是信号幅值的平方的平均值。
b) 离散时间信号的能量和功率可以通过计算信号的幅值序列的平方和和平方的
平均值得到。
2.2 习题答案:
a) 离散时间信号的自相关函数是信号与其自身经过不同时间延迟的乘积的和。
b) 离散时间信号的自相关函数可以用于确定信号的周期性和频率成分。
第三章:离散时间信号的频域分析
3.1 习题答案:
a) 离散时间信号的频谱是信号在频率域上的表示,可以通过对信号进行傅里叶变换得到。
b) 离散时间信号的频谱可以用于分析信号的频率成分和频谱特性。
3.2 习题答案:
a) 离散时间信号的频谱具有周期性,其周期等于采样频率。
b) 离散时间信号的频谱可以通过对信号进行离散傅里叶变换得到。
第四章:离散时间系统的频域分析
4.1 习题答案:
a) 离散时间系统的频率响应是系统在不同频率下的输出与输入之比。
b) 离散时间系统的频率响应可以通过对系统的冲激响应进行傅里叶变换得到。
4.2 习题答案:
a) 离散时间系统的频率响应可以用于分析系统的频率选择性和频率特性。
b) 离散时间系统的频率响应可以通过对系统的差分方程进行离散傅里叶变换得到。
通过以上习题的答案,我们可以更加深入地理解和掌握《数字信号处理(第三版)》中所介绍的内容。
数字信号处理作为一门重要的学科,对于现代科技的发
展和应用起到了重要的推动作用。
希望本文的内容能够对读者们的学习和研究有所帮助。
