高考文科三角函数知识点总结

合集下载

高中三角函数知识点总结《精华版》

高中三角函数知识点总结《精华版》一、三角函数的定义：1. 正弦函数（sin）：在单位圆上，其中一角的正弦值等于该角顶点的对边与斜边的比值。

2. 余弦函数（cos）：在单位圆上，其中一角的余弦值等于该角顶点的邻边与斜边的比值。

3. 正切函数（tan）：在单位圆上，其中一角的正切值等于该角顶点的对边与邻边的比值。

二、基本性质：1.三角函数的值域：正弦和余弦的值域为[-1,1]，正切的值域为实数集。

2. 正弦函数和余弦函数的关系：sin²θ + cos²θ = 13.三角函数的周期性：正弦和余弦函数的周期为2π，正切函数的周期为π。

三、三角函数与四象限：1. 在第一象限，sinθ和cosθ均为正数。

2. 在第二象限，sinθ为正，cosθ为负。

3. 在第三象限，sinθ和cosθ均为负数。

4. 在第四象限，sinθ为负，cosθ为正。

四、三角函数的图像及性质：1.正弦函数的图像：从原点出发向右为起始点，振动幅度为1，曲线在零点上下交替。

2.余弦函数的图像：从峰值（1或-1）出发向右为起始点，振动幅度为1，曲线在零点上下交替。

3.正切函数的图像：振动幅度无限增加，从0开始。

五、常见角的正弦、余弦和正切值的计算：1. 0度：sin0 = 0，cos0 = 1，tan0 = 0。

2. 30度：sin30° = 1/2，cos30° = √3/2，tan30° = 1/√33. 45度：sin45° = √2/2，cos45° = √2/2，tan45° = 14. 60度：sin60° = √3/2，cos60° = 1/2，tan60° = √35. 90度：sin90° = 1，cos90° = 0，tan90° = 无穷大。

六、三角函数的基本性质：1.奇偶性：正弦函数是奇函数，余弦函数是偶函数，正切函数是奇函数。

高考三角函数知识点总结

高考三角函数知识点总结一、基本概念和性质1.弧度制：单位圆上的弧所对应的圆心角的大小定义为该弧的弧度。

1弧度等于圆周的1/2π。

2. 三角函数：正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)、余切函数cot(x)、正割函数sec(x)和余割函数csc(x)。

3.三角恒等式：包括同角三角恒等式、余角三角恒等式、反三角函数同角恒等式等。

4.周期性：正弦函数、余弦函数、正割函数和余割函数的周期都是2π；正切函数和余切函数的周期是π。

二、基本关系式1.正弦函数：在直角三角形中，正弦函数是指对于一个锐角三角形，三角形的对边和斜边的比值。

- sin(x) = a / c，其中a是对边，c是斜边。

- sin(x) = y / r，其中y是斜边在y轴上的投影，r是半径。

2.余弦函数：在直角三角形中，余弦函数是指对于一个锐角三角形，三角形的邻边和斜边的比值。

- cos(x) = b / c，其中b是邻边，c是斜边。

- cos(x) = x / r，其中x是斜边在x轴上的投影，r是半径。

3.正切函数：在直角三角形中，正切函数是指对于一个锐角三角形，三角形的对边和邻边的比值。

- tan(x) = a / b，其中a是对边，b是邻边。

- tan(x) = y / x，其中y是斜边在y轴上的投影，x是斜边在x轴上的投影。

4.余切函数：余切函数是正切函数的倒数。

- cot(x) = 1 / tan(x)。

5.正割函数：在直角三角形中，正割函数是指对于一个锐角三角形，三角形的斜边和邻边的比值的倒数。

- sec(x) = 1 / cos(x)。

6.余割函数：在直角三角形中，余割函数是指对于一个锐角三角形，三角形的斜边和对边的比值的倒数。

- csc(x) = 1 / sin(x)。

三、平面内角与弧度制之间的关系1.弧度制与度数之间的转换：-弧度=度数×π/180-度数=弧度×180/π2.弧度制下的角的性质：-一个圆上的圆心角的弧度数等于该弧所对应的弧的弧度数。

高中数学- 三角函数公式总结

高中数学-三角函数公式总结一、任意角的三角函数在角α的终边上任取．．一点),(y x P ，记：22y x r +=，正弦：ry =αsin 余弦：rx =αcos 正切：xy=αtan 二、同角三角函数的基本关系式商数关系：αααcos sin tan =，平方关系：1cos sin 22=+αα三、诱导公式（奇变偶不变，符号看象限）⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值，等于α的同名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

⑵απ+2、απ-2、απ+23、απ-23的三角函数值，等于α的异名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin （2k π＋α）＝sin α（k ∈Z ）cos （2k π＋α）＝cos α（k ∈Z ）tan （2k π＋α）＝tan α（k ∈Z ）公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin （π＋α）＝－sin αcos （π＋α）＝－cos αtan （π＋α）＝tan α公式三：任意角α与-α的三角函数值之间的关系：sin （－α）＝－sin αcos （－α）＝cos αtan （－α）＝－tan α公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin （π－α）＝sin αcos （π－α）＝－cos αtan （π－α）＝－tan α公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin （2π－α）＝－sin αcos （2π－α）＝cos αtan （2π－α）＝－tan α微生筑梦公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin （π/2＋α）＝cos αsin （π/2－α）＝cos αcos （π/2＋α）＝－sin αcos （π/2－α）＝sin αtan （π/2＋α）＝－cot αtan （π/2－α）＝cot αsin （3π/2＋α）＝－cos αsin （3π/2－α）＝－cos αcos （3π/2＋α）＝sin αcos （3π/2－α）＝－sin αtan （3π/2＋α）＝－cot αtan （3π/2－α）＝cot α四、和角公式和差角公式βαβαβαsin sin cos cos )cos(⋅+⋅=-βαβαβαsin sin cos cos )cos(⋅-⋅=+βαβαβαsin cos cos sin )sin(⋅+⋅=+βαβαβαsin cos cos sin )sin(⋅-⋅=-βαβαβαtan tan 1tan tan )tan(⋅-+=+βαβαβαtan tan 1tan tan )tan(⋅+-=-五、二倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=ααα2tan 1tan 22tan -=六、辅助角公式)sin(cos sin 22ϕ++=+x b a x b x a 其中：角ϕ的终边所在的象限与点),(b a 所在的象限相同，22sin b a b +=ϕ，22cos b a a +=ϕ，ab=ϕtan 。

高三文科数学三角函数知识点归纳

高三文科数学三角函数知识点归纳
三角函数是高考数学历年来考察的重点，高三学生在复习这一块的知识时需要认真对待，下面是店铺给大家带来的高三文科数学三角函数知识点归纳，希望对你有帮助。

高三文科数学三角函数知识点
高三文科数学三角函数考试内容
角的概念的推广.弧度制.
任意角的三角函数.单位圆中的三角函线.同角三角函数的基本关系式.正弦、余弦的诱导公式.
两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切.
正弦函数、余弦函数的图像和性质.周期函数.函数y=Asin(ωx+φ)的图像.正切函数的图像和性质.已知三角函数值求角。

高三文科数学三角函数考试要求
(1)理解任意角的概念、弧度的意义能正确地进行弧度与角度的换算.
(2)掌握任意角的正弦、余弦、正切的定义;了解余切、正割、余割的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式;了解周期函数与最小正周期的意义.
(3)掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式.
(4)能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明.
(5)理解正弦函数、余弦函数、正切函数的图像和性质，会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图，理解
A.ω、φ的物理意义.
(6)会由已知三角函数值求角，并会用符号arcsinx\arc-cosx\arctanx表示.
(7)掌握正弦定理、余弦定理，并能初步运用它们解斜三角形.
(8)“同角三角函数基本关系式：sin2α+cos2α=1，
sinα/cosα=tanα,tanα•cotα=1”。

高中三角函数知识点归纳总结(通用10篇)

高中三角函数知识点归纳总结(通用10篇)高中数学三角函数知识点总结：三倍角公式篇一sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)高中数学三角函数知识点总结：三倍角公式推导篇二sin3a=sin(2a+a)=sin2acosa+cos2asina高中数学三角函数知识点总结：半角公式篇三tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)高中数学三角函数知识点总结：辅助角公式篇四Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t)，tant=A/B降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))高中数学三角函数知识点总结：和差化积篇五sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)高中三角函数知识点归纳篇六1.做高中数学题的时候千万不能怕难题！有很多人数学分数提不动，很大一部分原因是他们的畏惧心理。

文科三角函数知识点整理

文科三角函数知识点整理三角函数这玩意儿，在文科数学里可真是个让人又爱又恨的“小调皮”。

今天咱们就来好好整理整理它！先来说说正弦函数（sin）吧。

这就好比你去游乐场坐摩天轮，从最低点开始，随着摩天轮的转动，你的高度不断变化。

这个高度的变化规律就可以用正弦函数来描述。

想象一下，当你转到最高点时，那就是正弦函数的最大值 1；转到最低点时，就是最小值－1。

是不是有点意思？余弦函数（cos）也差不多。

还是那个摩天轮，这次咱们不看高度，看你离摩天轮中心的水平距离。

从最左边到最右边，再从最右边回到最左边，这就是余弦函数的变化。

正切函数（tan）呢，就像是你在斜坡上跑步。

斜坡越陡，正切值就越大；斜坡越平缓，正切值就越小。

咱们再来说说三角函数的诱导公式。

这就像是变魔术一样，看似复杂，其实有规律可循。

比如说，sin（π α）＝sinα ，cos（π α）＝cosα 。

就好像你和朋友玩捉迷藏，你从这边绕到那边，位置变了，但本质没变。

还有三角函数的图像，那可是非常直观的。

正弦函数的图像像波浪一样，起起伏伏；余弦函数的图像则像是被风吹动的旗帜，左右摆动。

记得我上学那会，有一次数学考试，就考到了三角函数的一个难题。

题目是这样的：已知sinα ＝ 1/2 ，且α在（0，π/2）区间内，求cosα和tanα 的值。

我当时一看，心里有点慌，这可咋办？但我静下心来，想到老师讲的知识点，先根据sin²α ＋cos²α ＝ 1 ，算出cosα ＝√3/2 ，然后再用tanα ＝sinα ／cosα ，算出tanα ＝√3/3 。

那次考试因为这道题，我数学成绩还不错呢！在解决三角函数的问题时，一定要记住特殊角的三角函数值。

像30°、45°、60°这些，那可是经常要用到的。

比如 sin30°＝ 1/2 ，cos30°＝√3/2 ，tan45°＝ 1 。

总之，文科里的三角函数虽然有点复杂，但只要咱们掌握了规律，多做练习，就一定能把它拿下！就像攻克一座城堡，只要找到突破口，就能一举成功！加油吧，同学们！。

高考文科三角函数知识点总结

三角函数知识点一．知识点1．角度制与弧度制的互化：,23600π= ,1800π=1rad ＝π180°≈57.30°=57°18ˊ． 1°＝180π≈0.01745（rad ）2.弧长及扇形面积公式弧长公式：r l .α= 扇形面积公式:S=r l .21α----是圆心角且为弧度制。

r-----是扇形半径3.任意角的三角函数设α是一个任意角，它的终边上一点p （x,y ）, r=22y x + (1)正弦sin α=r y 余弦cos α=r x 正切tan α=xy (2)各象限的符号：sin α cos α tan α4、三角函数线正弦线：MP; 余弦线：OM; 正切线： AT.xy+O— —+x yO — ++— +y O— ++ —(3) 若 o<x<2,则sinx<x<tanx16. 几个重要结论:5.同角三角函数的基本关系：（1）平方关系：s in 2α+ cos 2α=1。

（2）商数关系：ααcos sin =tan α（z k k ∈+≠,2ππα） 6.诱导公式：奇变偶不变，符号看象限()()1sin 2sin k παα+=，()cos 2cos k παα+=，()()tan 2tan k k παα+=∈Z ． ()()2sin sin παα+=-，()cos cos παα+=-，()tan tan παα+=． ()()3sin sin αα-=-，()cos cos αα-=，()tan tan αα-=-． ()()4sin sin παα-=，()cos cos παα-=-，()tan tan παα-=-．()5sin cos 2παα⎛⎫-=⎪⎝⎭，cos sin 2παα⎛⎫-= ⎪⎝⎭． ()6sin cos 2παα⎛⎫+= ⎪⎝⎭，cos sin 2παα⎛⎫+=- ⎪⎝⎭．7正弦函数、余弦函数和正切函数的图象与性质8.辅助角公式：)sin(cos sin 22ϕ++=+x b a x b x a （ab =ϕtan ）其中：角ϕ的终边所在的象限与点),(b a 所在的象限相同，22sin b a b +=ϕ，22cos b a a +=ϕ，ab =ϕtan 。

高中三角函数及解三角形知识点总结(高考复习)

3、三角形面积公式：
= 2 cos 2 α − 1 = 1 − 2 sin 2 α .
变形如下：
1 + cos 2α = 2 cos 2 α 升幂公式： 2 1 − cos 2α = 2sin α cos 2 α = 1 (1 + cos 2α ) 2 降幂公式： sin 2 α = 1 (1 − cos 2α ) 2
y = sin x 在 x ∈ [0, 2π ] 上的五个关键点为：
π 3π （0， 0）（，， 1 ）（， π， 0）（，，） -1（， 2π ， 0） . 2 2
-1-
§1.4.3、正切函数的图象与性质 1、记住正切函数的图象：
y
2、记住余切函数的图象：
y
y=tanx
y=cotx
y = A sin ω x
横坐标变为原来的 | 平移
ϕ ω
2− 3
§ 3.1.2 、两角和与差的正弦、余弦、正切公式
1 ω
|倍
个单位
1、 sin (α + β ) = sin α cos β + cos α sin β 2、 sin (α − β ) = sin α cos β − cos α sin β
r = x2 + y 2 ） sin α = x y x y ， cos α = ， tan α = ， cot α = y r r x
π sin + α = cos α , 2 π cos + α = − sin α . 2
§1.4.1、正弦、余弦函数的图象和性质 1、记住正弦、余弦函数图象：
ymax + ymin . 2
ymax − ymin ， 2

文科三角函数知识点整理

文科三角函数知识点整理一、三角函数的定义在平面直角坐标系中，设角α的顶点在坐标原点，始边与 x 轴正半轴重合，终边上任取一点 P（x，y），它与原点的距离为 r（r ＝√（x²＋ y²)，r ＞ 0），则角α的正弦、余弦、正切分别定义为：正弦（sinα）＝ y ／ r余弦（cosα）＝ x ／ r正切（tanα）＝ y ／ x （x ≠ 0）例如，角α的终边经过点 P（3，4），则 r ＝√（3²＋ 4²) ＝ 5，sinα ＝ 4 ／ 5，cosα ＝ 3 ／ 5，tanα ＝ 4 ／ 3。

二、特殊角的三角函数值要牢记一些特殊角的三角函数值，这在解题中经常会用到。

｜角度｜ 0°｜ 30°｜ 45°｜ 60°｜ 90°｜｜｜｜｜｜｜｜｜ sin 值｜ 0 ｜ 1/2 ｜√2/2 ｜√3/2 ｜ 1 ｜｜ cos 值｜ 1 ｜√3/2 ｜√2/2 ｜ 1/2 ｜ 0 ｜｜ tan 值｜ 0 ｜√3/3 ｜ 1 ｜√3 ｜不存在｜三、同角三角函数的基本关系1、平方关系：sin²α ＋cos²α ＝ 1这是一个非常重要的恒等式，无论α的取值如何，该等式都成立。

2、商数关系：tanα ＝sinα ／cosα （cosα ≠ 0）通过这两个基本关系，可以实现正弦、余弦、正切之间的相互转化。

四、诱导公式诱导公式是用于将任意角的三角函数转化为锐角三角函数的公式。

例如：sin(π ＋α) ＝sinα，cos(π ＋α) ＝cosα，tan(π ＋α) ＝tanαsin(α) ＝sinα，cos(α) ＝cosα，tan(α) ＝tanαsin(π α) ＝sinα，cos(π α) ＝cosα，tan(π α) ＝tanα掌握诱导公式的规律，可以大大简化三角函数的计算。

五、两角和与差的正弦、余弦、正切公式1、两角和的正弦：sin(α ＋β) ＝sinαcosβ ＋cosαsinβ2、两角差的正弦：sin(α β) ＝sinαcosβ cosαsinβ3、两角和的余弦：cos(α ＋β) ＝cosαcosβ sinαsinβ4、两角差的余弦：cos(α β) ＝cosαcosβ ＋sinαsinβ5、两角和的正切：tan(α ＋β) ＝（tanα ＋tanβ) ／（1 tanαtanβ)6、两角差的正切：tan(α β) ＝（tanα tanβ) ／（1 ＋tanαtanβ)这些公式在三角函数的化简、求值和证明中经常使用。

高三高考文科数学《三角函数》题型归纳与汇总

高三高考文科数学《三角函数》题型归纳与汇总高考文科数学题型分类汇总：三角函数篇本文旨在汇总高考文科数学中的三角函数题型，包括定义法求三角函数值、诱导公式的使用、三角函数的定义域或值域、三角函数的单调区间、三角函数的周期性、三角函数的图象变换和三角函数的恒等变换。

题型一：定义法求三角函数值这类题目要求根据三角函数的定义，求出给定角度的正弦、余弦、正切等函数值。

这类题目的难点在于熟练掌握三角函数的定义，以及对角度的准确度量。

题型二：诱导公式的使用诱导公式是指通过对已知的三角函数进行代数变形，得到新的三角函数值的公式。

这类题目需要熟练掌握各种诱导公式，以及灵活应用。

题型三：三角函数的定义域或值域这类题目要求确定三角函数的定义域或值域。

需要掌握各种三角函数的性质和图象，以及对函数的定义域和值域的概念和计算方法。

题型四：三角函数的单调区间这类题目要求确定三角函数的单调区间，即函数在哪些区间上单调递增或单调递减。

需要掌握各种三角函数的性质和图象，以及对函数单调性的判定方法。

题型五：三角函数的周期性这类题目要求确定三角函数的周期。

需要掌握各种三角函数的性质和图象，以及对函数周期的计算方法。

题型六：三角函数的图象变换这类题目要求根据给定的变换规律，确定三角函数图象的变化。

需要掌握各种三角函数的性质和图象，以及对图象变换的计算方法。

题型七：三角函数的恒等变换这类题目要求根据已知的三角函数恒等式，进行变形和推导。

需要掌握各种三角函数的恒等式，以及灵活应用。

2）已知角α的终边经过一点P，则可利用点P在单位圆上的性质，结合三角函数的定义求解．在求解过程中，需注意对角终边位置进行讨论，避免忽略或重复计算．例2已知sinα=0.8，且α∈[0,π2]，则cosα=．答案】0.6解析】∵sinα=0.8，∴cosα=±√1-sin²α=±0.6XXXα∈[0,π2]，∴cosα>0，故cosα=0.6易错点】忘记对cosα的正负进行讨论思维点拨】在求解三角函数值时，需注意根据已知条件确定函数值的正负，避免出现多解或无解的情况．同时，需根据角度范围确定函数值的取值范围，避免出现超出范围的情况．题型二诱导公式的使用例3已知tanα=√3，且α∈(0,π2)，则sin2α=．答案】34解析】∵ta nα=√3，∴α=π/30<α<π/2，∴0<2α<πsin2α=sin(π-2α)=sinπcos2α-cosπsin2α=-sin2α2sin2α=0，∴sin2α=0sin2α=3/4易错点】忘记利用诱导公式将sin2α转化为sin(π-2α)思维点拨】在解决三角函数的复合问题时，可利用诱导公式将一个三角函数转化为其他三角函数的形式，从而简化计算．同时，需注意根据角度范围确定函数值的取值范围，避免出现超出范围的情况．题型三三角函数的定义域或值域例4已知f(x)=2sinx+cosx，则f(x)的值域为．答案】[−√5,√5]解析】∵f(x)=2sinx+cosx=√5(sin(x+α)+sin(α-x))，其中tanα=-121≤sin(x+α)≤1，-1≤sin(α-x)≤15≤f(x)≤√5f(x)的值域为[−√5,√5]易错点】忘记利用三角函数的性质将f(x)转化为含有同一三角函数的形式思维点拨】在确定三角函数的定义域或值域时，可利用三角函数的性质将其转化为含有同一三角函数的形式，从而方便计算．同时，需注意对于复合三角函数，需先将其转化为含有同一三角函数的形式，再确定其定义域或值域．题型四三角函数的单调区间例5已知f(x)=sin2x，则f(x)在区间[0,π]上的单调递增区间为．答案】[0,π/4]∪[3π/4,π]解析】∵f'(x)=2cos2x=2(2cos²x-1)=4cos²x-2f'(x)>0的充要条件为cosx12f(x)在[0,π/4]∪[3π/4,π]上单调递增易错点】忘记将f'(x)化简为含有同一三角函数的形式，或对于三角函数的单调性判断不熟练思维点拨】在求解三角函数的单调区间时，需先求出其导数，并将其化简为含有同一三角函数的形式．然后，利用三角函数的单调性进行判断，得出函数的单调区间．题型五三角函数的周期性例6已知f(x)=sin(2x+π)，则f(x)的周期为．答案】π解析】∵sin(2x+π)=sin2xcosπ+cos2xsinπ=-sin2xf(x)的周期为π易错点】忘记利用三角函数的周期性质思维点拨】在求解三角函数的周期时，需利用三角函数的周期性质，即f(x+T)=f(x)，其中T为函数的周期．同时，需注意对于复合三角函数，需先将其转化为含有同一三角函数的形式，再确定其周期．题型六三角函数的图象变换例7已知f(x)=sinx，g(x)=sin(x-π4)，则g(x)的图象相对于f(x)的图象向左平移了．答案】π4解析】∵g(x)=sin(x-π4)=sinxcosπ4-cosxsinπ4g(x)的图象相对于f(x)的图象向左平移π4易错点】忘记利用三角函数的图象变换公式，或对于三角函数的图象不熟悉思维点拨】在求解三角函数的图象变换时，需利用三角函数的图象变换公式，即y=f(x±a)的图象相对于y=f(x)的图象向左（右）平移a个单位．同时，需对于各种三角函数的图象有一定的了解，以便准确判断图象的变化情况．题型七三角函数的恒等变换例8已知cosα=12，且α∈(0,π2)，则sin2α的值为．答案】34解析】∵cosα=12，∴sinα=√3/2sin2α=2sinαcosα=√3/2×1/2=3/4易错点】忘记利用三角函数的恒等变换公式思维点拨】在求解三角函数的恒等变换时，需熟练掌握三角函数的基本恒等式和常用恒等式，从而简化计算．同时，需注意根据已知条件确定函数值的正负，避免出现多解或无解的情况．已知角α的终边所在的直线方程，可以通过设出终边上一点的坐标，求出此点到原点的距离，然后利用三角函数的定义来解决相关问题。

(word完整版)三角函数最全知识点总结,推荐文档

三角函数、解三角形一、任意角和弧度制及任意角的三角函数1.任意角的概念(1)我们把角的概念推广到任意角，任意角包括正角、负角、零角．①正角：按__逆时针__方向旋转形成的角．②负角：按__顺时针__方向旋转形成的角．③零角：如果一条射线__没有作任何旋转__，我们称它形成了一个零角．(2)终边相同角：与α终边相同的角可表示为：{β|β＝α＋2kπ，k∈Z}，或{β|β＝α＋k·360°，k∈Z}．(3)象限角：角α的终边落在__第几象限__就称α为第几象限的角，终边落在坐标轴上的角不属于任何象限.象限角轴线角2．弧度制(1)1度的角：__把圆周分成360份，每一份所对的圆心角叫1°的角__.(2)1弧度的角：__弧长等于半径的圆弧所对的圆心角叫1弧度的角__.(3)角度与弧度的换算：360°＝__2π__rad,1°＝__π180＝(__180π__)≈57°18′.(4)若扇形的半径为r，圆心角的弧度数为α，则此扇形的弧长l＝__|α|·r__，面积S＝__12|α|r2__＝__12lr__.3．任意角的三角函数定义(1)设α是一个任意角，α的终边上任意一点(非顶点)P的坐标是(x，y)，它与原点的距离为r，则sinα＝__yr__，cosα＝__xr__，tanα＝__yx__.(2)三角函数在各象限的符号是：(3)三角函数线可以看作是三角函数的几何表示．正弦线的起点都在x轴上，余弦线的起点都是原点，正切线的起点都是(1,0)．如图中有向线段MP，OM，AT分别叫做角α的__正弦__线、__余弦__线和__正切__线．4．终边相同的角的三角函数sin(α＋k·2π)＝__sinα__，cos(α＋k·2π)＝__cosα__，tan(α＋k·2π)＝__tanα__(其中k∈Z)，即终边相同的角的同一三角函数的值相等．重要结论1．终边相同的角不一定相等，相等角的终边一定相同，在书写与角α终边相同的角时，单位必须一致．2．确定αk(k∈N*)的终边位置的方法(1)讨论法：①用终边相同角的形式表示出角α的范围．②写出αk的范围．③根据k的可能取值讨论确定αk的终边所在位置．(2)等分象限角的方法：已知角α是第m(m＝1,2,3,4)象限角，求αk是第几象限角．①等分：将每个象限分成k等份．②标注：从x轴正半轴开始，按照逆时针方向顺次循环标上1,2,3,4，直至回到x轴正半轴．③选答：出现数字m的区域，即为αk所在的象限．如α2判断象限问题可采用等分象限法．二、同角三角函数的基本关系式与诱导公式1．同角三角函数的基本关系式(1)平方关系：__sin 2x ＋cos 2x ＝1__. (2)商数关系：__sin xcos x ＝tan x __.2．三角函数的诱导公式1．同角三角函数基本关系式的变形应用：如sin x ＝tan x ·cos x ，tan 2x ＋1＝1cos 2x ，(sin x ＋cos x )2＝1＋2sin x cos x 等． 2．特殊角的三角函数值表“奇变偶不变，符号看象限”．“奇”与“偶”指的是诱导公式k ·π2＋α中的整数k 是奇数还是偶数．“变”与“不变”是指函数的名称的变化，若k 是奇数，则正、余弦互变；若k 为偶数，则函数名称不变．“符号看象限”指的是在k ·π2＋α中，将α看成锐角时k ·π2＋α所在的象限．4.sin x ＋cos x 、sin x －cos x 、sin x cos x 之间的关系sin x ＋cos x 、sin x －cos x 、sin x cos x 之间的关系为(sin x ＋cos x )2＝1＋2sin x cos x ，(sin x －cos x )2＝1－2sin x cos x ，(sin x ＋cos x )2＋(sin x －cos x )2＝2.因此已知上述三个代数式中的任意一个代数式的值，便可求其余两个代数式的值．三、两角和与差的三角函数二倍角公式1．两角和与差的正弦、余弦和正切公式2．二倍角的正弦、余弦、正切公式 (1)sin2α＝__2sin αcos α__；(2)cos2α＝__cos 2α－sin 2α__＝__2cos 2α__－1＝1－__2sin 2α__； (3)tan2α＝__2tan α1－tan 2α__(α≠k π2＋π4且α≠k π＋π2，k ∈Z )． 3．半角公式(不要求记忆) (1)sin α2＝±1－cos α2； (2)cos α2＝±1＋cos α2；(3)tan α2＝±1－cos α1＋cos α＝sin α1＋cos α＝1－cos αsin α.重要结论1．降幂公式：cos 2α＝1＋cos2α2，sin 2α＝1－cos2α2. 2．升幂公式：1＋cos2α＝2cos 2α，1－cos2α＝2sin 2α. 3．公式变形：tan α±tan β＝tan(α±β)(1∓tan α·tan β)． 1－tan α1＋tan α＝tan(π4－α)；1＋tan α1－tan α＝tan(π4＋α)cos α＝sin2α2sin α，sin2α＝2tan α1＋tan 2α，cos2α＝1－tan 2α1＋tan 2α，1±sin2α＝(sin α±cos x )2.4．辅助角(“二合一”)公式： a sin α＋b cos α＝a 2＋b 2sin(α＋φ)，其中cos φ＝，sin φ＝ 5.三角形中的三角函数问题在三角形中，常用的角的变形结论有：A ＋B ＝π－C ；2A ＋2B ＋2C ＝2π；A2＋B 2＋C 2＝π2.三角函数的结论有：sin(A ＋B )＝sin C ，cos(A ＋B )＝－cos C ，tan(A ＋B )＝－tan C ，sin A ＋B 2＝cos C 2，cos A ＋B 2＝sin C 2.A >B ⇔sin A >sin B ⇔cos A <cos B .四、三角函数的图象与性质1．周期函数的定义及周期的概念(1)对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x＋T)＝f(x)，那么函数f(x)就叫做__周期函数__.非零常数T叫做这个函数的__周期__.如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小__正周期__.(2)正弦函数、余弦函数都是周期函数，__2kπ(k∈Z，k≠0)__都是它们的周期，最小正周期是__2π__.2．正弦、余弦、正切函数的图象与性质π重要结论1．函数y ＝sin x ，x ∈[0,2π]的五点作图法的五个关键点是__(0,0)__、__(π2，1)__、__(π，0)__、__(3π2，－1)__、__(2π，0)__.函数y ＝cos x ，x ∈[0,2π]的五点作图法的五个关健点是__(0,1)__、__(π2，0)__、__(π，－1)__、__(3π2，0)__、__(2π，1)__.2．函数y ＝A sin(ωx ＋φ)和y ＝A cos(ωx ＋φ)的最小正周期为T ＝2π|ω|，函数y ＝tan(ωx ＋φ)的最小正周期为T ＝π|ω|.3．正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半周期，相邻的对称中心与对称轴之间的距离是14周期．而正切曲线相邻两对称中心之间的距离是半周期．4．三角函数中奇函数一般可化为y ＝A sin ωx 或y ＝A tan ωx 的形式，而偶函数一般可化为y ＝A cos ωx ＋b 的形式．五、函数y ＝A sin(ωx ＋φ)的图象及应用1．五点法画函数y ＝A sin(ωx ＋φ)(A >0)的图象(1)列表：(2)描点：__(－φω，0)__，__(π2ω－φω，A )__，(πω－φω，0)，(3π2ω－φω，－A )__，(2πω－φω，0)__.(3)连线：把这5个点用光滑曲线顺次连接，就得到y ＝A sin(ωx ＋φ)在区间长度为一个周期内的图象．(4)扩展：将所得图象，按周期向两侧扩展可得y ＝A sin(ωx ＋φ)在R 上的图象2．由函数y ＝sin x 的图象变换得到y ＝A sin(ωx ＋φ)(A >0，ω>0)的图象的步骤3．函数y ＝A sin(ωx ＋φ)(A >0，ω>0，x ∈[0，＋∞)的物理意义 (1)振幅为A . (2)周期T ＝__2πω__.(3)频率f ＝__1T __＝__ω2π__. (4)相位是__ωx ＋φ__. (5)初相是φ.重要结论1．函数y ＝A sin(ωx ＋φ)的单调区间的“长度 ”为T2.2．“五点法”作图中的五个点：①y ＝A sin(ωx ＋φ)，两个最值点，三个零点；②y ＝A cos(ωx ＋φ)，两个零点，三个最值点．3．正弦曲线y ＝sin x 向左平移π2个单位即得余弦曲线y ＝cos x .六、正弦定理、余弦定理1．正弦定理和余弦定理 ①a ＝__2R sin A __，b ＝__2R sin B __，c ＝__2R sin C __；②sin A ＝__a 2R __，sin B ＝__b2R__，sin C＝__c2R __；③ab c ＝__sin Asin B sin C __④a sin B ＝b sin A ，b sin C ＝c sin B ，a sin C ＝c sin Aa <b sin A a ＝b sin A b sin A < a <b a ≥b a >b a ≤b (1)S ＝12a ·h a (h a 表示a 边上的高)．(2)S ＝12ab sin C ＝12ac sin B ＝12bc sin A .(3)S ＝12r (a ＋b ＋c )(r 为内切圆半径)．重要结论在△ABC 中，常有以下结论 1．∠A ＋∠B ＋∠C ＝π.2．在三角形中大边对大角，大角对大边．3．任意两边之和大于第三边，任意两边之差小于第三边．4．sin(A ＋B )＝sin C ；cos(A ＋B )＝－cos C ；tan(A ＋B )＝－tan C ；sin A ＋B 2＝cos C 2，cos A ＋B 2＝sin C 2. 5．tan A ＋tan B ＋tan C ＝tan A ·tan B ·tan C .6．∠A >∠B ⇔a >b ⇔sin A >sin B ⇔cos A <cos B .7．三角形式的余弦定理sin 2A ＝sin 2B ＋sin 2C －2sin B sin C cos A ，sin 2B ＝sin 2A ＋sin 2C －2sin A sin C cos B ，sin 2C ＝sin 2A ＋sin 2B －2sin A sin B cos C .8．若A 为最大的角，则A ∈[π3，π)；若A 为最小的角，则A ∈(0，π3]；若A 、B 、C 成等差数列，则B ＝π3. 9.三角形形状的判定方法(1)通过正弦定理和余弦定理，化边为角(如a ＝2R sin A ，a 2＋b 2－c 2＝2ab cos C 等)，利用三角变换得出三角形内角之间的关系进行判断．此时注意一些常见的三角等式所体现的内角关系，如sin A ＝sin B ⇔A ＝B ；sin(A －B )＝0⇔A ＝B ；sin2A ＝sin2B ⇔A ＝B 或A ＋B ＝π2等． (2)利用正弦定理、余弦定理化角为边，如sin A ＝a 2R ，cos A ＝b 2＋c 2－a 22bc等，通过代数恒等变换，求出三条边之间的关系进行判断．(3)注意无论是化边还是化角，在化简过程中出现公因式不要约掉，否则会有漏掉一种形状的可能．。

高三文科数学三角函数概念、同角关系、诱导公式

二、三角函数定
义的应用原点）的角为，OB为终边的角为，那么 sin(+ )等于多少？
（第103页例1）
二、三角函数定义的应用
例2 直线y=2x+m和圆x2+y2=1交于以x轴正方向为始边，OA为终边（
典例分析
原点）的角为，OB为终边的角为 sin(+ )等于
典例分析
二、三角函数定义的应用
例3 如图，已知点A（3，4），C(2,0),
点B在第二象限，且OB=3，O为坐标原点，
记AOC= . (1)求sin2的值；
y
A
（2）若AB=7，求 BOC的面积.
B
O
C
x
典例分析
三、
－７例4
已知-
2
x
0, sin
x
cos
x
1 5
,
5 求sin x cos x 的值.
sin x cos x与方程思想
典例分析
sin x cos x与方程思想
复习回顾
二、三角函数定义的应用
1.齐次式的问题
一、同角关系的应用
2.已知一个角的三角函数值,求其它的三角函数值
典例分析
若角的终边落在射线y=二-、x三(角函x数定义0的)应上用，
in
1 cos2 的值为（第104页第6题）2 直线y=2x+m和圆x2+y2=1交于点A,B，以x轴正方向为始边，OA为终边（O是坐标
例5
已知（０，）,sin２
－24 , 25
－７
求 cos sin 的值.
5
三、
三角函数的概念同角三角函数的关系诱导
公式
单击此处添加副标题

高考文科数学三角函数知识点

高考文科数学三角函数知识点一、角度制和弧度制1.角度的定义：角度是用来度量平面上两条射线之间夹角的一种方式。

2.角度的度量方式：角度可以用角度制和弧度制来表示。

(1)角度制：一圆的角度被等分为360个等份，即1度(°)。

(2) 弧度制：一圆的弧长等于半径的角度被称为1弧度(rad)。

二、常用三角函数1. 正弦函数(sin)：在直角三角形中，对于非直角边为a，斜边为h的直角三角形，定义sinA=a/h。

2. 余弦函数(cos)：在直角三角形中，对于非直角边为b，斜边为h的直角三角形，定义cosA=b/h。

3. 正切函数(tan)：在直角三角形中，对于非直角边为a，非直角边为b的直角三角形，定义tanA=a/b。

4. 余切函数(cot)：cotA=1/tanA。

5. 正割函数(sec)：secA=1/cosA。

6. 余割函数(csc)：cscA=1/sinA。

三、三角函数的基本性质1.定义域和值域：对于正弦函数和余弦函数，其定义域为全体实数，值域为[-1,1]；对于正切函数和余切函数，其定义域为全体实数，但在一些点或区间上不存在值；对于正割函数和余割函数，其定义域为实数集合中除去余弦函数零点的点，值域为(-∞,-1]∪[1,+∞]；2.奇偶性：(1) 正弦函数和余切函数是奇函数，即sin(-x)=-sinx，cot(-x)=-cots。

(2) 余弦函数、正切函数和正割函数是偶函数，即cos(-x)=cosx，tan(-x)=-tanx，sec(-x)=secx。

3.周期性：正弦函数、余弦函数、正割函数和余割函数的周期均为2π；正切函数和余切函数的周期为π。

4.诱导公式：(1) 正弦函数和余弦函数的诱导公式：sin(A±B)=sinAcosB±cosAsinB，cos(A±B)=cosAcosB∓sinAsinB。

(2) 正切函数和余切函数的诱导公式：tan(A±B)=(tanA±tanB)/(1mpcosAcosB)，cot(A±B)=(cotAcotB-/+1)/(cotA±cotB)。

(完整版)高中三角函数知识点总结

(完整版)高中三角函数知识点总结高中三角函数知识点总结1. 基本三角函数概念- 三角函数是以单位圆为基础的函数，包括正弦函数、余弦函数和正切函数。

- 正弦函数（sin）：在直角三角形中，对于一个锐角，其对边与斜边的比值称为正弦值。

即：sinA = 对边/斜边。

- 余弦函数（cos）：在直角三角形中，对于一个锐角，其邻边与斜边的比值称为余弦值。

即：cosA = 邻边/斜边。

- 正切函数（tan）：在直角三角形中，对于一个锐角，其对边与邻边的比值称为正切值。

即：tanA = 对边/邻边。

2. 基本三角函数性质和公式- 三角函数的周期性：正弦函数和余弦函数的周期都是2π；正切函数的周期是π.- 三角函数的奇偶性：正弦函数是奇函数，余弦函数是偶函数，正切函数是奇函数。

- 三角函数的同角关系：sinA/cosA = tanA。

- 三角函数的和差化积公式和积化和差公式：具体公式可根据需要进行查阅。

3. 三角函数图像和性质- 正弦函数图像：在0到2π的区间内，正弦函数的图像为一条周期性的波浪线，最高点为1，最低点为-1，对应于最大值和最小值，0点对应于零值。

- 余弦函数图像：在0到2π的区间内，余弦函数的图像为一条周期性的波浪线，最高点为1，最低点为-1，对应于最大值和最小值，0点对应于最大值。

- 正切函数图像：在0到π的区间内，正切函数的图像无法在x=π/2和3π/2时定义，其他点对应的图像为一条连续的射线。

4. 三角函数的应用- 三角函数广泛应用于科学和工程领域中的周期性现象的描述和计算，例如电流的正弦波，声波的波动等。

- 在几何学中，三角函数也应用于测量角度和距离等问题的解决。

以上为高中三角函数的基本知识点总结，更详细的内容和公式可以参考相关教材或资料。

三角函数最全知识点总结

三角函数最全知识点总结三角函数是高中数学中的重要内容，主要包括正弦函数、余弦函数、正切函数等。

下面将对这些三角函数的定义、性质以及常用的解题方法进行总结。

一、正弦函数（sin）：1. 定义：在单位圆上，任选一点P与x轴正方向的夹角为θ，P点的纵坐标y即为θ的正弦值，记作sinθ。

正弦函数的定义域为实数集，值域为[-1,1]。

2. 周期性：sin(θ+2π)=sinθ，sin(θ+π)=-sinθ。

其中π为圆周率。

3. 奇偶性：sin(-θ)=-sinθ，即正弦函数关于原点对称。

4. 正负性：当θ为锐角时，sinθ>0；当θ为钝角时，sinθ<0。

5. 值域变化：当θ从0增加到π/2时，sinθ从0增加到1，然后再从1减小到0。

二、余弦函数（cos）：1. 定义：在单位圆上，任选一点P与x轴正方向的夹角为θ，P点的横坐标x即为θ的余弦值，记作cosθ。

余弦函数的定义域为实数集，值域为[-1,1]。

2. 周期性：cos(θ+2π)=cosθ，cos(θ+π)=-cosθ。

3. 奇偶性：cos(-θ)=cosθ，即余弦函数关于y轴对称。

4. 正负性：当θ为锐角时，cosθ>0；当θ为钝角时，cosθ<0。

5. 值域变化：当θ从0增加到π/2时，cosθ从1减小到0。

三、正切函数（tan）：1. 定义：正切值tanθ等于θ的正弦值除以θ的余弦值，即tanθ=sinθ/cosθ。

正切函数的定义域为实数集，值域为实数集。

2. 周期性：tan(θ+π)=tanθ。

3. 奇偶性：tan(-θ)=-tanθ，即正切函数关于原点对称。

4. 正负性：当θ为锐角时，tanθ>0；当θ为钝角时，tanθ<0。

四、反三角函数：1. 反正弦函数：定义域为[-1,1]，值域为[-π/2，π/2]。

记作arcsin x或sin⁻¹x。

2. 反余弦函数：定义域为[-1,1]，值域为[0,π]。

高考三角函数必备知识点

s i n c o s

2
1
y sin x
0
y
sin 2 cos2 ቤተ መጻሕፍቲ ባይዱ 1
t a n
t a n c o t 1
-1
2

3 2
2 x

2
1 0 -1
y cos x
2

3 2
2 x
6、两角和与差的正弦、余弦、正切
S( ) ： sin( ) sin cos cos sin C( ) ： cos(a ) cos cos sin sin
(2k 1) ,2k
2k , (2k 1)
x k , k Z
3 2
y
0
0
1
6 1 2
3 2
4
2 2 2 2
1
3
3 2
2
1
2 3
3 2
3 4
2 2 2 2
1
5 6

0
1
3 2
1

2
1 2
3 2 3 3
0
1
x k
2 2 2 2 2 2 2 2
4、余弦定理公式原形： a b c 2bc cos A , b a c 2ac cos B , c a b 2ab cos C
2
公式变形： cos A
b2 c 2 a 2 a 2 c 2 b2 a 2 b2 c 2 ， cos B ， cos C 2ab 2bc 2ac
1 cos 2 1 1 cos 2 2 2 2 1 cos 2 1 1 cos 2 cos 2 2 2 2 2 tan T2 ： tan 2 1 tan 2 sin 2 sin cos 1 sin 2 2

高考三角函数复习专题

三角函数复习专题一、核心知识点归纳：★★★1、正弦函数、余弦函数和正切函数的图象与性质：★★2.正、余弦定理：在ABC ∆中有: ①正弦定理：2sin sin sin a b cR A B C===R 为ABC ∆外接圆半径2sin 2sin 2sin a R A b R B c R C =⎧⎪=⎨⎪=⎩ ⇒ sin 2sin 2sin 2a A R b B R c C R ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩注意变形应用 ②面积公式：111sin sin sin 222ABC S abs C ac B bc A ∆===③余弦定理： 2222222222cos 2cos 2cos a b c bc A b a c ac B c a b ab C ⎧=+-⎪=+-⎨⎪=+-⎩ ⇒ 222222222cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩三、例题集锦：考点一：三角函数的概念1.如图,设A 是单位圆和x 轴正半轴的交点,Q P 、是单位圆上的两点,O 是坐标原点,6π=∠AOP ,[)παα,0,∈=∠AOQ ．1若34(,)55Q ,求⎪⎭⎫⎝⎛-6cos πα的值；2设函数()f OP OQ α=⋅,求()αf 的值域． 2．已知函数2()22sin f x x x =-.Ⅰ若点(1,P在角α的终边上,求()f α的值； Ⅱ若[,]63x ππ∈-,求()f x 的值域.考点二：三角函数的图象和性质3.函数()sin()(0,0,||)2f x A x A ωφωφπ=+>><部分图象如图所示．Ⅰ求()f x 的最小正周期及解析式；Ⅱ设()()cos 2g x f x x =-,求函数()g x 在区间[0,]x π∈上的最大值和最小值．考点三、四、五：同角三角函数的关系、诱导公式、三角恒等变换4．已知函数x x x f 2cos )62sin()(+-=π.1若1)(=θf ,求θθcos sin ⋅的值；2求函数)(x f 的单调增区间.3求函数的对称轴方程和对称中心 5.已知函数2()2sin cos 2cos f x x x x ωωω=-0x ω∈>R ，,相邻两条对称轴之间的距离等于2π．Ⅰ求()4f π的值；Ⅱ当 02x π⎡⎤∈⎢⎥⎣⎦，时,求函数)(x f 的最大值和最小值及相应的x 值． 6、已知函数2()2sin sin()2sin 12f x x x x π=⋅+-+ ()x ∈R . Ⅰ求函数()f x 的最小正周期及函数()f x 的单调递增区间；Ⅱ若0()23x f =,0ππ(, )44x ∈-,求0cos 2x 的值.7、已知πsin()410A +=,ππ(,)42A ∈． Ⅰ求cos A 的值； Ⅱ求函数5()cos 2sin sin 2f x x A x =+的值域．考点六：解三角形8．已知△ABC 中,2sin cos sin cos cos sin A B C B C B =+. Ⅰ求角B 的大小；Ⅱ设向量(cos , cos 2)A A =m ,12(, 1)5=-n ,求当⋅m n 取最小值时,)4tan(π-A 值.9．已知函数23cos sin sin 3)(2-+=x x x x f ()R x ∈． Ⅰ求)4(πf 的值；Ⅱ若)2,0(π∈x ,求)(x f 的最大值；Ⅲ在ABC ∆中,若B A <,21)()(==B f A f ,求AB BC 的值．10、在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c 分,且满足2cos cos c b Ba A-=． Ⅰ求角A 的大小；Ⅱ若a =求△ABC 面积的最大值．11、在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且b 2+c 2-a 2=bc ．9第题图Ⅰ求角A 的大小；Ⅱ设函数2cos 2cos 2sin 3)(2x x xx f +=,当)(B f 取最大值23时,判断△ABC 的形状．12、在ABC ∆中,内角A 、B 、C 所对的边分别为,,a b c ,已知1tan 2B =,1tan 3C =,且1c =. Ⅰ求tan A ； Ⅱ求ABC ∆的面积.13、在ABC ∆中,角A ,B ,C 所对应的边分别为a ,b ,c ,且274sin cos222A B C +-=． Ⅰ求角C 的大小； Ⅱ求sin sin A B +的最大值．高三文科---三角函数专题11.已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos2θ=A .45- B .35- C .35 D .452.如图,质点P 在半径为2的圆周上逆时针运动,其初始位置为)2,2(0-P ,角速度为1,那么点P 到x 轴距离d 关于时间t 的函数图象大致为3.动点(),A x y 在圆221x y +=上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间0t =时,点A 的坐标是13(,)22,则当012t ≤≤时,动点A 的纵坐标y 关于t 单位：秒的函数的单调递增区间是A 、[]0,1B 、[]1,7C 、[]7,12D 、[]0,1和[]7,124.函数f (x)Asin(wx ),(A,w,=+φφ）为常数,)0,0>>w A 的部分图象如图所示,则f (0)____的值是5.已知函数f (x)A tan(x )=ω+ϕω＞0,2π＜ϕ,y f (x)=的部分图象如下图,则f24π=__________. 6. 函数f x=sinx －cosx ＋6π的值域为A ．－2 ,2B .33C .－1,1D .－33 8.已知函数()sin(2)f x x ϕ=+,其中ϕ为实数,若()()6f x f π≤对x R ∈恒成立,且()()2f f ππ>,则()f x 的单调递增区间是 A ,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B ,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦C 2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ D ,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦14.定义在⎪⎭⎫⎝⎛20π,的函数y=6cosx 图像与y=5tanx 图像的交点为P,过点P 作PP 1⊥x轴于点P 1,直线PP 1与y=sinx 的图像交于点P 2,则线段P 1P 2的长为 .16.如图,四位同学在同一个坐标系中分别选定了一个适当的区间,各自作出三个函数sin 2y x =, sin()6y x π=+,sin()3y x π=-的图像如下,结果发现其中有一位同学作出的图像有错误,那么有错误．．的图像是 A B C D17.已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是20.设sin 1+=43πθ（）,则sin 2θ=A 79- B 19- C 19 D 7922.已知,2)4tan(=+πx 则x x2tan tan 的值为__________25.若tan θ＋1tan θ=4,则sin 2θ=A ．15B . 14C . 13D . 1226.已知α为第二象限角,33cos sin =+αα,则cos2α=A 555527.若02πα<<,02πβ-<<,1cos ()43πα+=,3cos ()42πβ-=则cos ()2βα+= A33 B 33-53 D 628. 设α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则)122sin(π+a 的值为． 29.在△ABC 中,角A 、B 、C 所对应的边为c b a ,,1若,cos 2)6sin(A A =+π 求A 的值；2若c b A 3,31cos ==,求C sin 的值.30.如图,△ABC 中,AB=AC=2,BC=3点D 在BC 边上,∠ADC=45°,则AD 的长度等于___.31.在ABC ∆中,内角A,B,C 所对的边分别是c b a ,,,已知8b=5c,C=2B,则cosC=A257 B 257- C 257± D 2524 34.设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且53cos =A ,135cos =B ,3=b 则c =35. 如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=A 、31010 B 、1010 C 、510 D 、51536. 在ABC ∆中,角,,A B C 所对边长分别为,,a b c , 若2222a b c +=,则cos C 的最小值为A .3. 22C . 12D . 12-37.在ABC 中,60,3B AC ==则2AB BC +的最大值为 . 39. 设ABC ∆的内角,,A B C 所对的边为,,a b c ；则下列命题正确的是①若2ab c >；则3C π<②若2a b c +>；则3C π<③若333a b c +=；则2C π<④若()2a b c ab +<；则2C π>⑤若22222()2a b c a b +<；则3C π>43. 已知函数()tan(2),4f x x =+πⅠ求()f x 的定义域与最小正周期；II 设0,4⎛⎫∈ ⎪⎝⎭πα,若()2cos 2,2f =αα求α的大小45. 设函数22())sin 4f x x x π=++. I 求函数()f x 的最小正周期；II 设函数()g x 对任意x R ∈,有()()2g x g x π+=,且当[0,]2x π∈时, 1()()2g x f x =-,求函数()g x 在[,0]π-上的解析式.47.设426f (x )cos(x )sin x cos x π=ω-ω+ω,其中.0>ω Ⅰ求函数y f (x )= 的值域Ⅱ若y f (x )=在区间322,ππ⎡⎤-⎢⎥⎣⎦上为增函数,求 ω的最大值.48. 函数2()6cos 33(0)2xf x x ωωω=->在一个周期内的图象如图所示,A 为图象的最高点,B 、C 为图象与x 轴的交点,且ABC ∆为正三角形.Ⅰ求ω的值及函数()f x 的值域； Ⅱ若083()f x =,且0102(,)33x ∈-,求0(1)f x +的值. 52. 已知,,a b c 分别为ABC ∆三个内角,,A B C 的对边,cos 3sin 0a C a C b c --= 1求A ； 2若2a =,ABC ∆的面积为3；求,b c .53.在∆ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ．已知cos A ＝23,sin B ＝5C ．Ⅰ求tan C 的值； Ⅱ若a 2求∆ABC 的面积．54.在△ABC中,角A ,B ,C 的对边分别为a ,b ,c .已知,sin()sin()444A b C cB a πππ=+-+= 1求证： 2B C π-=2若2a =,求△ABC 的面积.56.已知向量(cos sin ,sin )x x x ωωω=-a ,(cos sin ,23cos )x x x ωωω=--b ,设函数()f x λ=⋅+a b ()x ∈R 的图象关于直线πx =对称,其中ω,λ为常数,且1(,1)2ω∈.Ⅰ求函数()f x 的最小正周期；Ⅱ若()y f x =的图象经过点π(,0)4,求函数()f x 在区间3π[0,]5上的取值范围. 57.在ABC ∆中,已知3AB AC BA BC =． 1求证：tan 3tan B A =； 2若5cos 5C =，求A 的值．58. 已知△ABC 得三边长成公比为2的等比数列,则其最大角的余弦值为_____.59.已知ABC ∆ 的一个内角为120o ,并且三边长构成公差为4的等差数列,则ABC ∆的面积为_______60.已知等比数列{a n }的公比q=3,前3项和313.3S = I 求数列{a n }的通项公式；II 若函数()sin(2)(0,0)f x A x A p ϕϕπ=+><<<在6x π=处取得最大值,且最大值为a 3,求函数fx 的解析式.63.函数22xy sin x =-的图象大致是 64.函数fx=sin x ωϕ+的导函数()y f x '=的部分图像如图4所示,其中,P 为图像与y 轴的交点,A,C 为图像与x 轴的两个交点,B 为图像的最低点.1若6πϕ=,点P 的坐标为0,332,则ω= ； 2求∆ABC 面积65设ABC ∆的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=.I 求BII 若1sin sin 4A C =,求C .66在△ABC 中,内角A 、B 、C 的对边分别是a 、b 、c ,且222a b c =++.Ⅰ求A ;Ⅱ设a =S 为△ABC 的面积,求3cos cos S B C +的最大值,并指出此时B 的值.67在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且3cos()cos sin()sin()5A B B A B A c ---+=-.Ⅰ求sin A 的值;Ⅱ若a =5b =,求向量BA 在BC 方向上的投影68已知函数()sin cos f x x a x =+的一个零点是3π4. Ⅰ求实数a 的值;Ⅱ设22()[()]2sin g x f x x =-,求()g x 的单调递增区间.69在△ABC 中,内角,,A B C 所对的边分别为,,a b c ,已知sin (tan tan )tan tan B A C A C +=.Ⅰ求证：,,a b c 成等比数列； Ⅱ若1,2a c ==,求△ABC 的面积S .三角函数1、在ABC ∆中,已知内角3A π=,边BC =设内角B x =,面积为y .1求函数()y f x =的解析式和定义域； 2求y 的最大值.2、已知a ＝coos α,sin α,b ＝coos β,sin β,其中0＜α＜β＜π． 1求证：a ＋b 与a －b 互相垂直；2若k a ＋b 与a －k b 的长度相等,求β－α的值k 为非零的常数．3、已知3sin22B A ++cos 22BA -=2, cocacobs ≠0,求tanAtanB 的值; 5、已知ABC ∆中,1||=AC ,0120=∠ABC ,θ=∠BAC ,记→→•=BC AB f )(θ, 1求)(θf 关于θ的表达式； 2求)(θf 的值域；6、已知向量],2[),2cos ),122(cos(),2cos ),122(sin(ππππ∈-+=+=x x x b x x a ,函数b a x f ⋅=)(.I 若53cos -=x ,求函数)(x f 的值；II 将函数)(x f 的图象按向量c ＝)0)(,(π<<m n m 平移,使得平移后的图象关于原点对称,求向量c .9、在ABC ∆中,已知内角A 、B 、C 所对的边分别为a 、b 、c,向量(2sin ,m B =,2cos 2,2cos 12B n B ⎛⎫=- ⎪⎝⎭,且//m n ;I 求锐角B 的大小；II 如果2b =,求ABC ∆的面积ABC S ∆的最大值; 10、已知向量()()3cos2,1,1,sin2,,m a x n b a x a b R ==-∈,集合{}2cos ,22M x x x ππ⎡⎤=∈-⎢⎥⎣⎦,若函数()f x m n x M =∈在时,取得最大值3,最小值为－1,求实数,a b 的值16、在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -= I 求cos B 的值；II 若2=⋅BC BA ,且22=b ,求c a 和b 的值.21、已知向量m =()B B cos 1,sin -, 向量n = 2,0,且m 与n 所成角为错误!,其中A 、B 、C 是ABC ∆的内角;ＡＢＣ1201求角B 的大小;2求 C A sin sin +的取值范围;26、在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,C ＝2A,43cos =A , 1求B C cos ,cos 的值；2若227=⋅BC BA ,求边AC 的长; 30、已知ABC △的面积为3,且满足60≤⋅≤AC AB ,设AB 和AC 的夹角为θ． I 求θ的取值范围；II 求函数)4(sin 2)(2πθθ+=f －θ2cos 3的最大值与最小值．33、已知△ABC 的面积为３,且06,AB AC AB AC θ→→→→≤•≤设和的夹角为; 1求θ的取值范围；2求函数22()(sin cos )f θθθθ=+-的最大值和最小值; 36、已知A B 、是△ABC 的两个内角,向量2cos, sin 22A B A Ba +-=（）,若6||2a =. Ⅰ试问B A tan tan ⋅是否为定值若为定值,请求出；否则请说明理由； Ⅱ求C tan 的最大值,并判断此时三角形的形状. 38、在△ABC 中,已知35=BC ,外接圆半径为5. Ⅰ求∠A 的大小； Ⅱ若ABC AC AB ∆=⋅，求211的周长. 40、如图A 、B 是单位圆O 上的点,C 是圆与x 轴正半轴的交点,A 点的坐标为)54,53(,三角形AOB 为正三角形． Ⅰ求COA ∠sin ；Ⅱ求2||BC 的值．45、已知函数fx=4sin 24π42x ππ≤≤1求)(x f 的最大值及最小值；2若不等式|fx －m|<2恒成立, 求实数m 的取值范围49、已知函数fx ＝·,其中＝sin ωx ＋cos ωx,错误!cos ωx,＝cos ωx －sin ωx,2sin ωx ω＞0,若fx 相邻的对称轴之间的距离不小于错误!. 1求ω的取值范围；2在△ABC 中,a,b,c 分别为A,B,C 的对边,a ＝错误!,b+c ＝3,当ω最大时,fA ＝1,求△ABC 的面积.56、已知角C B A ,,为ABC ∆的三个内角,其对边分别为c b a ,,,若)2sin ,2cos (A A -=m ,)2sin ,2(cos A A =n ,32=a ,且21=⋅n m ．1若ABC ∆的面积3=S ,求c b +的值． 2求c b +的取值范围．59、在锐角△ABC 中,已知内角A 、B 、C 所对的边分别为a 、b 、c ,且tanA －tanB＝1＋tanA ·tanB ．1若a 2－ab ＝c 2－b 2,求A 、B 、C 的大小；2已知向量m ＝sinA,cosA,n ＝cosB,sinB,求｜3m －2n ｜的取值范围．62、已知函数0)6(,cos sin cos 2)(2=+=πf x x a x x f1求函数)(x f 的最小正周期及单调增区间；2若函数)(x f 的图象按向量)1,6(-=πm 平移后得到函数)(x g 的图象,求)(x g 的解析式.64、设向量)2,(),,0(),0,1(),sin ,cos 1(),sin ,cos 1(ππβπαββαα∈∈=-=+=c b a ,2sin,3,,2121βαπθθθθ-=-求且的夹角为与的夹角为与c b c a 的值;68已知A 、B 、C 为ABC ∆的三个内角,向量65(,cos )22A B A B +-=a ,且3|| 5.5=a 1求tan tan A B 的值；2求C 的最大值,并判断此时ABC ∆的形状.74、在△ABC 中,,0),1,(),cos ,sin 3(),2cos ,(cos πλ≤≤--x C x x B x x A 若△ABC 的重心在y 轴负半轴上,求实数λ的取值范围．76、在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若).(R k k BC BA AC AB ∈=⋅=⋅ Ⅰ判断△ABC 的形状； Ⅱ若k c 求,2=的值.77、在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且cos cos B C ba c=-+2. I 求角B 的大小；II 若b a c =+=134，,求△ABC 的面积.78、已知ABC ∆中,a 、b 、c 是三个内角A 、B 、C 的对边,关于x 的不等式2cos 4sin 60x C x C ++<的解集是空集． 1求角C 的最大值；2若72c =,ABC ∆的面积S =求当角C 取最大值时a b +的值． 84、在△ABC 中,角A ,B ,C 所对边分别为a ,b ,c ,且tan 21tan A c Bb+=． Ⅰ求角A ； Ⅱ若m (0,1)=-,n ()2cos ,2cos 2C B =,试求|m +n |的最小值． 90、已知锐角△ABC 三个内角为A 、B 、C,向量22sin ,cos sin pA A A 与向量sin cos ,1sin qA A A 是共线向量.Ⅰ求角A. Ⅱ求函数232sin cos 2C By B 的最大值.96、已知]),0[,0)(cos()(πωωπ∈Φ>Φ+=x x f 是R 上的奇函数,其图像关于直线43=x 对称,且在区间]41,41[-上是单调函数,求ω和Φ的值; 98、已知向量(1tan ,1),(1sin 2cos 2,3)x x x =-=++-b a ,记().f x =⋅b a1求fx 的值域及最小正周期；2若224f f ααπ⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭其中0,2πα⎛⎫∈ ⎪⎝⎭,求角.α。

三角函数相关知识点总结

三角函数相关知识点总结一、三角函数的定义。

1. 锐角三角函数。

- 在直角三角形中，设一个锐角为α。

- 正弦sinα=(对边)/(斜边)。

例如，在直角三角形ABC中，∠ C = 90^∘，∠A=α，BC为∠ A的对边，AB为斜边，则sinα=(BC)/(AB)。

- 余弦cosα=(邻边)/(斜边)，对于上述三角形，AC为∠ A的邻边，cosα=(AC)/(AB)。

- 正切tanα=(对边)/(邻边)=(BC)/(AC)。

2. 任意角三角函数（单位圆定义）- 设角α终边上一点P(x,y)，r=√(x^2)+y^{2}。

- sinα=(y)/(r)。

- cosα=(x)/(r)。

- tanα=(y)/(x)(x≠0)。

二、三角函数的基本性质。

1. 定义域。

- y = sin x和y=cos x的定义域都是R（全体实数）。

- y=tan x的定义域是<=ft{xx≠ kπ+(π)/(2),k∈ Z}。

2. 值域。

- y = sin x和y=cos x的值域都是[ - 1,1]。

- y=tan x的值域是R。

3. 周期性。

- y = sin x和y=cos x的最小正周期都是2π。

即sin(x + 2kπ)=sin x，cos(x +2kπ)=cos x，k∈ Z。

- y=tan x的最小正周期是π，tan(x + kπ)=tan x，k∈ Z。

4. 奇偶性。

- y=sin x是奇函数，因为sin(-x)=-sin x。

- y = cos x是偶函数，因为cos(-x)=cos x。

- y=tan x是奇函数，因为tan(-x)=-tan x。

5. 单调性。

- y=sin x在<=ft[-(π)/(2)+2kπ,(π)/(2)+2kπ](k∈ Z)上单调递增，在<=ft[(π)/(2)+2kπ,(3π)/(2)+2kπ](k∈ Z)上单调递减。

- y=cos x在[2kπ-π,2kπ](k∈ Z)上单调递增，在[2kπ,2kπ + π](k∈ Z)上单调递减。

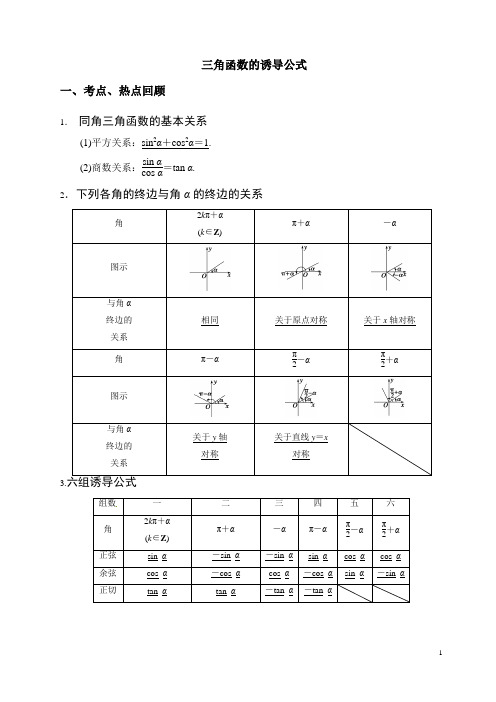
三角函数诱导公式-高三文科数学

三角函数的诱导公式一、考点、热点回顾1．同角三角函数的基本关系(1)平方关系：sin2α＋cos2α＝1.(2)商数关系：sin αcos α＝tan α.2．下列各角的终边与角α的终边的关系角2kπ＋α(k∈Z)π＋α－α图示与角α终边的关系相同关于原点对称关于x轴对称角π－απ2－απ2＋α图示与角α终边的关系关于y轴对称关于直线y＝x对称3.组数一二三四五六角2kπ＋α(k∈Z)π＋α－απ－απ2－απ2＋α正弦sin_α－sin_α－sin_αsin_αcos_αcos_α余弦cos_α－cos_αcos_α－cos_αsin_α－sin_α正切tan_αtan_α－tan_α－tan_α口诀函数名不变符号看象限函数名改变符号看象限三角函数诱导公式（k2π+α）的本质是：奇变偶不变（对k 而言，指k 取奇数或偶数），符号看象限（看原函数，同时把α看成是锐角）.牢记几个诱导公式：sin()sin ,παα-=cos()s ,co αα-=tan()tan ,παα+=sin()cos ,2παα-=sin()cos ,2παα+=二、典型例题+拓展训练典型例题1：若点P 在角2π3的终边上，且|OP |_____．＝2，则点P 的坐标是___________扩展1：已知角θ的顶点为坐标原点，始边为x 轴的正半轴，若P (4，y )是角θ终边上点，且sin θ＝－255，则y ＝________.2.下列与9π4的终边相同的角的表达式中正确的是( )A ．2k π＋45° (k ∈Z )B ．k ·360°＋94π (k ∈Z )C ．k ·360°－315°(k ∈Z )D ．k π＋5π4(k ∈Z ) 3.已知角α的终边经过点P (x ，－2) (x ≠0)，且cos α＝36x ，求sin α＋1tan α的值．4. (1)若θ是第二象限角，试判断sin cos θcos sin 2θ的符号；5. (1)y ＝sin x －32的定义域为________．典型例题2：已知α∈⎝ ⎛⎭⎪⎫π，3π2，tan α＝2，则cos α＝_______1. 若tan α＝2，则2sin α－cos αsin α＋2cos α的值为________．2. 已知α是第二象限的角，tan α＝－12，则cos α＝________.3. sin 43π·cos 56π·tan ⎝ ⎛⎭⎪⎫－43π的值是________．4. 已知cos ⎝ ⎛⎭⎪⎫π6－α＝23，则sin ⎝ ⎛⎭⎪⎫α－2π3＝________.5.已知在△ABC 中，sin A ＋cos A ＝15.(1)求sin A cos A 的值；(2)判断△ABC 是锐角三角形还是钝角三角形； (3)求tan A 的值．6.(1)已知tan α＝2，求sin 2α＋sin αcos α－2cos 2α； (2)已知sin α＝2sin β，tan α＝3tan β，求cos α.三、课堂训练1.(1)已知cos ⎝ ⎛⎭⎪⎫π6＋α＝33，求cos ⎝⎛⎭⎪⎫5π6－α的值； (2)已知π<α<2π，cos(α－7π)＝－35，求sin(3π＋α)·tan ⎝ ⎛⎭⎪⎫α－72π的值．2.(1)化简：tanπ＋αcos2π＋αsin ⎝⎛⎭⎪⎫α－3π2cos－α－3πsin－3π－α；(2)已知f (x )＝sin π－x cos2π－x tan －x ＋πcos ⎝ ⎛⎭⎪⎫－π2＋x ，求f ⎝⎛⎭⎪⎫－31π3的值．3. (1)已知tan α＝13，求12sin αcos α＋cos 2α的值；(2)化简：tanπ－αcos 2π－αsin ⎝⎛⎭⎪⎫－α＋3π2cos －α－πsin －π－α.4. 已知sin ⎝⎛⎭⎪⎫α＋π2＝－55，α∈(0，π)，求cos 2⎝ ⎛⎭⎪⎫π4＋α2－cos 2⎝ ⎛⎭⎪⎫π4－α2sin π－α＋cos 3π＋α的值．四、总结五、课后练习1. 化简015tan 115tan 1-+等于（）A. 3B. 23C. 3D. 12. 已知函数f(x)=sin(x+2π)，g(x)=cos(x －2π)，则下列结论中正确的是（） A ．函数y=f(x)·g(x)的最小正周期为2π B ．函数y=f(x)·g(x)的最大值为1C ．将函数y=f(x)的图象向左平移2π单位后得g(x)的图象D ．将函数y=f(x)的图象向右平移2π单位后得g(x)的图象3. 下列函数中，最小正周期为π，且图象关于直线3π=x 对称的是（）A ．)32sin(π-=x y B ．)62sin(π-=x y C ．)62sin(π+=x y D ．)62sin(π+=x y4. 函数x x y sin cos 2-=的值域是（）A 、[]1,1-B 、⎥⎦⎤⎢⎣⎡45,1C 、[]2,0D 、⎥⎦⎤⎢⎣⎡-45,15. 设0002012tan13cos66,,21tan 13a b c ===+则有（） A ．a b c >> B.a b c << C. b c a << D. a c b <<6. 已知sin 53=α,α是第二象限的角，且tan(βα+)=1,则tan β的值为（） A ．－7 B ．7 C ．－43 D ．437. 定义在R 上的函数)(x f 既是偶函数又是周期函数，若)(x f 的最小正周期是π，且当]2,0[π∈x 时，x x f sin )(=，则)35(πf 的值为（）A. 21- B23 C 23-D 218. 函数1cos sin xy x -=的周期是（） A ．2πB ．πC ．2πD ．4π9. 2002年8月，在北京召开的国际数学家大会会标如图所示，它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形，若直角三角形中较小的锐角为θ，大正方形的面积是1，小正方形的面积是θθ22cos sin ,251-则的值等于（）A ．1B ．2524- C ．257 D ．725-五、课后反馈表1、学生对老师形象气质的满意度（）A.非常满意B.比较满意C.一般D.比较不满意E.非常不满意2、学生对课程内容的满意度（）A.非常满意B.比较满意C.一般D.比较不满意E.非常不满意3、学生对授课教师的满意度（）A.非常满意B.比较满意C.一般D.比较不满意E.非常不满意4、学生对授课教师的精神状态满意度（）A.非常满意B.比较满意C.一般D.比较不满意E.非常不满意5、学生对课程进度的满意度（）A.非常满意B.比较满意C.一般D.比较不满意E.非常不满意学生签字：日期：。

(word完整版)高考文科三角函数知识点总结,推荐文档

三角函数知识点二．知识点1．角度制与弧度制的互化：,23600π= ,1800π=1rad ＝π180°≈57.30°=57°18ˊ． 1°＝180π≈0.01745（rad ）2.弧长及扇形面积公式弧长公式：r l .α= 扇形面积公式:S=r l .21α----是圆心角且为弧度制。

r-----是扇形半径3.任意角的三角函数设α是一个任意角，它的终边上一点p （x,y ）, r=22y x + (1)正弦sin α=r y 余弦cos α=r x 正切tan α=xy(2)各象限的符号：sin α cos α tan α4、三角函数线正弦线：MP; 余弦线：OM; 正切线： AT.5.同角三角函数的基本关系：（1）平方关系：s in 2α+ cos 2α=1。

xy+O— —+x yO — ++— +y O— ++ —(3) 若 o<x<2,则sinx<x<tanx16. 几个重要结论:（2）商数关系：ααcos sin =tan α（z k k ∈+≠,2ππα） 6.诱导公式：奇变偶不变，符号看象限()()1sin 2sin k παα+=，()cos 2cos k παα+=，()()tan 2tan k k παα+=∈Z ． ()()2sin sin παα+=-，()cos cos παα+=-，()tan tan παα+=． ()()3sin sin αα-=-，()cos cos αα-=，()tan tan αα-=-． ()()4sin sin παα-=，()cos cos παα-=-，()tan tan παα-=-．()5sin cos 2παα⎛⎫-=⎪⎝⎭，cos sin 2παα⎛⎫-= ⎪⎝⎭． ()6sin cos 2παα⎛⎫+=⎪⎝⎭，cos sin 2παα⎛⎫+=- ⎪⎝⎭． 7正弦函数、余弦函数和正切函数的图象与性质8.三角函数的伸缩变化先平移后伸缩sin y x =的图象ϕϕϕ<−−−−−−−→向左(>0)或向右(0)平移个单位长度得sin()y x ϕ=+的图象()ωωω−−−−−−−−−→横坐标伸长(0<<1)或缩短(>1)1到原来的纵坐标不变得sin()y x ωϕ=+的图象()A A A >−−−−−−−−−→纵坐标伸长(1)或缩短(0<<1)为原来的倍横坐标不变得sin()y A x ωϕ=+的图象(0)(0)k k k ><−−−−−−−→向上或向下平移个单位长度得sin()y A x k ϕ=++的图象．先伸缩后平移sin y x =的图象(1)(01)A A A ><<−−−−−−−−−→纵坐标伸长或缩短为原来的倍(横坐标不变)得sin y A x =的图象(01)(1)1()ωωω<<>−−−−−−−−−→横坐标伸长或缩短到原来的纵坐标不变得sin()y A x ω=的图象(0)(0)ϕϕϕω><−−−−−−−→向左或向右平移个单位得sin ()y A x x ωϕ=+的图象(0)(0)k k k ><−−−−−−−→向上或向下平移个单位长度得sin()y A x k ωϕ=++的图象．10．正弦定理：2sin sin sin a b cR A B C===. 11.余弦定理：2222cos a b c bc A =+-; 2222cos b c a ca B =+-;2222cos c a b ab C =+-.三角形面积定理.111sin sin sin 222S ab C bc A ca B ===.。