2020年中国矿业大学高等代数考试大纲
中国矿业大学(北京)806流体力学2020年考研专业课初试大纲

工程热 力学
《工程热力学》,朱明善等 编著,清华大学出版社,第1 版,1995年; 《工程热力学》,沈维道等 编著,高等教育出版社,第4 版,2007年
二、 考试范围
1.基本概念 热力系统,状态及平衡状态,状态参数及其特性,参数坐标图,热力过程及 准静态过程,热力循环。 2.热力学第一定律 闭口系热力学第一定律解析式,热力学第一定律应用于开口系统,稳定流动 能量方程式,焓,技术功,能量方程应用。 3.气体的性质与过程 理想气体状态方程及气体常数,理想气体的比热,理想气体的内能、焓和熵 的计算,四个典型热力过程,多变过程及多变指数。气体的理想压缩功,压 缩机的效率,活塞式压缩机余隙容积的影响,多级压缩和中间冷却。 4.热力学第二定律 过程的方向性,卡诺循环和卡诺定理,熵的导出,克劳修斯不等式,孤立系 统熵增原理,熵方程,火用及其计算。 5.气体动力循环 活塞式内燃机循环,燃气轮机装置循环,提高循环热效率的各种途径。 6.水蒸气 蒸汽的性质,蒸汽图表及其应用,水蒸气的热力过程。 7.蒸汽动力循环
三、 试题结构(包括考试时间,试题类型等)
1. 考试时间:180分钟,满分:150分 2. 题型结构 (1) 概念型题 重点考察学生对基本概念的理解程度。这个类型题的基本形式有以下几 种:填空、选择、判断等。 (2) 简答、分析型题 通过此类考题考察学生对于知识点的理解程度,及运用专业工程语言, 简单准确的叙述能力。
考试为笔试、闭卷形式。重点考察学生对基本概念、基本公式、基本计 得使用带有公
算方法的掌握和应用能力。学生应能对流体力学学科知识有系统的理解 式和文本存储
,深刻领会流体在静止、相对平衡、运动状态及不同假设条件下的数学 功能的计算器
描述方式,能从整体上把握学科各知识点间的联系,避免单纯的死记硬 。
《高等代数》考试大纲

五邑大学2021年硕士学位研究生招生《高等代数》课程考试大纲一、课程的性质,目的和任务高等代数是数学(数学与应用数学,数学教育)专业的一门重要基础课程。
通过本课程的教学,应培养学生良好的数学素养,打下较扎实的代数学理论基础,提高学生的抽象思维的能力和逻辑推理能力,并掌握较系统的代数基础知识,为学习后继课程服务。
二、基本要求这门课程大致分为两部分:多项式理论和线性代数。
前者以数域上一元多项式的因式分解理论为中心内容;后者主要讲授线性方程组的理论,向量空间和线性变换。
本课程应着重于基本理论的讲授和基本技能的培养和训练,不适求内容上的完备和全面.三、考试范围(一)多项式理论1. 数域 (A)2. 整除的概念 (A)3. 最大公因式. (A)4. 因式分解定理. (A)5. 重因式. (A)6. 多项式函数. (A)8. 复系数与实系数多项式的因式分解. (A)9. 有理系数多项式. (A)*10.多元多项式. (B)*11.对称多程式. (B)(二) 行列式1. 排列. (A)2. n阶行列式的定义和性质. (A)3. 行列式的依行和依列展开. (A)4. 行列式的计算. (A)5. Crammer法则(克莱姆法则). (A)6. Laplace(拉普拉斯)定理. 行列式的乘法规则. (A)(三)线性方程组1. 线性方程组的消元法. (A)2. n维向量空间 (A)3. 线性相关性. (A)4. 矩阵的秩. (A)5. 线性方组有解的判定定理. (A)6. 线性方程组解的结构. (A)7. 二元高次方程. (B)(四) 矩阵1. 矩阵的概念与运算. (A)2. 矩阵乘积的行列式与秩. (A)3. 矩阵的逆. (A)4. 矩阵的分块. (A)5. 初等矩阵. (A)(五) 二次型1. 二次型的矩阵表示. (A)2. 标准形. (A)3. 唯一性. (A)4. 正定二次型. (A)(六) 线性空间1. 线性空间的定义与简单性质. (A)2. 维数.基与坐标. (A)3. 基变换. (A)4. 线性子空间 (A)5. 子空间的交与和. (A)6. 子空间的直和. (A)7. 线性空间的同构. (A)(七) 线性变换1. 定义和例子 (B)2. 线性变换的运算. (A)3. 线性变换的矩阵. (A)4. 特征值与特征向量. (A)5. 对角矩阵. (A)6. 线性变换的值域与核. (A)7. 不变子空间. (A)8. Jordan标准形介绍. (B)(八) 入一矩阵1. 入一矩阵. (A)2. 入一矩阵在初等变换下的标准形. (A)3. 不变因子. (A)4. 矩阵相似条件. (A)5. 初等因子. (A)*6.Jordan标准形的理论推导. (C)(九) 欧几里得空间1. 定义与基本性质. (A)2. 标准正交基. (A)3. 同构. (A)4. 正交变换. (A)5. 子空间. (A)6. 对称矩阵的准形. (A)四、主要教材和参考书1. 北京大学数学力学系,高等代数(第二版),高教出版社。
高代知识点

《高等代数》复习参考提纲一、总体要求高等代数是数学各专业的一门重要基础理论课。
要求学生掌握高等代数的基本概念,基本理论,基本方法和基本技巧;熟练掌握矩阵和线性变换的关系,学会线性方程组,矩阵,线性变换问题的相互转化;理解具体与抽象、特殊与一般、有限与无限等辨证关系。
并善于应用这些理论和方法,具有较强的分析问题与解决问题的能力。
二、课程考试内容(一)多项式数域,整除的概念与性质,最大公因式,因式分解,重因式,多项式函数,有理系数多项式,多元多项式,对称多项式。
(二)行列式排列,n阶行列式的概念,n阶行列式的性质,行列式的计算,行列式按一行(列)展开,拉普拉斯(Lap lace)定理,克兰姆法则。
(三)线性方程组消元法,矩阵,矩阵的秩,线性方程组的初等变换等概念及性质,线性方程组有解判别定理。
n维向量的概念及运算;向量组的线性组合、线性表示、线性相关、线性无关等概念;向量组的线性相关性的判定;两个向量组的等价;向量组的极大无关组、秩的概念及性质;向量组的秩与矩阵的秩的关系。
线性方程组解的结构。
(四) 矩阵矩阵的概念,矩阵的运算,矩阵乘积的行列式与秩,矩阵的逆,矩阵的分块,初等矩阵,分块矩阵的初等变换及应用。
(五)二次型二次型的矩阵表示,标准形,唯一性,惯性定律,正定二次型。
(六)线性空间线性空间的概念与性质,维数,基,坐标,基变换,坐标变换,子空间,子空间的和与交,子空间的直和,线性空间的同构。
(七)线性变换线性变换的概念与性质,线性变换的运算,线性变换的矩阵,特征值与特征向量,矩阵相似对角矩阵的各种条件,线性变换的值域和核,不变子空间,Jordan标准形,最小多项式。
(八)λ-矩阵λ-矩阵的标准形,行列式因子,不变因子,初等因子,矩阵相似的条件,矩阵的有理标准形。
(九)欧几里得空间欧几里得空间的概念与性质,标准正交基,欧几里得空间的子空间与同构,正交变换与对称变换,Schimidt正交化方法,实对称矩阵的标准形,最小二乘法,酉空间。
中国矿业大学2020年硕士研究生招生自命题初试科目参考书目
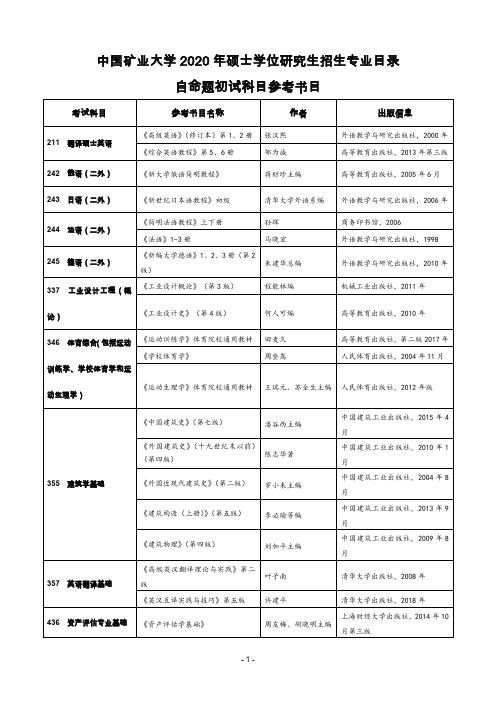
624 马克思主义基本原 《马克思主义基本原理概论》
马克思主义理论研究 高等教育出版社,2018 年版
-2-
考试科目
理
625 公共管理学 628 地史学 643 数学分析 644 普通物理
647 基础英语
参考书目名称
作者
出版信息
和建设工程重点教材
《马克思主义哲学》
马克思主义理论研究 高等教育出版社、人民出版社, 和建设工程重点教材 2009 年版
Enclusre Fire Dynamics.
Karlsson, B. and CRC Press, 2000
Quintiere, J.G.
830 运筹学
《管理运筹学》
魏晓平、宋学锋、王 中国矿业大学出版社,2011 年第
新宇、王桂强编
三版
832 管理学 833 微观经济学
《管理学原理》
机械工业出版社,2012 年 3 月第 陈传明、周小虎编著
孙桓、陈作模主编 高等教育出版社, 2013 年
《机械原理》(第 2 版)
王知行、邓宗全主编 高等教育出版社,2006 年
《机械原理教程》
申永胜主编
清华大学出版社,2005 年
《土地经济学》
汪应宏等
中国矿业大学出版社,2008
《土地经济学》(第七版)
毕宝德
中国人民大学出版社,2016
《土质学与土力学》(第四版)
《材料科学基础》(第 3 版)
刘智恩
西北工大出版社
《材料科学基础》
胡赓祥
上海交大出版社
《材料科学基础》
潘金生
清华大学出版社
《基础工业工程》第 2 版
易树平、郭伏
机械工业出版社,2015.6.1
2020云南专升本《高等代数》考试大纲

一、考试内容概述《高等代数》是数学与应用数学的重要的基础内容,其主要内容是一元多项式理论、行列式、线性方程组、矩阵、向量空间(亦称线性空间)、线性变换、欧氏空间、二次型等方面的基本概念、基本知识和一些数学的基本思想方法。
要求考生理解和掌握映射、数域、带余除法、最大公因式的性质、不可约多项式的定义及性质、重因式、多项式的有理根等相关知识;会应用行列式的性质计算行列式,掌握行列式的一些基本计算方法;理解线性方程组解的相关理论并掌握求解方法及解的表示;掌握矩阵理论并能灵活应用;理解向量空间和欧氏空间的一些基本概念并掌握相关知识的计算方法且能灵活应用;理解和掌握线性变换与矩阵的联系、矩阵相似、线性变换在不同基下的矩阵、矩阵的特征值、特征向量及子空间、正交矩阵等相关知识;掌握正定二次型的等价条件及二次型的标准形并会判定。
要求考生具备逻辑推理、抽象思维与综合分析问题的能力。
能运用高等代数中的基本知识、基本理论进行推理和论证。
考生还应熟练掌握高等代数中常用的计算方法,掌握基本运算中的技能、技巧,提高综合计算和解决问题的能力。
二、考试形式满分:150分(单科成绩)。
考试时间:120分钟。
三、试题难易程度分布较易试题约占50%中等试题约占30%较难试题约占20%四、内容比例基本概念约占3%一元多项式约占12%行列式约占16%线性方程组约占10%矩阵约占16%向量空间与欧式空间约占23%线性变换约占13%二次型约占7%五、参考教材北京大学数学系几何与代数教研室代数小组编,王萼芳、石生明修订:《高等代数》,高等教育出版社2003年7月第三版。
2.张和瑞、郝炳新编:《高等代数》,高等教育出版社2007年6月第五版。
六、考试内容及要求(一)基本概念考试内容:1.映射。
映射的定义,满射、单射与双射,映射的相等,映射的合成,逆映射。
2.数域。
数域的定义,最小的数域。
考试要求:1.熟记映射、满射、单射、双射的定义,理解它们之间的联系与区别。
考研《高等代数》(学术学位)考试大纲

(3)初等矩阵与初等变换
掌握矩阵的初等变换和初等矩阵的概念,明确二者关系。能熟练进行矩阵的初等变换,能利用初等变换求解线性方程组,并能进行有关证明。
(4) 相似矩阵与矩阵合同
三、主要参考书目
1、《高等代数》(第三版),北京大学数学系几何与代数教研室前代数小组著,高等教育出版社 2003 或之后版本
2、《高等代数(上下册)》(第二版),丘维声著,高等教育出版社,1999 或之后版本
硕士研究生入学考试自命题科目考试大纲
科目代码、名称:
专业类别:
■学术学位□专业学位
适用专业:
数学
一、基本内容
1、多项式
本部分要求掌握一元多项式及其整除问题、多项式函数、最大公因式、重因式和因式分解定理等有关概念和基本结论,能够进行多项式的有关计算和有关问题的证明。
2、行列式
(1)定义与性质
要求熟悉排列、逆序、对换等概念;理解行列式的定义;掌握行列式的性质。
9、欧几里得空间
掌握欧几里得空间的定义与性质,掌握内积、正交性、标准正交基的概念及有关计算方法,能证明有关性质和结论。
二、考试要求(包括考试时间、总分、考试方式、题型、分数比例等)
考试时间:180分钟
总分:150分
考试方式:笔试,闭卷
题型:填空题,计算与证明题
分数比例:填空题(60分)占40%,计算与证明题(90分)占60%。
(3)线性方程组解的结构
掌握线性方程组解的判定定理,会求有解的线性方程组的通解,熟练掌握线性方程组常用的解
法,并能证明有关结论。
4、矩阵
高等代数《高等代数》教学大纲

《高等代数》课程教学大纲Advanced Algebra执笔人:颜昌元编写日期:2012.7一、课程基本信息1.课程编号: 07010112,070101132.课程性质/类别:专业基础课/ 必修课3.学时/学分:160 学时/ 10 学分4.适用专业:数学与应用数学、信息与计算科学、统计学二、课程教学目标及学生应达到的能力《高等代数》是大学数学专业三门重要基础课程之一。
因其内容的抽象性和理论的结构化及应用之广泛,既是数学在其它学科应用的必需基础课程,又是数学修养的核心课程。
该课程的教学目标是使学生掌握代数基本知识和理论,逐步培养学生的抽象思维能力和逻辑推理能力,使学生获得较熟练的演算技能与初步的应用能力,为后续专业课程的学习打下基础,适当了解代数的一些历史与背景。
该课程应突出传授数学思想和数学方法,突出高等代数中等价分类、结构分解、同构对应的思想,揭示课程内部本质的有机联系。
在教学过程中根据具体教学内容,帮助学生体会人类认识客观世界的一般规律:从具体个例提升到抽象本质再应用到一般情形,及本课程中体现的唯物主义辩证法;帮助学生体会本课程统一性、简单性、对称性、整齐性、不变性、奇异性等数学的内在美。
三、课程教学内容与基本要求本课程开课时间:第一学年(共两学期),共160 学时;其中,第一学期,每周5学时,共80学时;第二学期,每周5学时,共 80学时。
(一)多项式 (20 学时)1.主要内容:(1)数域(2)一元多项式(3)整除的概念(4)最大公因式(5)因式分解定理(6)重因式(7)多项式函数(8)复系数与实系数多项式的因式分解(9)有理系数多项式2.基本要求:(1)熟练掌握和应用带余除法定理。
(2)熟练掌握最大公因式和互素的判别方法和性质。
(3)熟练掌握和应用因式分解定理。
(4)掌握不可约多项式的基本性质。
(5)掌握重因式和重根的联系。
(6)掌握复系数和实系数多项式的标准分解式;(7)掌握有理系数多项式的Gauss 引理,Eisenstein 判别法。
《高等代数》考试大纲

《高等代数》考试大纲(适用专业:数学与应用数学、应用统计学)第一章基本概念一.主要内容1、集合子集集的相等集合的交与并及其运算律笛卡儿积2、映射映射满射单射双射映射的相等映射的合成可逆映射映射可逆的充要条件3、数学归纳法自然数的最小数原理第一数学归纳法第二数学归纳法4、整数的一些整除性质5、数环和数域二. 考试要求(一)掌握1、集合的交与并及其运算律2、映射满射单射双射映射的相等映射的合成3、数环和数域的定义及性质4、数学归纳法的运用(二)理解1、集合的交与并及其运算律2、可逆映射映射可逆的充要条件3、数环和数域的判别(三)了解自然数的最小数原理第一数学归纳法、第二数学归纳法的证明整数的一些整除性质第二章多项式一. 主要内容1、一元多项式的定义和运算2、多项式的整除性整除的基本性质带余除法定理3、多项式的最大公因式最大公因式概念、性质辗转相除法多项式互素概念、性质4、多项式的唯一因式分解定理不可约多项式概念唯一因式分解定理典型分解式5、多项式的重因式多项式的重因式概念多项式有重因式的充要条件6、多项式函数与多项式的根多项式函数的概念余式定理综合除法多项式的根的概念根与一次因式的关系多项式根的个数7、复数域和实数域上多项式的因式分解(代数基本定理不证明)8、有理数域上多项式的可约性及有理根本原多项式的定义Gauss引理整系数多项式在有理数域上的可约性问题Eisenstein判别法有理数域上多顶式的有理根9、多元多项式多元多项式的概念字典排列法多元多项式的和与积的次数10、对称多项式对称多项式的概念初等对称多项式对称多项式基本定理二. 考试要求(一)掌握1、一元多项式的定义和运算2、整除的基本性质带余除法定理3、最大公因式概念、性质辗转相除法多项式互素概念、性质4、唯一因式分解定理典型分解式5、多项式的重因式概念多项式有重因式的充要条件6、余式定理综合除法多项式的根的概念7、复数域和实数域上多项式的因式分解有理数域上多顶式的有理根(二)理解1、不可约多项式概念2、多项式的重因式概念3、多项式函数与多项式的根4、多项式函数的概念5、本原多项式的定义 Gauss引理6、整系数多项式在有理数域上的可约性问题Eisenstein判别法(三)了解1、对称多项式的概念2、多元多项式的概念3、多元多项式的概念字典排列法初等对称多项式对称多项式基本定理三. 说明本章主要介绍数域上一元多项式的概念及其运算、整除性、因式分解和有理系数多项式有理根的求法,简单介绍了多元多项式及对称多项式。
高等代数课程教学大纲

《高等代数》课程教学大纲适用专业数学与应用数学(师范)、数学与应用数学总学时 168学分 10一、编写说明(一)本课程的性质、地位和作用高等代数是数学与应用数学专业(师范)、数学与应用数学专业的一门重要的专业基础课,其主要内容有多项式理论与线性代数两部分。
本课程的教学目的是使学生初步掌握基本的、系统的代数知识和抽象的严格的代数方法,为后继课程如近世代数、常微分方程、概率论与数理统计、泛函分析、计算方法等提供必须具备的代数知识,也为进一步学习数学与应用数学专业的各门课程所需要的抽象思维能力提供一定的训练。
高等代数课程是中学代数的继续和提高。
通过本课程的教学,要使学生加深对中学代数的理解。
本课程在教学中要求学生确切理解高等代数中的基本概念,不仅要正确掌握这些概念的内涵,还要了解这些概念的实际背景。
对于一些基本的重要概念,还要求了解它们产生与发展的过程及概念推广的原则;与中学代数有直接联系或者平行的概念,要求学生能与中学数学中相应概念加以比较,以确立较高的观点。
对于高等代数中的基本理论,要求学生掌握基本理论的结果,对于典型定理还要求掌握论证方法或思想,同时要求学生能了解严谨的理论体系,体会建立这种体系的抽象的代数方法。
通过本课程的教学,要求学生能显著地提高应用基本概念、基本理论作抽象论证的能力;较好地掌握基本的论证方法与基本的计算方法,特别要掌握基本的线性代数计算法。
(二)本大纲制订的依据根据本专业人才的培养目标所需要的基本理论和基本技能的要求,根据本课程的教学性质、条件和教学实践而制定。
(三)大纲内容选编原则与要求1.本大纲所列各单元讲授顺序与北京大学数学系几何与代数教研室代数小组编《高等代数》(高等教育出版社第二版)所列基本相同,讲授时可根据具体情况作适当调整。
2.为了避免教学上的难点过于集中,有些定理的掌握可以侧重于定理的结果和证明定理的方法,以达到掌握基本的代数方法的目的。
3.每一章的重点内容要重点讲解,在讲清概念的基础上,通过适当的练习(习题课、作业、问题探讨)以达到掌握高等代数中常用的计算方法、基本运算中的技能和技巧以及提高综合计算和解决问题的能力的目的。
中国矿业大学(北京)828高等代数2020年考研专业课初试大纲
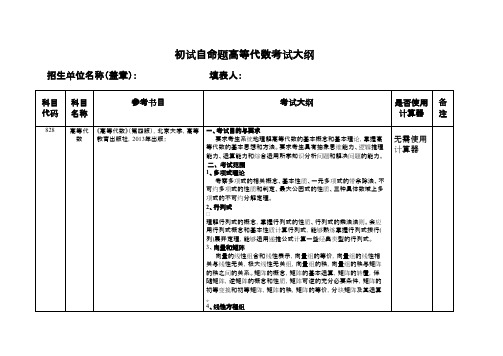
线性变换的概念和简单性质,线性变换的运算,线性变换的矩 阵,线性变换(矩阵)的特征值、特征向量和特征子空间,线性变换 的特征多项式及HamiltonCaylay定理,矩阵相似的概念及性质,矩阵可对角化的充分必要条 件,线性变换的值域与核,线性变换的不变子空间,矩阵的若当标 准型。 8、欧几里德空间 线性空间内积的定义及其性质,欧几里德空间的概念,标准正交基 ,施密特正交化过程,正交矩阵,正交变换及其性质,正交子空间、 正交补及其性质,实对称矩阵的特征值、特征向量,对角化,欧几 里德空间的同构。 主要参考书目: 《高等代数》,北京大学数学系几何与代数教研室代数小组编,2013 年8月第4版,高等教育出版社出版 三、试题结构
能力、运算能力和综合运用所学知识分析问题和解决问题的能力。
二、考试范围
1、多项式理论
考察多项式的相关概念、基本性质、一元多项式的带余除法、不
可约多项式的性质和判定、最大公因式的性质、三种具体数域上多
项式的不可约分解定理。
2、行列式
理解行列式的概念,掌握行列式的性质、行列式的乘法法则。会应
用行列式概念和基本性质计算行列式,能够熟练掌握行列式按行(
列)展开定理,能够运用递推公式计算一些经典类型的行列式。
3、向量和矩阵
向量的线性组合和线性表示,向量组的等价,向量组的线性相
关与线性无关,极大线性无关组,向量组的秩,向量组的秩与矩阵
的秩之间的关系。矩阵的概念,矩阵的基本运算,矩阵的转置,伴
随矩阵,逆矩阵的概念和性质,矩阵可逆的充分必要条件,矩阵的
初等变换和初等矩阵,矩阵的秩,矩阵的等价,分块矩阵及其运算
《高等代数》考试大纲

《高等代数》考试大纲一、《高等代数》的课程性质高等代数是数学与应用数学专业、信息与计算机科学专业和统计学专业一门重要基础课,是中学代数的继续和提高,但是又与中学代数有很大不同,表现在内容的深度和广度上,更主要表现在观点和方法上。
具体表现在内容的高度抽象性、推理的严密性和解题技巧的独特性。
本课程最活跃研究内容:数域上一元多项式理论、行列式、线性方程组、二次型、线性空间、线性变换矩阵、欧氏空间和双线性函数。
方法的特点:在阐述上更强调一般性原则,广泛使用公理化方法,用结构化方法揭示代数系统的内部构造,用矩阵表示作为主线,受整体、统一思想的支配,逐步抽象出高等代数的各个基本概念,揭示代数研究问题的基本方法。
二、《高等代数》课程的教学目的和要求高等代数的教学目的要求是:通过本课程的学习,不仅要求学生掌握一元多项式和线性代数的基础知识、基本理论和基本技能,而且要求学生初步熟悉和掌握抽象的、严格的代数方法,理解具体与抽象、特殊与一般、有限与无限的辩证关系。
培养学生整体思考问题的能力,使之理解代数思想、公理化方法,把握概念的内涵和外延,提高抽象思维、逻辑推理、分析问题和解决问题的能力,为进一步后继课程的学习及继续深造或从事教学工作打下坚实的基础。
三、《高等代数》课程的知识点与考核要求第一章:多项式1、考核知识点:(1)、一元多项式的定义、运算、性质,次数的定义和次数公式;(2)、多项式整除的定义,整除的性质,带余除法;(3)、最大公因子的定义、性质和求法;(4)、多项式互素的概念和性质;(5)、多项式的可约性,因式分解及唯一性定理,标准分解式;(6)、重因式的概念与判别法,求多项式重因式的方法;(7)、多项式函数、多项式根的概念,根的个数定理,多项式相等与根的关系,判别某数是多项式根的综合除法;(8)、复数域和实数域上不可约多项式的特征,因式分解定理;(9)、有理系数多项式是否可约的判别法,根与系数的关系,有理根的求法。
中国矿业大学004:化工学院2020硕士目录考试大纲(化工)

初试自命题科目考试大纲格式(物理化学A)
学院名称(盖章):填表人:
初试自命题科目考试大纲格式(无机与分析化学A)
学院名称(盖章):填表人:
初试自命题科目考试大纲格式(化工原理A)
学院名称(盖章):填表人:
初试自命题科目考试大纲(机械设计基础A)
学院名称(盖章):填表人:
初试自命题科目考试大纲格式(生物化学A)
学院名称(盖章):填表人:
学院名称(盖章):填表人:
学院名称(盖章):填表人:
初试自命题科目考试大纲格式(过程流体力学)
学院名称(盖章):填表人:
初试自命题科目考试大纲格式(工程热力学A)
招生单位名称(盖章):填表人:
初试自命题科目考试大纲格式(生物化学基础)
招生单位名称(盖章):填表人:。
2020年数学二考试大纲

2020年数学二考试大纲考试科目:高等数学、线性代数考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷内容结构高等数学 约78%线性代数 约22%四、试卷题型结构单项选择题 8小题,每小题4分,共32分填空题 6小题,每小题4分,共24分解答题(包括证明题) 9小题,共94分高等数学一、函数、极限、连续考试内容函数的概念及表示法 函数的有界性、单调性、周期性和奇偶性 复合函数、反函数、分段函数和隐函数 基本初等函数的性质及其图形 初等函数 函数关系的建立 数列极限与函数极限的定义及其性质 函数的左极限与右极限 无穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则 两个重要极限:0sin lim 1x x x →=, 1lim 1xx e x →∞⎛⎫+= ⎪⎝⎭函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质 考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.考试内容导数和微分的概念 导数的几何意义和物理意义 函数的可导性与连续性之间的关系 平面曲线的切线和法线 导数和微分的四则运算 基本初等函数的导数 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法 高阶导数 一阶微分形式的不变性 微分中值定理 洛必达(L'Hospital )法则 函数单调性的判别 函数的极值 函数图形的凹凸性、拐点及渐近线 函数图形的描绘 函数的最大值与最小值 弧微分 曲率的概念 曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle )定理、拉格朗日(Lagrange )中值定理和泰勒(Taylor )定理,了解并会用柯西(Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数的最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间(),a b 内,设函数()f x 具有二阶导数.当()0f x ''>时,()f x 的图形是凹的;当()0f x ''<时,()f x 的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆和曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念 不定积分的基本性质 基本积分公式 定积分的概念和基本性质 定积分中值定理 积分上限的函数及其导数 牛顿-莱布尼茨(Newton-Leibniz)公式 不定积分和定积分的换元积分法与分部积分法 有理函数、三角函数的有理式和简单无理函数的积分 反常(广义)积分 定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿-莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值.考试内容多元函数的概念 二元函数的几何意义 二元函数的极限与连续的概念 有界闭区域上二元连续函数的性质 多元函数的偏导数和全微分 多元复合函数、隐函数的求导法 二阶偏导数 多元函数的极值和条件极值、最大值和最小值 二重积分的概念、基本性质和计算考试要求1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).五、常微分方程考试内容常微分方程的基本概念 变量可分离的微分方程 齐次微分方程 一阶线性微分方程 可降阶的高阶微分方程 线性微分方程解的性质及解的结构定理 二阶常系数齐次线性微分方程 高于二阶的某些常系数齐次线性微分方程 简单的二阶常系数非齐次线性微分方程 微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.3.会用降阶法解下列形式的微分方程:()(),(,)n y f x y f x y '''== 和 (,)y f y y '''=.4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.线性代数一、行列式考试内容行列式的概念和基本性质 行列式按行(列)展开定理考试要求1.了解行列式的概念,掌握行列式的性质.2.会应用行列式的性质和行列式按行(列)展开定理计算行列式.二、矩阵考试内容矩阵的概念矩阵的线性运算矩阵的乘法方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算考试要求1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反对称矩阵和正交矩阵以及它们的性质.2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件.理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.4.了解矩阵初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.5.了解分块矩阵及其运算.三、向量考试内容向量的概念向量的线性组合和线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量的内积线性无关向量组的的正交规范化方法考试要求1.理解n维向量、向量的线性组合与线性表示的概念.2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.3.了解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.4.了解向量组等价的概念,了解矩阵的秩与其行(列)向量组的秩的关系.5.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.四、线性方程组考试内容线性方程组的克拉默(Cramer)法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组的基础解系和通解非齐次线性方程组的通解考试要求1.会用克拉默法则.2.理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.3.理解齐次线性方程组的基础解系及通解的概念,掌握齐次线性方程组的基础解系和通解的求法.4.理解非齐次线性方程组的解的结构及通解的概念.5.会用初等行变换求解线性方程组.五、矩阵的特征值和特征向量考试内容矩阵的特征值和特征向量的概念、性质相似矩阵的概念及性质矩阵可相似对角化的充分必要条件及相似对角矩阵实对称矩阵的特征值、特征向量及其相似对角矩阵考试要求1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵的特征值和特征向量.2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,会将矩阵化为相似对角矩阵.3.理解实对称矩阵的特征值和特征向量的性质.六、二次型考试内容二次型及其矩阵表示合同变换与合同矩阵二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性考试要求1.了解二次型的概念,会用矩阵形式表示二次型,了解合同变换与合同矩阵的概念.2.了解二次型的秩的概念,了解二次型的标准形、规范形等概念,了解惯性定理,会用正交变换和配方法化二次型为标准形.3.理解正定二次型、正定矩阵的概念,并掌握其判别法.。
硕士研究生入学考试大纲-853高等代数

目录I 考查目标 (2)II 考试形式和试卷结构 (2)III 考查内容 (2)IV. 题型示例及参考答案 (4)全国硕士研究生入学统一考试高等代数考试大纲I 考查目标要求考生比较系统地理解高等代数的基本概念和基本理论,掌握高等代数的基本思想和方法具有抽象思维能力、逻辑推理能力、运算能力和综合运用所学的知识分析问题和解决问题的能力。
II 考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间180分钟。
二、答题方式答题方式为闭卷、笔试。
三、试卷内容与题型结构计算题(30%)、证明题(70%)III 考查内容一、多项式1.熟练掌握多项式因式分解理论及整除理论。
2.掌握多项式、不可约多项式、最大公因式、重因式的概念;掌握整除、互素、不可约等概念的联系与区别。
3.掌握带余除法、辗转相除法、艾森斯坦因(Eisenstein)判别法。
4.会求两个多项式的最大公因式,会求有理系数多项式的有理根,会判别两个多项式互素。
二、行列式1.熟练掌握行列式的性质及行列式的计算。
2.掌握n阶行列式的定义。
3.掌握克拉默(Cramer)法则。
三、线性方程组1.熟练掌握向量线性相关性的概念、性质、判别法,会求向量组的秩及最大线性无关组。
2.掌握基础解系的概念及计算,熟练掌握线性方程组的解的判别定理,以及齐次和非齐次线性方程组的求解。
3.熟练掌握矩阵的秩的概念及计算。
四、矩阵1.熟练掌握矩阵、可逆矩阵、初等矩阵的概念与性质。
2.理解分块矩阵的概念,掌握分块矩阵的运算及思想方法。
3.熟练掌握矩阵的加法、减法、乘法,数乘、转置等运算。
4.熟练掌握可逆矩阵的判别方法及逆矩阵的计算。
5.能熟练使用矩阵的初等变换方法。
五、二次型1.掌握二次型的标准形、实二次型的规范形的概念。
2.熟练掌握正定二次型的概念、性质、判别方法。
3.掌握化二次型为标准形的思想方法。
4.理解合同矩阵的概念及背景。
六、线性空间1.掌握线性空间、子空间的概念及判定方法。
(完整word版)《高等代数》课程教学大纲

《高等代数》课程教学大纲课程编号:090085、090022总学时:162学分:8适用专业:数学与应用数学、信息与计算科学课程类型:专业必修课开课单位:一、课程的性质、目的与任务通过本课程的教学,使学生对高等代数乃至代数学的思想和方法有较深刻的认识, 提高他们的抽象思维、逻辑推理和运算的能力;使学生初步地掌握基本的、系统的代数知识和抽象的、严格的代数方法,进而加深对中学代数的理解;使学生能应用代数思想和方法去理解与处理有关的问题, 培养与提高代数的理论分析问题与解决问题的能力;使学生学习数学学科后续课程(如近世代数、离散数学、计算方法、偏微分方程、泛函分析等)提供一些所需要的基础理论和知识;使学生在智能开发、创新能力培养等方面获得重要的平台。
《高等代数》是数学与应用数学、信息与计算科学本科专业最重要的基础课程之一,是数学各专业报考研究生的必考课程之一,也是理论性、应用性很强的一门数学基础课。
讲授本课程的目的主要在于培养学生的代数基础理论和思想素质,基本掌握代数中的论证方法, 获得较熟练的演算技能和初步应用的技巧, 提高分析问题、解决问题的能力,为进一步学习其它数学知识打下坚实的基础。
本课程的主要任务是通过教学的主要环节(课堂讲授与讨论、习题课、作业、辅导答疑等),使学生学习和掌握多项式理论、线性代数的代数理论(行列式、线性方程组、矩阵、λ矩阵)及线性代数的几何理论(线性空间、线性变换、欧氏空间)。
二次型、-二、课程教学内容和基础要求(1)理解多项式的定义,掌握最大公因式,互素,不可约多项式, 因式分解等有关的一系列性质。
(2)理解行列式的定义, 掌握行列式的基本运算性质和行列式的行(列)展开性质;理解向量组的线性相关性,掌握线性方程组的通解求法;理解矩阵的概念和运算,掌握矩阵的可逆、矩阵的分块、矩阵的等价关系的性质及应用;理解二次型的定义,掌握二次型的标准形的求法及正定二次型的一系列性质。
(3)理解线性空间的定义,掌握交空间、和空间及直和的判定及性质;理解线性变换的定义及简单性质,掌握线性变换在不同基下的矩阵的性质、线性变换的值域与核的应用问题;会求矩阵的若当标准形;理解欧氏空间及对称变换的定义,掌握对称变换与实对称矩阵之间的关系的有关性质。
中国矿业大学考研真题—中国矿业大学(北京)

中国矿业大学(北京)力学与建造工程学院材料力学2003,2023年年——2023年年结构力学2004——2023年年土力学2002——2003,2023年年——2023年年管理概论2023年年建设项目管理基础2023年年——2023年年流体力学1997,2000城市计划1999——2000钻眼爆破2002工程地质学1998——2002水文工程地质学原理2004地下水动力学2003土壤学2003沉积学原理2004(加试)钢筋混凝土结构2002普通地质学2003能源地质学2003化学与环境工程学院无机化学1999——2023年年有机化学1999——2023年年物理化学1999——2000,2023年年普通化学2000,2023年年分析化学2000煤化学1999——2000化工原理1999——2000电路2001——2023年年第 1 页/共 5 页数字电路2000,2002——2023年年材料科学基础2023年年——2023年年环境学2023年年浮选1999——2000水处理工程1999——2000环境工程学1999——2000环境化学2003——2004(复试)文法学院二外法语2002——2023年年二外日语2003——2004,2023年年——2023年年(其中2023年年的试卷共9页,缺P8)二外俄语2023年年二外德语2000,2002——2004,2023年年——2023年年基础英语2003,2023年年——2023年年专业英语2023年年——2023年年翻译2004——2023年年民商法2023年年经济法与国际经济法2023年年国际经济法2023年年经济法2023年年科学技术史2023年年——2023年年科学技术哲学2023年年——2023年年政治学原理2002——2003,2023年年——2023年年政治学基本理论2023年年当代世界经济与政治2023年年——2023年年思想政治教诲学原理2002,2004——2023年年行政管理学2023年年马克思主义中国化的基本理论2023年年机电与信息工程学院电路2001——2023年年数字电路2000,2002——2023年年模拟电子技术2003——2023年年,2023年年机械原理2001——2002,2004——2023年年控制工程基础2023年年——2023年年材料科学基础2023年年——2023年年模拟电子技术2023年年——2023年年计算机组成与结构2002——2023年年数据结构2000——2023年年地球科学概论2004——2023年年计算机软件开辟基础2023年年——2023年年数据库技术2002遥感概论2003计算机在工程管理中的应用2004计算机在矿业中的应用2002理学院高等代数2023年年数学分析2023年年管理学院管理概论2001——2023年年(注:2003年名称为“管理学原理”;2004年名称为“管理学概论”)经济学原理2003——2023年年财务会计与管理会计学2023年年——2023年年会计学原理2003——2023年年(注:2000——2002年试卷名称为“会计学”)资源与安全工程学院第 3 页/共 5 页GIS基础2023年年,2023年年地球科学概论2004——2023年年水文地质学2001——2023年年测量学2004——2023年年计算机在测量中的应用2004——2023年年土地管理学2003,2023年年——2023年年计算机软件开辟基础2023年年——2023年年普通化学2000,2023年年环境学2023年年矿山压力及控制2023年年——2023年年计算机语言基础2023年年——2023年年安全系统工程2023年年——2023年年安全学原理2003材料力学2003,2023年年——2023年年结构力学2004——2023年年管理概论2023年年建设项目管理基础2023年年——2023年年材料科学基础2023年年——2023年年无机化学1999——2023年年有机化学1999——2023年年物理化学1999——2000,2023年年分析化学2000煤化学1999——2000化工原理1999——2000浮选1999——2000水处理工程1999——2000环境工程学1999——2000地球化学2002工业技术经济学2004采煤概论2001煤矿开采学2002煤田地质学2000地下工程2001第 5 页/共 5 页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初试自命题高等代数考试大纲
招生单位名称(盖章):填表人:
要求:1.参考书目应尽量考虑通用性和出版时间(出版时间不宜太早,以方便考生购买);非正式出版物以及正在出版过程中的书不能作参考书;参考书应注明书名、编著者、出版社、出版年份等。
如:《高级英语》(修订版)第1、2册,张汉熙主编,外国教学与研究出版社,2000年;
2.请标注是否允许考生使用无字典存储、编程和查询功能的计算器,如不标注理解为不允许使用计算器;绘图及其他科目考试时如有其他说
明的请在“备注”栏内标明。
