弦振动的实验研究
弦振动的研究实验报告

弦振动的研究实验报告实验目的:通过实验研究弦的振动特性,并分析弦振动时的动力学特点。
实验装置和材料:1. 弦:选用一根细长的弹性绳或细细的金属丝作为实验弦。
2. 振动源:使用一个固定在实验台上的振动源,可以通过电机或手动方式产生振动。
3. 能量传输装置:使用一个振动传输装置,将振动传输到实验弦上,如夹子、固定块等。
4. 振动探测器:使用一个合适的装置或传感器,用于测量弦的振动状态,如光电传感器、激光干涉仪等。
5. 数据采集设备:使用一个数据采集器,将振动数据进行记录和分析。
实验步骤:1. 将实验弦固定在实验台上,并将振动源固定在一端,确保弦能够自由振动。
2. 施加适量的拉力到弦上,以保证弦的紧绷度。
3. 使用振动源产生一定频率和振幅的振动,并将振动传输到实验弦上。
4. 启动数据采集设备记录弦的振动数据,包括振动频率、振幅和相位等。
5. 根据需要,可以改变振动源的频率和振幅,记录不同条件下的振动数据。
6. 对实验数据进行分析,绘制振动频率与振幅的关系图,并分析振动的谐波特性。
实验结果与分析:1. 实验数据表明,弦的振动频率与振幅呈正相关关系,即振动频率随着振幅的增加而增加。
2. 弦振动呈现出谐波特性,即振动状态可分解为基频振动和多个谐波振动的叠加。
3. 弦的振动模式与弦长度、拉力和材料特性有关,可以通过改变这些参数来调节振动频率和振幅。
结论:通过实验研究弦的振动特性,我们发现弦振动具有谐波特性,振动频率与振幅呈正相关关系。
弦的振动模式受到弦长度、拉力和材料特性的影响。
这些实验结果对于理解弦乐器的音色产生原理和振动系统的动力学特性具有重要意义。
弦振动特性实验报告

弦振动特性实验报告1. 实验目的通过实验,研究弦振动的基本特性,包括谐波产生、频率与长度、质点线密度的关系,以及波的传播速度与张力的关系。
2. 实验装置和材料- 弦振动装置- 引线- 引力滑块- 弯曲放大器- 定标尺- 振动发生器- 弦3. 实验原理弦的振动属于机械波的一种,是通过弦上质点的振动传递的。
当弦的一端被激发产生振动后,振动将以机械波的形式沿着弦传播。
3.1 谐波产生在实验中,激发弦振动的常用方法是通过振动发生器,将正弦波信号传递给弦。
由于弦上的质点受到激励,产生往返运动,形成谐振波。
3.2 频率与长度关系当弦的一端固定时,弦的长度可以影响波的频率。
根据弦的固定端和自由端来计算,可以得到以下公式:v = \frac{f \lambda}{T} = 2fL其中,v为波的传播速度,f为频率,\lambda为波长,T为张力,L为弦长。
3.3 质点线密度与频率关系质点线密度是指单位长度的弦所带有的质量。
一般情况下,质点线密度越大的弦,其频率越低。
根据公式可以得到:f = \frac{1}{2L}\sqrt{\frac{T}{\mu}}其中,\mu为质点线密度。
3.4 波的传播速度与张力关系当弦的长度和质点线密度一定时,可以通过调节弦的张力来改变波的传播速度。
根据公式可以得到:v = \sqrt{\frac{T}{\mu}}4. 实验步骤4.1 实验准备- 将弦振动装置固定在实验台上,并确保稳定和水平。
- 将弦挂在装置上,并且用定标尺测量弦的长度L。
- 调节振动发生器的频率为较低的值。
- 将引力滑块放在适当的位置,使其激起弦振动。
- 调节振动发生器的振幅和频率,使弦产生明显的振动。
4.2 测量波的频率和长度- 测量弦的长度L。
- 调节振动发生器的频率,使弦产生稳定的波形。
- 使用弯曲放大器,将弦上波的振动放大,方便观测。
- 使用定标尺,测量波的波长\lambda,注意使用两个节点之间的距离测量。
大学物理《弦振动》实验报告

大学物理《弦振动》实验报告大学物理《弦振动》实验报告(报告内容:目的、仪器装置、简单原理、数据记录及结果分析等)一.实验目的1.观察弦上形成的驻波2.学习用双踪示波器观察弦振动的波形3.验证弦振动的共振频率与弦长、张力、线密度及波腹数的关系二.实验仪器XY弦音计、双踪示波器、水平尺三实验原理当弦上某一小段受到外力拨动时便向横向移动,这时弦上的张力将使这小段恢复到平衡位置,但是弦上每一小段由于都具有惯性,所以到达平衡位置时并不立即停止运动,而是继续向相反方向运动,然后由于弦的张力和惯性使这一小段又向原来的方向移动,这样循环下去,此小段便作横向振动,这振动又以一定的速度沿整条弦传播而形成横波。
理论和实验证明,波在弦上传播的速度可由下式表示:=ρ1------------------------------------------------------- ①另外一方面,波的传播速度v和波长λ及频率γ之间的关系是:v=λγ-------------------------------------------------------- ②将②代入①中得γ=λ1-------------------------------------------------------③ ρ1又有L=n*λ/2 或λ=2*L/n代入③得γn=2L------------------------------------------------------ ④ ρ1四实验内容和步骤1.研究γ和n的关系①选择5根弦中的一根并将其有黄铜定位柱的一端置于张力杠杆的槽内,另一端固定在张力杠杆水平调节旋钮的螺钉上。
②设置两个弦码间的距离为60.00cm,置驱动线圈距离一个弦码大约5.00cm的位置上,将接受线圈放在两弦码中间。
将弦音计信号发生器和驱动线圈及示波器相连接,将接受线圈和示波器相连接。
③将1kg砝码悬挂于张力杠杆第一个槽内,调节张力杠杆水平调节旋钮是张力杠杆水平(张力杠杆水平是根据悬挂物的质量精确确定,弦的张力的必要条件,如果在张力杠杆的第一个槽内挂质量为m的砝码,则弦的张力T=mg,这里g是重力加速度;若砝码挂在第二个槽,则T=2mg;若砝码挂在第三个槽,则T=3mg…….)④置示波器各个开关及旋钮于适当位置,由信号发生器的信号出发示波器,在示波器上同时显示接收器接受的'信号及驱动信号两个波形,缓慢的增加驱动频率,边听弦音计的声音边观察示波器上探测信号幅度的增大,当接近共振时信号波形振幅突然增大,达到共振时示波器现实的波形是清晰稳定的振幅最大的正弦波,这时应看到弦的震动并听到弦振动引发的声音最大,若看不到弦的振动或者听不到声音,可以稍增大驱动的振幅(调节“输出调节”按钮)或改变接受线圈的位置再试,若波形失真,可稍减少驱动信号的振幅,测定记录n=1时的共振频率,继续增大驱动信号频率,测定并记录n=2,3,4,5时的共振频率,做γn图线,导出γ和n的关系。
弦振动研究实验报告

弦振动研究实验报告弦振动研究实验报告引言弦振动是物理学中一个重要的研究领域,对于理解声音、乐器演奏、结构工程等方面都具有重要意义。
本实验旨在通过实验观察和数据分析,探究弦振动的基本原理和特性。
实验目的1. 研究弦振动的基本原理和特性。
2. 通过实验观察和数据分析,验证弦振动的频率与弦长、张力和质量的关系。
3. 探究不同条件下弦振动的共振现象。
实验装置与方法本实验使用的装置包括弦线、定滑轮、振动发生器、频率计和质量块等。
具体实验步骤如下:1. 将弦线固定在两个支架上,并通过定滑轮使弦线保持水平。
2. 在弦线上固定一个质量块,调整张力。
3. 将振动发生器连接到弦线上,并调节频率。
4. 使用频率计测量弦线的频率。
5. 重复步骤2-4,改变质量块的质量、张力和弦长等条件。
实验结果与分析通过实验观察和数据分析,我们得到了以下结果:1. 频率与弦长的关系:在保持张力和质量不变的情况下,我们改变了弦长。
实验结果显示,随着弦长的增加,频率呈现出递减的趋势。
这与理论预测相符,即频率与弦长成反比关系。
2. 频率与张力的关系:在保持弦长和质量不变的情况下,我们改变了张力。
实验结果表明,随着张力的增加,频率也随之增加。
这符合理论预测,即频率与张力成正比关系。
3. 频率与质量的关系:在保持弦长和张力不变的情况下,我们改变了质量。
实验结果显示,随着质量的增加,频率呈现出递减的趋势。
这与理论预测相符,即频率与质量成反比关系。
4. 共振现象:我们在实验中发现了共振现象。
当振动发生器的频率与弦的固有频率相等时,弦会出现共振现象,振幅显著增大。
这说明共振频率与弦的固有频率相匹配。
结论通过本实验的观察和数据分析,我们得出以下结论:1. 弦振动的频率与弦长成反比关系,与张力和质量成正比关系。
2. 弦振动会出现共振现象,当振动发生器的频率与弦的固有频率相等时,振幅显著增大。
这些结论对于理解弦振动的基本原理和特性具有重要意义。
在实际应用中,我们可以根据这些关系来设计和调整乐器的音调,以及优化结构工程中的弦悬挂系统。
实验十四 弦振动的研究

比较 可知:在线密度为 、张力为 FT 的弦线上, 横波传播速度 的平方等于 FT 2 即
FT
(6)
3.弦振动规律 将式(1)代T
即
(7) 又将式(1’)代入式(6),整理后可得
1 FT
n 2l
FT
(8)
实验内容
1.测量弦的线密度 取2 m长和所用弦线为同一轴上的线,在 分析天平上称其质量m,求出线密度.
2.观察弦上的驻波
根据已知音叉频率 (一般为100 Hz)和已知 线密度 ,求弦长在20~30 cm附近,若要 弦的基频与音叉共振时,弦的张力 FT =? 参照上述计算的值,选适当的砝码挂在弦 上(弦长在130 cm左右),给电振音叉的线圈 上通以50 Hz,1—2 V的交流电,使音叉做受 迫振动,进行以下的观测:
振动体有一个基频和多个谐频的规律不只是
弦线上存在,而是普遍的现象.但基频相同 的各振动体,其各谐频的能量分布可以不同, 所以音色不同.例如具有同一基频的弦线和 音叉,其音调是相同的,但听起来声音不同 就是这个道理. 当弦线在频率为 的音叉驱动下振动时, 适当改变 FT 、l 和 ,则可能和强迫力发生 共振的不一定是基频,而可能是第一、第二、 第三、……谐频,这时弦上出现2,3,4,… 个半波区.
有变化,
式(2)将成为 FT 2 FT 1 0
,即 FT 2 FT 1 FT表 示张力不随时间和地点而变,为一定值.式 (3)将成为
dy dy d2y FT ( ) x dx FT ( ) x dx 2 dx dx dt
(4)
dy 将 ( ) x dx dx
弦的振动实验报告

弦的振动实验报告
实验目的
根据弦振动的微分方程和边界条件,计算弦振动的固有频率和振型,与实验结果对比,研究弦振动与结构及预紧力的参数关系。
实验内容
研究弦振动的固有频率与边界条件及弦的预紧力的关系,观察弦的节点及波峰波谷的形状。
实验原理
实验原理如图1所示,弦为一端固定,另一端悬挂重物(砝码),弦上固定有几种质量块,通过对弦上质量块激励,可以获得弦振动的共振频率;改变重物的质量,可以改变弦的预紧力,从而改变弦的共振频率。
通过观察可以了解弦的振型。
图1 实验装置简图
实验仪器
测试实验装置如图2所示,左侧为悬挂的重物。
取不同的悬挂重物,可以获得不同的预紧力,测取不同预紧力下弦的共振频率,可以得到弦的振动频率与预紧力的关系。
图2 实验装置图
图3 实验装置局部放大图
实验步骤
1:用非接触式激振器对准悬索的某一质量块,并保持初始间隙4-5mm,用标准砝码组弦丝张力1Kg.
2:激振器接入正弦信号后,对系统产生正弦激振力,系统将发生振动,激振信号频率由低到高缓慢调节,观察质量块的振动幅值及系统的振动形态,即可打找到系统在张力为1Kg时各阶固有频率和主振型.
3:然后增加砝码分别为2、3、4、5Kg,用同样的方法可找到张力为2、3、4、5Kg时的保阶固有频率和主振型。
实验数据记录和整理
通过眼睛观察弦在不同频率下的振动形态,得到其共振频率。
改变预紧力(增加砝码数),得到其固有频率。
表一不同预紧力下的弦的固有频率
砝码数/个2 3 4 5
一阶固有频率
/Hz
图4可观察得到的一阶振型。
弦振动的研究实验报告

弦振动的研究实验报告弦振动的研究实验报告引言弦振动作为物理学中的一个重要研究领域,其在音乐、工程、物理等多个领域都有广泛的应用。
本文将介绍一项关于弦振动的实验研究,通过实验数据和分析,探究弦振动的特性和规律。
实验目的本次实验的目的是通过调节弦的张力和长度,观察弦振动的频率和波形变化,进一步了解弦振动的特性,并验证弦振动的相关理论。
实验器材1. 弦:选择一根柔软且均匀的弦,如钢琴弦或者尼龙弦。
2. 弦激振器:用于激励弦振动的装置,可以是手摇的或者电动的。
3. 张力调节器:用于调节弦的张力,可以通过改变固定点的位置或者增加负重来实现。
4. 长度调节器:用于调节弦的长度,可以通过改变固定点的位置或者使用滑动支架来实现。
5. 频率计:用于测量弦振动的频率。
实验步骤1. 设置实验装置:将弦固定在两个支架上,并通过张力调节器调整弦的张力。
保持弦的长度初值为L0。
2. 激励弦振动:使用弦激振器在弦上施加横向力,使其振动。
可以调整激振器的频率和振幅。
3. 测量频率:使用频率计测量弦振动的频率。
记录下频率值f0。
4. 调整弦长度:通过滑动支架或者改变固定点的位置,改变弦的长度为L1,并再次测量频率f1。
5. 调整张力:通过增加负重或者改变固定点的位置,改变弦的张力,并测量频率f2。
6. 重复步骤4和5,记录不同长度和张力下的频率值。
实验结果与分析通过实验数据的记录和分析,我们可以得到以下结论:1. 弦的长度对振动频率的影响:当弦的长度增加时,振动频率减小。
这符合弦振动的基本原理,即弦的长度与振动频率呈反比关系。
2. 弦的张力对振动频率的影响:当张力增大时,振动频率也增大。
这是因为张力的增加会使弦的振动速度加快,从而导致频率的增加。
3. 弦的波形变化:通过观察弦的振动波形,我们可以发现当振动频率接近弦的固有频率时,波形呈现出共振现象,振幅增大。
这是由于共振频率与弦的固有频率相匹配,能量传递更加高效。
实验误差分析在实验过程中,可能存在一些误差,如频率计的精度限制、弦的材料和品质不同等。
弦振动实验报告

弦振动实验报告1. 引言本实验旨在研究弦振动现象的特性,并通过实验验证弦振动的数学模型。
通过测量不同条件下弦的振动频率和振动模式,我们可以深入理解弦振动的规律和特点,进一步探索其在物理学中的应用。
2. 实验装置与方法2.1 实验装置本实验使用的实验装置如下:•弦:一条细长而均匀的弦,可调节其长度和张力。
•弦轴:用于固定弦的一个端点,以保持弦的水平状态。
•调频器:用于调整弦的张力以改变振动频率。
•高斯计数器:用于测量弦的长度。
2.2 实验方法本实验分为以下几个步骤进行:1.将弦固定在弦轴上,并调整张力和长度,确保弦处于水平状态。
2.使用高斯计数器测量弦的长度,并记录下来。
3.调节调频器,改变弦的张力,使其产生不同的振动频率。
4.测量不同频率下弦的长度,并记录下来。
5.使用摄像设备记录弦的振动模式,并观察振动波形的变化。
6.对实验数据进行处理和分析,验证弦振动的数学模型。
3. 实验结果与分析3.1 弦长度与振动频率的关系在调节弦的张力时,记录了不同频率下弦的长度,如下表所示:弦的长度 (cm) 振动频率 (Hz)50 5040 6030 7020 8010 905 100根据实验数据,我们可以绘制出弦的长度与振动频率的关系曲线。
根据弦的线密度和张力可以推算出弦的波速,并进一步验证弦振动的规律。
3.2 弦的振动模式使用摄像设备记录了不同频率下弦的振动模式,并观察了振动波形的变化。
通过分析观察到的振动模式,可以发现随着振动频率的增加,弦的振动模式也会发生变化。
当振动频率为谐振频率时,弦会呈现出最大的振幅,形成共振现象。
4. 结论通过本实验的研究,我们得出以下结论:•弦的振动频率与其长度成反比关系。
•当弦的振动频率等于谐振频率时,弦呈现出最大振幅的共振现象。
•弦的振动模式随着振动频率的变化而变化。
这些结论进一步验证了弦振动的数学模型,并对弦振动现象的特性提供了实验依据。
5. 实验总结通过本次实验,我们学习了弦振动现象的特性,并通过实验验证了弦振动的数学模型。
物理实验:弦振动的研究
物理实验:弦振动的研究实验四弦振动的研究两列振幅相等的相干波,在同一直线上沿相反方向传播时,叠加形成驻波。
驻波是波的干涉现象中的一种重要现象,它在声学、光学、无线电工程和检测技术等方面都有广泛的应用,利用驻波现象可以测量波长、波速和频率。
一、实验目的1.了解固定均匀弦振动的传播规律,加深振动与波和干涉的概念。
2.了解固定均匀弦振动传播形成驻波的波形,加深对干涉的特殊形式——驻波的认识。
3.了解固定均匀弦振动固有频率的因素,测量均匀弦线上横波的传播速度及其线密度。
4.了解声音与频率之间的关系。
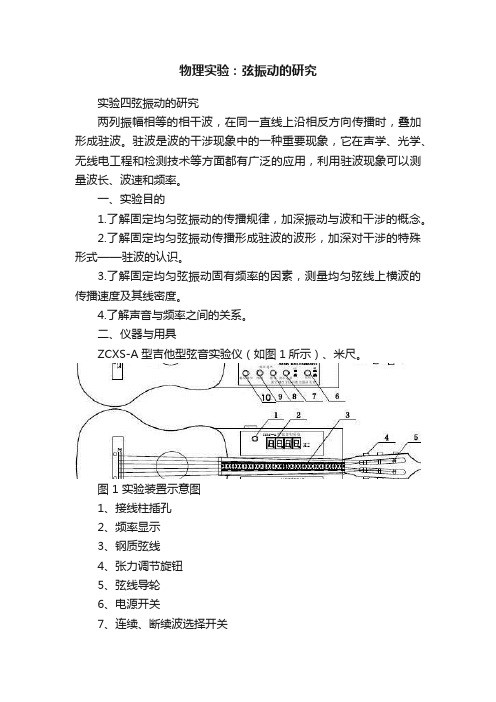
二、仪器与用具ZCXS-A型吉他型弦音实验仪(如图1所示)、米尺。
图 1 实验装置示意图1、接线柱插孔2、频率显示3、钢质弦线4、张力调节旋钮5、弦线导轮6、电源开关7、连续、断续波选择开关8、频段选择开关 9、频率微调旋钮 10、幅度调节旋钮 11、砝码盘实验装置如图1所示。
吉他上有四支钢质弦线,中间两支是用来测定弦线线密度,旁边两支用来测定弦线张力。
实验时,弦线3与音频信号源接通。
这样,通有正弦交变电流的弦线在磁场中就受到周期性的安培力的激励。
根据需要,可以调节频率选择开关和频率微调旋钮,从显示器上读出频率,通过调节幅度调节旋钮来改变正弦波发射强度。
移动劈尖的位置,可以改变弦线长度,并可适当移动磁钢的位置,使弦振动调整到最佳状态。
根据实验要求:挂有砝码的弦线可用来间接测定弦线线密度或横波在弦线上的传播速度;利用安装在张力调节旋钮上的弦线,可测定弦线的张力。
三、实验原理如图1所示,实验时,将弦线3(钢丝)绕过弦线导轮5与砝码盘11连接,并通过接线柱4接通正弦信号源。
在磁场中,通有电流的金属弦线会受到磁场力(称为安培力)的作用,若弦线上接通正弦交变电流时,则它在磁场中所受的与磁场方向和电流方向均为垂直的安培力,也随之发生正弦变化,移动劈尖改变弦长,当弦长是半波长的整倍数时,弦线上便会形成驻波。
移动磁钢的位置,将弦线振动调整到最佳状态,使弦线形成明显的驻波。
弦振动实验 报告

实 验 报 告班级 姓名 学号日期 室温 气压 成绩 教师 实验名称 弦 振 动 研 究【实验目的】1. 了解波在弦上的传播及驻波形成的条件2. 测量不同弦长和不同张力情况下的共振频率3. 测量弦线的线密度4. 测量弦振动时波的传播速度【实验仪器】弦振动研究试验仪及弦振动实验信号源各一台、双综示波器一台【实验原理】驻波是由振幅、频率和传播速度都相同的两列相干波,在同一直线上沿相反方向传播时叠加而成的特殊干涉现象。
当入射波沿着拉紧的弦传播,波动方程为()λπx ft A y -=2cos 当波到达端点时会反射回来,波动方程为 ()λπx ft A y +=2cos式中,A 为波的振幅;f 为频率;λ为波长;x 为弦线上质点的坐标位置,两拨叠加后的波方程为ft xA y y y πλπ2cos 2cos 221=+=这就是驻波的波函数,称为驻波方程。
式中,λπxA 2cos 2是各点的振幅 ,它只与x有关,即各点的振幅随着其与原点的距离x 的不同而异。
上式表明,当形成驻波时,弦线上的各点作振幅为λπxA 2cos 2、频率皆为f 的简谐振动。
令02cos 2=λπxA ,可得波节的位置坐标为()412λ+±=k x 2,1,0=k令12cos 2=λπxA ,可得波腹的位置坐标为2λkx ±= 2,1,0=k相邻两波腹的距离为半个波长,由此可见,只要从实验中测得波节或波腹间的距离,就可以确定波长。
在本试验中,由于弦的两端是固定的,故两端点为波节,所以,只有当均匀弦线的两个固定端之间的距离(弦长)L 等于半波长的整数倍时,才能形成驻波。
既有 2λn L =或 nL 2=λ 2,1,0=n 式中,L 为弦长;λ为驻波波长;n 为半波数(波腹数)。
另外,根据波动离乱,假设弦柔性很好,波在弦上的传播速度v 取决于线密度和弦的张力T ,其关系式为μTv =又根据波速、频率与波长的普遍关系式λf v =,可得μλTf v ==可得横波传播速度nL fv 2= 如果已知张力和频率,由式可得线密度22⎪⎪⎭⎫ ⎝⎛=Lfn T μ 如果已知线密度和频率,可得张力22⎪⎭⎫ ⎝⎛=n Lf T μ如果已知线密度和张力,由式可得频率μT L n f 2=【实验内容】一、 实验前准备 1. 选择一条弦,将弦的带有铜圆柱的一端固定在张力杆的U 型槽中,把带孔的一端套到调整螺旋杆上圆柱螺母上。
基础物理实验--关于弦振动的探究附图

如何做好这个实验呢?这里有图有真相~一、首先了解一下实验目的:1、观察弦振动形成的驻波。
熟悉其性质2、测定弦振动张力与波速的关系3、测定音叉的频率二、实验原理一、驻波的性质柔软均匀的弦线被拉紧,一端固定,另一端以一个固定频率振动,于是激起一个由振动端传至固定端然后反射回来的波,前进波和反射波不断在弦线上传播,并发生干涉。
为了简便可见,我们视前进波与反射波的振幅相等,通过调整绳线的压力,当弦线的长度为半波长的整数倍时,形成振幅最大又稳定的驻波,即弦与音叉共振。
前进波为;y1=Asin2p(t/T-x/λ)y2=Asin〔2p(t/T-(X+2l)/λ)-p〕y=y1+y2 经三角函数变换,得y=〔2Asin2p(l/λ)〕cos2p〔t/T-(x+l)/λ〕此式即驻波方程,式中余弦符号前面的系数是驻播上各点振动的振幅,可见,驻波上不同的点(不同l)以不同的振幅振动,振动的振幅依点的位置而按正弦规律变化,振动的最大值等于2A,叫波腹;最小值等于0,叫波节。
可见驻波上某些点始终以最大的振幅振动,某些点则始终静止。
处sin2p(l/λ)=0,是波节的位置,即l=0,λ、2、2λ/2、3λ/2......波节的位置;处sin2p(l/λ)=1,是波腹的位置,即l=λ/4、3λ/4、5λ/4、7λ/4.......是波腹的位置可见,波节与波节,波腹与波腹的距离,叫做驻波的波长,它等于形成这个驻波的两个横波波长的一半,因此利用驻波可以方便的测出横波波长二、音叉以固有频率做等幅简谐振动的原理音叉两臂间装有一个电磁铁N,磁铁的线圈一端接直流电源,一端接螺钉尖端的固定架,螺钉尖端可与音叉一臂上的弹片接触,电源另一极在音叉座驾上,通电后,调整尖端与音叉的距离(这是重要操作,音叉与尖端不能接触,但要足够近,以至于产生尖端放电,形成回路),电磁铁线圈有电流通过,音叉臂在电磁铁的吸引下使得尖端断开,电流中断,电磁铁失去吸引力,音叉臂弹回,弹片与尖端重新接触电路接通,电磁铁又吸引如此反复,使音叉以固有频率不断振动,而且每次振动都能得到电磁铁补给的能量,因此,音叉按照它的固有频率做等幅振动。
弦振动的实验研究

弦振动的实验研究弦是指一段又细又柔软的弹性长线,比如二胡、吉它等乐器上所用的弦。
用薄片拨动或者用弓在张紧的弦上拉动就可以使整个弦的振动,再通过音箱的共鸣,就会发出悦耳的声音。
对弦乐器性能的研究与改进,离不开对弦振动的研究,对弦振动研究的意义远不只限于此,在工程技术上也有着极其重要的意义。
比如悬于两根高压电杆间的电力线、大跨度的桥梁等,在一定程度上也是一根“弦”,它们的振动所带来的后果可不象乐器上的弦的振动那样使我们们感到愉快。
对于弦振动的研究,有助于我们理解这些特殊“弦”的振动特点、机制,从而对其加以控制。
同时,弦的振动也提供了一个直观的振动与波的模型,对它的分析、研究是处理其它声与振动问题的基础。
欧拉最早提出了弦振动的二阶方程,而后达朗贝尔等人通过对弦振动的研究开创了偏微分方程论。
本实验意在通过对一段两端固定弦振动的研究,了解弦振动的特点和规律。
预备问题1. 复习DF4320示波器的使用。
2. 什么是驻波?它是如何形成的?3. 什么是弦振动的模式?共振频率与哪些因素有关?4. 张力对波速有何影响?试比较以基频和第一谐频共振时弦中的波速。
一、 实验目的:1、了解驻波形成的条件,观察弦振动时形成的驻波;2、学会测量弦线上横波传播速度的方法:3、用作图法验证弦振动频率与弦长、频率与张力的关系。
二、实验原理一根两端固定并张紧的弦,静止时处于水平平衡位置,当在弦的垂直方向被拉离平衡位置后,弦会有回到平衡位置的趋势,在这种趋势和弦的惯性作用下,弦将在平衡位置附近振动。
令弦线长度方向为x 轴,弦被拉动的方向(与x 轴垂直的方向)为y 轴,如图1所示。
若设弦的长度为L ,线密度为ρ,弦上的张力为T ,对一小段弦线微元dl 进行受力分析,运用牛顿第二定律定律,可得在y 方向的运动微分方程()2222tydx dx x y T ∂∂=∂∂ρ (1) 若令ρ/2T v =, 上式可写为222221tyv x y ∂∂=∂∂ (2)y 图1(2)式反映了弦的位移y 与位置x 、时间t 的关系,其中)/(ρT v =代表了在弦线上横波传播的波速。
弦振动研究实验报告

弦振动研究实验报告导言弦振动是物理学中一个重要的研究领域,对于理解声学、乐器制作和波动理论等方面有着深远的影响。
本次实验旨在通过实际操作和数据测量,研究弦振动的基本特性和数学模型,并探讨其在实际应用中的意义。
实验装置与方法1. 实验装置本次实验使用了一根悬挂在两个固定点之间的细弦,以及一个固定好的频率发生器和一个震动传感器。
2. 实验步骤1) 将频率发生器连接至弦的一端,并设置合适的频率。
2) 将震动传感器固定在弦的中间位置上方,用于测量振动的频率。
3) 激发弦产生振动,并通过震动传感器采集数据。
4) 重复上述步骤,改变频率和弦长等参数,记录数据。
实验结果与分析通过采集的数据,我们得到了许多不同频率下弦的振动模式和波形。
通过对数据的处理和分析,我们得到了以下几方面的结论。
1. 弦振动的频率与弦长的关系在实验过程中,我们保持弦张力、线密度等参数不变,只改变弦长。
通过测量不同弦长下的频率,我们得到了频率与弦长的关系。
实验结果表明,频率与弦长成反比例关系,即弦长越长,频率越低。
2. 弦振动的频率与张力的关系在保持弦长不变的条件下,我们改变了弦的张力。
通过测量不同张力下的频率,我们得到了频率与张力的关系。
实验结果表明,频率与张力成正比例关系,即张力越大,频率越高。
3. 弦振动的波形特征在实验中,我们观察到了不同频率下的弦振动波形特征。
对于较低频率下的振动,弦呈现出单一的低音波形。
而对于较高频率下的振动,则呈现出分段性较明显的高音波形。
这一发现与波动理论中的谐波理论相一致,即弦振动可看作是一系列谐波波形的叠加。
实际应用与意义弦振动的研究在许多方面有着重要的应用和实际意义。
1. 声学研究弦振动是声学研究的基础,通过研究弦振动的频率、波形和音色特征,可以进一步理解声音的产生和传播机理。
同时,对于乐器制作、声音合成等方面也有着深远的影响。
2. 结构力学弦振动的研究有助于理解弦结构的稳定性和荷载传递机制。
对于建筑设计、桥梁工程和航空航天等领域都有重要意义。
弦振动实验研究报告

弦振动地研究一、实验目地1观察固定均匀弦振动共振干涉形成驻波时地波形,加深驻波地认识•2 了解固定弦振动固有频率与弦线地线密 p、弦长L和弦地张力T地关系, 并进行测量•二、实验仪器弦线,电子天平,滑轮及支架,砝码,电振音叉,米尺三、实验原理为了研究问题地方便,认为波动是从A 点发出地,沿弦线朝E端方向传播,称为入射波,再由E端反射沿弦线朝A端传播,称为反射波.入射波与反射波在同一条弦线上沿相反方向传播时将相互干涉,移动劈尖E 到适合位置•弦线上地波就形成驻波.这时,弦线上地波被分成几段形成波节和波腹.驻波形成如图(2)所示.b5E2RGbCAP设图中地两列波是沿X轴相向方向传播地振幅相等、频率相同振动方向一致地简谐波.向右传播地用细实线表示,向左传播地用细虚线表示,它们地合成驻波用粗实线表示.由图可见,两个波腹间地距离都是等于半个波长,这可从波动方程推导出来QEanqFDPw下面用简谐波表达式对驻波进行定量描述.设沿X轴正方向传播地波为入射波,沿X轴负方向传播地波为反射波,取它们振动位相始终相同地点作坐标原点“0”,且在X二0处,振动质点向上达最大位移时开始计时,则它们地波动方程分别为:DXDiTa9E3dY i = Acos2二(ft — x/ ) 丫2= Acos[2 二(ft + x/ 入)+ -:] 式中A为简谐波地振幅,f为频率,■为波长,X为弦线上质点地坐标位置.两波叠加后地合成波为驻波,其方程为:RTCrpUDGiTY i + 丫2 = 2Acos[2 二(x/ ■) + 二/2]Acos2二ft①由此可见,入射波与反射波合成后,弦上各点都在以同一频率作简谐振动,它们地振幅为丨2A cos[27:(x/ ■) +二/2] 与时间无关t,只与质点地位置x有关.5PCzVD7HxA由于波节处振幅为零,即:| cos[2二(x/ ■) +二/2] | = 02 二(x/ ■) + 二/2 = (2k+1)二/ 2 ( k=0. 2. 3. …)可得波节地位置为:x = k /2 ②而相邻两波节之间地距离为:X k +1 — X k= (k + 1)和./2 — k". / 2=和"/ 2 ③又因为波腹处地质点振幅为最大,即| cos[2二(x/ ■) +二/2] |=12二(x/ ) + 二/2= k二(k=0. 1.2. 3.…) 可得波腹地位置为:x = (2k-1) /4④这样相邻地波腹间地距离也是半个波长.因此,在驻波实验中,只要测得相邻两波节或相邻两波腹间地距离,就能确定该波地波长.jLBHrnAILg在本实验中,由于固定弦地两端是由劈尖支撑地,故两端点称为波节,所以,只有当弦线地两个固定端之间地距离(弦长)等于半波长地整数倍时,才能形成驻波,这就是均匀弦振动产生驻波地条件,其数学表达式为:XHAQX74J0XL= n / 2 ( n=1.2. 3. …)由此可得沿弦线传播地横波波长为:=2L/n ⑤式中n为弦线上驻波地段数,即半波数.根据波速、频率及波长地普遍关系式:V = f,将⑤式代入可得弦线上横波地传播速度:V = 2Lf/n ⑥另一方面,根据波动理论,弦线上横波地传播速度为:式中T为弦线中地张力,再由⑥⑦式可得V = (T/ P1/2⑦P为弦线单位长度地质量,即线密度.得1/2f = (T/ p) ( n/2L)T= p/ (n /2Lf )2即p= T(n/2Lf ) 2( n = 1.2. 3. …⑧LDAYtRyKfE由⑧式可知,当给定T、P L,频率f只有满足以上公式关系,且积储相应能量时才能在弦线上有驻波形成•四、实验内容1、测定弦线地线密度:用米尺测量弦线长度,用电子天平测量弦线质量,记录数据2、测定11个砝码地质量,记录数据3、组装仪器4、调节电振音叉频率,弦线长度和砝码数量得到多段驻波,用米尺测量驻波长度,记录频率,砝码质量,波数,波长.(靠近振动端地第一个驻波不完整,要从第二个驻波开始测量波长)Zzz6ZB2Ltk五、数据记录及处理1、弦线密度测定弦线总长:2.00m 总质量:0.383g c =0.383/2.00=0.1915 g/m2、砝码质量测定:兰州g=9.793m/s2 dvzfvkwMI12 5000.000 DOWIZ262_____________________Ar 1 ni7.338>^0715 _dir A EAC.1.2DD2.000 1.5001.000 0.5000.2000.4DDD.6000.E1000 v/m/sIgv-IgT® 象V=0.5001(+0.3SE60.S六、实验分析本实验结果基本符合经验公式,但还存在误差,分析有以下原因:1、未等挂在弦线上地砝码稳定就开始测量•2、未等形成地驻波稳定就开始记录数据.3、用米尺测量时读数不够精确.七、实验问题1、.如果要确定v与c地关系,实验应如何安排?答:应准备材质不同地弦线,在频率 f和张力T 一定地情况下,出现不同数量地驻波,测量对应波长L , V=2Lf,作出c— V图像“作为V地幕函数令(T =AV , 两边取对数得rqyn14ZNXIlg c =lgA+BlgV 作lg c— IgV图像求A,B.若B=V,A=T则公式推导正确.2、弦振动时,使N (波数)为偶数,将音叉转90°后,观察现象,并说明原因.答:旋转音叉90°波数变为N/2.原因是音叉带动地弦线由原来地左右摆动变成了前后摆动,形成地都是横波,原来左右振动一个周期形成两个波,旋转90°之后前后振动一个周期只形成了一个波,此时,电振音叉地振动频率不变,但是弦线地振动频率变为了原来地一半,所以波数减半.EmxvxOtOco版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理•版权为个人所有This article includes someparts, including text, pictures,and desig n. Copyright is pers onal own ership. sixE2yxpq5用户可将本文地内容或服务用于个人学习、研究或欣赏,以及其他非商业性或非盈利性用途,但同时应遵守著作权法及其他相关法律地规定,不得侵犯本网站及相关权利人地合法权利.除此以外,将本文任何内容或服务用于其他用途时,须征得本人及相关权利人地书面许可,并支付报酬.6ewMyirQFLUsers mayuse the contents or services of this article forpers onal study, research or appreciati on, and othernon-commercial or non -profit purposes, but at the same time, they shall abide by the provisi ons of copyright law and other releva nt laws, and shall not infringe upon the legitimate rights of this website and its releva nt obligees. In additi on, whe nany content or service of this article is used for other purposes, writte n permissi on and remun erati on shall be obta ined from the pers on con cer ned and the releva nt obligee. kavu42VRus转载或引用本文内容必须是以新闻性或资料性公共免费信息为使用目地地合理、善意引用,不得对本文内容原意进行曲解、修改,并自负版权等法律责任.y6v3ALoS89Reproducti on or quotati on of the content of this articlemust be reas on able and good-faith citati on for the use of n ewsor in formative public free in formati on .It shall notmisinterpret or modify the original intention of the content ofthis article, and shall bear legal liability such as copyright. M2ub6vSTnP。
弦振动的研究

3、计算波速 从以上测量中,选取合适的数据,用 两种方法求波速,说明其差异是否显著。 4、从测量纪录中,选一组数据 (T=40g),计算弦振动频率,求其与音 叉频率的百分差。
弦振动的研实验目的
1、观察弦振动时形成的驻波 2、验证弦振动的波长与张力 的关系 3、测量弦上横波的传播速度
实验仪器
• 电振音叉
• 弦线 • 滑轮 • 砝码 • 米尺
实验原理: 实验原理 由波动理论可以证明,横波沿着一条 拉紧的弦线传播时,波速v与弦线的张力T、 线密度ρ (单位长度的质量)间的关系为
T
实验内容: 实验内容: 1.观察驻波的形成和波形,波长的 变化。 (1)安装调试实验装置。如图所示, 接通电源后,调节螺钉 k ′ ,使音叉振 动; (2)改变弦线长(移动音叉)或砝码 质量,使之产生振幅最大且稳定的驻波 ,改变数次,观察波形、波长的变化情 况。
2、弦上横波的波长与张力的关系 增加砝码的质量,再细调弦长使其共 振,保持n=1或2个波段数,测出弦长l, 算出波长λ,重复测量取平均值。FT值 取20、40、60、80、100ɡ。 作 λ ~ FT 图,根据图求出斜率,求出 线密度ρ值,求其与测量值得百分差
v = FT
ρ
(1)
设f为弦线的波动频率;λ为弦线上传播 的横波波长,则根据v =fλ和(1)式得 1 F
λ=
T
f
ρ
当f、ρ一定时λ与 F 成正比。 形成驻波的条件:两列波,频率相同 ,振动方向相同,振幅基本相同,传播 方向相反。 λ l = n (n=1,2,3,……)时,得 当弦长 2 到稳定的最大幅度的驻波,波长 λ = 2l , n 则波速 v = f 2nl
弦振动研究实验报告

弦振动研究实验报告
实验目的:
研究弦的振动特性,分析弦的共振频率和振动模式,并确定弦的线密度。
实验装置:
弦、固定夹、串联铅垂测力计、固定器、震动源。
实验步骤:
1. 将弦固定在两个固定夹上,保持弦处于水平状态。
2. 使用串联铅垂测力计将弦与固定器连接,并调整垂直距离,使测力计可以测量到弦受力情况。
3. 在弦的中央位置敲击一下,产生振动。
4. 通过测量弦的共振频率和振幅来确定弦的共振特性。
5. 以不同的固定夹距离和弦长度进行多组实验,记录振动模式和测力计示数。
实验结果:
1. 测量了弦的共振频率和振幅,绘制了共振曲线。
2. 观察到了不同的振动模式,如基频、一次谐波、二次谐波等。
3. 记录了不同固定夹距离和弦长度下的测力计示数,进而计算得到弦的线密度。
实验讨论与分析:
1. 通过对弦的振动特性的研究,我们可以了解到弦的振动频率是与其长度和线密度有关的。
当固定夹距离一定时,弦长度越短,共振频率越高;线密度越大,共振频率越低。
2. 在实验中观察到了不同的振动模式,这与弦的基频和谐波有关。
基频是最低的振动模式,其他谐波是基频的整数倍。
3. 实验中测量了弦受力情况,通过示数可以计算弦的线密度,从而进一步研究弦的物理特性。
实验结论:
通过实验研究,我们得出了弦的振动特性与其长度和线密度有关的结论,并成功测量了弦的线密度。
这些结果对于理解和应用弦的振动现象具有重要意义。
弦振动的研究 实验报告

弦振动的研究实验报告弦振动的研究实验报告引言:弦振动是物理学中一个重要的研究领域,它涉及到声学、乐器制作、声波传播等多个方面。
本实验旨在通过对弦振动的实验研究,探索弦振动的特性和规律,为相关领域的研究提供实验数据和理论依据。
实验目的:1. 研究弦振动的基本特性,如频率、振幅等。
2. 探究弦振动与弦长、张力、质量等因素之间的关系。
3. 分析弦振动的波动性质,如波速、波长等。
实验装置:1. 弦:选用具有一定弹性的细绳或金属丝作为实验弦。
2. 弦轴:用于固定实验弦并调整张力的装置。
3. 振动源:通过手指或其他装置在弦上施加激励。
4. 测量仪器:包括频率计、示波器等,用于测量和记录实验数据。
实验步骤:1. 准备工作:调整弦轴的高度和张力,确保弦的平稳和稳定。
2. 施加激励:用手指或其他装置在弦上施加激励,使其振动起来。
3. 测量频率:使用频率计测量弦振动的频率,并记录数据。
4. 改变弦长:调整弦轴的位置,改变弦的长度,并重复步骤2和步骤3,记录数据。
5. 改变张力:调整弦轴的张力,改变弦的张力,并重复步骤2和步骤3,记录数据。
6. 改变质量:在弦上加挂一定质量的物体,改变弦的质量,并重复步骤2和步骤3,记录数据。
实验结果:通过实验测量和记录,我们得到了一系列关于弦振动的数据。
首先,我们观察到弦振动的频率与弦长成反比关系,即弦长越短,频率越高。
这与弦振动的基本特性相符。
其次,我们发现弦振动的频率与张力成正比关系,即张力越大,频率越高。
这也符合弦振动的基本规律。
最后,我们注意到弦振动的频率与质量无直接关系,即质量的增加并不会显著影响弦振动的频率。
讨论与分析:根据实验结果,我们可以得出以下结论:1. 弦振动的频率与弦长成反比关系,即频率和弦长满足频率公式 f = v / λ,其中 v 为波速,λ 为波长。
由于波速是一定的,所以当弦长减小时,波长必然增加,从而导致频率的增加。
2. 弦振动的频率与张力成正比关系,即频率和张力满足频率公式f = (1 / 2π) * √(T / μ),其中 T 为张力,μ 为线密度。
弦振动实验报告

弦振动实验报告实验13 弦振动得研究任何⼀个物体在某个特定值附近作往复变化,都称为振动。
振动就是产⽣波动得根源,波动就是振动得传播。
均匀弦振动得传播,实际上就是两个振幅相同得相⼲波在同⼀直线上沿相反⽅向传播得叠加,在⼀定条件下可形成驻波。
本实验验证了弦线上横波得传播规律:横波得波长与弦线中得张⼒得平⽅根成正⽐,⽽与其线密度(单位长度得质量)得平⽅根成反⽐、⼀、实验⽬得1、观察弦振动所形成得驻波。
2、研究弦振动得驻波波长与张⼒得关系、 3. 掌握⽤驻波法测定⾳叉频率得⽅法。
⼆。
实验仪器电动⾳叉、滑轮、弦线、砝码、钢卷尺等。
三。
实验原理1、两列波得振幅、振动⽅向与频率都相同,且有恒定得位相差,当它们在媒质内沿⼀条直线相向传播时,将产⽣⼀种特殊得⼲涉现象——形成驻波、如图3—13—1所⽰。
在⾳叉⼀臂得末端系⼀根⽔平弦线,弦线得另⼀端通过滑轮系⼀砝码拉紧弦线。
当接通电源,调节螺钉使⾳叉起振时,⾳叉带动弦线A端振动,由A 端振动引起得波沿弦线向右传播,称为⼊射波。
同时波在C 点被反射并沿弦线向左传播,称为反射波。
这样,⼀列持续得⼊射波与其反射波在同⼀弦线上沿相反⽅向传播,将会相互⼲涉、当C 点移动到适当位置时,弦线上就形成驻波。
此时,弦线上有些点始终不动,称为驻波得波节;⽽有些点振动最强,称为驻波得波腹。
2、图3—13-2所⽰为驻波形成得波形⽰意图。
在图中画出了两列波在T=0,T/4,T/2时刻得波形,细实线表⽰向右传播得波,虚线表⽰向左传播得波,粗实线表⽰合成波。
如取⼊射波与反射波得振动相位始终相同得点作为坐标原点,且在X=0处,振动点向上到达最⼤位移时开始计时,则它们得波动⽅程分别为:(3-13-1)(3-13-2)式中为波得振幅,为频率,λ为波长,为弦线上质点得坐标位置。
两波叠加后得合成波为驻波,其⽅程为:(3-13-3)由上式可知,⼊射波与反射波合成后,弦线上各点都在以同⼀频率作简谐振动,它们得振幅为,即驻波得振幅与时间⽆关,⽽与质点得位置有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弦振动的实验研究
弦是指一段又细又柔软的弹性长线,比如二胡、吉它等乐器上所用的弦。
用薄片拨动或者用弓在张紧的弦上拉动就可以使整个弦的振动,再通过音箱的共鸣,就会发出悦耳的声音。
对弦乐器性能的研究与改进,离不开对弦振动的研究,对弦振动研究的意义远不只限于此,在工程技术上也有着极其重要的意义。
比如悬于两根高压电杆间的电力线、大跨度的桥梁等,在一定程度上也是一根“弦”,它们的振动所带来的后果可不象乐器上的弦的振动那样使我们们感到愉快。
对于弦振动的研究,有助于我们理解这些特殊“弦”的振动特点、机制,从而对其加以控制。
同时,弦的振动也提供了一个直观的振动与波的模型,对它的分析、研究是处理其它声与振动问题的基础。
欧拉最早提出了弦振动的二阶方程,而后达朗贝尔等人通过对弦振动的研究开创了偏微分方程论。
本实验意在通过对一段两端固定弦振动的研究,了解弦振动的特点和规律。
预备问题
1. 复习DF4320示波器的使用。
2. 什么是驻波?它是如何形成的?
3. 什么是弦振动的模式?共振频率与哪些因素有关?
4. 张力对波速有何影响?试比较以基频和第一谐频共振时弦中的波速。
一、 实验目的:
1、了解驻波形成的条件,观察弦振动时形成的驻波;
2、学会测量弦线上横波传播速度的方法:
3、用作图法验证弦振动频率与弦长、频率与张力的关系。
二、实验原理
一根两端固定并张紧的弦,静止时处于水平平衡位置,当在弦的垂直方向被拉离平衡位置后,弦会有回到平衡位置的趋势,在这种趋势和弦的惯性作用下,弦将在平衡位置附近振动。
令弦线长度方向为x 轴,弦被拉动的方向(与x 轴垂直的方向)为y 轴,如图1所示。
若设弦的长度为L ,线密度为ρ,弦上的张力为T ,对一小段弦线微元dl 进行受力分析,运用牛顿第二定律定律,可得在y 方向的运动微分方程
()2222t
y
dx dx x y T ∂∂=∂∂ρ (1) 若令ρ/2
T v =, 上式可写为
2222
21t
y
v x y ∂∂=∂∂ (2)
y 图1
(2)式反映了弦的位移y 与位置x 、时间t 的关系,其中)/(ρT v =代表了在弦线上横波传播的波速。
对于两端固定的弦,满足上述方程的解为
)22cos()sin(
t L nv x L n A y n n ππ=, ,3,2,1=n (3) 若令 L
nv f n 2= ,n L
n 2=λ,(3)式又可写为
()t f x A y n n
n n πλπ
2cos )2sin(
= (4)
由(4)式可以看出,n f 代表了弦的振动频率,n λ代表了在弦上传播的机械波的波长。
两
端固定的弦的振动具有如下特点:对于某一固定的时间t 0,弦的位移随位置的变化为一正弦波形,最大波幅为A n cos (20t f n π)。
对于某一固定的位置x 0,弦表现为谐
振动,最大振幅为A n sin (n x λπ/20)。
在x o = 0,λ/2,λ,
3λ/2,2λ…等处的波幅为零,具有该种特点的波形,我们称之为驻波。
弦上始终为零的点称为波节,两相邻波节间的部分称为波腹,两相邻
波节间的距离正好为半个波长。
图2
给出了n 分别为1、2、3的三种弦振动的情形。
从图2不难看出,对于不同的n ,其波的形状不同,频率也不同,它代表着弦振动的一个状态。
所以,我们把一个个振动状态称之为弦振动的一个本征振动模式。
对应于n=1的频率,称为基频,对应于n=2,3,…的频率称为第一谐频、第二谐频,等等。
但基频较其他谐频强得多,因此它决定弦的频率,而各谐频则决定弦振动的音色。
弦的任何可能的振动状态都可以视为本征振动的线性叠加,这些本征振动中某一振动的强度会因初始条件或外界激励的不同而有所不同。
当用一频率与某一本征振动频率相同的周期性激励迫使弦振动时,弦上与激励频率相同的本征振动强度加强,这就是所谓的共振。
我们可以利用弦的共振特性对一些物理量进行测量。
如波长、波速等。
当弦上有n 个半波区时有(弦长等于半波长的整数倍时产生驻波)
n L 2=λ (5)
假设此时弦振动的频率为f ,弦上横波的传播的速度v ,则
n
L
f
f v 2==λ (6) 将ρ/T v =代入(6)式得弦振动的共振频率与弦长、弦张力和弦线密度的关系
图2 n=1,2,3时的三种振动状态
ρ
λT
f
1=
(7)
或 ρ
T
L n f 2=
(8)
上式中n f
f =
0为弦振动的基频
故有:ρT
L
f 210= (9)
三、实验仪器
FB301型弦振动实验仪一台、DF4320双踪示波器一台、FB303弦振动信号源一台
图中 1—调节螺杆 2—圆柱螺母 3—驱动传感器 4—弦 5—接收传感器
6—支撑板 7—拉力杆 8—悬挂物块 9—信号源 10—示波器
四、实验内容和步骤
1、研究弦振动时共振频率与弦长的关系
(1)将一根密度已知的弦固定在弦音计上,并在张力杆上悬挂一定质量的砝码,给弦一定的张
力,调张力杆水平,移动两桥的位置,先使弦长为60cm ,并把驱动传感器和接收传感器放在适当位置。
(2)按上图连接仪器,开启信号源、示波器预热约10分钟,由低到高调节其输出信号的频率,
当弦上产生n=1、2、3、4、5个半波区的情况下,即弦共振时(示波器上振幅达到最大),记下信号源输出信号的频率(你会发现示波器上读出的频率和信号源上的频率不相等,为什么?哪个是弦的共振频率?)。
(3)保持弦的张力不变,改变弦的长度,使弦长分别为60、 55、45、40cm 时重做步骤(2)。
(4)作ln 0f 与ln L 曲线,求出其斜率验证关系式(9)
(1)固定弦长,改变张力,使T=1、2、3、4、5Kmg 时,始终使弦线只出现一个驻波,测出共
振频率(基频)。
(2)作ln 0f 与ln T 曲线,求出其斜率验证关系式(9) 3、研究弦共振时弦线的动态线密度
利用表二的数据计算不同张力下弦线的线密度ρ
4、根据λf v =和ρ/T v =分别计算波速值,并分析产生误差的原因。
五、数据记录与处理
1、研究弦振动共振频率与弦长的关系
表一 基频与弦长的关系
弦线密度0ρ= 9.54×410-kg/m 物块悬挂位置 2 张力= 19.6牛顿
上表只作基频0f 与弦长的对数关系曲线。
基频0f 是驻波数为1的共振频率 作ln 0f 与ln L 曲线,求斜率验证关系式
表二 基频与张力的关系
以上两表中频率均为信号源的显示值,此值可以用示波器读出后与之比较
作ln 0f 与ln T 曲线验证关系式
3、根据λ.f v =和ρ/T v =分别计算波速值,并分析产生误差的原因
表三 ρ=9.54×10-4 kg/m
六、思考题
1、通过实验,说明弦线的共振频率和波速与哪些条件有关?。
