六年级小升初 图形与几何复习
六年级小升初几何图形知识点梳理

第二部份 空间与图形量的计量一、长度单位是用来测量物体的长度的。
常用的长度单位有:千米、米、分米、 厘米、毫米。
二、长度单位:三、面积单位是用来测量物体的恚面或平面图形的大小的。
常用面积单位:平方 千米、公顷、平方米、平方分米、平方厘米。
四、 测量和计算土地面积,通常用公顷作单位。
边长100米的正方形土地,面积是1公顷。
五、 测量和计算大面积的土地,通常用平方千米作单位。
边长woo 米的正方形 土地,面积是1平方千米。
六、面积单位:(100)七、 体积单位是用来测量物体所占空间的大小的。
常用的体积单位有;立方米、 立方分米(升)、立方厘米(臺升)。
八、 体枳单位;<1000)九、常用的质量单位有:吨、千克、克。
十、质量单位:十一、常用的时间单位有;世纪、年、季度、月、旬、日、时、分、秒。
十二、时间单位:(60)(一) 形的认识.测量十三、高级单位的名数改写成低级单位的名数应该乘以进率;低级单位的名数改写成高级单位的名数应该除以进率。
十四、常用计最单位用字母表示平面图形【认识.周长、面积】一、用直尺把两点连接起来,就得到一条线段;把线段的一端无限延长,可以得到一条射线;把线段的两端无限延长,可以得到一条直线。
线段、射线都是直线上的一部分。
线段有两个端点,长度是有限的;射线只有一个端点,直线没有端点,射线和直线都是无限长的。
二、从一点引出两条射线,就组成了一个角。
角的大小与两边叉开的大小有关,与边的长短无关。
角的大小的计量单位是O三、角的分类:小于90度的角是锐角;等于90度的角是直角;大于90度小于180度的角是钝角;等于180度的角是平角;等于360度的角是周角。
四、相交成直角的两条直线互相垂直;在同一平面不相交的两条直线互相平行。
五、三角形是由三条线段国成的图形。
围成三角形的每条线段叫做三角形的边,每两条线段的交点叫做三角形的顶点。
六、三角形按角分'可以分为锐角三角形、直角三角形和钝角三角形。
苏教版六年级数学小升初专题复习五几何初步知识
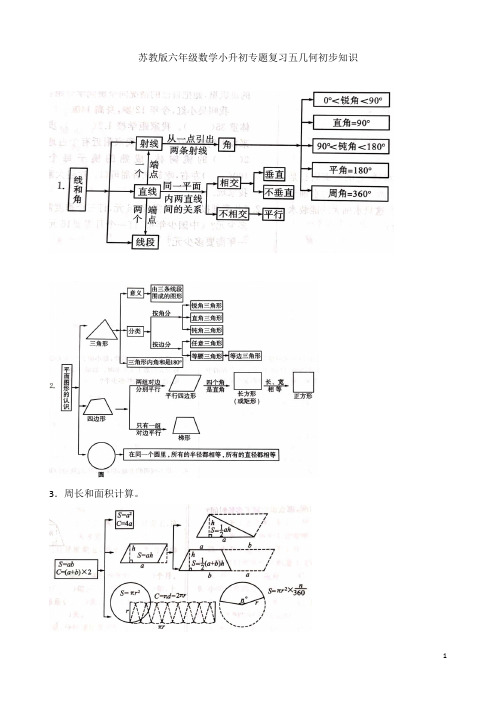
苏教版六年级数学小升初专题复习五几何初步知识3.周长和面积计算。
4.立体图形一、定义1.线段:用直尺把两点连接起来,就得到一条线段,线段长就是这两点间的距离。
两点间所有连线中线段最短。
2.射线:把线段的一端无限延长,可以得到条射线。
手电筒发出的光、太阳射出的光线都可看成是射线。
3.直线:把线段的两端无限延长,可以得到一条直线。
二、直线、线段、射线的比较名称三、同一平面上线与线的关系同一平面上的两条直线或平行或相交。
1.垂线:两条直线相交成直角时,这两条直线叫作互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足。
2.平行线:在同一平面内不相交的两条直线叫作平行线。
(1)平行线之间的距离处处相等;(2)平行线间垂线段最短,并且有无数条;(3)垂直于同一条直线的两条直线互相平行。
3.点到直线的连线中,垂线段最短4.线段AB的垂直平分线上的任意一点到线段两端的连线相等。
一、角的分类角:从一点起画两条射线,所组成的图形叫作角。
角两边叉开得越大,角越大;角的大小与角两边的长短无关。
二、角的测量利用量角器可以画角或量出角的度数。
首先将量角器的中心与角的顶点重合,然后再将量角器的零刻度线与角的一边重合,另一条边所对准的刻度就是这个角的度数。
注意要分清是内刻度线还是外刻度线。
三、画角画角的方法有很多,我们应该学会用量角器画指定大小的角。
画角时,首先要确定角的顶点,并画出角的一条边,然后将量角器的中心和零刻度线与角的顶点和画好的一条边都分别重合,数出量角器上所画角的度数,做好标记,然后连接顶点和标记,这样就画好了一个指定度数的角。
要注意美观。
形一、平行四边形和梯形(四边形)圆定义:两组对边分别平行的四边形叫作平行四边形。
只有一组对边平行的四边形叫作梯形。
二、三角形(由三条线段围成的图形)1.按角分2.按边分3.等腰三角形的特征和性质两腰相等,两底角相等,底边上的高是底边的垂直平分线。
4.等边三角形的特征和性质,5.三角形的一些特征和性质 (1)三角形具有稳定性; (2)三角形内角和是180º(3)三角形中任意两边之和大于第三边(4)在三角形中大角所对的边也大;在直角三角形中,斜边最长 (5)在等腰直角三角形中,斜边上的高等于斜边的一半三、圆(封闭的曲线图形) 1.圆的各部分名称在同一个圆内,有无数条直径和半径,所有的直径都相等,所有的半径都相等。
六年级数学小升初几何易错知识点汇总+图形求面积十大方法总结

易错知识点1线、角1 .直线没有端点,没有长度,可以无限延伸。
2. 射线只有一个端点,没有长度,射线可以无限延伸,并且射线有方向。
3. 在一条直线上的一个点可以引出两条射线。
4. 线段有两个端点,可以测量长度。
圆的半径、直径都是线段。
5 .角的两边是射线,角的大小与射线的长度没有关系,而是跟角的两边叉开的大小有关,叉得越大角就越大。
6 .几个易错的角边关系:(1)平角的两边是射线,平角不是直线。
(2)三角形、四边形中的角的两边是线段。
(3)圆心角的两边是线段。
7 .两条直线相交成直角时,这两条直线叫做互相垂直。
其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
8. 从直线外一点到这条直线所画的垂直线段的长度叫做点到直线的距离。
9. 在同一个平面上不相交的两条直线叫做平行线。
2 三角形1. 任何三角形内角和都是180度。
2 .三角形具有稳定的特性,三角形两边之和大于第三边,三角形两边之差小于第三边。
3. 任何三角形都有三条高。
4. 直角三角形两个锐角的和是90度。
5. 两个三角形等底等高,则它们面积相等。
6 .面积相等的两个三角形,形状不一定相同。
3正方形面积1 .正方形面积:边长×边长2 .正方形面积:两条对角线长度的积÷24三角形、四边形的关系1. 两个完全一样的三角形能组成一个平行四边形。
2. 两个完全一样的直角三角形能组成一个长方形。
3. 两个完全一样的等腰直角三角形能组成一个正方形。
4. 两个完全一样的梯形能组成一个平行四边形。
5 圆把一个圆割成一个近似的长方形,割拼成的长方形的长相当于圆周长的一半,宽相当于圆的半径。
则长方形的面积等于圆的面积,长方形的周长比圆的周长增加r ×2。
半圆的周长等于圆的周长的一半加直径。
半圆的周长公式:C=pd¸2+d或C=pr+2r在同一个圆里,半径扩大或缩小多少倍,直径和周长也扩大或缩小相同的倍数。
而面积扩大或缩小以上倍数的平方倍。
六年级下册数学-小升初平面几何知识复习(练习)冀教版

第一节 平面图形知识结构图如果一个图形沿着一条直线对折,两边的图形能够完全重合,这个图形叫做轴对称图形,这条直线叫做对称轴。
名称 对称轴 名称 对称轴 线段 1条 正方形 4条 角 1条 等腰梯形 1条 等腰三角形 1条 圆 无数条 等边三角形3条长方形2条锐角三角形直角三角形 钝角三角形 按角分按边分不等边三角形等腰三角形 等边三角形长方形周长:C=2(a+b) 面积:S=ab 正方形周长:C=2(a+b) 面积:S=a 2 平行四边形面积:S=12ah 梯形面积:S=12(a+b)h面积:S=12ah线:直线、射线、线段角:锐角、直角、 钝角、平角 、周角三角形四边形圆周长:C=2πr 面积:S=πr 2 组合图形(面积计算)平面图形【例题】1.判断,对的打“√”,错的打“×”。
1、直线比射线长。
------------------------------------------------------()2、四条边都相等的四边形是正方形。
--------------------------------------()3、面积相等的两个三角形,一定能拼成一个平行四边形。
--------------- ()4、一个三角形中最少有两个锐角。
------------------------------------------()5、有一组对边平行的四边形是梯形。
---------------------------------------()6、大于90度的角是钝角。
------------------------------------()7、角的两条边越长,角就越大。
------------------------------()8、从直线外一点向这条直线所画的线段,都叫做这点到直线的距离。
2.填空。
1、三角形的一个内角正好等于其余两个内角的和,这是一个()三角形。
2、一个等腰三角形,它的顶角是72º,它的底角是()度。
苏教版六年级下册数学课内+小升初专题讲义-第9讲 图形与几何(总复习)

第9讲图形与几何(总复习)【考点1】巧数图形【例1】数一数,下图中有()条直线,()条射线,()条线段。
【考点2】图形与格点【例1】如图是用橡皮筋在钉子板上围成的一个三角形,计算它的面积是多少?(每相邻两个小钉之间的距离都等于1个单位长度)【例2】右图中有28个点,其中每相邻的三点“∵”或“∴”所形成的三角形都是面积为1的等边三角形,试计算四边形ABCD的面积。
【规律总结】1.正方形格点多边形面积公式:2.三角形格点多边形面积公式:【实战练习】1.如图,每个小方格都是边长为1的正方形,求图中格点四边形ABCD的面积。
2.如图,每相邻三个点构成的三角形的面积都是1平方厘米,求阴影格点多边形的面积。
【考点3】用底高倍数法接图形题【例1】如图所示,三角形ABC的每边长都是96cm,用折线把这个三角形分割成面积相等的4个三角形,求线段CE与CF的长度之和。
【例2】如图,三角形ABC的面积为10厘米,AD与BF交于点E,且AE=ED,BD=CD,求图中阴影部分的面积和。
【例3】如图,把四边形ABCD的各边延长,使得AB=AE,BC=BF,CD=CG,DA=DH,得到一个大的四边形EFGH,若四边形ABCD的面积是5,试求四边形EFGH的面积。
【实战练习】1.如图,△ABC中,BD:DF:FC=2:3:4,已知△AFC的面积为48平方厘米,E为AF的中点。
求四边形ABDE的面积。
2.如图所示,=1,==,则=( )A. B. C. D.3.如图所示,直线DE把大三角形分成甲、乙两部分,甲与乙的面积比是。
4.如图所示,已知梯形ABCD的上底CD=3cm,下底AB=9cm,CF=2cm,.求梯形ABCD的面积。
【考点4】活用公式解图形问题【例1】用一块面积为36平方厘米的大圆铝板下料,如图,裁出7个同样大小的小圆形铝板,则余下的边角料的总面积是多少平方厘米?【例2】如图,等边△ABC的边长是1,现依次以A、C、B为圆心,以AB,CD,BE为半径画扇形,则阴影部分的面积为多少?(结果保留π)【实战练习】1.如图,半圆的直径为50厘米,阴影部分的周长是多少厘米?(结果保留π)2.如图,半圆的面积是14.13平方厘米,圆的面积是19.625平方厘米,那么长方形(阴影部分)的面积是多少平方厘米?课后巩固一、求下面各图中阴影部分的面积二.填空题1.经过一点可以画()条直线。
小升初数学《图形与几何》专题复习讲义(含答案)

小升初数学《图形与几何》专题复习讲义(含答案)一、填空题1、如图所示,有一个五边形ABCDE,其中M、N、P分别为边AE、BC、DE的中点,每块图形中的数表示该图形的面积(单位:平方厘米),则图中阴影部分的面积是()平方厘米2、如图所示,长方形ABCD的面积是56cm²。
BE=3cm,DF=2cm。
请你回答:三角形AEF的面积是()3、如图所示,一个正六边形分成6个相同的三角形,每个三角形又可以分成三个相同的小三角形,已知阴影部分的面积是18平方厘米,那么正六边形的面积是()平方厘米4、如图所示,在平行四边形ABCD中,点E是BC的中点,DF=2FC。
若的面积是10,则平行四边形的面积是()5、如图所示,正方形ABCD中,点E在边AD上,点F在边DC上,AE=2ED,DF=3FC,则△BFE的面积与正方形ABCD的面积的比值是()6、有一块长50.24厘米、宽18.84厘米的长方形硬纸板,横着可以卷成一个圆柱,竖着可以卷成一个圆柱,两种卷法表面积相差( )平方厘米(接头处忽略不计)7、一个半圆的周长是257厘米,它的面积是( )平方厘米8、一个圆柱的底面周长和一个圆锥的底面周长的比是3:4,它们的体积之比是9:7,那么圆柱和圆锥的高之比是( )9、如图所示,有3个圆从小到大的半径分别为1厘米,2厘米,3厘米。
阴影部分和非阴影部分面积之比是( )10、如图,圆的半径是1厘米,阴影部分的周长是( )厘米11、把一根长1米的圆柱铁棒锯成三段(每段仍然是圆柱体),表面积增加了0.36平方分米,这跟铁棒原来的体积是( )立方分米12、一个圆柱形水桶的侧面积是它的底面积的6倍,水桶的底面半径为1分米,这个水桶的容积是( )立方分米13、一个圆柱体,侧面积是37.68平方分米,高是2分米,它的表面积是( )平方分米14、一根横截面为正方形的方木长2.4米,锯下一个最大的正方体后,表面积减少了36平方分米,这跟方木原来的体积是( )立方分米15、一个长方体木块,长、宽、高分别是8分米、4分米、2分米,把它锯成若干个小正方体,然后拼成一个大正方体,那么拼成的大正方体的表面积是( )平方分米 二、解答题1、如图所示,梯形ABCD 的面积为45平方厘米,三角形AED 的面积是三角形ABE 面积的2倍,BE =4厘米,EC =9厘米,求三角形DEC 的面积。
六年级小升初 图形与几何复习

8. 如图阴影部分的面积是8cm,它的体积为
直径是20cm的圆锥形铁块,这个圆锥形铁块的高约是
cm。
cm3 。把它熔铸成底面
10. 一个圆扩大后,面积比原来多8倍,周长比原来多50.24厘米,这个圆原来的面积是
平
方厘米。
11. 如图,求阴影部分的面积。(单位:厘米)(π取3.14)
15.
一个正方体油罐,从里面量,棱长6分米。油罐里装的柴油占油罐容量的
2 3
,装了多少升柴油?
16. 一个长方形和一个圆的周长相等,已知长方形的长是10厘米,宽是5.7厘米。圆的面积是多
少?
17. 有一张长方形铁皮(如图),剪下图中两个圆及一块长方形,正好可以做成一个圆柱,这个圆
柱的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?
12. 将一个底面直径是20厘米,高为24厘米的金属圆锥体,全部浸没在直径是40厘米的圆柱形水
桶中,水面会升高多少厘米?
13. 半径为3厘米的圆,如果将半径扩大到原来的4倍,那么这个圆的周长和面积分别发生怎样的变
化?
14. 如图所示,直角三角形三条边分别长为3、4、5,求绕斜边旋转一周后所形成的物体体积。
18. 中心公园有一个圆形花坛,它的周长是37.68米,现在准备将它的周围增加1米,这样,花坛的
面积可增加多少平方米?
19. 从一块边长为4dm的正方形铁皮中剪下一个最大的圆,这块铁皮的利用率是多少?
20. 所有的圆都有无数条半径,无数条对称轴。 A. 正确 B. 错误
1. 如图,长方形的面积与圆的面积相等,已知阴影部分的面积是84.78cm2,圆的周长是( )cm
。
A. 18.84 B. 75.36 C. 37.68
六年级下册数学小升初专题复习 图形与几何精品PPT人教新课标

六年级下册数学小升初专题复习 图形与几何精品PPT人教新课标
复习周长和面积的含义。
平面图形面积与周长能比较大小吗?
半径为1㎝的圆的周长比面积大,这种说法对吗? 这种说法不对,因为周长和面积的意义不同,单位不同,不能 比较大小。
六年级下册数学小升初专题复习 图形与几何精品PPT人教新课标
六年级下册数学小升初专题复习 图形与几何精品PPT人教新课标
ONor No
Image
ImC÷ag2e
六年级下册数学小升初专题复习 图形与几何精品PPT人教新课标
从一张长3厘米,宽2.5厘米的长方形纸片上剪下一个最大
的正方形,求这个正方形的周长和面积。
这个最大的正方形以
正方形的周长=边长×4
长方形的宽为边长。
2.5×4=10(厘米)
正方形的面积=边长×边长 2.5×2.5=6.25(厘米²)
三角形的面积等于与 它等底等高的平行四 边形面积的一半。
答:三角形的面积是15cm²。
六年级下册数学小升初专题复习 图形与几何精品PPT人教新课标
六年级下册数学小升初专题复习 图形与几何精品PPT人教新课标
靠墙边围成一个花坛,围花坛的篱笆长43m,求这个花坛 的面积。
先求出梯形上下底的和
上底+下底=43-21=22(m)
圆
高
通过实验得到了周长与直径的关系:任意一个
圆的周面长积都=圆是周它率直×径半的径三×倍半多径一些。底这是一个
固定值,我们把它叫做圆周率, 它是一个定值,结
果为π. π=3.1415926…… 圆的周长=圆周率×直径=2×圆周率×半径
C=πd 或 C=2πr
六年级下册数学小升初专题复习 图形与几何精品PPT人教新课标
(完整版)小学六年级小学升初中小升初阴影面积专题复习经典例题图形面积几何图形(含答案)

阴影部分面积专题小学六年级小学升初中1. 求如图阴影部分的面积.(单位:厘米)2. 如图,求阴影部分的面积.(单位:厘米)3. 计算如图阴影部分的面积.(单位:厘米)4. 求出如图阴影部分的面积:单位:厘米.6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)11. 求下图阴影部分的面积.(单位:厘米)12. 求阴影部分图形的面积.(单位:厘米)r ------ io ------- 113. 计算阴影部分面积(单位:厘米)14. 求阴影部分的面积.(单位:厘米)15. 求下图阴影部分的面积:(单位:厘米)16. 求阴影部分面积(单位:厘米)17. (2012&泰县)求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积. 1526356分析阴影部分的面积等丁梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答…n 2解:(4+6) X4士2士2-3.14 X士2,2=10— 3.14 X4士2,=10-6.28 ,=3.72 (平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.1526356分析根据图形可以看出:阴影部分的面积等丁正方形的面积减去4个扇形的面积.正方形的面积等丁(10X 10) 100平方厘米,4个扇形的面积等丁半径为(10士2) 5厘米的圆的面积,即:3.14 X 5X 5=78.5 (平■方厘米). 解答解:扇形的半径是:10 士2,=5 (厘米);10X 10 -3.14 X 5X 5,100-78.5 ,=21.5 (平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.考点组合图形的面积.1526356分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等丁直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10 -2=5 (厘米),长方形的面积*X宽=10X 5=50 (平方厘米),半圆的面积=兀r2士2=3.14 X 52-2=39.25 (平■方厘米),阴影部分的面积=长方形的面积-半圆的面积,=50- 39.25 ,=10.75 (平方厘米);答:阴影部分的面积是10.75 .点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看届丁哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.1526356专题平■面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积-以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8X4-3.14 X42-2,=32 - 25.12 ,=6.88 (平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄活楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点圆、圆环的面积.1526356分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4 H 米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2X圆的面积”算出答案.解答解:S=^ r2_ ,_ . 2=3.14 X (4士2)=12.56 (平方厘米);阴影部分的面积=2个圆的面积,=2X 12.56 ,=25.12 (平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.1526356分析图一中阴影部分的面积=大正方形面积的一半-与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积-平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6X6-2-4X6-2=6 (平方厘米);图二中阴影部分的面积=(8+15) X (48士8)士 2 - 48=21 (平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.1526356分析由图意可知:阴影部分的面积皂圆的面积,乂因圆的半径为斜边上的高, 4利用同一个三角形的面积相等即可求出斜边上的高,也就等丁知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15X 20-2X2-25,=300+ 25,=12 (厘米);阴影部分的面积:lx 3.14 X 122,4=Lx 3.14 X 144,=0.785 X 144,=113.04 (平■方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积. 1526356 分析(1)圆环的面积等丁大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积-三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等丁圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:223.14 X (上)-3.14 X 〔萱),2 2=28.26 - 3.14 ,=25.12 (平方厘米);(2)阴影部分的面积:3.14 x 32--X (3+3) X3, 2=28.26 - 9,=19.26 (平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径. 9. 如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.1526356专题平■面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积-以10-2=5厘米为半径的半圆的面积-以3-2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14 X ( 10+3),=3.14 X 13,=40.82 (厘米);面积:ix 3.14 X [ (10+3) 士2]2—【X 3.14 X (10 士2) 2 2ix 3.14 X (3 士2) 2,=以 3.14 X (42.25 - 25 - 2.25),2=以 3.14 X 15,=23.55 (平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=兀r,得出图中两个小半圆的弧长之和等丁大半圆的弧长,是解决本题的关键.10. 求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.1526356■刀忻先用“3+3=6'求出大扇形的半径,然后根据“扇形的面积卫*”分别计360算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积-小扇形的面积=阴影部分的面积”解答即可.解:r=3, R=3+3=6 n=120,解答$喙新一点兀=—"■-□OU JuU=37.68 - 9.42 ,=28.26 (平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11. 求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.1526356分析先求出半圆的面积3.14 X (10士2)2-2=39.25平方厘米,再求出空白三角形的面积10X (10士2)士2=25平方厘米,相减即可求解.2解答解:3.14 X (10士2)士2 - 10X (10士2)士 2=39.25 - 25=14.25 (平■方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积北圆的面积-空白三角形的面积.12. 求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.1526356分析求阴影部分的面积可用梯形面积减去圆面积的1,列式计算即可.42解答解:(4+10) X4士2-3.14 X4 士4,=28 - 12.56 ,=15.44 (平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13. 计算阴影部分面积(单位:厘米)考点组合图形的面积.1526356专题平■面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积-三角形①的面积,平■行四边形的底和高分另U为10厘米和15厘米,三角形①的底和高分别为10厘米和(15-7)厘米,利用平■行四边形和三角形的面积公式即可求解.解答解:10X 15- 10X ( 15-7)士2,=150- 40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.考点梯形的面积.1526356分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等丁梯形的上底,代入梯形的面积公式即可求解.=96 士2,=48 (平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15. 求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.1526356分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2X 3-2=6 士2=3 (平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16. 求阴影部分面积(单位:厘米).考点组合图形的面积.1526356分析由图意可知:阴影部分的面积=梯形的面积-圆的面积,梯形的上底和高[4都等丁圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9) X4士2-3.14 X42x1,4=13X4士2-3.14 X4,=26 - 12.56 ,=13.44 (平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等丁圆的半径,且阴影部分的面积=梯形的面积-[圆的面积.17. (2012&泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.1526356分析由图可知,阴影部分的面积=梯形的面积-半圆的面积.梯形的面积(a+b)h,半圆的面积 m兀「2,将数值代入从而求得阴影部分的面积.解答解:*X(6+8) X (6士2)— 3.14 X (6士2)2=以14X3-以 3.14 X 9, 2 '=21 - 14.13,=6.87 (平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
六年级小升初 图形与几何复习

10. 圆的直径是一条直线。( )
A. ✓ B. ×
11. 如图,一个内直径是4cm的瓶子里,水的高度是14cm,把瓶盖拧紧倒置放平,无水部分是圆
柱形,高度是11cm.这个瓶子的容积是
mL。
12. 一根长1米,横截面直径是20厘米的木头浮在水面上,小明发现它正好是一半露出水面,请你
求出这根木头与水接触的面的面积是
平方厘米。
13. 已知长方形的长为10cm,宽为8cm,以10cm长的边所在直线为轴旋转一周,会得到一个
,它的表面积是
,体积是
。
14. 将一根高是1.5米的圆柱形木料沿直径劈成两个半圆柱后,(如图)发现表面积比原来增加了
60平方分米,原来这根木料的体积是
立方分米。
15. 一个圆柱的底面半径为4厘米,侧面展开后正好是一个正方形,这个圆柱的体积是
4. 把一根长2米的长方体木料锯成两段后,表面积增加了100平方厘米,它的体积是( ) A. 100立方厘米 B. 10000立方厘米 C. 2立方分米
5. 用三根同样长的铁丝,分别围成一个圆、一个长方形和一个三角形,围成的( )面积最大。 A. 三角形 B. 圆 C. 长方形
6. 图中瓶底的面积和圆锥形杯口的面积相等,将瓶子中的液体倒入圆锥形杯子中,能倒满( ) 杯。
。
16. 一个圆柱的底面面积是5cm2 , 它的高是10cm,则它的体积是
cm3。
17. 一个周长为62.8m的圆形花坛,要在花坛周围铺一条1.5m的小路,这条路的面积是多少m2?
18.
在比例尺是
1 1000
的图纸上,量得一个圆形花坛的直径是1厘米。这个花坛实际占地面积是多少
平方米?
19. 九河路中间的圆形大转盘,周长是251.2米,这个大转盘占地面积是多少平方米?
小升初数学图形与几何知识点分类复习《常见的立体图形》一大题量附答案
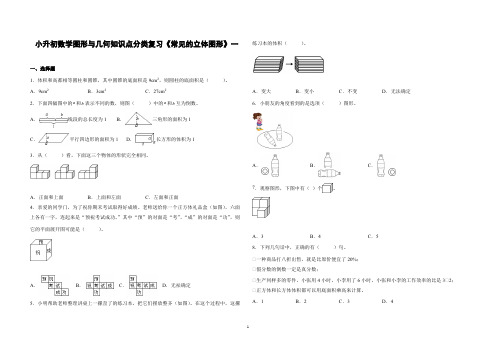
从正面看是 ,从左面看是 。
故答案为:A
【点睛】
本题考查了观察物体,能从三视图中将几何体还原是解题的关键。
12.D
【分析】
两面涂色的小正方体在大正方体的每条棱上除去两端的两个,正方体有12条棱,两面涂色的正方体的个数为:12×(4-2)个,计算出结果,即可解答。
【详解】
12×(4-2)
=12×2
46.一节通风管长1米,宽和高都是0.1米,做5节这样的通风管至少需要( )平方米铁皮。
47.把一个表面涂色的正方体每条棱都平均分成4份,切成同样大小的小正方体,3面涂色的小正方体有( )个,2面涂色的有( )个。
48.观察立体图形,下面的三幅图分别是从上面、左面和正面中的哪个方向看到的?填一填。
( ) ( ) ( )
根据分析可知,长方体酸奶盒体积:
4×5×10
=20×10
=200(立方厘米)
200立方厘米=200毫升
净含量<200毫升
故答案选:B
【点睛】
本这题考查长方体体积公式的应用,以及单位名数的互换,关键明确净含量要小于这个包装的体积。
11.A
【分析】
根据从正面和左面看到的图形,对比各选项中的几何体,直接选出正确选项即可。
49.数一数。
( )个, ( )个, ( )个, ( )个。
50.如图,把一个圆柱切成若干等份,拼成一个近似的长方体,圆柱的侧面积是( ) 。
四、作图题
51.在下图中画出长为3厘米,宽为2厘米,高为1厘米的长方体无盖纸盒的展开图(表格中每个小方格的边长为1厘米)。
五、解答题
52.一种常见的玩具陀螺是由圆柱和圆锥两部分组成的,圆柱的底面直径是4厘米,高是3厘米,圆锥的高是1.5厘米。
小升初数学图形与几何知识点分类复习《图形拼组问题》大题量附答案

小升初数学图形与几何知识点分类复习《图形拼组问题》一、选择题1.想要把一个长方形纸板剪成2个长方形纸板后,剪成的两个长方形纸板周长的和与原来长方形纸板的周长相比()。
A.增加了B.减少了C.与原来相等2.用两个完全一样的直角三角形拼成一个平行四边形,可以拼成两种平行四边形,问拼成的两个平行四边形面积相等吗?()A.相等B.不相等C.无法确定3.两个()的三角形可以拼成一个平行四边形。
A.形状相同B.面积相等C.周长相等D.等底等高4.两个周长是12厘米的正方形,拼成一个长方形,这个长方形的周长是()厘米。
A.24B.96C.185.把一个长10cm、宽8cm、高6cm的长方体,切成两个相等的长方体,它们的表面积之和比原来最多增加()平方厘米。
A.480B.160C.96D.806.先放两个正方体,在两个正方体的上面放两个圆柱,在两个圆柱的上面放一个长方体,在长方体上面放一个球,放对了的是()。
A.①B.①C.①7.在一张长方形纸上剪一刀,把它分成两部分,这两部分的形状不可能是()。
A.直角三角形B.等边三角形C.正方形D.直角梯形8.用20个相同的小正方形可以拼成()种长方形,20的因数有()个。
A.3;6B.4;5C.4;6D.5;69.左边的图形是用()个组成的。
A.4B.5C.610.把一张长方形的纸对折三次,折痕间的关系是()。
A.互相平行B.互相垂直C.可能互相平行,也可能互相垂直11.两个()的梯形一定能拼成一个平行四边形。
A.面积相等B.形状相同C.完全一样12.认真观察下图,共有()个。
A.6B.7C.813.以下几个图形中,不能单独密铺的是()。
A.B.C.D.14.下图中的大长方形是由4个完全相同的长方形拼成的,那么阴影部分与空白部分的面积比是()。
A.3①4B.4①5C.3①8D.3①515.一根绳子对折2次后,每段长4米,对折3次后,每段长()。
A.2米B.4米C.8米16.把一张圆形纸片剪拼成一个近似的梯形(如图),这个梯形的上、下底之和相当于圆的()。
六年级小升初数学总复习【图形与几何】专题训练(解析卷)

六年级小升初数学总复习【图形与几何】专题训练(解析卷)六年级小升初数学总复【图形与几何】专题训练【解析卷】直线型面积】1.在图中,平行四边形ABCD的边BC长10厘米,直角三角形ECB的直角边EC长8厘米。
已知阴影部分的总面积比三角形EFG的面积大10厘米2,求平行四边形ABCD的面积。
解答:因为阴影部分比三角形EFG的面积大10厘米2,都加上梯形FGCB后,根据差不变性质,所得的两个新图形的面积差不变,即平行四边形ABCD比直角三角形ECB的面积大10厘米2,所以平行四边形ABCD的面积等于10×8÷2+10=50(厘米2)。
2.图中,CA=AB=4厘米,三角形ABE比三角形CDE的面积大2厘米,求CD的长。
解答:连结CB。
三角形DCB的面积为4×4÷2-2=6(厘米2),CD=6÷4×2=3(厘米)。
3.有红、黄、绿三块同样大小的正方形纸片,放在一个正方形盒的底部,它们之间互相叠合。
已知露在外面的部分中,红色面积是20,黄色面积是14。
绿色面积是10,求正方形盒子底部的面积。
解答:把黄色正方形纸片向左移动并靠紧盒子的左边。
由于三个正方形纸片面积相等,所以原题图可以转化成下页右上图。
此时露出的黄、绿两部分的面积相等,都等于(14+10)÷2=12.因为绿:红=A∶黄,以是绿×黄=红×A,A=绿×XXX÷红12×12÷20=7.2.正方形盒子底部的面积是红+黄+绿+A=20+12+12+7.2=51.2.三角形的等积变换】:4.如左下图是两个相同的直角三角形叠在一起组成的,求阴影部分的面积。
单位:分米)谜底:32.5平方分米。
拓展:如图所示,已知正方形ABCD和正方形EFGC,且正方形EFGC的边长为6厘米,请问图中阴影部分面积是多少?答案:18平方厘米。
5.如图所示,在平行四边形ABCD中,DE=EF=FC,BG=GD.已知三角形GEF的面积是4平方厘米,求平行四边形的面积。
小升初总复习资料-图形与几何部分(1)图形的认识

图形与几何部分(1)图形的认识知识点:认识平行四边形1.()的两个梯形一定能拼成一个平行四边形。
[A]形状一样 [B]面积相等 [C]完全相同 [D] 任意2.两个完全一样的锐角三角形,可以拼成一个()。
[A] 长方形[B] 正方形[C] 平行四边形 [D] 梯形3.先画出这个平行四边形的一条高,再量出它的底和高各是多少厘米(取整厘米数)。
a=( )厘米 h=()厘米4.先观察下图,然后在三角形右边画出一个平行四边形 (用阴影表示),使平行四边形面积是三角形面积的2倍。
5.用木条钉成一个长方形,沿对角线拉成一个平行四边形。
这个平行四边形与原来的长方形相比:平行四边形的周长(),平行四边形面积()。
(括号里填“变大”、“变小”或“不变”)6.下面哪些图形是平行四边形?画出每个平行四边形的高。
7.如图,在平行四边形中,已知∠1=40 ,其他各个内角的度数分别是()、()、()。
知识点:认识梯形1. 两个()梯形可以拼成一个长方形。
[A] 等底等高[B]完全一样[C] 完全一样的直角 [D] 任意2.把一个平行四边形任意分割成两个梯形,这两个梯形的()总是相等的。
[A]高[B] 面积 [C] 上下两底的和 [D] 周长3.在一个等腰梯形中画一条线段,可以将它分割成两个完全一样的()。
[A]梯形[B] 平行四边形 [C] 三角形 [D] 长方形4. 右图中有()个平行四边形,()个梯形。
5. 按要求在下面图形中画一条线段,分成一个平行四边形和一个梯形知识点:三角形1.用木条给一个长方形窗户加固,若只考虑加固效果的话,采用()最好。
[B][A]2.在一个平行四边形内画一个最大的三角形,这个三角形的面积是这个平行四边形面积的()。
3.任意一个三角形都有( )条高。
4.在下面方格中画出一个与已知长方形面积相等的三角形(每个小方格代表1平方厘米)。
5.一个三角形中至少有()个锐角。
6.已知图中的三角形是原三角形面积的一半,请你把原来的三角形画完整。
小升初数学总复习归类精讲-第二章图形与几何(一)图形的认识和测量-平面图形的周长和面积 全国通用

平面图形的周长和面积课标要求1.掌握长方形、正方形的周长和面积计算公式,并能解决简单的实际问题,会估计给定的简单图形或不规则图形的面积。
2.掌握三角形、平行四边形、梯形的面积公式,并能解决简单的实际问题。
3.掌握圆、扇形的周长和面积的计算公式,并能解决简单的实际问题。
4.初步运用割、补、平移、旋转等数学方法,综合运用学过的周长、面积公式求组合图形的周长和面积。
考点1 长方形正方形的周长和面积计算1. 用边长是5厘米的两个正方形,拼成一个长方形,拼成的长方形的周长是( )厘米,面积是( )平方厘米。
2. 用两个完全一样的直角三角形拼成一个面积是20平方分米的长方形,已知直角三角形的一条直角边是8分米,则另一条直角边是( )分米。
3. 一张正方形纸先上下对折一次,再左右对折一次,得到的图形是( )形,它的面积是原来正方形的( ),它的周长是原来正方形的多少( )。
4. 下图中大圆的半径是5厘米,小圆的半径是3厘米。
长方形的周长是( )厘米。
5. 长方形的长和宽分别是a 分米、b 分米(a 、b 是不同的自然数),如果长方形的周长是200分米,那么长方形的面积是( )平方分米。
6. 一张正方形纸的边长是12厘米,在它的一个角上剪去一个长4厘米、宽3厘米的长方形后(长方形的边与正方形的边分别平行),剩余图形的周长是( )厘米。
7. 一个长方形的周长是72厘米,如果它的宽增加 ,长减少 ,周长仍和原来一样。
那么原来这个长方形的面积是( )。
8. 一个等腰三角形底和高的比是8:3,把它沿着底边上的高剪开,拼成一个长方形,这个长方形的面积是192平方厘米,长方形的周长是( )厘米。
419.选择(1)如下图,每个小正方形的面积是2cm2,涂色部分的面积是()cm2。
A.32B.24C.20D.10时(2)如下图,将四张长为16厘米、宽为2厘米的长方形纸条垂直相交平放在桌面上,则桌面被覆盖部分的面积是()。
A.72cm2B.128cm2C.124cm2D.112cm2(3)一根彩绳和A、B、C三个钉子围成如下图所示的三角形。
北师大版六年级下册数学小升初《图形与几何》复习检测(含答案)

六年级数学小升初《图形与几何》复习检测班级:学号:姓名: 成绩:一.填空题(每空1分,共25分)1.6.23m3=()dm3,3.5dm2=()m22.3点15分时针与分针成()度的角。
3.一个等腰三角形的底角是80°,它的顶角是()。
4.一个长方体水缸,长20厘米,宽15厘米,水深6厘米,将一块石头投入水中(石头完全浸入水)水面上升到8厘米,这块石头的体积是()立方厘米。
5.棱长 1 分米的正方体水缸装满水,往缸里放一块石头,缸里的水还剩35,根据以上信息,算出石头的体积应是()立方分米。
6.用圆规画一个周长是12.56厘米的圆,圆规两脚尖的距离应为()厘米.在一张长20厘米,宽15厘米的白纸上画这样的圆(圆不交叉重叠),最多能画()个。
7.一个平行四边形的面积是5.6平方米,高是2米,底是()米。
8.一个立体图形从正面看到的形状是,从左面看到的形状是,要搭成这个立体图形,至少要用( )个小正方体,最多可以用( )个小正方体。
9.在比例尺1:5000000的地图上,量得两地的距离是8厘米,两地的实际距离是()千米。
10.用6个边长是1平方厘米的正方形拼成长方形,长是()厘米,宽是()厘米,周长是()厘米。
11.一块平行四边形土地,底长250米,高80米,这块土地的面积是()公顷。
12.一个半径是4厘米的圆,按2:1的比放大后,放大后的圆的面积是()平方厘米;如果按()的比缩小后,圆的面积是3.14平方厘米。
13.小军将一张正方形纸对折两次,如下图所示,并在中央点打孔,再将它展开,请在括号里画出展开的图形。
14.一块平行四边形菜地,底是32.5分米,高是15.4分米.如果每平方米能收8千克青菜。
这块菜地一共可以收()千克青菜。
16.小明在一长方形纸上剪下一个面积最大的三角形,三角形面积与长方形面积的比是(),剪法有()种。
17.一个棱长8分米的正方体水缸,水深6分米,如放入一块石头完全浸入水中,水溢出18升,则石头的体积是()立方分米。
六年级小升初毕业考试总复习——几何图形专项复习(附答案)

六年级⼩升初毕业考试总复习——⼏何图形专项复习(附答案)六年级⼩升初毕业考试——⼏何图形专项训练→→→圆锥圆柱正⽅体长⽅体⽴体图形扇形圆环圆梯形正⽅形长⽅形平⾏四边形四边形三⾓形平⾯图形⼏何图形⼀、平⾯图形知识要点:1. 三⾓形(1)三⾓形具有稳定性。
(2)三⾓形的内⾓和是180°。
(3)三⾓形三边关系:在⼀个三⾓形中,任意两边之和⼤于第三边,任意两边之差⼩于第三边。
(4)三⾓形的⾯积=底×⾼÷22.四边形(1)长⽅形的周长=(长+宽)×2 长⽅形的⾯积=长×宽(2)正⽅形的周长=边长×4 正⽅形的⾯积=边长×边长(3)平⾏四边形的⾯积=底×⾼(4)梯形的⾯积=(上底+下底)×⾼÷23.圆(1)圆的周长:c=πd c=2πr 圆的⾯积:s=πr 2(2)圆环的⾯积=外圆⾯积-内圆⾯积 s=πR 2-πr 2或 s=π(R 2-r 2)(3)扇形的周长=半径×2+弧长 c=2r+2πr ×360οοn扇形的⾯积=圆⾯积×360οοn s=πr 2×360οοn28m 近似三⾓形了,真有意思!1.(西城2019年⼩学毕业数学测查卷)⼀个⽤草绳编织成的茶杯垫的上⾯是圆形,将它沿半径剪开,下⾯说法不正确...的是(). A.近似三⾓形的底相当于圆的周长 B.近似三⾓形的⾼相当于圆的半径 C.近似三⾓形的⾯积相当于圆的⾯积 D.近似三⾓形的⾯积相当于圆⾯和的212.(西城2019年⼩学毕业数学测查卷)⼀个长⽅体,有两个相对的⾯是正⽅形。
它的长是8cm.宽是5cm.这个长⽅体的表⾯积最少是( )cm 2.A.130B. 200C.210D. 2883.(西城2019年⼩学毕业数学测查卷)如下图⼩圆贴着⼤圆的内侧从A 点开始按箭头所指⽅向滚动(⼤圆不动....)。
图1 图2 图3①⼩圆⾃⾝⾄少需要滚动多少周才能回到A 点? (⽤你喜欢的⽅式说明理由)②⼩圆经过滚动回到A 点,请在图3中⽤圆规画出圆⼼......⾛过的轨迹。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.圆的半径扩大倍,这个圆的面积扩大( )
A.
B.
C.2.正方体的棱长扩大到原来的倍,它的表面积扩大到原来的( )。
A.
倍B.
倍C.倍
3.所有的车轮都做成圆形是利用了圆的( )特性。
A.曲线图形
B.容易加工
C.圆心到圆上任意一点的距离相等
4.圆柱的底面半径扩大倍,高也扩大倍,则该圆柱的体积扩大( )倍。
A.
B.
C.D.无法确定
5.
在下图中,以直线为轴旋转,可以得到圆柱体的是( )。
A.
B.
481216
224622238
C.
D.
6.一个圆柱,底面直径和高都是分米,这个圆柱的表面积是( )平方分米。
A.
B.
C.7.用一根同样长的铁丝分别围成长方形、正方形和圆,( )面积最大。
A.长方形
B.正方形
C.圆
D.无法比较
8.把一根棱长分米的正方体木料加工成一个最大的圆柱,这个圆柱的体积是
立方分米,
表面积是平方分米。
9.一块圆柱形橡皮泥,从侧面观察是一个边长为厘米的正方形,这个圆柱的表面积是
平
方厘米;如果把它捏成一个圆锥,这个圆锥的体积是立方厘米。
10.用一张边长是的正方形纸,剪成一个最大的圆,这个圆的周长是
,剪去圆后剩余的面积是。
11.求阴影的面积。
26π5π4π
446dm cm dm 2
12.一个长厘米,宽厘米的长方形,按的比放大,得到的长方形的周长是厘米,面
积是平方厘米。
13.一个三角形三个角的比是,最大的角是度。
14.把一个直径是厘米的圆分成若干等份,然后把它剪开,照如图的样子拼起来,周长是
,面积是。
15.在一个长厘米,宽厘米的长方体玻璃缸中,放入一个棱长为厘米的正方体铁块,这时水深为厘米,如果把这块铁从缸中取出,缸中的水深是多少厘米?
16.手工课上,小红用一张直径是的圆形纸片剪出如图所示的风车图案(空白部分),则被剪掉的纸片(阴影部分)的面积是多少?
17.一个长方体的所有棱长之和是厘米,长、宽、高的比是,这个长方体的体积是多
少?18.一个无盖的长方体玻璃鱼缸,长厘米,宽厘米,高厘米。
433
:13:4:54cm 5040102020cm 483
:2:1504030。
