湘教版数学九年级下册期末检测卷
湘教版九年级数学下册期末试卷及答案【完整版】

湘教版九年级数学下册期末试卷及答案【完整版】 班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.估计7+1的值在( )A .2和3之间B .3和4之间C .4和5之间D .5和6之间2.已知31416181279a b c ===,,,则a b c 、、的大小关系是( )A .a b c >>B .a c b >>C .a b c <<D .b c a >>3.若|321|20x y x y --++-=,则x ,y 的值为( )A .14x y =⎧⎨=⎩B .20x y =⎧⎨=⎩C .02x y =⎧⎨=⎩D .11x y =⎧⎨=⎩4.用配方法解方程2890x x ++=,变形后的结果正确的是( )A .()249x +=-B .()247x +=-C .()2425x +=D .()247x += 5.在数轴上,点A ,B 在原点O 的两侧,分别表示数a ,2,将点A 向右平移1个单位长度,得到点C .若CO=BO ,则a 的值为( )A .-3B .-2C .-1D .16.用配方法解方程2x 2x 10--=时,配方后所得的方程为( )A .2x 10+=()B .2x 10-=()C .2x 12+=()D .2x 12-=()7.如图,函数221y ax x =-+和y ax a =-(a 是常数,且0a ≠)在同一平面直角坐标系的图象可能是( )A .B .C .D .8.如图,⊙O 中,半径OC ⊥弦AB 于点D ,点E 在⊙O 上,∠E=22.5°,AB=4,则半径OB 等于( )A .2B .2C .22D .39.如图,函数 y 1=﹣2x 与 y 2=ax +3 的图象相交于点 A (m ,2),则关于 x 的不等式﹣2x >ax +3 的解集是( )A .x >2B .x <2C .x >﹣1D .x <﹣1 10.如图,矩形ABCD 的对角线AC ,BD 交于点O ,6AB =,8BC =,过点O 作OE AC ⊥,交AD 于点E ,过点E 作EF BD ⊥,垂足为F ,则OE EF +的值为( )A .485B .325C .245D .125二、填空题(本大题共6小题,每小题3分,共18分)1.计算:23a a ⋅=______________.2.分解因式:x 2﹣9x =________.3.已知关于x 的分式方程233x k x x -=--有一个正数解,则k 的取值范围为________.4.如图,四边形ACDF 是正方形,CEA ∠和ABF ∠都是直角,且点,,E A B 三点共线,4AB =,则阴影部分的面积是__________.5.如图,△ABC 中,AB=BC ,∠ABC=90°,F 为AB 延长线上一点,点E 在BC 上,且AE=CF ,若∠BAE=25°,则∠ACF=__________度.6.在平面直角坐标系中,四边形AOBC 为矩形,且点C 坐标为(8,6),M 为BC 中点,反比例函数k y x=(k 是常数,k ≠0) 的图象经过点M ,交AC 于点N ,则MN 的长度是__________.三、解答题(本大题共6小题,共72分)1.解分式方程:214111x x x ++=--2.已知关于x 的一元二次方程:x 2﹣2x ﹣k ﹣2=0有两个不相等的实数根.(1)求k 的取值范围;(2)给k 取一个负整数值,解这个方程.3.已知:如图,平行四边形ABCD ,对角线AC 与BD 相交于点E ,点G 为AD 的中点,连接CG ,CG 的延长线交BA 的延长线于点F ,连接FD .(1)求证:AB=AF;(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.4.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE,(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.5.某校为了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱乐器),现将收集到的数据绘制如下的两幅不完整的统计图.(1)这次共抽取学生进行调查,扇形统计图中的x .(2)请补全统计图;(3)在扇形统计图中“扬琴”所对扇形的圆心角是度;(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有名.6.山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:(1)每千克核桃应降价多少元?(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、B2、A3、D4、D5、A6、D7、B8、C9、D10、C二、填空题(本大题共6小题,每小题3分,共18分)1、a52、x(x-9)3、k<6且k≠34、85、706、5三、解答题(本大题共6小题,共72分)1、3x=-2、(1)k>﹣3;(2)取k=﹣2, x1=0,x2=2.3、(1)略;(2)结论:四边形ACDF是矩形.理由略.4、解:(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,∴四边形AEBD是平行四边形.∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC.∴∠ADB=90°.∴平行四边形AEBD是矩形.(2)当∠BAC=90°时,矩形AEBD是正方形.理由如下:∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,∴AD=BD=CD.∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.5、(1)200,15%;(2)统计图如图所示见解析;(3)36;(4)900.6、(1)4元或6元;(2)九折.。
湘教版九年级下册数学试题 期末质量评估试卷(一)(含答案)
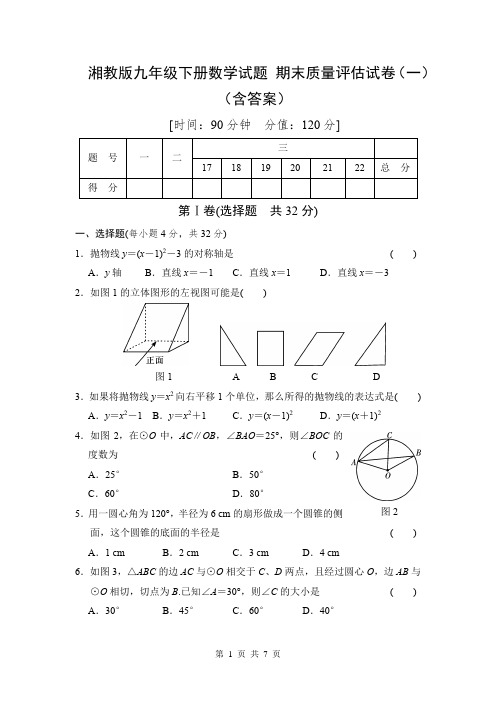
湘教版九年级下册数学试题期末质量评估试卷(一)(含答案)[时间:90分钟分值:120分]题号一二三171819202122总分得分第Ⅰ卷(选择题共32分)一、选择题(每小题4分,共32分)1.抛物线y=(x-1)2-3的对称轴是() A.y轴B.直线x=-1 C.直线x=1 D.直线x=-32.如图1的立体图形的左视图可能是()图1A B C D3.如果将抛物线y=x2向右平移1个单位,那么所得的抛物线的表达式是() A.y=x2-1 B.y=x2+1 C.y=(x-1)2D.y=(x+1)24.如图2,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为()A.25°B.50°C.60°D.80°5.用一圆心角为120°,半径为6 cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是() A.1 cm B.2 cm C.3 cm D.4 cm6.如图3,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是() A.30°B.45°C.60°D.40°图2图3图47.如图4所示,在平面直角坐标系中,二次函数y =ax 2+bx +c 的图象顶点为A (-2,-2),且过点B (0,2),则y 与x 的函数关系式为( )A .y =x 2+2B .y =(x -2)2+2C .y =(x -2)2-2D .y =(x +2)2-28.从1、2、3、4中任取两个不同的数,其乘积大于4的概率是( )A.16B.13C.12D.23第Ⅱ卷(非选择题 共88分)二、填空题(每小题4分,共32分)9.下列事件:①打雷后会下雨;②明天是晴天;③1小时等于60分钟;④从装有2个红球,2个白球的袋子中摸出一个蓝球.其中是确定性事件的是________.(填序号)10.如图5,对称轴平行于y 轴的抛物线与x 轴交于(1,0)、(3,0)两点,则它的对称轴为____________.图5图611.二次函数y =x 2-2x -3的图象如图6所示.当y <0时,自变量x 的取值范围是____________.12.如图7,在⊙O中,弦AB垂直平分半径OC,垂足为D,若☉O的半径为2,则弦AB的长为______.图7图813.某涵洞是抛物线形,如图8所示,现测得水面宽AB=8 m,涵洞顶点O到水面的距离为12 m,在图中的平面直角坐标系内,涵洞所在抛物线的函数解析式是____________.14.如图9,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=54°,则∠BAC的度数等于________.图9图1015.在一个不透明的口袋中,有3个完全相同的小球,他们的标号分别是2、3、4,从袋中随机地摸取一个小球然后放回,再随机的摸取一个小球,则两次摸取的小球标号之和为5的概率是__________.16.如图10,有一直径是 2 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:(1)AB的长为________m;(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为________m.三、解答题(共6小题,满分56分)17.(8分)如图11,AC ︵=CB ︵,D 、E 分别是半径OA 和OB 的中点,CD 与CE 的大小有什么关系?为什么?图1118.(8分)已知抛物线y =-x 2+bx +c 经过点A (3,0)、B (-1,0). (1)求抛物线的解析式; (2)求抛物线的顶点坐标.19.(8分)一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.(1)从袋中摸出一个球是黄球的概率;(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是13,求从袋中取出黑球的个数.20.(10分)已知二次函数y=x2-4x+3.(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;(2)求函数图象与x轴的交点A、B的坐标,及△ABC的面积.图1221.(10分)如图13,矩形ABCD的两边长AB=18 cm,AD=4 cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以2 cm/s的速度匀速运动,Q 在边BC上沿BC方向以1 cm/s的速度匀速运动,设运动时间为x s,△PBQ 的面积为y cm2.(1)求y关于x的函数关系式,并写出x的取值范围;(2)求△PBQ的面积的最大值.图1322.(12分)如图14,AB 是⊙O 的直径,点F 、C 是⊙O 上两点,且AF ︵=FC ︵=CB ︵,连接AC 、AF ,过点C 作CD ⊥AF 交AF 延长线于点D ,垂足为D . (1)求证:CD 是⊙O 的切线; (2)若CD =23,求⊙O 的半径.图14参考答案1.C 2.A 3.C 4.B 5.B 6.A7.D8.C 9.③④10.直线x=211.-1<x<312.2313.y=-34x214.36°15.2916.(1)1(2)1417.CD=CE,理由略.18.(1)y=-x2+2x+3;(2)抛物线的顶点坐标为(1,4).19.(1)从袋中摸出一个球是黄球的概率为1 4;(2)从袋中取出黑球的个数为2个.20.(1)顶点C的坐标是(2,-1),当x≤2时,y随x的增大而减少;当x>2时,y随x的增大而增大;(2)A点的坐标是(1,0),B点的坐标是(3,0),S△ABC=1. 21.(1)y=-x2+9x(0<x≤4);(2)△PBQ的最大面积是20 cm2.22.(1)证明略(2)⊙O的半径为4.。
湘教版九年级下册数学期末测试卷及含答案

湘教版九年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图仔细观察其中的两个尺规作图痕迹,两直线相交于点O,则下列说法中不正确的是()A.EF是△ABC的中位线B.∠BAC+∠EOF=180°C.O是△ABC的内心D.△AEF的面积等于△ABC的面积的2、如图,PA,PB分别切⊙O于点A,曰,PA=12,CD切⊙O于点E,交削,PB 于点C,D两点,则△PCD的周长是()A.12B.18C.24D.303、如图,扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为()A.3 πB.C.D.4 π4、已知如图抛物线y=ax2+bx+c,下列式子正确的是()A.a+b+c<0B.b 2﹣4ac<0C.c<2bD.abc>05、对称轴平行于y轴的抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )A.y =-2x 2 + 8x +3B.y =-2x 2–8x +3C.y = -2x 2 + 8x –5 D.y =-2x 2–8x +26、某学校在进行防溺水安全教育活动中,将以下几种在游泳时的注意事项写在纸条上并折好,内容分别是:①互相关心;②互相提醒;③不要相互嬉水;④相互比潜水深度;⑤选择水流湍急的水域;⑥选择有人看护的游泳池.小颖从这6张纸条中随机抽出一张,抽到内容描述正确的纸条的概率是()A. B. C. D.7、已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有2个,黑球有n个,随机地从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,经过大量重复试验发现摸出白球的频率稳定在0.4附近,则n的值为()A.2B.3C.4D.58、已知二次函数y=kx2-7x-7的图象和x轴有交点,则k的取值范围是()A.k>-B.k>- 且k≠0C.k≥-D.k≥- 且k≠09、如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是()A.CE=DEB.AE=OEC.D.△OCE≌△ODE10、将抛物线y =(x-4)2+2向右平移1个单位,再向下平移3个单位,则平移后抛物线的表达式为()A.y =(x-3) 2+5B.y =(x-3) 2-1C.y =(x-5) 2+5D.y =(x-5) 2-111、下列事件中,必然事件是( )、A.打开电视,它正在播广告B.掷两枚质地均匀的正方体骰子,点数之和一定大于6C.早晨的太阳从东方升起D.没有水分,种子发芽12、抛物线y=ax2﹣2ax+4(a>0),下列判断正确的是( )A.当x>2时,y随x的增大而增大B.当x<2时,y随x的增大而增大 C.当x>1时,y随x的增大而增大 D.当x<1时,y随x的增大而增大13、下列说法中,正确的是()A.将一组数据中的每一个数据都加同一个正数,方差变大B.为了解全市同学对书法课的喜欢情况,调查了某校所有女生C.“任意画出一个矩形,它是轴对称图形”是必然事件D.为了审核书稿中的错别字,选择抽样调查14、如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是()A.△ACD的外心B.△ABC的外心C.△ACD的内心D.△ABC的内心15、如图,⊙O的直径CD⊥AB,∠AOC=50°,则∠CDB大小为()A.25°B.30°C.40°D.50°二、填空题(共10题,共计30分)16、如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC= ________度.17、如图,在⊙O中,圆心角∠AOB=120°,弦AB=2 cm,则⊙O的半径是________.18、把抛物线先向上平移2个单位,再向右平移3个单位,所得抛物线的解析式为________19、如图,中,为的中点,以为圆心,长为半径画一弧交于点,若,,,则扇形的面积为________.20、在一个不透明的布袋中有除颜色外其它都相同的红、黄、蓝球共200个,某位同学经过多次摸球试验后发现,其中摸到红色球和蓝色球的频率稳定在35%和55%,则口袋中可能有黄球________个.21、如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为________ cm2.22、小李和小王在拼图游戏中,从如图三张纸片中任取两张,如拼成房子,则小李赢;否则,小王赢.你认为这个游戏公平吗?________(填“公平”或“不公平”)23、△ABC中,∠A=40°,若点O是△ABC的外心,则∠BOC=________°;若点I是△ABC的内心,则∠BIC=________°.24、对某批乒乓球的质量进行随机抽查,结果如下表所示:随机抽取的乒乓球数优等品数优等品率当越大时,优等品率趋近于概率________.(精确到)25、一个圆的半径为2,那么它的弦长d的取值范围________.三、解答题(共5题,共计25分)26、圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。
(全优)湘教版九年级下册数学期末测试卷及含答案(适用考试)

湘教版九年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、甲箱装有40个红球和10个黑球,乙箱装有60个红球、40个黑球和50个白球.这些球除了颜色外没有其他区别.搅匀两箱中的球,从箱中分别任意摸出一个球.正确说法是().A.从甲箱摸到黑球的概率较大B.从乙箱摸到黑球的概率较大C.从甲、乙两箱摸到黑球的概率相等D.无法比较从甲、乙两箱摸到黑球的概率2、在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣1(m>0)与x轴的交点为A,B.若横、纵坐标都是整数的点叫做整点,当抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,可得m的取值范围为()A. <m≤B. ≤m<C.0<m<D.0<m≤3、一个几何体由几个大小相同的小正方体搭成,其左视图和俯视图如图所示,则搭成这个几何体的小正方体的个数是A.3B.4C.5D.64、抛物线y=-2(x-3)2-4的顶点坐标是()A.(3,4)B.(-3,4)C.(3,-4)D.(2,4)5、将抛物线向左平移个单位,再向下平移个单位后所得抛物线的解析式为()A. B. C. D.6、抛掷一个质地均匀的正方体玩具(它的每个面上分别标有数字1,2,3,4,5,6),它落地时向上的数是3的概率是()A. B.1 C. D.7、抛物线经过点与,若,则b的最小值为()A.2B.C.4D.8、小张同学去展览馆看展览,该展览馆有2个验票口A、B(可进出),另外还有2个出口C、D(不许进).小张不从同一个验票口进出的概率是多少()A. B. C. D.9、下列说法中,正确的是()A.生活中,如果一个事件不是不可能事件,那么它就必然发生B.生活中,如果一个事件可能发生,那么它就是必然事件C.生活中,如果一个事件发生的可能性很大,那么它也可能不发生D.生活中,如果一个事件不是必然事件,那么它就不可能发生10、图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是()A.甲先到B点B.乙先到B点C.甲、乙同时到BD.无法确定11、如图,在等边三角形ABC中,点P是BC边上一动点(不与点B,C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是()A. B. C.D.12、如图,一张半径为1的圆形纸片在边长为的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是()A. B.4-π C.π D.13、有长24m的篱笆,一面利用围墙围成如图中间隔有一道篱笆的矩形花圃,设花圃的垂直于墙的一边长为x m,面积是s m2,则s与x的关系式是()A.s=﹣3x 2+24xB.s=﹣2x 2﹣24xC.s=﹣3x 2﹣24x D.s=﹣2x 2+24x14、一个扇形的圆心角为60°,弧长为2π厘米,则这个扇形的半径为()A.6厘米B.12厘米C. 厘米D. 厘米15、如图,二次函数的图象如图所示,下列结论:①;②;③一元二次方程有两个不相等的实数根;④当或时,.上述结论中正确的个数是()A.1个B.2个C.3个D.4个二、填空题(共10题,共计30分)16、如图,从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为________m.17、若⊙A的半径为5,圆心A的坐标为(3,4),点P的坐标是(5,8),则点P在⊙A________.18、已知抛物线y=x2﹣k的顶点为P,与x轴交于点A,B,且△ABP是正三角形,则k的值是________.19、已知△ABC的外心为O,内心为I,∠BOC=120°,∠BIC=________.20、如图,利用成直角的墙角(墙足够长),用10m长的栅栏围成一个矩形的小花园,花园的面积S(m2)与它一边长a(m)的函数关系式是________,面积S的最大值是________.21、AB是半圆O的直径,AB=8,点C为半圈上的一点将此半圆沿BC所在的直线折叠,若配给好过圆心O,则图中阴影部分的面积是________.22、如图是二次函数y=ax2+bx+c的部分图像,在下列四个结论中正确的是________.①不等式ax2+bx+c>0的解集是-1<x<5;②a-b+c>0;③b2-4ac>0;④4a+b <0.23、如图,AB是⊙O的直径,点C,D都在⊙O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AB的长是________.24、将二次函数化为的形式,则________.25、如图,AB为☉O的切线,切点为B,连接AO,AO与☉O交于点C,BD为☉O的直径,连接CD.若∠A=30°,☉O的半径为2,则图中阴影部分的面积为________.三、解答题(共5题,共计25分)26、篮球课上,朱老师向学生详细地讲解传球的要领时,叫甲、乙、丙、丁四位同学配合朱老师进行传球训练,朱老师把球传给甲同学后,让四位同学相互传球,其他人观看体会,当甲同学第一个传球时,求甲同学传给下一个同学后,这个同学再传给甲同学的概率27、如图,直线y= 与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,求横坐标为整数的点P的个数.28、”4.20芦山地震”发生后,各地积极展开抗震救援工作,一支救援车队经过如图1所示的一座拱桥,拱桥的轮廓是抛物线型,拱高6m,跨度20m,相邻两支柱间的距离均为5m,将抛物线放在所给的直角坐标系中(如图2所示),拱桥的拱顶在y轴上.(1)求拱桥所在抛物线的解析式;(2)求支柱MN的长度;(3)拱桥下地平面是双向行车道(正中间是一条宽2米的隔离带),其中的一条行车道能否并排行驶宽2m、高2.4m的三辆汽车(隔离带与内侧汽车的间隔、汽车间的间隔、外侧汽车与拱桥的间隔均为0.5m)?请说说你的理由.29、珍珍与环环两人一起做游戏,游戏规则如下:每人从1,2,3,4,5,6,7,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于她们各自选择的数,就再做一次上述游戏,直到决出胜负.若环环事先选择的数是5,用列表法或画树状图的方法,求她获胜的概率.30、已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).(1)求b、c的值;(2)求出该二次函数图象的顶点坐标和对称轴,并在所给坐标系中画出该函数的图象;(3)该函数的图像经过怎样的平移得到y=x2的图像?参考答案一、单选题(共15题,共计45分)1、B2、A3、B4、C5、C6、D7、D8、D9、C10、C11、C12、B13、A14、A15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、30、。
湘教版九年级下册数学期末测试卷及含答案

湘教版九年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为()A.3B.4C.D.2、把抛物线y=x2+1向右平移3个单位,再向下平移2个单位,得到抛物线()A.y=(x+3)2﹣1B.y=(x+3)2+3C.y=(x﹣3)2﹣1D.y=(x﹣3)2+33、将抛物线向左平移个单位后,再向上平移个单位,得到新抛物线的解析式为()A. B. C. D.4、如图,四边形ABCD是⊙O的内接四边形,∠ABC=100°,则∠ADC=()A.70°B.80°C.90°D.100°5、如图,在平面直角坐标系中,抛物线y=a(x-m)²+1(a<0)与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C,顶点是D,且∠DAB=45°,点C绕O逆时针旋转90°得到点C',当-2≤m≤5时,BC'的长度范围是( )A.0≤BC'≤1B.0≤BC'≤18C.1≤BC'≤D.2≤BC'≤6、已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有2个,黑球有n个.随机地从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀.经过大量重复试验发现摸出白球的频率稳定在0.4附近,则n的值为( )A.2B.3C.4D.57、如图所示是一个正方体展开图,图中六个正方形内分别标有“新”、“时”、“代”、“去”、“奋”、“斗”、六个字,将其围成一个正方体后,则与“奋”相对的字是()A.斗B.新C.时D.代8、如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为()A. B.2 C.2 D.89、如图,为的直径,弦,垂足为点,连接,若,,则的长度为()A.2B.1C.3D.410、在如图四个几何体中,主视图与俯视图都是圆的为()A. B. C. D.11、点P1(﹣1,y1),P2(3,y2),P3(5,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1, y2, y3的大小关系是()A.y3>y2>y1B.y3>y1=y2C.y1>y2>y3D.y1=y2>y312、将抛物线y=(x﹣1)2+4先向右平移4个单位长度,再向下平移3个单位长度,得到的抛物线的顶点坐标为()A.(5,4)B.(1,4)C.(1,1)D.(5,1)13、若对任意实数x,二次函数的值总是非负数,则的取值范围是()A. B. C. D.14、图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是()A.y=﹣2x 2B.y=2x 2C.y=﹣x 2D.y= x 215、在二次函数的图像中,若随的增大而增大,则的取值范围是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,AB为⊙0的直径,点C、D在⊙0上,且∠ADC=52°,则∠BAC=________°.17、小明的卷子夹里放了大小相同的试卷共12页,其中语文6页、数学4页、英语2页,他随机地从卷子夹中抽出1页,抽出的试卷恰好是数学试卷的概率为________.18、如图,若,则________,19、如图是一个正方体的表面展开图,如果正方体相对的面上标注的值相等,那么x+2y=________.20、如图,点A,B,C都在⊙O上,若OB=3,∠ABC=30°,则劣弧AC的长为________.21、二次函数y=2x2+bx+3的图象的对称轴是直线x=1,则常数b的值为________.22、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是________.23、如图,△ABC是定圆O的内接三角形,AD为△ABC的高线,AE平分∠BAC 交⊙O于E,交BC于G,连OE交BC于F,连OA,在下列结论中,①CE=2EF,②△ABG∽△AEC,③∠BAO=∠DAC,④为常量.其中正确的有________.24、将6×4的正方形网格如图所示放置在平面直角坐标系中,每个小正方形的边长为1,若点在第一象限内,且在正方形网格的格点上,若是钝角的外心,则的坐标为________.25、如图,抛物线y=x2﹣2x﹣3交x轴于A(﹣1,0)、B(3,0),交y轴于C(0,﹣3),M是抛物线的顶点,现将抛物线沿平行于y轴的方向向上平移三个单位,则曲线CMB在平移过程中扫过的面积为________(面积单位).三、解答题(共5题,共计25分)26、在四编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中机抽取一张.我们知道,满足的三个正整数a,b,c成为勾股数,请用“列表法”或“树状图法”求抽到的两张卡片上的数都是勾股数的概率(卡片用A,B,C,D表示).27、小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:(1)小明总共剪开了多少条棱?(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.28、如图,在⊙O中,,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.29、如图,某涵洞的截面是抛物线的一部分,现水面宽AB=1.6m,涵洞顶点O 到水面的距离为2.4m,求涵洞所在抛物线的解析式.30、在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:摸球的次数n 100 200 300 500 800 1000 3000摸到白球的次数m 63 124 178 302 481 599 1803摸到白球的频率0.63 0.62 0.593 0.604 0.601 0.599 0.601(1)请估计:当实验次数为5000次时,摸到白球的频率将会接近?;(精确到0.1)(2)假如你摸一次,你摸到白球的概率P(摸到白球)= ?;(3)试验估算这个不透明的盒子里黑球有多少只?参考答案一、单选题(共15题,共计45分)1、C2、C3、B4、B5、B6、B7、C8、C9、A10、D11、D12、D13、C14、C15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题,共计25分)26、29、30、。
湘教版九年级下册数学期末测试卷【参考答案】

湘教版九年级下册数学期末测试卷一、单选题(共15题,共计45分)1、如图,AB为⊙O的直径,点C在⊙O上,∠A=24°,则BC弧的度数为()A.66°B.48°C.33°D.24°2、一个袋子中装有6个黑球3个白球,这些球除颜色外,形状、大小、质地等完全相同,在看不到球的条件下,随机地从这个袋子中摸出一个球,摸到白球的概率为()A. B. C. D.3、如图,摆放的几何体的俯视图是()A. B. C. D.4、从下列四张卡片中任取一张,卡片上的图形是中心对称图形的概率为()A.0B.C.D.5、如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1, x2的值分别是()A.﹣2,1B.﹣3,1C.﹣1,1D.不能确定6、下列命题正确的个数是()①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧.A.1个B.2个C.3个D.4个7、下列函数中,不是二次函数的是()A.y=B.y=3﹣x+x 2C.y=﹣2x+3x 2D.y=(x﹣2)(x+2)﹣x 28、某一型号飞机着陆后滑行的距离S(单位:米)关于滑行的时间t(单位:秒)之间的函数解析式是S=﹣1.5t2+60t,则该型号飞机着陆后滑行()秒才能停下来.A.600B.300C.40D.209、给出下列4个命题:①相似三角形的周长之比等于其相似比;②方程x2-3x+5=0的两根之积为5;③在同一个圆中,同一条弦所对的圆周角都相等;④圆的内接四边形对角互补.其中,真命题为()A.①②④B.①③④C.①④D.①②③④10、如图,将边长相等的正方形、正五边形和正六边形摆放在平面上,则为A. B. C. D.11、如图,把抛物线y=x2沿直线y=x平移个单位后,其顶点在直线上的A 处,则平移后的抛物线解析式是()A.y=(x+1)2-1B.y=(x+1)2+1C.y=(x-1)2+1 D.y=(x-1)2-112、如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则2x﹣y的值为()A.-2B.6C.D.213、如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于()A.20°B.40°C.50°D.60°14、已知⊙O的半径为5,圆心O到直线AB的距离为6,则直线AB于⊙O的位置关系是()A.相交B.相切C.相离D.无法确定15、已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:x …-1 0 1 2 3 …y …10 5 2 1 2则当y≥5时,x的取值范围是( )A.x≤0B.0≤x≤4C.x≥4D.x≤0或x≥ 4二、填空题(共10题,共计30分)16、若二次函数的图象与x轴有且只有一个公共点,则m=________.17、在一个不透明的口袋中,有3个完全相同的小球,他们的标号分别是2,3,4,从袋中随机地摸取一个小球然后放回,再随机的摸取一个小球,则两次摸取的小球标号之和为5的概率是________.18、如图,△AOB和△ACD均为正三角形,顶点B,D在双曲线y= (x>0)上,则=________.19、如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,D为边AB的中点,以点A为圆心,以AD的长为半径画弧与腰AC相交于点E,以点B为圆心,以BD的长为半径画弧与腰BC相交于点F,则图中的阴影部分图形的面积为________.(结果保留π).20、如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,若用阴影部分围成一个圆锥,则该圆锥的底面半径为________.21、如图,有一块直角三角形土地,它两条直边米,米,某单位要沿着斜边修一座底面是矩形的大楼,、分别在边、上,这个矩形的面积最大值是________.22、二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确的结论有________.23、若△ABC的三边长为3、4、5,则△ABC的外接圆半径R与内切圆半径r的差为________.24、已知函数y= (m+3)x2+2x+1的图象与x轴只有一个公共点,则m的值为________.25、如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:3,则k值为________.三、解答题(共5题,共计25分)26、有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,从口袋中随机摸出一个小球,记下标号后放回,再从口袋中随机摸出一个小球,记下标号.用画树状图(或列表)的方法,求两次摸出的小球号码恰好都大于1的概率.27、已知,二次函数的表达式为y=4x2+8x.写出这个函数图象的对称轴和顶点坐标,并求图象与x轴的交点的坐标.28、如图,一块草地是长80 m,宽60 m的矩形,欲在中间修筑两条互相垂直的宽为xm的小路,这时草坪面积为y m2.求y与x的函数关系式,并写出自变量x的取值.29、如图,圆心角120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM 交AB于H,ON交CD于K,OM>OA.(1)证明:△AOH≌△COK;(2)若AB=2,求正六边形ABCDEF与扇形OMN重叠部分的面积.30、已知:如图,AB为⊙O的直径,OD∥AC.求证:点D平分.参考答案一、单选题(共15题,共计45分)1、B2、B3、B4、D5、B6、B7、D8、D9、C10、D11、C12、B13、B14、C15、D二、填空题(共10题,共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题,共计25分)26、27、28、。
湘教版九年级下册数学期末测试卷及含答案

湘教版九年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、已知抛物线y=-(x+3)2-5,则此抛物线的函数值有( )A.最小值-3B.最大值是-3C.最小值是-5D.最大值是-52、如图,△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,点E是线段AD上一点,以点E为圆心,r为半径作⊙E.若⊙E与边AB,AC相切,而与边BC相交,则半径r的取值范围是()A.r>B. <r≤4C. <r≤4D. <r≤3、已知二次函数y=ax2+bx+c+2的图象如图,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是()A.1B.2C.3D.44、某中学九年级舞蹈兴趣小组8名学生的身高分别为(单位:cm):168,165,168,166,170,170,176,170,则下列说法错误的是()A.这组数据的众数是170B.这组数据的中位数是169C.这组数据的平均数是169D.若从8名学生中任选1名学生参加校文艺会演,则这名学生的身高不低于170的概率为5、如图,在半径为的中,弦与交于点E,,,则CD的长是()A. B. C. D.6、如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么()A.a<0,b>0,c>0B.a>0,b<0,c>0C.a>0,b>0,c<0 D.a<0,b<0,c<07、如图,在平面直角坐标系中,已知抛物线的对称轴为,且经过点A(2,1),点是抛物线上的动点,的横坐标为,过点作轴,垂足为,交于点,点关于直线的对称点为,连接,,过点A作AE⊥x轴,垂足为E,则当()时,的周长最小.A.1B.1.5C.2D.2.58、如图,已知二次函数的部分图象与坐标轴交于A(3,0)和C(0,2)两点,对称轴为直线,当函数值>0时,自变量的取值范围是( )A. <3B.0≤<3C.-2<<3D.-1<<39、如图坐标平面上有一透明片,透明片上有一拋物线及一点P,且拋物线为二次函数y=x2的图形,P的坐标(2,4)。
湘教版九年级数学下册期末试卷及答案【完美版】

湘教版九年级数学下册期末试卷及答案【完美版】 班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.﹣3的相反数是( )A .13-B .13C .3-D .32.已知抛物线24y x bx =-++经过(2,)n -和(4, )n 两点,则n 的值为( )A .﹣2B .﹣4C .2D .43.已知α、β是方程x 2﹣2x ﹣4=0的两个实数根,则α3+8β+6的值为( )A .﹣1B .2C .22D .304.用配方法解方程2680x x --=时,配方结果正确的是( )A .2(3)17x -=B .2(3)14x -=C .2(6)44x -=D .2(3)1x -=5.实数a 在数轴上的对应点的位置如图所示.若实数b 满足a b a -<<,则b 的值可以是( )A .2B .-1C .-2D .-36.定义运算:21m n mn mn =--☆.例如2:42424217=⨯-⨯-=☆.则方程10x =☆的根的情况为( )A .有两个不相等的实数根B .有两个相等的实数根C .无实数根D .只有一个实数根7.如图,将含30°角的直角三角板ABC 的直角顶点C 放在直尺的一边上,已知∠A =30°,∠1=40°,则∠2的度数为( )A.55°B.60°C.65°D.70°8.按如图所示的运算程序,能使输出y值为1的是()A.11m n==,B.10m n==,C.12m n==,D.21m n==,9.若关于x的一元二次方程2210x x kb-++=有两个不相等的实数根,则一次函数y kx b=+的图象可能是:()A. B.C. D.10.如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC 边上的点F处.若AB=3,BC=5,则tan∠DAE的值为()A.12B.920C.25D.13二、填空题(本大题共6小题,每小题3分,共18分)1.64的算术平方根是__________.2.分解因式:2x 2﹣8=_______.3.若代数式1x x -有意义,则x 的取值范围为__________. 4.如图,直线AB ,CD 相交于点O ,EO ⊥AB 于点O ,∠EOD=50°,则∠BOC 的度数为__________.5.如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,若AB=8,CD=6,则BE=______.6.如图,平面直角坐标系中,矩形OABC 的顶点A (﹣6,0),C (0,23).将矩形OABC 绕点O 顺时针方向旋转,使点A 恰好落在OB 上的点A 1处,则点B 的对应点B 1的坐标为__________.三、解答题(本大题共6小题,共72分)1.解方程:23121x x =+-2.关于x 的一元二次方程2223()0m x mx m +++=-有两个不相等的实数根.(1)求m 的取值范围;(2)当m 取满足条件的最大整数时,求方程的根.3.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.4.如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.(1)求该二次函数的解析式;(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.5.老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.(1)求条形图中被遮盖的数,并写出册数的中位数;(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了人.6.某公司今年1月份的生产成本是400万元,由于改进技术,生产成本逐月下降,3月份的生产成本是361万元.假设该公司2、3、4月每个月生产成本的下降率都相同.(1)求每个月生产成本的下降率;(2)请你预测4月份该公司的生产成本.参考答案一、选择题(本大题共10小题,每题3分,共30分)1、D2、B3、D4、A5、B6、A7、D8、D9、B10、D二、填空题(本大题共6小题,每小题3分,共18分)1、2、2(x+2)(x ﹣2)3、0x ≥且1x ≠. 4、140°5、6、(6)三、解答题(本大题共6小题,共72分)1、x =52、(1)6m <且2m ≠;(2)12x =-,243x =-3、(1)略;(2)3. 4、(1)抛物线解析式为213222y x x =-++;(2)点D 的坐标为(3,2)或(-5,-18);(3)当t=85时,有S 1-S 2有最大值,最大值为165. 5、(1)条形图中被遮盖的数为9,册数的中位数为5;(2)选中读书超过5册的学生的概率为512;(3)36、(1)每个月生产成本的下降率为5%;(2)预测4月份该公司的生产成本为342.95万元.。
湘教版九年级下册数学期末测试卷(参考答案)
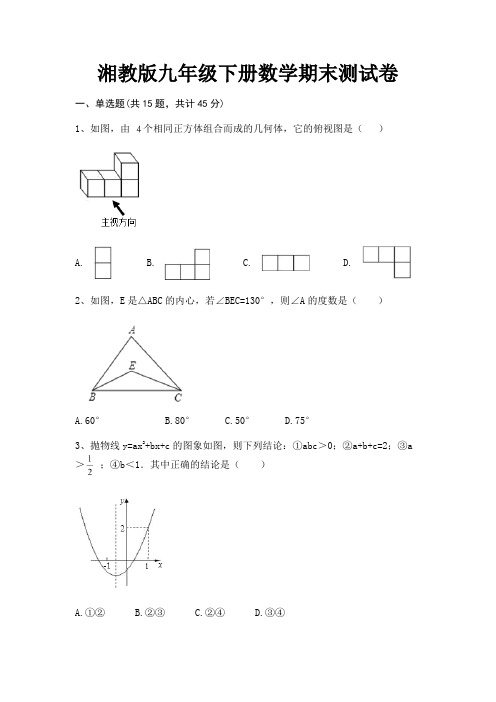
湘教版九年级下册数学期末测试卷一、单选题(共15题,共计45分)1、如图,由个相同正方体组合而成的几何体,它的俯视图是()A. B. C. D.2、如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是()A.60°B.80°C.50°D.75°3、抛物线y=ax2+bx+c的图象如图,则下列结论:①abc>0;②a+b+c=2;③a >;④b<1.其中正确的结论是()A.①②B.②③C.②④D.③④4、如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为()A.140°B.70°C.60°D.40°5、如图,弦AB的长等于⊙O的半径,点C在弧AMB上,则∠C的度数是()A.30ºB.35ºC.25ºD.60º6、关于二次函数y=2x2+x-1,下列说法正确的是()A.图象与y轴的交点坐标为(0,1)B.图象的对称轴在y轴的右侧C.当x<0时,y的值随x值的增大而减小D.y的最小值为-7、从地面竖直向上抛出一小球,小球的高度(单位:)与小球运动时间(单位:)之间的函数关系如图所示.下列结论:①小球在空中经过的路程是;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度时,.其中正确的是( )A.①④B.①②C.②③④D.②③8、下列立体图形中,主视图是三角形的是()A. B. C. D.9、下面所给几何体的俯视图是()A. B. C. D.10、已知点A(),B(),C()在二次函数的图象上,则的大小关系为()A. B. C. D.11、如图,为半圆O的直径,且,射线交半圆O 的切线于点E,交于F,若,则的半径长为()A. B. C. D.12、点P到⊙O上各点的最大距离为5,最小距离为1,则⊙O的半径为()A.2B.4C.2或3D.4或613、已知二次函数的y与x的部分对应值如表:x −1 0 2 3 4y 5 0 −4 −3 0下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A( ,2),B( ,3)是抛物线上两点,则,其中正确的个数是()A.2B.3C.4D.514、如图,CB为⊙O的切线,点B为切点,CO的延长线交⊙O于点A,若∠A=25°,则∠C的度数是()A.25°B.30°C.35°D.40°15、如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为()A. B. C.2 D.3二、填空题(共10题,共计30分)16、如下图,已知AB是⊙O的直径,,∠BOC = 40°,那么∠AOE等于 ________ .17、在平面直角坐标系 xOy 中,函数 y = x2的图象经过点M (x1 , y1) ,N(x2 , y2) 两点,若- 4< x1< -2, 0< x2<2 ,则 y1________ y2. (用“ < ”,“=”或“>”号连接)18、将抛物线平移,使它的顶点移到点P(-2,3),平移后新抛物线的表达式为________.19、请写出一个开口向上,并且与x轴交于、的抛物线的解析式:________.20、如图,扇形的圆心角为,是上的一点,则________ .21、如图,内接于,若,则的半径长为________.22、如图,已知为四边形的外接圆,若,则度数为________.23、已知电路AB由如图所示的开关控制,闭合a,b,c,d,e五个开关中的任意两个,则使电路形成通路的概率是________.24、由几个小正方体搭成的几何体,其主视图、左视图相同,均如图所示,则搭成这个几何体最少需要________ 个小正方体.25、如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2厘米的速度向左运动,最终点A与点M重合,则重叠部分面积y(厘米2)与时间t (秒)之间的函数关系式为________三、解答题(共5题,共计25分)26、圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。
湘教版九年级下册数学期末测试卷及含答案(适用考试)

湘教版九年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则的长为()A. πB.πC.D.2、如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac﹣b2<2a;④2b=3a.其中正确的结论是()A.①③B.②④C.①④D.②③3、如图是由5个相同的小正方体组成的几何体,该几何题的左视图是()A. B. C. D.4、如图,AB是⊙O的直径,CD是弦,如果弧AC=弧AD,∠C比∠D大36°,则∠A等于()A.24°B.27°C.34°D.37°5、如图,在⊙O,点A,B,C在⊙O上,若∠OAB=54°,则∠C( )A.54°B.27°C.36°D.46°6、尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连结OG.问:OG 的长是多少?大臣给出的正确答案应是()A. rB.(1+ )rC.(1+ )rD. r7、如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是()A. B. C. D.8、如图所示为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材料表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个。
湘教版九年级数学下册期末考试卷及答案【完整版】

湘教版九年级数学下册期末考试卷及答案【完整版】 班级: 姓名: 一、选择题(本大题共10小题,每题3分,共30分)1.若分式211x x -+的值为0,则x 的值为( ) A .0 B .1 C .﹣1 D .±12.已知抛物线24y x bx =-++经过(2,)n -和(4, )n 两点,则n 的值为( )A .﹣2B .﹣4C .2D .43.实数a ,b ,c 在数轴上的对应点的位置如图所示,则正确的结论是( )A .||4a >B .0c b ->C .0ac >D .0a c +>4.为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm )的平均数与方差为:x 甲=x 丙=13,x 乙=x 丁=15:s 甲2=s 丁2=3.6,s 乙2=s 丙2=6.3.则麦苗又高又整齐的是( )A .甲B .乙C .丙D .丁 5.如图,数轴上两点A,B 表示的数互为相反数,则点B 表示的( )A .-6B .6C .0D .无法确定6.已知直线y 1=kx+1(k <0)与直线y 2=mx (m >0)的交点坐标为(12,12m ),则不等式组mx ﹣2<kx+1<mx 的解集为( ) A .x>12 B .12<x<32 C .x<32 D .0<x<327.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A .B .C .D .8.如图,AB 为O 的直径,,C D 为O 上两点,若40BCD ∠︒=,则ABD ∠的大小为( ).A .60°B .50°C .40°D .20°9.如图,CB =CA ,∠ACB =90°,点D 在边BC 上(与B ,C 不重合),四边形ADEF 为正方形,过点F 作FG ⊥CA ,交CA 的延长线于点G ,连接FB ,交DE 于点Q ,给出以下结论:①AC =FG ;②S △FAB ∶S 四边形CBFG =1∶2;③∠ABC =∠ABF ;④AD 2=FQ ·AC ,其中正确结论的个数是( )A .1个B .2个C .3个D .4个10.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A .B .C .D .二、填空题(本大题共6小题,每小题3分,共18分)1.计算:3816-+=_____.2.因式分解:_____________. 3.以正方形ABCD 的边AD 作等边△ADE ,则∠BEC 的度数是__________.4.如图,已知菱形ABCD 的周长为16,面积为83,E 为AB 的中点,若P 为对角线BD 上一动点,则EP +AP 的最小值为__________.5.如图所示,在四边形ABCD 中,AD ⊥AB ,∠C=110°,它的一个外角∠ADE=60°,则∠B 的大小是__________.6.如图,点A 是反比例函数y=4x(x >0)图象上一点,直线y=kx+b 过点A 并且与两坐标轴分别交于点B ,C ,过点A 作AD ⊥x 轴,垂足为D ,连接DC ,若△BOC 的面积是4,则△DOC 的面积是__________.三、解答题(本大题共6小题,共72分)1.解方程:2142242x x x x +-+--=12.先化简,再求值:24211326x x x x -+⎛⎫-÷ ⎪++⎝⎭,其中21x =.3.已知:如图,四边形ABCD 中,AD ∥BC ,AD=CD ,E 是对角线BD 上一点,且EA=EC .(1)求证:四边形ABCD是菱形;(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.41.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形BCFD的面积.5.胜利中学为丰富同学们的校园生活,举行“校园电视台主待人”选拔赛,现将36名参赛选手的成绩(单位:分)统计并绘制成频数分布直方图和扇形统计图,部分信息如下:请根据统计图的信息,解答下列问题:(1)补全频数分布直方图,并求扇形统计图中扇形D对应的圆心角度数;(2)成绩在D区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.5.某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.(1)求出y与x的函数关系式;(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、B2、B3、B4、D5、B6、B7、D8、B9、D10、B二、填空题(本大题共6小题,每小题3分,共18分)1、22、3、30°或150°.4、235、40°6、32.三、解答题(本大题共6小题,共72分)1、x=1223、(1)略;(2)略.4、(1)略;(2)35、(1)补图见解析;50°;(2)3 5 .6、(1)y=﹣2x+80(20≤x≤28);(2)每本纪念册的销售单价是25元;(3)该纪念册销售单价定为28元时,才能使文具店销售该纪念册所获利润最大,最大利润是192元.。
湘教版九年级下册数学期末测试卷【有解析】

湘教版九年级下册数学期末测试卷一、单选题(共15题,共计45分)1、如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=4,则弦BC的长为()A.2B.4C.3D.42、如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内上的一点,若,则的度数是A. B. C. D.3、下列命题是真命题的是()A.多边形的内角和为360°B.若2 a﹣b=1,则代数式6 a﹣3 b﹣3=0 C.二次函数y=(x﹣1)2+2的图象与y轴的交点的坐标为(0,2) D.矩形的对角线互相垂直平分4、图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是()A.甲先到B点B.乙先到B点C.甲、乙同时到BD.无法确定5、抛物线y=-2(x-3)2-4的顶点坐标()A. B. C. D.6、下列关于二次函数y=x2﹣3的图象与性质的描述,错误的是( )A.该函数图象的开口向上B.函数值y随着自变量x的值的增大而增大 C.该函数图象关于y轴对称D.该函数图象可由函数y=x 2的图象平移得到7、图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线,桥拱与桥墩AC的交点C恰好在水面,有AC⊥ 轴。
若OA=10米,则桥面离水面的高度AC为()A. 米B. 米C. 米D. 米8、△ABC中,∠A=30°,∠B=60°,AC=6,则△ABC外接圆的半径为()A. B. C. D.39、如图所示几何体的左视图是()A. B. C. D.10、如图是某个几何体的三视图,则该几何体是()A.长方体B.圆锥C.圆柱D.三棱柱11、如图所示的几何体是由一个大正方体切去一个小正方体形成的,它的主视图是( )A. B. C. D.12、如图,直径AB为3的半圆,绕A点逆时针旋转60°,此时点B到了点B′处,则图中阴影部分的面积是()A.3πB.C.6πD.24π13、如图,已知∠AOB是⊙O的圆心角,∠AOB=60°,则圆周角∠ACB的度数是( )A.50°B.25°C.100°D.30°14、如图,是的切线,点A为切点,交于点B,,点C在上,.则等于()A.20°B.25°C.30°D.50°15、下列四个命题中,正确的有()A.圆的对称轴是直径B.半径相等的两个半圆是等弧C.三角形的外心到三角形各边的距离相等D.经过三个点一定可以作圆二、填空题(共10题,共计30分)16、如图所示,一个矩形区域ABCD,点E、F分别是AB、DC的中点,求一只蝴蝶落在阴影部分的概率为________17、在半径为4cm的圆中,长为4cm的弦所对的圆周角的度数为________18、已知,当________时,函数值随x的增大而减小.19、如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=________.20、如图,在中,⑴作AB和BC的垂直平分线交于点O;⑵以点O为圆心,OA长为半径作圆;⑶⊙O分别与AB和BC的垂直平分线交于点M,N;⑷连接AM,AN,CM,其中AN与CM交于点P.根据以上作图过程及所作图形,下列四个结论中,① ;② ;③点O是的外心;④点P是的内心.所有正确结论的序号是________.21、如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为________.22、在Rt△ABC中,∠C=90°,AC=12,BC=5,以点A为圆心作⊙A,要使B、C 两点中的一点在圆外,另一点在圆内,那么⊙A的半径长r的取值范围为________23、⊙O的半径为1,弦AB= ,C是在异于A、B圆上的点,则∠ACB的度数为________.24、如图,在一个正方形围栏中均匀地散步者许多米粒,正方形内有一个圆(正方形的内切园),一只小鸡仔围栏内啄食,则“小鸡正在院内”啄食的概率为________.25、如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线l相切.设半圆O1,半圆O2,…,半圆On的半径分别是r1, r2,…,r n ,则当直线l与x轴所成锐角为30°,且r1=1时,r2018=________.三、解答题(共5题,共计25分)26、如图,AB、CD是⊙O的直径,弦CE∥AB,的度数为70°.求∠EOC的度数.27、如图,已知E为圆内两弦AB和CD的交点,直线EF∥CB,交AD的延长线于F,FG切圆于G.求证:EF=FG.28、抛物线y=ax2+2x+c与其对称轴相交于点A(1,4),与x轴正半轴交于点B.(1)求这条抛物线的函数关系式;(2)在抛物线对称轴上确定一点C,使△ABC是等腰三角形,求出所有点C的坐标.29、已知抛物线y=x2﹣4x+a﹣2的最小值为0,求a的值.30、已知抛物线与x轴相交于两点A(1,0),B(-3,0),与y轴相交于点C(0,3).(1)求此抛物线的函数表达式;(2)如果点D(,m)是抛物线上的一点,求△ABD的面积.参考答案一、单选题(共15题,共计45分)1、B2、D3、B4、C5、C6、B7、B8、A9、B11、D12、B13、D14、B15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)28、29、30、。
湘教版九年级数学下册期末考试题及答案【完整版】

湘教版九年级数学下册期末考试题及答案【完整版】 班级: 姓名: 一、选择题(本大题共10小题,每题3分,共30分)1.2020的相反数是( )A .2020B .2020-C .12020D .12020- 2.已知x+1x =6,则x 2+21x =( ) A .38 B .36 C .34 D .323.下列计算正确的是( )A .a 2+a 3=a 5B .3221-=C .(x 2)3=x 5D .m 5÷m 3=m 24.关于x 的一元二次方程2(1)20x k x k ---+=有两个实数根12,x x ,()1212122(2)2x x x x x x -+--+3=-,则k 的值() A .0或2 B .-2或2 C .-2 D .25.关于x 的不等式x-b>0恰有两个负整数解,则b 的取值范围是( )A .32b -≤<-B .32b -<≤-C .32b -≤≤-D .-3<b<-26.一个等腰三角形的两条边长分别是方程27100x x -+=的两根,则该等腰三角形的周长是( )A .12B .9C .13D .12或97.如图,某小区计划在一块长为32m ,宽为20m 的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m 2.若设道路的宽为xm ,则下面所列方程正确的是( )A.(32﹣2x)(20﹣x)=570 B.32x+2×20x=32×20﹣570 C.(32﹣x)(20﹣x)=32×20﹣570 D.32x+2×20x﹣2x2=5708.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是()A.20°B.35°C.40°D.70°9.如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是()A.∠1=∠2 B.∠3=∠4 C.∠5=∠B D.∠B +∠BDC=180°10.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大.其中结论正确的个数是()A.4个B.3个C.2个D.1个二、填空题(本大题共6小题,每小题3分,共18分)1.81的平方根是__________.2.分解因式(xy ﹣1)2﹣(x+y ﹣2xy )(2﹣x ﹣y )=_______.3.抛物线23(1)8y x =-+的顶点坐标为____________.4.把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A ,且另三个锐角顶点B ,C ,D 在同一直线上.若AB=2,则CD=__________.5.如图,正六边形ABCDEF 的边长为1,以点A 为圆心,AB 的长为半径,作扇形ABF ,则图中阴影部分的面积为__________(结果保留根号和π).6.在平面直角坐标系中,点A (﹣2,1),B (3,2),C (﹣6,m )分别在三个不同的象限.若反比例函数y =k x(k ≠0)的图象经过其中两点,则m 的值为__________. 三、解答题(本大题共6小题,共72分)1.解方程:11322x x x-=---2.已知关于x 的一元二次方程2(3)0x m x m ---=.(1)求证:方程有两个不相等的实数根;(2)如果方程的两实根为1x ,2x ,且2212127x x x x +-=,求m 的值.3.在□ABCD ,过点D 作DE ⊥AB 于点E ,点F 在边CD 上,DF =BE ,连接AF ,BF.(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.4.如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.(1)求BC的长;(2)求证:PB是⊙O的切线.5.“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:(1)接受问卷调查的学生共有______人,条形统计图中m的值为______;(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为______;(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为______人;(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.61.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?(3)如果该企业要使每天的销售利润不低于4000元,那么销售单价应控制在什么范围内?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、B2、C3、D4、D5、A6、A7、A8、B9、A10、B二、填空题(本大题共6小题,每小题3分,共18分)1、±32、(y﹣1)2(x﹣1)2.3、(1,8)415、﹣3π6、-1三、解答题(本大题共6小题,共72分)1、无解2、(1)证明见解析(2)1或23、(1)略(2)略4、(1)2(2)略5、(1)60,10;(2)96°;(3)1020;(4)2 36、(1)y=﹣5x2+800x﹣27500(50≤x≤100);(2)当x=80时,y最大值=4500;(3)70≤x≤90.。
湘教版九年级下册数学期末测试卷(附解析)

湘教版九年级下册数学期末测试卷一、单选题(共15题,共计45分)1、已知抛物线y=ax2+bx+c(a<0)过A(-3,0)、O(1,0)、B(-5,)、C(5,)四点,则y1与y2的大小关系是()A. >B. =C. <D.不能确定2、抛物线y=x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为()A.y=x 2+4x+3B.y=x 2+4x+5C.y=x 2-4x+3D.y=x 2-4x-53、抛物线y=2(x+3)2+4的顶点坐标是( )A.(3,4)B.(-3,4)C.(3,-4)D.(-3,-4)4、下列条件中,能确定圆的是()A.以已知点O为圆心B.以1cm长为半径C.经过已知点A,且半径为2cm D.以点O为圆心,1cm为半径5、把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为()A.10 cmB.10cmC.10 cmD.8 cm6、在阳光下,小明和他爸爸在学校球场行走时,他们的影子一样长,晚上在该球场同一路灯下,关于他俩的影子以下说法正确的是()A.小明的影子比他爸爸的影子长B.小明的影子比他爸爸的影子短C.小明的影子比他爸爸的影子一样长D.不能确定谁的影子长7、实验的总次数、频数及频率三者的关系是()A.频数越大,频率越大B.频数与总次数成正比C.总次数一定时,频数越大,频率可达到很大D.频数一定时,频率与总次数成反比8、如图,在Rt△ACB中,∠ACB=90°,AC=6,BC=8,D,E分别在AC,BC上,且DE=6,以DE为直径的⊙O 交AB于点M,N,则弦长MN的最大值为()A.2.4B.4.8C.5D.69、原价为100元的某种药品经过连续两次降价后为64元,设平均每次降价的百分率为x,则下面所列方程正确的是()A.100(1﹣x)2=64B.64(1﹣x)2=100C.100(1﹣2x)=64 D.64(1﹣2x)=10010、若二次函数y=ax2+bx+c (a≠0)的图象与x轴有两个交点,坐标分别为(x1, 0),(x2, 0),且x1<x2,图象上有一点M (x, y)在x轴下方,则下列判断正确的是( )A.a>0B.b 2-4ac≥0C.x1<x<x2D.a(x-x1)( x-x2)<011、如图,AB是半圆O的直径,∠BAC=40°,则∠D的度数是()A.140°B.130°C.120°D.110°12、由若干边长相等的小正方体构成的几何体的主视图、左视图、俯视图如图所示,则构成这个几何体的小正方体有()个.A.5B.6C.7D.813、若方程ax2+bx+c=0的两个根是﹣4和2,那么二次函数y=ax2+bx+c的图象的对称轴是直线()A.x=﹣2B.x=﹣1C.x=0D.x=114、如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为()A.2B.4C.4D.815、如图,AB是⊙O的直径,C,D为⊙O上的点,,如果∠CAB=40°,那么∠CAD的度数为()A.25°B.50°C.40°D.80°二、填空题(共10题,共计30分)16、如图,AB、AC与⊙O相切于点B、C,∠A=50゜,P为⊙O上异于B、C的一个动点,则∠BPC的度数为________ 。
湘教版九年级数学下册期末考试卷及答案【A4打印版】

湘教版九年级数学下册期末考试卷及答案【A4打印版】班级:姓名:一、选择题(本大题共10小题,每题3分,共30分)1.﹣8的相反数是()A.8 B.18C.18-D.-82.若实数m、n满足02m=-,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是()A.12 B.10 C.8或10 D.63.下列结论成立的是()A.若|a|=a,则a>0 B.若|a|=|b|,则a=±bC.若|a|>a,则a≤0 D.若|a|>|b|,则a>b.4.某气象台发现:在某段时间里,如果早晨下雨,那么晚上是晴天;如果晚上下雨,那么早晨是晴天,已知这段时间有9天下了雨,并且有6天晚上是晴天,7天早晨是晴天,则这一段时间有()A.9天B.11天C.13天D.22天5.如果分式||11xx-+的值为0,那么x的值为()A.-1 B.1 C.-1或1 D.1或06.对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )A.c<﹣3 B.c<﹣2 C.c<14D.c<17.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()A.4个B.3个C.2个D.1个8.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是()A.12B.1 C.2D.29.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是()A.55°B.60°C.65°D.70°10.如图,能判定EB∥AC的条件是()A.∠C=∠1 B.∠A=∠2C.∠C=∠3 D.∠A=∠1二、填空题(本大题共6小题,每小题3分,共18分)181____________.2.分解因式:2x3﹣6x2+4x=__________.3.已知x=2是关于x的一元二次方程kx2+(k2﹣2)x+2k+4=0的一个根,则k 的值为__________.41.如图,圆锥侧面展开得到扇形,此扇形半径 CA=6,圆心角∠ACB=120°,则此圆锥高 OC 的长度是__________.5.如图,点A,B是反比例函数y=kx(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA,BC,已知点C(2,0),BD=2,S△BCD =3,则S△AOC=__________.6.如图,在矩形ABCD中,8AD=,对角线AC与BD相交于点O,AE BD⊥,垂足为点E,且AE平分BAC∠,则AB的长为__________.三、解答题(本大题共6小题,共72分)1.解分式方程:24 1x-+1=11xx-+2.已知关于x的一元二次方程x2+(2m+3)x+m2=0有两根α,β.(1)求m的取值范围;(2)若111αβ+=-,则m的值为多少?3.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.4.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;(2)求恒温系统设定的恒定温度;(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?5.某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:(1)九(1)班的学生人数为,并把条形统计图补充完整;(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是度;(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.6.去年在我县创建“国家文明县城”行动中,某社区计划将面积为23600m的一块空地进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的1.8倍,如果两队各自独立完成面积为2450m区域的绿化时,甲队比乙队少用4天.甲队每天绿化费用是1.05万元,乙队每天绿化费用为0.5万元.(1)求甲、乙两工程队每天各能完成多少面积(单位:2m)的绿化;(2)由于场地原因,两个工程队不能同时进场绿化施工,现在先由甲工程队绿化若干天,剩下的绿化工程由乙工程队完成,要求总工期不超过48天,问应如何安排甲、乙两个工程队的绿化天数才能使总绿化费用最少,最少费用是多少万元?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、A2、B3、B4、B5、B6、B7、A8、B9、C10、D二、填空题(本大题共6小题,每小题3分,共18分)1、32、2x(x﹣1)(x﹣2).3、﹣34、5、5.6、.三、解答题(本大题共6小题,共72分)1、无解.2、(1)34m≥-;(2)m的值为3.3、(1)略;(2)3.4、(1)y关于x的函数解析式为210(05)20(510)200(1024)x xy xxx⎧⎪+≤<⎪=≤<⎨⎪⎪≤≤⎩;(2)恒温系统设定恒温为20°C;(3)恒温系统最多关闭10小时,蔬菜才能避免受到伤害.5、(1)40,补全统计图见详解.(2)10;20;72.(3)见详解.6、(1)甲、乙两工程队每天各完成绿化的面积分别是90m2、50m2;(2)甲队先做30天,乙队再做18天,总绿化费用最少,最少费用是40.5万元.。
湘教版九下数学期末考试卷

湘教版九下数学期末考试卷一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 2.718281828459B. 1.414213562373C. 1.000000000000D. 0.3333333333332. 一个圆的半径为5,那么它的直径是多少?A. 10B. 15C. 20D. 253. 已知一个直角三角形的两个直角边分别为3和4,那么斜边的长度是?A. 5B. 6C. 7D. 84. 函数y=2x+3的斜率是?A. 2B. 3C. -2D. -35. 一个二次方程ax^2+bx+c=0的判别式是?A. b^2-4acB. a^2-4bcC. b^2+4acD. a^2+4bc6. 以下哪个是二次根式?A. √2B. √(-1)C. √(1/2)D. √(2x)7. 一个正方体的体积是27立方厘米,那么它的边长是?A. 3厘米B. 6厘米C. 9厘米D. 12厘米8. 以下哪个是反比例函数?A. y=k/xB. y=kxC. y=kx^2D. y=kx^(-1)9. 若一个数列是等差数列,且a3=5,a5=11,那么公差d是?A. 2B. 3C. 4D. 610. 一个函数的图像是一条直线,那么它的反函数图像是?A. 一条曲线B. 一条直线C. 无法确定D. 一个点二、填空题(每空2分,共20分)11. 一个圆的面积是π平方厘米,那么它的半径是______厘米。
12. 一个等腰三角形的两个底角相等,如果一个底角是40°,那么顶角是______度。
13. 一个数的平方根是5,那么这个数是______。
14. 一个正数的倒数是1/8,那么这个数是______。
15. 一个二次方程的根是x1=2和x2=-3,那么这个方程可以写成______。
三、解答题(共50分)16. 解方程:2x^2 - 7x + 3 = 0。
(10分)17. 证明:如果一个三角形的两边之和大于第三边,那么这个三角形是锐角三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解得
2 x1=2+
3
3
2
,x2=2-
3
3.∴函数
y=-3x2+12x-8
与
x
轴的交点坐标分别为(2+2
3
3,0),(2-2
3
3,0).
90×π×( 3)2
19.连接 OB,OC.∵∠BAC=45°,∴∠BOC=90°.∵⊙O 的直径为 2 3,∴OB=OC= 3.∴S 扇形 = OBC
360
3
1
3
33
21.(1)由题意可知:点 C 坐标为(0,1),点 F 坐标为(-6,2),设抛物线表达式为 y=ax2+c(a≠0),则有c=1, 36a+c=2.
解得a=316,∴抛物线表达式为 c=1.
y=316x2+1.
25
25
(2)∵点 A 的横坐标为-8,当 x=-8 时,y= 9 ,∴柱子 AD 的高度为 9 米.
16.如图,在矩形 ABCD 中,AB=5,BC=4,以 BC 为直径在矩形内作半圆,自点 A 作半圆的切线 AE,则 tan∠CBE=____________.
三、解答题(共 72 分) 17.(6 分)在直径为 1 米的圆柱形油槽内装入一些油后,截面如图所示,若油面宽 AB=0.6 米,求油的最大深度.
D.2 个
二、填空题(每小题 3 分,共 24 分) 9.抛物线 y=-12(x+3)2+2 的顶点坐标为____________. 10.身高相同的小明和小丽站在灯光下的不同位置,已知小明的投影比小丽的投影长,我们可以判定小明离灯较 ____________. 11.已知扇形的半径为 4 cm,圆心角为 120°,则此扇形的弧长是____________cm. 12.已知 a,b 可以取-2,-1,1,2 中的任意一个值(a≠b),则直线 y=ax+b 的图象不经过第四象限的概率是 ____________. 13.如图,AB 是⊙O 的直径,BC 为⊙O 的切线,∠ACB=40°,点 P 在边 BC 上,则∠PAB 的度数可能为____________.(写 出一个符合条件的度数即可)
AN= (k+2)2+4.当 AM=AN 时,解得 k=0;当 AM=MN 时, (k-2)2+4=4,解得
中考
k=2±2 3,则14k2=4±2 3;当 AN=MN 时, (k+2)2+4=4,解得 k=-2±2 3,则 k2=4±2 3.综上所述,
P 的纵坐标为 0 或 4+2 3或 4-2 3.
最大深度是 0.1 米.
18.(1)y=-3x2+12x-8=-3(x2-4x)-8=-3(x-2)2+12-8=-3(x-2)2+4.∴函数 y=-3x2+12x-8 的对称
轴为直线 x=2,顶点坐标为(2,4).
(2)令 x=0,则 y=-8.∴函数 y=-3x2+12x-8 与 y 轴的交点坐标为(0,-8).令 y=0,则-3x2+12x-8=0,
中考
22.(12 分)如图,AB,CD 是⊙O 的直径,点 E 在 AB 延长线上,FE⊥AB,BE=EF=2,FE 的延长线交 CD 延长线于点 G,DG=EG=3,连接 FD.
(1)求⊙O 的半径; (2)求证:DF 是⊙O 的切线.
23.(12 分)如图,已知 AB 是⊙O 的直径,弦 CD⊥AB 于点 E,F 是 CE 上的一点,且 FC=FA,延长 AF 交⊙O 于点 G, 连接 CG. (1)试判断△ACG 的形状(按边分类),并证明你的结论; (2)若⊙O 的半径为 5,OE=2,求 CF·CD 的值.
中考
期末测试
(时间:90 分钟 满分:120 分)
题号 一 二 三 总分 合分人 复分人
得分
一、选择题(每小题 3 分,共 24 分)
1.下列各式中,y 是 x 的二次函数的是( )
A.y=3x-1
1 B.y=x2
C.y=3x2+x-1
D.y=2x2+1x
2.下列事件:①在足球赛中,弱队战胜强队;②抛掷一枚硬币,落地后正面朝上;③任取两个正整数,其和大于 1;
参考答案
1.C 2.B 3.A 4.D 5.D 6.D 7.D 8.B 9.(-3,2) 10.远 11.83π 12.16 13.30°(满足 0°≤∠PAB≤50°即可) 14.2π 15.(75 3+360) 16.25 17.连接 OA,过点 O 作 OD⊥AB,交 AB 于点 C,交⊙O 于点 D.由题意,得 OA=OD=0.5 米,AC=12AB= 0.3 米,∴OC2=OA2-AC2.∴OC= OA2-AC2= 0.52-0.32=0.4(米).∴CD=OD-OC=0.5-0.4=0.1(米).∴油的
(1)求不等式组的解集,并写出它的所有整数解; (2)在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为正数的概率.
21.(8 分)桂林红桥位于桃花江上,是桂林两江四湖的一道亮丽的风景线,该桥的部分横截面如图所示,上方可看 作是一个经过 A,C,B 三点的抛物线,以桥面的水平线为 x 轴,经过抛物线的顶点 C 且与 x 轴垂直的直线为 y 轴, 建立直角坐标系,已知此桥垂直于桥面的相邻两柱之间距离为 2 米(图中用线段 AD,CO,BE 等表示桥柱),CO= 1 米,FG=2 米. (1)求经过 A,B,C 三点的抛物线的表达式; (2)求柱子 AD 的高度.
6.袋中有红球 4 个,白球若干个,它们只有颜色上的区别.从袋中随机地取出一个球,如果取到白球的可能性较
中考
大,那么袋中白球的个数可能是( )
A.3 个
B.不足 3 个
C.4 个
D.5 个或 5 个以上
7.如图,菱形 ABCD 的对角线 BD,AC 分别为 2,2 3,以 B 点为圆心的弧与 AD,DC 相切,则阴影部分的面积是( )
=4π,S△OBC=2× 3× 3=2.∴S 阴影=S 扇形 OBC-S△OBC=4π-2.
中考
20.(1)由①,得 x>-2.由②,得 x≤2.∴不等式组的解集为-2<x≤2.∴它的所有整数解为-1,0,1,2. (2)画树状图得:
∵共有 12 种等可能的结果,积为正数的有 2 种情况,∴积为正数的概率为122=16.
④长分别为 3,5,9 厘米的三条线段不能围成一个三角形.其中确定事件的个数是( )
A.1
B.2
C.3
D.4
3.(岳阳中考)已知一个几何体的三视图如图所示,则该几何体是( )
A.圆柱
B.圆锥
C.球
D.棱柱
︵ 4.如图,A,B,C 是⊙O 上的三点,且点 A 是BAC上与点 B,点 C 不同的一点,若△BOC 是直角三角形,则△BAC 必
(3)设 P(k,14k2).∵PA= 116k4+4,作 PH⊥MN 于点 H,连接 PM,PN,PA,则 PM=PN= 116k4+4.又 PH= 14k2,则 MH=NH= 116k4+4-(14k2)2=2.故 MN=4.∴M(k-2,0),N(k+2,0).又∵A(0,2),∴AM= (k-2)2+4,
14.如图,⊙O 的半径为 2,C1 是函数 y=12x2 的图象,C2 是函数 y=-12x2 的图象,则阴影部分的面积是____________.
中考
15.如图是一个上下底密封且为正六棱柱的纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为 ____________cm2.(结果可保留根号)
中考
24.(14 分)(长沙中考)如图,抛物线 y=ax2+bx+c(a≠0,a,b,c 是常数)的对称轴为 y 轴,且经过(0,0),( a, 1 16)(a>0)两点,点 P 在抛物线上运动,以 P 为圆心的⊙P 经过定点 A(0,2). (1)求 a,b,c 的值; (2)求证:点 P 在运动过程中,⊙P 始终与 x 轴相交; (3)设⊙P 与 x 轴相交于 M(x1,0),N(x2,0)(x1<x2)两点,当△AMN 为等腰三角形时,求圆心 P 的纵坐标.
A.2 3- 33π
B.4 3- 33π
C.4 3-π
D.2 3-π
8.如图所示的抛物线是二次函数 y=ax2+bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与
x 轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.其中正确的结论有( )
A.5 个
B.4 个
C.3 个
c=0, 解得
a2=116.
a=4, b=0, c=0.
∴二次函数的解析式为 y=14x2.
(2)证明:设 P(x,y),⊙P 的半径 r= x2+(y-2)2.又∵y=14x2,则 r= >14x2=y,∴点 P 在运动过程中,⊙P 始终与 x 轴相交.
x2+(14x2-2)2,化简得 r=
116x4+4
是( )
A.等腰三角形
B.锐角三角形
C.有一个角是 30°的三角形
D.有一个角是 45°的三角形
5.已知二次函数 y=ax2+bx+c 的部分图象如图所示,则关于 x 的一元二次方程 ax2+bx+c=0 的解为( )
A.x1=-3,x2=0
B.x1=3,x2=-1
C.x=-3
D.x1=-3,x2=1
∠G,∴△DFG≌△EOG.∴∠FDG=∠OEG=90°.∴DF⊥OD.∴DF 是⊙O 的切线.
︵︵ 23.(1)△ACG 是等腰三角形.证明:∵CD⊥AB,∴AD=AC.∴∠G=∠ACD.∵FC=FA,∴∠ACD=∠CAG.
∴∠G=∠CAG.∴AC=CG∴△ACG 是等腰三角形.
︵︵ (2)连接 AD,BC,CO.由(1),知AC=AD,∴AC=AD.∴∠D=∠ACD.又∵∠G=∠ACD,∴∠D=∠G=∠CAG.又∵∠ACF
=∠DCA,∴△ACF∽△DCA.∴AC∶CD=CF∶AC,即 AC2=CF·CD.∵CD⊥AB,∴AC2=AE2+
