minitab正交分析、响应分析
minitab doe案例

minitab doe案例
以下是一个使用Minitab进行DOE(实验设计)的案例:
案例:PCB板的镀铜线质量优化
1. 确定每个因子的高低水平,例如温度、时间、电流等。
2. 打开Minitab软件,创建一个新的DOE计划。
3. 选择合适的因子数、区组中心点数、角点仿行数和区组数,以满足实验需求。
4. 生成正交试验矩阵,并按照计划进行实验。
5. 将实验数据复制到Minitab中进行DOE分析。
6. 选择因子和响应,进行效应图和方差分析。
7. 根据分析结果,优化因子水平,以提高镀铜线的质量。
通过以上步骤,可以使用Minitab进行DOE,优化PCB板的镀铜线质量。
minitab部分因子设计,响应面设计,参数设计解读

北京信息科技大学经济管理学院《工程优化技术》课程结课报告成绩:_______________班级:__工商1002_____学号:__2010011713____姓名:__魏坡_______日期:_2013年6月7日_部分因子试验设计1.实验设计背景部分因子试验设计与全因子试验设计的不同之处在于大大减少了试验的次数,具体表现在试验设计创建阶段的不一致,下面主要就部分因子试验设计的创建进行讲述。
2.因子选择用自动刨床刨制工作台平面的工艺条件试验。
在用刨床刨制工作台平面试验中,考察影响其工作台平面光洁度的因子,并求出使光洁度达到最高的工艺条件。
3.实验方案共考察6个因子:A 因子:进刀速度,低水平1.2,高水平1.4(单位:mm/刀)B 因子:切屑角度,低水平10,高水平12(单位:度)C 因子:吃刀深度,低水平0.6,高水平0.8(单位:mm )D 因子:刀后背角,低水平70,高水平76(单位:度)E 因子:刀前槽深度,低水平1.4,高水平1.6(单位:mm )F 因子:润滑油进给量,低水平6,高水平8(单位:毫升/分钟) 要求:连中心点在内,不超过20次试验,考察各因子主效应和2阶交互效应AB 、AC 、CF 、DE 是否显著。
由于试验次数的限制,我们在因子点上只能做试验16次,另4次取中心点,这就是6224-+的试验,通过查部分因子试验分辨度表可知,可达分辨度为Ⅳ的设计。
具体操作为:选择 [统计]=>[DOE ]=>[因子]=>[创建因子设计],单击打开创建因子设计对话框。
在“设计类型”中选择默认2水平因子(默认生成元),在“因子数”中选定6。
单击“显示可用设计”就可以看到下图的界面,可以确认:用16次试验能够达到分辨度为Ⅳ的设计。
单击“设计”选项,选定1/4部分实施,在每个区组的中心点数中设定为4,其他的不进行设定,单击确定。
单击“因子”选项,设定各个因子的名称,并设定高、低水平值。
响应面法和实验设计软件Minitab 及 Design-Expert简介

Adj MS 4.0517 2.5962 4.4619 5.0970 0.9920 1.4760 0.5079
F 4.08 2.62 4.50 5.14
P 0.019 0.109 0.030 0.021
2.91 0.133
R-Sq(adj) = 59.4%
此值大于0.05,表示二次多 项式回归模型正确。
非线性回归结果
输出结果:二次多项式回归方差分析表
此值小于0.05的项显著有效,回归的整体、二次项和交叉 乘积项都显著有效,但是一次项的效果不显著。
Source Regression
Linear Square Interaction Residual Error Lack-of-Fit Pure Error Total S = 0.9960
响应面法的分类
中心复合试验设计 (central composite design,CCD);
Box-Behnken试验设计;
中心复合试验设计
中心复合试验设计也称为星点设计。其设计
表是在两水平析因设计的基础上加上极值点和 中心点构成的,通常实验表是以代码的形式编 排的, 实验时再转化为实际操作值,(一般水 平取值为 0, ±1, ±α, 其中 0 为中值, α 为极值, α=F*(1/ 4 )
其设计表是在两水平析因设计的基础上加上极值点和中心点构成的通常实验表是以代码的形式编排的实验时再转化为实际操作值一般水平取值为01其中0为中值为极值f14精品资料boxbehnkendesignboxbehnkendesign简称bbd也是响应面优化法常用的实验设计方法其设计表安排以三因素为例三因素用abc表示见下页表其中0是中心点分别是相应的高值和低值
2. 创建“中心复合”或“Box-Behnken”设计; 3. 确定试验运行顺序(Display Design); 4. 进行试验并收集数据; 5. 分析试验数据; 6. 优化因素的设置水平。
minitab正交试验设计

食品科学研究中实验设计的案例分析——正交设计优选白芨多糖包合丹皮酚最佳工艺以及包合物的鉴定[1]摘要:本实验采用用minitab软件设计L9(34)正交试验优选白芨多糖包合丹皮酚的最佳工艺,结果显示:以丹皮酚和白芨多糖的物料比、反应时间和反应温度为考察指标,得到优化工艺为:物料比1:6、反应时间4h、温度30℃,包封率可达29.38%,收得率74.29%。
关键词:正交设计 minitab1 正交试验因素水平的确定选择丹皮酚与白芨多糖的A物料比(W/W)、B反应时间(h)、C包合温度(℃)三个对试验结果影响较大的因素为考察对象,每个因素各取三个水平(表1)。
采用L9(34)正交试验表进行正交试验。
以所得包合物的收得率和药物包封率为考察指标,确定最佳工艺。
表一正交试验因素水平表水平因素A物料比(w/w)B反应时间(h)C反应温度(℃)1 1:2 2 302 1:43 403 1:64 502 正交试验设计步骤:1 选择统计—>DOE—>田口—>创建田口设计。
2 得出田口设计窗口,在这个窗口中我们可以设计正交试验,本试验选择3水平4因素,其中一个因素作为误差列。
3 点击显示可用设计,进入如下图的窗口,选择L9 2-44 点击“设计”选项,选择L9 3**4,这样我们就得到了L9(34)5 点击“因子”选项,得到如下图窗口,可以对其名称进行设计,如“A”改为“A物料比”6 设计完成,得到如下图的正交试验表7 导入数据(包封率和收得率)8 点击“DOE”—>“田口”—>“分析田口设计”,得到下图9 在响应数据位于栏中选择“包封率”10 在“项”选项中,选中A B C的内容,注意不要选中误差列,按下图进行设计。
11 点击确定,可得出下列的分析数据。
(再按上述8-11,对收得率进行分析,可得出另外一个分析数据)12 点击“统计”—>“方差分析”—>“一般线性模型”13 在“响应”栏中选择“包封率”,在“模型”栏中选择A B C D14 点击确定,得出方差分析数据,如下图。
MINITAB与正交试验(精选PPT)

这是设计正交试验表的基本准则 5
正交试验设计的基本步骤
1. 确定目标、选定因素(包括交互作用)、确定水平; 2. 选用合适的正交表; 3. 按选定的正交表设计表头,确定试验方案; 4. 组织实施试验; 5. 试验结果分析。
要求:能利用MINITAB完成正交试验的方差分析。
16
例1的上机操作
按正交表及试验结果输入数据。
17
不写C3 不写C5 要表明是交互作用
18
F<1 表示该因子的影响力比试验 误差更小,不必理会,(严重无统计 意义)去掉这些因子,将它们造成的 微小差异归到试验误差中(软件会自 动处理),则可突显其它因子的影响。
5 2 1 2 1 2 1 2 200
6 2 1 2 2 1 2 1 250
7 2 2 1 1 2 2 1 275
8 2 2 1 2 1 1 2 37153
第四步 分析正交试验结果 方法1 直观分析(极差分析) (1)计算极差,确定因素的主次顺序
第j列的极差
Rj
max i
Tij
min i
11
考虑交互作用AB和AC,则例1的表头可设计为
花菜留种的表头设计
列号 1 2 3 4 5 6 7
因子 A B A B C AC
D
按正交表 L8 27 得试验方案:
只需将各列中的数字“1”、“2”分别理解为所填因素 在试验中的水平数,每一行就是一个试验方案。
注:第6列为空白列,当随机误差列;也可把第7列 作空白列。一般要求至少有一个空白列。
B:喷药次数 发现病害即喷药
每半月喷一次
C:施肥次数 开花期施硫酸铵 D:进室时间 11月初
运用MiniTAB进行正交试验设计

利用Minitab进行正交试验设计1.试验设计试验设计可分为单因素问题试验设计与多因素试验设计。
常用的单因素试验设计方法有:对分法、0.618法等等。
常用的多因素试验设计方法有:曲面响应法、全因子试验法、正交试验设计等。
其中正交试验设计法是研究与处理多因素实验的一种科学方法。
利用规格化的表格—正交表,科学地挑选试验条件,合理安排实验。
该方法是在上世纪50年代由日本质量管量专家田口玄一提出的,由于其具有均衡分配、整齐可比的特点,所需工作量小,却可得到全面的试验分析结果,因而得到了广泛的应用,称为国际标准型正交试验法,又称为田口设计。
我国于上世纪70年代由数学家张里千教授经过简化得到了中国型正交试验法。
两者的主要区别在于中国型采用极差分析的方法对试验结果进行评价,计算量小、简单;田口型采用方差分析的方法,可得到因素间相互影响大小的结论。
常用的术语:【试验指标】作为试验研究过程的因变量,常为试验结果特征的量【因素】作试验研究过程的自变量,常常是造成试验指标按某种规律发生变化的那些原因【水平】试验中因素所处的具体状态或情况,又称为等级2. 利用Minitab进行正交试验设计a.启动b.创建正交设计表在这里选择3-Level Design,在因素数量上选择4 factors。
选择正交设计试验表,选Design:选择L9_3_4正交表设计:进行因素设计,选择Factor。
对因素名称和水平值进行设定,也可以不进行设定。
在options选项中选择将设计保存于工作表。
点击ok,在工作表区生成所需正交表。
在新的一列加入试验指标-试验结果。
并将试验结果的数据输入。
对试验结果进行分析,选择Analyze Taguchi Design。
出现分析设计对话框。
点击“选择”所要评价的试验指标。
设定分析的“选项”,这里选“望大”。
点击“确定”进行分析,在任务窗口出现均值和信噪比的分析结果,从结果可以看出磨制时间对指标的影响最大。
Minitab轻松完成正交试验极差分析和方差分析,可视化效果突出
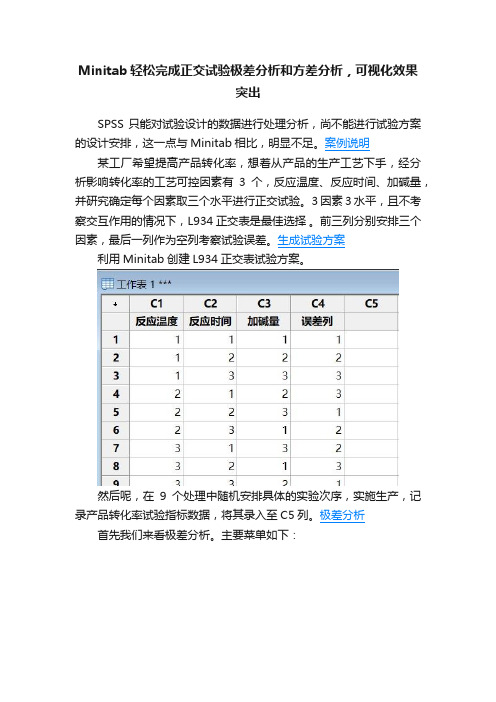
Minitab轻松完成正交试验极差分析和方差分析,可视化效果突出SPSS只能对试验设计的数据进行处理分析,尚不能进行试验方案的设计安排,这一点与Minitab相比,明显不足。
案例说明某工厂希望提高产品转化率,想着从产品的生产工艺下手,经分析影响转化率的工艺可控因素有3个,反应温度、反应时间、加碱量,并研究确定每个因素取三个水平进行正交试验。
3因素3水平,且不考察交互作用的情况下,L934正交表是最佳选择。
前三列分别安排三个因素,最后一列作为空列考察试验误差。
生成试验方案利用Minitab创建L934正交表试验方案。
然后呢,在9个处理中随机安排具体的实验次序,实施生产,记录产品转化率试验指标数据,将其录入至C5列。
极差分析首先我们来看极差分析。
主要菜单如下:极差分析结果:此表中数据是因素各水平下转化率平均值,Delta一行的数据即为极差了。
很明显,极差从大到小依次是:反应温度>加碱量>反应时间,也可以理解为三个试验因素的重要性顺序。
上图是因素水平-转化率均值趋势图,美观、直观,试验指标Y望大,越大越好,所以各因素优水平也很明显,分别是A3、B2、C2。
如果我们只使用极差分析来总结此处正交试验的结论,那么最优工艺组合是A3B2C2,该组合没有出现在已经实施的9个处理中,这恰好说明正交试验本身的科学性。
方差分析如果我们想搞清楚三个试验因素对转化率的影响在统计学上是不是显著,那么接下来需要进行方差分析。
minitab方差分析表。
最简单直接的解读方法是直接看最后一列,概率p值。
我们发现仅反应温度的p值小于0.05,也就是说统计上认为反应温度对试验指标转化率有显著影响,统计上有意义。
其他两个因素影响相对较小。
还没有完。
现在反应温度在统计上认为是一个相对很重要的因素,它下设3个水平,请问这3个水平差异表现如何?我们该选谁作为优水平呢?所以,需要多重比较。
这一步在minitab中比较麻烦,还需要再对试验数据进行一次【方差分析→一般线性模型】处理,然后单独进行一个多重比较的过程。
Minitab实现有交互作用的正交实验的设计与结果分析

Minitab实现有交互作用的正交实验的设计与结果分析一、本文概述Overview of this article正交实验设计是一种在多个因素中找出最优组合的高效实验设计方法。
通过正交表,我们可以合理安排实验,使得每个因素在每个水平下都能被充分考察,同时减少实验次数,提高实验效率。
在实际应用中,我们经常遇到有交互作用的因素,即两个或多个因素同时作用时,它们的效果会发生变化。
因此,在正交实验设计中考虑交互作用至关重要。
Orthogonal experimental design is an efficient experimental design method that finds the optimal combination among multiple factors. Through orthogonal tables, we can arrange experiments reasonably so that each factor can be fully examined at each level, while reducing the number of experiments and improving experimental efficiency. In practical applications, we often encounter interactive factors, that is, when two or more factors act simultaneously, theireffects will change. Therefore, considering interaction is crucial in orthogonal experimental design.本文将详细介绍如何在Minitab中实现有交互作用的正交实验设计,并对实验结果进行分析。
minitab正交分析、响应分析

Minitab 实验之试验设计实验目的:本实验主要引导学生利用Minitab 统计软件进行试验设计分析,包括全因子设计、部分因子设计、响应曲面设计、混料设计、田口设计以及响应优化,并能够对结果做出解释。
实验仪器:Minitab 软件、计算机 实验原理:“全因子试验设计”的定义是:所有因子的所有水平的所有组合都至少要进行一次试验的设计。
由于包含了所有的组合,全因子试验所需试验的总次数会比较多,但它的优点是可以估计出所有的主效应和所有的各阶交互效应。
所以在因子个数不太多,而且确实需要考察较多的交互作用时,常常选用全因子设计。
一般情况下,当因子水平超过2时,由于试验次数随着因子个数的增长而呈现指数速度增长,因而通常只作2水平的全因子试验。
进行2水平全因子设计时,全因子试验的总试验次数将随着因子个数的增加而急剧增加,例如,6个因子就需要64次试验。
但是仔细分析所获得的结果可以看出,建立的6因子回归方程包括下列一些项:常数项、主效应项有6项、二阶交互作用项15项、三阶交互项20项,…,6阶交互项1项,除了常数项、主效应项和二阶交互项以外,共有42项是3阶以及3阶以上的交互作用项,而这些项实际上已无具体的意义了。
部分因子试验就是在这种思想下诞生的,它可以使用在因子个数较多,但只需要分析各因子和2阶交互效应是否显著,并不需要考虑高阶的交互效应,这使得试验次数大大减少。
在实际工作中,常常要研究响应变量Y 是如何依赖于自变量,进而能找到自变量的设置使得响应变量得到最佳值(望大、望小或望目)。
如果自变量的个数较少(通常不超过3个),则响应曲面方法(response surface methodology ,RSM )是最好的方法之一,本方法特别适合于响应变量望大或望小的情形。
通常的做法是:先用2水平因子试验的数据,拟合一个线性回归方程(可以包含交叉乘积项),如果发现有弯曲的趋势,则希望拟合一个含二次项的回归方程。
其一般模型是(以两个自变量为例):22011221112221212y b b x b x b x b x b x ε=++++++这些项比因子设计的模型增加了各自的变量的平方项。
DOE(Minitab)全

DOE的定义
DOE: Design of Experiment 实验设计,收集数据的过程,这种过程主动的 改变流程输入(X)的设置,并且考察这些X的 改变对流程的输出(Y)有何影响。
y = f(x)
响应 因子 输出 输入
DOE研究的对象
受控因子 (Factor)
过程
噪音因子 (Noise)
在另一天将所有的实
件,使用三次测量的
验条件重新运行。
平均作为运行的响应。 彷行比重复好(通常成
本更高)
实验中的样本量通过防 行来控制
随机化
对于我们知道的噪音变量可以用Block降低其对实 验的影响。
对于我们不知道的噪音变量如湿度,电压变化这 一类潜伏变量可以用随机化,即打乱实验的顺序 降低其对实验的影响。
为什么随机化:示例
假设印刷电路板上的镀层厚度是您关心的响应。 在一个月内这个值趋向于下降。 如何解释这种下降趋势?(某种潜伏变量影响)
厚度与每月的第几天
为什么随机化:示例(续)
假设要在实验中评估浸泡温度的效果,小组首先 测试了50摄氏度,然后测试70摄氏度。(直观判 断70摄氏度的输出较小)
如果因子的数目很多,要运行全因子实验将变得 很困难,为了达到筛选关键因子的目的,可以按 照一定的方法从所有的处理中挑选出一部分运行, 这种实验方法很多,其中之一叫做部分因子实验 (Fractional Factorial Experiment)。
全因子实验--例子
在注塑成型工具中,注塑件表面的强度是个关键 质量指标,对其的要求是越高越好。
响应(Y) (Response)
DOE的目的
因子的显著性分析 确定对响应Y有重要影响的因子X
确定最佳条件 确定关键输入因子的设置从而使得响应Y最佳
正交实验(田口)与Minitab应用

假设要预测高尔夫球试验的结果。确定了认为会影响高尔夫球飞行距离的四个可控因子:核心材料、核心 直径、波纹数和表层厚度。由于要使信噪比和均值最大化,因此选择了以下因子设置:液体核心、核心直 径 118、392 个波纹以及表层厚度0 .06。具体 操作步骤如下: 1 打开工作表“高尔夫球 .MTW”。已保存了设计和响应信息。 2 选择统计 > DOE > 田口 > 预测田口结果。 3 取消选中标准差和标准差的自然对数。 4 单击项。确保项 A、B、C、D 和 AB 都位于所选项框中。单击确定。 4 单击水平。 5 在指定新因子水平的方法下,选择从列表中选择水平。 6 在水平下,单击第一行并根据下表选择因子水平。然后,使用沿该列下移并选择其余的因子水平. 7 在每个对话框中单击确定。
静态田口设计示例-06
2013-7-25 8
步骤5:分析静态田口设计(续)
(图形窗口的输出1)
结果解释: 在此示例中,秩表明核心直径对信噪比和均值的影响最大。 对于信噪比,表层厚度的影响次之,然后是核心材料和波 纹。对于均值,核心材料的影响次之,然后是波纹和表层 厚度
对于此示例,由于目标是增加球的飞行距离,因此您需要的 是能产生最高均值的因子水平。在田口试验中,始终都需要 使信噪比最大化。响应表中的水平平均值表明,当核心材料 为液体、核心直径为 118、有 392 个波纹以及表层厚度为 0.06 时,信噪比和均值达到最大。检查主效应图和交互作 用图可以确证这些结果。交互作用图表明,球核使用液体时, 飞行距离在核心直径为 118 时达到最大。
2013-7-25
1
2013-7-25
2
例1背景:您是高尔夫球制造商,现在正在进行一项旨在使球的飞行 距离最大化的新设计。您确定了四个控制因子,每个因子有两个水平: ●核心材料(液体与钨) ●核心直径(118 与 156) ●波纹数(392 与 422) ●表层厚度(0.03 与0.06) 您还想检验核心材料与核心直径之间的交互作用 。 响应为球的飞行距离(以英尺计)。 噪声因子为两种类型的高尔夫球棍:长打棒和 5 号铁头球棒。测量每种球棍打出 球的距离,在工作表中形成两个噪声因子列。 由于目标是使飞行距离最大化,因此选择望大信噪比 。
Minitab实现正交试验设计

Minitab实现正交试验设计Yearmay实验设计在学术研究、工程应用中有着十分广泛的应用。
由于自身的需要,Yearmay 开始了实验设计的学习。
并将学习笔记拿出来与大家分享。
希望与同样在学习的朋友进行交流。
空间地址:/yearmay。
若能得到行家的指正,荣幸之至;若对初学者有些帮助,深感欣慰。
正交试验需要进行以下一些工作:1)明确实验目的2)明确试验指标3)确定因子与水平4)选用合适的正交表,进行表头设计5)列出试验计划6)进行实验和记录试验结果7)数据分析在此以一具体事例,说明如何用minitab实现正交试验设计及分析的。
某化工厂希望寻找提高产品转化率的生产工艺条件。
1)实验目的提高转化率2)试验指标转化率。
转化率越大越好,这一指标是一个望大特性。
3)因子与水平经分析影响转化率的可能因子有三个,相对应的水平见表1表1 因子与水平因子一水平二水平三水平A:反应温度(℃)80 85 90B:反应时间(min)90 120 150C:加碱量(%) 5 6 74)选用正交表和设计表头由于因子均为3水平,故选用三水平正交表。
由正交表每列自由度f列等于各列的水平数减1,两交互作用的自由度等于两因素的自由度的乘积,则因子与交互作用的自由度之和为:fA+ fB + fC = fA+ fB + fC=6据选择正交表的必要条件,其行数n应满足:n>6。
为了避免表头出现混杂现象,并且尽量保证试验次数尽量少。
此例不考虑交互作用,表头设计见表2。
表2 表头设计表头设计 A B C列号 1 2 3 45)列出试验计划试验计划可用minitab帮助实现。
见图1。
图1图2图3图4图56)试验和记录为了减少或避免事先某些考虑不周及环境条件变化所引起的系统误差常采用试验次序随机化,本文采用试验编号随机抽签的方法来进行试验。
并将试验结果记录与C5中。
7)数据分析A)直观分析图6-1图6-2图7图8图9图10图11图12 B)方差分析图13图14图16图 17对于统计模型,必须对统计数据进行独立性检验、正态性检验以及等方差检验。
[工程科技]Minitab教程 全析因试验设计
![[工程科技]Minitab教程 全析因试验设计](https://img.taocdn.com/s3/m/1dce60276c85ec3a86c2c52f.png)
50
51
第四步:对选定模型进行分析解释
输出各因子的主效应图和交互效应图; 输出等高线图、响应曲面图; 实现最优化。
52
选择图形种类
53
选定显示主效应的响应变量和因子
54
选定显示交互效应的响应变量和因子
55
选定显示立方体图的响应变量和因子
56
各因子的主效应图
57
各因子的交互效应图
3
代码化的换算: 令中心值为M,半间距为D,则 代码值 = (真实值—M)/D 真实值 = M+D•代码值 k个因子的二水平全析因实验记为:2k实验 因子的数量
2k
因子的水平数
4
2k : 实验的运行次数
K
Std. Order 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
23
检查ANOVA表中的弯曲项, P值应大于0.05,说明无 弯曲项。否则应在模型中补上二次项; 检查拟合的总效果 多元全相关系数R2 (R-sq)和修正的多元全相关系数 R2adj (R-sq(adj))均越接近于1越好,两者之差越小越好。 检查s 或s2的值,越小越好。 检查各项效应的显著性 看Pareto图和正态分布图。
34
残差散点图和正态检验图
35
残差对于以自变量Press为横轴的散点图
36
第三步:模型要改进吗?
模型是否基本上可行? 剔除非显著因子和非显著交互作用后再进行计 算分析。 本例中仅A、B、AB为显著。据此修改拟合 模型中的 “选项”,做新的一轮计算分析。
37
38
第七章 试验设计方法的minitab软件操作

60 D 30 90
D -1 1
60
均值
30 -1 70 60 50 40 F 1 -1 K 1
E 30 90
E -1 1
60 F 30
F -1 1
K
30 -1 1 -1 1
从以上分析结果可知,D,E为关键因子,D,F因子有交互作用。
22
案例四:某化工品的合成工艺
在某化工的合成工艺中,为了提高产量,试验者选了3个因
y 553.370 4.304 A 0.331B 0.702C 0.007A2
31
4、用MINITAB进行图形分析
y 与 B, A 的等值线图
50
80 90 100 110 120 130 y < – – – – – – > 80 90 100 110 120 130 140 140
数据均值
1 2 20 15 A 10 5 20 15 D 10 5 1 2
D 1 2 A 1 2
9
6、对信噪比的主要影响分析
信噪比 主效应图
数据均值
A 34 33 32 31 30 1 C 34 33 32 31 30 1 2 1 2 2 1 D 2 B
信噪: 望大
从图中可以看出 A1B1C2 D1 组合最好。
y
y 与 B, A 的曲面图
保持值 C 0
45
40
保持值 C 0
140 120 100 50 40 200 250 A 300 30
B
35
80
B
30 200
220
240 A
260
280
300
32
5、对响应变量进行优化 响应优化
Minitab操作指南

R Chart by 测量人员
A B C UCL=4.792 4 2 0 _ R=1.467 LCL=0 498 500
测量读数 by 测量人员
Sample Range
496 A B 测量人员 C
Xbar Chart by 测量人员
A B C UCL=500.358 _ _ X=497.6
Sample Mean
• Gage Run Chart提供各测量数据的链图,帮助你分 析不同的操作者和工件之间测量结果的差异; • Gage R&R (Crossed) 用于分析当每一被测工件都可 以被多个操作者重复测量时的GR&R分析; • Gage R&R (Nested) 用于分析当每一被测工件不可 以被多个操作者重复测量(即进行破坏性测量)时的 GR&R分析;上述三种选择均针对计量型(连续型)数 据而言。 • Attribute Gage Study (Analytic Method)则是针 对计数型(逻辑型)数据的分析。
样本 1 2 3 4 5 6 7 8 9 10 X1 99.70 99.32 99.89 99.15 99.66 97.74 101.18 101.54 101.49 97.16 X2 98.72 100.97 99.83 99.71 100.80 98.82 100.24 100.96 100.67 98.26 X3 100.24 100.87 101.48 99.17 101.06 99.24 99.62 100.62 99.36 97.59 X4 101.28 99.24 99.56 99.30 101.16 98.64 99.33 100.67 100.38 100.09 X5 101.20 98.21 100.90 98.80 100.45 98.73 99.91 100.49 102.10 99.78
正交试验设计minitab

Minitab在正交试验设计中的应用
正交试验设计是一种常用的统 计方法,用于评估多个因素对 实验结果的影响。
Minitab提供了丰富的正交试 验设计工具,包括正交表生成、 数据输入、分析以及结果解读 等功能。
使用Minitab进行正交试验设 计,用户可以快速地确定关键 因素、优化实验条件并提高实 验效率。
具,包括正交试验设计。
02 正交试验设计的基本原理
正交表的选择
根据试验目的选择合适的正交表
正交表的选择应基于试验目的、因素数量和水平数,确保正交表具有足够的自 由度。
考虑试验精度和成本
选择正交表时,应平衡试验精度和成本,选择既能满足精度要求又具有较低成 本的方案。
试验方案的制定
确定试验因素和水平
明确试验的目标,如提 高产品性能、优化工艺
参数等。
选择正交表
根据试验因素和水平数 选择合适的正交表,确 保试验具有足够的代表
性和均衡性。
制定试验计划
执行试验
按照正交表的安排,确 定每个试验方案的试验
条件。
根据试验计划进行试验,响程度
利用Minitab的统计功能,计 算各因素对试验结果的影响程 度。
正交试验设计在Minitab中的应用
目 录
• 引言 • 正交试验设计的基本原理 • Minitab软件介绍 • 正交试验设计在Minitab中的实现 • 案例分析 • 结论与展望
01 引言
目的和背景
确定正交试验设计在 Minitab中的实施步 骤和具体应用。
探讨正交试验设计在 Minitab中的实际应 用案例。
分析正交试验设计在 Minitab中的优势和 局限性。
正交试验设计简介
正交试验设计是一种通过合理 安排试验因素和水平,以最小 试验次数获得最优解的统计方
响应面法和实验设计软件Minitab 及 DesignExpert简介

三因素下的立方点、轴向点和中心点
区组(block)
也叫块。设计包含正交模块,正交模块 可以允许独立评估模型中的各项及模块 影响,并使误差最小化。
但由于把区组也作为一个因素来安排, 增加了分析的复杂程度。
序贯试验(顺序试验)
先后分几段完成试验,前次试验设计的点上 做过的试验结果,在后续的试验设计中继续 有用。
立方点,也称立方体点、角点,即2水平对 应的“-1”和“+1”点。各点坐标皆为+1或-1。 在k个因素的情况下,共有2k个立方点
轴向点(axial point)
轴向点,又称始点、星号点,分布在轴向上。
除一个坐标为+α或-α外,其余坐标皆为0。
在k个因素的情况下,共有2k个轴向点。
中心点(center point)
这样做,每个因素的取值水平只有3个(-1,0,1),而 一般的CCD设计,因素的水平是5个(-α,-1,0,1,α), 这在更换水平较困难的情况下是有意义的。
这种设计失去了旋转性。但
保留了序贯性,即前一次在 立方点上已经做过的试验结 果,在后续的CCF设计中可 以继续使用,可以在二阶回
归中采用。
中心点的个数选择
旋转性(rotatable)设计
旋转设计具有在设计中心等距点上预测方差 恒定的性质,这改善了预测精度。
α的选取
在α的选取上可以有多种出发点,旋转性是
个很有意义的考虑。在k个因素的情况下,应 取
α = 2 k/4
当k=2, α =1.414;当k=3, α =1.682; 当k=4, α =2.000;当k=5, α =2.378
2. 创建“中心复合”或“Box-Behnken”设计; 3. 确定试验运行顺序(Display Design); 4. 进行试验并收集数据; 5. 分析试验数据; 6. 优化因素的设置水平。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
页眉内容Minitab 实验之试验设计实验目的:本实验主要引导学生利用 Minitab 统计软件进行试验设计分析,包括全因子 设计、部分因子设计、响应曲面设计、混料设计、田口设计以及响应优化,并能 够对结果做出解释。
实验仪器:Minitab 软件、计算机实验原理:“全因子试验设计”的定义是:所有因子的所有水平的所有组合都至少要进 行一次试验的设计。
由于包含了所有的组合,全因子试验所需试验的总次数会比 较多,但它的优点是可以估计出所有的主效应和所有的各阶交互效应。
所以在因 子个数不太多,而且确实需要考察较多的交互作用时,常常选用全因子设计。
一 般情况下,当因子水平超过 2 时,由于试验次数随着因子个数的增长而呈现指数 速度增长,因而通常只作 2 水平的全因子试验。
进行 2 水平全因子设计时,全因子试验的总试验次数将随着因子个数的增加 而急剧增加,例如,6 个因子就需要 64 次试验。
但是仔细分析所获得的结果可 以看出,建立的 6 因子回归方程包括下列一些项:常数项、主效应项有 6 项、二 阶交互作用项 15 项、三阶交互项 20 项,…,6 阶交互项 1 项,除了常数项、主 效应项和二阶交互项以外,共有 42 项是 3 阶以及 3 阶以上的交互作用项,而这 些项实际上已无具体的意义了。
部分因子试验就是在这种思想下诞生的,它可以 使用在因子个数较多,但只需要分析各因子和 2 阶交互效应是否显著,并不需要 考虑高阶的交互效应,这使得试验次数大大减少。
在实际工作中,常常要研究响应变量 Y 是如何依赖于自变量,进而能找到 自变量的设置使得响应变量得到最佳值(望大、望小或望目)。
如果自变量的个 数较少(通常不超过 3 个),则响应曲面方法(response surface methodology,RSM) 是最好的方法之一,本方法特别适合于响应变量望大或望小的情形。
通常的做法 是:先用 2 水平因子试验的数据,拟合一个线性回归方程(可以包含交叉乘积项), 如果发现有弯曲的趋势,则希望拟合一个含二次项的回归方程。
其一般模型是(以 两个自变量为例):这些项比因子设计的模型增加了各自的变量的平方项。
由于要估计这些项的 回归系数,原来因子设计所安排的一些设计点就不够用了,需要再增补一些试验 点。
这种先后分两阶段完成全部试验的策略就是“序贯试验”的策略。
适用于这 种策略的方法有很多种,其中最常用的就是中心复合设计(central composite design,CCD)。
稳健参数设计(robust parameter design)(也称健壮设计、鲁棒设计,简称参 数设计)是工程实际问题中很有价值的统计方法。
它通过选择可控因子的水平组 合来减少一个系统对噪声变化的敏感性,从而达到减小此系统性能波动的目的。
过程的输入变量有两类:可控因子和参数因子。
可控因子是指一旦选定就保持不 变的变量,它包括产品或生产过程设计中的设计参数,而噪声因子是在正常条件 下难以控制的变量。
在做参数设计时,就是把可控因子的设计当做研究的主要对 象,与此同时让噪声因子按照设定的计划从而系统改变其水平的方法来表示正常页眉内容条件下的变化,最终按照我们预定的望大、望小或望目地目标选出最佳设置。
田 口玄一博士在参数设计方法方面贡献非常突出,他在设计中引进信噪比的概念, 并以此作为评价参数组合优劣的一种测度,因此很多文献和软件都把稳健参数设 计方法称为田口方法(Taguchi design)。
在实际工作中,常常需要研究一些配方配比试验问题。
这种问题常出现在橡 胶、化工、制药、冶金等课题中。
例如不锈钢由铁、镍、铜和铬 4 种元素组成; 闪光剂由镁、硝酸钠、硝酸锶及固定剂组成;复合燃料、复合塑料、混纺纤维、 混泥土、粘结剂、药品、饲料等都是由多种成分按相应比例而不是其绝对数值; 而且显然所有分量之和总是为 1 的。
对于这种分量之和总是为 1 的试验设计,称 为混料设计(mixture design)。
实验内容和步骤:实验之一:全因子试验设计:例:改进热处理工艺提高钢板断裂强度问题。
合金钢板经热处理后将提高其断 裂其抗断裂性能,但工艺参数的选择是个复杂的问题。
我们希望考虑可能影响断 裂强度的 4 个因子,确认哪些因子影响确实是显著的,进而确定出最佳工艺条件。
这几个因子及其试验水平如下:A:加热温度,低水平:820,高水平:860(摄氏度) B:加热时间,低水平:2,高水平:3(分钟) C:转换时间,低水平:1.4,高水平:1.6(分钟) D:保温时间,低水平:50,高水平:60(分钟) 由于要细致考虑各因子及其交互作用,决定采用全因子试验,并在中心点处 进行 3 次试验,一共 19 次试验。
步骤 1:全因子设计的计划(创建) 选择[统计]=>[DOE]=>[因子]=>[创建因子设计],单击打开创建因子设计对话 框。
, 选择两水平因子(默认生成元),在因子数中选择 4,单击“设计”选项, 弹出“设计”选项对话框。
选择“全因子”试验次数为 16 的那行,并在“每个 区组的中心点数”中选择 3,其他项保持默认(本例中没有分区组,各试验点皆页眉内容不需要完全复制)。
单击确定。
单击“因子”选项打开,分别填写四个因子的名称及相应的低水平和高水平的设置。
单击确定。
“选项”选项可以使用折叠设计(这是一种减少混杂的方法)、指定部分(用 于设计生成)、使设计随机化以及在工作表中存储设计等;“结果”选项用于控制 会话窗口中显示的输出。
本例中这两项保持默认。
单击确定,计算机会自动对于试验顺序进行随机化,然后形成下列表格。
在表的最后一列,写上响应变量名(强 度),这就完成了全部试验的计划阶段的工作。
步骤 2:拟合选定模型按照上图的试验计划进行试验,将结果填入上表的最后一列,则可以得到试 验的结果数据(数据文件:DOE_热处理(全因)),如下:拟合选定模型的主要任务是根据整个试验的目的,选定一个数学模型。
通常首先可以选定“全模型”,就是在模型中包含全部因子的主效应及全部因子的二 阶交互效应。
在经过细致的分析之后,如果发现某些主效应和二阶交互效应不显 著,则在下次选定模型的时候,应该将不显著的主效应和二阶交互效应删除。
选择[统计]=>[DOE]=>[因子]=>[分析因子设计],打开分析因子设计对话框。
点击“项”选项后,在“模型中包含项的阶数”中选择 2(表示模型中只包 含 2 阶交互作用和主效应项,三阶以上交互作用不考虑),对默认的“在模型中 包括中心点”保持不选。
单击确定。
在“图形”选项中,“效应图”中选择“正态”和“Pareto”,“图中的标准差” 中选择“正规”,“残差图”中选择“四合一”,在“残差与变量”图中将“加热温度”、“加热时间”、“转换时间”和“保温时间”选入,单击确定。
在“存储”选项中,在“拟合值与残差”中选定“拟合值”和“残差”,在“模型信息”中选定“设计矩阵”。
单击确定。
结果如下:拟合因子: 强度 与 加热温度, 加热时间, 转换时间, 保温时间强度 的估计效应和系数(已编码单位)系数标项效应 系数 准误TP常量541.632 1.377 393.39 0.000加热温度20.038 10.019 1.500 6.68 0.000加热时间16.887 8.444 1.500 5.63 0.000转换时间3.813 1.906 1.500 1.27 0.240保温时间11.113 5.556 1.500 3.70 0.006加热温度*加热时间 0.737 0.369 1.500 0.25 0.812加热温度*转换时间 -0.487 -0.244 1.500 -0.16 0.875加热温度*保温时间 3.062 1.531 1.500 1.02 0.337加热时间*转换时间 1.263 0.631 1.500 0.42 0.685加热时间*保温时间 7.113 3.556 1.500 2.37 0.045转换时间*保温时间 0.837 0.419 1.500 0.28 0.787S = 6.00146 PRESS = 1778.45R-Sq = 92.49% R-Sq(预测) = 53.68% R-Sq(调整) = 83.11%强度 的方差分析(已编码单位)来源自由度 Seq SS Adj SS Adj MSFP页眉内容主效应4 3298.85 3298.85 824.71 22.90 0.0002因子交互作用6 252.17 252.17 42.03 1.17 0.408残差误差8 288.14 288.14 36.02弯曲1 9.92 9.92 9.92 0.25 0.633失拟5 169.72 169.72 33.94 0.63 0.709纯误差2 108.50 108.50 54.25合计18 3839.16强度 的估计系数(使用未编码单位的数据)项系数常量932.26加热温度-0.25063加热时间-111.262转换时间43.812保温时间-16.5637加热温度*加热时间 0.036875加热温度*转换时间 -0.121875加热温度*保温时间 0.0153125加热时间*转换时间 12.6250加热时间*保温时间 1.42250转换时间*保温时间 0.83750结果分析:分析要点一:分析评估回归的显著性。
包含三点: (1)看方差分析表中的总效果。
方差分析表中,主效应对应的概率P值为 0.000小于显著性水平0.05,拒绝原假设,认为回归总效果是显著的。
(2)看方差分析表中的失拟现象。
方差分析表中,失拟项的P值为0.709, 无法拒绝原假设,认为回归方程并没有因为漏掉高阶交互作用项而产生失拟现 象。
(3)看方差分析表中的弯曲项。
方差分析表中,弯曲项对应的概率P值0.633, 表明无法拒绝原假设,说明本模型中没有弯曲现象。
分析要点二:分析评估回归的总效果(1)两个确定系数R-Sq与R-Sq(调整),计算结果显示,这两个值分别为 92.49%和83.11%,二者的差距比较大,说明模型还有待改进的余地。
(2)对于预测结果的整体估计。
计算结果显示R-Sq和R-Sq(预测)分别为92.49%和53.68%,二者差距比较大;残差误差的SSE为288.14,PRESS 为 1778.45, 两者差距也比较大;说明在本例中,如果使用现在的模型,则有较多的点与模型 差距较大,模型应该进一步改进。
分析要点三:分析评估各项效应的显著性。
计算结果显示,4个主效应中, 加热温度、加热时间和保温时间是显著的,只有转换时间不显著;6个2因子水平 交互效应中,只有加热时间*保温时间是显著的。
