Matlab微积分问题的计算机求解实验
实验一B Matlab基本操作与微积分计算
实验一Matlab基本操作与微积分计算实验目的1.进一步理解导数概念及其几何意义.2.学习matlab的求导命令与求导法.3.通过本实验加深理解积分理论中分割、近似、求和、取极限的思想方法.4.学习并掌握用matlab求不定积分、定积分、二重积分、曲线积分的方法.5.学习matlab命令sum、symsum与int.实验内容一、变量1、变量MATLAB中变量的命名规则是:(1)变量名必须是不含空格的单个词;(2)变量名区分大小写;(3)变量名最多不超过19个字符;(4)变量名必须以字母打头,之后可以是任意字母、数字或下划线,变量名中不允许使用标点符号.1、创建简单的数组x=[a b c d e f ]创建包含指定元素的行向量x=first:step: last创建从first起,逐步加step计数,last结束的行向量, step缺省默认值为1x=linspace(first,last,n)创建从first开始,到last结束,有n个元素的行向量x=logspace(first,last,n)创建从first开始,到last结束,有n个元素的对数分隔行向量.注:以空格或逗号分隔的元素指定的是不同列的元素,而以分号分隔的元素指定了不同行的元素.2、数组元素的访问(1)访问一个元素: x(i)表示访问数组x的第i个元素.(2)访问一块元素: x(a :b :c)表示访问数组x的从第a个元素开始,以步长为b到第c个元素(但不超过c),b可以为负数,b缺损时为1.(3)直接使用元素编址序号: x ([a b c d]) 表示提取数组x的第a、b、c、d个元素构成一个新的数组[x (a) x (b) x(c) x(d)].3、数组的运算(1)标量-数组运算数组对标量的加、减、乘、除、乘方是数组的每个元素对该标量施加相应的加、减、乘、除、乘方运算.设:a=[a1,a2,…,an], c=标量, 则:a+c=[a1+c,a2+c,…,an+c]a .*c=[a1*c,a2*c,…,an*c]a ./c= [a1/c,a2/c,…,an/c](右除)a .\c= [c/a1,c/a2,…,c/an] (左除)a .^c= [a1^c,a2^c,…,an^c]c .^a= [c^a1,c^a2,…,c^an](2)数组-数组运算当两个数组有相同维数时,加、减、乘、除、幂运算可按元素对元素方式进行的,不同大小或维数的数组是不能进行运算的.设:a=[a1,a2,…,an], b=[b1,b2,…,bn], 则:a +b= [a1+b1,a2+b2,…,an+bn]a .*b= [a1*b1,a2*b2,…,an*bn]a ./b= [a1/b1,a2/b2,…,an/bn]a .\b=[b1/a1,b2/a2,…,bn/an]a .^b=[a1^b1,a2^b2,…,an^bn]三、矩阵1、矩阵的建立矩阵直接输入:从“[ ” 开始,元素之间用逗号“,”(或空格),行之间用分号“;”(或回车),用“ ]”结束.特殊矩阵的建立:a=[ ] 产生一个空矩阵,当对一项操作无结果时,返回空矩阵,空矩阵的大小为零.b=zeros (m,n) 产生一个m行、n列的零矩阵c=ones (m,n) 产生一个m行、n列的元素全为1的矩阵d=eye (m,n) 产生一个m行、n列的单位矩阵eye (n) %生成n维的单位向量eye (size (A)) %生成与A同维的单位阵2、矩阵中元素的操作(1)矩阵A的第r行A(r,:)(2)矩阵A的第r列A(:,r)(3)依次提取矩阵A的每一列,将A拉伸为一个列向量A(:)(4)取矩阵A的第i1~i2行、第j1~j2列构成新矩阵:A(i1:i2, j1:j2)(5)以逆序提取矩阵A的第i1~i2行,构成新矩阵:A(i2:-1:i1,:)(6)以逆序提取矩阵A的第j1~j2列,构成新矩阵:A(:, j2:-1:j1 )(7)删除A的第i1~i2行,构成新矩阵:A(i1:i2,:)=[ ](8)删除A的第j1~j2列,构成新矩阵:A(:, j1:j2)=[ ](9)将矩阵A和B拼接成新矩阵:[A B];[A;B]3、矩阵的运算(1)标量-矩阵运算同标量-数组运算.(2)矩阵-矩阵运算a. 元素对元素的运算,同数组-数组运算.(A/B %A右除B; B\A %A左除B)b. 矩阵运算:矩阵加法:A+B矩阵乘法:A*B方阵的行列式:det(A)方阵的逆:inv(A)方阵的特征值与特征向量:[V,D]=eig[A] A 的转置 A’ A 的n 次幂A^n 四、导数及偏导数计算 1.学习matlab 命令.建立符号变量命令sym 和syms 调用格式: x=sym(‘x’), 建立符号变量x ;syms x y z , 建立多个符号变量x,y,z ; matlab 求导命令diff 调用格式:diff (函数()f x ) , 求()f x 的一阶导数()f x ';diff (函数()f x , n ) , 求()f x 的n 阶导数()()n f x (n 是具体整数); diff (函数(,)f x y ,变量名x ), 求(,)f x y 对x 的偏导数f x∂∂; diff (函数(,)f x y , 变量名x ,n ) ,求(,)f x y 对x 的n 阶偏导数n n fx∂∂;matlab 求雅可比矩阵命令jacobian ,调用格式:jacobian ([(,,)f x y z ;(,,)g x y z ;(,,)h x y z ], [,,x y z ])给出: f f f x y z gg g x y z h h h xyz ⎛⎫∂∂∂ ⎪∂∂∂ ⎪ ⎪∂∂∂⎪∂∂∂ ⎪ ⎪∂∂∂ ⎪∂∂∂⎝⎭2.求一元函数的导数. (1)()y f x =的一阶导数. 例1.1 设()x f x e =,用定义计算(0)f '. 解:()f x 在某一点0x 的导数定义为极限: 000()()limx f x x f x x∆→+∆-∆我们记h x =∆,输入命令:syms h;limit((exp(0+h)-exp(0))/h,h,0) 得结果:ans=1.可知(0)1f '= 例1.2 求ln(sin )y x =的导数. 解: 输入命令:dy_dx=diff(log(sin(x))). 得结果:dy_dx=cos(x)/sin(x).在matlab 中,函数x ln 用log(x)表示,而log10(x)表示x lg .例1.3 求下列函数的导数: %利用matlab 命令diff 一次可以求出若干个函数的导数.1.1y =2.22cos 2cos2y x x =+.3.xy sin 34=.4.xy ln ln 4=. 解: 输入命令:a=diff([sqrt(x^2- 2*x+5),cos(x^2)+2*cos(2*x),4^(sin(x)),log(log(x))]). 得结果:a=[1/2/(x^2-2*x+5)^(1/2)*(2*x-2), -2*sin(x^2)*x-4*sin(2*x), 4^sin(x)*cos(x)*log(4), 1/x/log(x)].由本例可以看出,matlab 函数是对矩阵或向量进行操作的,a(i)表示向量a 的第i 个分量.函数向量的第i 个函数的导数为导数向量中对应的元素。
实验六 matlab数值微分积分实验

软件学院 MATLAB 程序设计 课程实验报告 201 ~201 学年 第 学期 级 专业班级: 学号: 姓名:实验六 数值微分积分实验一、实验目的1.掌握基本的插值与拟合方法2.掌握使用数学工具Matlab 进行实际问题的插值和拟合建模二、实验内容1.解微分方程2. 求解积分三、实验环境1.工具软件:MATLAB2012b四、实验步骤1. 解微分方程(1)微分方程的解析解dsolve(‘方程1’, ’方程2’,…‘方程n ’, ‘初始条件…’, ‘自变量’)求微分方程的特解⎪⎩⎪⎨⎧===++15)0(',0)0(029422y y y dx dy dx y d(2)求微分方程组的通解⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=+-=+-=z y x dtdz z y x dt dy zy x dt dx 244354332(3)常微分方程的数值解[t ,x]=solver (’f ’, ts, x0, options )解微分方程组⎪⎪⎩⎪⎪⎨⎧===-=-==1)0(,1)0(,0)0(51.0'''321213312321y y y y y y y y y y y y(4)实例-微分方程设位于坐标原点的甲舰向位于x 轴上点A(1, 0)处的乙舰发射导弹,导弹头始终对准乙舰.如果乙舰以最大的速度v 0(是常数)沿平行于y 轴的直线行驶,导弹的速度是5v 0,求导弹运行的曲线方程,并绘图表示。
2. 求解积分(1) quad 函数、quadl 函数quad8函数来求定积分例:被积函数f(x)=x*sin(x)/(1+cos(x)*cos(x)),x 的范围自定义(2) 梯形积分函数trapzX = sort(rand(1,101)*pi);Y = sin(X);Z = trapz(X,Y);(3)dblquad 函数用于求二重积分的数值解自变量范围:pi <= x <= 2*pi, 0 <= y <= pi ;被积函数z = y*sin(x)+x 2*cos(y)(4)triplequad 函数用于求三重积分的数值解五、分析与思考1、什么是解析解?什么是数值解?六、实验总结。
计算方法实验报告matlab

计算方法实验报告matlab《使用MATLAB进行计算方法实验报告》摘要:本文利用MATLAB软件进行了一系列计算方法实验,包括数值积分、微分方程求解、线性代数计算等。
通过实验结果分析,我们验证了各种计算方法的准确性和稳定性,为进一步研究和应用这些方法提供了可靠的数值支持。
引言:计算方法是现代科学和工程中不可或缺的一部分,它们通过数值计算的方式解决了许多复杂的数学问题。
MATLAB作为一种强大的数值计算工具,被广泛应用于各种计算方法的实验和研究中。
本文将利用MATLAB进行一系列计算方法实验,验证其在数值计算中的有效性和实用性。
实验一:数值积分在本实验中,我们将使用MATLAB对一些常见的积分问题进行数值求解,比较不同数值积分方法的精度和收敛速度。
通过实验结果的分析,我们将评估各种数值积分方法的适用范围和优缺点。
实验二:微分方程求解微分方程是自然界和工程领域中常见的数学模型,其数值求解方法对于模拟和预测系统行为至关重要。
在本实验中,我们将使用MATLAB对一些典型的微分方程进行数值求解,并比较不同数值方法的稳定性和精度。
实验三:线性代数计算线性代数是现代科学和工程中的基础学科,其在数据处理、信号处理、优化等领域中有着广泛的应用。
在本实验中,我们将利用MATLAB进行一些常见的线性代数计算,比如矩阵求逆、特征值分解等,验证其数值计算的准确性和效率。
结论:通过以上一系列的实验,我们验证了MATLAB在计算方法实验中的有效性和实用性。
我们发现,MATLAB提供了丰富的数值计算工具和函数库,能够满足各种计算方法实验的需求。
同时,我们也发现不同的计算方法在不同的问题上有着各自的优势和局限性,需要根据具体问题选择合适的方法。
希望本文的实验结果能够为相关领域的研究和应用提供一定的参考和借鉴。
实验四 用matlab计算积分

实验四 用matlab 计算积分4.1积分的有关理论定积分:积分是微分的无限和,函数)(x f 在区间],[b a 上的积分定义为∑⎰=→∆∆==ni ii x bax f dx x f I i 1)max()(lim)(ξ其中.,,2,1),,(,,1110n i x x x x x b x x x a i i i i i i n =∈-=∆=<<<=--ξ从几何意义上说,对于],[b a 上非负函数)(x f ,记分值I 是曲线)(x f y =与直线b x a x ==,及x 轴所围的曲边梯形的面积。
有界连续(或几何处处连续)函数的积分总是存在的。
微积分基本定理(Newton-Leibniz 公式):)(x f 在],[b a 上连续,且],[),()('b a x x f x F ∈=,则有)()()(a F b F dx x f ba-=⎰这个公式表明导数与积分是一对互逆运算,它也提供了求积分的解析方法:为了求)(x f 的定积分,需要找到一个函数)(x F ,使)(x F 的导数正好是)(x f ,我们称)(x F 是)(x f 的原函数或不定积分。
不定积分的求法有学多数学技巧,常用的有换元积分和分部积分法。
从理论上讲,可积函数的原函数总是存在的,但很多被积函数的原函数不能用初等函数表示,也就是说这些积分不能用解析方法求解,需用数值积分法解决。
在应用问题中,常常是利用微分进行分析,而问题最终归结为微分的和(即积分)。
一些更复杂的问题是含微分的方程,不能直接积分求解。
多元函数的积分称为多重积分。
二重积分的定义为∑∑⎰⎰∆∆=→∆+∆ijji j i y x Gy x f dxdy y x f i i ),(lim ),(0)max(22ηξ当),(y x f 非负时,积分值表示曲顶柱体的体积。
二重积分的计算主要是转换为两次单积分来解决,无论是解析方法还是数值方法,如何实现这种转换,是解决问题的关键。
Matlab微积分问题计算机求解实验

>> q2=quad('quad1',0,1)
【例】求exp(-x2)在[0,1]上的积分。
数值积分
3、编写被积函数表达式,函数名为f=@(x).exp(-x.^2);
>> q2=quad(f,0,1)
数值积分
(2)梯形法(被积函数由一个表格定义)
trapz函数采用梯形法求取数值积分,适用于由表格形式定义的函数关系的求定积分问题,求值速度快, 但精度差。
syms x; f=abs(x)/x;%给出待展开的函数 xx=[-pi:pi/200:pi]; xx=xx(xx~=0); xx=sort([xx,-eps,eps]);
Fourier级数的Matlab程序
yy=subs(f,x,xx);%计算f(x)的值 for i=1:20
[A,B,F]=fseries(f,x,n); y=subs(F,x,xx); subplot(4,5,n); plot(xx,yy);%画出f(x)的图像 hold on plot(xx,y);%画出Fourier级数的图像 end
K ex2dx 0
计算积分
21
( x1)2
练习:
e 2 dx,
0 2
e2t 2 x 2 1
dx
cost (2 x 2 3 x 1)2
符号求和
symsum(u,n,n0,nn): symsum(f,a,b): 关于默认变量求和
例:计算级数
S 1 及其前100项的部2 分和 n n 1
>> syms n; f=1/n^2;
>> S=symsum(f,n,1,inf)
>> S100=symsum(f,n,1,100)
MATLAB第三章

第三章微积分问题的计算机求解一、实验内容:题目1.试求出如下极限。
①limx→∞(3x +9x )1/ x,②lim x→∞[(x+2)x+2(x+3)x+3 ]/(x+5)2x+5【分析】:该题为单变量函数的极限。
极限问题可以用limit()函数直接求出。
要注意该函数的调用格式为:L=limit(fun,x,x0)(求极限),L=limit(fun,x,x0,’left’或’right’)(求极限)。
还需注意一开始要对函数的字符进行申明。
【解答】:(1)输入如下语句:>> syms x;f=(3^x+9^x)^(1/x);L=limit(f,x,inf)语句运行后显示如下:L =9(2)输入如下语句:>>syms x;f=(x+2)^(x+2)*(x+3)^(x+3)/(x+5)^(2*x+5);>> L=limit(f,x,inf)语句运行后显示如下:L =exp(-5)题目2.试求下面的双重极限。
①lim x→−1y→2 (x2y+xy3)/(x+y) 3,②limx→0 y→0 xy /√(xy+1)−1,③limx→0y→0 [1−cos(x2+y2)]/(x2+y2)e x2+y2。
【分析】:该题为多变量函数的极限问题。
他可以用嵌套使用limit()函数来解决。
在MATLAB上可以用L=limit(limit(f,x,x0),y,y0)或者L=limit(f,y,y0),x,x0)来解决。
其思想是所有的先关于X求导,再所有的关于y求导。
【解答】:(1)输入如下语句:>> syms x y>> f=(x^2*y+x*y^3)/(x+y)^3;>> L=limit(limit(f,x,-1),y,2)语句运行后显示如下:L =-6(2)输入如下语句:>> syms x yf=(x*y)/(sqrt(x*y+1)-1);L=limit(limit(f,x,0),y,0)按ENTER键,语句运行后显示如下:L =2(3)输入如下语句:>> syms x yf=(1-cos(x^2+y^2))/(sqrt(x^2+y^2)*exp(x^2+y^2));L=limit(limit(f,x,0),y,0)按ENTER键,语句运行后显示如下:L =题目3.求出下面函数的导数。
微积分问题的MATLAB求解
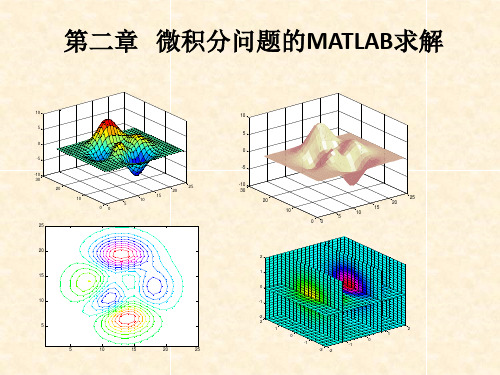
0-1规划(bintprog)
非线性最小二乘 lsqnonlin lsqcurvefit
其他规划ga gamultiobj simulannealbnd patternsearch threshacceptbnd 上下界 约束 fminbnd fmincon lsqnonlin lsqcurvefit
fun
H
A,b
Aeq,beq vlb,vub X0 x1,x2 options
A矩阵和b向量分别为线性不等式约束: linprog,quadprog,fgoalattain, fmincon,fminimax AX≤b中的系数矩阵和右端向量 Aeq矩阵和beq向量分别为线性等式约 束Aeq*X=beq中的系数矩阵和右端向量 X的下限和上限向量 迭代初始点坐标 函数最小化的区间 优化选项参数结构 linprog,quadprog,fgoalattain, fmincon,fminimax linprog,quadprog,fgoalattain, fmincon,fminimax,lsqcurvefit, lsqnonlin 除fminbnd外所有函数 fminbnd 所有优化函数
内寻找一个近似零点。 solve(f)求解表达式f的代数方程,求解变量为默认变量。 solve(f,x)求解变量为x sovle(f1,f2,...,fn,x1,x2,...,xn)求解f1,f2,...,fn表示的代数方程组。
例如:
三. 微商的计算
3.1符号导数
diff函数用于对符号表达式求导数,该函数的调用形式为: diff(f)没有指定变量和导数阶数,系统按照findsym函数指示的默认变量求一阶导数 diff(f,x) diff(f,n)按findsym函数指示的默认变量求n阶导数,n必须为正整数。 diff(f,x,n)
用MATLAB解微积分问题的实验报告4

>>xa=-2:0.2:2;ya=-2:0.5:2;[x,y]=meshgrid(xa,ya); >>z=x.*exp(-x.^2-y.^2); >>[px,py]=gradient(z,xa,ya); %画出函数的方向导数 >>contour(x,y,z),hold on,quiver(x,y,px,py),hold off 3.梯形积分法 指令: z=trapz (x, y) x 是表示积分区间的离散化向量; y 也是与 x 同 维数的向量,表示被积函数;z 返回积分近似值 实验原理:先将积分区间分解为几个小区间,用每个小区间上梯形 面积之和作为积分近似值 例如:求积分
2 2 2 2 xe(x +y ) dxdy 0 −2
和
������ 1 1 (ysint 0 0 −1
+ zcost) dtdydz
建立 M 文件,内容如下: fun=inline('x.*exp(x.^2+y.^2)','x','y'); dblquad(fun,0,2,-2,2) fun=inline('y.*sin(t)+z.*cos(t)','t','y','z'); triplequad(fun,0,pi,0,1,-1,1) 实验结果: (保存之后,运行结果如下: ) ans=881.8304
������, ������ ������������求解
������ ������−������ ������ ( −������ − ������−������ ������
������ ������ +������ ������
微积分问题的MATLAB求解

研究背景
微积分的相关知识 微积分是研究微分学与积分学的统称,其在自然科学, 经济学和工程学领域有着广泛应用。微积分的思想早在 17世纪就已经产生了。为了解决当时存在的科学问题, 费马、笛卡尔等著名的数学家做了大量的研究,积累了 很多理论成果。最终,牛顿和莱布尼茨被认为是独立的 微积分的发明者。 微积分主要有三大分支,即极限、微分学、积分学。微 积分的基本公式为
S symsum( fk , k, k0 , kn )
4.序列求积问题可用符号运算工具箱提供的symprod()。该函数调用格式为
P symprod ( fn , n, a,b)
微积分问题的MATLAB求解
论文要点——曲线积分及MATLAB求解
曲线积分一般分为第一类曲线积分和曲面积分的现成函数。论文中介 绍了曲线、曲面积分的概念,引入了将他们转换为一般积分问题的算 法,并介绍了如何利用符号运算工具箱直接求解曲线。在这里将通过 例子介绍第一类曲线积分的求解方法。
同样,我们也可以求解参数方程, 隐函数,多元函数Jacobi矩阵, Hess偏导数矩阵的导数
微积分问题的MATLAB求解
论文内容——积分问题的解析解
传统的积分求解方法需要灵活熟练的掌握积分知识,本文将从不定积分,定积分,多重 积分三个方面介绍积分问题的客观求解方法。
MATLAB符号运算工具箱提供了一个int()函数,可以直接用来求取符号函数的不定积分, 调用格式为F=int(f,x)
得出的结果为
y(x) 386459 x8 515273 x7 3067 x6 4087 x5 34 x4 23 x3 4 x2 1 x 918540 1224720 7290 9720 81 54 9 3
matlab第3章 微积分问题的计算机求解

2/28/2024星期六, 2008-9- 6, 13:07:55
Slide 1 (of 147)
18/159
3.2.1 函数的导数和高阶导数
如果函数和自变量都已知,且均为符号变 量,则可以用diff()函数解出给定函数的 各阶导数 函数语法
或
2/28/2024星期六, 2008-9- 6, 13:07:55
单变量函数Taylor级数展开 多变量函数Taylor级数展开
Fourier级数展开 级数求和的计算 序列求积问题
2/28/2024星期六, 2008-9- 6, 13:07:55
Slide 1 (of 147)
54/159
3.4.1 单变量函数 的Taylor幂级数展开
Slide 1 (of 147)
40/159
3.3.1 不定积分的推导
函数int()可以被用于计算不定积分
MATLAB函数
积分
多重积分,嵌套调用;更多重循环
2/28/2024星期六, 2008-9- 6, 13:07:55
Slide 1 (of 147)
41/159
例 3.21
函数 求其一阶导数,再积分
48/159
例 3.25
求解 MATLAB求解(早期版本)
直接公式求解
2/28/2024星期六, 2008-9- 6, 13:07:55
Slide 1 (of 147)
49/159
3.3.3 多重积分问题的 MATLAB求解
函数int()仍可以被用于计算多重积分
注意:需要根据实际情况先选择积分顺 序,可积的部分作为内积分,然后再处 理外积分。否则,会的不出解析解
Slide 1 (of 147)
用matlab计算微积分

是int,其调用格式为: int(f,x) int函数求函数f对变量x的不定积分。
例4 求不定积分
x x dx
2 4
解: 原 式 x 1 x 2 dx
1 1 x 2 d (1 x 2 ) 2
3 1 2 . .(1 x 2 ) 2 2 3 3 1 (1 x 2 ) 2 c 3
在MATLAB中,求定积分的函数是int,
例 6 求积分
1 0
1
2
3 2x x 1
dx, dx,
3 2x x
2
syms x; int(1/(3+2*x+x^2),x,0,1) int(1/(3+2*x+x^2),x,-inf,inf)
2x 1 例7求定积分 cost (2 x 2 3 x 1)2 dx
因式分解
因式分解
factor(f)
syms x; f=x^6+1; factor(f)
factor 也可用于正整数的分解
s=factor(100) factor(sym('12345678901234567890'))
大整数的分解要转化成符号常量
函数展开
函数展开
expand(f)
多项式展开
>> syms x; f=(x+1)^6; >> expand(f)
三角函数展开
>> syms x y; f=sin(x+y); >> expand(f)
合并同类项
合并同类项
collect(f,v): 按指定变量 v 进行合并 collect(f): 按默认变量进行合并
实验二MATLAB中的极限和微分积分运算

Matlab中可以通过命令[d,p,q]=gcd(a,b)来获得上述 的三个数,比如[d,p,q]=gcd(12,32)运行得到
实验二 MATLAB中的极限、微分和积分运算
2021/4/21
1
一、实验目的 熟悉MATLAB软件中关于极限、微分运算和不定积 分、定积分的基本命令,掌握利用MATLAB软件进 行求极限和微分运算的方法。掌握利用MATLAB软 件进行求不定积分、定积分等积分运算的方法。
南京邮电大学
2021/4/21
南京邮电大学
2021/4/21
18
综合实验
1.定积分近似计算的Monte Carlo方法
b
s
a
f (x)dx
H (b a) m
南京邮电大学
2021/4/21
19
例1 近似计算 1exdx 0
a=0;b=1;m=1000; s=0;H=exp(1);%s设置为落在曲边梯形内的点数 for i=1:m
a
3
5
7
9 11 13 15 17 19
b
4 12 24 40 60 84 112 144 180
c
5 13 25 41 61 85 113 145 181
可以证明,此时勾股数的通项可表示为
{a, b, c} {2u 1,2u2 2u,2u2 2u 1}
南京邮电大学
2021/4/21
29
c-b=2的情况留着自己讨论,现在给出c-b=3时的勾股 数,可以得到下表
实验4__MATLAB在微积分学的应用

二重极限: 二重极限: 数学模型
matlab表达式 表达式
【例3-3】求出二元函数极限值 】
syms x y a; f=exp(-1/(y^2+x^2))*(sin(x)^2/x^2)*... (1+1/y^2)^(x+a^2*y^2); L=limit(limit(f,x,1/sqrt(y)),y,inf)
例 3-9 求解∫ 0 dx∫ 0 - syms x y z;
1
1− x 2
dy∫
1− x − 2 y 0
xdz
int(int(int(x,z,0,1-x-2*y),y,0,(1-x)/2),x,0,1)
4.方程求解问题 方程求解问题
默认以x,y, 作为变量 默认以 ,z…作为变量
solve('2*x=4')
数学问题的解析解与数值解(略)
数学家和其他科学技术工作者的区别 数学家:理论严格证明、存在性 工程技术人员:如何直接得出解 解析解不能使用的场合
– 不存在 – 数学家解决方法,引入符号erf(a) – 工程技术人员更感兴趣积分的值 数值解
解析解不能使用的场合
– – – – 解析解不存在:无理数,无限不循环小数 π 数学家:尽量精确地取值,小日本60亿位 工程技术人员:足够精确即可 祖充之 3.1415926,阿基米德的~3.1418
solve('a*x^2 + b*x + c')
solve('a*x^2 + b*x + c','b') S = solve('x + y = 1','x - 11*y = 5')
微 积 分 MATLAB 实 验

微积分MATLAB实验MAO YUHUI微积分MATLAB实验(2005年11月修改稿)§1 MATLAB 导引一、关于数学软件在当今众多数学类科技应用软件中,就其原始内核而言,可分为两大类:一类是数学解析型软件,如 Mathematica、Maple、Mathcad 等,它们以符号计算见长;另一类是数值计算型软件,如MATLAB等,它们对大批数据具有较强的管理、计算和可视化能力.这四种软件在数学软件市场据于主导地位.本附录采用的实验软件是MATLAB.二、关于MATLAB1980 年前后,MATLAB的首创者Cleve Moler 博士在美国新墨西哥大学讲授线性代数课程时,为学生构思开发了矩阵计算专用软件MATLAB ( MATrix LABoratory , 矩阵实验室 ),使学生不致花费太多的时间在繁琐的运算与编程上.至1983年,Cleve Moler和John Little 采用C语言改写了MATLAB的内核.不久,他们成立了Mathworks公司,并将MATLAB 正式推向市场.MATLAB软件从1984年推出第一个版本到目前的MATLAB 7.1,总共已发布了十余个版本.随着版本不断更新,MATLAB 的功能越来越多,使用起来也越来越方便.MATLAB由主包、动态仿真(Simulink)以及功能各异的工具箱(Toolbox)组成.Toolbox的内容非常广泛,涉及数学、控制、通讯、经济、地理、信号处理、图象处理、神经网络等多种学科的数十种工具和模块集,为用户提供了丰富而实用的资源.此外,借助Maple的威力,MATLAB也具有相当强的扩展符号运算的功能.下面介绍使用MATLAB的基本知识.三、启动MATLAB安装完毕MATLAB软件后,在Windows桌面上会自动创建MATLAB快捷方式图表.由此启动MATLAB后出现指令窗“MATLAB”.在提示符“》”(或光标位置符“|”)后,便可输入指令(程序).四、数据的输入和输出MATLAB的基本数据结构是矩阵,向量被看作是特殊的矩阵.有多种方法输入(产生)和输出矩阵,下面介绍几种最基本的方法.(1)直接写入矩阵输入矩阵时,用方括号[]作为矩阵的定界符,用逗号或空格分隔各列,用分号分隔各行.例如键入A=[1, 2, 3; 4, 5, 6; 7, 8, 9 ]或A=[1 2 3; 4 5 6; 7 8 9 ]均产生一个3 3矩阵A⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321; 键入a =[10, 11, 12]则产生一个1⨯3向量.屏幕显示为注1.在MATLAB 中,大写字母与小写字母是不能混同的( 如上面的A与a 互不相 同 );注2.上面输入矩阵A与a 的句末不加任何标点而直接“ 回车”,MATLAB 将立即在其后输出(屏幕显示)A与a 的结果.若在句末加分号“ ;”而后再“回车”,则结果不会被输出.这两种方式同样适用于其它类似的情形.注3.用小矩阵可以合并成大矩阵,例如上面已经输入了矩阵A和a ,则有其中a' 是 a 的转置.(2)利用冒号“:”产生矩阵例如,输入 x = 1 : 5 ,将产生一个元素值由1到5增量为1的行向量x =[1,2,3,4,5];输入 x = 2: 0.5:4,将产生一个元素值由2到4增量为0.5的行向量x =[2,2.5,3,3.5,4];输入 x = 6:-0.2:5,则产生一个元素值由6到5增量为-0.2的行向量x =[6,5.8,5.6,5.4,5.2,5].利用冒号也可以从大矩阵中抽取子矩阵.例如上面已经输入了矩阵C,则指令D =C( 2 : 3,2 : 4 )将产生一个2⨯3的子矩阵,其元素是C的第2行至第3行、第2列至第4列.屏幕显示为:(3)获取(或定义)矩阵元素可用小括号标识矩阵的单个元素.例如, 相继输入C (2, 3 ) 和a(5)=-a(1)后,屏幕分别显示为:注1“ans = 6”表示矩阵C中位于第2行、第3列的元素为6;其中“ans”是MATLAB的一个内部变量,意即“答案(answer)”.注2定义了新元素 a (5) = -a (1) = -10 后,原来维数为3的向量a,其维数自动扩大为5了,未定义的 a(4)则自动置为0,输出的a = [ 10 11 12 0 -10 ] 就是经扩维后得到的新向量.在MATLAB中没有维数说明语句,它会自动确定矩阵的维数.(4)特殊矩阵●size(A)查询矩阵A的维数.●ones()产生全1矩阵.用法如下:ones ( n ) 产生全1(n⨯n) 矩阵;ones ( m, n ) 产生全1(m⨯n)矩阵;ones (size (A)) 产生与A同维数的全1矩阵.● zeros () 产生全0矩阵,用法同上.● eye () 产生单位矩阵(主对角线元素为1,其他元素为0),用法同上. ● diag () 产生对角矩阵:若v 是n 元向量(行向量或列向量),则diag ( v ) 是一个 n 阶的方阵,其主对角线元素为 v ,其他元素为0.(5)几个内部永久变量 ● pi 即圆周率π.● eps 浮点相对精度.对于大多数PC 机的IEEE 算术标准,eps = 16521022.22--⨯≈.● inf 无穷大.产生 inf 的方法之一是 1/0,除数为0时不会导致终止运行, 但会给出警告信息.● NaN 非数( Not a Number ).由0/0、inf /inf 或 inf - inf 得到.五、矩阵运算和数组运算矩阵的代数运算在MATLAB 中分为“矩阵运算”和“数组运算”两种操作.其中,矩阵运算是按照线性代数运算法则定义的;数组运算是按元素逐个执行的.两者的区别主要体现在相乘、相除与乘方三种运算上.列表如下:六、数组函数和矩阵函数数组函数 f (A)是对数组A( 矩阵或向量 )的元素逐个执行运算 f .数组函数表下列矩阵函数的意义与线性代数中的定义相同.矩阵函数表七、数据可视化MATLAB具有很强的绘图功能.[例一]绘制正弦曲线和二次曲线的图形.x=-pi:pi/100:pi;y=sin(x);subplot(1,2,1), plot(x,y);%把正弦曲线绘在一行二列的1号子窗口 x1=-1:0.1:1;y1=x1.^2;subplot(1,2,2),plot(x1,y1) %把二次曲线绘在一行二列的2号子窗口注 上面绘图程序还可简化为:y=sin([-pi:pi/100:pi]); y1=[-1:0.1:1].^2;subplot(1,2,1), plot(y);supplot(1,2,2), plot(y1)[例二]绘制下列曲面的图形:2222)sin(yx y x z ++=.clf; %清除当前图形窗口[x,y]= meshgrid(-8:0.5:8); %生成网格点坐标(x,y ) r=sqrt(x.^2+y.^2)+eps; z=sin(r)./r;mesh(x,y,z); colormap([1,0,0]) %绘出曲面网线图(红色)八、关于MATLAB NotebookMathworks 公司开发的MATLAB Notebook 成功地把Microsoft Word 与MATLAB 集成为一个整体,为文字处理、科学计算、工程设计营造了一个完美统一的工作环境.Notebook 是“活”的笔记本.在该笔记本中的计算指令可随时修改、即时解算,并能方便地作出图示.这对于撰写科技报告、论文和编写理工学科的教材讲义都是十分宝贵的. Notebook 文件又称为 M-book ( 它使用了Word 中的 M-book .dot 模板 ).在MATLAB 文件夹中打开子文件夹Notebook ,就会看到M-book .把它发送为桌面快捷方式,以便使用时作快速访问.先启动MATLAB ,然后启动M-book ( 在Word 窗口的菜单栏里会出现“Notebook ”). 在英文状态下输入一组指令;然后用鼠标把它们选中,再按[Ctrl +Enter ]组合键;那组指令变成绿色,并会被执行(计算所得结果显示为蓝色,若出现红色文字,那是出错提示). 这类操作也可以在[Notebook ]下拉菜单中去选择.有关MATLAB 编程,请大家到下一节丰富多彩的例子中去体会、学习.§2 微积分 MATLAB 实验演示一、用可视化程序绘制下列曲线和曲面的图形( 1 ) ]5,5[]5.0,5.0[,3,32-∈-∈+==t t t t y t x 与.clf; syms t; x=t^2; y=3*t+t^3;subplot(1,2,1); ezplot(x,y,[-0.5,0.5]); grid; subplot(1,2,2); ezplot(x,y,[-5,5]); grid( 2 ) 0333=-+y x y x 及其渐近线 01=++y x . clf; syms x y; hold on;ezplot(x^3 + y^3–3*x*y,[-2,2]); ezplot(x+y+1,[-2,2]); grid( 3 ) 曲面 2222y x y x y x z +-= .[ 基本法 ]clf; u= -10:0.5:10; [x,y]=meshgrid(u,u); z=x.*y.*(x.^2-y.^2)./(x.^2+y.^2+eps);mesh(x,y,z); colormap([1,0,1])[ 符号函数法( 并显示等高线 ) ]clf;syms x y; colormap([1,0,0]);ezmeshc(x*y*(x^2-y^2)/(x^2+y^2));二、计算极限、导数和积分( 1 ) 求极限:nn h n x M hx h x L )1(lim ,)ln()ln(lim0-=-+=∞→→和 . syms h n xL=limit('(log(x+h)-log(x))/h',h,0) M=limit('(1-x/n)^n',n,inf)L =1/xM =exp(-x)( 2 ) 22d d ,d d ,d d ,sin xyC a y B x y A ax y ====求. syms a x; y=sin(a*x); A=diff(y,x) B=diff(y,a) C=diff(y,x,2)A = cos(a*x)*aB = cos(a*x)*xC = -sin(a*x)*a^2( 3 ) 计算以下不定积分、定积分、反常积分:x x x x I d )22(1222⎰+-+=, x xx xJ d cos sin cos 2/0⎰π+=, ⎰+∞-=d e 2xK x .syms xf=(x^2+1)/(x^2-2*x+2)^2; g=cos(x)/(sin(x)+cos(x)); h=exp(-x^2); I=int(f)J=int(g,0,pi/2)K=int(h,0,inf)I =1/4*(2*x-6)/(x^2-2*x+2)+3/2*atan(x-1) J =1/4*piK =1/2*pi^(1/2)三、符号求和与 Taylor 展开( 1 ) 求级数∑∞=121n n的和S, 以及前十项的部分和S1. syms kS=symsum('1/k^2',1,inf)S1=symsum('1/k^2',1,10)S =1/6*pi^2S1 =1968329/1270080注 当级数的通项较简单时,上面程序中加单引号的 ' 1 / k^2 ' 可以省略单引号.在其他类似情形下,同样如此.( 2 ) 求级数∑∞=-2)1(n nn n x 的和函数S2.syms kS2=symsum('x^k/k/(k-1)',k,2,inf)S2=simplify(S2)S2 =1/2*x^2*(2/x*(-log(1-x)/x-1)*(x-1)-1/(x-1)*(-2*x+2)) S2 =-log(1-x)*x+log(1-x)+x注 最末的 “ simplify( S2 )”为简化函数,用来简化上面得到的“S2” .( 3 ) 设 x x g xx f sin 4e )(,21)(=+=.给出 f ( x ) 在 x = 1 处的3阶Taylor展开式和g ( x ) 在x = 0 处的Taylor 展开式的前面三个非零项 .syms xf=1/(2+x^4); Tf=taylor(f,4,1) g=exp(sin(x)); Tg=taylor(g,3,0)Tf =7/9-4/9*x-2/27*(x-1)^2+44/81*(x-1)^3 Tg =1+x+1/2*x^2四、Taylor 逼近与Fourier 逼近的直观演示( 1 ) 用Taylor 多项式逼近 y = sin x . 已知正弦函数的Taylor 逼近式为∑=----=≈nk k k k x x P x 1121!)12()1()(sin .下面给出这个逼近过程的直观图形:clf; syms x t;ezplot(t,0,[0,2*pi]); hold on; A=[1.5 3 4 4 5.4]; for n=1:5 P=0;for k=1:1:nP=P+(-1)^(k-1)*x^(2*k-1)/prod(1:(2*k-1)); end;( 2 ) 用 Fourier 多项式逼近矩形波 )(x f .设 )(x f 在一个周期上为⎪⎩⎪⎨⎧ππ-=π<<<<π--=.,0,,00,10,1)(x x x x f对它作Fourier 级数展开,得到∑∞=--π=1)12sin(1214)(k x k k x f .下面在一个周期上,将Fourier 级数的前一项、前两项和前七项分别进行叠加,从图 象上可以清晰地看到这个逼近过程 .clf; syms x tN=[1 2 7]; hold on;ezplot(t,0,[-pi,pi]); ezplot(0,t,[-2.5,2.5]); for n=1:3 F=0;for k=1:1:N(n)F=F+4*sin((2*k-1)*x)/(2*k-1)/pi; end;五、函数项序列一致收敛的直观启示例如,已知三个函数序列:{}{}{}{}{}.),0[,)1(1)(;]1,0[,e)(;]5,0[,e )(222222222∞+∈⎭⎬⎫⎩⎨⎧+-=∈=∈=--x x n x n x h x x n x g x x n x f n x n n x n n通过作出它们的图象,根据一致收敛的几何意义来观察它们的一致收敛性. ( 1 ) 作出 {})(x f n 的一族曲线如下:clf; hold on; x=0:0.02:5; for n=1:8y=n*x.^2.*exp(-n.*x); plot(x,y); end ;由图可见,{})(x f n 中每条曲线的峰值将随着 ∞→n 而趋于0 , 故{})(x f n 能在 [ 0, 5 ] 上一致收敛 于 0 .( 2 ) 作出 {})(x g n 的一族曲线如下 :clf; hold on;x=0:0.01:1; for n=5:-1:1y=n^2*x.*exp(-n^2*x.^2); plot(x,y); end ;由图可见,)(x g n 的峰值将随着 ∞→n 而趋于∞+,故在 x = 0 的任意小右邻域内,{})(x g n 不可能一致收敛;但是对于任意小的正数 a , {})(x g n 在 [ a , 1 ] 上仍有可能一致收敛 于 0 .( 3 ) 作出 {})(x h n 的一族曲线如下:clf; hold on; x=0:0.01:3; for n=1:1:5y=(1-n^2*x.^2)./(1+n^2*x.^2).^2; plot(x,y); end ;由图可见,极限函数在x = 0 处不连续,故 在x = 0 的任意小右邻域内, {})(x h n 不可能一致收敛;但在任何 [)()∞+⊂∞+,0,a 上, {})(x h n 仍有可能一致收敛 于 0 .实 验 作 业1.用可视化程序绘制下列曲线和曲面的图形:(1)]2,2[,1323-∈+--=x x x x y ;(2)222y x z -=.2.已知plot 3是三维曲线图函数.请你先想一想:由指令pi])*[0,8t,cos(t),n(t),ezplot3(si t;syms能绘出怎样的曲线?再把此指令键入MATLAB 指令窗,看看实际绘出的曲线与你所想的结果是否相同?3.著名的莫比乌斯带(如图) 的一个参数描述是:⎪⎩⎪⎨⎧===+=.)2/(sin ,sin ,cos ,)2/cos(t s b z t r y t r x t s b a r其中b a ,为常数,例如取 1,2==b a ;参数]2,0[,]1,1[π∈-∈t s .请你用符号函数绘图法绘制出它的 图形.4.用MATLAB 求极限:xx L xx e-+=→10)1(lim .5.用MATLAB 求下列积分: (1)⎰++2x-x 2x)(1d x (化简结果);(2)⎰+∞2sin x x d .6.用MATLAB 求幂级数∑∞=+---1212114)1(n n n n x 的和函数(化简结果).。
MATLAB实验04多元函数微积分-8页word资料

实验04 多元函数微积分一实验目的 (2)二实验内容 (2)三实验准备 (2)四实验方法与步骤 (3)五练习与思考 (7)一 实验目的1 了解多元函数、多元函数积分的基本概念,多元函数的极值及其求法;2 理解多元函数的偏导数、全微分等概念,掌握积分在计算空间立体体积或表面积等问题中的应用;3 掌握MATLAB 软件有关求导数的命令;4 掌握MATLAB 软件有关的命令.二 实验内容1 多元函数的偏导数,极值;2 计算多元函数数值积分;3计算曲线积分,计算曲面积分.三 实验准备1 建立符号变量命令为sym 和syms ,调用格式为: x=sym('x') 建立符号变量x ;syms x y z 建立多个符号变量x ,y ,z ; 2 matlab 求导命令diff 的调用格式: diff(函数(,)f x y ,变量名x)求(,)f x y 对x 的偏导数fx∂∂; diff(函数(,)f x y ,变量名x,n) 求(,)f x y 对x 的n 阶偏导数n n fx∂∂;3 matlab 求雅可比矩阵命令jacobian 的调用格式: jacobian([f;g;h],[],,x y z )给出矩阵f f f x y zg g g x y zh h h xyz ⎛⎫∂∂∂ ⎪∂∂∂ ⎪ ⎪∂∂∂ ⎪∂∂∂ ⎪ ⎪∂∂∂ ⎪∂∂∂⎝⎭4 MATLAB 中主要用int 进行符号积分,常用格式如下: ① int(s)表示求符号表达式s 的不定积分② int(s,x)表示求符号表达式s 关于变量x 的不定积分③ int(s,a,b)表示求符号表达式s 的定积分,a ,b 分别为积分的上、下限④ int(s,x,a,b)表示求符号表达式s 关于变量x 的定积分,a,b 分别为积分的上、下限5 MATLAB 中主要用trapz,quad,quad8等进行数值积分,常用格式如下:① trapz(x,y)采用梯形积分法,其中x 是积分区间的离散化向量,y 是与x 同维数的向量、用来表示被积函数.② quad8('fun',a,b,tol)采用变步长数值积分,其中fun 为被积函数的M 函数名,a,b 分别为积分上、下限,tol 为精度,缺省值为1e-3.③ dblquad('fun',a,b,c,d)表示求矩形区域的二重数值积分,其中fun 为被积函数的M 函数名,a ,b 分别为x 的上、下限,c ,d 分别为y 的上、下限.使用help int ,help trapz ,help quad 等查阅有关这些命令的详细信息.四 实验方法与步骤例1 定义二元函数23z x y =+.解 (1)方法一:syms x y;z=x.^2+y.^3; (2)方法二:编写M 文件fun7.m 定义函数function z=fun7(x,y) z=x.^2+y.^3;(3)方法三:利用inline 函数:f=inline('x.^2+y.^3'). 注:不同定义方式,调用格式不完全相同. 例2 绘出函数23z x y =+的图形.解 程序为:x=linspace(-10,10,40);y=x;[X,Y]=meshgrid(x, y); Z=fun7(X,Y);surf(X,Y,Z),shading interp 结果如图2-10所示.图2-10例3 设222u x y yz =++,求uy∂∂.解 输入命令:syms x y z;diff(x^2+2*y^2+y*z,y),得ans=4*y+z.利用jacobian 命令:jacobian(x^2+2*y^2+y*z,[x y]),得ans=[2*x,4*y+z],即矩阵,u u x y ⎛⎫∂∂ ⎪∂∂⎝⎭例4 设642232z x y x y =-+,求22222,,z z zx y x y∂∂∂∂∂∂∂.解 求22zx∂∂的程序为:syms x y;diff(x^6-3*y^4+2*x^2*y^2,x,2)结果为: ans=30*x^4+4*y^2 求22zy ∂∂的程序为:syms x y;diff(x^6-3*y^4+2*x^2*y^2,y,2) 结果为:ans=-36*y^2+4*x^2 求2z x y ∂∂∂的程序为:syms x y;diff(diff(x^6-3*y^4+2*x^2*y^2,x),y) 结果:为ans=8*x*y.注:diff(x^6-3*y^4+2*x^2*y^2,x,y)是求zy∂∂,而不是求2z x y ∂∂∂例5 设由,x y 所确定的z 的隐函数为2225xy y z ++=,求,z zx y∂∂∂∂.解 令()22,,25F x y z xy y z =++-''/x z zF F x∂=-∂ 输入命令:syms x y z;a=jacobian(x*y+y^2+2*z^2-5,[x,y,z])可得矩阵()''',,x y z F F F =[y,x+2*y,4*z] 利用公式''''/,/x z y z z zF F F F x y∂∂=-=-∂∂可得 求zx ∂∂的程序为:-a(1)/a(3),结果为:-1/4*y/z ; 求zy∂∂的程序为:-a(2)/a(3),结果为:1/4*(-x-2*y)/z. 例6 求(1)()222122()312(12)f x x x x =-+-在点()2,2-临近的极小值.(2)222()()(1)f x y x x =-+-在55x -≤≤内的极值.解 求多元函数(,)z f x y =的极值点X 和极小值minf ,可用如下方法 方法一:X=fminsearch('f',x0),用的是Nelder-Mead 单纯形搜索法求解; 方法二:X=fminunc('f',x0),用的是BFGS 拟牛顿迭代法求解. 其中[](1),(2),(3),,()X x x x x n =,x0是初始点. 若求极大值点,用(-1)乘函数,再求极小值点.(1)程序如下:f='(x(1)^2-3*x(2))^2+12*(1-2*x(2))^2'; x=fminsearch(f,[-2,2]),minf=eval(f) 结果为:x =-1.2247 0.5000, minf =2.1879e-009结果说明在1 1.2247x =-,20.5x =时,函数的极小值为0.(2)先作函数的图形,程序如下: [x,y]=meshgrid(-5:0.5:5); f=(y-x.^2).^2+(1-x).^2; surf(x,y,f);结果如图2-11所示. 以下程序为求函数的极小值: 图2-11f='(x(2)-x(1).^2).^2+(1-x(1)).^2';x=fminsearch(f,[0.2,0.3]),minf=eval(f),shading interp 结果为:x=[1.0000,1.0000],minf=4.1546e-010 说明在1,1x y ==时,函数的极小值为0. 例8 计算积分221(1)d d x y xy x y +≤+⎰⎰.解 先将被积函数转化为二次积分:)22111(1)d d 1d d x y x y x y x y y x -+≤⎛⎫++=++ ⎪⎝⎭⎰⎰⎰,程序为:clear; syms x y;iy=int(1+x*y,y,-sqrt(1-x^2),sqrt(1-x^2));int(iy,x,-1,1) 结果为:ans=π.例9 求对弧长的曲线积分:(1)计算2d ,:2cos ,3sin Ly s L x t y t ==⎰。
【MATLAB】实验五:数值微积分与方程数值求解

实验五 数值微积分与方程数值求解一、实验目的1. 掌握求数值导数和数值积分的方法。
2. 掌握代数方程数值求解的方法。
3. 掌握常微分方程数值求解的方法。
二、实验内容要求:命令手工 ( )输入1. 求函数在指定点的数值导数。
232()123,1,2,3026x x x f x x x x x==2. 用数值方法求定积分。
(1) 210I π=⎰的近似值。
(2) 2220ln(1)1x I dt xπ+=+⎰3. 分别用三种不同的数值方法解线性方程组。
6525494133422139211x y z u x y z u x y z u x y u +-+=-⎧⎪-+-=⎪⎨++-=⎪⎪-+=⎩4. 求非齐次线性方程组的通解。
1234123412342736352249472x x x x x x x x x x x x +++=⎧⎪+++=⎨⎪+++=⎩解:先建立M 函数文件,然后命令窗口中写命令。
121/119/112/115/111/1110/11100010X k k --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,其中12,k k 为任意常数。
5. 求代数方程的数值解。
(1) 3x +sin x -e x =0在x 0=1.5附近的根。
(2) 在给定的初值x 0=1,y 0=1,z 0=1下,求方程组的数值解。
23sin ln 70321050y x y z x z x y z ⎧++-=⎪+-+=⎨⎪++-=⎩ans =1289/6826. 求函数在指定区间的极值。
(1) 3cos log ()xx x x x f x e ++=在(0,1)内的最小值。
(2) 33212112122(,)2410f x x x x x x x x =+-+在[0,0]附近的最小值点和最小值。
(以下选作题,是微分方程的数值解)7. 求微分方程的数值解。
x 在[1.0e-9,20]2250(0)0'(0)0xd y dy y dx dx y y ⎧-+=⎪⎪⎪=⎨⎪=⎪⎪⎩解:M 文件:运行结果:8. 求微分方程组的数值解,并绘制解的曲线。
matlab 《数学实验》报告9-matlab的极限和微分运算

matlab 《数学实验》报告9-matlab的极限和微分运算《数学实验》报告学号姓名成绩实验内容:Matlab的极限和微分运算。
一实验目的熟悉MATLAB软件中关于极限和微分运算的基本命令,掌握利用MATLAB软件求极限和微分运算的方法。
二预备知识(1)求函数的极限和微分的运算。
(2) Matlab基本命令limit,初等函数的表示方法。
三实验内容与要求1.求下列极限,将完成实验的程序写到文件sy31.m中xarctanF,(1); 1limxx,0Matlab命令结果clear%µÚ?þÖÖ???? =syms x atan(x)/xf=atan(x)/x ans =limit(f,'x',0) 1121,x,,F,(2) ,,2lim1,x,,x,0Matlab命令结果1clear F2 =syms x ((1+x)/(1-x))^(1/x) F2=((1+x)/(1-x))^(1/x) ans =limit(F2,'x',0) exp(2)xln(1x),F,(3) 3lim2x,0sinxMatlab命令结果 clear F3 =syms x x*log(1+x)/sin(x^2) F3=x*log(1+x)/sin(x^2) ans = limit(F3,'x',0) 1xarctanF,(4) 4limxx,,Matlab命令结果 clear F4 =syms x atan(x)/xF4=atan(x)/x ans =limit(F4,'x',inf) 011,,limF,,(5) ,,531x,1x,,,x1,Matlab命令结果 clear F5 =1/(1-x)-1/(1-x^3) syms xF5=1/(1-x)-1/(1-x^3) ans =limit(F5,'x',1) NaN2、求下列函数的倒数,将完成实验的程序写到文件sy32.m中3(1); y,cosx,cos3x1Matlab命令结果2clear%diyi y1 =syms x cos(x)^3-cos(3*x) y1=(cos(x))^3-cos(3*x) ans = diff(y1,x) -3*cos(x)^2*sin(x)+3*sin(3*x) (2) y,xsinxlnx2 Matlab命令结果 clear%dier y2 =syms xy2=x*sin(x)*log(x) x*sin(x)*log(x)diff(y2,x) ans =sin(x)*log(x)+x*cos(x)*log(x)+sin(x)xxe,1(3)y, 3sinxMatlab命令结果 clear%disan y3 =syms x (x*exp(x)-1)/sin(x) y3=(x*exp(x)-1)/sin(x) ans =diff(y3,x)(exp(x)+x*exp(x))/sin(x)-(x*exp(x)-1)/sin(x)^2*cos(x)x,,4(4),计算; y,ecosxy4Matlab命令结果 clear%disi y3 =exp(x)*cos(x) syms xans = y3=exp(x)*cos(x)diff(y3,x,4) -4*exp(x)*cos(x)2,,20y,xsin2x(5),计算 yMatlab命令结果 clear%diwu y5 =syms x x^2*sin(2*x)y5=x^2*sin(2*x) ans =-99614720*sin(2*x)-20971520*x*cos(2*x)+1048576*x^2*sindiff(y5,x,20) (2*x)3谣言:吃太咸了会得病,导语:“人体每日摄入食盐不应过多,否则易患多种疾病。
用MATLAB微分方程问题的计算机求解

实验报告131、实验名称:用MATLAB 微分方程问题的计算机求解。
2、实验目的:学会如何运用matlab 求解微分方程通解以及求解四阶定步长方程。
3、实验内容:一、试求解下面微分方程的通解以及满足()()()00,2,10===y x x π 条件下的解析解。
()()()()()⎪⎩⎪⎨⎧=+++=+++--te t x t x t y t y t e t y t x t x t x t t 4cos 6424sin 3)(4)(5)(66&&&&& 程序和结果如下:syms t[x,y]=dsolve('D2x+5*Dx+4*x+3*y=exp(-6*t)*sin(4*t)','2*Dy+y+4*Dx+6*x=exp(-6*t)*cos(4*t)')结果如下:x =-681/40820*exp(-6*t)*sin(4*t)+1013/40820*exp(-6*t)*cos(4*t)+C1*exp(t)+C2*exp(-13/4*t-1/4*t*57^(1/2))+C3*exp(-13/4*t+1/4*t*57^(1/2))y =279/4082*exp(-6*t)*sin(4*t)-433/4082*exp(-6*t)*cos(4*t)-10/3*C1*exp(t)-5/8*C2*e xp(-13/4*t-1/4*t*57^(1/2))-1/8*C2*exp(-13/4*t-1/4*t*57^(1/2))*57^(1/2)-5/8*C3*ex p(-13/4*t+1/4*t*57^(1/2))+1/8*C3*exp(-13/4*t+1/4*t*57^(1/2))*57^(1/2)二、请给出求解下面微分方程的Matlab 命令,并绘制y(t)曲线:()()()000,20,22)3(====++-y y y e y y t y ty y ty &&&&&&试选择四阶定步长Runge-Kutta 算法求解该方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算极限
f ( x) limit(f,x,a): 计算 lim xa limit(f,a): 当默认变量趋向于 a 时的极限 limit(f): 计算 a=0 时的极限 limit(f,x,a,'right'): 计算右极限 limit(f,x,a,'left'): 计算左极限
例:计算
ln( x h ) ln( x ) L lim , h0 h
Fourier级数的Matlab程序
3.
4.
e
( x 1)2 2 2 1
dx
2 a cos
2
0
d d
4 0
0
r 2 (1 cos )sin dr
5.
n 1 n 1 ( 1) n ( x 1) n 1
数值积分
函数quad()采用递推自适应Simpson法计算积分,精度较 高,较常使用。
梯形法
q = trapz(Y) q = trapz(X,Y)
X=0:0.01:1; Y=exp(-X.^2); q=trapz(X,Y)
其中向量X,Y定义函数关系Y=f(X)。 【例】求exp(-x2)在[0,1]上的积分。
上机作业
取一定数量的点,利用梯形数值积分 公式近似计算圆周率pi
1 π 4 dx 0 1 x2
数值积分
【例】计算二重定积分
1
1
[ e
2
2
x2 2
sin( x 2 y )dx]dy
①(1) 建立一个函数文件fxy.m: function f=fxy(x,y) f=exp(-x.^2/2).*sin(x.^2+y); (2) 调用dblquad函数求解。 I=dblquad('fxy',-2,2,-1,1) ② >> f=inline('exp(-x.^2/2).*sin(x.^2+y)') >> I=dblquad(f,-2,2,-1,1)
if a+b subs(f,x,x+L+a); end A=int(f,x,-L,L);%f(x)在[-pi,pi]内展开 B=[]; for i=1:n an=int(f*cos(i*pi*x/L),x,-L,L)/L; bn=int(f*sin(i*pi*x/L),x,-L,L)/L; end
Fourier级数的Matlab程序
x 2, y 1
计算积分
int(f,v,a,b): 计算定积分
b
a
f ( v )dv
int(f,a,b): 计算关于默认变量的定积分
int(f,v): 计算不定积分
f (v )dv
int(f): 计算关于默认变量的不定积分
例:计算
x2 1 I 2 dx 和 K 2 ( x 2 x 2)
数值积分
【例】求exp(-x2)在[0,1]上的积分。 3、编写被积函数表达式,函数名为 f=@(x).exp(-x.^2);
>> q2=quad(f,0,1)
数值积分
(2) (被积函数由一个表格定义) trapz函数采用梯形法求取数值积分,适用于由表格形式定 义的函数关系的求定积分问题,求值速度快,但精度差。
Fourier级数的Matlab程序
yy=subs(f,x,xx);%计算f(x)的值 for i=1:20 [A,B,F]=fseries(f,x,n); y=subs(F,x,xx); subplot(4,5,n); plot(xx,yy);%画出f(x)的图像 hold on plot(xx,y);%画出Fourier级数的图像 end
,
符号表达式的数值化
对符号求值的命令为vpa,即Variable precision arithmetic
R=vpa(A)或 R=vpa(A,d)
对符号表达式A求给定精度的值;d:输出数值的有效位数 Vpa的默认精度是23位。
digits(25); p=vpa(pi) w=vpa('(1+sqrt(5))/2',4)
2
( x 1)2 2
符号求和
symsum(u,n,n0,nn):
n n0
u
nn
n
symsum(f,a,b): 关于默认变量求和
1 例:计算级数 S 2 及其前100项的部分和 n 1 n >> syms n; f=1/n^2; >> S=symsum(f,n,1,inf) >> S100=symsum(f,n,1,100) x S 2 例:计算函数级数 n 1 n
>> syms n x; f=x/n^2; >> S=symsum(f,n,1,inf)
Taylor级数展开
taylor(f): 求f在默认自变量=0处的5阶 Taylor级数展开式定积分
taylor(f,n,x): 求f在默认自变量x=0处的
n-1阶Taylor级数展开式定积分
taylor(f,n,x,a): 求f在默认自变量x=a处
q = quad(fun,a,b) q = quad(fun,a,b,tol)
功能:求一元函数fun的积分q,积分上限和下限分别为a和 b,绝对误差为tol,默认时取值10^-6 ,函数fun是待求解 的对象,可以是字符串、内联函数、M函数文件名的函数句 柄。
Simpson Formula
数值积分
>> a=sym('a'); >> b=sym('b'); >> c=sym('c');
例: >> syms a b 达式的建立:
建立符号表达式通常有以下2种方法: (1) 用 sym 函数直接建立符号表达式。 (2) 使用已经定义的符号变量组成符号表达式。
例: >> y=sym('sin(x)+cos(x)')
1
π 4
1 0
1 x dx
2
数值积分
(3)二重积分的数值求解
dblquad函数就可以直接求出上述二重定积分的数 值解。该函数的调用格式为:
I=dblquad(f,a,b,c,d,tol,trace)
功能:该函数求f(x,y)在[a,b]×[c,d]区域上的二重定 积分。参数tol,trace的用法与函数quad完全相同。 trace控制是否展现积分过程,若取非0则展现积分过 程,取0则不展现,缺省时取trace=0。
x M lim1 n n
n
>> syms x h n; >> L=limit((log(x+h)-log(x))/h,h,0) >> M=limit((1-x/n)^n,n,inf)
计算导数
diff g=diff(f,v):求符号表达式 f 关于 v 的导数 g=diff(f):求符号表达式 f 关于默认变量的导数 g=diff(f,v,n):求 f 关于 v 的 n 阶导数
Fourier级数的Matlab程序
具体程序: function[A,B,F]=fseries(f,x,n,a,b) if nargin==3 a=-pi; b=pi; end %若输入为3个参数,表示函数f(x)在[pi,pi]内进行展开 L=(b-a)/2;
Fourier级数的Matlab程序
例:指出下面各条语句的输出结果 >> f=sym('2*u'); >> subs(f,'u',2) >> f2=subs(f,'u','u+2') >> a=3; >> subs(f2,'u',a+2) >> subs(f2,'u','a+2') >> syms x y >> f3=subs(f,'u',x+y) >> subs(f3,[x,y],[1,2])
数学实验
上海电力学院数理系
dhy0826@
微积分实验
1 2 3 4 5
符号表达式基础操作 符号微积分 数值积分
卫星轨道的长度
国土面积的计算
符号对象的建立
符号对象的建立:sym 和 syms sym 函数用来建立单个符号变量,一般调用格式为:
符号变量 = sym(A) 参数 A 可以是一个数或数值矩阵,也可以是字符串
【例】求exp(-x2)在[0,1]上的积分。 1、f=inline(‘exp(-x.^2)’);%内联函数 q1=quad(f,0,1)
数值积分
【例】求exp(-x2)在[0,1]上的积分。 2、编写被积函数表达式,函数名为 quad1.m function f = quad1(x) f=exp(-x.^2); >> q2=quad('quad1',0,1)
的n-1阶Taylor级数展开式定积分
>> syms x; taylor(exp(x),x,7,-1)
上机作业
1. 2.
2 f 2 y f ( x, y) x ln( x e ), 求 xy x 2, y 1
1 cos x lim x00 x(1 cos x )
1 2
符号表达式的替换
用给定的数据替换符号表达式中的指定的符号变量
subs(f,x,a) 用 a 替换字符函数 f 中的字符变量 x a 是可以是 数/数值变量/表达式 或 字符变量/表达式
