霍尔元件灵敏度的测量
霍尔元件测速原理说明及应用

霍尔元件测速原理说明及应用霍尔元件是一种具有特殊结构和特殊材料的电子元件,是由半导体材料组成的。
霍尔元件的测速原理是基于霍尔效应。
霍尔效应是指当电流通过垂直于磁场的导体时,导体两侧产生电压差。
霍尔元件利用霍尔效应,可以将电流和磁场转换为电压信号。
霍尔元件的结构一般由霍尔片和固定在霍尔片上的金属触点组成。
霍尔片一般是在P型或N型半导体上叠加一层接近绝缘的金属层,这两个结构相对于磁场磁通线垂直。
当通过霍尔元件的电流流过时,霍尔片两侧会产生电压差。
这个电压差与磁场的强度、电流的大小及方向,以及霍尔元件的几何尺寸相关。
应用方面,霍尔元件主要用于测速和位置检测。
以下是几个常见的应用示例:1.汽车速度传感器:霍尔元件可以用来检测汽车轮胎凹凸不平引起的震动,从而测量汽车的速度。
它可以代替传统的速度传感器,具有精度高、反应快和不易受环境影响等优点。
2.磁盘驱动器:霍尔元件可用于检测磁盘的转速。
通过检测旋转磁盘上的磁头是否通过霍尔元件附近的磁场来测量转速。
这对于磁盘驱动器的控制和数据读取非常重要。
3.电动机控制:霍尔元件可以用于检测电动机的转速。
通过将霍尔元件固定在电动机旋转轴上,可以通过检测每个霍尔元件通过磁场所产生的电压来测量电动机的转速。
4.位置检测:通过将霍尔元件固定在物体上,可以实时检测物体的位置。
这在一些自动控制系统中很有用,比如门禁系统、自动灯光调节和行车记录仪。
霍尔元件在工业和生活中有很广泛的应用。
它具有高灵敏度、快速响应、抗干扰能力强等优点,可以实现非接触测量和控制。
随着科技的进步和应用领域的扩大,霍尔元件的应用将会更加广泛。
霍尔效应及霍尔元件基本参数的测量

霍尔效应及霍尔元件基本参数的测量086041B班D组何韵摘要:霍尔效应是磁电效应的一种,利用这一现象制成的各种霍尔元件,广泛地应用于工业自动化技术、检测技术及信息处理等方面.霍尔效应是研究半导体材料性能的基本方法.本实验的目的在于了解霍尔效应的原理及有关霍尔器件对材料的要求,使用霍尔效应试验组合仪,采用“对称测量法”消除副效应的影响,经测量得到试样的V H—I M和V H—I S曲线,并通过实验测定的霍尔系数,判断出半导体材料试样的导电类型、载流子浓度及载流子迁移率等重要参数.关键词:霍尔效应hall effect,半导体霍尔元件semiconductor hall effect devices,对称测量法symmetrical measurement,载流子charge carrier,副效应secondary effect美国物理学家霍尔(Hall,Edwin Herbert,1855-1938)于1879年在实验中发现,当电流垂直于外磁场通过导体时,在导体的垂直于磁场和电流方向的两个端面之间会出现电势差,这一现象便是霍尔效应.这个电势差也被叫做霍尔电势差.霍尔的发现震动了当时的科学界,许多科学家转向了这一领域,不久就发现了爱廷豪森(Ettingshausen)效应、能斯托(Nernst)效应、里吉-勒迪克(Righi-Leduc)效应和不等位电势差等四个伴生效应.在霍尔效应发现约100年后,德国物理学家克利青(Klaus von Klitzing, 1943-)等在研究极低温度和强磁场中的半导体时发现了量子霍耳效应,这是当代凝聚态物理学令人惊异的进展之一,克利青为此获得了1985年的诺贝尔物理学奖.之后,美籍华裔物理学家崔琦(Daniel Chee Tsui,1939- )和美国物理学家劳克林(Robert ughlin,1950-)、施特默(Horst L. St rmer,1949-)在更强磁场下研究量子霍尔效应时发现了分数量子霍尔效应,这个发现使人们对量子现象的认识更进一步,他们为此获得了1998年的诺贝尔物理学奖.最近,复旦校友、斯坦福教授张首晟与母校合作开展了“量子自旋霍尔效应”的研究.“量子自旋霍尔效应”最先由张首晟教授预言,之后被实验证实.这一成果是美国《科学》杂志评出的2007年十大科学进展之一.如果这一效应在室温下工作,它可能导致新的低功率的“自旋电子学”计算设备的产生.目前工业上应用的高精度的电压和电流型传感器有很多就是根据霍尔效应制成的,误差精度能达到0.1%以下.一、霍尔效应的原理1.霍尔效应霍尔效应从本质上讲是运动的带电粒子在磁场中受洛伦兹力作用而引起的偏转.置于磁场中的载流体,如果电流方向与磁场垂直,则在垂直于电流和磁场的方向会产生一附加的横向电场,即霍尔电场E H ,这个现象被称为霍尔效应.在x方向通以电流I S ,在z方向加磁场B,则在y方向即试样A-A’电极两侧因一号电荷的聚集而产生附加电场.电场的指向取决于式样的导电类型,如图1示.霍尔电场E H 阻止载流子继续向侧面偏移,平衡时载流子所受电场力等于洛仑兹力B v e eE H =得B v E H =其中v 为载流子在电流方向的平均漂移速率.设试样宽b(y 方向的长度)厚d (z 方向的长度),载流子浓度为n ,则I S =nbd v e 得nbdeI v S=,由此得到, dBI ne nde B I b E V S S H H 1===. V H 与I S B 乘积成正比,与试样厚度d 成反比,比例系数R H =1/ne 称为图1E H <0, N 型E H >0, P 型霍尔系数,是反映材料霍尔效应强弱的重要参数.)/(1034C cm BI dV R S H H ⨯=,其中磁场单位用T. 2. R H 与其他参数的关系(1) 由R H 的符号判断导电类型:三元组(I S ,B,E H )满足右手螺旋法则,则导电类型为N 型,反之为P 型. (2) 由R H 求载流子的浓度:假定所有载流子的漂移速度相同,则eR n H 1=.若考虑载流子的统计分布,须引入3π /8的修正因子.(3) 结合电导率σ求载流子的迁移率μ.由σ=ne μ得μ=|Rh|σ.3. 霍尔效应与材料性能为得到较大的霍尔电压,根据其产生原理,可以采取下述方法: (1) 关键是选取R H 较大的材料,而R H =μρ(其中ρ为电阻率),金属导体μ和ρ都很小,不良导体ρ较大,但μ太小,都不适合做霍尔元件.只有半导体μ和ρ大小适中,是制作霍尔元件的较理想材料.由于电子的迁移率比空穴的迁移率大,一般霍尔元件采用N 型材料.(2) 其次是减小d ,因此常用薄膜型霍尔器件.一般,用霍尔灵敏度)mV/(mA.T)(1nedK H =来表示器件的灵敏度.二、霍尔效应的副效应上述推导是从理想情况出发的,实际情况要复杂得多,在产生霍尔电压H V 的同时,还伴生有四种副效应,副效应产生的电压叠加在霍尔电压上,造成系统误差.为便于说明,画一简图如图2所示.(1)爱廷豪森(Ettingshausen)效应引起的电势差E V .由于电子实际上并非以同一速度v 沿X 轴负向运动,速度大的电子回转半径大,能较快地到达接点3的侧面,从而导致3侧面较4侧面集中较多能量高的电子,结果3、4侧面出现温差,产生温差电动势E V .E V 的正负与I 和B 的方向有关.(2)能斯托(Nernst)效应引起的电势差N V .焊点1、2间接触电阻可能不同,通电发热程度不同,故1、2两点间温度可能不同,于是引起热扩散电流.与霍尔效应类似,该热扩散电流也会在3、4点间形成电势差N V .若只考虑接触电阻的差异,则N V 的方向仅与B 的方向有关. (3)里吉-勒迪克(Righi-Leduc)效应产生的电势差R V .在能斯托效应的热扩散电流的载流子由于速度不同,一样具有爱廷豪森效应,又会在3、4点间形成温差电动势R V . R V 的正负仅与B 的方向有关,而与I 的方向无关.(4)不等位电势差效应引起的电势差0V .由于制造上困难及材料的不均匀性,3、4两点实际上不可能在同一条等势线上.因此,即使未加磁场,当I 流过时,3、4两点也会出现电势差0V . 0V 的正负只与电流方向I 有关,而与B 的方向无关.x综上所述,在确定的磁场B 和电流I 下,实际测出的电压是H V 、E V 、N V 、R V 和0V 这5种电压的代数和. 根据副效应的性质,采用电流和磁场换向的对称测量法,尽量消减它们的影响.具体做法如下:① 给样品加(+B 、+I )时,测得3、4两端横向电压为1V =H V +E V +N V +R V +0V ;② 给样品加(+B 、-I )时,测得3、4两端横向电压为2V =-H V -E V +N V +R V -0V ;③ 给样品加(-B 、-I )时,测得3、4两端横向电压为3V =H V +E V -N V -R V -0V ;④ 给样品加(-B 、+I )时,测得3、4两端横向电压为4V =-H V -E V -N V -R V +0V ;由以上四式可得1V —2V +3V -4V =4H V +4E VH V =41(1V —2V +3V -4V )-E V通常E V 比H V 小得多,可以略去不计,因此霍尔电压为H V =41(1V —2V +3V -4V ).三、 具体实验过程实验采用霍尔实验组合仪,给定的霍尔元件长l=1.5mm, 宽b=1.5mm, 厚d=0.2mm,KH=184mV/(mA.T).1.首先根据仪器性能,连接测试仪与试验以之间的各种连线,注意接线对应连接.2.实验中使用换向开关改变电源正负极的连接从而改变电流和磁场的方向,可以实现对称测量.在作V H—I S曲线和V H—I M曲线时,使用控制变量法.3.将测试仪的功能切换置于“V H”.当I M=500mA(磁感应强度B)保持不变时,调整I S,用换向开关改变电流和磁场的方向,测1V,2V,3V,4V.列表记录数据如下:作V H—I S曲线注意到随着B和I S 的方向的改变,测得的1V,2V,3V,4V大小不同,这是由于霍尔效应的副效应引起的,最后用44 32 1V VVVVH-+-=得到可消除副效应对结果的影响.4.当I S=3.00mA保持不变时,调整I M ,再次用换向开关改变电流和磁场的方向,测1V,2V,3V,4V列表记录数据如下:I M (A)V1(mV) V2(mV) V3(mV) V4(mV)44321VVVVVH-+-=(mv)+B, +I S +B, -I S -B, -I S -B, +I S0.100 -2.11 0.35 -0.35 2.11 -1.23 0.150 -2.71 0.95 -0.95 2.71 -1.83 0.200 -3.32 1.57 -1.56 3.32 -2.440.250 -3.93 2.17 -2.17 3.93 -3.05 0.300 -4.54 2.78 4.55 -2.78 -3.66 0.350 -5.16 3.40 -3.40 5.16 -4.28 0.400 -5.77 4.01 -4.01 5.77 -4.89 0.450 -6.39 4.62 -4.62 6.39 -5.50 0.500-7.005.24-5.247.00-6.12作V H —I M 曲线判断霍尔片的导电类型:当I S >0,I M >0时,V H 小于零 ,则霍尔片为N 型半导体。
霍尔效应灵敏度kh值

霍尔效应灵敏度kh值霍尔效应灵敏度kh值是描述霍尔元件对磁场灵敏度的一个重要参数。
在应用中,我们经常需要根据具体的应用需求选择合适的霍尔元件,而kh值就是评估霍尔元件灵敏度的重要参考指标之一。
我们来了解一下霍尔效应。
霍尔效应是指当电流通过金属或半导体材料时,如果材料中存在垂直于电流方向的磁场,那么在材料两侧会产生一种电势差,这种现象被称为霍尔效应。
而霍尔元件则是利用霍尔效应来实现磁场测量的一种器件。
霍尔效应的灵敏度可以通过kh值来表示,kh值定义为在单位磁感应强度下霍尔电压的变化率,通常以mV/T为单位。
kh值越大,说明霍尔元件对磁场的灵敏度越高,即单位磁感应强度下霍尔电压的变化越大。
在实际应用中,kh值的选择取决于所测量磁场的强度范围以及所需的测量精度。
如果需要测量较小的磁场强度,就需要选择具有较高kh值的霍尔元件,以提高测量的灵敏度。
反之,如果测量范围较大,对精度要求较低,可以选择kh值较小的霍尔元件。
kh值还与霍尔元件的几何尺寸和材料特性有关。
一般来说,小尺寸的霍尔元件具有较高的kh值,因为其电流分布较为均匀,磁场作用效果较好。
而材料的特性如载流子浓度、迁移率等也会影响kh值。
高载流子浓度和迁移率的材料通常具有较高的kh值,因为它们能够有效地感受到磁场的作用。
在实际选择霍尔元件时,除了考虑kh值外,还需要考虑其他因素,如工作温度范围、响应时间、线性度等。
不同的应用场景可能对这些参数有不同的要求,因此在选择霍尔元件时需要综合考虑。
总结一下,霍尔效应灵敏度kh值是评估霍尔元件对磁场灵敏度的一个重要参数。
kh值越大,说明霍尔元件对磁场的灵敏度越高。
在选择霍尔元件时,需要根据具体应用需求选择合适的kh值,同时还需要考虑其他因素如工作温度范围、响应时间等。
通过合理选择霍尔元件,我们可以实现对磁场的准确测量和控制。
大一下物理实验【实验报告】 霍尔效应的研究及利用霍尔效应测磁场

东南大学物理实验报告姓名学号指导老师日期座位号报告成绩实验名称:霍尔效应的研究及利用霍尔效应测磁场目录预习报告...................................................2~5 实验目的 (2)实验仪器 (2)实验中的主要工作 (2)预习中遇到的问题及思考 (3)实验原始数据记录 (4)实验报告…………………………………………6~12 实验原理………………………………………………………实验步骤………………………………………………………实验数据处理及分析…………………………………………讨论……………………………………………………………预习报告实验目的:1.了解霍尔效应的基本原理以及有关霍尔元件对材料要求的知识。
2.了解霍尔效应及其消除办法。
3.确定试样的导电类型,载流子浓度以及迁移率。
4.利用霍尔效应测量磁场,并研究载流线圈组的磁场分布。
实验仪器(包括仪器型号):实验中的主要工作:1.霍尔效应的研究:(1)、测量霍尔元件的灵敏度;(2)、测量半导体材料的电导率;(3)、确定所用霍尔元件的电导类型,计算霍尔系数R,载H流子浓度n及载流子迁移率 。
2.利用霍尔效应测磁场:(1)、根据仪器的使用方法调整好测磁实验仪;(2)、测定一对共轴线圈轴线上的磁场分布;(3)、测量长直螺线管轴线上的磁场分布。
①取I=10mA和适当的I M,测量螺线管轴线磁场上的分布,做B-X曲线,并分析结果②测定B=CI M中螺线管常数C预习中遇到的问题及思考:1.霍尔效应实验中有哪些副效应?通过什么方法消除它?答:霍尔元件通常为一矩形薄片,由于材料本身的不均匀以及电压输出的对称性,会在电极位置产生不等位电势差,在研究固体的导电性质时还发现一些热电、热磁效应伴随着霍尔效应一起出现,这样实验中从A、A`测得的电压U并不等于真实的霍尔电压,而是包含了由各种副效应引起的虚假电压。
一般来说附加电压的正负与霍尔原件工作电流及磁感应强度B的方向有关,可以采用对称测量法进行修正。
霍尔传感器测量方法

霍尔传感器测量方法1. 霍尔传感器简介霍尔传感器是一种测量磁场强度的电子设备,通常用于测量物体的位移、速度和位置等物理量。
该传感器利用霍尔效应,在磁场中沿器件通电方向的正交方向上产生电位差,从而实现对磁场的测量。
2. 霍尔传感器类型目前市面上常见的霍尔传感器主要有线性霍尔传感器和角度霍尔传感器两种类型。
线性霍尔传感器通常用于测量物体的位移和速度等,而角度霍尔传感器则适用于测量物体的角度位置信息。
3. 霍尔传感器测量原理霍尔传感器的测量原理主要基于霍尔效应。
当将一个导电物品(如铜线)放在磁场中时,这个物体沿磁场方向在两端会出现电场差(电势差),这种现象称为霍尔效应。
引入实验条件后简单来讲就是:将霍尔元件(霍尔晶体管)放置于磁场中,由于磁场的作用,霍尔元件会在一个方向上堆积电荷,产生一定的电势差。
这个电势差与磁场强度成正比,可以通过测量电势差的大小来得到磁场强度的值。
4. 霍尔传感器测量方法在使用霍尔传感器时,需要通过接线将传感器与测量仪器相连。
此外,还需要将传感器放置在被测物体的表面或近距离接近被测物体。
当磁场作用于传感器时,传感器将会产生一个电势差信号。
使用测量仪器来测量这个信号的大小,就可以得到磁场强度的数值。
根据不同的应用需求,可以使用不同的测量仪器来进行精度更高的测量。
5. 霍尔传感器的优势霍尔传感器具有很高的灵敏度和线性度,能够快速响应磁场信号,同时也具有很好的可靠性和稳定性。
此外,霍尔传感器不受温度和湿度等环境因素的影响,因此在不同环境下都能够获得较好的测量精度。
同时,霍尔传感器还具有很小的体积和重量,适用于小型化、轻量化的应用领域。
6. 霍尔传感器的应用领域目前,霍尔传感器已经被广泛应用于汽车、机械制造、电子、医疗、环保等多个领域。
在汽车领域,霍尔传感器可用于测量车速、发动机转速、车辆加速度和制动效果等信息;在机械领域,霍尔传感器可用于测量机械部件的运动状态和位置信息;在电子领域,霍尔传感器可用于测量电流、电压等电学量;在医疗领域,霍尔传感器可用于监测心率和血压等生物信息;在环保领域,霍尔传感器可用于监测水质和空气质量等环境信息。
实验二 霍尔系数和电阻率的测量
实验二 霍尔系数和电阻率的测量把通有电流的半导体置于磁场中,如果电流方向与磁场垂直,则在垂直于电流和磁场的方向会产生一附加的横向电场,这个现象称为霍尔效应。
随着半导体物理学的发展,霍尔系数和电导率的测量已成为研究半导体材料的主要方法之一。
通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流子浓度、载流子迁移率等主要参数。
若能测量霍尔系数和电导率随温度变化的关系,还可以求出材料的杂质电离能和材料的禁带宽度。
一、实验目的1. 了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识;2. 学习用“对称测量法”消除副效应的影响,测量并绘制试样的V H -I S 和V H -I M 曲线;3. 确定试样的导电类型、载流子浓度以及迁移率。
二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子和空穴)被约束在固体材料中,这种偏转就导致在垂直于电流和磁场的方向上产生正负电荷的积累,从而形成附加的横向电场,即霍尔电场。
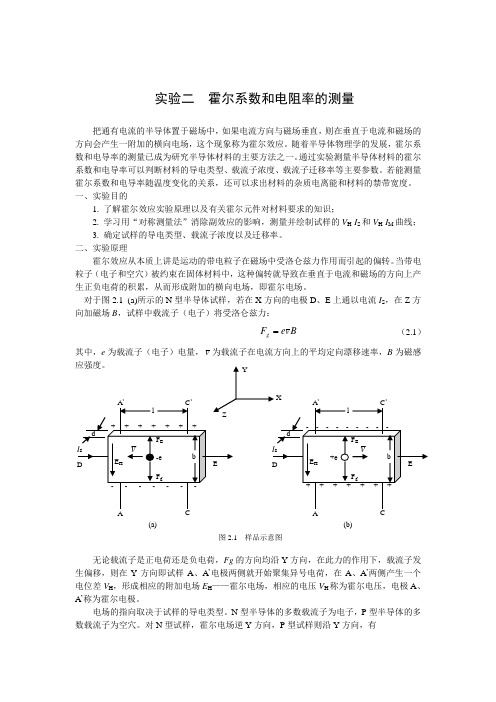
对于图2.1 (a)所示的N 型半导体试样,若在X 方向的电极D 、E 上通以电流I S ,在Z 方向加磁场B ,试样中载流子(电子)将受洛仑兹力:B v e F g (2.1)其中,e 为载流子(电子)电量,v 为载流子在电流方向上的平均定向漂移速率,B 为磁感无论载流子是正电荷还是负电荷,Fg 的方向均沿Y 方向,在此力的作用下,载流子发生偏移,则在Y 方向即试样A 、A ’电极两侧就开始聚集异号电荷,在A 、A ’两侧产生一个电位差V H ,形成相应的附加电场E H ——霍尔电场,相应的电压V H 称为霍尔电压,电极A 、A ’称为霍尔电极。
电场的指向取决于试样的导电类型。
N 型半导体的多数载流子为电子,P 型半导体的多数载流子为空穴。
对N 型试样,霍尔电场逆Y 方向,P 型试样则沿Y 方向,有(a) (b) 图2.1 样品示意图I S (X)、B (Z) E H (Y) < 0 (N 型)E H (Y) > 0 (P 型)显然,该电场是阻止载流子继续向侧面偏移。
霍尔效应及霍尔元件基本参数的测量实验报告

霍尔效应及霍尔元件基本参数的测量实验报告实验目的:1. 了解霍尔效应的基本原理及其在霍尔元件中的应用;2. 学习使用霍尔元件测量磁场强度和电流的方法;3. 掌握测量霍尔元件输出电压与磁场强度、电流之间的关系。
实验器材:1. 霍尔元件;2. 恒流源;3. 磁场调节装置;4. 数字多用表。
实验原理:霍尔效应是指当载流子在导体中受到垂直于电流方向的磁场力作用时,在导体横向产生电场差,进而产生电势差。
这一效应被应用在霍尔元件中,通过测量霍尔元件的输出电压,可以间接测量磁场强度和电流。
实验步骤:1. 将恒流源的正极和负极分别连接到霍尔元件的两个引脚上;2. 将数字多用表的电压测量端口连接到霍尔元件的输出引脚上;3. 将磁场调节装置放置在霍尔元件附近,通过调节磁场的强度,使其垂直于电流方向;4. 打开恒流源,调节电流的大小;5. 在不同的电流和磁场强度下,记录霍尔元件的输出电压。
实验数据处理:1. 将实验记录的电流和霍尔元件的输出电压整理成表格;2. 绘制电流和霍尔元件输出电压的关系曲线;3. 利用最小二乘法拟合曲线,得到电流和输出电压之间的线性关系;4. 根据线性关系,计算出霍尔元件的灵敏度和霍尔系数。
实验结果与讨论:根据实验数据处理的结果,可以得到霍尔元件的灵敏度和霍尔系数。
实验还发现,在磁场强度较小的情况下,霍尔元件的输出电压与磁场强度呈线性关系;当磁场强度较大时,输出电压可能存在饱和现象,即不再随磁场强度的增大而线性增加。
结论:通过本次实验,我们成功测量了霍尔元件的基本参数,包括灵敏度和霍尔系数。
同时,我们也验证了霍尔元件输出电压与磁场强度、电流之间的关系,进一步加深了对霍尔效应的理解。
这些实验结果对于霍尔元件的应用和相关工程设计具有重要的参考价值。
霍尔元件 标准

霍尔元件标准
霍尔元件是一种基于霍尔效应的磁传感器,可以用于测量磁场和电流。
以下是霍尔元件的主要参数:
1. 灵敏度:霍尔元件的输出电压与输入磁场强度的比值,单位为mV/mT。
2. 线性范围:输入的磁场强度在一定范围内,输出电压与输入磁场强度成线性关系。
3. 响应速度:霍尔元件对磁场变化的响应速度,单位为ms。
4. 温度稳定性:霍尔元件在不同温度下的输出电压变化率,单位为mV/℃。
5. 长期稳定性:霍尔元件在长时间工作后的输出电压变化率。
此外,霍尔元件还有不同的材料和尺寸可供选择,以满足不同的应用需求。
例如,常用的半导体材料N型硅、N型锗、锑化铟、砷化铟和不同比例亚
砷酸铟和磷酸铟组成的In型固溶体等。
其中N型锗容易加工,其霍尔常数、温度性能、输出线性都较好,应用非常普遍。
在使用霍尔元件时,需要注意以下几点:
1. 避免在强磁场或高温环境中使用,以免影响其性能。
2. 安装时要保证其与磁铁或导磁材料之间的气隙均匀,以免影响测量精度。
3. 在使用前应先进行校准,以确保测量结果的准确性。
4. 在使用过程中要定期检查其工作状态,及时发现并处理问题。
总之,选择合适的霍尔元件需要考虑其参数、应用环境和实际需求等因素。
大学物理实验报告实验14霍尔元件灵敏度测定及应用

大学物理实验教案实验名称: 霍尔元件灵敏度测定及应用一 目的1、 进一步了解霍尔效应;2、 掌握霍尔元件灵敏度及其特性的测量方法。
3、 测定电磁铁磁场特性二 仪器V AA H 电压测量双路恒流电源,SH500霍尔效应实验装置,MR-1磁阻效应实验装置。
三 原理1、 霍尔效应及其霍尔灵敏度将金属片置于磁场中,让磁场垂直通过薄片平面。
沿薄片的纵向通以电流,则在薄片的两侧面会出现微弱的电压。
这就是霍尔效应,横向产生的电压叫霍尔电压,符号V H 。
d IB R V HH = (1)霍尔系数R H =(en )-1=C ;n 为薄片中载流子的浓度,e 为电子带电量,d 为薄片的厚度。
V H =K H IB (2)K H ——霍尔灵敏度,它表示该元件产生霍尔效应的强弱,即在单位磁感应强度B 和单位控制电流I 时,产生霍尔电压的大小。
2、 电磁铁气隙的磁场本实验利用电磁铁装置产生一个已知的磁场 r ML L NI B μμ210+= (3)μ0——真空磁导率;N ——励磁线圈的匝数;I M ——线圈中的励磁电流;L 1——气隙距离; L 2——铁芯磁路平均长度;μr ——铁芯相对磁导率;本实验μr =15003、 电磁铁气隙中心的磁场系数M CH H H M I I K V I B R == (4)R ——中心磁场的磁场系数四 教学内容(一) 磁感应强度一定,变化控制电流时霍尔元件灵敏度测定接好线路,并打开恒流源后面的开关,在一定的I CH ,I M 值下,调节霍尔元件在气隙里的位置和角度,使霍尔电压V H 显示的数值最大为止。
1、 I M =200mA ,依次改变:I CH =0.50,1.00,1.50,2.00,2.50,3.00,3.50,4.00,4.50,5.00,5.50,6.00,6.50,7.00mA ,测量出相应的霍尔电压V H 的值。
2、 利用开关k 1,k 2依次改变I M 与I CH 电流的方向,记录相应的数值。
霍尔元件灵敏度参数单位

霍尔元件灵敏度参数单位霍尔元件是一种用来测量磁场的传感器元件。
它的灵敏度是指在给定的电场条件下,每个磁场单位变化对该元件输出电压的影响程度。
霍尔元件的灵敏度通常以电压/V(V/T)表示,其中V/T是对磁场单位的度量。
本文将详细介绍霍尔元件的灵敏度参数单位,并对其进行全面的分析。
一、霍尔元件的工作原理霍尔元件是由一块晶体片制成的,它包含有金属触点和感应结构。
当感应结构过电流时,它会在两个触点之间产生横向电场(霍尔电场),这个电场会受到磁场的影响,从而引起触点之间的电势差产生变化。
这种电势差的变化可以通过读取该元件的输出电压来衡量。
霍尔元件的灵敏度参数单位通常有两种:一种是电压/V(V/T),另一种是电流/A(V/A T)。
其中电压/V(V/T)是对于每个磁场单位的电势差变化量的度量,而电流/A(V/A T)是入射磁场下输出电流与磁力度之间的比例。
S = ΔV/ΔB其中S表示霍尔元件的灵敏度,ΔV表示输入磁场单位下的输出电势差变化量,ΔB表示磁场单位的变化量。
该公式可以用来计算霍尔元件在不同磁场条件下的灵敏度,从而确定将使用什么样的元件来实现所需的测量精度。
霍尔元件的灵敏度参数受多种因素影响,其中包括:1. 硅片的薄膜质量:硅片的薄膜质量会影响霍尔晶体的导电性、生长质量和磁场响应。
2. 温度:温度是影响霍尔元件灵敏度的一个重要因素。
在不同的温度下,霍尔元件的灵敏度会发生变化。
3. 磁场的方向和大小:不同方向和大小的磁场对霍尔元件的灵敏度有影响。
对于特定方向和大小的磁场,霍尔元件会表现出不同的灵敏度值。
4. 霍尔元件的尺寸和形状:霍尔元件的尺寸和形状也会对其灵敏度产生影响。
对于不同的尺寸和形状的霍尔元件,其灵敏度也不同。
霍尔元件的灵敏度参数单位是电压/V(V/T)和电流/A(V/A T)。
灵敏度受多种因素影响,包括硅片的薄膜质量、温度、磁场的方向和大小以及霍尔元件的尺寸和形状。
了解这些因素对霍尔元件灵敏度的影响可以帮助我们选择合适的元件来实现所需的测量精度。
霍尔元件

【示范中的测量数据及计算结果仅作为书写报告的参考,不可抄袭】实验19 霍尔元件测磁场一、仪器条件记录:1.霍尔元件灵敏度:H K = 6.170mv/ mA ·T ;H K ∆=1.0mv/ mA ·T 2.螺线管参数:单位长度上线圈的匝数n =4101538.1⨯ 匝/米;△n =4100077.0⨯匝/米;总长L =0.26 cm3.霍尔元件位置:标尺分度值:cm 1.0; 读数误差:cm 05.0;位置:X=15.00cm ,4.霍尔元件工作电流: I S =5.00mA, △IS =I S ·0.5%=0.025mA 二、B —I M 关系测量数据记录:三、最小二乘法处理:1. 测量关系式:M S H H I I nK V 0μ=用bx a y +=进行线性回归,y 表示H V ,x 表示M I ,S H I nK b 0μ= (1)计算机显示记录:a =1.222222 E-02 a U =2.182641 E-02 (程序中a 的A 类不确定度作为a U )b =0.01245 b U =4.584464E-05(2)计算结果表示: a =(1.2±2.2)×10-2 mV ;b =(1.245±0.005)×10-2mV/mAE b =0.4%【对a 的合理性讨论:a U a ±中包含0,从另一个侧面说明实验没有显著的系统误差存在。
】2.真空磁导率0μ 的计算和测量结果表示:(1)0μ 的计算式:16342010650.121000.56.170101538.110245.1----⋅⋅⨯=⨯⨯⨯⨯⨯=⋅=A m T I nK bS H μ (2)不确定度计算:因为测量关系式为乘除关系,可用先计算相对不确定度的方法来进行不确定度传递:222222220⎪⎪⎭⎫ ⎝⎛∆+⎪⎪⎭⎫⎝⎛∆+⎪⎭⎫ ⎝⎛∆+=+++=SS HH b I KH n b I I K K n n E E E E E E sμ %93.000.5025.06.1701.01538.10077.0245.1005.02222=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=0μU =0μ×0μE =1.2650×10-6×0.93%=0.012×10-6 T ·m ·A -1(3)0μ测量结果:四、测量值0μ与理论值0μ'的比较及讨论: (1)测量结果的正确度:理论值:16170102566.1104----⋅⋅⨯=⋅⋅⨯='A m T A m T πμ 0000μμμ''-=A ⨯100%==-566.12566.1265.120.67% (2)一致性讨论:0μ=(12.65±0.12)×10-7 T ·m ·A -10μ' ‘=12.566×10-7 T ·m ·A -1 00μμδ'-==0.084×10-7 T ·m ·A -1 0μ =(12.65±0.12)×10-7 T ·m ·A -1; 0μE =0.93%△=0μU =0.12×10-7T ·m ·A -1∵δ<△∴0μ与0μ' ‘在相对不确定度 0.93%下一致五、实验结论:本实验根据(I M ,B )数据进行作图,从实验关系图可以看出, I M 与B 数据点具有很好的线性相关性;测得真空磁导率0μ为12.65×10-7T ·m ·A -1,相对不确定度达0.93%, 测量值0μ与理论值0μ' ‘在相对不确定为0.93%下一致。
霍尔元件灵敏度kh计算公式

霍尔元件灵敏度kh计算公式1. 引言霍尔元件是一种基于霍尔效应的传感器,可以测量磁场强度和电流。
由于其具有高精度、高灵敏度、无触点化以及长寿命等优点,已广泛应用于电流、速度、位置和角度等物理量的测量中。
在霍尔元件中,灵敏度是一个很重要的参数,决定了霍尔元件的测量精度。
本文将介绍霍尔元件灵敏度的概念、计算公式和影响因素。
2. 灵敏度的概念在霍尔元件中,灵敏度(kh)是指磁场引起的霍尔电压与磁场强度之比。
通俗的说,就是指当磁场发生变化时,霍尔电压的变化程度。
灵敏度的单位为mV/T,表示每个特定的磁场单位强度中,霍尔电压变化的程度。
3. 灵敏度的计算公式在实际应用中,霍尔元件的灵敏度可以通过以下公式进行计算:kh = Vh / B其中,kh是霍尔元件的灵敏度(mV/T),Vh是磁场引起的霍尔电压(mV),B是磁场强度(T)。
在这个公式中,霍尔电压Vh是比较容易测量的,而磁场强度B则需要加以注意。
由于磁场的各种特殊性质,可以对其进行多种不同的测量。
在实际计算时,应根据实际使用情况选择合适的测量方法。
4. 影响灵敏度的因素在霍尔元件中,灵敏度受到多种因素的影响。
以下是一些常见的因素:4.1 磁场强度范围在不同的磁场强度下,霍尔元件的灵敏度是不同的。
通常,当磁场强度较小时,灵敏度较高;当磁场强度较大时,灵敏度较低。
4.2 工作温度霍尔元件的工作温度也会对其灵敏度产生影响。
在一定范围内,随着工作温度的升高,霍尔元件的灵敏度会下降。
因此,在实际应用中,应尽可能确保霍尔元件的工作温度稳定。
4.3 带宽范围带宽是指霍尔元件能够测量的电流频率范围。
在带宽范围内,灵敏度是比较稳定的。
但是,在带宽范围外,灵敏度会逐渐降低。
4.4 制造质量霍尔元件的制造质量对其灵敏度有重要影响。
高质量的霍尔元件,能够保证精度稳定、温度性能好等优点,从而具有更高的灵敏度。
5. 结论本文对霍尔元件的灵敏度进行了介绍,包括灵敏度的概念、计算公式和影响因素。
霍尔效应及霍尔元件基本参数的测量

霍尔效应及霍尔元件基本参数的测量086041B班D组何韵摘要:霍尔效应是磁电效应的一种,利用这一现象制成的各种霍尔元件,广泛地应用于工业自动化技术、检测技术及信息处理等方面.霍尔效应是研究半导体材料性能的基本方法.本实验的目的在于了解霍尔效应的原理及有关霍尔器件对材料的要求,使用霍尔效应试验组合仪,采用“对称测量法”消除副效应的影响,经测量得到试样的V H—I M和V H—I S曲线,并通过实验测定的霍尔系数,判断出半导体材料试样的导电类型、载流子浓度及载流子迁移率等重要参数.关键词:霍尔效应hall effect,半导体霍尔元件semiconductor hall effect devices,对称测量法symmetrical measurement,载流子charge carrier,副效应secondary effect美国物理学家霍尔(Hall,Edwin Herbert,1855-1938)于1879年在实验中发现,当电流垂直于外磁场通过导体时,在导体的垂直于磁场和电流方向的两个端面之间会出现电势差,这一现象便是霍尔效应.这个电势差也被叫做霍尔电势差.霍尔的发现震动了当时的科学界,许多科学家转向了这一领域,不久就发现了爱廷豪森(Ettingshausen)效应、能斯托(Nernst)效应、里吉-勒迪克(Righi-Leduc)效应和不等位电势差等四个伴生效应.在霍尔效应发现约100年后,德国物理学家克利青(Klaus von Klitzing, 1943-)等在研究极低温度和强磁场中的半导体时发现了量子霍耳效应,这是当代凝聚态物理学令人惊异的进展之一,克利青为此获得了1985年的诺贝尔物理学奖.之后,美籍华裔物理学家崔琦(Daniel Chee Tsui,1939- )和美国物理学家劳克林(Robert ughlin,1950-)、施特默(Horst L. St rmer,1949-)在更强磁场下研究量子霍尔效应时发现了分数量子霍尔效应,这个发现使人们对量子现象的认识更进一步,他们为此获得了1998年的诺贝尔物理学奖.最近,复旦校友、斯坦福教授张首晟与母校合作开展了“量子自旋霍尔效应”的研究.“量子自旋霍尔效应”最先由张首晟教授预言,之后被实验证实.这一成果是美国《科学》杂志评出的2007年十大科学进展之一.如果这一效应在室温下工作,它可能导致新的低功率的“自旋电子学”计算设备的产生.目前工业上应用的高精度的电压和电流型传感器有很多就是根据霍尔效应制成的,误差精度能达到0.1%以下.一、霍尔效应的原理1.霍尔效应霍尔效应从本质上讲是运动的带电粒子在磁场中受洛伦兹力作用而引起的偏转.置于磁场中的载流体,如果电流方向与磁场垂直,则在垂直于电流和磁场的方向会产生一附加的横向电场,即霍尔电场E H ,这个现象被称为霍尔效应.在x方向通以电流I S ,在z方向加磁场B,则在y方向即试样A-A’电极两侧因一号电荷的聚集而产生附加电场.电场的指向取决于式样的导电类型,如图1示.霍尔电场E H 阻止载流子继续向侧面偏移,平衡时载流子所受电场力等于洛仑兹力B v e eE H =得B v E H =其中v 为载流子在电流方向的平均漂移速率.设试样宽b(y 方向的长度)厚d (z 方向的长度),载流子浓度为n ,则I S =nbd v e 得nbdeI v S=,由此得到, dBI ne nde B I b E V S S H H 1===. V H 与I S B 乘积成正比,与试样厚度d 成反比,比例系数R H =1/ne 称图1E H <0, N 型E H >0, P 型为霍尔系数,是反映材料霍尔效应强弱的重要参数.)/(1034C cm BI dV R S H H ⨯=,其中磁场单位用T. 2. R H 与其他参数的关系(1) 由R H 的符号判断导电类型:三元组(I S ,B,E H )满足右手螺旋法则,则导电类型为N 型,反之为P 型. (2) 由R H 求载流子的浓度:假定所有载流子的漂移速度相同,则eR n H 1=.若考虑载流子的统计分布,须引入3π /8的修正因子.(3) 结合电导率σ求载流子的迁移率μ.由σ=ne μ得μ=|Rh|σ.3. 霍尔效应与材料性能为得到较大的霍尔电压,根据其产生原理,可以采取下述方法: (1) 关键是选取R H 较大的材料,而R H =μρ(其中ρ为电阻率),金属导体μ和ρ都很小,不良导体ρ较大,但μ太小,都不适合做霍尔元件.只有半导体μ和ρ大小适中,是制作霍尔元件的较理想材料.由于电子的迁移率比空穴的迁移率大,一般霍尔元件采用N 型材料.(2) 其次是减小d ,因此常用薄膜型霍尔器件.一般,用霍尔灵敏度)mV/(mA.T)(1nedK H =来表示器件的灵敏度.二、霍尔效应的副效应上述推导是从理想情况出发的,实际情况要复杂得多,在产生霍尔电压H V 的同时,还伴生有四种副效应,副效应产生的电压叠加在霍尔电压上,造成系统误差.为便于说明,画一简图如图2所示.(1)爱廷豪森(Ettingshausen)效应引起的电势差E V .由于电子实际上并非以同一速度v 沿X 轴负向运动,速度大的电子回转半径大,能较快地到达接点3的侧面,从而导致3侧面较4侧面集中较多能量高的电子,结果3、4侧面出现温差,产生温差电动势E V .E V 的正负与I 和B 的方向有关.(2)能斯托(Nernst)效应引起的电势差N V .焊点1、2间接触电阻可能不同,通电发热程度不同,故1、2两点间温度可能不同,于是引起热扩散电流.与霍尔效应类似,该热扩散电流也会在3、4点间形成电势差N V .若只考虑接触电阻的差异,则N V 的方向仅与B 的方向有关. (3)里吉-勒迪克(Righi-Leduc)效应产生的电势差R V .在能斯托效应的热扩散电流的载流子由于速度不同,一样具有爱廷豪森效应,又会在3、4点间形成温差电动势R V . R V 的正负仅与B 的方向有关,而与I 的方向无关.(4)不等位电势差效应引起的电势差0V .由于制造上困难及材料的不均匀性,x3、4两点实际上不可能在同一条等势线上.因此,即使未加磁场,当I 流过时,3、4两点也会出现电势差0V . 0V 的正负只与电流方向I 有关,而与B 的方向无关.综上所述,在确定的磁场B 和电流I 下,实际测出的电压是H V 、E V 、N V 、R V 和0V 这5种电压的代数和. 根据副效应的性质,采用电流和磁场换向的对称测量法,尽量消减它们的影响.具体做法如下:① 给样品加(+B 、+I )时,测得3、4两端横向电压为1V =H V +E V +N V +R V +0V ;② 给样品加(+B 、-I )时,测得3、4两端横向电压为2V =-H V -E V +N V +R V -0V ;③ 给样品加(-B 、-I )时,测得3、4两端横向电压为3V =H V +E V -N V -R V -0V ;④ 给样品加(-B 、+I )时,测得3、4两端横向电压为4V =-H V -E V -N V -R V +0V ;由以上四式可得1V —2V +3V -4V =4H V +4E VH V =41(1V —2V +3V -4V )-E V通常E V 比H V 小得多,可以略去不计,因此霍尔电压为H V =41(1V —2V +3V -4V ).三、 具体实验过程实验采用霍尔实验组合仪,给定的霍尔元件长l=1.5mm, 宽b=1.5mm, 厚d=0.2mm,KH=184mV/(mA.T).1.首先根据仪器性能,连接测试仪与试验以之间的各种连线,注意接线对应连接.2.实验中使用换向开关改变电源正负极的连接从而改变电流和磁场的方向,可以实现对称测量.在作V H—I S曲线和V H—I M曲线时,使用控制变量法.3.将测试仪的功能切换置于“V H”.当I M=500mA(磁感应强度B)保持不变时,调整I S,用换向开关改变电流和磁场的方向,测1V,2V,3V,4V.列表记录数据如下:作V H—I S曲线注意到随着B和I S 的方向的改变,测得的1V,2V,3V,4V大小不同,这是由于霍尔效应的副效应引起的,最后用44 32 1V VVVVH-+-=得到可消除副效应对结果的影响.4.当I S=3.00mA保持不变时,调整I M ,再次用换向开关改变电流和磁场的方向,测1V,2V,3V,4V列表记录数据如下:I M (A)V1(mV) V2(mV) V3(mV) V4(mV)44321VVVVVH-+-=(mv)+B, +I S +B, -I S -B, -I S -B, +I S0.100 -2.11 0.35 -0.35 2.11 -1.23 0.150 -2.71 0.95 -0.95 2.71 -1.83 0.200 -3.32 1.57 -1.56 3.32 -2.440.250 -3.93 2.17 -2.17 3.93 -3.05 0.300 -4.54 2.78 4.55 -2.78 -3.66 0.350 -5.16 3.40 -3.40 5.16 -4.28 0.400 -5.77 4.01 -4.01 5.77 -4.89 0.450 -6.39 4.62 -4.62 6.39 -5.50 0.500-7.005.24-5.247.00-6.12作V H —I M 曲线判断霍尔片的导电类型:当I S >0,I M >0时,V H 小于零 ,则霍尔片为N 型半导体。
霍尔元件的灵敏度测量原理

霍尔元件的灵敏度测量原理霍尔元件是一种基于霍尔效应的传感器,用于测量磁场的强度和方向。
它的灵敏度是指对于磁场的变化,传感器输出信号的变化程度。
本文将详细介绍霍尔元件的灵敏度测量原理。
首先,我们需要了解一下霍尔效应。
霍尔效应是指当电流通过导体时,如果该导体处于磁场中,会在导体的两侧产生电势差,这个现象就被称为霍尔效应。
霍尔元件中常用的是纵向霍尔效应,即磁场方向与电流方向垂直。
在霍尔元件中,通常有三个引脚,分别是电源引脚(Vcc)、接地引脚(GND)和输出引脚(OUT)。
电源引脚连接正电源,接地引脚连接地线,输出引脚连接电路的输入端。
在测量霍尔元件的灵敏度时,我们需要将霍尔元件放置在已知磁场中,并通过测量输出信号的变化来确定其灵敏度。
具体步骤如下:1. 构建实验电路。
首先,将霍尔元件与其他电路连接起来,例如,将电源引脚连接正电源,接地引脚连接地线,输出引脚连接电路的输入端。
2. 定义基准信号。
在没有外部磁场作用时,测量霍尔元件输出的基准信号,将其作为后续测量的基准值。
3. 放置霍尔元件。
将霍尔元件放置在已知磁场中,并保持稳定。
可以使用磁铁或电磁铁产生磁场,确保磁场强度可控且恒定。
4. 测量输出信号。
通过连接的电路,测量霍尔元件输出的信号大小和方向。
可以使用示波器或模拟信号处理器来获取输出信号。
5. 计算灵敏度。
通过比较基准信号和测量信号的差异,计算出霍尔元件的灵敏度。
通常,灵敏度被定义为单位磁场变化引起的电压变化。
需要注意的是,为了获得准确的灵敏度测量结果,我们应该尽量避免外界因素对测量的干扰。
例如,应保持磁场稳定且恒定,避免其它磁场源的影响;还要注意电源稳定和抗干扰电路的设计,以减小测量误差。
此外,为了获得更准确的灵敏度测量结果,可以进行多次测量并取平均值。
同时,还可以通过改变磁场的强度来测量不同磁场下的输出信号,以确定灵敏度的变化规律。
总之,霍尔元件的灵敏度测量原理是通过将霍尔元件放置在已知磁场中,测量输出信号的变化来确定其灵敏度。
霍尔元件灵敏度的测量

西北工业大学设计性基础物理实验报告班级:11051401 姓名:日期: 2016.05.27霍尔元件灵敏度的测量一、实验目的测量置于螺线管中部霍尔元件的灵敏度。
二、实验仪器(名称、型号及参数)可调直流双路输出稳压电源一台(E1:0-5V E2:0-20V)数字式万用表(限用直流电流2mA量程档)未知阻值的电阻R0直流多值电阻箱3个(只有R1阻值准确)TH-S螺线管磁场实验仪单刀单掷开关、导线三、实验原理1.霍尔效应任何导体中通过电流时,若存在垂直于电流方向的磁场,则导体内部产生与电流和磁场方向都垂直的电场。
2.测量计算方法当霍尔电场力与洛伦兹力平衡时,霍尔片中载流子不再迁移,霍尔片上下两个平面间会形成霍尔电压,且霍尔电压与电场强度成正比,流过器件的霍尔电流与电子定向运动速度成正比,则U H=K H I S B其中K H为比例系数,即霍尔元件的灵敏度。
3.不等位电位差可以通过取霍尔电压平均值来消除。
四、实验内容与方法1、测量未知电阻R0、万用表内阻r如图1连接线路,取U=4V,R1=2KΩ,测量I1,取下R0,替换为R2,,调节数值使万用表读数与前一致,则R2数值为R0。
如图2连接线路,调节R1=2KΩ,得到I2;调节R1’=3KΩ,得到I3,计算可得r。
2、测量励磁电流、霍尔电流、霍尔电压如图3连接电路,调节R1=4KΩ,根据等势点,可得励磁电流I M。
如图4连接电路,取R1=200Ω,根据R1和万用表内阻的比例可得霍尔电流I S。
如图5连接电路,将图4和图3连接到一起,取合适的R2值使得万用表读数为0,取R=1Ω此时R两端电压为霍尔电压,使用图6电路图得到电流表示数,计算霍尔电压。
五、实验数据记录与处理(列表记录数据并写出主要处理过程)图1:I1=1.845mA R0=9.5Ω图2:I2=1.847mA I3=1.251mA R1=2000Ω R1’=3000Ω解方程组得r=98.99Ω图3:R1=4000Ω I=0.965mA I M==0.963mA图4:R1=200Ω I万=0.698mA I s=0.698+6.98=7.678mA图5、图6:R2=13111.5Ω I万=0.002mA R=R万98.99Ω U=0.02*98.99=1.98V六、实验分析与讨论1.霍尔元件电流端电阻数百欧姆,其工作电流不能超过10mA,以免损坏霍尔元件,应详细计算出各个电路中保护电阻的大概数值之后进行测量。
霍尔效应实验说明书

霍尔效应实验霍尔效应是导电材料中的电流与磁场相互作用而产生电动势的效应。
1879年美国霍普金斯大学研究生霍尔在研究金属导电机构时发现了这种电磁现象,故称霍尔效应。
后来曾有人利用霍尔效应制成测量磁场的磁传感器,但因金属的霍尔效应太弱而未能得到实际应用。
随着半导体材料和制造工艺的发展,人们又利用半导体材料制成霍尔元件,由于它的霍尔效应显著而得到实用和发展,现在广泛用于非电量检测、电动控制、电磁测量和计算装置方面。
在电流体中的霍尔效应也是目前在研究中的“磁流体发电”的理论基础。
近年来,霍尔效应实验不断有新发现。
1980年原西德物理学家冯·克利青(K.Von Klitzing )研究二维电子气系统的输运特性,在低温和强磁场下发现了量子霍尔效应,这是凝聚态物理领域最重要的发现之一。
目前对量子霍尔效应正在进行深入研究,并取得了重要应用,例如用于确定电阻的自然基准,可以极为精确地测量光谱精细结构常数等。
在磁场、磁路等磁现象的研究和应用中,霍尔效应与其元件是不可缺少的,利用它观测磁场直观、干扰小、灵敏度高、效果明显。
[实验目的]1、了解霍尔效应原理与测量霍尔元件有关参数.2、测绘霍尔元件的s H I V -,M H I V -曲线了解霍尔电势差H V 与霍尔元件控制(工作)电流s I 、励磁电流M I 之间的关系。
3、学习利用霍尔效应测量磁感应强度B 与磁场分布。
4、判断霍尔元件载流子的类型,并计算其浓度和迁移率。
5、学习用“对称交换测量法”消除负效应产生的系统误差。
[实验原理]霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力的作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直电流和磁场的方向上产生正负电荷在不同侧的聚积,从而形成附加的横向电场。
如右图(1)所示,磁场B 位于Z 的正向,与之垂直的半导体薄片上沿X 正向通以电流s I (称为控制电流或工作电流),假设载流子为电子(N 型半导体材料),它沿着与电流s I 相反的X 负向运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图1:I1=1.845mA R0=9.5Ω
图2:I2=1.847mA I3=1.251mA R1=2000Ω R1’=3000Ω
解方程组得r=98.99Ω
图3:R1=4000Ω I=0.965mA IM= =0.963mA
图4:R1=200Ω I万=0.698mA Is=0.698+6.98=7.678mA
图5、图6:R2=13111.5Ω I万=0.002mA R=R万98.99Ω U=0.02*98.99=1.98V
六、实验分析与讨论
1.霍尔元件电流端电阻数百欧姆,其工作电流不能超过10mA,以免损坏霍尔元件,应详细计算出各个电路中保护电阻的大概数值之后进行测量。
2.霍尔电极不对称,两极间有附加的不等电位差,应多次测量,取平均值来消除该误差,但是因为实验时间有限,因此只测量一次,存在误差。
西北工业大学
设计性基础物理实验报告
班级:11051401姓名:日期:2016.05.27测量置于螺线管中部霍尔元件的灵敏度。
二、实验仪器(名称、型号及参数)
可调直流双路输出稳压电源一台(E1:0-5V E2:0-20V)
数字式万用表(限用直流电流2mA量程档)
未知阻值的电阻R0
3.由于焊点之间接触电阻不同导致焊点之间温度不同,由能斯特方程,会在两板间形成附加的电势差,引起实验误差。
直流多值电阻箱3个(只有R1阻值准确)
TH-S螺线管磁场实验仪
单刀单掷开关、导线
三、实验原理
1.霍尔效应
任何导体中通过电流时,若存在垂直于电流方向的磁场,则导体内部产生与电流和磁场方向都垂直的电场。
2.测量计算方法
当霍尔电场力与洛伦兹力平衡时,霍尔片中载流子不再迁移,霍尔片上下两个平面间会形成霍尔电压,且霍尔电压与电场强度成正比,流过器件的霍尔电流与电子定向运动速度成正比,则
UH=KHISB
其中KH为比例系数,即霍尔元件的灵敏度。
3.不等位电位差可以通过取霍尔电压平均值来消除。
四、实验内容与方法
1、测量未知电阻R0、万用表内阻r
如图1连接线路,取U=4V,R1=2KΩ,测量I1,取下R0,替换为R2,,调节数值使万用表读数与前一致,则R2数值为R0。
如图2连接线路,调节R1=2KΩ,得到I2;调节R1’=3KΩ,得到I3,计算可得r。
2、测量励磁电流、霍尔电流、霍尔电压
如图3连接电路,调节R1=4KΩ,根据等势点,可得励磁电流IM。
如图4连接电路,取R1=200Ω,根据R1和万用表内阻的比例可得霍尔电流IS。
如图5连接电路,将图4和图3连接到一起,取合适的R2值使得万用表读数为0,取R=1Ω此时R两端电压为霍尔电压,使用图6电路图得到电流表示数,计算霍尔电压。
