地下水运动的基本规律重力水运动的基本规律达西
地下水运动的基本规律

断面的水头,水头差为h;两断面相距L; (5)下端出口测定流量为Q。
0
0
图4-1 达西实验装置图
5.4.1.2 实验成果
Q KA h KAI L
Q AV
V KI
5.4.2 达西公式中各项的物理意义
5.4.2.1 渗透流速(V) >>在达西定律表达公式中,渗透流速是一个宏观概念,并且
它很容易测量。 >>因此,必须把它与单个水质点在砂粒中寻路而曲折前进的
地下水迹线示意图
5.1.2.3 二者区别
流线和迹线都是流场中的一簇曲线,都与流 体的运动有关,但各自代表了不同的概念:
>>流线反映的是某时刻流体的流速向量,迹线 是反映流体中某一质点不同时间走过的轨迹;
>>因此流线可看作水质点运动的摄影,迹线则 可看作对水质点运动所拍摄的电影。
5.1.3 过水断面与流量
5.4 地下水运动的基本规律
5.4.1 达西定律
达西定律是法国水利学家H.Darcy通过大量的实验,得到的线 性渗透定律。
5断面面积A;
(2)上游置一个稳定的溢水装置→保持稳定
水头;
(3)实验上端进水,下端出水→示意流线;
(4)圆筒中上、下断安装测压管→测定两个
>>稳定流条件下,流体的流线与迹线重合!
>>严格说来,自然界中的地下水都属于非稳定流,但是, 但为了便于分析和运算,也可以将某些运动要素变化微小的 渗流,近似地看作稳定流。
5.1.7 均匀流与非均匀流
>>均匀流——在实际水流中,如果流线是彼此平行的直线, 而且在同一流线上的点,其实际流速相等,即沿水流方向实 际流速的大小和方向皆不变。显然,在均匀流中,质点的时 变加速度和位变加速度都等于零。亦即流体在运动过程中, 其运动要素不随坐标位置而改变!
地下水的运动规律

地下水在岩层空隙中流动的现象称为渗流。在岩层 空隙中渗流时,水的质点有秩序的、互不混杂的流动, 称为层流运动。在具有狭小空隙的岩土(如砂、裂隙不 大的基岩)中流动时,重力水受到介质的吸引力较大, 水的质点排列较有秩序,故做层流运动。水的质点无秩 序的、互相混杂的流动,称为紊流运动。做紊流运动时, 水流所受阻力作用比层流状态作用大,消耗的能量较多。 在宽大的空隙中(大的溶穴、宽大裂隙及卵砾石孔隙 中),水的流速较大时,容易出现紊流运动。
时间内渗流量为
q V /t
图5-9 达西渗透试验装置图
同时读取断面1-1和断面2-2处的侧压管水头值 h1 和 h2 ,h h1 h2 为两断面之间的水头损失。 达西分析了大量试验资料,发现土中单位时间内渗透的渗流量q与圆筒断面积A及水头损失h
成正比,与断面间距l成反比,即
q kA h kAi l
地下水运动时,其运动规律服从达西定律或非线性 渗透ห้องสมุดไป่ตู้律。
地下水在土体孔隙中渗透时,由于渗透阻力的作用,运
动时必然伴随着能量的损失。为了揭示水在土体中的渗透规律,
法国工程师达西(H. Darcy)做了大量的试验研究,于1856年
总结得出渗透能量损失与渗透速度之间的相互关系,即达西定
律。达西渗透试验的装置如图5-9所示。
装置中的①是横截面积为A的直立圆筒,其上端开口,在
其侧壁装有两支相距为l的侧压管。筒底以上一定距离处装一
滤板②,滤板上填放颗粒均匀的砂土。水由上端注入圆筒,多
余的水从溢水管③溢出,使筒内的水位维持一个恒定值。渗透
过砂层的水从短水管④流入量杯⑤中,并以此来计算单位时间
内渗流量q。设 t 时间内流入量杯的水体体积为V,则单位
4第五章--达西定律PPT课件

IH1H2 Hh
L12
LL
单位渗透途径上的机械能损失,也即机械能的损失率。
V=KI,当岩石性质一定时,K为常数,I大,V也大;
➢说明渗透水流流动速度越大,沿渗流途径的机械能损耗 越大,反之, I越大,驱动水流运动的速度越大。
能量损失:内摩擦消耗和岩石固体边界对水流的摩擦阻
力消耗。
2损021失/6/7 的能量最终转变为热能而消耗掉。
O’
5.2 重力水运动的基本定律
一、达西定律
法国水力学家H.Darcy,1856年通过大 量的水通过均匀砂柱渗流实验得出;
实验条件
➢ 等径圆筒装入均匀砂样,断面为ω;
➢ 上下各置一个稳定的溢水装置——保持 稳定水流;
➢ 实验时上端进水,下端出水;
➢ 砂筒中安装了2个测压管;
➢ 下端测出水量(outflow)——Q。
总势能 总机械能
几何意义 位置水头 压强水头 流速水头 测压管水头 总水头
2V
2 2
2g
p2
2
Hp2 H2
2
Z2
4
0
某砾石含水层中,V = 1.65cm/s
V2 11.652 0.0001c4m
2g 2980
V2
p
2g
z
Hp
在渗流场中:
断面1
p
H Hp Z
2021/6/7
O
5
p1
H1
Z1
过水断面ω 与实际过水断面ω ' 过水断面ω :砂柱的横切面积,是指水流通过的包括岩石 骨架与空隙在内的整个断面。 实际过水断面ω ′:扣除结合水所占据范围以外的空隙面积, 也就是重力水所占据的空隙面积 。
水文地质学基础 第四章 地下水运动的基本规律.
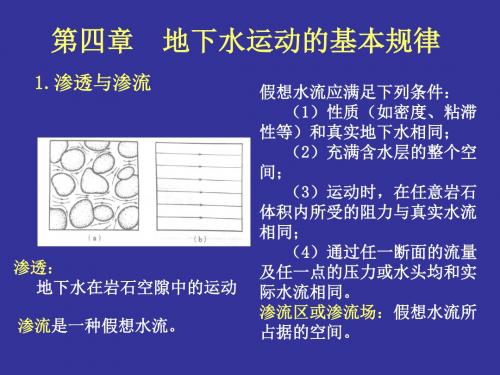
1.渗透与渗流
渗透: 地下水在岩石空隙中的运动
渗流是一种假想水流。
假想水流应满足下列条件: (1)性质(如密度、粘滞
性等)和真实地下水相同; (2)充满含水层的整个空
间; (3)运动时,在任意岩石
体积内所受的阻力与真实水流 相同;
(4)通过任一断面的流量 及任一点的压力或水头均和实 际水流相同。 渗流区或渗流场:假想水流所 占据的空间。
• 流线:是渗流场中某一瞬时的一条线,线上各水 质点在此瞬时的流向均与此线相切。
• 迹线:则是对水质点运动所拍的电影。在稳定流 条件下,流线与迹线重合。
一、均质各向同,流线与等水头线构成 正交网格。 • 分析均质各向同性介质中的稳定流网。 • 徒手绘制定性流网
地下水的运动绝大多数服从Darcy定律。
二、非线性渗透定律—哲才(Chezy)定律
地下水在较大的空隙中运动且流速较大时,呈紊 流运动,此时的渗流服从哲才定律。有:
1
Q KI 2
1
V KI 2
即此时渗透流速V与水力梯度I的1/2次方成正比.
4.2 流 网
• 流网:在渗流场的某一典型剖面或切面上,由一 系列等水头线与流线组成的网格.
2.层流和紊流
层流运动:水质点作有秩序的、互不混杂的流动. 紊流运动:水质点无秩序的、互相混杂的流动.
地下水在岩石空隙中的运动速度一般较慢,大多为层流 运动。只有在大裂隙、溶洞中地下水流速大,才可能出现紊 流运动。此外,在抽水井附近小范围内,当降深很大时,流 速增大,也可出现紊流现象。
3. 稳定流和非稳定流
实际流速,ω有:
Q Kw h KwI Vw L
Q= ω/·u= ω·ne·u=
4.水文地质学基础-地下水的基本运动规律

4.1 重力水运动的基本规律
渗透系数(K)的影响因素:
d0 —— 孔隙直径;γ——水的重率;μ——动力粘滞系数
K与岩石空隙性质、水的某些物理性质有关。
(1)孔隙直径大则渗透性强,取决于最小孔隙直径。 (2)圆管通道:形状弯曲而变化时,渗透性较差。 (3)颗粒分选性:比对孔隙度的影响要大。 (4)水的物理性质:粘滞性大的液体K<粘滞性小的液体
4.1 重力水运动的基本规律
4.1.4渗透系数 渗透系数(K)是水力梯度等于1时的渗透流速,单位:m/d,cm/s. 关系: V = K I 1)I为定值时,K大,V大;K小,V小(V=KI); 2)V为定值时,K大,I小等水位线疏;K小,I大等水位线密。 渗透系数可定量说明岩石的渗透性:K大→渗透性强;K小→渗 透性弱。
Q K ω I K M 1 I H H H H b a b K a 2 L K 2 2 Ha H b 2L
4.2 流 网
流线(flow line, stream line)是渗流场中某一瞬时的一条 线,线上各个水质点在此时刻的流向均与此线相切。 迹线(path line)是渗流场中某一时间段内某一水质点的运动 轨迹。
h1 0
K
M
h2
0’ L
dh dx 单宽流量为: v K dh dh q v K M 1 KM dx dx
qdx KMdh
L
0
qdx KMdh
h1 L h2 0 h1
h2
分离变量并积分:
q dx KM dh h1 h2 q KM KMI L
0 h1 L h2
h1 h2 h1 h2 qK KM I 2 L
达西实验指导

实验二达西实验前面我们已经知道了地下水储存在岩石的空隙中,那么地下水在岩石空隙中是怎样运动(渗流或渗透)的呢?也就是地下水运动的基本规律是什么呢?早在1856年,法国水力学家达尔西(Darcy)通过大量的实验,得到了水在孔隙介质中运动的线性渗透定律——达西定律。
达西定律表述的是通过过水断面的流量与水力梯度、过水断面面积和介质的渗透性质之间的关系。
为了定量描述岩石的渗透性质,提出了渗透系数的概念。
岩石渗透系数是定量描述岩石透水性能的物理指标,岩石空隙越大、连通性越好,则渗透系数越大,单位时间内通过过水断面的水量越多。
渗透系数在数值上等于水力坡度为1时的渗流速度。
所以渗透系数具有速度的单位。
渗透系数是诸多有关水文计算问题(水井涌水量、矿坑涌水量及水库、渠道渗流量等)中不可缺少的、重要的水文地质参数。
渗透系数可以通过抽水试验、物理模拟、数值模拟等不同的方法求得。
现在我们来进行达西实验。
一、实验目的(1)掌握实验室测定孔隙介质渗透系数的方法,加深对岩石渗透系数的认识。
(2)验证达西定律,从而提高对直线渗透定律的理解。
在野外确定渗透系数常用的方法有:井孔抽水、注水及试坑渗水、压水试验等方法。
这些方法所得资料可靠,精度高,但效率低,成本高。
在室内常用达西仪、戚姆仪及渗压仪、渗流槽等实验方法测定。
现在我们采用达西仪来测定岩石的渗透系数。
二、实验原理达西通过大量实验,得到圆筒过水断面的渗流量Q 与圆筒断面F 和水力坡度I 成正比,并和土壤的透水性能有关,所建立基本关系式如下:KFI Q =; 或KI FQv ==式中:v---为渗流简化模型的断面平均流速;K---为岩石的渗透系数,反映了孔隙介质透水性能。
三、仪器结构达西仪共由四部分组成(见图2)马氏瓶试样筒测压板 测压管管供水管排水管排水孔 水槽量筒吸球过滤板 测压孔图2 达西仪1.供水器装置(马氏瓶):以法国物理学家Mariotte的马利奥特瓶装置,是一种能控制水位又能自动连续补给水的量测装置。
水文地质学

《水文地质学基础》读书报告一、地球上的水及其循环地球上的水的分布可分为浅部层圈水与深部层圈水。
浅部层圈水:从大气圈到地壳上半部,包括大气水、地表水、地下水以及生物体中的水,以液态为主,也呈气态与固态形式存在。
深部层圈水:分布于地壳下部到下地幔,以被压密的气水溶液的形式存在。
浅部层中自由态的水与深部层中的特殊高温高压下离解状态下的水以及地壳矿物内部的结合水相互转化相互联系,因此广义上的水圈包括地球各圈层中以各种不同状态存在且相互转化的所有的水。
地球上的水循环即地球上各圈层中的水相互联系相互转化的过程,可分为水文循环和地质循环。
水文循环的对象为浅部层圈水中的大气水、地表水和地壳岩石空隙中的地下水。
循环过程为蒸发(海洋蒸发、水面蒸发、土面蒸发、叶面蒸发等)→大气中水汽转移→降水→入渗→地表径流或地下径流→蒸发。
水文循环按循环途径长短可分为大循环和小循环。
海洋与大陆之间的水分交换为大循环;海洋或大陆内部的水分交换为小循环。
是分子态水的转换,更替速度较快。
地质循环为地球浅层圈与深层圈之间水的相互转化过程。
常伴有水分子的分解与合成,转换速度缓慢。
与水文循环有关的气象因素包括大气圈的结构(主要因素是对流层的物理状态和运动规律)、大气的热源(太阳短波辐射以及地表长波辐射)、主要的气象要素(气温、气压、湿度、蒸发、降水)。
水文因素主要是径流。
表征地表径流的特征值有:流量;径流总量;径流模数;径流深度;径流系数。
我国水文循环概况:由于季风的控制,我国大部分地区旱季雨季分明,降水集中。
我国水资源在时间上分配不均。
雨季降水丰沛,旱季降水稀少。
此外,我国降水在空间上分布也不均匀,从东南沿海向西北内陆递减。
降水是地下水补给的最重要来源,因此一个地区地下水资源的丰富程度通常决定于该地区降水量的多寡。
一个地区地下水资源通常是多年水文循环的结果,我们在研究一个地区的地下水状况时必须从整个地球或某个较大尺度区域的水文循环角度出发,从整体上把握地下水形成、流动以及污染物迁移转化的复杂性。
地下水运动基本定律、基本微分方程和数学模型

第二节 数学模型
导水系数T
当水力坡度为1时,通过整个含水层上 的单位宽度流量。即:
T=K·M
第二节 数学模型
水的状态方程 对于给定质量的水体积,增加一个压力
dPw,水体积产生一定的压缩,根据质量守 恒定律:
ρVw=常数 取全微分有:
ρdVw+Vwdρ=0
由于dPw=dH
第二节 数学模型
达西定律的实质是水流在流动过程中消耗的 能量与流速和渗流长度成正比,与含水层的 渗透系数成反比。
HH1H2
vL K
达西定律的适用范围
Re ud
第一节 达西定律
当雷诺数Re<100时,适用; 当雷诺数Re>100时,不适用; 在天然情况下,绝大多数地下水运动服从达西定律。
第二节 数学模型
地下水渗流连续性方程 表示:在渗流场中的 任何局部,都必须满足质量守恒和能量守恒。
第二节 数学模型
对于稳定渗流,且假定n、ρ不变,则为地
下水稳定流的连续性方程:
x(K x H x) y(K y H y) z(K z H z) 0
第二节 数学模型
形式相似,意义有所差别
x(Tx H x) y(Ty H y)* H t
承压水二维流的微分方程:
第二节 数学模型
当水头变化很小时,即ΔH<0.1h时,对均质 各向同性的潜水有
2xH2 2yH2 T THt
T=Kh h为潜水含水层平均厚度
第二节 数学模型
H(x,y),t0 z,H t0(x,y),z
第二节 数学模型
注:对于稳定流来说,定解条件中没有初始条 件,因为地下水作稳定流时其运动要素是不随 时间而变化的。
《水文地质学》课程笔记 (2)

《水文地质学》课程笔记第一章绪论一、水文地质学的研究对象1. 地下水- 定义:地下水是指在地表以下岩石空隙和土壤孔隙中储存的水。
- 特点:地下水具有隐蔽性、循环性、动态性、可再生性和不可替代性。
- 研究内容:地下水的水位、流量、水质、水温、化学成分、运动规律等。
- 分类:根据埋藏条件,地下水可分为潜水、承压水等类型。
2. 岩土- 定义:岩土是指地球表层及其内部的岩石和土壤。
- 特性:岩土的物理性质(如密度、孔隙度、渗透性)、化学性质(如酸碱度、氧化还原性)和力学性质(如抗压强度、抗剪强度)。
- 研究内容:岩土的结构、组成、分布、成因、水文地质特性等。
3. 水资源- 定义:水资源是指地球表层可供人类利用的水。
- 特点:水资源具有时空分布不均、可再生性和有限性。
- 研究内容:水资源的评价、开发、利用、管理和保护。
4. 水文地质环境- 定义:水文地质环境是指地球表层地下水、岩土、气候、生态等因素相互作用的综合体。
- 研究内容:水文地质环境的调查、评价、监测、预测和调控。
二、地下水的功能1. 供水- 地下水是重要的饮用水源,尤其在干旱和半干旱地区。
- 地下水供水稳定,受气候变化影响较小。
2. 农业灌溉- 地下水灌溉可以提高作物产量,保障粮食安全。
- 地下水灌溉系统简单,易于管理。
3. 生态保护- 地下水维持河流、湖泊、湿地等生态系统的稳定。
- 地下水是许多生态系统的重要补给来源。
4. 灾害防治- 地下水可以调节地表水循环,减轻洪水和干旱灾害。
- 地下水开采可以降低地面沉降和海水入侵的风险。
5. 工业生产- 地下水用于冷却、洗涤、制造等多种工业用途。
- 地下水的水质稳定,适合特定工业需求。
6. 科研价值- 地下水研究为地质学、气候学、生态学等领域提供重要信息。
- 地下水是研究地球历史和地质作用的天然实验室。
三、水文地质学发展简史1. 古代阶段- 早期人类对地下水的利用主要限于井、泉等自然出露点。
- 古代文明(如古埃及、美索不达米亚)已有简单的地下水开发利用技术。
4第五章 达西定律

渗透系数K( 渗透系数 (coefficient of permeability) )
也有称为水力传导度( 也有称为水力传导度(Hydraulic Conductivity) ) V=KI,当I=1时,K=V ;因此 在数值上是当 时的 因此K在数值上是当 在数值上是当I=1时的 , 时 渗透流速。 渗透流速。 具有流速量纲[L/T],常用单位 具有流速量纲 ,常用单位cm/s,m/d; I一定,K大,则V也大, Q 也大,因此,渗透系数 K 一定, 大 也大, 也大,因此, 一定 也大 是表征岩石透水性的定量指标; 愈大 愈大, 是表征岩石透水性的定量指标;K愈大,则表明岩石的 透水能力愈强; 透水能力愈强; 影响渗透系数的因素
通过变水头,多次实验得出:出水端的流量 与砂柱 与砂柱、 通过变水头,多次实验得出:出水端的流量Q与砂柱、测 压管水头之间的关系为: 压管水头之间的关系为: (1) )
h Q = Kω L
Q ——渗流量; ω——砂柱断面面积; 渗流量; 砂柱断面面积; 渗流量 砂柱断面面积 h ——水头损失(m); ——渗流途径; 水头损失( ); );L 渗流途径; 水头损失 渗流途径 K——渗透系数。 渗透系数。 渗透系数 由水力学中水动力学基本原理: 由水力学中水动力学基本原理:
ω′ = ωne
有效孔隙度n 重力水流动的空隙体积( 有效孔隙度 e:重力水流动的空隙体积(不包括不连通的死孔隙和不 流动结合水所占据的空间)与岩石体积之比。 流动结合水所占据的空间)与岩石体积之比。
。
ω
ω′
渗透流速V与实际流速u 渗透流速V与实际流速u
Q = ωV = ω′ ⋅ u
ω′ = ωne
Q A
Q=KIW
HA 0 B
第四章 地下水运动的基本规律

5.作流网
1)根据边界条件绘制容易确定的等水头线或流线。 a.定水头边界:地表水体的断面一般可看作等水头面,因此,河渠的湿周必定是一条等水头线。 b.隔水边界:无水流通过(通量为零),而流线本身就是“零通量”边界,因此,平行隔水边界可 绘出流线。 c.地下水面边界:边界比较复杂。当无入渗补给及蒸发排泄,有侧向补给,作稳定流动时,地下水 面是一条流线;当有入渗补给时,它既不是流线,也不是等水头线。
等水头线、流线与各类边界的关系 1-含水层 2-隔水层 3-潜水面 4-等水头线 5-流线 6-河渠水面 7-降水入渗
2)流线总是由源指向汇的,因此,根据补给区(源:发散 流线处)和排泄区(汇:吸收流线处)可以判断流线的趋 向。渗流场中具有一个以上补给点或排泄点时,首先要确 定分流线,分流线是虚拟的隔水边界(分水或分流处为流 线)。 3)根据流线跟等水头线正交这一规则,在已知流线与等水 头线间插补其余部分。 如果我们规定相邻两条流线之间通过的流量相等,则 流线的疏密可以反映地下径流强度(流线密代表径流强, 流线疏代表径流弱),等水头线的密疏则说明水力梯度的 大小(等水头线密代表水力梯度大,等水头线疏代表水力 梯度小)。
承压含水层和潜水含水层的渗透压强来自水头6.水头(H)和水力梯度(I) 1)水头(H) a.水力学中的水头为: H=Z+P/r+ɑu2/2g Z:位置高度;ɑ动能修正系数;g:重力加速度; u:地下水的实际速度。 b.地下水总水头(H) 地下水实际流速很小,因此水力学中的ɑu2/2g与前两项相比微不足 道,可以忽略不计。因此地下水总水头(H)在数值上就等于测压管 水头,即:H≈Z+P/r。 2)水力梯度(I) 地下水在渗透过程中,不断克服阻力而消耗机械能,出现水头损失。 水力梯度(I) 为沿渗透途径水头损失与相应渗透途径长度的比值, 即: I=h/L,h:水头差,h=H1-H2 水在空隙中运动时,必须克服水与隙壁以及流动快慢不同的水质点 之间的摩擦阻力(这种摩擦阻力随地下水流速增加而增大),从而消 耗机械能,造成水头损失。因此,水力梯度可以理解为水流通过单位 长度渗透途径为克服摩擦阻力所耗失的机械能。从另一个角度,也可 以将水力梯度理解为驱动力,即克服摩擦阻力使水以一定速度流动的 力量。既然机械能消耗于渗透途径上,因此求算水力梯度I 时,水头 差必须与相应的渗透途径相对应。
第四章地下水运动的基本规律

4.2 饱水带重力水运动的基本规律-达西定律
一、线性渗透定律-达西定律 1.达西定律 H.Darcy—法国水力学家,1856年通过大量的室内实验得出的线性渗 透定律 实验条件 1)等径圆筒装入均匀砂样,断面为ω 2)上下各置一个稳定的溢水装置——保持稳定水流 3)实验时上端进水,下端出水——示意流线 4)砂筒中安装了2个测压管 5)下端测出水量-Q 根据实验结果,得到下列关系式:
第四章 地下水运动的基本规律
4.1 地下水运动-渗流运动要素 4.2 饱水带重力水运动的基本规律-达西定律 4.3 流网 4.4 饱水粘性土中结合水的运动规律
4.1 地下水运动-渗流运动要素
一、地下水存在及运动
1.岩石空隙介质:三种。 2.地下水在岩石空隙介质中的存在形式:强、弱结合水;毛细水;重 力水。
Q-渗透流量(出口处流量,即为通过砂柱各断面的流量); ω-过水断面(在实验中相当于砂柱横断面积); h -水头损失( h = H1 − H2 ,即上下游过水断面的水头差); L -渗透途径(上下游过水断面的距离); I -水力梯度(相当于h / L ,即水头差除以渗透途径); K -渗透系数
2)水力梯度(I)
地下水在渗透过程中,不断克服阻力而消耗机械能,出现水头损失。 水力梯度(I) 为沿渗透途径水头损失与相应渗透途径长度的比值, 即: I=h/L,h:水头差,h=H1-H2
水在空隙中运动时,必须克服水与隙壁以及流动快慢不同的水质点 之间的摩擦阻力(这种摩擦阻力随地下水流速增加而增大),从而消 耗机械能,造成水头损失。因此,水力梯度可以理解为水流通过单位 长度渗透途径为克服摩擦阻力所耗失的机械能。从另一个角度,也可 以将水力梯度理解为驱动力,即克服摩擦阻力使水以一定速度流动的 力量。既然机械能消耗于渗透途径上,因此求算水力梯度I 时,水头 差必须与相应的渗透途径相对应。
水资源利用与保护考试知识点整理

1.1水资源的定义狭义:是指人类在一定的经济技术条件下能够直接使用的淡水。
广义:是指在一定的经济技术条件下能够直接或间接使用的各种水和水中物质,在社会生活和生产中具有使用价值和经济价值的水都可称为水资源。
1.2 水资源的特性1、资源的循环性2、储量的有限性3、时空分布的不均匀性4、利用的多样性5、利、害的两重性1.3 水资源的属性:1.自然属性,2可利用性3数量与质量的兼顾性4时变性2.1 小循环——是指由海洋表面蒸发的水汽 , 又以降水形式落入海洋 ; 或者由大陆表面 ( 包括陆地水体表面、土面及植物叶面等 ) 蒸发的水气 , 仍以降水形式落回陆地表面。
这种发生在局部范围内的水循环过程称为小循环大循环——则是由海洋表面蒸发的水汽 , 随气流带到大陆上空 , 形成降水落回地面 , 再通过径流 ( 地表的及地下的)返回海洋的过程这种发生在海陆之间的循环过程称为大循环 2.2更替周期是指在补给停止的条件下,各类水从水体中排干所需要的时间 2.3全球上任一区域在一定时间内,进入的水量与输出水量之差等于该区域内 的蓄水变化量,这一关系称为水量平衡。
2.4中国水资源面临主要问题1、水资源开发过度,生态破坏严重2、城市供水集中,供需矛盾尖锐3、地下水过量开采,环境地质问题突出4、水资源污染严重、水环境日益恶化5、水资源开发利用缺乏统筹规划和有效管理2.5我国水资源特点及解决途径1.总量丰富,人均不足2.时空分布不均匀,资源组合不合理3.水土流失严重4.水污染加剧,生态环境恶化3.1水资源评价包括:(1)水资源数量评价(确定可利用的水资源的数量)(2)水资源质量评价(3)水资源利用评价及综合评价。
原则:地表水与地下水统一评价、水量水质并重、水资源可持续利用与社会经济发展和生态环境保护相协调的。
3.2多年平均条件下,水资源量的收支项主要为降水、蒸发和径流。
平衡条件下,收支在数量上是相等的。
降水、径流和蒸发是决定区域水资源状态的三要素。
吉林大学 水文地质学基础复习提纲

离子毫克当量浓度:毫克当量(mEq)表示某物质和1mg氢的化学活性或化合力相当的量。
1mg氢,23mg钠,39mg钾,20mg钙和35mg氯都是1mEq。
其换算公式如下:mEq/L=(mg/L)×原子价/化学结构式量mg/L=(mEq/L)×化学结构式量/原子价mg/L = mmol/l×化学结构式量所以mEq/L=mmol/L×原子价(注:化学结构式量=原子量或分子量)总硬度:除Na+、K+外水中溶释的全部金属离子总量,Ca2+、Mg2+通常是硬度的主要组成部分。
【总硬度】={[Ca2+]+[Mg2+](mEq/L)}*50 mg/L以CaCO3计表示的硬度含量。
总碱度:指水中所含能与强酸发生中和作用的全部物质,即能接受质子H+的物质的总量。
【总碱度】={[HCO3-]+[CO32-]+[OH-](mEq/L)}*50 mg/L以CaCO3计表示的总碱度。
达西定律(线性渗透定律)(重力水运动的基本定律)及其适用范围渗透流量Q或流速V与水力梯度I的一次方成正比,Q=KIω=K△Hω/L,V=KI=K△H/L。
适用范围:雷诺数Re小于1—10之间的某一数值的层流运动。
达西实验的使用条件:渗流介质为均质砂,渗透系数K为常数;过水断面ω为常数;水力梯度I=(H1-H2)/L为常数;渗流为层流运动,稳定流。
悬挂毛细水的涵义:细粒层次与粗粒层次交互成层时,在一定条件下,由于上下弯液面毛细力的作用,在细土层中会保留与地下水面不相连接的毛细水,这种毛细水称为悬挂毛细水毛细上升高度的涵义:毛细管中的水表面是一个弯月面,从而使其表面积增大,而一旦液面增大,水的表面张力和收缩作用,促使液面要恢复水平,于是使得毛管内水随之上升,以减少表面积,这样直到表面张力向上的拉引作用与管内升高的液柱重量达到平衡为止,管内的水才停止上升。
(这种使液体在管内上升的湿润力就是毛管力。
H =2σcosθ/rρg式中:r——毛管半径,m。
水文地质课件习题四 地下水运动的基本规律

习题四地下水运动的基本规律一、名词解释1.渗流:地下水在岩石空隙中的运动。
2.渗流场:发生渗流的区域。
3.层流运动:在岩层空隙中流动时,水的质点作有秩序的、互不混杂的流动。
4.紊流运动:在岩层空隙中流动时,水的质点作无秩序地、互相混杂的流动。
5.稳定流:水在渗流场内运动,各个运动要素(水位、流速、流向)不随时间改变。
6.非稳定流:水在渗流场中运动,各个运动要素随时间变化的水流运动。
7.渗透流速:地下水通过某一过水断面的平均流速。
8.有效空隙度:重力水流动的孔隙体积与岩石体积之比。
9.水力梯度:沿渗透途径水头损失与相应渗透途径之比。
10.渗透系数:水力坡度等于1时的渗透流速。
11.流网:在渗流场的某一典型剖面或切面上由一系列流线和等水头线组成的网。
12.流线:流场中某一瞬时的一条线,线上各水质点的流向与此线相切。
13.迹线:渗流场中某一段时间内某一质点的运动轨迹。
14.层状非均质:介质场内各岩层内部为均质各项同性,但不同岩层渗透性不同。
二、填空1.据地下水流动状态,地下水运动分为层流和紊流。
2.据地下水运动要素与时间的关系,地下水运动分为稳定流和非稳定流。
3.水力梯度为定值时,渗透系数愈大,渗透流速就愈大。
4.渗透流速为定值时,渗透系数愈大,水力梯度愈小。
5.渗透系数可以定量说明岩石的渗透性能。
渗透系数愈大,岩石的透水能力愈强。
6.流网是由一系列流线与等水头线组成的网格。
7.流线是渗流场中某一瞬时的一条线,线上各水质点在此瞬时的流向均与此线相切。
迹线是渗流场中某一时间段内某一水质点的运动轨迹。
8.在均质各向同性介质中,地下水必定沿着水头变化最大的方向,即垂直于等水头线的方向运动,因此,流线与等水头线构成正交网格。
9.流线总是由源指向汇。
10.如果规定相邻两条流线之间通过的流量相等,则流线的疏密可以反映径流强度,等水头线的疏密则说明水力梯度的大小。
三. 判断题1.在岩层空隙中渗流时,水作平行流动,称作层流运动。
第4章 地下水运动的基本规律

由水力学:
Q V
V
Q
即(对地下水也适用) 达西定律也可以另一种形式表达(流速):
V KI 式中:V––––渗透流速,m/d,cm/s;
K––––渗透系数,m/d,cm/s; I––––水力梯度,无量纲(比值)。 具体到实际问题:
关于有效孔隙度ne: 1)ne<n; 2)一般重力释水时,空隙中有结合水、毛 细水,所以 <ne; 3)对于粘性土,空隙细小、结合水所占的 比例大,所以ne很小,尽管n很大; 4)对于空隙大的岩层(如大的溶隙、裂 隙),ne≈≈n。
在各向同性介质中,流线与等水头线正交;在各向 异性介质中,流线与等水头线斜交
流网的画法: 1.均质各向同性介质中的流网(稳定流) 均质各向同性介质中流线与等水头线构成 正交网格。 水文地质边界: a. 定水头边界H(t)= c;(一类边界) b. 隔水边界,零通量边界;(二类边界) c. 地下水面边界。
2)流线由源指向汇:根据补给区、排泄区判 断流线的趋向(由补给区指向排泄区)。
2、层状非均质介质中的流网 1)两层介质,渗透系数K2>K1,K2=3K1; K2中流线密度为K1的3倍,因此,K2径流强, 流量大,更多的流量通过渗透性好的介质。
2)两块介质: a. K1中等水位(头)线密,间隔数为K2的3 倍;K1中水力梯度大,K2中水力梯度小; b. 在渗透较差的K1中,消耗的机械能大,是 K2的3倍。
叙述粘性土渗透流速(V)与水力梯度(I)主要存在的三种关系? 叙述流网的画法,以及利用流网图可解决的问题? 在等厚的承压含水层中,实际过水断面面积为400平方米的流量为10000立 方米/天,含水层的孔隙度为0.25,试求含水层的实际水流速度和渗透速 度。 一底板水平的含水层,观测孔A、B、C 彼此相距1000米,A位于B的正南 方,C则在AB线的东面。A、B、C的地面高程分别是95、ll0和135米,A中 水位埋深为5米,B中和C中的水位埋深分别是30米和35米,试确定通过三 角形ABC的地下水流的方向,并计算其水力梯度。 有三个地层,每个25米厚,互相叠置,如果在这个层组中设置一个不变流 速的垂向水流场,使其顶部h=120米,底部h=100米,试计算内部两个边 界处的h值(设顶部地层的渗透系数为0.0001米/天,中部地层为0.0005米 /天,底部地层为0.001米/天)。 考虑一个饱和、均质、各向同性、长方形、垂向剖面ABCDA。其上部边界 为AB,底部边界为DC,左侧边界为AD,右侧边界为BC,使DC的距离为 AD的两倍。BC和DC是不透水的。AB是一个不变水头边界,h=100米。 AD被分为两个相等的长度,其上半部分为不透水,下半部分是不变水头边 界,h=40米。试示意绘出流网图。 已知一等厚、均质、各向同性的承压含水层,其渗透系数为15米/天,孔 隙度为0.2,沿着水流方向的两观测孔A、B间距L=1200米,其水位标高分 别为Ha=5.4米,Hb=3米。试求地下水的渗透速度和实际速度。 已知一等厚、均质、各向同性的承压含水层,其渗透系数为20米/天,A、 B两断面间距为5000米,两断面处的承压水头分别为130.2米和125.2米。 试计算两断面间的水力梯度和单宽流量。
水文地质学---地下水运动的基本规律

(以此种情况居多)
说明:只要施加微小的水力梯度,结合水就会流动,但 此时的V十分微小;随着I加大,曲线斜率(K)逐渐增大,然
后趋于定值
较多的学者认为,粘性土(包括相当致密的粘土在内)中
的渗透,通常仍然服从达西定律。例如,奥尔逊曾用高岭土作
渗透试验,加压固结使高岭土孔隙度从58.8%降到22.5%,施 加水力梯度I =0.2~40,结果得出V - I 关系为一通过原点的直
第四章 地下水运动的基本规律
4.1.6 达西定律的适用范围 1<Re<10,层流,适用,地下水低速运动,粘 滞力占优势; 10<Re<100,层流,不适用,地下水流速增大, 为过渡带,由粘滞力占优势的层流转变为以惯性 力占优势的层流运动; Re>100,紊流,不适用。
达西定律是描述层流状态下渗透流速与水头损失关系的 规律,即渗流速度V与水力坡度I成线性关系只适用于层流范 围。在水利工程中,绝大多数渗流,无论是发生于砂土中或 一般的粘性土中,均属于层流范围,故达西定律均可适用。 但以下两种情况可认为超出达西定律适用范围。
第四章 地下水运动的基本规律 ①从微观角度研究地下水运动的难度有两个方面:
A)要获得微观角度每一个空间点的水流运动参数,首 先必须获得空隙的几何参数(查明每一个空隙与固体颗粒 之间的边界位置等) B)从微观角度来看地下水流在空间上是不连续的。固 体颗粒部分是没有水流的,因此从微观角度地下水的运动 参数在空间上是不连续的,有很多地方运动参数是零。 也就是说描述水流运动的物理量是非连续函数,因此 基于连续函数的许多微积分方法无法应用。
普通水流的流向是从总水头高的地方流向总水头低的地方 水流量的大小取决于水头差和水头损失 地下水水的流向也是从高水头流向低水头 流量的大小也取决于水头差和水头损失 普通水流在管道中运动取决于管道大小、形状及管壁的粗糙度 渗流运动取决于多孔介质空隙大小、形状以及其连通性
地下水类型运动规律

地下水类型运动规律一、地下水的类型和运动规律1、地下水的类型:按地下水的物理性质划分为:气态水、吸着水、薄膜水、毛细管水、重力水、固态水;按地下水的赋存特征划分为:上层滞水、潜水、承压水。
2、运动规律:地下水运动分为层流和紊流。
地下水在土中或微小裂隙中以不大的速度连续渗透时为层流运动;在岩石的裂隙或空洞内流淌,会产生紊流。
地下水的渗流速度一般符合达西定律。
二、地下水对工程的影响1,潜水上升,引起盐渍化,增大腐蚀性。
2,河谷阶地、斜坡及岸边,潜水上升,增大浸湿范围,破坏岩土体的结构和强度。
3,粉土、粉、细砂层中,潜水上升,会产生液化。
4,水位上升,可能使基础上浮使建筑物失稳。
5,膨胀土区,水位上升或土体水分增减,使膨胀岩土产生不匀称胀缩变形。
6,寒冷地区,潜水上升,冻结,地面隆起。
解冻降低抗压强度和抗剪强度。
导致建筑物开裂、失稳。
7,地下水位在压缩层范围内突然下降,增加自重应力,使基础产生附加沉降,导致变形破坏。
另外基坑支护中的地下水的影响、地表塌陷、地面沉降都可能与地下水有关。
一、地下水的类型和运动规律1、地下水的类型:按地下水的物理性质划分为:气态水、吸着水、薄膜水、毛细管水、重力水、固态水;按地下水的赋存特征划分为:上层滞水、潜水、承压水。
2、运动规律:地下水运动分为层流和紊流。
地下水在土中或微小裂隙中以不大的速度连续渗透时为层流运动;在岩石的裂隙或空洞内流淌,会产生紊流。
地下水的渗流速度一般符合达西定律。
二、地下水对工程的影响1,潜水上升,引起盐渍化,增大腐蚀性。
2,河谷阶地、斜坡及岸边,潜水上升,增大浸湿范围,破坏岩土体的结构和强度。
3,粉土、粉、细砂层中,潜水上升,会产生液化。
4,水位上升,可能使基础上浮使建筑物失稳。
5,膨胀土区,水位上升或土体水分增减,使膨胀岩土产生不匀称胀缩变形。
6,寒冷地区,潜水上升,冻结,地面隆起。
解冻降低抗压强度和抗剪强度。
导致建筑物开裂、失稳。
7,地下水位在压缩层范围内突然下降,增加自重应力,使基础产生附加沉降,导致变形破坏。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章地下水运动的基本规律
第一节重力水运动的基本规律
(1)达西定律
达西定律是由法国水力学家H.Darcy于1856年通过大量的室内实验得出的。
达西实验装置与条件:
等径圆筒装入均匀砂样,圆筒断面为ω;
上下各置一个稳定的溢水装置——保持实验过程水流的稳定;
水流实验时,上端进水,下端出水——参见图4-1,示意流线(图中兰色线);
砂筒中,安装了2个测压管;
下端出水口,测定出水量Q。
实验过程:(1)通过改变水头,稳定测量出水量;(2)改变试样筒内的砂样(粒
径变化),重复实验。
实验结果:出水端的流量Q与砂柱断面为ω、测压管水头之间的关系为:
图4—1 达西试验示意图
(4—1)
式中:——渗透流量(出口处流量,即为通过砂柱各断面的流量);
——过水断面(在实验中相当于砂柱横断面积);
——水头损失(,即上下游过水断面的水头差);
——渗透途径(上下游过水断面的距离);
——渗透系数(与砂柱样品有关的系数)。
(4—1)为达西定律表达方法之一。
达西公式的变化形式:
由水力学中水动力学基本原理:
(4—2)
——水力梯度,相当于/,即水头差除以渗透途径。
(4—2)代入(4—1)有:
(4—3)
(4—1)与(4—3)为达西定律的不同表达方法。
由(4—3)达西公式表明:渗透流量(Q)与渗透系数(K)、过水断面(ω)
及水力梯度(I)成正比。
从水力学已知,通过某一断面的流量等于流速与过水断面的乘积,即:
(4—4)
即。
比照公式(4—4)与(4—1),达西定律又可以表达为:
(4—5)
式中:称作渗透流速,即单位面积上的流量——也称为比流量。
由(4—5)式表明:渗透流速与水力梯度一次方成正比关系,故达西定律又
称为线性渗透定律。
下面探讨达西公式(4—5)式中各项的物理涵义。
(2)渗透流速(V)
过水断面ω :砂柱的横切面积,是指水流通过的包括岩石骨架与空隙在内
的整个断面。
实际过水断面:扣除结合水所占据范围以外的空隙面积,也就是重力水
所占据的空隙面积。
实际过水断面ω′与过水断面ω的关系,可以表示为:(参
见图4-2,插图4-1)
图4—2 过水断面(斜阴线部分)与实际过水断面(直阴线部分)颗粒边缘涂黑部分(最好改为红色)为夸大表示的结合水
A 过水断面(水流可以穿越颗粒)
B 实际过水断面(水流只沿孔隙运动)
插图4-1 过水断面与实际过水断面动画
有效孔隙度:重力水流动的空隙体积(不包括结合水占据的空间)与岩石
体积之比。
既然不是实际的过水断面,可知也并非真实的流速,而是假设水流通过包括颗粒骨架与空隙在内的整个断面()。
因此,渗透流速是一种虚拟流速。
渗透流速与实际流速:令通过实际过水断面的流速为实际平均流速,则有:
而
既:
两者的关系:达西流速小于实际流速;u和V都是平均流速。
通常渗流计算时用渗透流速V,研究地下水污染时用实际流速u。
(3)水力梯度(I)
水力梯度的概念:是沿渗透途径上的水头损失与相应渗透途径的长度之比;即单位渗透途径上的机械能损失,也即机械能的损失率。
根据(4—5)式V=KI,可知,当岩石性质一定时,K为常数,I大,V也大;说明渗透水流流动速度越大,沿渗流途径的机械能损耗越大;换言之, I越大,驱动水流运动的速度越大。
水头损失构成:水质点间内摩擦的消耗和岩石固体边界对水流的摩擦阻力消耗。
损失的能量最终转变为热能而消耗掉。
(4)渗透系数(K)
由公式(4—5)V=KI可知,渗透系数K在数值上是当I=1时的渗透流速。
当I一定时,K大,则V也大,Q也大,因此,渗透系数K是表征岩石透水性的定量指标。
K愈大,表明岩石的透水能力愈强。
松散岩石渗透系数的常见值可参见表4—1。
表4—1 松散岩石渗透系数参考值
第二节流网
(1)基本概念
渗流场:地下水的流动空间,它包含两种内容:一是空间的含水介质场(介质场—K),二是水流的势能量场(势场—H),这二者共同构成地下水的流动特征,可以用达西定律V=KH/L 来描述V=f(K,H)。
流网是描述渗流场中地下水流动状况的有效工具。
流网概念:在渗流场中,由一系列等水头线与流线组成的网格,称为流网。
等水头线:在某时刻,渗流场中水头相等的各点的连线(水势场的分布)。
流线:某时刻在渗流场中画出的一条空间曲线,该曲线上各个水质点的流速方向都与这条曲线相切(某时刻各点流向的连线)。
迹线:流体水质点在渗流场中某一时间段内的运动轨迹。
稳定流条件下,流线与迹线重合。
(2)二维流网
平面流网:通常在潜水等水位线图和承压水等测压水位线图上,加上流向来表示。
剖面流网:当含水层厚度较大时,需要刻画垂向水流特征,通常用剖面流网来表示。
(3)流网的基本要求
a)在各向同性介质中,流线与等水头线正交;在各向异性介质中,流线与等水头线斜交;
b)相邻两条等水位线的水头差相等,相邻两条流线间流量相等。
(4)二维流网的绘制——剖面流网为例
精确地绘制定量流网需要充分掌握有关的边界条件及参数,但在实测资料较少的情况下,也可徒手绘制定性流网。
尽管这种信手流网并不精确,但往往可以提供我们许多有用的水文地质信息,是水文地质分析的有效工具。
为了讨论的方便。
在此仅限于分析均质各向同性介质中剖面稳定流流网为例。
a. 边界性质分析
定水头边界:地表水体的断面(如河渠的湿周,图4—3,a);
隔水边界:
潜水含水层底板、承压含水层隔水顶底板(图4—3,b);
无入渗、无蒸发稳定流动条件下潜水面(图4—3,c);
分流线是水力零通量面——虚拟的隔水边界(图4—4)。
地下水面边界:
当无入渗及蒸发,有侧向补给,稳定流动时是一条流线(图4—3,c);
当有入渗补给时,它既不是流线,也不是等水头线(图4—3,d)。
图4—3 等水头线、流线与各类边界的关系
1—含水层;2—隔水层;3—潜水面;4—等水头线;5—流线;6—河渠水面;7—降水入渗
b. 绘制步骤(参见河间地块流网图P40,图4-4,参照幻灯片):
寻找已知边界(湿周,隔水边界,水位线);
分水线、源、汇的确定;流线总是由源指向汇;
画出渗流场周边流线,按照边界性质将流线或等水头线与边界相连;
中间内插其它流线,等单宽流量控制流线根数;
确定等水头差间隔,根据流线与等水头线正交的规则,画出等水头线。
(5)流网图的信息与应用
流网它反映了渗流场中地下水的流动状况,同时也是介质场与势场的综合反映。
从图4-4河间地块流网图可以获得以下信息:
(1)由分水岭到河谷,流向从由上向下到接近水平再向上;(2)在分水岭地带打井,井中水位随井深加大而降低,河谷地带井水位则随井深加大而抬升;(3)由分水岭到河谷,流线愈来愈密集,流量增大,地下径流加强;(4)由地表向深部,地下径流减弱;(5)由分水岭出发的流线,渗透途径最长,平均水力梯度最小,地下水径流交替最弱,近流线末端河谷下方,地下水的矿化度最高。
理解上述流网提供的信息,思考以下问题:
确定任意点的水头值(H),了解其在流场中的变化规律
比较图4-4中:与的大小?
确定水力梯度 I 的大小,及其在流场中的变化规律
比较图4-4中:与的大小?
确定渗透流速V的大小,及其在流场中的变化规律。
比较与的大小?
渗流场内的流量分布情况——参照流线的疏密(分布)情况分析
污染物质的运移追踪。
图4—4 河间地块流网图
1—流线;2—等水头线;3—分流线;4—潜水面;5—河水位;6—井、涂兰部分有水;7—代表矿化度大小的符号,圆圈愈多,矿化度愈大;8—降水入渗;9—绘制流网的大致顺序
(6)层状非均质介质中的流网(自学内容)
层状非均质:指介质场内各岩层内部渗透性均为均质各向同性的,但不同层介质的渗透性不同。
以两层含水介质,剖面二维流(图4—5)为例分析。
设两岩层渗透系数分别为及,而且。
图4—5 层状非均质介质中两种条件下的流网
1—隔水层;2—弱透水层;3—强透水层;4—等水头线;5—流线;6—测压水位线
图4—5(a):及两层厚度相等(上下分层,并联关系)
基本原理:,I不变,ω相同,,故。
流线特征:层流线密度为的3倍(,流线根数反映流量的大小);
等水头线特征:等水头线间隔分布一致(I不变)
与均质介质的流网比较:均质介质中流线相对均匀分布;层状非均质中流线分层均匀分布(相当于并联效果)
图4—5(b):及两层长度相等(沿程变化,成串联关系)
基本原理:,和ω相同,故,由于,故。
流线特征:两层流线数相等(相同)
等水头线特征:层中等水头线的间隔数为层的3倍()
与均质介质的流网比较:均质介质中等水头线均匀分布;层状非均质中等水头线分段均匀分布(相当于串联效果)。
