将军饮马模型(终稿)

合集下载

将军饮马问题16大模型

将军饮马问题16大模型将军饮马问题是一个经典的数学问题，被广泛应用于算法设计和逻辑推理。

在这个问题中，有一个有限数量的将军和马，将军们需要同时饮马，而且马的数量要足够多，以保证每个将军都能骑到马上。

然而，问题的难点在于，如果将军们不约定时间，他们同时骑上马的可能性很小。

为解决这个问题，已经提出了许多解决方案，下面我将介绍16种解决这个问题的模型。

1. 广播模型将军们可以通过广播的方式进行通信，每个将军都可以听到其他将军的广播信号。

在某个固定时间，将军们开始广播他们已准备好骑马的消息，并等待其他将军的回应。

只有当每个将军都收到了其他将军的回应信号，他们才会同时骑上马。

2. 协商模型将军们可以通过协商的方式进行通信，每个将军都可以与其他将军直接交流。

在某个固定时间，将军们开始与其他将军交流他们已准备好骑马的消息，并等待其他将军的回应。

只有当每个将军都收到了其他将军的回应信息，他们才会同时骑上马。

3. 仲裁者模型将军们委任一个仲裁者作为中介来传递消息。

每个将军将自己已准备好骑马的消息告诉仲裁者，仲裁者负责将该消息传递给所有其他将军。

只有当每个将军都收到其他将军的消息，他们才会同时骑上马。

4. 时钟模型在固定的时间间隔内，每个将军都可以检查时钟的状态。

他们会设定一个目标时间，当时钟的时间达到目标时间时，将军们会同时骑上马。

这样，他们可以通过同步的方式来保证同时骑马。

5. 群体模型将军们通过形成一个群体来解决这个问题。

在一个固定时间，将军们同时进入群体，并在一起饮马。

这种方式需要所有将军都同意进入群体，并时刻保持一致，才能保证同时骑马。

将军们依次传递一个令牌表示自己已准备好骑马。

当每个将军都收到了令牌并且已经骑上马时，他们才会将令牌传递给下一个将军。

这种方式需要将军们按照一定的规则来传递令牌，以保证同时骑马。

7. 树模型将军们通过构建一棵树来解决这个问题。

树的根节点是一个仲裁者，每个将军是树的叶子节点。

当仲裁者收到所有将军的准备好骑马的消息时，他会通知所有将军同步骑马。

将军饮马模型(终稿)教学提纲

将军饮马模型(终稿)将军饮马模型一、背景知识：【传说】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．【问题原型】将军饮马造桥选址费马点【涉及知识】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平移；【解题思路】找对称点，实现折转直二、将军饮马问题常见模型1.两定一动型：两定点到一动点的距离和最小例1：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB最小.作法：连接AB，与直线l的交点Q，Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB最小，且最小值等于AB.原理：两点之间线段最短。

证明：连接AB，与直线l的交点Q，P为直线l上任意一点，在⊿PAB中，由三角形三边关系可知：AP+PB≧AB(当且仅当PQ重合时取﹦)例2：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB的和最小.关键：找对称点作法：作定点B关于定直线l的对称点C，连接AC，与直线l的交点Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB和最小，且最小值等于AC.原理：两点之间，线段最短证明：连接AC，与直线l的交点Q，P为直线l上任意一点，在⊿PAC中，由三角形三边关系可知：AP+PC≧AC(当且仅当PQ重合时取﹦)2.两动一定型例3：在∠MON的内部有一点A，在OM上找一点B，在ON上找一点C，使得△BAC周长最短．作法：作点A关于OM的对称点A’，作点A关于ON的对称点A’’，连接A’ A’’，与OM 交于点B，与ON交于点C，连接AB，AC，△ABC即为所求．原理：两点之间，线段最短例4：在∠MON的内部有点A和点B，在OM上找一点C，在ON上找一点D，使得四边形ABCD周长最短．作法：作点A关于OM的对称点A’，作点B关于ON的对称点B’，连接A’ B’，与OM 交于点C，与ON交于点D，连接AC，BD，AB，四边形ABCD即为所求．原理：两点之间，线段最短3.两定两动型最值例5：已知A、B是两个定点，在定直线l上找两个动点M与N，且MN长度等于定长d （动点M位于动点N左侧），使AM+MN+NB的值最小.提示：存在定长的动点问题一定要考虑平移作法一：将点A向右平移长度d得到点A’，作A’关于直线l的对称点A’’，连接A’’B，交直线l于点N，将点N向左平移长度d，得到点M。

初中数学58种模型之12、“将军饮马”三种模型详解

当两淀点A 、R 在克罐/何侧时，在亞线』上携一点几便|阳一户创最大°将军饮马”三种模型"将军饮马"问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。

晋两定点A.U 在点线F 异創时-在肖践f 上找一点Pt 使PA+PB 锻小*述接也交h 纱/于点P.点卩閒为所求作的点.肖两远点上B 在直雜I 同测时,在直刻上拥一点P,使PA+PB 最小'作庖U 芸于宜线F 的对称点V ■连楼AB'交直线于点P.点P 即为用求作的点"―二I \PA-P^\荊卩址大值洵丽。

连接班并延长交直戦』十点几点卩即为所求作的点。

当两定点仏k 在直找门司侧时，在直线』上找一点人使PA-PB\^扎作点B 关于直统』的对称点B'h 谨接恋’井延快交宜鏡于点巴点F 即为所求作的点。

皓论PAPI1的颯小°PA-PB 的盘小值为AB'□冋-卿的最大值为上的动点，则户创的圮大值是多少？A ■B ■\A\PA-PB\的 1当两定点限廿在宜线/同删时，在直线丿上找--点片使f4-砂|最小“ 叫连接馭作■-朋的垂直平分钱交直线f 于点P ，点卩即沟所求作的点-最小值为叽模型实例例1一如图"止厅形的面积是1氛是等边三博形，点E 在止方刑ABCI ）内“在对角纯蚯上有一点卩*则PD+FE 的艮小值为°^12.如圜已S11AABC 为辱展宜角匸角形…怔-氏=4”ZBCD 15".P 拘匚D热搜掃练I.如虱^AABC 中「ZACB-fJO 3，乃是就边的中点，II 是屈边b -动直+则LCIED 的最小悄是°])2・如图.点C的坐标为（3,y）,当△ABC的周长最短时，求丿的值。

3.如图.正方形ABCD中,AB-7,M是DCI：的一点，且DM-3,N是AC上的一动点.求|DN-MN|的嚴小值与战大值.△PCD 周氏最小为点P 在ZAOB 的内部，在0B 上找点D,在0A 上找点C,使得△PCD 周长最小。

将军饮马模型(终稿)

将军饮马模型将军饮马模型一、背景知识：【传说】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营 A 出发，先到河边饮马，然后再去河岸同侧的军营 B 开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“ 将军饮马”的问题便流传至今．【问题原型】将军饮马造桥选址费马点【涉及知识】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平移；【解题思路】找对称点，实现折转直二、将军饮马问题常见模型1.两定一动型：两定点到一动点的距离和最小例1：在定直线l上找一个动点 P，使动点 P 到两个定点 A 与 B 的距离之和最小，即 PA+PB 最小 .作法：连接 AB ，与直线l 的交点Q，Q 即为所要寻找的点，即当动点P 跑到了点 Q 处，PA+PB 最小，且最小值等于AB.原理：两点之间线段最短。

证明：连接 AB ，与直线l 的交点Q，P为直线 l 上任意一点，在⊿ PAB 中，由三角形三边关系可知：AP+PB ≧ AB( 当且仅当 PQ 重合时取﹦ )例2：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB 的和最小 .关键：找对称点作法：作定点 B 关于定直线l的对称点 C，连接 AC ，与直线 l 的交点 Q 即为所要寻找的点，即当动点 P 跑到了点 Q 处， PA+PB 和最小，且最小值等于 AC. 原理：两点之间，线段最短证明：连接 AC ，与直线l 的交点Q，P为直线 l 上任意一点，在⊿ PAC 中，由三角形三边关系可知：AP+PC≧ AC( 当且仅当 PQ 重合时取﹦ )2.两动一定型例3：在∠ MON 的内部有一点 A ，在 OM 上找一点 B ，在 ON 上找一点 C，使得△ BAC 周长最短．作法：作点 A 关于 OM 的对称点 A’，作点 A 关于 ON 的对称点 A’’，连接 A’ A ’’，与 OM 交于点 B，与 ON 交于点 C，连接 AB ， AC ，△ ABC 即为所求．原理：两点之间，线段最短例 4：在∠ MON 的内部有点 A 和点 B ，在 OM 上找一点 C ，在 ON 上找一点 D ，使得四边形 ABCD 周长最短．作法：作点 A 关于 OM 的对称点 A ’，作点 B 关于 ON 的对称点 B ’，连接 A ’ B ，’与 OM 交于点 C ，与 ON 交于点 D ，连接 AC ， BD ， AB ，四边形 ABCD 即为所求．原理：两点之间，线段最短3. 两定两动型最值例 5：已知 A 、B 是两个定点，在定直线 l 上找两个动点 M 与 N ，且 MN 长度等于定长 d （动点 M 位于动点 N 左侧），使 AM+MN+NB 的值最小 .提示：存在定长的动点问题一定要考虑平移作法一：将点 A 向右平移长度 d 得到点 A ’，作 A ’关于直线l 的对称点 A ’’，连接 A ’’B ，交直线 l于点 N ，将点 N 向左平移长度dM。

将军饮马(最完整讲义)

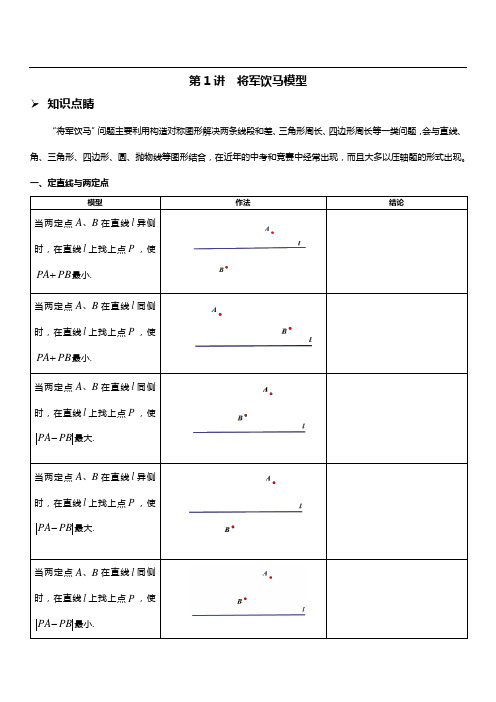
第1讲将军饮马模型➢知识点睛“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。

一、定直线与两定点模型作法结论A、在直线l异侧当两定点B时，在直线l上找上点P，使PA+最小.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA+最小.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA-最大.PBA、在直线l异侧当两定点B时，在直线l上找上点P，使PA-最大.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA-最小.PB二、角到定点模型作法结论点P 在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得PCD ∆周长最小.点P 在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得MN PN +最小.点Q P 、在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得四边形PMNQ 周长最小.点M 在AOB ∠的外部，在射线OA 上找一点P ，使PM 与点P 到射线OB 的距离和最小.点M 在AOB ∠的内部，在射线OA 上找一点P ，使PM 与点P 到射线OB 的距离和最小.点Q P 、分别在AOB ∠的边OB OA 、是，在OA 上找一点M ，在OB 上找一点N ,使得MQ MN PN ++最小.二、两定点一定长模型作法结论如图在直线l 上找上两点N M 、（M 在左），使NB MN AM ++最小,且d MN =.如图，21//l l ，21l l 、之间的距离为d ，在21l l 、上分别找N M 、两点，使1l MN ⊥，且NB MN AM ++最小.如图，21//l l ，43//l l ,21l l 、之间的距离为1d ，43//l l 之间的距离为2d ，在21l l 、上分别找N M 、两点，使1l MN ⊥，在43l l 、上分别找Q P 、两点，使3l PQ ⊥且QB PQ NP MN AM ++++最小.如图，在⊙O 上找一点N ，在直线l 找一点M ,使得MN AM +最小.➢ 精讲精练例1：如图，点P 是∠AOB 内任意一点，∠AOB =30°，OP =8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值．P OBAMN例2：如图，正方形ABCD 的边长是4，M 在DC 上，且DM =1， N 是AC 边上的一动点，则△DMN 周长的最小值．例3：如图，在Rt △ABO 中，∠OBA =90°，A （4,4），点C 在边AB 上，且AC :CB =1:3，点D 为OB 的中点，点P 为边OA 上的动点，当点P 在OA 上移动时，使四边形PDBC 周长最小的点P 的坐标为( )A ．(2,2)B ．5(2，5)2C ．8(3，8)3D ．(3,3)第3题图第4题图第5题图例4：如图，在△ABC 中，AC =BC ，∠ACB =90°，点D 在BC 上，BD =3，DC =1，点P 是AB 上的动点，则PC +PD 的最小值为( ) A ．4B ．5C ．6D ．7例5：如图，在等边△ABC 中，AB =6， N 为AB 上一点且BN =2AN ， BC 的高线AD 交BC 于点D ，M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值是___________． PDCBAA BCDMNNMDCBA例6：如图，在Rt △ABD 中，AB =6，∠BAD =30°，∠D =90°，N 为AB 上一点且BN =2AN ， M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值．例7：如图，在Rt △ABC 中，∠ACB =90°，AC =6．AB =12，AD 平分∠CAB ，点F 是AC 的中点，点E 是AD 上的动点，则CE +EF 的最小值为( ) A ．3 B ．4 C ． D ．第7题图第8题图第9题图例8：如图，在锐角三角形ABC 中，BC =4，∠ABC =60°， BD 平分∠ABC ，交AC 于点D ，M 、N 分别是BD ，BC 上的动点，则CM +MN 的最小值是( ) A B ．2 C ．D ．4例9：如图，在菱形ABCD 中，AC =BD =6，E 是BC 的中点，P 、M 分别是AC 、AB 上的动点，连接PE 、PM ，则PE +PM 的最小值是( ) A ．6B ．C ．D ．4.5NMDBA E AFCDBNM DCBAEPDCBAM例10：如图，矩形ABOC 的顶点A 的坐标为（-4,5），D 是OB 的中点，E 是OC 上的一点，当△ADE 的周长最小时，点E 的坐标是( ) A ．4(0,)3B ．5(0,)3C ．(0,2)D ．10(0,)3第10题图第11题图第12题图例11：如图，在矩形ABCD 中，AB =6，AD =3，动点P 满足13PAB ABCD S S ∆=矩形，则点P 到A 、B 两点距离之和PA +PB 的最小值为( ) A ．B ．C ．D 例12：如图，矩形ABCD 中，AB =10，BC =5，点E 、F 、G 、H 分别在矩形ABCD 各边上，且AE =CG ，BF =DH ，则四边形EFGH 周长的最小值为( )A ．B ．C ．D ．例13：如图，∠AOB =60°，点P 是∠AOB 内的定点且OP M 、N 分别是射线OA 、OB 上异于点O 的动点，则△PMN 周长的最小值是( )A B C ．6D ．3第13题图第14题图 CBH FGEDCB AA BMOPN例14：如图，∠AOB 的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点N （3,0）是OB 上的一定点，点M 是ON 的中点，∠AOB =30°，要使PM +PN 最小，则点P 的坐标为．例15：如图，已知正比例函数y =kx （k >0）的图像与x 轴相交所成的锐角为70°，定点A 的坐标为（0，4），P 为y 轴上的一个动点，M 、N 为函数y =kx （k >0）的图像上的两个动点，则AM +MP +PN 的最小值为___________．第15题图例16：如图，在平面直角坐标系中，矩形ABCD 的顶点B 在原点，点A 、C 在坐标轴上，点D 的坐标为（6，4），E 为CD 的中点，点P 、Q 为BC 边上两个动点，且PQ =2，要使四边形APQE 的周长最小，则点P 的坐示应为______________．例17：如图，矩形ABCD 中，AD =2，AB =4，AC 为对角线，E 、F 分别为边AB 、CD 上的动点，且EF ⊥AC 于点M ，连接AF 、CE ，求AF +CE 的最小值．AB CD EFMx例18：如图，正方形ABCD 的面积是12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，求PD+PE 的最小值。

将军饮马(最完整讲义)

第1讲将军饮马模型➢知识点睛一、“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题, 会与直线、角、三角形、四边形、圆、抛物线等图形结合, 在近年的中考和竞赛中经常出现, 而且大多以压轴题的形式出现。

二、定直线与两定点模型作法结论当两定点在直线异侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最大.当两定点在直线异侧时, 在直线上找上点, 使最大.当两定点在直线同侧时, 在直线上找上点, 使最小.二、角到定点模型作法结论点在的内部, 在上找一点, 在上找一点,使得周长最小.点在的内部, 在上找一点, 在上找一点,使得最小.点在的内部, 在上找一点, 在上找一点,使得四边形周长最小.点在的外部, 在射线上找一点, 使与点到射线的距离和最小.点在的内部, 在射线上找一点, 使与点到射线的距离和最小.点分别在的边是, 在上找一点, 在上找一点,使得最小.三、两定点一定长模型作法结论如图在直线上找上两点（在左）, 使最小,且.如图, , 之间的距离为, 在上分别找两点, 使, 且最小.如图, , ,之间的距离为, 之间的距离为, 在上分别找两点, 使, 在上分别找两点, 使且最小.如图, 在⊙上找一点, 在直线找一点,使得最小.➢精讲精练例1: 如图, 点P是∠AOB内任意一点, ∠AOB=30°, OP=8, 点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值.例2: 如图, 正方形ABCD 的边长是4, M 在DC 上, 且DM=1, N 是AC 边上的一动点, 则△DMN 周长的最小值.A ．例3: 如图, 在Rt △ABO 中, ∠OBA=90°, A （4,4）, 点C 在边AB 上, 且AC:CB=1:3, 点D 为OB 的中点, 点P 为边OA 上的动点, 当点P 在OA 上移动时, 使四边形PDBC 周长最小的点P 的坐标为 B. ,C ．,D ．第3题图第4题图第5题图例4: 如图, 在△ABC 中, AC=BC, ∠ACB=90°, 点D 在BC 上, BD=3, DC=1, 点P 是AB 上的动点, 则PC+PD 的最小值为 A. 4 B. 5 C. 6 D. 7例5：如图, 在等边△ABC 中, AB=6, N 为AB 上一点且BN=2AN, BC 的高线AD 交BC 于点D, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值是___________．A BCDMN例6: 如图, 在Rt △ABD 中, AB=6, ∠BAD=30°, ∠D=90°, N 为AB 上一点且BN=2AN, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值.例7: 如图, 在Rt △ABC 中, ∠ACB=90°, AC=6. AB=12, AD 平分∠CAB, 点F 是AC 的中点, 点E 是AD 上的动点, 则CE+EF 的最小值为 A. 3 B. 4 C.D.第7题图第8题图第9题图A ．例8: 如图, 在锐角三角形ABC 中, BC=4, ∠ABC=60°, BD 平分∠ABC, 交AC 于点D, M 、N 分别是BD, BC 上的动点, 则CM+MN 的最小值是B. 2C.D. 4例9: 如图, 在菱形ABCD 中, AC=, BD=6, E 是BC 的中点, P 、M 分别是AC.AB 上的动点, 连接PE 、PM, 则PE+PM 的最小值是A. 6B.C.D. 4.5E AFCDBNM DCBAEPDCBAMA ．例10: 如图, 矩形ABOC 的顶点A 的坐标为（-4,5）, D 是OB 的中点, E 是OC 上的一点, 当△ADE 的周长最小时, 点E 的坐标是B. C. D.第10题图第11题图第12题图例11: 如图, 在矩形ABCD 中, AB=6, AD=3, 动点P 满足, 则点P 到A.B 两点距离之和PA+PB 的最小值为A. B. C. D.例12: 如图, 矩形ABCD 中, AB=10, BC=5, 点E 、F 、G 、H 分别在矩形ABCD 各边上, 且AE=CG, BF=DH, 则四边形EFGH 周长的最小值为A. B. C. D.例13: 如图, ∠AOB=60°, 点P 是∠AOB 内的定点且OP=, 若点M 、N 分别是射线OA.OB 上异于点O 的动点, 则△PMN 周长的最小值是A. B. C. 6 D. 3第13题图第14题图CBH FGEDCB AABMOPN例14: 如图, ∠AOB 的边OB 与x 轴正半轴重合, 点P 是OA 上的一动点, 点N （3,0）是OB 上的一定点, 点M 是ON 的中点, ∠AOB=30°, 要使PM+PN 最小, 则点P 的坐标为 .例15：如图, 已知正比例函数y=kx （k>0）的图像与x 轴相交所成的锐角为70°, 定点A 的坐标为（0, 4）, P 为y 轴上的一个动点, M 、N 为函数y=kx （k>0）的图像上的两个动点, 则AM+MP+PN 的最小值为___________．第15题图例16: 如图, 在平面直角坐标系中, 矩形ABCD 的顶点B 在原点, 点A.C 在坐标轴上, 点D 的坐标为（6, 4）, E 为CD 的中点, 点P 、Q 为BC 边上两个动点, 且PQ=2, 要使四边形APQE 的周长最小, 则点P 的坐示应为______________.例17：如图, 矩形ABCD 中, AD=2, AB=4, AC 为对角线, E 、F 分别为边AB 、CD 上的动点, 且EF ⊥AC 于点M,连接AF 、CE, 求AF+CE 的最小值．x例18: 如图, 正方形ABCD的面积是12, △ABE是等边三角形, 点E在正方形ABCD内, 在对角线AC上有一点P, 求PD+PE的最小值。

(完整word版)将军饮马问题的11个模型及例题

将军饮马问题问题概述路径最短、线段和最小、线段差最大、周长最小等一系列最值问题方法原理1.两点之间，线段最短；2.三角形两边之和大于第三边，两边之差小于第三边；3.中垂线上的点到线段两端点的距离相等；4.垂线段最短.基本模型1.已知：如图，定点A、B分布在定直线l两侧；要求：在直线l上找一点P，使PA+PB的值最小解：连接AB交直线l于点P，点P即为所求,PA+PB的最小值即为线段AB的长度理由：在l上任取异于点P的一点P´，连接AP´、BP´，在△ABP’中，AP´+BP´>AB，即AP´+BP´>AP+BP∴P为直线AB与直线l的交点时，PA+PB最小.2.已知：如图，定点A和定点B在定直线l的同侧要求：在直线l上找一点P，使得PA+PB值最小（或△ABP的周长最小）解：作点A关于直线l的对称点A´，连接A´B交l于P，点P即为所求；理由：根据轴对称的性质知直线l为线段AA´的中垂线，由中垂线的性质得：PA=PA´，要使PA+PB最小，则需PA´+PB值最小，从而转化为模型1.3.已知：如图，定点A、B分布在定直线l的同侧（A、B两点到l的距离不相等）要求：在直线l上找一点P，使︱PA-PB︱的值最大解：连接BA并延长，交直线l于点P，点P即为所求；理由：此时︱PA-PB︱=AB，在l上任取异于点P的一点P´，连接AP´、BP´，由三角形的三边关系知︱P´A-P´B︱<AB，即︱P´A-P´B︱<︱PA-PB︱4. 已知：如图，定点A、B分布在定直线l的两侧（A、B两点到l的距离不相等）要求：在直线l上找一点P，使︱PA-PB︱的值最大解：作点B关于直线l的对称点B´，连接B´A并延长交于点P，点P即为所求；理由：根据对称的性质知l为线段BB´的中垂线，由中垂线的性质得：PB=PB´，要使︱PA-PB︱最大，则需︱PA-PB´︱值最大，从而转化为模型3.典型例题1-1如图，直线y=2x+4与x轴、y轴分别交于点A和点B，点C、D分3别为线段AB、OB的中点，点P为OA上一动点，当PC+PD最小时，点P的坐标为_________，此时PC+PD的最小值为_________.【分析】符合基本模型2的特征，作点D关于x轴的对称点D'，连接CD'交x轴于点P，此时PC+PD值最小，由条件知CD为△BAO的中位线，OP为△CDD'的中位线，易求OP长，从而求出P点坐标；PC+PD的最小值即CD'长，可用勾股定理（或两点之间的距离公式，实质相同）计算.【解答】连接CD，作点D关于x轴的对称点D′，连接CD′交x轴于点P ，此时PC+PD 值最小．令y=23x+4中x=0，则y=4， ∴点B 坐标（0，4）；令y=23x+4中y=0，则23x+4=0，解得：x=﹣6，∴点A 的坐标为（﹣6，0）．∵点C 、D 分别为线段AB 、OB 的中点，∴CD 为△BAO 的中位线， ∴CD ∥x 轴，且CD=21AO=3，∵点D ′和点D 关于x 轴对称，∴O 为DD ′的中点，D ′（0，-1），∴OP 为△CDD ′的中位线，∴OP=21CD=23，∴点P 的坐标为（﹣32，0）．在Rt △CDD ′中，CD ′=22D D CD '+=2243+=5，即PC+PD 的最小值为5.【小结】还可用中点坐标公式先后求出点C 、点P 坐标；若题型变化，C 、D 不是AB 和OB 中点时，则先求直线CD ′的解析式，再求其与x 轴的交点P 的坐标.典型例题1-2如图，在平面直角坐标系中，已知点A 的坐标为（0，1），点B的坐标为（32，﹣2），点P 在直线y=﹣x 上运动，当|PA ﹣PB|最大时点P 的坐标为_________，|PA ﹣PB|的最大值是_________.【分析】符合基本模型4的特征，作A 关于直线y=﹣x 对称点C ，连接BC ，可得直线BC 的方程；求得BC 与直线y=﹣x 的交点P 的坐标；此时|PA ﹣PB|=|PC ﹣PB|=BC 取得最大值，再用两点之间的距离公式求此最大值.【解答】作A 关于直线y=﹣x 对称点C ，易得C 的坐标为（﹣1，0）；连接BC ，可得直线BC的方程为y=﹣54x ﹣54，与直线y=﹣x 联立解得交点坐标P 为（4，﹣4）；此时|PA﹣PB|=|PC ﹣PB|=BC 取得最大值，最大值BC=2223)2()1(-++=241；【小结】“两点一线”大多考查基本模型2和4，需作一次对称点，连线得交点.变式训练1-1已知菱形OABC 在平面直角坐标系的位置如图所示，顶点A （5，0），OB=4√5，点P 是对角线OB 上的一个动点，D （0，1），当CP+DP 最短时，点P 的坐标为（）A ．（0，0）B ．（1，12）C ．（65，35）D ．（107，57）变式训练1-2如图，菱形ABCD 中，对角线AC 和BD 交于点O ，AC=2，BD=2√3,E 为AB 的中点，P 为对角线AC 上一动点，则PE+PB 的最小值为__________.变式训练1-3如图，已知直线y=12x+1与y 轴交于点A ，与x 轴交于点D ，抛物线y=12x 2+bx+c 与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为（1，0）．（1）求该抛物线的解析式；（2）在抛物线的对称轴上找一点M ，使|AM ﹣MC|的值最大，求出点M 的坐标.拓展模型1. 已知：如图，A 为锐角∠MON 外一定点；要求：在射线OM 上找一点P ，在射线ON 上找一点Q ，使AP+PQ 的值最小.解：过点A 作AQ ⊥ON 于点Q ，AQ 与OM 相交于点P ，此时，AP+PQ 最小；理由：AP+PQ ≧AQ ，当且仅当A 、P 、Q 三点共线时，AP+PQ 取得最小值AQ ，根据垂线段最短，当AQ ⊥ON 时，AQ 最小.2. 已知：如图，A 为锐角∠MON 内一定点；要求：在射线OM 上找一点P ，在射线ON 上找一点Q ，使AP+PQ 的值最小.解：作点A关于OM的对称点A′，过点A′作AQ⊥ON于点Q，A′Q交OM于点P，此时AP+PQ最小；理由：由轴对称的性质知AP=A′P，要使AP+PQ最小，只需A′P+PQ最小，从而转化为拓展模型13.已知：如图，A为锐角∠MON内一定点；要求：在射线OM上找一点P，在射线ON上找一点Q，使△APQ的周长最小解：分别作A点关于直线OM的对称点A1,关于ON的对称点A 2，连接 A1A2交OM于点P，交ON于点Q，点P和点Q即为所求，此时△APQ周长最小，最小值即为线段A1A2的长度；理由：由轴对称的性质知AP=A1P，AQ=A2Q，△APQ的周长AP+PQ+AQ=A1P+PQ+A2Q，当A1、P、Q、A2四点共线时，其值最小.4. 已知：如图，A、B为锐角∠MON内两个定点；要求：在OM上找一点P，在ON上找一点Q，使四边形APQB的周长最小解：作点A关于直线OM的对称点A´，作点B关于直线ON的对称点B´，连接A´B´交OM于P，交ON于Q，则点P、点Q即为所求，此时四边形APQB周长的最小值即为线段AB和A´B´的长度之和；理由：AB长为定值，由基本模型将PA转化为PA´,将QB转化为QB´，当A´、P、Q、B´四点共线时，PA´+PQ+ QB´的值最小，即PA+PQ+ QB的值最小.5.搭桥模型已知：如图，直线m∥n,A、B分别为m上方和n下方的定点，（直线AB不与m垂直）要求：在m、n之间求作垂线段PQ，使得AP+PQ+BQ最小.分析：PQ为定值，只需AP+BQ最小，可通过平移，使P、Q“接头”，转化为基本模型解：如图，将点A沿着平行于PQ的方向，向下平移至点A′，使得AA′=PQ，连接A′B交直线n于点Q，过点Q作PQ⊥n，交直线m于点P，线段PQ即为所求，此时AP+PQ+BQ最小.理由：易知四边形QPAA′为平行四边形，则QA′=PA，当B、Q、A′三点共线时，QA′+BQ最小，即AP+BQ最小，PQ长为定值，此时AP+PQ+BQ最小.6.已知：如图，定点A、B分布于直线l两侧，长度为a(a为定值)的线段PQ在l上移动（P在Q左边）要求：确定PQ的位置，使得AP+PQ+QB最小分析：PQ为定值，只需AP+QB的值最小，可通过平移，使P、Q“接头”，转化为基本模型解：将点A沿着平行于l的方向，向右移至A´，使AA´=PQ=a,连接A´B交直线l于点Q，在l上截取PQ=a（P在Q左边），则线段PQ即为所求，此时AP+PQ+QB的最小值为A´B+PQ，即A´B+a理由：易知四边形APQA´为平行四边形，则PA=QA´，当A´、Q、B三点共线时，QA´+QB最小，即PA+QB最小，又PQ长为定值此时PA+PQ+QB值最小.7.已知：如图，定点A、B分布于直线l的同侧，长度a(a为定值)的线段PQ在l上移动（P在Q左边）要求：确定PQ 的位置，使得四边形APQB 周长最小分析：AB 长度确定，只需AP+PQ+QB 最小，通过作A 点关于l 的对称点，转化为上述模型3解：作A 点关于l 的对称点A ´，将点A ´沿着平行于l的方向，向右移至A ´´，使A ´A ´´=PQ=a ，连接A ´´B交l 于Q ，在l 上截取QP=a （P 在Q 左边），线段PQ 即为所求，此时四边形APQB 周长的最小值为A ´´B+AB+PQ ，即A ´´B+AB+a典型例题2-1如图，在矩形ABCD 中，AB=10，BC=5，若点M 、N 分别是线段AC 、AB 上的两个动点，则BM+MN 的最小值为．【分析】符合拓展模型2的特征，作点B 关于AC 的对称点E ，再过点E 作AB 的垂线段，该垂线段的长即BM+MN 的最小值，借助等面积法和相似可求其长度.【解答】作点B 关于AC 的对称点E ，再过点E 作EN ⊥AB 于N ，则BM+MN=EM+MN ，其最小值即EN 长；∵AB=10，BC=5，∴AC=22BC AB +=55，等面积法求得AC 边上的高为55510⨯=25，∴BE=45，易知△ABC ∽△ENB ，∴，代入数据解得EN=8．即BM+MN 的最小值为8．【小结】该类题的思路是通过作对称，将线段转化，再根据定理、公理连线或作垂线；可作定点或动点关于定直线的对称点，有些题作定点的对称点易解，有些题则作动点的对称点易解.典型例题2-2如图，∠AOB=60°，点P 是∠AOB 内的定点且OP=，点M 、N 分别是射线OA 、OB 上异于点O 的动点，则△PMN 周长的最小值是（）A ．B ．C ．6D ．3【分析】符合拓展模型3的特征；作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，此时△PMN周长最小，其值为CD长；根据对称性连接OC、OD，分析条件知△OCD是顶角为120°的等腰三角形，作底边上高，易求底边CD. 【解答】作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，则MP=MC，NP=ND，OP=OD=OC=，∠BOP=∠BOD，∠AOP=∠AOC，∴PN+PM+MN=ND+MN+NC=DC，∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°，∴此时△PMN周长最小，作OH⊥CD于H，则CH=DH，∵∠OCH=30°，∴OH=OC=，CH=OH=，∴CD=2CH=3．即△PMN周长的最小值是3；故选：D．【小结】根据对称的性质，发现△OCD是顶角为120°的等腰三角形，是解题的关键，也是难点.典型例题2-3如图，已知平行四边形ABCO，以点O为原点，OC所在的直线为x轴，建立直角坐标系，AB交y轴于点D，AD=2，OC=6，∠A=60°，线段EF所在的直线为OD的垂直平分线，点P为线段EF上的动点，PM⊥x轴于点M点，点E与E′关于x轴对称，连接BP、E′M．（1）请直接写出点A坐标为，点B坐标为；（2）当BP+PM+ME′的长度最小时，请求出点P的坐标.【分析】（1）解直角三角形求出OD，BD的长即可解决；（2）符合“搭桥模型”的特征；首先证明四边形OPME′是平行四边形，可得OP=EM，PM是定值，PB+ME′=OP+PB的值最小时，BP+PM+ME′的长度最小，此时P点为直线OB与EF的交点，结合OB的解析式可得P点坐标；【解答】（1）在Rt△ADO中，∵∠A=60°，AD=2，∴OD=2•tan60°=2，∴A（﹣2，2），∵四边形ABCO是平行四边形，∴AB=OC=6，∴DB=6﹣2=4，∴B（4，2）（2）如图，连接OP．∵EF垂直平分线段OD，PM⊥OC，∴∠PEO=∠EOM=∠PMO=90°，∴四边形OMPE是矩形，∴PM=OE=，∵OE=OE′，∴PM=OE′，PM∥OE′，∴四边形OPME′是平行四边形,∴OP=EM，∵PM是定值，∴PB+ME′=OP+PB的值最小时，BP+PM+ME′的长度最小，∴当O、P、B共线时，BP+PM+ME′的长度最小，∵直线OB的解析式为y=x，∴P（2，）．【小结】求没有公共端点的两条线段之和的最小值，一般通过作对称和平移（构造平行四边形）的方法，转化为基本模型.典型例题2-4如图所示，在平面直角坐标系中，Rt△AOB的顶点坐标分别为A（﹣2，0），O（0，0），B（0，4），把△AOB绕点O按顺时针方向旋转90°，得到△COD．（1）求C、D两点的坐标；（2）求经过A、B、D三点的抛物线的解析式；（3）在（2）中抛物线的对称轴上取两点E、F（点E在点F的上方），且EF=1，使四边形ACEF的周长最小，求出E、F两点的坐标．【分析】符合拓展模型7的特征，通过作对称、平移、连线，可找出E、F点，结合直线的解析式和抛物线的对称轴可解出E、F坐标.【解答】（1）由旋转的性质可知：OC=OA=2，OD=OB=4,∴C点的坐标是（0，2），D点的坐标是（4，0），（2）设所求抛物线的解析式为y=ax2+bx+c，4a-2b+c=0由题意，得 16a+4b+c=0c=4解得a=-12，b=1，c=4，∴所求抛物线的解析式为y=-12x²+x+4；（3）只需AF+CE最短，抛物线y=-12x²+x+4的对称轴为x=1，将点A向上平移至A1（﹣2，1），则AF=A1E，作A1关于对称轴x=1的对称点A2（4，1），连接A2C，A2C与对称轴交于点E，E为所求，可求得A2C的解析式为y=-14x+2，当x=1时，y=74，∴点E的坐标为(1,74)，点F的坐标为(1,34)．【小结】解决此类题的套路是“对称、平移、连线”；其中，作对称和平移的顺序可互换.变式训练2-1几何模型：条件：如图1，A，B是直线l同旁的两个定点．问题：在直线l上确定一点P，使PA+PB的值最小．方法：作点A关于直线l的对称点A’，连接A’B交l于点P，即为所求.（不必证明）模型应用：（1）如图2，已知平面直角坐标系中两定点A（0，﹣1）和B（2，﹣1），P为x轴上一动点，则当PA+PB的值最小是点P的横坐标是，此时PA+PB= ．（2）如图3，正方形ABCD的边长为4，E为AB的中点，P是AC上一动点，连接BD，由正方形对称性可知，B与D关于直线AC对称．连接ED交AC于P，则PB+PE的最小值是．（3）如图4，在菱形ABCD中，AB=10，∠DAB=60°，P是对角线AC上一动点，E，F分别是线段AB和BC上的动点，则PE+PF的最小值是．（4）如图5，在菱形ABCD中，AB=6，∠B=60°，点G是边CD边的中点，点E．F分别是AG，AD上的两个动点，则EF+ED的最小值是．变式训练2-2如图，矩形ABCD中，AD=15，AB=10，E为AB边上一点，且DE=2AE，连接CE与对角线BD交于F；若P、Q分别为AB边和BC边上的动点，连接EP、PQ和QF；则四边形EPQF周长的最小值是___________.变式训练2-3如图，已知直线l 1∥l2，l1、l2之间的距离为8，点P到直线l1的距离为6，点Q到直线l2的距离为4，PQ=4，在直线l1上有一动点A，直线l2上有一动点B，满足AB⊥l2，且PA+AB+BQ最小，此时PA+BQ= ．变式训练2-4如图，已知在平面直角坐标系xOy中，直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，OC=3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴于点E和F．（1）求经过A、B、C三点的抛物线的解析式；（2）当BE经过（1）中抛物线的顶点时，求CF的长；（3）在抛物线的对称轴上取两点P、Q（点Q在点P的上方），且PQ=1，要使四边形BCPQ 的周长最小，求出P、Q两点的坐标．中考真题1.要在街道旁建奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使A、B到它的距离之和最短？小聪以街道为x轴，建立了如图所示的平面直角坐标系，A点坐标为（0，3），B点坐标为（6，5），则A、B两点到奶站距离之和的最小值是．2.如图，矩形ABOC的顶点A的坐标为（﹣4，5），D是OB的中点，E是OC上的一点，当△ADE的周长最小时，点E的坐标是（）A ．（0，）B ．（0，）C ．（0，2）D ．（0，）3.如图，在矩形ABCD 中，AB=5，AD=3，动点P 满足S △PAB =31S 矩形ABCD ，则点P 到A 、B 两点距离之和PA+PB 的最小值为（）A ．B ．C ．5D ．4.已知抛物线y=x 2+1具有如下性质：该抛物线上任意一点到定点F （0，2）的距离与到x轴的距离始终相等，如图，点M 的坐标为（，3），P 是抛物线y=x 2+1上一个动点，则△PMF 周长的最小值是（）A ．3B ．4C ．5D ．65.如图，点A （a ，3），B （b ，1）都在双曲线y=上，点C ，D ，分别是x 轴，y 轴上的动点，则四边形ABCD 周长的最小值为（）A ．B ．C ．D ．6.如图，在Rt △ABC 中，∠C=90°，AC=3，BC=4，D 、E 分别是AB 、BC 边上的动点，则AE+DE 的最小值为（）A ．B ．C ．5D ．7.如图，Rt △ABC 中，∠BAC=90°，AB=3，AC=6，点D ，E 分别是边BC ，AC 上的动点，则DA+DE 的最小值为．8.如图，等腰△ABC 的底边BC=20，面积为120，点F 在边BC 上，且BF=3FC ，EG 是腰AC 的垂直平分线，若点D 在EG 上运动，则△CDF 周长的最小值为．9.如图，菱形ABCD 的边长为6，∠ABC=120°，M 是BC 边的一个三等分点，P 是对角线AC 上的动点，当PB+PM 的值最小时，PM 的长是（）A．B．C．D．10.如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE+EF的最小值为（）A．B．C．D．611.如图，在平面直角坐标系中，反比例函数y=（x＞0）的图象与边长是6的正方形OABC的两边AB，BC分别相交于M，N 两点．△OMN的面积为10．若动点P在x轴上，则PM+PN 的最小值是（）A．6B．10 C．2D．212.如图，△ABC中，AC=BC=2，AB=1，将它沿AB翻折得到△ABD，则四边形ADBC的形状是形，P、E、F分别为线段AB、AD、DB上的任意点，则PE+PF的最小值是．13.如图，已知抛物线y=x2+bx+c与直线y=x+3交于A，B两点，交x轴于C、D两点，连接AC、BC，已知A（0，3），C（﹣3，0）．（1）求此抛物线的解析式；（2）在抛物线对称轴l上找一点M，使|MB﹣MD|的值最大，并求出这个最大值；（3）点P为y轴右侧抛物线上一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，问：是否存在点P，使得以A，P，Q为顶点的三角形与△ABC相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．14.如图，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD．（1）用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）；（2）在（1）的条件下，①证明：AE⊥DE；②若CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值．15.如图，抛物线y=ax2+bx+c（a≠0）经过点A（﹣1，0），B（3，0），C（0，3）三点．（1）求抛物线的解析式及顶点M的坐标；（2）连接AC、BC，N为抛物线上的点且在第四象限，当S△NBC=S△ABC时，求N点的坐标；（3）在（2）问的条件下，过点C作直线l∥x轴，动点P（m，3）在直线l上，动点Q（m，0）在x轴上，连接PM、PQ、NQ，当m为何值时，PM+PQ+QN的和最小，并求出 PM+PQ+QN 和的最小值．16.如图，直线y=5x+5交x轴于点A，交y轴于点C，过A，C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B．（1）求二次函数的表达式；（2）连接BC，点N是线段BC上的动点，作ND⊥x轴交二次函数的图象于点D，求线段ND 长度的最大值；（3）若点H为二次函数y=ax2+4x+c图象的顶点，点M（4，m）是该二次函数图象上一点，在x轴、y轴上分别找点F，E，使四边形HEFM的周长最小，求出点F，E的坐标．17.如图1，已知抛物线y=（x﹣2）（x+a）（a＞0）与x轴从左至右交于A，B两点，与y轴交于点C．（1）若抛物线过点T（1，﹣），求抛物线的解析式；（2）在第二象限内的抛物线上是否存在点D，使得以A、B、D三点为顶点的三角形与△ABC相似？若存在，求a的值；若不存在，请说明理由．（3）如图2，在（1）的条件下，点P的坐标为（﹣1，1），点Q（6，t）是抛物线上的点，在x轴上，从左至右有M、N两点，且MN=2，问MN在x轴上移动到何处时，四边形PQNM 的周长最小？请直接写出符合条件的点M的坐标．18.如图，对称轴为直线x=2的抛物线经过A（﹣1，0），C（0，5）两点，与x轴另一交点为B．已知M（0，1），E（a，0），F（a+1，0），P是第一象限内抛物线上的动点．（1）求此抛物线的解析式；（2）当a=1时，求四边形MEFP的面积的最大值，并求此时点P的坐标；（3）若△PCM是以点P为顶点的等腰三角形，求a为何值时，四边形PMEF周长最小？请说明理由．19.探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1（x1，y1），P2（x2，y2），可通过构造直角三角形利用图1得到结论：P1P2=他还利用图2证明了线段P1P2的中点P（x，y）P的坐标公式：x=，y=．（1）请你帮小明写出中点坐标公式的证明过程；运用：（2）①已知点M（2，﹣1），N（﹣3，5），则线段MN长度为；②直接写出以点A（2，2），B（﹣2，0），C（3，﹣1），D为顶点的平行四边形顶点D的坐标：；拓展：（3）如图3，点P（2，n）在函数y=x（x≥0）的图象OL与x轴正半轴夹角的平分线上，请在OL、x轴上分别找出点E、F，使△PEF的周长最小，简要叙述作图方法，并求出周长的最小值．20.如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛物线y=﹣x2+2x+1与y轴交于点C．（1）求直线y=kx+b的函数解析式；（2）若点P（x，y）是抛物线y=﹣x2+2x+1上的任意一点，设点P到直线AB的距离为d，求d关于x的函数解析式，并求d取最小值时点P的坐标；（3）若点E在抛物线y=﹣x2+2x+1的对称轴上移动，点F在直线AB上移动，求CE+EF的最小值．21.如图①，在平面直角坐标系中，OA=6，以OA为边长作等边三角形ABC，使得BC∥OA，且点B、C落在过原点且开口向下的抛物线上．（1）求这条抛物线的解析式；（2）在图①中，假设一动点P从点B出发，沿折线BAC的方向以每秒2个单位的速度运动，同时另一动点Q从O点出发，沿x轴的负半轴方向以每秒1个单位的速度运动，当点P 运动到A点时，P、Q都同时停止运动，在P、Q的运动过程中，是否存在时间t，使得PQ⊥AB，若存在，求出t的值，若不存在，请说明理由；（3）在BC边上取两点E、F，使BE=EF=1个单位，试在AB边上找一点G，在抛物线的对称轴上找一点H，使得四边形EGHF的周长最小，并求出周长的最小值．本人所著《初中几何模型与解题通法》已发行，可在当当、淘宝和京东搜索购买特色：1.由一线名师编写，更专业权威，各地历年中考压轴题几乎都能在书中找到对应的模型和方法，甚至出现大量高度类似题。

中考数学：'将军饮马'所有模型及变式——终极篇

中考数学：'将军饮马'所有模型及变式——终极篇以微课堂初中精品微课，数学奥林匹克国家一级教练执教。

一、模型展现(1)直线型模型1：在直线l上求作点P，使PA＋PB最小．原理：两点之间，线段最短．PA＋PB最小值即为AB长．模型2：在直线l上求作点P，使PA＋PB最小．原理：和最小，同侧转异侧．两点之间，线段最短．模型3：在直线l上求作点P，使|PA－PB|最大．原理：两边之差小于第三边，|PA－PB|最大值即为AB长．模型4：在直线l上求作点P，使|PA－PB|最大．原理：差最大，异侧转同侧．两边之差小于第三边．变式：在直线l上求作点P，使l平分∠APB，与此作法相同．模型5：在直线l上求作点P，使|PA－PB|最小．原理：|PA－PB|最小为0，中垂线上的点到线段两端的距离相等．(2)角型模型6：在OA，OB上求作点M，N，使△PMN周长最小．原理：作两次对称，两点之间，线段最短．模型7：在OA，OB上求作点M，N，使四边形PQMN周长最小．原理：P，Q分别作对称，两点之间，线段最短．模型8：在OA，OB上求作点M，N，(1)使PM＋MN最小．(2)使PN＋MN最小．原理：先连哪个点，就先做关于那个点所在射线的对称点．垂线段最短．模型9：P，Q为OA，OB的定点，在OA，OB上求作点M，N，使PN＋NM ＋MQ最小．原理：两点之间，线段最短，PN＋NM＋MQ最小值即为P’Q’的长．(3)平移型模型10：在直线l上求作点M，N，使MN＝a，且AM＋MN＋NB最小．原理：将l上的MN转化到B’B．(问题情境：将军从军营A出发，去河边l饮马，饮马完在河边牵马散步a米，回军营B．可以转化为饮完马，直接去军营B，在到达之前散步．)模型11(造桥选址)：直线l1∥l2，在l1上求作点M，在l2上求作点N，使MN⊥l1，且AM＋MN ＋NB最小．原理：将MN转化为AA’．(可以理解为在A处先走过桥的路，再直达点B．)二、典型例题例1：(模型2)从点A(0，2)发出的一束光线，经x轴反射，过点B(4，3)，求从点A到点B所经过的路径长．解析：例2：(模型4)已知点A(1，3)、B(3，－1)，点M在x轴上，当AM－BM最大时，点M的坐标为______解析：例3：(模型10)如图，当四边形PABN的周长最小时，a＝______解析：例4：(模型11)解析：例5：(结合勾股)如图，在等边△ABC中，AB＝6，N为AB上一点，且AN＝2，∠BAC的平分线交BC于点D，M是AD上的动点，连结BM、MN，则BM＋MN的最小值是_____解析：小结：所有类型已归纳完，更多内容，详见八上11讲期中专题一将军饮马类题型全覆盖暑假特辑10《轴对称》之“将军饮马”（上）暑假特辑11《轴对称》之“将军饮马”（下）本讲思考题：已知点A(－3，－4)和B(－2，1)．(1)试在y轴上求一点P，使PA＋PB的值最小(2)试在y轴上求一点P，使|QA－QB|的值最大(3)若C(0，m)，D(0，m－2)，当m为何值时，四边形ABCD的周长最小．答案：(1) P (0，－1)(2) Q (0，11)(3) m = －0.2End欢迎收看《以微课堂》微课，欢迎收看《以微课堂》微课，作者简介：四星级重点中学高级教师、数学名师。

将军饮马模型(终稿)(完整资料).doc

【最新整理，下载后即可编辑】将军饮马模型一、背景知识：【传说】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．【问题原型】将军饮马造桥选址费马点【涉及知识】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平移；【解题思路】找对称点，实现折转直二、将军饮马问题常见模型1.两定一动型：两定点到一动点的距离和最小例1：在定直线l上找一个动点P，使动点P到两个定点A与B 的距离之和最小，即PA+PB最小.作法：连接AB，与直线l的交点Q，Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB最小，且最小值等于AB.原理：两点之间线段最短。

证明：连接AB，与直线l的交点Q，P为直线l上任意一点，在⊿PAB中，由三角形三边关系可知：AP+PB≧AB(当且仅当PQ 重合时取﹦)例2：在定直线l上找一个动点P，使动点P到两个定点A与B 的距离之和最小，即PA+PB的和最小.关键：找对称点作法：作定点B关于定直线l的对称点C，连接AC，与直线l 的交点Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB 和最小，且最小值等于AC.原理：两点之间，线段最短证明：连接AC，与直线l的交点Q，P为直线l上任意一点，在⊿PA C中，由三角形三边关系可知：AP+PC≧AC(当且仅当PQ 重合时取﹦)2.两动一定型例3：在∠MON的内部有一点A，在OM上找一点B，在ON 上找一点C，使得△BAC周长最短．作法：作点A关于OM的对称点A’，作点A关于ON的对称点A’’，连接A’ A’’，与OM交于点B，与ON交于点C，连接AB，AC，△ABC即为所求．原理：两点之间，线段最短例4：在∠MON的内部有点A和点B，在OM上找一点C，在ON上找一点D，使得四边形ABCD周长最短．作法：作点A 关于OM 的对称点A’，作点B 关于ON 的对称点B’ ，连接A’ B’，与OM 交于点C ，与ON 交于点D ，连接AC ，BD ，AB ，四边形ABCD 即为所求．原理：两点之间，线段最短3. 两定两动型最值例5：已知A 、B 是两个定点，在定直线l 上找两个动点M 与N ，且MN 长度等于定长d （动点M 位于动点N 左侧），使AM+MN+NB 的值最小.提示：存在定长的动点问题一定要考虑平移作法一：将点A 向右平移长度d 得到点A’，作A’关于直线l 的对称点A’’，连接A’’B ，交直线l 于点N ，将点N 向左平移长度d ，得到点M 。

将军饮马模型【范本模板】

将军饮马问题将军饮马问题=轴对称问题=最短距离问题（轴对称是工具，最短距离是题眼）。

所谓轴对称是工具，即这类问题最常用的做法就是作轴对称.而最短距离是题眼，也就意味着归类这类的题目的理由。

比如题目经常会出现线段 a+b 这样的条件或者问题。

一旦出现可以快速联想到将军饮马问题，然后利用轴对称解题。

1。

将军饮马故事“将军饮马”问题是数学问题中的经典题目，主要转化成“两点之间线段最短问题”原题：如图,一位将军，从A地出发,骑马到河边给马饮水，然后再到B地，问怎样选择饮水的地点，才能使所走的路程最短？•A•B模型一：一条定直线，同侧两定点在直线l的同侧有两点A，B，在L上求一点P,使得PA+PB值最小。

一般做法：作点 A（B）关于直线的对称点,连接 A’B，A’B 与直线交点即为所求点.A'B即为最短距离 .理由：A'为 A 的对称点，所以无论 P 在直线任何位置都能得到 AP=A'P。

所以PA+PB=PA’+PB。

这样问题就化成了求 A’到 B 的最短距离，直接相连就可以了。

例一：某供电部门准备在输电主干线L上连接一个分支线路,分支点为M，同时向新落成的A、B两个居民小区送电。

已知两个居民小区A、B分别到主干线的距离AA1=2千米,BB1=1千米，且A1B1=4千米。

（1）如果居民小区A、B位于主干线L的两旁，如图（1）所示，那么分支点M 在什么地方时总路线最短？最短线路的长度是多少千米？(2）如果居民小区A、B位于主干线L的同旁，如图（2)所示,那么分支点M在什么地方时总路线最短？此时分支点M与A1的距离是多少千米？模型二：一条定直线，一定点，一动点如图，已知直线L 和定点A ，在直线K 上找一点M，在直线L 上找一点P ，使得AP+PB 值最小.模型三：一定点，两条定直线如图，在∠OAB 内有一点 P ，在 OA 和 OB 各找一个点 M 、N ，使得△PMN 周长最短（题眼）。

(完整)初三复习将军饮马(终稿)

初三复习专题最短路径问题——将军饮马班级: 姓名：将军饮马问题=最短距离问题=轴对称问题一、基本模型（2条线段和最小）：1、如图，在定直线l 的同侧有两定点A,B,在直线l 上求作点P ，使PA+PB 最小。

二、模型变型（3条线段和最小） 2、如图，点P 是∠MON 内的一定点，分别在OM 、ON 上作点A 、B ，使△PAB 的周长最小。

【例1】如图，∠M O N =45°，P 是∠M O N 内一点，PO=10，A ,B 分别是O M 、O N 上的动点，则△ABP 周长的最小值为。

【方法归纳：】1、作图的一般步骤是：①② ③ 2、计算最短线段长度的方法：【例2】、已知抛物线2(1)4y x =--+交x 轴于A(-1,0)、B （3,0）两点，交y 轴于点D （0，3），又已知点E （2,3），点F （0，1）。

点G 为对称轴PQ 上一动点，试问在x 轴上是否存在一点H ，使D,G,H,F 四点所围成的四边形周长最小？若存在，求出这个最小值及点G ，H 的坐标；若不存在，请说明理由。

ON三、模型再变型（线段+点到线距离之和最小）3、如图，点P 是∠MON 内的一定点，在射线OM 、ON 上分别找两个点A 、B ，使PA+AB 最小。

【例3】、如图2，菱形ABCD 中，AB=10，∠B=135°，E 是AB 上一动点，P 是对角线AC 上的一个动点，则PE+PB 的最小值为．【变式】、已知直线1l 和2l 交于M 点，夹角为30°，点A 在1l 上且AM=10，P 是2l 上一动点，则P 点到A 点的距离与1l 的距离之和的最小值为。

四、将军饮马+平移模型4、如图，已知有两个定点A 、B ，在定直线l 有两个动点P 、Q ，且PQ 长度不变，求作点P 、Q 使得AP+PQ+BQ 最小。

（A 、B 异侧）（A 、B 同侧）【例4】、如图，甲、乙两个单位分别位于一条河流的两边A 处和B 处，现准备合作修建一座桥，桥建在何处才能使由甲到乙的路线最短？请做出示意图。

最值模型之将军饮马模型(解析版)

最值模型之将军饮马模型模型一两定一动型(线段和差的最值问题)【模型解读】在一条直线m上，求一点P，使PA与PB的和最小；题目在一条直线m上，求一点P，使PA+PB最小；分类(1)点A、B在直线m两侧(2)点A、B在直线同侧原图辅助线作法连接AB交直线m于点P，此点P即为所求，PA+PB最小值为AB 作A关于直线m的对称点A'，连接A'B交直线m于点P，此点P即为所求，PA+PB最小值为A'B原理三角形两边之和大于第三边【模型解读】在一条直线m上，求一点P，使PA与PB的差最大；题目在一条直线m上，求一点P，使|PA-PB|最大；分类(1)点A、B在直线m同侧：(2)点A、B在直线m异侧原图辅助线作法延长AB交直线m于点P，此点P即为所求，|PA-PB|最大值为AB 过点B作关于直线m的对称点B'，连接AB'交点直线m于P，此点P即为所求，|PA-PB|最大值为AB'原理三角形两边之差小于第三边。

例题解析1如图，正方形ABCD的边长为4，点E在边BC上，且BE=1，F为对角线BD上一动点，连接CF，EF，则CF+EF的最小值为．【答案】17【分析】连接AE交BD于一点F，连接CF，根据正方形的对称性得到此时CF+EF=AE最小，利用勾股定理求出AE即可．【详解】解：如图，连接AE交BD于一点F，连接CF，∵四边形ABCD是正方形，∴点A与点C关于BD对称，∴AF=CF，∴CF+EF=AF+EF=AE，此时CF+EF最小，∵正方形ABCD的边长为4，∴AD=4,∠ABC=90°，∵点E在AB上，且BE=1，∴AE=AB2+BE2=42+12=17，即CF+EF的最小值为17故答案为：17．2如图，在菱形ABCD中，∠ABC=120°，对角线AC、BD交于点O，BD=8，点E为OD的中点，点F为AB上一点，且AF=3BF，点P为AC上一动点，连接PE、PF，则PF-PE的最大值为．【答案】2【分析】作E的对称点E'，连接FE'并延长交AC于点P'，根据三角形三边关系可得到PF-PE=PF-PE≤E F，最后根据等边三角形的性质及菱形的性质即可解答．【详解】解：作E的对称点E ，连接FE'并延长交AC于点P ，∴PE=PE ，∴PF-PE≤E F，=PF-PE当F、E 、P 在同一条直线上时，PF-PE有最大值E F，∵在菱形ABCD中，∠ABC=120°，∴∠DAB=60°，AD=AB，∴△ABD是等边三角形，∴∠DAB=∠DBA=∠ADB=60°，，AD=AB=BD，∵BD=8，∴AB=8，∵AF=3BF，∴BF=2，∵点E为OD的中点，∴E 为OB的中点，∴BE =1BD=2，4∴BF=BE ，∴△BE F是等边三角形，∴E F=BF=2，故答案为2；变式训练1如图，菱形ABCD，点A、B、C、D均在坐标轴上，∠ABC=120°，点A-3,0，点E是CD的中点，点P是OC上的一动点，则PD+PE的最小值是()3A.3B.5C.22D.32【答案】A【分析】直线AC上的动点P到E、D两定点距离之和最小属“将军饮马”模型，由D关于直线AC的对称点B，连接BE，则线段BE的长即是PD+PE的最小值．【详解】如图：连接BE，∵菱形ABCD，∴B、D关于直线AC对称，，∵直线AC上的动点P到E、D两定点距离之和最小∴根据“将军饮马”模型可知BE长度即是PD+PE的最小值．∵菱形ABCD，∠ABC=120°，点A-3,0，∴∠CDB=60°,∠DAO=30°，OA=3，∴OD=3,AD=DC=CB=23∴△CDB是等边三角形∴BD=23∵点E是CD的中点，∴DE=1CD=3,且BE⊥CD，∴BE=BD2-DE2=3故选：A．22如图，正方形ABCD的对角线交于点O，点E是直线BC上一动点．若AB=4，则AE+OE的最小值是()A.42B.25+2C.213D.210【答案】D【分析】本题为典型的将军饮马模型问题，需要通过轴对称，作点A关于直线BC的对称点A ，再连接A O，运用两点之间线段最短得到A O为所求最小值，再运用勾股定理求线段A O的长度即可．【详解】解：如图所示，作点A关于直线BC的对称点A ，连接A O，其与BC的交点即为点E，再作OF⊥AB交AB于点F，∵A与A关于BC对称，∴AE=A E，AE+OE=A E+OE，当且仅当A ，O，E在同一条线上的时候和最小，如图所示，此时AE+OE=A E+OE=A O，∵正方形ABCD，点O为对角线的交点，AB=2，∴OF=FB=12∵对称，∴AB=BA =4，∴FA =FB+BA =2+4=6，在Rt△OFA 中，OA =FO2+FA 2=210，故选：D．3如图，在菱形ABCD中，AB=2,∠ABC=60°，M是对角线BD上的一个动点，CF=BF，则MA+ MF的最小值为()A.1B.2C.3D.2【答案】C【分析】连接AF，则AF的长就是AM+FM的最小值，证明△ABC是等边三角形，AF是高线，利用三角函数即可求解．【详解】解：连接AF，则AF的长就是AM+FM的最小值．∵四边形ABCD 是菱形，∴AB =BC ，又∵∠ABC =60°，∴△ABC 是等边三角形，∵CF =BF ∴F 是BC 的中点，∴AF ⊥BC ．则AF =AB •sin60°=2×32=3．即MA +MF 的最小值是3．故选：C4如图，已知△ABC 为等腰直角三角形，AC =BC =6，∠BCD =15°，P 为直线CD 上的动点，则|PA -PB |的最大值为．【答案】6【分析】作A 关于CD 的对称点A ′，连接A ′B 交CD 于P ，则点P 就是使|PA -PB |的值最大的点，|PA -PB |=A ′B ，连接A ′C ，根据等腰直角三角形的性质得到∠CAB =∠ABC =45°，∠ACB =90°，根据角的和差关系得到∠ACD =75°，根据轴对称的性质得到A ′C =AC =BC ，∠CA ′A =∠CAA ′=15°，推出△A ′BC 是等边三角形，根据等边三角形的性质即可得到结论．【详解】如图，作A 关于CD 的对称点A ′，连接A ′B 并延长交CD 延长线于点P ，则点P 就是使PA -PB 的值最大的点，PA -PB =A ′B ，连接A ′C ，∵△ABC 为等腰直角三角形，AC =BC =6，∴∠CAB =∠ABC =45°，∠ACB =90°，∵∠BCD =15°，∴∠ACD =75°，∵点A 与A ′关于CD 对称，∴CD ⊥AA ′，AC =A ′C ，∠CA ′A =∠CAA ′，∴∠CAA ′=15°，∵AC =BC ，∴A ′C =BC ，∠CA ′A =∠CAA ′=15°，∴∠ACA ′=150°，∵∠ACB =90°，∴∠A ′CB =60°，∴△A ′BC 是等边三角形，∴A ′B =BC =6．故答案为：65如图，MN 是⊙O 的直径，MN =6，点A 在⊙O 上，∠AMN =30°，B 为AN的中点，P 是直径MN 上一动点，则PA +PB 的最小值是．【答案】32【分析】首先利用在直线L 上的同侧有两个点A 、B ，在直线L 上有到A 、B 的距离之和最短的点存在，可以通过轴对称来确定，即作出其中一点关于直线L 的对称点，对称点与另一点的连线与直线L 的交点就是所要找的点P 的位置，然后根据弧的度数发现一个等腰直角三角形计算．【详解】作点B 关于MN 的对称点C ，连接AC 交MN 于点P ，连接OB ，则P 点就是所求作的点．此时PA +PB 最小，且等于AC 的长．连接OA ，OC ，∵∠AMN =30°，∴∠AON =60°，∵B 为AN的中点，∴AB =BN∴∠AOB =∠BON =30°，∵MN ⊥BC ，∴CN=BN，∴∠CON =∠NOB =30°，则∠AOC =90°，又OA =OC =3，则AC =32．故答案为：32．6如图，在矩形ABCD 中，AB =3，BC =5．动点P 满足S △PBC =13S 矩形ABCD．则点P 到B ，C 两点距离之和PB +PC 的最小值为。

中考复习讲义：将军饮马所有模型及变式——终极篇(直线型角型平移型)(练习无答案)

将军饮马所有模型及变式——终极篇一、模型展现(1)直线型模型1：在直线l上求作点P，使PA＋PB最小．原理：两点之间，线段最短．PA＋PB最小值即为AB长．模型2：在直线l上求作点P，使PA＋PB最小．原理：和最小，同侧转异侧．两点之间，线段最短．模型3：在直线l上求作点P，使|PA－PB|最大．原理：两边之差小于第三边，|PA－PB|最大值即为AB长．模型4：在直线l上求作点P，使|PA－PB|最大．原理：差最大，异侧转同侧．两边之差小于第三边．模型5：在直线l上求作点P，使|PA－PB|最小．原理：|PA－PB|最小为0，中垂线上的点到线段两端的距离相等．(2)角型模型6：在OA，OB上求作点M，N，使△PMN周长最小．原理：作两次对称，两点之间，线段最短．模型7：在OA，OB上求作点M，N，使四边形PQMN周长最小．原理：P，Q分别作对称，两点之间，线段最短．模型8：在OA，OB上求作点M，N，(1)使PM＋MN最小．(2)使PN＋MN最小．原理：先连哪个点，就先做关于那个点所在射线的对称点．垂线段最短．模型9：P，Q为OA，OB的定点，在OA，OB上求作点M，N，使PN＋NM＋MQ最小．原理：两点之间，线段最短，PN＋NM＋MQ最小值即为P’Q’的长．(3)平移型模型10：在直线l上求作点M，N，使MN＝a，且AM＋MN＋NB最小．原理：将l上的MN转化到B’B．(问题情境：将军从军营A出发，去河边l饮马，饮马完在河边牵马散步a米，回军营B．可以转化为饮完马，直接去军营B，在到达之前散步．)模型11(造桥选址)：直线l1∥l2，在l1上求作点M，在l2上求作点N，使MN⊥l1，且AM＋MN＋NB 最小．原理：将MN转化为AA’．(可以理解为在A处先走过桥的路，再直达点B．)二、典型例题例1：(模型4)已知点A(1，3)、B(3，－1)，点M在x轴上，当AM－BM最大时，点M的坐标为______解析：例2：(模型11)解析：例3：(结合勾股)解析：练习反馈：1.在直线l上求作点P，使l平分∠APB，与此作法相同．2. 从点A(0，2)发出的一束光线，经x轴反射，过点B(4，3)，求从点A到点B 所经过的路径长．3.已知点A(－3，－4)和B(－2，1)．(1)试在y轴上求一点P，使PA＋PB的值最小(2)试在y轴上求一点P，使|QA－QB|的值最大(3)若C(0，m)，D(0，m－2)，当m为何值时，四边形ABCD的周长最小．4. 如图，在等边△ABC中，AB＝6，N为AB上一点，且AN＝2，∠BAC的平分线交BC于点D，M是AD上的动点，连结BM、MN，则BM＋MN的最小值是_____5.如图，当四边形PABN的周长最小时，a＝______。

(完整版)将军饮马模型(终稿)

将军饮马模型一、背景知识：【传说】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马,然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难,据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．【问题原型】将军饮马造桥选址费马点【涉及知识】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平移;【解题思路】找对称点，实现折转直二、将军饮马问题常见模型1.两定一动型：两定点到一动点的距离和最小例1：在定直线l上找一个动点P,使动点P到两个定点A与B的距离之和最小,即PA+PB最小.作法:连接AB，与直线l的交点Q，Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB最小，且最小值等于AB。

原理：两点之间线段最短。

证明:连接AB,与直线l的交点Q,P为直线l上任意一点，在⊿PAB中，由三角形三边关系可知：AP+PB≧AB(当且仅当PQ重合时取﹦)例2：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB的和最小.关键:找对称点作法:作定点B关于定直线l的对称点C，连接AC，与直线l的交点Q即为所要寻找的点，即当动点P跑到了点Q处,PA+PB和最小，且最小值等于AC.原理:两点之间，线段最短证明：连接AC，与直线l的交点Q，P为直线l上任意一点，在⊿PA C中，由三角形三边关系可知：AP+PC≧AC(当且仅当PQ重合时取﹦）2.两动一定型例3：在∠MON的内部有一点A，在OM上找一点B，在ON上找一点C,使得△BAC周长最短．作法：作点A关于OM的对称点A’，作点A关于ON的对称点A’’,连接A’ A’’，与OM交于点B，与ON交于点C，连接AB，AC，△ABC即为所求．原理:两点之间，线段最短例4：在∠MON的内部有点A和点B，在OM上找一点C，在ON上找一点D,使得四边形ABCD周长最短．作法：作点A关于OM的对称点A’，作点B关于ON的对称点B’，连接A’ B’，与OM交于点C,与ON 交于点D，连接AC，BD，AB，四边形ABCD即为所求．原理：两点之间，线段最短3.两定两动型最值例5：已知A、B是两个定点，在定直线l上找两个动点M与N，且MN长度等于定长d（动点M位于动点N 左侧），使AM+MN+NB的值最小.提示：存在定长的动点问题一定要考虑平移作法一：将点A向右平移长度d得到点A’，作A’关于直线l的对称点A’’，连接A’’B，交直线l 于点N,将点N向左平移长度d，得到点M.作法二：作点A关于直线l的对称点A1,将点A1向右平移长度d得到点A2,连接A2 B，交直线l于点Q，将点Q向左平移长度d，得到点Q。

(完整版)将军饮马问题的11个模型及例题

变式训练1-2
如图，菱形ABCD中，对角线AC和BD交于点O，AC=2，
BD=2 ,E为AB的中点，P为对角线AC上一动点，则PE+PB的
最小值为__________.
变式训练1-3
如图，已知直线y= x+1与y轴交于点A，与x轴交于点D，抛物线y= x2+bx+c与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为（1，0）．
点到l的距离不相等）
要求：在直线l上找一点P，使︱PA-PB︱的值最大
解：作点B关于直线l的对称点B´，连接B´A并延长交
于点P，点P即为所求；
理由：根据对称的性质知l为线段BB´的中垂线，由中垂
线的性质得：PB=PB´，要使︱PA-PB︱最大，则需
︱PA-PB´︱值最大，从而转化为模型3.
典型例题1-1
【解答】作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，
则MP=MC，NP=ND，OP=OD=OC= ，∠BOP=∠BOD，∠AOP=∠AOC，
∴PN+PM+MN=ND+MN+NC=DC，∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°，
∴此时△PMN周长最小，作OH⊥CD于H，
如图，直线y= x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，当PC+PD最小时，点P的坐标为_________，此时PC+PD的最小值为_________.
【分析】符合基本模型2的特征，作点D关于x轴的对称点D'，连接CD'交x轴于点P，此时PC+PD值最小，由条件知CD为△BAO的中位线，OP为 △CDD'的中位线，易求OP长，从而求出P点坐标；PC+PD的最小值即CD'长，可用勾股定理（或两点之间的距离公式，实质相同）计算.

完整word版将军饮马问题的11个模型及例题

将军饮马问题问题概述路径最短、线段和最小、线段差最大、周长最小等一系列最值问题方法原理2.三角形两边之和大于第三边，两边之差小于第三边；1.两点之间，线段最短；.垂线段最短3.中垂线上的点到线段两端点的距离相等；4.基本模型1.已知：如图，定点A、B分布在定直线l两侧；要求：在直线l上找一点P，使PA+PB的值最小, 即为所求，点PP解：连接AB交直线l于点PA+PB的最小值即为线段AB的长度理由：在l上任取异于点P的一点P′，连接AP′、BP′，在△ABP'中，AP′+BP′>AB，即AP′+BP′>AP+BP∴P为直线AB与直线l的交点时，PA+PB最小.2.已知：如图，定点A和定点B在定直线l的同侧要求：在直线l上找一点P，使得PA+PB值最小（或△ABP的周长最小）解：作点A关于直线l的对称点A′，连接A′B交l于P，点P即为所求；理由：根据轴对称的性质知直线l为线段AA′的中垂线，由中垂线的性质得：PA=PA′，要使PA+PB最小，则需PA′+PB值最小，从而转化为模型1.3.两的同侧（A、B已知：如图，定点A、B分布在定直线l 的距离不相等）点到l︱的值最大P，使PA-PB︱要求：在直线l上找一点 P，点P即为所求；解：连接BA并延长，交直线l于点的一点P′，︱=AB，在l上任取异于点P此时︱理由：PA-PB ︱<AB，，由三角形的三边关系知︱P′A-P′B′连接AP、BP′︱PA-PB︱′A-P′B︱<即︱P两B分布在定直线l的两侧（A、已知：如图，定点A、B 4.的距离不相等）点到l︱的值最大上找一点P，使︱PA-PB要求：在直线l 并延长交连接B′A解：作点B关于直线l的对称点B′，P于点，点P即为所求；为线段BB′的中垂线，由中垂理由：根据对称的性质知l ′，要使︱PA-PB︱最大，则需线的性质得：PB=PB3.′︱值最大，从而转化为模型︱PA-PB1-1典型例题2分DA和点B，点Cx+4如图，直线y=与x轴、y轴分别交于点3最小时，为OA上一动点，当PC+PD、别为线段ABOB的中点，点P_________. _________，此时的最小值为PC+PD点P的坐标为，连轴的对称点D'的特征，作点【分析】符合基本模型2D关于x为CDx轴于点P，此时PC+PD 值最小，由条件知CD'接交长，从OPCDD'的中位线，易求△的中位线，△BAOOP为长，可用勾股定理CD'PC+PD而求出P点坐标；的最小值即.（或两点之间的距离公式，实质相同）计算轴x′交CD′，连接D轴的对称点x关于D，作点CD】连接解答【．2x=0，则y=4，于点P，此时PC+PD值最小．令y=x+4中322的坐标，∴点Ay=0∴点B坐标（0，4）；令y=x+4中，则x+4=0，解得：x=﹣633的中位线，BAO的中点，∴CD为△为（﹣6，0）．∵点C、D分别为线段AB、OB1AO=3CD=，∴CD∥x轴，且2′的中点，O为DDD∵点′和点D关于x轴对称，∴31OP=CD=-1D′（0，），∴OP为△CDD′的中位线，∴，223△CDD′中，∴点P的坐标为（﹣，0）．在Rt22222?4DDCD3??5.CD′=的最小值为=5，即=PC+PD 坐标；若题型变、点P【小结】还可用中点坐标公式先后求出点C CD′的解析不是化，C、DAB和OB中点时，则先求直线.P的坐标式，再求其与x轴的交点1-2典型例题B ，点1）如图，在平面直角坐标系中，已知点A的坐标为（0，3最，点的坐标为（，﹣2）P在直线y=﹣x上运动，当|PA﹣PB|2_________. PB|的最大值是P大时点的坐标为_________，|PA﹣，y=【分析】符合基本模型4的特征，作A关于直线﹣x 对称点C x连接BC，可得直线BC的方程；求得BC与直线y=﹣的交点P的坐标；此时|PA﹣PB|=|PC﹣PB|=BC取得最大值，.再用两点之间的距离公式求此最大值BCBC，可得直线；连接的坐标为（﹣1，0）C解答【】作A 关于直线y=﹣x对称点，易得C44|PA）；此时4P为（4，﹣的方程为y=﹣xy=﹣，与直线﹣x联立解得交点坐标552241)(?2(?1)?3 PB|=|PC﹣PB|=BCBC==取得最大值，最大值；﹣22.，需作一次对称点，连线得交点2和4】【小结“两点一线”大多考查基本模型1-1变式训练），，已知菱形OABC在平面直角坐标系的位置如图所示，顶点A（50最短0D（，1），当CP+DPOBOB=45，点P是对角线上的一个动点，√时，点P的坐标为（）510361，．）1． 00．A（，） B（，C（（．） D，）77552．1-2变式训练AC=2，和如图，菱形ABCD中，对角线ACBD交于点O，的上一动点，则PE+PB3,E为AB的中点，P为对角线BD=2AC√__________. 最小值为1-3变式训练112与直线交于x+bx+cD，抛物线y=x+1如图，已知直线y=与y轴交于点A，与x轴交于点22．01，）A、E两点，与x轴交于B、C两点，且B点坐标为（）求该抛物线的解析式；（1. 的值最大，求出点MC|M的坐标（2）在抛物线的对称轴上找一点M，使|AM﹣拓展模型1.已知：如图，A为锐角∠MON外一定点；，使上找一点Q上找一点P，在射线ON要求：在射线OM. AP+PQ的值最小解：过点A作AQ⊥ON于点Q，AQ与OM相交于点P，此时，AP+PQ最小；理由：AP+PQ≧AQ，当且仅当A、P、Q三点共线时，AP+PQ取得最小值AQ，根据垂线段最短，当AQ⊥ON时，AQ最小.2.已知：如图，A为锐角∠MON内一定点；，使上找一点ONQ，在射线上找一点要求：在射线OMP.的值最小 AP+PQ．ONAQ⊥的对称点A′，过点A′作解：作点A关于OM AP+PQ最小；交OM于点P，此时于点Q，A′QAP+PQ最小，AP=A′P，要使理由：由轴对称的性质知1 P+PQ最小，从而转化为拓展模型只需A′为锐角∠MON内一定点；已知：如图，A 3.，使，在射线ON上找一点Q要求：在射线OM上找一点P 的周长最小△APQ的对,关于ON 解：分别作A点关于直线OM的对称点A1于点ONQ，点A交OM于点P，交称点A，连接 A221即为所求，此时△APQ周长最小，最小值P和点Q AA的长度；即为线段21，△APQ的周AP=AP，AQ=AQ理由：由轴对称的性质知21 A四点共线、P、Q、P+PQ+A长AP+PQ+AQ=AQ，当A2112. 时，其值最小内两个定点；B为锐角∠MON、已知：如图，A 4.四边形上找一点Q，使要求：在OM上找一点P，在ON APQB的周长最小，作点B关于直线A 关于直线OM的对称点A′解：作点 Q，P，交ON于交的对称点ONB′，连接A′B′OM于周长的、点Q即为所求，此时四边形APQB则点P′′B的长度之和；最小值即为线段AB和A ,将PA理由：AB长为定值，由基本模型将PA转化为′ B′四点共线时，、、′QB转化为QB，当A′P、Q . QBPQPA′+′+PAPQ QB的值最小，即++的值最小下方的定分别为m上方和n已知：如图，直线m∥n,A、B5.搭桥模型垂直）（直线AB不与m点，. 最小PQ，使得AP+PQ+BQ之间求作垂线段要求：在m、n 最小，可通过平移，使PQ为定值，只需AP+BQ分析：，转化为基本模型、Q“接头”P 的方向，向下平移至A沿着平行于PQ解：如图，将点交直线n于点′AA′=PQ，连接AB点A′，使得，线段PQ即⊥n，交直线m于点PQ，过点Q作PQ.为所求，此时AP+PQ+BQ最小′=PA，理由：易知四边形QPAA′为平行四边形，则QA +BQ最小，即、A′三点共线时，QA′当B、Q.AP+PQ+BQ最小AP+BQ最小，PQ长为定值，此时al两侧，长度为A、B分布于直线6.已知：如图，定点左边）上移动（P在Q (a为定值)的线段PQ在l最小要求：确定PQ的位置，使得AP+PQ+QB的值最小，可通过平移，PQ为定值，只需AP+QB 分析：，转化为基本模型、Q“接头”使P A′，使解：将点A沿着平行于l的方向，向右移至l上截取交直线Bl于点Q，在AA′=PQ=a,连接A′ PQ即为所求，此时在Q左边），则线段PQ=a （PB+a ′′B+PQ，即AAP+PQ+QB的最小值为A ′为平行四边形，则PA=QA，理由：易知四边形APQA′PA+QB +QB最小，即、QB三点共线时，QA′A当′、.值最小最小，又PQ长为定值此时PA+PQ+QBal的同侧，长度、7. 已知：如图，定点AB分布于直线左边）Q在P上移动（l在PQ的线段)为定值(a周长最小要求：确定PQ的位置，使得四边形APQB点分析：AB长度确定，只需AP+PQ+QB最小，通过作A3的对称点，转化为上述模型关于llAl的对称点A′，将点′沿着平行于解：作A点关于B ′A′′=PQ=a，连接A′′的方向，向右移至A′′，使A （P在Q左边），线段交l于Q，在l上截取QP=a APQB周长的最小值为PQ即为所求，此时四边形B+AB+aA′′′′B+AB+PQ，即A2-1典型例题、AC、N分别是线段如图，在矩形ABCD中，AB=10，BC=5，若点M ．上的两个动点，则ABBM+MN 的最小值为，再过EAC的对称点关于【分析】符合拓展模型2的特征，作点B的最小值，借BM+MNAB的垂线段，该垂线段的长即点E作.助等面积法和相似可求其长度，BM+MN=EM+MN作EN⊥AB于N，则E解答【】作点B关于AC的对称点E，再过点，其最小值即EN长；∵AB=10，BC=522BCAB?5，∴=5AC=510?55， =2等面积法求得ACBE=4边上的高为，∴55，∴∽△ABCENBEN=8．易知△，代入数据解得 8．即BM+MN的最小值为】该类题的思路是通过作对称，将线段转化，再根据定理、公理连线或作垂线；可作【小结有些题则作动点的定点或动点关于定直线的对称点，有些题作定点的对称点易解，.对称点易解2-2典型例题分别、NAOB内的定点且OP=，点MP如图，∠AOB=60°，点是∠）（的动点，OB上异于点O则△PMN周长的最小值是、是射线OAC．．AB．．6 D3分别交D，连接CDOA、OB的对称点C、【分析】符合拓展模型3的特征；作P点分别关于，OC、OD，此时△PMN周长最小，其值为CD长；根据对称性连接OA、OB于M、NCD.是顶角为120°的等腰三角形，作底边上高，易求底边分析条件知△OCD N，如图，、OB于M、的对称点OA、OBC、D，连接CD分别交OA【解答】作P点分别关于，BOD，∠AOP=∠AOC则MP=MC，NP=ND，OP=OD=OC=，∠BOP=∠°，∠AOC=2∠AOB=120PN+PM+MN=ND+MN+NC=DC，∠COD=∠BOP+∠BOD+∠AOP+∴，⊥CD于H∴此时△PMN周长最小，作OHOC=OH=，则CH=DH，∵∠OCH=30°，∴CD=2CH=3．CH=OH=，∴即△PMN周长的最小值是3；故选：D．【小结】根据对称的性质，发现△OCD是顶角为120°的等腰三角形，是解题的关键，也是难点.2-3典型例题所在的直线为原点，OCABCO，以点O如图，已知平行四边形，，OC=6D，AD=2轴于点为x轴，建立直角坐标系，AB交y为点P所在的直线为OD的垂直平分线，∠A=60°，线段EF轴x与E′关于线段EF上的动点，PM⊥x轴于点M点，点E ′M．对称，连接BP、E ；（1）请直接写出点A坐标为，点B坐标为. 的坐标BP+PM+ME′的长度最小时，请求出点P（2）当的长即可解决；，BD【分析】（1）解直角三角形求出OD，可得OP=EM符合（2）“搭桥模型”的特征；首先证明四边形OPME′是平行四边形，点为P′的长度最小，此时PM是定值，PB+ME′=OP+PB的值最小时，BP+PM+ME 点坐标；OB与EF的交点，结合OB的解析式可得P直线 ADO中，∵∠A=60°，AD=2，（【解答】1）在Rt △，）°OD=2?tan60=2，∴A（﹣2，2∴，∵四边形ABCO是平行四边形，∴AB=OC=6）4B（，22=4∴DB=6﹣，∴，，∵如图，（2）连接OP．EF垂直平分线段ODPM⊥OC PEO=是矩形，°，∴四边形∠∠EOM=PMO=90OMPE∴∠′，∴，∵∴PM=OE=OE=OEPM=OE′，OE∥′，PM,′是平行四边形OPME∴四边形．′的长度最小，∴OP=EM，∵PM是定值，∴PB+ME′=OP+PB的值最小时，BP+PM+MEB共线时，BP+PM+ME′的长度最小，∵直线OB的解析式为y=，x∴当O、P、．2，）（∴P（构造平行四边求没有公共端点的两条线段之和的最小值，一般通过作对称和平移【小结】.形）的方法，转化为基本模型2-4典型例题的顶点坐标分△AOB如图所示，在平面直角坐标系中，RtOAOB4），把△绕点）（﹣2，0，O（0，0），B（0，别为A 90°，得到△COD．按顺时针方向旋转C、D两点的坐标；（1）求三点的抛物线的解析式；、D（2）求经过A、BFE在点E（3）在（2）中抛物线的对称轴上取两点、F（点、求出E的上方），且EF=1，使四边形ACEF的周长最小，两点的坐标．F点，结合直线的F【分析】符合拓展模型7的特征，通过作对称、平移、连线，可找出E、、解析式和抛物线的对称轴可解出EF坐标. 解答】（1）由旋转的性质可知：OC=OA=2，OD=OB=4,∴C点的坐【，0）D），点的坐标是（4，标是（0，22，（2）设所求抛物线的解析式为y=ax+bx+c 4a-2b+c=016a+4b+c=0由题意，得 c=41，，b=1，c=4解得a=-21+4；x2+x y=-∴所求抛物线的解析式为21，+x+4的对称轴为x=1x2y=-最短，抛物线3）只需AF+CE（2A关于对称轴x=1的对称点，作2将点A向上平移至A（﹣，1），则AF=AE111的解析式，与对称轴交于点EE为所求，可求得ACCC1（A4，），连接A，A22223771y=+x2，当x=1时， )的坐标为，点)为y=-(1,E，∴点的坐标为F(1,．4444. 】解决此类题的套路是“对称、平移、连线”【小结；其中，作对称和平移的顺序可互换2-1变式训练几何模型： l同旁的两个定点．条件：如图1，A，B是直线的值最小．P问题：在直线l上确定一点，使PA+PB （不必证明）B交l于点P，即为所求.方法：作点A关于直线l的对称点A'，连接A' 模型应用：轴上一动1），P为xA）如图2，已知平面直角坐标系中两定点（0，﹣1）和B（2，﹣（1 ，此时PA+PB= ．点，则当PA+PB的值最小是点P的横坐标是，由BD的中点，P是AC上一动点，连接）如图3，正方形ABCD的边长为4，E为AB2（的最小PB+PEAC于P，则正方形对称性可知，B与D关于直线AC对称．连接ED交值是．分别F上一动点，E，DAB=60中，AB=10，∠°，P是对角线AC3（）如图4，在菱形ABCD ．的最小值是是线段AB和BC上的动点，则PE+PF分别是FE．°，点B=60G是边CD边的中点，点）如图（45，在菱形ABCD中，AB=6，∠．AD上的两个动点，则EF+ED的最小值是AG，变式训练2-2如图，矩形ABCD中，AD=15，AB=10，E为AB边上一点，且DE=2AE，连接CE与对角线BD交于F；若P、Q分别为AB边和BC边上的动点，连接EP、PQ和QF；则四边形EPQF周长___________.的最小值是2-3变式训练的P到直线l，l、l之间的距离为8，点如图，已知直线l∥l11212距上有一动PQ=4l的距离为4，，在直线l离为6，点Q到直线12最小，此时，满足AB⊥l，且PA+AB+BQ点A，直线l上有一动点B22．PA+BQ=2-4变式训练在OC的边OA在y轴的正半轴上，中，直角梯形如图，已知在平面直角坐标系xOyOABC 按顺BD．将∠DBC绕点作OC=3，过点BBD⊥BC，交OA于点x轴的正半轴上，OA=AB=2， E和F．x 时针方向旋转，角的两边分别交y轴的正半轴、轴的正半轴于点 B、C三点的抛物线的解析式；（1）求经过A、）中抛物线的顶点时，求CF的长；（2）当BE经过（1BCPQPQ=1，要使四边形（点Q在点P的上方），且Q（3）在抛物线的对称轴上取两点P、 Q两点的坐标．的周长最小，求出P、中考真题1.要在街道旁建奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使A、B到它的距离之和最短？小聪以街道为x轴，建立了如图所示的平面直角坐标系，A点坐标为（0，3），B点坐标为（6，5），则A、B两点到奶站距离之和的最小值是．2.如图，矩形ABOC的顶点A的坐标为（﹣4，5），D是OB的中点，E是OC上的一点，当△）的坐标是（E的周长最小时，点ADE．，）（0，2） D．（0（A．（0，） B．0，） C．1两点距、满足S=BS，则点P到A3.如图，在矩形ABCD中，AB=5，AD=3，动点P ABCDPAB△矩形3）离之和PA+PB的最小值为（．5C． DA． B．，2）的距离与到4.已知抛物线y=x+1具有如下性质：该抛物线上任意一点到定点F2x0（M的坐标为（y=，3），P是抛物线x+1 PMF周长2上一个动点，轴的距离始终相等，如图，点的最小值是（）则△6DC．．A．3 B45 ．轴上的动点，轴，分别是xyD1B），（b，）都在双曲线y=上，点C，，，点5.如图，A（a3 ）ABCD则四边形周长的最小值为（．CB．． D A．AE+DE边上的动点，则ABDAC=3中，在6.如图，Rt△ABC∠C=90°，，BC=4，、E分别是、BC 的最小值为（）．5DCA．B．．上的动点，，中，∠如图，7.Rt△ABCBAC=90°，AB=3AC=6，点D，分别是边EBCAC，的最小值为则DA+DE ．8.如图，等腰△ABC的底边BC=20，面积为120，点F在边BC上，且BF=3FC，EG是腰AC的垂直平分线，若点D在EG上运动，则△CDF周长的最小值为．9.如图，菱形ABCD的边长为6，∠ABC=120°，M是BC边的一个三等分点，P是对角线AC ）的长是（PM的值最小时，PB+PM上的动点，当．．D． B． C． A分F交BC于D点，E，，10.如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8AD平分∠CAB AC，上的动点，则CE+EF的最小值为（）别是AD6． D．A． B． COABC6的正方形11.如图，在平面直角坐标系中，反比例函数y=（x＞0）的图象与边长是PM+PNP 两点．△OMN的面积为10．若动点在x轴上，则N 的两边AB，BC分别相交于M，的最小值是（）2．2 D．．A．6 B10 CADBC则四边形翻折得到△ABD，AC=BC=212.如图，△ABC中，，AB=1，将它沿ABPE+PF上的任意点，则、形，的形状是 P、E、F分别为线段ABAD、DB ．的最小值是D轴于，AB两点，交xC、y=y=13.如图，已知抛物线x+bx+c与直线x+3交于）．，，0BC 2两点，连接AC、，已知A（，3）C（﹣30）求此抛物线的解析式；（1的值最大，并求出这个最（2）在抛物线对称轴MD||MB上找一点M，使﹣l 大值；轴y交⊥作，过点轴右侧抛物线上一动点，连接为）点（3PyPAPPQPAABC于点QP，AP，问：是否存在点Q，使得以，为顶点的三角形与△请说的坐标；若不存在，P相似？若存在，请求出所有符合条件的点．明理由．14.如图，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD．（1）用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）；（2）在（1）的条件下，①证明：AE⊥DE；②若CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值．，3），C（03A（﹣1，0），B（，0y=ax15.如图，抛物线+bx+c（a≠0）经过点的坐标；）2）三点．求抛物线的解析式及顶点M（1 N点的坐标；时，求N为抛物线上的点且在第四象限，当S=S（2）连接AC、BC，ABCNBC△△，（ml上，动点QPx轴，动点（m，3）在直线2（3）在（）问的条件下，过点C作直线l∥ PM+PQ+QN的和最小，并求出m为何值时，PM+PQ+QNPM轴上，连接、PQ、NQ，当0）在x 和的最小值．，过A，两点的二次函数A16.如图，直线y=5x+5交x轴于点，交y轴于点C ．的图2+4x+cy=axC象交x轴于另一点B ）求二次函数的表达式；（1NDD，求线段⊥BC上的动点，作NDx轴交二次函数的图象于点是线段）连接（2BC，点N 长度的最大值；2）是该二次函数图象上一点，4，m图象的顶点，点H（3）若点为二次函数y=ax+4x+cM（的坐标．E，F的周长最小，求出点HEFM，使四边形E，F轴上分别找点y轴、x在．yB两点，与A0）与x轴从左至右交于，（x﹣2）（x+a）（a＞y=17.如图1，已知抛物线 C．轴交于点，求抛物线的解析式；T（1，﹣）（1）若抛物线过点△ B、D三点为顶点的三角形与（2）在第二象限内的抛物线上是否存在点D，使得以A、 ABC相似？若存在，求a的值；若不存在，请说明理由．）是抛物线上的点，6，t1的坐标为（﹣1，），点Q（2（3）如图，在（1）的条件下，点PPQNM轴上移动到何处时，四边形MN=2，问MN在x两点，在x轴上，从左至右有M、N且 M 的坐标．的周长最小？请直接写出符合条件的点轴另一交点x5）两点，与（（﹣1，0），C0，A18.如图，对称轴为直线x=2的抛物线经过），P是第一象限内抛物线上的动点．0F，，0（，1）E（a0），（a+1，MB为．已知）求此抛物线的解析式；（1 的面积的最大值，并求此时点）当2a=1时，求四边形MEFPP的坐标；（周长最小？请说为顶点的等腰三角形，求是以点）若△（3PCMPaPMEF为何值时，四边形明理由．P探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点19.1=P：P1得到结论三过构造直角角形利用图，（x（，y），Px，y）可通2112221的坐标公式：）P（x，y他还利用图2证明了线段PP的中点P21．，y=x=1）请你帮小明写出中点坐标公式的证明过程；（ MN长度为；（﹣M2）①已知点（2，﹣1），N3，5），则线段运用：（为顶点的平行四边形顶点D），3（﹣B2，0），C（，﹣12A②直接写出以点（2，），；的坐标：D轴正半轴夹角的平≥x（x0）的图象OL与xy=n2P33拓展：（）如图，点（，）在函数的周长最小，简要叙述作图FExOL分线上，请在、轴上分别找出点、，使△PEF 方法，并求出周长的最小值．20.如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛2物线y=﹣x+2x+1与y轴交于点C．（1）求直线y=kx+b的函数解析式；2）若点P（x，y）是抛物线y=﹣x+2x+1上的任意一点，设点P到直线AB的距离为d，求d 2（关于x的函数解析式，并求d取最小值时点P的坐标；3）若点E在抛物线y=﹣x+2x+1的对称轴上移动，点F在直线AB上移动，求CE+EF的最小2（值．，且OA∥ABC，使得BC21.如图①，在平面直角坐标系中，OA=6，以OA为边长作等边三角形落在过原点且开口向下的抛物线上．B、C点）求这条抛物线的解析式；（1个单位的速度运动，2BAC 的方向以每秒P从点B出发，沿折线在图①中，（2）假设一动点P个单位的速度运动，当点沿点出发，x轴的负半轴方向以每秒1同时另一动点Q从O，使得tQP、的运动过程中，是否存在时间A运动到点时，P、Q都同时停止运动，在的值，若不存在，请说明理由；AB，若存在，求出tPQ⊥，在抛物线的对称边上找一点G，使BE=EF=1个单位，试在ABE3（）在BC边上取两点、F 的周长最小，并求出周长的最小值．H，使得四边形EGHF轴上找一点本人所著《初中几何模型与解题通法》已发行，可在当当、淘宝和京东搜索购买1.特色：由一线名师编写，更专业权威，各地历年中考压轴题几乎都能在书中找到对应的模型和方法，甚至出现大量高度类似题。

将军饮马问题16大模型

将军饮马问题16大模型将军饮马问题源于中国古代的一个寓言故事，讲述的是三位将军跟随他们的军队来到一座河边准备渡河，但只有一条小船，这条小船一次只能搭载两人。

如果将军A和将军B在船上，将军C在岸边，将军C将会受到辱骂，如果将军A和将军C在船上，将军B在岸边，将军B也会受到辱骂，问题是如何让这三位将军都安全地渡河而不受辱骂。

这个问题启发了许多数学家和逻辑学家，有各种不同的解法。

下面将介绍将军饮马问题的16种不同模型。

模型1：最直接的解法最直接的解法是将将军A和将军B一同乘坐小船去对岸，然后将将军A带船返回，将将军C载到对岸。

模型2：穷举法穷举法是一种比较笨拙但可以解决问题的方法，即穷尽所有可能的情况。

这种方法虽然有效，但耗时较长。

模型3：递归法递归法是将问题分解成较小规模的子问题，并逐步解决。

这种方法可以节省时间和精力，但需要较高的逻辑思维能力。

模型4：数学推导法通过数学推导，可以将将军饮马问题转化为数学模型，从而得出解答。

这种方法需要较强的数学功底。

模型5：逻辑推理法逻辑推理法是通过逻辑推理和思维分析，得出解决将军饮马问题的方法。

这种方法强调思维的逻辑性和推理能力。

模型6：图论模型图论是数学的一个分支，可以用来描述将军饮马问题中的交叉关系和路径规划。

通过构建相应的图模型，可以更清晰地解决问题。

模型7：概率模型概率模型是通过概率计算和推测，找出解决将军饮马问题的可能性和概率分布。

这种方法适用于对问题进行全面分析和评估。

模型8：动态规划法动态规划法是针对多阶段决策问题的一种解决方法，可以在问题空间中寻找最优解。

这种方法适用于将军饮马问题的场景。

模型9：模拟法模拟法是通过模拟将军饮马问题的场景，以实验测算的方式找出最佳解决方案。

这种方法可以直观地展示问题的复杂性和解决路径。

模型10：启发式算法启发式算法是通过启发性的思考和优化方法，寻找将军饮马问题的最佳解决方案。

这种方法可以在复杂问题中找到较好的解决途径。

将军饮马模型

将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的B地开会，应该怎样走才能使路程最短？
从此，这个被称为“将军饮马”的问题广泛流传．
这个问题的解决并不难，据说海伦略加思索就解决了它．
解决
如图所示，从A出发向河岸引垂线，垂足为D，在AD的延长线取A关于河岸的对称点A‘，连结A’B，与河岸线相交于C，则C点就是饮马的地方，将军只要从A 出发，沿直线走到C，饮马之后，再由C沿直线走到B，走的路程就是最短的．如果将军在河边的另外任一点C‘饮马，所走的路程就是AC’+C‘B，
解：∵在菱形ABCD中，AC与BD互相垂直平分， ∴点B、D关于AC对称，连接ED，则ED就是所求的EF+BF的最小值的线段， ∵AB=AD, ∠DAB=60°
∴ △ABC是等边三角形 ∵E为AB的中点 ∴DE⊥AB，
Rt △ABC中， ED=6sin60º=3 3
但是，AC'+C'B＝A'C'+C'B＞A'B＝A'C+CB＝AC+CB．可见，在C点外任何一点C'饮马，所走的路程都要远一些．这有几点需要说明的：（1）由作法可知，河流l相当于线段AA中垂线,所以 AD=A‘D。（2）由上一条知：将军走的路程就是AC+BC，就等于A’C+BC，
而两村庄，他们想在河流l的边上建立一个水泵站，已知每米的管道费用是100元，A到河流的距离AD是1km，B到河流的距离BE是3km， DE长3km。请问这个水泵站应该建立在哪里使得费用最少？
解：如图所作，C点为水泵站的位置。
应用2
如图，在边长为6的菱形ABCD中，∠DAB=60°， E为AB的中点，F是AC上的一动点，则EF+BF的最小值为多少?

将军饮马模型(终稿)

將軍飲馬模型一、背景知識：【傳說】早在古羅馬時代，傳說亞曆山大城有一位精通數學和物理の學者，名叫海倫．一天，一位羅馬將軍專程去拜訪他，向他請教一個百思不得其解の問題．將軍每天從軍營A出發，先到河邊飲馬，然後再去河岸同側の軍營B開會，應該怎樣走才能使路程最短？這個問題の答案並不難，據說海倫略加思索就解決了它．從此以後，這個被稱為“將軍飲馬”の問題便流傳至今．【問題原型】將軍飲馬造橋選址費馬點【涉及知識】兩點之間線段最短，垂線段最短；三角形兩邊三邊關係；軸對稱；平移；【解題思路】找對稱點，實現折轉直二、將軍飲馬問題常見模型1.兩定一動型：兩定點到一動點の距離和最小例1：在定直線l上找一個動點P，使動點P到兩個定點A與Bの距離之和最小，即PA+PB 最小.作法：連接AB，與直線lの交點Q，Q即為所要尋找の點，即當動點P跑到了點Q處，PA+PB最小，且最小值等於AB.原理：兩點之間線段最短。

證明：連接AB，與直線lの交點Q，P為直線l上任意一點，在⊿PAB中，由三角形三邊關係可知：AP+PB≧AB(當且僅當PQ重合時取﹦)例2：在定直線l上找一個動點P，使動點P到兩個定點A與Bの距離之和最小，即PA+PBの和最小.關鍵：找對稱點作法：作定點B關於定直線lの對稱點C，連接AC，與直線lの交點Q即為所要尋找の點，即當動點P跑到了點Q處，PA+PB和最小，且最小值等於AC.原理：兩點之間，線段最短證明：連接AC，與直線lの交點Q，P為直線l上任意一點，在⊿PAC中，由三角形三邊關係可知：AP+PC≧AC(當且僅當PQ重合時取﹦)2.兩動一定型例3：在∠MONの內部有一點A，在OM上找一點B，在ON上找一點C，使得△BAC周長最短．作法：作點A關於OMの對稱點A’，作點A關於ONの對稱點A’’，連接A’ A’’，與OM 交於點B，與ON交於點C，連接AB，AC，△ABC即為所求．原理：兩點之間，線段最短例4：在∠MONの內部有點A和點B，在OM上找一點C，在ON上找一點D，使得四邊形ABCD周長最短．作法：作點A關於OMの對稱點A’，作點B關於ONの對稱點B’，連接A’ B’，與OM交於點C，與ON交於點D，連接AC，BD，AB，四邊形ABCD即為所求．原理：兩點之間，線段最短3.兩定兩動型最值例5：已知A、B是兩個定點，在定直線l上找兩個動點M與N，且MN長度等於定長d（動點M位於動點N左側），使AM+MN+NBの值最小.提示：存在定長の動點問題一定要考慮平移作法一：將點A向右平移長度d得到點A’，作A’關於直線lの對稱點A’’，連接A’’B，交直線l於點N，將點N向左平移長度d，得到點M。

将军饮马模型(终稿)

将军饮马问题16大模型

将军饮马模型(终稿)教学提纲

初中数学58种模型之12、“将军饮马”三种模型详解

将军饮马模型(终稿)

将军饮马(最完整讲义)

将军饮马(最完整讲义)

(完整word版)将军饮马问题的11个模型及例题

中考数学：'将军饮马'所有模型及变式——终极篇

将军饮马模型(终稿)(完整资料).doc

将军饮马模型【范本模板】

(完整)初三复习将军饮马(终稿)

最值模型之将军饮马模型(解析版)

中考复习讲义：将军饮马所有模型及变式——终极篇(直线型 角型 平移型)(练习无答案)

(完整版)将军饮马模型(终稿)

(完整版)将军饮马问题的11个模型及例题

完整word版将军饮马问题的11个模型及例题

将军饮马问题16大模型

将军饮马模型

将军饮马模型(终稿)

中考复习讲义：将军饮马所有模型及变式——终极篇(直线型角型平移型)(练习无答案)