空间相干性.ppt
合集下载
3杨氏空间相干性and分振幅干涉ok
3.普通光源的空间展宽越大，其光场的空间相干范
围越小 4.理想点光源照明的空间里波面上各点是完全相干 的
8
▲
薄膜干涉分振幅干涉
入射光束被薄膜分解为两束光,在空间交叠而形成干涉场
9
10
1. 点光源的薄膜干涉
点光源的薄膜干涉是非定域干涉。
干涉条纹-同心圆
薄膜两面不平行仍然是非定域的
11
点光源的薄膜干涉
n1 1
n2 1 38
ng 1 50
两束反射光强度相同
5500 h 1000 A0 4n 4 1 38
32
2 2
2 (2m 1) 4.8 107
m
4 1.32 0.52
7
(2m 1) 1.0 10 m
m=1时有
hmin 1.0 10 m
7
27
从法向观察，i=0:
2nh 2 m
4nh 4 1.30 1.0 107 5.20 107 2m 1 2m 1 2m 1
26
[例]在白光下，观察一层折射率为 1.30的薄油膜，若观 察方向与油膜表面法线成300角时，可看到油膜呈蓝色(波 长为4800A), 试求油膜的最小厚度，如果从法向观察，反 射光呈什么颜色?
解: 需考虑额外程差。根据明纹条件
L 2h n n sin i
2 2 1 2
h
(2m 1) 4 n sin i
n1 n2 ng
增反膜 如图（b） 高膜（H）
n1 n2 ng
n2 h
无
4
n2 h
有
4
L L0
光的相干性PPT课件
.
2
3.5.1 光的相干性 (Coherence of light) 影响条纹可见度的最主要因素是用于干涉实验的光 源特性；光源的大小和复色性。
1.光源大小对条纹可见度的影响—光的空间相干性 2.光源非单色性对条纹可见度的影响—光的时间相干性
.
3
1.光源大小对条纹可见度的影响—光的空间相干性
在杨氏干涉实验中，如果采用点光源，则通过于涉 系统将产生清晰的干涉条纹，V = l。如果采用扩展 光源，其干涉条纹可见度将下降。
2
(151)
V 随 的变化曲线如图所示。或者说，对一定的 ，
V 随着k 变化，k 增大，可见度 V 下降：
V 1
0
. 2/
37
2.光源非单色性对条纹可见度的影响—光的时间相干性
当Δk = 0，光源为单色光源时，V = 1； 当0< Δk< 2/Δ时，0 <V<1； 当Δk = 2/Δ时，V = 0。
V
1
0
2 b
.
19
1.光源大小对条纹可见度的影响—光的空间相干性 当光源是扩展光源时，光场平面上具有空间相干性 的各点的范围与光源的大小成反比。
V πbsinπb (141)
.
20
1.光源大小对条纹可见度的影响—光的空间相干性
对于一定的光波长和干涉装置，当光源宽度 b 较大， 且满足
b R d
I0dx 是元光源通过 S1 或 S2 在干涉场上所产生的光
强度； 是元光源发出的光波经 S1 和 S2 到达 P 点
的光程差。
I I1 I2 2I1 I2c o sc o s= I1 I2 + 2 I1 2 (3 )
.
9
3-8光场的空间相干性
结论：
（1）若要通过双孔直接看太阳,双孔间距 时才能看到干涉条纹。 d 0 . 0 5 5 m m （2）在双孔前面加上狭缝，限制太阳光源 的有效宽度，构成杨氏干涉装置，才 能在双孔间距较大时看到干涉条纹。
d f D sin u I ( x ) 2 bI [ 1 cos 2 fx ] 0 u IM Im sin u 反衬度： IM Im u bd u 时 , 0 R
bd 其中 ： u R
R 即： b 时，干涉条纹反衬度为零。 d
§8光源宽度对干涉条纹的影响 及光场的空间相干性
8.1 光源宽度对干涉条纹的影响
1）光源在Y方向展宽时反衬度不变
2）光源在X方向展宽时反衬度下降
（1）仅有两个点源时的反衬度
随两个点源错开距离的增加，两套干涉 图样非相干迭加的反衬度逐渐下降。 两套干涉图样错开半个条纹间距时， 反衬度下降为零。
（2）证明：
则：I I I 4 I A B 0
IM Im 0 两套条纹峰谷相对时 IM Im
（3）线光源时的反衬度
设任一点光源距中心点的位移为 此点光源在屏幕上任一点P的相位差为
s
k [( r r ) (R R 2 1 1 2)]
d d d D k [ x s )] 2 (x s )] D R D R 这个点光源在屏幕上的光强分布为： d D dI 2 I ( 1 cos( 2 ( x s ))) ds 0 D R
d
6）例题：
2 已知太阳的视角约为 ' b R 1 0 r a d， 估算太阳光射到地面上时的相干线度和 相干面积？ 取白光的中心波长 解： 为太阳光的平均波长 0 .5 5 m 相干线度为： d ' 5 5 m 0 . 0 5 5 m m
时空相干性
可见度与相干光波的相对强度、光源的大小和单色性有关。 1、两相干光的强度对干涉条纹可见度的影响 I I1 I 2 2 I1I 2 cos 对理想的单色点光源 I I1 I 2 ① I1 I 2 4I1
A1 2 A ( A1 A2 ) 2 ( A1 A2 ) 2 2 A1 A2 2 2 2 2 2 2 ( A1 A2 ) ( A1 A2 ) ( A1 A2 ) A1 1 A 2
相干长度coherentlength由光源的单色性决定的产生可见度不为零的干涉条纹的最大光程差是光源单色性的量度决定了产生干涉现象的最大光程差
§3—5 干涉条纹的可见度 时间相干性和空间相干性 一、干涉条纹的可见度 2 I ( A A ) I I max 1 2 max min 定义： V 2 I ( A A ) I max I min min 1 2
y
y
d
-1N 0M 0N 0L +1L
y
y
单色光相邻 两条纹间距
单色光源 r1 L b0 / 2 M r
2
b0 计算如下：
d
x r1
r
·
r2
0
+1L △y / 2
此时L点的一 级明纹的极大 在 M 点的一级 极小 y
y 处 2
r
L点一级明纹：(r2 r2 ) (r1 r1) r r
2 I1I 2 I I 0 2 I1I 2 cos I 0 (1 cos ) I 0 (1 V cos ) I0
可见度差 Imin (V < 1) -4 -2 0 2 4
Imax
2
空间相干性
16
式中 =p/D,是扩展光源对Q1 , Q2 连线中点的张角。此时，d 0 称为横向相干宽度。
扩展光源的空间相干性
在二维光源的情况下，引入相干面积的概念度 量空间相干性。相干面积为 Ac 定义为：
Ac
D
Ap
2
17
其中Ap为光源面积。说明光场中处于相干面积 内任意两点处的光场总是相关的（即只要杨氏实验 中的两孔位于相干面积之内，总可以发生干涉）。
3
4
其中 r1 r2 / c, r12 是函数12 的实部，且 12 = V1 t V2 * t
上式12 称为光束的互相干函数。
P1与P2 重合时，有： 11 = V1 t V2 * t 11 称为自相干函数。取 =0，则 11 0 =I1 , 22 0 =I 2 。
11
此时，干涉条纹的可见度为：
pd sin D v pd D
12
由此式可见随着光源的扩展，条纹对比度下降。
扩展光源的空间相干性
将（ ）式作图（得图3）。可见，当光源宽度小于p D / 4d 12 时可见度v 0.9, 这时条纹有足够好的对比度。
0 1
A2 e
i w0t 2
,
2 2 (1与2随机)，1 =A1 ，I 2 =A 2， 1 ( P , 0)V2 *( P2 , 0) =0， 12 =0， I V 1
即两个独立的光源本身的场不具有空间相干性。但当它们的 辐射经过相当距离的传播后可以获得一定的空间相干性。
扩展光源的空间相干性
2
3
考虑场的平稳性，在取平均时可移动时间原点，有：
空间相干性
2d
明条纹中心的位置
k = 0,±1,±2
暗条纹中心的位置
分波前双光束 干涉，是不定 域干涉。
§3.3 分波前干涉
2） 洛埃镜实验
光栏
p
当屏幕W移至B处， S 从 S 和 S’ 到B点的 d
光程差为零，但是 观察到暗条纹，验 S'
证了反射时有半波
损失存在。
p'
Q'
A MB
Q
D
W
结论：它们也是分波前双光束干涉。是不定域干涉。
A'
b o'
B'
S1
B
o
S2
A
D
b 内各点均可视为点光源而在屏幕上形成一套干涉 条纹，总的效果等效于各套干涉条纹的非相干叠加
§3.4 空间相干性
定量地，考虑极端的A’、B’的情况
对A’，条纹下移：
OP = -Db/(2R)
A'
S1
b o'
d
p′
o
对B’，条纹下移：
B'
S2
p
OP’ = Db/(2R)
R
D
即由宽b的光源形成的干涉，零级极大的宽度为：
∆x’ = Db/R
光源变大，干涉条纹变宽
§3.4 空间相干性
点光源双缝干涉中条纹的宽度为： ∆x = Dλ
d
当 ∆x’ > ∆x 时，将无法观察到干涉条纹。
有限的b值必须满足∆x’ < ∆x ，即：
Db/R < Dλ/d
b
≡
b0
=
R d
λ
——光源的极限宽度
b < b0 时，才能观察到干涉条纹。
1-5 光波的时间相干性与空间相干性(1)
第1章 光的干涉
7/11/2013
空间相干性
空间相干性：是描述光场中在光的传播路径上空间横 向两点在同一时刻光振动的关联程度；亦即是说，对 给定宽度的扩展d0’光源，在它照明的空间中在横向 波面上多大的范围内提取出来的两个次光源S1和S2还 是相干的？(两次波源间距小于或等于dmax) 空间相关性也称横向相干性； 空间相干性与光源的线度有关，光束窄－空间相 干性好；实验中常通过限制光束的宽度，来提高 光场的空间相干性； 光的空间相干性与时间相干性是不能严格分割的。实 际光源既有一定的宽度，也的一定的谱线宽度，光场 的空间相干性和时间相干性是同时存在的。实际干涉 中需同时考虑。
波长为的单色光，j级明纹的位置 波长为＋的单色光，j级明 纹的位置 j级明纹的宽度
j
d
r0 yj j ( ) d
y j
r0 j d
随着干涉级j的增大，同一级干涉的宽度增大，可见度下降. 第1章 光的干涉
7/11/2013
j+1
+ +
条纹分辨的极限
光的干涉15干涉条纹的可见度光波的时间相干性和空间相干性151干涉的可见度152光源的非单色性对干涉条纹的影响153时间相干性154光源线度对干涉条纹的影响155空间相干性光的空间相干性与时间相干性是共存的可用相干体积进行度量相干体积相干长度相干面积返回首页可见度
1.5 干涉条纹的可见度 光波的时间相干性和空间相干性
P
a S S1 b S2
P0
7/11/2013
具体分析
第1章 光的干涉
P
具体分析
S1 S S2 P0
波列a 经s1、s2分波面后次波列a1、a2。
7/11/2013
空间相干性
空间相干性：是描述光场中在光的传播路径上空间横 向两点在同一时刻光振动的关联程度；亦即是说，对 给定宽度的扩展d0’光源，在它照明的空间中在横向 波面上多大的范围内提取出来的两个次光源S1和S2还 是相干的？(两次波源间距小于或等于dmax) 空间相关性也称横向相干性； 空间相干性与光源的线度有关，光束窄－空间相 干性好；实验中常通过限制光束的宽度，来提高 光场的空间相干性； 光的空间相干性与时间相干性是不能严格分割的。实 际光源既有一定的宽度，也的一定的谱线宽度，光场 的空间相干性和时间相干性是同时存在的。实际干涉 中需同时考虑。
波长为的单色光，j级明纹的位置 波长为＋的单色光，j级明 纹的位置 j级明纹的宽度
j
d
r0 yj j ( ) d
y j
r0 j d
随着干涉级j的增大，同一级干涉的宽度增大，可见度下降. 第1章 光的干涉
7/11/2013
j+1
+ +
条纹分辨的极限
光的干涉15干涉条纹的可见度光波的时间相干性和空间相干性151干涉的可见度152光源的非单色性对干涉条纹的影响153时间相干性154光源线度对干涉条纹的影响155空间相干性光的空间相干性与时间相干性是共存的可用相干体积进行度量相干体积相干长度相干面积返回首页可见度
1.5 干涉条纹的可见度 光波的时间相干性和空间相干性
P
a S S1 b S2
P0
7/11/2013
具体分析
第1章 光的干涉
P
具体分析
S1 S S2 P0
波列a 经s1、s2分波面后次波列a1、a2。
1.4 干涉条纹的可见度,光波的时间相干性和空间相干性
r0 ( y y ) j j ( ) d
r0 r0 ( j 1) j ( ) d d
即j
S1 S2
j+1级 j级 j-1级
y j 1 ( y y ) j
当波长为 + 的第j 级与 的第j +1级条纹 重合时，可见度降为零，无法观察到条纹
可见度下降。 为什么是非相干叠加？
以杨氏实验为例
设光源的波长为
对
，其波长范围为
,j 级亮纹的位置为 r0 y j d
对 ,j 级亮纹的位置为
r0 y y j ( ) d
则第j 级明条纹的宽度为
r0 y j d
第j 级明条纹的宽度为
对于持续时间为光程对于有一定波长范围的非单色光源波列的长至少应等于最大光程差才有可能观在这个时间内传到p点的两列波具有相干性否则不具有相干性称该光波场具有时间相干性相干时间144光源的线度对干涉条纹的影响在前面的讨论中我们采用的是点光源或线光源但实际上光源总是具有一定的宽度的我们可以把它看成由很多线光源构成各个线光源在屏幕上形成各自的干涉花样这些干涉花样具有一定的位移位移量的大小与线光源到s的距离有关这些干涉花样的非相干叠加使总的干涉花样模糊不清甚至会使干涉条纹的可见度降为零
对于有一定波长范围的非单色光源，波列的长 度 L 至少应等于最大光程差 max ，才有可能观 j 察到 级以下的干涉条纹，由此可得
0
L0 max
L0 2 2 , 0 c c
（相干时间）
在这个时间内传到p点的两列波具有相干性，否则， 不具有相干性，称该光波场具有时间相干性
严格的单色光是具有确定的频率和波长的简谐波，它在时 间和空间上都是无始无终的，形成了无限长波列。然而 从微观机制看，实际的光源中的原子或分子等微观客体， 每次发射的光波波列都是有限长的。即使在非常稀薄的 气体中相互作用几乎可以忽略的情况下，它们发射的波 列所持续的时间 也不会超过 10^(-8)秒。 0
r0 r0 ( j 1) j ( ) d d
即j
S1 S2
j+1级 j级 j-1级
y j 1 ( y y ) j
当波长为 + 的第j 级与 的第j +1级条纹 重合时，可见度降为零，无法观察到条纹
可见度下降。 为什么是非相干叠加？
以杨氏实验为例
设光源的波长为
对
，其波长范围为
,j 级亮纹的位置为 r0 y j d
对 ,j 级亮纹的位置为
r0 y y j ( ) d
则第j 级明条纹的宽度为
r0 y j d
第j 级明条纹的宽度为
对于持续时间为光程对于有一定波长范围的非单色光源波列的长至少应等于最大光程差才有可能观在这个时间内传到p点的两列波具有相干性否则不具有相干性称该光波场具有时间相干性相干时间144光源的线度对干涉条纹的影响在前面的讨论中我们采用的是点光源或线光源但实际上光源总是具有一定的宽度的我们可以把它看成由很多线光源构成各个线光源在屏幕上形成各自的干涉花样这些干涉花样具有一定的位移位移量的大小与线光源到s的距离有关这些干涉花样的非相干叠加使总的干涉花样模糊不清甚至会使干涉条纹的可见度降为零
对于有一定波长范围的非单色光源，波列的长 度 L 至少应等于最大光程差 max ，才有可能观 j 察到 级以下的干涉条纹，由此可得
0
L0 max
L0 2 2 , 0 c c
（相干时间）
在这个时间内传到p点的两列波具有相干性，否则， 不具有相干性，称该光波场具有时间相干性
严格的单色光是具有确定的频率和波长的简谐波，它在时 间和空间上都是无始无终的，形成了无限长波列。然而 从微观机制看，实际的光源中的原子或分子等微观客体， 每次发射的光波波列都是有限长的。即使在非常稀薄的 气体中相互作用几乎可以忽略的情况下，它们发射的波 列所持续的时间 也不会超过 10^(-8)秒。 0
光学课间 干涉条纹的可见性、光波的时间相干性和空间相干性
b b0
五、空间相干性（spatial coherence）
当光源的极限宽度 b0 间的最大距离为
d max r b0
确定时，对应的双缝之
s d d max 时，光源 s1 和 s2 为相干光源；d d max 时， 1
和 s2 为非相干光源。
空间相干性描述光场中光的传播路径上横向两点 在同一时刻光振动的关联程度，又称为横向相干性。
二、光源的非单色性对干涉条纹的影响
▲
光的非单色性
、
1、理想的单色光 2、准单色光、谱线宽度 准单色光：在某个中心波长（频率）附近有一定波长 （频率）范围的光。
I0
谱线宽度：
I0 2
I
谱线宽度
0
0
3、造成谱线宽度的原因：
●
自然宽度（有能级的宽度造成）
Ej Ei
●
·
Ej
光波场的时间相干性和光源的单色性紧密相连因为波列是沿光的传播方向通过空间固定点的所以时间相干性是光场的纵向相干性四光源线度对干涉条纹的影响
§1—5 干涉条纹的可见性、光波的时间相干性和空间相干性 一、干涉条纹的可见度（对比度，反衬度）(contrast) 定义
V I max I min I max I min
I max ( A1 A 2 )
I min ( A1 A 2 )
2
描述干涉花样的强弱对比
2
( A1 A 2 ) ( A1 A 2 )
2
2 2
( A1 A 2 ) ( A1 A 2 )
2
A 2 1 A2 A 1 1 A2
五、空间相干性（spatial coherence）
当光源的极限宽度 b0 间的最大距离为
d max r b0
确定时，对应的双缝之
s d d max 时，光源 s1 和 s2 为相干光源；d d max 时， 1
和 s2 为非相干光源。
空间相干性描述光场中光的传播路径上横向两点 在同一时刻光振动的关联程度，又称为横向相干性。
二、光源的非单色性对干涉条纹的影响
▲
光的非单色性
、
1、理想的单色光 2、准单色光、谱线宽度 准单色光：在某个中心波长（频率）附近有一定波长 （频率）范围的光。
I0
谱线宽度：
I0 2
I
谱线宽度
0
0
3、造成谱线宽度的原因：
●
自然宽度（有能级的宽度造成）
Ej Ei
●
·
Ej
光波场的时间相干性和光源的单色性紧密相连因为波列是沿光的传播方向通过空间固定点的所以时间相干性是光场的纵向相干性四光源线度对干涉条纹的影响
§1—5 干涉条纹的可见性、光波的时间相干性和空间相干性 一、干涉条纹的可见度（对比度，反衬度）(contrast) 定义
V I max I min I max I min
I max ( A1 A 2 )
I min ( A1 A 2 )
2
描述干涉花样的强弱对比
2
( A1 A 2 ) ( A1 A 2 )
2
2 2
( A1 A 2 ) ( A1 A 2 )
2
A 2 1 A2 A 1 1 A2
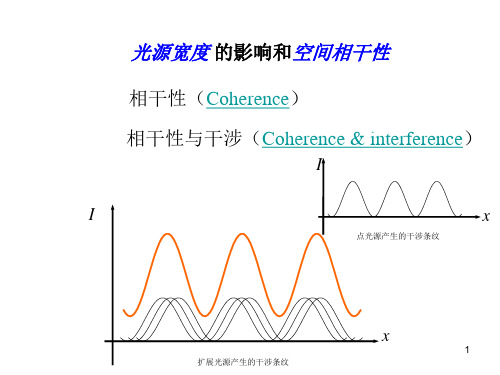
光源宽度 的影响和空间相干性
b2
2I 0b1
sin b / b /
cos 2
d D
x
K sin b b
3
讨论：
K sin b b
1）光源的临界宽度：条纹可见度为0时的光源宽度
临界宽度bc
2）光源的允许宽度：能够清晰地观察到干涉条纹时， 允许的光源宽度
允许宽度bp
4
4
2、空间相干性（Spatial Coherence )
c发出的光线到 P：
光程差 (r2 r1 ) (r2 r1)
其中 d x, ' d x' x'
D
l
被称为干涉孔径角
2
设I 0为单位宽度光源在P平面上的光强值， c处的元光源在P点的光强：dI 2I0dx'[1 cos k( )]
宽度为b的整个光源在P点的光强：
b 2
I 2I 0[1 cos k ( )]dx'
光源宽度 的影响和空间相干性
相干性（Coherence） 相干性与干涉（Coherence & interference）
I
I
x
点光源产生的干涉条纹纹可见度的影响
dx' S' c
x' b S0 β
r1' r2'
S1 d
l1
l2
S2
l
r1
r2
D
P
x
O
S''
若通过光波场横向两点的光在空间相遇时能够发生
干涉，则称通过空间两点的光具有空间相干性。
bc /
bc
k
5
干涉系统不变量 bc e d
x'
2I 0b1
sin b / b /
cos 2
d D
x
K sin b b
3
讨论：
K sin b b
1）光源的临界宽度：条纹可见度为0时的光源宽度
临界宽度bc
2）光源的允许宽度：能够清晰地观察到干涉条纹时， 允许的光源宽度
允许宽度bp
4
4
2、空间相干性（Spatial Coherence )
c发出的光线到 P：
光程差 (r2 r1 ) (r2 r1)
其中 d x, ' d x' x'
D
l
被称为干涉孔径角
2
设I 0为单位宽度光源在P平面上的光强值， c处的元光源在P点的光强：dI 2I0dx'[1 cos k( )]
宽度为b的整个光源在P点的光强：
b 2
I 2I 0[1 cos k ( )]dx'
光源宽度 的影响和空间相干性
相干性（Coherence） 相干性与干涉（Coherence & interference）
I
I
x
点光源产生的干涉条纹纹可见度的影响
dx' S' c
x' b S0 β
r1' r2'
S1 d
l1
l2
S2
l
r1
r2
D
P
x
O
S''
若通过光波场横向两点的光在空间相遇时能够发生
干涉，则称通过空间两点的光具有空间相干性。
bc /
bc
k
5
干涉系统不变量 bc e d
x'
论述光的空间相干性和时间相干性PPT课件
本质：空间相干性源于扩展光源不同部分发光的独立性； 时间相干性源于发光过程在时间上的断续性。
效果：空间相干性表现在光波场的横向，并集中于分波前干涉； 时间相干性表现在光波场的纵向，并集中于分振幅干涉。
结语
数学描述： 空间相干性：相干线度： dc l / b 相干孔径角： / b 相干性反比公式：b
时间相干性
设由分光源S′，S″所发出的单色相干光的平均持续 时间为τ ,则平均波列长度为Lc=cτ ，c为光速。在不 考虑光源线度对干涉条纹清晰度影响的情况下，若光 源S′发出的光传播到光屏EE′上P点所用时间为t1，光 源S″发出的光传播到光屏EE′上P点所用时间为 t1 +Δ t，则当Δ t<τ 时,两列光波在P点能形成干涉条 纹；Δ t越接近于τ ，条纹越不清楚；当Δ t>τ 时，两 列光波位相间无确定关系，不能产生干涉现象。
相干光源：能够观察到干涉条纹的理想光源，是从一 无限小的点光源发出无限长光波列，用光学方法将其分为 两束，再实现同一波列的相遇迭加，能得到稳定的干涉条 纹的光源。
概述
实际的相干光源和理想的相干光源有两点重要的不同， 一是理想相干光源所发出的是无限长光波列，而实际相干 光源所发出的是有限长光波列；二是理想相干光源为一几 何点，而实际相干光源总有一定的线度。因此，我们应注 意以下两方面的问题： (1)由于实际相干光源所发出的光波列为有限长，若两束 光到达观察点的光程差超过一个波列的长度，在该处就不 能实现相干迭加。所以，波列长度和光程差的大小是影响 干涉条纹清晰度的一个重要因素。
概述
(2)由于实际相干光源有一定的线度,即使光源上的每个点 所发出的光都是无限长波列,能保持恒定的位相差而形成 稳定的干涉条纹,但由于光源上不同点发出的光所形成的 干涉条纹分布不同,迭加的结果仍使条纹看不清楚.所以, 光源的线度以及干涉装置的结构,是影响干涉条纹清晰度 的另一个重要因素
效果：空间相干性表现在光波场的横向，并集中于分波前干涉； 时间相干性表现在光波场的纵向，并集中于分振幅干涉。
结语
数学描述： 空间相干性：相干线度： dc l / b 相干孔径角： / b 相干性反比公式：b
时间相干性
设由分光源S′，S″所发出的单色相干光的平均持续 时间为τ ,则平均波列长度为Lc=cτ ，c为光速。在不 考虑光源线度对干涉条纹清晰度影响的情况下，若光 源S′发出的光传播到光屏EE′上P点所用时间为t1，光 源S″发出的光传播到光屏EE′上P点所用时间为 t1 +Δ t，则当Δ t<τ 时,两列光波在P点能形成干涉条 纹；Δ t越接近于τ ，条纹越不清楚；当Δ t>τ 时，两 列光波位相间无确定关系，不能产生干涉现象。
相干光源：能够观察到干涉条纹的理想光源，是从一 无限小的点光源发出无限长光波列，用光学方法将其分为 两束，再实现同一波列的相遇迭加，能得到稳定的干涉条 纹的光源。
概述
实际的相干光源和理想的相干光源有两点重要的不同， 一是理想相干光源所发出的是无限长光波列，而实际相干 光源所发出的是有限长光波列；二是理想相干光源为一几 何点，而实际相干光源总有一定的线度。因此，我们应注 意以下两方面的问题： (1)由于实际相干光源所发出的光波列为有限长，若两束 光到达观察点的光程差超过一个波列的长度，在该处就不 能实现相干迭加。所以，波列长度和光程差的大小是影响 干涉条纹清晰度的一个重要因素。
概述
(2)由于实际相干光源有一定的线度,即使光源上的每个点 所发出的光都是无限长波列,能保持恒定的位相差而形成 稳定的干涉条纹,但由于光源上不同点发出的光所形成的 干涉条纹分布不同,迭加的结果仍使条纹看不清楚.所以, 光源的线度以及干涉装置的结构,是影响干涉条纹清晰度 的另一个重要因素
3-3时间相干性和空间相干性
§3--3时间相干性和空间相干性Temporal Coherence and Spatial Coherence ）一）问题的提出：S 2d 1r 2r 1）单色光入射时，只能在中央条纹附近看到有限的为数不多的几条干涉条纹。
2）单缝或双缝宽度增大时，干涉条纹变得模糊起来。
S 1DX O为什么？二）时间相干性XO S 1S 2d D指由原子一次发光所持续的时间来确定的光的相干性问题--原子发光时间越长，观察到清楚的干涉条纹就越多，时间相干性就越好。
1r 2r 1)两波列的光程差为零（)21r r =可产生相干叠加。
X OS 1S 2d D1r 2r )(12L r r <−能参与产生相干叠加的波列长度减小干涉条纹变模糊了！P若是明纹，则明纹不亮；若是暗纹；暗纹不暗原因：XOS 1S 2dD1r 2r )(12L r r ≥−波列不能在P 点叠加产生干涉。
干涉条纹消失了！原因：P此乃高干涉级条纹看不清或消失的原因之一L<δ结论：产生光的干涉还须加一附加条件：tc L Δ=L<δ结论：产生光的干涉还须加一附加条件：tc L Δ=E 2E 1E 3tc L Δ=1）波列长度L 又称相干长度。
L 越长，光波的相干叠加长度越长，干涉条纹越清晰，相干性也越好。
注意：2）原子一次发光的时间Δt 称为相干时间。
Δt 越大，相干长度越长，相干性越好，因此用这种原子一次持续发光的时间来描述这种相干性故称为时间相干性。
三）空间相干性S 1S 2d DXOIb光源总是有一定的线度的，当光源线度不大时：从S 和S’发出的光产生的干涉条纹叠加后，仍能分辩清楚明暗条纹。
SS’S 1S 2d DXOIb当光源线度b 较大时：从S 和S’发出的光产生的干涉条纹叠加后，干涉条纹对比度降低，明暗条纹变得模糊。
SS’S 1S 2d DXOI b当光源线度b 增大到某一限度时：干涉条纹消失，S 和S’发出的光的光程差之差差λ/2SS’可见：为了产生清晰的干涉条纹，光源的线度受到一定限度。
光学 1.6 光的时间空间相干性
L max Lc
相干长度与光谱宽度的关系
Lc max 2 2 k | |(7)Fra bibliotek(8)
相干时间
Lc 2 1 t0 0 c c c | |
max
(9)
（ 0发光时间或寿命）
(9)式表明，波列的空间长度和持续时间（寿命）是与谱线 的宽度成反比的。 由此可见，“波列长度是有限的”和“光是非单色的”两 种说法完全等效，它们是光源同样性质的不同表述。它们实 际上是分别在时域和频域之间的描述.其之间的关系傅立叶变 换. 5、时间相干性 ① 定义：时间相干性是指沿传播方向多大距离内的两个点 分出来的光才能满足相干条件。 ② 量度：时间相干性用相干波长（波列长度，最大光程差） 或用相干时间（波列持续时间）来衡量 。
x
dx S r
b
S
r
S
S1
d
z
S2
r0
图6.6 扩展光源的相干性
r0
r r d
bd d 2 bd d r0 2r0 r0
当光程差等于半个波长：
b d / 2 r0
d2 略去二阶小量 2r0
（3）
（2）光源的非单色性，光源的线度。 3、所谓相干性，一般可理解为来自不同时刻或不同空间位 置的光场之间的相关性。具体来说，当我们把同一光源发出 的光分成两束，然后在空间某一点叠加时，如果可以形成干 涉条纹，我们就说着两束光是相干的，反之就是非相干的。 把来自不同时刻的光场之间的相关性称为时间相干性；把来 自不同空间位置的光场之间的相关性，称为空间相干性。
(10)
bd r0 2
临界宽度bc
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
扩展光源
• 若杨氏实验中用的是扩展光源，它的宽度 0 ',d 0 '= 2 d ' 为 d ，则扩展光源可分成许多相 距为 d ' 的线光源对，由于每对线光源在屏幕 上的干涉图样的可见度为零，所以整个光源 再屏幕上的干涉图样的可见度也为零，因此， 无法观察到干涉图样，这个扩展光源的宽度 称为临界宽度。其值为： d 0'
' '
d ' r20 a d r10 a , 2 ' ' ' 而： r10 + r2 0 = r0
' '
d ( ' ' ' \ d’+ r10 + r2 0 ) a = r0 a 2 1 ' d 即： a = ' d + 2 r0
即：
1 a = ' r0
' d d + 2
d 0 ' = 2 d ' = r 0 ' l / d
对于临界宽度，可求得所对应的双缝之间的 最大距离：
由d =
0
r
'
0
d
l 得：d
max
=
r
'
0
l
d
0
讨论：双缝距离与
• 若缝之间的距离等于或大 于 d max ，则观察不到干 涉条纹，即光场中狭缝s
2
1、
d max = r 0 ' l / d 0 '
（1）当两个线光源相互靠近时，两套 干涉条纹相互错开距离较小 （2）当两个线光源远距离时，两套干 涉条纹相互错开距离增大 （3）当一套条纹亮纹与另一套条纹暗 纹重合， ,即两套条纹，零级相互错开 半个条纹宽度时合成光强度成为均匀， 干涉条纹消失。
Q d = r2 - r1 d a (a sin a )
1、
的关系
和s 处的光矢量在同一时 刻无确定的相位关系。由 于s 和s 发出的光波来自 同一束光源，故与宽度为 d 0 ' 的光源对应的光场空 间相干性较差。
1、
2
• 若双缝s s 之间的 距离小于 d max ，则 在屏幕上能观察到 干涉条纹，说明s s 的光场是相干的， 或者说这是光场具 有空间相干性
2
ad d 2 ad l \ d da = ' + ' ' = 2 r0 r0 r0
d ( 又 Q a tg a = )
r0
'
l if : d = 2 ，
此时Ｖ＝０
ad = l then : ' 2 r0
即：
r0 l d’= 2d
'
临界宽度：
r0 d0 = 2a = d l
'
a V 0
光的空间相干性
一、光的空间相干性和光的时间相干性是共存的。 在杨氏双缝实验中，观察屏幕上离O点较远位置处的y 点干涉条纹时，不仅涉及空间相干性，而且涉及时间相干 性。
y
S
s1
d
r1
r2
r0
y
s2
0
杨氏双缝实验
（点光源或者线光源）
二、光源的线度对空间相干性的影响 两个线光源的情况：
此时
V=0
s和s’ 间的距离为d‘
2
1、
2
光的空间相干性Βιβλιοθήκη • 综上所述：在光的传播路径上空间 横向两点在同一时刻光振动的关联 程度，又叫作：横向相干性。
1）而且光的空间相干性和光源的线度有关。 2)为了改善干涉条纹的可见度，通常在光源前放置 狭缝s以减小光源的线度，提高光场的空间相干性
谢谢观看 敬请批评
制作者：闫新正 参与者：A0941全班同学