相干照明与非相干照明的比较
中山大学信息光学习题课后答案--习题4-5-6作业
习 题 44.1 尺寸为a b ⨯的不透明矩形屏被单位振幅的单色平面波垂直照明，求出紧靠零后的平面上透射光场的角谱。
4.2 采用单位振幅的单色平面波垂直照明具有下述透过率函数的孔径，求菲涅耳衍射图样在孔径轴上的强度分布：(1) 00(,)t x y = (2) 001,(,)0,a t x y ⎧⎪≤=⎨⎪⎩其它4.3 余弦型振幅光栅的复振幅透过率为：00()cos(2/)t x a b x d π=+式中，d 为光栅的周期，0a b >>。
观察平面与光栅相距z 。
当z 分别取下述值时，确定单色平面波垂直照明光栅，在观察平面上产生的强度分布。
(1) 22r d z z λ== (2) 22r z d z λ== (3) 242r z d z λ== 式中：r z 为泰伯距离。
4.4 参看下图，用向P 点会聚的单色球面波照明孔径∑。
P 点位于孔径后面距离为z 的观察平面上，坐标为(0,)b 。
假定观察平面相对孔径的位置是在菲涅耳区内，证明观察平面上强度分布是以P 点为中心的孔径的夫琅禾费衍射图样。
4.5 方向余弦为cos ,cos αβ，振幅为A 的倾斜单色平面波照明一个半径为a 的圆孔。
观察平面位于夫琅禾费区，与孔径相距为z 。
求衍射图样的强度分布。
4.6 环形孔径的外径为2a ，内径为2a ε(01)ε<<。
其透射率可以表示为：001,()0,a r a t r ε≤≤⎧=⎨⎩其他度分布。
4.7 下图所示孔径由两个相同的圆孔构成。
它们的半径都为a ，中心距离为d ()d a >>。
采用单位振幅的单色平面波垂直照明孔径，求出相距孔径为z 的观察平面上夫琅禾费衍射图样的强度分布并画出沿y 方向截面图。
4.8 参看下图，边长为2a 的正方形孔径内再放置一个边长为a 的正方形掩模，其中心落在(,)x y ''点。
采用单位振幅的单色平面波垂直照射，求出与它相距为z 的观察平面上夫琅禾费射图样的光场分布。
中国科学院大学《高等物理光学》期末知识点总结
20 讲题目：平面波与球面波；空间频率；角谱：波的叠加；空间频率的丢失：卷积的物理意义；抽样定理；衍射与干涉；透过率函数；近场与远场衍射；“傅里叶变换与透镜”；対易：衍射的分析法：空品対易；全息；阿贝成像原理（4f 系统）；泽尼克相衬显微镜；CTF;OTF;非相干与相干成像系统；衍射的计算机实验；衍射的逆问题；叠层成像（Ptychography）；如何撰写科技文章面有限短距离 z 处得观察平面上，坐标是(0, b).求观察平面上的光强分布，并说明该光强分布与孔径是什么关系;若该孔径是两个矩形孔，求观察平面上的光强分布，并画出沿 y 轴方向的𝐴𝑘光强分布曲线。
解：孔径平面上透射波的光场分布为U(𝑥0 , 𝑦0 ) = exp(−𝑗𝑘𝑧) exp {−𝑗 [𝑥0 2 +𝑧抽样定理：利用梳状函数对连续函数𝑔(𝑥, 𝑦)抽样，得𝑔𝑠 (𝑥, 𝑦) = 𝑐𝑜𝑚𝑏 ( ) 𝑐𝑜𝑚𝑏 ( ) 𝑔(𝑥, 𝑦)抽样U(x, y) =函数𝑔𝑠 ,由δ函数的阵列构成，各个空间脉冲在𝑥方向和y方向的间距分别为𝑋, 𝑌。
每个δ函数下的体积正比于该点 g 的函数值。
利用卷积定理，抽样函数𝑔𝑠 的频谱为空间域函数的抽样，导致函数频谱𝐺的周期性复𝑛 𝑚现，以频率平面上( , )点为中心重复𝐺见图。
相干光与非相干光在光学成像中的比较与优化
相干光与非相干光在光学成像中的比较与优化光学成像是一种常见的图像获取技术，广泛应用于医学、生物学、材料科学等领域。
在光学成像中，相干光和非相干光是两种常见的光源。
它们在成像质量、分辨率以及应用范围上存在一些差异。
本文将对相干光和非相干光在光学成像中的比较与优化进行探讨。
首先，我们来了解一下相干光和非相干光的特点。
相干光是指光波的振动方向、频率和相位都保持一致的光源。
相干光的特点是波前的干涉和衍射现象明显，可以实现高分辨率的成像。
非相干光则是指光波的振动方向、频率和相位都是随机的，没有明显的干涉和衍射现象。
非相干光的特点是亮度均匀，适合用于照明和全息成像。
在光学成像中，相干光和非相干光的选择取决于具体的应用需求。
相干光成像适用于需要高分辨率的情况，如显微镜观察细胞结构、纳米材料表征等。
相干光成像的原理是利用光的干涉和衍射现象，通过重构波前信息来获取高分辨率的图像。
相干光成像技术包括干涉显微镜、全息显微镜等。
这些技术可以实现纳米级别的分辨率，对于细胞和材料的研究具有重要意义。
然而，相干光成像也存在一些限制。
由于相干光的干涉和衍射现象，它对样品的透明度和形貌要求较高。
对于不透明或表面粗糙的样品，相干光成像的效果会受到限制。
此外，相干光成像还受到散射和折射等因素的影响，可能导致成像的模糊和畸变。
因此，在实际应用中，需要根据具体样品的特点来选择相干光成像技术，并进行优化和改进。
与相干光相比，非相干光成像更加简单和实用。
非相干光成像不受样品的透明度和形貌的限制，适用于各种材料和样品的成像。
非相干光成像技术包括传统的光学显微镜、X射线成像、CT扫描等。
这些技术具有广泛的应用范围，可以用于生物医学、材料科学、工业检测等领域。
非相干光成像的优势在于成像速度快、成本低廉，并且可以实现大范围的样品扫描。
然而，非相干光成像也存在一些局限性。
由于非相干光的特点是亮度均匀，它的分辨率相对较低。
对于需要高分辨率的应用，非相干光成像可能无法满足要求。
相干成像与非相干成像的比较
光学信息处理
第三章
Transfer Function of Optical Imaging System
光学成像系统的传递函数
§ 6. 相干成像与非相干成像的比较
a.截止频率
相 干： Hc (,)=F{hi(xi,yi)}
非相干：
ℋ (,)=
2
jφ )
x 1 .92
x 1 .92
由于相位差的影响，应具体问题具体分析，不能瑞利判据来表述分辨 率。
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
§ 6. 相干成像与非相干成像的比较
相干成像与非相干成像由于照明方式有本质的不同，是不 能直接进行比较的！ 这里主要是从量上进行对比，以加深对几个同名参数的 理解与记忆！
§ 6. 相干成像与非相干成像的比较
b.像的强度谱
例题：物体的复振幅透过率为：t1 ( x )
cos
2
x b
当此物通过一横向放大率为1的光学系统成像，系统的出瞳是半径为
di b
ห้องสมุดไป่ตู้
a
2di b
的圆孔， di 为出瞳到像面的距离，试问对该物体成像，是采用相干照明好还是
非相干照明好？
在相干照明下：
c
a di
§ 6. 相干成像与非相干成像的比较
c.分辨率
非相干： I( x ) [ 2J1( x 1.92 ) ] 2 [ 2J1( x 1.92 ) ] 2
x 1.92
x 1.92
可以用瑞利判据： σ 1 .22 λ d i
D
相 干：
I( x )
[ 2 J 1 ( x 1 .92 ) ] [ 2 J 1 ( x 1 .92 ) ] exp(
相干光与非相干光的特性比较
相干光与非相干光的特性比较光学是研究光的传播和性质的学科，随着科技的发展和应用的推广，光学在各个领域都扮演着重要的角色。
在光学中，有两种重要的光的性质，分别是相干光和非相干光。
它们具有不同的特性和应用，下面将对它们进行比较和探讨。
相干光是指光的振动方向、频率、相位等参数在时间和空间上保持一致的光。
它具有相同的相位、频率和振动方向，波前是平行的。
相干光可以通过干涉和衍射现象进行研究，例如洛伦兹衍射和杨氏实验。
相干光的干涉现象可以用来测量物体的形状和厚度，广泛应用于光学显微镜、激光干涉测量等领域。
非相干光是指光的振动方向、频率、相位等参数在时间和空间上没有任何关联的光。
它是由多个不同的光源发出的光波叠加而成的。
非相干光具有不同的相位、频率和振动方向，波前是随机的。
非相干光在物体上形成均匀照明的效果，适用于照明和成像等领域。
例如，在医学影像中，X射线和γ射线等都属于非相干光。
非相干光也可以用于光学标准源中，用于校准仪器的。
相比之下，相干光和非相干光有着截然不同的特性和应用。
首先，相干光的干涉效应明显，能够产生干涉条纹，而非相干光则不能。
这是由于相干光的波前具有一定的几何结构，可以使光波叠加形成明暗条纹。
而非相干光的波前是随机的，叠加后无法形成干涉现象。
其次，相干光在照明领域的应用相对较少，非相干光则广泛应用于照明和成像。
由于相干光的波前是平行的，不能形成均匀照明的效果。
而非相干光的波前是随机的，可以在物体表面形成均匀的照明作用，使得物体的细节更加清晰。
此外，相干光还具有相干性、干涉性和倾向性等特点，非相干光则没有这些特性。
相干光的相位差会导致干涉现象，而非相干光的波前差异可以忽略不计。
在实际应用中，科学家和工程师需要根据具体需求选择相干光或非相干光。
例如，相干光在干涉测量和光学显微镜等领域发挥重要作用，可以提供高分辨率的测量结果。
而非相干光在照明和成像等领域广泛应用，可以提供均匀的照明效果和清晰的成像细节。
18-成像系统5-相干照明与非相干照明的比较
衍射受限系统的非相干传递函数
调制传递函数（ 调制传递函数（MTF） ）
一般为复函数, (fx, fy)一般为复函数 可写为 一般为复函数 (fx, fy) = m(fx, fy)exp[jφ(fx, fy)] (
的模) 其中 m(fx, fy)(即OTF的模 称为调制传递函数 ( 即 的模 称为调制传递函数MTF （Modulation Transfer Function） ） 相应地, 称为相位传递函数。 相应地 φ(fx, fy)称为相位传递函数。 称为相位传递函数
[
]
衍射受限系统的非相干传递函数
调制传递函数（ 调制传递函数（MTF） ）
~ 2 m ∴ I i ( xi ) = ∫ h ( x ) dx + e j 2πf 0 xi H c ★ H c + C.C. 2 −∞
+∞
+∞
[
]
HC★HC一般是复函数
H C★ C = H C H C • e jφ H ★
光栅
+∞
（无限窄的单缝∥y0轴的阵列，周期 = 0.01mm）求像的强度分布 无限窄的单缝∥ 轴的阵列，周期d ）求像的强度分布. 思路: 首先求出物(几何像 强度的频谱,并确定系统的 几何像)强度的频谱 并确定系统的OTF与 思路 首先求出物 几何像 强度的频谱 并确定系统的 与 的值→ 截止频率→在通频带内对于每个物频谱分量求出OTF的值→ 的值 截止频率→在通频带内对于每个物频谱分量求出 求出像频谱→ 求出像频谱→综合出像强度 单位强度的平面波垂直照明.几何光学理想像分布 解: (1) M=1, 单位强度的平面波垂直照明 几何光学理想像分布 等于物体的强度透过率. 等于物体的强度透过率 Ig(x0)=∑δ(x0-nd) (2) 输入的归一化频谱 输入的归一化频谱:
非相干光源,相干光源 直流电与交流电的关系
非相干光源,相干光源直流电与交流电的关系非相干光源和相干光源是光学领域中常用的两种光源。
它们在光的性质、产生原理和应用方面有着明显的区别。
而直流电和交流电是电学领域中两种常见的电流形式，它们在电流的产生、传输和应用方面也有着不同的特点。
下面将分别对非相干光源和相干光源以及直流电和交流电进行详细的介绍和比较。
非相干光源是指光波的相位关系是随机的光源。
它的特点是光波的相位差是随机的，不具有相干性。
常见的非相干光源有白炽灯、荧光灯等。
非相干光源产生的光波是由许多不同频率、不同相位的光波叠加而成的。
由于光波的相位差是随机的，所以非相干光源的光波是不稳定的，无法形成明确的干涉和衍射图样。
非相干光源的光强分布是均匀的，不具有明显的干涉和衍射效应。
非相干光源的应用主要集中在照明、摄影等领域。
相干光源是指光波的相位关系是确定的光源。
它的特点是光波的相位差是确定的，具有相干性。
常见的相干光源有激光器、干涉仪等。
相干光源产生的光波是由具有相同频率、相同相位的光波叠加而成的。
由于光波的相位差是确定的，所以相干光源的光波是稳定的，能够形成明确的干涉和衍射图样。
相干光源的光强分布具有明显的干涉和衍射效应。
相干光源的应用主要集中在干涉、衍射、激光技术等领域。
直流电是指电流方向恒定的电流。
它的特点是电流的方向和大小都保持不变。
直流电的产生可以通过直流发电机、电池等设备实现。
直流电的传输和应用主要集中在电池供电的电子设备、直流电机、电解等领域。
直流电的优点是电流方向稳定，容易控制和使用。
但是直流电的传输距离有限，损耗较大。
交流电是指电流方向周期性变化的电流。
它的特点是电流的方向和大小随时间呈周期性变化。
交流电的产生可以通过交流发电机实现。
交流电的传输和应用主要集中在电网供电的家庭、工业、交通等领域。
交流电的优点是传输距离远，损耗小。
交流电的缺点是电流方向和大小变化较快，不易控制和使用。
综上所述，非相干光源和相干光源在光的性质、产生原理和应用方面有着明显的区别。
5.6__相干成像和非相干成像的比较 PPT课件
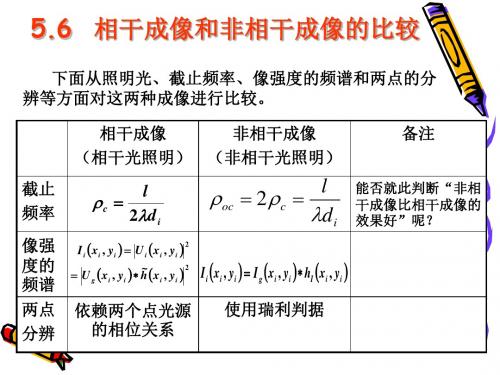
相干光照明下，
像的强度为
Ii U g h~ 2
像强度的频谱为 Gi , Gg , H , Gg , H ,
瞳是半径为a 的圆形孔径，并且 di a 2di
b
b
。d i
为出瞳到像面的距离， 为照明光波波长，请问对
该物体成像，采用相干光和非相干光照明，哪一种方
式更好？
t1x
x
分析：首先，该系统的出瞳是圆孔.
相干光照明时， 截止频率为
c
a
di
a
因为题目给出了条件：di a 2di
（相干光照明） （非相干光照明）
备注
截止 频率
像强 度的 频谱 两点 分辨
c
l
2d i
oc
2c
l
di
能否就此判断“非相 干成像比相干成像的 效果好”呢？
Ii xi , yi Ui xi , yi 2
U g xi , yi h~xi , yi 2 Ii xi , yi Ig xi , yi hI xi , yi
b
b
所以得到
1 2
c
1 b
c
（1）
接着，将物函数分解为余弦函数的线性组合，即将其展 开成傅立叶级数，得
tix
cos 2
x b
4
1 2
1 cos 4
13
x b
1 cos 6
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B: t 2 x cos 2 x b
试用作图法定性分析
对于相干照明，这个呈余弦分布的复振幅能不受影响地通 过系统成像。对于非相干照明，此物也能通过系统成像， 但幅度要受到衰减。故相干照明优于非相干照明.
§3-8 相干与非相干成像系统的比较
3. 两点分辨 Resolution
评判系统成像质量的一个重要指标 瑞利分辨判据: 用来表示理想非相干成像光学系统的分辨极限。 对于衍射受限的圆形光瞳，点 I I (0) 2 J1 ( x) , x rk a / z x 光源在像面上产生艾里斑分布：
2
对两个强度相等的非相干点源，若一个点源产生的艾里斑中心恰 与第二个点源产生的艾里斑的第一个零点（x = 3.83)重合，则认 为这两个点源刚好能够分辨。此时总的强度分布：
像的频谱: 相干 Gc f x , f y Ggc f x , f y H c f x , f y ☆ Ggc f x , f y H c f x , f y 非相干 Gi f x , f y [Ggc ( f x , f y ) ☆ Ggc ( f x , f y )][ H c ( f x , f y ) ☆ H c ( f x , f y )] 在两种情况下像强度的频谱可能很不相同. 成像结果不仅依赖于系统的结构与照明光的相干性， 而且也与物的空间结构有关。
x0
其中f 0
x0 d i
只有相应于光瞳开孔的空频带分量才能通过系统，像方复振 幅才有相应的分量。 非相干成像系统是一个有衰减的低通滤波器，其传递函数值 在零频时恒为1，在其它频率处的值均小于1。无论光瞳的形 状如何。
#
对空间频率分量的传递作用（滤波器）
如何理解？ 非相干系统考虑的是像强度的频谱，不是复振幅的频谱。只 要光瞳不是≡0，有光通过光瞳到达像面，就会有像强度的平 均值，即像频谱的零频分量。
2 J ( x 1.92 ) 2 J1 ( x 1.92 ) I ( x) 1 x 1.92 x 1.92
2 2
像面上得到的最小分辨 极限σ 等于艾里斑图 1.22 d i 样的中心亮斑半径，即： D
中心凹 陷大小 为峰值 的19%
i
( fx, fy )
g
( fx, f y )
i
( fx, f y )
(归一化)
§3-8 相干与非相干成像系统的比较 Review (续)
相干成像 传递 CTF P(d i f x , di f y ) 频 函数 理想 带通滤波器 非相干成像
P( ,) P( d f , d OTF P( ,)dd
间隔为2/b的梳
中心在+1/b, 半宽为2/b的sinc
f cut a d i
相干照明: 几何像的频谱即为T1 相干截止频率
（注意: a是半径）
1 a f cut 2 b d i b
d i
b
a
2d i b
所以只有零频分量能够通过，像面上将没有条纹结构。
§3-8 相干与非相干成像系统的比较
#
§3-8 相干与非相干成像系统的比较
对空间频率分量的传递作用 例：P80-81 例3.5/3.6题
有两个物体
A: x 分别通过衍射受限系统 t1 x cos 2 b 成像(1:1) 系统的出瞳是 x 半径为a的圆孔, 并且: t 2 x cos 2 d i 2d i b a b b
i x
i
f 光瞳总面积
有衰减的低通滤波器, MTF=|OTF|<1 截止频率: CTF 由光瞳函数决定 边长l的方瞳: f cut 域 直径l的圆瞳: f cut
l 2d i l 2d i
扩展到CTF的二倍
l f cut ' d i
l f cut ' d i
2
I i ( xi , yi ) ~ ~ , ~ h x ~ , y ~ 2 d~ d~ I g x0 y0 x0 i y0 x0 y0 i
复振幅 Gi ( f x ,f y ) Gg ( f x ,f y ) H C ( f x ,f y ) 频 频谱
像强度 I i Gi ( f x , f y )★ Gi ( f x , f y ) 频谱 (Gg H ) ★ (Gg H ) 域
2 b 2 b 2
b f x comb f x 2 2
b 1 1 1 b 1 b b comb f x sinc ( f x ) sin c ( f x ) 2 b 2 b 2 2 2 2
f x f x 1 f x 2 1 f x 2 i
2 b 2 b
' 但f cut
fx
(fx)的截止频率为
f
' cut
2a 2 2 f cut d i b
所以正负1级强度谱可以通过， 4 像面上有条纹结构，但对比度 b 较原物为低。
B:
di:出瞳到像面的距离, λ :波长 讨论：从像强度的频谱分析入手 物A:
x t1 x cos 2 b
讨论它们在相干照明和非相干照明下成像，哪一种光照为好？
~ 2 b 基频: f 0 b 2
t1(x)
1
x x b t1 x cos 2 rect x n b b 2 2 n
#
成像质量要做具体分析, 主要从频域考虑
§3-8 相干与非相干成像系统的比较 1. 截止频率 Cutoff Frequency
OTF的截止频率是CTF截止频率的两倍。 但这并不意味着非相干照明一定比相干照明好。 不同系统的截止频率是对不同物理量传递而言的, 无法从数值上做简单比较 对于相干系统,截止频率指能够传递的复振幅呈周 期变化的最高频率。对于非相干系统，指能够传递的强度 呈余弦变化的最高频率。 对于二者的最后可观察量都是强度，因此直接对像强 度进行比较是恰当的。 但即使比较的物理量一致，也难判断绝对好坏。
对空间频率分量的传递作用: 例
非相干光照明： 物A的强度透过率：
t g x t1 x cos2 2
2
x 1 2 1 cos 2 x , b 2 b
~ 2 b f b 2
采用单位强度的平面波垂直照明， I ~ 1 1 cos(2 2 ~ ) x0 g x0 像强度就是物的强度透过率: 2 b 像的归一化强度频谱:
2
φ =0：完全不能分辨 两个点 φ =π /2：刚好能够分辨； 源的相 φ =π ：比非相干照明时 对相位 分辨得更为清楚。 差 瑞利分辨判据仅适用于 非相干成像系统
作业
设系统的出瞳是边长为2a的方形 孔径，用图解方法解例3.6题。并取 a = 5 mm, b = 0.2 mm, = 5x10-4 mm, di = 103 mm, 分别计算相干照明和非 相干照明时，像面条纹的对比度。
#
§3-8 相干与非相干成像系统的比较
2. 像强度的频谱 Frequency Spectrum of Image Intensity
像强度:
2 ~ I c ( xi , yi ) U g ( xi , yi ) h ( xi , yi ) 相干照明
I i ( xi , yi ) I g ( xi , yi ) hI ( xi , yi ) 非相干照明
2 2 comb x b b
-b/4 0 b/4
§3-8 相干与非相干成像系统的比较
对空间频率分量的传递作用: 例
t1的频谱
T1 f x
t1 x 1 f x 1 1 f x 1 b sin c b
必须注意 CTF是对物复振幅频谱的传递能力 OTF是对物强度谱的传递能力。 同一物函数若振幅谱的最高空频为f0，则强度谱的最高空频 通常为2 f0，扩展到二倍（注意有特例）。 而对于同一形状的对称光瞳（方孔或圆孔）OTF的截止频 率均为CTF的二倍。故截止频率也是相当的（注意有特例）。 但在通频带内，CTF无衰减，OTF有衰减，降低了对比度。 实际成像清晰度还与物的空间结构有关。以下例证明。
§3-8 相干与非相干成像系统的比较 Review
相干成像
i i i 像的 ~ 空 复振幅 U g ~0 , ~0 h xi ~0 , yi ~0 d~0 d~0 x y x y x y
非相干成像
U (x , y )
域
像强度 I i ( xi , yi )
U i ( xi , yi )
本章复习
基本概念 • 透镜的位相变换，透镜的傅里叶变换性质 • 衍射受限系统, 阿贝成像理论 • 相干成像系统的点扩展函数, 相干传递函数 • 非相干成像系统的点扩展函数, 光学传递函数,调制传 递函数 基本技能 • 简单孔径和光栅的夫琅和费衍射图样的计算和画图 （频谱平面） • 简单光瞳的相干/光学传递函数及相应的截止频率 综合能力 • 基于频谱分析的成像系统像质评价（相干照明、非相 干照明）
§3-8 相干与非相干成像系统的比较
对空间频率分量的传递作用: 例
A: x t1 x cos 2 b
1 2 I g ~0 1 cos(2 ~0 ) x x 2 b
对物A而言，非相干光照明优于相干照明。
原因: 此特殊物体的振幅谱与强度谱有相同的空频， 该空频高于CTF的截止频率，而低于OTF的截止频率。
#
§3-8 相干与非相干成像系统的比较
对空间频率分量的传递作用