考点点拨 考例回顾(3)
Grammar and usage

The attributive clause when, introduced by when, where and why. why.
定语从句中关系副词的用法
1. 定语从句中关系副词有: 定语从句中关系副词有: when, where, why 2. 关系副词在定语从句中所作的成份: 关系副词在定语从句中所作的成份: 关系副词在定语从句中都作状语。 关系副词在定语从句中都作状语。 when 作时间状语 where 作地点状语; ______作时间状语;______ 作地点状语; 作时间状语; why ________ 作原因状语。如: 作原因状语。
Practice two
Use proper prepositions and relative pronouns to fill in the blanks. 1. Do you like the book _________ she on which spent $10? 2. Do you like the book for which ________ she paid $10?
to whom 1. Do you know the boy________ she was talking? 2. Do you know the boy (that) she talking to was________ ? 3. The pencil (which / that) he was __________ writing with suddenly broke.
思考 是否所有的介词+关系代词都能用关系 是否所有的介词 关系代词都能用关系 副词代替? 副词代替 at which 1.The painting (________ I looked) was painted by me. about which 2.The book (___________ I heard) was written twenty years ago.
专题 概率的进一步认识章末重难点题型(举一反三)

专题概率的进一步认识章末重难点题型【举一反三】【考点1 可能性的大小】【方法点拨】可能性等于所求情况数与总情况数之比,关键是求出每种情况的可能性.【例1】(春金坛区期中)如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,估计下列4个事件发生的可能性大小,其中事件发生的可能性最大的是()A.指针落在标有5的区域内B.指针落在标有10的区域内C.指针落在标有偶数或奇数的区域内D.指针落在标有奇数的区域内【变式1-1】(春市北区期末)我国南方地区冬至的传统习俗是吃汤圆,其寓意团团圆圆冬至这一天,小红家煮了30个汤圆,其中有12个黑芝麻馅的,14个枣泥馅的,4个豆沙馅的,煮完之后的汤圆看起来都一样,小红盛了1个汤圆,下列各种描述正确的是()A.她吃到黑芝麻馅汤圆和枣泥馅汤圆可能性一样大B.她吃到枣泥馅汤圆比豆沙馅汤圆的可能性大很多C.她不可能吃到豆沙馅汤圆D.她一定能吃到枣泥馅汤圆【变式1-2】(资阳)在一个布袋中装有红、白两种颜色的小球,它们除颜色外没有任何其他区别.其中红球若干,白球5个,袋中的球已搅匀.若从袋中随机取出1个球,取出红球的可能性大,则红球的个数是()A.4个B.5个C.不足4个D.6个或6个以上【变式1-3】(张店区一模)从淄博汽车站到银泰城有甲,乙,丙三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从淄博汽车站到银泰城的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:线路/公交车用时的频数/公交车用时30≤t≤3535≤t≤4040≤t≤4545≤t≤50合计甲59 151 166 124 500乙50 50 122 278 500丙45 265 167 23 500 早高峰期间,乘坐线路上的公交车,从淄博汽车站到银泰城“用时不超过45分钟”的可能性最大.()A.甲B.乙C.丙D.无法确定【考点2 确定与不确定事件】【方法点拨】必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.【例2】(秋十堰期末)下列说法中不正确的是()A.抛掷一枚硬币,硬币落地时正面朝上是随机事件B.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件C.任意打开九年级下册数学教科书,正好是第38页是确定事件D.一个盒子中有白球m个,红球6个,黑球n个(每个除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是6【变式2-1】(春常熟市期末)下列事件中,属于必然事件的是()A.如果a,b都是实数,那么,a+b=b+aB.同时抛掷两枚质地均匀的骰子,向上一面的点数之和为13C.抛枚质地均匀的硬币20次,有10次正面向上D.用长为4cm,4cm,9cm的三条线段围成一个等腰三角形【变式2-2】(春滨湖区期末)下列事件中,属于随机事件的是()A.一组对边平行且一组对角相等的四边形是平行四边形B.一组对边平行另一组对边相等的四边形是平行四边形C.矩形的两条对角线相等D.菱形的每一条对角线平分一组对角【变式2-3】(襄城区模拟)下列事件中是不可能事件的是()A.任意画一个四边形,它的内角和是360°B.若a=b,则a2=b2C.掷一枚质地均匀的硬币,落地时正面朝上D.一只袋子里共装有3个小球,它们的标号分别为1,2,3,从中摸出一个小球,标号为5【考点3 概率与方程】【方法点拨】随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.【例3】(齐齐哈尔)在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.已知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为()A.27 B.23 C.22 D.18【变式3-1】(南安市模拟)不透明袋子中装有若干个红球和6个蓝球,这些球除了颜色外,没有其他差别,从袋子中随机摸出一个球,摸出蓝球的概率是0.6,则袋子中有红球()A.4个B.6个C.8个D.10个【变式3-2】(大洼区三模)在一个不透明的袋中有4个白球和n个黄球,它们除颜色外其余均相同.若从中随机摸出一个球,摸到黄球的概率为,则n=()A.10 B.8 C.6 D.4【变式3-3】(厦门一模)一个不透明盒子里装有a只白球、b只黑球、c只红球,这些球仅颜色不同.从中随机摸出一只球,若P(摸出白球)=,则下列结论正确的是()A.a=1 B.a=3 C.a=b=c D.a=(b+c)【考点4 几何概型】【方法点拨】如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型。
专题03 全等三角形章末重难点题型提高练习(举一反三)

专题03 全等三角形章末重难点题型汇编【举一反三】【人教版】【考点1 利用全等三角形的性质求角】【方法点拨】全等三角形的性质:(1)全等三角形的对应边相等、对应角相等;(2)全等三角形的周长相等、面积相等;(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
【例1】(2019春•临安区期中)如图,△ACB≌△A′CB′,∠ACB=70°,∠ACB′=100°,则∠BCA′的度数为()A.30°B.35°C.40°D.50°【变式1-1】(2018秋•绍兴期末)如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是()A.55°B.60°C.65°D.70°【变式1-2】(2018秋•厦门期末)如图,点F,C在BE上,△ABC≌△DEF,AB和DE,AC和DF是对应边,AC,DF交于点M,则∠AMF等于()A.2∠B B.2∠ACB C.∠A+∠D D.∠B+∠ACB【变式1-3】(2018秋•桐梓县校级期中)如图,△ABC≌△A′B′C,∠ACB=90°,∠B=50°,点B′在线段AB上,AC,A′B′交于点O,则∠COA′的度数是()A.50°B.60°C.70°D.80°【考点2 全等三角形的判定条件】【方法点拨】寻找并证明全等三角形还缺少的条件,其基本思路是:(1)有两边对应相等,找夹角对应相等,或第三边对应相等.前者利用SAS判定,后者利用SSS判定. (2)有两角对应相等,找夹边对应相等,或任一等角的对边对应相等.前者利用ASA判定,后者利用AAS 判定.(3)有一边和该边的对角对应相等,找另一角对应相等.利用AAS判定.(4)有一边和该边的邻角对应相等,找夹等角的另一边对应相等,或另一角对应相等.前者利用SAS判定,后者利用AAS判定.【例2】(2019春•沙坪坝区校级期中)如图,在△ABC和△AED中,已知∠1=∠2,AC=AD,添加一个条件后,仍然不能证明△ABC≌△AED,这个条件是()A.AB=AE B.BC=ED C.∠C=∠D D.∠B=∠E【变式2-1】(2019秋•潘集区期中)在△ABC与△DEF中,给出下列四组条件:(1)AB=DE,AC=DF,BC=EF(2)AB=DE,∠B=∠E,BC=EF(3)∠B=∠E,BC=EF,∠C=∠F(4)AB=DE,∠B=∠E,AC=DF,其中能使△ABC≌△DEF的条件共有()A.1组B.2组C.3组D.4组【变式2-2】(2018春•渝中区校级期中)如图,点B、F、C、E在一条直线上,∠A=∠D,∠B=∠E,再添一个条件仍不能证明△ABC≌△DEF的是()A.AB=DE B.BC=EF C.∠ACB=∠DFE D.AC=DF【变式2-3】(2018秋•鄂尔多斯期中)如图,已知AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加一个条件,则下列所添条件不恰当的是()A.BD=CE B.∠ABD=∠ACE C.∠BAD=∠CAE D.∠BAC=∠DAE【考点3 全等三角形判定的应用】【方法点拨】解决此类题型的关键是理解题意,利用全等三角形的判定.【例3】(2019春•郓城县期末)如图所示,要测量河两岸相对的两点A、B的距离,因无法直接量出A、B 两点的距离,请你设计一种方案,求出A、B的距离,并说明理由.【变式3-1】(2019春•峄城区期末)如图,点C、E分别在直线AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结CF,再找出CF 的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.小华的想法对吗?为什么?【变式3-2】(2019春•槐荫区期末)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.【变式3-3】如图,两根长12m的绳子,一端系在旗杆上的同一位置,另一端分别固定在地面上的两个木桩上(绳结处的误差忽略不计),现在只有一把卷尺,如何来检验旗杆是否垂直于地面?请说明理由.【考点4 利用AAS证明三角形全等】【方法点拨】两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)【例4】(2018秋•仙游县期中)如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC ≌△BEC(不添加其他字母及辅助线),你添加的条件是.并证明结论.【变式4-1】(2018春•揭西县期末)如图,∠ABC=∠ACB,∠ADE=∠AED,BE=CD,试说明:△ABD≌△ACE.【变式4-2】(2018秋•杭州期中)如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE.【变式4-3】(2018•雁塔区校级二模)如图,在四边形ABCD中,点E在AD上,其中∠BAE=∠BCE=∠ACD =90°,且BC=CE,求证:△ABC≌△DEC.【考点5 利用SAS证明三角形全等】【方法点拨】两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)【例5】(2018春•金山区期末)如图,已知CA=CD,CB=CE,∠ACB=∠DCE,试说明△ACE≌△DCB的理由.【变式5-1】(2018春•黄岛区期末)如图,点E在AB上,AC=AD,∠CAB=∠DAB,那么△BCE和△BDE全等吗?请说明理由.【变式5-2】(2018秋•仪征市校级月考)如图,已知点B、F、C、E在同一直线上,AC、DF相交于点G,AB ⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE,说明△ABC与△DEF全等的理由.【变式5-3】(2019秋•东莞市校级月考)如图:△ABC和△EAD中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.求证:△ABD≌△AEC.【考点6 利用ASA证明三角形全等】【方法点拨】两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)【例6】(2019秋•利辛县期末)如图,已知AB=AC,∠ABE=∠ACD,BE与CD相交于O,求证:△ABE≌△ACD.【变式6-1】(2018•双柏县二模)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED;【变式6-2】(2019•陕西模拟)如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC≌△DEC.【变式6-3】(2019秋•乐清市校级期中)如图,△ABC的两条高AD、BE相交于点H,且AD=BD,求证:△BDH≌△ADC.【考点7 利用SSS证明三角形全等】【方法点拨】三边对应相等的两个三角形全等(可简写成“SSS”)【例7】(2019春•渝中区校级月考)如图,AB=CD,AE=CF,E、F是BD上两点,且BF=DE.求证:△ABE≌△CDF.【变式7-1】(2019秋•扶余县校级月考)如图,在△ABC中,AD=AE,BE=CD,AB=AC.(1)求证:△ABD≌△ACE;(2)求证:∠BAE=∠CAD.【变式7-2】(2019秋•保亭县校级月考)如图,AB=AD,DC=BC,∠B与∠D相等吗?为什么?【变式7-3】(2019秋•蓬江区校级期末)如图,在△ABC中,∠C=90°,D、E分别为AC、AB上的点,且AD=BD,AE=BC,DE=DC,求证:DE⊥AB.【考点8 利用HL证明三角形全等】【方法点拨】对于特殊的直角三角形,判定它们全等时,还有HL定理(斜边、直角边定理):有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”)【例8】(2018秋•思明区校级月考)如图,在四边形ABCD中,AD⊥BD,AC⊥CB,BD=AC.求证:△ABD ≌△BAC;【变式8-1】(2019秋•睢宁县校级月考)如图,Rt△ABC中,∠C=90°,BC=2,一条直线MN=AB,M、N分别在AC和过点A且垂直于AC的射线AP上运动.问点M运动到什么位置,才能使△ABC和△AMN 全等?并证明你的结论.【变式8-2】(2019秋•合浦县期末)如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.【变式8-3】(2019春•醴陵市期末)如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点E,AF⊥CD交CD的延长线于点F.求证:△ABE≌△ADF.【考点9 全等三角形的判定与性质综合】【例9】(2019•南岸区)如图,在△ABC和△ABD中,∠BAC=∠ABD=90°,点E为AD边上的一点,且AC=AE,连接CE交AB于点G,过点A作AF⊥AD交CE于点F.(1)求证:△AGE≌△AFC;(2)若AB=AC,求证:AD=AF+BD.【变式9-1】(2019•福州模拟)(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA =∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由.【变式9-2】(2018秋•天台县期末)如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,若AD=a,DE=b,(1)如图1,求BE的长,写出求解过程;(用含a,b的式子表示)(2)如图2,点D在△ABC内部时,直接写出BE的长.(用含a,b的式子表示)【变式9-3】(2019春•道外区期末)如图,四边形ABCD中,∠ABC=∠BCD=90°,点E在BC边上,∠AED =90°(1)求证:∠BAE=∠CED;(2)若AB+CD=DE,求证:AE+BE=CE;(3)在(2)的条件下,若△CDE与△ABE的面积的差为18,CD=6,求BE的长.【考点10 动点问题中的全等三角形应用】【例10】(2019春•平川区期末)如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP 全等?【变式10-1】(2019春•永新县期末)△ABC中,AB=AC,∠A=40°,D、E分别是AB,AC上的不动点.且BD+CE=BC,点P是BC上的一动点.(1)当PC=CE时(如图1),求∠DPE的度数;(2)若PC=BD时(如图2),求∠DPE的度数还会与(1)的结果相同吗?若相同,请写出求解过程;若不相同,请说明理由.【变式10-2】(2019春•宝安区期中)如图,在四边形ABCD中,AD=BC=10,AB=CD,BD=14,点E从D 点出发,以每秒2个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒5个单位的速度沿C →B→C,作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.(1)试证明:AD∥BC;(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.【变式10-3】(2018秋•十堰期末)在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.(1)如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE=.(2)设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.【考点1 利用全等三角形的性质求角】【方法点拨】全等三角形的性质:(1)全等三角形的对应边相等、对应角相等;(2)全等三角形的周长相等、面积相等;(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
数的开方知识点章末重难点题型(举一反三)
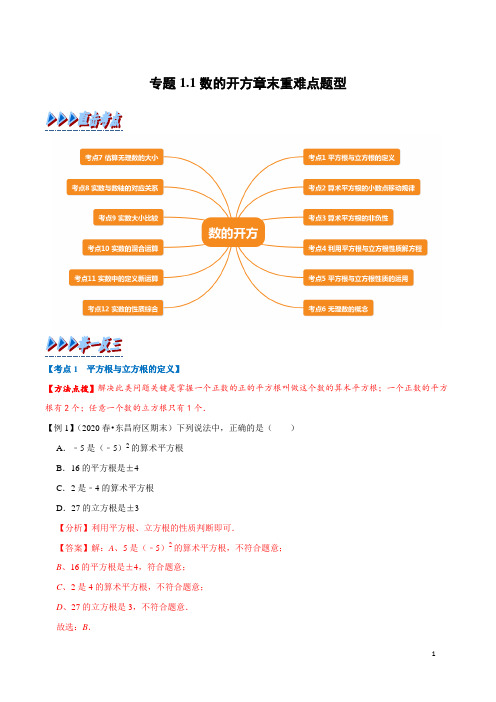
专题1.1数的开方章末重难点题型【考点1 平方根与立方根的定义】【方法点拨】解决此类问题关键是掌握一个正数的正的平方根叫做这个数的算术平方根;一个正数的平方根有2个;任意一个数的立方根只有1个.【例1】(2020春•东昌府区期末)下列说法中,正确的是()A.﹣5是(﹣5)2的算术平方根B.16的平方根是±4C.2是﹣4的算术平方根D.27的立方根是±3【分析】利用平方根、立方根的性质判断即可.【答案】解:A、5是(﹣5)2的算术平方根,不符合题意;B、16的平方根是±4,符合题意;C、2是4的算术平方根,不符合题意;D、27的立方根是3,不符合题意.故选:B.【点睛】此题考查了立方根,平方根,以及算术平方根,熟掌握各自的性质是解本题的关键. 【变式1-1】(2020春•南昌期末)下列结论中,其中正确的是( ) A .√81的平方根是±9 B .√100=±10C .立方根等于本身的数只有0.1D .√−63=−√63【分析】根据平方根,立方根的定义逐项计算可判断求解.【答案】解:A .∵√81=9,9的平方根为±3,∴√81的平方根为±3,故原说法错误; B .√100=10,故原说法错误;C .立方根等于本身的数只有0,﹣1,1,故原说法错误;D .√−63=−√63,故原说法正确. 故选:D .【点睛】本题主要考查平方根,立方根,根据平方根及立方根的定义逐项计算可判断求解. 【变式1-2】(2020春•海安市期中)下列说法:①±3都是27的立方根;②116的算术平方根是±14;③−√−83=2;④√16的平方根是±4;⑤﹣9是81的算术平方根,其中正确的有( ) A .1个B .2个C .3个D .4个【分析】根据平方根,算术平方根,立方根的定义找到错误选项即可. 【答案】解:①3是27的立方根,原来的说法错误; ②116的算术平方根是14,原来的说法错误;③−√−83=2是正确的;④√16=4,4的平方根是±2,原来的说法错误; ⑤9是81的算术平方根,原来的说法错误. 故其中正确的有1个. 故选:A .【点睛】考查立方根,平方根,算术平方根的知识;用到的知识点为:一个正数的正的平方根叫做这个数的算术平方根;一个正数的平方根有2个;任意一个数的立方根只有1个. 【变式1-3】(2020春•沭阳县期末)下列说法正确的是( ) A .若√a 2=−a ,则a <0B .若√a 2=a ,则a >0C.√a4b8=a2b4D.3的平方根是√3【分析】根据平方根和算术平方根的定义分别对每一项进行分析,即可得出答案.【答案】解:A、若√a2=−a,则a≤0,故本选项错误;B、若√a2=a,则a≥0,故本选项错误;C、√a4b8=a2b4,故本选项正确;D、3的平方根是±√3,故本选项错误;故选:C.【点睛】此题考查了平方根和算术平方根,熟练掌握平方根和算术平方根定义是解本题的关键.【考点2算术平方根的小数点移动规律】【方法点拨】解决此类问题关键是掌握一个被开方数的小数点向左或向右移动两位,它的算术平方根的小数点就相应地向左或向右移动1位;【例2】(2020春•嘉祥县期末)由√3≈1.732,得√300≈17.32,则√0.03≈,√30000≈.从以上结果可以发现,被开方数的小数点向左或向右移动位,它的算术平方根的小数点就相应地向左或向右移动1位.【分析】根据算术平方根的定义进行解答即可.【答案】解:∵√300≈17.32,∴√0.03≈0.1732,√30000≈173.2,从以上结果可以发现,被开方数的小数点向左或向右移动两位,它的算术平方根的小数点就相应地向左或向右移动1位;故答案为:0.1732,173.2,两.【点睛】此题考查了算术平方根的定义,掌握算术平方根的定义是本题的关键.【变式2-1】(2020春•海淀区校级期末)如表所示,被开方数a的小数点位置移动和它的算术平方根√a的小数点位置移动规律符合一定的规律,若√a=180,且−√3.24=−1.8,则被开方数a的值为.a…0.0000010.011100100001000000…√a…0.0010.11101001000…【分析】根据题意和表格中数据的变化规律,可以求得a的值.【答案】解:∵√a=180,且−√3.24=−1.8,∴√3.24=1.8,∴√32400=180,∴a =32400, 故答案为:32400.【点睛】本题考查算术平方根,解答本题的关键是明确算术平方根的定义,求出相应的a 的值. 【变式2-2】(2020春•唐县期末)若√25.36=5.036,√253.6=15.906,则√253600=( ) A .50.36B .503.6C .159.06D .1.5906【分析】根据已知等式,利用算术平方根定义判断即可得到结果. 【答案】解:∵√25.36=5.036,∴√253600=√25.36×√10000=5.036×100=503.6, 故选:B .【点睛】本题考查了算术平方根.解题的关键是掌握算术平方根的定义以及算术平方根的被开方数小数点移动的规律.【变式2-3】(2020春•杭州期中)设√5=m ,√7=n ,则√0.056可以表示为( ) A .mn 25B .mn 20C .mn 15D .mn 10【分析】首先把小数化为分数,为便于开方根据分数基本性质,分子分母同时扩大10倍,再根据二次根式的性质与化简,即可求得结论.【答案】解:√0.056=√561000=√56010000=√560100=√16×5×7100=4×√5×√7100=mn25; 故选:A .【点睛】本题考查了二次根式的性质与化简,解决本题的关键是二次根式化简时把小数化为分数,注意尝试怎样拆分数据可简便运算. 【考点3算术平方根的非负性】【方法点拨】解决此类问题关键是掌握算术平方根,绝对值,偶次乘方均具有非负性.【例3】(2020春•滨城区期末)若实数x ,y 满足|x ﹣3|+√=0,则(x +y )3的平方根为( ) A .4B .8C .±4D .±8【分析】利用绝对值的性质以及二次根式的性质得出x ,y 的值,进而利用平方根的定义得出答案. 【答案】解:∵|x ﹣3|+√y −1=0, ∴x ﹣3=0,y ﹣1=0, ∴x =3,y =1,则(x +y )3=(3+1)3=64,64的平方根是:±8.故选:D.【点睛】此题主要考查了算术平方根以及绝对值的性质,正确把握相关定义是解题的关键.【变式3-1】(2019春•潍城区期中)已知实数x和y满足√x2−4+(y3+8)2=0,则x+y的值为()A.0B.﹣4C.0或﹣4D.±4【分析】根据非负数的性质即可求出答案.【答案】解:由题意可知:x2﹣4=0,y3+8=0,∴x=±2,y=﹣2,∴x+y=0或﹣4,故选:C.【点睛】本题考查非负数的性质,解题的关键是熟练运用非负数的性质,本题属于基础题型.【变式3-2】(2020春•海勃湾区期末)已知(2a+b)2与√3b+12互为相反数,则b a=.【分析】根据相反数的概念列出算式,根据非负数的性质求出a、b的值,计算即可.【答案】解:由题意得,(2a+b)2+√3b+12=0,则2a+b=0,3b+12=0,解得,a=2,b=﹣4,则b a=(﹣4)2=16,故答案为:16.【点睛】本题考查了非负数的性质和相反数,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.【变式3-3】(2020春•竹溪县期末)已知:实数a、b满足关系式(a﹣2)2+|b+√3|+√2009−c=0,求:b a+c+8的值.【分析】根据算术平方根,绝对值,偶次方的非负性求解a,b,c的值,再代入计算即可求解.【答案】解:由题意得a−2=0,b+√3=0,2009−c=0,解得a=2,b=−√3,c=2009,∴b a+c+8=(−√3)2+2009+8=2020.【点睛】本题主要考查算术平方根,绝对值,偶次方的非负性,代数式求值,求解a,b,c的值是解题的关键.【考点4利用平方根与立方根性质解方程】【方法点拨】解决此类问题关键是注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.立方根的性质:一个正数的立方根式正数,一个负数的立方根是负数,0的立方根式0. 【例4】(2020春•广丰区期末)计算下列各式的x 的值: (1)12x 2=8;(2)13(x +1)3=﹣9.【分析】(1)方程变形后,利用平方根定义开方即可求出解; (2)方程利用立方根的定义化简即可求出解. 【答案】解:(1)方程变形得:x 2=16, 开方得:x =±4;(2)方程变形得:(x +1)3=﹣27, 开立方得:x +1=﹣3, 解得:x =﹣4.【点睛】此题考查了立方根,以及平方根,熟练掌握各自的定义是解本题的关键. 【变式4-1】(2020春•越秀区期末)求下列各式中x 的值 (1)25x 2=4; (2)(x +1)3=﹣27.【分析】(1)根据等式的性质,可得平方的形式,根据开方运算,可得答案; (2)根据开立方运算,可得一元一次方程,根据解方程,可得答案. 【答案】解:(1)方程两边都除以25,得 x 2=425, 开方得, x =±25;(2)开立方得, x +1=﹣3, 移项得, x =﹣4.【点睛】本题主要考查立方根和平方根的知识点,解答本题的关键是注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.立方根的性质:一个正数的立方根式正数,一个负数的立方根是负数,0的立方根式0.【变式4-2】(2020春•蕲春县期中)求下列各式中的x : (1)4(x +2)2﹣16=0; (2)(2x ﹣1)3+2627=1. 【分析】(1)先求出(x +2)的值,然后解方程即可; (2)求出(2x ﹣1)的值,解方程即可得出x 的值. 【答案】解:(1)由题意得,4(x +2)2=16, ∴(x +2)2=4, ∴x +2=±2, 解得x =0或﹣4;(2)由题意得,(2x ﹣1)3=127, ∴2x ﹣1=13, ∴x =23.【点睛】此题考查了平方根的知识,属于基础题,解答本题的关键是掌握一个正数的平方根有两个,不要漏解.【变式4-3】(2020春•西城区校级期中)解方程: (1)(x ﹣4)2=6; (2)13(x +3)3−9=0.【分析】(1)根据平方根的定义解答即可;(2)把方程整理为(x +3)3=27,再根据立方根的定义解答即可. 【答案】解:(1)(x ﹣4)2=6, x −4=±√6,∴x =4+√6或x =4−√6;(2)13(x +3)3−9=0,13(x +3)3=9,(x+3)3=27,3,x+3=√27x+3=3,∴x=0.【点睛】本题主要考查了平方根与立方根,注意一个正数有两个平方根,它们互为相反数.【考点5平方根与立方根性质的运用】【方法点拨】解决此类问题关键是注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.立方根的性质:一个正数的立方根是正数,一个负数的立方根是负数,0的立方根式0.【例5】(2020春•石城县期末)已知4a+1的平方根是±3,b﹣1的算术平方根为2.(1)求a与b的值;(2)求2a+b﹣1的立方根.【分析】(1)首先根据4a+1的平方根是±3,可得:4a+1=9,据此求出a的值是多少;然后根据b﹣1的算术平方根为2,可得:b﹣1=4,据此求出b的值是多少即可.(2)把(1)中求出的a与b的值代入2a+b﹣1,求出算术的值是多少,进而求出它的立方根是多少即可.【答案】解:(1)∵4a+1的平方根是±3,∴4a+1=9,解得a=2;∵b﹣1的算术平方根为2,∴b﹣1=4,解得b=5.(2)∵a=2,b=5,∴2a+b﹣1=2×2+5﹣1=8,3=2.∴2a+b﹣1的立方根是:√8【点睛】此题主要考查了立方根、平方根、算术平方根的含义和求法,要熟练掌握.【变式5-1】(2020春•安定区期末)已知4a+7的立方根是3,2a+2b+2的算术平方根是4.(1)求a,b的值;(2)求6a+3b的平方根.【分析】(1)运用立方根和算术平方根的定义求解.(2)根据平方根,即可解答.【答案】解:(1)∵4a+7的立方根是3,2a+2b+2的算术平方根是4,∴4a+7=27,2a+2b+2=16,∴a=5,b=2;(2)由(1)知a=5,b=2,∴6a+3b=6×5+3×2=36,∴6a+3b的平方根为±6.【点睛】本题考查了平方根、算术平方根,解决本题的关键是熟记平方根、算术平方根的定义.【变式5-2】(2020春•盐池县期末)已知2a+1的平方根是±3,3a+2b﹣4的立方根是﹣2,求4a﹣5b+8的立方根.【分析】先根据平方根,立方根的定义列出关于a、b的二元一次方程组,再代入进行计算求出4a﹣5b+8的值,然后根据立方根的定义求解.【答案】解:∵2a+1的平方根是±3,3a+2b﹣4的立方根是﹣2,∴2a+1=9,3a+2b﹣4=﹣8,解得a=4,b=﹣8,∴4a﹣5b+8=4×4﹣5×(﹣8)+8=64,∴4a﹣5b+8的立方根是4.【点睛】本题考查了平方根,立方根的定义,列式求出a、b的值是解题的关键.【变式5-3】(2020春•汉川市期末)已知3a+4a+5a+6a+7a+8a=165,且a+11的算术平方根是m,5a+2的立方根是n.求n m的平方根.【分析】先由3a+4a+5a+6a+7a+8a=165,即33a=165得出a=5,再结合a+11的算术平方根是m,5a+2的立方根是n得出m、n的值,代入求解可得.【答案】解:∵3a+4a+5a+6a+7a+8a=165,即33a=165,∴a=5,又a+11的算术平方根是m,即16的算术平方根是m,∴m=4,∵5a +2的立方根是n ,即27的立方根是n , ∴n =3,则n m =34=81的平方根为±9.【点睛】本题主要考查立方根,解题的关键是掌握立方根、平方根及算术平方根的定义. 【考点6无理数的概念】【方法点拨】解决此类问题关键是掌握无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,√2,0.8080080008…(每两个8之间依次多1个0)等形式. 【例6】(2020春•陇西县期末)在以下实数227,3.14159265,√93,√36,π3中,无理数的个数为( )A .1个B .2个C .3个D .4个【分析】根据无理数是无限不循环小数,可得答案. 【答案】解:227是分数,属于有理数;3.14159265是有限小数,属于有理数; √36=6,是整数,属于有理数; 无理数有:√93,π3共2个.故选:B .【点睛】此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,√2,0.8080080008…(每两个8之间依次多1个0)等形式.【变式6-1】(2020春•崇川区校级期末)在√16,−π2,﹣5.1⋅8⋅,−√93,47,0.317311731117…,这几个数中,无理数的个数是( ) A .1B .2C .3D .4【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【答案】解:√16=4,是整数,属于有理数;−5.1.8.是循环小数,属于无理数;47是分数,属于有理数;无理数有:−π2,−√93,0.317311731117…共3个.故选:C.【点睛】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.【变式6-2】(2020•开平区一模)如图是一个无理数生成器的工作流程图,根据该流程图,下面说法:①当输出值y为√3时,输入值x为3或9;②当输入值x为16时,输出值y为√2;③对于任意的正无理数y,都存在正整数x,使得输入x后能够输出y;④存在这样的正整数x,输入x之后,该生成器能够一直运行,但始终不能输出y值.其中错误的是()A.①②B.②④C.①④D.①③【分析】根据运算规则即可求解.【答案】解:①x的值不唯一.x=3或x=9或81等,故①说法错误;②输入值x为16时,√16=4,√4=2,即y=√2,故②说法正确;③对于任意的正无理数y,都存在正整数x,使得输入x后能够输出y,如输入π2,故③说法错误;④当x=1时,始终输不出y值.因为1的算术平方根是1,一定是有理数,故④原说法正确.其中错误的是①③.故选:D.【点睛】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.【变式6-4】(2019春•南昌期中)如图是一个无理数筛选器的工作流程图.(1)当x为16时,y值为;(2)是否存在输入有意义的x值后,却输不出y值?如果存在,写出所有满足要求的x值;如果不存在,请说明理由;(3)当输出的y值是√3时,判断输入的x值是否唯一,如果不唯一,请写出其中的两个.【分析】(1)根据运算规则即可求解;(2)根据0的算术平方根是0,即可判断;(3)根据运算法则,进行逆运算即可求得无数个满足条件的数.【答案】解:(1)当x=16时,√16=4,√4=2,故y值为√2.故答案为:√2;(2)当x=0,1时,始终输不出y值.因为0,1的算术平方根是0,1,一定是有理数;(3)x的值不唯一.x=3或x=9.【点睛】本题考查了二次根式有意义的条件,正确理解给出的运算方法是关键.【考点7估算无理数的大小】【方法点拨】解决此类问题关键是掌握无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,√2,0.8080080008…(每两个8之间依次多1个0)等形式.【例7】(2020•玄武区二模)下列整数中,与6−√11最接近的是()A.2B.3C.4D.5【分析】用逼近法即可进行无理数大小的估算.【答案】解:∵9<11<16,∴3<√11<4,∵3.52=12.25>11,∴3<√11<3.5∴2.5<6−√11<3.∴与6−√11最接近的是3.故选:B.【点睛】本题考查了估算无理数的大小,估算无理数大小要用逼近法.【变式7-1】(2020•福州模拟)若a<√28−√7<a+1,其中a为整数,则a的值是()A.1B.2C.3D.4【分析】先把√28−√7化简,再估算√7的范围即可.【答案】解:√28−√7=2√7−√7=√7,∵22<7<32,∴2<√7<3,∵a<√28−√7<a+1,其中a为整数,∴a=2.故选:B.【点睛】此题主要考查了估算无理数的大小,正确估算√7的范围是解答本题的关键.【变式7-2】(2020春•郯城县期中)阅读下面的文字,解答问题,例如:∵√4<√7<√9,即2<√7<3,∴√7的整数部分为2,小数部分为(√7−2).请解答:(1)√17的整数部分是,小数部分是.(2)已知:5−√17小数部分是m,6+√17小数部分是n,且(x+1)2=m+n,请求出满足条件的x的值.【分析】(1)直接利用估算无理数的大小的方法分别得出答案;(2)直接利用(1)中所求即可得出m,n的值,进而得出x的值.【答案】解:(1)∵√16<√17<√25,∴4<√17<5,∴√17的整数部分是:4,小数部分是:√17−4;故答案为:4,√17−4;(2)∵5−√17小数部分是m,6+√17小数部分是n,∴m=5−√17,n=6+√17−10=√17−4,∴m+n=1,∴(x+1)2=1,解得:x=0或﹣2.【点睛】此题主要考查了估算无理数的大小,正确得出无理数的取值范围是解题关键.【变式7-3】(2020春•延平区期中)阅读下面的文字,解答问题.大家知道√2是无理数,而无理数是无限不循环小数,因此√2的小数部分我们不可能全部地写出来,于是小明用√2−1来表示√2的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为√2的整数部分是1,将这个数减去其整数部分,差就是小数部分.请解答:(1)若√13的整数部分为a,小数部分为b,求a2+b−√13的值.(2)已知:10+√3=x+y,其中x是整数,且0<y<1,求x﹣y的值.【分析】(1)先估算出√13的范围,求出a、b的值,再代入求出即可;(2)先估算出√3的范围,再求出x、y的值,再代入要求的式子进行计算即可.【答案】解:(1)∵3<√13<4,∴a=3,b=√13−3,∴a2+b−√13=32+√13−3−√13=6;(2)∵1<√3<2,又∵10+√3=x+y,其中x是整数,且0<y<1,∴x=11,y=√3−1,∴x﹣y=11﹣(√3−1)=12−√3.【点睛】本题考查了估算无理数的大小,能估算出√13,√3的范围是解此题的关键.【考点8实数与数轴的对应关系】【例8】(2020春•孟村县期中)如图,在数轴上,AB=AC,A,B两点对应的实数分别是√3和﹣1,则点C 对应的实数是()A.2√3B.2√3−2C.√3+1D.2√3+1【分析】求出AB的距离,再求出点C所表示的数.【答案】解:AB =√3−(﹣1)=√3+1,∵AB =AC ,A 所表示的实数为√3,点C 在点A 的右侧, ∴点C 所表示的数为:√3+(√3+1)=2√3+1, 故选:D .【点睛】考查数轴表示数的意义,理解绝对值的意义是解决问题的前提,【变式8-1】(2020春•西城区校级期中)如图,3,√11在数轴上的对应点分别为C ,B ,点C 是AB 的中点,则点A 表示的数是( )A .−√11B .3−√11C .√11−3D .6−√11【分析】设点A 表示的数是x ,再根据中点坐标公式即可得出x 的值. 【答案】解:设点A 表示的数是x ,∵数轴上表示3、√11的对应点分别为C 、B ,点C 是AB 的中点, ∴√11+x2=3, 解得x =6−√11. 故选:D .【点睛】本题考查的是实数与数轴,熟知数轴上的点与实数是一一对应关系是解答此题的关键. 【变式8-2】(2019秋•桂林期末)在数轴上,点A 表示实数3,以点A 为圆心,2+√5的长为半径画弧,交数轴于点C ,则点C 表示的实数是( ) A .5+√5B .1−√5C .√5−1或5+√5D .1−√5或5+√5【分析】在数轴上利用左减右加的规律计算点C 表示的实数. 【答案】解:根据题意得:3+2+√5=5+√5,3﹣(2+√5)=1−√5, 则点C 表示的实数是5+√5或1−√5, 故选:D .【点睛】此题考查了实数与数轴,熟练掌握左减右加的规律是解本题的关键.【变式8-3】(2020春•定州市校级期末)如图,一只蚂蚁从点A 沿数轴向右直爬2个单位长度到达点B ,点A 表示−√2,设点B 所表示的数为m . (1)求m 的值. (2)求|m ﹣1|+m +6的值.【分析】(1)根据正负数的意义计算;(2)根据绝对值的意义和实数的混合运算法则计算.【答案】解:(1)由题意A 点和B 点的距离为2,A 点的坐标为−√2,因此B 点坐标m =2−√2. (2)把m 的值代入得:|m ﹣1|+m +6 =|2−√2−1|+2−√2+6, =|1−√2|+8−√2, =√2−1+8−√2, =7.【点睛】本题考查了数轴、绝对值和实数的混合运算,熟练掌握数轴的意义和实数的运算法则是解题的关键.【考点9实数大小比较】【例9】(2020春•西城区校级期中)比较下列实数的大小(填上>、<或=). ①π 3.14159;②√5034;③√22 √33. 【分析】根据实数大小比较的法则进行比较即可. 【答案】解:①π>3.14159;②∵4=√643∴√503<4; ③(√22)2=12,(√33)2=13,∵12>13, ∴√22>√33. 故答案为:>;<;>.【点睛】此题主要考查了实数的比较大小,关键是掌握正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小.【变式9-1】(2019秋•沧州期末)5−√2,2+√52,2+√2的大小关系是( )A .2+√2>2+√52>5−√2 B .5−√2>2+√52>2+√2C .2+√52>5−√2>2+√2 D .5−√2>2+√2>2+√52【分析】先根据√52<√2,利用不等式的性质可以判断第2个和第3个数的大小,最后由作差法可得第一个数和第3个数的大小. 【答案】解:∵5<8, ∴√5<√8, ∴√52<√2, ∴2+√52<2+√2,∵(5−√2)﹣(2+√2)=3﹣2√2>0, ∴5−√2>2+√2>2+√52; 故选:D .【点睛】本题考查了实数大小的比较,先观察每个数的特点,常利用作差法,不等式的性质,作商法,数轴法等比较两个数的大小.【变式9-2】(2020春•文登区期中)已知0<x <1,则√x 、1x 、x 2、x 的大小关系是( )A .√x <x 2<x <1xB .x <x 2<1x<√xC .x 2<x <√x <1xD .1x<√x <x 2<x【分析】根据0<x <1,可得:0<x 2<x <√x <1,1x>1,据此判断即可.【答案】解:∵0<x <1, ∴0<x 2<x <√x <1,1x >1,∴x 2<x <√x <1x. 故选:C .【点睛】此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.【变式9-3】(2020•黄州区校级模拟)已知min {√x ,x 2,x }表示取三个数中最小的那个数,例如:当x =9,min {√x ,x 2,x }=min {√9,92,9}=3﹒当min {√x ,x 2,x }=116时,则x 的值为( ) A .116B .18C .14D .12【分析】本题分别计算√x=116,x2=116,x=116的x值,找到满足条件的x值即可.首先从x的值代入来求,由x≥0,则x=01,2,3,4,5,则可知最小值是0,最大值是6.【答案】解:当√x=116时,x=1256,x<√x,不合题意;当x2=116时,x=±14,当x=−14时,x<x2,不合题意;当x=14时,√x=12,x2<x<√x,符合题意;当x=116时,x2=1256,x2<x,不合题意,故选:C.【点睛】本题主要考查实数大小比较,算术平方根及其最值问题,解决此题时,注意分类思想的运用.【考点10实数的混合运算】【方法点拨】在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.正确化简各数是解题关键.【例10】(2020春•巩义市期末)计算﹣12﹣(﹣2)3×18+√−273×|−13|+|1−√3|【分析】直接利用立方根以及对值的性质分别化简得出答案.【答案】解:原式=﹣1+8×18−3×13+√3−1=﹣1+1﹣1+√3−1=√3−2.【点睛】此题主要考查了实数运算,正确化简各数是解题关键.【变式10-1】(2020春•孝南区期末)计算:3×(√4−√3)×√1−19 273−|√3−2|【分析】直接利用立方根的性质、二次根式的性质分别化简得出答案.【答案】解:原式=3×(2−√3)×23−(2−√3)=4﹣2√3−2+√3=2−√3.【点睛】此题主要考查了实数运算,正确化简各数是解题关键.【变式10-2】(2020春•潮南区期末)计算:(﹣1)2020+(﹣2)3×18−√−273×(−√19).【分析】首先计算乘方、开方,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.【答案】解:(﹣1)2020+(﹣2)3×18−√−273×(−√19)=1+(﹣8)×18−(﹣3)×(−13) =1﹣1﹣1 =﹣1.【点睛】此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.正确化简各数是解题关键.【变式10-3】(2020春•营山县期末)计算:√−83−√1−1625+|2−√5|+√(−4)2 【分析】直接利用立方根以及二次根式的性质、绝对值的性质分别化简得出答案. 【答案】解:原式=﹣2−35+√5−2+4 =−35+√5.【点睛】此题主要考查了实数运算,正确化简各数是解题关键. 【考点11实数中的定义新运算】【例11】(2020•青海)对于任意两个不相等的数a ,b ,定义一种新运算“⊕”如下:a ⊕b =√a+b √a−b,如:3⊕2=√3+23−2=√5,那么12⊕4= .【分析】先依据定义列出算式,然后再进行计算即可. 【答案】解:12⊕4=√12+4√12−4=√2.故答案为:√2.【点睛】本题主要考查的是算术平方根的性质,根据定义运算列出算式是解题的关键. 【变式11-1】(2020春•房县期末)对于能使式子有意义的有理数a ,b ,定义新运算:a △b =3a+ba−3b.如果|x +1|+√y −3+|xz +2|=0,则x △(y △z )= .【分析】先根据绝对值、二次根式的非负性,求出x 、y 、z 的值,再根据新运算的规定计算x △(y △z )的值.【答案】解:∵|x +1|≥0,√y −3≥0,|xz +2|≥0, 又∵|x +1|+√y −3+|xz +2|=0, ∴|x +1|=0,√y −3=0,|xz +2|=0.∴x +1=0,y ﹣3=0,xz +2=0. ∴x =﹣1,y =3,z =2. ∵y △z =3y+z3−3z =−113. x △(y △z )=﹣1△(−113)=3×(−1)−113−1−3×(−113)=−20310=−23. 故答案为:−23.【点睛】本题考查了绝对值、二次根式的非负性及实数的混合运算,理解并运用新定义运算的规定是解决本题的关键.【变式11-2】(2020春•西城区校级期中)对任意两个实数a ,b 定义两种运算:a ⊕b ={a(若a ≥b)b(若a <b),a ⊗b ={b(若a ≥b)a(若a <b),并且定义运算顺序仍然是先做括号内的,例如(﹣2)⊕3=3,(﹣2)⊗3=﹣2,((﹣2)⊕3)⊗2=2.那么(√5⊕2)⊗√273等于( ) A .3√5B .3C .√5D .6【分析】直接利用已知运算公式进而分析得出答案. 【答案】解:(√5⊕2)⊗√273=√5⊗√273=√5⊗3 =√5. 故选:C .【点睛】此题主要考查了实数运算,正确运用公式是解题关键.【变式11-3】(2019春•临渭区校级月考)对实数a、b,定义“★”运算规则如下:a★b={b(a≤b)√a2−b2(a>b),则√7★(√2★√3)=()A.1B.2C.﹣1D.﹣2【分析】先依据法则知√2★√3=√3,据此得出原式=√7★√3,再次利用法则计算可得.【答案】解:∵√2<√3,∴√2★√3=√3,则原式=√7★√3=√(√7)2−(√3)2=√7−3=√4=2,故选:B.【点睛】本题主要考查实数的运算,解题的关键是掌握实数的混合运算顺序和运算法则及对新定义的理解.【考点12实数的性质综合】【例12】(2019春•嘉祥县期末)如图①是由8个同样大小的立方体组成的魔方,体积为8.(1)求出这个魔方的棱长;(2)图①中阴影部分是一个正方形ABCD,求出阴影部分的面积及其边长.(3)把正方形ABCD放到数轴上,如图②,使得点A与﹣1重合,那么点D在数轴上表示的数为.【分析】(1)根据立方体的体积公式,直接求棱长即可;(2)根据棱长,求出每个小正方体的边长,进而可得小正方形的对角线,即阴影部分图形的边长,即可得解;(3)用点A表示的数减去边长即可得解.【答案】解:(1)设魔方的棱长为x,则x3=8,解得:x=2;(2)∵棱长为2,∴每个小立方体的边长都是1,∴正方形ABCD的边长为:√2,∴S正方形ABCD=(√2)2=2;(3)∵正方形ABCD的边长为√2,点A与﹣1重合,∴点D在数轴上表示的数为:﹣1−√2,故答案为:﹣1−√2.【点睛】本题主要考查实数与数轴、立方根的综合应用,解决此题的关键是能求出每个小正方形的边长.【变式12-1】如图,4×4方格中每个小正方形的边长都为1.(1)直接写出图(1)中正方形ABCD的面积及边长;(2)在图(2)的4×4方格中,画一个面积为8的格点正方形(四个顶点都在方格的顶点上);并把图(2)中的数轴补充完整,然后用圆规在数轴上表示实数√8.【分析】(1)根据面积求出正方形的边长,再根据边长的长和面积公式即可求出答案;(2)根据勾股定理和正方形的面积公式即可画出图形,利用圆规,以O为圆心,正方形的边长为半径画弧可得实数√8的位置.【答案】解:(1)正方形的边长是:√5,面积为:√5×√5=5.(2)见图:在数轴上表示实数√8,【点睛】本题考查了三角形的面积,实数与数轴,用到的知识点是勾股定理,以及勾股定理的应用,在直角三角形中,两直角边的平方和等于斜边的平方.【变式12-2】如图甲,这是由8个同样大小的立方体组成的魔方,总体积为64cm3.(1)这个魔方的棱长为cm;(2)图甲中阴影部分是一个正方形ABCD,求这个正方形的边长;(3)把正方形ABCD放置在数轴上,如图乙所示,使得点A与数1重合,则D在数轴上表示的数为.【分析】(1)魔方是个正方体,正方体的体积等于棱长的三次方;(2)这个正方形ABCD的边长是小立方体一个面的对角线的长度;(3)点D表示的数是负数,它的绝对值比正方形ABCD的边长少1.【答案】解:(1)设魔方的棱长为acm,根据题意得a3=64∴a=4故答案为4.(2)设小正方体的棱长为bcm,根据题意得8b3=64∴b=2∴所以根据勾股定理得CD2=22+22∴CD=√8答:这个正方形的边长是√8cm.(3)由(2)知,AD=√8∴点D对应的数的绝对值是√8-1,∵点D对应的数是负数∴点D对应的数是1﹣√8故答案为1﹣√8.【点睛】本题考查了正方体的体积、实数与数轴之间的关系和勾股定理.正方体的体积=棱长的立方.实数与数轴上的点是一一对应的关系,要在数轴上表示一个实数,要知道这个实数的正负性和绝对值.。
复习被动语态

GRAMMAR被动语态(一)被动语态常与时态、主谓一致等一起考查。
我们先通过下面的表格来复习一下不同时态的被动语态的构成形式。
下面我们以高考题为例,对被动语态的用法作个总结和延伸。
考点一:在时态中的应用【考例回顾】1. In the last few years thousands of films ______ all over the world. (天津2011)A. have producedB. have been producedC. are producingD. are being produced2. Experiments of this kind ______ in both the U.S. and Europe well before the Second World War. (北京2011)A. have conductedB. have been conductedC. had conductedD. had been conducted【点拨】1. 答案为B。
时间状语In the last few years常与现在完成时连用;films与produce 之间是被动关系,故用现在完成时的被动语态。
2. 答案为D。
根据句意,此动作是在二战之前发生,故用过去完成时;experiments 与conduct之间是被动关系,故用过去完成时的被动语态。
考点二:在动词不定式中的应用【考例回顾】1. If they win the final tonight, the team are going to tour around the city ______ by their enthusiastic supporters. (浙江2011)A. being cheeredB. be cheeredC. to be cheeredD. were cheered2. There were many talented actors out there just waiting ______.(江西2010)A. to discoverB. to be discoveredC. discoveredD. being discovered【点拨】1. 答案为C。
专题02 二次函数章末重难点题型(举一反三)(解析版)

专题02 二次函数章末重难点题型【举一反三】【考点1 二次函数的概念】二次函数的定义:一般地,形如y =ax 2+bx +c (a 、b 、c 是常数,a ≠0)的函数,叫做二次函数.其中x 、y 是变量,a 、b 、c 是常量,a 是二次项系数,b 是一次项系数,c 是常数项.y ═ax 2+bx +c (a 、b 、c 是常数,a ≠0)也叫做二次函数的一般形式.【例1】(2019秋•泰兴市校级月考)下列函数关系式中,y 是x 的二次函数是( )A .2y ax bx c =++B .21y x x =-C .2325y x x ++D .2(32)(43)12y x x x =+--【思路点拨】根据二次函数的定义,可得答案.【答案】解:A 、a =0时,不是二次函数,故A 错误;B 、不是二次函数,故B 错误;C 、是二次函数,故C 正确;D 、不含二次项,不是二次函数,故D 错误;故选:C .【方法总结】本题考查了二次函数的定义,利用了二次函数的定义,二次函数:y =ax 2+bx +c (a ≠0)是二次函数.【变式1-1】(2019秋•文水县期中)已知函数:①2y ax =;②23(1)2y x =-+;③22(3)2y x x =+-;④21y x x =+.其中,二次函数的个数为( ) A .1个 B .2个 C .3个 D .4个【思路点拨】根据形如y =ax 2+bx +c (a ≠0)的函数为二次函数即可得到结论.【答案】解:根据定义②y =3(x ﹣1)2+2;③y =(x +3)2﹣2x 2是二次函数故选:B .【方法总结】本题考查二次函数的定义,解题的关键正确理解二次函数的定义,本题属于基础题型.【变式1-2】(2019秋•苍溪县期中)已知函数||(2)1m y m x mx =-+-,其图象是抛物线, 则m 的取值是( )A .2m =B .2m =-C .2m =±D .0m ≠【思路点拨】根据二次函数最高次数是二次,二次项的系数不等于零,可得方程,根据解方程,可得答案.【答案】解:∵函数y =(m ﹣2)x |m |+mx ﹣1,其图象是抛物线,∴|m |=2且m ﹣2≠0,解得m =﹣2.故选:B .【方法总结】本题考查了二次函数的定义,利用了二次函数的定义:形如y =ax 2+bx +c (a ≠0)是二次函数,注意二次项的系数不等于零是解题关键.【变式1-3】(2019秋•南康区期中)若22(2)32my m x x -=-+-是二次函数,则m 等于( ) A .2- B .2 C .2±D .不能确定 【思路点拨】根据二次函数的定义求解即可.【答案】解:由题意,得m 2﹣2=2,且m ﹣2≠0,解得m =﹣2,故选:A .【考点2 二次函数与一次函数图象】【例2】(2019秋•花都区期中)在同一直角坐标系中2y ax b =+与(0,0)y ax b a b =+≠≠图象大致为( )A .B .C .D .【思路点拨】本题由一次函数y =ax +b 图象得到字母系数的正负,再与二次函数y =ax 2+b 的图象相比较看是否一致.【答案】解:A 、由抛物线可知,a <0,b <0,由直线可知,a <0,b <0,故本选项正确;B 、由抛物线可知,a <0,b >0,由直线可知,a >0,b >0,故本选项错误;C 、由抛物线可知,a >0,b <0,由直线可知,a >0,b >0,故本选项错误;D 、由抛物线可知,a >0,b >0,由直线可知,a <0,b >0,故本选项错误.故选:A .【方法总结】本题考查了一次函数和二次函数的图象.解答该题时,一定要熟记一次函数、二次函数的图象的性质.【变式2-1】(2018秋•厦门期中)在同一平面直角坐标系中,函数2y ax bx =+与y bx a =-+的图象可能是()A .B .C .D .【思路点拨】首先根据图形中给出的一次函数图象确定a 、b 的符号,进而运用二次函数的性质判断图形中给出的二次函数的图象是否符合题意,根据选项逐一讨论解析,即可解决问题.【答案】解:A 、对于直线y =﹣bx +a 来说,由图象可以判断,a >0,b <0;而对于抛物线y =ax 2+bx 来说,对称轴x =﹣>0,在y 轴的右侧,符合题意,图形正确.B 、对于直线y =﹣bx +a 来说,由图象可以判断,a <0,b >0;而对于抛物线y =ax 2+bx 来说,图象应开口向下,故不合题意,图形错误.C 、对于直线y =﹣bx +a 来说,由图象可以判断,a <0,b <0;而对于抛物线y =ax 2+bx 来说,对称轴=﹣<0,应位于y 轴的左侧,故不合题意,图形错误,D 、对于直线y =﹣bx +a 来说,由图象可以判断,a >0,b <0;而对于抛物线y =ax 2+bx 来说,图象应开口向下,故不合题意,图形错误.故选:A .【方法总结】此主要考查了一次函数、二次函数图象的性质及其应用问题;解题的方法是首先根据其中一次函数图象确定a 、b 的符号,进而判断另一个函数的图象是否符合题意;解题的关键是灵活运用一次函数、二次函数图象的性质来分析、判断、解答.【变式2-2】(2019秋•沂水县期中)在同一直角坐标系中,一次函数y ax c =+和二次函数2()y a x c =+的图象大致为( )A .B .C .D .【思路点拨】本题形数结合,一次函数y =ax +b ,可判断a 、c 的符号;根据二次函数y =a (x +c )2的图象位置,可得a ,c .经历:图象位置﹣系数符号﹣图象位置.【答案】解:A 、函数y =ax +c 中,a >0,c >0,y =a (x +c )2中,a <0,c <0,故A 错误;B 、函数y =ax +c 中,a <0,c >0,y =a (x +c )2中,a >0,c >0,故B 正确;C 、函数y =ax +c 中,a >0,c <0,y =a (x +c )2中,a >0,c >0,故C 错误;D 、函数y =ax +c 中,a <0,c >0,y =a (x +c )2中,a >0,c <0,故D 错误.故选:B .【方法总结】此题考查二次函数图象,利用一次函数,二次函数系数及常数项与图象位置之间关系是解题关键.【变式2-3】(2016秋•工业园区期中)如图,一次函数y x =与二次函数2y ax bx c =++图象相交于A 、B两点,则函数2(1)y ax b x c =+-+的图象可能是( )A .B .C .D .【思路点拨】由直线y =x 与抛物线y =ax 2+bx +c 有两个交点,且两交点的横坐标均为负数可知:方程ax 2+bx +c =x ,即ax 2+(b ﹣1)x +c =0有两个同为异号的实数根,根据二次函数的图象与一元二次方程的根之间的关系即可得.【答案】解:由图象知直线y =x 与抛物线y =ax 2+bx +c 有两个交点,且两交点的横坐标均为负数, ∴方程ax 2+bx +c =x ,即ax 2+(b ﹣1)x +c =0有两个同为异号的实数根,∴函数y =ax 2+(b ﹣1)x +c 的图象与x 轴的负半轴有两个交点,故选:B .【方法总结】本题主要考查二次函数的图象与一元二次方程的根之间的关系,由题目已知图象得出方程ax 2+bx +c =x ,即ax 2+(b ﹣1)x +c =0有两个同为异号的实数根是解题的关键.【考点3 二次函数的增减性】【例3】(2018春•利津县期末)设1(2,)A y -,2(1,)B y ,3(2,)C y 是抛物线2(1)y x k =-++上的三点,则1y ,2y ,3y 的大小关系为( )A .123y y y >>B .132y y y >>C .231y y y >>D .312y y y >>【思路点拨】由二次函数解析式可知抛物线开口向下,且对称轴为x =﹣1.根据图象上的点的横坐标距离对称轴的远近来判断纵坐标的大小.【答案】解:∵二次函数线y =﹣(x +1)2+k ,∴该二次函数的抛物线开口向下,且对称轴为:x =﹣1.∵A (﹣2,y 1),B (1,y 2),C (2,y 3)是抛物线y =﹣(x +1)2+k 上的三点,而三点横坐标离对称轴x =3的距离按由近到远为:(﹣2,y 1)、(1,y 2)、(2,y 3),∴y 1>y 2>y 3故选:A .【方法总结】本题考查了函数图象上的点的坐标与函数解析式的关系,同时考查了函数的对称性及增减性.【变式3-1】(2019秋•宣威市校级月考)已知二次函数21572y x x =--+,若自变量x 分别取1x ,2x ,3x ,且1230x x x <<<,则对应的函数值1y ,2y ,3y 的大小关系正确的是( )A .123y y y >>B .123y y y <<C .231y y y >>D .231y y y <<【思路点拨】先根据抛物线的性质得到抛物线对称轴,则x >﹣时,y 随x 的增大而减小,于是由0<x 1<x 2<x 3即可得到y 1,y 2,y 3的大小关系.【答案】解:抛物线的对称轴为直线x =﹣=﹣,而抛物线开口向下,所以当x >﹣时,y 随x 的增大而减小,所以当0<x 1<x 2<x 3时,y 1>y 2>y 3.故选:A . 【方法总结】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.【变式3-2】(2018秋•建昌县期中)已知抛物线2(0)y ax bx c a =++<过(3,0)A -,(1,0)B ,1(5,)C y -,2(2,)D y -四点,则1y 与2y 的大小关系是( )A .12y y >B .12y y =C .12y y <D .不能确定【思路点拨】根据A (﹣3,0)、B (1,0)两点可确定抛物线的对称轴,再根据开口方向,C 、D 两点与对称轴的远近,判断y 1与y 2的大小关系.【答案】解:∵抛物线过A (﹣3,0)、B (1,0)两点,∴抛物线的对称轴为x ==﹣1,∵a <0,抛物线开口向下,离对称轴越远,函数值越小,比较可知C 点离对称轴远,对应的纵坐标值小,即y 1<y 2.故选:C .【方法总结】此题主要考查了二次函数图象上点的坐标特征,比较抛物线上两点纵坐标的大小,关键是确定对称轴,开口方向,两点与对称轴的远近.【变式3-3】(2018•南海区期中)已知二次函数2y ax bx c =++中,其函数y 与自变量x 之间的部分对应值如下表所示: x ⋯0 1 2 3 ⋯ y⋯ 5 2 1 2 ⋯ 点1(A x ,1)y 、2(B x ,2)y 在函数的图象上,则当101x <<,223x <<时,1y 与2y 的大小关系正确的是()A .y 1≥y 2B .y 1>y 2C .y 1<y 2D .y 1≤y 2【思路点拨】根据题意知图象过(0,5)(1,2)(2,1),代入得到方程组,求出方程组的解即可得到抛物线的解析式,化成顶点式得到抛物线的对称轴,根据对称性得到A 的对称点,利用增减性即可得出答案.【答案】解:根据题意知图象过(0,5)(1,2)(2,1), 代入得:且,解得:a =1,b =﹣4,c =5,∴抛物线的解析式是y =x 2﹣4x +5=(x ﹣2)2+1,∴抛物线的对称轴是直线x =2,∵0<x 1<1,2<x 2<3,0<x 1<1关于对称轴的对称点在3和4之间,当x >2时,y 随x 的增大而增大,∴y 1>y 2,故选:B .【方法总结】本题主要考查对二次函数图象上点的坐标特征,解二元一次方程组,用待定系数法求二次函数的解析式等知识点的理解和掌握,能根据二次函数的对称性判断两点的纵坐标的大小是解此题的关键.【考点4 二次函数图象的平移】【例4】(2018秋•花都区期中)抛物线22y x =-经过平移得到22(1)3y x =--+,平移方法是( )A .向左平移1个单位,再向下平移3个单位B .向左平移1个单位,再向上平移3个单位C .向右平移1个单位,再向下平移3个单位D .向右平移1个单位,再向上平移3个单位【思路点拨】由抛物线y =﹣2x 2得到顶点坐标为(0,0),而平移后抛物线y =﹣2(x ﹣1)2+3的顶点坐标为(1,3),根据顶点坐标的变化寻找平移方法.【答案】解:∵抛物线y =﹣2x 2得到顶点坐标为(0,0),而平移后抛物线y =﹣2(x ﹣1)2+3的顶点坐标为(1,3),∴平移方法为向右平移1个单位,再向上平移3个单位.故选:D .【方法总结】本题考查了抛物线的平移规律.关键是确定平移前后抛物线的顶点坐标,寻找平移规律.【变式4-1】(2019•天津校级期中)已知抛物线243y x x =-+与x 轴相交于点A ,B (点A 在点B 左侧),顶点为M .平移该抛物线,使点M 平移后的对应点M '落在x 轴上,点B 平移后的对应点B '落在y 轴上,则平移后的抛物线解析式为( )A .221y x x =++B .221y x x =+-C .221y x x =-+D .221y x x =--【思路点拨】直接利用抛物线与坐标轴交点求法结合顶点坐标求法分别得出A ,B ,M 点坐标,进而得出平移方向和距离,即可得出平移后解析式.【答案】解:当y =0,则0=x 2﹣4x +3,(x ﹣1)(x ﹣3)=0,解得:x 1=1,x 2=3,∴A (1,0),B (3,0),y =x 2﹣4x +3=(x ﹣2)2﹣1,∴M 点坐标为:(2,﹣1),∵平移该抛物线,使点M 平移后的对应点M '落在x 轴上,点B 平移后的对应点B '落在y 轴上,∴抛物线向上平移一个单位长度,再向左平移3个单位长度即可,∴平移后的解析式为:y =(x +1)2=x 2+2x +1.故选:A .【方法总结】此题主要考查了抛物线与坐标轴交点求法以及二次函数的平移,正确得出平移方向和距离是解题关键.【变式4-2】(2018秋•鼓楼区校级期中)在平面直角坐标系中,如果抛物线22y x =不动,而把x 轴、y 轴分别向下、向右平移2个单位长度,那么在新坐标系下抛物线的解析式为( )A .22(2)2y x =-+B .22(2)2y x =+-C .22(2)2y x =--D .22(2)2y x =++【思路点拨】根据平移确定出抛物线的顶点在新坐标系中的坐标,然后利用顶点式解析式写出即可.【答案】解:抛物线y =2x 2的顶点坐标为(0,0),∵把x 轴、y 轴分别向下、向右平移2个单位,∴在新坐标系中抛物线的顶点坐标为(﹣2,﹣2),∴抛物线的解析式为y =2(x +2)2﹣2.故选:D .【方法总结】本题考查了二次函数图象与几何变换,利用顶点的变化确定函数解析式的变化更简便易懂.【变式4-3】(2018秋•襄州区期中)将二次函数2y x bx c =++的图象先向左平移3个单位长度,再向上平移2个单位长度得到二次函数221y x x =-+的图象,用b ,c 的值分别是( )A .14b =,8c =-B .2b =-,4c =C .8b =-,14c =D .4b =,2c =-【思路点拨】把二次函数y =x 2﹣2x +1的图象先向右平移3个单位长度,再向下平移2个单位长度得到y =x 2+bx +c 的图象.【答案】解:∵y =x 2﹣2x +1=(x ﹣1)2,∴二次函数y =x 2﹣2x +1的图象的顶点坐标为(1,0),把点(1,0)先向右平移3个单位长度,再向下平移2个单位长度所得对应点的坐标为(4,﹣2), ∴原抛物线解析式为y =(x ﹣4)2﹣2,即y =x 2﹣8x +14,即b =﹣8,c =14.故选:C .【方法总结】本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a 不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.【考点5 二次函数的图象与a ,b ,c 的关系】【例5】(2018秋•渝中区校级期中)已知二次函数的图象如下所示,下列5个结论:①0abc >;②0b a c -->;③42a c b +>-;④30a c +>;⑤()(1a b m am b m +>+≠的实数),其中正确的结论有( )A .①②③B .②③④C .②③⑤D .③④⑤【思路点拨】由抛物线对称轴的位置判断ab 的符号,由抛物线与y 轴的交点判断c 的符号,然后根据对称轴及抛物线与x 轴交点情况进行推理,进而对所得结论进行判断.【答案】解:①∵对称轴在y 轴的右侧,∴ab <0,由图象可知:c>0,∴abc<0,故①不正确;②当x=﹣1时,y=a﹣b+c<0,∴b﹣a﹣c>0,故②正确;③由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0,∴4a+c>﹣2b,故③正确;④∵x=﹣=1,∴b=﹣2a,∵a﹣b+c<0,∴a+2a+c<0,3a+c<0,故④不正确;⑤当x=1时,y的值最大.此时,y=a+b+c,而当x=m时,y=am2+bm+c,所以a+b+c>am2+bm+c(m≠1),故a+b>am2+bm,即a+b>m(am+b),故⑤正确.故②③⑤正确,故选:C.【方法总结】本题主要考查了图象与二次函数系数之间的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴和抛物线与y轴的交点、抛物线与x轴交点的个数确定,熟练掌握二次函数的性质是关键.【变式5-1】(2018秋•苍溪县期中)二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac ﹣b2<0;②3b+2c<0;③m(am+b)+b≤a;④(a+c)2<b2;其中正确结论的个数有()个.A .1B .2C .3D .4【思路点拨】利用二次函数图象的相关知识与函数系数的联系,需要根据图形,逐一判断.【答案】解:∵抛物线和x 轴有两个交点,∴b 2﹣4ac >0,∴4ac ﹣b 2<0,∴①正确;∵把x =1代入抛物线得:y =a +b +c <0,∴2a +2b +2c <0, ∵﹣=﹣1,∴b =2a ,∴3b +2c <0,∴②正确;∵抛物线的对称轴是直线x =﹣1,∴y =a ﹣b +c 的值最大,即把x =m 代入得:y =am 2+bm +c ≤a ﹣b +c ,∴am 2+bm +b ≤a ,即m (am +b )+b ≤a ,∴③正确;∵a +b +c <0,a ﹣b +c >0,∴(a +c +b )(a +c ﹣b )<0,则(a +c )2﹣b 2<0,即(a +c )2<b 2,故④正确;故选:D .【方法总结】此题主要考查了二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特殊点的关系,也要掌握在图象上表示一元二次方程ax 2+bx +c =0的解的方法,同时注意特殊点的运用.【变式5-2】(2018秋•江岸区期中)已知二次函数2(0)y ax bx c a =++≠,过(1,1)(2y ,2)y .①若10y >时,则0a b c ++>②若a b =时,则12y y <③若10y <,20y >,且0a b +<,则0a >④若21b a =-,3c a =-,且10y >,则抛物线的顶点一定在第三象限上述四个判断正确的有( )个.A .1B .2C .3D .4【思路点拨】①若y 1>0时,当x =1时,y 1=a +b +c ,此时,确定不了y 的值,∴a +b +c >0,正确; ②若a =b 时,即函数的对称轴是x =﹣,分两种情况,a =b >0,则y 2>y 1,否则,故y 1<y 2,故错误; ③若y 1<0,y 2>0,即:a +b +c <0,4a +2b +c >0,而a +b <0,即:﹣2a <0,a >0,正确;④若b =2a ﹣1,c =a ﹣3,且y 1>0,即:a +b +c >0,把b 、c 的值代入上式得:a >1,则b >1,c >﹣2,代入顶点坐标即可求解,正确.【答案】解:①若y 1>0时,当x =1时,y 1=a +b +c >0此时,正确;②若a =b 时,即函数的对称轴是x =﹣,也确定不了y 1、y 2的大小,故y 1<y 2,错误;③若y 1<0,y 2>0,即:a +b +c <0,4a +2b +c >0,解得:﹣3a ﹣b <0,而a +b <0,即:﹣2a <0,∴a >0,正确;④若b =2a ﹣1,c =a ﹣3,且y 1>0,即:a +b +c >0,把b 、c 的值代入上式得:a >1,则b >1,c >﹣2,顶点的x 坐标=﹣<0,顶点的y 坐标==﹣2﹣<0,故顶点一定在第三象限,正确;故选:C .【方法总结】本题考查的是二次函数图象与系数的关系,涉及到函数基本性质、解不等式等相关知识,难度较大.【变式5-3】(2019•凉山州)二次函数2y ax bx c =++的部分图象如图所示,有以下结论:①30a b -=;②240b ac ->;③520a b c -+>;④430b c +>,其中错误结论的个数是( )A.1 B.2 C.3 D.4【思路点拨】①对称轴为x=﹣,得b=3a;②函数图象与x轴有两个不同的交点,得△=b2﹣4ac>0;③当x=﹣1时,a﹣b+c>0,当x=﹣3时,9a﹣3b+c>0,得5a﹣2b+c>0;④由对称性可知x=1时对应的y值与x=﹣4时对应的y值相等,当x=1时a+b+c<0,4b+3c=3b+b+3c =3b+3a+3c=3(a+b+c)<0;【答案】解:由图象可知a<0,c>0,对称轴为x=﹣,∴x=﹣=﹣,∴b=3a,①正确;∵函数图象与x轴有两个不同的交点,∴△=b2﹣4ac>0,②正确;当x=﹣1时,a﹣b+c>0,当x=﹣3时,9a﹣3b+c>0,∴10a﹣4b+2c>0,∴5a﹣2b+c>0,③正确;由对称性可知x=1时对应的y值与x=﹣4时对应的y值相等,∴当x=1时a+b+c<0,∵b=3a,∴4b+3c=3b+b+3c=3b+3a+3c=3(a+b+c)<0,∴4b+3c<0,④错误;故选:A .【方法总结】本题考查二次函数的图象及性质;熟练掌握从函数图象获取信息,将信息与函数解析式相结合解题是关键.【考点6 二次函数与一元二次方程之间的关系】【例6】(2019春•天心区校级期中)函数2y ax bx c =++的图象如图所示,那么关于一元二次方程220ax bx c ++-=的根的情况是( )A .有两个不相等的实数根B .有两个异号的实数根C .有两个相等的实数根D .没有实数根【思路点拨】由图可知ax 2+bx +c ﹣2=0的根的情况即图中图象和x 轴交点的横坐标,为两个不相等的正数.【答案】解:∵函数的顶点的纵坐标为3,∴直线y =3与函数图象只有一个交点,∴y =ax 2+bx +c ﹣2,相当于函数y =ax 2+bx +c 的图象向下平移2个单位,∴方程ax 2+bx +c ﹣2=0的根为两个不相等的实数根.故选:A .【方法总结】本题考查了二次函数与一元二次方程的知识,关键是通过看图象直线y =3与抛物线的交点个数.【变式6-1】(2019春•安吉县期中)如图,抛物线2y x mx =-+的对称轴为直线2x =,若关于x 的一元二次方程20(x mx t t +-=为实数)在13x <<的范围内有解,则t 的取值范围是( )A .﹣5<t ≤4B .3<t ≤4C .﹣5<t <3D .t >﹣5【思路点拨】先利用抛物线的对称轴方程求出m 得到抛物线解析式为y =﹣x 2+4x ,配方得到抛物线的顶点坐标为(2,4),再计算出当x =1或3时,y =3,结合函数图象,利用抛物线y =﹣x 2+4x 与直线y =t 在1<x <3的范围内有公共点可确定t 的范围.【答案】解:∵抛物线y =﹣x 2+mx 的对称轴为直线x =2, ∴﹣=2,解得m =4,∴抛物线解析式为y =﹣x 2+4x ,抛物线的顶点坐标为(2,4),当x =1时,y =﹣x 2+4x =3;当x =3时,y =﹣x 2+4x =3,∵关于x 的一元二次方程x 2+mx ﹣t =0(t 为实数)在1<x <3的范围内有解,∴抛物线y =﹣x 2+4x 与直线y =t 在1<x <3的范围内有公共点,∴3<t ≤4.故选:B .【方法总结】本题考查了抛物线与x 轴的交点:把求二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)与x 轴的交点坐标问题转化为解关于x 的一元二次方程.也考查了二次函数的性质.【变式6-2】(2018秋•福清市期中)函数21y x x =+-中x 与y 的对应关系如下表所示,方程210x x +-=两实数根中有一个正根1x ,下列对1x 的估值正确的是( ) x ⋯0.5 0.55 0.6 0.65 0.7 0.75 ⋯ y ⋯ 0.25- 0.1475- 0.04- 0.0725 0.19 0.3125 ⋯A .10.50.55x <<B .10.550.6x <<C .10.60.65x <<D .10.650.7x << 【思路点拨】利用x =0.6时,y =x 2+x ﹣1=﹣0.04;x =0.65时,y =x 2+x ﹣1=0.0725,从而可判断当0.6<x <0.65时,y =x 2+x ﹣1的值能等于0,从而得到方程x 2+x ﹣1=0一个正根x 1的范围.【答案】解:∵x =0.6时,y =x 2+x ﹣1=﹣0.04;x =0.65时,y =x 2+x ﹣1=0.0725,∴当0.6<x <0.65时,y =x 2+x ﹣1的值能等于0,∴方程x 2+x ﹣1=0两实数根中有一个正根x 1,则0.6<x 1<0.65.故选:C .【方法总结】本题考查了抛物线与x 轴的交点:把求二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)与x 轴的交点坐标问题转化解关于x 的一元二次方程即可求得交点横坐标.【变式6-3】(2019秋•萧山区期中)已知关于x 的方程2()()0x m x n +--=,存在a ,b 是方程2()()0x m x n +--=的两个根,则实数m ,n ,a ,b 的大小关系可能是( )A .m a b n <<<B .m a n b <<<C .a m b n <<<D .a m n b <<<【思路点拨】令抛物线解析式中y =0,得到方程的解为a ,b ,即为抛物线与x 轴交点的横坐标为a ,b ,再由抛物线开口向上得到a <x <b 时y 小于0,得到x =m 与n 时函数值大于0,即可确定出m ,n ,a ,b 的大小关系.【答案】解:令函数y =2+(x ﹣m )(x ﹣n )=x 2﹣(m +n )x +mn +2,∴抛物线开口向上,令y =0,根据题意得到方程(x ﹣m )(x ﹣n )=﹣2的两个根为a ,b ,∵当x =m 或n 时,y =2>0,∴实数m ,n ,a ,b 的大小关系为m <a <b <n .故选:A .【方法总结】本题考查了一元二次方程的根与系数之间的关系,难度较大,熟练掌握抛物线的性质是解本题的关键.【考点7 二次函数解析式】【例7】经过(4,0)A ,(2,0)B -,(0,3)C 三点的抛物线解析式是 .【思路点拨】根据A 与B 坐标特点设出抛物线解析式为y =a (x ﹣2)(x ﹣4),把C 坐标代入求出a 的值,即可确定出解析式.【答案】解:根据题意设抛物线解析式为y =a (x +2)(x ﹣4),把C (0,3)代入得:﹣8a =3,即a =﹣,则抛物线解析式为y =﹣(x +2)(x ﹣4)=﹣x 2+x +3,故答案为y =﹣x 2+x +3.【方法总结】此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.【变式7-1】若二次函数2y ax bx c =++的x 与y 的部分对应值如下表: x 7- 6- 5- 4-3- 2- y 27- 13- 3- 3 53 则二次函数的解析式为 .【思路点拨】取三组对应值(﹣4,3)、(﹣3,5)、(﹣2,3)代入y=ax2+bx+c得到关于a、b、c 的方程组,然后解方程组求出a、b、c的值,从而得到抛物线解析式.【答案】解:把(﹣4,3)、(﹣3,5)、(﹣2,3)代入y=ax2+bx+c得,解得.所以抛物线解析式为y=﹣2x2﹣12x﹣13.故答案为y=﹣2x2﹣12x﹣13.【方法总结】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.【变式7-2】(2019秋•荣成市期中)二次函数在32x=时,有最小值14-,且函数的图象经过点(0,2),则此函数的解析式为.【思路点拨】由条件可知其顶点坐标为(,),可设顶点式,再把点(0,2)代入可求得函数的解析式.【答案】解:∵二次函数在x=时,有最小值,∴抛物线的顶点是(,),∴设此函数的解析式为y=a(x﹣)2﹣,∵函数图象经过点(0,2),∴2=a(0﹣)2﹣,解得a=1,∴此函数的解析式为y=(x﹣)2﹣,即y=x2﹣3x+2.故答案为y=x2﹣3x+2.【方法总结】本题主要考查了用待定系数法求二次函数解析式,在已知抛物线顶点坐标的情况下,通常用顶点式设二次函数的解析式.【变式7-3】(2013秋•潜山县校级月考)抛物线2y ax bx c =++与x 轴两个交点为(1,0)-,(3,0),其形状与抛物线22y x =相同,则抛物线解析式为 . 【思路点拨】根据抛物线形状相同则a 的值相同,再将(﹣1,0),(3,0)代入抛物线求出b ,c 的值即可.【答案】解:∵抛物线y =ax 2+bx +c 与x 轴两个交点为(﹣1,0),(3,0),其形状与抛物线y =2x 2相同,∴或,∴解得:或,∴抛物线解析式为:y =2x 2﹣4x ﹣6或y =﹣2x 2+4x +6.故答案为:y =2x 2﹣4x ﹣6或y =﹣2x 2+4x +6.【方法总结】此题主要考查了待定系数法求二次函数解析式,得出a 的值是解题关键.【考点8 二次函数的应用—销售问题】【例8】(2018秋•鼓楼区校级期中)某公司投资销售一种进价为每件15元的护眼台灯.销售过程中发现,每月销售量y (件)与销售单价x (元)之间的关系可近似的看作一次函数:20800y x =-+,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.(1)设该公司每月获得利润为w (元),求每月获得利润w (元)与销售单价x (元)之间的函数关系式,并确定自变量x 的取值范围.(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?【思路点拨】(1)由题意得,每月销售量与销售单价之间的关系可近似看作一次函数,利润=(定价﹣进价)×销售量,从而列出关系式;(2)首先确定二次函数的对称轴,然后根据其增减性确定最大利润即可;【答案】解:(1)由题意,得:w =(x ﹣15)•y =(x ﹣15)•(﹣20x +800)=﹣20x 2+1100x ﹣12000, 即w =﹣20x 2+1100x ﹣12000(15≤x ≤24);(2)对于函数w =﹣20x 2+1100x ﹣12000(15≤x ≤24)的图象的对称轴是直线x =27.5又∵a =﹣20<0,抛物线开口向下.∴当15≤x≤24时,W随着x的增大而增大,∴当x=24时,W=2880,答:当销售单价定为24元时,每月可获得最大利润,最大利润是2880元.【方法总结】此题考查二次函数的性质及其应用,还考查抛物线的基本性质,另外将实际问题转化为求函数最值问题,从而来解决实际问题.【变式8-1】(2019春•宿豫区期中)某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件,设衬衫的单价降x元,每天获利y元.(1)如果商场里这批衬衫的库存只有44件,那么衬衫的单价应降多少元,才能使得这批衬衫一天内售完,且获利最大,最大利润是多少?(2)如果商场销售这批衬衫要保证每天盈利不少于1200元,那么衬衫的单价应降多少元?【思路点拨】(1)列出y=44(40﹣x)=﹣44x+1760,根据一次函数的性质求解;(2)根据题意列出y=(20+2x)(40﹣x)=﹣2(x﹣15)2+1250,结合二次函数的性质求解;【答案】解:(1)y=44(40﹣x)=﹣44x+1760,∵20+2x≥44,∴x≥12,∵y随x的增大而减小,∴当x=12时,获利最大值1232;答:如果商场里这批衬衫的库存只有44件,那么衬衫的单价应12元,才能使得这批衬衫一天内售完,且获利最大1232元;(2)y=(20+2x)(40﹣x)=﹣2(x﹣15)2+1250,当y=1200时,1200=﹣2(x﹣15)2+1250,∴x=10或x=20,∵当x<15时,y随x的增大而增大,当x>15时,y随x的增大而减小,当10≤x≤20时,y≥1200,答:如果商场销售这批衬衫要保证每天盈利不少于1200元,那么衬衫的单价应降不少于10元且不超过20元;【方法总结】本题考查一次函数和二次函数的性质;能够从情境中列出函数关系式,借助函数的性质解决实际问题;【变式8-2】(2019春•安吉县期中)为建设美丽家园,某社区将辖区内的一块面积为21000m 的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为2()x m ,种草所需费用1y (元)与2()x m 的函数关系图象如图所示,栽花所需费用2y (元)与2()x m 的函数关系式为220.012030000(01000)y x x x =--+.(1)求1y (元)与2()x m 的函数关系式;(2)设这块21000m 空地的绿化总费用为W (元),请利用W 与x 的函数关系式,求绿化总费用W 的最大值.【思路点拨】(1)根据函数图象利用待定系数法即可求得y 1(元)与x (m 2)的函数关系式(2)总费用为W =y 1+y 2,列出函数关系式即可求解【答案】解:(1)依题意当0≤x ≤600时,y 1=k 1x ,将点(600,18000)代入得18000=600k 1,解得k 1=30 ∴y 1=30x当600<x ≤1000时,y 1=k 2x +b ,将点(600,18000),(1000,26000)代入得 ,解得∴y 1=20x +600综上,y 1(元)与x (m 2)的函数关系式为:(2)总费用为:W =y 1+y 2∴W = 整理得故绿化总费用W的最大值为32500元【方法总结】本题主要考查二次函数在生活中的实际应用.根据函数解析式即可求最大值,但要注意自变量的取值范围.【变式8-3】(2019秋•沂源县期末)某公司生产的某种商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:时间t(天) 1 3 5 10 36 ⋯94 90 86 76 24 ⋯日销售量m(件)未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1=t+25(1≤t≤20且t 为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣t+40(21≤t≤40且t为整数).下面我们就来研究销售这种商品的有关问题:(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的表达式;(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?【思路点拨】(1)从表格可看出每天比前一天少销售2件,所以判断为一次函数关系式;(2)日利润=日销售量×每件利润,据此分别表示前20天和后20天的日利润,根据函数性质求最大值后比较得结论.【答案】解:(1)经分析知:m与t成一次函数关系.设m=kt+b(k≠0),将t=1,m=94,t=3,m=90代入,解得,∴m=﹣2t+96;(2)前20天日销售利润为P1元,后20天日销售利润为P2元,则P1=(﹣2t+96)(t+25﹣20)=﹣(t﹣14)2+578,∴当t=14时,P1有最大值,为578元.。
六年级下册数学试题-小升初考点点拨:工程问题(含答案)全国通用

工程问题例题精讲【例题 1】在参与奥运场馆建设中,张师傅生产一个零件用 1/2 小时,李师傅生产一个零件用 1/3 小时,张师傅和李师傅工作效率的比是多少?A.3:2 B.2:3 C.1:6【答案】解:1/3:1/2=2:3.答:张师傅和李师傅工作效率的比是 2:3.【例题 2】加工一批零件,甲乙合作 24 天可以完成,现在由甲先做16 天,然后由乙方再做 12 天,还剩下这批零件的 2/5 没有完成.已知甲每天比乙多加工 3 个零件,求这批零件的个数.【答案】甲、乙合作12 天,完成了总工程的几分之几:1/24×12=1/2甲 1 天能完成全工程的几分之几:(1-2/5-1/2)÷(16-12)=1/40 乙 1 天可完成工程的几分之几:1/24-1/40=1/60 这批零件共多少个:3÷(1/40-1/60)=360(个)答:这批零件共有 360 个。
【例题 3】一项工程,甲、乙、丙三人合作 13 天完成,如丙休息 2 天,乙就要多做 4 天,或由甲、乙两人合做多做 1 天.这项工程由乙独做多少天完成?【答案】解:乙丙效率比 1/4:1/2=1:2,甲乙效率比为(4-1):1=3:1,所以甲:乙:丙=3:1:2,则乙单独做需要:13÷1/(3+1+2)=78(天)答:这项工程由乙独做 78 天完成.举一反三【变式 1】修一条路,甲队每天修这条路的 1/9,照这样计算,甲队要天可以完成;乙队每天修这条路的 1/10,照这样计算,乙队要多少天可以完成?【答案】解:1÷1/9=9(天) 1÷1/10=10(天)答:甲队要 9 天可以完成;乙队要 10 天可以完成【变式 2】一项工程,甲队单独做 10 天完成,乙队每天完成这项工程的 1/8,甲乙两队单独完成这项工程的时间比是多少?【答案】解:10:(1÷1/8)=10:8,=5:4;答:甲乙两队单独完成这项工程的时间比是 5:4.【变式 3】一项工程甲单独做 12 天可以完成,如果甲单独做 3 天,余下的工作由乙去做,乙再用 6 天可以做完,若甲单独做 6 天,余下的工作乙要做几天?【答案】乙的工作效率为:(1-1/12×3)÷6=1/8 (1-1/12×6)÷1/8=4(天)答:余下的工作乙要做 4天。
中考英语-介词-超全考点梳理+易错点拨

中考英语-介词-超全考点梳理+易错点拨一、表示时间的介词1. in,on,at,overat用于表示时刻、时间的某一点at lunch在午饭时at breakfast早餐时at noon正午时at night在夜间at that time那时at the moment此刻,目前at the same time同时at times偶尔,有时at nine在九点钟at first开始的时候,起初at last最后►We usually have lunch at noon/ at twelve. 我们通常中午吃午饭(十二点吃午饭)。
注意:表示时间的名词前有this, last, next, every等修饰时,其前面不加介词。
this morning今天早上last Monday上周一every week每周on用于表示某天,某一天的上、下午(指具体的某一时,一律用on)on Monday 在周一on Monday evening 在周一晚上on Tuesday morning 在周二早上on June 6在6月6日on May 4,2016 在2016年5月4日on a cold night在一个寒冷的夜晚on that day在那天on Christmas Day在圣诞节那天on time准时on the night of July(the)first 在七月一日的夜晚►We didn’t listen to the lecture on Wednesday afternoon. 周三下午我们没去听演讲。
in用于表示周、月、季节、年和泛指的上午、下午、晚上(指在一段时间内)。
in the week在这周in the holiday在假期中in May 在五月in 1995在1995年in summer在夏季in Spring在春季in autumn在秋季in winter在冬季in September, 1995 在1995年9月in the morning 在上午in the afternoon 在下午in the evening在晚上in the 21st century在二十一世纪in time及时in an hour一个小时后in a minute一会儿,立刻►The plane took off on time.飞机准时起飞了。
言语理解与表达高频考点梳理

言语理解与表达高频考点梳理在 2021 年国考行测科目中,言语理解与表达共考查了 40 题,占行测科目总题量的 30%左右。
其中中心理解题、语句排序题、逻辑填空题为 2021 年乃至近五年国考言语的高频题型,本文将为大家介绍每类题型高频考点的重要解题技巧。
国考言语理解与表达各题型近五年考查数量(副省/地市)高频考点一:中心理解之对策。
中心理解题在近五年国考言语模块中考查的题量为 5-12 道,在总题量 40 中的占比还是相对较高的,属于言语模块的高频题型。
既然叫做中心理解题,顾名思义就是要找到文段中心,即文段中心句。
我们可以借助转折关联词、因果关联词、对策标志词、主题词、程度词等等特殊信息寻找中心句。
通过对近年国考真题考点的统计发现,国考试题考查最多的当属对策这一知识点,比如19 年地市卷 43 题、46 题、57 题,19 年副省卷 37 题、40 题、48 题;20 年地市卷 51 题,20 年副省卷 48 题;21 年地市卷 42 题、43 题、60 题,21 年副省卷 38 题。
对于对策文段来说,文段中心就是对策本身,那么如何找到文段的对策呢?(一)通过必要条件关联词引导对策:只有……才……其中,“只有”和“才”之间的内容为对策,即文段中心。
(二)引导对策的其他标志词:1.应该、应当、应、需要、要、必须 + 做法2.通过 / 采取……手段 / 途径 / 措施 / 方式 / 方法 / 渠道,才能……3.前提、基础、保障4.负有……的义务 /……的必由之路 /……的法门之一 / 要领之一 / 势在必行(三)对策文段常见的行文脉络:1.提出问题 + 分析问题 + 解决问题2.提出问题 + 解决问题 + 解释说明(意义效果)3.对策 + 正反论证 / 原因论证(四)反面论证标志:如果/倘若/一旦……+不好的结果具体应用:把前面的做法反过来,即为正确答案如:小编的父母说“如果你在 12 点之前不回家,回家就会遭遇一场混合双打(反面提对策)”,强调的就是“12 点前必须回家”。
轴对称、平移与旋转知识点章末重难点题型(举一反三)

专题1.5 轴对称、平移与旋转章末重难点题型【考点1 判断轴对称图形】【方法点拨】掌握轴对称图形的概念:把一个图形沿着某一条直线翻折,如果直线两旁的部分能够互相重合,那么称这个图形是轴对称图形,这条直线就是对称轴。
注意:理解轴对称图形的定义应注意两点:(1)轴对称图形是一个图形,反映的是这个图形自身的性质。
(2)符合要求的“某条直线”可能不止一条,但至少要有一条。
【例1】(2019春•相城区期中)下列图形中,不是轴对称图形的是()A.B.C.D.【分析】根据关于某条直线对称的图形叫轴对称图形,进而判断得出即可.【答案】解:A、是轴对称图形,不合题意;B、不是轴对称图形,符合题意;C、是轴对称图形,不合题意;D、是轴对称图形,不合题意;故选:B.【点睛】此题主要考查了轴对称图形,轴对称图形的关键是寻找对称轴,对称轴可使图形两部分折叠后重合.【变式1-1】(2018秋•思明区校级期中)如图,四个手机应用图标中是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念判断即可.【答案】解:A、B、C不是轴对称图形,D是轴对称图形,故选:D.【点睛】本题考查的是轴对称图形的概念,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.【变式1-2】(2018秋•开封期中)下列四个图形中,不是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念求解.【答案】解:A、是轴对称图形,故本选项错误;B、是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项正确;D、是轴对称图形,故本选项错误;故选:C.【点睛】本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.【变式1-3】(2018秋•宜兴市校级期中)下列图形中,不是轴对称图形的有()A.1个B.2个C.3个D.4个【分析】根据轴对称图形的概念求解.【答案】解:只有第1个不是轴对称图形.故选:A.【点睛】本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.【考点2 轴对称性质的应用】【方法点拨】掌握轴对称的性质:1.成轴对称的两个图形全等。
2021年高中英语 Unit 4 Making the news 考点点拨 考例回顾试题

2021年高中英语 Unit 4 Making the news 考点点拨考例回顾试题1. Later you can cover a story and submit the article yourself. (P26)【考点】cover在此意为“报道”,它还可意为“遮盖;包含,涉及;足以支付;行走(一段距离)”等。
【考例】—Do you have enough to ______ all your daily expenses?—Oh yes, enough and to spare.A. coverB. spendC. fillD. offer(山东xx)【点拨】选A。
问句意为:你有足够的钱来支付日常开支吗?enough and to spare 意为“绰绰有余”。
2. Meanwhile you have to prepare the next question depending on what the person says. (P26)【考点】meanwhile其间;同时。
【考例】 The ines of skilled workers went up. ______, unskilled workers saw their earnings fall.A. MoreoverB. ThereforeC. MeanwhileD. Otherwise (浙江xx)【点拨】选C。
moreover而且;therefore因此;otherwise否则。
句意为:熟练工的收入在上升,与此同时非熟练工的收入在下降。
3. Have you ever had a case where someone accused your journalists of getting the wrong end of the stick? (P26)【考点】case情况,病例,案例,可构成短语in case,表示“万一”。
[2007--2018真题]文化史考点精练3 宋明理学(原卷版)
![[2007--2018真题]文化史考点精练3 宋明理学(原卷版)](https://img.taocdn.com/s3/m/b0cd5ee04028915f814dc21f.png)
考点3 程朱理学与陆王心学【考点图解】【名师点拨】一、.全面评价宋明理学(1)积极:①宋明理学具有和谐意识,强调人与自然、家庭、国家的和谐意识。
②宋明理学具有忧患意识,鼓舞历代仁人志士胸怀天下,奋发进取,为理想不懈追求。
③宋明理学崇尚道德,重义轻利,强调自我约束,可以促进文明的进步。
④宋明理学强调身体力行,强调自主自强的精神,对中国文化起了推动和促进作用。
(2)消极:①尊卑等级观念。
②重男轻女的观念。
③轻视自然科学的观念。
④轻视个体自由的观念。
⑤重礼轻法的观念等封建伦理,是维护君主专制的工具、摧残扼杀人性、压抑思想进步。
二、.全面认识程朱理学和陆王心学的关系程朱理学陆王心学相同点本质都以儒家的纲常伦纪来约束社会,维护专制统治,遏制人们的自然欲求内容都继承了孔孟“仁”“礼”的儒学发展的新形式,以维护封建统治影响都有助于维护专制统治,扼杀人的自然欲求;都强调社会责任和历史使命,对塑造中华民族性格起了积极作用不同点理学思想“理”是世界的本原“心”是万物的本原方法论强调“格物致知”“发明本心”或“致良知”道德观主张人应以外在的天理为行为规范主张应以“内心”的自修、自省达到良知哲学范畴客观唯心主义思想主观唯心主义思想【历年真题】1.(2018·天津高考·1)朱熹在《四书章句集注》中说:“盖国以民为本,社稷亦为民而立,而君之尊又系于二者之存亡,故其轻重如此。
”这一说法( )A.强调了君主至尊的观念 B.体现了儒家传统的民本思想C.呼应了“存天理,灭人欲”的主张 D.推动了儒家思想的新发展2.(2018.4·浙江高考·7)思想家王守仁说:“夫良知者,即所谓是非之心,人皆有之,不待学而有,不待虑而得者也”“致吾心良知之天理于事事物物,则事事物物皆得其理矣。
致吾心之良知者,致知也”。
其主张( )①重建儒学信仰②人人都有良知③无私则无心④道德自我完善A.①② B.③④C.①③ D.②④3.(2017·江苏高考·4)孔子主张“克己复礼”“为仁由己”。
上海市七年级第一学期数学专题03 与数有关的排列规律重难点题型(举一反三)(解析版)
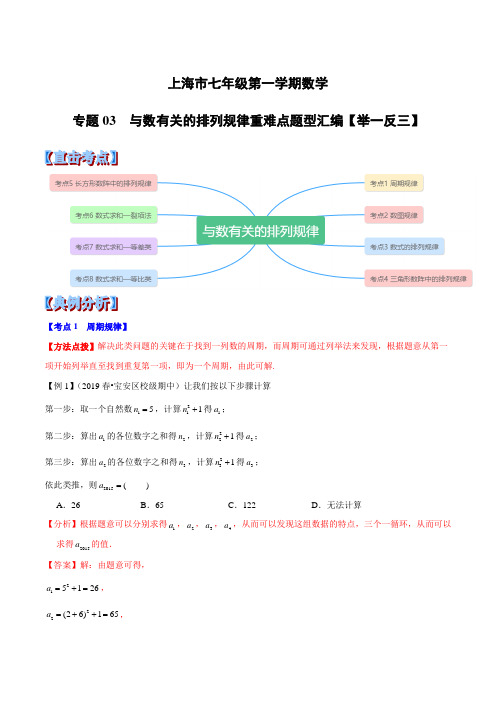
上海市七年级第一学期数学专题03 与数有关的排列规律重难点题型汇编【举一反三】【考点1 周期规律】【方法点拨】解决此类问题的关键在于找到一列数的周期,而周期可通过列举法来发现,根据题意从第一 项开始列举直至找到重复第一项,即为一个周期,由此可解. 【例1】(2019春•宝安区校级期中)让我们按以下步骤计算 第一步:取一个自然数15n =,计算211n +得1a ;第二步:算出1a 的各位数字之和得2n ,计算221n +得2a ; 第三步:算出2a 的各位数字之和得3n ,计算231n +得3a ; 依此类推,则2015(a = ) A .26B .65C .122D .无法计算【分析】根据题意可以分别求得1a ,2a ,3a ,4a ,从而可以发现这组数据的特点,三个一循环,从而可以求得2015a 的值. 【答案】解:由题意可得,215126a =+=, 22(26)165a =++=,23(65)1122a =++=, 24(122)126a =+++=,⋯201536712∴÷=⋯, 201565a ∴=,故选:B .【点睛】本题考查规律性:数字的变化类,解题的关键是明确题意,求出前几个数,观察数的变化特点,求出2015a 的值.【变式1-1】(2018秋•景德镇期中)对于每个正整数n ,设()f n 表示(1)n n +的末位数字.例如:f (1)2(12=⨯ 末位数字),f (2)6(23=⨯的末位数字),f (3)2(34=⨯的末位数字),⋯⋯则f (1)f +(2)f +(3) (2016)f +⋯+的值是( )A .4028B .4030C .4032D .4038【分析】首先根据已知得出规律,f (1)2(12=⨯的末位数字),f (2)6(23=⨯的末位数字),f (3)2(34=⨯的末位数字),f (4)0=,f (5)0=,f (6)2=,f (7)6=,f (8)2=,f (9)0=,⋯,进而求出即可.【答案】解:f Q (1)2(12=⨯的末位数字),f (2)6(23=⨯的末位数字),f (3)2(34=⨯的末位数字),f (4)0=,f (5)0=,f (6)2=,f (7)6=,f (8)2=,f (9)0=,⋯,∴每5个数一循环,分别为2,6,2,0,0⋯,201654031∴÷=⋯,f ∴(1)f +(2)f +(3)(2016)f +⋯+ 262002622=++++++++⋯+403(262)2=⨯+++ 4032=.故选:C .【点睛】此题主要考查了数字变化规律,根据已知得出数字变化以及求出f (1)f +(2)f +(3)(2016)403(262)2f +⋯+=⨯+++是解题关键.【变式1-2】(2019秋•台州期中)在一列数:1a ,2a ,3a ,⋯,n a 中,13a =,27a =,从第三个数开始,每一个数都等于它前两个数之积的个位数字,则这一列数中的第2016个数是( ) A .9B .3C .7D .1【分析】本题可分别求出3n =、4、5⋯时的情况,观察它是否具有周期性,再把2016代入求解即可. 【答案】解:依题意得:13a =,27a =,31a =,47a =,57a =,69a =,73a =,87a =; 周期为6; 20166336÷=,所以201669a a ==. 故选:A .【点睛】本题考查了找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.而具有周期性的题目,找出周期是解题的关键. 【变式1-3】(2018春•雨花区校级期中)有一列数1a ,2a ,3a ,⋯,n a ,⋯满足13a =,211111132a a ===---,之后每一个数是1与前一个数的差的倒数,即111n na a +=-,则20202018(a a -= ) A .72-B .73 C .76-D .72【分析】根据差倒数的定义分别求出前几个数,便不难发现,每3个数为一个循环组依次循环,再根据规律求出2020a 与2018a ,然后将它们相减即可得解. 【答案】解:13a =Q , 211111132a a ∴===---, 312131()2a ==--, 413213a ==-,511132a ==--, ⋯,所以这列数的周期为3,又202036731÷=⋯,201836722÷=⋯, 20203a ∴=,201812a =-,20202018173()22a a ∴-=--=.故选:D.【点睛】本题考查了数字的变化规律,理解差倒数的定义并求出每3个数为一个循环组依次循环是解题的关键.【考点2 数图规律】【方法点拨】解决此类问题在于通过数图找到数与数之间的关系式.【例2】(2018秋•常熟市期中)根据图中数字的规律,则x y+的值是()A.729 B.550 C.593 D.738【分析】观察发现,图中第二行左边的数比第一行数的平方大1,第二行右边的数=第二行左边的数⨯第一行的数+第一行的数,依此规律先求x,再求y即可.【答案】解:2521Q,12522=+=⨯+;2=+,7217441741=⨯+;2=+,22837663761=⨯+;2∴=+=,6588528x8165y=⨯+=,+=+=.65528593x y故选:C.【点睛】考查了规律型:数字的变化类,关键是由图形得到第二行左边的数比第一行数的平方大1,第二行右边的数=第二行左边的数⨯第一行的数+第一行的数.【变式2-1】(2018秋•瑶海区期中)观察下面“品”字形中各数之间的规律,根据观察到的规律得出a的值为()A.19 B.21 C.32 D.41【分析】由图可知:上边的数与左边的数的和正好等于右边的数,上边的数为连续的奇数,左边的数为12,22,32,⋯,由此可得a,b.【答案】解:Q上边的数为连续的奇数1,3,5,7,9,左边的数为12,22,32,⋯,5∴==,b232Q上边的数与左边的数的和正好等于右边的数,a∴=+=,93241故选:D.【点睛】此题考查数字变化规律,观察出上边的数与左边的数的和正好等于右边的数是解题的关键.【变式2-2】(2018秋•沙坪坝区校级期中)如图所示,下列各三角形的三个数之间均具有相同的规律,根据此规律最后一个三角形中y的值是()A.418 B.420 C.424 D.422【分析】根据已知图形得出左边三角形中的数字即为序数,而右边三角形数是序数与1的和,下方三角形数是上面两个三角形中数字乘积与2的和,据此可得.【答案】解:Q观察可知:左边三角形的数字规律为:1,2,3,4⋯,n,右边三角形的数字规律为:2,3,4,5,⋯,1n+,下边三角形的数字规律为:122n n++,⨯+,232⨯+,⋯,(1)2⨯+,452⨯+,342y∴=⨯+=,20212422故选:D.【点睛】本题主要考查数字的变化规律,解题的关键是掌握左边三角形中的数字即为序数,而右边三角形数是序数与1的和,下方三角形数是上面两个三角形中数字乘积与2的和.【变式2-3】(2018秋•汉滨区期中)下面每个表格中的四个数都是按相同规律填写的根据此规律确定x的值为()A.252 B.209 C.170 D.135【分析】首先根据图示,可得第n个表格的左上角的数等于n,左下角的数等于1n+;右上角的数分别为4,6,8,10,22⋯+,由此求出n;最后根据每个表格中右下角的数等于左下角的数与右上角的数的积n加上左上角的数,求出x的值是多少即可.【答案】解:由分析可知,2220a=,a+=,解得910b ∴=,20209x b a ∴=+=,故选:B .【点睛】此题主要考查了探寻数字规律问题,注意观察总结出规律,并能正确的应用规律. 【考点3 数式的排列规律】【方法点拨】解决此类问题在于通过数式的排列规律找到数与数之间的关系. 【例3】(2018秋•江城区期中)观察下列三行数: 0,3,8,15,24,⋯① 2,5,10,17,26,⋯② 0,6,16,30,48,⋯③(1)第①行数按什么规律排的,请写出来? (2)第②、③行数与第①行数分别对比有什么关系? (3)取每行的第n 个数,求这三个数的和.【分析】(1)通过计算得到2011=-,2321=-,2831=-,21541=-,22451=-,即每个数为它的序号数的平方减1;(2)观察易得第①行的数加2得到第②行的数;第①行的数乘2得到第③行的数;(3)先表示出第①行的第n 个数21n -,再表示出第②、③行的第n 个数,然后求它们的和. 【答案】解:(1)2011=-,2321=-,2831=-,21541=-,22451=-,⋯; (2)第②行的数是第①行相应的数加2所得;第③行的数是第①行相应的数乘2所得; (3)2221122(1)n n n -+-++- 242n =-.【点睛】本题考查了规律型-数字的变化类:充分利用表中数据,分析它们之间的联系,然后归纳出一般的变化规律.【变式3-1】(2018秋•汉滨区期中)仔细观察下列三组数 第一组:1,4,9,16,25⋯⋯ 第二组:1,8,27,64,125⋯⋯ 第三组:2-,8-,18-,32-,50-⋯⋯ (1)写出每组的第6个数各是多少?(2)第二组的第100个数是第一组的第100个数的多少倍?(3)取每组的第20个数,计算这三个数的和.【分析】(1)第一组按21,22,23,24,排列,第二组按31,32,33,34,排列第三组,通过观察可以发现,此题实际上就是第一组中的数乘2-得来的;(2)利用(1)中规律得出第二组的第100个数是第一组的第100个数即可得出答案; (3)进而得出每组数的第20个数,即可得出答案. 【答案】解:(1)第一组按21,22,23,24,排列, 第二组按31,32,33,34,排列第三组按21(2)⨯-,22(2)⨯-,23(2)⨯-排列;∴每组的第6个数是:2636=,36216=,26(2)72⨯-=-;(2)第二组的第100个数是第一组的第100个数的32100100100÷=(倍); (3)每组数的第20个数分别为:220,320,220(2)⨯-232202020(2)∴++⨯- 322020=- 7600=.【点睛】此题主要考查了数字变化规律,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.第三组的规律最难找,要细心观察. 【变式3-2】(2018秋•福州期中)观察下列三行数,并完成后面的问题: ①2-,4,8-,16,32-,⋯; ②1,2-,4,8-,16,⋯; ③0,3-,3,9-,15⋯;(1)根据排列规律,分别写出上面三行数的第6个数;(2)设x 、y 、z 分别表示第①、②、③行数的第2019个数字,计算x y z ++的值.【分析】(1)利用数字的排列规律得到第①行数的第n 个数字为(2)n -,第②行数的第n 个数字为1(2)n --,第③行数的第n 个数字为1(2)1(n n ---为正整数),然后n 取6即可; (2)当n 取2019得到x 、y 、z 的值,然后计算它们的和.【答案】解:(1)第①行数的第6个数为64;第②行数的第6个数为32-;第③行数的第6个数为33-;(2)第①行数的第2019个数字为2019(2)-,即2019(2)x =-, 第②行数的第2019个数字为2018(2)-,即2018(2)y =-, 第③行数的第2019个数字为2018(2)1--,即2018(2)1z =--,所以20192018201820192018201820192019(2)(2)(2)122212211x y z ++=-+-+--=-++-=-+-=-.【点睛】本题考查了规律型:数字的变化类:探寻数列规律:认真观察、仔细思考,善用联想是解决这类问题的方法.【变式3-3】(2018秋•洪山区期中)观察下面三行数2-、 4 、8-、 16 、32-、 64 、⋯①0 、 6 、6-、 18 、30-、 66 、⋯② 5 、1-、11、13-、 35 、61-、⋯⋯③ (1) 第①行数的第 7 个数是 ;(2) 设第②行数中有一个数为a ,第③行数中对应位置的数为b ,则a 和b 之间等量关系为 ; 设第①行数的第n 个数为x ,取每行的第n 个数, 这三个数的和是 ; (3) 根据 (2) 中的结论, 若取每行的第 9 个数, 计算这三个数的和 .【分析】(1) 利用第①行数字的规律得到第①行数的第n 个数为(2)n-,然后n 取 7 即可得到第 7 个数; (2) 第②行和第③行的对应位置上的数的和为 5 ,从而得到a 与b 的关系;第①行数的第n 个数为x ,则第②行数的第n 个数为2x +,第③行数的第n 个数为3x -,然后把它们相加即可;(3) 由于第①行数的第 9 个数为9(2)-,即9(2)512x =-=-,然后利用 (2) 的结论计算这三个数的和 .【答案】解: (1) 第①行数的第 1 个数为1(2)-,第 2 个数为2(2)-,第 3 个数为3(2)-,第 4 个数为4(2)-,第 5 个数为5(2)-,第 6 个数为6(2)-,⋯ 所以第 7 个数为7(2)128-=-; (2)2b a =+;第①行数的第n 个数为x , 第②行数的第n 个数为2x +, 第③行数的第n 个数为3x -,所以这三个数的和235x x x x =+++-=+; 故答案为128-;2b a =+;5x +.(3) 第①行数的第 9 个数为9(2)-,即9(2)512x =-=-, 所以这三个数的和5125507=-+=-.【点睛】本题考查了规律型: 数字的变化类: 认真观察、 仔细思考, 利用数字与序号数的关系解决这类问题 .【考点4 三角形数阵中的排列规律】【例4】(2018秋•厦门期中)观察下面一组数:1-,2,3-,4,5-,6,7-,⋯,将这组数排成如图的形式,按照如图规律排下去,(1)第10行中从左边数第4个数是 ; (2)前7行的数字总和是 .【分析】(1)奇数为负,偶数为正,每行的最后一个数的绝对值是这个行的行数n 的平方,所以第9行最后一个数字的绝对值是81,第10行从左边第4个数是(814)85-+=-. (2)找到前7行的数字个数,再两个一组计算即可求解. 【答案】解:(1)2981=, (814)85-+=-.故第10行中从左边数第4个数是85-. 故答案为:85-;(2)2(135791112)21725++++++÷⨯-=-. 故前7行的数字总和是25-. 故答案为:25-.【点睛】本题是对数字变化规律的考查,观察出每一行的最后一个数的绝对值等于行数的平方是解题的关键.【变式4-1】(2018秋•江阴市期中)如图, 将正整数按如图所示规律排列下去, 若用有序数对(,)n m 表示n 排从左到右第m 个数 . 如(4,3)表示 9 ,则(20,8)表示 .【分析】根据(3,2)表示整数 5 ,对图中给出的有序数对进行分析, 可以发现: 对所有数对(,)[]m n n m …有:(m ,(1))(1231)2m m n m n n -=+++⋯+-+=+;由此方法解决问题即可 . 【答案】解: 若用有序数对(,)m n 表示从上到下第m 排, 从左到右第n 个数,对如图中给出的有序数对和(3,2)表示正整数 5 、(4,3)表示整数 9 可得,(3,3(31)2)252⨯-=+= (4,4(41)3)392⨯-=+=;⋯,由此可以发现, 对所有数对(,)m n (n m …)有:(m ,(1))(1231)2m m n m n n -=+++⋯+-+=+, 2019(20,8)81982⨯∴=+=. 故答案为: 198 .【点睛】此题考查对数字变化类知识点的理解和掌握, 解答此类题目的关键是根据题目中给出的图形、 数值、 数列等已知条件, 认真分析, 找出规律, 解决问题 .【变式4-2】(2018秋•上杭县期中)将整数按如图方式进行有规律的排列,第2行最后一个数是4-,第3行最后一个数是9,第4行最后一个数是16-,⋯,依此类推,第21行的第21个数是 .【分析】根据图形得出第n 行最后一个数为12(1)n n +-g ,据此知第20行最后一个数为400-,继而由奇数行的序数为奇数的数为正数可得答案.【答案】解:根据题意知第n 行最后一个数为12(1)n n +-g ,当20n =时,即第20行最后一个数为400-,又奇数行的序数为奇数的数为正数,∴第21行的第21个数是421,故答案为:421.【点睛】本题主要考查数字的变化规律,解题的关键是根据已知数列得出第n 行最后一个数为12(1)n n +-g .【变式4-3】(2018秋•二七区校级期中)观察如图中的数列排放顺序,根据其规律猜想:第10行第8个数应该是 .【分析】由n 行有n 个数,可得出第10行第8个数为第53个数,结合奇数为正偶数为负,即可求出结论.【答案】解:第1行1个数,第2行2个数,第3行3个数,⋯,∴第9行9个数,∴第10行第8个数为第1239853+++⋯++=个数.又Q 第21n -个数为21n -,第2n 个数为2n -,∴第10行第8个数应该是53.故答案为:53.【点睛】本题考查了规律型中数字的变化类,根据数的变化找出变化规律是解题的关键.【考点5 长方形数阵中的排列规律】【例5】(2018秋•高邮市期中)如图1,在五列若干行的表格中,将2、4、6、8、10、12、⋯⋯若干个偶数有规律的放入.(1)第7行第二列的数是.(2)若用a表示第三列的某一个数,则该数左上角的与右下角的两个数的和为;(3)若小颖用图2所示的33⨯的方框框住的9个数之和等于612,求这个方框内右下角的那个数.【分析】(1)本题的规律是第3列的数字每下一格是上一格多8,奇数行是从小到大,偶数行是从大到小;(2)第3列数的左上角与右上角的和都是中间数的2倍,依此即可求解;(3)框中间的数字是第3列的数字.【答案】解:(1)由题意得中间数字的规律为48(1)84+-=-n n当7n-=,n=时,8452因此第七行第3列为52,所以第七行第2列为50.故答案为:50;(2)由题意得第3列数的左上角与右上角的和都是中间数的2倍,即为2a.故答案为:2a;(3)设中间数为x,则这9个数的和为9612x=,解得68x=,n-=,8468解得9n=.所以68在第9行第3列上一个数为60,上一行为第8行,偶数行是从大到小,所以这个方框的右上角为58.【点睛】本题考查了关于数字的变化规律:先要观察各行各列的数字的特点,得出数字排列的规律,然后确定所给数字的位置.【变式5-1】(2018秋•新洲区期中)把2016个正整数1、2、3、4、⋯⋯、2016按如图方式排列成一个表,用一方框按如图所示的方式任意框住9个数.(方框只能平移)(1)若框住的9个数中,正中间的一个数为39,则:这九个数的和为.(2)方框能否框住这样的9个数,它们的和等于2016?若能,请写出这9个数;若不能,请说明理由.(3)若任意框住9个数的和记为S,则:S的最大值与最小值之差等于.【分析】(1)找出所框数字上下两行间的数量关系,左右数字间的数量关系,即可写出另外的八个数,进而求出它们的和;(2)由(1)可知方框框住这样的9个数的和是正中间的一个数的9倍,代入2016求出中间的数,由÷=,可得出224为32行的第7个数,即224后面不存在数,从而得出方框框住这样的9个数.它224732们的和不能等于2016;(3)分别求出S的最大值与最小值,再相减即可.【答案】解:(1)313233383940454647351++++++++=.故答案为:351;(2)设正中间的数为a,则a a a a a a a a a a-+-+-+-+++++++++=,(8)(7)(6)(1)(1)(6)(7)(8)9由题意得92016a=,解得224a=.=⨯Q,224732∴是表中第32行的最后一个数,224∴不能框住这样的9个数,它们的和等于2016;(3)若任意框住9个数的和记为S,则S的最小值为9981⨯=.Q,20167288÷=∴在第288行的最后一个数,2016⨯--=,S∴的最大值为9(201617)18072∴-=.180728117991即S的最大值与最小值之差为17991.故答案为:17991.【点睛】本题考查了一元一次方程的应用以及规律型中图形的变化类,观察表格,得出方框中框住的9个数与正中间数的关系是解题的关键.【变式5-2】(2018秋•黄陂区期中)如图(1)2018在第行,第列;(2)由五个数组成的“+”中:①这五个数的和可能是2019吗,为什么?②如果这五个数的和是60,直接写出这五个数;(3)如果这五个数的和能否是2025,若能请求出这5个数;若不能请说明理由.【分析】(1)观察图表,发现每9个数排成一行,用2018除以9,根据商与余数即可确定行数与列数;(2)①根据五个数的和是中间数的5倍,可知这五个数的和不可能是2019;②先根据五个数的和是中间数的5倍,求出中间数,再根据中间数与其它数的关系,求出其余4个数;(3)假设这五个数的和是2025,根据五个数的和是中间数的5倍,求出中间数是405,发现405在第9列,所以不存在.【答案】解:(1)201892242÷=⋯,故2018在第2241225+=行,第2列.故答案为:225,2;(2)①不可能,因为这五个数的和是中间数的5倍,而2019不是5的整数倍,所以这五个数的和不可能是2019.②60512÷=-=,129312111-=,+=,1211312921+=.故这五个数分别是3,11,12,13,21;(3)因为20255405=⨯,而405945=⨯,所以405在第45行,第9列,所以不存在.【点睛】本题考查了一元一次方程的应用以及规律型:数字的变化类,解题的关键是:(1)找出5个数的和与中间数的关系;(2)用含x 的代数式表示出其它4个数;(3)通过解一元一次方程来判定5个数的和能否为给定的各数.【变式5-3】(2018秋•雨花区校级期中)把正整数1,2,3,4⋯⋯,排列成如图1所示的一个表,从上到下分别称为第1行、第2行、⋯,从左到右分别称为第1列、第2列、⋯⋯.用图2所示的方框在图1中框住16个数,把其中没有被阴影覆盖的四个数分别记为A 、B 、C 、D .设A x =.(1)在图1中,2018排在第 行第 列;排在第m 行第n 列的数为 ,其中1m …,18n 剟,且都是正整数;(直接写出答案)(2)若23357A B D ++=,求出C 所表示的数;(3)在图(2)中,被阴影覆盖的这些数的和能否为4212?如果能,请求出这些数中最大的数,如果不能,请说明理由.【分析】(1)每行8个数,201882522=⨯+,2018排在第253行第2列;第m 行第8列数为8m ,第m 行第n 列为88m n +-;(2)设A x =,可以依据A 、B 、C 、D 四个数排列的规律依次用含x 的代数式表达,再根据题意列方程求解即可;(3)根据题意列方程求出x ,如果x 为正整数,并且不在第6、7、8列,才能符合题目要求.【答案】解:(1)201882522=⨯+Q ,2018排在第253行第2列;根据数字排列规律:第m 行最后一列数字为8m ,∴排在第m 行第n 列的数为88m n +-;故答案为:253,2;88m n +-;(2)由题意得:A x =,24B x =+,27C x =+,3D x =+,23357A B D ++=Q ,2(24)3(3)357x x x ∴++++=,解得:50x =,27502777C x ∴=+=+=.(3)这些数的和不能为4212;Q 被阴影覆盖的这些数的和1289101116171819252612162x x x x x x x x x x x x x =+++++++++++++++++++++++=+若121624212x +=,则337.5x =不是正整数,不符合题意.【点睛】本题关键要理解题意,弄清楚数字的排列规律.【考点6 数式求和—裂项法】【例6】(2018秋•开封期中)请观察下列算式,找出规律并填空:111122=-⨯,1112323=-⨯,1113434=-⨯,1114545=-⨯,⋯⋯则: (1)第10个算式是 ;(2)第n 个算式为 ;(3)根据以上规律解答下题:111112233420172018+++⋯⋯+⨯⨯⨯⨯ 【分析】(1)由已知等式得出:连续整数乘积的倒数等于较小整数倒数与较大整数的倒数的差,据此可得;(2)利用所得规律求解可得;(3)利用所得规律展开,两两相消求解可得.【答案】解:(1)根据题意知,第10个算式是11110111011=-⨯, 故答案为:11110111011=-⨯; (2)第n 个算式为111(1)1n n n n =-++, 故答案为:111(1)1n n n n =-++; (3)原式111111112233420172018=-+-+-+⋯+- 112018=- 20172018=. 【点睛】本题考查了数字的变化类题目,解决此类题目的关键是认真观察题目提供的算式,然后从中整理出规律,并利用此规律解题.【变式6-1】(2018秋•潮州期中)观察下列等式:111122=-⨯,1112323=-⨯,1113434=-⨯,将以上三个等式两边分别相加得:1111111113111223342233444++=-+-+-=-=⨯⨯⨯. (1)猜想并写出:1(1)n n =+ (2)直接写出下列各式的计算结果: ①111112233420112012+++⋯+=⨯⨯⨯⨯ ②1111122334(1)n n +++⋯+=⨯⨯⨯⨯+ (3)探究并计算:111124466820182020+++⋯+⨯⨯⨯⨯ 【分析】(1)先根据题中所给出的列子进行猜想,写出猜想结果即可;(2)根据①中的猜想计算出结果;(3)根据乘法分配律提取14,先拆项,再抵消即可求解; 【答案】解:(1)由111122=-⨯,1112323=-⨯,1113434=-⨯猜想出:111(1)1n n n n =-++; 故答案为:111n n -+; (2)直接写出下列各式的计算结果: ①11112011122334201120122012+++⋯+=⨯⨯⨯⨯, ②1111122334(1)1n n n n +++⋯+=⨯⨯⨯⨯++; 故答案为:20112012,1n n +; (3)111124466820182020+++⋯+⨯⨯⨯⨯ 11111111(1)42233410091010=-+-+-+⋯+- 1100941010=⨯ 10094040=. 【点睛】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.【变式6-2】(2018秋•兴庆区校级期中)观察下列等式: 第一个等式:1111(1)1323a ==⨯-⨯第二个等式:21111()35235a ==⨯-⨯ 第三个等式:31111()57257a ==⨯-⨯ ⋯⋯按以上规律解答下列问题:(1)列出第五个等式:5a =(2)计算12345a a a a a ++++的结果.(3)计算1231n n a a a a a -+++⋯⋯++的结果.【分析】(1)连续奇数乘积的倒数等于各自倒数差的一半,据此可得;(2)利用所得规律将原式裂项求和即可得;(3)利用所得规律将原式裂项求和即可得.【答案】解:(1)根据题意知,第5个等式为1111()9112911=⨯-⨯, 故答案为:1111()9112911=⨯-⨯. (2)12345a a a a a ++++11111111111111(1)()()()()232352572792911=⨯-+⨯-+⨯-+⨯-+⨯- 1111111111(1)23355779911=⨯-+-+-+-+- 11(1)211=⨯- 110211=⨯ 511=; (3)1231n n a a a a a -+++⋯⋯++11111111111(1)()()()2323525722121n n =⨯-+⨯-+⨯-+⋯⋯+⨯--+ 11111111(1)2335572121n n =⨯-+-+-+⋯+--+ 11(1)221n =⨯-+ 12221n n =⨯+ 21n n =+.【点睛】本题主要考查数字的变化规律,解题的关键是根据已知等式得出规律:1111()(2)22n n n n =-++. 【变式6-3】(2018秋•安徽期中)阅读并验证下列计算:1111212=-⨯,1112323=-⨯,1113434=-⨯,⋯ 计算:111112233420172018+++⋯+⨯⨯⨯⨯ 1111111112233420172018=-+-+-+⋯+- 112018=- 20172018= 理解上述解题力法,思考其中的规律,完成下列任务:(1)1111122334(1)n n +++⋯+=⨯⨯⨯⨯+ (直接填得数) (2)计算:111110111112121399100+++⋯+⨯⨯⨯⨯; (3)填空:①111113355720172019+++⋯+=⨯⨯⨯⨯ ; ②111114477103134+++⋯+=⨯⨯⨯⨯ . 【分析】(1)先根据得出的规律展开,再合并,最后求出即可;(2)先根据得出的规律展开,再合并,最后求出即可;(3)先根据得出的规律展开,再合并,最后求出即可.【答案】解:(1)11111111111111122334(1)22334111n n n n n n n +++⋯+=-+-+-+⋯+-=-=⨯⨯⨯⨯++++; (2)11111111111111910111112121399100101111121213991001010010+++⋯+=-+-+-+⋯+-=-=⨯⨯⨯⨯; (3)①111111111111111009(1)(1)1335572017201823355720172019220192019+++⋯+=⨯-+-+-+⋯+-=⨯-=⨯⨯⨯⨯; ②11111111111111(1)(1)144771031343447313433434+++⋯+=⨯-+-+⋯+-=⨯-=⨯⨯⨯⨯; 故答案为:1n n +;10092019;1134. 【点睛】本题考查了数字的变化类,有理数的混合运算,能根据已知算式得出规律是解此题的关键.【考点7 数式求和—等差类】【例7】(2018秋•赣榆区期中)问题探究:观察下面由“※”组成的图案和算式,解答问题:2213134()22++===22151359()32+++=== 2217135716()42++++=== ⋯问题解决:(1)试猜想1357949++++⋯+的结果为 ;(2)若n 表示正整数,请用含n 的代数式表示13579(21)(21)n n +++++⋯+-++的结果.问题拓展:(3)请用上述规律计算:1017101920172019++⋯++.【分析】(1)根据已知得出连续奇数的和等于数字个数的平方;(2)根据已知得出连续奇数的和等于数字个数的平方,得出答案即可;(3)利用以上已知条件得出1017101920132015(135********)(135********)++⋯++=+++⋯++-+++⋯++,求出即可.【答案】解:(1)221491357929()256252+++++⋯+===, 故答案为:625;(2)2212113579(21)(21)()(1)2n n n n +++++++⋯+-++==+; (3)1017101920132019++⋯++(135********)(135********)=+++⋯++-+++⋯++222019112015()()22++=- 221010508=-762036=.【点睛】此题主要考查了数字变化规律,培养学生通过特例分析从而归纳总结出一般结论的能力.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目的难点.【变式7-1】(2018秋•蒙城县期中)从2开始,连续的偶数相加,它们和的情况如下表:加数的个数n 连续偶数的和S(1)如果8n=时,那么S的值为;(2)根据表中的规律猜想:用n的代数式表示S的公式为:24682=++++⋯+=;S n(3)根据上题的规律计算30030230420102012+++⋯++的值(要有计算过程).【分析】(1)当8n=时,表示出S,计算得到S的值;(2)根据表格得到从2开始的偶数之和为偶数个数乘以个数加1,用n表示出即可;(3)将所求式子表示为(24629830030230420102012)(246298)+++⋯+++++⋯++-+++⋯+,用上述规律计算,即可得到结果.【答案】解:(1)当8S=+++++++=⨯=;n=时,那么2468101214168972(2)根据表格中的等式得:2468(1)=++++⋯++;S n n(3)30030230420102012+++⋯++=+++⋯+++++⋯++-+++⋯+ (24629830030230420102012)(246298)=⨯-⨯=-=.10061007149150101304222350990692故答案为:(1)72;(2)(1)n n+.【点睛】此题考查了规律型:数字的变化类,本题的规律为:从2开始的连续偶数之和为偶数个数乘以偶数个数加1.【变式7-2】(2018秋•殷都区期中)探索规律,观察下面由※组成的图案和算式,解答问题:2+==13422++==135932+++==13571642++++==13579255⋯(1)请猜想1357919+++++⋯+=;(2)请猜想13579(21)(21)(23)+++++⋯+-++++=;n n n(3)请计算:101103197199++⋯++.【分析】(1)(2)观察数据可知,从1开始的连续奇数的和等于首尾两个奇数的和的一半的平方,然后计算即可得解;(3)用从1开始到199的和减去从1开始到99的和,列式计算即可得解. 【答案】解:(1)21191357919()1002++++++⋯+==;(2)2212313579(21)(21)(23)()(2)2n n n n n +++++++⋯+-++++==+;(3)221199199101103197199()()100002500750022++++⋯++=-=-=.故答案为:100;2(2)n +.【点睛】本题是对数字变化规律的考查,观察出结果的底数与算式中首尾两个数的关系是解题的关键. 【变式7-3】(2018秋•射阳县期中)从2开始,连续的偶数相加,它们的和的情况如下表:加数m 的个数和()S1 212=⨯2 24623+==⨯3 2461234++==⨯4 24682045+++==⨯52468103056++++==⨯(1)按这个规律,当8m =时,和为(2)从2开始,m 个连续偶数相加,它们的和S 与m 之间的关系,用公式表示出来为 (3)应用上述公式计算 ①246200+++⋯+ ②102104106200+++⋯+【分析】(1)仔细观察给出的等式可发现从2开始连续两个偶数和12⨯,连续3个偶数和是23⨯,连续4个,5个偶数和为34⨯,45⨯,从而推出当8m =时,和的值;(2)根据分析得出当有m 个连续的偶数相加是,式子就应该表示成:2462(1)m m m +++⋯+=+. (3)根据已知规律进行计算,得出答案即可. 【答案】解:(1)2222+=⨯Q , 246232(21)+==⨯=⨯+, 24612343(31)++==⨯=⨯+, 246820454(41)+++==⨯=⨯+, 8m ∴=时,和为:8972⨯=;故答案为:72;(2)∴和S 与m 之间的关系,用公式表示出来:2462(1)m m m +++⋯+=+; 故答案为:(1)S m m =+; (3)①246200+++⋯+ 100101=⨯, 10100=;②24630015015122650+++⋯+=⨯=Q , 102104106200∴+++⋯+.(246200)(246100)=+++⋯+-+++⋯+ 101005051=-⨯,7550=.【点睛】此题主要考查了数字规律,要先从简单的例子入手得出一般化的结论,然后根据得出的规律去求特定的值是解题关键. 【考点8 数式求和—等比类】【例8】(2018秋•宝安区期中)(1)①观察一列数1,2,3,4,5,⋯,发现从第二项开始,每一项与前一 项之差是一个常数,这个常数是 ;根据此规律,如果(n a n 为正整数)表示这个数列的第n 项,那么 18a = ,n a = ;②如果欲求1234n ++++⋯+的值,可令1234S n =++++⋯+⋯① 将①式右边顺序倒置,得4321S n =+⋯++++⋯② 由②加上①式,得2S = ; S ∴= ;由结论求123455++++⋯+= ;(2)①观察一列数2,4,8,16,32,⋯,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果(n a n 为正整数)表示这个数列的第n 项,那么18a = ,n a = ; ②为了求23201813333++++⋯⋯+的值,可令23201813333M =++++⋯⋯+,则 23201933333M =+++⋯⋯+,因此2019331M M -=-,所以2019312M -=,即 201923201831133332-++++⋯⋯+=. 仿照以上推理,计算235115555++++⋯⋯+【分析】(1)①根据数列中每一项与前一项之差是1求解可得;②将对应位置的数相加,其和为1n +,共n 个数,再将两边除以2即可得; (2)①根据数列中每一项与前一项之比是2求解可得;②令235115555M =++++⋯⋯+,将等式两边乘以5后相减,再进一步求解可得.【答案】解:(1)①数列1,2,3,4,5,⋯中,每一项与前一项之差是一个常数,这个常数是1, 如果(n a n 为正整数)表示这个数列的第n 项,那么1818a =,n a n =; ②令1234S n =++++⋯+⋯①将①式右边顺序倒置,得4321S n =+⋯++++⋯② 由②加上①式,得2(1)S n n =+; (1)2n n S +∴=, 由结论求555612345515402⨯++++⋯+==, 故答案为:①1,18,n ;②(1)n n +,(1)2n n +,1540; (2)①数列2,4,8,16,32,⋯,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是2, 如果(n a n 为正整数)表示这个数列的第n 项,那么18182a =,2n n a =; ②令235115555M =++++⋯⋯+, 则235255555M =+++⋯⋯+, 52551M M ∴-=-, 52451M ∴=-,∴52514M -=,即52235151155554-++++⋯⋯+=.故答案为:①2,182,2n .【点睛】本题主要考查数字的变化规律,解题的关键是掌握两个数列中的等差和等比的规律,并熟练掌握求和的方法.【变式8-1】(2018秋•和平区期中)观察下列各等式: 312111124==⨯⨯33221129234+==⨯⨯33322112336344++==⨯⨯⋯用你发现的规律解答下列问题:(1)填空:333331123(1)(4n n +++⋯+-+=⨯ 2)(⨯ 2)(n 为正整数);(2)计算:①333331234950+++⋯++; ②3333324698100+++⋯++【分析】(1)括号内是两个连续的自然数,最小的数与等号左边的最大底数相同; (2)①根据规律得所有底数和的平方,计算即可; ②提公因式32,可得结论.【答案】解:(1)33333221123(1)(1)(4n n n n n +++⋯+-+=⨯⨯+为正整数);故答案为:n ,1n +; (2)计算:①333331234950+++⋯++;2(12350)=+++⋯+, 250(501)[]2+=, 21275=, 1625625=,②3333324698100+++⋯++,333332(12350)=+++⋯+,81625625=⨯,13005000=.【点睛】此题考查算式的规律,注意结果与等式左边的各个数的关系是解题的关键,并进一步利用规律解决问题.【变式8-2】(2019秋•中原区校级期中)观察下面的几个式子 23131⨯=⨯223(12)5(12)⨯+=⨯+ 2223(123)7(123)⨯++=⨯++ 22223(1234)9(1234)⨯+++=⨯+++(1)根据上面的规律,第5个式子为: ; (2)根据上面的规律,第n 个式子为: ;(3)利用你发现的规律写出2222123n +++⋯+= ;(4)利用你发现的规律求出22222135739++++⋯+的值并写出过程. 【分析】(1)根据已知等式的规律可得; (2)根据已知等式的规律可得;(3)将(2)中所得等式两边都除以3,再整理可得; (4)将原式变形为2222222222222222123440(2440)1234404(1220)++++⋯+-++⋯+=++++⋯+-⨯++⋯+, 利用所得规律计算可得.【答案】解:(1)第5个式子为:222223(12345)11(12345)⨯++++=⨯++++, 故答案为:222223(12345)11(12345)⨯++++=⨯++++;(2)根据上面的规律,第n 个式子为:222223(1234)(21)(1234)n n n ⨯++++⋯+=+⨯++++⋯+, 故答案为:222223(1234)(21)(1234)n n n ⨯++++⋯+=+⨯++++⋯+; (3)2222(21)(123)1(1)(1)(21)123(21)3326n n n n n n n n n ++++⋯+++++++⋯+==⨯+⨯=, 故答案为:(1)(21)6n n n ++;(4)原式22222222123440(2440)=++++⋯+-++⋯+。
专题 整式的乘除章末重难点题型(举一反三)(原卷版)

专题 整式的乘除章末重难点题型【考点1 幂的基本运算】【方法点拨】同底数幂的乘法法则:nm nmaa a +=•(n m ,都是正整数)同底数幂相乘,底数不变,指数相加。
注意底数可以是多项式或单项式。
幂的乘方法则:mnnm aa =)((n m ,都是正整数)幂的乘方,底数不变,指数相乘。
积的乘方法则:nnnb a ab =)((n 是正整数) 积的乘方,等于各因数乘方的积。
同底数幂的除法法则:nm nmaa a -=÷(n m a ,,0≠都是正整数,且)n m同底数幂相除,底数不变,指数相减。
【例1】(黔东南州期中)下列运算正确的是( ) A .x 2+x 3=x 5 B .(﹣2a 2)3=﹣8a 6C .x 2•x 3=x 6D .x 6÷x 2=x 3【变式1-1】(蜀山区期中)下列运算中,正确的是( ) A .3x 3•2x 2=6x 6 B .(﹣x 2y )2=x 4y C .(2x 2)3=6x 6D .x 5÷x =2x 4【变式1-2】(淄博期中)下列运算正确的是( ) A .a 2•a 3=a 6B .(﹣a 2)3=﹣a 5C .a 10÷a 9=a (a ≠0)D .(﹣bc )4÷(﹣bc )2=﹣b 2c 2【变式1-3】(成安县期中)下列运算正确的是( ) A .(﹣2ab )•(﹣3ab )3=﹣54a 4b 4 B .5x 2•(3x 3)2=15x 12C .(﹣0.16)•(﹣10b 2)3=﹣b 7D .(2×10n )(×10n )=102n【考点2 因式分解的概念】 【方法点拨】因式分解:(1)把一个多项式化成几个整式的积的形式,叫做把这个多项式因式分解,也叫把这个多项式分解因式. (2)分解因式是对多项式而言的,且分解的结果必须是整式的积的形式. (3)分解因式时,其结果要使每一个因式不能再分解为止.。
《点拨》 第三章 一元一次方程 基础复习

第三章一元一次方程复习一、自主检测1.(2008·温州)方程3x的解是( )-4=1A.1-x D.2=x==x B.1=x C.2-2.(2010·泸州)若23=-m的解,则m的值为( )1=20x是关于x的方程+x1A.-1 B.0 C.1 D.33.(2009·吉林)A种饮料比B种饮料单价少1元,小峰买了2瓶A种饮料和3瓶B种饮料,一共花了13元.如果设B种饮料为x元/瓶,那么下面所列方程正确的是( ) A.13(2=)1+xx3+)13(2=+-xx B.13C.132=(3-+xx)1+xx D.13)12=(3+*4.(2009·张家界)对于正实数a,b作新定义:b-a+*,在此定义下,若9 *=bbaax=55,则x的值为______.5.(2010·泸州)由于电子技术的飞速发展,计算机的成本不断降低,若每隔3年计算机的1,现价为2400元的某款计算机,3年前的价格为______元.价格降低36.(2008·济南)解方程:0-+x.1(2=)17.(2008·北京)京津城际铁路将于2008年8月1日开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京的行驶时间与预计时间相同,如果这次试车时,由天津返回北京比去天津时平均每小时多行驶40千米,那么这次试车时由北京到天津的平均速度是每小时多少千米?二、考点典例考点1:方程的相关概念及等式的性质典例1 下列各式不是方程的是( )A .1373=+xB .014=--m xC .532=+D .35=+y x考点2:一元一次方程的解法(重点)典例2 (2010·泰安模拟)解方程:151423=+--x x考点3:-元一次方程的应用(重点,热点)典例3 (2009·北京)列方程或方程组解应用题:北京市实施交通管理新措施以来,全市公共交通客运量显著增加.据统计,2008年10月11日至2009年2月28日期间,地面公交日均客运量与轨道交通日均客运量总和为1696万人次,地面公交日均客运量比轨道交通日均客运量的4倍少69万人次,在此期间,地面公交和轨道交通日均客运量各为多少万人次?三、课标新题课标新型题一:最佳方案设计题【例1】(热点题)为庆祝新中国成立六十周年,甲、乙两个班统一组织文艺演出(每名学生都参加),甲和乙两个班共92人(其中甲班人数多于乙班人数,且甲班人数不够90人),现准备统一购买演出服装,下面是某服装厂给出的演出服装的价格表:如果两个班单独购买服装,一共应付5000元.(1)甲、乙两个班各有多少学生?(2)如果甲班有10名学生被抽调去参加书法绘画比赛以致不能参加演出,请你为两个班设计一种最省钱的购买服装的方案.课标新型题二:计算评估题【例2】学习了一元一次方程后,甲、乙、丙、丁四位同学解方程x x 535.044.2=--, 他们的解法分别如下: 甲的解法:把小数化为整数,得x x 65424=--,去分母,得x x 30)4(120=--,去括号,得x x 304120=+-,移项,合并同类项,得12431-=-x ,系数化为1,得4=x . 乙的解法:原方程化为x x 5354010512=--,去分母,得12-x x 3)4010(=-,去括号,得x x 3401012=+-,移项,合并同类项,得5213-=-x ,系数化为l ,得4=x . 丙的解法:原方程化为x x 5354010512=--,去分母,得12+x x 34010=-,移项,合并同类项,得287=x ,系数化为1,得x =4.丁的解法:原方程化为x x 6.02)4(4.2=⨯--,去括号,得x x 6.0824.2=+-,移项,合并同类项,得4.106.2-=-x ,系数化为1,得x =4.以上四位同学的结果都相同,能说明他们的解法是正确的吗?若他们的解法有问题,请指出来.四、易错专攻1.(易混点,2010·河北)小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的1元纸币为x 张,根据题意,下面所列方程正确的是( )A .48)12(5=-+x xB .48)12(5=-+x xC .48)5(12=-+x xD .48)12(5=-+x x2.(易误点)方程512+-=-x x 的解为______.3.(易混点)已知2是关于x 的方程02=-a x 的解,则a 的值为______.4.(易混点,2009·重庆)某公司销售A ,B ,C 三种产品,在去年的销售中,高新产品C 的销售金额占总销售金额的40%.由于受国际金融危机的影响,今年A ,B 两种产品的销售金额都将比去年减少20%,因而高新产品C 是今年销售的重点.若要使今年的总销售金额与去年持平,那么今年高新产品C 的销售金额应比去年增加______%.5.(易漏点)解方程:246231x x x -=+--五、过关测试一、选择题1.(2010·宁波模拟)方程012=+x 的解是( )A .21=xB .21-=x C .2=x D .2-=x 2.下列方程是一元一次方程的是( )A .8=xyB .752=+C .2312+=+x x D .623=+y x 3.已知等式mb ma =,下列变形正确的是( )A .b a =B .11-=+mb maC .mb ma -=D .mb ma -=-114.(2010·长沙模拟)关于x 的方程032312=--=+x a x 与的解相同,则a 的值是( ) A .7 B .O C .1 D .-15.解方程6)]12()1[(2)23(=+--++x x x ,得x 等于( )A.2B.4C.6D.8二、填空题6.(2010·苏州)若代数式73+x 的值为-2,则x =______.7.如果312=-x ,823=+y ,那么y x 32+=______.8.某商店销售一批服装,每件售价150元,打8折出售后,每件仍可获利20元,设这种服装的成本价为每件x 元,则x 满足的方程是____________________.三、解答题9.解方程:(1))1()23(21--=-x x (2)12.01.023.03-=+--x x四、课标新型题10.(定义新运算)a ,b ,c ,d 为实数,现规定一种新的运算:bc ad d c b a-=,那么当185)1(42=-x 时,x =______.。
高三数学考点-二元一次不等式(组)与简单的线性规划问题

7.3二元一次不等式(组)与简单的线性规划问题1.二元一次不等式表示的平面区域(1)一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的________.我们把直线画成虚线以表示区域________边界直线.当我们在坐标系中画不等式Ax+By+C≥0所表示的平面区域时,此区域应________边界直线,则把边界直线画成________.(2)由于对直线Ax+By+C=0同一侧的所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得的符号都________,所以只需在此直线的同一侧取一个特殊点(x0,y0)(如原点)作为测试点,由Ax0+By0+C的________即可判断Ax +By+C>0表示的是直线Ax+By+C=0哪一侧的平面区域.2.线性规划(1)不等式组是一组对变量x,y的约束条件,由于这组约束条件都是关于x,y的一次不等式,所以又可称其为线性约束条件.Z=Ax+By是要求最大值或最小值的函数,我们把它称为________.由于Z=Ax+By是关于x,y的一次解析式,所以又可叫做________.另外注意:线性约束条件除了用一次不等式表示外,也可用一次方程表示.(2)一般地,求线性目标函数在线性约束条件下的________的问题,统称为线性规划问题.(3)满足线性约束条件的解(x,y)叫做________,由所有可行解组成的集合叫做________.其中,使目标函数取得最大值或最小值的可行解都叫做这个问题的________.线性目标函数的最值常在可行域的边界上,且通常在可行域的顶点处取得;而求最优整数解首先要看它是否在可行域内.(4)用图解法解决简单的线性规划问题的基本步骤:①首先,要根据_________________ (即画出不等式组所表示的公共区域).②设__________,画出直线l0.③观察、分析、平移直线l0,从而找到最优解.④最后求得目标函数的__________.(5)利用线性规划研究实际问题的解题思路:首先,应准确建立数学模型,即根据题意找出__________条件,确定__________函数.然后,用图解法求得数学模型的解,即__________,在可行域内求得使目标函数__________.自查自纠1.(1)平面区域不包括包括实线(2)相同符号2.(1)目标函数线性目标函数(2)最大值或最小值(3)可行解可行域最优解(4)①线性约束条件画出可行域②z=0④最大值或最小值(5)约束线性目标画出可行域取得最值的解(2016·济南模拟)已知点(-3,-1)和点(4,-6)在直线3x -2y -a =0的两侧,则a 的取值范围为( ) A .(-24,7) B .(-7,24)C .(-∞,-7)∪(24,+∞)D .(-∞,-24)∪(7,+∞)解:根据题意知(-9+2-a )(12+12-a )<0,即(a +7)(a -24)<0,解得-7<a <24.故选B .(2017·全国卷Ⅲ)设x ,y 满足约束条件⎩⎪⎨⎪⎧3x +2y -6≤0,x ≥0,y ≥0,则z =x -y 的取值范围是( )A .[-3,0]B .[-3,2]C .[0,2]D .[0,3]解:绘制不等式组表示的可行域,结合目标函数的几何意义可得函数在点A (0,3) 处取得最小值z =0-3=-3. 在点B (2,0) 处取得最大值z =2-0=2.故选B .(2016·北京)若x ,y 满足⎩⎪⎨⎪⎧2x -y ≤0,x +y ≤3,x ≥0,则2x +y 的最大值为( )A .0B .3C .4D .5解:作出可行域如图中阴影部分所示,则当z =2x +y 经过点P (1,2)时,取最大值,z max =2×1+2=4.故选C .(2017·全国卷Ⅲ)若x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥0,x +y -2≤0,y ≥0,则z =3x -4y 的最小值为________.解:由题意,画出可行域如图,目标函数为z =3x -4y ,则直线y =34x -z4纵截距越大,z 值越小.由图可知,在A (1,1)处取最小值,故z min =3×1-4×1=-1.故填-1.(2017届云南四川贵州百校大联考)设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y -2≥0,2x +y -4≤0,4x -y +1≥0,则目标函数z =y -3x 的最大值是________.解:作可行域如图所示,由目标函数z=y-3x得直线y=3x+z,当直线y=3x+z平移经过点A⎝⎛⎭⎫12,3时,目标函数z=y-3x取得最大值为32.故填32.类型一二元一次不等式(组)表示的平面区域(2016·郑州模拟)在平面直角坐标系xOy中,满足不等式组⎩⎪⎨⎪⎧|x|≤|y|,|x|<1的点(x,y)的集合用阴影表示为下列图中的()解:|x|=|y|把平面分成四部分,|x|≤|y|表示含y轴的两个区域;|x|<1表示x=±1所夹含y轴的区域.故选C.【点拨】关于不等式组所表示的平面区域(可行域)的确定,可先由“直线定界”,再由“不等式定域”,定域的常用方法是“特殊点法”,且一般取坐标原点O(0,0)为特殊点.不等式组⎩⎪⎨⎪⎧x+y-2≥0,x+2y-4≤0,x+3y-2≥0表示的平面区域的面积为________.解:不等式组所表示的平面区域如图中阴影部分所示,易求得|BD|=2,C点坐标(8,-2),所以S△ABC=S△ABD+S△BCD=12×2×(2+2)=4.故填4.类型二利用线性规划求线性目标函数的最优解(2017·天津)设变量x,y满足约束条件⎩⎪⎨⎪⎧2x+y≥0,x+2y-2≥0,x≤0,y≤3,则目标函数z=x+y的最大值为()A.23 B .1 C.32D .3解:可行域为四边形ABCD 及其内部,所以直线z =x +y 过点B (0,3)时取最大值3.故选D .【点拨】线性规划问题有三类:(1)简单线性规划,包括画出可行域和考查截距型目标函数的最值,有时考查斜率型或距离型目标函数;(2)线性规划逆向思维问题,给出最值或最优解个数求参数取值范围;(3)线性规划的实际应用. 一般情况下,目标函数的最大或最小值会在可行域的端点或边界上取得.(2017·北京)若x ,y 满足⎩⎪⎨⎪⎧x ≤3,x +y ≥2,y ≤x , 则x + 2y 的最大值为( )A .1B .3C .5D .9解:如图,画出可行域,z =x +2y 表示斜率为-12的一组平行线,当过点C (3,3)时,目标函数取得最大值z max=3+2×3=9.故选D .类型三 含参数的线性规划问题(1)(北京西城区2017届期末)实数x ,y 满足⎩⎪⎨⎪⎧x ≤3,x +y ≥0,x -y +6≥0. 若z =ax +y 的最大值为3a +9,最小值为3a-3,则a 的取值范围是( ) A .[-1,0] B .[0,1]C .[-1,1]D .(-∞,-1]∪[1,+∞)解:作出不等式组对应的平面区域如图,由z =ax +y 得y =-ax +z .因为z =ax +y 的最大值为3a +9,最小值为3a -3, 所以当直线y =-ax +z 经过点B (3,9)时直线截距最大, 当经过点A (3,-3)时,直线截距最小. 则直线y =-ax +z 的斜率-a 满足, -1≤-a ≤1,即-1≤a ≤1.故选C .(2)在平面直角坐标系中,若不等式组⎩⎪⎨⎪⎧x +y -1≥0,x -1≤0,ax -y +1≥0 (a 为常数)所表示的平面区域的面积等于2,则a 的值为( )A .-5B .1C .2D .3解:如图可得阴影部分即为满足x -1≤0与x +y -1≥0的可行域,而直线ax -y +1=0恒过点(0,1),故看作直线绕点(0,1)旋转,若不等式组所表示的平面区域内的面积等于2,则它是三角形,设该三角形为△ABC ,因为△ABC 的点A 和B的坐标分别为A (0,1)和B (1,0),且S △ABC =2,设点C 的坐标为C (1,y ),则12×1×y =2⇒y =4,将点C (1,4)代入ax -y +1=0得a =3.故选D .【点拨】例3(1)考查了简单的线性规划中的斜率问题,通过y =-ax +z 得到参数-a 是动直线y =-ax +z 的斜率,z =ax +y 的最大值为3a +9,则动直线y =-ax +z 纵截距的最大值为3a +9,最优解在三个端点处取得;例3(2)中的ax -y +1=0,即为y =ax +1,其中a 为动直线的斜率,利用数形结合的方法求解.注意把握两点:①参数的几何意义;②条件的合理转化.(1)已知x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥0,x +y ≤2,y ≥0. 若z =ax +y 的最大值为4,则a =( )A .3B .2C .-2D .-3解:画出不等式组所表示的可行域如图中阴影部分所示,因为目标函数z =ax +y 的最大值为4,即目标函数对应直线与可行域有公共点时,在y 轴上的截距的最大值为4,所以作出过点D (0,4)的直线,由图可知,目标函数在点B (2,0)处取得最大值,有a ×2+0=4,得a =2.故选B .(2)若变量x ,y 满足约束条件⎩⎪⎨⎪⎧y ≤x ,x +y ≤4,y ≥k ,且z =2x +y 的最小值为-6,则k =________.解:易得出约束条件中三条直线两两所成的交点(k ,k ),(4-k ,k ),(2,2),且可行域如图,则k ≤2.最小值在点(k ,k )处取得,3k =-6,得k =-2.故填-2.类型四 非线性目标函数的最优解问题(2016·江苏)已知实数x ,y 满足⎩⎪⎨⎪⎧x -2y +4≥0,2x +y -2≥0,3x -y -3≤0,则x 2+y 2的取值范围是________.解:可行域如图中阴影部分所示,x 2+y 2为可行域中任一点(x ,y )到原点(0,0)的距离的平方.由图可知,x 2+y 2的最小值为原点到直线AC 的距离的平方,即⎝ ⎛⎭⎪⎫|-2|52=45.易求得B (2,3),最大值为OB 2=22+32=13.故填⎣⎡⎦⎤45,13. 【点拨】线性规划问题,首先明确可行域对应的是封闭区域还是开放区域,分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值或范围.即:一画,二移,三求.其关键是准确作出可行域,理解目标函数的意义.常见的目标函数有:(1)截距型:形如z =ax +by .求这类目标函数的最值常将函数z =ax +by 转化为直线的斜截式:y =-a b x +zb ,通过求直线的截距的最值间接求出z 的最值.(2)距离型:形如z =(x -a )2+(y -b )2 .(3)斜率型:形如z =y -bx -a ,本题属于距离形式.(2015·全国卷Ⅰ)若x ,y 满足约束条件⎩⎪⎨⎪⎧x -1≥0,x -y ≤0,x +y -4≤0,则yx的最大值为________.解:作出可行域如图中阴影部分所示,由斜率的意义知,yx是可行域内一点与原点连线的斜率,由图可知,点A (1,3)与原点连线的斜率最大,故yx的最大值为3.故填3.类型五 线性规划与整点问题设实数x ,y 满足不等式组⎩⎪⎨⎪⎧x +2y -5>0,2x +y -7>0,x ≥0,y ≥0, 若x ,y 为整数,则3x +4y 的最小值为( )A .14B .16C .17D .19解:画出可行域如图,令3x +4y =z ,y =-34x +z4,过x 轴上的整点(1,0),(2,0),(3,0),(4,0),(5,0)处作格子线,可知当y =-34x +z4过(4,1)时有最小值(对可疑点(3,2),(2,4),(4,1)逐个试验),此时z min =3×4+4=16.故选B .【点拨】求解整点问题,对作图精度要求较高,可行域内的整点要找准,最好使用“网点法”先作出可行域中的各整点.设不等式组⎩⎪⎨⎪⎧x >0,y >0,y ≤-nx +3n (n ∈N *) 所表示的平面区域为D n ,记D n 内的整点(即横坐标和纵坐标均为整数的点)个数为a n (a n ∈N *),则数列{a n }的通项公式为a n =______.解:直线y =-nx +3n =-n (x -3),过定点(3,0),由y =-nx +3n >0得x <3,又x >0,所以x =1或x =2.直线x =2交直线y =-nx +3n 于点(2,n ),直线x =1交直线y =-nx +3n 于点(1,2n ),所以整点个数a n =n +2n =3n .故填3n.类型六 线性规划在实际问题中的应用(2015·陕西)某企业生产甲、乙两种产品均需用A ,B 两种原料.已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )甲 乙 原料限额 A (吨) 3 2 12 B (吨)128A.12万元 B .16万元 C .17万元 D .18万元解:设每天生产甲、乙两种产品分别为x 、y 吨,利润为z 元,则⎩⎪⎨⎪⎧3x +2y ≤12,x +2y ≤8,x ≥0,y ≥0,目标函数为z =3x +4y .作出二元一次不等式组所表示的平面区域(阴影部分),即可行域.由z =3x +4y 得y =-34x +z 4,平移直线y =-34x 至经过点B 时,直线y =-34x +z4的纵截距最大,此时z 最大,解方程组⎩⎪⎨⎪⎧3x +2y =12,x +2y =8, 得⎩⎪⎨⎪⎧x =2,y =3, 即B (2,3).所以z max =3x +4y =6+12=18.即每天生产甲、乙两种产品分别为2吨、3吨,能够获得最大利润,最大的利润是18万元.故选D . 【点拨】对于此类有实际背景的线性规划问题,可行域通常是位于第一象限的一个凸多边形区域,此时变动直线的最佳位置一般通过这个凸多边形在第一象限的某个顶点.(2016·全国卷Ⅰ)某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料.生产一件产品A 需要甲材料1.5 kg ,乙材料1 kg ,用5个工时;生产一件产品B 需要甲材料0.5 kg ,乙材料0.3 kg ,用3个工时.生产一件产品A 的利润为2 100元,生产一件产品B 的利润为900元.该企业现有甲材料150 kg ,乙材料90 kg ,则在不超过600个工时的条件下,生产产品A 、产品B 的利润之和的最大值为________元.解:设某高科技企业生产产品A 和产品B 分别为x 件,y 件,生产产品A 、产品B 的利润之和为z 元,依题意得⎩⎪⎨⎪⎧1.5x +0.5y ≤150,x +0.3y ≤90,5x +3y ≤600,x ∈N ,y ∈N , 即⎩⎪⎨⎪⎧3x +y ≤300,10x +3y ≤900,5x +3y ≤600,x ∈N ,y ∈N ,目标函数z =2 100x +900y .作出可行域如图所示.当直线z =2 100x +900y经过点M (60,100)时,z 取得最大值.z max =2 100×60+900×100=216 000.故生产产品A 、产品B 的利润之和的最大值为216 000元.故填216 000.1.解客观题可利用特殊点判断二元一次不等式(组)表示的平面区域所在位置,如果直线Ax +By +C =0不经过原点,则把原点代入Ax +By +C ,通过Ax +By +C 的正负和不等号的方向,来判断二元一次不等式(组)表示的平面区域所在的位置.2.求目标函数z =ax +by (ab ≠0)的最值,将函数z =ax +by 转化为直线的斜截式:y =-a b x +zb,通过求直线的截距z b 的最值间接求出z 的最值.最优解一般在顶点或边界取得.但要注意:①当b >0时,截距zb取最大值,z 也取最大值;截距z b 取最小值,z 也取最小值;②当b <0时,截距z b 取最大值,z 取最小值;截距zb 取最小值时,z 取最大值.3.如果可行域是一个多边形,那么一般在其顶点处目标函数取得最大值或最小值.最优解一般是多边形的某个顶点,到底是哪个顶点为最优解,有三种解决方法:第一种方法:将目标函数的直线平行移动,最先通过或最后通过可行域的一个便是. 第二种方法:利用围成可行域的直线斜率来判断.特别地,当线性目标函数的直线与可行域某条边重合时,其最优解可能有无数组.第三种方法:将可行域所在多边形的每一个顶点P i 逐一代入目标函数Z P i =mx +ny ,比较各个ZP i ,得最大值或最小值.1.(2015·烟台模拟)不等式组⎩⎪⎨⎪⎧y ≤-x +2,y ≤x -1,y ≥0所表示的平面区域的面积为( )A .1 B.12 C.13 D.14解:作出不等式组对应的区域为如图△BCD ,由题意知x B =1,x C =2.由⎩⎪⎨⎪⎧y =-x +2,y =x -1, 得y D =12,所以S △BCD =12×(x C -x B )×12=14.故选D . 2.(湖北孝感市2017届期中)已知实数x ,y 满足⎩⎪⎨⎪⎧y ≤x ,x +y ≤1,y ≥-1, 则目标函数z =2x -y 的最大值为( )A .-3 B.12 C .5 D .6解:作出不等式组表示的平面区域,得到如图的△ABC 及其内部,其中A (-1,-1),B (2,-1),C (0.5,0.5),将直线2x -y =0进行平移,当其经过点B 时,目标函数z 达到最大值.所以z 最大值=5.故选C .3.(2016·天津)设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x -y +2≥0,2x +3y -6≥0,3x +2y -9≤0.则目标函数z =2x +5y 的最小值为( )A .-4B .6C .10D .17解:可行域为一个三角形ABC 及其内部,其中A (0,2),B (3,0),C (1,3),根据目标函数的几何意义,可知当直线y =-25x +z5过点B (3,0)时,z 取得最小值2×3-5×0=6.故选B .4.(2017·浙江)若x ,y 满足约束条件⎩⎪⎨⎪⎧x ≥0,x +y -3≥0,x -2y ≤0,则z =x +2y 的取值范围是( )A .[0,6]B .[0,4]C .[6,+∞)D .[4,+∞)解:如图,可行域为一开放区域,所以直线过点(2,1)时取最小值4,无最大值.故选D .5.(2016·浙江)在平面上,过点P 作直线l 的垂线所得的垂足称为点P 在直线l 上的投影.由区域⎩⎪⎨⎪⎧x -2≤0,x +y ≥0,x -3y +4≥0中的点在直线x +y -2=0上的投影构成的线段记为AB ,则|AB |=( ) A .2 2 B .4 C .3 2 D .6解:如图△PQR 为线性区域,区域内的点在直线x +y -2=0上的投影构成了线段AB .由⎩⎪⎨⎪⎧x -3y +4=0,x +y =0得Q (-1,1),由⎩⎪⎨⎪⎧x =2,x +y =0得R (2,-2),|AB |=|RQ |=(-1-2)2+(1+2)2=3 2.故选C .6.(2016·商丘模拟)已知a >0,x ,y 满足约束条件⎩⎪⎨⎪⎧x ≥1,x +y ≤3,y ≥a (x -3),若z =2x +y 的最小值为1,则a =( )A.14B.12C .1D .2解:作出可行域如图中阴影部分所示,当直线z =2x +y 通过A (1,-2a )时,z 取最小值,z min =2×1+(-2a )=1,所以a =12.故选B .7.(2016·全国卷Ⅲ)若x ,y 满足约束条件⎩⎪⎨⎪⎧x -y +1≥0,x -2y ≤0,x +2y -2≤0,则z =x +y 的最大值为________.解:画出可行域,如图所示阴影部分,易得A (0,1),B (-2,-1),C ⎝⎛⎭⎫1,12,可得z =x +y 在C 点处取得最大值为32.故填32.8.(山西四校2017届联考)已知y =-2x -z 满足约束条件⎩⎪⎨⎪⎧x +y -2≤0,x -2y -2≤0,2x -y +2≥0, 若2x +y +k ≥0恒成立,则实数k的取值范围为________.解:可行域为一个三角形ABC 及其内部,其中A (2,0),B (-2,-2),C (0,2),直线z =-2x -y 过点B 时取最大值6,而2x +y +k ≥0恒成立等价于k ≥[-(2x +y )]max =6.故填[6,+∞).9.(2016·昆明模拟)已知变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥0,x -2y +2≥0,x -y ≤0,求z =2x -y 的最大值.解:作出可行域如图中阴影部分所示.当直线过点B (2,2)时,z =2x -y 取得最大值2.10.变量x ,y 满足⎩⎪⎨⎪⎧x -4y +3≤0,3x +5y -25≤0,x ≥1.(1)假设z 1=4x -3y ,求z 1的最大值;(2)设z 2=yx ,求z 2的最小值;(3)设z 3=x 2+y 2,求z 3的取值范围.解:作出可行域如图中阴影部分,联立易得A ⎝⎛⎭⎫1,225,B (1,1),C (5,2). (1)z 1=4x -3y ⇔y =43x -z 13,易知平移y =43x 至过点C 时,z 1最大,且最大值为4×5-3×2=14.(2)z 2=y x 表示可行域内的点与原点连线的斜率大小,显然直线OC 斜率最小.故z 2的最小值为25.(3)z 3=x 2+y 2表示可行域内的点到原点距离的平方,而2=OB 2<OA 2<OC 2=29.故z 3∈[2,29].11.(2015·广东模拟)某工厂生产甲、乙两种产品,每种产品都有一部分是一等品,其余是二等品,已知甲产品为一等品的概率比乙产品为一等品的概率大0.25,甲产品为二等品的概率比乙产品为一等品的概率小0.05. (1)分别求甲、乙产品为一等品的概率P 甲,P 乙;(2)已知生产一件产品需要用的工人数和资金数如表所示,且该厂有工人32名,可用资金55万元.设x,y分工人(名)资金(万元)甲420乙85解:(1)依题意得⎩⎪⎨⎪⎧甲乙1-P甲=P乙-0.05,解得⎩⎪⎨⎪⎧P甲=0.65,P乙=0.4,故甲产品为一等品的概率P甲=0.65,乙产品为一等品的概率P乙=0.4.(2)依题意得x,y应满足的约束条件为⎩⎪⎨⎪⎧4x+8y≤32,20x+5y≤55,x≥0,y≥0,且z=0.65x+0.4y.作出以上不等式组所表示的平面区域(如图阴影部分),即可行域.作直线l:0.65x+0.4y=0即13x+8y=0,把直线l向上方平移到l1的位置时,直线经过可行域内的点M,且l1与原点的距离最大,此时z取最大值.解方程组⎩⎪⎨⎪⎧x+2y=8,4x+y=11,得⎩⎪⎨⎪⎧x=2,y=3.故M的坐标为(2,3),所以z的最大值为z max=0.65×2+0.4×3=2.5.当实数x,y满足⎩⎪⎨⎪⎧x+2y-4≤0,x-y-1≤0,x≥1时,1≤ax+y≤4恒成立,则实数a的取值范围是________.解:作出可行域为一三角形,且易求出三个顶点坐标分别为(1,0),⎝⎛⎭⎫1,32,(2,1),都代入1≤ax+y≤4得⎩⎪⎨⎪⎧1≤a≤4,1≤a+32≤4,1≤2a+1≤4.解不等式组可得1≤a≤32.故填⎣⎡⎦⎤1,32.项目用量产品。
2014届高考数学总复习(考点引领+技巧点拨)第三章 三角函数、三角恒等变换及解三角形第3课时三角函数图象

《最高考系列 高考总复习》2014届高考数学总复习(考点引领+技巧点拨)第三章 三角函数、三角恒等变换及解三角形第3课时三角函数的图象和性质1. (必修4P 25练习2改编)函数f(x)=3sin ⎝ ⎛⎭⎪⎫x 2-π4,x ∈R 的最小正周期为________. 答案:4π解析:函数f(x)=3sin ⎝ ⎛⎭⎪⎫x 2-π4的最小正周期为T =2π12=4π. 2. (必修4P 39第2题改编)将函数y =sinx 的图象上所有的点向右平行移动 π10个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是____________________.答案:y =sin ⎝ ⎛⎭⎪⎫12x -π10 解析:∵ 向右平移π10个单位,∴ 用x -π10代替y =sinx 中的x ;∵ 各点横坐标伸长到原来的2倍,∴ 用12x 代替y =sin ⎝ ⎛⎭⎪⎫x -π10中的x ,∴ y =sin ⎝ ⎛⎭⎪⎫12x -π10.3. (必修4P 45第9题改编)如图,它表示电流I =Asin(ωt +φ)(A>0,ω>0)在一个周期内的图象,则I =Asin(ωt +φ)的解析式为________________.答案:I =3sin ⎝⎛⎭⎪⎫100π3t +π3解析:由图可知A =3,ω=100π3.代入⎝ ⎛⎭⎪⎫150,0和⎝ ⎛⎭⎪⎫120,0,解得φ=π3,于是I =3sin ⎝⎛⎭⎪⎫100π3t +π3.4. (必修4P 32练习6改编)函数y =cos ⎝ ⎛⎭⎪⎫2x -π4的单调递增区间是________.答案:⎣⎢⎡⎦⎥⎤-3π8+k π,π8+k π(k∈Z )解析:-π+2k π≤2x -π4≤2k π,即-3π8+k π≤x ≤π8+k π(k∈Z ),所求单调递增区间是⎣⎢⎡⎦⎥⎤-3π8+k π,π8+k π(k∈Z ).5. (必修4P 32第5题改编)函数y =2sinx ⎝ ⎛⎭⎪⎫π6≤x ≤2π3的值域是________.答案:[1,2]解析:根据正弦函数图象,可知x =π6时,函数取到最小值1;x =π2时,函数取到最大值2.1. 周期函数的定义周期函数的概念:对于函数y =f(x),如果存在一个不为零的常数T ,使得当x 取定义域内的每一个值时,f(x +T)=f(x)都成立,则称y =f(x)为周期函数;函数y =Asin(ωx +φ)和y =Acos(ωx +φ)的周期均为T =2π|ω|;函数y =Atan(ωx +φ)的周期为T =π|ω|2. 三角函数的图象和性质“五点法”作图原理:在确定正弦函数y =sinx 在[0,2π]上的图象形状时,起关键作用的五个点是(0,0)、 ⎛⎭⎪⎫π2,1、(π,0)、 ⎛⎭⎪⎫3π2,-1、 (2π,0).余弦函数呢?4. 函数 y =Asin(ωx +φ)的特征若函数y =Asin(ωx +φ) (A >0,ω>0,x ∈(-∞,+∞))表示一个振动量时,则A 叫做振幅,T =2πω叫做周期,f =1T叫做频率,ωx +φ叫做相位,φ叫做初相.[备课札记]题型1 依据三角函数的图象求解析式例1 (2013·南京三模)已知函数f(x)=2sin(ωx +φ)(ω>0)的部分图象如图所示,则ω=________.答案:23解析:由图象可知函数的四分之三周期为15π8-⎝ ⎛⎭⎪⎫-3π8=34T ,T =3π,ω=2π3π=23.变式训练已知函数y =Asin(ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象如图所示,则ω=________.答案:3解析:由图知,A =2,将(0,2)、⎝ ⎛⎭⎪⎫π12,2代入函数,得⎩⎪⎨⎪⎧2sin ⎝ ⎛⎭⎪⎫π12w +φ=2,2sin φ=2,∴ ⎩⎪⎨⎪⎧φ=π4,ω=3.题型2 三角函数的图象变换例2 为了得到函数y =2sin ⎝ ⎛⎭⎪⎫x 3+π6(x∈R )的图象,只需把函数y =2sinx (x∈R )的图象上所有的点经过怎样的变换得到?解:y =2sinx 用6x p +代替x ,左移 6p个单位 y =2sin ⎝ ⎛⎭⎪⎫x +π6再用3p 代替x ,各点横坐标伸长到原来的3倍。
高考英语语法词汇专项突破:01表解不定式考点及其时态语态突破(含高考真题)

高考英语语法词汇专项突破:表解不定式考点及其时态语态全突破+巩固训练养成良好的答题习惯,是决定高考英语成败的决定性因素之一。
做题前,要认真阅读题目要求、题干和选项,并对答案内容作出合理预测;答题时,切忌跟着感觉走,最好按照题目序号来做,不会的或存在疑问的,要做好标记,要善于发现,找到题目的题眼所在,规范答题,书写工整;答题完毕时,要认真检查,查漏补缺,纠正错误。
Part 1:不定式考点【高考链接1】【考例1】(2023新高考I卷)Nanxiang aside, the best Xiao long bao have a fine skin, allowing them____ (lift) out of the steamer basket without allowing them tearing or spilling any of their contents.答案与解析:to be lifted。
考查非谓语动词。
句根据搭配allow sb. to do sth.“允许某人做某事”可知,空格需用动词不定式作宾语补足语,补足语lift out与宾语them(指代小笼包)是逻辑上的动宾关系,空格需填动词不定式的被动式to be lifted,故填to be lifted。
意:除了南翔,最好的小笼包有一个精致的,可以让它们从蒸笼篮中拿出来,而不会撕裂或溢出里面的东西。
【考例2】(2022全国甲卷)A visually-challenged man from Beijing recently hiked (徒步) 40 days to Xi’an, as a first step (journey) the Belt and Road route (路线) by foot.答案与解析:to journey。
考查非谓语动词。
step前面有序数词first,应用不定式,作后置定语。
故填to journey。
小说阅读考点3:分析小说环境,赏析环境描写的手法及作用(含答案)

小说阅读考点3:分析小说环境,赏析环境描写的手法及作用(含答案)考点三分析小说环境,赏析环境描写的手法及作用文本展示典例阅读下面的文字,完成问题。
(20分)峡谷XXX山被直着劈开,于是当中有七八里谷地。
大约是那刀有些弯,结果谷地中央高出如许,愈近峡口,便愈低。
XXX冷气漫出峡口,收掉一身黏汗。
峡口处,倒一棵大树,连根拔起,似XXX出了什么不测之事,把大树唬得跑,一跤仰翻在那里。
峡顶一线蓝天,深得令人不敢久看。
一只鹰在空中移来移去。
峭壁上草木不甚生长,石头生铁般锈着。
一块巨石和百十块斗大石头,昏死在峡壁根,一动不动。
巨石上伏着两只四脚蛇,眼睛眨也不眨,只偶尔吐一下舌芯子,与石头们赛呆。
因有人在峡中走,壁上时时落下些许小石,声音左右荡着升上去。
那鹰却忽地不见去向。
顺路上去,有三五人家在高处。
临路立一幢石屋,门开着,却像睡觉的人。
门口一幅布旗静静垂着。
靠近人家,便有稀松的石板垫路。
中午的阳光慢慢挤进峡谷,阴气浮开,地气熏上来,石板有些颤。
似乎有了XXX,细听却什么也不响。
忍不住干咳一两声,总是自讨没趣。
一天下都静着,不要谁来多舌。
走近了,方才辨出布旗上有个藏文字,布色已经晒退,字色也相去不远,随旗沉甸甸地垂着。
愈来愈近,一到上坡,马慢下来。
骑手轻轻一夹,马上了石板,蹄铁连珠般脆响。
XXX耸一耸向上走,骑手就一坐一坐随它。
蹄声在峡谷中回转,又响又高。
那只鹰又出现了,慢慢移来移去。
骑手走过眼前,结结实实一脸黑肉,直鼻紧嘴,细眼高颧,眉睫似漆。
皮袍裹在身上,胸微敞,露出油灰布衣。
手隐在袖中,并不拽缰。
藏靴上一层细土,脚尖直翘着。
眼睛遇着了,脸一短,肉横着默默一笑,立即复原,似乎咔嚓一响。
XXX 走上去,屁股锦缎一样闪着。
到了布旗下,骑手俯身移下马,将缰绳缚在门前木桩上。
XXX了脖子立着,甩一甩尾巴,曲一曲前蹄,倒换一下后腿。
骑手望望门,那门不算大,骑手似乎比门宽着许多,可拐着腿,左右一晃,竟进去了。
屋里极暗,不辨大小。
专题03 《勾股定理》重难考点(解析版)

八年级数学上册北师大版版链接教材精准变式练专题03 勾股定理重难考点【典例1】如图所示,等腰直角△ABC 中,∠ACB =90°,E 、F 为AB 上两点(E 左F 右),且∠ECF =45°,求证:222AE BF EF +=.【点拨】由于∠ACB =90°,∠ECF =45°,所以∠ACE +∠BCF =45°,若将∠ACE 和∠BCF 合在一起则为一特殊角45°,于是想到将△ACE 旋转到△BCF 的右外侧合并,或将△BCF 绕C 点旋转到△ACE 的左外侧合并,旋转后的BF 边与AE 边组成一个直角,联想勾股定理即可证明. 【解析】解:(1)222AE BF EF +=,理由如下:将△BCF 绕点C 旋转得△ACF ′,使△BCF 的BC 与AC 边重合,即△ACF ′≌△BCF ,∵ 在△ABC 中,∠ACB =90°,AC =BC , ∴ ∠CAF ′=∠B =45°,∴ ∠EAF ′=90°. ∵ ∠ECF =45°,∴ ∠ACE +∠BCF =45°. ∵ ∠ACF ′=∠BCF ,∴ ∠ECF ′=45°. 在△ECF 和△ECF ′中45CE CE ECF ECF CF CF =⎧⎪'∠=∠=⎨⎪'=⎩°∴ △ECF ≌△ECF ′(SAS),∴ EF =EF ′.典例解读在Rt △AEF ′中,222AE F A F E ''+=, ∴ 222AE BF EF +=.【总结】若一个角的内部含有同顶点的半角,(如平角内含直角,90°角内含45°角,120°角内含60°角),则常常利用旋转法将剩下的部分拼接在一起组成又一个半角,然后利用角平分线、全等三角形等知识解决问题.【典例2】如图,在△ABC 中,∠ACB=90°,AC=BC ,P 是△ABC 内的一点,且PB=1,PC=2,PA=3,求∠BPC的度数.【解析】解:如图,做∠ECB=∠PCA ,且使CE=CP ,连结EP ,EB在△APC 和△BEC 中PCA ECB AC BCPC EC =⎧⎪∠=∠⎨⎪=⎩∴△APC ≌△BEC ∴△PCE为等腰直角三角形∴∠CPE=45°,PE 2=PC 2+CE 2=8 又∵PB 2=1,BE 2=9 ∴PE 2+ PB 2= BE 2则∠BPE=90°∴∠BPC=135°【总结】本题考查了勾股定理的逆定理,通过观察所要求的角度,作出辅助线,把PA 、PB 、PC 的长度转化为一个三角形三条边,构造出直角三角形是解题的关键,当然此题也可以利用旋转的思想来解,即将△APC 绕点C 旋转,使CA 与CB 重合即△APC ≌△BEC.【典例3】如图,已知四边形ABCD 中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD 的面积.【点拨】连接AC ,在直角三角形ABC 中,由AB 及BC 的长,利用勾股定理求出AC 的长,再由AD 及CD 的长,利用勾股定理的逆定理得到三角形ACD 为直角三角形,根据四边形ABCD 的面积=直角三角形ABC 的面积+直角三角形ACD 的面积,即可求出四边形的面积. 【解析】解:连接AC ,如图所示: ∵∠B=90°,∴△ABC 为直角三角形, 又∵AB=3,BC=4,∴根据勾股定理得:AC 2=25, 又∵CD=12,AD=13,∴AD 2=132=169,CD 2+AC 2=122+52=144+25=169, ∴CD 2+AC 2=AD 2,∴△ACD 为直角三角形,∠ACD=90°, 则S 四边形ABCD =S △ABC +S △ACD =21AB •BC+21AC •CD=21×3×4+21×5×12=36. 故四边形ABCD 的面积是36.【总结】此题考查了勾股定理,以及勾股定理的逆定理,熟练掌握勾股定理及勾股定理的逆定理是解本题的关键.【典例4】如图:正方形ABCD 中,E 是DC 中点,F 是EC 中点.求证:∠BAF=2∠EAD.【解析】证明:取BC 中点G ,连结AG 并延长交DC 延长线于H∵ ∠ABG=∠HCG ,BG=CG ,∠AGB=∠HGC ∴ △GAB ≌△HCG ∴ ∠GAB=∠H ,AB=CH 又∵ AB=AD ,∠B=∠D ,BG=DE ∴ △ABG ≌△ADE ∴ ∠GAB=∠DAE在Rt ADF △中,设AD a =,由勾股定理得:222222325()41654AF AD DF a a aAF a=+=+==∴又544a HF CH CF a a =+=+= ∴ AF=HF ∴ ∠FAH=∠H ∴ ∠FAH=∠DAE ∴ ∠BAF=2∠DAE【总结】要证∠BAF=2∠EAD ,一般方法是在∠BAF 中取一个角使之等于∠EAD ,再证明另一个角也等于∠EAD ,另一种方法是把小角扩大一倍,看它是否等于较大的角.【典例5】如图所示,牧童在A 处放牛,其家在B 处,A 、B 到河岸的距离分别为AC =400米,BD =200米,CD =800米,牧童从A 处把牛牵到河边饮水后再回家.试问在何处饮水,所走路程最短?最短路程是多少?【点拨】作点A 关于直线CD 的对称点G ,连接GB ,交CD 于点E ,利用“两点之间线段最短”可知应在E 处饮水,再根据对称性知GB 的长为所走的最短路程,然后构造直角三角形,利用勾股定理可解决. 【解析】解:作点A 关于直线CD 的对称点G ,连接GB 交CD 于点E ,由“两点之间线段最短”可以知道在E 点处饮水,所走路程最短.说明如下:在直线CD 上任意取一异于点E 的点I ,连接AI 、AE 、BE 、BI 、GI 、GE . ∵ 点G 、A 关于直线CD 对称,∴ AI =GI ,AE =GE .由“两点之间线段最短”或“三角形中两边之和大于第三边”可得GI +BI >GB =AE +BE ,于是得证. 最短路程为GB 的长,自点B 作CD 的垂线,自点G 作BD 的垂线交于点H ,在直角三角形GHB 中, ∵ GH =CD =800,BH =BD +DH =BD +GC =BD +AC =200+400=600, ∴ 由勾股定理得222228006001000000GB GH BH =+=+=. ∴ GB =1000,即最短路程为1000米.【总结】这是一道有关极值的典型题目.解决这类题目,一方面要考虑“两点之间线段最短”;另一方面,证明最值,常常另选一个量,通过与求证的那个“最大”“最小”的量进行比较来证明,如本题中的I 点.本题体现了勾股定理在实际生活中的应用.【典例6】台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.如图台风中心在我国台湾海峡的B 处,在沿海城市福州A 的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C 移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问:(1)该城市是否会受到台风影响?请说明理由.(2)若会受到台风影响,那么台风影响该城市的持续时间有多长? (3)该城市受到台风影响的最大风力为几级? 【解析】解:(1)该城市会受到台风影响. 理由:如图,过点A 作AD ⊥BC 于D 点, 则AD 即为该城市距离台风中心的最短距离.在Rt △ABD 中,因为∠B=30°,AB=240.∴AD=12AB=12×240=120(千米).由题可知,距台风中心在(12-4)×25=200(千米)以内时,则会受到台风影响.因为120<200,因此该城市将会受到影响.(2)依题(1)可知,当点A距台风中心不超过200千米时,会受台风影响,故在BC上作AE=AF=200;台风中心从点E移动到点F处时,该城市会处在台风影响范围之内.(如图)由勾股定理得,2222220012025600DE AE AD=-=-=DE=160(千米).所以EF=2×160=320(千米).又知台风中心以20千米/时的速度移动.所以台风影响该城市320÷20=16(小时).(3)∵AD距台风中心最近,∴该城市受到这次台风最大风力为:12-(120÷25)=7.2(级).答:该城市受台风影响最大风力7.2级.【总结】本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到直角三角形中,运用勾股定理使问题解决.【教材知识必背】【教材知识必会】一、勾股定理教材知识链接1.勾股定理:直角三角形两直角边a b 、的平方和等于斜边c 的平方.(即:222a b c +=) 2.勾股定理的应用勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用是: (1)已知直角三角形的两边,求第三边;(2)利用勾股定理可以证明有关线段平方关系的问题; (3)解决与勾股定理有关的面积计算; (4)勾股定理在实际生活中的应用. 二、勾股定理的逆定理 1.勾股定理的逆定理如果三角形的三边长a b c 、、,满足222a b c +=,那么这个三角形是直角三角形. 要点诠释:应用勾股定理的逆定理判定一个三角形是不是直角三角形的基本步骤: (1)首先确定最大边,不妨设最大边长为c ; (2)验证:22a b +与2c 是否具有相等关系:若222a b c +=,则△ABC 是以∠C 为90°的直角三角形; 若222a b c +>时,△ABC 是锐角三角形; 若222a b c +<时,△ABC 是钝角三角形. 2.勾股数满足不定方程222x y z +=的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以x y z 、、为三边长的三角形一定是直角三角形. 要点诠释:常见的勾股数:①3、4、5; ②5、12、13;③8、15、17;④7、24、25;⑤9、40、41.如果(a b c 、、)是勾股数,当t 为正整数时,以at bt ct 、、为三角形的三边长,此三角形必为直角三角形.观察上面的①、②、④、⑤四组勾股数,它们具有以下特征: 1.较小的直角边为连续奇数;2.较长的直角边与对应斜边相差1.3.假设三个数分别为a b c 、、,且a b c <<,那么存在2a b c =+成立.(例如④中存在27=24+25、29=40+41等)三、勾股定理与勾股定理逆定理的区别与联系区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理;联系:勾股定理与其逆定理的题设和结论正好相反,两者互为逆定理,都与直角三角形有关.【变式1】已知凸四边形ABCD 中,∠ABC =30°,∠ADC =60°,AD =DC ,求证:222BD AB BC =+.【答案】解:将△ABD 绕点D 顺时针旋转60°.由于DC =AD ,故点A 转至点C .点B 转至点E ,连结BE . ∵ BD =DE ,∠BDE =60° ∴ △BDE 为等边三角形,BE =BD易证△DAB ≌△DCE ,∠A =∠2,CE =AB ∵ 四边形ADCB 中∠ADC =60°,∠ABC =30° ∴ ∠A +∠1=360°-60°-30°=270° ∴ ∠1+∠2=∠1+∠A =270° ∴ ∠3=360°-(∠1+∠2)=90° ∴222BC CE BE += ∴ 222BC AB BD +=精准变式题【变式2】如图所示,在△ABC 中,AB :BC :CA=3:4:5,且周长为36cm ,点P 从点A 开始沿边向B 点以每秒1cm 的速度移动;点Q 从点B 沿BC 边向点C 以每秒2cm 的速度移动,如果同时出发,问过3秒时,△BPQ 的面积为多少?【答案】解:设AB 为3xcm ,BC 为4xcm ,AC 为5xcm ,∵周长为36cm , AB+BC+AC=36cm , ∴3x+4x+5x=36, 得x=3,∴AB=9cm ,BC=12cm ,AC=15cm , ∵AB 2+BC 2=AC 2, ∴△ABC 是直角三角形,过3秒时,BP=9﹣3×1=6(cm ),BQ=2×3=6(cm ), ∴S △PBQ =21BP •BQ=21×(9﹣3)×6=18(cm 2). 故过3秒时,△BPQ 的面积为18cm 2.【变式3】如图所示,正方形ABCD 的AB 边上有一点E ,AE =3,EB =1,在AC 上有一点P ,使EP +BP 最短.求EP +BP 的最小值.【答案】解:根据正方形的对称性可知:BP =DP ,连接DE ,交AC 于P ,ED =EP +DP =EP +BP , 即最短距离EP +BP 也就是ED .∵ AE =3,EB =1,∴ AB =AE +EB =4,∴ AD =4,根据勾股定理得:222223425ED AE AD =+=+=. ∵ ED >0,∴ ED =5,∴ 最短距离EP +BP =5.1.在△ABC 中,若1,2,122+==-=n c n b n a ,则△ABC 是( )A . 锐角三角形B . 钝角三角形C . 等腰三角形D . 直角三角形 【答案】D ;【解析】因为()()2222221111c a n n n n -=++-+-+=422n b =,所以222c a b -=,222a b c +=,由勾股定理的逆定理可知:△ABC 是直角三角形.2. 如图,每个小正方形的边长为1,A 、B 、C 是小正方形的顶点,则∠ABC 的度数为( ) A .90° B .60° C .45° D .30°【答案】C ;【解析】连接AC ,计算AC 2=BC 2=5,AB 2=10,根据勾股定理的逆定理,△ABC 是等腰直角三角形,∴∠ABC =45°.3.下列满足条件的三角形中,不是直角三角形的是( ) A .三内角之比为1:2:3 B .三边长的平方之比为1:2:3 C .三边长之比为3:4:5 D .三内角之比为3:4:5【答案】D ;【解析】解:A 、因为根据三角形内角和定理可求出三个角分别为30度,60度,90度,所以是直角三角形,综合提升变式练故正确;B 、因为其符合勾股定理的逆定理,所以是直角三角形,故正确;C 、因为其符合勾股定理的逆定理,所以是直角三角形,故正确;D 、因为根据三角形内角和公式得三个角中没有90°角,所以不是直角三角形,故不正确.故选D .4.如图,一牧童在A 处牧马,牧童家在B 处,A 、B 处距河岸的距离AC 、BD 的长分别为500m 和700m ,且C 、D 两地的距离为500m ,天黑前牧童从A 点将马牵引到河边去饮水后,再赶回家,那么牧童至少要走( )A .2900mB . 1200mC . 1300mD . 1700m【答案】C ;【解析】作A 点关于河岸的对称点A ′,连接BA ′交河岸与P ,则PB+PA=PB+PA ′=BA ′最短,如图,BB ′=BD+DB ′=1200,B ′A ′=500,BA ′=1300(m ).5. 直角三角形的两条直角边长为a ,b ,斜边上的高为h ,则下列各式中总能成立的是( )A .ab =h 2B .a 2+b 2=h 2C .111a b h += D .222111a b h += 【答案】D ;【解析】解:根据直角三角形的面积可以导出:ab c h=.再结合勾股定理:a 2+b 2=c 2.进行等量代换,得a 2+b 2= 222a b h.两边同除以a 2b 2,得222111a b h +=. 6.如图,Rt △ABC 中,∠C =90°,CD ⊥AB 于点D ,AB =13,CD =6,则(AC +BC)2等于( )A .25B .325C .2197D .405【答案】B ;【解析】()222222AC BC AC BC AC BC AB AB CD +=++⋅=+⋅=169+2×13×6=325. 7. 已知三角形的三边长为a b c 、、,由下列条件能构成直角三角形的是( )A .()()2222221,4,1a m b m c m =-==+B .()()222221,4,1a m b m c m =-==+C .()()222221,2,1a m b m c m =-==+D .()()2222221,2,1a m b m c m =-==+ 【答案】B ;【解析】()()22141m m m -+=+8.如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S 1、S 2、S 3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S 4、S 5、S 6.其中S 1=16,S 2=45,S 5=11,S 6=14,则S 3+S 4=( )A .86B .64C .54D .48【答案】C ;【解析】解:如图1,S 1=AC 2,S 2=AB 2,S 3=BC 2, ∵BC 2=AB 2﹣AC 2,∴S 2﹣S 1=S 3,如图2,S4=S5+S6,∴S3+S4=45﹣16+11+14=54.故选C.9.如图,AB=5,AC=3,BC边上的中线AD=2,则△ABC的面积为______.【答案】6;【解析】延长AD到E,使DE=AD,连结BE,可得△ABE为直角三角形.10.如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将直角边AB折叠使它落在斜边AC上,折痕为AD,则BD=______.【答案】3;【解析】设点B落在AC上的E点处,设BD=x,则DE=BD=x,AE=AB=6,CE=4,CD=8-x,在Rt△CDE中根据勾股定理列方程.11.已知:△ABC中,AB=15,AC=13,BC边上的高AD=12,BC=_______.【答案】14或4;【解析】当△ABC是锐角三角形时,BC=9+5=14;当△ABC是钝角三角形时,BC=9-5=4.12.如图,E是边长为4cm的正方形ABCD的边AB上一点,且AE=1cm,P为对角线BD上的任意一点,则AP+EP 的最小值是cm.【答案】5【解析】作E点关于直线BD的对称点E′,连接AE′,则线段AE′的长即为AP+EP的最小值5.13.如图,长方体的底面边长分别为1cm 和2cm,高为4cm,点P在边BC上,且BP=14BC.如果用一根细线从点A开始经过3个侧面缠绕一圈到达点P,那么所用细线最短需要cm.【答案】5【解析】∵长方体的底面边长分别为1cm 和2cm,高为4cm,点P在边BC上,且BP=14BC,∴AC=4cm,PC=34BC=3cm,根据两点之间线段最短,AP=5.14.小明把一根70cm长的木棒放到一个长宽高分别为30cm,40cm,50cm的木箱中,他能放进去吗?答:(选填“能”或“不能”).【答案】能;【解析】解:可设放入长方体盒子中的最大长度是xcm ,根据题意,得x 2=502+402+302=5000,702=4900,因为4900<5000,所以能放进去.15.如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,该图形的面积等于 .【答案】96;【解析】连接AC ,在Rt △ACD 中,AD=8,CD=6,∴AC 2=100,在△ABC 中,∵AC 2+BC 2=102+242=262=AB 2,∴△ABC 为直角三角形;∴图形面积为:S △ABC ﹣S △ACD =×10×24﹣×6×8=96.16. 如图所示,在△ABC 中,AB =5,AC =13,BC 边上的中线AD =6,∠BAD =________.【答案】90°;【解析】延长AD 到M ,使DM =AD ,易得△ABD ≌△MCD .∴ CM =AB =5 AM =2AD =12在△ACM 中22251213+= 即222CM AM AC +=∴∠AMC =∠BAD=90°17.能够成为直角三角形边长的三个正整数,我们称之为一组勾股数,观察表格所给出的三个数a,b,c,a<b<c.(1)试找出它们的共同点,并证明你的结论;(2)写出当a=17时,b,c的值.3,4,5 32+42=525,12,13,52+122=1327,24,25 72+242=2529,40,41 92+402=412……17,b,c 172+b2=c2【解析】解:(1)以上各组数的共同点可以从以下方面分析:①以上各组数均满足a2+b2=c2;②最小的数(a)是奇数,其余的两个数是连续的正整数;③最小奇数的平方等于另两个连续整数的和,如32=9=4+5,52=25=12+13,72=49=24+25,92=81=40+41…由以上特点我们可猜想并证明这样一个结论:设m为大于1的奇数,将m2拆分为两个连续的整数之和,即m2=n+(n+1),则m,n,n+1就构成一组简单的勾股数,证明:∵m2=n+(n+1)(m为大于1的奇数),∴m2+n2=2n+1+n2=(n+1)2,∴m,n,(n+1)是一组勾股数;(2)运用以上结论,当a=17时,∵172=289=144+145,∴b=144,c=145.18.如图等腰△ABC的底边长为8cm,腰长为5cm,一个动点P在底边上从B向C以0.25cm/s的速度移动,请你探究,当P运动几秒时,P点与顶点A的连线PA与腰垂直.【解析】解:如图,作AD⊥BC,交BC于点D,∵BC=8cm,∴BD=CD=BC=4cm,∴AD=3,分两种情况:当点P运动t秒后有PA⊥AC时,∵AP2=PD2+AD2=PC2﹣AC2,∴PD2+AD2=PC2﹣AC2,∴PD2+32=(PD+4)2﹣52∴PD=2.25,∴BP=4﹣2.25=1.75=0.25t,∴t=7秒,当点P运动t秒后有PA⊥AB时,同理可证得PD=2.25,∴BP=4+2.25=6.25=0.25t,∴t=25秒,∴点P运动的时间为7秒或25秒.19.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若一直重型运输卡车P沿道路ON方向行驶的速度为18千米/时.(1)求对学校A的噪声影响最大时卡车P与学校A的距离;(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.【解析】解:(1)过点A作AD⊥ON于点D,∵∠NOM=30°,AO=80m,∴AD=40m,即对学校A的噪声影响最大时卡车P与学校A的距离为40米;(2)由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD=BC,OA=80m,∵在Rt△AOD中,∠AOB=30°,∴AD=OA=×80=40m,在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD===30m,故BC=2×30=60米,即重型运输卡车在经过BD时对学校产生影响.∵重型运输卡车的速度为18千米/小时,即=300米/分钟,∴重型运输卡车经过BD时需要60÷300=0.2(分钟)=12(秒).答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒.cm,CD=15cm,将这四根木条用小钉绞合在一起,20.如图1,四根长度一定....的木条,其中AB=6构成一个四边形ABCD(在A、B、C、D四点处是可以活动的).现固定AB边不动,转动这个四边形,使它的形状改变,在转动的过程中有以下两个特殊位置.位置一:当点D在BA的延长线上时,点C在线段AD上(如图2);位置二:当点C在AB的延长线上时,∠C=90°.(1)在图2中,若设BC 的长为x ,请用x 的代数式表示AD 的长;(2)在图3中画出位置二的准确..图形;(各木条长度需符合题目要求) (3)利用图2、图3求图1的四边形ABCD 中,BC 、AD 边的长.【解析】解:(1)∵ 在四边形ABCD 转动的过程中,BC 、AD 边的长度始终保持不变,BC =x , ∴ 在图2中,AC =BC -AB =x -6,AD =AC +CD =x +9.(2)位置二的图形见图3.(3)∵ 在四边形ABCD 转动的过程中,BC 、AD 边的长度始终保持不变, ∴ 在图3中,BC =x ,AC =AB +BC =6+x ,AD =x +9.在△ACD 中,∠C =90°由勾股定理得222AC CD AD +=.∴ 222(6)15(9)x x ++=+.整理,得2212362251881x x x x +++=++.化简,得6x =180.解得 x =30.即 BC =30.∴ AD =39.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点点拨考例回顾
1. Since then, finding ways to grow more rice has been his goal. (P10)
[考点] 动词-ing短语在句中作主语。
[考例] Eugene’s never willing to alter any of his opinions. It’s no use ______ with him. (上海2006)
A. to argue
B. arguing
C. argued
D. having argued
(注意:斜体部分为最佳选项。
下同)
[点拨] It’s no use doing sth.做某事没用。
其中it为形式主语,动词-ing 短语为真正的主语。
2. He enjoys listening to violin music, playing mah-jong, swimming and reading. (P10)
[考点] 动词-ing短语作宾语。
[考例1] —There is a story here in the paper about a 110-year-old man.
—My goodness! I can’t imagine ______ that old. (江苏2006)
A. to be
B. to have been
C. being
D. having been
[点拨] imagine doing sth. 想象做某事。
imagine后面接动词-ing形式作宾语,也可接名词、代词或从句,但不接动词不定式。
[考例2] The parents suggested ______ in the hotel room but their kids were anxious to camp out during the trip.(上海2006春)
A. sleep
B. to sleep
C. sleeping
D. having slept
[点拨] suggest doing sth. 建议做某事。
suggest后面接动词-ing形式作宾语,也可接名词、代词或从句,但不接动词不定式。
3. He therefore gives millions of yuan to equip others for their research in agriculture. (P10)
[考点] therefore adv. 因此;所以;因而,表示因果关系。
[考例] Progress so far has been very good. ______, we are sure that the project will
be completed on time.
(浙江2006)
A. However
B. Otherwise
C. Therefore
D. Besides
[点拨] 题意是“至今情况进展良好,因此我们确信能按时完成这项工程。
” 前后两句为因果关系,故选therefore;however然而,可是;otherwise否则,要不然,二者均表示转折关系;besides而且,也不符合题意。
4. They focus on keeping their soil rich and free of disease. (P14)
[考点] 动词-ing短语作介词的宾语。
[考例1] Isn’t it time you got down t o ______ the papers?
(重庆2006)
A. mark
B. be marked
C. being marked
D. marking
[点拨] get down to doing sth. 开始着手干某事,to在这个短语中是介词, 后可跟动词-ing形式、名词或代词。
又因mark the papers“判试卷”与逻辑主语you是主动关系,故排除选项C。
[考例2] According to a recent U.S. survey, children spent up to 25 hours a week ______ TV. (上海2004)
A. to watch
B. to watching
C. watching
D. watch
[点拨] spend time / money (in) doing sth.花费时间或金钱干某事。
doing sth. 作介词in的宾语。
