辽宁省营口市开发区第一高级中学2018届高三上学期第一次月考数学(理)试卷+Word版含答案
营口市一中2018-2019学年上学期高三数学10月月考试题

(1)求 f ( x) 的单调区间和极值; (2)求 f ( x) 在 x 1, 2 上的最小值. (3)设 g ( x) f ( x) f '( x) ,若对 k , 及 x 0,1 有 g ( x) 恒成立,求实数 的取值范围. 2 2
3 5
3 【解析】因为 ( x +1) (n Î N ) 的展开式中 x 项系数是 C3 n ,所以 C n = 10 ,解得 n = 5 ,故选 A.
n
*
3
6. 【答案】 C 【解析】
(1 i ) 2 2i 2i (3 i ) 2 6i 1 3 i. 3i 3 i (3 i )(3 i ) 10 5 5
21.如图所示,两个全等的矩形 ABCD 和 ABEF 所在平面相交于 AB , M AC , N FB ,且
AM FN ,求证: MN / / 平面 BCE .
22.已知函 f(x)=
,求不等式 f(x)<4 的解集.
第 4 页,共 16 页
23. ∠ABC= 如图, 在四棱锥 O﹣ABCD 中, 底面 ABCD 四边长为 1 的菱形, M 为 OA 的中点,N 为 BC 的中点. (Ⅰ)证明:直线 MN∥平面 OCD; (Ⅱ)求异面直线 AB 与 MD 所成角的大小; (Ⅲ)求点 B 到平面 OCD 的距离.
第 9 页,共 16 页
故答案是:8. 16.【答案】 y=﹣1.7t+68.7 【解析】解: = , = =63.6.
OA⊥底面 ABCD, OA=2, ,
第 5 页,共 16 页
营口市一中 2018-2019 学年上学期高三数学 10 月月考试题(参考答案) 一、选择题
【化学】辽宁省营口市开发区第一高级中学2018届高三上学期第一次月考

辽宁省营口市开发区第一高级中学2018届高三上学期第一次月考时间:90分钟分值:100分第I卷选择题(第1卷包括18小题,每小题3分,共54分。
选项中,只有一项是符合题目要求的)可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 S 32 Cl 35.5 K 39 Ca 40 Mn 55 Fe 56 Cu 64 I 127 Ba 1371.化学与社会、生活密切相关。
下列说法正确的是( )A.稀豆浆、食盐水均可产生丁达尔效应B.利用生物质能就是间接利用太阳能C.钢铁在潮湿的空气中主要发生化学腐蚀D.纯铝质轻,耐腐蚀性强,可直接用作航天材料2.下列说法不正确的是()A.明矾水解形成的Al(OH)3胶体能吸附水中悬浮物,可用于水的净化B.苏打和氢氧化铝胶囊,可以作内服药治疗胃酸过多C.Al2O3和MgO的熔点均很高,可用于制作耐高温材料D.NaHCO3可用作发酵粉、泡沫灭火剂材料、治疗胃酸过多的药物3.下列离子的检验方法合理的是( )A.向某溶液中滴入KSCN溶液呈血红色,说明不含Fe2+B.用酸性KMnO4溶液检验FeCl3溶液中是否含有FeCl2C.向某溶液中加入NaOH溶液,得红褐色沉淀,说明溶液中含有Fe3+D.向某溶液中加入NaOH溶液得白色沉淀,又观察到颜色逐渐变为红褐色,说明该溶液中只含有Fe2+,不含有Mg2+4.分别用等量的铁与足量的稀硫酸和足量的CuO制备单质铜,有人设计了以下两种方案:①,②。
对制备得到Cu的量,下列判断正确的是()A.一样多B.①多C.②多D.无法判断5.某溶液中含有较大量的Cl-、CO32-、OH-等三种阴离子,如果只取一次该溶液就能够分别将三种阴离子依次检验出来,下列实验操作顺序正确的是()①滴加Mg(NO3)2溶液②过滤③滴加AgNO3溶液④滴加Ba(NO3)2溶液A.①②④②③B.④②①②③C.①②③②④D.④②③②①6.下列过程中没有发生化学变化的是()A.氯气作水杀菌消毒剂B.硅胶作袋装食品的干燥剂C.二氧化硫作纸浆的漂白剂D.肥皂水作蚊虫叮咬处的清洗剂7.下列化学现象及解释错误的是( )8.要除去CO2中含有的少量的SO2杂质,可选用的一组试剂是( )①NaOH溶液②NaHCO3溶液③Na2CO3溶液④HNO3酸化的Ba(NO3)2溶液⑤氨水⑥酸性KMnO4溶液A.②⑥B.②③C.②④⑥D.②③⑥9.在一定条件下X既能与Y又能与Z发生氧化还原反应,且都有单质生成的是()10.①石油的分馏②煤的干馏③石油的裂化④铝热反应⑤由乙烯变为聚乙烯⑥氧气转变为臭氧⑦乙烯催熟果实⑧苯遇溴水⑨海水蒸馏法制取淡水A.①②③④B.①②⑤⑦C.①⑧⑨D.①②⑥⑨11.X、Y、Z、R、W是原子序数依次增大的五种短周期元素。
辽宁省营口市开发区第一高级中学2017-2018学年高一上学期第一次月考物理试卷

2017-2018学年度上学期第一次月考高一物理试卷时间:90分钟满分:100分第I卷(选择题共56分)一、选择题(共14小题,每小题4分,共56分,在每小题给出的4个选项中,第1-8小题只有一个选项符合题目要求,第9-14小题有多个选项符合要求,全部选对的得4分,选不全的得2分,有选错或不答的得0分)1、松原的查干湖和白城的向海同为国家级自然保护区,近些年旅游事业蓬勃发展,吸引大批海内外游客。
设游客甲从白城乘火车去松原,运行184km。
游客乙驾车从松原火车站赶往白城火车站行程190km,如图,若二人恰好同时出发且同时到达,则甲乙在两地之间运动的过程中 ( )A.研究甲的行驶路程时可将火车看作质点B.甲的平均速率等于乙的平均速率C.甲、乙的平均速度相同D.题中的“190km”指的是位移2、下列所给的图像中能反映作直线运动的物体不能回到初始位置的是()3、某人用手表估测火车的加速度,先观测3min,发现火车前进540m,隔3min后,又观测1min,发现火车前进360m,,若火车在这7min内做匀加速直线运动,则加速度为()A. .0.01m/s2 B 0.03m/s2 C.0.5m/s2 D.0.6m/s24、2017年珠海直通潮汕的高铁正式开通,假设列车在某段距离中做匀加速直线运动,速度由5m/s 增加到10m/s 时位移为x 。
则当速度由10m/s 增加到15m/s 时,它的位移是( )A.3x/2B. 2xC. 5x/3D.3x5、一物体做加速直线运动,依次通过A 、B 、C 三点,AB=BC ,物体在AB 段的加速度为a 1,所用时间为t 1,在BC 段的加速度为a 2,所用时间为t 2,且物体在B 点的速度为 V B =(V A +V C )/2,则下列正确的是( )6、A 、B 两辆汽车在平直公路上朝同一方向运动,如图所示为两车运动的v —t图象,下面对阴影部分的说法正确的是( )A .若两车从同一点出发,它表示两车再次相遇前的最大距离B .若两车从同一点出发,它表示两车再次相遇前的最小距离C .若两车从同一点出发,它表示两车再次相遇时离出发点的距离D .表示两车出发时相隔的距离7、汽车从静止开始以加速度a 做匀加速直线运动.当速度达到v 后立即以大小为a 的加速度做匀减速直线运动,直到静止.在整个加速阶段和整个减速过程中,下列物理量不相同的是( )A.位移B.加速度C.经历时间D.平均速度8、如图所示,A 、B 两物体相距x=7m ,物体A 以V A =4m/s 的速度向右匀速运动,而物体B 此时的速度V B =10m/s ,物体B 只在摩擦阻力作用下向右做匀减速运动,加速度大小为a=2m/s 2 ,那么物体A 追上物体B 所用的时间为( )A .7sB .8sC .9sD .10s9、下列所描述的运动中可能的是( )A .速度变化很大,加速度很小B .速度变化的方向为正,加速度方向为负C .速度越来越快,加速度越来越小D .加速度越来越大,速度越来越小A .a 1=a 2 t 1=t 2B .a 1>a 2 t 1>t 2C .a 1<a 2 t 1<t 2D .a 1<a 2 t 1>t 210、如图所示是汽车与自行车在同一直线上、从同一地点同向运动、同时计时的v-t图象,由图象可知()A.在2s末二者距离最大 B.在4s末二者速度相同C.在2s末二者相遇 D.在4s末二者相遇11、关于自由落体运动,下列说法中正确的是()A.初速度为零的竖直向下的运动是自由落体运动B.只在重力作用下的竖直向下的运动是自由落体运动C.自由落体运动在任意相等的时间内速度变化量相等D.自由落体运动是初速度为零、加速度为g的匀加速直线运动12、质点做直线运动的位移x与时间t的关系为x=6t+2t2(各物理量均采用国际单位制单位),则该质点()A.在第1s内的位移大小是6m B.前2s内的平均速度大小是10m/sC.在任意相邻1s内的位移差都是4m D.在任意1s内的速度增量都是6m/s13、如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的位置,连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中的信息,下列判断正确的是()A.位置“1”是小球释放的初始位置B.小球做匀加速直线运动C.小球下落的加速度为d/T2D.小球在位置“3”的速度为7d/2T14、我国“蛟龙号”深潜器经过多次试验,终于在2012年6月24日以7020m深度创下世界最新纪录(国外最深不超过6500m),预示着可以征服全球99.8%的海底世界,假设在某次实验时,深潜器内的显示屏上显示出了从水面开始下潜到最后返回水面10min内全过程的深度曲线(a)和速度图像(b),如图示则有()A.(a)图中h3代表本次最大深度。
营口市高级中学2018-2019学年高三上学期11月月考数学试卷含答案
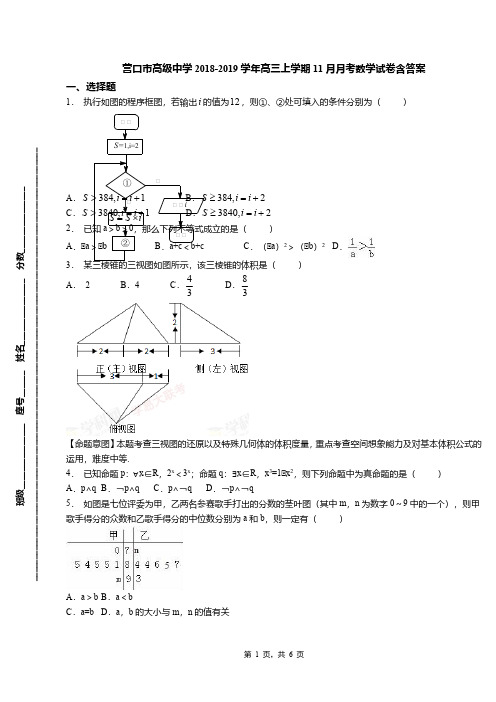
营口市高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1. 执行如图的程序框图,若输出的值为,则①、②处可填入的条件分别为()i 12A .S 384,2i i ≥=+C .S 3840,2i i ≥=+2.)A .﹣C .(﹣a )2>(﹣b )2D .3. )A . 2B .4C .D .3438【命题意图】本题考查三视图的还原以及特殊几何体的体积度量,重点考查空间想象能力及对基本体积公式的运用,难度中等.4. 已知命题p :∀x ∈R ,2x <3x ;命题q :∃x ∈R ,x 3=1﹣x 2,则下列命题中为真命题的是( )A .p ∧qB .¬p ∧qC .p ∧¬qD .¬p ∧¬q5. 如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m ,n 为数字0~9中的一个),则甲歌手得分的众数和乙歌手得分的中位数分别为a 和b ,则一定有()A .a >bB .a <bC .a=bD .a ,b 的大小与m ,n 的值有关班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________6. 若变量x y ,满足约束条件22024010x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩,则目标函数32z x y =-的最小值为( )A .-5B .-4C.-2D .37. 已知=(2,﹣3,1),=(4,2,x ),且⊥,则实数x 的值是( )A .﹣2B .2C .﹣D .8. 已知集合A={0,m ,m 2﹣3m+2},且2∈A ,则实数m 为( )A .2B .3C .0或3D .0,2,3均可9. 设n S 是等比数列{}n a 的前项和,425S S =,则此数列的公比q =( )A .-2或-1B .1或2C.1±或2D .2±或-110.设a=sin145°,b=cos52°,c=tan47°,则a ,b ,c 的大小关系是( )A .a <b <cB .c <b <aC .b <a <cD .a <c <b11.已知双曲线kx 2﹣y 2=1(k >0)的一条渐近线与直线2x+y ﹣3=0垂直,则双曲线的离心率是( )A .B .C .4D .12.已知一组函数f n (x )=sin n x+cos n x ,x ∈[0,],n ∈N *,则下列说法正确的个数是()①∀n ∈N *,f n (x )≤恒成立②若f n (x )为常数函数,则n=2③f 4(x )在[0,]上单调递减,在[,]上单调递增.A .0B .1C .2D .3二、填空题13.当下社会热议中国人口政策,下表是中国人民大学人口预测课题组根据我过2000年第五次人口普查预测的15﹣64岁劳动人口所占比例:年份20302035204020452050年份代号t 12345所占比例y6865626261根据上表,y 关于t 的线性回归方程为 附:回归直线的斜率和截距的最小二乘估计公式分别为: =, =﹣.14.满足tan (x+)≥﹣的x 的集合是 . 15.抛物线y 2=4x 上一点M 与该抛物线的焦点F 的距离|MF|=4,则点M 的横坐标x= .16.函数的定义域是,则函数的定义域是__________.111]()y f x =[]0,2()1y f x =+17.已知、、分别是三内角的对应的三边,若,则a b c ABC ∆A B C 、、C a A c cos sin -=的取值范围是___________.3cos()4A B π-+【命题意图】本题考查正弦定理、三角函数的性质,意在考查三角变换能力、逻辑思维能力、运算求解能力、转化思想.18.已知一个算法,其流程图如图,则输出结果是 .三、解答题19.已知m ∈R ,函数f (x )=(x 2+mx+m )e x .(1)若函数f (x )没有零点,求实数m 的取值范围;(2)若函数f (x )存在极大值,并记为g (m ),求g (m )的表达式;(3)当m=0时,求证:f (x )≥x 2+x 3. 20.已知函数f (x )=ax 2+2x ﹣lnx (a ∈R ).(Ⅰ)若a=4,求函数f (x )的极值;(Ⅱ)若f ′(x )在(0,1)有唯一的零点x 0,求a 的取值范围;(Ⅲ)若a ∈(﹣,0),设g (x )=a (1﹣x )2﹣2x ﹣1﹣ln (1﹣x ),求证:g (x )在(0,1)内有唯一的零点x 1,且对(Ⅱ)中的x 0,满足x 0+x 1>1.21.已知复数z1满足(z1﹣2)(1+i)=1﹣i(i为虚数单位),复数z2的虚部为2,且z1z2是实数,求z2.22.如图,点A是以线段BC为直径的圆O上一点,AD⊥BC于点D,过点B作圆O的切线,与CA的延长线相交于点E,点G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.(1)求证:BF=EF;(2)求证:PA是圆O的切线.23.已知椭圆的离心率,且点在椭圆上.(Ⅰ)求椭圆的方程;(Ⅱ)直线与椭圆交于、两点,且线段的垂直平分线经过点.求(为坐标原点)面积的最大值.24.设f(x)=x2﹣ax+2.当x∈,使得关于x的方程f(x)﹣tf(2a)=0有三个不相等的实数根,求实数t的取值范围.营口市高级中学2018-2019学年高三上学期11月月考数学试卷含答案(参考答案)一、选择题题号12345678910答案D C B B C B A B D A题号1112答案A D二、填空题13. y=﹣1.7t+68.7 14. [kπ,+kπ),k∈Z .15. 3 .-16.[]1,117.18. 5 .三、解答题19.20.21.22.23.24.。
辽宁省营口市开发区第一高级中学2018届高三上学期第一次月考物理试卷Word版含答案

2017-2018学年度上学期第一次月考高三物理试卷时间 :90 分钟满分 : 100分第Ⅰ卷(选择题共40分)一.选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,第1~6题只有一项符合题目要求,第7~10题有多个选项符合题目要求。
全部选对的得4分,选对但不全的得2分,有选错的得0分.1. 甲、乙两辆汽车沿同一平直路面行驶,其v-t图象如图所示,下列对汽车运动状况的描述正确的是()A.在第10 s末,乙车改变运动方向B.在第10 s末,甲、乙两车相距150 mC.在第20 s末,甲、乙两车相遇D.若开始时乙车在前,则两车可能相遇两次2. 如图所示,长为L的轻绳悬挂一个质量为m的小球,开始时绳竖直,小球与倾角θ=45°且静止于水平面的三角形物块刚好接触.现用水平恒力F向左推动三角形物块,直至轻绳与斜面平行,此时小球的速度大小为v.重力加速度为g,不计所有的摩擦.下列说法中正确的是()A.上述过程中,推力F做的功为FLB.上述过程中,斜面对小球做的功等于小球增加的动能C.上述过程中,推力F做的功等于小球增加的机械能D.轻绳与斜面平行时,绳对小球的拉力大小为mg sin45°3如图所示,粗糙水平地面上的长方体物块将一重为G的光滑圆球抵在光滑竖直的墙壁上,现用水平向右的拉力F缓慢拉动长方体物块,在圆球与地面接触之前,下面的相关判断正确的是()A.球对墙壁的压力逐渐减小B.水平拉力F逐渐减小C.地面对长方体物块的摩擦力逐渐增大D.地面对长方体物块的支持力逐渐增大4. 如图所示,质量为M ,倾角为θ的斜劈在水平面上以一定的初速度向右滑动的过程中,质量为m 的光滑小球在斜面上恰好保持与斜劈相对静止,已知斜劈与地面的动摩擦因数是μ,则下列说法正确的是( )A .小球与斜面间的压力是mg cos θB .小球与斜面的加速度大小是g cos θC .地面对斜劈的支持力一定大于(M +m )gD .地面与斜劈间的动摩擦因数是μ=tan θ5. 质量为m 的炮弹沿水平方向飞行,其动能为E k ,突然在空中爆炸成质量相同的两块,其中一块向后飞去,动能为E k 2,另一块向前飞去,则向前的这块的动能为( ) A.E k 2 B .94E k C .92E k D.9+422E k 6.为研究太阳系内行星的运动,需要知道太阳的质量,已知地球半径为R ,地球质量为m ,太阳与地球中心间距为r ,地球表面的重力加速度为g ,地球绕太阳公转的周期为T 。
辽宁省营口市开发区第一高级中学2017-2018学年高一上学期第一次月考数学试卷(精品解析)

2017-2018学年度上学期第一次月考高一数学试卷一、选择题(本题共有12小题,每小题5分,共60分)1.给出下列四个关系式:(1);(2);(3);(4),其中正确的个数是()A. 1B. 2C. 3D. 4【答案】B【解析】【分析】由字母所代表的集合类型、集合与元素和集合与集合间的关系以及空集的意义进行判断即可.【详解】(1)R为实数集,为实数,所以正确;(2)Z、Q分别为两个集合,集合间不能用属于符号,所以错误;(3)空集中没有任何元素,所以错误;(4)空集为任何集合的子集,所以正确.故选B.【点睛】本题考查集合与元素、集合与集合间关系的判断,掌握特殊集合的表示方法以及注意表示集合与元素、集合与集合间关系的符号的区别.2.设集合,则()A. B. C. D.【答案】D【解析】【分析】由交集的性质可知即属于集合A又属于集合B,所以将坐标代入各自的表达式,即可求出参数值. 【详解】由交集的性质可知,,将其代入两个集合可得:,解得:a=2,b=3.故选D.【点睛】本题考查交集的性质与代入求值,将点代入集合即可求得参数值,注意计算的准确性.3.下列函数中,在(-∞,0)上单调递减的是()A. B. C. D.【答案】B【解析】【分析】分别根据解析式的性质判断单调性,将分式型解析式化为反比例型函数,一次函数由斜率判断,二次函数由对称轴与开口方向判断.【详解】A选项:,定义域错误;B选项:一次函数斜率为负数,故单调递减,正确;C选项:对称轴为,定义域不在对称轴一侧,所以错误;D选项,图像开口朝下,对称轴为y轴,所以在该定义域内单调递增,所以错误.故选B.【点睛】本题考查单调性的判断,首先可根据定义域进行判断,其次常见的分式类型可考虑化简为反比例型函数分析,一次函数与二次函数都有固定的分析方式.4.设函数,的定义域都为R,且是奇函数,是偶函数,则下列结论正确的是A. 是偶函数B. ||是奇函数C. ||是奇函数D. ||是奇函数【答案】C【解析】试题分析:∵f(x)是奇函数,g(x)是偶函数,∴f(-x)=-f(x),g(-x)=g(x),f(-x)•g(-x)=-f(x)•g(x),故函数是奇函数,故A错误,|f(-x)|•g(-x)=|f(x)|•g(x)为偶函数,故B错误,f(-x)•|g(-x)|=-f(x)•|g(x)|是奇函数,故C正确.|f(-x)•g(-x)|=|f(x)•g(x)|为偶函数,故D错误考点:函数奇偶性的判断5.集合A满足的集合有()个.A. 1B. 2C. 3D. 4【答案】D【解析】【分析】由集合A与两集合的关系可将其可能性一一列出,即可求得其个数.【详解】由集合A与两集合的关系将其一一列出:,共四个.故选D.【点睛】本题考查集合间的关系,由集合间的关系确定其可能含有的元素,求出集合,注意集合也是集合本身的子集.6.函数的定义域是()A. B. C. D.【答案】B【解析】【分析】由根号下式子大于等于0,分母不等于0,0没有零次方三个知识点即可列式求出定义域.【详解】由题意可得:,解得:且.故选B.【点睛】本题考查定义域的求法,一般有解析式的函数定义域有以下几种情况:①偶次根式被开方数大于等于0;②分母不等于0,;③0没有0次方;④对数函数真数大于0.7.已知函数,则的解析式是()A. 3x+2B. 3x+1C. 3x-1D. 3x+4【答案】A【解析】【分析】由配凑法将解析式化为关于2x+1的形式,即可直接得出解析式.【详解】将解析式变型:,所以.故选A.【点睛】本题考查配凑法求解析式,只需将解析式化为关于左侧括号内式子的形式,进行直接代换即可.8.已知,其中表示不超过的最大整数,则=()A. 2B. 3C.D. 6【答案】D【解析】【分析】由该特殊符号的性质求出的值,带入解析式即可求出函数值.【详解】由特殊符号的性质:,所以.故选D.【点睛】本题考查新定义函数及函数的代入求值,由题意求解即可,注意负数的大小关系.9.如图,U是全集,A、B、C是U的子集,则阴影部分表示的集合是()A. B.C. D.【答案】B【解析】【分析】由图像可知阴影部分为集合B在集合A中的补集与集合C的交集,或集合B在全集中的补集与集合A的交集,再与集合C取交集.【详解】由图像可知:集合B在全集中的补集与集合A的交集,再与集合C取交集,用符号可表示为:.故选B.【点睛】本题考查由韦恩图判断集合的关系,本题阴影部分有多种表示方法,可根据选项进行分析逐个判断即可.10.若函数的定义域为,值域为,则的取值范围是()A. B. C. D.【答案】C【解析】试题分析:,二次函数的对称轴方程为,对于定义域为,值域为,由二次函数的性质可知.故本题答案选C.考点:二次函数的最值.11.若函数为奇函数,且在上是增函数,又的解集为()A. B.C. D.【答案】A【解析】【分析】由函数奇偶性性质,结合特殊值,在坐标系中作出函数简图,由奇函数性质化简不等式,借助图像即可求出解集.【详解】由奇函数的性质以及特殊点可作出如下简图:由奇函数定义化简解析式:,即与x异号即可,由图像可知当或时与x异号.故选A.【点睛】本题考查奇函数的定义以及图像特点,由题意作出图像可极大降低题目的难度,便于快速求出结果.12.已知符号函数sgn=,是R上的增函数,,则()A. sgn sgnB. sgn- sgnC. sgn sgnD. sgn- sgn【答案】B【解析】【分析】分类讨论x与ax的大小,结合单调性分析的正负,代入函数,分析与原函数关系即可.【详解】当时,,由单调性:,此时,当时,,此时:,当时,,由单调性:,此时,所以.故选B.【点睛】本题考查新定义函数以及函数的单调性,由单调性结合新函数的性质即可得出结论,也可以采用特殊值的方式验证其关系,得出结论.二、填空题(本题共有4小题,每小题5分,共20分)13.函数的值域为___________.【答案】【解析】【分析】利用换元法将函数换元构造出新函数,由新函数的定义域结合二次函数的性质求出最值即可得到值域. 【详解】设,则,所以原函数可化为:,由二次函数性质,当时,函数取最大值4,由性质可知函数无最小值,所以值域为:.【点睛】本题考查换元法求函数值域,当函数解析式中含有根式时,一般考虑换元法,用换元法时要注意一定写出参数的取值范围.14.函数的定义域为,则函数的定义域为__________.【答案】【解析】【分析】由两函数括号内式子范围相同可列式求出的定义域.【详解】由题意知中括号内式子的范围为,所以中的范围也是,因此解不等式:,解得:,即为的定义域.【点睛】本题考查复合函数的定义域,复合函数定义域要利用括号内范围相同的原则,列出不等式,即可求解.15.已知的定义域为R,定义若的最小值是___________.【答案】-1【解析】【分析】由函数的表达式可知为定义域中各自取两函数中较大的部分,结合图像分析,即图像在另一图像上方的部分,有图像即可判断最值.【详解】在坐标系中作出两函数图像如下图:由解析式可知,该函数为两函数中较大的部分,由图像可知上方的直线为函数图像,故最小值为-1. 【点睛】本题考查新定义函数,注意对新函数的理解,通过作图的方式辅助解题,即可得出最值.16.定义在上的函数满足.若当时。
辽宁省营口开发区第一高级中学2017-2018学年高二上学期第一次月考数学试题

2017—2018学年度上学期第一次月考高 二 数 学 试 卷满分150分 考试时间120分钟一、选择题(共12个小题,每题5分,共60分,每题只有一个正确答案)1.若a >b >0,c <d <0,则一定有( )A. a c >b dB. a c <b dC. a d >b cD. a d <b c2.设集合M ={x |x 2-3x -4<0},N ={x |0≤x ≤5},则M ∩N =( )A .(0,4]B .[0,4)C .[-1,0)D .(-1,0]3.《莱因德纸草书》是世界上最古老的数学著作之一,书中有一道这样的题目:把100个面包分给五个人,使每个人所得成等差数列,最大的三份之和的17是最小的两份之和,则最小的一份的量是( )A.53B.103C.56D.1164.等差数列{a n }的前n 项和为S n ,若a 1=2,S 3=12,则a 6等于( )A .8B .10C .12D .145.若直线x a +y b=1(a >0,b >0)过点(1,1),则a +b 的最小值等于( ) A . 4 B .3 C . 2 D .56.在等差数列{a n }中,已知a 4+a 8=16,则该数列前11项和S 11=( )A .58B .88C .143D .1767.已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则a 1+a 10=( )A .7B .5C .-5D .-78.在数列{ n a }中,已知12a =,1122n n n a a a --=+,(2)n ≥,则n a 等于( )A21n + B 2n C 3n D 31n + 9.在如图所示的锐角三角形空地中,欲建一个面积不小于300 m 2的内接矩形花园(阴影部分),则其边长x (单位:m)的取值范围是( )A .[15,20]B .[12,25]C .[10,30]D .[20,30]10.设等差数列{a n }的前n 项和为S n ,若S m -1=-2,S m =0,S m +1=3,则m =( )A . 5B .4C .3D .611.已知等比数列{a n }的各项均为不等于1的正数,数列{b n }满足b n =lg a n ,b 3=18,b 6=12,则数列{b n }的前n 项和的最大值等于( )A .126B .130C .132D .13412.已知数列{}n a 是递增数列,且对n N ∈+,都有2n a n n λ=+,则实数λ的取值范围是A 7(,)2-+∞ B (1,)-+∞ C (2,)-+∞ D (3,)-+∞二、填空题(共4个小题,每题5分,共20分)13.已知数列{a n }满足a 1=1,且a n =a n -1+2n -1 (n ≥2 ),则a 20=________.14.中位数为1 010的一组数构成等差数列,其末项为2 015,则该数列的首项为________.15.对于不等式2221(2)3238t t x x t -≤-+≤-,则对区间[0,2]上的任意x 都成立的实数t 的取值范围是_______.16.等差数列{a n }的公差d ≠0满足a 1、a 3、a 13成等比数列,若a 1=1,S n 是{a n }的前n 项和,则2163n n S a ++的最小值为________.三、填空题(共6个题,17题10分,其余每题12分,共70分) 17 设{}n a 是公比为正数的等比数列,12a =,32 4.a a =+(1)求{}n a 的通项公式;(2)设{}n b 是首项为1,公差为2的等差数列,求数列{}n n a b +的前n 项和.n S18 设a≠b ,解关于x 的不等式a 2x +b 2(1-x )≥[ax +b (1-x )]2.19设S n 是等差数列{a n }的前n 项和,已知313S 与414S 的等比中项为515S ,且313S 与414S 的等差中项为1,求数列{a n }的通项公式。
2018-2019学年辽宁省营口市开发区第一中学高三数学文联考试题含解析

2018-2019学年辽宁省营口市开发区第一中学高三数学文联考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知x为锐角,,则a的取值范围为()A.[-2,2] B.C.(1,2] D.(1,2)参考答案:C由,可得:又,∴∴的取值范围为故选:C2. 有下列说法:(1)“”为真是“”为真的充分不必要条件;(2)“”为假是“”为真的充分不必要条件;(3)“”为真是“”为假的必要不充分条件;(4)“”为真是“”为假的必要不充分条件。
其中正确的个数为()A.1 B.2 C. 3D. 4参考答案:D略3. 若、、是互不相同的空间直线,、是不重合的平面,则下列结论正确的是A.B.C.D.参考答案:D略4. 点A,B,C,D均在同一球面上,且AB,AC,AD两两垂直,且AB=1,AC=2,AD=3,则该球的表面积为( )A.7πB.14πC.D.参考答案:B【考点】球内接多面体.【专题】计算题;方程思想;综合法;空间位置关系与距离.【分析】三棱锥A﹣BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,然后解答即可.【解答】解:三棱锥A﹣BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,d==,它的外接球半径是,外接球的表面积是4π()2=14π故选:B.【点评】本题考查球的表面积,考查学生空间想象能力,是基础题.5. 定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则(A)f(sin)<f(cos) (B)f(sin1)>f(cos1)(C)f(cos)<f(sin) (D)f(cos2)>f(sin2)参考答案:答案:D6. 直线l与圆相交于A,B两点,若弦AB的中点,则直线l的方程为:A. B. C.D.参考答案:C7. 已知圆C:x2+y2﹣2x﹣4y=0,则下列点在圆C内的是()A.(4,1)B.(5,0)C.(3,4)D.(2,3)参考答案:D【考点】点与圆的位置关系.【分析】由题意化简得:(x﹣1)2+﹙y﹣2)2=5,将选项,代入,可得结论.【解答】解:由题意化简得:(x﹣1)2+﹙y﹣2)2=5,将选项,代入,可得(2,3)在圆C内,故选D.【点评】本题考查点与圆的位置关系,考查学生的计算能力,比较基础.8. 如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有()A.10 B.12 C.13 D.15参考答案:C9. 等比数列{a n}的前n项和为S n,已知S3=a2+10a1,a5=9,则a1=()A.B.C.D.参考答案:C【考点】89:等比数列的前n项和.【分析】设等比数列{a n}的公比为q,利用已知和等比数列的通项公式即可得到,解出即可.【解答】解:设等比数列{a n}的公比为q,∵S3=a2+10a1,a5=9,∴,解得.∴.故选C.10. 抛物线的弦与过弦的断点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的断点的来两条切线的交点在其准线上,设抛物线,弦过焦点,且其阿基米德三角形,则的面积的最小值为()A. B. C. D.参考答案:B略二、填空题:本大题共7小题,每小题4分,共28分11. 设向量=(1,﹣2),=(a,﹣1),=(﹣b,0),其中O为坐标原点,a>0,b>0,若A、B、C三点共线,则+的最小值为.参考答案:8【考点】基本不等式.【分析】A、B、C三点共线,则=λ,化简可得2a+b=1.根据+=(+)(2a+b),利用基本不等式求得它的最小值【解答】解:向量=(1,﹣2),=(a,﹣1),=(﹣b,0),其中O为坐标原点,a>0,b>0,∴=﹣=(a﹣1,1),=﹣=(﹣b﹣1,2),∵A、B、C三点共线,∴=λ,∴,解得2a+b=1,∴+=(+)(2a+b)=2+2++≥4+2=8,当且仅当a=,b=,取等号,故+的最小值为8,故答案为:812. 函数f(x)=ax2+bx﹣1,且0≤f(1)≤1,﹣2≤f(﹣1)≤0,则z=的取值范围是.参考答案:[,2]【考点】简单线性规划;二次函数的性质.【分析】利用已知条件得到a,b的不等式组,利用目标函数的几何意义,转化求解函数的范围即可.【解答】解:函数f(x)=ax2+bx﹣1,且0≤f(1)≤1,﹣2≤f(﹣1)≤0,可得0≤a+b﹣1≤1,﹣2≤a﹣b﹣1≤0,即,表示的可行域如图:,则z==,令t=,可得z==+.t≥0.,又b=1,a=0成立,此时z=,可得z∈[,2]故答案为:[,2].13. 对于函数定义域中任意的(),有如下结论:①;②;③>0;④<.当时,上述结论中正确结论的序号是参考答案:答案:②③14. 已知一几何体的三视图如图所示,则该几何体的体积为________.参考答案:略15. 若|x+1|+|x﹣3|>k对任意的x∈R恒成立,则实数k的取值范围为.参考答案:(﹣∞,4)考点:函数恒成立问题.专题:计算题;函数的性质及应用;不等式的解法及应用.分析:|x+1|+|x﹣3|>k对任意的x∈R恒成立,等价于(|x+1|+|x﹣3|)min>k,利用不等式的性质即可求得最小值.解答:解:|x+1|+|x﹣3|>k对任意的x∈R恒成立,等价于(|x+1|+|x﹣3|)min>k,∵|x+1|+|x﹣3|≥|(x+1)﹣(x﹣3)|=4,∴k<4,即实数k的取值范围是(﹣∞,4),故答案为:(﹣∞,4).点评:该题考查函数恒成立问题、绝对值不等式的性质,考查转化思想,属基础题.16. 不等式的解集是___________.参考答案:(-1,3)略17. 如图,已知PA、PB是圆O的切线,A、B分别为切点,C为圆O上不与A、B重合的另一点,若∠ACB = 120°,则∠APB=参考答案:三、解答题:本大题共5小题,共72分。
营口市开发区第一高级中学2018-2019学年上学期期中高考数学模拟题

营口市开发区第一高级中学2018-2042学年上学期期中高考数学模拟题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1. 设集合{}|||2A x R x =∈≤,{}|10B x Z x =∈-≥,则A B =( )A.{}|12x x <≤B.{}|21x x -≤≤C. {}2,1,1,2--D. {}1,2【命题意图】本题考查集合的概念,集合的运算等基础知识,属送分题.2. 拋物线E :y 2=2px (p >0)的焦点与双曲线C :x 2-y 2=2的焦点重合,C 的渐近线与拋物线E 交于非原点的P 点,则点P 到E 的准线的距离为( ) A .4 B .6 C .8 D .103. 已知集合,则( )ABC D4. 将函数)63sin(2)(π+=x x f 的图象向左平移4π个单位,再向上平移3个单位,得到函数)(x g 的图象, 则)(x g 的解析式为( )A .3)43sin(2)(--=πx x g B .3)43sin(2)(++=πx x g C .3)123sin(2)(+-=πx x g D .3)123sin(2)(--=πx x g【命题意图】本题考查三角函数的图象及其平移变换理论,突出了对函数图象变换思想的理解,属于中等难度.5. 1F ,2F 分别为双曲线22221x y a b-=(a ,0b >)的左、右焦点,点P 在双曲线上,满足120PF PF ⋅=,若12PF F ∆的内切圆半径与外接圆半径之比为12,则该双曲线的离心率为( )C. 1D. 1【命题意图】本题考查双曲线的几何性质,直角三角形内切圆半径与外接圆半径的计算等基础知识,意在考查基本运算能力及推理能力.6. 若关于x 的不等式07|2||1|>-+-++m x x 的解集为R ,则参数m 的取值范围为( ) A .),4(+∞ B .),4[+∞ C .)4,(-∞ D .]4,(-∞【命题意图】本题考查含绝对值的不等式含参性问题,强化了函数思想、化归思想、数形结合思想在本题中的应用,属于中等难度.7. 已知抛物线C :y x 82=的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若2=,则=QF ( ) A .6B .3C .38D .34 第Ⅱ卷(非选择题,共100分)8. ABC ∆的外接圆圆心为O ,半径为2,OA AB AC ++为零向量,且||||OA AB =,则CA 在BC 方向上的投影为( )A .-3 B. C .3 D9. 已知i z 311-=,i z +=32,其中i 是虚数单位,则21z z 的虚部为( ) A .1- B .54 C .i - D .i 54 【命题意图】本题考查复数及共轭复数的概念,复数除法的运算法则,主要突出对知识的基础性考查,属于容易题.10.已知函数1)1(')(2++=x x f x f ,则=⎰dx x f 1)(( )A .67-B .67C .65D .65- 【命题意图】本题考查了导数、积分的知识,重点突出对函数的求导及函数积分运算能力,有一定技巧性,难度中等.11.已知变量,x y 满足约束条件20170x y x x y -+≤⎧⎪≥⎨⎪+-≤⎩,则y x 的取值范围是( )A .9[,6]5B .9(,][6,)5-∞+∞ C .(,3][6,)-∞+∞ D .[3,6]12.“3<-b a ”是“圆056222=++-+a y x y x 关于直线b x y 2+=成轴对称图形”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件【命题意图】本题考查圆的一般方程、圆的几何性质、常用逻辑等知识,有一定的综合性,突出化归能力的考查,属于中等难度.二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.在正方形ABCD 中,2==AD AB ,N M ,分别是边CD BC ,上的动点,当4AM AN ⋅=时,则MN 的取值范围为 .【命题意图】本题考查平面向量数量积、点到直线距离公式等基础知识,意在考查坐标法思想、数形结合思想和基本运算能力.14.在ABC ∆中,90C ∠=,2BC =,M 为BC 的中点,1sin 3BAM ∠=,则AC 的长为_________. 15.81()x x-的展开式中,常数项为___________.(用数字作答) 【命题意图】本题考查用二项式定理求指定项,基础题. 16.已知函数22tan ()1tan xf x x=-,则()3f π的值是_______,()f x 的最小正周期是______. 【命题意图】本题考查三角恒等变换,三角函数的性质等基础知识,意在考查运算求解能力.三、解答题(本大共6小题,共70分。
2018届高三理科数学上第一次月考试卷

2018届高三理科数学上第一次月考试卷安徽省无为县2018届高三数学上学期第一次月考试题理(考试时间:120分钟满分:150分)第I卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合,则()A. B. . D.2已知复数,,若复数,则实数的值为()A. B.6. D.3. 如图是某个几何体的三视图,则这个几何体体积是()A. B..D.4. 已知等边与等边同时内接于圆中,且,若往圆内投掷一点,则该点落在图中阴影部分内的概率为()A. B . . D.5. 已知等比数列,且,贝U的值为()A.2B.4.8D.166. 我国古代数学著作《九算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的(单位:升),则输入的值为()A. 4.5B . 6. 7.5D . 97 .已知角a终边与单位圆x2+y2=1的交点为,则=( )A. B . . D. 1&设,满足约束条件若的最大值为2,则的值为 ()A. B . . D.9、已知向量,,,若与的夹角为60°,且,则实数的值为()A. B. . 6 D. 410 .函数的图象如图所示,则下列结论成立的是()A . a>0, b>0,v 0B. a v 0, b>0,> 0.a v 0, b>0,v 0D. a v 0, b v0, v 011.四面体中,,,,则四面体外接球的表面积为()A. B. . D.12 .已知定义域为R的函数g( x),当x € (- 1,1]时,且g (x+2) =g (x)对∀x € R恒成立,若函数 f(x) =g (x)-( x+1)在区间[-1, 5]内有6个零点,则实数的取值范围是( )A. ( , )B. (-^, ] U (,+^). [ , ) D.[,] 第口卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知函数的两个零点分别为、n (v n),则二14. 已知数列为等差数列,为等比数列,且,记数列的前项和为,若,则数列的最大项为第_____________ 项.15. 若的展开式中各项系数的和为32,则展开式中只含字母且的次数为1的项的系数为_____________16. 已知双曲线的右焦点为,过点向双曲线的一条渐进线引垂线,垂足为,交另一条渐近线于,若,则双曲线的离心率为.三、解答题(本大题共6小题,共70分.解答应写出字说明、证明过程或演算步骤.)17. (本小题满分12分)在厶AB中,角A, B,所对的边分别为a, b,且sin2A+sin2=sin2B - sinAsin .(1)求B的大小;(2)设/ BA的平分线AD交B于D, AD=2 , BD=1,求sin / BA的值.18、(本小题满分12分)2016年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:满意度评分低于60分60分到79分80分到89分不低于90分满意度等级不满意基本满意满意非常满意已知满意度等级为基本满意的有680人.(I)若市民的满意度评分相互独立,以满意度样本估计全市市民满意度.现从全市市民中随机抽取4人,求至少有2人非常满意的概率;(H)在等级为不满意市民中,老年人占13.现从该等级市民中按年龄分层抽取15人了解不满意的原因,并从中选取3人担任整改督导员,记X为老年督导员的人数,求X 的分布列及数学期望E(X);19 (本小题满分12分)如图,已知四棱锥S- ABD中,SA!平面ABD/ AB=Z BD=90°,且SA=AB=B=2D=2E 是边SB的中点.(I)求证:E//平面SAD;(2)求二面角D- E- B的余弦值大小.20. (本小题满分12分)已知是抛物线上的一点,以点和点为直径的圆交直线于,两点,直线与平行,且直线交抛物线于,两点.(I)求线段的长;(H)若,且直线与圆相交所得弦长与相等,求直线的方程.21 .(本小题满分12 分)函数f (x) =lnx+ +ax (a€ R), g (x) =ex+ .(I)讨论f (x)的极值点的个数;(2)若对于∀x > 0,总有f (x) < g (x). (i ) 求实数a的取值范围;(ii )求证:对于∀x >0,不等式ex+x2 -( e+1) x+ > 2 成立.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分(本小题满分10分).22. 以直角坐标系的原点为极点,轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线的参数方程为,(为参数,),曲线的极坐标方程为.(1)求曲线的直角坐标方程;(2)设直线与曲线相交于,两点,当变化时,求的最小值.23. 已知函数.(1)若,使得成立,求的范围;(2)求不等式的解集高三数学(理科)参考答案选择题一、1-5 BAD 6-10 BAA 11-12二、填空题13 14.14 15.-7 16.三、解答题17. 解:(本小题满分12分)(1)在厶AB中,I sin2A+sin2=sin2B —sinAsin ,••• a2+2=b2 —a,…/. sB==—=—,…••• B€( 0, n),…•B=.…(2)在厶ABD中,由正弦定理:,•sin / BAD===,…•s/ BA=s2Z BAD=1- 2sin2 / BAD=1- 2X =,…•sin / BA===. …18. 解:(1)由频率分布直方图可知则10X (0.035 + a + 0.020 + 0.014 + 0.004 + 0.002) = 1 ,所以a= 0.025 ,所以市民非常满意的概率为0.025 X 10= 14.又市民的满意度评分相互独立,故所求事件的概率P= 1- 189256 = 67256.6分(2)按年龄分层抽样抽取15人进行座谈,则老年市民抽15X 13= 5人,从15人中选取3名整改督导员的所有可能情况为315,由题知X的可能取值为0,1,2,3 ,P(X= 0) = 310315 =2491 , P(X = 1) = 15210315 = 4591,P(X = 2) = 25110315 = 2091 , P(X= 3) = 35315= 291,X分布列为X0123P2491291所以E(X) = 0 X 2491 + 1 X 4591 + 2 X 2091 + 3 X 291 = 1.8分12分19【解答】证明:(1)取SA中点F,连结EF, FD,••• E是边SB的中点,••• EF// AB,且EF= AB,又•••/ AB=Z BD=90° ,••• AB// D,又••• AB=2D,且EF=D,•••四边形EFD是平行四边形,••• FD// E,又FD⊂平面SAD E⊄平面SAD••• E//面SAD解:(2)在底面内过点A作直线A// B,则AB丄A,又SU平面ABD以AB, A, AS所在直线分别为x, y, z轴,建立空间直角坐标系,则A(0,0,0),B(2, 0,0),(2, 2, 0),D(1, 2,0), D(1, 2, 0), E( 1, 0, 1),则=(0, 2, 0), = (- 1, 0, 1), = (- 1, 0,),= (-1, - 2 , 1), 设面BE的一个法向量为=(x , y , z),贝U ,取x=1,得=(1, 0 , 1),同理求得面DE的一个法向量为=(0 , 1 , 2),s V > ==,由图可知二面角D- E- B是钝二面角,•••二面角D- E- B的余弦值为-.20.解:(20.解:(I)设,圆方程为令,得,「•,,(H)设直线的方程为,,,则由消去,得,•••,•••,则,•••,解得或,当或时,当到直线的距离,•••圆心到直线的距离等于直线的距离,•••,又,消去得,求得,此时,,直线的方程为,综上,直线的方程为或.21. 解:(1)由题意得f (x) =x+ +a=,当a2 - 4< 0,即-2< a< 2时,f (x) > 0恒成立,无极值点;当a2 - 4> 0,即a v- 2 或a>2 时,① a v- 2时,设方程x2+ax+仁0两个不同实根为x1 ,x2,不妨设x1 v x1 , x2,贝» x1+x2= - a>0, x1x2=1 >0, 故0v x1 v x2,• x1 , x2是函数的两个极值点.② a> 2时,设方程x2+ax+1=0两个不同实根为x1 , x2,则x1+x2= - a v 0, x1x2=1 >0,故x1 v 0, x2 v 0, 故函数没有极值点.综上,当a v- 2时,函数有两个极值点;当a>- 2时,函数没有极值点.(2) (i ) f (x) < g (x)等价于ex - Inx+x2 > ax,由x> 0, 即卩a< 对于∀x > 0恒成立,设 $ (x) = (x > 0),『(x)=,••• x > 0,.・.x €( 0, 1)时,$ (x)v 0, $ (x)单调递减,x €( 1, +8)时,$ (x)> 0, $ (x)单调递增,••• $ (x) > $ (1) =e+1,••• a< e+1 .(ii )( ii )由(i )知,当a=e+1 时有f (x) < g (x), 即:ex+ x2 > lnx+ x2+ (e+1) x ,等价于ex+x2 - (e+1) x > Inx…①当且仅当x=1时取等号,以下证明:lnx+ > 2,设B (x) =lnx+ ,贝» 0 '( x)=—=,•••当x €( 0, e)时0 (x)v 0, 0 (x)单调递减,x €( e, +8)时0 (x)> 0, 0 (x)单调递增,•0 (x) > 0 (e) =2,•lnx+ >2,②当且仅当x=e时取等号;由于①②等号不同时成立,故有ex+x2 — (e+1)x+ >2.22. ........................................ 解:(I )由,得4分曲线的直角坐标方程为... 5分(II )将直线的参数方程代入,得.... 6分设两点对应的参数分别为,贝U ,,……7分..... 9分.精品文档.当时,的最小值为2. ................ 10分23. 解:(I )……3分当时,,所以 ......... 4分••• .... 5分(II )即由(I )可知,当时,的解集为空集;…当时,的解集为;……8分当时,的解集为.……9分综上,不等式的解集为 ...... 10分2016全新精品资料-全新公文范文-全程指导写作 -独家原创11 / 11。
辽宁省营口市高一上学期数学第一次月考试卷

辽宁省营口市高一上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2018高三上·广东月考) 若集合,,则()A .B .C .D .2. (2分) (2017高一上·张掖期末) 如图所示,U是全集,A,B是U的子集,则阴影部分所表示的集合是()A . A∩BB . A∪BC . B∩(∁UA)D . A∩(∁UB)3. (2分)(2019·定远模拟) 设集合,,则()A .B .C .D .4. (2分) (2017高一上·广州月考) 下列各组函数中,表示同一函数的是()A .B .C .D .5. (2分)函数的定义域为()A .B .C .D .6. (2分) (2018高二上·莆田月考) 若关于x的不等式x2+ax-2>0在区间[1,5]上有解,则a的取值范围是()A . (- ,+∞)B . [- ,1]C . (1,+∞)D . (-∞, ]7. (2分)已知定义域为R的函数y=g(x)满足以下条件:①∀x∈R,g(3﹣x)=g(3+x)②g(x)=g(x+2)③当x∈[1,2]时,g(x)=﹣2x2+4x﹣2,若方程g(x)=loga(x+1)(a>0,且a≠1)在[0,+∞)上至少有5个不等的实根,则实数a的取值范围为()A . 0<a<B . 0<a≤C . 0<a<D . a≥8. (2分) (2017高一上·雨花期中) 已知函数f(x)= ,则f(f())()A .B .C .D .9. (2分)(2013·新课标Ⅰ卷理) 执行程序框图,如果输入的t∈[﹣1,3],则输出的s属于()A . [﹣3,4]B . [﹣5,2]C . [﹣4,3]D . [﹣2,5]10. (2分) (2018高一上·河北月考) 函数的奇偶性是()A . 奇函数B . 偶函数C . 既不是奇函数也不是偶函数D . 既是奇函数又是偶函数11. (2分)对于函数(其中),选取的一组值计算和,所得出的正确结果一定不可能是()A . 4和6B . 2和1C . 2和4D . 1和312. (2分) (2016高一上·临川期中) 已知函数f(x)= ,若f(f(0))=6,则a的取值等于()A . ﹣1B . 1C . 2D . 4二、填空题 (共4题;共4分)13. (1分)已知数列A:a1 , a2 ,…an(n>2),记集合TA={x|x=ai+aj ,1≤i<j≤n},则当数列A:2,4,6,8,10时,集合TA的元素个数是________.14. (1分)已知函数f(x)=ax﹣k的图象过点(1,3)和(0,2),则函数f(x)的解析式为________.15. (1分)对于函数f(x),若存在区间A=[m,n],使得{y|y=f(x),x∈A}=A,则称函数f(x)为“同域函数”,区间A为函数f(x)的一个“同城区间”.给出下列四个函数:①f(x)=cos x;②f(x)=x2﹣1;③f(x)=|x2﹣1|;④f(x)=log2(x﹣1).存在“同域区间”的“同域函数”的序号是________ (请写出所有正确的序号)16. (1分)若函数y=f(x)的定义域为R,对于∀x∈R,f'(x)<ex ,且f(x+1)为偶函数,f(2)=1,则不等式f(x)<ex的解集为________.三、解答题 (共6题;共70分)17. (10分)已知集合A={x|x2+4ax﹣4a+3=0},B={x|x2+(a﹣1)x+a2=0},C={x|x2+2ax﹣2a=0},其中至少有一个集合不为空集,求实数a的取值范围.18. (15分)设函数f(x)=|1﹣2x|﹣3|x+1|,f(x)的最大值为M,正数a,b满足+=Mab.(Ⅰ)求M;(Ⅱ)是否存在a,b,使得a6+b6=?并说明理由.19. (15分) (2016高一上·台州期中) 已知函数f(x)= (a>0)在其定义域上为奇函数.(1)求a的值;(2)判断函数f(x)的单调性,并给出证明.20. (10分) (2019高一上·上饶期中) 某镇在政府“精准扶贫”的政策指引下,充分利用自身资源,大力发展养殖业,以增加收入,政府计划共投入72万元,全部用于甲、乙两个合作社,每个合作社至少要投入15万元,其中甲合作社养鱼,乙合作社养鸡,在对市场进行调研分析发现养鱼的收益M、养鸡的收益N与投入a(单位:万元)满足,N= a+20.设甲合作社的投入为x(单位:万元),两个合作社的总收益为f(x)(单位:万元).(1)当甲合作社的投入为25万元时,求两个合作社的总收益;(2)试问如何安排甲、乙两个合作社的投入,才能使总收益最大,最大总收益为多少万元?21. (10分) (2017高一上·中山月考) 某种商品在天内每克的销售价格 (元)与时间的函数图象是如图所示的两条线段(不包含两点);该商品在 30 天内日销售量 (克)与时间 (天)之间的函数关系如下表所示:第天5152030销售量克35252010(注:日销售金额=每克的销售价格×日销售量)(1)根据提供的图象,写出该商品每克销售的价格 (元)与时间的函数关系式;(2)根据表中数据写出一个反映日销售量随时间变化的函数关系式;(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的值.22. (10分) (2016高一上·荆州期中) 已知函数f(x)的定义域为(﹣1,1),对任意x,y∈(﹣1,1),有f(x)+f(y)=f().且当x<0时,f(x)>0.(1)验证函数f(x)=lg 是否满足这些条件;(2)若f()=1,f()=2,且|a|<1,|b|<1,求f(a),f(b)的值.(3)若f(﹣)=1,试解关于x的方程f(x)=﹣.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共70分) 17-1、答案:略18-1、答案:略19-1、答案:略19-2、答案:略20-1、答案:略20-2、答案:略21-1、21-2、21-3、答案:略22-1、答案:略22-2、答案:略22-3、答案:略。
辽宁省营口开发区一高中高三数学入学摸底考试试题 理 新人教A版

辽宁省营口开发区一高中高三数学入学摸底考试试题 理新人教A 版数 学(理)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,I 是全集,,,M P S 是的3个子集,则阴影部分所表示的集合是( )A.()M P SB.()M P SC.()MP C I S D.()MP C I S2.已知复数211iz i=+-,则2320121z z z z ++++⋅⋅⋅+的值为( ) A.1i + B.1 C.i D.i - 3.下列有关命题说法正确的是( ) A."1"x =-是2"560"x x --=的必要不充分条件B.命题2000",10"x R x x ∃∈++<的否定是2000",10"x R x x ∀∈++>C.ABC ∆的三个内角为,,A B C ,则cos2cos2A B <是A B >的充要条件D.函数()()sin f x x x x R =-∈有3个零点4.已知各项不为0的等差数列{}n a 满足:()271222a a a =+,数列{}n b 的等比数列,且77b a =,则59b b =( )A.16B.8C.4D.25.如右图所示的程序框图,输出S 的结果的值为( )A.0B.1C.12-D.126.若()1123ln 21a x dx a x ⎛⎫+=+> ⎪⎝⎭⎰,则a 的值是( )A.2B.3C.4D.67.一个盒子里有6只好晶体管,4只坏晶体管,任取两次,每次取一只,每次取后不放回,则若已知第一只是好的,则第二只也是好的概率为( )A.23B.512C.59D.798.设M 是ABC ∆的任一点,且23,30AB AC BAC ⋅=∠=︒,设,,MBC MAC MAB ∆∆∆的面积分别为,,x y z ,且12z =,则在平面直角坐标系中,以,x y 为坐标的点(),x y 的轨迹图形是阴影P SMI( )DCBA9.设函数()ππ2cos23f x x⎛⎫=-⎪⎝⎭,若对于任意的x R∈,都有()()()12f x f x f x<<,则12||x x-的最小值为( )A.4B.2C.1D.1210.已知双曲线()222210,0x ya ba b-=>>,,M N是双曲线上关于原点对称的两点,P是双曲线上的动点,且直线,PM PN的斜率分别为1212,,0k k k k≠,若12||||k k+的最小值为1,则双曲线的离心率为( )D.3211.棱长为,然后在正四面体和该球形成的空隙处各放入一小球,则这些球的最大半径为( )12.若122012222n aa a=++⋅⋅⋅+,其中12,,,na a a⋅⋅⋅为两两不等的非负整数,令1sin,niix a==∑11cos,tann ni ii iy a z a====∑∑,则,,x y z的大小关系是( )A.x y z<< B.y z x<< C.x z y<< D.z x y<<二、填空题(本大题共4小题,每小题5分,共20分)13.已知312ax xx x⎛⎫⎛⎫+-⎪⎪⎝⎭⎝⎭展开式中各项系数和为3,则61xax⎛⎫-⎪⎝⎭的展开式中的常数项为________14.已知实数,x y满足121,yy xx y m≥⎧⎪≤-⎨⎪+≤⎩如果目标函数z x y=-的最小值为1-,则实数m=________15.若圆()2221:240C x y ax a a R+++-=∈与圆()2222:210C x y by b b R+-+-=∈外切,则a b+的最大值为________(16题图)俯视图左视图主视图32416.已知一个四面体的三视图如图所示,则这个四面体的体积为________三、解答题(本大题共6小题,共70分.解答题应写出文字说明,证明过程或演算步骤.) 17.(本小题12分)已知在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,cos cos cos B c B b C =+ (1)求角B 的大小;(2)设向量()()cos ,cos 2,12,5m A A n ==-,求当m n ⋅取最大值时,tan C 的值.18.(本小题12分)随机调查某社区80个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别有关系,得到下面的数据表:休闲方式性别看电视 看书 合计男 10 50 60 女 10 10 20 合计 20 60 80(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X ,求X 的分布列和期望;(2)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?参考公式: ()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++参考数据:()20P K K ≥0.15 0.10 0.05 0.025 0.010 0K2.0722.7063.8415.0426.63519.(本小题12分)如图,在三棱锥P ABC -中,,AB AC D =为BC 的中点,PO 平面ABC ,垂足O 落在线段AD 上,已知8,4,3,2BC PO AO OD ====(1)证明:AP BC ⊥;(2)在线段AP 上是否存在点M ,使得二面角A MC B --为直二面角?若存在,求出AM 的长;若不存在,请说明理由.20.(本小题12分)如图,抛物线21:4C y x =的焦点到准线的距离与椭圆()22222:10x y C a b a b +=>>的长半轴相等,设椭圆的右顶点为12,,A C C 在第一象限的交点为,B O 为坐标原点,且OAB ∆(1)求椭圆2C 的标准方程;(2)过点A 作直线l 交1C 于,C D 两点,射线,OC OD 分别交2C 于,E F 两点. (I)求证:O 点在以EF 为直径的圆的内部;(II)记,OEF OCD ∆∆的面积分别为12,S S ,问是否存在直线l ,使得213S S =?请说明理由.21.(本小题12分)已知,a R ∈函数()()()ln 1,ln 1x af x xg x x e x x=+-=-+ (1)判断函数()f x 在(]0,e 上的单调性;(2)是否存在实数()00,x ∈+∞,使曲线()y g x =在点0x x =处的切线与y 轴垂直?若存在,求出0x 的值;若不存在,请说明理由.请考生在第22,23,24题中任选一题做答.如果多做,则按所做的第一题记分.做答时,用2B 铅笔在答题卡上把所选题目对应的题号涂黑. 22.(本小题10分)选修4—1:几何证明选讲如图,已知1O 与2O 外切于点P ,AB 是两圆的外公切线,,A BP OD C BA为切点, AB 与12O O 的延长线相交于点C ,延长AP 交2O 于点D ,点E 在AD 延长线上,(1)求证:ABP ∆是直角三角形; (2)若9,4,4AB AC AP AE AP PD ⋅=⋅==,求EC AC的值.23.(本小题10分)选修4—4:坐标系与参数方程在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建坐标系,已知曲线()2:sin 2cos 0C a a ρθθ=>,已知过点()2,4P --的直线l 的参数方程为:2,4x y ⎧=-⎪⎪⎨⎪=-⎪⎩直线l 与曲线C 分别交于,M N(1)写出曲线C 和直线l 的普通方程;(2)若||,||,||PM MN PN 成等比数列,求a 的值.24.(本小题10分)选修4—5:不等式选讲已知函数()||f x x a =-(1)若不等式()f x m ≤的解集为{}|15x x -≤≤,求实数,a m 的值; (2)当2a =时,解关于x 的不等式()()()20f x t f x t t +≥+≥.高三第六次模拟考试理科数学试题答案 CBCAAA CABBCD13.52-14.515.16.817.(1)π4B =(2)234310cos 55m n A ⎛⎫⋅=--+ ⎪⎝⎭,∴当3cos 5A =时,取最大值.此时4tan 3A =,()tan tan 7C A B ∴=-+=18.(1)0,1,2,3X =,且每个男性在这一时间段以看书为休闲方式的概率为56P = 根据题意可得5~3,6X B ⎛⎫⎪⎝⎭,()3315,0,1,2,366kkk P X k C k -⎛⎫⎛⎫∴=== ⎪⎪⎝⎭⎝⎭55362EX np ∴==⨯=(2)提出假设0H :休闲方式与性别无关系. 28.889 6.635K ≈>因为当0H 成立时,2 6.635K ≥的概率约为0.01,所以我们有99%的把握认为相关 19.(1),,,AD BC PO BC BC PAD BC PA ⊥⊥⊥⊥平面故(2)在平面PAB 内作BM PA ⊥于M ,连CM ,得AP ⊥平面BMC BMC APC ∴⊥平面平面,ADB AB POD PBD ∆=∆∆在R t 中,勾股定理得在R t R t 中,勾股定理得222236,6PB PO OD DB PB =++==得,5POA PA ∆=在R t 中,得1cos cos 2,33BPA PM PB BPA AM PA PM ∠=∴=∠=∴=-=又,综上所述,存在点M 符合题意,3AM = 20.(1)2p =,得椭圆的长半轴2a =1||2OAB B B S OA y y ∆=⨯⨯=∴=代入抛物线求得23B ⎛ ⎝⎭∴椭圆2C 方程为22:143x y +=(2)(I)设直线l 的方程为:2x my =+,由224x my y x=+⎧⎨=⎩得2480,y my --=设()()1122121212,,,4,84C x y D x y y y m y y x x ∴+==-∴= 121240,90OC OD x x y y COD ∴⋅=+=-<∴∠>︒又,90,EOF COD EOF ∠=∠∴∠>︒∴O 点在以EF 为直径的圆的内部 (II)11221||||sin ||||21||||||||sin 2E F OC OD CODS y y S y y OE OF EOF ⋅∠==⋅⋅∠,直线OC 的斜率为1114y x y =∴直线OC 的方程为14y y x ⋅=.由1224143y y x x y ⋅⎧=⎪⎪⎨⎪+=⎪⎩得222212643643,364364E F y y y y ⨯⨯==++2222222164312148,121483E F S m y y m S ⎛⎫⨯+∴⋅=∴=⎪+⎝⎭,222221121481111,3333S m m R S +∈∴≥∴≥> ∴不存在直线l 使得213S S =21.()()()221ln 1,0,,a a x af x x x f 'x x x x x-∴=+-∈+∞∴=-+= ①若0,a ≤则()0f 'x >,()f x 在(]0,e 上单调递增②若0a e <<,当()0,x a ∈时,()0,f 'x <函数()f x 在区间()0,a 上单调递减, 当(],x a e ∈时,()0,f 'x >函数()f x 在区间(],a e 上单调递增 ③若a e ≥,则()0,f 'x ≤函数()f x 在区间(]0,e 上单调递减.(2)()1ln 11x g'x x e x ⎛⎫=+-+ ⎪⎝⎭,由(1)易知,当1a =时,()f x 在()0y +∞上的最小值:()()min 10f x f == 即()00,x ∈+∞时,001ln 10.x x +-≥又()000,10x e g x >∴≥>, 曲线()y g x =在点0x x =处的切线与y 轴垂直等价于方程()00g'x =有实数解. 而()00g'x >,即方程()00g'x =无实数解,故不存在. 23.(1)22,2y ax y x ==- (2)1a =24.(1)2,3a m ==(2)0,;0,,22t t x R t x ⎛⎤=∈>∈-∞- ⎥⎝⎦。
辽宁省大连经济技术开发区2018届高三数学上学期第一次月考试题 理(无答案)

辽宁省大连经济技术开发区2018届高三数学上学期第一次月考试题理(无答案)一选择题(每小题5分,共计60分) 1.已知集合{}{}22|,032|2<≤-=≥--=x x B x x x A ,则=B A ( )A .]1,2[-- B . )2,1[- C..]1,1[- D .)2,1[2. 已知x ,y R ∈,且0x y >>,则( )A.110x y-> B.sin sin 0x y -> C.11()()022x y-< D.ln ln 0x y +>3.下列函数中,在区间(0,)+∞上为增函数的是( )A .y =.2(1)y x =- C .2x y -=D .0.5log (1)y x =+4. 如图,函数()f x 的图象为折线ACB ,则不等式()()2log 1f x x +≥的解集是( )A{}|10x x -<≤ B .{}|11x x -≤≤C{}|11x x -<≤ D .{}|12x x -<≤5. 已知)(),(x g x f 分别是定义在R 上的偶函数和奇函数,且1)()(23++=-x x x g x f ,则=+)1()1(g f ( )A. 3-B. 1-C. 1D. 36. 已知432a =,254b =,1325c =,则( )(A )b ac << (B )a b c <<(C )b c a << (D )c a b <<7. 设命题p :2,2nn N n ∃∈>,则p ⌝为( )(A )2,2nn N n ∀∈> (B )2,2nn N n ∃∈≤(C )2,2nn N n ∀∈≤ (D )2,=2n n N n ∃∈8. 已知命题:p 对任意x R ∈,总有20x>;:"1"q x >是"2"x >的充分不必要条件则下列命题为真命题的是( ).A p q ∧ .B p q ⌝∧⌝ .C p q ⌝∧ .D p q ∧⌝9. “1x >”是“12log (2)0x +<”的( )A 、充要条件B 、充分不必要条件C 、必要不充分条件D 、既不充分也不必要条件 10. 命题“*x n ∀∈∃∈,R N,使得2n x >”的否定形式是( )A 、∀x ∈R,∃n ∈N +,2n x < B .*x n ∀∈∀∈,R N ,2n x <C 、∃x ∈R, ∃n ∈N +,2n x<, D .*x n ∃∈∀∈,R N ,2nx <11. 以平面直角坐标系的原点为极点,x 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线l 的参数方程是13x t y t =+⎧⎨=-⎩(t 为参数),圆C 的极坐标方程是θρcos 4=,则直线l被圆C截得的弦长为( ) A .14B .142 C .2 D .2212. 曲线1cos 2sin x y θθ=-+⎧⎨=+⎩,(θ为参数)的对称中心( )A .在直线2y x =上 B .在直线2y x =-上C .在直线1y x =-上D .在直线1y x =+上二、填空题(每小题5分,共计20分) 13.在极坐标中,圆8sin ρθ=上的点到直线()3R πθρ=∈距离的最大值是 .14.在极坐标系中,直线cos sin 10ρθθ--=与圆2cos ρθ=交于A ,B 两点,则||AB =——15.不等式152x x ---<的解集是____16. 若实数x,y 满足xy=1,则2x +22y 的最小值为______________. 三、解答题(共计70分)17(10分)设a,b 为正数,且a+b=1,求证:1a 2++12+b ≤22 18,(12分)已知函数()||||f x x x =+1--2.(1)求不等式()f x ≥1的解集; (2)若不等式()f x x x m 2≥-+的解集非空,求m 的取值范围.19,(12分)已知在平面直角坐标系xOy 中,直线l 的参数方程是⎪⎪⎩⎪⎪⎨⎧+==242222t y t x (t 是参数),以原点O 为极点,x 轴正半轴极轴建立极坐标系,曲线C 的极坐标方程)4cos(2πθρ+=.(Ⅰ)判断直线l 与曲线C 的位置关系;(Ⅱ)设M 为曲线C 上任意一点,求y x +的取值范围. 20、(12分)已知命题p:关于x 的方程x2-ax+4=0有实根;命题q:关于x 的函数y=2x2+ax+4在[3,+∞)上是增函数,若p 或q 真,p 且q 假,求实数a 的取值范围。
2018年辽宁省营口市开发区中学高一数学理期末试题含解析

2018年辽宁省营口市开发区中学高一数学理期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设集合A={x|﹣1≤x≤2},B={x|0≤x≤4},则A∩B=()A.{x|0≤x≤2}B.{x|1≤x≤2}C.{x|0≤x≤4}D.{x|1≤x≤4}参考答案:A【考点】交集及其运算.【专题】计算题.【分析】找出A和B解集中的公共部分,即可确定出两集合的交集.【解答】解:∵A={x|﹣1≤x≤2},B={x|0≤x≤4},∴A∩B={x|0≤x≤2}.故选A【点评】此题考查了交集及其运算,比较简单,是一道基本题型.2. 将函数的图像上各点的横坐标伸长为原来的2倍,再向右平移个单位,得到的函数图像的一个对称中心为( )A.B. C. D.参考答案:D将函数的图象上各点的横坐标伸长为原来的倍,可得函数的图象,向右平移个单位,得到函数的图象,令,可得,故所得函数的对称中心为,令,可得函数图象的一个对称中心为,故选D.3. 下列函数中,既是偶函数又在(0,+∞)上是单调递减的是()A. B. C. D.参考答案:C【分析】先判断各函数奇偶性,再找单调性符合题意的即可。
【详解】首先可以判断选项D,不是偶函数,排除;然后,由图像可知,在上不单调,在上单调递增,只有选项C:符合,故选C。
【点睛】本题主要考查函数的性质,奇偶性和单调性。
4. 定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有<0.则()A.f(0.76)<f(log0.76)<f(log60.5)B.f(0.76)<f(60.5)<f(log0.76)C.f(log0.76)<f(0.76)<f(60.5)D.f(log0.76)<f(60.5)<f(0.76)参考答案:D【考点】奇偶性与单调性的综合.【专题】综合题;转化思想;综合法;函数的性质及应用.【分析】先由奇偶性将问题转化到[0,+∞),再由函数在区间上的单调性比较.【解答】解:∵任意的x1,x2∈[0,+∞)(x1≠x2),有<0∴f(x)在[0,+∞)上是减函数,又∵0.76<60.5<|log0.76|∴,故选:D【点评】本题主要考查用奇偶性转化区间和单调性比较大小,在比较大小中,用单调性的较多,还有的通过中间桥梁来实现的,如通过正负和1来解决.5. 设集合A={x|1≤x≤2},B={x|x≤a},若A?B,则a的取值范围是()A.{a|a≥2}B.{a|a>2} C.{a|a≥1}D.{a|a≤2}参考答案:A【考点】集合的包含关系判断及应用.【分析】利用集合的包含关系直接求解.【解答】解:∵集合A={x|1≤x≤2},B={x|x≤a},A?B,∴a≥2.∴a的取值范围是{a|a≥2}.故选:A.6. 已知奇函数f(x)在[-1,0]上为单调递减函数,又α、β为锐角三角形两内角且,则下列结论正确的是()A.f(cos α)>f(cos β) B.f(sin α)>f(sin β)C.f(sin α)>f(cos β) D.f(sin α)<f(cos β)参考答案:B7. 设函数,其中均为非零的常数,若,则的值是()A. 5B. 3C. 1D. 不确定参考答案:A【分析】化简表达式,将所得结果代入的表达式中,由此求得的值.【详解】由于,故,所以..【点睛】本小题主要考查三角函数的诱导公式,考查化归与转化的数学思想方法,属于中档题.8. 已知f(x)=ax7-bx5+cx3+2,且f(-5)=m,则f(5)+f(-5)的值为()A.0 B.4C.2m D.-m+4参考答案:B略9. (5分)已知集合A={x|﹣3≤x≤1},B={x|x≤2},则集合A∪B()A.{x|﹣3≤x≤1}B.{x|﹣3≤x≤2}C.{x|x<1} D.{x|x≤2}参考答案:D考点:并集及其运算.专题:集合.分析:利用并集的定义求解.解答:∵集合A={x|﹣3≤x≤1},B={x|x≤2},∴A∪B={x|x≤2}.故选:D.点评:本题考查并集的求法,是基础题,解题时要注意不等式性质的合理运用.10. 如图,A,B两点为山脚下两处水平地面上的观测点,在A,B两处观察点观察山顶点P的仰角分别为,若,,且观察点A,B之间的距离比山的高度多100米,则山的高度为()A. 100米B. 110米C. 120米D. 130米参考答案:A【分析】设山的高度为,求出AB=2x,根据,求出山的高度.【详解】设山的高度为,如图,由,有.在中,,有,又由观察点之间的距离比山的高度多100,有.故山的高度为100.故选:A【点睛】本题主要考查解三角形的实际应用,意在考查学生对该知识的理解掌握水平,属于基础题.二、填空题:本大题共7小题,每小题4分,共28分11. 直线xsinα﹣y+1=0的倾角的取值范围.参考答案:[0,]∪[)【考点】直线的倾斜角.【分析】由直线方程求出直线斜率的范围,再由正切函数的单调性求得倾角的取值范围.【解答】解:直线xsinα﹣y+1=0的斜率为k=sinα,则﹣1≤k≤1,设直线xsinα﹣y+1=0的倾斜角为θ(0≤θ<π),则﹣1≤tanθ≤1,∴θ∈[0,]∪[).故答案为:[0,]∪[).【点评】本题考查直线的倾斜角,考查了直线倾斜角和斜率的关系,训练了由直线斜率的范围求倾斜角的范围,是基础题.12. 从分别写有1,2,3,4的4张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为_____.参考答案:【分析】先求出别写有1,2,3,4的4张卡片中随机抽取1张,放回后再随机抽取1张,基本事件的个数,然后再求出抽得的第一张卡片上的数大于第二张卡片上的数的基本事件的个.数,运用古典概型公式求出概率.【详解】写有1,2,3,4的4张卡片中随机抽取1张,放回后再随机抽取1张,基本事件的个数为,抽得的第一张卡片上的数大于第二张卡片上的数的基本事件为:,共个,因此抽得的第一张卡片上的数大于第二张卡片上的数的概率为.【点睛】本题考查了古典概型概率的计算公式,考查了有放回抽样,属于基础题.13. 已知= .参考答案:1【考点】对数的运算性质.【专题】计算题.【分析】首先分析题目已知2x=5y=10,求的值,故考虑到把x和y用对数的形式表达出来代入,再根据对数的性质以及同底对数和的求法解得,即可得到答案.【解答】解:因为2x=5y=10,故x=log210,y=log510=1故答案为:1.【点评】此题主要考查对数的运算性质的问题,对数函数属于三级考点的内容,一般在高考中以选择填空的形式出现,属于基础性试题同学们需要掌握.14. 设ω∈R+,若函数f ( x ) = sin ωx在区间[ –,]上是增加的,则ω的取值范围是。
辽宁省辽宁省营口市开发区第一高级中学2017-2018学年高一下学期第一次月考数学试卷

2017—2018学年度下学期高一第一次月考数学试卷时间:120分钟满分:150分第I卷一、选择题(共12小题,每题5分,共60分)1、我国古代数学名著《数学九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得粒内夹谷•粒,则这批米内夹谷约为()A. I 石B. I「石C. m 石D.1365 石2、如果下边程序执行后输出的结果是:,那么在程序药:二了后面的“条件”应为1=12 s = l DOLOOP UNTIL M条件”PRINT 4END「 B. ■i.'-C.・J = . 'D. W3、为了考察两个变量与'之间的线性关系,甲、乙两同学各自独立做了 '次和.次试验,并且利用线性回归方法,求得回归直线分别为、.已知两人得到的试验数据中变量和'的数据的平均值相等,且分别都是、、,那么下列说法正确的是()2D 4) 6U K0 100 腔豹甘A.直线和一定有公共点•B. 直线和相交,但交点不- -定是C. 必有直线-D. 直线山与必定重合4、某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100]. 若低于60分的人数是15人,则该班的学生人数是()A.45B.50C.55D.605、某人手表停了,他打开电视机,想利用电视机上整点显示时间来校正他的手表,则他等待不超过一刻钟的概率为().A1 m1^1^ 1A. •B. .C. :D.6、甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为,再由乙猜甲刚才所想的数字,把乙猜的数字记为-,其中込,若生:,就称甲、乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为()A. 士B. 丐C. rD. 77、集合P={a|2kir<u<C2k+l)兀底册,Q={口卜4壬!玉4},则PnQ =( )A. •B. ' - '■ < :乞「或上二C. - :• * ID. -8、从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )A.至少有1个黑球与都是黑球B. 至少有1个黑球与至少有1个红球C.恰有1个黑球与恰有2个黑球D. 至少有1个黑球与都是红球9..H-. 等于(A. t应啦-liinyB. tany-tanxD. I lany|-|t3nx|10、已知函数「是定义在上的偶函数,且在区间| 上是增函数,令C.E —D.hr11、设•'是第—象限角,且■「:•:— ;:,贝%是( )A.第一象限角B. 第二象限角C.第三象限角D.第四象限角sin(-a-2S)- sin(^J-a)j tan 2( 2n-a)12、已知• 是方程";.= .:的根,则| 的值是(cos(2-a) ■ cos (S+a) -cot(n-a) A JD33A.^B.■- C. [或可 D. '7'第n 卷二、填空题(共 4小题,每小题5分,共20分)13、 某校早上「•开始上课,假设该校学生小张与小王在早上 •之间到校,且每人在该时间段的任何时刻到校是等可能的 ,则小张比小王至少早 分钟到校的概率为 _________________ .(用数字作答)14、 袋中有形状、大小都相同的.只球,其中 只白球,1只红球一只黄球,从中一次随机摸出_ 只球,则这一只球颜色不同的概率为 _________________________ 15、 函数:■■ I'.■: 的定义域为 _______________________________ .16、 若 WY:,化简:I - :>-.n u C'的结果是 ___________________________ .三、解答题(共70分)17、(本小题满分10分)计算: 1.3S 善+丄5瞥警;2. i 「in || ■ '. I :I I-Ji :.siniTK,x<()f(x-l) + l f x>0求证:m :..20、(本小题满分12分)城市公交车的数量太多容易造成资源的浪费 ,太少又难以满足乘客 的需求,为此,某市公交公司在某站台的 60名候车的乘客中随机抽取 15人,将他们的候车时 间作为样本分成5组,如下表所示:A.卜;i 「B. c<b<a 12分)设=18、(本小题满分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017—2018学年度上学期第一次月考高 三 数 学 试 卷(理)满分150分 考试时间120分钟第1卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合A =⎩⎨⎧⎭⎬⎫x ⎪⎪12<2x <2,B ={x |lg x >0},则A ∪B =( ) A .{x |x >-1} B .{x |-1<x <1} C .∅ D .{x |-1<x <1或x >1} 2.如果命题“p 且q ”是假命题,“非p ”是真命题,那么( )A .命题p 一定是真命题B .命题q 一定是真命题C .命题q 一定是假命题D .命题q 可以是真命题也可以是假命题 3.若函数f (x )=⎩⎪⎨⎪⎧(14)x ,x ∈[-1,0),4x , x ∈[0,1],则f (log 43)等于( )A.13 B .3 C.14 D .4 4.下面结论中,正确结论的个数为( )①命题p :“∃x ∈R ,x 2-3x +2≥0”的否定为¬p :“∀x ∈R ,x 2-3x +2<0”; ②命题:“∀x ∈M ,P (x )”的否定为:“∃x ∈M ,P (x )”; ③若¬p 是q 的必要条件,则p 是¬q 的充分条件; ④“M >N ”是“log 2M >log 2N ”的充分不必要条件. A .1 B .2 C .3 D .45.已知函数f (x )=⎩⎪⎨⎪⎧x 2+4x ,x ≥0,4x -x 2,x <0.若f (2-a 2)>f (a ),则实数a 的取值范围是( ) A .(-∞,-1)∪(2,+∞) B .(-1,2)C .(-2,1)D .(-∞,-2)∪(1,+∞)6.条件p :|x |>1,条件q :x <-2,则¬p 是¬q 的( )A .充分条件但非必要条件B .必要条件但非充分条件C .充要条件D .既非充分条件又非必要条件7.已知函数f (x )=ax 3+bx 2+c ,其导函数f ′(x )的图象如下图所示,则( )A .函数f (x )的有极小值a +b +cB .函数f (x )的有极小值cC .函数f (x )的有最大值a +b +cD .函数f (x )的有最大值c8.f (x )是定义在[-2,2]上的奇函数,且满足f (3-2x )+f (1-x )>0,当f (x )是增函数时,x 的范围为( )A .[12,43)B .[-2,43)C .[-1,52]D .(-∞,43)9.直线y =4x 与曲线y =x 3在第一象限内围成的封闭图形的面积为( )A .2 2B .4 2C .2D .410.若函数f (x )=kx -ln x 在区间(1,+∞)单调递增,则k 的取值范围是( )A .(-∞,-2]B .(-∞,-1]C .[2,+∞)D .[1,+∞)11.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p 与加工时间t (单位:分钟)满足函数关系p =at 2+bt +c (a ,b ,c 是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为( )A .3.50分钟B .4.00分钟C .3.75分钟D .4.25分钟12. 设方程10x=|lg(-x )|的两个根分别为x 1,x 2,则( )A .0<x 1x 2<1B .x 1x 2=1C .x 1x 2>1D .x 1x 2<0第Ⅱ卷【非选择题共90分)本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须作答.第22题、23题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置上.13.已知曲线y =x 24-3ln x 的一条切线的斜率为12,则切点的横坐标为________.14.已知定义域为R 的偶函数f (x )在[0,+∞)上是增函数,且f (12)=0,则不等式f (log 4x )>0的解集为________________15.若函数f (x )=x 3+x 2-ax -4在区间(-1,1)内恰有一个极值点,则实数a 的取值范围为________________16.已知定义在R 上的可导函数f (x )的导函数为f ′(x ),若对于任意实数x ,有f (x )>f ′(x ),且y =f (x )-1为奇函数,则不等式f (x )<e x的解集为_______________三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)17.已知函数f (x )=x 3+ax 2+bx +c 在点x 0处取得极小值-5,其导函数y =f ′(x )的图象经过点(0,0),(2,0).(1)求a ,b 的值;(2)求x 0及函数f (x )的表达式.18. 设二次函数f (x )=ax 2+bx +c 的图象过点(0,1)和(1,4),且对于任意的实数x ,不等式f (x )≥4x 恒成立.(1)求函数f (x )的表达式;(2)设g (x )=kx +1,若F (x )=log 2[g (x )-f (x )]在区间[1,2]上是增函数,求实数k 的取值范围.19.(本小题满分12分)已知函数f (x )=log a 1-mxx -1是奇函数(a >0,且a ≠1).(1)求m 的值;(2)判断f (x )在区间(1,+∞)上的单调性并加以证明; (3)当a >1时,f (x )在[2,+∞)上取得最大值4,求a 的值.20.在1999年10月12日“世界60亿人口日”提出了“人类对生育的选择决定世界未来”的主题,控制人口急剧增长的紧迫任务摆在我们的面前.(1)世界人口在过去40年内翻了一番,问每年人口平均增长率是多少?(2)我国人口在1998年底达到12.48亿,若将人口平均增长率控制在1%以内,我国人口在2008年底至多有多少亿?21.已知函数f (x )=x 2+a (x +ln x ),a ∈R . (1)当a =-1时,求f (x )的单调区间; (2)若f (x )>12(e +1)a ,求a 的取值范围.请考生在22、23二题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑.22.(本小题满分l0分)选修4—4:坐标系与参数方程在直角坐标系xOy 中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,已知 圆C 的极坐标方程为ρ=4sin θ.从极点作圆C 的弦,记各条弦中点的轨迹为曲线C 1. (I)求C 1的极坐标方程;(II)已知曲线l 的参数方程为cos sin x t y t αα=⎧⎨=⎩,(0≤α<π,t 为参数,且t ≠0),1与C 交于点A ,l 与C 1交于点B ,且α的值.23.(本小题满分10分)选修4—5:不等式选讲 已知a ,b ,c 均为正实数,且2221111a b c++=.(I)证明:111a b c++ (Ⅱ)求证:222222a b c b c a++≥1.高三理科数学 参考答案1D 2D 3B 4B 5C 6A 7B 8A 9D 10D 11C 12A11解析:由实验数据和函数模型知,二次函数p =at 2+bt +c 的图象过点(3,0.7),(4,0.8),(5,0.5),分别代入解析式,得⎩⎪⎨⎪⎧0.7=9a +3b +c ,0.8=16a +4b +c ,0.5=25a +5b +c ,解得⎩⎪⎨⎪⎧a =-0.2,b =1.5,c =-2.所以p =-0.2t 2+1.5t -2=-0.2(t -3.75)2+0.8125, 所以当t =3.75分钟时,可食用率p 最大,故选B. 13 314 {x |0<x <12或x >2}15 [1,5) 16 (0,+∞)解析 因为y =f (x )-1为奇函数,且定义域R ,所以0=f (0)-1,所以f (0)=1.设h (x )=f (x )e x ,则h ′(x )=e x (f ′(x )-f (x ))(e x )2,因为f (x )>f ′(x ),所以函数h (x )是R 上的减函数,所以不等式f (x )<e x 等价于f (x )e x <1=f (0)e 0,即h (x )<h (0),所以x >0,故(0,+∞)17解 (1)由题设可得f ′(x )=3x 2+2ax +b ……………….2分 ∵f ′(x )的图象过点(0,0),(2,0),∴⎩⎪⎨⎪⎧b =0,12+4a +b =0,解得a =-3,b =0. ……………….6分(2)由f ′(x )=3x 2-6x >0,得x >2或x <0. ……………….8分∴在(-∞,0)上f ′(x )>0,在(0,2)上f ′(x )<0,在(2,+∞)上f ′(x )>0,∴f (x )在(-∞,0),(2,+∞)上递增,在(0,2)上递减,因此f (x )在x =2处取得极小值,所以x 0=2,由f (2)=-5,得c =-1.∴f (x )=x 3-3x 2-1. ……………….12分18解 (1)f (0)=c =1,f (1)=a +b +c =4,. ……………….2分∴f (x )=ax 2+(3-a )x +1.f (x )≥4x 即ax 2-(a +1)x +1≥0恒成立得⎩⎪⎨⎪⎧a >0,(a +1)2-4a ≤0,解得a =1. ∴f (x )=x 2+2x +1. . ……………….6分 (2)F (x )=log 2[g (x )-f (x )]=log 2[-x 2+(k -2)x ]. 由F (x )在区间[1,2]上是增函数,得h (x )=-x 2+(k -2)x 在区间[1,2]上为增函数且恒为正实数,. ……………….8分 ∴⎩⎨⎧k -22≥2,h (1)=-1+k -2>0,解得k ≥6.∴实数k 的取值范围为[6,+∞).. ……………….12分 19【解析】 (1)∵f (x )是奇函数, ∴f (-x )=-f (x )在其定义域内恒成立,即log a 1+mx -x -1=-log a 1-mx x -1恒成立,. ……………….2分∴1-m 2x 2=1-x 2恒成立,∴m =-1,或m =1(舍去),∴m =-1. . ……………….4分(2)由(1)得f (x )=log a x +1x -1(a >0,且a ≠1),任取x 1,x 2∈(1,+∞),且x 1<x 2,令t (x )=x +1x -1,则t (x 1)=x 1+1x 1-1,t (x 2)=x 2+1x 2-1,∴t (x 1)-t (x 2)=x 1+1x 1-1-x 2+1x 2-1=2(x 2-x 1)(x 1-1)(x 2-1),∵1<x 1<x 2,∴x 1-1>0,x 2-1>0,x 2-x 1>0. ∴t (x 1)>t (x 2),即x 1+1x 1-1>x 2+1x 2-1,∴当a >1时,log a x 1+1x 1-1>log a x 2+1x 2-1,即f (x 1)>f (x 2),f (x )在(1,+∞)上是减函数;当0<a <1时,f (x )在(1,+∞)上是增函数.. ……………….8分(3)由(2)知f (x )在[2,+∞)上单调递减, 故当x =2时,f (x )取到最大值. 即f (x )max =f (2)=4,∴log a 2+12-1=4,log a 3=4,即a 4=3,∴a =43.. ……………….12分20【解析】 (1)设每年人口平均增长率为x ,n 年前的人口数为y , 即y ·(1+x )n =60,则当n =40时,y =30,.. ……………….3分 即30(1+x )40=60,∴(1+x )40=2, 两边取对数,则40lg(1+x )=lg2, 则lg(1+x )=lg240=0.007525,∴1+x ≈1.017,得x =1.7%... ……………….6分 (2)依题意,y ≤12.48(1+1%)10,得lg y ≤lg12.48+10lg1.01=1.1392,.. ……………….8分 ∴y ≤13.78,故人口至多有13.78亿.答:每年人口平均增长率为1.7%,2008年人口至多有13.78亿... ……………….12分21解 (1)由题意得x ∈(0,+∞),当a =-1时,f (x )=x 2-x -ln x , ∴f ′(x )=2x 2-x -1x.令f ′(x )<0,则0<x <1;令f ′(x )≥0,则x ≥1,∴f (x )的单调递减区间是(0,1),单调递增区间是[1,+∞)... ……………….4分(2)①当a =0时,f (x )=x 2,显然符合题意; ②当a >0时,当0<x <e -1-1a<1时,f (x )<1+a +a ln x <1+a +a ⎝⎛⎭⎫-1-1a =0<12(e +1)a ,不符合题意;.. ……………….6分③当a <0时,则f ′(x )=2x 2+ax +ax ,令f ′(x )=0,则存在x 0∈(0,+∞),使得2x 20+ax 0+a =0,即f ′(x 0)=0,令f ′(x )<0,则0<x <x 0;令f ′(x )>0,则x >x 0, ∴f (x )min =f (x 0)=x 20+a (x 0+ln x 0)=12a [(x 0-1)+2ln x 0], ∵f (x )>12(e +1)a ,∴x 0+2ln x 0-(e +2)<0,∴0<x 0<e ,∵2x 20+ax 0+a =0,∴a =-2x 20x 0+1. 设y =-2x 20x 0+1,则y ′=-2x 20+4x 0(x 0+1)2<0,∴函数y =-2x 20x 0+1在(0,e)上单调递减,∴y =-2x 20x 0+1∈⎝ ⎛⎭⎪⎫-2e 2e +1,0,即a ∈⎝ ⎛⎭⎪⎫-2e 2e +1,0. 综上所述,实数a 的取值范围为⎝ ⎛⎦⎥⎤-2e 2e +1,0... ……………….12分22.解:(Ⅰ)设1C 上任意一点的极坐标为()θρ, 则点()θρ,2在圆C 上,故θρsin 42=,所以1C 的极坐标方程为)0(sin 2≠=ρθρ..................................................................................4分(Ⅱ)B A ,两点的极坐标分别为),sin 2(),,sin 4(ααααB A , 又因为πα<≤0,所以ααααsin 2sin 2sin 2sin 4==-=AB =3,故23sin =α,所以323ππα或=...............................................................................10分23.证明:(Ⅰ)acbc ab c b a 222)111(2222++≥++ ac bc ab c b a 111111222++≥++∴ 又acbc ab c b a c b a 222111)111(2222+++++=++)(2221113c b a ++≤ 由题中条件知1111222=++cb a ,3)111(2≤++∴c b a即3111≤++cb a ...................................................................................................................5分(Ⅱ)22422422121ba b a a b a =⋅≥+同理:224221c b c b ≥+,224221ac a c ≥+)111(2111222222424242cb ac b a a c c b b a ++≥+++++∴ 21424242≥+++∴ac c b b a 1424242≥++∴ac c b b a .............................................................................................................10分。
