离散数学例题
(完整版)离散数学题目及答案

数理逻辑习题判断题1.任何命题公式存在惟一的特异析取范式 ( √ ) 2. 公式)(q p p →⌝→是永真式 ( √ ) 3.命题公式p q p →∧)(是永真式 ( √ ) 4.命题公式r q p ∧⌝∧的成真赋值为010 ( × ) 5.))(()(B x A x B x xA →∃=→∀ ( √ )6.命题“如果1+2=3,则雪是黑的”是真命题 ( × ) 7.p q p p =∧∨)( ( √ )8.))()((x G x F x →∀是永真式 ( × ) 9.“我正在撒谎”是命题 ( × ) 10. )()(x xG x xF ∃→∀是永真式( √ )11.命题“如果1+2=0,则雪是黑的”是假命题 ( × ) 12.p q p p =∨∧)( ( √ )13.))()((x G x F x →∀是永假式 ( × )14.每个命题公式都有唯一的特异(主)合取范式 ( √ ) 15.若雪是黑色的:p ,则q →p 公式是永真式 ( √ ) 16.每个逻辑公式都有唯一的前束范式 ( × ) 17.q →p 公式的特异(主)析取式为q p ∨⌝ ( × ) 18.命题公式 )(r q p →∨⌝的成假赋值是110 ( √ ) 19.一阶逻辑公式)),()((y x G x F x →∀是闭式( × )单项选择题1. 下述不是命题的是( A )A.花儿真美啊! B.明天是阴天。
C.2是偶数。
D.铅球是方的。
2.谓词公式(∀y)(∀x)(P(x)→R(x,y))∧∃yQ(x,y)中变元y (B)A.是自由变元但不是约束变元B.是约束变元但不是自由变元C.既是自由变元又是约束变元D.既不是自由变元又不是约束变元3.下列命题公式为重言式的是( A )A.p→ (p∨q)B.(p∨┐p)→qC.q∧┐q D.p→┐q4.下列语句中不是..命题的只有(A )A.花儿为什么这样红?B.2+2=0C.飞碟来自地球外的星球。
离散数学练习题(含答案)

离散数学练习题(含答案)题目1. 对于集合 $A={1,2,3,...,10}$ 和 $B={n|n是偶数,2<n<8}$,求 $A \cap B$ 的元素。
2. 存在三个可识别的状态A,B,C。
置换群 $S_3$ 作用在状态集上。
定义四个动作:$α: A → C, β: A → B, γ: C→ A, δ: B→ C$。
确定式子,描述 $\{α,β,γ,δ\}$ 的乘法表。
3. 证明 $\forall n \in \mathbb{N}$,合数的个数不小于$n$。
4. 给定一个无向带权图,图中每个节点编号分别是$1,2,...,n$,证明下列结论:a. 如果从节点$i$到$j$只有一条权值最小的路径,则这条路径的任意子路径都是最短路径。
b. 如果从节点$i$到$j$有两条或两条以上权值相等的路径,则从$i$到$j$的最短路径可能不唯一。
答案1. $A \cap B = \{2,4,6\}$。
2. 乘法表:3. 对于任意$n$,我们可以选择$n+1$个连续的自然数$k+1,k+2,...,k+n,k+n+1$中的$n$个数,其中$k \in \mathbb{Z}$。
这$n$个数构成的$n$个正整数均为合数,因为它们都至少有一个小于它自身的因子,所以不是质数。
所以合数的个数不小于任意$n$。
4.a. 根据题意,从$i$到$j$只有一条权值最小的路径,即这条最短路径已被确定。
如果从这条路径中任意取出一段子路径,假设这段子路径不是这个节点到$j$的最短路径,那么存在其他从$i$到$j$的路径比这段子路径更优,又因为这条路径是最短路径,所以这段子路径也一定不优于最短路径,矛盾。
所以从这条路径中任意取出的子路径都是最短路径。
b. 如果从节点$i$到$j$有多条权值相等的路径,则这些路径权值都是最短路径的权值。
因为所有最短路径的权值相等,所以这些路径的权值就是最短路径的权值。
所以从$i$到$j$的最短路径可能不唯一。
离散数学cp规则例题

离散数学cp规则例题
题目:
有20个人参加全英锦标赛,其中有4个人只参加了A组比赛,7个人只参加了B组比赛,5个人只参加了C组比赛,而且没
有人同时参加了A、B、C三个组的比赛。
求:
a) 参加了至少一组比赛的人数;
b) 只参加了A组和B组比赛的人数;
c) 只参加了B组和C组比赛的人数;
d) 参加了A组比赛但没有参加B组和C组比赛的人数。
解答:
a) 根据题意,只参加了A组比赛的人数为4,只参加了B组
比赛的人数为7,只参加了C组比赛的人数为5,因此参加了
至少一组比赛的人数为4+7+5=16。
b) 只参加了A组和B组比赛的人数为4(只参加了A组比赛)+7(只参加了B组比赛)-0(同时参加了A、B两组比赛)
=11。
c) 只参加了B组和C组比赛的人数为7(只参加了B组比赛)+5(只参加了C组比赛)-0(同时参加了B、C两组比赛)
=12。
d) 参加了A组比赛但没有参加B组和C组比赛的人数为4-0(同时参加了A、B两组比赛)-0(同时参加了A、C两组比赛)=4。
《离散数学》典型例题
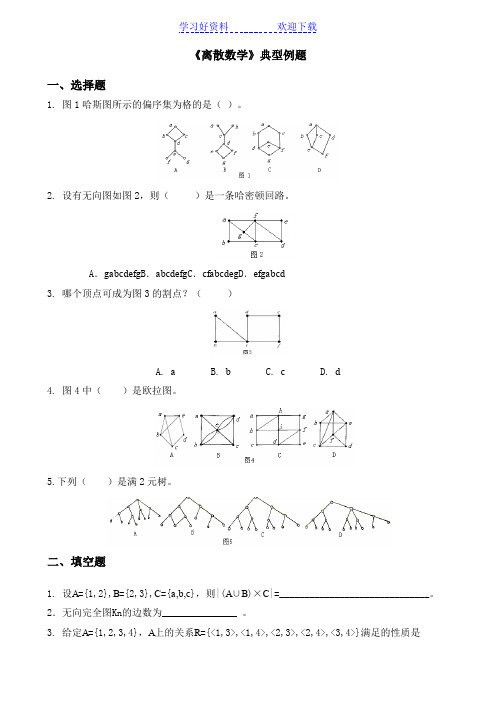
《离散数学》典型例题一、选择题1. 图1哈斯图所示的偏序集为格的是()。
2. 设有无向图如图2,则()是一条哈密顿回路。
A.gabcdefg B.abcdefg C.cfabcdeg D.efgabcd3. 哪个顶点可成为图3的割点?()A. aB. bC. cD. d4. 图4中()是欧拉图。
5.下列()是满2元树。
二、填空题1. 设A={1,2},B={2,3},C={a,b,c},则|(A∪B)×C|=______________________________。
2.无向完全图Kn的边数为_______________ 。
3. 给定A={1,2,3,4},A上的关系R={<1,3>,<1,4>,<2,3>,<2,4>,<3,4>}满足的性质是_________________________。
4. 设A ={a,b,c },F 是A 上的二元关系,F ={<a,a >,<b,b >,<c,c >},则其自反闭包为r (F )=______________________________。
5. 设A 和B 是有穷集合,|A |=m ,|B |=n ,A 到B 有_______多少个不同一对一映射。
三、判断题1.每个正整数都可以唯一地表示为素数的乘积。
( )2.集合X 上的关系R 如果是自反的、反对称的、传递的则称此关系为相容关系。
( )3.一条基本回路一定是简单回路,但一条简单回路不一定是基本回路。
( )4.树是不包含回路的连通图,在(n ,m )树中必有m=n+1( )5.一个有限群<G ,*>的阶n 一定被它的任一个子群的阶m 所等分。
( )四 、综合题1. 求公式(~P →Q) →(Q →~P)的主析取范式和主合取范式。
2. 6个人一起吃饭,围绕圆桌就餐,有多少种就座方式?如果要从4种不同的菜系中点足6道菜,问有多少种点法?3. 一个面包店里有5种不同口味的面包,要挑选8个面包,并且至少有2个奶油味面包和不超过2个咸味面包。
离散数学——精选推荐

1.设G有16条边,有三个四度顶点,四个三度顶点,其余顶点的度数都小于3,问G中至少有几个顶点?答:总度数=16*2=323*4+4*3=24(32-24)/2=4 至少有3+4+4=11至少有11个顶点2.设9阶无向图G中,每个顶点的度数不是5就是6,证明G中至少有5个六度定点或者至少有6个5度顶点证明,因为:4*6+5*5=24+25=49不可能,所以当n6<4 时,n5>=6 满足条件当n6>=5时,满足条件得证3.空间不可能存在奇数个面而且每个面均有奇数条棱的多面体答:假如有奇数个面n 每个面都有奇数个棱mi(I=1,2,…n),那么m1+m2+…+mn= D mi为奇数,n奇数,所以D为奇数但对于上式来说,每条棱都记了两次,那么D=2*(总棱数) 为偶数矛盾所以空间不可能存在奇数个面而且每个面均有奇数条棱的多面体4.在一次象旗比赛中,任意两个选手之间至多只下一盘棋,又每个人至少下一盘,证明总能找到两名选手,他们下过的盘数是相同的证明:建一个图的模型:每个选手相当于图的顶点,选手下的盘数相当于顶点得度数,两个选手的对局相当于两个顶点的边,已知顶点的度数是1----n-1, 选手有n个,根据鸽巢原理可知,比存在两个顶点的度数相同,也就是总能找到两名选手,他们下过的盘数是相同的。
5.设n阶无向简单图G为3次图(3-正则图),边数m和n满足以下关系2n-3=m问G有几种非同构的情况?并证明你的结论解:3n=2m 2n-3=m => n=6 m=9所以G是6阶3正则图.设G1,G2均为无向简单图,G1同构于G2 等价于G1的补图同构于G2的补图。
所以可知有两种同构的情况6.下面给出的两个整数列,哪个是可图化的,对于可图化的请至少给出三个非同构的图1)d=(1,2,2,4,4,5) 可图化2)d=(1,1,2,2,3,3,5) 不可图化非同构的图,赫赫在BBS上没法画!7.判断下列三个整数列中哪些是可以简单图化的?对于可简单图化的试给出两个非同构的图.1)(6,6,5,5,3,3,2)(6,6,5,5,3,3,2)<=>(5,4,4,2,2,1)<=><3,3,1,1,0)<=>,<2,0,0,0> 显然不可以简单图化2)(5,3,3,2,2,1)<=>(2,2,1,1,0)<=>(1,0,1,0) 显然可以简单图化(赫赫,图在BBS没法画)3)(3,3,2,2,2,2)<=>(2,1,1,2,2)(不符合定理的条件,可先调整顶点次序)<=>(2,2,2,1,1)(根据课本例题)<=>(1,1,1,1)显然(1,1,1,1)是可简单图化的8.9题(略)大家一定要画呀,挺好的一道题呀!!!10,现有5个4阶的无向简单图,他们均有3条边,证明这5个图中至少有两个是同构的证明:可以得知,这样的非同构的图有3个,所以得证(图省略)11.设G为n阶自补图,证明n=4k或者n=4k+1其中k为正整数。
《离散数学》题库及答案

《离散数学》题库及答案一、选择或填空(数理逻辑部分)1、下列哪些公式为永真蕴含式?()(1)Q=>Q→P(2)Q=>P→Q(3)P=>P→Q(4)P(PQ)=>P答:(1),(4)2、下列公式中哪些是永真式?()(1)(┐PQ)→(Q→R)(2)P→(Q→Q)(3)(PQ)→P(4)P→(PQ)答:(2),(3),(4)3、设有下列公式,请问哪几个是永真蕴涵式()(1)P=>PQ(2)PQ=>P(3)PQ=>PQ(4)P(P→Q)=>Q(5)(P→Q)=>P(6)P(PQ)=>P答:(2),(3),(4),(5),(6)4、公式某((A(某)B(y,某))zC(y,z))D(某)中,自由变元是(变元是()。
答:某,y,某,z5、判断下列语句是不是命题。
若是,给出命题的真值。
((1)北京是中华人民共和国的首都。
(2)陕西师大是一座工厂。
),约束)(3)你喜欢唱歌吗?(4)若7+8>18,则三角形有4条边。
(5)前进!(6)给我一杯水吧!答:(1)是,T(2)是,F(3)不是(4)是,T(5)不是(6)不是6、命题“存在一些人是大学生”的否定是(),而命题“所有的人都是要死的”的否定是()。
答:所有人都不是大学生,有些人不会死7、设P:我生病,Q:我去学校,则下列命题可符号化为()。
(1)只有在生病时,我才不去学校(2)若我生病,则我不去学校(3)当且仅当我生病时,我才不去学校(4)若我不生病,则我一定去学校答:(1)QP(2)PQ(3)PQ(4)PQ8、设个体域为整数集,则下列公式的意义是()。
(1)某y(某+y=0)(2)y某(某+y=0)答:(1)对任一整数某存在整数y满足某+y=0(2)存在整数y对任一整数某满足某+y=09、设全体域D是正整数集合,确定下列命题的真值:(1)某y(某y=y)()(2)某y(某+y=y)()(3)某y(某+y=某)()(4)某y(y=2某)()答:(1)F(2)F(3)F(4)T10、设谓词P(某):某是奇数,Q(某):某是偶数,谓词公式某(P(某)Q(某))在哪个个体域中为真()2(1)自然数(2)实数(3)复数(4)(1)--(3)均成立答:(1)11、命题“2是偶数或-3是负数”的否定是()。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项不是离散数学的研究对象?A. 图论B. 组合数学C. 微积分D. 逻辑学答案:C2. 在逻辑学中,下列哪个命题是真命题?A. 如果今天是周一,那么明天是周二。
B. 如果今天是周一,那么明天是周三。
C. 如果今天是周一,那么明天是周四。
D. 如果今天是周一,那么明天是周五。
答案:A3. 在集合论中,下列哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 在图论中,下列哪个术语描述的是图中的顶点集合?A. 边B. 路径C. 子图D. 顶点答案:D二、填空题(每题5分,共20分)1. 如果一个集合A包含5个元素,那么它的子集个数是______。
答案:322. 在逻辑学中,如果命题P和命题Q都是真命题,那么复合命题“P且Q”的真值是______。
答案:真3. 在图论中,如果一个图的顶点数为n,那么它的最大边数是______。
答案:n(n-1)/24. 如果一个二叉树的深度为3,那么它最多包含______个节点。
答案:7三、简答题(每题10分,共30分)1. 请简述什么是图的连通性,并给出一个例子。
答案:图的连通性是指在图中任意两个顶点之间都存在一条路径。
例如,在一个完全图K3中,任意两个顶点之间都可以通过一条边直接连接,因此它是连通的。
2. 解释什么是逻辑蕴含,并给出一个例子。
答案:逻辑蕴含是指如果一个命题P为真,则另一个命题Q也必须为真。
例如,命题P:“如果今天是周一”,命题Q:“明天是周二”。
如果今天是周一,那么根据逻辑蕴含,明天必须是周二。
3. 请描述什么是二叉搜索树,并给出它的一个性质。
答案:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
它的一个性质是中序遍历可以得到一个有序序列。
四、计算题(每题15分,共30分)1. 给定一个集合A={1, 2, 3, 4, 5},请计算它的幂集,并列出所有元素。
离散数学试题总汇及答案

离散数学试题总汇及答案一、单项选择题(每题2分,共20分)1. 在集合{1,2,3}和{3,4,5}的笛卡尔积中,元素(2,4)是否存在?A. 存在B. 不存在C. 无法确定D. 以上都不对2. 函数f: A→B是单射的,当且仅当对于任意的a1, a2∈A,若f(a1)=f(a2),则a1=a2。
A. 正确B. 错误C. 无法确定D. 以上都不对3. 以下哪个命题是真命题?A. 所有的狗都会游泳。
B. 有些狗不会游泳。
C. 所有的狗都不会游泳。
D. 以上都不是真命题。
4. 如果p蕴含q为假,那么p和q的真值可以是?A. p为真,q为假B. p为假,q为真C. p为真,q为真D. p为假,q为假5. 以下哪个图是连通图?A. 一个孤立点B. 两个不相连的点C. 一个包含三个点且每对点都相连的图D. 以上都不是连通图6. 在有向图中,如果存在从顶点u到顶点v的路径,那么称v是u的后继顶点。
A. 正确B. 错误C. 无法确定D. 以上都不对7. 以下哪个等价关系是集合{1,2,3}上的?A. {(1,1), (2,2), (3,3)}B. {(1,2), (2,1), (2,2), (3,3)}C. {(1,1), (2,3), (3,2), (3,3)}D. {(1,1), (2,2), (3,3), (1,3)}8. 以下哪个命题是假命题?A. 所有的鸟都有羽毛。
B. 有些鸟不会飞。
C. 所有的哺乳动物都是温血动物。
D. 以上都不是假命题。
9. 在图论中,一个图的生成树是包含图中所有顶点的最小连通子图。
A. 正确B. 错误C. 无法确定D. 以上都不对10. 如果命题p和q互为逆否命题,那么它们具有相同的真值。
A. 正确B. 错误C. 无法确定D. 以上都不对二、填空题(每题2分,共20分)1. 集合{1,2,3}和{3,4,5}的并集是________。
2. 函数f: A→B是满射的,当且仅当对于任意的b∈B,存在a∈A,使得f(a)=________。
离散数学试题及答案解析

离散数学试题及答案解析一、选择题1. 在集合{1,2,3,4}中,含有3个元素的子集有多少个?A. 4B. 8C. 16D. 32答案:B解析:含有3个元素的子集可以通过组合数公式C(n, k) = n! / [k!(n-k)!]来计算,其中n为集合的元素个数,k为子集中的元素个数。
在本题中,n=4,k=3,所以C(4, 3) = 4! / [3!(4-3)!] = 4。
2. 下列哪个命题是真命题?A. 所有偶数都是整数。
B. 所有整数都是偶数。
C. 所有整数都是奇数。
D. 所有奇数都是整数。
答案:A解析:偶数是指能被2整除的整数,因此所有偶数都是整数,选项A是真命题。
选项B、C和D都是错误的,因为并非所有整数都是偶数或奇数。
二、填空题1. 逻辑运算符“非”(NOT)的真值表是:当输入为真时,输出为______;当输入为假时,输出为真。
答案:假解析:逻辑运算符“非”(NOT)是一元运算符,它将输入的真值取反。
如果输入为真,则输出为假;如果输入为假,则输出为真。
2. 命题逻辑中,合取词“与”(AND)的真值表是:当两个命题都为真时,输出为真;否则输出为______。
答案:假解析:合取词“与”(AND)是二元运算符,只有当两个命题都为真时,输出才为真;如果其中一个或两个命题为假,则输出为假。
三、简答题1. 解释什么是等价关系,并给出一个例子。
答案:等价关系是定义在集合上的一个二元关系,它满足自反性、对称性和传递性。
例如,考虑整数集合上的“同余”关系。
对于任意整数a,b,如果a和b除以同一个正整数n后余数相同,则称a和b模n同余。
这个关系是自反的(a同余a),对称的(如果a同余b,则b同余a),并且是传递的(如果a同余b且b同余c,则a同余c)。
2. 什么是图的连通性?一个图是连通的需要满足什么条件?答案:图的连通性是指在无向图中,任意两个顶点之间都存在一条路径。
一个图是连通的需要满足以下条件:图中的任意两个顶点v和w,都可以通过图中的边相互到达。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题2分,共20分)1. 在集合论中,下列哪个符号表示属于关系?A. ∈B. ∉C. ⊆D. ∩答案:A2. 对于命题逻辑,下列哪个是真值表的表示方法?A. 真值表B. 逻辑图C. 布尔代数D. 集合论答案:A3. 以下哪个是图论中的基本单位?A. 点B. 线C. 面D. 体答案:A4. 函数f(x) = x^2 + 3x + 2在x=-1处的值是:A. 0C. 4D. 6答案:C5. 在关系数据库中,以下哪个操作用于删除表中的记录?A. SELECTB. INSERTC. UPDATED. DELETE答案:D6. 以下哪个是离散数学中的归纳法证明方法?A. 直接证明法B. 反证法C. 归纳法D. 构造性证明法答案:C7. 在逻辑中,以下哪个是析取命题?A. P ∧ QB. P ∨ QC. ¬PD. P → Q答案:B8. 以下哪个是图的遍历算法?B. BFSC. Dijkstra算法D. Floyd算法答案:B9. 在集合{1, 2, 3}上,以下哪个是幂集?A. {∅, {1}}B. {1, 2}C. {1, 2, 3}D. 所有选项答案:D10. 以下哪个是递归算法的特点?A. 不能自我调用B. 必须有一个终止条件C. 必须有一个基本情况D. 所有选项答案:D二、填空题(每空2分,共20分)1. 在离散数学中,_________ 表示一个命题的否定。
答案:¬P2. 如果集合A和集合B的交集为空集,那么A和B被称为_________。
答案:不相交3. 一个函数f: A → B是_________,如果对于集合B中的每个元素b,集合A中至少有一个元素a与之对应。
答案:满射4. 在图论中,一个没有环的连通图被称为_________。
答案:树5. 一个命题逻辑公式是_________,如果它在所有可能的真值分配下都是真的。
答案:重言式6. 一个关系R在集合A上是_________,如果对于A中的任意两个元素a和b,如果(a, b)属于R,则(b, a)也属于R。
离散数学初步例题和知识点总结

离散数学初步例题和知识点总结离散数学是现代数学的一个重要分支,它在计算机科学、信息科学、密码学等领域都有着广泛的应用。
下面我们通过一些例题来讲解离散数学中的部分重要知识点。
一、集合论集合是离散数学中的基本概念之一。
例 1:设集合 A ={1, 2, 3, 4},B ={3, 4, 5, 6},求 A ∪ B 和 A∩ B。
解:A ∪ B ={1, 2, 3, 4, 5, 6},A ∩ B ={3, 4}集合的运算包括并集、交集、差集等。
并集是将两个集合中的所有元素合并在一起,去掉重复的元素;交集是两个集合中共同拥有的元素组成的集合。
知识点:集合的基本运算规则1、交换律:A ∪ B = B ∪ A,A ∩ B =B ∩ A2、结合律:(A ∪ B) ∪ C = A ∪(B ∪ C),(A ∩ B) ∩ C = A ∩ (B ∩ C)3、分配律:A ∩ (B ∪ C) =(A ∩ B) ∪(A ∩ C),A ∪(B ∩C) =(A ∪ B) ∩ (A ∪ C)二、关系关系是集合元素之间的某种联系。
例 2:设集合 A ={1, 2, 3},R 是 A 上的关系,R ={(1, 1),(1, 2),(2, 2),(2, 3),(3, 3)},判断 R 是否具有自反性、对称性和传递性。
解:R 具有自反性,因为对于 A 中的每个元素 a,都有(a, a) ∈ R;R 不具有对称性,因为(1, 2) ∈ R 但(2, 1) ∉ R;R 具有传递性,因为(1, 2) ∈ R 且(2, 3) ∈ R ,同时(1, 3) ∈ R 。
知识点:1、自反关系:对于集合中的每个元素 a,都有(a, a) ∈ R 。
2、对称关系:若(a, b) ∈ R ,则(b, a) ∈ R 。
3、传递关系:若(a, b) ∈ R 且(b, c) ∈ R ,则(a, c) ∈ R 。
三、函数函数是一种特殊的关系。
例 3:设函数f: R → R ,f(x) = x^2 ,求 f(-2),f(0),f(3)。
离散数学期末考试题及答案

离散数学期末考试题及答案一、单项选择题(每题2分,共20分)1. 集合{1, 2, 3}的子集个数是:A. 3B. 4C. 8D. 2^3答案:C2. 命题逻辑中,命题p∧(q∨¬p)的真值表中,真值个数为:A. 1B. 2C. 3D. 4答案:B3. 函数f: A→B中,若A={1, 2},B={a, b},则f是单射的必要条件是:A. |A| ≤ |B|B. |A| < |B|C. |A| = |B|D. |A| > |B|答案:B4. 以下哪个图是无向图?A. 有向图B. 无向图C. 完全图D. 树答案:B5. 在图论中,一个图的生成树是:A. 包含图中所有顶点的最小连通子图B. 包含图中所有边的最小连通子图C. 包含图中所有顶点和边的连通子图D. 包含图中所有顶点和边的无环子图答案:A6. 以下哪个命题是真命题?A. 所有偶数都是整数B. 所有整数都是偶数C. 所有奇数都是整数D. 所有整数都是奇数答案:A7. 在布尔代数中,以下哪个运算符表示逻辑与?A. ∨B. ∧C. ¬D. →答案:B8. 有限状态机中,状态的转移是由以下哪个决定的?A. 当前状态B. 输入符号C. 当前状态和输入符号D. 输出符号答案:C9. 以下哪个是图的遍历算法?A. 深度优先搜索B. 广度优先搜索C. 动态规划D. 分治算法答案:A10. 在集合论中,以下哪个符号表示集合的交集?A. ∪B. ∩C. ×D. ÷答案:B二、填空题(每题2分,共20分)1. 集合{1, 2, 3}的幂集是{∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}},其中包含元素个数最多的子集是_。
答案:{1, 2, 3}2. 在命题逻辑中,如果p和q都为真,则p∨q的真值为_。
答案:真3. 函数f: A→B中,若A={1, 2},B={a, b, c},则f是满射的必要条件是_。
离散数学考试试题及答案

离散数学考试试题及答案一、单项选择题(每题5分,共20分)1. 在离散数学中,以下哪个概念不是布尔代数的基本元素?A. 逻辑与B. 逻辑或C. 逻辑非D. 逻辑异或答案:D2. 下列哪个命题不是命题逻辑中的命题?A. 所有学生都是勤奋的B. 有些学生是勤奋的C. 学生是勤奋的D. 勤奋的学生答案:D3. 在集合论中,以下哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 以下哪个图不是无向图?A. 简单图B. 完全图C. 有向图D. 多重图答案:C二、填空题(每题5分,共20分)1. 如果一个命题的逆否命题为真,则原命题的________为真。
答案:逆命题2. 在图论中,如果一个图的任意两个顶点都由一条边连接,则称这个图为________图。
答案:完全3. 一个集合的幂集是指包含该集合的所有________的集合。
答案:子集4. 如果一个函数的定义域和值域都是有限集合,那么这个函数被称为________函数。
答案:有限三、简答题(每题10分,共30分)1. 请简述什么是图的欧拉路径。
答案:欧拉路径是一条通过图中每条边恰好一次的路径。
2. 解释什么是二元关系,并给出一个例子。
答案:二元关系是指定义在两个集合之间的关系,它将第一个集合中的元素与第二个集合中的元素联系起来。
例如,小于关系就是一个二元关系。
3. 请说明什么是递归函数,并给出一个简单的例子。
答案:递归函数是一种通过自身定义来计算函数值的函数。
例如,阶乘函数就是一个递归函数,定义为:n! = n * (n-1)!,其中n! = 1当n=0时。
四、计算题(每题10分,共30分)1. 计算以下逻辑表达式:(P ∧ Q) ∨ ¬R答案:首先计算P ∧ Q,然后计算¬R,最后计算两者的逻辑或。
2. 给定集合A = {1, 2, 3},B = {2, 3, 4},求A ∪ B。
答案:A ∪ B = {1, 2, 3, 4}3. 已知函数f(x) = 2x + 3,求f(5)。
《离散数学》试卷及答案精选全文完整版

H(x):x是身体健康的;
S(x):x是科学家
C(x):x是事业获得成功的人
置换规则。
3、设集合|A|=101,S ,且|S|为奇数,则这样的S有2101/2或2100个。
4、设mi是公式G的的主析取范式中的一个极小项,则mi的对偶式不一定是(填“是”/“不是”/“不一定是” ) G的主合取范式中的一个极大项。
5、由3个元素组成的有限集上所有的等价关系有5个
6、给定解释I如下: (1) Di:={2,3}; (2) a=3; (3) 函数f(x)为f(2)=2,f(3)=3; (4) 谓词:F(x)为F(2):=1,F(3):=0;G(x,y)为当i=j时,G(i,j):=1;当i≠j时,G(i,j):=0;其中i,j=2,3;
ac>0并且cu>0
若u>0,则c>0,a>0,因此有ac>0;
若u<0,则c<0,a<0, 也有ac>0;
因此有(a+bi)R(u+vi)
所以R在C*是传递的。所以R是C*上的等价关系。
2、在一阶逻辑自然推理系统F中,构造下面推理的证明。个体域是人的集合。
“每位科学家都是勤奋的,每个勤奋又身体健康的人在事业中都会获得成功。存在着身体健康的科学家。所以,存在着事业获得成功的人。”(15分)
2.设A={1,2,3…10},定义A上的二元关系R={<x,y>|x,y∈A∩x+y=10},试讨论R关于关系的五个方面的性质并说明理由(5分)
解答:R={<1,9>,<9,1>,<2,8>,<8, 2 >,<3,7>,<7,3>,<4,6>,<6, 4 >,<5, 5 >}
离散数学试题及答案解析

离散数学试题及答案解析一、单项选择题(每题2分,共10分)1. 集合A={1,2,3},集合B={2,3,4},则A∩B等于:A. {1,2,3}B. {2,3}C. {1,4}D. {3,4}答案:B2. 以下哪个命题是真命题?A. 所有天鹅都是白色的。
B. 有些天鹅不是白色的。
C. 所有天鹅都不是白色的。
D. 没有天鹅是白色的。
答案:B3. 函数f: A→B的定义域是A,值域是B,那么f是:A. 单射B. 满射C. 双射D. 既不是单射也不是满射答案:D4. 逻辑表达式(p∧q)→r的逆否命题是:A. ¬r→¬(p∧q)B. ¬r→¬p∨¬qC. r→(p∧q)D. ¬r∧¬p∨¬q答案:B5. 有限集合A={a, b, c}的子集个数为:A. 3B. 4C. 7D. 8答案:D二、填空题(每题3分,共15分)1. 如果一个关系R在集合A上是自反的,那么对于A中的每一个元素a,都有___________。
答案:(a, a)∈R2. 命题逻辑中,合取(AND)的逻辑运算符用___________表示。
答案:∧3. 在图论中,一个连通图是指图中任意两个顶点之间都存在___________。
答案:路径4. 集合{1, 2, 3}的幂集包含___________个元素。
答案:85. 如果一个函数f是单射,那么对于任意的x1, x2∈A,如果f(x1)=f(x2),则x1___________x2。
答案:=三、解答题(每题10分,共20分)1. 证明:若p是q的充分条件,q是r的充分条件,则p是r的充分条件。
证明:假设p成立,由于p是q的充分条件,所以q成立。
又因为q是r的充分条件,所以r成立。
因此,p成立可以推出r成立,即p是r的充分条件。
2. 给定一个有向图,其中包含顶点A、B、C、D,边为(A, B),(B, C),(C, D),(D, A),(A, C)。
离散数学考试试题及答案

离散数学考试试题及答案一、选择题(每题2分,共20分)1. 在集合论中,以下哪个选项表示“属于”关系?A. ⊆B. ⊂C. ∈D. ⊇答案:C2. 以下哪个命题是真命题?A. p ∧ ¬pB. p ∨ ¬pC. p → ¬pD. ¬(p → q) → p答案:B3. 以下哪个选项是命题逻辑中的德摩根定律?A. ¬(p ∨ q) = ¬p ∧ ¬qB. ¬(p ∧ q) = ¬p ∨ ¬qC. ¬(p → q) = p ∧ ¬qD. ¬(p ∨ q) = ¬p ∨ ¬q答案:A4. 以下哪个选项是命题逻辑中的蕴含等价?A. p → q ≡ ¬p ∨ qB. p → q ≡ ¬q → ¬pC. p → q ≡ p ∨ ¬qD. p → q ≡ ¬p ∧ q答案:A5. 以下哪个选项是关系的性质?A. 反身性B. 对称性C. 传递性D. 所有选项都是答案:D6. 以下哪个选项是图论中的有向图?A. 无向图中的边没有方向B. 有向图中的边有方向C. 混合图中的边既有方向也有无方向D. 所有选项都是答案:B7. 在图论中,以下哪个选项是树的性质?A. 树是无环的B. 树是连通的C. 树是无向图D. 所有选项都是答案:D8. 以下哪个选项是布尔代数的基本运算?A. 与(AND)B. 或(OR)C. 非(NOT)D. 所有选项都是答案:D9. 以下哪个选项是组合数学中的排列?A. 从n个不同元素中取出m个元素的组合B. 从n个不同元素中取出m个元素的排列C. 从n个相同元素中取出m个元素的组合D. 从n个相同元素中取出m个元素的排列答案:B10. 以下哪个选项是集合论中的幂集?A. 一个集合的所有子集的集合B. 一个集合的所有真子集的集合C. 一个集合的所有超集的集合D. 一个集合的所有子集的个数答案:A二、简答题(每题10分,共30分)1. 简述命题逻辑中的等价命题是什么?答案:等价命题是指两个命题在所有可能的真值赋值下都具有相同真值的命题。
离散数学例题

例1证明p→(q→r) ⇔ (p∧q)→r证p→(q→r)⇔⌝p∨(⌝q∨r) (蕴涵等值式,置换规则)⇔ (⌝p∨⌝q)∨r(结合律,置换规则)⇔⌝(p∧q)∨r(德摩根律,置换规则)⇔ (p∧q)→r(蕴涵等值式,置换规则)今后在注明中省去置换规则注意:用等值演算不能直接证明两个公式不等值例2 证明p→(q→r) 与(p→q)→r 不等值证方法一真值表法, 见例1(2)方法二观察法. 观察到000, 010是左边的成真赋值,是右边的成假赋值方法三先用等值演算化简公式,然后再观察p→(q→r) ⇔⌝p∨⌝q∨r(p→q)→r ⇔⌝(⌝p∨q)∨r⇔(p∧⌝q)∨r更容易看出前面的两个赋值分别是左边的成真赋值和右边的成假赋值例3 用等值演算法判断下列公式的类型(1) q∧⌝(p→q)(2) (p→q)↔(⌝q→⌝p)(3) ((p∧q)∨(p∧⌝q))∧r)解(1) q∧⌝(p→q)⇔q∧⌝(⌝p∨q) (蕴涵等值式)⇔q∧(p∧⌝q) (德摩根律)⇔p∧(q∧⌝q) (交换律,结合律)⇔p∧0 (矛盾律)⇔ 0 (零律)矛盾式(2) (p→q)↔(⌝q→⌝p)⇔ (⌝p∨q)↔(q∨⌝p) (蕴涵等值式)⇔ (⌝p∨q)↔(⌝p∨q) (交换律)⇔ 1重言式(3) ((p∧q)∨(p∧⌝q))∧r)⇔ (p∧(q∨⌝q))∧r(分配律)⇔p∧1∧r(排中律)⇔p∧r(同一律)可满足式,101和111是成真赋值,000和010等是成假赋值.例4 求下列公式的析取范式与合取范式(1) (p→⌝q)∨⌝r;(2) (p→⌝q)→r解(1) (p→⌝q)∨⌝r ⇔ (⌝p∨⌝q)∨⌝r(消去→)⇔⌝p∨⌝q∨⌝r(结合律)最后结果既是析取范式(由3个简单合取式组成的析取式),又是合取范式(由一个简单析取式组成的合取式)(2) (p→⌝q)→r⇔ (⌝p∨⌝q)→r(消去第一个→)⇔⌝(⌝p∨⌝q)∨r(消去第二个→)⇔ (p∧q)∨r(否定号内移——德摩根律) 析取范式⇔ (p∨r)∧(q∨r) (∨对∧分配律)合取范式例 5 求公式A=(p→⌝q)→r的主析取范式解(p→⌝q)→r⇔ (p∧q)∨r(析取范式)①⇔((p∧q)∧(⌝r∨r))∨((⌝p∨p)∧(⌝q∨q)∧r)⇔((p∧q∧⌝r)∨(p∧q∧r))∨((⌝p∧⌝q∧r)∨(⌝p∧q∧r)∨(p∧⌝q∧r)∨(p∧q∧r))⇔m6∨m7 ∨m1∨m3∨m5∨m7 ②排序,得(p→⌝q)→r⇔m1∨m3∨m5∨m6∨m7(主析取范式)注①:一个公式的真值为T的指派所对应的极小项的析取即为主析取范式例 6 结合下表求G:(P→Q)↔R的主析取范式P Q R(P→Q)↔R真值的指派所对应的极小项0 0 000 0 1 1 ⌝P∧⌝Q∧R0 1 000 1 11⌝P∧Q∧R1 0 01P∧⌝Q∧⌝R1 0 101 1 001 1 11P∧Q∧R将极小项全部进行析取后,便得到所求的主析取范式:G:(P→Q)↔R⇔(┐P∧┐Q∧R)∨(┐P∧Q∧R)∨(P∧┐Q∧┐R)∨(P∧Q∧R)注②:n个命题变项的极小项或极大项的关系为:⌝m i ⇔M i, ⌝M i ⇔m i注③:极小项(极大项)的性质:(1)每个极小项(极大项)的成真(成假)赋值有且仅有一个;(2)两个不同的极小项的合取(极大项的析取)构成的命题形式为矛盾式(重言式);(3)所有极小项的析取(极大项的合取)构成的命题形式为重言式(矛盾式)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学例题
一、证明对任意集合A,B,C,有
a)A-B)-C=A-(B∪C);
b)(A-B)-C=(A-C)-B;
c)(A-B)-C=(A-C)-(B-C)。
证明
a)(A-B)-C=(A∩~B)∩~C
=A∩(~B∩~C)
=A∩~(B∩C)
=A-B∪C)
b)(A-B)-C=A∩~B∩~C
=A∩~C∩~B
=(A-C)-B
c)(A-C)-(B-C)
=(A∩~C)∩~(B∩~C)
=(A∩~C)∩(~B∪C)
=(A∩~C∩~B)∪(A∩~C∩C)
=A∩~B∩~C
=(A-B)-C
二、设命题公式G=(P→Q)∪(Q∪(P→R)),求G的主析取范式
G=(P→Q)∪(Q∪(P→R))
=(P∪Q)∪(Q∪(P∪R))
=(P∪Q)∪(Q∪(P∪R))
=(P∪Q)∪(Q∪P)∪(Q∪R)
=(P∪Q∪R)∪(P∪Q∪R)∪(P∪Q∪R)∪(P∪Q∪R)∪(P∪Q∪R)∪(P∪Q∪ R) =(P∪Q∪R)∪(P∪Q∪R)∪(P∪Q∪R)∪(P∪Q∪R)∪(P∪Q∪R)
=m3∪m4∪m5∪m6∪m7=(3,4,5,6,7).
三、假设f和g是函数,证明f∩g也是函数。
证明
f∩g={<x,y>|x∪dom f∪x∪dom g∪y=f(x)∪y=g(x)}
={<x,y>|x∪dom f∩dom g∪y=f(x)=g(x)}
令h=f∩g,则
dom h={x|x∪dom f∩dom g,f(x)=g(x)}
若y1 =y2 ,因为f是函数,故必有y1 =/f(x1 ),y2 =/f(x2 ),且x1 ≠x2 ,所以h=f∩g
是一个函数。
因为dom h存在且y1 ≠y2 时x1 ≠x2 ,即h={<x,y>|x∪
Dom h,y=h(x)=f(x)=g(x)}
四、设函数f:R→R,若x≤y=>f(x)≤f(y),则称函数f是单调递增的。
设f和g是在R 上单调递增,证明
1)若(f十g)(x)=f(x)+g(x),则f+g是单调递增;
2)复合函数f○g是单调递增:
3)f和g的乘积不一定是单调递增。
证明
1)因为f和g是单调递增,若x≤y,则有f(x)≤f(y),g(x)≤g(y),
(f+g)(x)=f(x)十g(x)≤f(y)+g(y)=(f十g)(y)
所以f+g是单调递增。
2)若x≤y,则f(x)≤f(y)且g(x)≤g(y),
f○g(x)=f(g(x))≤f(g(y))=f○g(y)
所以f○g是单凋递增。
3)令f(x)=g(x)=x,则f和g是单调递增,但其积函数
g*g(x)=f(x)*g(x)=x2
在R上不是单凋递增。
五、设R和S是集合A={a,b,c,d}上的关系,其中R={(a,a),(a,c),(b,c),(c,d)},
S={(a,b),(b,c),(b,d),(d,d)}.
计算R•S,R∪S,R-1,S-1•R-1.
R•S={(a,b),(c,d)},
R∪S={(a,a),(a,b),(a,c),(b,c),(b,d),(c,d),(d,d)},
R-1={(a,a),(c,a),(c,b),(d,c)},
S-1•R-1={(b,a),(d,c)}.
六、若f:A→B是双射,则f-1 :B→A是双射。
证明
因为f:A→B是双射,则f-1 是B到A的函数。
下证f-1是双射。
对任意x∪A,必存在y∪B使f(x)=y,从而f-1 (y)=x,所以f-1 是满射。
对任意的y1、y2∪B,若f-1 (y1)=f-1 (y2)=x,则f(x)=y1,f(x)=y2。
因为f:A→B 是函数,则y1=y2。
所以f-1 是单射。
综上可得,f-1 :B→A是双射。
七、设函数g:A→B,f:B→C,则:
(1)f。
g是A到C的函数;
(2)对任意的x∪A,有fg(x)=f(g(x))。
证明
(1)对任意的x∪A,因为g:A→B是函数,则存在y∪B使<x,y>∪g。
对于y∪B,因f:B→C是函数,则存在z∪C使<y,z>∪f。
根据复合关系的定义,由<x,y>∪g和<y,z>∪f得<x,z>∪g*f,即<x,z>∪f g。
所以Df。
g=A。
对任意的x∪A,若存在y1、y2∪C,使得<x,y1>、<x,y2>∪fg=g*f,则存在t1使得<x,t1>∪g 且<t1,y1>∪f,存在t2使得<x,t2>∪g且<t2,y2>∪f。
因为g:A→B是函数,则t1=t2。
又因f:B→C是函数,则y1=y2。
所以A中的每个元素对应C中惟一的元素。
综上可知,f。
g是A到C的函数。
(2)对任意的x∪A,由g:A→B是函数,有<x,g(x)>∪g且g(x)∪B,又由f:B→C是函数,得<g(x),f(g(x))>∪f,于是<x,f(g(x))>∪g*f=f。
g。
又因f。
g是A到C的函数,则可写为
f。
g(x)=f(g(x))。
