哈尔滨市2018年初中升学考试(含答案)
专题08 文言文阅读-2019年中考语文阅读写作练手资料汇编(解析版)

专题08 文言文阅读(一)江苏省淮安市2018年初中毕业试卷阅读【甲】【乙】两部分文字,完成下面小题。
【甲】明有奇巧人曰王叔远,能以径寸之木,为.宫室、器皿、人物,以至鸟兽、木石,罔不因.势象形,各具情态。
尝贻余核舟一,盖大苏泛赤壁云。
舟首尾长约八分有奇,高可二黍许。
中轩敞者为舱,箬篷覆之。
旁开小窗,左右各四,共八扇。
启窗而观,雕栏相望焉。
闭之,则右刻“山高月小,水落石出”,左刻“清风徐来,水波不兴”,石青糁之。
【乙】沪邑元宵灯火,以伞灯为最。
灯作伞形,或圆,或.六角,咸以五色锦笺缀成,磨薄令如蝉翼,上镂人物、花鸟,细若茧丝。
一灯之制,经岁始成,虽费百金不惜,但伞灯之出最迟,每俟诸灯兴阑,于百花生日前后始盛。
多至二三百盏,间以五彩吴绫折枝花灯,偶缀禽、鱼、蝉、蝶,飞舞若生。
又扎彩为亭,高可.三四丈,名曰“抬阁”,间饰龙凤,以云母石为鳞甲,上下通明,光照数丈;或二层,或三层,每层以纹绣孩童,扮演杂剧,常扮《长生殿·玉环拜月》,兽炉中香烟一缕,烟际现月宫,姮娥立殿左,左右侍女,各执宫扇,肩上立牛女二星,望之如在霄汉也。
每灯过处,绵亘数里,光耀如昼。
笙箫鼓乐声彻夜不绝。
而自通商后,无复有此盛事矣。
同里张秋浦茂才《岁事衢歌》有“月夜笙箫步绿塍,珠常垂处小楼凭。
吴绫输与谈笺纸,妙擅江乡算伞灯。
”盖伞灯之制,纸贵于绫,谈笺,邑之土产也。
雨苍氏曰:琐事耳,而插一叹想句,便寓绝大感慨。
【注释】①锦笺,精致华美的纸。
②兴阑,兴尽。
③绫,比绸缎还薄的一种丝织品。
④抬阁:一种民间的游艺项目。
在木制的小阁里有人扮饰戏曲人物,由别人抬着游行。
⑤姮娥,嫦娥。
⑥茂才:秀才。
⑦塍:田埂。
⑧擅:独揽,独占。
(选自毛祥麟《墨余录》,有删改)7. 请用“/”标出下面句子的朗读停顿。
(只标—处)笙箫鼓乐声彻夜不绝8. 解释文中加点词语。
①为.宫室(_____)②罔不因.势象形(_____)③或.六角(_____)④高可.三四丈(_____)19. 把下列句子翻译成现代汉语。
2018年各省地市中考语文名著阅读试题汇编(一)

2018年各省地市中考语文名著阅读试题汇编(一)湖南省怀化市2018年初中毕业学业考试语文试卷7. 名著导读。
(1)《格列佛游记》的作者是______,讲述的是____国船医格列佛因海难等原因流落到小人国,__________,飞岛及马(慧骃)国等地的经历。
(2)“人最宝贵的东西是生命,生命对于我们只有一次。
一个人的生命应当这样度过……”这句话是出自尼古拉·奥斯特洛夫斯基的小说______,该小说以主人公______的生活经历为线索,展现了从1915到1930前后苏俄广阔的历史画面和人民艰苦的斗争生活。
【答案】 (1)斯威夫特英大人国(2)《钢铁是怎样炼成的》保尔·柯察金【解析】这是一道名著阅读试题。
(1)此题考查学生对名著的阅读和理解。
用心读《课程标准》推荐的名著,了解关键情节,经典片段和名言警句,才能轻松应对试题。
《格列佛游记》是英国作家乔纳森·斯威夫特创作的一部长篇游记体讽刺小说,讲述的是英国船医格列佛在小人国、大人国、飞岛国以及马(慧骃)国等地的经历,反映了18世纪前半期英国统治阶级的腐败和罪恶。
(2)名著学习中要注意积累的广泛性。
既要注意表面的知识,如作者、背景、写作特色、涉及人物及故事情节;还要知道一些细节,并且及时做笔记,做到积少成多,常读常新,逐步深化印象。
做题时才能信手拈来,得心应手。
这段文字是《钢铁是怎样炼成的》的主人公保尔的内心独白,告诉我们要珍惜生命,不要虚度年华。
江苏省淮安市2018年初中毕业暨中等学校招生文化统一考试语文试题3.班级开展名著阅读交流活动,请积极参与,充分展示自我。
(8分)【我来对一对】【甲】“俺只指望痛打这厮一顿,不想三拳真个打死了他。
洒家须吃官司,又没人送饭,不如及早撒开。
”拔步便走,回头指着郑屠尸道:“你诈死,洒家和你慢慢理会。
”—头骂,一头大踏步去了。
(节选自《水浒传》第3回) (1)《水浒传》的“回目”有形式整齐的特点,请根据【甲】段内容,补全“回目”。
专题10 化学综合计算(模拟检测)-2018中考化学十大难点突破(解析版)

专题10 化学综合计算1.【江苏省盐城市大丰亭湖区2018届九年级4月一模】为测定某过氧化氢溶液中氢元素的质量分数,某同学向100g 过氧化氢溶液中加入5g 二氧化锰固体,充分搅拌至不再产生气泡为止,称得剩余固液混合物的质量为101.3g ,则该过氧化氢溶液中氢元素的质量分数为( ) A. 6% B. 11.1% C. 20% D. 10.7% 【答案】D【解析】根据题意,反应中产生的氧气质量=100g+5g-101.3g=3.7g , 设:生成3.7g 的氧气需要过氧化氢的质量为x , 2H 2O 2 MnO 2 2H 2O+O 2↑ 68 32 X 3.7g6832 3.7xg=x=7.87g 7.87g 的过氧化氢中氢元素的质量=7.87g×1212162⨯⨯+⨯×100%=0.46g100g 过氧化氢溶液中水的质量=100g-7.87g=92.13g ,92.13g 的水中氢元素的质量=92.13g×1212161⨯⨯+⨯×100%=10.23g , 过氧化氢溶液中氢元素的质量分数=0.4610.23100g gg+×100%=10.7% ,故选D 。
2.【吉林省农安县三岗中学2017—2018学年第二学期九年级化学模拟】工业用CaO 和硝酸反应制Ca(NO 3)2·4H 2O 晶体,为确保制备过程既不补充水分,又无水剩余,则应选用的硝酸质量分数 A. 30% B. 63% C. 70% D. 84% 【答案】C3.【江苏省丹徒区实业实验学校2018届九年级12月月考】碱式碳酸镁晶体成分的确定 【查阅资料】(1)Mg(OH)2:白色固体,难溶于水,受热会分解成氧化镁和水;(2)MgCO 3: 白色固体,微溶于水,受热会分解成氧化镁和二氧化碳; (3)MgCO 3的热稳定性比Mg(OH)2的热稳定性更强。
工业生产中得到的碱式碳酸镁晶体是xMgCO 3•yMg(OH)2•zH 2O ,为精确测量晶体的组成,小组同学取4.66g 该晶体,用热分析仪对固体进行热分解(加热使之逐步分解,首先失去结晶水,最后完全反应),测定剩余固体质量与分解温度之间关系。
哈尔滨市2018年中考化学真题试题(含解析)

黑龙江省哈尔滨市2018年中考化学真题试题可能用到的相对原子质量:H-1 C-12 O-16 Na—23 S—32 K-39 Cu-64一、选择题1。
2018年6月9日“迷人的哈尔滨之夏”旅游文化时尚活动正式开幕,吸引了众多游客而来,下图是几处著名的景观,下列描述中用到的材料属于复合材料的是A.哈尔滨火车站大理石地面B.中央大街欧式铁制艺术门柱C。
防洪纪念塔钢筋混凝土底座D.哈尔滨大剧院铝合金外壳A。
A B。
B C。
C D。
D【答案】C【解析】复合材料是人们运用先进的材料制备技术将不同性质的材料组分优化组合而成的新材料。
A、大理石主要成分是碳酸钙,不是复合材料,不符合题意;B、铁制艺术门柱属于金属材料,不符合题意;C、钢筋混凝土底座属于复合材料,符合题意;D、铝合金外壳属于金属材料,不符合题意.故选C。
2。
下列实验操作错误的是A.液体的量取B.取用固体粉末C。
检验氢气的纯度D。
倾倒二氧化碳A. AB. B C。
C D。
D【答案】B【解析】A、读数时,视线与凹液面的最低处保持水平,正确;B、取用固体粉末,将药品送到试管底部,错误;C、检验氢气的纯度,用拇指堵住试管口,靠近火焰,移开拇指,如果听到“噗”的声音,说明是纯净的氢气,正确;D、由于二氧化碳的密度比空气的密度大,可像倒液体一样,将二氧化碳从集气瓶倒入烧杯中,下层蜡烛先熄灭,正确。
故选B。
3. 下列过程中只发生物理变化的是A。
电解水B.铁钉生锈C。
品红在水中扩散D。
测定空气里氧气含量A. A B。
B C. C D. D【答案】C【解析】有新物质生成的变化是化学变化,无新物质生成的变化是物理变化。
A、电解水时有新物质生成,属于化学变化,不符合题意;B、铁钉生锈有新物质生成,属于化学变化,不符合题意;C、品红在水中扩散,无新物质生成,属于物理变化,符合题意;D、测定空气里氧气含量,所用物质是红磷,红磷燃烧生成新物质,属于化学变化,不符合题意。
故选C。
2018年黑龙江省哈尔滨市中考数学试卷(带答案解析)

2018年黑龙江省哈尔滨市中考数学试卷参考答案与试题解析一、选择题(每小题3分,共计30分)1.(3分)﹣57的绝对值是( )A .57B .75C .−57D .−75【解答】解:|−57|=57,故选:A .2.(3分)下列运算一定正确的是( ) A .(m +n )2=m 2+n 2 B .(mn )3=m 3n 3C .(m 3)2=m 5D .m•m 2=m 2【解答】解:A 、(m +n )2=m 2+2mn +n 2,故此选项错误; B 、(mn )3=m 3n 3,正确; C 、(m 3)2=m 6,故此选项错误; D 、m•m 2=m 3,故此选项错误; 故选:B .3.(3分)下列图形中既是轴对称图形又是中心对称图形的是( )A .B .C .D .【解答】解:A 、此图形既不是轴对称图形也不是中心对称图形,此选项不符合题意;B 、此图形不是轴对称图形,是中心对称图形,此选项不符合题意;C 、此图形既是轴对称图形,又是中心对称图形,此选项符合题意;D 、此图形是轴对称图形,但不是中心对称图形,此选项不符合题意; 故选:C .4.(3分)六个大小相同的正方体搭成的几何体如图所示,其俯视图是()A.B.C.D.【解答】解:俯视图从左到右分别是2,1,2个正方形.故选:B.5.(3分)如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为()A.3 B.3√3 C.6 D.9【解答】解:连接OA,∵PA为⊙O的切线,∴∠OAP=90°,∵∠P=30°,OB=3,∴AO=3,则OP=6,故BP=6﹣3=3.故选:A.6.(3分)将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )A .y=﹣5(x +1)2﹣1B .y=﹣5(x ﹣1)2﹣1C .y=﹣5(x +1)2+3D .y=﹣5(x ﹣1)2+3【解答】解:将抛物线y=﹣5x 2+1向左平移1个单位长度,得到y=﹣5(x +1)2+1,再向下平移2个单位长度,所得到的抛物线为:y=﹣5(x +1)2﹣1. 故选:A .7.(3分)方程12x =2x+3的解为( )A .x=﹣1B .x=0C .x=35 D .x=1【解答】解:去分母得:x +3=4x , 解得:x=1,经检验x=1是分式方程的解, 故选:D .8.(3分)如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,BD=8,tan ∠ABD=34,则线段AB 的长为( )A .√7B .2√7C .5D .10【解答】解:∵四边形ABCD 是菱形, ∴AC ⊥BD ,AO=CO ,OB=OD , ∴∠AOB=90°, ∵BD=8, ∴OB=4,∵tan ∠ABD=34=AOOB,∴AO=3,在Rt △AOB 中,由勾股定理得:AB=√AO 2+OB 2=√32+42=5, 故选:C .9.(3分)已知反比例函数y=2k−3x的图象经过点(1,1),则k 的值为( )A .﹣1B .0C .1D .2【解答】解:∵反比例函数y=2k−3x的图象经过点(1,1), ∴代入得:2k ﹣3=1×1, 解得:k=2, 故选:D .10.(3分)如图,在△ABC 中,点D 在BC 边上,连接AD ,点G 在线段AD 上,GE ∥BD ,且交AB 于点E ,GF ∥AC ,且交CD 于点F ,则下列结论一定正确的是( )A .AB AE =AG AD B .DF CF =DG ADC .FG AC =EG BD D .AE BE =CF DF【解答】解:∵GE ∥BD ,GF ∥AC , ∴△AEG ∽△ABD ,△DFG ∽△DCA ,∴AE AB =AG AD ,DG DA =DF DC , ∴AE BE =AG DG =CF DF. 故选:D .二、填空题(每小题3分,共计30分)11.(3分)将数920000000科学记数法表示为 9.2×108 . 【解答】解:920000000用科学记数法表示为9.2×108,故答案为;9.2×10812.(3分)函数y=5xx−4中,自变量x 的取值范围是 x ≠4 .【解答】解:由题意得,x ﹣4≠0, 解得,x ≠4, 故答案为:x ≠4.13.(3分)把多项式x 3﹣25x 分解因式的结果是 x (x +5)(x ﹣5) 【解答】解:x 3﹣25x =x (x 2﹣25) =x (x +5)(x ﹣5).故答案为:x (x +5)(x ﹣5).14.(3分)不等式组{x −2≥15−2x >3x −15的解集为 3≤x <4 .【解答】解:{x −2≥1①5−2x >3x −15②∵解不等式①得:x ≥3, 解不等式②得:x <4,∴不等式组的解集为3≤x <4, 故答案为;3≤x <4.15.(3分)计算6√5﹣10√15的结果是 4√5 .【解答】解:原式=6√5﹣10×√55=6√5﹣2√5=4√5,故答案为:4√5.16.(3分)抛物线y=2(x +2)2+4的顶点坐标为 (﹣2,4) . 【解答】解:∵y=2(x +2)2+4, ∴该抛物线的顶点坐标是(﹣2,4),故答案为:(﹣2,4).17.(3分)一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,张兵同学掷一次骰子,骰子向上的一面出现的点数是3的倍数的概率是 13.【解答】解:掷一次骰子,向上的一面出现的点数是3的倍数的有3,6,故骰子向上的一面出现的点数是3的倍数的概率是:26=13.故答案为:13.18.(3分)一个扇形的圆心角为135°,弧长为3πcm ,则此扇形的面积是 6π cm 2.【解答】解:设扇形的半径为Rcm , ∵扇形的圆心角为135°,弧长为3πcm ,∴135π×R 180=3π,解得:R=4, 所以此扇形的面积为135π×42360=6π(cm 2),故答案为:6π.19.(3分)在△ABC 中,AB=AC ,∠BAC=100°,点D 在BC 边上,连接AD ,若△ABD 为直角三角形,则∠ADC 的度数为 130°或90° . 【解答】解:∵在△ABC 中,AB=AC ,∠BAC=100°, ∴∠B=∠C=40°,∵点D 在BC 边上,△ABD 为直角三角形, ∴当∠BAD=90°时,则∠ADB=50°, ∴∠ADC=130°, 当∠ADB=90°时,则 ∠ADC=90°,故答案为:130°或90°.20.(3分)如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,AB=OB ,点E 、点F 分别是OA 、OD 的中点,连接EF ,∠CEF=45°,EM ⊥BC 于点M ,EM 交BD 于点N ,FN=√10,则线段BC 的长为 4√2 .【解答】解:设EF=x ,∵点E 、点F 分别是OA 、OD 的中点, ∴EF 是△OAD 的中位线, ∴AD=2x ,AD ∥EF , ∴∠CAD=∠CEF=45°,∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AD=BC=2x , ∴∠ACB=∠CAD=45°, ∵EM ⊥BC , ∴∠EMC=90°,∴△EMC 是等腰直角三角形, ∴∠CEM=45°, 连接BE , ∵AB=OB ,AE=OE ∴BE ⊥AO ∴∠BEM=45°, ∴BM=EM=MC=x , ∴BM=FE ,易得△ENF ≌△MNB ,∴EN=MN=12x ,BN=FN=√10,Rt △BNM 中,由勾股定理得:BN 2=BM 2+MN 2,∴(√10)2=x 2+(12x)2,x=2√2或﹣2√2(舍),∴BC=2x=4√2.故答案为:4√2.三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)21.(7分)先化简,再求代数式(1﹣1a−2)÷a2−6a+92a−4的值,其中a=4cos30°+3tan45°.【解答】解:当a=4cos30°+3tan45°时,所以a=2√3+3原式=a−3a−2•2(a−2)(a−3)2=2 a−3=√3 322.(7分)如图,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.(1)在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D 均在小正方形的顶点上;(2)在图中画出以线段AB为一腰,底边长为2√2的等腰三角形ABE,点E在小正方形的顶点上,连接CE,请直接写出线段CE的长.【解答】解:(1)如图所示,矩形ABCD即为所求;(2)如图△ABE即为所求,CE=4.23.(8分)为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:(1)本次调查共抽取了多少名学生?(2)通过计算补全条形统计图;(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?【解答】解:(1)本次调查的学生总人数为24÷20%=120人;(2)“书法”类人数为120﹣(24+40+16+8)=32人,补全图形如下:(3)估计该中学最喜爱国画的学生有960×40120=320人.24.(8分)已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点G,∠BGE=∠ADE.(1)如图1,求证:AD=CD;(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE 面积的2倍.【解答】解:(1)∵∠BGE=∠ADE,∠BGE=∠CGF,∴∠ADE=∠CGF,∵AC⊥BD、BF⊥CD,∴∠ADE+∠DAE=∠CGF+∠GCF,∴∠DAE=∠GCF,∴AD=CD;(2)设DE=a,则AE=2DE=2a ,EG=DE=a ,∴S △ADE =12AE•DE=12•2a•a=a 2,∵BH 是△ABE 的中线, ∴AH=HE=a , ∵AD=CD 、AC ⊥BD , ∴CE=AE=2a ,则S △ADC =12AC•DE=12•(2a +2a )•a=2a 2=2S △ADE ;在△ADE 和△BGE 中, ∵{∠AED =∠BEGDE =GE ∠ADE =∠BGE ,∴△ADE ≌△BGE (ASA ), ∴BE=AE=2a ,∴S △ABE =12AE•BE=12•(2a )•2a=2a 2,S △BCE =12CE•BE=12•(2a )•2a=2a 2,S △BHG =12HG•BE=12•(a +a )•2a=2a 2,综上,面积等于△ADE 面积的2倍的三角形有△ACD 、△ABE 、△BCE 、△BHG .25.(10分)春平中学要为学校科技活动小组提供实验器材,计划购买A 型、B 型两种型号的放大镜.若购买8个A 型放大镜和5个B 型放大镜需用220元;若购买4个A 型放大镜和6个B 型放大镜需用152元. (1)求每个A 型放大镜和每个B 型放大镜各多少元;(2)春平中学决定购买A 型放大镜和B 型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A 型放大镜?【解答】解:(1)设每个A 型放大镜和每个B 型放大镜分别为x 元,y 元,可得:{8x +5y =2204x +6y =152,解得:{x =20y =12,答:每个A 型放大镜和每个B 型放大镜分别为20元,12元;(2)设购买A型放大镜m个,根据题意可得:20a+12×(75﹣a)≤1180,解得:x≤35,答:最多可以购买35个A型放大镜.26.(10分)已知:⊙O是正方形ABCD的外接圆,点E在AB̂上,连接BE、DE,点F在AD̂上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.(1)如图1,求证:∠CBE=∠DHG;(2)如图2,在线段AH上取一点N(点N不与点A、点H重合),连接BN交DE于点L,过点H作HK∥BN交DE于点K,过点E作EP⊥BN,垂足为点P,当BP=HF时,求证:BE=HK;(3)如图3,在(2)的条件下,当3HF=2DF时,延长EP交⊙O于点R,连接BR,若△BER的面积与△DHK的面积的差为74,求线段BR的长.【解答】(1)证明:如图1,∵四边形ABCD是正方形,∴∠A=∠ABC=90°,∵∠F=∠A=90°,∴∠F=∠ABC,∵DA平分∠EDF,∴∠ADE=∠ADF,∵∠ABE=∠ADE,∴∠ABE=∠ADF,∵∠CBE=∠ABC+∠ABE,∠DHG=∠F+∠ADF,∴∠CBE=∠DHG;(2)如图2,过H 作HM ⊥KD ,垂足为点M , ∵∠F=90°, ∴HF ⊥FD , ∵DA 平分∠EDF , ∴HM=FH , ∵FH=BP , ∴HN=BP , ∵KH ∥BN , ∴∠DKH=∠DLN , ∴∠ELP=∠DLN , ∴∠DKH=∠ELP , ∵∠BED=∠A=90°, ∴∠BEP +∠LEP=90°, ∵EP ⊥BN ,∴∠BPE=∠EPL=90°, ∴∠LEP +∠ELP=90°, ∴∠BEP=∠ELP=∠DKH , ∵HM ⊥KD ,∴∠KMH=∠BPE=90°, ∴△BEP ≌△HKM , ∴BE=HK ;(3)解:如图3,连接BD , ∵3HF=2DF ,BP=FH , ∴设HF=2a ,DF=3a , ∴BP=FH=2a ,由(2)得:HM=BP ,∠HMD=90°, ∵∠F=∠A=90°,∴tan ∠HDM=tan ∠FDH ,∴HM DM =FH DF =23,∴DM=3a ,∵四边形ABCD 为正方形, ∴AB=AD ,∴∠ABD=∠ADB=45°,∵∠ABF=∠ADF=∠ADE ,∠DBF=45°﹣∠ABF ,∠BDE=45°﹣∠ADE , ∴∠DBF=∠BDE , ∵∠BED=∠F ,BD=BD , ∴△BED ≌△DFB , ∴BE=FD=3a ,过H 作HS ⊥BD ,垂足为S ,∵tan ∠ABH=tan ∠ADE=AH AB =23,∴设AB=3√2m ,AH=2√2m ,∴BD=√2AB=6m ,DH=AD ﹣AH=√2m ,∵sin ∠ADB=HS DH =√22,∴HS=m ,∴DS=√DH 2−HS 2=m , ∴BS=BD ﹣DS=5m ,∴tan ∠BDE=tan ∠DBF=HS BS =15,∵∠BDE=∠BRE ,∴tanBRE=BP PR =15,∵BP=FH=2a , ∴RP=10a ,在ER 上截取ET=DK ,连接BT ,由(2)得:∠BEP=∠HKD , ∴△BET ≌△HKD , ∴∠BTE=∠KDH , ∴tan ∠BTE=tan ∠KDH ,∴BP PT =23,即PT=3a , ∴TR=RP ﹣PT=7a ,∵S △BER ﹣S △DHK=74,∴12BP•ER ﹣12HM•DK=74, ∴12BP•(ER ﹣DK )=12BP•(ER ﹣ET )=74, ∴12×2a ×7a=74, 解得:a=12(负值舍去),∴BP=1,PR=5, 则BR=√12+52=√26.27.(10分)已知:在平面直角坐标系中,点O 为坐标原点,点A 在x 轴的负半轴上,直线y=﹣√3x +72√3与x 轴、y 轴分别交于B 、C 两点,四边形ABCD 为菱形.(1)如图1,求点A 的坐标;(2)如图2,连接AC ,点P 为△ACD 内一点,连接AP 、BP ,BP 与AC 交于点G ,且∠APB=60°,点E 在线段AP 上,点F 在线段BP 上,且BF=AE ,连接AF 、EF ,若∠AFE=30°,求AF 2+EF 2的值;(3)如图3,在(2)的条件下,当PE=AE 时,求点P 的坐标.【解答】解:(1)如图1中,∵y=﹣√3x+7√3 2,∴B(72,0),C(0,7√32),∴BO=72,OC=7√32,在Rt△OBC中,BC=√OC2+OB2=7,∵四边形ABCD是菱形,∴AB=BC=7,∴OA=AB﹣OB=7﹣72=72,∴A(﹣72,0).(2)如图2中,连接CE、CF.∵OA=OB,CO⊥AB,∴AC=BC=7,∴AB=BC=AC,∴△ABC是等边三角形,∴∠ACB=60°,∵∠APB=60°,∵∠PAG+∠APB=∠AGB=∠CBG+∠ACB,∴∠PAG=∠CBG,∵AE=BF,∴△ACE≌△BCF,∴CE=CF,∠ACE=∠BCF,∴∠ECF=∠ACF+∠ACE=∠ACF+∠BCF=∠ACB=60°,∴△CEF是等边三角形,∴∠CFE=60°,EF=FC,∵∠AFE=30°,∴∠AFC=∠AFE+∠CFE=90°,在Rt△ACF中,AF2+CF2=AC2=49,∴AF2+EF2=49.(3)如图3中,延长CE交FA的延长线于H,作PQ⊥AB于Q,PK⊥OC于K,在BP设截取BT=PA,连接AT、CT、CF、PC.∵△CEF是等边三角形,∴∠CEF=60°,EC=CF,∵∠AFE=30°,∠CEF=∠H+∠EFH,∴∠H=∠CEF﹣∠EFH=30°,∴∠H=∠EFH,∴EH=EF,∴EC=EH,∵PE=AE,∠PEC=∠AEH,∴△CPE≌△HAE,∴PC∥FH,∵∠CAP=∠CBT,AC=BC,∴△ACP≌△BCT,∴CP=CT,∠ACP=∠BCT,∴∠PCT=∠ACB=60°,∴△CPT是等边三角形,∴CT=PT,∠CPT=∠CTP=60°,∵CP∥FH,∴∠HFP=∠CPT=60°,∵∠APB=60°,∴△APF是等边三角形,∴∠CFP=∠AFC﹣∠∠AFP=30°,∴∠TCF=∠CTP﹣∠TFC=30°,∴∠TCF=∠TFC,∴TF=TC=TP,∴AT⊥PF,设BF=m,则AE=PE=m,∴PF=AP=2m,TF=TP=m,TB=2m,BP=3m,在Rt△APT中,AT=√AP2−TP2=√3m,在Rt△ABT中,∵AT2+TB2=AB2,∴(√3m)2+(2m)2=72,解得m=√7或﹣√7(舍弃),∴BF=√7,AT=√21,BP=3√7,sin∠ABT=ATAB =√217,∵OK=PQ=BP•sin∠PBQ=3√7×√217=3√3,BQ=√BP2−PQ2=6,∴OQ=BQ﹣BO=6﹣72=52,∴P(﹣52,3√3)。
黑龙江省部分地市2018年中考语文真题精选汇编写作专题(含解析)

写作专题哈尔滨市作文24. 从下面两题中任选一题作文。
(1)命题作文痴迷,就是深深的迷恋。
徜徉书海,醉心音乐,欣赏比赛,学习技能……痴迷其中的那份快乐难以割舍,痴迷其中的那份执著不易改变。
因为这份痴迷,生活有了更多的色彩;因为这份痴迷,世界多了进步的动力。
请以“不变的是那份痴迷”为题写一篇文章。
要求:①将题目抄写在答题卡作文纸的第一行(题目前空四格)②文体自选(诗歌、戏剧除外)③不得抄袭,不要套作④不少于600字⑤文中不得出现真实的人名、校名(2)给材料作文美丽的大森林是百鸟共同的家园。
这天,乌鸦飞到森林南面,发现一棵枝繁叶茂的大树,它决定在此安家。
不久,又飞来一只猫头鹰,它对正在忙碌的乌鸦霸道地说:“喂,这是我早看中的地盘,你赶快离开!”为此,它们争吵到百鸟之王面前,百鸟之王平静地听完它们的叙述,对乌鸦说:“森林这么大,可以栖息的大树有很多,你救礼让一下又何妨?大家相处,贵在礼让。
”接着,它又对猫头鹰说:“你也要自律一些,对待别人不能那么粗暴,大家和谐相处,不好吗?”从此以后,大森林中很少再听到争吵声,鸟儿们礼让、自律,逐渐养成了良好的习惯,大森林便一直鸟语花香,和乐安宁。
这个故事至少给我们这样一些启示:人与人之间要和谐相处;礼让是人应具备的美德;要严于律己,宽以待人;应该养成良好的习惯。
请根据以上材料,自选角度,写一篇文章。
要求:①所写文章主旨必须从所给材料中提炼,但不要对材料扩写、续写和改写,不得抄袭,不要套作②立意自定,题目自拟,文体自选(诗歌、戏剧除外)③不少于600字④文中不得出现真实的人名、校名【答案】参考例文不变的是那份痴迷“问世间情为何物,直教人生死相许”,这大概是对痴迷爱情的典型描绘了。
而这些人,往往被称作“情痴”。
当三毛与荷西定情撒哈拉时,我们赞许她是个勇敢且不畏艰苦的女人,但却不能说她是个“情痴”。
而当荷西亡去,三毛“居则九曲回肠,出则若有所失”时,我们感慨她对荷西深沉的爱,但却不能说她是个“情痴”。
三年中考语文真题:名著阅读与文学、文化常识(原卷版)[2018-2020年分项详解](黑龙江专用)
](https://img.taocdn.com/s3/m/5dc103274028915f814dc2e4.png)
三年中考语文真题:名著阅读与文学、文化常识(原卷版)[2018-2020年分项详解](黑龙江专用)精品资源·备战中考『2018-2020·『2018-2020·分项详解』『三年中考·真题试炼』编在前面:历年的中考卷可以让学生认识到中考的题型,命题风格,各知识板块的分值分布,考查的重点及难点。
这对于初三学生备战中考具有很大的指导意义。
而且历年的中考真题还有中考风向标的作用,学生可以通过中考试卷分析命题趋势自我预测一下可能会出现的重点难点。
这对于学生来说帮助非常大。
很多学生在初三在复习阶段会买很多的预测试卷儿或者是模拟题。
虽然也能够帮助学生扩展题面见识更多的题型,但是这些复习资料是与中考真题相比是无法比拟的。
利用好中考真题可以获得事半功倍的效果。
老师通常会在中考第二轮复习期间要求学生做至少三遍中考真题,每一遍都会有不同的侧重点。
通常第一遍就是按照中考节奏去完成试卷。
目的就是为了让学生能够掌握中考的节奏。
了解中考题试卷难易的题型分布等。
中考真题通常是80%是基础题型,20%是难题。
第一遍做中考真题并不强调分数的重要性。
主要是要把握中考的做题节奏,合理安排时间。
第二遍通常要注重准确率。
因为通过第一遍做题和对答案以后,需要花时间对错题进行分析,对难题做出归纳总结。
掌握中考真题的做题思路和方法。
而且在做第二遍的时候,要尽可能的去缩短时间。
同时避免再犯第一次做题的错误,以能够锻炼做题的速度和准确率。
做第三遍的时候就要要求百分之百的正确率。
因为经过前两次的反复练习,对中考真题已经很熟悉。
尤其是对中考试卷进行研究以后,那么对于平时的模拟考试,就会显得非常简单。
一般情况下模拟考试的题型都能够在之前的中考真题中找到真实题型!需要注意的是,如果在第三次,做中考真题的时候还会出现错误,那就需要好好地反省一下了。
中考真题的作用是独一无二的,你做再多的模拟试卷都不如做一套中考真题作用大,所以在考试前一定要认真做中考真题,并总结分析真题规律!专题04名著阅读与文学、文化常识(原卷版)【2020年黑龙江绥化市初中毕业学业考试语文试题】2.下列文学文化常识说法错误的一项是( )A. 清明既是节气又是节日,和它有关的诗句有“清明时节雨纷纷,路上行人欲断魂”等。
黑龙江哈尔滨中考地理2018年试题word版答案或解析精编

2018年黑龙江省哈尔滨市中考地理试卷一、选择题(本大题共25小题,每小题2分,共50分。
在每小题给出的四个选项中,只有一项是最符合题目要求的)1.(2分)南北半球的分界线是()A.本初子午线B.赤道C.回归线D.极圈2.(2分)2018年海南博鳌亚洲论坛,有汉语、法语、英语、俄语等多种工作语言,世界上使用最广泛的语言是()A.汉语B.法语C.英语D.俄语3.(2分)2018年6月14日世界杯足球赛将在俄罗斯举行,查找俄罗斯在世界中的地理位置应选择的地图是()A.世界气候图B.世界政区图C.世界地形图D.世界河流图4.(2分)如图所示,夏季炎热干燥、冬季温和多雨的气候类型是()A.温带季风气候B.温带海洋性气候C.地中海气候D.热带草原气候5.(2分)下列地区中年降水量最多的是()A.赤道地区B.两极地区C.回归线附近大陆西岸D.中纬度地区大陆内部6.(2分)澳大利亚羊毛产量和出口量均占世界首位,羊肉的产量和出口量也占世界前列,因此澳大利亚被称为()A.世界活化石博物馆B.骑在羊背上的国家C.坐在矿车上的国家D.世界上最小的大陆7.(2分)世界上信仰人数最多的宗教是()A.佛教B.伊斯兰教C.基督教D.印度教8.(2分)小明从哈尔滨乘火车去北京旅游,应选择的铁路线是()A.京哈线B.京沪线C.京广线D.京九线9.(2分)下列词语中,描述气候的是()A.阴雨连绵B.四季如春C.艳阳高照D.暴风骤雨10.(2分)我国的人口地理分界线是()A.黑河﹣﹣腾冲一线B.200毫米年等降水量线C.贺兰山D.昆仑山11.(2分)下列关于亚洲叙述错误的是()A.世界上面积最大的大洲B.世界上人口最多的大洲C.地势中部低、四周高D.河流呈放射状流向周边海洋12.(2分)解决我国水资源南方多、北方少、空间分布不均的跨流域调水工程是()A.南水北调工程B.防治水污染C.倡导节约用水D.植树种草13.(2分)那达慕节是下列哪个民族的传统节日()A.傣族B.藏族C.蒙古族D.汉族14.(2分)我国以北京、天津、唐山为工业中心的工业基地是()A.京津唐工业基地B.长江三角洲工业基地(沪宁杭)C.辽中南工业基地D.珠江三角洲工业基地15.(2分)海南省终年如夏,黑龙江省北部冬季寒冷而漫长,造成两地气候差异的主要因素是()A.地形因素B.纬度因素C.海陆因素D.人类活动16.(2分)世界上含沙量最大,下游有“地上河”的河流是()A.黑龙江B.长江C.黄河D.松花江17.(2分)下列关于日本的叙述错误的是()A.多火山、地震的岛国B.工业区主要分布在太平洋沿岸及濑户内海沿岸C.位于太平洋板块和亚欧板块交界处D.资源丰富的大国18.(2分)下列地区叙述错误的是()A.西亚石油主要分布在波斯湾及其沿岸地区B.东南亚是华人、华侨最大的聚居地C.印度是世界第一人口大国D.大洋洲是陆地上面积最小的大洲19.(2分)关于非洲叙述错误的是()A.高原大陆B.热带大陆C.白色人种为主D.尼罗河是世界第一长河20.(2分)读图分析,下列叙述错误的是()A.唐山是我国的直辖市B.雄安新区包括雄县、容城、安新C.北京是我国的政治中心D.北京大约在雄县的正北方向21.(2分)下列景观属于中国的世界自然遗产的是()A.九寨沟B.长城C.丽江古城D.秦始皇陵兵马俑22.(2分)下列聚落建筑风格与自然环境关系对应不正确的是()A.北极地区一一冰屋B.内蒙古草原一一四合院C.东南亚地区一一高架屋D.黄土高原一一窑洞23.(2分)关于我国国情叙述错误的是()A.我国陆地面积约960万平方千米B.我国耕地主要分布在东部C.我国有55个民族D.我国自然资源总量丰富、人均不足24.(2分)下列叙述错误的是()A.我国最大的湖泊是青海湖B.我国最大的河流是黄河C.我国第一大渔场是舟山渔场D.我国最大的沙漠是塔克拉玛干沙漠25.(2分)中国葡萄酒领军企业张裕在全球布局35万亩葡萄基地,全球累积销量5亿瓶,实现了亚洲、欧洲、美洲、大洋洲等地的产品布局,在全球有13座酒庄、21间生产工厂,张裕目前拥有21个主流品牌产品在70多个国家销售。
2018年黑龙江省哈尔滨市中考语文试卷含答案

绝密★启用前黑龙江省哈尔滨市2018年初中升学考试语文本试卷满分120分,考试时间120分钟。
一、积累与运用(25分)1.下列词语中加点字的注音和书写完全正确的一项是(3分)( )A .嫩.(n èn )芽 酬和.(h é) 人声鼎.(d ǐng )沸 B .精致.(zh ì) 和煦.(x ù) 囊萤.(y íng )映雪 C .籍.(j í)贯 妖娆.(r áo ) 微不足道.(d ào ) D .宽恕.(sh ù) 伦.(l ún )理 迫不急.(j í)待 2.对病句的修改不正确的一项是(3分)( )A .通过这次活动,使同学们认识到“诵读经典”很重要。
将“重要”改为“必要”。
B .在世乒赛上,中国队囊括并包揽了所有项目的金牌。
删掉“囊括并”或“并包揽”。
C .保护水资源刻不容缓,每个人都应作为江河卫士。
将“作为”改为“成为”。
D .教师要善于引导学生质疑问难,解决问题并深入研究。
将“解决问题”和“深入研究”调换位置。
3.《三国演义》中的人物和情节对应不正确的一项是(3分)( )A .诸葛亮——火烧新野B .曹操——火烧乌巢C .关羽——火烧赤壁D .陆逊——火烧连营4.对下面这首元曲理解有误的一项是(3分)( )山坡羊潼关怀古张养浩峰峦如聚,波涛如怒,山河表里潼关路。
望西都,意踌躇。
伤心秦汉经行处,宫阙万间都做了土。
兴,百姓苦;亡,百姓苦。
A .这首元曲借凭吊潼关古迹,抒发了作者的感慨。
B .“聚”“怒”从视觉和听觉两个方面写出潼关的险要。
C .“望西都,意踌躇”写作者驻马远望,感慨横生的样子。
D .“兴,百姓苦;亡,百姓苦”的意思是:只有改朝换代,人们才能摆脱痛苦的生活。
5.下面情境下,语言表达最准确、得体的一项是(3分) ( )【情境】学校周边有些露天摊位售卖油炸和烧烤食品,放学后,总有一些学生去购买,班主任老师担心学生多吃此类食品会影响身体健康,她对学生们说: A .“油炸和烧烤食品,质次价高,花钱买这类东西吃,不合算,你们就不要买了。
2018年各省地市中考语文诗词阅读试题汇编

2018年各省地市中考语文诗词阅读试题汇编湖南怀化市2018年初中毕业学业考试语文试卷阅读下面的诗歌,完成下列小题。
渔家傲·秋思范仲淹塞下秋来风景异,衡阳雁去无留意。
四面边声连角起,千嶂里,长烟落日孤城闭。
浊酒一杯家万里,燕然未勒归无计。
羌管悠悠霜满地,人不寐,将军白发征夫泪。
10. 下面对这首词的理解,不恰当的一项是()A. 词的上片中“长烟落日孤城闭”,与“大漠孤烟直,长河落日圆”的意境相似。
B. 词的下片中“羌管悠悠霜满地”,写出了边关虽寒冷,但有羌管鸣奏,生活并不艰苦。
C. “塞下秋来风景异”中的“异”字,写出了边塞秋天的景物与江南一带不同。
D. “千嶂里”中的“千嶂”是指崇山峻岭。
11. 这首词的上下片分别以什么表达方式为主,全词表达了作者怎样的思想感情?【答案】10. B 11. 上片侧重描写;下片侧重抒情。
表达了词人思念家乡、功业难成(壮志难酬)的哀伤,有凄清悲凉之感,也含蓄地表达了他对朝廷腐朽、软弱,不修武备、不重边功的愤懑之情。
【解析】10. 本题考查诗词关键句赏析,诗词句子赏析需要我们在了解诗词的结构和作者思想情感的基础上作答,并且要结合写作背景。
B项有误,“羌管悠悠霜满地”,写出了边关寒冷,生活很艰苦。
11. 本题考查辨析表达方式和赏析作者感情。
本词上阙写景,突出了边塞风光的“异”,这是描写的表达方式。
下阙抒情,“浊酒一杯家万里,燕然未勒归无计”写出了征人矛盾的心情,既思念家乡又为国担忧;“羌管悠悠霜满地,人不寐,将军白发征夫泪”一句更体现了对家乡的思念之情,还从侧面反映了边塞生活的艰苦。
湖北省孝感市2018年中考语文试题二、阅读理解(47分)(一)古诗词赏析(3分)次北固山下(作者:王湾)客路青山外,行舟绿水前。
潮平两岸阔,风正一帆悬。
海日生残夜,江春入旧年。
乡书何处达?归雁洛阳边。
8.本诗表达了诗人的情感。
(1分)9.明代胡应麟在《诗薮·内编》里说,本诗颈联“形容景物,妙绝千古”,你能从炼字上说说它妙在哪里吗?(2分)【答案】8.思乡9.妙在诗中用“日”“春”作为新生的美好事物的象征,并且用“生”“入”两字使之拟人化。
哈尔滨市2018年中考英语试题(含答案)

黑龙江省哈尔滨市2018年中考英语试题考生须知:1.本试卷满分为100分,考试时间为100分钟。
2。
答题前,考生先将自己的“姓名"、“考号”、“考场”、“座位号"在答题卡上填写清楚。
将“条形码”准确粘贴在条形码区域内。
3。
请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题纸上答题无效。
4。
选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫来黑色字迹的签字笔书写,字体工整、笔迹清楚。
5。
保持卡面整洁,不要折叠、不要弄脏、不要弄皱,不准使用涂改液、修正带、刮纸刀。
第I卷一、单项选择(本题共20分,每小题1分)选择最佳答案。
()1。
Boys and girls, work hard。
I m sure your parents will___ you in the future.A。
be famous as B。
be proud of C. keep in touch()2。
—-—--What are you going to do next month?———--I am going to travel to Germany,which is ______ European country。
A。
a B. an c. the()3。
——-—Hi,Helen。
When were you born?—---I was born_________ February, 2003。
I’m 15 years old.A。
on B。
in C. at( )4.----Alice,which season do you like best?————Autumn。
The fallen _______ are like a thick blanket on the ground. What beautiful scenery it is!A. leaf B。
leafs C。
2018年黑龙江省哈尔滨市中考物理试卷-答案

黑龙江省哈尔滨市2018年初中升学考试理综物理部分答案解析一、选择题1.【答案】C【解析】长度测量中刻度尺的零刻度线没有与木块的左边缘对齐,木块的左边缘与0.50 cm刻度线对齐,右-=,A错误;天平标尺的分度值是边缘与2.50 cm刻度线对齐,则木块的长度为2.50cm0.50cm 2.00 cmm=++=,B错误;读数时视线与温度计中液柱的液面相平,温度为0.2 g,物体的质量20g20g 1.6g41.6g30℃,C正确;电能表记录消耗的电能为1 866.6 kW h,D错误。
【考点】物理仪器的读数。
2.【答案】B【解析】手影是由光的直线传播形成的,A正确;从不同角度看到光屏上的像,是因为光在光屏上发生了漫反射,B错误;凹透镜对光线有发散作用,故平行光经凹透镜后会发散,C正确;因为在反射中光路是可逆的,所以在同一块镜子中,人能看到猫,猫也能看到人,D正确。
【考点】光现象的综合知识。
3.【答案】C【解析】呼出的“白气”是水蒸气液化形成的小水珠,A错误;用雪制成的雕塑自然变小,是因为雪直接变成水蒸气消散在空气中,是升华现象,B错误;雪是水蒸气凝华形成的小冰晶,凝华放热,C正确;冰在熔化过程中吸热,但温度不变,D错误。
【考点】物态变化。
4.【答案】C【解析】以球门为参照物,射向球门的球相对于球门的位置发生变化,故球是运动的,A错误;质量与物体所处的位置和运动状态无关,B错误;球被顶出后,在空中继续运动是因为球具有惯性,C正确;由于物体间力的作用是相互的,故踢球时,球对脚和脚对球都有力的作用,D错误。
【考点】力和运动的相关知识。
5.【答案】D【解析】机翼上凸下平的设计使其上方流速快压强小,下方流速慢压强大,从而获得向上的升力,A正确;螺旋桨的响声会对环境造成声污染,是噪声,B正确;随着海拔的升高,空气变得稀薄,大气压减小,C正确;太阳能电池板将太阳能转化为电能,D错误。
【考点】物理知识的实际应用。
黑龙江省哈尔滨市2018年八年级下期中数学试卷(五四制)及答案

黑龙江省哈尔滨市2018年八年级下期中数学试卷(五四制)及答案.2015-2016学年黑龙江省哈尔滨市嵩山中学八年级(下)期中数学试卷(五四学制)一.选择题(每题3分,共30分)1.下列四组线段中,可以构成直角三角形的是()、、15 7、8C.1、、23 B.3、4、A.16 D.、2.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是().45° DCB.90°.120°A.60°2+mx﹣1=0是一元二次方程,则m的取值范围是(的方程(m﹣1)x )3.若关于x0m≠1D.1≠B.m=1 C.m≥A.m2+8x+9=0,变形后的结果正确的是( x )4.用配方法解方程2222=25).((x+4)x+4=7 7 B.(x+4)D=﹣9 C.A.(x+4)﹣=5.下列不能判断四边形ABCD是平行四边形的是()A.AB=CD,AD=BC B.AB∥CD,AD=BC C.AB∥CD,AD∥BC D.∠A=∠C,∠B=∠D6.在Rt△ABC中,∠C=90°,AB=15,AC:BC=3:4,则这个直角三角形的面积是()108D.C.54 A.24 B.48 7.如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的)长度为(2cm..4cm DA.8cm B.6cm C8.下列所给的方程中,没有实数根的是()2222﹣5x+2=0.4x.3x﹣4x+1=0 D1=0 A.x+x=0 B.5x﹣4x﹣C9.如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD 的面积为20,A坐标为(﹣2,0),则顶点C的坐标为() 2)7,3),4 D.())A.(4,3 B.(5,4 C.(6)个. 10.下列命题中正确的有(①直角三角形中两条直角边的平方和等于斜边的平方;②一组对边相等,一组对角相等的四边形是平行四边形;③两条对角线互相垂直的四边形是菱形;④三角形的中位线平行于三角形的第三边;⑤对角线相等且互相平分的四边形是矩形.5..4 D2 A.B.3 C分)30二、填空题(每题3分,共(填“真命题”,等边对等角”的逆命题是11.命题“在同一个三角形中,是或“假命题”)2. =2x的根为12.方程x,那么这个直角三角形斜边上8cm.已知一个直角三角形的两条直角边分别为136cm、.的高为AC+BD= ,则△OCD的周长为27cm,对角线?ABCD中,AC、BD交于一点O,AB=11cm在14..cm,则20边的中点.若△ABC的周长为,ABC的ABBC,CA分别是△,15.如图,DE,F.的周长为△DEF元,则平均每次降元,由于两次降价,现在每盒8116.某药品原来每盒的售价为100.价的百分数为,,已知FBCD折叠,沿直线如图将矩形17.ABCDAE顶点恰好落在边上处,CE=3AB=8 3.则BF=18.参加足球联赛的每两队之间都进行两场比赛,共要比赛90场,共有个队参加比赛.19.矩形的一个内角平分线把矩形的一条边分成长为3和5两部分,则该矩形的面积是.20.如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,则EB= .三、解答题(21题8分,22、23题7分,24题8分,25、26、27题每题10分,共60分)21.用适当方法解下列方程2﹣7xx﹣1=0 (1)2+12x+9=814x(2)22+6x+9 4x+1=x﹣(3)4x22.2x)=(5x(4)(﹣4)﹣22.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E均在小正方形的顶点上.(1)在方格纸中画出以AB为一边的直角三角形ABC,点C在小正方形的顶点上,且;5的面积为△ABC(2)在方格纸中画出以DE为一边的锐角等腰三角形DEF,点F在小正方形的顶点上,且△DEF的面积为10.连接CF,请直接写出线段CF的长. 4分别相BCAD、,EF过点O与23.如图,平行四边形ABCD的对角线AC、BD相交于点O.,求证:OE=OF交于点E、F∥,NF,MG∥AD、N分别在AB、AD上,且BM=DN24.已知,四边形ABCD是菱形,点M.NF相交于点EMG分别在BC、CD上,与FAB,点、G是菱形;,求证:四边形AMEN(1)如图1在不添加任何辅助线的情况下,请直接写出面积相等的四边形.AC2,连接(2)如图40件,每件盈利.百货商店服装柜在销售中发现:某品牌童装平均每天可售出2025元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施.经市场调查发现:件.21如果每件童装降价元,那么平均每天就可多售出元,那么每天可售出多少件,每天可盈利多少元?)现在每件童装降价5(1元,那么每件童装应降价多少元?(2)要想平均每天销售这种童装盈利1200.已ABEACD,等边△及斜边ABC的直角边ACAB向外作等边△△26.如图,分别以Rt.DFAB,垂足为F,连接EF知∠BAC=30°,⊥;)AC=EF求证:(1是平行四边形;ADFE)四边形(2.AC3()⊥DF 5轴正半轴上,在x,在平面直角坐标系中,点O为坐标原点,点A27.已知:如图1的面积,且菱形OABCOC为邻边作菱形OABC点C在第一象限,且∠COA=60°,以OA、.为18两点的坐标;B、C(1)求的方向BAA点出发沿射线CB匀速运动,同时动点Q从点出发沿射线(2)动点P从C所在直线和AC和AC,PQ个单位匀速运动,P、Q两点的运动速度均为2/秒,连接PQDQE,请将△Q的运动时间为tBQ 为线段的中点,连接DE,设动点P、D交于点,点E的取值范围;的式子表示,并直接写出t的面积S用含t为Q、F、BPtFyQFQ23()在()的条件下,过点作⊥轴于点,当为何值时,以、顶点的四边形为平行四边形?62015-2016学年黑龙江省哈尔滨市嵩山中学八年级(下)期中数学试卷(五四学制)参考答案与试题解析一.选择题(每题3分,共30分)1.下列四组线段中,可以构成直角三角形的是()、1C.1、3 B.3、4、5 A.1、2、 D.67、8、【考点】勾股定理的逆定理.【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,这个就是直角三角形.222,∴该三角形不符合勾股定理的逆定理,故不可以构成直+231【解答】解:A、∵≠角三角形;222,∴该三角形符合勾股定理的逆定理,故可以构成直角三角形;+4=5B、∵3222≠(+1C)、∵,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角1形;222,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角形.6≠+78D、∵故选B.2.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是()CB.90°.120° DA.45°.60°【考点】平行四边形的性质.【分析】首先设平行四边形中两个内角的度数分别是x°,2x°,由平行四边形的邻角互补,即可得方程x+2x=180,继而求得答案.【解答】解:设平行四边形中两个内角的度数分别是x°,2x°,则x+2x=180,,解得:x=60∴其中较小的内角是:60°..故选A 72+mx﹣1=0是一元二次方程,则m的取值范围是(1)x )3.若关于x的方程(m﹣ 1≠0A.m.B.m=1 C.m≥1Dm≠【考点】一元二次方程的定义.【分析】根据一元二次方程的定义可得m﹣1≠0,再解即可.【解答】解:由题意得:m﹣1≠0,,1解得:m≠.故选:A2+8x+9=0,变形后的结果正确的是( 4.用配方法解方程x)2222=25x+4)=7 D.﹣9 C.(x+4)(A.x+4).=﹣7 B(x+4)(=【考点】解一元二次方程﹣配方法.【分析】方程移项后,利用完全平方公式配方即可得到结果.22+8x=﹣x9,【解答】解:方程x,整理得:+8x+9=022=7,,即(x+4配方得:x)+8x+16=7 C故选5.下列不能判断四边形ABCD是平行四边形的是()A.AB=CD,AD=BC B.AB ∥CD,AD=BC C.AB∥CD,AD∥BC D.∠A=∠C,∠B=∠D【考点】平行四边形的判定.【分析】直接根据平行四边形的判定定理判断即可.【解答】解:平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.∴C能判断,平行四边形判定定理1,两组对角分别相等的四边形是平行四边形;∴D能判断;能判定;平行四边形判定定理2,两组对边分别相等的四边形是平行四边形;∴A,对角线互相平分的四边形是平行四边形;平行四边形判定定理3,一组对边平行相等的四边形是平行四边形;4平行四边形判定定理.故选B8)则这个直角三角形的面积是(:BC=3:4,中,6.在Rt△ABC∠C=90°,AB=15,AC108D..48 C.54 .A24 B【考点】勾股定理.2222的值,继而x+BC,求出=ABAC=3x【分析】设,则BC=4x,然后根据勾股定理得到AC根据三角形的面积公式求出答案.,BC=4xAC=3x【解答】解:设,则222,+BC=AB根据勾股定理有AC2222,=15,得:x=94x即(3x)+()2.=54则△ABC的面积4x=6x=×3x×.C故选:7.如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的)长度为(2cm4cm D..6cm C.A.8cm B【考点】矩形的性质.【分析】根据矩形的性质、等边三角形的判定只要证明△DOC是等边三角形即可解决问题.【解答】解:∵四边形ABD是矩形,∴BD=AC,OA=OC,OB=OD,∵BD=8cm,,∴OD=4cm ∵∠DOC=∠AOB=60°,是等边三角形,∴△DOC,∴CD=OD=4cm.故选C9).下列所给的方程中,没有实数根的是( 82222﹣4x5x+2=0﹣4x+1=0 D﹣﹣4x1=0 C.3xA.x.+x=0 B.5x【考点】根的判别式.2﹣4ac的值,然后根据△的意义分别判断即可.【分析】分别计算出判别式△=b2﹣4×1×=10=1>0,所以方程有两个不相等的实数根;【解答】解:A、△2,所以方程有两个不相等的实数根;)=36>054)﹣4××(﹣1、△B=(﹣2,所以方程有两个不相等的实数根;04)﹣×3×1=4>C、△=(﹣42,所以方程没有实数根.<02=﹣74D、△=(﹣5)﹣×4×.D故选9.如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,)的坐标为( 0),则顶点C且菱形ABCD的面积为20,A坐标为(﹣2,A.(4,3) B.(5,4) C.(6,4) D.(7,3)【考点】菱形的性质;坐标与图形性质.【分析】过点C作x轴的垂线,垂足为E,由面积可求得CE的长,在Rt△BCE中可求得BE的长,可求得AE,结合A点坐标可求得AO,可求出OE,可求得C点坐标.【解答】解:如图,过点C作x轴的垂线,垂足为E,,S=20∵ABCD菱形∴AB?CE=20,即5CE=20,,CE=4∴在Rt△BCE中,BC=AB=5,CE=4,∴BE=3,∴AE=AB+BE=5+3=8.,0),又∵A(﹣2,∴OA=2∴OE=AE ﹣OA=8﹣2=6, 10,)∴C(6,4.故选C)个. 10.下列命题中正确的有(①直角三角形中两条直角边的平方和等于斜边的平方;②一组对边相等,一组对角相等的四边形是平行四边形;③两条对角线互相垂直的四边形是菱形;④三角形的中位线平行于三角形的第三边;⑤对角线相等且互相平分的四边形是矩形.5..2 B3 C.4 DA.【考点】命题与定理.【分析】①由勾股定理判定;②直接利用全等三角形的判定与性质以及利用平行四边形的性质求出即可;【解答】解:①直角三角形中两条直角边的平方和等于斜边的平方,故①正确;②一组对边相等,一组对角相等的四边形不一定是平行四边形,所以②错误;③对角线互相垂直的平行四边形是菱形,所以③错误;④三角形的中位线平行于三角形的第三边,且等于第三边的一半,所以④正确;⑤对角线相等且互相平分的四边形是矩形,⑤正确;.故选B分)分,共30二、填空题(每题3在同一个三角形中,等角 11.命题“在同一个三角形中,等边对等角”的逆命题是(填“真命题”或“假命题”)真对等边,是【考点】命题与定理.【分析】把一个命题的条件和结论互换就得到它的逆命题,再分析题设是否能推出结 11论,从而得出命题的真假.“在同一个三角形中”,等边对等角”的逆命题是:【解答】解:“在同一个三角形中,等角对等边,是真命题;故答案为:“在同一个三角形中,等角对等边;真.2 x=0,的根为12.方程xx=2x=2 .21【考点】解一元二次方程﹣因式分解法.【分析】移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.2,x【解答】解:=2x2,﹣x2x=0x(x﹣2)=0,x=0,或x﹣2=0,x=0,x=2,21故答案为:x=0,x=2.2113.已知一个直角三角形的两条直角边分别为6cm、8cm,那么这个直角三角形斜边上的高为 4.8cm .【考点】勾股定理.【分析】根据勾股定理可求出斜边.然后由于同一三角形面积一定,可列方程直接解答.【解答】解:∵直角三角形的两条直角边分别为6cm,8cm,∴斜边为,=10(cm),设斜边上的高为h则直角三角形的面积为×6×8=×10h,,h=4.8cm解得:这个直角三角形斜边上的高为4.8cm.故答案为:4.8cm.14.在?ABCD中,对角线AC、BD交于一点O,AB=11cm,△OCD的周长为27cm,则AC+BD=12.32 cm【考点】平行四边形的性质.,即可求CD的长,由条件△OCD的周长为27【分析】首先由平行四边形的性质可求出的长,再根据平行四边的对角线互相平分即可求出平行四边形的两条对角线出OD+OC的和.是平行四边形,【解答】解:∵四边形ABCD,,OA=OC,OB=OD∴AB=CD=11cm,的周长为OCD27cm ∵△,11=16cm∴OD+OC=27﹣,∵BD=2DO,AC=2OC,=32cm∴BD+AC=2(OD+OC).32故答案为:,则20,BCCA边的中点.若△ABC的周长为,15.如图,D,EF分别是△ABC的AB,.10 △DEF的周长为【考点】三角形中位线定理.倍,从的各边长为△DEF的各边长的2【分析】根据三角形的中位线定理,可得△ABC的周长即可.而得出△DEF,BC=2DFAC=2DE分别是△A BC三边的中点,∴AB=2EF,,E【解答】解:∵点D、、F,DE+EF+DF=10∵AB+AC+BC=20,∴.10故答案为16.某药品原来每盒的售价为100元,由于两次降价,现在每盒81元,则平均每次降价的百分数为 10% .【考点】一元二次方程的应用.【分析】设平均每次降价的百分率为x,那么第一次降价后的单价是原来的(1﹣x), 132,根据题意列方程解答即可.那么第二次降价后的单价是原来的(1﹣x),根据题意列方程得【解答】解:设平均每次降价的百分率为x2=81﹣x)100×(1,(不符合题意,舍去)x解得=0.1=10%,x=1.921.故答案为:10%,CE=3处,已知,AB=8沿直线AE折叠,顶点D恰好落在BC边上F17.如图将矩形ABCD.则BF= 6.【考点】勾股定理;翻折变换(折叠问题)表可以根据勾股定理求出,然后用xx的式子表示,CF【分析】设BC=x,AF可用含的长.BF中,利用勾股定理,可建立关于x的方程,即可得出△示出BF,在RtABF;3=5,DE=EF=8﹣【解答】解:由折叠的性质知:AD=AF,CF=4CE=3,由勾股定理可得:△RtCEF中,EF=DE=5,在;4BF=x﹣若设AD=AF=x,则BC=x,中,由勾股定理可得:ABF 在Rt△222,﹣8+(x4)=x,解得x=10.4=6故BF=x﹣.故答案为:690场,共有.参加足球联赛的每两队之间都进行两场比赛,共要比赛10 个队参18加比赛.【考点】一元二次方程的应用.【分析】设共有x个队参加比赛,根据每两队之间都进行两场比赛结合共比了90场即可得出关于x的一元一次方程,解之即可得出结论.【解答】解:设共有x个队参加比赛, 14,(x﹣1)根据题意得:2=90×x2,90=0﹣x整理得:x﹣.x=10或x=﹣9(舍去)解得:.10故答案为:两部分,则该矩形的面积195.矩形的一个内角平分线把矩形的一条边分成长为3和 24或40 是.【考点】矩形的性质.【分析】矩形的四个角都是直角,内角平分线,可组成等腰直角三角形,因此矩形的宽可有两种情况.【解答】解:∵矩形的一个内角平分线把矩形的一条边分成长为3和5两部分,∴矩形的长为8,宽为5或3.∴面积为40或24..24故答案为:40或20.如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=. AB=3,则EB=∠BAD=30°,AC=5,【考点】全等三角形的判定与性质.【分析】如图,作DM⊥AC于M,DN⊥AB于N.首先证明Rt△DMC≌Rt△DNB,推出CM=BN,△ADM≌△ADN,推出AM=AB,再证明DE∥AC,推出∠ADE=∠CAD=∠DAB=30°,推出AE=DE,推出∠DEN=60°,在Rt△ADN中,可得DN=AN?tan30°=,在Rt△EDN中,可得DE=DN,由此即可解决问题.÷cos30°=【解答】解:如图,作DM⊥AC于M,DN⊥AB于N. 15,于N,DN⊥AB∠∵∠CAD=BAD=30°,DM⊥AC于M,DN=DM∴中,DNBDMC和Rt△在Rt△,,DNB≌Rt△∴Rt△DMC,CM=BN∴,ADM同理可证△≌△ADN,∴AM=AB,AC+AB=AM+CM+AN﹣BN=2AM=8∴,∴AM=AN=4,∠DBN∵∠DCM=,∠2∴∠1=,2CDE=∵∠∠,CDE∴∠1=∠,AC∴DE∥∠DAB=30°,ADE=∠CAD=∴∠,∴AE=DE∴∠DEN=60°,,ADN在Rt△中,DN=AN?tan30°=,DE=DN÷cos30°=EDN在Rt△中,,AE=∴.﹣∴EB=ABAE=3﹣= 16.故答案为分,共10、27题每题题8分,25、26三、解答题(21题8分,22、23题7分,24分)60.用适当方法解下列方程2121=0 ﹣﹣)(1x7x2+12x+9=81)4x(222+6x+9 ﹣(3)4x4x+1=x22.)(=5﹣(4)(x﹣4)2x【考点】解一元二次方程﹣因式分解法;解一元二次方程﹣配方法;解一元二次方程﹣公式法.)公式法求解可得;(1【分析】)直接开平方法求解可得;2()直接开平方法求解可得;3()直接开平方法求解可得.(4,c=﹣1,)∵a=1b=﹣7,【解答】解:(1,011×(﹣)=53>∴△=49﹣4×;x=∴2,2x+3)=81(2)∵(,92x+3=9∴或2x+3=﹣;6x=﹣x=3解得:或22,)(12x3()∵(﹣)=x+3,2x1=x+32x∴﹣或﹣3x﹣1=﹣;x=4解得:﹣x=或17,﹣5x﹣4=2x)∵x﹣4=5﹣2x或(4.x=3或x=1解得:22.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E均在小正方形的顶点上.(1)在方格纸中画出以AB为一边的直角三角形ABC,点C在小正方形的顶点上,且;的面积为5△ABC(2)在方格纸中画出以DE为一边的锐角等腰三角形DEF,点F在小正方形的顶点上,且△DEF的面积为10.连接CF,请直接写出线段CF的长.【考点】作图—应用与设计作图;等腰三角形的性质;勾股定理.【分析】(1)直接利用旋转的性质得出对应点位置,进而得出答案;(2)利用等腰三角形的性质得出对应点位置进而结合勾股定理得出答案.即为所求;ABC1)如图所示:△(【解答】解:,即为所求;DFE2()如图所示:△.=CF= 18分别相、BC过点O与AD的对角线AC、BD相交于点O,EF23.如图,平行四边形ABCD.,求证:OE=OFE、F交于点【考点】平行四边形的性质;全等三角形的判定与性质.【分析】要证明线段相等,只需证明两条线段所在的两个三角形全等即可.为平行四边形,【解答】证明:∵ABCD,,OA=OC∴AD∥BC,CFOAEO=∠∴∠EAO=∠FCO,∠,)(AAS ∴△AEO≌△CFO.OE=OF∴∥NFAD,∥、AD上,且BM=DN,MG分别在是菱形,点24.已知,四边形ABCDM、NAB.E与MGNF相交于点、、AB,点FG分别在BCCD上,是菱形;AMEN1(1)如图,求证:四边形在不添加任何辅助线的情况下,请直接写出面积相等的四边形.,连接AC22()如图19【考点】菱形的判定与性质.【分析】(1)由MG∥AD,NF∥AB,可证得四边形AMEN是平行四边形,又由四边形ABCD是菱形,BM=DN,可得AM=AN,即可证得四边形AMEN是菱形;(2)易得四边形CGEF是菱形;即可得S=S,S=S,S=S,继而求得答ADC△△CEG△AEMABC△AEN△△CEF案.【解答】(1)证明:∵MG∥AD,NF∥AB,∴四边形AMEN是平行四边形,∵四边形ABCD是菱形,∴AB=AD,,∵BM=DN,﹣BM=ADDN∴AB﹣,AM=AN∴∴四边形AMEN是菱形;(2)解:∵四边形AMEN是菱形,,S=S∴AEN△AEM△同理:四边形CGEF是菱形,∴S=S,CEG△CEF△∵四边形ABCD是菱形,∴S=S,ADCABC△△∴S=S,S=S,S=S,S=S,S=S ABFN四边形DNFCADGE四边形四边形MBFEDNEG四边形四边形MBCE四边形ABFE四边形DNEC四边形四边形MBCG.ADGM四边形25.百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施.经市场调查发现:件.元,那么平均每天就可多售出2如果每件童装降价1(1)现在每件童装降价5元,那么每天可售出多少件,每天可盈利多少元?元,那么每件童装应降价多少元?)要想平均每天销售这种童装盈利(21200【考点】一元二次方程的应用.【分析】(1)根据每件童装降价1元,平均每天就可多售出2件,得出每件童装降价 20元,即可得出每天的盈利;40×20+52=30件,再根据每件盈利5元,每天可售出(2)设每件应降价x元,每天可以多销售的数量为2x件,每件的利润为(40﹣x),每件的利润×数量建立方程求出其解即可.=由总利润【解答】解:(1)∵每件童装降价1元,平均每天就可多售出2件,件;2=3020+5×5∴每件童装降价元,每天可售出;30=1050(元)(40﹣5)×∴每天可盈利:元,由题意,得x2)设每件应降价(,)=1200x)(20+2x(40﹣,=10,x=20解得:x21∴为增大销量,减少库存,元.20∴每件童装应降价26.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已.DF,垂足为F,连接知∠BAC=30°,EF⊥AB;1)AC=EF求证:((2)四边形ADFE是平行四边形;.DFAC⊥(3)【考点】平行四边形的判定与性质;全等三角形的判定与性质;等边三角形的性质.【分析】(1)首先Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又因为△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后即可证明△AFE≌△BCA,再根;AC=EF据全等三角形的性质即可证明(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形; 21.DFAC⊥得AE∥DF,可以得∠AGD=90°,则(3)先求∠EAC=90°,由?ADFE中,∠BAC=30°,△ABC【解答】证明:(1)∵Rt,AB=2BC∴又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF,AB=AE,,∴AF=BC在Rt△AFE和Rt△BCA中,∵,∴△AFE≌△BCA(HL),;AC=EF∴(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°,ABEF⊥又∵,AD∥∴EF∵AC=EF,AC=AD,,∴EF=AD∴四边形ADFE是平行四边形;(3)∵∠EAC=∠EAF+∠BAC=60°+30°=90°,∵四边形ADFE是平行四边形,,∥FD∴AE∴∠EAC=∠AGD=90°,∴AC⊥DF.27.已知:如图1,在平面直角坐标系中,点O为坐标原点,点A在x轴正半轴上, 22点C在第一象限,且∠COA=60°,以OA、OC为邻边作菱形OABC,且菱形OABC的面积.为18两点的坐标;C)求B、(1(2)动点P从C点出发沿射线CB匀速运动,同时动点Q从A点出发沿射线BA的方向匀速运动,P、Q两点的运动速度均为2个单位/秒,连接PQ和AC,PQ和AC所在直线交于点D,点E为线段BQ的中点,连接DE,设动点P、Q的运动时间为t,请将△DQE的取值范围;的式子表示,并直接写出t的面积S用含t(3)在(2)的条件下,过点Q作QF⊥y轴于点F,当t为何值时,以P、B、F、Q为顶点的四边形为平行四边形?【考点】四边形综合题.【分析】(1)如图1,过点C作CD⊥OA于点D,解直角三角形求出OD、CD的长即可解决问题.(2)分两种情形讨论即可①如图2中,当0≤t≤3时.②如图3中,当t>3时.分别想办法构建方程即可解决问题.(3)分三种情形①如图4中,当0≤t≤3时.②当t>3时,由PB=QF时.③当点Q在y 轴左侧时,构建PB=QF构建方程即可解决问题.,于点⊥CDOAD作,过点)如图(【解答】解:11C,OA=OC=BC=xxOABC设菱形的边长为,则 23∵∠COA=60°,∴CD=OC?sin60°=,x18∵菱形OABC的面积为,,∴x?x=18解得:x=±6,,∴OA=OC=BC=6,OD=OC?cos60°=3,×∴CD=6=33,B的坐标为:(,C的坐标为:(393),点);∴点(2)①如图2中,当0≤t≤3时,作PK∥AB交AC于K,则△PCK是等边三角形.作.H⊥AB于DH,DQAKPD=∠∠PK=PC=AQ,∠PDK=ADQ,∠∵,≌△QDA∴△PDK,DH=AD?sin60°=t=3﹣﹣DK=AD=(62t)t(3﹣),EQ=6+2tBQ=()=3+t,∴2?QE?DH=﹣t.+∴S=②如图3中,当t>3时,作PK∥AB交AC于K,则△PCK是等边三角形.作DH ⊥AB于.H 24,PDK≌△QDA由△,DH=AD?sin60°=36)=t﹣(BQ=6+2t)=3+t,∴(DK=AD=2t﹣(t3),EQ=﹣2.∴tS=﹣?QE?DH=S=.综上所述,,﹣,FQ=OK=6t.则⊥≤0≤t3时,作QKOA于KAK=t中,当)①如图(34是平行四边形,PBQF时,四边形当PB=FQ.t2t=66∴﹣﹣,解得t=0 25,t=4﹣t,解得时,由PB=QF时,2t﹣6=63②当t>,此种情形不存在.t=0﹣6,解得6=2tPB=QFQ③当点在y轴左侧时,由可得,t﹣为顶点的四边形为平行四边形.Q、、、时,以或综上所述,当t=04sPBF26日1752017年月 27。
2018年哈尔滨市南岗区中考数学一模试卷-有答案

2018年黑龙江省哈尔滨市南岗区中考数学一模试卷一、选择题(本大题共10小题,每小题3分,共30分)1.(3分)2018南1月24日是腊八节,这天哈尔滨市的最低气温是﹣35℃,最高气温是﹣24℃,这一天哈尔滨市的温差为()A.9℃B.10℃C.11℃D.59℃2.(3分)下列计算正确的是()A.3a﹣2a=a B.=C.(2a)3=2a3D.a6÷a3=a23.(3分)下列图形中,是中心对称图形的是()A.B.C. D.4.(3分)抛物线y=x2﹣2x﹣1的对称轴是()A.x=1 B.x=﹣1 C.x=2 D.x=﹣25.(3分)如图所示的几何体的主视图是()A.B.C.D.6.(3分)分式方程=的解为()A.5 B.13 C.D.7.(3分)如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=,则小车上升的高度是()A.5米 B.6米 C.6.5米D.12米8.(3分)一种药品原价每盒25元,经过两次降价后每盒16元,两次降价的百分率相同,设每次降价的百分率为x,则符合题意的方程为()A.16(1+2x)=25 B.25(1﹣2x)=16 C.16(1+x)2=25 D.25(1﹣x)2=169.(3分)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点,若∠DAB=50°,则∠ABC的大小是()A.55°B.60°C.65°D.70°10.(3分)如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为()A.B.C.D.二、填空题(本大题共10小题,每小题3分,共30分)11.(3分)地球绕太阳公转的速度约为110000千米/时,将这个数用科学记数法表示为.12.(3分)函数y=中,自变量x的取值范围是.13.(3分)把多项式a2b﹣4ab+4b分解因式的结果是.14.(3分)计算:﹣4的结果是.15.(3分)若反比例函数y=的图象经过点(﹣1,﹣2),则k的值为.16.(3分)不等式组的解集是.17.(3分)从,0,﹣,3.14,6这5个数中随机抽取一个数,抽到的有理数的概率是.18.(3分)若一个扇形的圆心角为60°,面积为6π,则这个扇形的半径为.19.(3分)在△ABC中,AB=2,AC=3,cos∠ACB=,则∠ABC的大小为度.20.(3分)如图,在▱ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=,AE=7,tan∠EAF=,则线段BF的长为.三、解答题(其中21-25题各6分,26题10分,共计40分)21.(6分)先化简,再求代数式(1﹣)÷的值,其中x=2cos30°﹣tan45°.22.(6分)如图,在方格纸中,每一个小正方形的边长为1,△ABC的三个顶点都在小方格的顶点上,按要求画一个三角形.(1)将△ABC先向右平移4个单位,再向上平移1个单位,在图1中画出示意图;(2)以点C为旋转中心,将△ABC顺时针旋转90°,在图2中画出示意图.23.(6分)某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问题卷调查,调查结果分为“A非常了解”、“B了解”、“C基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.(1)这次调查的市民有多少人?(2)补全条形统计图;(2)若该市约有市民950万人,请你根据抽样调查的结果,估计该市有多少万人对“社会主义核心价值观”达到“A非常了解”的程度.24.(6分)如图,点E在菱形ABCD的对角线BD上,连接AE,且AE=BE,⊙O是△ABE的外接圆,连接OB.(1)求证:OB⊥BC;(2)若BD=,tan∠OBD=2,求⊙O的半径.25.(6分)某运输公司承担了某标段的土方运输任务,公司已派出大小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车每次共35吨,3辆大型渣土运输车和2辆小型渣土运输车每次共运40吨.(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?(2)该运输公司决定派出大小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不小于150吨,问该运输公司最多派出几辆小型渣土运输车?26.(10分)在平面直角坐标系中,点O为坐标原点,直线y=﹣x+12与x轴,y轴分别相交于点A,B,∠ABO的平分线与x轴相交于点C.(1)如图1,求点C的坐标;(2)如图2,点D,E,F分别在线段BC,AB,OB上(点D,E,F都不与点B重合),连接DE,DF,EF,且∠EDF+∠OBC=90°,求证:∠FED=∠AED;(3)如图3,在(2)的条件下,延长线段FE与x轴相交于点G,连接DG,若∠CGD=∠FGD,BF:BE=5:8,求直线DF的解析式.2018年黑龙江省哈尔滨市南岗区中考数学一模试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分,共30分)1.(3分)2018南1月24日是腊八节,这天哈尔滨市的最低气温是﹣35℃,最高气温是﹣24℃,这一天哈尔滨市的温差为()A.9℃B.10℃C.11℃D.59℃【解答】解:﹣24﹣(﹣35)=﹣24+35=11(℃),故选:C.2.(3分)下列计算正确的是()A.3a﹣2a=a B.=C.(2a)3=2a3D.a6÷a3=a2【解答】解:A、3a﹣2a=a,故本选项正确;B、与不是同类项,不能合并,故本选项错误;C、(2a)3=8a3≠2a3,故本选项错误;D、a6÷a3=a3≠a2,故本选项错误.故选:A.3.(3分)下列图形中,是中心对称图形的是()A.B.C. D.【解答】解:A、不是中心对称图形,故本选项不符合题意;B、不是中心对称图形,故本选项不符合题意;C、是中心对称图形,故本选项符合题意;D、不是中心对称图形,故本选项不符合题意;故选:C.4.(3分)抛物线y=x2﹣2x﹣1的对称轴是()A.x=1 B.x=﹣1 C.x=2 D.x=﹣2【解答】解:抛物线y=x2﹣2x﹣1的对称轴是直线x=﹣=1.故选:A.5.(3分)如图所示的几何体的主视图是()A.B.C.D.【解答】解:从正面看易得第一层有2个正方形,第二层也有2个正方形.故选:B.6.(3分)分式方程=的解为()A.5 B.13 C.D.【解答】解:去分母得:5(x+2)=3(2x﹣1),解得:x=13,经检验x=13是分式方程的解,故选:B.7.(3分)如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=,则小车上升的高度是()A.5米 B.6米 C.6.5米D.12米【解答】解:如图AC=13,作CB⊥AB,∵cosα==,∴AB=12,∴BC===5,∴小车上升的高度是5m.故选:A.8.(3分)一种药品原价每盒25元,经过两次降价后每盒16元,两次降价的百分率相同,设每次降价的百分率为x,则符合题意的方程为()A.16(1+2x)=25 B.25(1﹣2x)=16 C.16(1+x)2=25 D.25(1﹣x)2=16【解答】解:第一次降价后的价格为:25×(1﹣x);第二次降价后的价格为:25×(1﹣x)2;∵两次降价后的价格为16元,∴25(1﹣x)2=16.故选:D.9.(3分)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点,若∠DAB=50°,则∠ABC的大小是()A.55°B.60°C.65°D.70°【解答】解:连接OC,∵点C为的中点,∴∠BOC=∠DAB=50°,∵OC=OB,∴∠ABC=∠OCB=65°,故选:C.10.(3分)如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△D HE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S 四边形MNKP =y ,则y 关于x 的函数图象大致为( )A .B .C .D .【解答】解:∵AE=x ,∴y=S 正方形ABCD ﹣2(S △AEF +S △BGF +S △CGH +S △DEH )=2×2﹣2×[•x•(2﹣x )+•x•(2﹣x )+x•(2﹣x )+x•(2﹣x )] =4x 2﹣8x +4 =4(x ﹣1)2, ∵0<x <2, ∴0<y <4,∵是二次函数,开口向上, ∴图象是抛物线,即选项A 、B 、C 错误;选项D 符合, 故选:D .二、填空题(本大题共10小题,每小题3分,共30分)11.(3分)地球绕太阳公转的速度约为110000千米/时,将这个数用科学记数法表示为 1.1×105 .【解答】解:将110000用科学记数法表示为:1.1×105. 故答案为:1.1×105.12.(3分)函数y=中,自变量x 的取值范围是 x ≠﹣3 .【解答】解:由题意得,x +3≠0, 解得x ≠﹣3. 故答案为:x ≠﹣3.13.(3分)把多项式a2b﹣4ab+4b分解因式的结果是b(a﹣2)2.【解答】解:a2b﹣4ab+4b=b(a2﹣4a+4)=b(a﹣2)2.故答案为:b(a﹣2)2.14.(3分)计算:﹣4的结果是2.【解答】解:原式=4﹣2=2故答案为:215.(3分)若反比例函数y=的图象经过点(﹣1,﹣2),则k的值为2.【解答】解:把点(﹣1,﹣2)代入解析式可得k=2.16.(3分)不等式组的解集是0<x<5.【解答】解:∵解不等式①得:x>0,解不等式②得:x<5,∴不等式组的解集为0<x<5,故答案为:0<x<5.17.(3分)从,0,﹣,3.14,6这5个数中随机抽取一个数,抽到的有理数的概率是.【解答】解:∵在,0,﹣,3.14,6这5个数中只有0、3.14和6为有理数,∴从,0,﹣,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是.故答案为:.18.(3分)若一个扇形的圆心角为60°,面积为6π,则这个扇形的半径为6.【解答】解:扇形的面积==6π.解得:r=6,故答案为:619.(3分)在△ABC中,AB=2,AC=3,cos∠ACB=,则∠ABC的大小为30或150度.【解答】解:如图,作AD⊥BC于点D,在Rt△ACD中,∵AC=3、cos∠ACB=,∴CD=ACcos∠ACB=3×=2,则AD===1,若点B在AD左侧,∵AB=2、AD=1,∴∠ABC=30°;若点B在AD右侧,则∠AB′D=30°,∴∠AB′C=150°,综上,∠ABC的度数为30°或150°,故答案为:30或150.20.(3分)如图,在▱ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=,AE=7,tan∠EAF=,则线段BF的长为.【解答】解:过F作FG⊥AE于G,延长AE、BC交于H,在Rt△AFG中,∵tan∠EAF=,∴设FG=5x,AG=2x,由勾股定理得:,∴x1=1,x2=﹣1(舍),∴AG=2,FG=5,∵AE=7,∴EG=5,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠D=∠DCH,∠DAE=∠H,∵DE=EC,∴△ADE≌△HCE,∴EH=AE=7,Rt△FGH中,∵FG=5,GH=5+7=12,∴FH=13,∵CF=2BF,设BF=a,则CF=2a,AD=CH=3a,∴2a+3a=13,a=,∴BF=,故答案为:.三、解答题(其中21-25题各6分,26题10分,共计40分)21.(6分)先化简,再求代数式(1﹣)÷的值,其中x=2cos30°﹣tan45°.【解答】解:原式=×=∵x=2cos30°﹣tan45°=﹣1,∴原式==22.(6分)如图,在方格纸中,每一个小正方形的边长为1,△ABC的三个顶点都在小方格的顶点上,按要求画一个三角形.(1)将△ABC先向右平移4个单位,再向上平移1个单位,在图1中画出示意图;(2)以点C为旋转中心,将△ABC顺时针旋转90°,在图2中画出示意图.【解答】解:(1)如图1,△A′B′C′为所作;(2)如图2,△A″B″C为所作.23.(6分)某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问题卷调查,调查结果分为“A非常了解”、“B了解”、“C基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.(1)这次调查的市民有多少人?(2)补全条形统计图;(2)若该市约有市民950万人,请你根据抽样调查的结果,估计该市有多少万人对“社会主义核心价值观”达到“A非常了解”的程度.【解答】解:(1)280÷56%=500(人),(2)对“社会主义核心价值观”达到“A.非常了解”的人数为:500﹣280﹣60=160(人),补全条形统计图如下:(3)950×=304(万人),答:该市大约有304万人对“社会主义核心价值观”达到“A.非常了解”的程度.24.(6分)如图,点E在菱形ABCD的对角线BD上,连接AE,且AE=BE,⊙O是△ABE的外接圆,连接OB.(1)求证:OB⊥BC;(2)若BD=,tan∠OBD=2,求⊙O的半径.【解答】(1)证明:连接OA、OE,设OE交AB于F,∵AE=BE,∴∠AOE=∠BOE,∵OA=OB,∴AF=BF,OE⊥AB,∴∠OFB=∠BFE=90°,∴∠BEF+∠EBF=90°,∵四边形ABCD是菱形,∴∠CBD=∠ABD,∵OB=OE,∴∠OBE=CEB,∴∠OBE+∠CBD=90°,∴∠OBC=90°,∴OB⊥BC;(2)解:连接AC交BD于G,∵四边形ABCD是菱形,∴AB=BC,AC⊥BD,BG=BD=,∴∠BGC=90°,∴∠GCB+∠GBC=90°,∵∠OBD+∠CBG=90°,∴∠GCB=∠OBD,在Rt△BCG中,tan∠GCB=tan∠OBD=2,∴=2,∴CG=,∴BC===8,∴AB=8,∴BF=4,在Rt△BEF中,tan∠BEF=tan∠OBD=2,∴=2,∴EF=2,设⊙O的半径为r,在Rt△BOF中,OF2+BF2=OB2,(r﹣2)2+42=r2,解得:r=5,即⊙O的半径为5.25.(6分)某运输公司承担了某标段的土方运输任务,公司已派出大小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车每次共35吨,3辆大型渣土运输车和2辆小型渣土运输车每次共运40吨.(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?(2)该运输公司决定派出大小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不小于150吨,问该运输公司最多派出几辆小型渣土运输车?【解答】解:(1)设一辆大型渣土运输车一次运输x吨,一辆小型渣土运输车一次运输y吨,,解得.即一辆大型渣土运输车一次运输10吨,一辆小型渣土运输车一次运输5吨;(2)设该运输公司派出a辆小型渣土运输车,由题意可得,10(20﹣a)+5a≥150,解得a≤10.∵a是整数,∴a最大为10,∴该运输公司最多派出10辆小型渣土运输车.26.(10分)在平面直角坐标系中,点O为坐标原点,直线y=﹣x+12与x轴,y轴分别相交于点A,B,∠ABO的平分线与x轴相交于点C.(1)如图1,求点C的坐标;(2)如图2,点D,E,F分别在线段BC,AB,OB上(点D,E,F都不与点B重合),连接DE,DF,EF,且∠EDF+∠OBC=90°,求证:∠FED=∠AED;(3)如图3,在(2)的条件下,延长线段FE与x轴相交于点G,连接DG,若∠CGD=∠FGD,BF:BE=5:8,求直线DF的解析式.【解答】解:(1)如图1中,作CH⊥AB于H.由题意A(9,0),B(0,12),在Rt△AOB中,AB===15,tan∠OAB===,∵∠CBH=∠CBO,∠CHB=∠COB,CB=CB,∴△O BC≌△HBC,∴BH=OB=12,OC=CH,AH=15﹣12=3,在Rt△ACH中,tan∠CAH==,∠CH=4,∴OC=CH=4,∴点C坐标为(4,0).(2)解:如图2中,过点D分别作DM⊥y轴于点M,DN⊥AB于点N,在NA上截取NP=FM,连接PD.∵∠EDF+∠OBC=90°,∠BDM+∠OBC=90°,∴∠EDF=∠BDM,同理∠BDN=∠BDM=∠MDN,∴∠EDF=∠MDN,∵∠DBM=∠DBN,DM⊥OB,DN⊥AB,∴DM=DN,∵∠FMD=∠PND=90°,NP=FM,∴△DFM≌△DPN,∴DF=DP,∠FDM=∠PDN,∴∠FDM+∠FDN=∠PDN+∠FDN,即∠FDP=∠MDN,∴∠EDF=∠FDP=∠EDP,∵DE=DE,∴△DEF≌△DEP,∴∠FED=∠AED.(3)解:如图3中,过点F作FQ⊥BE于点Q,过点D作DM⊥y轴于M,DN⊥AB于N,DR⊥EF于R,DS⊥OG于点S,过点A作AT⊥BC交BC的延长线于T,连接AD.∵∠DEF=∠DEA,DR⊥EF,DN⊥EA,∴DR=DN,同理DR=DS,∴DN=DS,∴∠BAD=∠OAD,同理∠OFD=∠DFG,在Rt△ACT中,AC=9﹣4=5,tan∠ACT=tan∠BCO==3,=3,设CT=m,则AT=3m.∵CT2+AT2=AC2,∴m2+(3m)2=52,解得m=或﹣(舍弃),∴CT=,AT=,∵∠ADC=∠ABD+∠BAD=(∠OBA+∠BAO)=×90°=45°,∴∠DAT=45°=∠ADC,∴DT=AT=,∴CD=DT﹣CT=,同理可得,CS=1,DS=3=OM,∴OS=4﹣1=3,∴点D坐标(3,3),设BF=5n,则BE=8n,在Rt△BFQ中,cos∠FBQ===,∴BQ=4n=EQ,∴FQ⊥AB,∠BFQ=∠EFQ,∴∠DFQ=∠DFC+∠EFQ=(∠OFG+∠BFE)=×180°=90°,∴∠DFQ=∠BQF=90°,∴DF∥AB,设直线DF的解析式为y=﹣x+b,∴3=﹣×3+b,解得b=7,∴直线DF的解析式为y=﹣x+7.。
2018年哈尔滨市中考数学试题及答案

哈 尔 滨 市 2018 年 初 中 升 学 考 试数 学 试 卷考生须知:1.本试卷满分为120分,考试时间为120分钟。
2.答题前,考生先将自己的”姓名”、“考号”、“考场"、”座位号”在答题卡上填写清楚,将“条形码”准确粘贴在条形码区域内。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题纸上答题无效。
4.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
5.保持卡面整洁,不要折叠、不要弄脏、不要弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷选择题(共30分)(涂卡)一、选择题(每小题3分,共计30分) 1.75-的绝对值是( ). (A)75 (B)57 (C)75- (D)57- 2.下列运算一定正确的是( ).(A)()222n m n m +=+ (B)()333n m mn = (C)()523m m = (D)22m m m =⋅3.下列图形中既是轴对称图形又是中心对称图形的是( ).4.六个大小相同的正力体搭成的几何体如图所示,其俯视图是( ).5. 如图,点P 为⊙O 外一点,PA 为⊙0的切线,A 为切点,PO 交⊙0于点B ,∠P=30°,OB=3,则线段BP 的长为( ). (A)3 (B)33 (C)6 (D)9 6.将抛物线y=-5x 2+l 向左平移1个单位长度,再向下平移2个单位长度, 所得到的抛物线为( ).(A) y=-5(x+1)2-1 (B)y=-5(x-1)2-1 (C)y=-5(x+1)2+3 (D)y=-5(x-1)2+3 7.方程3221+=x x 的解为( ). (A)x=-1 (B)x=0 (C) x=53 (D)x=1 8.如图,在菱形ABCD 中,对角线AC 、BD 相交于点0,BD=8,tan ∠ABD=43, 则线段AB 的长为( ).(A)7 (B)27 (C)5 (D)109.已知反比例函数xk y 32-=的图象经过点(1,1),则k 的值为( ). (A)-1 (B)0 (C)1 (D)210.如图,在△ABC 中,点D 在BC 边上,连接AD,点G 在线段AD 上,GE ∥BD,且交AB 于点E,GF ∥AC,且交CD 于点F,则下列结论一定正确的是( ).(A)AD AGAE AB = (B)AD DGCF DF =(C)BD EG AC FG = (D)DFCF BE AE =第Ⅱ卷非选择题(共90分)二、填空题(每小3分,共计30分)11.将数920 000 000用科学记数法表示为 . 12.函数45y -=x x 中,自变量x 的取值范围是 . 13.把多项式x 3-25x 分解因式的结果是 .14.不等式组{1215325≥---x x x >的解集为 . 15.计算5110-56的结果是 . 16.抛物线y=2(x+2)2+4的顶点坐标为 .17.一枚质地均匀的正方体骰子,骰子的六个面上分別刻有1到6的点数,张兵同学掷一次骰子,骰 子向上的一面出现的点数是3的倍数的概率是 .18.一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是 .19.在△ABC 中, AB=AC,∠BAC=100°,点D 在BC 边上,连接AD,若△ABD 为直角三角形,则∠ADC 的 度数为 .20. 如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点0,AB=OB ,点E 、点F 分别是OA 、OD 的中点,连接EF,∠CEF=45°EM ⊥BC 于点M,EM 交BD 于点N,FN=10,则线段BC 的长为 .三、解答题(其中21~22题各7分,23~24题备8分,25-27题各10分,共计60分21(本题7分)先化简,再求代数式429621-12-+-÷⎪⎭⎫ ⎝⎛-a a a a 的值,其中a=4cos30°+3tan45°. 22.(本题7分)如图,方格纸中每个小正方形的边长均为1,线段AB 的两个端点均在小正方形的顶点上.(1) 在图中画出以线段AB 为一边的矩形ABCD(不是正方形),且点C 和点D 均在小正方形的顶点上;(2) 在图中画出以线段AB 为一腰,底边长为22的等腰三角形ABE,点E 在小正方形的顶点上.连接CE,请直接写出线段CE 的长.23.(本题8分)为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图.请你根据图中提供的信息回答下列问题:(1)本次调查共抽取了多少名学生?(2)通过计算补全条形统计图;(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?24.(本题8分)已知:在四边形ABCD 中,对角线AC 、BD 相交于点E ,且AC ⊥BD,作BF ⊥CD 垂足为点F,BF 与AC 交于点G.∠BGE=∠ADE.(1)如图1,求证:AD=CD ;(2)如图2,BH 是△ABE 的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE 面积的2倍.25.(本题10分)春平中学要为学校科技活动小组提供实验器材,计划购买A 型,B 型两种型号的放大镜,若购买8个A 型放大镜和5个B 型放大镜需用220元;若购买4个A 型放大镜和6个B 型放大镜需用152元.(1)求每个A 型放大镜和每个B 型放大镜各多少元?(2)春平中学决定购买A 型放大镜和B 型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A 型放大镜?26.(本题10分)已知:⊙O 是正方形ABCD 的外接圆,点E 在弧AB 上,连接BE 、DE,点F 在弧AD 上,连接BF,DF,BF 与DE 、DA 分别交于点G 、点H,且DA 平分∠EDF.(1)如图1,求证:∠CBE=∠DHG;(2)如图2,在线段AH 上取一点N (点N 不与点A 、点H 重合),连接BN 交DE 于点L,过点H 作HK ∥BN 交DE 于点K,过点E 作EP ⊥BN 垂足为点P ,当BP=HF 时,求证:BE=HK;(3)如图3,在(2)的条件下,当3HF=2DF 时,延长EP 交⊙0于点R,连接BR,若△BER 的面积与△DHK 的面积的差为47,求线段BR 的长.27.(本题10分)已知:在平面直角坐标系中,点0为坐标原点,点A 在x 轴的负半轴上,直线3273+-=x y 与x 轴、y 轴分别交于B 、C 两点,四边形ABCD 为菱形.(1)如图1,求点A 的坐标;(2)如图2,连接AC,点P 为△ACD 内一点,连接AP 、BP,BP 与AC 交于点G,且∠APB=60°,点E 在线段AP 上,点F 在线投BP 上,且BF=AE.连接AF 、EF,若∠AFE=30°,求AF 2+EF 2的值;(3)如图3在(2)的条件下,当PE=AE 时,求点P 的坐标.一、选择题(每小题3分,共计30分)1.(3.00分)﹣的绝对值是()A.B.C.D.【分析】计算绝对值要根据绝对值的定义求解,第一步列出绝对值的表达式,第二步根据绝对值定义去掉这个绝对值的符号.【解答】解:||=,故选:A.【点评】本题主要考查了绝对值的定义,绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0,比较简单.2.(3.00分)下列运算一定正确的是()A.(m+n)2=m2+n2B.(mn)3=m3n3C.(m3)2=m5D.m•m2=m2【分析】直接利用完全平方公式以及积的乘方运算法则、同底数幂的乘除运算法则分别计算得出答案.【解答】解:A、(m+n)2=m2+2mn+n2,故此选项错误;B、(mn)3=m3n3,正确;C、(m3)2=m6,故此选项错误;D、m•m2=m3,故此选项错误;故选:B.【点评】此题主要考查了完全平方公式以及积的乘方运算、同底数幂的乘除运算,正确掌握运算法则是解题关键.3.(3.00分)下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】观察四个选项中的图形,找出既是轴对称图形又是中心对称图形的那个即可得出结论.【解答】解:A、此图形既不是轴对称图形也不是中心对称图形,此选项不符合题意;B、此图形不是轴对称图形,是中心对称图形,此选项不符合题意;C、此图形既是轴对称图形,又是中心对称图形,此选项符合题意;D、此图形是轴对称图形,但不是中心对称图形,此选项不符合题意;故选:C.【点评】本题考查了中心对称图形以及轴对称图形,牢记轴对称及中心对称图形的特点是解题的关键.4.(3.00分)六个大小相同的正方体搭成的几何体如图所示,其俯视图是()A.B.C.D.【分析】俯视图有3列,从左到右正方形个数分别是2,1,2.【解答】解:俯视图从左到右分别是2,1,2个正方形.故选:B.【点评】本题考查了简单组合体的三视图,培养学生的思考能力和对几何体三种视图的空间想象能力.5.(3.00分)如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为()A.3B.3C.6D.9【分析】直接利用切线的性质得出∠OAP=90°,进而利用直角三角形的性质得出OP 的长.【解答】解:连接OA,∵PA为⊙O的切线,∴∠OAP=90°,∵∠P=30°,OB=3,∴AO=3,则OP=6,故BP=6﹣3=3.故选:A.【点评】此题主要考查了切线的性质以及圆周角定理,正确作出辅助线是解题关键.6.(3.00分)将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为()A.y=﹣5(x+1)2﹣1B.y=﹣5(x﹣1)2﹣1C.y=﹣5(x+1)2+3D.y=﹣5(x ﹣1)2+3【分析】直接利用二次函数图象与几何变换的性质分别平移得出答案.【解答】解:将抛物线y=﹣5x2+1向左平移1个单位长度,得到y=﹣5(x+1)2+1,再向下平移2个单位长度,所得到的抛物线为:y=﹣5(x+1)2﹣1.故选:A.【点评】此题主要考查了二次函数图象与几何变换,正确记忆平移规律是解题关键.7.(3.00分)方程=的解为()A.x=﹣1B.x=0C.x=D.x=1【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:x+3=4x,解得:x=1,经检验x=1是分式方程的解,故选:D.【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.8.(3.00分)如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=8,tan∠ABD=,则线段AB的长为()A.B.2C.5D.10【分析】根据菱形的性质得出AC⊥BD,AO=CO,OB=OD,求出OB,解直角三角形求出AO,根据勾股定理求出AB即可.【解答】解:∵四边形ABCD是菱形,∴AC⊥BD,AO=CO,OB=OD,∴∠AOB=90°,∵BD=8,∴OB=4,∵tan∠ABD==,∴AO=3,在Rt△AOB中,由勾股定理得:AB===5,故选:C.【点评】本题考查了菱形的性质、勾股定理和解直角三角形,能熟记菱形的性质是解此题的关键.9.(3.00分)已知反比例函数y=的图象经过点(1,1),则k的值为()A.﹣1B.0C.1D.2【分析】把点的坐标代入函数解析式得出方程,求出方程的解即可.【解答】解:∵反比例函数y=的图象经过点(1,1),∴代入得:2k﹣3=1×1,解得:k=2,故选:D.【点评】本题考查了反比例函数图象上点的坐标特征,能根据已知得出关于k的方程是解此题的关键.10.(3.00分)如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是()A.=B.=C.=D.=【分析】由GE∥BD、GF∥AC可得出△AEG∽△ABD、△DFG∽△DCA,根据相似三角形的性质即可找出==,此题得解.【解答】解:∵GE∥BD,GF∥AC,∴△AEG∽△ABD,△DFG∽△DCA,∴=,=,∴==.故选:D.【点评】本题考查了相似三角形的判定与性质,利用相似三角形的性质找出==是解题的关键.二、填空题(每小题3分,共计30分)11.(3.00分)将数920000000科学记数法表示为9.2×108.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:920000000用科学记数法表示为9.2×108,故答案为;9.2×108【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12.(3.00分)函数y=中,自变量x的取值范围是x≠4.【分析】根据分式分母不为0列出不等式,解不等式即可.【解答】解:由题意得,x﹣4≠0,解得,x≠4,故答案为:x≠4.【点评】本题考查的是函数自变量的取值范围,掌握分式分母不为0是解题的关键.13.(3.00分)把多项式x3﹣25x分解因式的结果是x(x+5)(x﹣5)【分析】首先提取公因式x,再利用平方差公式分解因式即可.【解答】解:x3﹣25x=x(x2﹣25)=x(x+5)(x﹣5).故答案为:x(x+5)(x﹣5).【点评】此题主要考查了提取公因式法以及公式法分解因式,正确应用公式是解题关键.14.(3.00分)不等式组的解集为3≤x<4.【分析】先求出每个不等式的解集,再求出不等式组的解集即可.【解答】解:∵解不等式①得:x≥3,解不等式②得:x<4,∴不等式组的解集为3≤x<4,故答案为;3≤x<4.【点评】本题考查了解一元一次不等式组,能根据不等式的解集得出不等式组的解集是解此题的关键.15.(3.00分)计算6﹣10的结果是4.【分析】首先化简,然后再合并同类二次根式即可.【解答】解:原式=6﹣10×=6﹣2=4,故答案为:4.【点评】此题主要考查了二次根式的加减,关键是掌握二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变.16.(3.00分)抛物线y=2(x+2)2+4的顶点坐标为(﹣2,4).【分析】根据题目中二次函数的顶点式可以直接写出它的顶点坐标.【解答】解:∵y=2(x+2)2+4,∴该抛物线的顶点坐标是(﹣2,4),故答案为:(﹣2,4).【点评】本题考查二次函数的性质,解答本题的关键是由顶点式可以直接写出二次函数的顶点坐标.17.(3.00分)一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,张兵同学掷一次骰子,骰子向上的一面出现的点数是3的倍数的概率是.【分析】共有6种等可能的结果数,其中点数是3的倍数有3和6,从而利用概率公式可求出向上的一面出现的点数是3的倍数的概率.【解答】解:掷一次骰子,向上的一面出现的点数是3的倍数的有3,6,故骰子向上的一面出现的点数是3的倍数的概率是:=.故答案为:.【点评】本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.18.(3.00分)一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是6πcm2.【分析】先求出扇形对应的圆的半径,再根据扇形的面积公式求出面积即可.【解答】解:设扇形的半径为Rcm,∵扇形的圆心角为135°,弧长为3πcm,∴=3π,解得:R=4,所以此扇形的面积为=6π(cm2),故答案为:6π.【点评】本题考查了扇形的面积计算和弧长的面积计算,能熟记扇形的面积公式和弧长公式是解此题的关键.19.(3.00分)在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADC的度数为130°或90°.【分析】根据题意可以求得∠B和∠C的度数,然后根据分类讨论的数学思想即可求得∠ADC的度数.【解答】解:∵在△ABC中,AB=AC,∠BAC=100°,∴∠B=∠C=40°,∵点D在BC边上,△ABD为直角三角形,∴当∠BAD=90°时,则∠ADB=50°,∴∠ADC=130°,当∠ADB=90°时,则∠ADC=90°,故答案为:130°或90°.【点评】本题考查等腰三角形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用等腰三角形的性质和分类讨论的数学思想解答.20.(3.00分)如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AB=OB,点E、点F分别是OA、OD的中点,连接EF,∠CEF=45°,EM⊥BC于点M,EM交BD 于点N,FN=,则线段BC的长为4.【分析】设EF=x,根据三角形的中位线定理表示AD=2x,AD∥EF,可得∠CAD=∠CEF=45°,证明△EMC是等腰直角三角形,则∠CEM=45°,证明△ENF≌△MNB,则EN=MN=x,BN=FN=,最后利用勾股定理计算x的值,可得BC的长.【解答】解:设EF=x,∵点E、点F分别是OA、OD的中点,∴EF是△OAD的中位线,∴AD=2x,AD∥EF,∴∠CAD=∠CEF=45°,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=2x,∴∠ACB=∠CAD=45°,∵EM⊥BC,∴∠EMC=90°,∴△EMC是等腰直角三角形,∴∠CEM=45°,连接BE,∵AB=OB,AE=OE∴BE⊥AO∴∠BEM=45°,∴BM=EM=MC=x,∴BM=FE,易得△ENF≌△MNB,∴EN=MN=x,BN=FN=,Rt△BNM中,由勾股定理得:BN2=BM2+MN2,∴,x=2或﹣2(舍),∴BC=2x=4.故答案为:4.【点评】本题考查了平行四边形的性质、等腰直角三角形的判定和性质、全等三角形的判定与性质、勾股定理;解决问题的关键是设未知数,利用方程思想解决问题.三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分) 21.(7.00分)先化简,再求代数式(1﹣)÷的值,其中a=4cos30°+3tan45°.【分析】根据分式的运算法则即可求出答案,【解答】解:当a=4cos30°+3tan45°时,所以a=2+3原式=•==【点评】本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.22.(7.00分)如图,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.(1)在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;(2)在图中画出以线段AB为一腰,底边长为2的等腰三角形ABE,点E在小正方形的顶点上,连接CE,请直接写出线段CE的长.【分析】(1)利用数形结合的思想解决问题即可;(2)利用数形结合的思想解决问题即可;【解答】解:(1)如图所示,矩形ABCD即为所求;(2)如图△ABE即为所求;【点评】本题考查作图﹣应用与设计、等腰三角形的性质、勾股定理、矩形的判定和性质等知识,解题的关键是学会利用思想结合的思想解决问题,属于中考常考题型.23.(8.00分)为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:(1)本次调查共抽取了多少名学生?(2)通过计算补全条形统计图;(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?【分析】(1)由“诗词”的人数及其所占百分比可得总人数;(2)总人数减去其他种类的人数求得“书法”的人数即可补全条形图;(3)用总人数乘以样本中“国画”人数所占比例.【解答】解:(1)本次调查的学生总人数为24÷20%=120人;(2)“书法”类人数为120﹣(24+40+16+8)=32人,补全图形如下:(3)估计该中学最喜爱国画的学生有960×=320人.【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.24.(8.00分)已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.(1)如图1,求证:AD=CD;(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.【分析】(1)由AC⊥BD、BF⊥CD知∠ADE+∠DAE=∠CGF+∠GCF,根据∠BGE=∠ADE=∠CGF得出∠DAE=∠GCF即可得;(2)设DE=a,先得出AE=2DE=2a、EG=DE=a、AH=HE=a、CE=AE=2a,据此知S△ADC=2a2=2S△ADE ,证△ADE≌△BGE得BE=AE=2a,再分别求出S△ABE、S△ACE、S△BHG,从而得出答案.【解答】解:(1)∵∠BGE=∠ADE,∠BGE=∠CGF,∴∠ADE=∠CGF,∵AC⊥BD、BF⊥CD,∴∠ADE+∠DAE=∠CGF+∠GCF,∴∠DAE=∠GCF,∴AD=CD;(2)设DE=a,则AE=2DE=2a,EG=DE=a,∴S△ADE=AE•DE=•2a•a=a2,∵BH是△ABE的中线,∴AH=HE=a,∵AD=CD、AC⊥BD,∴CE=AE=2a,则S=AC•DE=•(2a+2a)•a=2a2=2S△ADE;△ADC在△ADE和△BGE中,∵,∴△ADE≌△BGE(ASA),∴BE=AE=2a,=AE•BE=•(2a)•2a=2a2,∴S△ABES△ACE=CE•BE=•(2a)•2a=2a2,S△BHG=HG•BE=•(a+a)•2a=2a2,综上,面积等于△ADE面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG.【点评】本题主要考查全等三角形的判定与性质,解题的关键是掌握等腰三角形的判定与性质及全等三角形的判定与性质.25.(10.00分)春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜.若购买8个A型放大镜和5个B型放大镜需用220元;若购买4个A型放大镜和6个B型放大镜需用152元.(1)求每个A型放大镜和每个B型放大镜各多少元;(2)春平中学决定购买A型放大镜和B型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A型放大镜?【分析】(1)设每个A型放大镜和每个B型放大镜分别为x元,y元,列出方程组即可解决问题;(2)由题意列出不等式求出即可解决问题.【解答】解:(1)设每个A型放大镜和每个B型放大镜分别为x元,y元,可得:,解得:,答:每个A型放大镜和每个B型放大镜分别为20元,12元;(2)设购买A型放大镜m个,根据题意可得:20a+12×(75﹣a)≤1180,解得:x≤35,答:最多可以购买35个A型放大镜.【点评】本题考查二元一次方程组的应用、一元一次不等式的应用等知识,解题的关键是理解题意,列出方程组和不等式解答.26.(10.00分)已知:⊙O是正方形ABCD的外接圆,点E在上,连接BE、DE,点F在上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.(1)如图1,求证:∠CBE=∠DHG;(2)如图2,在线段AH上取一点N(点N不与点A、点H重合),连接BN交DE于点L,过点H作HK∥BN交DE于点K,过点E作EP⊥BN,垂足为点P,当BP=HF时,求证:BE=HK;(3)如图3,在(2)的条件下,当3HF=2DF时,延长EP交⊙O于点R,连接BR,若△BER的面积与△DHK的面积的差为,求线段BR的长.【分析】(1)由正方形的四个角都为直角,得到两个角为直角,再利用同弧所对的圆周角相等及角平分线定义,等量代换即可得证;(2)如图2,过H作HM⊥KD,垂足为点M,根据题意确定出△BEP≌△HKM,利用全等三角形对应边相等即可得证;(3)根据3HF=2DF,设出HF=2a,DF=3a,由角平分线定义得到一对角相等,进而得到正切值相等,表示出DM=3a,利用正方形的性质得到△BED≌△DFB,得到BE=DF=3a,过H作HS⊥BD,垂足为S,根据△BER的面积与△DHK的面积的差为,求出a的值,即可确定出BR的长.【解答】(1)证明:如图1,∵四边形ABCD是正方形,∴∠A=∠ABC=90°,∵∠F=∠A=90°,∴∠F=∠ABC,∵DA平分∠EDF,∴∠ADE=∠ADF,∵∠ABE=∠ADE,∴∠ABE=∠ADF,∵∠CBE=∠ABC+∠ABE,∠DHG=∠F+∠ADF,∴∠CBE=∠DHG;(2)如图2,过H作HM⊥KD,垂足为点M,∵∠F=90°,∴HF⊥FD,∵DA平分∠EDF,∴HM=FH,∵FH=BP,∴HN=BP,∵KH∥BN,∴∠DKH=∠DLN,∴∠ELP=∠DLN,∴∠DKH=∠ELP,∵∠BED=∠A=90°,∴∠BEP+∠LEP=90°,∵EP⊥BN,∴∠BPE=∠EPL=90°,∴∠LEP+∠ELP=90°,∴∠BEP=∠ELP=∠DKH,∵HM⊥KD,∴∠KMH=∠BPE=90°,∴△BEP≌△HKM,∴BE=HK;(3)解:如图3,连接BD,∵3HF=2DF,BP=FH,∴设HF=2a,DF=3a,∴BP=FH=2a,由(2)得:HM=BP,∠HMD=90°,∵∠F=∠A=90°,∴tan∠HDM=tan∠FDH,∴==,∴DM=3a,∵四边形ABCD为正方形,∴AB=AD,∴∠ABD=∠ADB=45°,∵∠ABF=∠ADF=∠ADE,∠DBF=45°﹣∠ABF,∠BDE=45°﹣∠ADE,∴∠DBF=∠BDE,∵∠BED=∠F,BD=BD,∴△BED≌△DFB,∴BE=FD=3a,过H作HS⊥BD,垂足为S,∵tan∠ABH=tan∠ADE==,∴设AB=3m,AH=2m,∴BD=AB=6m,DH=AD﹣AH=m,∵sin∠ADB==,∴HS=m,∴DS==m,∴BS=BD﹣DS=5m,∴tan∠BDE=tan∠DBF==,∵∠BDE=∠BRE,∴tanBRE==,∵BP=FH=2a,∴RP=10a,在ER上截取ET=DK,连接BT,由(2)得:∠BEP=∠HKD,∴△BET≌△HKD,∴∠BTE=∠KDH,∴tan∠BTE=tan∠KDH,∴=,即PT=3a,∴TR=RP﹣PT=7a,∵S△BER﹣S△DHK=,∴BP•ER﹣HM•DK=,∴BP•(ER﹣DK)=BP•(ER﹣ET)=,∴×2a×7a=,解得:a=(负值舍去),∴BP=1,PR=5,则BR==.【点评】此题属于圆综合题,涉及的知识有:正方形的性质,角平分线性质,全等三角形的判定与性质,三角形的面积,锐角三角函数定义,熟练掌握各自的性质是解本题的关键.27.(10.00分)已知:在平面直角坐标系中,点O为坐标原点,点A在x轴的负半轴上,直线y=﹣x+与x轴、y轴分别交于B、C两点,四边形ABCD为菱形.(1)如图1,求点A的坐标;(2)如图2,连接AC,点P为△ACD内一点,连接AP、BP,BP与AC交于点G,且∠APB=60°,点E在线段AP上,点F在线段BP上,且BF=AE,连接AF、EF,若∠AFE=30°,求AF2+EF2的值;(3)如图3,在(2)的条件下,当PE=AE时,求点P的坐标.【分析】(1)利用勾股定理求出BC的长即可解决问题;(2)如图2中,连接CE、CF.想办法证明△CEF是等边三角形,AF⊥CF即可解决问题;(3)如图3中,延长CE交FA的延长线于H,作PQ⊥AB于Q,PK⊥OC于K,在BP 设截取BT=PA,连接AT、CT、CF、PC.想办法证明△APF是等边三角形,AT⊥PB即可解决问题;【解答】解:(1)如图1中,∵y=﹣x+,∴B(,0),C(0,),∴BO=,OC=,在Rt△OBC中,BC==7,∵四边形ABCD是菱形,∴AB=BC=7,∴OA=AB﹣OB=7﹣=,∴A(﹣,0).(2)如图2中,连接CE、CF.∵OA=OB,CO⊥AB,∴AC=BC=7,∴AB=BC=AC,∴△ABC是等边三角形,∴∠ACB=60°,∵∠AOB=60°,∴∠APB=∠ACB,∵∠PAG+∠APB=∠AGB=∠CBG+∠ACB,∴∠PAG=∠CBG,∵AE=BF,∴△ACR≌△BCF,∴CE=CF,∠ACE=∠BCF,∴∠ECF=∠ACF+∠ACE=∠ACF+∠BCF=∠ACB=60°,∴△CEF是等边三角形,∴∠CFE=60°,EF=FC,∵∠AFE=30°,∴∠AFC=∠AFE+∠CFE=90°,在Rt△ACF中,AF2+CF2=AC2=49,∴AF2+EF2=49.(3)如图3中,延长CE交FA的延长线于H,作PQ⊥AB于Q,PK⊥OC于K,在BP 设截取BT=PA,连接AT、CT、CF、PC.∵△CEF是等边三角形,∴∠CEF=60°,EC=CF,∵∠AFE=30°,∠CEF=∠H+∠EFH,∴∠H=∠CEF﹣∠EFH=30°,∴∠H=∠EFH,∴EH=EF,∴EC=EH,∵PE=AE,∠PEC=∠AEH,∴△CPE≌△HAE,∴∠PCE=∠H,∴PC∥FH,∵∠CAP=∠CBT,AC=BC,∴△ACP≌△BCT,∴CP=CT,∠ACP=∠BCT,∴∠PCT=∠ACB=60°,∴△CPT是等边三角形,∴CT=PT,∠CPT=∠CTP=60°,∵CP∥FH,∴∠HFP=∠CPT=60°,∵∠APB=60°,∴△APF是等边三角形,∴∠CFP=∠AFC﹣∠∠AFP=30°,∴∠TCF=∠CTP﹣∠TFC=30°,∴∠TCF=∠TFC,∴TF=TC=TP,∴AT⊥PF,设BF=m,则AE=PE=m,∴PF=AP=2m,TF=TP=m,TB=2m,BP=3m,在Rt△APT中,AT==m,在Rt△ABT中,∵AT2+TB2=AB2,∴(m)2+(2m)2=72,解得m=或﹣(舍弃),∴BF=,AT=,BP=3,sin∠ABT==,∵OK=PQ=BP•sin∠PBQ=3×=3,BQ==6,∴OQ=BQ﹣BO=6﹣=,∴P(﹣,3)【点评】本题考查一次函数综合题、等边三角形的判定和性质、全等三角形的判定和性质、勾股定理、菱形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会构建方程解决问题,属于中考压轴题.。
哈尔滨市69中2018年七年级下期中数学试卷(含答案)

2017—2018学年度(下)69中学七年级期中数学测试一、选择题(每题3分,共计30分) 1.-2-等于( )A.-2B.21C.2D. 21 2.下列计算中正确的是( )A.325a b ab +=B.235325a a a +=C.54xy xy xy -= D .532x x -= 3.单项式323z xy π-的系数和次数分别是( )A. 3π,6B. 3,7C. -3π,6D. -3,74.下列各式:52x +,2xy -,0.1,3a ,x2,122-+y x ,其中单项式有( ) A. 2个 B. 3个 C. 4个 D. 5个5.下面简单几何体的主.视图(正面看)是 ( )6.已知2y 32x 和32m x y - 是同类项,则m的值是( )A.1B.2C.3D.47、若21(2)02x y -++=,则2015()xy 的值为( ) A. -1 B. 1 C. -2015 D. 20158.下列正确的是( )A. 若b a =,则b a =B. 若22b a =,则b a =10.已知数轴上有P 、Q 两点,点P 与点Q 的距离为3,点P 与原点O 的距离为2,则所有满足条件的点Q 与原点O 的距离之和为( ) A. 0 B. 5 C. 6 D. 12二、填空题(每题3分,共计30分)11.地球上的海洋面积约为361000000平方千米,361000000这个数用科学记数法可表示为__________________.12.用四舍五入法将3.836精确到0.01,所得的近似数为_____________.13.比较大小:-54 _____ -32 14.两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是60km/h ,水流速度是a km/h ,4h 后甲船比乙船多航行___________km.15.一个两位数,个位上的数是a ,十位上的数比个位上的数大3,这个两位数__________.A .B .C .D .16.若x-2y=3,则6-2x+4y=____________.17.多项式1)2(32++-x m y x m是一个四次二项式,那么m =__________.18. 若m 、n 互为相反数(m 、n 都不为0),x 、y 互为倒数,3=z ,则=-+-+2522z xy nm n m _______________. 19.已知6=x ,92=y ,且x y y x -=-,则=-y x ________________. 20.观察下列等式12-02=1+0=1 22-12=2+1=3 32-22=3+2=5 42-32=4+3=7 52-42=5+4=9 ……若字母n 表示自然数,请把你观察到的规律用含字母n 的等式表示出来___________________三、解答题(第21题每题3分共计12分,第22题每题6分,第23题、24题每题7分,第25题每题8分,第26、27题每题10分,共计60分)21、(1)()()231224⨯÷-+- (2)131486412⎛⎫⨯ ⎪⎝⎭-+-(-)(3)223247x x x x -+- (4)22225(3)2(7)a b ab a b ab ---22.计算.(1) 4×(-3)2-13+|(-12)|(2)23.先化简,再求值:2222)232(243y x y x xy xy y x --+-,其中3=x ,31-=y .23100)32(9425)1(-⨯-÷-⨯-24.某商店有一种商品每件成本a 元,原来按成本每件增加b 元定出售价,销售70件后,由于库存积压,降价打“八折”出售,又销售80件.(1)该商店销售150件这种商品的总售价为多少元?(2)销售150件这种商品共盈利多少元?25、 有理数a 、b 、c 在数轴上对应点的位置如图所示,化简:c b a b a a c ---+--.26.小亮房间窗户的窗帘如图(1)所示,它是由两个四分之一圆组成(半径相同)的.(1)用代数式表示窗户能射进阳光的面积: ;(结果保留π)(2)当23=a ,1=b 时,求窗户能射进阳光的面积是多少;(取π=3) (3)小亮又设计了如图(2)所示的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算,此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)27.已知数轴上点A 、点B 对应的数分别为-4、6,点P 为数轴上一动点,其对应的数为x.(1)若点P 到点A 的距离与点P 到点B 的距离相等,求x 的值;(2)若点E 以每秒5个单位长度的速度从点A 出发沿数轴向右运动,点F 以每秒2个单位长度的速度从点B 出发沿数轴向右运动,求点E 、点F 同时出发,几秒后点E 与点F 相距4个单位长度?(3)在(2)的条件下,点P 以每秒4个单位长度的速度从原点出发沿数轴向右运动,求点E 、点F 、点P 同时出发,几秒后点P 到点E 的距离与点P 到点F 的距离相等?选择题:ACCBC AACBD填空题:11、12、3.8413、14、8a15、11a+3016、017、-218、-319、-9或-3 20、21、(1)0 (2)-24 (3)(4)81061.3⨯〈1n 21n -1n 22+=++=+n n )(x 9-x 72223ab b a-备用图2 备用图122、(1)2123 (2)-3 23、原式=22-y x ,当x=3,y=31-时,原式=-1 24、(1)134a+134b(2)134b-16a25、a+2b 26、(1)(2)89 (3)是更大,大 27、(1)x=1 (2)t=2或314 (3)2或3108b -ab 2π16b 2π。
哈尔滨市2018-2019学年八年级下期中数学测试卷(附答案)

2018-2019学年黑龙江省哈尔滨市嵩山中学八年级(下)期中数学试卷(五四学制)一.选择题(每题3分,共30分)1.下列四组线段中,可以构成直角三角形的是()A.1、2、3 B.3、4、5 C.1、1、D.6、7、82.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是()A.60°B.90°C.120° D.45°3.若关于x的方程(m﹣1)x2+mx﹣1=0是一元二次方程,则m的取值范围是()A.m≠1 B.m=1 C.m≥1 D.m≠04.用配方法解方程x2+8x+9=0,变形后的结果正确的是()A.(x+4)2=﹣7 B.(x+4)2=﹣9 C.(x+4)2=7 D.(x+4)2=255.下列不能判断四边形ABCD是平行四边形的是()A.AB=CD,AD=BC B.AB∥CD,AD=BC C.AB∥CD,AD∥BC D.∠A=∠C,∠B=∠D 6.在Rt△ABC中,∠C=90°,AB=15,AC:BC=3:4,则这个直角三角形的面积是()A.24 B.48 C.54 D.1087.如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的长度为()A.8cm B.6cm C.4cm D.2cm8.下列所给的方程中,没有实数根的是()A.x2+x=0 B.5x2﹣4x﹣1=0 C.3x2﹣4x+1=0 D.4x2﹣5x+2=09.如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(﹣2,0),则顶点C的坐标为()A.(4,3) B.(5,4) C.(6,4) D.(7,3)10.下列命题中正确的有()个.①直角三角形中两条直角边的平方和等于斜边的平方;②一组对边相等,一组对角相等的四边形是平行四边形;③两条对角线互相垂直的四边形是菱形;④三角形的中位线平行于三角形的第三边;⑤对角线相等且互相平分的四边形是矩形.A.2 B.3 C.4 D.5二、填空题(每题3分,共30分)11.命题“在同一个三角形中,等边对等角”的逆命题是,是(填“真命题”或“假命题”)12.方程x2=2x的根为.13.已知一个直角三角形的两条直角边分别为6cm、8cm,那么这个直角三角形斜边上的高为.14.在▱ABCD中,对角线AC、BD交于一点O,AB=11cm,△OCD的周长为27cm,则AC+BD= cm.15.如图,D,E,F分别是△ABC的AB,BC,CA边的中点.若△ABC的周长为20,则△DEF 的周长为.16.某药品原来每盒的售价为100元,由于两次降价,现在每盒81元,则平均每次降价的百分数为.17.如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=.18.参加足球联赛的每两队之间都进行两场比赛,共要比赛90场,共有个队参加比赛.19.矩形的一个内角平分线把矩形的一条边分成长为3和5两部分,则该矩形的面积是.20.如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,则EB=.三、解答题(21题8分,22、23题7分,24题8分,25、26、27题每题10分,共60分)21.用适当方法解下列方程(1)x2﹣7x﹣1=0(2)4x2+12x+9=81(3)4x2﹣4x+1=x2+6x+9(4)(x﹣4)2=(5﹣2x)2.22.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E 均在小正方形的顶点上.(1)在方格纸中画出以AB为一边的直角三角形ABC,点C在小正方形的顶点上,且△ABC的面积为5;(2)在方格纸中画出以DE为一边的锐角等腰三角形DEF,点F在小正方形的顶点上,且△DEF 的面积为10.连接CF,请直接写出线段CF的长.23.如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O与AD、BC分别相交于点E、F,求证:OE=OF.24.已知,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E.(1)如图1,求证:四边形AMEN是菱形;(2)如图2,连接AC在不添加任何辅助线的情况下,请直接写出面积相等的四边形.25.百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.(1)现在每件童装降价5元,那么每天可售出多少件,每天可盈利多少元?(2)要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?26.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证:(1)AC=EF;(2)四边形ADFE是平行四边形;(3)AC⊥DF.27.已知:如图1,在平面直角坐标系中,点O为坐标原点,点A在x轴正半轴上,点C在第一象限,且∠COA=60°,以OA、OC为邻边作菱形OABC,且菱形OABC的面积为18.(1)求B、C两点的坐标;(2)动点P从C点出发沿射线CB匀速运动,同时动点Q从A点出发沿射线BA的方向匀速运动,P、Q两点的运动速度均为2个单位/秒,连接PQ和AC,PQ和AC所在直线交于点D,点E为线段BQ的中点,连接DE,设动点P、Q的运动时间为t,请将△DQE的面积S用含t的式子表示,并直接写出t的取值范围;(3)在(2)的条件下,过点Q作QF⊥y轴于点F,当t为何值时,以P、B、F、Q为顶点的四边形为平行四边形?2018-2019学年黑龙江省哈尔滨市嵩山中学八年级(下)期中数学试卷(五四学制)参考答案与试题解析一.选择题(每题3分,共30分)1.下列四组线段中,可以构成直角三角形的是()A.1、2、3 B.3、4、5 C.1、1、D.6、7、8【考点】勾股定理的逆定理.【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,这个就是直角三角形.【解答】解:A、∵12+22≠32,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角形;B、∵32+42=52,∴该三角形符合勾股定理的逆定理,故可以构成直角三角形;C、∵12+12≠()2,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角形;D、∵62+72≠82,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角形.故选B.2.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是()A.60°B.90°C.120° D.45°【考点】平行四边形的性质.【分析】首先设平行四边形中两个内角的度数分别是x°,2x°,由平行四边形的邻角互补,即可得方程x+2x=180,继而求得答案.【解答】解:设平行四边形中两个内角的度数分别是x°,2x°,则x+2x=180,解得:x=60,∴其中较小的内角是:60°.故选A.3.若关于x的方程(m﹣1)x2+mx﹣1=0是一元二次方程,则m的取值范围是()A.m≠1 B.m=1 C.m≥1 D.m≠0【考点】一元二次方程的定义.【分析】根据一元二次方程的定义可得m﹣1≠0,再解即可.【解答】解:由题意得:m﹣1≠0,解得:m≠1,故选:A.4.用配方法解方程x2+8x+9=0,变形后的结果正确的是()A.(x+4)2=﹣7 B.(x+4)2=﹣9 C.(x+4)2=7 D.(x+4)2=25【考点】解一元二次方程﹣配方法.【分析】方程移项后,利用完全平方公式配方即可得到结果.【解答】解:方程x2+8x+9=0,整理得:x2+8x=﹣9,配方得:x2+8x+16=7,即(x+4)2=7,故选C5.下列不能判断四边形ABCD是平行四边形的是()A.AB=CD,AD=BC B.AB∥CD,AD=BC C.AB∥CD,AD∥BC D.∠A=∠C,∠B=∠D【考点】平行四边形的判定.【分析】直接根据平行四边形的判定定理判断即可.【解答】解:平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.∴C能判断,平行四边形判定定理1,两组对角分别相等的四边形是平行四边形;∴D能判断;平行四边形判定定理2,两组对边分别相等的四边形是平行四边形;∴A能判定;平行四边形判定定理3,对角线互相平分的四边形是平行四边形;平行四边形判定定理4,一组对边平行相等的四边形是平行四边形;故选B.6.在Rt△ABC中,∠C=90°,AB=15,AC:BC=3:4,则这个直角三角形的面积是()A.24 B.48 C.54 D.108【考点】勾股定理.【分析】设AC=3x,则BC=4x,然后根据勾股定理得到AC2+BC2=AB2,求出x2的值,继而根据三角形的面积公式求出答案.【解答】解:设AC=3x,则BC=4x,根据勾股定理有AC2+BC2=AB2,即(3x)2+(4x)2=152,得:x2=9,则△ABC的面积=×3x×4x=6x2=54.故选:C.7.如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的长度为()A.8cm B.6cm C.4cm D.2cm【考点】矩形的性质.【分析】根据矩形的性质、等边三角形的判定只要证明△DOC是等边三角形即可解决问题.【解答】解:∵四边形ABD是矩形,∴BD=AC,OA=OC,OB=OD,∵BD=8cm,∴OD=4cm,∵∠DOC=∠AOB=60°,∴△DOC是等边三角形,∴CD=OD=4cm,故选C.8.下列所给的方程中,没有实数根的是()A.x2+x=0 B.5x2﹣4x﹣1=0 C.3x2﹣4x+1=0 D.4x2﹣5x+2=0【考点】根的判别式.【分析】分别计算出判别式△=b2﹣4ac的值,然后根据△的意义分别判断即可.【解答】解:A、△=12﹣4×1×0=1>0,所以方程有两个不相等的实数根;B、△=(﹣4)2﹣4×5×(﹣1)=36>0,所以方程有两个不相等的实数根;C、△=(﹣4)2﹣4×3×1=4>0,所以方程有两个不相等的实数根;D、△=(﹣5)2﹣4×4×2=﹣7<0,所以方程没有实数根.故选D.9.如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(﹣2,0),则顶点C的坐标为()A.(4,3) B.(5,4) C.(6,4) D.(7,3)【考点】菱形的性质;坐标与图形性质.【分析】过点C作x轴的垂线,垂足为E,由面积可求得CE的长,在Rt△BCE中可求得BE的长,可求得AE,结合A点坐标可求得AO,可求出OE,可求得C点坐标.【解答】解:如图,过点C作x轴的垂线,垂足为E,=20,∵S菱形ABCD∴AB•CE=20,即5CE=20,∴CE=4,在Rt△BCE中,BC=AB=5,CE=4,∴BE=3,∴AE=AB+BE=5+3=8.又∵A(﹣2,0),∴OA=2,∴OE=AE﹣OA=8﹣2=6,∴C(6,4),故选C.10.下列命题中正确的有()个.①直角三角形中两条直角边的平方和等于斜边的平方;②一组对边相等,一组对角相等的四边形是平行四边形;③两条对角线互相垂直的四边形是菱形;④三角形的中位线平行于三角形的第三边;⑤对角线相等且互相平分的四边形是矩形.A.2 B.3 C.4 D.5【考点】命题与定理.【分析】①由勾股定理判定;②直接利用全等三角形的判定与性质以及利用平行四边形的性质求出即可;【解答】解:①直角三角形中两条直角边的平方和等于斜边的平方,故①正确;②一组对边相等,一组对角相等的四边形不一定是平行四边形,所以②错误;③对角线互相垂直的平行四边形是菱形,所以③错误;④三角形的中位线平行于三角形的第三边,且等于第三边的一半,所以④正确;⑤对角线相等且互相平分的四边形是矩形,⑤正确;故选B.二、填空题(每题3分,共30分)11.命题“在同一个三角形中,等边对等角”的逆命题是在同一个三角形中,等角对等边,是真(填“真命题”或“假命题”)【考点】命题与定理.【分析】把一个命题的条件和结论互换就得到它的逆命题,再分析题设是否能推出结论,从而得出命题的真假.【解答】解:“在同一个三角形中,等边对等角”的逆命题是:“在同一个三角形中”,等角对等边,是真命题;故答案为:“在同一个三角形中,等角对等边;真.12.方程x2=2x的根为x1=0,x2=2.【考点】解一元二次方程﹣因式分解法.【分析】移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.【解答】解:x2=2x,x2﹣2x=0,x(x﹣2)=0,x=0,或x﹣2=0,x1=0,x2=2,故答案为:x1=0,x2=2.13.已知一个直角三角形的两条直角边分别为6cm、8cm,那么这个直角三角形斜边上的高为4.8cm.【考点】勾股定理.【分析】根据勾股定理可求出斜边.然后由于同一三角形面积一定,可列方程直接解答.【解答】解:∵直角三角形的两条直角边分别为6cm,8cm,∴斜边为=10(cm),设斜边上的高为h,则直角三角形的面积为×6×8=×10h,解得:h=4.8cm,这个直角三角形斜边上的高为4.8cm.故答案为:4.8cm.14.在▱ABCD中,对角线AC、BD交于一点O,AB=11cm,△OCD的周长为27cm,则AC+BD= 32cm.【考点】平行四边形的性质.【分析】首先由平行四边形的性质可求出CD的长,由条件△OCD的周长为27,即可求出OD+OC 的长,再根据平行四边的对角线互相平分即可求出平行四边形的两条对角线的和.【解答】解:∵四边形ABCD是平行四边形,∴AB=CD=11cm,OA=OC,OB=OD,∵△OCD的周长为27cm,∴OD+OC=27﹣11=16cm,∵BD=2DO,AC=2OC,∴BD+AC=2(OD+OC)=32cm,故答案为:32.15.如图,D,E,F分别是△ABC的AB,BC,CA边的中点.若△ABC的周长为20,则△DEF 的周长为10.【考点】三角形中位线定理.【分析】根据三角形的中位线定理,可得△ABC的各边长为△DEF的各边长的2倍,从而得出△DEF的周长即可.【解答】解:∵点D、E、F分别是△A BC三边的中点,∴AB=2EF,AC=2DE,BC=2DF,∵AB+AC+BC=20,∴DE+EF+DF=10,故答案为10.16.某药品原来每盒的售价为100元,由于两次降价,现在每盒81元,则平均每次降价的百分数为10%.【考点】一元二次方程的应用.【分析】设平均每次降价的百分率为x,那么第一次降价后的单价是原来的(1﹣x),那么第二次降价后的单价是原来的(1﹣x)2,根据题意列方程解答即可.【解答】解:设平均每次降价的百分率为x,根据题意列方程得100×(1﹣x)2=81解得x1=0.1=10%,x2=1.9(不符合题意,舍去),故答案为:10%.17.如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=6.【考点】勾股定理;翻折变换(折叠问题).【分析】设BC=x,AF可用含x的式子表示,CF可以根据勾股定理求出,然后用x表示出BF,在Rt△ABF中,利用勾股定理,可建立关于x的方程,即可得出BF的长.【解答】解:由折叠的性质知:AD=AF,DE=EF=8﹣3=5;在Rt△CEF中,EF=DE=5,CE=3,由勾股定理可得:CF=4,若设AD=AF=x,则BC=x,BF=x﹣4;在Rt△ABF中,由勾股定理可得:82+(x﹣4)2=x2,解得x=10,故BF=x﹣4=6.故答案为:6.18.参加足球联赛的每两队之间都进行两场比赛,共要比赛90场,共有10个队参加比赛.【考点】一元二次方程的应用.【分析】设共有x个队参加比赛,根据每两队之间都进行两场比赛结合共比了90场即可得出关于x的一元一次方程,解之即可得出结论.【解答】解:设共有x个队参加比赛,根据题意得:2×x(x﹣1)=90,整理得:x2﹣x﹣90=0,解得:x=10或x=﹣9(舍去).故答案为:10.19.矩形的一个内角平分线把矩形的一条边分成长为3和5两部分,则该矩形的面积是24或40.【考点】矩形的性质.【分析】矩形的四个角都是直角,内角平分线,可组成等腰直角三角形,因此矩形的宽可有两种情况.【解答】解:∵矩形的一个内角平分线把矩形的一条边分成长为3和5两部分,∴矩形的长为8,宽为5或3.∴面积为40或24.故答案为:40或24.20.如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,则EB=.【考点】全等三角形的判定与性质.【分析】如图,作DM⊥AC于M,DN⊥AB于N.首先证明Rt△DMC≌Rt△DNB,推出CM=BN,△ADM≌△ADN,推出AM=AB,再证明DE∥AC,推出∠ADE=∠CAD=∠DAB=30°,推出AE=DE,推出∠DEN=60°,在Rt△ADN中,可得DN=AN•tan30°=,在Rt△EDN中,可得DE=DN÷cos30°=,由此即可解决问题.【解答】解:如图,作DM⊥AC于M,DN⊥AB于N.∵∠CAD=∠BAD=30°,DM⊥AC于M,DN⊥AB于N,∴DN=DM,在Rt△DMC和Rt△DNB中,,∴Rt△DMC≌Rt△DNB,∴CM=BN,同理可证△ADM≌△ADN,∴AM=AB,∴AC+AB=AM+CM+AN﹣BN=2AM=8,∴AM=AN=4,∵∠DCM=∠DBN,∴∠1=∠2,∵∠CDE=∠2,∴∠1=∠CDE,∴DE∥AC,∴∠ADE=∠CAD=∠DAB=30°,∴AE=DE,∴∠DEN=60°,在Rt△ADN中,DN=AN•tan30°=,在Rt△EDN中,DE=DN÷cos30°=,∴AE=,∴EB=AB﹣AE=3﹣=.故答案为.三、解答题(21题8分,22、23题7分,24题8分,25、26、27题每题10分,共60分)21.用适当方法解下列方程(1)x2﹣7x﹣1=0(2)4x2+12x+9=81(3)4x2﹣4x+1=x2+6x+9(4)(x﹣4)2=(5﹣2x)2.【考点】解一元二次方程﹣因式分解法;解一元二次方程﹣配方法;解一元二次方程﹣公式法.【分析】(1)公式法求解可得;(2)直接开平方法求解可得;(3)直接开平方法求解可得;(4)直接开平方法求解可得.【解答】解:(1)∵a=1,b=﹣7,c=﹣1,∴△=49﹣4×1×(﹣1)=53>0,∴x=;(2)∵(2x+3)2=81,∴2x+3=9或2x+3=﹣9,解得:x=3或x=﹣6;(3)∵(2x﹣1)2=(x+3)2,∴2x﹣1=x+3或2x﹣1=﹣x﹣3,解得:x=4或x=﹣;(4)∵x﹣4=5﹣2x或x﹣4=2x﹣5,解得:x=3或x=1.22.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E 均在小正方形的顶点上.(1)在方格纸中画出以AB为一边的直角三角形ABC,点C在小正方形的顶点上,且△ABC的面积为5;(2)在方格纸中画出以DE为一边的锐角等腰三角形DEF,点F在小正方形的顶点上,且△DEF 的面积为10.连接CF,请直接写出线段CF的长.【考点】作图—应用与设计作图;等腰三角形的性质;勾股定理.【分析】(1)直接利用旋转的性质得出对应点位置,进而得出答案;(2)利用等腰三角形的性质得出对应点位置进而结合勾股定理得出答案.【解答】解:(1)如图所示:△ABC即为所求;(2)如图所示:△DFE,即为所求;CF==.23.如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O与AD、BC分别相交于点E、F,求证:OE=OF.【考点】平行四边形的性质;全等三角形的判定与性质.【分析】要证明线段相等,只需证明两条线段所在的两个三角形全等即可.【解答】证明:∵ABCD为平行四边形,∴AD∥BC,OA=OC,∴∠EAO=∠FCO,∠AEO=∠CFO,∴△AEO≌△CFO(AAS),∴OE=OF.24.已知,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E.(1)如图1,求证:四边形AMEN是菱形;(2)如图2,连接AC在不添加任何辅助线的情况下,请直接写出面积相等的四边形.【考点】菱形的判定与性质.【分析】(1)由MG∥AD,NF∥AB,可证得四边形AMEN是平行四边形,又由四边形ABCD是菱形,BM=DN,可得AM=AN,即可证得四边形AMEN是菱形;=S△AEN,S△CEF=S△CEG,S△ABC=S△ADC,继而求得答案.(2)易得四边形CGEF是菱形;即可得S△AEM【解答】(1)证明:∵MG∥AD,NF∥AB,∴四边形AMEN是平行四边形,∵四边形ABCD是菱形,∴AB=AD,∵BM=DN,∴AB﹣BM=AD﹣DN,∴AM=AN,∴四边形AMEN 是菱形;(2)解:∵四边形AMEN 是菱形,∴S △AEM =S △AEN ,同理:四边形CGEF 是菱形,∴S △CEF =S △CEG ,∵四边形ABCD 是菱形,∴S △ABC =S △ADC ,∴S 四边形MBFE =S 四边形DNEG ,S 四边形MBCE =S 四边形DNEC ,S 四边形MBCG =S 四边形DNFC ,S 四边形ABFE =S 四边形ADGE ,S 四边形ABFN =S 四边形ADGM .25.百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.(1)现在每件童装降价5元,那么每天可售出多少件,每天可盈利多少元?(2)要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?【考点】一元二次方程的应用.【分析】(1)根据每件童装降价1元,平均每天就可多售出2件,得出每件童装降价5元,每天可售出20+5×2=30件,再根据每件盈利40元,即可得出每天的盈利;(2)设每件应降价x 元,每天可以多销售的数量为2x 件,每件的利润为(40﹣x ),由总利润=每件的利润×数量建立方程求出其解即可.【解答】解:(1)∵每件童装降价1元,平均每天就可多售出2件,∴每件童装降价5元,每天可售出20+5×2=30件;∴每天可盈利:(40﹣5)×30=1050(元);(2)设每件应降价x 元,由题意,得(40﹣x )(20+2x )=1200,解得:x 1=10,x 2=20,∴为增大销量,减少库存,∴每件童装应降价20元.26.如图,分别以Rt △ABC 的直角边AC 及斜边AB 向外作等边△ACD ,等边△ABE .已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证:(1)AC=EF;(2)四边形ADFE是平行四边形;(3)AC⊥DF.【考点】平行四边形的判定与性质;全等三角形的判定与性质;等边三角形的性质.【分析】(1)首先Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又因为△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后即可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF;(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF ⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形;(3)先求∠EAC=90°,由▱ADFE得AE∥DF,可以得∠AGD=90°,则AC⊥DF.【解答】证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC,又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF,AB=AE,∴AF=BC,在Rt△AFE和Rt△BCA中,∵,∴△AFE≌△BCA(HL),∴AC=EF;(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°又∵EF⊥AB,∴EF∥AD,∵AC=EF,AC=AD,∴EF=AD,∴四边形ADFE是平行四边形;(3)∵∠EAC=∠EAF+∠BAC=60°+30°=90°,∵四边形ADFE是平行四边形,∴AE∥FD,∴∠EAC=∠AGD=90°,∴AC⊥DF.27.已知:如图1,在平面直角坐标系中,点O为坐标原点,点A在x轴正半轴上,点C在第一象限,且∠COA=60°,以OA、OC为邻边作菱形OABC,且菱形OABC的面积为18.(1)求B、C两点的坐标;(2)动点P从C点出发沿射线CB匀速运动,同时动点Q从A点出发沿射线BA的方向匀速运动,P、Q两点的运动速度均为2个单位/秒,连接PQ和AC,PQ和AC所在直线交于点D,点E为线段BQ的中点,连接DE,设动点P、Q的运动时间为t,请将△DQE的面积S用含t的式子表示,并直接写出t的取值范围;(3)在(2)的条件下,过点Q作QF⊥y轴于点F,当t为何值时,以P、B、F、Q为顶点的四边形为平行四边形?【考点】四边形综合题.【分析】(1)如图1,过点C作CD⊥OA于点D,解直角三角形求出OD、CD的长即可解决问题.(2)分两种情形讨论即可①如图2中,当0≤t≤3时.②如图3中,当t>3时.分别想办法构建方程即可解决问题.(3)分三种情形①如图4中,当0≤t≤3时.②当t>3时,由PB=QF时.③当点Q在y轴左侧时,构建PB=QF构建方程即可解决问题.【解答】解:(1)如图1,过点C作CD⊥OA于点D,设菱形OABC的边长为x,则OA=OC=BC=x,∵∠COA=60°,∴CD=OC•sin60°=x,∵菱形OABC的面积为18,∴x•x=18,解得:x=±6,∴OA=OC=BC=6,∴CD=6×=3,OD=OC•cos60°=3,∴点C的坐标为:(3,3),点B的坐标为:(9,3);(2)①如图2中,当0≤t≤3时,作PK∥AB交AC于K,则△PCK是等边三角形.作DH⊥AB 于H.∵PK=PC=AQ,∠PDK=∠ADQ,∠KPD=∠DQA,∴△PDK≌△QDA,∴DK=AD=(6﹣2t)=3﹣t,DH=AD•sin60°=(3﹣t),EQ=BQ=(6+2t)=3+t,∴S=•QE•DH=﹣t2+.②如图3中,当t>3时,作PK∥AB交AC于K,则△PCK是等边三角形.作DH⊥AB于H.由△PDK≌△QDA,∴DK=AD=(2t﹣6)=t﹣3,DH=AD•sin60°=(t﹣3),EQ=BQ=(6+2t)=3+t,∴S=•QE•DH=t2﹣.综上所述,S=.(3)①如图4中,当0≤t≤3时,作QK⊥OA于K.则AK=t,FQ=OK=6﹣t,当PB=FQ时,四边形PBQF是平行四边形,∴6﹣2t=6﹣t,解得t=0.②当t>3时,由PB=QF时,2t﹣6=6﹣t,解得t=4,③当点Q在y轴左侧时,由PB=QF可得,t﹣6=2t﹣6,解得t=0,此种情形不存在.综上所述,当t=0或4s时,以P、B、F、Q为顶点的四边形为平行四边形.2017年5月17日。
2018年黑龙江省哈尔滨市中考数学试题及参考答案案
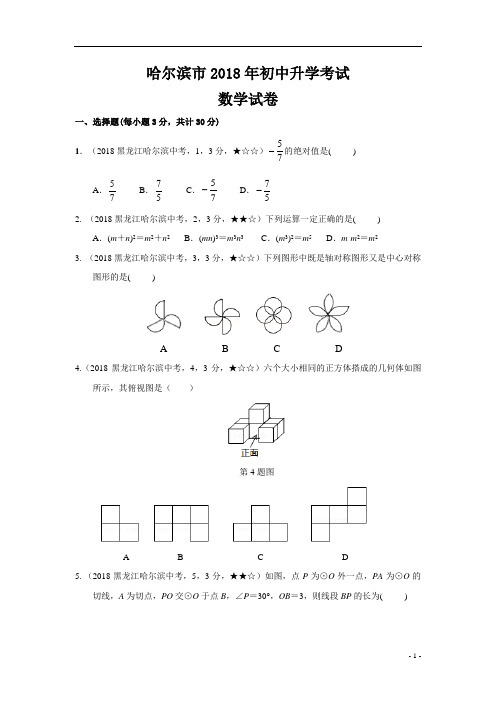
哈尔滨市2018年初中升学考试数学试卷 一、选择题(每小题3分,共计30分)1.(2018黑龙江哈尔滨中考,1,3分,★☆☆)75-的绝对值是( ) A .75 B .57 C .75- D .57- 2. (2018黑龙江哈尔滨中考,2,3分,★★☆)下列运算一定正确的是( )A .(m +n )2=m 2+n 2B .(mn )3=m 3n 3C .(m 3)2=m 5D .m ·m 2=m 23. (2018黑龙江哈尔滨中考,3,3分,★☆☆)下列图形中既是轴对称图形又是中心对称图形的是( )A B C D4.(2018黑龙江哈尔滨中考,4,3分,★☆☆)六个大小相同的正方体搭成的几何体如图所示,其俯视图是( )第4题图A B C D5. (2018黑龙江哈尔滨中考,5,3分,★★☆)如图,点P 为⊙O 外一点,PA 为⊙O 的切线,A 为切点,PO 交⊙O 于点B ,∠P =30°,OB =3,则线段BP 的长为( )第5题图A .3B .33C .6D .96. (2018黑龙江哈尔滨中考,6,3分,★☆☆)将抛物线y =-5x 2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )A .y =-5(x +1)2-1B .y =-5(x -1)2-1C .y =-5(x +1)2+3D .y =-5(x -1)2+37. (2018黑龙江哈尔滨中考,7,3分,★☆☆)方程3221+=x x 的解为( ) A .x = -1 B .x =0 C .x =53 D .x =1 8. (2018黑龙江哈尔滨中考,8,3分,★★☆)如图,在菱形ABCD 中,对角线AC 、BD相交于点O ,BD =8,tan ∠ABD =43,则线段AB 的长为( )第8题图A 7B .7C .5D .109. (2018黑龙江哈尔滨中考,9,3分,★☆☆)已知反比例函数y =xk 32-的图象经过点(1,1),则k 的值为( )A .-1B .0C .1D .210. (2018黑龙江哈尔滨中考,10,3分,★★☆)如图,在△ABC 中,点D 在BC 边上,连接AD ,点G 在线段AD 上,GE //BD ,且交AB 于点E ,GF ∥AC ,且交CD 于点F ,则下列结论一定正确的是( )第10题图A .AE AB =AD AG B .CF DF =AD DGC .AC FG =BDEG D .BE AE =DF CF 二、填空题(每小题3分,共计30分)11. (2018黑龙江哈尔滨中考,11,3分,★☆☆)将数920 000 000用科学记数法表示为_________________.12. (2018黑龙江哈尔滨中考,12,3分,★☆☆)函数y =45-x x 中,自变量x 的取值范围是_________________.13. (2018黑龙江哈尔滨中考,13,3分,★☆☆)把多项式x 3-25x 分解因式的结果是_________________.14. (2018黑龙江哈尔滨中考,14,3分,★☆☆)不等式组⎩⎨⎧--≥-1532512x x x >的解集为_________________.15. (2018黑龙江哈尔滨中考,15,3分,★☆☆)计算65-1051的结果是_________________.16. (2018黑龙江哈尔滨中考,16,3分,★☆☆)抛物线y =2(x +2)2+4的顶点坐标为_________________.17. (2018黑龙江哈尔滨中考,17,3分,★☆☆)一枚质地均匀的正方体骰子,骰子的六 个面上分别刻有1到6的点数.张兵同学掷一次骰子,骰子向上的一面出现的点数是3的倍数的概率是_________.18. (2018黑龙江哈尔滨中考,18,3分,★☆☆)一个扇形的圆心角为135°,弧长为3π cm ,则此扇形的面积是___________cm 2.19. (2018黑龙江哈尔滨中考,19,3分,★★☆)在△ABC 中,AB =AC ,∠BAC =100°,点D 在BC 边上,连接AD ,若△ABD 为直角三角形,则∠ADC 的度数为_________________.20. (2018黑龙江哈尔滨中考,20,3分,★★☆)如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,AB =OB ,点E 、点F 分别是OA 、OD 的中点,连接EF ,∠CEF =45°,EM ⊥BC 于点M ,EM 交BD 于点N ,FN =10,则线段BC 的长为_________________.第20题图三.解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)21.(2018黑龙江哈尔滨中考,21,7分,★★☆)先化简,再求代数式(121--a )÷42962-+-a a a 的值,其中a =4cos 30°+3tan 45°.22. (2018黑龙江哈尔滨中考,22,7分,★★☆)如图,方格纸中每个小正方形的边长均为1,线段AB 的两个端点均在小正方形的顶点上.(1)在图中画出以线段AB 为一边的矩形ABCD (不是正方形),且点C 和点D 均在小正方形的项点上;(2)在图中画出以线段AB 为一腰,底边长为22的等腰三角形ABE ,点E 在小正方形的顶点上.连接CE ,请直接写出线段CE 的长.第22题图23. (2018黑龙江哈尔滨中考,23,8分,★★☆)为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书祛、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图.请你根据图中提供的信息回答下列问题:(1)本次调查共抽取了多少名学生?(2)通过计算补全条形统计图;(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名.第23题图24.(2018黑龙江哈尔滨中考,24,8分,★★☆)已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点G,∠BGE =∠ADE.(1)如图1,求证:AD=CD;(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.第24题图25.(2018黑龙江哈尔滨中考,25,10分,★★☆)春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜.若购买8个A型放大镜和5个B 型放大镜雷用220元;若购买4个A型放大镜和6个B型放大镜需用152元.(1)求每个A 型放大镜和每个B 型放大镜各多少元;(2)春平中学决定购买A 型放大镜和B 型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A 型放大镜?26. (2018黑龙江哈尔滨中考,26,10分,★★★)已知:⊙O 是正方形ABCD 的外接圆,点E 在AB 上,连接BE 、DE ,点F 在AD 上,连接BF 、DF 、BF ,与DE 、DA 分别交于点G 、点H ,且DA 平分∠EDF .(1)如图1,求证:∠CBE =∠DHG ;(2)如图2,在线段AH 上取一点N (点N 不与点A 、点H 重合),连接BN 交DE 于点L ,过点H 作HK ∥BN 交DE 于点K ,过点E 作EP ⊥BN ,垂足为点P ,当BP =HF 时,求证:BE =HK ;(3)如图3,在(2)的条件下,当3HF =2DF 时,延长EP 交⊙O 于点R ,连接BR ,若△BER 的面积与△DHK 的面积的差为47,求线段BR 的长.第26题图27. (2018黑龙江哈尔滨中考,27,10分,★★★)已知:在平面直角坐标系中,点O 为坐标原点,点A 在x 轴的负半轴上,直线y =3 x +327与x 轴、y 轴分别交于B 、C 两点,四边形ABCD 为菱形.(1)如图1,求点A 的坐标;(2)如图2,连接AC ,点P 为△ACD 内一点,连接AP 、BP ,BP 与AC 交于点G ,且∠APB =60°,点E 在线段AP 上,点F 在线段BP 上,且BF =AF ,连接AF 、EF ,若∠AFE =30°,求AF 2+EF 2的值;(3)如图3,在(2)的条件下,当PE =AE 时,求点P 的坐标.第27题图哈尔滨市2018年初中升学考试数学试卷答案全解全析 1.答案:A解析:在数轴上,表示75-的点距离原点75个单位长度,根据绝对值的定义,75-的绝对值是75.故选:A. 考查内容:绝对值.命题意图:本题考查了绝对值的定义,难度较小.2.答案:B解析:根据完全平方公式,(m +n )2=m 2+2mn+n 2,选项A 错误;根据积的乘方性质,(mn )3=m 3n 3 ,选项B 正确;根据幂的乘方性质,(m 3)2=m 6,选项C 错误;根据同底数幂的乘法法则,m ·m 2=m 3,选项D 错误.故选:B.考查内容:同底数幂的乘法;幂的乘方与积的乘方;完全平方公式.命题意图:本题考查完全平方公式与幂的性质的识记,难度较小.易错警示:此类问题容易出错的地方是分不清各种运算的法则,对符号、底数、指数处理不当,特别容易混淆幂的运算性质,如:同底数幂的乘法是底数不变,指数相加;而幂的乘方是底数不变,指数相乘.3.答案:C解析:选项A既不是轴对称图形,也不是中心对称图形,选项B是中心对称图形,不是轴对称图形,选项D是轴对称图形,不是中心对图形.故选:C.考查内容:轴对称图形;中心对称图形.命题意图:本题考查了轴对称图形和中心对称图形的识别能力,难度较小.4.答案:B解析:根据俯视图定义,俯视图有3列,从左到右分别是2,1,2个正方形,故选B.考查内容:简单几何体的三视图.命题意图:本题考查学生的观察能力和对几何体三种视图的识别能力,难度较小.5.答案:A解析:如图,连接OA,则OA= OB=3.∵PA为⊙O的切线,∴∠OAP=90°.∵∠P=30°,∴OP=2OA=6,∴BP= OP﹣OB =6﹣3=3.故选A.考查内容:切线的性质;直角三角形30°角的性质.命题意图:本题考查添加辅助线进行圆的有关计算的能力,难度较小.6.答案:A解析:根据抛物线的平移规律:“左加右减,上加下减”,将抛物线y=﹣5x2+1向左平移1个单位长度,得到y=﹣5(x+1)2+1,再向下平移2个单位长度,得到y=﹣5(x+1)2+1﹣2,即y=﹣5(x+1)2﹣1,故选A.考查内容:抛物线的平移命题意图:本题考查抛物线平移规律的识记能力,难度较小.7.答案:D解析:去分母,得x+3=4x,解方程,得x=1.检验:当x=1时,2x(x+3)≠0,x=1是分式方程的解,故选D.考查内容:分式方程的解法.命题意图:本题考查解分式方程以及转化思想的渗透,注意验根.难度较小.8.答案:C解析:∵四边形ABCD 是菱形,∴AC ⊥BD ,AO=CO=12AC ,BO=OD=12BD=4,在Rt △ABO 中,∵tan ∠ABO =AO BO,∴344AO =,∴AO=3.∴,故选C.考查内容:菱形的性质;勾股定理;锐角三角函数. 命题意图:本题考查综合利用几何图形的性质计算的能力,难度中等.9.答案:D解析:∵反比例函数y=x k 32-的图象经过点(1,1),∴2311k -=,即2k ﹣3=1×1, 解得k=2,故选D .考查内容:反比例函数图象上点的坐标特征.命题意图:本题考查反比例函数图象上点的坐标特征,能根据已知得出关于k 的方程是解此题的关键,难度较小.10.答案:D解析:∵GE ∥BD , ∴BE AE =GD AG .∵GF ∥AC ,∴GD AG =DF CF ,∴BE AE =DF CF .故选:D. 考查内容:平行线分线段成比例定理.命题意图:本题考查利用平行线分线段成比例定理确定成比例线段的能力,难度较小.11.答案:9.2×108解析:科学记数法是写成±a ×10n 的形式,其中1≤a <10,n 为整数.此数为九位整数,所以n =8,a =9.2.考查内容:科学记数法命题意图:本题考查学生掌握科学记数法的表示方法的能力,难度小.12.答案:x ≠4解析:根据分母不为0时,分式有意义,得x ﹣4≠0,解得x≠4.考查内容:函数自变量的取值范围命题意图:本题考查学生根据函数关系式确定自变量的取值范围的能力,难度较小.13.答案:x (x +5)(x -5)解析:x 3﹣25x=x (x 2﹣25)=x (x+5)(x ﹣5).考查内容:多项式的因式分解.命题意图:本题考查学生掌握因式分解的方法和步骤的能力,难度较小.14.答案:3≤x <4解析:2152315x x x -≥⎧⎨->-⎩①②,解不等式①,得x≥3,解不等式②,得x <4, 根据“大小小大中间找”,得不等式组的解集为3≤x <4.考查内容:一元一次不等式组的解法.命题意图:本题考查学生解一元一次不等式组的能力,难度中等.15.答案:45解析:65-1051=65-10×55=65-25=45. 考查内容:二次根式的加减法命题意图:本题考查学生二次根式的性质以及运算能力,难度中等.16.答案:(-2,4)解析:由顶点式y =a (x -h )2+k 可知,y =2(x +2)2+4中h =-2,k =4,所以顶点坐标为(-2,4).考查内容:二次函数的函数表达式.命题意图:本题考查由二次函数的顶点式直接写出顶点坐标的能力,难度较小.17.答案:31 解析:掷一次骰子,向上的一面出现的点数是3的倍数的有3,6, 概率是26=31. 考查内容:概率公式.命题意图:本题考查利用概率公式求不确定事件的概率的能力,难度较小.18.答案:6π解析:设扇形的半径为Rcm ,由弧长公式,得135180R π⨯=3π,解得R=4, 所以扇形的面积为S=21354360π⨯=6π(cm 2). 考查内容:弧长的计算;扇形面积的计算.命题意图:本题考查利用扇形面积公式和弧长公式进行计算的能力,难度较小.一题多解:设扇形的半径为rcm ,由弧长公式,得135180r π⨯=3π,解得r=4,所以扇形的面积为S=12lr=12×3π×4=6π(cm2).19.答案:130°或90°.解析:△ABD为直角三角形,分两种情况考虑:①当∠ADB=90°时,如图1,∠ADC=180°﹣∠ADB=90°;②当∠BAD=90°时,如图2,在△ABC中,∵AB=AC,∠BAC=100°,∴∠B=∠C=1801002-=40°,∴∠ADC=∠BAD+∠B=90°+40°=130°.综合起来,∠ADC的度数为90°或130°.考查内容:等腰三角形的性质;三角形的外角.命题意图:本题考查利用等腰三角形的性质计算的能力,注意分类讨论的数学思想,难度中等.20.答案:42解析:连接BE,∵AB=OB,点E是OA的中点,∴BE⊥AO,∠BEC=90°.又∵点F是OD的中点,∴EF是△OAD的中位线,∴EF∥AD,EF=12AD.∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∴EF∥BC,EF=12BC,∴∠ACB=∠CEF=45°,∴∠EBC=180°﹣∠BEC﹣∠ACB=45°,∴EB=EC,△EBC是等腰直角三角形.∵EM⊥BC,∴EM=12BC=BM=CM.∴EF=EM= BM.∵EF∥BC,∴∠EFN=∠MBN.在△EFN与△MBN中,∵ENF MNBEFN MBNEF MB∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EFN≌△MBN(AAS),∴EN=MN=12EM,BN=FN=10.设EF=x,则BM=EM=EF=x,MN=12x,AD=BC=2x,在Rt△MBN中,由勾股定理,得BM2+MN2=BN2,∴x2+(12x)2=(10)2,解得x=22或﹣22(舍去),∴BC=2x=42.考查内容:平行四边形的性质;三角形的中位线;全等三角形的判定与性质;等腰直角三角形的判定与性质;勾股定理. 命题意图:本题考查综合利用平行四边形的性质、等腰直角三角形的性质、全等三角形的判定与性质计算线段长度的能力,注意方程思想的应用,难度较大.21.解析:原式=429621222-+-÷⎪⎭⎫ ⎝⎛----a a a a a a =9642232+--⋅--a a a a a =()()232223--⋅--a a a a =32-a ,当a= 4cos 30°+3tan 45°=4×23+3×1=32+3时, 原式=33322-+=33. 考查内容:分式的运算;特殊角的三角函数值.命题意图:本题考查熟练运用分式的运算法则进行运算的能力,难度中等.方法归纳:分式化简求值时需注意的问题:①化简求值,一般是先将分式化为最简分式或整式,再代入求值.化简时不能因跨度太大而缺少必要的步骤,代入求值的模式一般为“当……时,原式=……”.②代入求值,有直接代入法、整体代入法等常用方法.解题时可根据题目的具体条件选择合适的方法.当未知数的值没有明确给出时,所选取的未知数的值必须使原式中的各分式及化简过程中出现的分式都有意义,且除式的分子不能为0.22.解析:(1)如图所示,矩形ABCD 即为所求;(2)如图△ABE 即为所求,CE=4.考查内容:矩形的判定与性质;等腰三角形的性质;勾股定理.命题意图:本题考查利用等腰三角形的性质、勾股定理、矩形的判定和性质等知识进行作图的能力,难度中等.23.解析:(1)24÷20%=120(名),∴本次调查共抽取了120名学生.(2)120-24-40-16-8=32(名),∴最喜爱书法的学生有32名.补全条形统计图如图所示:(3)960×12040=320(名),∴估计该中学最喜爱国画的学生有320名. 考查内容:条形统计图;扇形统计图;用样本估计总体.命题意图:本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,难度中等.24.解析:(1)证明:∵AC ⊥BD ,∴∠AED =∠DEC =∠BEG =90°,∴∠BGE +∠EBG =90°.∵BF ⊥CD ,∴∠BFD =90°,∴∠BDF +∠EBC =90°,∴∠BCE =∠BDF .∵∠BGE =∠ADE ,∴∠ADE =∠BDF .∵DE =DE ,∴△ADE ≌△CDE ,∴AD =CD . (2)△ACD ,△ABE ,△BCE ,△GBH .附理由:设DE=a ,则AE=2DE=2a ,EG=DE=a ,∴S △ADE =12AE•DE=12•2a•a=a . ∵BH 是△ABE 的中线,∴AH=HE=a .∵AD=CD ,AC ⊥BD ,∴CE=AE=2a ,则S △ADC =12AC•DE=12•(2a+2a )•a=2a 2=2S △ADE ;在△ADE 和△BGE 中, ∵AED BEG DE GE ADE BGE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADE ≌△BGE (ASA ),∴BE=AE=2a ,∴S △ABE =12AE•BE=12(2a )•2a=2a 2,S △BCE =12CE•BE=12(2a )•2a=2a 2,S △BHG =12HG•BE=12(a+a )•2a=2a 2. 综上,面积等于△ADE 面积的2倍的三角形有△ACD 、△ABE 、△BCE 、△BHG . 考查内容:全等三角形的判定与性质;等腰三角形的判定与性质.命题意图:本题主要利用全等三角形的判定与性质和等腰三角形的判定与性质进行证明和计算的能力,难度中等偏上.25.解析:(1)解:设每个A 型放大镜x 元,每个B 型放大镜y 元.根据题意得⎩⎨⎧=+=+1526422058y x y x ,解得⎩⎨⎧==1220y x ,∴每个A 型放大镜20元,每个B 型放大镜12元.(2)解:设可以购买a 个A 型放大镜,则购买B 型放大镜(75-a )个. 根据题意得20a +12(75-a ) ≤1180,解得a ≤35.∴最多可以购买35个A 型放大镜. 考查内容:二元一次方程组的应用;一元一次不等式的应用.命题意图:本题考查利用二元一次方程组和一元一次不等式的知识解决实际问题的能力,难度中等偏上.26.解析:(1)证明:∵四边形ABCD 是正方形,∴∠A =∠ABC =90°.∵∠F =∠A =90°,∴∠F =∠ABC .∵DA 平分∠EDF ,∴∠ADE =∠ADF .∵∠ABE =∠ADE ,∴∠ABE =∠ADF .又∵∠CBE =∠ABC +∠ABE ,∠DHG =∠F +∠ADF ,∴∠CBE =∠DHG .(2)证明:如图,过H 作HM ⊥KD ,垂足为点M .∵∠F =90°,∴HF ⊥FD .又∵DA 平分∠EDF ,∴HM =FH .∵FH =BP ,∴HM =BP .∵KH ∥BN ,∴∠DKH =∠DLN .∵∠ELP =∠DLN ,∴∠DKH =∠ELP .∵∠BED =∠A =90°,∴∠BEP +∠LEP =90°.∵EP ⊥BN ,∴∠BPE =∠EPL =90°,∴∠LEP +∠ELP =90°,∴∠BEP =∠ELP =∠DKH .∵HM ⊥KD ,∴∠KMH =∠BPE =90°,∴△BEP ≌△HKM (AAS ),∴BE =HK .(3)解:如图,连接BD ,∵3HF =2DF ,BP =FH ,∴设HF =2a ,DF =3a ,∴BP =FH =2a .由(2)得HM =BP ,∠HMD =90°.∵∠F =∠A =90°,∴tan ∠HDM =tan ∠FDH ,∴DM HM =DFFH=32 ,∴DM =3a ,∴四边形ABCD 是正方形,∴AB =AD ,∴∠ABD =∠ADB =45°. ∵∠ABF =∠ADF =∠ADE ,∠DBF =45°-∠ABF ,∠BDE =45°-∠ADE ,∴∠DBF =∠BDE .∵∠BED =∠F ,BD =BD ,∴△BED ≌△DFB ,∴BE =FD =3a .过点H 作HS ⊥BD ,垂足为点S .∵tan ∠ABH =tan ∠ADE =ABAH =32,∴设AB =32m ,AH =22m , ∴BD =2AB =6m ,DH =AD -AH =2m ,sin ∠ADB =DH HS =22 ,∴HS =m ,∴ DS =22HS DH -=m ,∴BS =BD -DS =5m ,∴tan ∠BDE =tan ∠DBF =BSHS =51.∵∠BDE =∠BRE .∵tan ∠BRE =PR BP =51.∵BP =FH =2a ,∴RP =10a ,在ER 上截取ET =DK ,连接BT ,由(2)得∠BEP =∠HKD ,∴△BET ≌△HKD ,∴∠BTE =∠KDH ,∴tan ∠BTE =tan ∠KDH ,∴PT BP =32 ,∴PT =3a ,∴TR =RP -PT =7a .∵S △BER -S △KDH =47,∴21BP ·ER 21-HM ·DK =47,∴21BP (ER -DK )=21BP (ER -ET )=47,∴21×2a ×7a =47,∴a 2=41,解得a 1=21,a 2=21-(舍去),∴BP =1,PR =5,∴BR =22RP BP +=2251+=26.考查内容:圆的有关性质;正方形的性质;全等三角形的性质;三角形的面积公式;锐角三角函数定义.命题意图:本题考查综合利用圆的有关性质、三角形的性质、正方形的性质计算和证明的能力,综合性强,难度较大.27.解析:(1)∵y =3-x +327 ,∴B (27,0)C (0,273),∴BO = 27,CO =273 . 在Rt △BCO 中,BC =22CO BO +=2232727⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=7.∵四边形ABCD 为菱形,∴AB =BC =7 ,∴AO =AB -BO =727-=27 ,∴A (27-,0).(2) ∵AO =27=BO ,CO ⊥AB ,∴AC =BC =7,∴AB =AC =BC ,∴△ABC 为等边三角形, ∴∠ACB =60°.∵∠APB =60°,∴∠APB =∠ACB .∵∠PAG +∠APB =∠AGB =∠CBG +∠ACB ,∴∠PAG =∠CBG ,连接CE 、CF ,∵AE =BF ,∴△ACE ≌△BCF ,∴CE =CF ,∠ACE =∠BCF ,∴∠ECF =∠ACF +∠ACE =∠ACF +∠BCF =∠ACB =60°,∴△CEF 为等边三角形,∴∠CFE =60°,EF =FC .∵∠AFE =30°,∴∠AFC =∠AFE +∠CFE =90°.在Rt △ACF 中,∴AF 2+CF 2=AC 2=72=49,∴AF 2+EF 2=49.(3) 由(2)知△CEF 为等边三角形,∴∠CEF =60°,EC =EF ,延长CE 、FA 交于点H .∵∠AFE =30°,∠CEF =∠H +∠EFH ,∴∠H =∠CEF -∠EFH =30°,∴∠H =∠EFH ,∴EH =EF ,∴EC =EH .连接CP ,∵PE =AE ,∠CEP =∠HEA ,∴△CPE ≌△HAE ,∴∠PCE =∠H ,∴CP ∥FH , ∴∠HFP =∠CPF ,在BP 上截取TB =AP ,连接TC ,由(2)知∠CAP =∠CBT .∵AC =BC ,∴△ACP ≌△BCT ,∴CP =CT ,∠ACP =∠BCT ,∴∠PCT =∠ACP +∠ACT =∠BCT +∠ACT =∠ACB =60°,∴△CPT 为等边三角形,∴CT =PT ,∠CPT =∠CTP =60°.∵CP ∥FH ,∴∠HFP =∠CPT =60°. ∵∠APB =60°,∴∠APB =∠AFP ,∴AP =AF ,∴△APF 为等边三角形,∴∠CFP =∠AFC -∠AFP =90°-60°=30°,∴∠TCF =∠CTP -∠TFC =60°-30°=30°,∴∠TCF =∠TFC ,∴TF =TC =TP .连接AT ,则AT ⊥BP .设BF =m ,则AE =PE =m ,∴PF =AP =2m ,∴TF =TP =m ,TB =2m ,BP =3m ,在Rt △APT 中,AT =22TP AP -=()222m m -=3m ,在Rt △ABT 中,AT 2+TB 2=AB 2,∴(3m )2+(2m )2=72,∴m 1=-7(舍去),m 2=7.∴BF =7,AT =21,BP =37,sin ∠ABT =AB AT =721. 作PQ ⊥AB ,垂足为点Q ,作PK ⊥OC ,垂足为点K ,则四边形PQOK 为矩形,则OK =PQ =BP ·sin ∠PBQ =37×721=33,BQ =22PQ BP -=()()223373-=6 , OQ =BQ -BO =6-27=25,∴P (25-,33).考查内容:一次函数;等边三角形的判定和性质、全等三角形的判定和性质、勾股定理、菱形的性质.命题意图:本题考查综合利用一次函数、等边三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识解决问题的能力,注意构造全等三角形的应用,难度较大 .。
黑龙江省哈尔滨市工业大学附属中学2018-2019学年九年级上册期中英语试题(含答案)

哈工大附中2018——2019学年度九年级 (上)期中英语试卷考试时间(100分钟)试卷满分(100分)一.单项选择(本题共20分,每小题1分)( ) 1. Boys and girls, you are working hard all day. I know you _____ getting up early and going to bed late. Try your best, and I’m sure youwill have a bright future.A. used toB. are used toC. are used for( ) 2. -- If you work hard , you can be ________ honor to all of us.--- I hope so.A. /B. aC. an( ) 3. --- We took a trip ___________ a sunny morning.--- I remember. You enjoyed yourselves that day.A. inB. onC. at( ) 4. --- You are so excellent! We take __________ in you.---- Without your help, I can’t succeed.A. pridesB. a prideC. pride( ) 5.--- The book is very interesting. I have read it.---- Really? When _________ you ________ it?A. have, boughtB. did, buyC. will, buy( ) 6.--- ________ I finish my work today?--- No, you needn’t. You can finish it tomorrow.A.WillB. CanC. Must( ) 7.--- It’s so hot, please open the door.--- OK. I’ll keep the door ___.A. openedB. openC. opening( ) 8.--- When will you be free, this Saturday or Sunday?---- _________ day is OK. I have time on weekends.A.EitherB. NeitherC. Both( ) 9.--- As middle school students, no matter what difficulties we face, we should stick to __________ our dreams.---- I agree with you. Nothing is more important than our dreams.A. followedB. followingC. follow( ) 10. With the development of technology, _______ dictionaries are more and more popular.A. electricB. electricityC. electronic共12页第1页( ) 11.--- What is this passage about?--- It’s _________ about some useful methods in learning English.A. hardlyB. especiallyC. mainly( ) 12.---Traffic accidents cannot be avoided ________ everyone followsthe traffic rules.--- That’s true. As students, we must follow the rules on our way toand back from school.A. ifB. thoughC. unless( ) 13.---Can you tell me something about the city from ______ you come?--- Certainly. I’m from Harbin. People call it Ice City, because it is famous for itsice and snow in winter.A. whichB. thatC. where( ) 14.---- He wanted to know ___________ with you yesterday.---- I failed in English exam, I was very sad.A. what’s the matterB. what the mat ter wasC. what was the matter( )15. It is one of the most important topics in western countries. When English people meet each other, they often talk about it. Especially whenthey meet strangers for the first time. Therefore, this western topic is___.A. weatherB. ageC. work( )16. Reflection(反思) for exams is a good way to improve yourself.Every time you finish an English exam, you should _______ to get a better result next time.①prepare a notebook which you can use to collect and correct your wrong problems②learn all the answers of the exam by heart③care about the mark itself only④ask the teacher for the ways to work out problems⑤practice more exercises of the same typeA. ①②④B. ①④⑤C. ②③⑤( )17. Jim got ¥90 pocket money by working in a park every month. He spent two thirds of it in shopping on the Internet. The rest money wasused to do the following things. From the chart we know that he spent ____ in( )18. Which underlined letter has a different sound from the others?A. aheadB. increaseC. heat共12页第2页( )19. Which pair of the words with the underlined letters has the samesound?A. double doubtB. novel localC. brand land( )20. Which word of the following has a different stress from the others?A. Recent.B. Request.C. Create.二、完形填空(本题共十分,每空一分)Dreams are special things that only belong to human beings. Hall, a super intelligent(智能) computer in a science fiction movie that almost has understood all of human beings’ feelings, always confuses if he has dreams. After an accident, he realizes what a dream is. It’s not what you see during your sleep, but something when you are __21__. At last, he helps save the members of a spaceship and dies for a pretty dream to build a new world. Dreams are __22__ important for a person that we must have one dream or two. With a dream, we know __23__ we should do. __24__ a dream, we’ll lose the power to go ahead. How to realize our dreams is a serious problem. Here __25__ my three pieces of advice.First, we must make sure we have a prac tical dream. It’s __26__ too far for us to reach nor too near to need any hard work.Second, we need to make plans to make them __27__. A long plan makes us always know the necessary big steps toward the final goal. A short plan helps us keep getting a little step closer to the dream.Third, we should have a good __28__. That means we should always be active and never give up whenever we come across problems or even failure. Also, we should never be careless and keep working hard even when we get success.Dreams are so beautiful and meaningful for all of us that we will be excited __29__ we are just imagining about them. But the most important one is to take action. So let’s begin our trip to __30__ right now.()21. A. sleepy B. asleep C. awake()22. A. very B. so C. such()23. A. what B. why C. how()24. A. With B. Including C. Without()25. A. was B. is C. are()26. A. either B. whether C. neither()27. A. realize B. come true C. come up()28. A. expression B. attitude C. education()29. A. therefore B. when C. because()30. A. successful B. succeeding C. success三.阅读理解(共20分)(A)共12页第3页Mr. Smith was a cook. He worked in a restaurant. Once he decided to go to a village to spend his holidays when it was very hot in the town. One afternoon Mr. Smith walked in a forest, and found it was very cool. He went farther and farther. Suddenly he saw a bear coming to him. He tried his best to run away. And soon the bear disappeared but he lost his way. He came out of the forest when the sun set. He didn't know how to get to the village and was very hungry. Just then he saw an old man working in the fields."Hi! Old man," shouted Mr. Smith. "Where does the road go?""I never notice it can move. It has lain here for hundreds of years," answered the old man."How far is the village from here?""I don't know," said the old man. "I haven't measured it."M r. Smith became angry. He shouted. “What do you know? You are the most foolish in the world, I think.""Maybe I am," said the old man with a smile on his face, "___________"根据短文内容选择最佳答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈尔滨市2018年初中升学考试(含答案)可能用到的相对原子质量:H-1 C-12 O-16 Na-23 S-32 K-39 Cu-64一、选择题(1-15小题,每小题2分,共30分,每小题只有一个正确答案)1.2018年6月9日“迷人的哈尔滨之夏”旅游文化时尚活动正式开幕,吸引了众多A.哈尔滨火车站大理B.中央大街欧式铁C.-----------------------------------------(A )D.倾倒二氧化碳A.电解水B.铁钉生锈C.品红在水中扩散D.测定空气里氧气含量B.用熟石灰改良酸性土C.(B )A.元素周期表有7个周期16个族B.贵重设备、精密仪器失火最好用水基型灭火器灭火C.使用脱硫煤可以减少酸雨的产生D.我国科学院院士张青莲为相对原子质量的测定作出了卓越的贡献6.下列实验现象描述正确的是---------------------------------------( A )A.氢氧化钠固体放置于空气中:表面潮湿并逐渐溶解B.高锰酸钾放入汽油中:很快溶解形成紫色溶液C.将二氧化碳通入紫色石蕊溶液中:紫色石蕊溶液变蓝色D.涤纶和羊毛燃烧:都可闻到一股烧毛发的焦糊味7.下列有关叙述、对应的方程式,所属基本反应类型都正确的是-----( B )A.拉瓦锡研究空气成分 HgO △ Hg + O 2↑ 分解反应B.生石灰作干燥剂2O == Ca(OH)2 化合反应C.三氧化硫与氢氧化钠溶液反应 SO 3 + NaOH == Na 2SO 3 + H 2O 复分解反应D.葡萄糖在人体内氧化 C 6H 12O 6 + 6O 2 酶 6CO 2 + 6H 2O 氧化反应8.“关爱生命,注意安全,拥抱健康”-( D )A.正确使用含氟牙膏可以预防龋齿B.水体污染会直接危害人体健康C.炒菜时油锅中的油不慎着火,可用锅盖盖灭或放入较多的蔬菜D.如缺乏维生素C ,会引起夜盲症 9.碳酸饮料中含有碳酸,下列有关叙述正确的是-------------------------(B )A.碳酸由碳、氢、氧三种原子构成B.碳酸分子中碳、氢、氧原子的个数比1:2:3C.碳酸中碳元素的质量分数最大D.碳酸是有机高分子化合物 10.下列关于能源、资源的叙述正确的是---------------------------(A )A.常用来炼铁的矿石有赤铁矿、磁铁矿B.是由炼制可得到汽油、柴油、煤焦油等C.海洋是地球上最大的储水库,海水中含有的化学元素有100多种D.人们正在利用和开发的其他能源有水能、太阳能、风能、地热能、可燃冰等是-------------------------------------------------------( C )A.乙中含有少量甲,可用冷却热饱和溶液的方法提纯甲B.t 3℃时,甲的溶液溶质质量分数一定大于乙的溶液溶质质量分数C.t 3℃时,将等质量的甲、乙两种物质的饱和溶液分别降温至t 2℃,析出晶体的质量甲一定大于乙D.t 1℃时,乙的不饱和溶液只有通过蒸发溶剂的方法才能转变成饱和溶液中钠元素质量分数为23%,180℃时,将样品加热一段时间后称得固体质量为87.6g ,则分解的碳酸氢钠占原碳酸氢钠的质量分数为(2NaHCO 3 △ Na 2CO 3 + H 2O + CO 2↑)( B )A.33.6%B.40%C.47.3%D.60%二、非选择题(请根据题意填写空白,28-35小题,共40分)28.(5分)“科技兴国、科技创新、不负嘱托!”习总书记来到哈尔滨为哈尔滨科技创新带来活力。
哈工大学生设计制造的小卫星升空,哈工程大学研发的世界上速度最快的无人艇试航,石墨烯研发成功……都是哈尔滨的骄傲! (1)利用火箭发射卫星,火箭使用肼(N 2H 4)作燃料,氧气作氧化剂,在一定条件下反应生成空气中含量最多的气体和一种常用来作溶剂的物质,同时放出巨大能量把火箭送入太空,该反应的化学方程式为N 2H 4+O 2一定条件N 2+2H 2O , 反应前后氧元素的化合价分别为 0价、-2价 ,火箭升空过程中的能量转化为 化学能 →内能→ 机械能 。
(2)钛和钛合金是制造火箭、导弹、航天飞机的重要材料,主要利用了它们具有 A 等性能(填字母)A.熔点高、密度小、机械性能好B.熔点低、硬度大、韧性好C.密度大、耐磨、耐腐蚀(3)石墨烯可被用于制造透明电极、液晶显示屏、触摸屏、有机光伏电池和有机发光二极管等,是由于石墨烯具有较高的 导电能力 和透光性。
29.(5分)“他已褪去少年的青涩,淋漓尽致的表演充满了成长的力量。
”20岁的哈尔滨小伙博洋,自2018年年初的四大洲花样滑冰锦标赛自由滑比赛中完美发挥,全场零失误,一举夺得冠军。
(1)运动员每日饮食需要营养的严格配比,牛肉炖柿子是运动员比较喜爱的一道美食,其中西红柿富含的营养素可以起到调节新陈代谢, 预防疾病 和维持身体健康的作用。
而牛肉中富含的营养素(除水外)主要是 蛋白质 。
(2)大米是由水稻磨制而成的,水稻在种植过程中需施加钾肥,其主要作用是保证各种代谢过程的顺利进行,促进植物生长,增强抗病虫害抗倒伏能力等功能,若还需使水稻叶色浓绿,则能同时提供这两种营养元素的复合肥是KNO3(填化学式)。
(3)如果运动员穿的衣服面料是由一种纤维材料制成的,具有强度高、弹性好、耐磨、耐化学腐蚀的性能,则制作该面料的纤维种类为C(填字母)。
A.羊毛纤维B.棉纤维C.合成纤维乙丙(1)在甲、丙图中将相关粒子图形补充完整甲补充一个氧分子、丙中补充一个水分子(2)A、B、C、D对应的物质都是由分子构成的(3)画出比一个C分子多两个质子的离子结构示意图。
31.(4分)分类、类比、推理都是学习化学常用的方法。
(1)化学实验的设计除考虑实验目的外,还要考虑实验安全,减少对环境的污染等因素,据此应将下列实验中的A与 C (填“B”或“C”或“D”)归为一类,依铁丝在氧气中燃烧一氧化碳还原氧化铁稀释浓硫酸B C D尾气中含有一氧化碳,其原因是有些含碳的化合物不充分燃烧会生成CO (用文字叙述);汽车用燃料中不含氮元素,尾气中却含有一氧化氮,产生一氧化氮的原因是N2+O2放电或高温2NO (用化学方程式表示,条件是“放电或高温”)。
32.(7分)实验室现有石灰石、稀盐酸、火柴、药匙、升降台、木条、棉花、镊子及以下仪器:①②③④⑤⑥⑦⑧(1)若要制取二氧化碳,应选择的仪器有①锥形瓶和②④(填序号),还需补充的仪器是玻璃片(填名称)(2)若补充一种药品还能制取氧气,发生反应的化学方程式为2KMnO4△K2MnO4+MnO2+O2↑。
(3)将制取氧气和检验氧气的装置图补充完整(4)用排水法收集氧气,当观察到导管口有连续切均匀的气泡冒出时,开始收集,气体逸出的原因是由于试管内温度升高且且生成氧气,使试管内压强,大于外界大气压,在压强差的作用下,气体逸出。
33.(4分)右图中A、B、C、D、E、F分别表示初中化学常见的六种物质,B、C、D、E分别属于酸、碱、盐、氧化物四种类别中的一种,A是目前提取量最大的金属,B由两种元素组成,C是大理石的主要成分。
(图中用“—”表示两种物质之间能发生化学反应,用“→”或“”表示一种物质能转化为另一种物质,部分反应物和生成物及反应条件已略去,图中部分反应需要在溶液中进行,物质是溶液的只考虑溶质)。
请回答下列问题。
(1)分别写出A、C、E、F物质的化学式A Fe C CaCO3 E CO2 F C 。
(2)写出B与C发生反应的化学方程式 CaCO3+2HCl===CaCl2+H2O+CO2↑。
(3)写出过量A的粉末与B发生反应的实验现象黑色固体减少不消失,溶液由无色变成浅绿色,固体表面有气泡冒出。
34.(6分)化学是以实验为基础的科学,实验是科学探究的重要手段。
某化学兴趣小组在一次活动中进行了如图所示的探究实验。
【实验探究】【收集证据】A 烧杯中发生反应的化学方程式(1) H 2SO 4+Ba(OH)2=BaSO 4↓+2H 2O 。
根据C 试管中的现象能得出B 烧杯的溶液中一定没有的离子是(2) H +、SO 42- (填符号)。
滴加氢氧化钡溶液的实验现象(3) A 黄色溶液中出现白色沉淀D 试管中出现红褐色沉淀,溶液黄色逐渐变为无色 。
【结论应用】通过上述实验现象可以得出,在此过程中(4)在同一反应容器中同时存在碱与酸和碱与盐的反应时,酸碱反应一般是优先于酸与盐的反应 (从宏观角度回答)。
根据这个结论,若向C 试管溶液中加入氯化钡溶液有白色沉淀产生,则B 烧杯的溶液中一定含有的离子是(5) Cl -、Fe 3+、SO 42-、H + (填符号)。
【归纳总结】经讨论我们能够总结出,根据明显的实验现象可以得出许多结论。
一般来说,常根据(6) 明显的实验现象证明有新的物质生成 ,证明物质发生了化学变化。
35.(6分)为测定某硫酸铜样品中硫酸铜的含量(杂质不溶于水,不含铜元素,不与其他物质发生反应),进行了如下实验(1)上述实验过程中发生反应的化学方程式为 H 2SO 4+2KOH===K 2SO 4+2H 2O 、2KOH+CuSO 4===Cu(OH)2↓+K 2SO 4 。
(2)根据已知条件列出求解C 烧杯中参加反应的硫酸铜质量(X)的比例式160/98=x/4.9g 。
(3)配制上述实验所用的氢氧化钾溶液,需要质量分数为20%的氢氧化钾溶液的质量为 28g 。
(4)样品中硫酸铜的质量分数为 80% 。
(5)D 烧杯溶液中溶质的质量分数为 8.7% 。
(6)若用湿法冶金的方法冶炼出100kg 含杂质4%的铜,需要这种硫酸铜的质量为 300kg 。
