理论力学点的合成运动
理论力学--运动学总结
速度瞬心位置的确定总结
瞬时平动
几点注意 1、基点法是速度分析的基本方法;
2、速度投影法 应用起来简单,但必须知道待求速度 点的方位,致命的弱点—是不能求图形的角速度 2、当平面几何简单时,分析速度可采用瞬心法; 瞬心法既可以求某点的速度,也可以求刚体运动 的角速度; 4、确定速度瞬心的速度是该点的绝对运动速度; 5、具体分析时三种方法灵活运用;
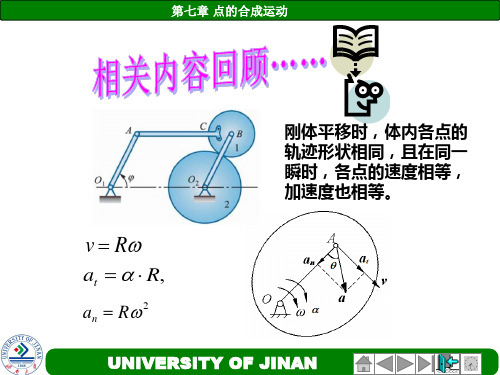
(1)刚体的基本运动 平动
v A vB
aA aB
各点的轨迹相同;
可简化为一个点的运动。
定轴转动
v R
a R
an R 2
轮系的传动比:
1 n1 R1 Z 2 i12 2 n2 R2 Z1
各处不打滑时: 接触点有相同的线速度和相同的切向加速度。
(2)刚体的平面运动 1. 定义 任一点到某固定平面的距离保持不变。
B点的加速度分析
D
C
a a 2 a a 2 ae 2 ar 2
n
aa 2 ae 2
O1
30°
ar 2
B
aa 2cos60 aa2cos30 ae 2
n
aa 2
1
30° O2
n
A
a a2 O2 B 2
n 2 aa2 O2 B2
ae2 657mm/ s
2
三、刚体的运动
va=v
vCA
动点:滑块C 动系:固结于AE
u=vA
vr
vC' A
ωAE
分析三种运动
牵连运动:刚体的平面运动
牵连转动
va ( vA vCA ) vr
va cos vCA v A sin
理论力学第八章点的合成运动

3
实例三
描述一个长杆在平面内同时作直线运动和回转运动的合成运动,讨论合成运动对 杆心运动特性的影响。
合成运动中的矢量操作
在合成运动中,我们经常需要进行矢量的加法、减法和乘法等操作。这些操作可以帮助我们推导、计算和分析 合成运动的各种特性。
合成运动的应用及展望
应用
合成运动的概念和原理广泛应用于物理学、工程学和运动学等领域,为我们理解和解决复杂 的运动问题提供了有力的工具。
点的合成运动的基本概念
点的合成运动是指多个点以各自不同的速度和方向同时运动,并在同一时间 到达相对位置的运动方式。它是合成运动的基本形式之一。
合成运动的示意图和公式推导
示意图
通过示意图展示合成运动的过程和结果,帮助加深 理解。
公式推导
推导合成运动的公式,使我们能够定量描述和计算 合成运动的各个特性。
质点运动的合成运动
质点的合成运动是指质点在运动过程中,同时具有平移运动和旋转运动的一 种复杂运动形式。在合成运动中,质点的运动轨迹会呈现出特定的形态和规 律。
质点合成运动实例分析
1
实例一
分析一个小球在倾斜平面上同时进行滚动和滑动的合成运动,探讨其运动规律和 性质。
2
实例二
研究一个弹射体在水平飞行过程中受到重力和空气阻力合成运动的影响,揭示合 成运动对物体运动轨迹的影响。
理论力学第八章点的合成 运动
欢迎大家来到本次关于理论力学第八章点的合成运动的精彩演讲。在本次演 讲中,我们将深入探讨合成运动的定义、基本概念、示意图与公式推导,以 及质点运动的合成运动等内容。
合成运动的定义
合成运动是指由多个简单的运动相结合而成的复杂运动。它将两个或多个运 动矢量合成为一个合成矢量,从而形成全新的运动方式。
理论力学7-2
z
M M '
rM z '
r'
O' x'
k ' rO ' i '
j'
y'
O
y
UNIVERSITY OF JINAN
第七章 点的合成运动
1. 动系做平移时 i 0, j 0, k 0
' k ' 0 2 x' i ' y ' j ' z
ve vr va ro
vB ve r O l l l
UNIVERSITY OF JINAN
第七章 点的合成运动
绝对加速度 相对加速度
n 2 aa aa O r
方向由A指向O
ar ?
n e 2 e
方向水平
2 O r2
v 牵连加速度 a l
l
方向由B指向D
v R vr aa R R 2 v R 2 r 2vr R
2 a 2
UNIVERSITY OF JINAN
第七章 点的合成运动
加速度合成定理(Theorem of composition of accelerations)
1. 动系做平移时
aa ae ar
2. 两个不相关的物体,求二者的相对速度。 根据题意, 选择所求相对运动速度的点为动点, 动系 固结于另一物体上。
UNIVERSITY OF JINAN
第七章 点的合成运动
3. 相对于运动物体在运动的物体上有一动点,求该点的绝 对运动。则取该点取为动点,动系固结于另一个运动物体 上。
理论力学基础点的合成运动

1
平动和转动的区别
2
它们之间的关系对于理解合成运动具有
重要意义;
3
运动学基本公式
4
位置、速度、加速度等运动学基本公式 是研究合成运动的基础知识。
牛顿第二定律
合力产生加速度,加速度与力成正比。 一切合成运动都符合牛顿第二定律;
匀速圆周运动的分解
它是所有曲线合成运动的基础,掌握分 解方法可以为其他曲线合成运动的研究 提供启示;
结论和总结
合成运动是力学基础点之一,但不同于其他运动,它是由多个运动步骤组 成的复杂过程,因此有其独特的研究方法和工具。对合成运动理论及其实 际应用的深度理解和掌握,具有重要意义。 ——陈晓明,中国科技大学教授
机器人动作设计
机器人动作设计中需要进行多种复杂的合成运动分析与控制。合成运动理论可以指导机器人 的运动规划、轨迹跟踪和动作执行。
运动传感设计
合成运动分解是一种重要的运动测量技术。在车辆安全、物流配送、航空监控等领域,合成 运动传感器为复杂运动测量提供了有效手段。
合成运动的实验方法和技术
1
高速相机
观测高速运动的一种重要方法。运用指定的曝光时间和快门速度,拍摄合成运动 过程中的关键帧。
2
追踪仪器
用于测量运动物体的位置、速度和加速度等多种参数,对于合成运动的分析和控 制有着重要作用。
3
动力学仿真软件
自动地计算合成运动的轨迹、速度、加速度等参数。可以模拟物体的运动过程, 为结构设计和工艺分析提供有力支持。
合成运动的分类和特点
线性合成运动
由两个或两个以上直线运动叠 加而成;
圆周合成运动
由两个或两个以上曲线运动叠 加而成;
复合合成运动
由不同类型直线运动或曲线运 动叠加而成。
理论力学第七章

例题
点的复合运动
例 题 7-1
3. 速度分析。
绝对速度va:va=OA · =r ω ,方 ω 向垂直于OA,沿铅垂
方向向上。
牵连速度ve:ve为所要求的未知量, 方向垂直于O1B 。 相对速度vr:大小未知,方向沿摇杆 O1B 。 应用速度合成定理
va ve vr
13
例题
点的复合运动
2. 运动分析。 绝对运动-以O为圆心的圆周运动。 相对运动-沿杆BC直线运动。 牵连运动-平动。
24
ω0
O
30
C
例题
点的复合运动
例 题 8-10
3. 速度分析。
α
ω
60
绝对速度va:va = ω0 r,垂直于OA向下。
D A E 牵连速度ve: ve= vB,垂直于BD向右下。
B
vr vB v a
a
a
n ae sin 30 cos 30
2 3o l r 3l
所以杆BD的角加速度
t ae l
2 3 o r (l r )
3l 2
27
例题
点的复合运动
习题课
28
第七章
一、基本概念
点的合成运动习题课
1.一个动点,两个坐标系,三种 运动 2.速度合成定理
v2 B
v1
30
vr 与 va 的夹角 ve
60
M
β
ve sin 60 46 12 arcsin vr
va
vr
18
§7-3点的加速度合成定理
先分析 k’ 对时间的导数。
' drA rA rO k vA e rA dt ' ' drO dk e (rO k ) dt dt 因为 v drO r O e O dt
理论力学第六章 点的合成运动 [同济大学]
![理论力学第六章 点的合成运动 [同济大学]](https://img.taocdn.com/s3/m/63fd0a4dbe1e650e53ea9909.png)
解: 从例6-2已知得: 1 =
vr r 3 , 2
ω 4
O
解: 从上例已知得: 1 =
r
M
ω 4
va
A
aaτ =0 ,
3 , 4
aan=2r aen=
ωr 8
x’
2
ac 21vr 2 r
va
30°
3 1 1/ s2 8
2
动点取A,
va v A
ar
dvr d 2 x ' ' d 2 y ' ' d 2 z ' ' 2 r 2 j 2 k dt dt dt dt
dx ' di ' dy ' dj' dz ' dk ' dt dt dt dt dt dt
ar ω vr
a a ae a r ac; ac= 2vr
ve
a n a ae a rn a rτ
矢量
1.瞬时状态; 2.可解两个未知量 (大小,方向)。
例6-5 曲柄滑道机构,OA=01A=r=10cm, =30°,=4, 求: 转到30°时直杆的加速度a。 va vr 动点取A; 绝对:圆周; ve 解:相对:圆周;牵连:直线。 [速度] =
a a ae a r ac; aa a an ae aen ar arn ac;
例6-8 曲柄绕O转动,並通过滑块M带动滑槽绕O′摆动, ’ y 求摆动到30°时的角加速度1。
例6-9 将例6-8滑槽改变为图示牛头刨床机构,MA=2r, 求:刨床刨刀的速度,加速度。
vr
dv e dω dr r ω dt dt dt α r ω v e ω v r ae ω v r
理论力学点的合成运动

例 8-4 曲柄OA以匀角速度 w绕O轴转动,其上
套有小环 M,而小环 M又在固定的大圆环上运动,大 圆环的半径为 R。
试求当曲柄与水平线成的角 j ωt 时,小环 M
的绝对速度和相对曲柄 OA 的相对速度。
A
M w
R
O
j
C
解:(1)选择动点及 动系: 小环M为动点,动系固连在 OA上。
(2)分析三种运动:绝 对运动为圆周运动,相对运 动为沿OA的直线运动,牵连 运动为定轴转动。
y
OA杆转动的角速度为
O
wOA
ve OC
ve 2r
3u 6r
y
wOA B
j va vr
A
r ve C
x
u x
8.3 牵连运动是平动时点的加速度合成定理
在图8-9中,设 Oxyz为定系,Oxyz为动系且作平
动,M为动点。动点M在动系中的坐标为 x、y 、z, 动系单位矢量为 i、 j、k。动系平动,i、j、k 的
Oxyz 作某种运动,在瞬时t,动系连同相对轨迹AB在
定系中的I位置,动点则在曲线 AB
上的 M 点。经过时间间 隔 t ,动系运动到定系 中的II位置,动点运动到
点 M。 如果在动系上观
察点M 的运动,则它沿 曲线 AB 运动到点 M2。
z B
M2
vr
z
M O
A
O I
x
va
M B
ve M1
z
O x A
例 8-1 汽车以速度 v1 沿直线的道路行驶,雨滴 以速度 v2 铅直下落,试求雨滴相对于汽车的速度。
v1
解: 因为雨滴相对运动的汽车有运动,所以本题 为点的合成运动问题,可应用点的速度合成定理求解。
3理论力学 第八章点的合成运动解析

? ? tg ?1 v?
v平
[例8-2] 曲柄摆杆机构
φ
已知:OA= r , ? , OO1=l 图示瞬时OA? O
求:摆杆O1B角速度? 1
解:取套筒A点为动点,摆杆O1B为动系.基座为静系。
绝对速度va = r ?
相对速度vr = ?
方向? OA 方向//O1B
牵连速度ve = ?
方向? O1B
由速度合成定理 va ? vr ? ve 作出速度平行四边形 如图示。
r
ve ? va sin? ? r? ?
r2? l2
又?ve ? O1 A?? 1,
? ? 1 ? Ov1eA?
1? r 2 ?l2
r 2?
r2?
l2
?
r
r 2?
2 ? l2
(
)
[例8-3]圆盘凸轮机构
已知:OC=e , R ? 3e , ? (匀角速度)
vr
va
A veva
B
aa
ar
va
A
Baen
ae?
练习三
解:
A
?
?
o
B
A
? ?
o
ve ? OB??
va
B
vr
动系:OA杆; 动点:滑块B
A
? ?
arn
o
aen ? OB?? 2
ar?
B
aa
a?e ? OB??
[例8-1] 桥式吊车。 已知:小 车水平运行,速度为v平, 物块A相对小车垂直上升 的速度为v? 。求物块A的运 行速度。
一、实例 : M点运动
地面: 摆线, 车箱: 圆。
二、复合运动的一般模型
理论力学第7章(点的合成运动)

点的速度合成定理是瞬时矢量式,共包括大小‚方向
六个元素,已知任意四个元素,就能求出其他两个。 二、应用举例
[例] 桥式吊车 已知:小
车水平运行,速度为v平, 物块A相对小车垂直上升 的速度为v。求物块A的 运行速度。
解:选取动点: 物块A 动系: 小车 静系: 地面 相对运动: 直线; 相对速度vr =v 方向 牵连运动: 平动; 牵连速度ve=v平 方向 绝对运动: 曲线; 绝对速度va 的大小, 方向待求。
由速度合成定理 va= vr+ ve , 作出速度平行四边形 如图示。
v a v e tg 30 0 2 3 e 3 v AB 2 3 e ( ) 3
动点:AB杆上的A点 动系:偏心轮
绝对运动:直线 相对运动:圆周(曲线) 牵连运动:定轴转动
铰接四边形O1A=O2B=100mm, O1O2=AB,杆 O1A以等角速度 ω =2rad/s绕轴O1转动。 AB杆上有一套筒C,此套筒与杆CD相铰接 ,机构的各部件都在同一铅垂平面内。
)
[例3] 圆盘凸轮机构 已知:OC=e , R 3e , (匀角速度) 图示瞬时, OCCA 且 O、A、B三点共线。 求:从动杆AB的速度。
解:动点取直杆上A点,动系固结于圆盘, 静系固结于基座。 绝对速度 va = ? 待求,方向//AB 相对速度 vr = ? 未知,方向CA 牵连速度 ve =OA=2e , 方向 OA
y
O C
x
x
合成运动:相对某一参考体的运动可由相对于其它参考 体的几个运动组合而成,称这种运动为合成运动
动点:要研究的点
两个参考系: 一般把固定在地球上的坐标系称为静参考系; 用 Oxyz表示; 固定在相对地球运动的参考体上的坐标系称为动参考系; 用 Oxyz 表示。
理论力学8

求曲柄在水平位置瞬时,摇杆O1B绕O1轴的角速度1及滑块A相
对摇杆O1B的相对速度。
运动学/点的合成运动
解:
选取动点: OA 上的A点 动系: O1B 定系: 基座
运 绝对运动:圆周运动 动 分 相对运动:直线运动 析 牵连运动:定轴转动 :
运动学/点的合成运动
另一方面,在实际问题中,不仅要在固联在地面上
的参考系上还要在相对于地面运动着的参考系上观察和
研究物体的运动。下面先看几个例子。
沿直线轨道纯滚动 的圆轮,研究轮缘上A 点的运动,对于地面上 的观察者,是旋轮线轨 迹,对站在轮心上的观 察者是圆。
A点的运动可看成随轮心的平移与绕轮心转动的合成。
运动学/点的合成运动
MM MM1 M1M 将上式两边同时除以t并取 t0得
lim MM lim MM1 t 0 t t 0 t
lim
M1M
t 0 t
va ve vr
即:在任一瞬时动点的绝对速度等于牵连速度与相对速
度的矢量和,这就是点的速度合成定理。
点的速度合成定理是瞬时矢量式,共包括大小‚方向 六个元素,已知任意四个元素,就能求出其它两个。
运动学/点的合成运动
例如,直管OB以匀角速度绕定轴O转动,小球M
以速度u在直管OB中作相对的匀速直线运动,如图示。 将动坐标系固结在OB管上,以小球M为动点。随着动 点M的运动,牵连点在动坐标系中的位置在相应改变。 设小球在t1、t2瞬时分别到达M1、M2位置,则动点的 牵连速度分别为
ve1 OM1
运动学/点的合成运动
第八章
点的合成运动
在前两章中研究点和刚体的运动时,认为地球( 参考体)固定不动,将坐标系(参考系)固连于地面。 因此,点和刚体的运动是相对固定参考系而言的。
理论力学.

2.速度分析: vavevr
大小:rω ? ?
方向:√ √ √
v e v as i n rs in
1
ve r2
O1A l2 r2
例7-4
已知:如图所示半径为R、偏心距为e的凸轮,以角速度ω 绕O轴转动,杆AB能在滑槽中上下平移,杆的端点A始终 与凸轮接触,且OAB成一直线。 求:在图示位置时,杆AB的速度。
求:当连线OM在水平位置时, 圆盘边缘上的点M的绝对速度。
D
C
M
B A
解: 1.运动分析:
动点:M点 ; 动系:固连于框架BACD;
绝对运动:未知;
相对运动:以O为圆心的圆周运动;
牵连运动:绕AB轴的定轴转动。
2.速度分析
C
vavevr
大小: ? Rω2 Rω 1
方向: ? √ √
vave 2 vr2R1 222
用铰链连接。当曲柄OA以匀角速度ω绕固定轴O转动时,
滑块在摇杆O1B上滑动,并带动杆O1B绕定轴O1摆动。设曲
柄长为OA=r,两轴间距离OO1=l。
求:曲柄在水平位置时摇杆的角 加速度。
解:
1.运动分析:
§动 绝牵点对连7-M运 运4相动动牵对、:连于相D运E地对动的面动绝运是水作动定平空点对、轴平间牵转移曲:运连动。线运时运滑动动点动的块:加速以度A合O;成点为动圆系心:,与O摇A杆为半固O径1 连B的;圆周运动;
arctvvaer)na( rct a1 2)n(
D M
B A
点的速度合成定理的解题步骤
1.选取动点、动参考系和定参考系; 2.分析三种运动和三种速度;
绝对运动、相对运动、牵连运动 绝对速度、相对速度、牵连速度 3.应用速度合成定理,做出速度平行四边形; 绝对速度为平行四边形的对角线 4.利用速度平行四边形中的几何关系解出未知数。
理论力学点的合成运动

B
va
O
vr
r
v
ve
A
C
第二节 点的速度合成定理
一、点的速度合成定理 在任一瞬时,动点的绝对速度等于其牵连速度和相对速度
的矢量和,即
va ve vr
二、运用点的速度合成定理的解题步骤
1. 适当选取动点和动系; 说明:选择动点、动系的基本原则 —— 1)动点、动系之间应有相对运动; 2)相对轨迹应简单易认; 3)在分析机构运动时,应选择常接触点为动点。
2
va
ve
vr C
O
[例6] 绕轴 O 转动的圆盘及直杆 OA 上均有一导槽,两导槽间有一
活动销子 M ,导槽与转轴之间的距离 b = 0.1m。图示位置时,圆
盘及直杆的角速度分别为 1 = 9 rad/s 和 2 = 3 rad/s。试求此瞬时
销子 M 的速度。
2
解: 1)选择动点与动系 动点:活动销子 M 动系:分别固连于圆盘和
O
2)运动分析 绝对运动: 圆周运动 相对运动: 沿滑槽 DE 的直线运动 牵连运动: 滑杆 CDE 的水平平移
3)速度分析
va
vr
va ve vr
4)求解未知量 将上述速度矢量方程两边分 别向 x、y 轴投影,得
ve
O
va sin ve vr cos 60 va cos vr sin 60
二、绝对运动、相对运动与牵连运动
1. 绝对运动
2. 相对运动 相对运动:动点相对于动系的运动 相对速度:动点相对于动系的速度,记作 vr 相对加速度:动点相对于动系的加速度,记作 ar
3. 牵连运动 牵连运动:动系相对于定系的运动。 牵连点:动系中与动点重合的点 牵连速度:牵连点相对于定系的速度,记作 ve 牵连加速度:牵连点相对于定系的加速度,记作 ae
理论力学 点的合成运动

例1. 梯子 AB 长 L , 重 P,一端 B 靠在光滑的铅垂墙上, 另一端 A 放在摩擦系数为 f 的水平地面上,问梯子与水 平线所成的倾角 多大时,梯子能处于平衡?
y
解:
对象:梯子 P , NB , NA , FAmax
B
P m NA RAmax
分析力:
NB
L 列方程: m A ( F ) N B L sin P cos 0 2
摩擦角和自锁现象
2.利用摩擦角判断物体是否平衡的两条规律
全约束力的作用线范围
0 m
m
m
R
若某接触面上的主动力的合力作用线在摩 擦角的范围之内,则不论此力有多大,物体 将永远平衡。--自锁现象
螺旋千斤顶 tg 1 f
m
f 0.1
5 43
例2. 已知排挡齿轮宽为 b,自重忽略不计,能在直径为 d 的轴上左右滑动。若齿轮与轴之间的摩擦系数为 f,求不 使齿轮被卡住,水平推力 P 的作用线离轴线的距离 a 的 y 范围。
解:
对象:排挡齿轮
d
NA A
P
a FA b
B m
分析力: P , NB , NA , FB , FA
FB NB
x
列方程:
Y N N 0 Y P F F 0
A B A B
RBmax
d mA ( F ) P(a ) N Bb FB d 0 2 FB fN B 摩擦定律: FA fN A
由式得 NA = NB 代入式
b a 2f
由式得 FA = FB = P/2 齿轮平衡
B A RBAmax RAmax RAmax RBAx 画封闭力三角形:
理论力学:第6章 点的合成运动

·1·第6章 点的合成运动6.1 主要内容6.1.1 点的绝对运动、相对运动和牵连运动1.定系和动系若存在两个有相对运动的坐标系,则可指定其中一个为定系,另一个即为动系。
但工程上一般以固定在地面上的坐标系为定系,相对于定系运动着的坐标系称为动系。
2.动点和牵连点动点为研究的对象,牵连点是动点在动系上的重合点,随动点的相对运动而变,是动系上的点,不同瞬时,有不同的牵连点。
3.三种运动的关系动点相对于定系的运动定义为绝对运动;动点相对于动系的运动定义为相对运动;动系相对于定系的运动定义为牵连运动。
本章的主要任务就是建立这三者之间的定量关系,从而用来解决工程实际某些运动分析问题。
6.1.2 点的速度合成定理动点的绝对速度等于它的牵连速度与相对速度的矢量和。
这就是点的速度合成定理。
a e r =+v v v6.1.3 牵连运动为平移时,点的加速度合成定理当牵连运动为平移时,动点的绝对加速度等于牵连加速度与相对加速度的矢量和。
a e r =+a a a6.1.4 牵连运动为转动时,点的加速度合成定理当牵连运动为转动时,动点的绝对加速度等于牵连加速度、相对加速度与科氏加速度的矢量和,这就是牵连运动为转动时点的加速度合成定理。
a e r C =++a a a a其中r C v a ⨯=ω2。
当取平动动系时0=e ω;0=C a 。
6.2 基本要求1.掌握运动合成与分解的基本概念和方法,准确理解本章阐述的若干概念。
2.明确动点与动系的选择原则,能在具体问题中恰当地选择动点与动系,并正确地分析三种运动。
3.熟练掌握点的速度合成定理和牵连运动为平动时的加速度合成定理及其应用。
4.掌握科氏加速度的概念和计算,准确应用牵连运动为转动时的加速度合成定理及其应用。
6.3 重点讨论应用点的合成运动理论解决实际问题时,其关键是正确地选择动点和动系。
选择原则因具体情况不同而略有区别。
常见的问题有三种题型。
1.两个独立运动的物体,研究两者的相对运动。
理论力学8—点的合成运动

(2) 应用速度合成定理时,可利用速度平行四边形中的 几何关系解出未知数。也可以采用投影法:即等式左 右两边同时对某一轴进行投影,投影的结果相等。
7.2 点的速度合成定理
通常选动点和动系主要有以下几种情况: 1. 有一个很明显的动点,在题中很容易发现;
2. 有一个不变的接触点,可选该点为动点;
3. 没有不变的接触点,此时应选相对轨迹容易确 定的点为动点; 4. 必须选某点为动点,而动系要取两次; 5. 根据题意,必须取两次动点和动系; 6. 两个不相关的动点,可根据题意来确定;
=ωt, 已知:r,相对速度v,
求:点M的绝对运动方程。
t0
0。
解:
动点:M 点 动 系 : O x y
相对运动方程
OO x O M cos 1 1 O y M sin 1
代入
vt r
=ωt, 已知:r,相对速度v,
求:点M的绝对运动方程。
vt x r 1 cos r y r sin vt r
第 7 章
点的合成运动
8.1 相对运动· 牵连运动· 绝对运动
8.2 点的速度合成定理
8.3 点的加速度合成定理
7.1 相对运动· 牵连运动· 绝对运动
一、方法及思想起源
运动合成的思想我们 大家都很熟悉,比如说右 边直升飞机螺旋桨端的P 点,其运动就可以分解为: “随螺旋桨一起相对飞机 机身的运动”和“随机身 一起在空中的移动”。你 们可以试着点击一下图片, 看看运动合成的情况。
A
y`
转轮
x
现在我们可以这样陈述:动点A相对于坐标架xoy的运动(螺旋 线),可以分解为动点相对于坐标架x`oy`的运动(直线运动)和坐 标架x`oy`相对于坐标架xoy的运动(定轴转动)。
理论力学(第7版)第七章 点的合成运动

ar ~ d 2r dt 2
xi j k y z
ae
d 2 rM dt 2
xi yj zk rO
?
√ √ √ √ 将加速度矢量式投影到法线上,得
a a sin a e cos
大小 方向
aa a e a r a r ? a0 R? √
?
n
n
ar
n
aa (ae cos ar n ) / sin
整理得
a AB
2 3 8 v0 aa (a0 ) 3 3 R
称为动参考系,简称动系。例如在行驶的 汽车。以o’x’y’z’坐标系表示。
[注]: 1、参考系须指明固结于哪个参考体上,选择参 考体是选择参考系的关键。 2、动系与参考体有区别:参考体是有限的,而 参考坐标系是无限大的,故动系无限大。
3
7-1 相对运动 牵连运动 绝对运动
二、三种运动
1.绝对运动:动点对定系的运动 2.相对运动:动点对动系的运动
2 (aa aen )sin 30 3O r (l r ) aet cos 30 3l
BD
2 aet 3O r (l r ) BD 3l 2
28
7-4 牵连运动是定轴时点的加速度合成定理 科氏加速度
1、牵连运动为转动情况:
定理推导:
rM rM
r xi yj z k
3、 v a v e v r 大小 r ? ?
ve r 2 1 2 O1 A l r 2
方向 OA O1B //O1B ve va sin r sin
理论力学第六章点的合成运动

PDF 文件使用 "pdfFactory Pro" 试用版本创建
例6-6:三角楔块可在光滑地面滑动,现在楔块上放一物块可
沿光滑斜面滑下,当t=0,x=0,y=h,v2=0,a1=10cm/s2 , a2=10 2cm/s2,试求:物块轨迹方程。
解: aax= a1+ a2 cos450 =20cm/s2;
υϖa = υϖe +υϖr
绝对速度
相对速度
牵连速度
速度合成定理 —— 动点的绝对速度等于其牵连速 度与相对速度的的矢量和。
22
PDF 文件使用 "pdfFactory Pro" 试用版本创建
例6-1:雨铅垂下落,客车以匀速v行驶,在无风时下雨打在 窗玻璃上 的夹角为θ,试求:雨的速度。
10
PDF 文件使用 "pdfFactory Pro" 试用版本创建
运动的分解:动点动系的选择
11
PDF 文件使用 "pdfFactory Pro" 试用版本创建
若选杆为动系,圆上一点为动点
12
PDF 文件使用 "pdfFactory Pro" 试用版本创建
例6-5:曲柄滑道机构,OA=O1A=r=10cm, θ= ϕ , ω=4π, 试求:ϕ 转到300时直杆的加速度a。
解:动点取A; 绝对:圆周;
va
vr
相对:圆周;牵连:平动;
ve
ω
[速度]
y: vacos300=vrcos300;
va= ω r=40 π; vr= va= ω r=40 π ,
选法2 Х
19
PDF 文件使用 "pdfFactory Pro" 试用版本创建
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章点的合成运动一、是非题1、不论牵连运动的何种运动,点的速度合成定理v a=v e+v r皆成立。
()2、在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相对加速度的矢量和。
()3、当牵连运动为平动时,相对加速度等于相对速度对时间的一阶导数。
()4、用合成运动的方法分析点的运动时,若牵连角速度ωe≠0,相对速度υr≠0,则一定有不为零的科氏加速度。
()5、若将动坐标取在作定轴转动的刚体上,则刚体内沿平行于转动轴的直线运动的动点,其加速度一定等于牵连加速度和相对加速度的矢量和。
()6、刚体作定轴转动,动点M在刚体内沿平行于转动轴的直线运动,若取刚体为动坐标系,则任一瞬时动点的牵连加速度都是相等的。
()7、当牵连运动定轴转动时一定有科氏加速度。
()8、如果考虑地球自转,则在地球上的任何地方运动的物体(视为质点),都有科氏加速度。
()二、选择题1、长L的直杆OA,以角速度ω绕O轴转动,杆的A端铰接一个半径为r的圆盘,圆盘相对于直杆以角速度ωr,绕A轴转动。
今以圆盘边缘上的一点M为动点,OA为动坐标,当AM垂直OA时,点M的相对速度为。
①υr=Lωr,方向沿AM;②υr=r(ωr-ω),方向垂直AM,指向左下方;③υr=r(L2+r2)1/2ωr,方向垂直OM,指向右下方;④υr=rωr,方向垂直AM,指向在左下方。
2、直角三角形板ABC,一边长L,以匀角速度ω绕B轴转动,点M以S=Lt的规律自A向C运动,当t=1秒时,点M的相对加速度的大小αr= ;牵连加速度的大小αe = ;科氏加速度的大小αk = 。
方向均需在图中画出。
①Lω2;②0;③3Lω2;④23 L ω2。
3.圆盘以匀角速度ω0绕O 轴转动,其上一动点M 相对于圆盘以匀速u 在直槽内运动。
若以圆盘为动系,则当M 运动到A 、B 、C 各点时,动点的牵连加速度的大小 ,科氏加速度的大小 。
①相等;②不相等;③处于A ,B 位置时相等。
4.一动点在圆盘内运动,同时圆盘又绕直径轴x以角速度ω转动,若AB ∥OX ,CD ⊥OX ,则当动点沿 运动时,可使科氏加速度恒等于零。
①直线CD 或X 轴;②直线CD 或AB ;③直线AB 或X 轴;④圆周。
三、填空题1.直角曲杆O 1AB 以匀角速度ω1绕O 1轴转动,则在图示位置(AO 1垂直O 1O 2)时,摇杆O 2C 的角速度为 。
2.已知杆OC 长L 2,以匀角速度ω绕O 转动,若以C 为动点,AB 为动系,则当AB 杆处于铅垂位置时点C 的相对速度为υr = ,方向用图表示;牵连速度υe = ,方向用图表示。
3.在图示平面机构中,杆AB=40cm ,以ω1=3rad/s的匀角速度绕A 轴转动,而CD 以ω2=1rad/s 绕B 轴转动BD=BC=30cm ,图示瞬时AB ⊥CD 。
若取AB 为动坐标,则此时D 点的牵连速度的大小为 ,牵连加速度的大小为 (方向均须在图中画出)。
4.系统按S=a+bsin ωt 、且φ=ωt (式中a 、b 、ω均为常量)的规律运动,杆长L ,若取小球A 为动点,物体B 为动坐标系,则牵连加速度 e = ,相对加速度 r = (方向均须由图表示)。
5.曲柄连杆机构在图示位置时,曲柄的角速度为ω0若以AB 为动系,套筒M 相对于AB 的速度为u r ,则套筒M的科氏加速度k 的大小为 。
6.已知半径为R 的圆盘平面与铅直轴成30°角,以匀角速度ω转动。
轮缘上有一点M ,以相对于盘的速度u r沿圆盘边缘运动。
则M 点经过水平直径AB 的端点A 时的科氏加速度为 (方向在图上表示)。
四、计算题1.直角曲杆OCD 在图示瞬时以角速度ω0(rad/s )绕O 轴转动,使AB 杆铅锤运动。
已知OC=L (cm )。
试求φ=45°时,从动杆AB 的速度。
2.矩形板ABCD 边BC=60cm ,AB=40cm 。
板以匀角速度ω=0.5(rad/s )绕A 轴转动,动点M 以匀速u=10cm/s沿矩形板BC 边运动,当动点M 运动到BC 边中点时,板处于图示位置,试求该瞬时M 点的绝对速度。
3.杆CD 可沿水平槽移动,并推动杆AB 绕轴A 转动,L 为常数。
试用点的合成运动方法求图示位置θ=30°时,CD 杆的绝对速度u 。
4.沿铅直轨道运动的T 字杆AB ,其上的销钉C 插在半径为R 的圆槽内,带动物块D 沿水平方向运动。
在图示位置,AB 杆的速度为u,方向如图示, =30°。
试求此瞬时物块D 的速度。
5.联合收获机的平行四边形机械在铅垂面内运动。
已知:曲柄OA=O 1B=500mm ,OA 转速n=36r/min ,收获机的水平速度u=2km/h 。
试求在图示位置 =30°时,AB杆的端点M 的水平速度和铅垂直速度。
6.直角杆OAB 可绕O 轴转动,圆弧形杆CD 固定,小环M 套在两杆上。
已知:OA=R ,小环M 沿DC 由D 往C作匀速运动,速度为u=R 31,并带动OAB 转动。
试求OA 处于水平线OO 1位置时,杆OAB 上A 点的速度。
7.图示轮O 1和O 2,半径均为r ,轮O 1转动角速度为ω,并带动O 2转动。
某瞬时在O 1轮上取A 点,在O 2轮上与O 2A 垂直的半径上取B 点,如图所示。
试求:该瞬时(1)B 点相对于A 点的相对速度;(2)B 点相对于轮O 1的相对速度。
8.在图示平面机构中,已知:AD=BE=L ,且AD平行BE ,OF 与CE 杆垂直。
当 =60°时,BE 杆的角速度为ω、角加速度为 。
试求止瞬时OF 杆的速度与加速度。
9.具有半长R=0.2m 的半圆形槽的滑块,以速度u 0=1m/s ,加速度 0=2m/s 2水平向右运动,推动杆AB 沿铅垂方向运动。
试求在图示 =60°时,AB 杆的速度和加速度。
10.图示一曲柄滑块机构,在滑块上有一圆弧槽,圆弧的半径R=3cm ,曲柄OP=4cm 。
当 =30°时,曲柄OP 的中心线与圆弧槽的中心弧线MN 在P 点相切,这时,滑块以速度u=0.4m/s 、加速度 0=0.4m/s 2向左运动。
试求在此瞬时曲柄OP 的角速度ω与角加速度 。
11.小车上有一摆杆OM ,已知:OM=R=15cm ,按t 2cos 31 规律摆动,小车按X=21t 2+15t 沿X 轴方向运动,式中 以rad 计,X 以cm 计,t 以s 计。
试求:t=1/6s 时摆杆端点M 的速度和加速度。
12.荡木AB 在图示平图内摆动,小车沿直线运动。
已知:AB=CD ,AC=BD=2.5m 。
在图示位置时,CA 的角速度和角加速度分别为ω=1rad/s 、2/3s rad ,小车G 的速度和加速度分别为u 0=3m/s 、 0=1m/s 2(方向如图所示), =45°,β=30°,GE=3m 。
试求该瞬时小车G 相对于荡木AB 的速度和加速度。
13.圆盘O 轴转动,图示位置时角速度ω=2rad/s 、角加速度 =1rad/s 2,B 点沿槽(b=20cm )的速度为30cm/s 、加速度为40cm/s 2,方向如图示。
试求图示瞬时(c=10cm )动点B 的绝对速度和绝对加速度。
14.当杆OC 转动时,通过杆OC 上的销子A 带动EBD 绕B 摆动,在图示瞬时,杆OC 的角速度ω=2rad/s ,角加速度为零,BA ⊥OC ,AB=L=15cm , =45°。
试求该瞬时EBD 的角速度ωB 和角加速度ωB 。
15.半径r 的圆环以匀角速度ω绕垂直于 纸面的O轴转动,OA 杆固定于水平方向,小环M 套在大圆环及杆上。
试用点的合成运动方法求当OC 垂直于CM 时,小环M 的速度和加速度。
16.已知:OA 杆以匀角速度ω0=2rad/s 绕O 轴转动,半径r=2cm 的小轮沿OA 杆作无滑动的滚动,轮心相对OA杆的运用规律b=4t 2(式中b 以cm 计,t 以s 计)。
当t=1s时, =60°,试求该瞬时轮心O 1的绝对速度和绝对加速度。
17.圆形板按 =t-0.5t 3绕过水平直径的轴AB 转动,动点M 沿板上半径为R=30cm 圆槽按OM=b=10t 2cos 2的规律运动,式中 以rad 计,b 以cm 计,t 以s 计。
当t=1/8s 时圆形板位于图示位置。
试求该瞬时动点M 的加速度在X 、Y 、Z 各坐标轴上的投影。
第六章 点的合成运动参考答案一、是非题答案1.对 2.错 3.对 4.错 5.对 6.错 7.错 8.错二、选择题1.④ 2.②;①;④ 3.②;① 4.③三、填空题1.02.u r =L ·ω; u e =L ·ω(图略)3.150cm/s; 450cm/s 24.);cos(2t b s a e0,22 r n r a L L a a k =0(图略)。
5.a k =06.a k =2ωu r sin30°=ω·u r四、计算题1.解:以AB 杆上的A 点为动点,动系固连于OCD 杆。
根据r e a V V V得:V a =V e =OA ·ω0=1.41ω0L cm/s方向:铅直向下2.解:动点:M ,动系:ABCD ,牵连转动3.解:以CD 杆上的D 点为动点,动系固连于AB 杆,根据r e a V V V 由速度分析图,知V a =uu=2Ve=2ωL/sin =4ωL方向:水平向右4.解:取销钉C 为动点,动系固连于物块D ,据速度分析图 得 Ve=Vtg =0.58V (→)方向:水平向右5.解:动点M ,动系:收获机,牵连平动u r =0.5×2π×36/60=1.38cm/su s =0.56m/su x =u r cos30°-u e =1.07m/su r =- u r sin30°=-0.94m/s6.解:动点:小环M ,动系:OAB ,牵连转动a u =e u +r u∴u a =u e cos =u e cos45°u a =3/22R u aω0=u a /OM= /3,顺时针u A =OA ·ω0=R /3↑7.解:(1)动点:B 点, 动系:O 1轮上的A 点,牵连平均a u =e u +r u∴u r =(u e 2+u a 2)1/2= r 2=45° (2)动点:B 点,动系:轮O 1,牵连转动a u =e u +r u u e =ω·[(2r)2+r 2]1/2= r 5u a =r ωu r =[ u e 2+u a 2-2u e u a cos(e u a u)]1/2 = r 228.解:取滑块上的F 点为动点,动系固连于CDE 杆,牵连运动为平动1.由r e a V V V (1)∵CDE 平动,∴V e =V E = ωL ∴21cos L V V e a 2.由r e n e a (2) 而a e n =a E n =ω2L , a e =a E = L(2)式在铅垂投影,得a a =a e n sin -a e cos =0.866L ω2-0.5L ↓9.解:取AB 杆上的A 点为动点,动系固连于滑块上,牵连运动为平动1.由r e a V V V (1)得A 点速度则V a =V e tg30°=m/s 577.0331 而V r =V e /cos30°=m /s 16.13/322.由nr r e a (2)得A 点加速度将(2)式向n 方向投影得:a a cos30°=a e sin30°+a r n而 a e =a 0 a r n =Vr 2/R∴ a e =(a e sin30°+a r n )/cos30=8.85 m/s 210.解:取曲柄端点P 为动点,动系固连于滑块,牵运动为平动1.由r e a V V V (1) 得P 点速度则V a =V e sin30°=0.2 m/s∴rad/s 5/ P O V a而V r =V e cos30°=0.23 m/s2.由n r r e n a a (2) 得P 点加速度分析将(2)式向X 轴投影得a a =a e sin30°-a r n而a r n =V r 2/R=4 m/s 2∴ a a =0.2-4=-3.8 m/s 2∴ = a a / P O =-3.8/0.04=-95 rad/s 211.解:动点M ,动系:小车,牵连平均t=1/6s 时:12.解:动点:G ,动系:AB ,牵连平动13.解:取B 为动点,动系固连于圆盘,速度及加速度分析14.解:取销子A 为动点,EBD 为动系(1)计算EBD 角速度 B据r e a V V VV a =L =30 cm/sV e =30 cm/s, Vr=230 cm/s, B =V e /L=2 (rad/s)(2)计算EBD 角加速度 Bk r n e e a(*) 将(*)式在k投影得15.解:以小环M 为动点,圆环为动系(1)求M V(2)求M16.解:动点:轮心O 1,动系:OA 杆,牵连转动17.解:动点:M ,动系:圆板,牵连转动t=1/8s 时:b=10 (cm), = b/R = 10 /30= /3 (rad) 22202sin 220 t u r(cm/s) 方向与图示相反33402cos 240t r (cm/s 2) 方向与图示相反。
