方差分析资料报告几个案例
实验4--方差分析报告

学院:数学与统计学院专业:数学与应用数学学号::君波实验六方差分析一、实验目的通过本次实验,了解如何进展各种类型均值的比拟与检验。
二、实验性质必修,根底层次三、主要仪器与试材计算机与SPSS软件四、实验容单因素方差分析五、实验学时2学时单因素方差分析(One-Way ANOVA过程)1.某城市从4个排污口取水,进展某种处理后检测大肠杆菌数量,单位面积菌落数如下表所示,请分析各个排污口的大肠杆菌数量是否有差异。
排污口 1 2 3 4 大肠杆菌数量9,12,7,5 20,14,18,12 12,7,6,10 23,13,16,21实验步骤:首先建立“数据视图〞→单击“分析(A)〞→选择“比拟均值〔M〕〞→选择“单因素ANOV A〞→将“大肠杆菌数量〞选入到“因变量列表(E)〞→将“排污口〞选入到“因子〞中→在“选项〔O〕〞中的“描述性〔D〕〞、“方差同质性检验〔H〕〞、“均值图〔M〕〞上打勾→点击“继续〞→点击“确定〞。
运行过程与结果:变量视图:数据视图:运行结果:结果分析:①在“描述〞图表中给出了四个排污口的大肠杆菌数量的根本描述性统计量。
包括样本容量、样本均值、标准差、标准误差、均值的95%的置信区间、最小值和最大值;②在“方差齐性检验〞图表中P值为0.329,假如我们给定显著性水平为0.05,P大于0.05,承受原假设,认为四个总体的方差相等;③在“ANOVA〞图表中假如取显著性水平0.05,因为P=0.003,所以P小于0.05,拒绝原假设,认为各个排污口的大肠杆菌数量存在显著差异;④在“均值图〞中可以看出第四个排污口大肠杆菌数量最多,第一个排污口大肠杆菌数量最少。
2.某连锁商场有五个连锁分店。
希望比拟这五个分店的营业额是否一样,调查人员各自独立地从这五个分店中取得12个营业日的日营业额,资料见下表:连锁店营业日第一分店第二分店第三分店第四分店第五分店1 924 994 1160 1072 9492 1094 1270 1185 1011 11213 1000 1261 1292 961 11594 948 1034 1319 1229 10495 1066 1542 1101 1238 9526 923 1258 1246 1035 10977 823 1215 1340 1240 11448 1035 978 1019 947 9589 1130 1316 1224 1110 91710 1019 1005 967 955 107711 985 944 1221 1091 96712 957 1295 1210 916 1039以α=的显著性水平检验“这五个分店的日营业额一样〞这一假设。
方差分析介绍及案例分析

P
(6) <0.05 >0.05 >0.05
q0.05,(57,3)=3.40
q0.05,(57,2)=2.83
结论
总的说来,三种治疗方案的治疗婴幼儿贫血 疗效有差别。而这种差别主要来自A方案和C
方案。这一结论可用下列形式表示:
A 1.840 B 1.415 C 0.930
多个实验组与一个对照组均数间的 两两比较
单因素多个样本均数的比较 (analysis of one way variance)
处理因素只有一个 属于完全随机设计:随机抽样 随机分组 随机试验
C X
2
N
2
SS总 X C
SS组间 ni X i X
2
2
Xi
ni
2
C
SS组内 si ni 1 SS总 SS组间
总=总例数-1=20-1=19 处理=处理组数-1=4-1=3 配伍=配伍组数-1=5-1=4 误差=总-处理-配伍=19-3-4=12
列方差分析表
变异来源 总 处理 配伍 误差 表 6.8 两因素方差分析表 SS MS 0.74128 19 0.41084 3 0.13695 0.11233 4 0.02808 0.21811 12 0.01818 F 7.53 1.54 P < 0.01 > 0.05
1.840 0.913 15.8482
1.415 1.297 31.9669 59.3755
0.930 0.78 11.5626
变异分解
组间变异
总变异
组内变异
SS总=SS组间+SS组内
方差分析举例范文

方差分析举例范文方差分析(Analysis of Variance, ANOVA)是一种用于比较两个或以上样本均值是否存在显著差异的统计方法。
它通过分析变量的方差来推断不同处理条件(或不同组)之间的均值是否差异显著。
下面将给出三个不同领域的方差分析举例。
1.生物学实验:假设我们对一种新药的有效性进行测试,研究对象分为三组,分别服用不同剂量的药物A、B、C。
我们想要知道不同剂量的药物是否对指标变量(例如疼痛程度)产生显著影响。
我们将随机选取若干个人,将他们分配到三组中,并测量他们的疼痛程度。
在完成实验后,我们可以使用方差分析来比较每个组的均值差异是否显著。
如果方差分析结果显示剂量组之间的差异是显著的,那么我们可以得出结论:不同剂量的药物会对疼痛程度产生显著影响。
2.教育研究:假设我们正在比较两种不同的教学方法对学生学习成绩的影响。
一个学校将两个班级随机分配到两个教学组,一组采用传统的讲授式教学方法,另一组采用互动式教学方法。
在教学实验结束后,我们可以通过方差分析来比较两组学生的平均成绩是否有显著差异。
如果方差分析结果显示两个组之间的差异是显著的,那么我们可以得出结论:互动式教学方法对学生成绩的影响较传统教学方法更好。
3.工程研究:假设我们正在评估两种不同材料的耐磨性能。
我们可以将两种材料随机分配到两个实验组,并通过对每个组进行多次磨损实验来测量其耐磨性能。
然后,我们可以使用方差分析来比较两组材料的平均耐磨性能是否有显著差异。
如果方差分析的结果表明两种材料之间的差异是显著的,那么我们可以得出结论:这两种材料的耐磨性能是不同的,其中一种材料更加耐磨。
总结:方差分析是一种用于比较多个组之间平均值差异的有力工具,它可以应用于各个领域。
在生物学实验中,方差分析可以用于比较不同处理条件对一些指标变量的影响;在教育研究中,方差分析可以用于比较不同教学方法对学生成绩的影响;在工程研究中,方差分析可以用于比较不同材料性能的差异。
单因素方差分析报告完整实例

什么是单因素方差分析单因素方差分析是指对单因素试验结果进行分析,检验因素对试验结果有无显著性影响的方法。
单因素方差分析是两个样本平均数比较的引伸,它是用来检验多个平均数之间的差异,从而确定因素对试验结果有无显著性影响的一种统计方法。
单因素方差分析相关概念●因素:影响研究对象的某一指标、变量。
●水平:因素变化的各种状态或因素变化所分的等级或组别。
●单因素试验:考虑的因素只有一个的试验叫单因素试验。
单因素方差分析示例[1]例如,将抗生素注入人体会产生抗生素与血浆蛋白质结合的现象,以致减少了药效。
下表列出了5种常用的抗生素注入到牛的体内时,抗生素与血浆蛋白质结合的百分比。
现需要在显著性水平α = 0.05下检验这些百分比的均值有无显著的差异。
设各总体服从正态分布,且方差相同。
在这里,试验的指标是抗生素与血浆蛋白质结合的百分比,抗生素为因素,不同的5种抗生素就是这个因素的五个不同的水平。
假定除抗生素这一因素外,其余的一切条件都相同。
这就是单因素试验。
试验的目的是要考察这些抗生素与血浆蛋白质结合的百分比的均值有无显著的差异。
即考察抗生素这一因素对这些百分比有无显著影响。
这就是一个典型的单因素试验的方差分析问题。
单因素方差分析的基本理论[1]与通常的统计推断问题一样,方差分析的任务也是先根据实际情况提出原假设H0与备择假设H1,然后寻找适当的检验统计量进行假设检验。
本节将借用上面的实例来讨论单因素试验的方差分析问题。
在上例中,因素A(即抗生素)有s(=5)个水平,在每一个水平下进行了n j = 4次独立试验,得到如上表所示的结果。
这些结果是一个随机变量。
表中的数据可以看成来自s个不同总体(每个水平对应一个总体)的样本值,将各个总体的均值依次记为,则按题意需检验假设不全相等为了便于讨论,现在引入总平均μ其中:再引入水平A j的效应δj显然有,δj表示水平A j下的总体平均值与总平均的差异。
利用这些记号,本例的假设就等价于假设不全为零因此,单因素方差分析的任务就是检验s个总体的均值μj是否相等,也就等价于检验各水平A j的效应δj是否都等于零。
方差分析实例详解

方差分析计算实例一、单因素方差分析二、双因素方差分析一、单因素方差分析(一)完全随机试验设计1、重复数相同(1)实例:不同浇水量对某蔬菜产量的影响试验,设置5个浇水量A、B、C、D、E;每个浇水量设置四个小区,小区采用完全随机试验设计;各小区产量见下表(单位:kg)(2)基本参数计算处理数k=5,重复数n=4220.0250.9750.485,11.143χχ==(3)方差同质性检验2220.0250.975,c χχχ≤≤五个处理的方差无显著差异平方和计算:(4)方差分析自由度计算:方差分析表:22222222/()/()(45.2869.5288.55108.48130.12)/4441.95/(45)1089.89t i ij SS T n x nk =−=++++−⨯=∑∑1107.051089.8917.16e T t SS SS SS =−=−=222222()/()16.6115.9531.11441.95/(45)1107.05T ijij SS x x nk =−=+++−⨯=∑∑1514t df k =−=−=(1)5(41)15e df k n =−=−=145119T df nk =−=⨯−=变异来源平方和自由度均方F 值F 0.05处理间1089.894272.47238.213.056误差17.1615 1.14总变异1107.0519F 值大于F 0.05,五个处理蔬菜产量平均值差异显著。
将五个处理小区产量平均值从大到小排列,采用字母标记法表示各均值间差异是否显著,均值间的差值大于LSD ,差异显著,标记不同的字母;均值间的差值小于LSD ,差异不显著,标记相同的字母。
标记字母时,第一个值标a ,用最大值减第二个值,差值若大于LSD 则标b ,差值若小于LSD 则标a ,再以最大值减第三个值,直到出现大于LSD 值,标记b ,再以该值为标准向上比较,若差值大于LSD 就停止比较,若小于LSD 值则在a 后面加上b ,直至出现差值大于LSD 就停止比较;再以最上面标记b 的均值为标准在向下比较;直到所有的平均值都标记字母。
方差分析研究几个案例

方差分析方法方差分析是统计分析方法中,最重要、最常用地方法之一.本文应用多个实例来阐明方差分析地应用.在实际操作中,可采用相应地统计分析软件来进行计算.1. 方差分析地意义、用途及适用条件1.1 方差分析地意义方差分析又称为变异数分析或F检验,其基本思想是把全部观察值之间地变异(总变异),按设计和需要分为二个或多个组成部分,再作分析.即把全部资料地总地离均差平方和(SS)分为二个或多个组成部分,其自由度也分为相应地部分,每部分表示一定地意义,其中至少有一个部分表示各组均数之间地变异情况,称为组间变异(MS组间);另一部分表示同一组内个体之间地变异,称为组内变异(MS组内),也叫误差.SS除以相应地自由度(υ),得均方(MS).如MS组间>MS组内若干倍(此倍数即F值)以上,则表示各组地均数之间有显著性差异.方差分析在环境科学研究中,常用于分析试验数据和监测数据.在环境科学研究中,各种因素地改变都可能对试验和监测结果产生不同程度地影响,因此,可以通过方差分析来弄清与研究对象有关地各个因素对该对象是否存在影响及影响地程度和性质.1.2 方差分析地用途1.2.1 两个或多个样本均数地比较.1.2.2 分离各有关因素,分别估计其对变异地影响.1.2.3 分析两因素或多因素地交叉作用.1.2.4 方差齐性检验.1.3 方差分析地适用条件1.3.1 各组数据均应服从正态分布,即均为来自正态总体地随机样本(小样本).1.3.2 各抽样总体地方差齐.1.3.3 影响数据地各个因素地效应是可以相加地.1.3.4 对不符合上述条件地资料,可用秩和检验法、近似F值检验法,也可以经过变量变换,使之基本符合后再按其变换值进行方差分析.一般属Poisson分布地计数资料常用平方根变换法;属于二项分布地百分数可用反正弦函数变换法;当标准差与均数之间呈正比关系,用平方根变换法又不易校正时,也可用对数变换法.2. 单因素方差分析(单因素多个样本均数地比较)根据某一试验因素,将试验对象按完全随机设计分为若干个处理组(各组地样本含量可相等或不等),分别求出各组试验结果地均数,即为单因素多个样本均数.用方差分析比较多个样本均数地目地是推断各种处理地效果有无显著性差异,如各组方差齐,则用F检验;如方差不齐,用近似F值检验,或经变量变换后达到方差齐,再用变换值作F检验.如经F检验或近似F值检验,结论为各总体均数不等,则只能认为各总体均数之间总地来说有差异,但不能认为任何两总体均数之间都有差异,或某两总体均数之间有差异.必要时应作均数之间地两两比较,以判断究竟是哪几对总体均数之间存在差异.在环境科学研究中,常常要分析比较不同季节对江、河、湖水中某种污染物地含量有无显著性影响;各种气象条件如风向、风速、温度对大气中某种污染物含量地影响等问题.我们把季节、风向、风速、温度等称为因素.仅按不同季节,或不同地风向,或不同地温度来分组,称为单因素.例1 某年度某湖不同季节湖水中氯化物含量(mg/L)测定结果如表—6.1所示.试比较不同季节湖水中氯化物含量有无显著性差异.从表—1地测定结果可见有三种变异:1. 组内变异:每个季节内部地各次测定结果不尽相同,但显然不是季节地影响,而只是由于误差(如个体差异、随机测量误差等)所致.2. 组间变异:各个季节地均数也不相同,说明季节对湖水中氯化物地含量可能有一定地影响,也包括误差地作用.3.总变异:32次测定结果都不尽相同,既可能受季节地影响,也包括误差地作用.不同季节湖水中氯化物含量地均数之间地变异究竟是由于误差所致,还是由于不同季节地影响,可以用方差分析来解决此问题.方差分析可表示:⑴从总变异中分出组间变异和组内变异,并用数量表示变异地程度.⑵将组间变异和组内变异进行比较,如二者相差甚微,说明季节影响不大;如二者相差较大,组间变异比组内变异大得多,说明季节影响不容忽视.以下是三种变异地计算方法:3.1 多个方差地齐性检验已知多个样本(理论上均来自正态总体)方差,可以据此推断它们所分别代表地总体方差是否相等,即多个方差地齐性检验.其常用于:⑴说明多组变量值地变异度有无差异.⑵方差齐性检验.以例1为例(各组样本含量相等),如表—4所示.3.确定P值:根据υ=4—1=3,查附表—12得P<0.005.4.判断结果:由于P<0.005,因此,四组方差不齐.3.2 近似F值检验(F'检验)以例2为例,如表—6所示.公式26最常用,公式27适用于原数据中有小值和零时.K为常数,可以根据需要选用合适地数值.⑵对数变换地用途:①当几个样本均数作比较时,如样本方差不齐,尤其是当标准差与均数之比地比值接近时,必须经对数变换以缩小各方差之间地差别,达到方差齐后才能进行t检验或方差分析.②适用于呈对数正态分布地资料.③在曲线拟合中,对数变换常常是直线化地重要手段,如指数曲线、双曲线、logistic曲线地直线化等.例3 欲用t检验比较某河丰水期和枯水期地河水BOD5(mg/L)含量均数,资料如表—7所示.此数据能否直接用t检验方法?如不能,试作变量变换.二者比较接近,可以试用对数变换.⑶将X作“lgX +1”变换后,再作方差齐性检验,得F=1.72,P>0.05,两组方差齐,可以用变换值作两样本均数比较地t检验.2.平方根变换以原数据地平方根作为统计分析地变量值,称为平方根变换.⑴平方根变换地形式:⑶百分数地概率单位变换:主要用于S形或反S形曲线地直线化、正态性检验,尤其适用于剂量反应曲线地直线化.⑷百分数地logit变换:主要用于S形或反S形曲线地直线化.⑸反双曲正切变换:用于两直线相关系数地比较与合并.4. 两因素方差分析(双因素多个样本均数地比较)将试验对象按性质相同或相近者组成配伍组,每个配伍组有三个或三个以上试验对象,然后随机分配到各个处理组.这样,分析数据时将同时考虑两个因素地影响,试验效率较高.例5 某市为了研究一日中不同时点以及不同区域大气中氮氧化物含量地变化情况,该市环保所于某年1月15~19日,在市区选择了7个采样点,对大气中氮氧化物地含量进行测定.表—9为各个采样点每个时点五天地平均含量,试分析不同时点、不同区域氮氧化物含量之间有无显著性差异.5. 多因素方差分析(多因素多个样本均数地比较)在环境科学研究中,所研究地事物或现象往往是比较复杂地多因素问题,而各种因素本身尚有程度地差别,其间往往又存在交互作用.当研究地因素在三个或三个以上时,可以用正交试验法.正交试验是一种高效、快速地多因素试验方法.正交试验地设计与分析见另外章节.“多因素多个样本均数地比较”不仅可以用于正交试验,也可以用于拉丁方试验分析与析因试验分析等.6.多个样本均数间地两两比较(多重比较)经方差分析后,如果各总体均数有显著性差异时,常需进一步确定哪两个总体均数间有显著性差异,哪两个之间无显著性差异.因此,可以利用方差分析提供地信息作样本均数间地两两比较.以例5为例:(每组样本含量相等)经方差分析后,认为不同时点以及不同区域地氮氧化物含量之间均有高度显著性差异.现在需要进一步检验不同时点地氮氧化物含量均数两两之间有无显著性差异.检验步骤如下:1.检验假设:各时点地氮氧化物含量均数之间两两相等.⑷q值地计算方法与上例相同.3.确定P值与判断结果如表—13所示.版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.TIrRGchYzg 用户可将本文地内容或服务用于个人学习、研究或欣赏,以及其他非商业性或非盈利性用途,但同时应遵守著作权法及其他相关法律地规定,不得侵犯本网站及相关权利人地合法权利.除此以外,将本文任何内容或服务用于其他用途时,须征得本人及相关权利人地书面许可,并支付报酬.7EqZcWLZNXUsers may use the contents or services of this article for personal study, research or appreciation, and othernon-commercial or non-profit purposes, but at the same time, they shall abide by the provisions of copyright law and other relevant laws, and shall not infringe upon the legitimate rights of this website and its relevant obligees. In addition, when any content or service of this article is used for other purposes, written permission and remuneration shall be obtained from the person concerned and the relevant obligee.lzq7IGf02E转载或引用本文内容必须是以新闻性或资料性公共免费信息为使用目地地合理、善意引用,不得对本文内容原意进行曲解、修改,并自负版权等法律责任.zvpgeqJ1hkReproduction or quotation of the content of this article must be reasonable and good-faith citation for the use of news or informative public free information. It shall not misinterpret or modify the original intention of the content of this article, and shall bear legal liability such as copyright.NrpoJac3v1。
单因素方差分析完整实例

单因素方差分析完整实例假设有一家医院的研究人员想要比较三种不同药物对高血压患者的降压效果。
为了进行实验,他们随机选择了60名患有高血压的病人,并将他们随机分成三组。
第一组患者接受药物A的治疗,第二组患者接受药物B的治疗,第三组患者接受药物C的治疗。
在治疗开始前,研究人员记录了每个患者的收缩压数据。
第一步是对数据进行描述性统计分析。
研究人员计算了每一组的平均值、标准差和样本量。
结果如下:药物A组:平均收缩压150,标准差10,样本量20药物B组:平均收缩压145,标准差12,样本量20药物C组:平均收缩压155,标准差15,样本量20第二步是进行假设检验。
研究人员的零假设是所有药物的降压效果相同,即三组的平均收缩压相等。
备择假设是至少有一组的平均收缩压不同。
为了进行单因素方差分析,我们需要计算组内方差和组间方差,然后进行F检验。
组内方差反映了每一组内部数据的离散程度,组间方差反映了不同组之间平均值的差异程度。
组内方差的计算方法是对每一组的方差进行平均,然后再对所有组的方差进行加权平均。
组间方差的计算方法是对所有组的平均值进行方差分析。
我们通过公式计算出组内方差为10.08,组间方差为58.67、接下来我们计算F值,F值是组间方差除以组内方差的比值。
F=组间方差/组内方差=58.67/10.08=5.81第三步是通过查找F分布表来计算p值。
根据自由度为2(组数-1)和df = 57(总样本量-组数)的F分布表,我们可以找到在F = 5.81条件下的p值。
假设我们选择显著性水平为0.05,我们发现在F分布表上,F=5.81对应的p值小于0.05、因此,我们拒绝零假设,接受备择假设。
这意味着至少有一组的平均收缩压与其他组有显著差异。
最后一步是进行事后检验。
由于我们有三组进行比较,我们可以使用事后检验方法来确定哪两组之间存在显著差异。
常用的事后检验方法包括Tukey HSD检验、Duncan检验等。
综上所述,单因素方差分析可以帮助我们判断不同组之间是否存在显著差异。
方差分析--实例

例6.1 测定东北、内蒙古、河北、安徽、贵州5个地区黄鼬冬季针毛的长度,每个地区随机抽取4个样本,测定的结果列于表6-1。
试比较各地区黄鼬针毛长度的差异显著性。
表6-1 不同地区黄鼬冬季针毛长度(单位:mm)
地区东北内蒙古河北安徽贵州合计
1 32.0 29.
2 25.5 23.
3 22.3
2 32.8 27.4 26.1 25.1 22.5
3 31.2 26.3 25.8 25.1 22.9
4 30.4 26.7 26.7 25.
5 23.7
∑x126.4 109.6 104.1 99.0 91.4 530.5
n 4 4 4 4 4 20
x31.60 27.40 26.03 24.75 22.85 26.53 ∑X23997.44 3007.98 2709.99 2453.16 2089.64 14258.21
例6.2 园艺研究所调查了3个品种草莓的维生素C含量(mg/100g),测定结果列于表6-2。
试分析不同品种之间维生素C含量是否有显著性差异。
表6-2 不同品种草莓维生素C含量(单位:mg/100g)
例6.3 研究三种不同日粮对猪日增重的影响,每种日粮饲喂5头猪,三种日粮分别用TR1、TR2、TR3表示。
相关数据如下表所示:
TR1 TR2 TR3
270 290 290
300 250 340
280 280 330
280 290 300
270 280 300 总和 1400 1390 1560 4350
n 5 5 5 15
y280 278 312 290。
方差分析示例

方差分析spss实例操作(2013-09-18 13:45:02)转载▼分类:数据挖掘标签:实例含量总胆固醇spss18方差分析方差分析方差分析的应用条件各样本是相互独立的随机样本;ν各组样本均来自正态总体;ν各组的总体方差相等ν各单元格样本含量比较大(ν>30)且各单元格样本含量相同的情况下,方差是否相等对结果影响几乎没有方差分析的基本思想全部数据的总变异分成多个部分(离均差平方和SS)ν均方MS=SS/dfν各部分变异的MS与随机误差的MS做比,形成F统计量ν注意:H0为各组总体均数不全相等ν完全随机设计方差分析ν多组样本均数两两比较ν随机区组设计方差分析ν析因设计方差分析ν例题:ν某人研究北京机关工作人员血脂水平,随机抽取不同年龄组男性受试者各10名,检测他们的总胆固醇(TC)的含量(mmol/L),其结果如下:ν青年组5.00 4.85 4.93 5.18 4.95 4.78 5.18 4.89 5.07 5.21ν中年组5.12 5.13 4.89 5.20 4.99 5.14 5.16 4.98 5.16 5.25ν老年组5.24 5.26 5.23 5.10 5.31 5.23 5.21 4.98 5.15 5.19ν请问:三个年龄组的总胆固醇平均含量之间的差别是否具有统计学意义?ν完全随机设计方差分析库结构ν分组检验正态性1、将数据粘贴到excel分组总胆固醇1 51 4.851 4.931 5.181 4.951 4.781 5.181 4.891 5.071 5.212 5.122 5.132 4.892 5.22 4.992 5.142 5.162 4.982 5.162 5.253 5.243 5.263 5.233 5.13 5.313 5.233 5.213 4.983 5.153 5.192、打开SPSS 18,打开数据,点击【分析】【比较均值】【单因素ANOVA】【因变量列表】选【总胆固醇】【因子】选【分组】点击【两两比较】勾选【LSD】【S-N-K】【Dunnett】【继续】点击【选项】勾选【方差同质性检验】点击【继续】【确定】经检验,F=5.897,P=0.008,在检验水准为0.05的水平下,差异有统计学意义,拒绝H0,接受H1,可以认为三组的TC水平不全相等============================例题:ν研究者欲比较生物蛋白粉饲料、血浆蛋白粉饲料和普通饲料喂养断奶仔猪的增重效果。
方差分析案例---精品模板
“地域”与“抑郁”朱平辉改编自西南财大网(案例分析者刘玲同学)一、案例简介美国人作了一项调查,研究地理位置与患抑郁症之间的关系。
他们选择了60个65岁以上的健康人组成一个样本,其中20个人居住在佛罗里达,20个人居住在纽约、20个人居住在北卡罗来纳.对中选的每个人给出了测量抑郁症的一个标准化检验,搜集到表1中的资料,较高的得分表示较高的抑郁症水平.研究的第二部分考虑地理位置与患有慢性病的65岁以上的人患抑郁症之间的关系,这些慢性病诸如关节炎、高血压、心脏失调等。
这种身体状况的人也选出60个组成样本,同样20个人居住在佛罗里达,20个人居住在纽约、20个人居住在北卡罗来纳。
这个研究记录的抑郁央视主持人崔永元对外公开其患有抑郁症后,使人们对这种精神疾病有了更多的关注.通过对以上两个数据集统计分析,你能从中看出什么结论?你对该疾病有什么认识?二、抑郁症的相关知识抑郁症有两种含义,广义的抑郁症包括情感性精神病、抑郁性神经症、反应性抑郁症、更年期抑郁症等;狭义的则仅指情感性精神病抑郁症。
抑郁症在国外是一种十分常见的精神疾病,据报告,其患病率最高竟占人群的10%左右,而且社会经济情况较好的阶层,患病率越高。
世界卫生组织预测,抑郁症将成为21世纪人类的主要杀手.全世界患有抑郁症的人数在不断增长,而抑郁症患者中有10-15%面临自杀的危险……引起抑郁症的原因有很多,为了了解地理位置对抑郁症是否有影响,我们做如下的案例分析:三、地理位置与患抑郁症之间是否有关系作为对65岁以上的人长期研究的一部分,在纽约洲北部地区的Wentworth医疗中心的社会学专家和内科医生进行了一项研究,以调查地理位置与患抑郁症之间的关系。
选择了60个相当健康的人组成一个样本,其中20人居住在佛罗里达,20人居住在纽约,20人居住在北卡罗米纳。
对中选的人给出了测量抑郁症的一个标准化实验,搜集到表1中的资料,较高的分表示较高的抑郁症水平。
研究的第二部分考虑地理位置与患有慢性病的65岁以上的人患抑郁症之间的关系,这些慢性病诸如关节炎、高血压、心脏失调等。
方差分析实例

方差分析实例
案例分析一:
方差分析实例
某化工厂化验室检验过程中要确定温度(记为因子A)对检验结果的影响。
现让同一个检验人员从同一批样品中随机抽取三个样品,用同一种测量方法、同一台仪器,在四个温度水平(记为A1、A2、A3、A4)下对三个样品主要成分进行测量,数据如下表,其中,含量的单位为%,温度单位为℃,测定结果的显著性水平α=0.05。
温度和含量的数据分析图含量(%)
从数据图可清晰得知,温度对样品中主要成分的含量的测量结果有着显著的影响,即温度越高,样品含量越大。
为了减少决策风险,对于
该结论还需进行方差分析。
(二)组间方差齐性检验
1、计算A1~A4的极差R1~R4,
2、平均极差R ,
3、根据α=0.05,m=3,查“均值-极差控制图系数表”得D3、D4,
4、计算上临界值:D4*R;下临界值:D3*R
5、验证R1~R4是否在上下临界值直间,即D3R﹤R1,R2,R3,R4﹤D4R,则证明每个水平内样品的测定数据方差是一致的。
(三)计算因子A在每一温度水平下不同样本测定数据的和Ti及总和Tn
(四)依次计算平方和Sr、S A、Se及自由度fr、f A、fe
(五)计算各均方及F比值并列出方差分析表
F=105.685
(六)根据F=105.685,对于给定的显著性水平α=0.05,查F 分布表F1-α(F A,Fe),可得1-α=0.95,F0.95(3,8)=4.07,F﹥F0.95(3,8),因此,温度对含量测定结果的影响是显著的。
spss多因素方差分析报告报告材料例子
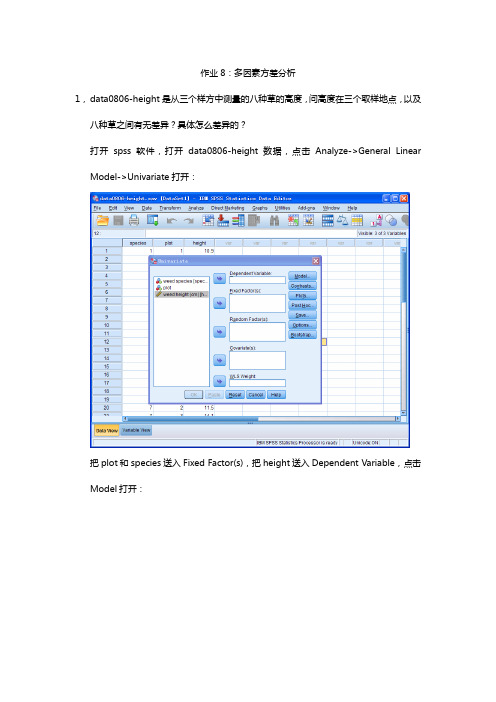
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue 回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
实习报告五(单因素方差分析)

实习报告五(单因素方差分析)
一、问题:某高原研究组将籍贯相同、年龄相同、身高体重接近的30名新战士随机分为三组,甲组为对照组,按常规训练,乙组为锻炼组,每天除常规训练外,接受中速长跑与健身操锻炼,丙组为药物组,除常规训练外,服用抗疲劳药物,一月后测定第一秒用力肺活量(L),结果见表。
试比较三组第一秒用力肺活量有无差别。
二、数据:
三组战士的第一秒用力肺活量(L)
三、统计处理:该实际问题涉及“处理方式”一个因素,为单因素实验,对照组、锻炼组、药物组为该因素的三个水平,所考察的随机变量,即实验指标是第一秒肺活量,为连续性随机变量,目的是考察三个水平下指标间是否具有显著差异,以此判断高原地区不同的处理方式对肺功能对作用是否有显著差别,所进行对分析为单因素方差分析。
四、结果及分析:
表1
表3
表4
分析:从表1中可以得到三个不同分组的一些相关描述统计量:平均值、标准差、样本容量等。
表2为方差齐性检验,由于Sig>0.05,接受原假设,认为方差具有齐性。
可以运用Tukey法进行多重比较。
从表3中可以看出,F = 3.729 ,P=0.037<0.05,拒绝原假设(三个分组的高原战士第一秒用力肺活量总体均数相等),结论: 三个分组的高原战士第一秒用力肺活量总体均数至少有部分不相等。
表4为多重比较,Tukey和Scheffe法,本题中例数相等,应运用Tukey法进行多重比较。
可以从表4中看出,对照组和药物组之间、药物组和锻炼组之间没有显著差异;对照组和锻炼组之间具有显著差异,且锻炼组的第一秒用力肺活量比对照组高。
市场研究的方差分析实例

实例分析一、单因子分析一项研究三个电视广告(A、B、C)效果的研究,安排了10个消费者观看每个我们利用SPSS对数据进行方差分析,得到以下结果0.000<0.05,即是,样本均值相等的零假设被拒绝。
即三个电视广告不是同样有效的。
二、N因子方差分析1、研究课题:职业、性别对周薪水的影响2、数据统计: (1)(2)(1)在Levene检验中,显著性p=0.856,显著性水平a=0.05,p值远大于a值,落在大概率范围内,处于接受域,因此接受H0假设,误差与方差相等。
得到了方差分析的前提,可以继续进行方差分析。
(2)在表2中,主体间效应的检验,发现因子1性别,p1=0.000小于a=0.05,落在拒绝域上,因此拒绝H01,可得性别对于周薪水的影响是显著的。
因子2职业,p2=0.000小于a=0.05,同样落在拒绝域上,因此拒绝H02,可得职业对于周薪水的影响是显著的。
因子1与因子2的交互效应,p3=0.011小于a值,落在拒绝域上,因此拒绝H03,可得性别与职业间的交互效应是显著的。
三、协方差分析1、课题:考虑年龄因素下,体重对胆固醇含量有无影响体重超重组标识为2,体重正常组标识为12、数据统计(2)(3)(4)3、数据分析(1)在图表2中,以x=年龄,y=胆固醇,得到散点图,从图中可以明显看出,年龄与胆固醇含量存在明显线性关系。
因此,需要将连续变量年龄列入影响胆固醇含量的因素中,所以,年龄应作为协变量进行分析。
(2)在Levene检验中,显著性p=0.375,显著性水平a=0.05,p值远大于a值,落在大概率范围内,处于接受域,因此接受H0假设,误差与方差相等。
得到了方差分析的前提,可以继续进行协方差分析。
(3)表4中,主体间效应的检验,发现因子体重,p1=0.038小于a=0.05,落在拒绝域上,因此拒绝H01,可得体重对于胆固醇含量的影响是显著的。
协变量年龄,p2=0.000小于a=0.05,落在拒绝域上,因此拒绝H02,可得年龄对于胆固醇含量的影响也是显著的。
析因设计的方差分析报告

析因设计(factorial design): 是将两个或多个实验因素的各水平进行
组合,对各种可能的组合都进行实验,从而 探讨各实验因素的主效应(main effect), 以及各因素间的交互作用(interaction)的研 究设计类型。
图形上标出,以直观描述交互效应。
--水平轴:因素A --单图(线段,separate lines):因素B --多图(分图,separate plots):无 4) Post Hoc(对比)按钮: 用于某处理因素多个水平间的多重比较。本例的研究因 素均为两水平,所以无需此步骤。
5)Options(选项)按钮,弹出单变量选项对话框。 --显示均值:结果输出所选因素的均数、标准误、可信
对于因素B(纯苯染毒): H0:染毒与不染毒的大鼠吞噬指数的总体均数相等 H1:染毒与不染毒的大鼠吞噬指数的总体均数不等
对于交互作用AB: H0:因素A和因素B无交互作用 H1:因素A和因素B有交互作用
均取 0.05
计算检验统计量
表9-4 例1的两因素析因设计方差分析表
确定P值,作出推断结论
方差分析的基本思想
• 变异分解: SS总 SS处理 SS误差
SSA SSB SSAB SS误差
• 自由度的分解:
总 A B AB 误差
方差分析的基本步骤
建立检验假设,确定检验水准
对于因素A(升白细胞药物): H0:给药与不给药的大鼠吞噬指数的总体均数相等 H1:给药与不给药的大鼠吞噬指数的总体均数不等
若i :表示因素A的水平(i=1,2,…,a), j :表示因素B的水平(j=1,2,…,b), k:表示因素A和因素B各水平组合下的观察单位数(k=1, 2,…,n)。
方差分析

一、完全随机化设计资料的方差分析
例2-18:某妇幼保健院用甲、乙和丙三种方案治疗血红蛋白
含量不满10g的婴幼儿贫血患者,甲方案为每公斤体重每天口
服2.1%硫酸亚铁1ml,乙方案为每公斤体重每天口服2.5%硫 酸亚铁0.6ml,丙方案为每公斤体重每天口服2g鸡肝粉,治疗 一月后,记录下每名受试者血红蛋白的上升克数,资料见表 2-13,问三种治疗方案对婴幼儿贫血的是否相同?
3.84
2.67 5.77 4.11
3.68
2.42 5.81 4.12
0.16
0.25 -0.04 -0.01
0.0256
0.0625 0.0016 0.0001
11
12
4.95
3.25
5.32
2.85
-0.37
0.40 (Σd ) 2.06
0.1369
0.1600 ( Σd2 )1.5916
2.某医生研究野木瓜用于手术后的镇痛疗效,以哌替啶作 为对照,观察两药的镇痛时间(h),得到下表结果,问野
例2-19 在抗基因突变药物筛选试验中,用20只狼
疮鼠按不同窝别分为5组,分别观察三种药物对狼 疮鼠抗FCR基因突变效果,数据见表2-16,问三 种药物是否有抗基因突变作用?
比较与完全随机化设计资料 有何区别?
总变异可以分解为处理因素的变异、区组间的 变异,以及误差 :
变异来源 总 处理 区组 误差
3.横轴上,标准正态曲线下从0到1.96的面积为:
A.95%
B.45%
C.97.5%
D.47.5%
E.49.5%
4.要评价某市一名8岁男孩的身高是否偏高或偏矮,应选用的统计方法是: A.用该市8岁男孩身高的95%或99%正常值范围来评价
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方差分析方法
方差分析是统计分析方法中,最重要、最常用的方法之一。
本文应用多个实例来阐明方差分析的应用。
在实际操作中,可采用相应的统计分析软件来进行计算。
1. 方差分析的意义、用途及适用条件
1.1 方差分析的意义
方差分析又称为变异数分析或F检验,其基本思想是把全部观察值之间的变异(总变异),按设计和需要分为二个或多个组成部分,再作分析。
即把全部资料的总的离均差平方和(SS)分为二个或多个组成部分,其自由度也分为相应的部分,每部分表示一定的意义,其中至少有一个部分表示各组均数之间的变异情况,称为组间变异(MS组间);另一部分表示同一组个体之间的变异,称为组变异(MS组),也叫误差。
SS除以相应的自由度(υ),得均方(MS)。
如MS组间>MS组若干倍(此倍数即F值)以上,则表示各组的均数之间有显著性差异。
方差分析在环境科学研究中,常用于分析试验数据和监测数据。
在环境科学研究中,各种因素的改变都可能对试验和监测结果产生不同程度的影响,因此,可以通过方差分析来弄清与研究对象有关的各个因素对该对象是否存在影响及影响的程度和性质。
1.2 方差分析的用途
1.2.1 两个或多个样本均数的比较。
1.2.2 分离各有关因素,分别估计其对变异的影响。
1.2.3 分析两因素或多因素的交叉作用。
1.2.4 方差齐性检验。
1.3 方差分析的适用条件
1.3.1 各组数据均应服从正态分布,即均为来自正态总体的随机样本(小样本)。
1.3.2 各抽样总体的方差齐。
1.3.3 影响数据的各个因素的效应是可以相加的。
1.3.4 对不符合上述条件的资料,可用秩和检验法、近似F值检验法,也可以经过变量变换,使之基本符合后再按其变换值进行方差分析。
一般属Poisson分布的计数资料常用平方根变换法;属于二项分布的百分数可用反正弦函数变换法;当标准差与均数之间呈正比关系,用平方根变换法又不易校正时,也可用对数变换法。
2. 单因素方差分析(单因素多个样本均数的比较)
根据某一试验因素,将试验对象按完全随机设计分为若干个处理组(各组的样本含量可相等或不等),分别求出各组试验结果的均数,即为单因素多个样本均数。
用方差分析比较多个样本均数的目的是推断各种处理的效果有无显著性差异,如各组方差齐,则用F检验;如方差不齐,用近似F值检验,或经变量变换后达到方差齐,再用变换值作F检验。
如经F检验或近似F值检验,结论为各总体均数不等,则只能认为各总体均数之间总的来说有差异,但不能认为任何两总体均数之间都有差异,或某两总体均数之间有差异。
必要时应作均数之间的两两比较,以判断究竟是哪几对总体均数之间存在差异。
在环境科学研究中,常常要分析比较不同季节对江、河、湖水中某种污染物的含量
有无显著性影响;各种气象条件如风向、风速、温度对大气中某种污染物含量的影响等问题。
我们把季节、风向、风速、温度等称为因素。
仅按不同季节,或不同的风向,或不同的温度来分组,称为单因素。
例1 某年度某湖不同季节湖水中氯化物含量(mg/L)测定结果如表—6.1所示。
试比较不同季节湖水中氯化物含量有无显著性差异。
从表—1的测定结果可见有三种变异:
1. 组变异:每个季节部的各次测定结果不尽相同,但显然不是季节的影响,而只是由于误差(如个体差异、随机测量误差等)所致。
2. 组间变异:各个季节的均数也不相同,说明季节对湖水中氯化物的含量可能有一定的影响,也包括误差的作用。
3.总变异:32次测定结果都不尽相同,既可能受季节的影响,也包括误差的作用。
不同季节湖水中氯化物含量的均数之间的变异究竟是由于误差所致,还是由于不同季节的影响,可以用方差分析来解决此问题。
方差分析可表示:
⑴从总变异中分出组间变异和组变异,并用数量表示变异的程度。
⑵将组间变异和组变异进行比较,如二者相差甚微,说明季节影响不大;如二者相差较大,组间变异比组变异大得多,说明季节影响不容忽视。
以下是三种变异的计算方法:
3.1 多个方差的齐性检验
已知多个样本(理论上均来自正态总体)方差,可以据此推断它们所分别代表的总体方差是否相等,即多个方差的齐性检验。
其常用于:
⑴说明多组变量值的变异度有无差异。
⑵方差齐性检验。
以例1为例(各组样本含量相等),如表—4所示。
3.确定P值:根据υ=4—1=3,查附表—12得P<0.005。
4.判断结果:由于P<0.005,因此,四组方差不齐。
3.2 近似F值检验(F'检验)
以例2为例,如表—6所示。
公式26最常用,公式27适用于原数据中有小值和零时。
K为常数,可以根据需要选用合适的数值。
⑵对数变换的用途:
①当几个样本均数作比较时,如样本方差不齐,尤其是当标准差与均数之比的比值接近时,必须经对数变换以缩小各方差之间的差别,达到方差齐后才能进行t检验或方差分析。
②适用于呈对数正态分布的资料。
③在曲线拟合中,对数变换常常是直线化的重要手段,如指数曲线、双曲线、logistic 曲线的直线化等。
例3 欲用t检验比较某河丰水期和枯水期的河水BOD5(mg/L)含量均数,资料如表—7所示。
此数据能否直接用t检验方法?如不能,试作变量变换。
二者比较接近,可以试用对数变换。
⑶将X作“lgX +1”变换后,再作方差齐性检验,得F=1.72,P>0.05,两组方差齐,可以用变换值作两样本均数比较的t检验。
2.平方根变换
以原数据的平方根作为统计分析的变量值,称为平方根变换。
⑴平方根变换的形式:
⑶百分数的概率单位变换:主要用于S形或反S形曲线的直线化、正态性检验,尤其适用于剂量反应曲线的直线化。
⑷百分数的logit变换:主要用于S形或反S形曲线的直线化。
⑸反双曲正切变换:用于两直线相关系数的比较与合并。
4. 两因素方差分析(双因素多个样本均数的比较)
将试验对象按性质相同或相近者组成配伍组,每个配伍组有三个或三个以上试验对象,然后随机分配到各个处理组。
这样,分析数据时将同时考虑两个因素的影响,试验效率较高。
例5 某市为了研究一日中不同时点以及不同区域大气中氮氧化物含量的变化情况,该市环保所于某年1月15~19日,在市区选择了7个采样点,对大气中氮氧化物的含量进行测定。
表—9为各个采样点每个时点五天的平均含量,试分析不同时点、不同区域氮氧化物含量之间有无显著性差异。
5. 多因素方差分析(多因素多个样本均数的比较)
在环境科学研究中,所研究的事物或现象往往是比较复杂的多因素问题,而各种因素本身尚有程度的差别,其间往往又存在交互作用。
当研究的因素在三个或三个以上时,可以用正交试验法。
正交试验是一种高效、快速的多因素试验方法。
正交试验的设计与分析见另外章节。
“多因素多个样本均数的比较”不仅可以用于正交试验,也可以用于拉丁方试验分析与析因试验分析等。
6.多个样本均数间的两两比较(多重比较)
经方差分析后,如果各总体均数有显著性差异时,常需进一步确定哪两个总体均数间有显著性差异,哪两个之间无显著性差异。
因此,可以利用方差分析提供的信息作样本均数间的两两比较。
以例5为例:(每组样本含量相等)经方差分析后,认为不同时点以及不同区域的氮氧化物含量之间均有高度显著性差异。
现在需要进一步检验不同时点的氮氧化物含量均数两两之间有无显著性差异。
检验步骤如下:
1.检验假设:各时点的氮氧化物含量均数之间两两相等。
⑷q值的计算方法与上例相同。
3.确定P值与判断结果如表—13所示。
