小学奥数繁分数计算定义及解题技巧

六年级奥数。计算

六年级奥数。

计算.突破繁分数(ABC级).学生版突破繁分数一、定义繁分数是指分子和分母中至少有一个含有分数的分数，其中主分数线比其他分数线长，书写位置要取中。

在运算过程中，主分线要对准等号。

如果分子和分母都是繁分数，最长的主分线被称为中主分线，依次向上为上一主分线，向下为下一主分线，两端的为末主分线。

分数除法的运算也可以写成繁分数的形式。

二、繁分数化简繁分数化简是将繁分数化为最简分数或整数的过程。

有以下四种方法：1.找出中主分线，确定分母和分子部分，分别进行计算，能约分的要约分，最后写成“分子部分÷分母部分”的形式，再求出最终结果。

也可以改写成分数除法的运算式进行计算。

2.根据分数的基本性质，同时扩大繁分数的分子和分母相同的倍数（即分子部分与分母部分所有分母的最小公倍数），去掉分母，然后化为最简分数或整数。

3.逐次进行化简，由下至上，由左到右。

4.如果分子和分母都是小数，可以将它们都化成整数进行计算。

如果是分数和小数混合出现的形式，可以按照分数、小数四则混合运算的方法进行处理。

在化简时，分子和分母要统一成小数或整数，然后进行约分。

如果分子部分和分母部分都有小数位，可以同时扩大1000倍，变成整数进行约分。

化简时要注意小数点的位置。

繁分数的运算涉及分数和小数的定义和运算，需要注意多级分数的处理。

在处理繁分数时，可以先算短分数线，再算长分数线。

找到最长的分数线，将其上视为分子，下视为分母。

一般情况下，分数的乘、除运算使用真分数或假分数，而不使用带分数。

因此，需要将带分数化为假分数。

有时将分数线视为除号，可以使繁分数的运算更加直观。

对于定义新运算，只需按照题目中的定义进行运算即可。

繁分数是数，不是除法式子。

除法算式应包括被除数、除数和除号，通过运算得出商数。

因此，除法算式和一个数是不同的。

繁分数的定义可以这样表述：繁分数是分子或分母含有分数，或分子和分母都含有分数的数。

在一个繁分数中，最长的分数线是主分数线，主分数线上下的数或运算都分别看作是繁分数的分子和分母。

小学奥数繁分数的定义分析及练习【三篇】

小学奥数繁分数的定义分析及练习【三篇】
导读：本文小学奥数繁分数的定义分析及练习【三篇】，仅供参考，如果觉得很不错，欢迎点评和分享。

【篇一】一、繁分数是数，而不是除法式子
一个有意义的除法算式应包括定义范围内的被除数、除数和除号，它是一种运算表达形式。

只有通过运算后，才能得出一个商数来，所以除法算式和一个数是两回事。

二、繁分数定义的表述
根据繁分数的特点和内涵，考虑到既有分数的“形”，又有分子部分分母部分含有分数的特殊情况，它的定义可以这样表述：如分数形式，分子或分母含有分数，或分子与分母都含有分数的数，叫繁分数。

在一个繁分数里，最长的分数线叫做繁分数的主分数线，主分数线上下不管有多少个数或运算，都把它们分别看作是繁分数的分子和分母。

【篇二】【简化繁分数】
（1990年马鞍山市小学数学竞赛试题）讲析：如果分别计算出分子与分母的值，则难度较大。

观察式子，可发现分子中含有329×274，分母中含有275×326.于是可想办法化成相同的数：
（全国第三届“华杯赛”复赛试题）
讲析：可把小数化成分数，把带分数都化成假分数，并注意将分
子分母同乘以一个数，以消除各自中的分母。

于是可得
【篇三】例3 简化
（全国第三届“华杯赛”复赛试题）讲析：由于分子分母部分都比较复杂，所以只能分别计算。

计算时，哪一步中能简算的，就采用简算的办法去计算。

（北京市第一届“迎春杯”小学数学竞赛试题）讲析：连分数简化，通常要从最下层的分母开始，自下而上逐步简化。

依此法计算，题目的得数是2（计算过程略）。

小学繁分数化简专题

小学奥数知识点汇编第一章计算1.1四则混合运算1.1.1繁分数的化简技巧繁分数的定义如果分数形式中，分子或分母含有四则运算或分数，或分子与分母都含有四则运算或分数的数，叫“繁分数”；其对应于“简分数”。

1.1.1.2繁分数化简的基本方法1.1.1.2.1可利用分数与除法的关系把繁分数写成分子除以分母的形式。

141.1.1.2.2利用分数的基本性质，去掉分子、分母上分数的分母后化为最简分数。

一般情况下,分子、分母所乘上的适当非零整数为分子、分母部分的两个分数分母的最小公倍数。

1.1.1.3繁分数化简的常用技巧 1.1.1.3.1化带分数为假分数：繁分数中的分子或分母若含有带分数，则把带分数化为假分数再化简。

,1 6 6 , -1155 - 5 - 5 -18 9 28 8 “ 40 -202— 153331.1.1.3.2化小数为分数：繁分数中的分子或分母若含有小数，则一般可把小数化成分数再化简。

3 3200.15 20 — 20 31 3 _ 3 3155—20 4 4 46例: 76 5 • - 6 14 X 57 14 7 5125 例:67 5 14 614 7 5 14 1412 51.1.133化分数为小数：繁分数中的分子或分母部分所含有的分数可化为有限小数，则可把分子或分母中的分数化为小数再化简。

0.15 0.15 15 1■ - --- — _3 一 0.75 一 75 一 541.1.1.3.4化小数为整数：若分子、分母都是小数还可以利用分数的基本性质，分子与分母同时扩大相同的倍数，把小数化成整数再化简。

-2.4 _ 24 _ 2 3.6 _ _ 31.1.1.3.5化复杂为简单：繁分数的分子或分母部分若含有加减运算，则先加减运算再按繁分数化简方法进行化简。

繁分数的分子、分母都是连乘运算可以分子、分母直接约分化简。

1 3 1 30.26(2)厘 4 1 0.52 1.5 72走进奥数繁分数1_ 1 _ 1_ 1 _ 1_ 1 _ 12 丄1-亠11-丄1-丄5-292922222 —J \J222 22 2122 1555221.1.1.3.6化多层为单层：化简复杂的繁分数要学会分层化简O12767 17 “ 70——20 =1 _ 6 20 63201.5 3.75 0.26 0.52 1.5 7.51 1 1 12 12 4346 6 2 上20 一 20根据实际问题列出的分数，有时它的分子或分母里又含有分数，或者分子和分母里都含有分数，我们把这样的分数叫做繁繁分数中，把分子部分和分母部分分开的那条分数线，叫做繁分数的主分数线（也叫主分线）。

小学奥数繁分数运算典型问题解析【三篇】

小学奥数繁分数运算典型问题解析【三篇】
导读：本文小学奥数繁分数运算典型问题解析【三篇】，仅供参考，如果觉得很不错，欢迎点评和分享。

【篇一】第一届“华罗庚金杯”少年数学邀请赛.决赛一试第1题
【篇二】计算：【分析与解析】注意，作为被除数的这个繁分数的分子、分母均含有19又9分之5，于是，我们想到改变预算顺序，如果分子与分母在19又9分之5后的两个数字的运算结果一致，那么作为被除数的这个繁分数的值为1；如果不一致，也不会增加我们的计算量，所以我们决定改变作为被除数的繁分数的预算顺序。

而作为除数的繁分数，我们注意两个加数的分母相似，于是统一通分为1995×0.5 具体过程如下图：
【篇三】北京市第三届“迎春杯”数学竞赛.决赛第1题挑战级数：★
3、计算：
【解析与分析】。

六年级奥数繁分数的运算讲座

六年级奥数繁分数的运算讲座繁分数的运算繁分数的运算，涉及分数与小数的定义新运算问题，综合性较强的计算问题．1．繁分数的运算必须注意多级分数的处理，如下所示：甚至可以简单地说：“先算短分数线的，后算长分数线的”．找到最长的分数线，将其上视为分子，其下视为分母．2．一般情况下进行分数的乘、除运算使用真分数或假分数，而不使用带分数．所以需将带分数化为假分数．3．某些时候将分数线视为除号，可使繁分数的运算更加直观．4．对于定义新运算，我们只需按题中的定义进行运算即可．．本讲要求大家对分数运算有很好的掌握，可参阅《思维导引详解》五年级[第1讲循环小数与分数]．1．计算：【分析与解】原式=2．计算：【分析与解】注意，作为被除数的这个繁分数的分子、分母均含有．于是，我们想到改变运算顺序，如果分子与分母在后的两个数字的运算结果一致，那么作为被除数的这个繁分数的值为1；如果不一致，也不会增加我们的计算量．所以我们决定改变作为被除数的繁分数的运算顺序．而作为除数的繁分数，我们注意两个加数的分母相似，于是统一通分为199×0．具体过程如下：原式=== = =3．计算：【分析与解】原式= = =4．计算：已知= ，则x等于多少?【分析与解】方法一：交叉相乘有88x+66=96x+6，x=1．2．方法二：有，所以；所以，那么12．．求这10个数的和．【分析与解】方法一：== ===方法二：先计算这10个数的个位数字和为；再计算这10个数的十位数字和为4×9=36，加上个位的进位的3，为；再计算这10个数的百位数字和为4×8=32，加上十位的进位的3，为；再计算这10个数的千位数字和为4×7=28，加上百位的进位的3，为；再计算这10个数的万位数字和为4×6=24，加上千位的进位的3，为；再计算这10个数的十万位数字和为4×=20，加上万位的进位的2，为；再计算这10个数的百万位数字和为4×4=16，加上十万位的进位的2，为；再计算这10个数的千万位数字和为4×3=12，加上百万位的进位的1，为；再计算这10个数的亿位数字和为4×2=8，加上千万位的进位的1，为；最后计算这10个数的十亿位数字和为4×1=4，加上亿位上没有进位，即为．所以，这10个数的和为493827191．6如图1-1，每一线段的端点上两数之和算作线段的长度，那么图中6条线段的长度之和是多少? 【分析与解】因为每个端点均有三条线段通过，所以这6条线段的长度之和为：7我们规定，符号“○”表示选择两数中较大数的运算，例如：3．○29=29○3=3．符号“△”表示选择两数中较小数的运算，例如：3△29=29△3=29．请计算：【分析与解】原式8．规定（3）=2×3×4，（4）=3×4×，()=4××6，(10)=9×10×11，…．如果，那么方框内应填的数是多少?【分析与解】=9．从和式中必须去掉哪两个分数，才能使得余下的分数之和等于1?【分析与解】因为，所以, , , 的和为l，因此应去掉与10．如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数，例如189291929．那么在所有这种数中。

创新思维·小学奥数·解题思路和知识点归纳(运算法则方法、技巧与规律)

第八讲：运算法则或方法（技巧与规律）一、繁分数化简方法繁分数化简的方法，一般有以下两种方法。

（1）利用分数基本性质，把繁分数的分子、分母同乘以所有分母的最小公倍数，从而化简繁分数。

（2）利用分数与除法的关系，将繁分数化简。

这是因为繁分数实际上是分数除法的另一种表示形式的缘故。

例如【求连分数的值的方法】由数列a 0，a 1，……及b 1，b 2，……所组成的表达式称为“连分数”。

它可简记为为连分数的值。

连分数有两种，一是有限连分数，二是无限连分数。

例如，求有限连分数的值，也称化简连分数，它的化简方法与繁分数的化简方法基本相同。

一般是从最下面的分母运算开始，逐步向上计算。

例如上面的这个有限连分数：求无限连分数的值，就是求它的有限层的值作为它的近似值。

当层次愈多时，就愈接近它的值。

注意：繁分数和连分数，都不是“分数”定义里所定义的一种分数。

分解为两个单位分数的和，可按以下步骤去完成：的任意两个约数a 1，a 2；（2）扩分：将单位分数的分子、分母同乘以两约数的和（a 1+a 2），（3）拆分：将扩分后所得的分数，按照同分母分数相加的法则反过来（4）约分：将拆开后的两个分数约分，便得到两个单位分数。

注意：（1）因大于1的自然数的约数有时不止2个，有多个，从中任取两个约数的取法也有多种，只要每次取出的两个约数之间不成比例，则将一个单位分数拆成两个单位分数的和的结果也各不相同。

例如，15的约数有1，3，5，15四个，从中任取两个的取法有（1，3）、（1，5）、（1，15）、（3，5）、（3，15）、（5，15）六种，而取（1，3）和（5，15）、（1，5）和（3，15）是成比例（2）若要将单位分数拆成两个相等的单位分数之和，那只要在扩分时，分子、分母同乘以分母的任何一个约数的2倍或乘以2即可。

拆成n 个单位分数的和的方法和步骤与拆成两个单位分数的方法和步骤相同，不同点只在扩分时，分子、分母同乘以分母A 的n 个约数的和（a 1+a 2+…+a n ）。

第26讲繁分数的计算带答案

第二十六讲繁分数的计算--------巧取倒数法【知识要点】一个分数的分子或分母还含有分数或四则混合运算的分数叫做繁分数.通常无法用运算定律和运算性质进行计算,因此繁分数的运算过程就是化简的过程,要分别对分子和分母逐步进行计算,其间需要扎实的基本功：概念清楚,运算迅速正确,而且还需要探索和掌握一些灵活的解题方法,化“繁”为“简”.繁分数由分子部分、分母部分和分隔分子与分母的主分数线三部分构成.繁分数化简的目的是使分子部分与分母部分都不再含有分数.连分数是一类特殊的繁分数,它的化简也用到繁分数化简的方法.【典型例题】例1计算11413123---(1995年小学数学奥林匹克总决赛计算试题)解析从下往上,依层化简125131221;33;3335/355-==-=-=154311244;.4312/512124312-=-==练习一1.试计算114131212-+-+(1997年小学数学奥林匹克总决赛计算试题)解析原式1111511456 444131533423==== ---++-.2.计算111121345++++(1998年小学数学奥林匹克总决赛计算试题)解析原式111157116822511112115722568321====++++++.例2已知==+++xx则,1184112111.(1999年小学数学奥林匹克决赛试题)解析181313,11,;111118812221444x xx=∴+=+=+++++++进而我们有:1222,134x+=++12135,,.134244x xx=+==+练习二1.已知:==+++xx则,2518412111.(2000年北大少年数学邀请赛第二试试题)解析因为1181257171184,11,,22,11112518181877122421444xx xx=∴+==+=+==+++++++++14173,,.74424x xx=+==+注1 可以将上述过程简化为以下计算:25718473131,2,1,.1818774442x x=+=+=+=+=2.已知167,196121314xx=++++求的值.解析962967929291;676729299922=1+;=2+;=3+;=4+所以2x=.【课后精练与思考题】计算53793649++-(1996年小学数学奥林匹克总决赛计算试题)解析5552533337936363657679(79)5115553649+=+=+=+⨯+⨯+⨯-.1。

六年级奥数第04讲繁分数

学生课程讲义
课程名称
六年级奥数
上课时间
任课老师
沈老师
第04讲，本讲课题：繁分数
内容概要
了解什么是繁分数，掌握繁分数化简的基本方法，来为初中整式的学习打下良好基础。
分子和分母中还含有分数或四则混合运算的分数叫做繁分数,通常无法应用运算定律和运算性质进行计算,因此繁分数的运算过程就是化简的过程,要分别对分子和分母逐步进行运算,其间需要扎实的基本功:概念清楚,运算迅速正确,而且还需要探索和掌握一些灵活的解题方法,化“繁”为“简”。
【例1】计算：
【例2】
随ห้องสมุดไป่ตู้练习1
计算下列各式：
【例3】计算
【例4】
随堂练习2
（2）
【例5】计算：
【例6】
其中A、B、C都是大于0且互不相同的自然数，则（A+B）÷C＝
随堂练习3
（1）
（2）计算：
练习题

小学奥数01繁分数化简

小学奥数知识点汇编第一章计算1.1四则混合运算1.1.1繁分数的化简技巧1.1.1.1繁分数的定义如果分数形式中，分子或分母含有四则运算或分数，或分子与分母都含有四则运算或分数的数，叫“繁分数”；其对应于“简分数”。

1.1.1.2繁分数化简的基本方法1.1.1.2.1可利用分数与除法的关系把繁分数写成分子除以分母的形式。

例：7614576=÷76145=×512514= 1.1.1.2.2利用分数的基本性质，去掉分子、分母上分数的分母后化为最简分数。

一般情况下，分子、分母所乘上的适当非零整数为分子、分母部分的两个分数分母的最小公倍数。

例：51214145147614576=⨯⨯= 1.1.1.3繁分数化简的常用技巧1.1.1.3.1化带分数为假分数：繁分数中的分子或分母若含有带分数，则把带分数化为假分数再化简。

2094018153815563856322511-=-=⨯⨯-=-=-1.1.1.3.2化小数为分数：繁分数中的分子或分母若含有小数，则一般可把小数化成分数再化简。

51153204320203432034315.0-=-=⨯⨯-=-=-1.1.1.3.3化分数为小数：繁分数中的分子或分母部分所含有的分数可化为有限小数，则可把分子或分母中的分数化为小数再化简。

51751575.015.04315.0-=-=-=- 1.1.1.3.4化小数为整数：若分子、分母都是小数还可以利用分数的基本性质，分子与分母同时扩大相同的倍数，把小数化成整数再化简。

3236246.34.2-=-=- 1.1.1.3.5化复杂为简单：繁分数的分子或分母部分若含有加减运算，则先加减运算再按繁分数化简方法进行化简。

繁分数的分子、分母都是连乘运算可以分子、分母直接约分化简。

（１）37020672016720167204205646351413221=⨯=÷==-+=-+ （２）412121115.75.152.026.075.35.12175.152.026.0433211=⨯⨯⨯⨯=⨯⨯⨯⨯=⨯⨯⨯⨯ 1.1.1.3.6化多层为单层：化简复杂的繁分数要学会分层化简。

繁分数计算方法

繁分数计算方法繁分数，也称为复分数，是数学中的一种特殊数形式。

它由一个有理数和一个虚部组成，通常表示为a+bi的形式，其中a为实部，b为虚部。

繁分数在代数学和电路理论等领域有重要应用。

本文将介绍繁分数的计算方法，从基本运算到特殊运算，逐步进行详细说明。

一、基本运算1. 繁分数的加法：将两个繁分数的实部与虚部分别相加，得到结果的实部和虚部。

假设有两个繁分数A=3+2i，B=1+4i，首先将它们的实部相加：3+1=4，然后将它们的虚部相加：2+4=6，因此A+B=4+6i。

2. 繁分数的减法：将两个繁分数的实部与虚部分别相减，得到结果的实部和虚部。

假设有两个繁分数A=3+2i，B=1+4i，首先将它们的实部相减：3-1=2，然后将它们的虚部相减：2-4=-2，因此A-B=2-2i。

3. 繁分数的乘法：将两个繁分数按照复数乘法法则相乘，得到结果的实部和虚部。

假设有两个繁分数A=3+2i，B=1+4i，按照复数乘法法则进行计算：(3+2i)(1+4i)=3+12i+2i+8i^2，化简后得到：3+12i+2i-8=3+14i-8= -5+14i，因此A*B= -5+14i。

4. 繁分数的除法：将两个繁分数按照复数除法法则相除，得到结果的实部和虚部。

假设有两个繁分数A=3+2i，B=1+4i，按照复数除法法则进行计算：(3+2i)/(1+4i)=((3+2i)(1-4i))/((1+4i)(1-4i))，化简后得到：(3+2i-12i-8)/(1-16i^2)，进一步化简为：(-5-10i)/(17)，所以A/B=(-5/17)+(-10/17)i。

二、特殊运算1. 繁分数的共轭：将繁分数的虚部取负数，得到共轭繁分数。

假设有一个繁分数A=3+2i，将它的虚部取负数，得到共轭繁分数：A*=3-2i。

2. 繁分数的模：将繁分数表示的复数看作平面上的向量，可以用勾股定理计算繁分数的模，即平面上的长度。

假设有一个繁分数A=3+2i，根据勾股定理：|A|=√(3^2+2^2)=√(9+4)=√13。

繁分数

繁分数的化简与计算
一、繁分数的概念
所谓繁分数就是，分数的分子或分母中又含有分数的，繁分数是更复杂的分数，在繁分数中，用较长的分数线分出分子部分和分母部分，这较长的分数线我们称它为主分数线。
பைடு நூலகம்
4 1 5
2 3
主分数线
7 1 1 4 18 2 6 1 3 5 13 - 3 3 4 16
例2. 化简下面的繁分数
7.2 0.85 4.2 0.84 3.4 5.4
把分子、分母部分同时扩大10000倍（小数点向右移动四位）
7.2 0.85 4.2 72 85 42 5 0.84 3.4 5.4 84 34 54 3
1 0.96 4 0.8 由于分子部分和分母部分小数的位数不同，所以以小数位数多的为准。（分子、 2 分母同时扩大10000倍） 0.9 0.03 1 0.96 4 0.8 0.96 4.5 0.8 96 45 8 2 128 0.9 0.03 0.9 0.03 9 30
1
1 12 1 5 29 29 2 2 2 12 12 12 5 5
1
1
例1. 化简下面各题。四、例题选讲 7 1 11 1 4 4 3 3 12 7 7 7 15 5 1 7 12 15 12 7 4 4 1 4 1 1 11 5 5 33 15
1 例 3. 化简 1
1
11 1 1 1 1 1 11 1 11 1 1 1 2 11 1 1 2 2 1 11 1 1 2 1 1 1 1 1 1 1 3 11 3 1 1 2 3 1 1 1 2 3 1 12 2 1 11 2 1 1 2 3 12 1 1 3 3 2 11 1 1 3 1 11 1 1 3 1 3 4 1 1 3 3 11 3 4

第四讲_繁分数的计算(精品文档)_共2页

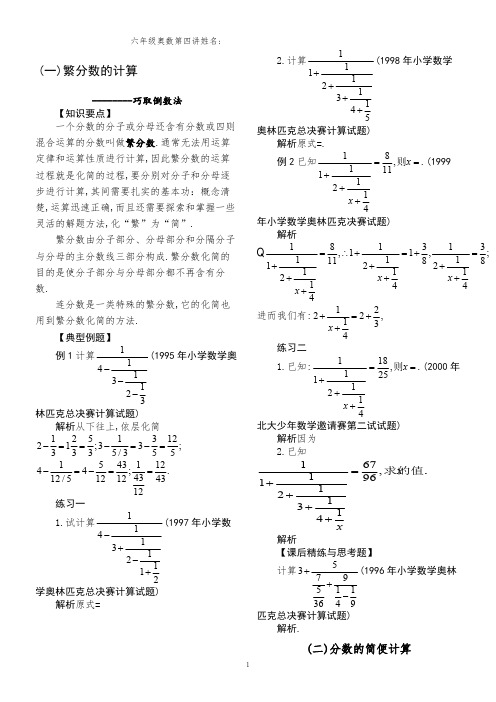
计算 3 5 (1996 年小学数学奥林
7 5

1
9
1
36 4 9
匹克总决赛计算试题)
解析.
(二)分数的简便计算
1
六年级奥数第四讲姓名:
+= +……+= = 1＋2＋3＋4＋5＋6＋7＋8＋9= += 1＋＋…＋= +……+= += += += ＋= = 1+－= ＋（）＋（）＋…＋（＋…＋）= 71×＋61×＋51×＋41×＋31×= 1×1×1×1×……×1×1= （1＋）×（1＋）×（1＋）×…×（1＋）× （1－）×（1－）×…×（1—）×（1—）= （1＋＋）×（＋）－（1＋）×（＋）= (9-×4)＋（8－×5）＋……＋（4－×9）= ＋…＋＋……＋= ＋……＋－－……－=
2
解析原式=
2.计算
1
(1998 年小学数学
1
2

3
1
1 4
1
1
5
奥林匹克总决赛计算试题)
解析原式=.
例 2 已知
1
8 ,则x .(1999
1 1
11
2 1
x 1
4
年小学数学奥林匹克决赛试题)
解析
Q
1
8 ,1 1 1 3 , 1 3 ;
1
2

1 1
x
1
11
灵活的解题方法,化“繁”为“简”.
繁分数由分子部分、分母部分和分隔分子
与分母的主分数线三部分构成.繁分数化简的
目的是使分子部分与分母部分都不再含有分
数.
连分数是一类特殊的繁分数,它的化简也

小六奥数繁分数的运算

精锐讲义编号：学员编号: 年级：小六课时数：3学员姓名辅导科目：奥数学科教师：课题繁分数的运算授课时间：备课时间教学目标教学目标：能够利用简单的分数运算定律进行复杂的繁分数的运算教学内容繁分数的运算，涉及分数与小数的定义新运算问题，综合性较强的计算问题．1．繁分数的运算必须注意多级分数的处理，如下所示：甚至可以简单地说：“先算短分数线的，后算长分数线的”．找到最长的分数线，将其上视为分子，其下视为分母．2．一般情况下进行分数的乘、除运算使用真分数或假分数，而不使用带分数．所以需将带分数化为假分数． 3．某些时候将分数线视为除号，可使繁分数的运算更加直观．4．对于定义新运算，我们只需按题中的定义进行运算即可．1．计算：71147 182621358 1333416⨯+⨯-÷【分析与解】原式=712372317 461224 1488128 131233+⨯=⨯=-2．计算：【分析与解】注意，作为被除数的这个繁分数的分子、分母均含有5199．于是，我们想到改变运算顺序，如果分子与分母在5199后的两个数字的运算结果一致，那么作为被除数的这个繁分数的值为1；如果不一致，也不会增加我们的计算量．所以我们决定改变作为被除数的繁分数的运算顺序．而作为除数的繁分数，我们注意两个加数的分母相似，于是统一通分为1995×0.5．具体过程如下：原式=5919(3 5.22)19930.4 1.6910()52719950.5199519(65.22)950+-⨯÷+⨯-+=5191.3219930.440.40.59()519950.419950.5191.329-⨯⨯⨯÷+⨯⨯-=199320.41()19950.5+÷⨯=0.410.5÷=1143．计算：1111111987-+-【分析与解】原式=11198711986-+=198613973-=198739734．计算：已知=181111+12+1x+4=，则x 等于多少?【分析与解】方法一：1118x 68114x 112x 7111+11148x 62+214x 1x+4+====+++++++交叉相乘有88x+66=96x+56，x=1．25．方法二：有11131118821x 4+==+++，所以18222133x 4+==++；所以13x 42+=，那么x =1.25．5．求944,43,443,...,44...43 个这10个数的和．【分析与解】方法一：944+43+443...44...43++ 个= 1044(441)(4441)...(44...41)+-+-++-个= 104444444...44...49++++-个=1094(999999...999...9)99⨯++++- 个=1004[(101)(1001)(10001)...(1000...01)]99⨯-+-+-++-- 个=914111.1009=49382715919⨯- 个.方法二：先计算这10个数的个位数字和为39+4=31⨯；再计算这10个数的十位数字和为4×9=36，加上个位的进位的3，为36339+=；再计算这10个数的百位数字和为4×8=32，加上十位的进位的3，为32335+=；再计算这10个数的千位数字和为4×7=28，加上百位的进位的3，为28331+=；再计算这10个数的万位数字和为4×6=24，加上千位的进位的3，为24327+=；再计算这10个数的十万位数字和为4×5=20，加上万位的进位的2，为20222+=；再计算这10个数的百万位数字和为4×4=16，加上十万位的进位的2，为16218+=；再计算这10个数的千万位数字和为4×3=12，加上百万位的进位的1，为12113+=；再计算这10个数的亿位数字和为4×2=8，加上千万位的进位的1，为819+=；最后计算这10个数的十亿位数字和为4×1=4，加上亿位上没有进位，即为4．所以，这10个数的和为4938271591．6.如图1-1，每一线段的端点上两数之和算作线段的长度，那么图中6条线段的长度之和是多少?【分析与解】因为每个端点均有三条线段通过，所以这6条线段的长度之和为：1173(0.60.875)1+0.75+1.8+2.625=6.175=63440⨯+++=7.我们规定，符号“○”表示选择两数中较大数的运算，例如：3．5○2.9=2.9○3.5=3.5．符号“△”表示选择两数中较小数的运算，例如：3.5△2.9=2.9△3.5=2.9．请计算：23155(0.625)(0.4)333841235(0.3)( 2.25)3104⨯+【分析与解】原式 1550.6255155725384218384122562.253⨯=⨯÷=+8．规定（3）=2×3×4，（4）=3×4×5，(5)=4×5×6，(10)=9×10×11，…．如果111(16)(17)(17)-=⨯，那么方框内应填的数是多少? 【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9．从和式11111124681012+++++中必须去掉哪两个分数，才能使得余下的分数之和等于1? 【分析与解】因为1116124+=，所以12,14,16,112的和为l ，因此应去掉18与110.10．如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数，例如1.892915929．那么在所有这种数中。

繁分数的运算

繁分数的运算，涉及分数与小数的定义新运算问题，综合性较强的计算问题．1．繁分数的运算必须注意多级分数的处理，如下所示：甚至可以简单地说：“先算短分数线的，后算长分数线的”．找到最长的分数线，将其上视为分子，其下视为分母．2．一般情况下进行分数的乘、除运算使用真分数或假分数，而不使用带分数．所以需将带分数化为假分数．3．某些时候将分数线视为除号，可使繁分数的运算更加直观．4．对于定义新运算，我们只需按题中的定义进行运算即可．5．本讲要求大家对分数运算有很好的掌握，可参阅《思维导引详解》五年级[第1讲循环小数与分数]．1．计算：711471826213581333416⨯+⨯-÷【分析与解】原式=7123723174612241488128131233+⨯=⨯=-2．计算：【分析与解】注意，作为被除数的这个繁分数的分子、分母均含有5199．于是，我们想到改变运算顺序，如果分子与分母在5199后的两个数字的运算结果一致，那么作为被除数的这个繁分数的值为1；如果不一致，也不会增加我们的计算量．所以我们决定改变作为被除数的繁分数的运算顺序．而作为除数的繁分数，我们注意两个加数的分母相似，于是统一通分为1995×0.5．具体过程如下：原式=5919(3 5.22)19930.41.6910()52719950.5199519(6 5.22)950+-⨯÷+⨯-+=5191.3219930.440.40.59()519950.419950.5191.329-⨯⨯⨯÷+⨯⨯-=199320.41()19950.5+÷⨯=0.410.5÷=1143．计算：1111111987-+-【分析与解】原式=11198711986-+=198613973-=198739734．计算：已知=181111+12+1x+4=，则x等于多少?【分析与解】方法一：1118x68114x112x7111+11148x62+214x1x+4+====+++++++交叉相乘有88x+66=96x+56，x=1．25．方法二：有11131118821x4+==+++，所以18222133x4+==++；所以13x42+=，那么x=1.25．5．求944,43,443,...,44...43个这10个数的和．【分析与解】方法一： 944+43+443...44...43++个=1044(441)(4441)...(44...41)+-+-++-个=104444444...44...49++++-个=1094(999999...999...9)99⨯++++-个 =1004[(101)(1001)(10001)...(1000...01)]99⨯-+-+-++--个 =914111.1009=49382715919⨯-个.方法二：先计算这10个数的个位数字和为39+4=31⨯；再计算这10个数的十位数字和为4×9=36，加上个位的进位的3，为36339+=；再计算这10个数的百位数字和为4×8=32，加上十位的进位的3，为32335+=；再计算这10个数的千位数字和为4×7=28，加上百位的进位的3，为28331+=；再计算这10个数的万位数字和为4×6=24，加上千位的进位的3，为24327+=；再计算这10个数的十万位数字和为4×5=20，加上万位的进位的2，为20222+=；再计算这10个数的百万位数字和为4×4=16，加上十万位的进位的2，为16218+=；再计算这10个数的千万位数字和为4×3=12，加上百万位的进位的1，为12113+=；再计算这10个数的亿位数字和为4×2=8，加上千万位的进位的1，为819+=；最后计算这10个数的十亿位数字和为4×1=4，加上亿位上没有进位，即为4．所以，这10个数的和为4938271591．6.如图1-1，每一线段的端点上两数之和算作线段的长度，那么图中6条线段的长度之和是多少?【分析与解】因为每个端点均有三条线段通过，所以这6条线段的长度之和为：1173(0.60.875)1+0.75+1.8+2.625=6.175=63440⨯+++=7.我们规定，符号“○”表示选择两数中较大数的运算，例如：3．5○2.9=2.9○3.5=3.5．符号“△”表示选择两数中较小数的运算，例如：3.5△2.9=2.9△3.5=2.9．请计算：23155(0.625)(0.4)333841235(0.3)( 2.25)3104⨯+【分析与解】原式1550.6255155725384218384122562.253⨯=⨯÷=+8．规定（3）=2×3×4，（4）=3×4×5，(5)=4×5×6，(10)=9×10×11，…．如果111(16)(17)(17)-=⨯，那么方框内应填的数是多少?【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9．从和式11111124681012+++++中必须去掉哪两个分数，才能使得余下的分数之和等于1? 【分析与解】因为1116124+=，所以12,14,16,112的和为l，因此应去掉18与110.10．如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数，例如1.892915929．那么在所有这种数中。