高中数学 考前归纳总结 解三角形易错题剖析
常见常新题型__注重解题方法——解三角形易错点扫描

ʏ江苏省高邮市第一中学 袁达飞解三角形问题是高考中的常见题型,主要利用正弦定理㊁余弦定理来求解未知边角的关系或具体值,由于解三角形需要综合应用正余弦定理和有关角的一些变换,所以经常会出现一些顾此失彼的错误,现归纳如下,供同学们学习时参考㊂易错点一㊁忽视解的讨论致误例1 在әA B C中,已知a =2,b =2,A =45ʎ,求B ㊂错解:由正弦定理知s i n B =b s i n Aa=2s i n 45ʎ2=12㊂又0<B <180ʎ,故B =30ʎ或150ʎ㊂剖析:上述解法中忽现了A +B +C =180ʎ这一隐含条件,当B =150ʎ时,A +B =195ʎ,与三角形的内角和为180ʎ矛盾㊂正解:由正弦定理知s i n B =b s i n Aa=2s i n 45ʎ2=12㊂又0<B <180ʎ,故B =30ʎ或B =150ʎ㊂若B =150ʎ,则A +B >180ʎ,应舍去㊂故B =30ʎ㊂易错点二㊁忽视三角形中角的范围致误例2 在әA B C 中,已知(a 2+b 2)㊃s i n (A -B )=(a 2-b 2)s i n C ,判断әA B C 的形状㊂错解:原式可化为(a 2+b 2)(s i n A c o s B-c o s A c o s B )=(a 2-b 2)(s i n A c o s B +c o s A s i n B ),即a 2s i n B c o s A =b 2s i n A c o s B ㊂由正弦定理得b 2s i n 2As i n 2B㊃s i n B c o s A =b 2s i n A c o s B ,化简得s i n A c o s A =s i n B c o s B ,即s i n 2A =s i n 2B ,所以A =B ㊂所以әA B C 是等腰三角形㊂剖析:上述解法忽略了角的范围,s i n 2A=s i n 2B 是2A =2B 的必要但不充分条件,另外,有些同学也可能由于逻辑关系不清而出现以下错误的判断:由s i n 2A =s i n 2B ,得2A =2B ,又2A +2B =π,且A =B ,A +B =π2,所以әA B C 是等腰直角三角形㊂正解:将条件都化为有关角的关系形式,前面同错解,得s i n 2A =s i n 2B ㊂因为A ,B 是三角形的内角,所以2A =2B 或2A =π-2B ,即A =B 或A +B =π2㊂故әA B C 是等腰三角形或直角三角形㊂易错点三㊁忽视隐含条件致误例3 在不等边әA B C中,a 为最大边,若a 2<b 2+c 2,则角A 的取值范围是㊂错解:因为a 2<b 2+c 2,所以b 2+c 2-a2>0,则c o s A =b 2+c 2-a22b c>0㊂又因为A 为әA B C 的内角,故A 为锐角,所以0<A <90ʎ㊂剖析:上述解法忽视了隐含条件:三角形的内角和为180ʎ,所以最大边所对的角应该大于60ʎ㊂正解:前面同错解,得0ʎ<A <90ʎ㊂又因为a 为最大边,所以A >60ʎ㊂所以60ʎ<A <90ʎ㊂故A 的取值范围是(60ʎ,90ʎ)㊂易错点四㊁忽视角之间的关系致误例4 在әA B C 中,若s i n 2A s i n 2B =t a n Ata n B ,则әA B C 的形状为㊂错解:已知s i n 2A s i n 2B =t a n A ta n B =s i n A c o s Bc o s A s i n B ㊂因为s i n A >0,s i n B >0,所以s i n A c o s A =s i n B c o s B ,即s i n 2A =s i n 2B ,所以2A =2B ,即A =B ㊂故әA B C 为等腰三角形㊂剖析:上述解法忽视了 在әA B C 中,由72解题篇 易错题归类剖析 高考数学 2023年10月Copyright ©博看网. All Rights Reserved.s i n 2A =s i n 2B ,可以得到2A +2B =π这种情况,导致漏解,结果错误㊂正解:前面同错解,得s i n 2A =s i n 2B ㊂所以2A =2B 或2A +2B =π,则A =B 或A +B =π2,故әA B C 为等腰三角形或直角三角形㊂易错点五㊁忽视三角形中三边的基本关系致误例5 已知钝角三角形的三边长分别是2a +1,a ,2a -1,求实数a 的取值范围㊂错解:因为2a +1,a ,2a -1是三角形的三边,所以2a +1>0,a >0,2a -1>0,解得a >12㊂又2a +1是三边长的最大值,设该边所对的角为θ,则c o s θ=a 2+(2a -1)2-(2a +1)22a (2a -1)<0,解得12<a <8㊂剖析:不是任意的三个正数都能作为三角形的三条边长,还需要满足三角形三边的基本关系,即两边之和大于第三边㊂上述解法中少了这个约束条件㊂正解:前面同错解,得12<a <8㊂又a +(2a -1)>2a +1,解得a >2㊂综上可得,实数a 的取值范围是(2,8)㊂易错点六㊁实际问题中题意不明致误图1例6 如图1,在海岛A 上有一座海拔1k m的山,山顶设有一个观察站P ,上午11时,测得一轮船在岛北30ʎ东㊁俯角为60ʎ的B 处,到11时10分,又测得该船在岛北60ʎ西㊁俯角为30ʎ的C 处㊂(1)求该船的航行速度;(2)又经过一段时间后,船到达海岛的正西方向的D 处,试问:此时船距海岛A 有多远?易错分析:有的同学对题意没有理解透彻,方位确定不了,不能观察出әB A C 是直角三角形;有的同学在求A D 的长时不能放在әA C D 中利用正弦定理求解㊂剖析:实际应用问题中的有关名词㊁术语不能混淆㊂①仰角和俯角:与目标视线在同一铅直平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫做仰角,目标视线在水平视线下方时叫做俯角㊂②方向角:从指定方向线到目标方向线的水平角㊂③方位角:从指定方向线顺时针到目标方向线的水平角㊂④坡度:坡面与水平面所成的二面角的度数㊂正解:(1)在R tәP A B 中,øA P B =60ʎ,P A =1,所以A B =3(k m )㊂在R t әP A C 中,øA P C =30ʎ,所以A C=P A ㊃t a n 30ʎ=33(k m )㊂在әA C B 中,øC A B =30ʎ+60ʎ=90ʎ,所以B C =A C 2+A B 2=332+32=303(k m )㊂所以该船的航行速度为303ː16=230(k m /h)㊂(2)øD A C =90ʎ-60ʎ=30ʎ㊂s i n øD C A =s i n (180ʎ-øA C B )=s i n øA C B =A B B C =3303=31010㊂s i n øC D A =s i n (øA C B -30ʎ)=s i n øA C B ㊃c o s 30ʎ-c o s øA C B ㊃s i n 30ʎ=31010㊃32-1-310102㊃12=33-11020㊂在әA C D 中,由正弦定理得A Ds i n øD C A=A C s i n øC D A ,所以A D =A C ㊃s i n øD C As i n øC D A=33㊃3101033-11020=9+313(k m )㊂故当船到达海岛的正西方向的D 处时,船与海岛A 的距离为9+313k m ㊂(责任编辑 王福华)82 解题篇 易错题归类剖析 高考数学 2023年10月Copyright ©博看网. All Rights Reserved.。
高考数学(理)总复习:解三角形(解析版)

高考数学(理)总复习:解三角形题型一 利用正、余弦定理解三角形 【题型要点解析】关于解三角形问题,一般要用到三角形的内角和定理,正、余弦定理及有关三角形的性质,常见的三角变换方法和原则都适用,同时要注意“三统一”,即“统一角、统一函数、统一结构”,这是使问题获得解决的突破口.【例1】△ABC 的内角A 、B 、C 所对的边分别为a ,b ,c ,已知sin(A +C )=8sin 2B2,(1)求cos B ;(2)若a +c =6,△ABC 的面积为2,求b .【解析】 (1)由题设及A +B +C =π,sin B =8sin 2B2,故sin B =4(1-cos B ).上式两边平方,整理得17cos 2B -32cos B +15=0, 解得cos B =1(舍去),cos B =1517.(2)由cos B =1517得sin B =817,故S △ABC =12ac sin B =417ac .又S △ABC =2,则ac =172.由余弦定理及a +c =6得:b 2=a 2+c 2-2ac cos B=(a +c )2-2ac (1+cos B )=36-2×172×⎪⎭⎫ ⎝⎛+17151 =4.所以b =2.题组训练一 利用正、余弦定理解三角形1.在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若sin A =223,a =2,S △ABC=2,则b 的值为( )A.3B.322 C .2 2D .2 3【解析】 ∵在锐角△ABC 中,sin A =223,S △ABC =2,∴cos A =1-sin 2A =13,12bc sin A =12bc ·223=2,∴bc =3①,由余弦定理得a 2=b 2+c 2-2bc cos A ,∴(b +c )2=a 2+2bc (1+cos A )=4+6×⎪⎭⎫⎝⎛+311=12, ∴b +c =23②.由①②得b =c =3,故选A. 【答案】 A2.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知sin A sin B +sin B sin C +cos 2B =1.若C =2π3,则ab=________.【解析】 ∵sin A sin B +sin B sin C +cos 2B =1,∴sin A sin B +sin B sin C =2sin 2B . 由正弦定理可得ab +bc =2b 2,即a +c =2b ,∴c =2b -a ,∵C =2π3,由余弦定理可得(2b -a )2=a 2+b 2-2ab cos 2π3,可得5a =3b ,∴a b =35. 【答案】 353.已知△ABC 是斜三角形,内角A ,B ,C 所对的边的长分别为a ,b ,c .若c sin A =3a cos C .(1)求角C ;(2)若c =21,且sin C +sin(B -A )=5sin 2A ,求△ABC 的面积.【解析】 (1)根据a sin A =c sin C,可得c sin A =a sin C , 又∵c sin A =3a cos C ,∴a sin C =3a cos C , ∴sin C =3cos C ,∴tan C =sin Ccos C =3,∵C ∈(0,π),∴C =π3.(2)∵sin C +sin(B -A )=5sin 2A ,sin C =sin (A +B ), ∴sin (A +B )+sin (B -A )=5sin 2A , ∴2sin B cos A =2×5sin A cos A . ∵△ABC 为斜三角形, ∴cos A ≠0,∴sin B =5sin A . 由正弦定理可知b =5a ,① ∵c 2=a 2+b 2-2ab cos C ,∴21=a 2+b 2-2ab ×12=a 2+b 2-ab ,②由①②解得a =1,b =5,∴S △ABC =12ab sin C =12×1×5×32=534.题型二 正、余弦定理的实际应用 【题型要点解析】应用解三角形知识解决实际问题一般分为下列四步:(1)分析题意,准确理解题意,分清已知与所求,尤其要理解题中的有关名词术语,如坡度、仰角、俯角、视角、方位角等;(2)根据题意画出示意图,并将已知条件在图形中标出;(3)将所求的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识正确求解;(4)检验解出的结果是否具有实际意义,对结果进行取舍,得出正确答案.【例2】某学校的平面示意图如图中的五边形区域ABCDE ,其中三角形区域ABE 为生活区,四边形区域BCDE 为教学区,AB ,BC ,CD ,DE ,EA ,BE .为学校的主要道路(不考虑宽度).∠BCD =∠CDE =2π3,∠BAE =π3,DE =3BC =3CD =910km.(1)求道路BE 的长度;(2)求生活区△ABE 面积的最大值.【解析】 (1)如图,连接BD ,在△BCD 中,BD 2=BC 2+CD 2-2BC ·CD cos ∠BCD =27100,∴BD =3310km.∵BC =CD ,∴∠CDB =∠CBD =π-2π32=π6,又∠CDE =2π3,∴∠BDE =π2.∴在Rt △BDE 中, BE =BD 2+DE 2=335(km). 故道路BE 的长度为335km.(2)设∠ABE =α,∵∠BAE =π3,∴∠AEB =2π3-α.在△ABE 中,易得AB sin ∠AEB =BE sin ∠BAE =335sinπ3=65,∴AB =65sin ⎪⎭⎫⎝⎛-απ32,AE =65sin α.∴S △ABE =12AB ·AE sin π3=9325sin ⎪⎭⎫⎝⎛-απ32·sin α =9325⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-4162sin 21πα≤9325⎪⎭⎫ ⎝⎛+4121 =273100(km 2). ∵0<α<2π3,∴-π6<2α-π6<7π6.∴当2α-π6=π2,即α=π3时,S △ABE 取得最大值,最大值为273100km 2,故生活区△ABE面积的最大值为273100km 2题组训练二 正、余弦定理的实际应用1.如图,为了估测某塔的高度,在同一水平面的A ,B 两点处进行测量,在点A 处测得塔顶C 在西偏北20°的方向上,仰角为60°;在点B 处测得塔顶C 在东偏北40°的方向上,仰角为30°.若A ,B 两点相距130 m ,则塔的高度CD =________m.【解析】设CD =h ,则AD =h3,BD =3h ,在△ADB 中,∠ADB =180°-20°-40°=120°,∴由余弦定理AB 2=BD 2+AD 2-2BD ·AD ·cos 120°,可得1302=3h 2+h 23-2×3h ×h 3×⎪⎭⎫⎝⎛-21,解得h =1039,故塔的高度为1039 m.【答案】 10392.如图,在第一条海防警戒线上的点A ,B ,C 处各有一个水声监测点,B ,C 两点到A 的距离分别为20千米和50千米,某时刻,B 收到发自静止目标P 的一个声波信号,8秒后A ,C 同时接收到该声波信号,已知声波在水中的传播速度是1.5千米/秒.(1)设A 到P 的距离为x 千米,用x 表示B ,C 到P 的距离,并求x 的值;(2)求P 到海防警戒线AC 的距离. 【解析】 (1)依题意,有P A =PC =x , PB =x -1.5×8=x -12. 在△P AB 中,AB =20, cos ∠P AB =P A 2+AB 2-PB 22P A ·AB=x 2+202-(x -12)22x ·20=3x +325x ,同理,在△P AC 中,AC =50,cos ∠P AC =P A 2+AC 2-PC 22P A ·AC =x 2+502-x 22x ·50=25x .∵cos ∠P AB =cos ∠P AC , ∴3x +325x =25x,解得x =31. (2)作PD ⊥AC 于点D ,在△ADP 中,由cos ∠P AD =2531,得sin ∠P AD =1-cos 2∠P AD =42131, ∴PD =P A sin ∠P AD =31×42131=421.故静止目标P 到海防警戒线AC 的距离为421千米. 题型三 三角函数与解三角形问题 【题型要点】解三角形与三角函数的综合题,其中,解决与三角恒等变换有关的问题,优先考虑角与角之间的关系;解决与三角形有关的问题,优先考虑正弦、余弦定理.【例3】在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且满足sin A -sin C b =sin A -sin Ba +c .(Ⅰ)求C ;(Ⅱ)若cos A =17,求cos(2A -C )的值.【解析】 (Ⅰ)由sin A -sin C b =sin A -sin B a +c 及正弦定理得a -c b =a -ba +c ,∴a 2-c 2=ab -b 2,整理得a 2+b 2-c 2=ab ,由余弦定理得cos C =a 2+b 2-c 22ab =12,又0<C <π,所以C =π3.(Ⅱ)由cos A =17知A 为锐角,又sin 2A +cos 2A =1,所以sin A =1-cos 2A =437,故cos2A=2cos 2A -1=-4749,sin2A =2sin A cos A =2×437×17=8349,所以cos(2A -C )=cos ⎪⎭⎫ ⎝⎛-32πA =cos2A cos π3+sin2A sin π3=-4749×12+8349×32=-2398.题组训练三 三角函数与解三角形问题已知函数f (x )=sin ⎪⎭⎫⎝⎛+62πx +cos 2x . (1)求函数f (x )的单调递增区间;(2)在△ABC 中,内角A ,B ,C 的对边为a ,b ,c ,已知f (A )=32,a =2,B =π3,求△ABC 的面积.【解析】 (1)f (x )=sin ⎪⎭⎫⎝⎛+62πx +cos 2x =sin 2x cos π6+cos 2x sin π6+cos 2x=32sin 2x +32cos 2x =3⎪⎪⎭⎫ ⎝⎛+x x 2cos 232sin 21 =3sin ⎪⎭⎫⎝⎛+32πx . 令-π2+2k π≤2x +π3≤π2+2k π⇒-5π12+k π≤x +π3≤π12+k π,k ∈Z .f (x )的单调递增区间为:⎥⎦⎤⎢⎣⎡++-ππππk k 12,125,k ∈Z .(2)由f (A )=32,sin ⎪⎭⎫ ⎝⎛+32πA =12, 又0<A <2π3,π3<2A +π3<5π3,因为2A +π3=5π6,解得:A =π4.由正弦定理a sin A =bsin B ,得b =6,又由A =π4,B =π3可得:sin C =6+24.故S △ABC =12ab sin C =3+32.题型四 转化与化归思想在解三角形中的应用 【题型要点】利用正弦、余弦定理解三角形的模型示意图如下:【例4】 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若a cos 2C 2+c cos 2A 2=32b .(1)求证:a ,b ,c 成等差数列;(2)若∠B =60°,b =4,求△ABC 的面积. 【解析】 (1)证明:a cos 2C 2+c cos 2A2=a ·1+cos C 2+c ·1+cos A 2=32b ,即a (1+cos C )+c (1+cos A )=3b . ①由正弦定理得:sin A +sin A cos C +sin C +cos A sin C =3sin B , ② 即sin A +sin C +sin(A +C )=3sin B , ∴sin A +sin C =2sinB.由正弦定理得,a +c =2b , ③ 故a ,b ,c 成等差数列.(2)由∠B =60°,b =4及余弦定理得: 42=a 2+c 2-2ac cos 60°,∴(a +c )2-3ac =16, 又由(1)知a +c =2b ,代入上式得4b 2-3ac =16. 又b =4,所以ac =16, ④∴△ABC 的面积S =12ac sin B =12ac sin 60°=4 3.题组训练四 转化与化归思想在解三角形中的应用 如图,在平面四边形ABCD 中,AD =1,CD =2,AC =7.(1)求cos ∠CAD 的值;(2)若cos ∠BAD =-714,sin ∠CBA =216,求BC 的长.【解析】 (1)在△ADC 中,由余弦定理,得cos ∠CAD =AC 2+AD 2-CD 22AC ·AD =7+1-427=277. (2)设∠BAC =α,则α=∠BAD -∠CAD . 因为cos ∠CAD =277,cos ∠BAD =-714,所以sin ∠CAD =1-cos 2∠CAD =217,sin ∠BAD =1-cos 2∠BAD =32114. 于是sin ∠BAC =sin (∠BAD -∠CAD )=sin ∠BAD cos ∠CAD -cos ∠BAD ·sin ∠CAD =32114×277-⎪⎪⎭⎫ ⎝⎛-1417×217=32. 在△ABC 中,由正弦定理得,BC =AC ·sin ∠BACsin ∠CBA=7×32216=3. 【专题训练】 一、选择题1.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c ,且b 2=a 2+bc ,A =π6,则内角C 等于( )A.π6 B.π4 C.3π4D.π4或3π4【解析】 在△ABC 中,由余弦定理得a 2=b 2+c 2-2bc cos A ,即a 2-b 2=c 2-2bc cos A ,由已知,得a 2-b 2=-bc ,则c 2-2bc cos π6=-bc ,即c =(3-1)b ,由正弦定理,得sin C=(3-1)sin B =(3-1)sin ⎪⎭⎫⎝⎛-C 65π, 化简,得sin C -cos C =0,解得C =π4,故选B.【答案】 B2.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知b =2,c =22,且C =π4,则△ABC 的面积为( )A.3+1B.3-1 C .4 D .2【解析】 法一 由余弦定理可得(22)2=22+a 2-2×2×a cos π4,即a 2-22a -4=0,解得a =2+6或a =2-6(舍去),△ABC 的面积S =12ab sin C =12×2×(2+6)sin π4=12×2×22×(6+2)=3+1,选A.法二 由正弦定理b sin B =c sin C ,得sin B =b sin C c =12,又c >b ,且B ∈(0,π),所以B =π6,所以A =7π12,所以△ABC 的面积S =12bc sin A =12×2×22sin 7π12=12×2×22×6+24=3+1.【答案】 A3.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若△ABC 的面积为S ,且2S =(a +b )2-c 2,则tan C 等于( )A.34B.43C .-43D .-34【解析】 因为2S =(a +b )2-c 2=a 2+b 2-c 2+2ab ,则结合面积公式与余弦定理,得ab sin C =2ab cos C +2ab ,即sin C -2cos C =2,所以(sin C -2cos C )2=4,sin 2C -4sin C cos C +4cos 2C sin 2C +cos 2C =4,所以tan 2C -4tan C +4tan 2C +1=4,解得tan C =-43或tan C =0(舍去),故选C.【答案】 C4.如图,在△ABC 中,C =π3,BC =4,点D 在边AC 上,AD =DB ,DE ⊥AB ,E 为垂足.若DE =22,则cos A 等于( )A.223B.24 C.64D.63【解析】 依题意得:BD =AD =DE sin A =22sin A ,∠BDC =∠ABD +∠A =2∠A .在△BCD 中, BC sin ∠BDC =BD sin C ,则4sin 2A =22sin A ×23=423sin A ,即42sin A cos A =423sin A,由此解得cos A =64,选C.【答案】 C5.如图所示,为测一建筑物的高度,在地面上选取A ,B 两点,从A ,B 两点分别测得建筑物顶端的仰角为30°,45°,且A ,B 两点间的距离为60 m ,则该建筑物的高度为( )A .(30+303) mB .(30+153) mC .(15+303) mD .(15+153) m【解析】 设建筑物高度为h ,则h tan 30°-h tan 45°=60,即(3-1)h =60,所以建筑物的高度为h =(30+303)m.【答案】 A6.在三角形ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若20aBC →+15bCA →+12cAB →=0,则三角形ABC 中最小角的正弦值等于( )A.45B.34C.35D.74【解析】 ∵20aBC →+15bCA →+12cAB →=0,∴20a (AC →-AB →)+15bCA →+12cAB →=0, ∴(20a -15b )AC →+(12c -20a )AB →=0.∵AC →与AB →不共线,∴⎩⎪⎨⎪⎧20a -15b =0,12c -20a =0⇒⎩⎨⎧b =43a ,c =53a ,∴三角形ABC 中最小角为角A , ∴cos A =b 2+c 2-a22bc =169a 2+259a 2-a 22×43×53a 2=45,∴sin A =35,故选C. 【答案】 C 二、填空题7.在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,若(a +b -c )(a +b +c )=ab ,c =3,当ab 取得最大值时,S △ABC =________.【解析】 因为(a +b -c )(a +b +c )=ab ,a 2+b 2-c 2=-ab ,所以cos C =-12,所以sinC =32,由余弦定理得(3)2=a 2+b 2+ab ≥3ab ,即ab ≤1,当且仅当a =b =1时等号成立.所以S △ABC =34. 【答案】348.已知△ABC 中,AB =1,sin A +sin B =2sin C ,S △ABC =316sin C ,则cos C =________. 【解析】 ∵sin A +sin B =2sin C ,由正弦定理可得a +b =2c .∵S △ABC =316sin C ,∴12ab sin C =316sin C ,sin C ≠0,化为ab =38.由余弦定理可得c 2=a 2+b 2-2ab cos C =(a +b )2-2ab-2ab cos C ,∴1=(2)2-2×38(1+cos C ),解得cos C =13.【答案】139.已知a ,b ,c 分别为△ABC 的三个内角A ,B ,C 的对边,a =2,且(2+b )(sin A -sin B )=(c -b )·sin C ,则△ABC 面积的最大值为________.【解析】 由正弦定理得(2+b )(a -b )=(c -b )c , 即(a +b )·(a -b )=(c -b )c ,即b 2+c 2-a 2=bc , 所以cos A =b 2+c 2-a 22bc =12,又A ∈(0,π),所以A =π3,又b 2+c 2-a 2=bc ≥2bc -4,即bc ≤4,故S △ABC =12bc sin A ≤12×4×32=3,当且仅当b =c =2时,等号成立,则△ABC 面积的最大值为 3. 【答案】310.如图,△ABC 中,AB =4,BC =2,∠ABC =∠D =60°,若△ADC 是锐角三角形,则DA +DC 的取值范围是________.【解析】 在△ABC 中,由余弦定理得AC 2=AB 2+BC 2-2AB ·BC cos ∠ABC =12,即AC =2 3.设∠ACD =θ(30°<θ<90°),则在△ADC 中,由正弦定理得23sin 60°=DA sin θ=DCsin (120°-θ),则DA +DC =4[sin θ+sin(120°-θ)]=4⎪⎪⎭⎫ ⎝⎛+θθcos 23sin 23=43sin(θ+30°),而60°<θ+30°<120°,43sin 60°<DA +DC ≤43sin 90°,即6<DA +DC ≤4 3.【答案】 (6,43] 三、解答题11.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a >b ,a =5,c =6,sin B =35. (1)求b 和sin A 的值;(2)求sin ⎪⎭⎫⎝⎛+42πA 的值. 【解析】 (1)在△ABC 中,因为a >b ,故由sin B =35,可得cos B =45.由已知及余弦定理,有b 2=a 2+c 2-2ac cos B =13,所以b =13.由正弦定理a sin A =b sin B ,得sin A =a sin B b =31313.所以b 的值为13,sin A 的值为31313.(2)由(1)及a <c ,得cos A =21313,所以sin 2A =2sin A cos A =1213,cos 2A =1-2sin 2A =-513.故sin ⎪⎭⎫⎝⎛+42πA =sin 2A cos π4+cos 2A sin π4=7226. 12.如图,在四边形ABCD 中,∠DAB =π3,AD ∶AB =2∶3,BD =7,AB ⊥BC .(1)求sin ∠ABD 的值;(2)若∠BCD =2π3,求CD 的长.【解析】(1)∵AD ∶AB =2∶3,∴可设AD =2k ,AB =3k .又BD =7,∠DAB =π3,∴由余弦定理,得(7)2=(3k )2+(2k )2-2×3k ×2k cos π3,解得k =1,∴AD =2,AB =3,sin ∠ABD =AD sin ∠DABBD=2×327=217.(2)∵AB ⊥BC ,∴cos ∠DBC =sin ∠ABD =217,∴sin ∠DBC =277,∴BD sin ∠BCD =CDsin ∠DBC,∴CD=7×27732=433.。
相似三角形的性质易错点剖析

靼 似 王 角 曲 悭 质 籍 最
… .
湖蔓 盔: 曼德吏. 撞 塑 主… 一 邹 ±
正解 : AA B C的三 边 长 按 从 小 到 大 的顺 序 排 列 为 3 、
DE
,
3
=
号 : ,  ̄ , - A B = 6 ( c m ) D E _ 4 . 5 ( c m )
综上所述 , △A B C 的第 三边 长 为 8 .
剖析 : 相似三角形 的对应 边成 比例 , 边的对应 , 没有
易错点三 、 错 记 相 似 三 角 形 的 面积 比 而 出错 到位 , 找 错 了对 应 边 , A E与 C E不 是 对 应 边 . 例 3 如 图, 已 知 AA D E 与
C. 2:l
m — 数掌大童界 。 p 。 ◆ . . . + 。 D .4:l .
C 的两 边分 别为 6 , 1 0 , 若 这两 个三 角形相 似 , 求 △A B
C 的第 三积 比等于 相似 比的平 方 , 一 些同学 由于错记为相 似三 角形 的面积 比等 于相似 比而
正 解 : 由 题 意 得 : = = 器 , 3 = 2 = , 得 曰 AABC的 相 似 比 为 1: 2, 则 AA D E
=
9 ( c m) , D E=3( c m) , B D= 9—3= 6 ( c m) .
-
 ̄AA B C 的面 积 比为 ( ) .
大 小 关 系对 应 并 进 行 分 类 讨 论 导 致 漏 解 .
高考数学易错点第8讲:三角函数与解三角形
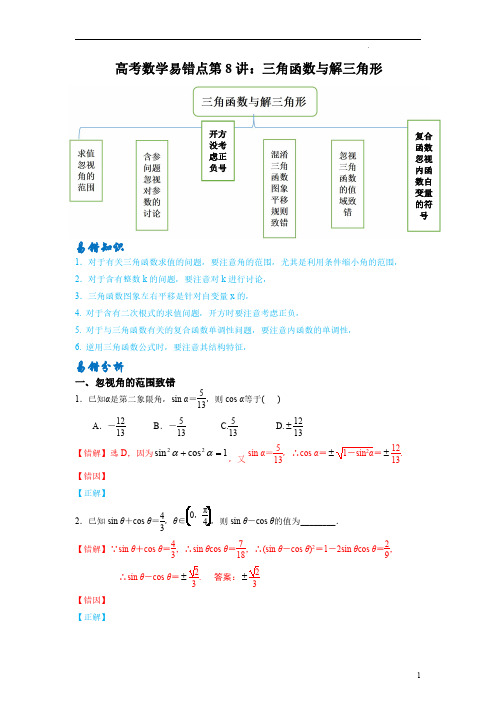
高考数学易错点第8讲:三角函数与解三角形易错知识1.对于有关三角函数求值的问题,要注意角的范围,尤其是利用条件缩小角的范围,2.对于含有整数k 的问题,要注意对k 进行讨论,3.三角函数图象左右平移是针对自变量x 的,4.对于含有二次根式的求值问题,开方时要注意考虑正负,5.对于与三角函数有关的复合函数单调性问题,要注意内函数的单调性,6.逆用三角函数公式时,要注意其结构特征,易错分析一、忽视角的范围致错1.已知α是第二象限角,sin α=513,则cos α等于()A .-1213B .-513C.513D.±1213【错解】选D ,因为1cos sin 22=+αα,又sin α=513,∴cos α=±1-sin 2α=±1213.【错因】【正解】2.已知sin θ+cos θ=43,θsin θ-cos θ的值为________.【错解】∵sin θ+cos θ=43,∴sin θcos θ=718,∴(sin θ-cos θ)2=1-2sin θcos θ=29,∴sin θ-cos θ=±23.答案:±23【错因】【正解】开方没考虑正负号复合函数忽视内函数自变量的符号3.已知θ∈(0,π),=43,则sinθ+cosθ=________.【错解】由题知=43=1+tanθ1-tanθ⇒tanθ=17,又因为θ∈(0,π),=17,sin2θ=1θ=210,θ=7210,或⎪⎪⎩⎪⎪⎨⎧-==1027cos102sinθθ,所以sinθ+cosθ=425或523-答案:425或523-【错因】【正解】4.在△ABC中,若C=3B,则cb的取值范围为()A.(0,3)B.(1,3)C.(1,3)D.(3,3)【错解】选A由正弦定理可得,cb=sin Csin B=sin3Bsin B=sin(B+2B)sin B=sin B·cos2B+cos B·sin2Bsin B =cos2B+2cos2B=4cos2B-1.又0<B<180°,∴≤0cos2B≤1,又c b>0,∴0<c b<3.【错因】【正解】二、对于含有二次根式的求值问题,开方时没有注意正负5.化简:2sin8+1+2cos8+2=()A.4cos4B.-2sin4-4cos4C.4sin4D.2sin4+4cos4【错解】选D原式=21+2sin4cos4+4cos24=2sin24+cos24+2sin4cos4+2cos4=2sin4+2cos4+2cos4=2sin4+4cos4.【错因】【正解】6.若3π2<θ<5π2,则12+1212+12cosθ等于()A.sinθ4B.cosθ4C.-sinθ4D.-cosθ4【错解】选B 由二倍角公式得12+12cos θ=1+cos θ2=cos 2θ2=cos θ2,∴12+1212+12cos θ=4cos 2212cos 21212θθ⨯=+=cos θ4【错因】【正解】三、三角函数图象左右平移时忽视自变量x 的系数致错7.为了得到函数y =sinx y =sin 2x 的图象()A .向右平移π6个单位B .向右平移π3个单位C .向左平移π6个单位D .向左平移π3个单位【错解】选B根据左加右减可知,为了得到函数y =sinx 可以将函数y =sin 2x 的图象向右平移π3个单位.【错因】【正解】8.要得到y =cos y =sin 12x 的图象()A .向左平移π3个单位B .向右平移π3个单位C .向左平移4π3个单位D .向右平移4π3个单位【错解】选A因为y =)3(21cos π+x ,故要得到y =cos只需将函数y =sin 12x 的图象向左平移π3个单位.【错因】【正解】四、涉及到整数k 的问题,忽视对k 的讨论致错9.已知角α为第一象限角,则α2是第________象限角.【错解】∵α是第一象限角,∴2k π<α<π2+2k π,k ∈Z ,∴k π<α2<π4+k π,k ∈Z ,则α2是第一象限角.答案:一【错因】【正解】10.(忽视对k 的讨论)已知A =sin (k π+α)sin α+cos (k π+α)cos α(k ∈Z),则A 的值构成的集合是________.【错解】A =sin αsin α+cos αcos α=2.答案:{2}【错因】【正解】五、含参问题忽视对参数的讨论致错11.已知角α的终边过点P (-4m,3m )(m ≠0),则2sin α+cos α=________.【错解】易知OP =(-4m )2+(3m )2=5m ,则sin α=5353=m m,cos α=5454-=-m m .故2sin α+cos α=25.答案:25【错因】【正解】六、三角函数的单调性问题中,忽视自变量x 的系数为负值致错12.函数f (x )=sin ________.【错解】要求f (x )=sin 的单调递增区间,只需令-π2+2k π≤π6-x ≤π2+2k π(k ∈Z ),可得3π-+2k π≤x ≤2π3+2k π(k ∈Z ),所以函数f (x )=sin 3[π-+2k π,2π3+2k π](k ∈Z ).答案:3[π-+2k π,2π3+2k π](k ∈Z ).【错因】【正解】七、判断三角形形状时考虑不全致错13.已知在△ABC 中,三个内角为A ,B ,C ,sin 2A =sin 2B ,则△ABC 是()A .等腰三角形B .等边三角形C .直角三角形D .等腰或直角三角形【错解】选A 因为sin 2A =sin 2B ,所以2A =2B ,解得A =B ,所以△ABC 是等腰三角形.【错因】【正解】八、忽视正切函数本身的定义域14.已知函数f(x)=lg(tan x-1)+9-x2,则f(x)的定义域是____.【错解】∵函数f(x)=lg(tan x-1)+9-x2,x-1>0,-x2≥0,∴⎪⎩⎪⎨⎧≤≤-∈+≥33,4xZkkxππ,∴x∈]343[π-,∴函数y=f(x)的定义域为]343[,π-.答案:]343[,π-【错因】【正解】易错题通关1π+π4≤α≤kπ+π2,k∈(阴影部分)是()2.在△ABC中,若sin2A=sin2C,则△ABC的形状是()A.等边三角形B.等腰三角形C.直角三角形D.等腰三角形或直角三角形3.已知角θ的顶点与原点重合,始边与x轴非负半轴重合,若A(-1,y)是角θ终边上的一点,且sinθ=-31010,则y=()A.3B.-3C.1D.-14.已知θ是第三象限角,且cos(π+θ)=13,则tanθ=()A.24B.2C.22 D.105.已知α终边与单位圆的交点α是第二象限角,则1-sin2α+2+2cos2α的值等于()A.15B.-15C.3D.-36.设α角属于第二象限,且|cosα2|=-cosα2,则α2角属于()A.第一象限B.第二象限C.第三象限D.第四象限7.已知sin α,cos α是方程x 2-2kx +k 2+k =0的两根,则k 的值为()A.1±32 B.1-32C .1±3D .1+38.若θ∈(0,π),tan θ+1tan θ=6,则sin θ+cos θ=()A .233B .-233C .±233D .239.在△ABC 中,cos A =513,sin B =35,则cos C 的值为()A.1665B .-5665C .-1665D.1665或-566510.已知cos α=255,sin β=1010,且α∈0,π2,β∈0,π2,则α+β的值是()A.3π4B.π4C.7π4D.5π411.已知φ∈R,则“φ=0”是“y =sin(x +φ)为奇函数”的()A .充分不必要条件B .充要条件C .必要不充分条件D .既不充分也不必要条件12.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a cos A =b cos B ,且c 2=a 2+b 2-ab ,则△ABC 的形状为()A .等腰三角形或直角三角形B .等腰直角三角形C .直角三角形D .等边三角形13.把函数f (x )=2cos 2x -π4的图象向左平移m (m >0)个单位,得到函数g (x )=2sin 2x -π3的图象,则m 的最小值是()A.724π B.1724π C.524π D.1924π14.已知ω>0,函数f (x )=sin ωx +π4在区间π2,π上单调递减,则实数ω的取值范围是()A.12,54B.12,34C .0,12D .(0,2]15.已知函数y =sin(ωx +φ)ω>0,|φ|<π2的图象的一部分如图所示,则ω,φ的值分别为()A .1,π3B .1,-π3C .2,-π3D .2,π316.已知函数f (x )=sinωx +π6(ω>0),对任意x ∈R ,都有f (x )≤f π3,并且f (x )在区间-π6,π3上不单调,则ω的最小值是()A .1B .3C .5D .717.(多选)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若b =23,c =3,A +3C =π,则下列结论正确的是()A .cos C =33B .sin B =23C .a =3D .S △ABC =218.(多选题)如图是函数y =sin(ωx +φ)的部分图象,则sin(ωx +φ)=()A .B .2C .xD .219.若0<α<π2,-π<β<-π2,=13,=-33,则()A .-539B.539C .-33D.3320.已知角α的终边经过点(3a -9,a +2),且cos α≤0,sin α>0,则实数a 的取值范围是________.21.已知函数f (x )=2sin(ωx +φ)(ω>0,-π<φ<0)的相邻两个零点间的距离为π2,且-2,则φ=________.22.化简sin (n π+α)cos (n π-α)cos[(n +1)π-α](n ∈Z)的结果为________.23.在锐角△ABC 中,BC =2,sin B +sin C =2sin A ,则中线AD 长的取值范围是________.24.若sin 2α=55,sin(β-α)=1010,且α∈π4,π,β∈π,3π2,则α+β的值是________.25.设f (x )=m x m -1(m ≠0).(1)若m =2,求函数f (x )的零点;(2)当x ∈0,π2时,-3≤f (x )≤4恒成立,求实数m 的取值范围.参考答案一、忽视角的范围致错1.已知α是第二象限角,sin α=513,则cos α等于()A .-1213B .-513C.513D.±1213【错解】选D ,因为1cos sin 22=+αα,又sin α=513,∴cos α=±1-sin 2α=±1213.【错因】没有注意条件α是第二象限角,【正解】选A∵α是第二象限角,则cos α>0,∴cos α=-1-sin 2α=-1213.2.已知sin θ+cos θ=43,θsin θ-cos θ的值为________.【错解】∵sin θ+cos θ=43,∴sin θcos θ=718,∴(sin θ-cos θ)2=1-2sin θcos θ=29,∴sin θ-cos θ=±23.答案:±23【错因】没有注意由条件θsin θ<cos θ,【正解】∵sin θ+cos θ=43,∴sin θcos θ=718,∴(sin θ-cos θ)2=1-2sin θcos θ=29,又θsin θ<cos θ,∴sin θ-cos θ=-23.答案:-233.已知θ∈(0,π),=43,则sin θ+cos θ=________.【错解】由题知=43=1+tan θ1-tan θ⇒tan θ=17,又因为θ∈(0,π),=17,sin 2θ=1θ=210,θ=7210,或⎪⎪⎩⎪⎪⎨⎧-==1027cos 102sin θθ,所以sin θ+cos θ=425或523-答案:425或523-【错因】没有注意由tan θ=17>0可以缩小角的范围,即可推出θ【正解】由题知=43=1+tan θ1-tan θ⇒tan θ=17,又因为θ∈(0,π),且tan θ>0,所以θ∈=17,sin 2θ=1θ=210,θ=7210,所以sin θ+cos θ=8210=425.答案:4254.在△ABC 中,若C =3B ,则cb的取值范围为()A .(0,3)B .(1,3)C .(1,3)D .(3,3)【错解】选A由正弦定理可得,c b =sin C sin B =sin 3B sin B =sin (B +2B )sin B =sin B ·cos 2B +cos B ·sin 2Bsin B=cos 2B +2cos 2B =4cos 2B -1.又0<B <180°,∴≤0cos 2B ≤1,又c b >0,∴0<cb<3.【错因】忽略了A +B +C =180°及条件C =3B ,【正解】选B由正弦定理可得,c b =sin C sin B =sin 3B sin B =sin (B +2B )sin B =sin B ·cos 2B +cos B ·sin 2Bsin B=cos 2B +2cos 2B =4cos 2B -1.又A +B +C =180°,C =3B ,∴0°<B <45°,∴22cos B <1,∴1<4cos 2B -1<3,即1<cb<3.二、对于含有二次根式的求值问题,开方时没有注意正负5.化简:2sin 8+1+2cos 8+2=()A .4cos 4B .-2sin 4-4cos 4C .4sin 4D .2sin 4+4cos 4【错解】选D原式=21+2sin 4cos 4+4cos 24=2sin 24+cos 24+2sin 4cos 4+2cos 4=2sin 4+2cos 4+2cos 4=2sin 4+4cos 4.【错因】开方时没有考虑2cos 4、sin 4+cos 4的正负,【正解】选B原式=21+2sin 4cos 4+4cos 24=2sin 24+cos 24+2sin 4cos 4+2|cos 4|=2|sin 4+cos 4|+2|cos 4|,∵π<4<3π2,∴sin 4+cos 4<0,cos 4<0,∴原式=-2(sin 4+cos 4)-2cos 4=-2sin 4-4cos 4.6.若3π2<θ<5π2,则12+1212+12cos θ等于()A .sinθ4B .cosθ4C .-sinθ4D .-cosθ4【错解】选B 由二倍角公式得12+12cos θ=1+cos θ2=cos 2θ2=cos θ2,∴12+1212+12cos θ=4cos 2212cos 21212θθ⨯=+=cos θ4【错因】没有用3π2<θ<5π2去求θ2、θ2的范围,【正解】选A∵3π2<θ<5π2,∴3π4<θ2<5π4,3π8<θ4<5π8,∴cos θ>0,cos θ2<0,sin θ4>0,∴12+12cos θ=1+cos θ2=cos 2θ2=-cos θ2,∴12+1212+12cos θ=1-cosθ22=sin 2θ4=sin θ4.三、三角函数图象左右平移时忽视自变量x 的系数致错7.为了得到函数y =sinx y =sin 2x 的图象()A .向右平移π6个单位B .向右平移π3个单位C .向左平移π6个单位D .向左平移π3个单位【错解】选B根据左加右减可知,为了得到函数y =sinx 可以将函数y =sin 2x 的图象向右平移π3个单位.x,【正解】选A ∵函数y =x sin 2∴为了得到函数y =sinx 可以将函数y =sin 2x 的图象向右平移π6个单位.8.要得到y =cos y =sin 12x 的图象()A .向左平移π3个单位B .向右平移π3个单位C .向左平移4π3个单位D .向右平移4π3个单位【错解】选A因为y =)3(21cos π+x ,故要得到y =cos只需将函数y =sin 12x 的图象向左平移π3个单位.【错因】函数图象平移变换时,没注意函数的名称是不一致的,不能直接进行平移,【正解】选Cy =+π6+y =cos图象,只需将函数y =sin 12x 的图象向左平移4π3个单位.四、涉及到整数k 的问题,忽视对k 的讨论致错9.已知角α为第一象限角,则α2是第________象限角.【错解】∵α是第一象限角,∴2k π<α<π2+2k π,k ∈Z ,∴k π<α2<π4+k π,k ∈Z ,则α2是第一象限角.答案:一【错因】没有对k 分情况讨论,【正解】∵α是第一象限角,∴2k π<α<π2+2k π,k ∈Z ,∴k π<α2<π4+k π,k ∈Z ,当k 为偶数时,α2是第一象限角;当k 为奇数时,α2是第三象限角.综上,α2是第一或第三象限角.答案:一或三10.(忽视对k 的讨论)已知A =sin (k π+α)sin α+cos (k π+α)cos α(k ∈Z),则A 的值构成的集合是________.【错解】A =sin αsin α+cos αcos α=2.答案:{2}【错因】没有对k 分情况讨论,【正解】当k 为奇数时:A =-sin αsin α-cos αcos α=-2.当k 为偶数时:A =sin αsin α+cos αcos α=2.答案:{-2,2}五、含参问题忽视对参数的讨论致错11.已知角α的终边过点P (-4m,3m )(m ≠0),则2sin α+cos α=________.【错解】易知OP =(-4m )2+(3m )2=5m ,则sin α=5353=m m,cos α=5454-=-m m .故2sin α+cos α=25.答案:25【错因】没有对参数m 分情况讨论,【正解】易知OP =(-4m )2+(3m )2=5|m |,则sin α=3m5|m |,cos α=-4m 5|m |.当m >0时,sin α=35,cos α=-45,2sin α+cos α=25;当m <0时,sin α=-35,cos α=45,∴2sin α+cos α=-25.故2sin α+cos α=±25.答案:±25六、三角函数的单调性问题中,忽视自变量x 的系数为负值致错12.函数f (x )=sin________.【错解】要求f (x )=sin的单调递增区间,只需令-π2+2k π≤π6-x ≤π2+2k π(k ∈Z ),可得3π-+2k π≤x ≤2π3+2k π(k ∈Z ),所以函数f (x )=sin3[π-+2k π,2π3+2k π](k ∈Z ).答案:3[π-+2k π,2π3+2k π](k ∈Z ).【错因】没有注意自变量x 的系数是负数,【正解】因为f (x )=f (x )=sin只需要求y =sin的单调递减区间.令π2+2k π≤x -π6≤3π2+2k π(k ∈Z ),可得2π3+2k π≤x ≤5π3+2k π(k ∈Z ),所以y =sin2π3+2k π,5π3+2k π(k ∈Z ),此即为函数f (x)=sin答案:2π3+2k π,5π3+2k π(k ∈Z )七、判断三角形形状时考虑不全致错13.已知在△ABC 中,三个内角为A ,B ,C ,sin 2A =sin 2B ,则△ABC 是()A .等腰三角形B .等边三角形C .直角三角形D .等腰或直角三角形【错解】选A因为sin 2A =sin 2B ,所以2A =2B ,解得A =B ,所以△ABC 是等腰三角形.【错因】sin 2A =sin 2B 时,有两种可能:2A =2B 或2A =π-2B ,【正解】选D因为sin 2A =sin 2B ,所以2A =2B 或2A =π-2B ,解得A =B 或A +B =π2,所以△ABC 是等腰或直角三角形.八、忽视正切函数本身的定义域14.已知函数f (x )=lg (tan x -1)+9-x 2,则f (x )的定义域是____.【错解】∵函数f (x )=lg (tan x -1)+9-x 2,x -1>0,-x 2≥0,∴⎪⎩⎪⎨⎧≤≤-∈+≥33,4x Z k k x ππ,∴x ∈]343[π-,∴函数y =f (x )的定义域为]343[,π-.答案:]343[,π-【错因】没有考虑x y tan =的定义域,【正解】∵函数f (x )=lg (tan x -1)+9-x 2,x -1>0,-x 2≥0,π+π4<x <k π+π2(k ∈Z ),3≤x ≤3,∴x -3π4,-∴函数y =f (x )-3π4,--3π4,-易错题通关1π+π4≤α≤k π+π2,k ∈(阴影部分)是()【答案】C【解析】当k =2n (n ∈Z)时,2n π+π4≤α≤2n π+π2(n ∈Z),此时α的终边和π4≤α≤π2的终边一样;当k =2n +1(n ∈Z)时,2n π+π+π4≤α≤2n π+π+π2(n ∈Z),此时α的终边和π+π4≤α≤π+π2的终边一样,结合选项知选C.2.在△ABC 中,若sin 2A =sin 2C ,则△ABC 的形状是()A .等边三角形B .等腰三角形C .直角三角形D .等腰三角形或直角三角形【答案】D【解析】因为sin 2A =sin 2C ⇒sin 2A =sin(π-2C ),所以A =C 或A +C =π2.当A =C 时,三角形为等腰三角形;当A +C =π2时,三角形为直角三角形.3.已知角θ的顶点与原点重合,始边与x 轴非负半轴重合,若A (-1,y )是角θ终边上的一点,且sin θ=-31010,则y =()A .3B .-3C .1D .-1【答案】B【解析】因为sin θ=-31010<0,A (-1,y )是角θ终边上一点,所以y <0,由三角函数的定义,得y y 2+1=-31010.解得y =-3.4.已知θ是第三象限角,且cos(π+θ)=13,则tan θ=()A.24B .2C .22 D.10【答案】C【解析】cos(π+θ)=-cos θ=13,所以cos θ=-13,又θ是第三象限角,所以sin θ=-1-cos 2θ=-=-223,所以tan θ=sin θcos θ=-223-13=22.5.已知α终边与单位圆的交点α是第二象限角,则1-sin 2α+2+2cos 2α的值等于()A.15B .-15C .3D .-3【答案】C【解析】因为α终边与单位圆的交点α是第二象限角,所以sin α=35,cos α=-45,则1-sin 2α+2+2cos 2α=1-2sin α·cos α+2(1+cos 2α)=(sin α-cos α)2|sin α-cos α|+2|cos α|=75+85=3.6.设α角属于第二象限,且|cos α2|=-cos α2,则α2角属于()A .第一象限B .第二象限C .第三象限D .第四象限【答案】C【解析】∵α是第二象限角,∴90°+k ·360<α<180°+k ·360°,k ∈Z ,∴45°+k ·180°<α2<90°+k ·180°,k ∈Z.当k =2n ,n ∈Z 时,α2在第一象限;当k =2n +1,n ∈Z 时,α2在第三象限,∴α2在第一象限或在第三象限,∵|cos α2|=-cos α2,∴cos α2<0,∴α2角在第三象限.7.已知sin α,cos α是方程x 2-2kx +k 2+k =0的两根,则k 的值为()A.1±32 B.1-32C .1±3D .1+3【答案】B【解析】α+cos α=2k ,αcos α=k 2+k ,∵sin 2α+cos 2α=(sin α+cos α)2-2sin αcos α=4k 2-2(k 2+k )=1,即2k 2-2k -1=0,解得k =2±234=1±32.∵sin α+cos α=2sin ∴sin α+cos α∈[-2,2],即2k ∈[-2,2],∴k ∈-22,22,∴k =1-32.9.若θ∈(0,π),tan θ+1tan θ=6,则sin θ+cos θ=()A .233B .-233C .±233D .23【答案】A【解析】因为tan θ+1tan θ=sin θcos θ+cos θsin θ=sin 2θ+cos 2θsin θcos θ=6,所以sin θcos θ=16,又θ∈(0,π),则sin θ>0,cos θ>0,所以sin θ+cos θ>0.所以(sin θ+cos θ)2=1+2sin θcos θ=43,所以sin θ+cos θ=233.9.在△ABC 中,cos A =513,sin B =35,则cos C 的值为()A.1665B .-5665C .-1665D.1665或-5665【答案】A【解析】在△ABC 中,由cos A =513,sin B =35,可得sin A =1-cos 2A =1213,因为sin B <sin A 且A 为锐角,则b <a ,所以A >B ,所以B 为锐角,所以cos B =1-sin 2B =45,则cos C =cos [π-(A +B )]=-cos(A +B )=-cos A cos B +sin A sin B =-513×45+1213×35=1665.10.已知cos α=255,sin β=1010,且αβα+β的值是()A.3π4B.π4C.7π4D.5π4【答案】B【解析】因为αβ所以sin α=1-cos 2α=55,cos β=1-sin 2β=31010,cos(α+β)=cos αcos β-sin αsin β=255×31010-55×1010=22.又0<α+β<π,故α+β=π4.11.已知φ∈R,则“φ=0”是“y =sin(x +φ)为奇函数”的()A .充分不必要条件B .充要条件C .必要不充分条件D .既不充分也不必要条件【答案】A【解析】当φ=0时,y =sin(x +φ)为奇函数;当y =sin(x +φ)是奇函数时,φ=k π,k ∈Z ,所以“φ=0”是“y =sin(x +φ)为奇函数”的充分不必要条件,故选A.13.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a cos A =b cos B ,且c 2=a 2+b 2-ab ,则△ABC 的形状为()A .等腰三角形或直角三角形B .等腰直角三角形C .直角三角形D .等边三角形【答案】D【解析】因为a cos A =b cos B ,所以sin A cos A =sin B cos B ,即sin 2A =sin 2B ,又A ,B ∈(0,π),故可得A =B 或A +B =π2.由c 2=a 2+b 2-ab ,得cos C =12,又C ∈(0,π),故可得C =π3.综上所述,A =B =C =π3.故三角形ABC 是等边三角形.13.把函数f (x )=2cos x m (m >0)个单位,得到函数g (x )=2sin x 图象,则m 的最小值是()A.724π B.1724π C.524π D.1924π【答案】B【解析】选B把函数f (x )=2cosx m (m >0)个单位,得到f (x )=2cos2(x +m )-π4=2cos x +2mg (x )=x 2cos π2-x 2x 由2m -π4=-5π6+2k π,k ∈Z ,得m =-7π24+k π,k ∈Z ,∵m >0,∴当k =1时,m 最小,此时m =π-7π24=17π24.14.已知ω>0,函数f (x )=sin 在区间π2,π上单调递减,则实数ω的取值范围是()A.12,54B.12,34C ,12D .(0,2]【答案】A【解析】由π2≤x ≤π,得π2ω+π4≤ωx +π4≤πω+π4,由题意π2ω+π4,πω+π4⊆2k π+π2,2k π+3π2(k ∈Z ).当k =0+π4≥π2,+π4≤3π2,得12≤ω≤54.15.已知函数y =sin(ωx +φ>0,|φ|则ω,φ的值分别为()A .1,π3B .1,-π3C .2,-π3D .2,π3【答案】D【解析】由图象知,T 4=7π12-π3=π4,即T =π,所以2πω=π,即ω=2.2×π3+φ=k π,k ∈Z ,又|φ|<π2,故φ=π3,故选D.16.已知函数f(x )=(ω>0),对任意x ∈R ,都有f (x )≤并且f (x )在区间-π6,π3上不单调,则ω的最小值是()A .1B .3C .5D .7【答案】D【解析】由题意,f f (x )的最大值,∴ωπ3+π6=2k π+π2,k ∈Z ,即ω=6k +1,k ∈Z .∵ω>0,∴k ∈N .当k =0时,ω=1,f(x )=sin 在-π6,π3上单调递增,不符合题意;当k =1时,ω=7,f(x )=sinx ω的最小值是7.17.(多选)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若b =23,c =3,A +3C =π,则下列结论正确的是()A .cos C =33B .sin B =23C .a =3D .S△ABC =2【答案】AD【解析】选AD 由A +3C =π,得B =2C .根据正弦定理b sin B =c sin C,得23sin C =3×2sin C cos C ,又sin C >0,故cos C =33,sin C =63,故A 正确;sin B =sin 2C =2sin C cos C =223,故B 错误;由余弦定理得c 2=a 2+b 2-2ab cos C ,将b =23,c =3代入得a 2-4a +3=0,解得a =3或a =1.若a =3,则A =C =π4,且B =π2,与sin B =223矛盾,所以a =1,故C 错误;S △ABC =12ab sin C =12×1×23×63=2,故D 正确.故选A 、D.18.(多选题)如图是函数y =sin(ωx +φ)的部分图象,则sin(ωx +φ)=()A .B .2C .xD .2【答案】BC【解析】由题图可知,函数的最小正周期T =π,∴2π|ω|=π,ω=±2.当ω=2时,y =sin(2x +φ)×π6+0,∴2×π6+φ=2k π+π,k ∈Z ,即=2k π+2π3,k ∈Z ,∴y =x 故A 错误;由x sin π2sin 2B 正确;由x x +π2+cos x C 正确;由x x cos πx cos 2D 错误.综上可知,正确的选项为B 、C.20.若0<α<π2,-π<β<-π2,=13,=-33,则()A .-539B.539C .-33D.33【答案】D【解析】∵0<α<π2,-π<β<-π2,则π4<π4+α<3π4,π2<π4-β2<3π4,∴=223,=63,因此,=13×+223×63=33.20.已知角α的终边经过点(3a -9,a +2),且cos α≤0,sin α>0,则实数a 的取值范围是________.【答案】(-2,3]【解析】∵cos α≤0,sin α>0,∴角α的终边落在第二象限或y 轴的正半轴上.∴a -9≤0,+2>0,∴-2<a ≤3.21.已知函数f (x )=2sin(ωx +φ)(ω>0,-π<φ<0)的相邻两个零点间的距离为π2,且-2,则φ=________.【答案】-π4【解析】由题意T =2×π2=π,ω>0,所以ω=2πT=2,-π4+2,-π4+φ=2k π-π2,k ∈Z ,又-π<φ<0,所以φ=-π4.22.化简sin (n π+α)cos (n π-α)cos[(n +1)π-α](n ∈Z)的结果为________.【答案】(-1)n +1sin α(n ∈Z)【解析】①当n =2k (k ∈Z)时,原式=sin (2k π+α)cos (2k π-α)cos[(2k +1)π-α]=sin αcos α-cos α=-sin α.②当n =2k +1(k ∈Z)时,原式=sin[(2k +1)π+α]cos[(2k +1)π-α]cos[(2k +2)π-α]=(-sin α)(-cos α)cos α=sin α.综上,化简的结果为(-1)n +1sin α(n ∈Z).23.在锐角△ABC 中,BC =2,sin B +sin C =2sin A ,则中线AD 长的取值范围是________.【答案】3【解析】设AB =c ,AC =b ,BC =a =2,对sin B +sin C =2sin A 运用正弦定理,得b +c =2a =4,解得c =4-b ,结合该三角形为锐角三角形,得到不等式组2+c 2=b 2+(4-b )2>4,2+4=(4-b )2+4>b 2,2+4>c 2=(4-b )2,解得32<b <52,故bc =b (4-b )=-b 2+4b ,结合二次函数的性质,得到154<bc ≤4.运用向量得到AD ―→=12(AB ―→+AC ―→),所以|AD ―→|=12AB 2―→+AC 2―→+2|AB ―→|·|AC ―→|·cos ∠BAC=12b 2+c 2+2bc ·b 2+c 2-42bc=122b 2+2c 2-4=1228-4bc ,结合bc 的范围,得|AD ―→|的范围为324.若sin 2α=55,sin(β-α)=1010,且α∈π4,π,β∈π,3π2,则α+β的值是________.【答案】7π4【解析】∵α∈π4,π,β∈π,3π2,∴2α∈π2,2π,又0<sin 2α=55<12,∴2ααβ-α∴cos 2α=-1-sin 22α=-255.又sin(β-α)=1010,∴β-α∴cos(β-α)=-1-sin 2(β-α)=-31010,∴cos(α+β)=cos[2α+(β-α)]=cos 2αcos(β-α)-sin 2αsin(β-α)=-255×-55×1010=22.又αβ∈π,3π2,∴α+βα+β=7π4.25.设f (x )=m x m -1(m ≠0).(1)若m =2,求函数f (x )的零点;(2)当x ∈0,π2时,-3≤f (x )≤4恒成立,求实数m 的取值范围.解:(1)由m =2⇒f (x )=x 1,令f (x )=0,则x =-12,即2x -π3=2k π+2π3或2x -π3=2k π+4π3(k ∈Z ),解得x =k π+π2或x =k π+5π6(k ∈Z ),21∴f (x )的零点是x =k π+π2或x =k π+5π6(k ∈Z ).(2)由0≤x ≤π2可得-π3≤2x -π3≤2π3,所以-12≤x1.①当m >0时,易得m 2-1≤f (x )≤2m -1,由-3≤f (x )≤4x )min ≥-3,x )max ≤4,1≥-3,-1≤4,,解得0<m ≤52;②当m <0时,可得2m -1≤f (x )≤m 2-1,由-3≤f (x )≤4x )min ≥-3,x )max ≤4,-1≥-3,1≤4,,解得-1≤m <0.综上可得,m的取值范围是[-1,0),52.。
「正弦定理」用正弦定理解三角形常见的四个题型以及易错点分析.doc

「正弦定理」用正弦定理解三角形常见的四个题型以及易错点分析
【方法总结】利用正弦定理解决“已知三角形的任意两边与其中一边的对角求其他边与角”的问题时,可能出现一解、两解或无解的情况,应结合“三角形大边对大角”来判断解的情况,做到正确取舍.
【变式2】满足a=4,b=3和A=45°的△ABC的个数为( ).
A.0个B.1个
C.2个D.无数多个
题型三利用正弦定理判断三角形的形状
【方法总结】依据条件中的边角关系判断三角形的形状时,主要有以下两种途径:
(1)利用正弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;
(2)利用正弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形得出内角的关系,从而判断出三角形的形状,此时要注意应用A+B+C=π这个结论.在两种解法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.题型四利用正弦定理求最值或范围
【题后反思】在三角形中解决三角函数的取值范围或最
值问题的方法:
(1)利用正弦定理理清三角形中基本量间的关系或求出某些量.
(2)将要求最值或取值范围的量表示成某一变量的函数(三角函数),从而转化为函数的值域或最值的问题.【易错点分析】忽视等价转化而致误
当两个角的某三角函数值相等时,我们并不能肯定这两个角一定相等,一定要根据两个角的取值范围结合诱导公式写出所有的情况.
灵活运用诱导公式sin(2kπ+α)=sin α(k∈Z),sin(π-α)=sin α是解三角形的关键,当出现sin A=sin B时,一是易忽略A、B的范围;二是易忽略A+B=π时,sin A=sin B同样成立.。
(完整版)高三复习:解三角形-知识点、题型方法归纳,推荐文档

333绵阳市开元中学高 2014 级高三一轮复习③ tan (A + B )= - tan C ;④sinA + BC = cos , ⑤cosA +B = sinC 《解三角形》知识点、题型与方法归纳制卷:王小凤学生姓名:7.实际问题中的常用角 (1)仰角和俯角2 22 2 一、知识点归纳(★☆注重细节,熟记考点☆★)1. 正弦定理及其变形在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下文的叫俯角(如图①)asin A = b sin B = c sin C= 2R (R 为三角形外接圆半径) 变式:(1) a = 2R sin A , b = 2R sin B , c = 2R sin C (边化角公式)(2)sin A = a ,sin B =2Rb , sin C =c 2R 2R (角化边公式) (2) 方位角(3)a : b : c = sin A : sin B : sin C(4) a = sin A , a = sin A , b =sin B b sin B c sin C c sin C2. 正弦定理适用情况: (1) 已知两角及任一边;(2) 已知两边和一边的对角(需要判断三角形解的情况). 3. 余弦定理及其推论从指北方向顺时针转到目标方向线的水平角,如 B 点的方位角为 α(如图②)注:仰角、俯角、方位角的区别是:三者的参照不同。
仰角与俯角是相对于水平线而言的, 而方位角是相对于正北方向而言的。
(3) 方向角:相对于某一正方向的水平角(如图③)如: ①北偏东 即由指北方向顺时针旋转到达目标方向;a 2 =b 2 +c 2 - 2bc cos Acos A =b 2 +c 2 - a 22bc②“东北方向”表示北偏东(或东偏北) 45︒ .(4) 坡度:坡面与水平面所成的二面角的度数(如图④,角 θ 为坡角)b 2 = a 2 +c 2 - 2ac cos B c 2 = a 2 + b 2 - 2ab cos Ccos B =a 2 + c 2 -b 22ac a 2 + b 2 - c 2二、题型示例(★☆注重基础,熟记方法☆★)4. 余弦定理适用情况:cos C =2ab1.在V ABC 中,若∠A =60°,∠B =45°,BC =3 2,则 AC = ()(1)已知两边及夹角;(2)已知三边.注.解三角形或判定三角形形状时,可利用正余弦定理实现边角转化(这也是正余弦定理的作用),统一成边的形式或角的形式.5. 常用的三角形面积公式A.4B .2C .D . 2 2.在V ABC 中, a 2 = b 2 + c 2 + 3bc ,则∠A 等于()A .60°B .45°C .120°D .150°(1) S ∆ABC = 1 ⨯ 底⨯高;2 (2) 1 1 1 abcS = ab sin C = ac sin B = bc sin A = (R 为∆A 接BC 圆半径 )(两边夹一角);2 2 2 4R6. 三角形中常用结论(1) a + b > c , b + c > a , a + c > b (即两边之和大于第三边,两边之差小于第三边) (2) 在∆A ,BC 即大边A 对> 大B ⇔角,a >大b 角⇔对s 大in 边A >)sin B ( (3) 在∆ABC 中, A + B + C = ,所以①sin (A + B )= sin C ;② cos (A + B )= -cos C ;3. 设V ABC 的内角 A , B , C 所对的边分别为a , b , c , 若b cos C + c cos B = a sin A , 则V ABC 的形状为( )A. 锐角三角形B .直角三角形C .钝角三角形D .不确定4. 若△ABC 的三个内角满足sin A : sin B : sin C = 3 : 5 : 7 ,则△ABC ()3考点一:正弦定理、余弦定理的简单应用 考点二:利用正弦定理、余弦定理判断三角形的形状3 3 33 3 14 15 3 14 15考点四:利用正余弦定理求角2 考点三:利用正余弦定理求三角形的面积A. 一定是锐角三角形 B .一定是直角三角形 C .一定是钝角三角形D .可能是锐角三角形,也可能是钝角三角形∴∠ADB =180°-(45°+30°)=105°.DBAB在△DAB 中,由正弦定理,得sin ∠DAB =sin ∠ADB ,cos A bAB ·sin ∠DAB 5(3+\r(3))·sin 45°5. 在∆ABC 中,若cos B =a ,则△ABC 是()A. 等腰三角形 B .等边三角形C .直角三角形D .等腰三角形或直角三角形6. 在∆ABC 中, AB =, AC = 1 , ∠A = 30︒ ,则∆ABC 面积为() ∴DB =sin ∠ADB = sin 105°5(3+\r(3))·sin 45°=sin 45°cos 60°+cos 45°sin 60°=2=10 3(海里).又∠DBC =∠DBA +∠ABC =30°+(90°-60°)=60°,BC =20 3(海里), 在△DBC 中,由余弦定理,得 CD 2=BD 2+BC 2-2BD ·BC ·cos ∠DBCA.B.C.或 D .或 12424 2=300+1 200-2×10 3×20 3×2=900, 7. 已知∆ABC 的三边长a = 3, b = 5, c = 6 ,则∆ABC 的面积为() ∴CD =30(海里),A .B . 2C .D . 2 30∴需要的时间 t =30=1(小时).故救援船到达 D 点需要 1 小时.8. 在锐角中∆ABC ,角 A , B 所对的边长分别为a , b .若2a sin B = 3b ,则角等于 ()三、高考真题赏析A.B.C.D.1.(2016 年ft 东)在△ABC 中,角 A ,B ,C 的对边分别为 a ,b ,c ,已知tan A tan B126 4 3 2(tan A + tan B ) = + cos B .cos A9.在△ABC 中,若 a =18,b =24,A =45°,则此三角形有 ( )(Ⅰ)证明:a +b =2c ;(Ⅱ)求 cos C 的最小值.A .无解B .两解C .一解D .解的个数不确定1【解析】(Ⅰ)由2(tanA + tanB) = tanA tanB+ 得10. 在∆ABC ,内角 A , B , C 所对的边长分别为a , b , c . a sin B cos C + c sin B cos A = ∠B = ()b , 且a > b ,则2 2 ⨯ sinC =sinA cosB+ sinB cosA, A.B.C. 2D. 5cosAcosB cosAcosB cosAcosB 2sin C = sin B + sin C a + b = 2c633 6所以,由正弦定理,得.a 2 +b 2 -c 2 (a + b )2 - 2ab - c32c 3c 23 1(Ⅱ)由cos C == = - 1 ≥ - 1 = - 1 = .11. 如图:A ,B 是海面上位于东西方向相距5(3 + 3 )海里的两个观测点,现位于 A 点北偏东45︒ ,B 点2ab2ab2ab 2( a + b )2 2 2 2北偏西60︒ 的 D 点有一艘轮船发出求救信号,位于 B 点南偏西60︒ 且与 B 点相距20 船立即前往营救,其航行速度为每小时 30 海里,该救援船到达 D 点需要多长时间?解 由题意知 AB =5(3+ 3)海里,∠DBA =90°-60°=30°,∠DAB =90°-45°=45°,1海里的 C 点的救援所以cos C 的最小值为 .22.(2016 年四川)在△ABC 中,角 A ,B ,C 所对的边分别是 a ,b ,c ,且cos A + cos B = sin C. a b c3 3 5 3(\r(3)+1)3+1 考点五:正余弦定理实际应用问题(I)证明:sin A sin B sin C ;3 3 Ctan tan tan 5(II )若b 2 + c 2 - a 2 = 6bc ,求tan B .5∆ABC 中, D 是 BC 上的点, AD 平分∠BAC , ∆ABD 面积是∆ADC 面积的 2 倍.a =b =c (Ⅰ) 求sin ∠B ;(Ⅱ)若 AD = 1 , DC =2 ,求 BD 和 AC 的长.【解析】(I )证明:由正弦定理 sin A sin Bsin C 可知sin ∠C2cos A + cos B = sin C = 1原式可以化解为 sin A sin B sin C∵ A 和 B 为三角形s i 内n A 角sin , B ∴sin A sin B ≠ 0 则,两边同时乘以,可得sin B cos A + sin A cos B = sin A sin B 由和角公式可知, sin B cos A + sin A cos B = sin (A + B )= sin (- C )= sin C原式得证。
解三角形解答题易错点剖析

2
0
°+θ)⇒
2
1
3
2
2
c
o
s θ- s
i
nθ =
4
4
s
i
n
·
θ
3
1
2
t
a
n θ+ 3t
a
nθ-1
c
o
sθ- s
i
nθ ⇒2
2
2
=0⇒t
a
nθ=
- 3± 1
1
。
4
又θ 为锐角,
故t
a
nθ=
- 3+ 1
1
。
4
二、解三角形的最值问题易错点
例 3
已 知 锐 角 △ABC 的 内 角 A ,
B,
2
2
C 所对的边分别 为a,
1,
3,
2;
4,
2,
1,
创新定义的数列抽象 出 其 中 内 含 的 等 差 (比)
4,
3,
1;
3,
1,
2,
4;
3,
1,
4,
2;
3,
2,
1,
4;
3,
2,
4,
1;
共2
3;
4,
2,
3,
1;
4,
3,
1,
2;
4,
3,
2,
1,
4 个 数 列,
然后借助 数 列 的 性 质 或 基 本 量 运 算 求 解;将
数列,
培养同学们
运用数学 知 识 解 决 实 际 问 题 的 能 力,积 累 数
学活动经 验。 并 把 知 识 应 用 于 实 践,提 升 同
高考数学压轴专题(易错题)备战高考《三角函数与解三角形》图文解析

数学《三角函数与解三角形》知识点练习一、选择题1.已知函数f (x )=sin 2x +sin 2(x 3π+),则f (x )的最小值为( ) A .12B .14CD【答案】A 【解析】 【分析】先通过降幂公式和辅助角法将函数转化为()11cos 223f x x π⎛⎫=-+ ⎪⎝⎭,再求最值. 【详解】已知函数f (x )=sin 2x +sin 2(x 3π+), =21cos 21cos 2322x x π⎛⎫-+⎪-⎝⎭+,=1cos 2111cos 22223x x π⎛⎛⎫-=-+ ⎪ ⎝⎭⎝⎭, 因为[]cos 21,13x π⎛⎫+∈- ⎪⎝⎭, 所以f (x )的最小值为12. 故选:A 【点睛】本题主要考查倍角公式及两角和与差的三角函数的逆用,还考查了运算求解的能力,属于中档题.2.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若(a ﹣c cos B )sin A =c cos A sin B ,则△ABC 的形状一定是( ) A .钝角三角形 B .直角三角形C .等腰三角形D .锐角三角形【答案】C 【解析】 【分析】根据题意,由(cos )sin cos sin a c B A c A B -=变形可得sin sin a A c C =,进而由正弦定理可得22a c =,即a c =,即可得答案. 【详解】根据题意,在ABC ∆中,(cos )sin cos sin a c B A c A B -=,sin cos sin cos sin (cos sin cos sin )sin()sin a A c B A c A B c B A A B c A B c C =+=+=+=,即有sin sin a A c C =,又由正弦定理可得22a c =,即a c =. 故选:C . 【点睛】本题主要考查三角形的形状判断,考查正弦定理的应用,意在考查学生对这些知识点的理解掌握水平,属于基础题.3.函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象的交点横坐标的和为( ) A .53π B .2πC .76π D .π【答案】B 【解析】 【分析】根据两个函数相等,求出所有交点的横坐标,然后求和即可. 【详解】令sin cos2x x =,有2sin 12sin x x =-,所以sin 1x =-或1sin 2x =.又[],2x ππ∈-,所以2x π=-或32x π=或6x π=或56x π=,所以函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象交点的横坐标的和3522266s πππππ=-+++=,故选B. 【点睛】本题主要考查三角函数的图象及给值求角,侧重考查数学建模和数学运算的核心素养.4.若函数()sin 2f x x =向右平移6π个单位后,得到()y g x =,则关于()y g x =的说法正确的是( ) A .图象关于点,06π⎛⎫- ⎪⎝⎭中心对称 B .图象关于6x π=-轴对称C .在区间5,126ππ⎡⎤--⎢⎥⎣⎦单调递增 D .在5,1212ππ⎡⎤-⎢⎥⎣⎦单调递增 【答案】D 【解析】 【分析】利用左加右减的平移原则,求得()g x 的函数解析式,再根据选项,对函数性质进行逐一【详解】函数()sin 2f x x =向右平移6π个单位,得()sin 2()sin(2)63g x x x ππ=-=-. 由23x π-=k π,得26k x ππ=+()k ∈Z ,所以,06π⎛⎫- ⎪⎝⎭不是()g x 的对称中心,故A 错; 由23x π-=2k ππ+, 得212k x π5π=+()k ∈Z ,所以()g x 的图象不关于6x π=-轴对称,故B 错;由222232k x k πππππ-≤-≤+,得1212k x k π5ππ-≤≤π+()k ∈Z , 所以在区间5,126ππ⎡⎤--⎢⎥⎣⎦上()g x 不单调递增,在5,1212ππ⎡⎤-⎢⎥⎣⎦上单调递增, 故C 错,D 对; 故选:D . 【点睛】解答三角函数问题时一般需将解析式化简为sin()y A x B ωϕ=++或cos()y A x B ωϕ=++,从而可利用正(余)弦型周期计算公式2||T πω=周期,对正弦型函数,其函数图象的对称中心为,k B πϕω-⎛⎫⎪⎝⎭,且对称中心在函数图象上,而对称轴必经过图象的最高点或最低点,此时函数取得最大值或最小值.5.如图,边长为1正方形ABCD ,射线BP 从BA 出发,绕着点B 顺时针方向旋转至BC ,在旋转的过程中,记([0,])2ABP x x π∠=∈,BP 所经过的在正方形ABCD 内的区域(阴影部分)的面积为()y f x =,则函数()f x 的图像是( )A .B .C .D .【答案】D 【解析】 【分析】根据条件列()y f x =,再根据函数图象作判断. 【详解】 当0,4x π⎡⎤∈⎢⎥⎣⎦时,()112y f x tanx ==⨯⨯; 当,42x ππ⎛⎤∈⎥⎝⎦时,()11112y f x tanx ==-⨯⨯; 根据正切函数图象可知选D. 【点睛】本题考查函数解析式以及函数图象,考查基本分析识别能力,属基本题.6.函数sin 26y x π⎛⎫=+ ⎪⎝⎭的图象可由函数32cos 2y x x =-的图象( ) A .向右平移3π个单位,再将所得图象上所有点的纵坐标伸长到原来的2倍,横坐标不变得到 B .向右平移6π个单位,再将所得图象上所有点的纵坐标伸长到原来的2倍,横坐标不变得到 C .向左平移3π个单位,再将所得图象上所有点的纵坐标缩短到原来的12,横坐标不变得到 D .向左平移6π个单位,再将所得图象上所有点的纵坐标缩短到原来的12,横坐标不变得到 【答案】D 【解析】 【分析】合并3sin2cos2y x x =-得:2sin 26y x π⎛⎫=-⎪⎝⎭,利用平移、伸缩知识即可判断选项。
2020年高考理科数学 《解三角形》题型归纳与训练及答案解析

2020年高考理科数学 《解三角形》题型归纳与训练【题型归纳】题型一 正弦定理、余弦定理的直接应用例1ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知2sin()8sin2BA C +=. (1)求cos B(2)若6a c +=,ABC ∆面积为2,求b . 【答案】(1)15cos 17B =(2)2b =. 【解析】由题设及A B C π++=得2sin 8sin2BB =,故sin 4(1cos )B B =-. 上式两边平方,整理得217cos 32cos 150B B -+=, 解得cos 1B =(舍去),15cos 17B =.(2)由15cos 17B =得8sin 17B =,故14sin 217ABC S ac B ac ∆==. 又2ABC S ∆=,则172ac =. 由余弦定理及6a c +=得22222cos ()2(1cos )b a c ac B a c ac B =+-=+-+1715362(1)4217=-⨯⨯+=. 所以2b =.【易错点】二倍角公式的应用不熟练,正余弦定理不确定何时运用 【思维点拨】利用正弦定理列出等式直接求出例2 ABC △的内角,,A B C 的对边分别为,,a b c ,若2cos cos cos b B a C c A =+,则B = . 【答案】π3【解析】1π2sin cos sin cos sin cos sin()sin cos 23B B AC C A A C B B B =+=+=⇒=⇒=.【易错点】不会把边角互换,尤其三角恒等变化时,注意符号。
【思维点拨】边角互换时,一般遵循求角时,把边换成角;求边时,把角转换成边。
例3在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,若b =1,c =3,C =23π,则S △ABC =________.【答案】34【解析】因为c >b ,所以B <C ,所以由正弦定理得b sin B =c sin C ,即1sin B =3sin 2π3=2,即sin B =12,所以B=π6,所以A =π-π6-2π3=π6.所以S △ABC =12bc sin A =12×3×12=34. 【易错点】大边对大角,应注意角的取值范围【思维点拨】求面积选取公式时注意,一般选取已知角的公式,然后再求取边长。
收集2解三角形重难点,易错点突破(含答案解析)

专题1-2 解三角形重难点、易错点突破(建议用时:60分钟)三角形定“形”记根据边角关系判断三角形的形状是一类热点问题.解答此类问题,一般需先运用正弦、余弦定理转化已知的边角关系,再进一步判断三角形的形状,这种转化一般有两个通道,即化角为边或化边为角.下面例析这两个通道的应用.1.通过角之间的关系定“形”例1 在△ABC 中,已知2sin A cos B =sin C ,那么△ABC 一定是( ) A .直角三角形 B .等腰三角形 C .等腰直角三角形 D .正三角形2.通过边之间的关系定“形”例2 在△ABC 中,若sin A +sin C sin B =b +ca ,则△ABC 是( )A .锐角三角形B .直角三角形C .等腰三角形D .等腰三角形或直角三角形细说三角形中解的个数解三角形时,处理“已知两边及其一边的对角,求第三边和其他两角”问题需判断解的个数,这是一个比较棘手的问题.下面对这一问题进行深入探讨. 1.出现问题的根源我们作图来直观地观察一下.不妨设已知△ABC 的两边a ,b 和角A ,作图步骤如下:①先做出已知角A ,把未知边c 画为水平的,角A 的另一条边为已知边b ;②以边b 的不是A 点的另外一个端点为圆心,边a 为半径作圆C ;③观察圆C 与边c 交点的个数,便可得此三角形解的个数. 显然,当A 为锐角时,有如图所示的四种情况:当A 为钝角或直角时,有如图所示的两种情况:根据上面的分析可知,由于a ,b 长度关系的不同,导致了问题有不同个数的解.若A 为锐角,只有当a 不小于b sin A 时才有解,随着a 的增大得到的解的个数也是不相同的.当A 为钝角时,只有当a 大于b 时才有解. 2.解决问题的策略 (1)正弦定理法已知△ABC 的两边a ,b 和角A ,求B . 根据正弦定理a sin A =b sin B,可得sin B =b sin A a.若sin B>1,三角形无解;若sin B=1,三角形有且只有一解;若0<sin B<1,B有两解,再根据a,b的大小关系确定A,B的大小关系(利用大边对大角),从而确定B的两个解的取舍.(2)余弦定理法已知△ABC的两边a,b和角A,求c.利用余弦定理可得a2=b2+c2-2bc cos A,整理得c2-2bc cos A-a2+b2=0.适合问题的上述一元二次方程的解c便为此三角形的解.(3)公式法当已知△ABC的两边a,b和角A时,通过前面的分析可总结三角形解的个数的判断公式如下表:A<90°A≥90°a≥ba<ba>b a≤b a>b sin A a=b sin A a<b sin A一解二解一解无解一解无解3.实例分析例在△ABC中,已知A=45°,a=2,b=2(其中角A,B,C的对边分别为a,b,c),试判断符合上述条件的△ABC有多少个?挖掘三角形中的隐含条件解三角形是高中数学的重要内容,也是高考的一个热点.由于我们对三角公式比较熟悉,做题时比较容易入手.但是公式较多且性质灵活,解题时稍有不慎,常会出现增解、错解现象,其根本原因是对题设中的隐含条件挖掘不够.下面结合例子谈谈解三角形时,题目中隐含条件的挖掘. 隐含条件1.两边之和大于第三边例1 已知钝角三角形的三边a =k ,b =k +2,c =k +4,求k 的取值范围.隐含条件2.三角形的内角范围 例2 已知△ABC 中,B =30°,AB =23,AC =2,则△ABC 的面积是________.例3 在△ABC 中,tan A tan B =a 2b 2,试判断三角形的形状.例4 在△ABC 中,B =3A ,求b a的取值范围.正弦、余弦定理三应用有些题目,表面上看不能利用正弦、余弦定理解决,但若能构造适当的三角形,就能利用两定理,题目显得非常容易,本文剖析几例. 1.平面几何中的长度问题例1 如图,在梯形ABCD 中,CD =2,AC =19,∠BAD =60°,求梯形的高.2.求范围例2 如图,等腰△ABC 中,底边BC =1,∠ABC 的平分线BD 交AC 于点D ,求BD 的取值范围(注:0<x <1时,f (x )=x -1x为增函数).3.判断三角形的形状例3 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若AB →·AC →=BA →·BC →=k ,(k ∈R ). (1)判断△ABC 的形状; (2)若c =2,求k 的值.专题1-2 解三角形重难点、易错点突破参考答案三角形定“形”记例1 分析 通过三角形恒等变换和正弦、余弦定理,把条件式转化,直至能确定两角(边)的关系为止,即可判断三角形的形状.解析 方法一 利用正弦定理和余弦定理 2sin A cos B =sin C 可化为2a ·a 2+c 2-b 22ac=c ,即a 2+c 2-b 2=c 2,即a 2-b 2=0,即a 2=b 2,故a =b . 所以△ABC 是等腰三角形.故选B. 方法二 因为在△ABC 中,A +B +C =π, 即C =π-(A +B ),所以sin C =sin(A +B ). 由2sin A cos B =sin C ,得2sin A cos B =sin A cos B +cos A sin B , 即sin A cos B -cos A sin B =0,即sin(A -B )=0. 又因为-π<A -B <π, 所以A -B =0,即A =B . 所以△ABC 是等腰三角形,故选B. 答案 B点评 根据角的三角函数之间的关系判断三角形的形状,一般需通过三角恒等变换,求出角(边)之间的关系. 例2分析 先运用正弦定理化角为边,根据边之间的关系即可判断三角形的形状. 解析 在△ABC 中,由正弦定理,可得sin A +sin C sin B =a +c b =b +ca ,整理得a (a +c )=b (b +c ),即a 2-b 2+ac -bc =0,(a -b )(a +b +c )=0. 因为a +b +c ≠0,所以a -b =0,即a =b ,所以△ABC 是等腰三角形.故选C. 答案 C点评 本题也可化边为角,但书写复杂,式子之间的关系也不易发现.细说三角形中解的个数例 分析 此题为“已知两边和其中一边的对角”解三角形的问题,可以利用上述办法来判断△ABC 解的情况.解 方法一 由正弦定理a sin A =bsin B ,可得sin B =22sin 45°=12<1. 又因为a >b ,所以A >B ,故B =30°, 符合条件的△ABC 只有一个. 方法二 由余弦定理得 22=c 2+(2)2-2×2×c cos 45°,即c 2-2c -2=0,解得c =1±3.而1-3<0,故仅有一解,符合条件的△ABC 只有一个.方法三 A 为锐角,a >b ,故符合条件的△ABC 只有一个.挖掘三角形中的隐含条件例1 [错解] ∵c >b >a 且△ABC 为钝角三角形, ∴C 为钝角. 由余弦定理得cos C =a 2+b 2-c 22ab=k 2+(k +2)2-(k +4)22k (k +2)=k 2-4k -122k (k +2)<0.∴k 2-4k -12<0,解得-2<k <6. 又∵k 为三角形的边长, ∴k >0.综上所述,0<k <6.[点拨] 忽略了隐含条件:k ,k +2,k +4构成一个三角形,需满足k +(k +2)>k +4.即k >2而不是k >0. [正解] ∵c >b >a ,且△ABC 为钝角三角形, ∴C 为钝角. 由余弦定理得cos C =a 2+b 2-c 22ab=k 2-4k -122k (k +2)<0.∴k 2-4k -12<0,解得-2<k <6.由两边之和大于第三边得k +(k +2)>k +4,∴k >2, 综上所述,k 的取值范围为2<k <6.温馨点评 虽然是任意两边之和大于第三边,但实际应用时通常不用都写上,只需最小两边之和大于最大边就行了.例2 [错解] 由正弦定理,得sin C =AB sin B AC =32. ∴C =60°,∴A =90°.则S △ABC =12AB ·AC ·sin A =12×23×2×1=23.[点拨] 上述解法中在用正弦定理求C 时丢了一解.实际上由sin C =32可得C =60°或C =120°,它们都满足条件.[正解] 由正弦定理,得sin C =AB sin B AC=32.∴C =60°或C =120°. 当C =60°时,A =90°,∴S △ABC =12AB ·AC ·sin A =23.当C =120°时,A =30°, ∴S △ABC =12AB ·AC ·sin A =3. 故△ABC 的面积是23或3.温馨点评 利用正弦定理理解“已知两边及其中一边对角,求另一角”问题时,由于三角形内角的正弦值都为正的,而这个内角可能为锐角,也可能为钝角,容易把握不准确出错.例3 [错解] tan A tan B =a 2b 2⇔sin A cos B cos A sin B =sin 2A sin 2B ⇔cos B cos A =sin Asin B ⇔sin A cos A =sin B cos B ⇔sin 2A =sin2B , ∴A =B .∴△ABC 是等腰三角形.[点拨] 上述错解忽视了满足sin 2A =sin 2B 的另一个角之间的关系:2A +2B =180°. [正解] tan A tan B =a 2b 2⇔sin A cos B cos A sin B =sin 2A sin 2B ⇔cos B cos A =sin Asin B ⇔sin A cos A =sin B cos B⇔sin 2A =sin 2B ⇔2A =2B 或2A +2B =180°. ∴A =B 或A +B =90°.∴△ABC 是等腰三角形或直角三角形.温馨点评 在△ABC 中,sin A =sin B ⇔A =B 是成立的,但sin 2A =sin 2B ⇔2A =2B 或2A +2B =180°. 例4 [错解] 由正弦定理得b a =sin B sin A =sin 3A sin A =sin (A +2A )sin A=sin A cos 2A +cos A sin 2Asin A=cos 2A +2cos 2A =4cos 2A -1. ∵0≤cos 2A ≤1, ∴-1≤4cos 2A -1≤3, ∵b a>0,∴0<b a≤3.[点拨] 忽略了三角形内角和为180°,及角A 、B 的取值范围,从而导致b a 取值范围求错. [正解] 由正弦定理得b a =sin B sin A =sin 3A sin A=sin (A +2A )sin A =sin A cos 2A +cos A sin 2A sin A=cos 2A +2cos 2A =4cos 2A -1. ∵A +B +C =180°,B =3A .∴A +B =4A <180°,∴0°<A <45°.∴22<cos A <1, ∴1<4cos 2 A -1<3,∴1<ba <3.温馨点评 解三角形问题,角的取值范围至关重要.一些问题,角的取值范围隐含在题目的条件中,若不仔细审题,深入挖掘,往往疏漏而导致解题失败.正弦、余弦定理三应用例1 分析 如图,过点D 作DE ⊥AB 于点E ,则DE 为所求的高.由∠BAD =60°,知∠ADC =120°,又边CD 与AC 的长已知,故△ACD 为已知两边和其中一边的对角,可解三角形.解Rt △ADE ,需先求AD 的长,这只需在△ACD 中应用余弦定理.解 由∠BAD =60°,得∠ADC =120°,在△ACD 中,由余弦定理得AC 2=AD 2+CD 2-2AD ·CD ·cos ∠ADC ,即19=AD 2+4-2AD ×2×⎝ ⎛⎭⎪⎫-12, 解得AD =3或AD =-5(舍去).在△ADE 中,DE =AD ·sin 60°=332.点评 依据余弦定理建立方程是余弦定理的一个妙用,也是函数与方程思想在解三角形中的体现.2.求范围例2 分析 把BD 的长表示为∠ABC 的函数,转化为求函数的值域.解 设∠ABC =α.因为∠ABC =∠C ,所以∠A =180°-2α,∠BDC =∠A +∠ABD =180°-2α+α2=180°-3α2, 因为BC =1,在△BCD 中,由正弦定理得BD =sin αsin 3α2=2sin α2cos α2sin αcos α2+cos αsin α2=2cos α24cos 2α2-1=24cos α2-1cos α2, 因为0°<α2<45°,所以22<cos α2<1, 而当cos α2增大时,BD 减小,且当cos α2=22时, BD =2;当cos α2=1时,BD =23, 故BD 的取值范围是⎝ ⎛⎭⎪⎫23,2. 点评 本题考查:(1)三角知识、正弦定理以及利用函数的单调性求值域的方法;(2)数形结合、等价转化等思想.例3 解 (1)∵AB →·AC →=cb cos A ,BA →·BC →=ca cos B .又AB →·AC →=BA →·BC →,∴bc cos A =ac cos B ,∴b cos A =a cos B .方法一 ∴sin B cos A =sin A cos B ,即sin A cos B -cos A sin B =0,∴sin(A -B )=0,∵-π<A -B <π,∴A =B .∴△ABC 为等腰三角形.方法二 利用余弦定理将角化为边, ∵b cos A =a cos B ,∴b ·b 2+c 2-a 22bc =a ·a 2+c 2-b 22ac ,∴b 2+c 2-a 2=a 2+c 2-b 2,∴a 2=b 2,∴a =b .∴△ABC 为等腰三角形.(2)由(1)知:a =b .∴AB →·AC →=bc cos A =bc ·b 2+c 2-a 22bc =c 22=k , ∵c =2,∴k =1.。
【二轮复习材料】解三角形中常见错误错因之浅析

解三角形中常见易错点分析先研究下面的问题.已知:在ABC ∆中,,150,8,4===A b a 解ABC ∆. 根据正弦定理,14150sin 8sin sin ===a Ab B , 因为 1800<<B ,所以 90=B ,于是60)(180-=+-=B A C ,解到这里,让我们惊讶的是所计算出来的角C 竟然是负角.问题出在何处呢?是我们利用正弦定理出现错误?分析已知条件,我们注意到8,4==b a ,这里150,=<A b a ,由三角形的性质,应该有,B A <因而B 也应该是一个钝角,而在一个三角形中是不可能有两个钝角的.这说明满足已知条件的三角形是不存在的.从上面的分析我们发现,在利用正弦定理和余弦定理解三角形时,要正确理解题设条件,不能简单的套用公式,否则解题时将出现严重失误.下面就解三角形时,容易出现的错误做一归纳,并就错因做一分析,以引起同学们关注.易错点1:不能挖掘隐含条件,进一步缩小角的范围例1 在ABC ∆中,已知53sin ,135cos ==B A ,求C cos 的值. 【错解】因为1312A sin ,135cos ==所以A .又54cos 53sin ±==B B ,所以 ①当.6516)sin sin cos (cos )A cos(cos ,54cos =--=+-==B A B A B C B 时 ②当.6556)sin sin cos (cos )A cos(cos ,54cos =--=+-=-=B A B A B C B 时 【分析1】在ABC ∆中,因为1312A sin A ,0135cos =>=为锐角,所以则A .又,53sin =B 所以B A sin sin >,由正弦定理知b a >,由三角形的性质有B A >,所以B 角不可能为钝角,因此54cos -≠B . 【分析2】忽略对题中隐含条件的挖掘,事实上当时54cos -=B ,22135cos ,2254cos -=︒-<-=B 所以︒<<︒180135B又2160cos ,21135cos ,135cos =︒<==A A ,所以,180B A ,9060︒>+︒<<︒即A 矛盾,应舍去. 【正解】由错解和分析知:6516cos =C . 例2 已知角A,B,C 为ABC ∆的三个内角,其对应边分别为c b a ,,.若m =)2sin ,2cos(A A -,n =)2sin ,2(cos A A ,32=a ,m ·n 21= ,求b+c 的取值范围. 【错解】由正弦定理得432sin 32sin sin sin ====πA a C cB b 又3ππ=-=+A C B ,所以4)3sin(4)3sin(4sin 4sin 4sin 4≤+=-+=+=+ππB B BC B c b【分析】在求c b +的范围时,没有注意到角B 的范围.【正解】接上最后一步。
查补易混易错点02 三角函数与解三角形(解析版)

查补易混易错点02 三角函数、平面向量与解三角形 1.三角函数(1)角与弧度:了解任意角的概念和弧度制,能进行弧度与角度的互化,体会引入弧度制的必要性。
(2)三角函数概念和性质①借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义,能画出这些三角函数的图象,了解三角函数的周期性、奇偶性、最大(小)值。
借助单位圆的对称性,利用定义推导出诱导公式(α ±2π,α ±π的正弦、余弦、正切)。
②借助图象理解正弦函数在、余弦函数[0,2]π上、正切函数在(,)22ππ-上的性质。
③结合具体实例,了解sin()y A x ωϕ=+的实际意义;能借助图象理解参数ω,φ,A 的意义,了解参数的变化对函数图象的影响。
(3)同角三角函数的基本关系式:理解同角三角函数的基本关系式22sin sin cos 1,tan cos xx x x x+==。
(4)三角恒等变换①经历推导两角差余弦公式的过程,知道两角差余弦公式的意义。
②能从两角差的余弦公式推导出两角和与差的正弦、余弦、正切公式,二倍角的正弦、余弦、正切公式,了解它们的内在联系。
③能运用上述公式进行简单的恒等变换(包括推导出积化和差、和差化积、半角公式,这三组公式不要求记忆)。
2.平面向量及应用 (1)向量概念①通过对力、速度、位移等的分析,了解平面向量的实际背景,理解平面向量的意义和两个向量相等的含义。
②理解平面向量的几何表示和基本要素。
(2)向量运算①借助实例和平面向量的几何表示,掌握平面向量加、减运算及运算规则,理解其几何意义。
②通过实例分析,掌握平面向量数乘运算及运算规则,理解其几何意义。
理解两个平面向量共线的含义。
③了解平面向量的线性运算性质及其几何意义。
④通过物理中功等实例,理解平面向量数量积的概念及其物理意义,会计算平面向量的数量积。
STEP01 课标解读⑤通过几何直观,了解平面向量投影的概念以及投影向量的意义(参见案例9)。
高考数学压轴专题(易错题)备战高考《三角函数与解三角形》难题汇编附答案解析
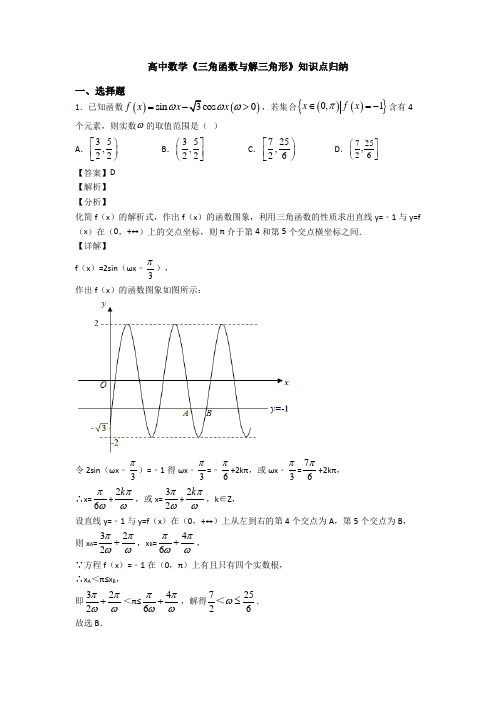
高中数学《三角函数与解三角形》知识点归纳一、选择题1.已知函数()()sin 3cos 0x f x x ωωω=->,若集合()(){}0,1x f x π∈=-含有4个元素,则实数ω的取值范围是( ) A .35,22⎡⎫⎪⎢⎣⎭B .35,22⎛⎤⎥⎝⎦C .725,26⎡⎫⎪⎢⎣⎭D .725,26⎛⎤⎥⎝⎦【答案】D 【解析】 【分析】化简f (x )的解析式,作出f (x )的函数图象,利用三角函数的性质求出直线y=﹣1与y=f (x )在(0,+∞)上的交点坐标,则π介于第4和第5个交点横坐标之间. 【详解】 f (x )=2sin (ωx ﹣3π), 作出f (x )的函数图象如图所示:令2sin (ωx ﹣3π)=﹣1得ωx ﹣3π=﹣6π+2kπ,或ωx ﹣3π=76π+2kπ, ∴x=6πω+2k πω,或x=32πω+2k πω,k ∈Z , 设直线y=﹣1与y=f (x )在(0,+∞)上从左到右的第4个交点为A ,第5个交点为B , 则x A =322ππωω+,x B =46ππωω+, ∵方程f (x )=﹣1在(0,π)上有且只有四个实数根, ∴x A <π≤x B ,即322ππωω+<π≤46ππωω+,解得72526ω≤<. 故选B .【点睛】本题考查了三角函数的恒等变换,三角函数的图象与性质,属于中档题.2.要得到函数y =sin (2x +9π)的图象,只需将函数y =cos (2x ﹣9π)的图象上所有点( ) A .向左平移518π个单位长度 B .向右平移518π个单位长度 C .向左平移536π个单位长度 D .向右平移536π个单位长度 【答案】D 【解析】 【分析】先将函数cos 29y x π⎛⎫=- ⎪⎝⎭转化为7sin 218y x π⎛⎫=+⎪⎝⎭,再结合两函数解析式进行对比,得出结论. 【详解】 函数75cos 2sin 2sin 2sin 299218369y x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=-+=+=++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ∴要得到函数sin 29y x π⎛⎫=+ ⎪⎝⎭的图象,只需将函数cos 29y x π⎛⎫=- ⎪⎝⎭的图象上所有点向右平移536π个单位长度,故选D . 【点睛】本题考查函数()sin y A x b ωϕ=++的图象变化规律,关键在于能利用诱导公式将异名函数化为同名函数,再根据左右平移规律得出结论.3.已知ABC V 的三条边的边长分别为2米、3米、4米,将三边都增加x 米后,仍组成一个钝角三角形,则x 的取值范围是( ) A .102x << B .112x << C .12x << D .01x <<【答案】D 【解析】 【分析】根据余弦定理和三角形三边关系可求得x 的取值范围. 【详解】将ABC V 的三条边的边长均增加x 米形成A B C '''V ,设A B C '''V 的最大角为A '∠,则A '∠所对的边的长为()4x +米,且A '∠为钝角,则cos 0A '∠<,所以()()()()()2222342340x x x x x x x ⎧+++<+⎪+++>+⎨⎪>⎩,解得01x <<.故选:D. 【点睛】本题考查利用余弦定理和三角形三边关系求参数的取值范围,灵活利用余弦定理是解本题的关键,考查计算能力,属于中等题.4.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若(a ﹣c cos B )sin A =c cos A sin B ,则△ABC 的形状一定是( ) A .钝角三角形 B .直角三角形 C .等腰三角形 D .锐角三角形【答案】C 【解析】 【分析】根据题意,由(cos )sin cos sin a c B A c A B -=变形可得sin sin a A c C =,进而由正弦定理可得22a c =,即a c =,即可得答案. 【详解】根据题意,在ABC ∆中,(cos )sin cos sin a c B A c A B -=, 变形可得:sin cos sin cos sin (cos sin cos sin )sin()sin a A c B A c A B c B A A B c A B c C =+=+=+=,即有sin sin a A c C =,又由正弦定理可得22a c =,即a c =. 故选:C . 【点睛】本题主要考查三角形的形状判断,考查正弦定理的应用,意在考查学生对这些知识点的理解掌握水平,属于基础题.5.已知在锐角ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,若2cos cos b C c B =,则111tan tan tan A B C++的最小值为( ) ABCD.【答案】A 【解析】 【分析】先根据已知条件,把边化成角得到B,C 关系式,结合均值定理可求. 【详解】∵2cos cos b C c B =,∴2sin cos sinCcos B C B =, ∴tan 2tan C B =.又A B C π++=, ∴()()tan tan tan A B C B C π=-+=-+⎡⎤⎣⎦22tan tan 3tan 3tan 1tan tan 12tan 2tan 1B C B BB C B B +=-=-=---, ∴21112tan 111tan tan tan 3tan tan 2tan B A B C B B B -++=++27tan 36tan B B =+. 又∵在锐角ABC ∆中, tan 0B >,∴27tan 36tan B B +≥=,当且仅当tan 2B =时取等号,∴min111tan tan tan 3A B C ⎛⎫++=⎪⎝⎭,故选A. 【点睛】本题主要考查正弦定理和均值定理,解三角形时边角互化是求解的主要策略,侧重考查数学运算的核心素养.6.已知函数sin(),0()cos(),0x a x f x x b x +≤⎧=⎨+>⎩的图像关于y 轴对称,则sin y x =的图像向左平移( )个单位,可以得到cos()y x a b =++的图像( ). A .4π B .3π C .2π D .π【答案】D 【解析】 【分析】根据条件确定,a b 关系,再化简()cos y x a b =++,最后根据诱导公式确定选项. 【详解】 因为函数()()(),0,0sin x a x f x cos x b x ⎧+≤⎪=⎨+>⎪⎩的图像关于y 轴对称,所以sin cos 22a b ππ⎛⎫⎛⎫-+=+ ⎪ ⎪⎝⎭⎝⎭,()()sin cos a b ππ-+=+,即sin cos sin cos b a a b ,==,因此π2π()2a b k k Z +=+∈, 从而()()cos sin y x a b sinx x π=++=-=+,选D. 【点睛】本题考查偶函数性质、诱导公式、三角函数图象变换,考查基本分析识别能力,属中档题.7.已知函数()sin()R,0,0,||2f x A x x A πωϕωϕ⎛⎫=+∈>>< ⎪⎝⎭的图象(部分)如图所示,则ω,ϕ分别为( )A .,3πωπϕ==B .2,3πωπϕ==C .,6πωπϕ==D .2,6πωπϕ==【答案】C 【解析】 【分析】由最大值可确定振幅A ,由周期确定ω,由1()23f =确定ϕ. 【详解】 由图可得,2A =,5114632T =-=,所以22T πω==,ωπ=,又1()23f =,所以12sin()23πϕ⨯+=,2,32k k Z ππϕπ+=+∈,即2,6k k Z πϕπ=+∈, 又2πϕ<,故6π=ϕ. 故选:C 【点睛】本题考查由图象确定正弦型函数解析式中的参数问题,考查学生逻辑推理能力,是一道中档题.8.锐角ABC ∆中,角A 、B 、C 所对的边分别为,,a b c ,若()sin 303A B C π⎛⎫+++= ⎪⎝⎭,2b =26c +=,则角B =( )A .6π B .4π C .3π D .512π 【答案】B 【解析】 【分析】先由()sin 03A B C π⎛⎫+++= ⎪⎝⎭求出3A π=,然后用余弦定理算出a =再用余弦定理算出cos B 即可. 【详解】因为()sin 03A B C π⎛⎫+++= ⎪⎝⎭所以11sin sin 022A A A A A +==所以tan A =0,2A π⎛⎫∈ ⎪⎝⎭,所以3A π=所以由余弦定理得:22222co 12322s a b c bc A -=+-=+=⎝⎭所以a =所以222232cos 22a c b B ac +-+-===因为0,2B π⎛⎫∈ ⎪⎝⎭,所以4B π=故选:B 【点睛】本题考查的是利用余弦定理解三角形,数据不特殊,计算能力是解题的关键.9.将函数()()sin 0,π2f x x ϕωϕω⎛⎫=+>< ⎪⎝⎭的图象向右平移6π个单位长度后,所得图象关于y 轴对称,且1π2f ω⎛⎫=- ⎪⎝⎭,则当ω取最小值时,函数()f x 的解析式为( )A .()sin 26f x x π⎛⎫=+⎪⎝⎭B .()sin 2π6f x x ⎛⎫=- ⎪⎝⎭C .()sin 4π6f x x ⎛⎫=+ ⎪⎝⎭D .()sin 4π6f x x ⎛⎫=- ⎪⎝⎭【答案】C 【解析】 【分析】由题意利用函数()sin y A x ωφ=+的图象变换规律,可得所得函数的解析式,由12f πω⎛⎫=- ⎪⎝⎭,求出φ,再根据所得图象关于y 轴对称求出ω,可得()f x 的解析式.【详解】解:将函数()()sin (0,)2f x x πωφωφ=+><的图象向右平移6π个单位长度后,可得sin 6y x ωπωφ⎛⎫=-+ ⎪⎝⎭的图象;∵所得图象关于y 轴对称,∴62k ωππφπ-+=+,k Z ∈.∵()1sin sin 2f ππφφω⎛⎫=-=+=- ⎪⎝⎭,即1sin 2φ=,26ππφφ<=,. ∴63k ωπππ-=+,620k ω=-->,则当ω取最小值时,取1k =-,可得4ω=, ∴函数()f x 的解析式为()sin 46f x x π⎛⎫=+ ⎪⎝⎭. 故选C . 【点睛】本题主要考查函数()sin y A x ωφ=+的图象变换规律,正弦函数的性质,属于中档题.10.在三角形ABC 中,给出命题:p “2ab c >”,命题:q “3C π<”,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A 【解析】 【分析】由余弦定理将2c 化为222cos a b ab C +-,整理后利用基本不等式求得12cos 2C +>,求出C 范围,即可判断充分性,取4a =,7b =,6c =,则可判断必要性不成立,两者结合可得正确的选项. 【详解】充分性:由余弦定理,2222cos c a b ab C =+-, 所以2ab c >,即222cos ab a b ab C >+-,整理得,2212cos a b C ab++>,由基本不等式,222a b ab ab+≥=,当且仅当a b =时等号成立, 此时,12cos 2C +>,即1cos 2C >,解得3C π<, 充分性得证;必要性:取4a =,7b =,6c =,则164936291cos 247562C +-==>⨯⨯,故3C π<,但228ab c =<,故3C π<推不出2ab c >.故必要性不成立; 故p 是q 的充分不必要条件. 故选:A 【点睛】本题主要考查充分必要条件的判断、余弦定理的应用和基本不等式的应用,考查学生分析转化能力,属于中档题.11.在ABC ∆中,060,A BC D ∠==是边AB 上的一点,CD CBD =∆的面积为1,则BD 的长为( ) A .32B .4C .2D .1【答案】C 【解析】1sin 1sin2BCD BCD ∠=∴∠=2242BD BD ∴=-=∴=,选C12.若函数()sin()f x A x ωϕ=+(其中0A >,||)2πϕ<图象的一个对称中心为(3π,0),其相邻一条对称轴方程为712x π=,该对称轴处所对应的函数值为1-,为了得到()cos2g x x =的图象,则只要将()f x 的图象( )A .向右平移6π个单位长度 B .向左平移12π个单位长度C .向左平移6π个单位长度 D .向右平移12π个单位长度【答案】B 【解析】 【分析】由函数的图象的顶点坐标求出A ,由周期求出ω,由五点法作图求出ϕ的值,可得()f x 的解析式,再根据函数()sin y A x ωϕ=+的图象变换规律,诱导公式,得出结论. 【详解】根据已知函数()()sin f x A x ωϕ=+(其中0A >,)2πϕ<的图象过点,03π⎛⎫ ⎪⎝⎭,7,112π⎛⎫-⎪⎝⎭, 可得1A =,1274123πππω⋅=-, 解得:2ω=. 再根据五点法作图可得23πϕπ⋅+=,可得:3πϕ=,可得函数解析式为:()sin 2.3f x x π⎛⎫=+⎪⎝⎭故把()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移12π个单位长度, 可得sin 2cos236y x x ππ⎛⎫=++= ⎪⎝⎭的图象, 故选B . 【点睛】本题主要考查由函数()sin y A x ωϕ=+的部分图象求解析式,由函数的图象的顶点坐标求出A ,由周期求出ω,由五点法作图求出ϕ的值,函数()sin y A x ωϕ=+的图象变换规律,诱导公式的应用,属于中档题.13.若,2παπ⎛⎫∈ ⎪⎝⎭,2cos2sin 4παα⎛⎫=- ⎪⎝⎭,则sin 2α的值为( )A .78-B .78C .18-D .18【答案】A 【解析】 【分析】利用二倍角公式及两角差的正弦公式化简得到cos sin 4αα+=,再将两边平方利用二倍角正弦公式计算可得; 【详解】解:因为2cos2sin 4παα⎛⎫=-⎪⎝⎭所以()222cos sin sincos cossin 44ππαααα-=-所以()())2cos sin cos sin cos sin αααααα-+=- ,cos sin 02παπαα⎛⎫∈-≠ ⎪⎝⎭Q ,所以cos sin 4αα+=所以()21cos sin 8αα+=,即221cos 2cos sin sin 8αααα++=,11sin 28α+= 所以7sin 28α=- 故选:A 【点睛】本题考查两角和差的正弦公式、二倍角公式的应用,属于中档题;14.已知sin α,sin()10αβ-=-,,αβ均为锐角,则β=( ) A .512πB .3π C .4π D .6π 【答案】C 【解析】 【分析】 由题意,可得22ππαβ-<-<,利用三角函数的基本关系式,分别求得cos ,cos()ααβ-的值,利用sin[(]sin )ααββ=--,化简运算,即可求解.【详解】由题意,可得α,β均为锐角,∴-2π <α-β<2π.又sin(α-β),∴cos(α-β).又sin α=5,∴cos α=5, ∴sin β=sin[α-(α-β)]=sin αcos(α-β)-cos αsin(α-β)=-×10⎛⎫- ⎪ ⎪⎝⎭.∴β=4π. 【点睛】本题主要考查了三角函数的化简、求值问题,其中熟记三角函数的基本关系式和三角恒等变换的公式,合理构造sin[(]sin )ααββ=--,及化简与运算是解答的关键,着重考查了推理与运算能力,属于基础题.15.在OAB ∆中,已知OB =u u u v 1AB u u u v=,45AOB ∠=︒,点P 满足(),OP OA OB λμλμ=+∈R u u u v u u u v u u u v ,其中λ,μ满足23λμ+=,则OP u u u v的最小值为( )ABCD【答案】A 【解析】 【分析】根据OB =u u u r,1AB =uu u r ,45AOB ∠=︒,由正弦定理可得OAB ∆为等腰直角三角形,进而求得点A 坐标.结合平面向量的数乘运算与坐标加法运算,用λ,μ表示出OP u u u r.再由23λμ+=,将OP u u u r 化为关于λ的二次表达式,由二次函数性质即可求得OP u u u r的最小值.【详解】在OAB ∆中,已知OB =u u u r,1AB =uu u r ,45AOB ∠=︒由正弦定理可得sin sin AB OBAOB OAB=∠∠u u u r u u u rsin OAB =∠,解得sin 1OAB ∠=即2OAB π∠=所以OAB ∆为等腰直角三角形以O 为原点,OB 所在直线为x 轴,以OB 的垂线为y 轴建立平面直角坐标系如下图所示:则点A 坐标为22,22⎛ ⎝⎭所以2222OA ⎛= ⎝⎭u u u r ,)2,0OB =u u ur因为(),OP OA OB λμλμ=+∈R u u u r u u u r u u u r则)222,022OP λμ⎛ =+ ⎝⎭u u u r 222,22λμλ⎛⎫⎪ ⎪⎝⎭= 则2222222OP λμλ⎛⎫=++⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭u u u r 2222λλμμ=++因为23λμ+=,则32μλ=- 代入上式可得()()22322232λλλλ+-+-218518λλ-=+299555λ⎛⎫=-+ ⎪⎝⎭所以当95λ=时, min 9355OP ==u u u r 故选:A 【点睛】本题考查了平面向量基本定理的应用,正弦定理判断三角形形状,平面向量的坐标运算,属于中档题.16.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,用现代式子表示即为:在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,则ABC ∆的面积S =根据此公式,若()cos 3cos 0a B b c A ++=,且2222a b c --=,则ABC ∆的面积为( )AB.CD.【答案】A 【解析】 【分析】根据()cos 3cos 0a B b c A ++=,利用正弦定理边化为角得sin cos cos sin 3sin cos 0A B A B C A ++=,整理为()sin 13cos 0C A +=,根据sin 0C ≠,得1cos 3A =-,再由余弦定理得3bc =,又2222a b c --=,代入公式=S . 【详解】由()cos 3cos 0a B b c A ++=得sin cos cos sin 3sin cos 0A B A B C A ++=, 即()sin 3sin cos 0A B C A ++=,即()sin 13cos 0C A +=, 因为sin 0C ≠,所以1cos 3A =-, 由余弦定理22222cos 23a b c bc A bc --=-==,所以3bc =, 由ABC ∆的面积公式得S ===故选:A 【点睛】本题主要考查正弦定理和余弦定理以及类比推理,还考查了运算求解的能力,属于中档题.17.将函数cos y x =的图象先左移4π,再纵坐标不变,横坐标缩为原来的12,所得图象的解析式为( ) A .sin 24y x π⎛⎫=+⎪⎝⎭B .13sin 24y x π⎛⎫=+⎪⎝⎭C .1sin 24y x π⎛⎫=+ ⎪⎝⎭D .3sin 24y x π⎛⎫=+ ⎪⎝⎭ 【答案】D【分析】根据三角函数的平移伸缩变换法则得到答案. 【详解】cos sin 2y x x π⎛⎫==+ ⎪⎝⎭向左平移4π个单位,故变为3sin 4y x π⎛⎫=+ ⎪⎝⎭,纵坐标不变,横坐标缩为原来的12,变为3sin 24y x π⎛⎫=+ ⎪⎝⎭. 故选:D . 【点睛】本题考查了三角函数的平移伸缩变换,意在考查学生对于平移伸缩变换的理解和掌握.18.函数()22sin 3cos 2f x x x =+-,2,36x ππ⎡⎤∈-⎢⎥⎣⎦的值域为( ) A .40,3⎡⎤⎢⎥⎣⎦B .41,3⎡⎤⎢⎥⎣⎦C .51,4⎡⎤⎢⎥⎣⎦D .50,4⎡⎤⎢⎥⎣⎦【答案】A 【解析】 【分析】化简得到()23sin 2sin 1f x x x =-++,设sin t x =,利用二次函数性质得到答案. 【详解】根据22sin cos 1x x +=,得()23sin 2sin 1f x x x =-++,2,36x ππ⎡⎤∈-⎢⎥⎣⎦, 令sin t x =,由2,36x ππ⎡⎤∈-⎢⎥⎣⎦,得1sin 1,2x ⎡⎤∈-⎢⎥⎣⎦, 故[]0,1t ∈,有2321y t t =-++,[]0,1t ∈,二次函数对称轴为13t =, 当13t =时,最大值43y =;当1t =时,最小值0y =, 综上,函数()f x 的值域为40,3⎡⎤⎢⎥⎣⎦. 故选:A . 【点睛】本题考查了三角函数值域,换元可以简化运算,是解题的关键.19.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,且222b c a bc +=+若2sin sin sin B C A ⋅=,则ABC ∆的形状是()A .等腰三角形B .直角三角形C .等边三角形D .等腰直角三角形【解析】 【分析】直接利用余弦定理的应用求出A 的值,进一步利用正弦定理得到:b =c ,最后判断出三角形的形状. 【详解】在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c , 且b 2+c 2=a 2+bc .则:2221222b c a bc cosA bc bc +-===,由于:0<A <π,故:A 3π=.由于:sin B sin C =sin 2A , 利用正弦定理得:bc =a 2, 所以:b 2+c 2﹣2bc =0, 故:b =c ,所以:△ABC 为等边三角形. 故选C . 【点睛】本题考查了正弦定理和余弦定理及三角形面积公式的应用,主要考查学生的运算能力和转化能力,属于基础题型.20.已知曲线1:sin C y x =,21:cos 23C y x π⎛⎫=- ⎪⎝⎭,则下面结论正确的是( )A .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CB .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CC .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移3π个单位长度,得到曲线2CD .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移3π个单位长度,得到曲线2C 【答案】D【分析】根据三角函数的周期变换和左右平移变换依次得到各选项中所得的函数解析式,从而得到正确选项. 【详解】A 中,将sin y x =横坐标缩短到原来的12倍得:sin 2y x =;向右平移3π个单位长度后得:2sin 2sin 2sin 2cos 233266y x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=-=--=-- ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,A 错误;B 中,将sin y x =横坐标伸长到原来的2倍得:1sin2y x =;向右平移3π个单位长度后得:11121sin sin cos cos 232622632y x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=-=--=- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,B 错误;C 中,将sin y x =横坐标缩短到原来的12倍得:sin 2y x =;向左平移3π个单位长度后得:2sin 2sin 2sin 2cos 233266y x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=+=+=++=+ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,C 错误;D 中,将sin y x =横坐标伸长到原来的2倍得:1sin2y x =;向左平移3π个单位长度后得:1111sin sin cos cos 232622623y x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+=+=-+=- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,D 正确. 故选:D 【点睛】本题考查三角函数的周期变换和平移变换的问题,关键是能够准确掌握变换原则,得到变换后的函数解析式.。
《解三角形》常见题型总结

《解三角形》常见题型总结1。
1正弦定理和余弦定理1。
1.1正弦定理【典型题剖析】考察点1:利用正弦定理解三角形例1 在ABC 中,已知A :B:C=1:2:3,求a :b :c 。
【点拨】 本题考查利用正弦定理实现三角形中边与角的互化,利用三角形内角和定理及正弦定理的变形形式 a :b :c=sinA: sinB: sinC 求解。
解:::1:2:3,A .,,,6321::sin :sin :sin sin:sin:sin::1 2.63222A B C B C A B C a b A B C πππππππ=++=∴===∴====而【解题策略】要牢记正弦定理极其变形形式,要做到灵活应用。
例2在ABC 中,已知C=30°,求a+b 的取值范围。
【点拨】 此题可先运用正弦定理将a+b 表示为某个角的三角函数,然后再求解。
解:∵C=30°sin sin sin a b c A B C === ∴sinA ,b=2°-A ).∴a+b=2[sinA+sin(150°—·2sin75°·cos(75°-A )=2cos (75°—A )① 当75°-A=0°,即A=75°时,a+b取得最大值2② ∵A=180°—(C+B)=150°—B ,∴A <150°,∴0°<A <150°,∴—75°<75°-A <75°,∴cos75°<cos(75°-A)≤1,∴>2cos75°=2×4. 综合①②可得a+b考察点2:利用正弦定理判断三角形形状例3在△ABC 中,2a ·tanB=2b ·tanA ,判断三角形ABC 的形状。
【点拨】通过正弦定理把边的关系转化为角的关系,利用角的关系判断△ABC 的形状。
解三角形方法与技巧例题和知识点总结

解三角形方法与技巧例题和知识点总结一、解三角形的基本概念在平面几何中,三角形是一个非常重要的图形。
解三角形就是通过已知的三角形的一些元素(如边、角),求出其他未知元素的过程。
三角形中的基本元素包括三个角(通常用 A、B、C 表示)和三条边(通常用 a、b、c 表示)。
解三角形的主要依据是三角形的内角和定理(A + B + C = 180°)以及正弦定理和余弦定理。
二、正弦定理正弦定理的表达式为:\(\frac{a}{\sin A} =\frac{b}{\sin B} =\frac{c}{\sin C}\)。
正弦定理可以用于以下两种情况:1、已知两角和一边,求其他两边和一角。
例如:在三角形 ABC 中,已知角 A = 30°,角 B = 45°,边 c =10,求边 a 和边 b。
首先,根据三角形内角和定理,角 C = 180° 30° 45°= 105°。
然后,利用正弦定理\(\frac{a}{\sin A} =\frac{c}{\sin C}\),可得\(a =\frac{c\sin A}{\sin C} =\frac{10\times\sin 30°}{\sin 105°}\)。
同样,\(\frac{b}{\sin B} =\frac{c}{\sin C}\),\(b =\frac{c\sin B}{\sin C} =\frac{10\times\sin 45°}{\sin 105°}\)。
2、已知两边和其中一边的对角,求另一边的对角和其他边。
例如:在三角形 ABC 中,已知边 a = 6,边 b = 8,角 A = 30°,求角 B。
由正弦定理\(\frac{a}{\sin A} =\frac{b}{\sin B}\),可得\(\sin B =\frac{b\sin A}{a} =\frac{8\times\sin 30°}{6} =\frac{2}{3}\)。
高三数学三角形中的常见错解剖析专题辅导

三角形中的常见错解剖析斯华清解三角形问题是个难点,怎样才能突破这个难点呢?只有正确理解三角形中的边角关系,即三角形中的边角等量关系、边角的不等关系及内角和关系,才能克服难点,下面就解三角形问题中的常见错误进行分析,以期对同学们的学习有所帮助。
一、不注意三角形的边角关系,造成角的范围变化而致错例1 在△ABC 中,B 2sin A 2sin =,试判断三角形的形状。
错解:由A 2sin B 2sin =,得A 2B 2=,所以B A =,知此三角形为等腰三角形。
剖析:上面的式子不是等价变换,未考虑三角形中角的范围而致错。
由已知得A 2B 2=或A 2B 2-π=,所以A=B 或2B A π=+。
故△ABC 是等腰三角形或直角三角形。
例2 A 、B 、C 为△ABC 的内角,且53A cos =,135B sin =,求C cos 的值。
错解:由53A cos =,知⎪⎭⎫⎝⎛π∈2,0A ,得54A sin =,135B sin =,知()π∈,0B ,所以1312B cos ±=,从而()6516B sin A sin B cos A cos B A cos C cos -=+-=+-=或6556C cos =。
剖析1:由于135B sin =,54A sin =,故A sinB sin <,两边乘以ABC △外接圆的直径2R ,得A B a b A sin R 2B sin R 2<⇔<⇔<。
故角B 一定是锐角,于是1312B cos =,知6516C cos -=。
剖析2:由2253A cos 21<=<且π<<A 0,而余弦函数在[]π,0上为减函数,得3A 4π<<π,由21135B sin 0<=<,得6B 0π<<或π<<πB 65。
所以2B A 4π<+<π或34B A 1213π<+<π(不合题意),显然B 为锐角。
备战2024年高考数学考试易错题专题06 解三角形及应用(3大易错点分析)(解析版)

专题06解三角形及应用易错点一:易忽视三角形解的个数(解三角形多解情况)1.方法技巧:解三角形多解情况在△ABC 中,已知a ,b 和A 时,解的情况如下:A 为锐角A 为钝角或直角图形关系式sin a b Asin b A a ba b a b a b解的个数一解两解一解一解无解2.在解三角形题目中,若已知条件同时含有边和角,但不能直接使用正弦定理或余弦定理得到答案,要选择“边化角”或“角化边”,变换原则常用:(1)若式子含有sin x 的齐次式,优先考虑正弦定理,“角化边”;(2)若式子含有,,a b c 的齐次式,优先考虑正弦定理,“边化角”;(3)若式子含有cos x 的齐次式,优先考虑余弦定理,“角化边”;(4)代数变形或者三角恒等变换前置;(5)含有面积公式的问题,要考虑结合余弦定理使用;(6)同时出现两个自由角(或三个自由角)时,要用到A B C .技巧:正弦定理和余弦定理是解三角形的两个重要工具,它沟通了三角形中的边角之间的内在联系,正弦定理能够解决两类问题问题1:已知两角及其一边,求其它的边和角。
这时有且只有一解。
问题2:已知两边和其中一边的对角,求其它的边和角,这是由于正弦函数在在区间 0, 内不严格格单调,此时三角形解的情况可能是无解、一解、两解,可通过几何法来作出判断三角形解的个数。
题设三角形中,已知一个角A 和两个边b a ,,判断三角形个数,遵循以下步骤第一步:先画一个角并标上字母A 第二步:标斜边(非对角边)b 第三步:画角的高,然后观察(A b a sin ,)易错提醒:利用正弦定理解三角形时,若已知三角形的两边及其一边的对角解三角形时,易忽视三角形解的个数.故选:ABD变式2.在ABC 中,内角,A A .若A B ,则cos A B .若2BC BA AB ,则角1.在ABC 中,已知3cos 5A ,sinB a ,若cosC 有唯一值,则实数a 的取值范围为()由BD DC ,可得OD OBOC 由2cos OB AB O OC AB B P 可得cos AB DP OP OD AB B sin2A =sin2B 《正弦定理》①正弦定理:R CcB b A a 2sin sin sin ②变形:acA C c b CB b a B A sin sin ,sin sin ,sin sin ③变形:C B A c b a sin :sin :sin :: ④变形:CcB b A aC B A c b a sin sin sin sin sin sin⑤变形:B c C b A c C a A b B a sin sin ,sin sin ,sin sin 《余弦定理》①余弦定理:Cab c b a B ac b c a A bc a c b cos 2,cos 2,cos 2222222222②变形:abc b a C ac b c a B bc a c b A 2cos ,2cos ,2cos 222222222核心问题:什么情况下角化边什么情况下边化角?⑴当每一项都有边且次数一样时,采用边化角⑵当每一项都有角《sin 》且次数一样时,采用角化边⑶当每一项都是边时,直接采用边处理问题⑷当每一项都有角《sin 》及边且次数一样时,采用角化边或变化角均可三角形面积公式①A bc S B ac S C ab S ABC ABC ABC sin 21,sin 21,sin 21 ② rl c b a r S ABC2121 其中l r ,分别为ABC 内切圆半径及ABC 的周长推导:将ABC 分为三个分别以ABC 的边长为底,内切圆与边相交的半径为高的三角形,利用等面积法即可得到上述公式③RabcC B A R S ABC 4sin sin sin 22(R 为ABC 外接圆的半径)推导:将A R a sin 2 代入ACB a S ABCsin sin sin 212可得C B A R S ABC sin sin sin 22 将C R c B R b A R a sin 2sin 2,sin 2 ,代入CB A R S ABC sin sin sin 22 可得RabcS ABC 4④CBA c SBC A b S A C B a S ABC ABC ABC sin sin sin 21,sin sin sin 21,sin sin sin 21222 ⑤海伦公式 c p b p a p p S ABC (其中 c b a p 21)推导:根据余弦定理的推论ab c b a C 2cos 222222222121cos 121sin 21ab c b a ab C ab C ab S ABCc b a b a c a c b c b a c b a ab 4124122222令 c b a p 21,整理得c p b p a p p S ABC 正规方法:面积公式+基本不等式① C c ab ab c C ab b a C ab c b a C ab S cos 122cos 2cos 2sin 212222222② B b ac ac b B ac c a B ac b c a B ac S cos 122cos 2cos 2sin 212222222③ A a bc bc a A bc c b Abc a c b A bc S cos 122cos 2cos 2sin 212222222易错提醒:当解题过程中出现类似于sin2A =sin2B 这样的情况要注意结合三角形内角范围进行讨论,另外当题设中出现锐角三角形时一定要注意条件之间的相互“限制”1.在ABC 中,sin sin 2,2B A c a ,则()A .B 为直角B .B 为钝角C .C 为直角D .C 为钝角易错点三:实际问题中题意不明致误(利用解三角形知识解决实际问题)解三角形的实际应用问题的类型及解题策略1、求距离、高度问题(1)选定或确定要创建的三角形,要先确定所求量所在的三角形,若其他量已知则直接解;若有未知量,则把未知量放在另一确定三角形中求解.有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的量.(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.2、求角度问题(1)分析题意,分清已知与所求,再根据题意画出正确的示意图,这是最关键、最重要的一步,画图时,要明确仰角、俯角、方位角以及方向角的含义,并能准确找到这些角.(2)将实际问题转化为可用数学方法解决的问题后,注意正、余弦定理的综合应用.易错提醒:实际问题应用中有关名词、术语也是容易忽视和混淆的。
高中数学-解三角形知识点汇总及典型例题

解三角形的必备知识和典型例题及详解一、知识必备:1.直角三角形中各元素间的关系:在△ABC 中,C =90°,AB =c ,AC =b ,BC =a 。
(1)三边之间的关系:a 2+b 2=c 2。
(勾股定理) (2)锐角之间的关系:A +B =90°; (3)边角之间的关系:(锐角三角函数定义) sin A =cos B =c a ,cos A =sin B =c b ,tan A =ba。
2.斜三角形中各元素间的关系:在△ABC 中,A 、B 、C 为其内角,a 、b 、c 分别表示A 、B 、C 的对边。
(1)三角形内角和:A +B +C =π。
(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等R Cc B b A a 2sin sin sin ===(R 为外接圆半径) (3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍a 2=b 2+c 2-2bc cos A ; b 2=c 2+a 2-2ca cos B ; c 2=a 2+b 2-2ab cos C 。
3.三角形的面积公式:(1)∆S =21ah a =21bh b =21ch c (h a 、h b 、h c 分别表示a 、b 、c 上的高); (2)∆S =21ab sin C =21bc sin A =21ac sin B ;4.解三角形:由三角形的六个元素(即三条边和三个内角)中的三个元素(其中至少有一个是边)求其他未知元素的问题叫做解三角形.广义地,这里所说的元素还可以包括三角形的高、中线、角平分线以及内切圆半径、外接圆半径、面积等等.主要类型: (1)两类正弦定理解三角形的问题:第1、已知两角和任意一边,求其他的两边及一角. 第2、已知两角和其中一边的对角,求其他边角. (2)两类余弦定理解三角形的问题:第1、已知三边求三角.第2、已知两边和他们的夹角,求第三边和其他两角.②当0116≈B 时,180()180(40116)24=-+≈-+=C A B ,0sin 20sin2413().sin sin40==≈a C c cm A 点评:应用正弦定理时(1)应注意已知两边和其中一边的对角解三角形时,可能有两解的情形;(2)对于解三角形中的复杂运算可使用计算器 题型2:三角形面积例2.在∆ABC 中,sin cos A A +=22,AC =2,3=AB ,求A tan 的值和∆ABC 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题1、在△ABC 中,已知2a =,b =22,C =15°,求A 。
错解:由余弦定理,得ca ba b 222215=+-c o s °
48228=+-=-×× ∴c =-62。
又由正弦定理,得s i n s i n A a C c =
=12 而0000018030150A A A <<=,∴=或。
分析:由题意b a
>,∴B A >。
因此A =150°是不可能的。
错因是没有认真审题, 未利用隐含条件。
在解题时,要善于应用题中的条件,特别是隐含条件,全面细 致
地分析问题,避免错误发生。
正解:同上c A b a
=-=>6212
,,∵s i n , 000018030B A A A ><<=∴,且,∴。
例题2、在△ABC 中,若a b
A B 22=ta n ta n ,试判断△ABC 的形状。
错解:由正弦定理,得s i n s i n t a n t a
n 22A B A B = 即s i n s i n s i n c o s c o s s i n s i n s i n 2200A B A A B B A B =>>·,∵,
∴,即s i n c o s s i n c o s s i n s i n A A B B A B
==22。
∴2A =2B ,即A =B 。
故△ABC 是等腰三角形。
分析:由s i n s i n 22A B
=,得2A =2B 。
这是三角变换中常见的错误,原因是不熟悉 三角函数的性质,三角变换生疏。
正解:同上得s i n s i n 22A B =,∴2A =22k B π+
或222A k B k Z =+-∈ππ
()。
∵000<<<<==A b k A B ππ,,∴,则或A B =-π
2。
故△ABC 为等腰三角形或直角三角形。
例题3、在△ABC 中,A =60°,b =1,S A B C △=3,求a b c A B C
++++s i n s i n s i n 的值。
错解:∵A =60°,b =1,S A B C △=3,又S A B C △=12
b c A s i n , ∴312=c s i n 60°,解得c =4。
由余弦定理,得a b cb c A =+-=+-22
2116860c o s c o s °=13 又由正弦定理,得s i n s i n C B ==6393239,。
∴a b c A B C ++++=++
++s i n s i n s i n 1314323239639。
分析:如此复杂的算式,计算困难。
其原因是公式不熟、方法不当造成的。
正解:由已知可得c a ==413,。
由正弦定理,得 2136023
9
3R a A ===s i n s i n °。
∴a b c
A B C R ++++==s i n s i n s i n 22393。
例题4、在△ABC 中,c =+62,C =30°,求a +b 的最大值。
错解:∵C =30°,∴A +B =150°,B =150°-A 。
由正弦定理,得a
A b
A sin sin()sin =-=+15062
30°°
∴a A =+262()s i n ,b A =+-262150()s i n ()°
又∵s i n s i n ()A A ≤-≤11501,° ∴a b +≤+++=+262262462()()()。
故a b +的最大值为462()+。
分析:错因是未弄清A 与150°-A 之间的关系。
这里A 与150°-A 是相互制约的,
不是相互独立的两个量,sinA 与sin(150°-A)不能同时取最大值1,因此所得的
结果也是错误的。
正解:∵C =30°,∴A +B =150°,B =150°-A 。
由正弦定理,得a A b A sin sin()sin =-=+1506230°°
因此a b A A +=++-262150()[s i n s i n ()]
°
sin 75cos(75)
cos(75)4
(875)8A A A =-=-=+-≤+°°·°° ∴a +b 的最大值为843+。
例题5、在不等边△ABC 中,a 为最大边,如果a b c
222
<+,求A 的取值范围。
错解:∵a b c b c a 2222220
<++->,∴。
则 c o s A b c a b c =+->22220,由于cos A 在(0,180)上为减函数 且cos90090A =<°,∴°
又∵A 为△ABC 的内角,∴0°<A <90°。
分析:错因是审题不细,已知条件弱用。
题设是a 为最大边,而错解中只把a 看做是三
角形的普通一条边,造成解题错误。
正解:由上面的解法,可得A <90°。
又∵a 为最大边,∴A >60°。
因此得A 的取值 范围是(60°,90°)。
例题6、在△ABC 中,cos cos A b B α=,判断△ABC 的形状。
错解:在△ABC 中,∵aA bB c o s c o s
=,由正弦定理 得22R A A R B B
s i n c o s s i n c o s = ∴s i n s i n 222222180A B A B A B ==+=,∴且°
∴A =B 且A +B =90°
故△ABC 为等腰直角三角形。
分析:对三角公式不熟,不理解逻辑连结词“或”、“且”的意义,导致结论错误。
正解:在△ABC 中,∵aA bB c o s c o s =,由正弦定理,
得2222R A A R B BA B s i n c o s s i n c o s s i n s i n ==,∴。
∴2A =2B 或2A +2B =180°,∴A =B 或A +B =90°。
故△ABC 为等腰三角形或直角三角形。
例题7 若a ,b ,c 是三角形的三边长,证明长为a b c ,,的三条线段能构成锐角三角
形。
错解:不妨设0<≤≤a b c
,只要考虑最大边的对角θ为锐角即可。
c o s ()()()θ=+-=+-a b c a b a b c a b
22222。
由于a ,b ,c 是三角形的三边长,
根据三角形三边关系,有a b c
+>,即c o s θ>0。
∴长为a b c ,,的三条线段能构成锐角三角形。
分析:三条线段构成锐角三角形,要满足两个条件:①三条边满足三角形边长关系;②
最长线段的对角是锐角。
显然错解只验证了第二个条件,而缺少第一个条件。
正解:由错解可得c o s θ>0
又∵abc abcabc abc +-=+-++++
()()
==> 即长为a b c ,,的三条线段能构成锐角三角形。
