01.专题一坐标曲线题

合集下载

练习01曲线运动之运动合成图像-2021年高考物理一轮复习习题课(必修2)

曲线运动习题课--运动合成图像练习1、（多选）质量为m＝2 kg的物体在光滑的水平面上运动，在水平面上建立xOy坐标系，t ＝0时物体位于坐标系的原点O.物体在x轴和y轴方向的分速度v x、v y随时间t变化的图线如图甲、乙所示．则()A．t＝0时，物体速度的大小为3 m/sB．t＝8 s时，物体速度的大小为4 m/sC．t＝8 s时，物体速度的方向与x轴正向夹角为37°D．t＝8 s时，物体的位置坐标为(24 m,16 m)2、有一个质量为2 kg的质点在x－y平面上运动，在x方向的速度图象和y方向的位移图象分别如图甲、乙所示，下列说法正确的是()A．质点所受的合外力为3 NB．质点的初速度为3 m/sC．质点做匀变速直线运动D．质点初速度的方向与合外力的方向垂直3、质量为2 kg的质点在x-y平面上运动，x方向的速度—时间图像和y方向的位移—时间图像分别如图所示，则质点()A．初速度为4 m/sB．所受合外力为4 NC．做匀变速直线运动D．初速度的方向与合外力的方向垂直4．(多选)如图甲所示，在杂技表演中，猴子沿竖直杆向上运动，其v -t图像如图乙所示，同时人顶着杆沿水平地面运动的x -t图像如图丙所示。

若以地面为参考系，下列说法正确的是()A．猴子的运动轨迹为直线B．猴子在0～2 s内做匀变速曲线运动C．t＝0时猴子的速度大小为8 m/sD．猴子在0～2 s内的加速度大小为4 m/s25、(多选)在一光滑水平面内建立平面直角坐标系，一物体从t＝0时刻起，由坐标原点O(0,0)开始运动，其沿x轴和y轴方向运动的速度－时间图象如图3甲、乙所示，下列说法中正确的是()图3A．前2 s内物体沿x轴做匀加速直线运动B．后2 s内物体继续做匀加速直线运动，但加速度沿y轴方向C．4 s末物体坐标为(4 m,4 m)D．4 s末物体坐标为(6 m,2 m)6、(多选)质量为0.2 kg的物体在水平面上运动，它的两个正交分速度图线分别如图所示，由图可知()A．最初4 s内物体的位移为8 2 mB．从开始至6 s末物体都做曲线运动C．最初4 s内物体做曲线运动，接下来的2 s内物体做直线运动D．最初4 s内物体做直线运动，接下来的2 s内物体做曲线运动7.一个质点从水平面内的xOy坐标系的原点出发开始运动，其沿x轴正方向的分速度随时间变化的图象及沿y轴正方向的位移随时间变化的图象如图6甲、乙所示，一条直线过坐标原点、与x轴正方向成30°角，如图丙所示。

专题01 用几何意义探究反比例函数中k值问题的多种解法(解析版)

专题01 用几何意义探究反比例函数中k 值问题的多种解法如图，反比例函数k y x =（k >0），A 、C 是第一象限上两点，S △OAB =S △OCD =2k ；S △OAC =S 梯形ABDC 在已知面积或比例线段解答反比例函数的问题中，善于利用k 与面积的关系，往往可以事半功倍．典例1．知面积比值，求k 值（2022•山东聊城中考真题）如图，直线与反比例函数在第一象限内的图象交于点，与y 轴交于点B ，过双曲线上的一点C 作x 轴的垂线，垂足为点D ，交直线于点E ，且．()30y px p =+¹()0k y k x=>()2,A q 3y px =+:3:4AOB COD S S =△△(1)求k ，p 的值；(2)若OE 将四边形BOCE 分成两个面积相等的三角形，求点C 的坐标．【答案】(1)，；(2)点C 的坐标为(4，2)【解析】【方法一】坐标法（1）解：∵直线与y 轴交点为B ，∴，即．∵点A 的横坐标为2，∴．∵，∴△COD 的面积为4，设，∴，解得．∵点在双曲线上，∴，把点代入，得，∴，；8k =12p =3y px =+()0,3B 3OB =13232AOB S =´´=V :3:4AOB COD S S =△△,k C m m æöç÷èø142k m m×=8k =()2,A q 8y x=4q =()2,4A 3y px =+12p =8k =12p =（2）解：由（1）得8,C m m æöç÷èø，∴．∵OE 将四边形BOCE 分成两个面积相等的三角形，∴，∵32BOE S m =△，，∴，解得或（不符合题意，舍去），∴点的坐标为（4，2）．【方法二】k 的几何意义法解：（1）由题意知，△ABO 的面积为3，又，得：△OCD 的面积为4，故k =2S △OCD =8，所以，A （2,4），把点代入，得（2）如图，过A ，E 作y 轴垂线，垂足为M ，N则四边形ODEN 为矩形，所以，S △OEN =S △OED ，又S △OBE =S △OCE ，所以S △BEN =S △OCD =4，1,32E m m æö+ç÷èøBOE COE S S =△△13422COE m S m æö=+-ç÷èø△3134222m m m æö=+-ç÷èø4m =4m =-C :3:4AOB COD S S =△△()2,4A 3y px =+12p =所以S △ABM =1，∵AM ∥NE ，∴△ABM ∽△EBN ，其面积比为1:4，∴AM ：NE =1:2，即NE =4，∴C 点坐标为（4,2）典例2．知比例线段，求k 值（2022•贵州铜仁中考真题）如图，点A 、B 在反比例函数k y x=的图象上，AC y ^轴，垂足为D ，BC AC ^．若四边形AOBC 的面积为6，12AD AC =，则k 的值为_______．【答案】3．【解析】【方法一】坐标法设点,k A a a æöç÷èø，∵AC y ^轴，∴AD a =，k OD a =，∵12AD AC =，∴AC 2a =，∴CD =3a ，∵BC AC ^．AC y ^轴，∴BC ∥y 轴，∴点B 3,3æöç÷èøk a a ，∴233k k k BC a a a=-=，∵AOD AOBC OBCD S S S =+V 四边形梯形，四边形AOBC 间面积为6，∴12136232k k a k a a æö+´=+ç÷èø，解得：3k =．【方法二】k 的几何意义法如图，连接OC ，延长CB 交x 轴于E ，则S △AOD =S △BOE =12k ，因为AD ：AC =1:2，所以S △AOC =2S △AOD =k ，S △BOC =6-k ，又四边形DOEC 为矩形，OC 为对角线，所以，S △COD =S △COE ，所以12k +k =6-k +12k ，解得：k =3．典例3．知面积值，求k 值（2022•内蒙古呼伦贝尔中考真题）如图，在平面直角坐标系中，Rt OAB △的直角顶点B 在x 轴的正半轴上，点O 与原点重合，点A 在第一象限，反比例函数k y x=（0x >）的图象经过OA 的中点C ，交AB 于点D ，连接CD ．若ACD △的面积是1，则k 的值是_________．【答案】43．【解析】【方法一】坐标法解：设C （m ，k m），因为C 为OA 中点，所以A （2m ，2k m），则D （2m ，2k m ），又△ACD 的面积为1，所以12122k k m m m æö×-=ç÷èø，解得：k =43【方法二】k 的几何意义法解：连接OD ，过C 作CE AB ∥，交x 轴于E ，∵∠ABO ＝90°，反比例函数k y x =（x ＞0）的图象经过OA 的中点C ，1ACD S =V ，∴12COE BOD S S k ==△△，1ACD OCD S S ==V V ，2OC =OA ，∵CE AB ∥，∴△OCE ∽△OAB ，∴221124OCE S OC S OA æöæö===ç÷ç÷èøèø△△O A B ，∴4OCE OAB ACD OCD OBD S S S S S ==++V V V V V ，∴1141122k k ´=++，∴k ＝43，故答案为：43．1.（2022•辽宁锦州中考真题）如图，在平面直角坐标系中，△AOB 的边OB 在y 轴上，边AB 与x 轴交于点D ，且BD =AD ，反比例函数y =k x(x >0)的图像经过点A ，若S △OAB =1，则k 的值为___________．【答案】2．【解析】【方法一】坐标法解：设A(a，b) ，如图，作A过x轴的垂线与x轴交于C，则：AC=b，OC=a，AC∥OB，∴∠ACD=∠BOD=90°，∠ADC=∠BDO，∴△ADC≌△BDO，∴S△ADC=S△BDO，∴S△OAC=S△AOD+ S△ADC=S△AOD+ S△BDO= S△OAB=1，∴12×OC×AC=12ab=1，∴ab=2，∵A(a，b) 在y=kx上，∴k=ab=2 ．【方法二】k的几何意义法由上知，S△AOC=1，所以，k=2S△AOC=2故答案为：2．2.（2022•辽宁鞍山中考真题）如图，在平面直角坐标系中，O 是坐标原点．在Rt OAB V 中，90OAB Ð=°，边OA 在y 轴上，点D 是边OB 上一点，且:1:2OD DB =，反比例函数()0ky x x=>的图象经过点D 交AB 于点C ，连接OC ．若4OBC S =△，则k 的值为_________．【答案】1．【解析】【方法一】坐标法解：∵反比例函数()0k y x x=>的图象经过点D ，∠OAB ＝90°，∴D （m ，k m ），∵OD ：DB ＝1：2，∴B （3m ，3k m），∴AB ＝3m ，OA ＝3k m ，∴反比例函数()0k y x x =>的图象经过点D 交AB 于点C ，∠OAB ＝90°，∴12AOC S k =△，∵4OBC S △＝，∴4AOB AOC S S -△△＝，即1313422k m k m ´×-=，解得k ＝1【方法二】k 的几何意义法如图，过D 作DE ⊥x 轴，则DE ∥AB ，因为OD ：BD =1:2，所以DE ：AB =1:3，所以S △ODE ：S △OAB =1：9，又S △ODE =S △OAC =12k ，所以12k +4=92k ，解得：k =13.（2022•江苏南通中考真题）平面直角坐标系中，已知点是函数图象上的三点．若，则k 的值为___________．【答案】【解析】【方法一】坐标法解：∵点是函数图象上的三点，∴，，∴m ＝n ，∴，，∴点B 、C 关于原点对称，∴设直线BC 的解析式为，代入得：，解得：，∴直线BC 的解析式为，xOy (,6),(3,2),(3,2)--A m m B m n C m n (0)k y k x=¹2ABC S =△34(,6),(3,2),(3,2)--A m m B m n C m n (0)k y k x =¹260k m =>6k mn =(3,2)B m m (3,2)C m m --()0y kx k =¹(3,2)B m m 23m mk =23k =23y x =不妨设m ＞0，如图，过点A 作x 轴的垂线交BC 于D ，把x ＝m 代入得：，∴D （m ，），∴AD ＝，∴，∴，∴，而当m ＜0时，可得，故答案为：．【方法二】由题意知，S △OAB =12632m n m m ×-×，O 为BC 中点，因为所以，S △OAB =12632m n m m ×-×=1，即291mn m -=①，又632m m m n k ×=×=②，23y x =23y m =23m 216633m m m -=()11633223ABC S m m m =´×+=V 218m =2136684k m ==´=34k =342ABC S =△由①②可得：4.（2022•湖北十堰中考真题）如图，正方形ABCD 的顶点分别在反比例函数()110k y k x=>和()220k y k x =>的图象上．若BD y ∥轴，点D 的横坐标为3，则12k k +=（）A ．36B ．18C ．12D ．9【答案】B ．【解析】【方法一】解：连接AC ，与BD 相交于点P ，设PA =PB =PC =PD =t （t ≠0）．∴点D 的坐标为（3，23k ），∴点C 的坐标为（3-t ，23k +t ）．∵点C 在反比例函数y =2k x 的图象上，34k=∴（3-t ）（23k +t ）=k 2，化简得：t =3-23k ，∴点B 的纵坐标为23k +2t =23k +2（3-23k ）=6-23k ，∴点B 的坐标为（3，6-23k ），∴3×（6-23k ）=1k ，整理，得：1k +2k =18．【方法二】先利用D 点坐标，表示出A 和C 点坐标，再根据四边形ABCD 为正方形，BD 与y 轴平行，知AC 平行于x 轴，那么，A 和C 点的纵坐标相等，进而求解23,3k D æöç÷èø，13,3k B æöç÷èø，122123,636k k k C k k æöç÷--ç÷-ç÷-èø，121123,636k k k A k k æöç÷-+ç÷-ç÷+èø所以2112123366k k k k k k =---+，整理得：()212212180k k k k ---=即()()1212108k k k k -+=-因为()120k k -¹所以()12018k k +-=，即1218k k +=5.（2022•黑龙江龙东中考真题）如图，在平面直角坐标系中，点O 为坐标原点，平行四边形OBAD 的顶点B 在反比例函数3y x =的图象上，顶点A 在反比例函数k y x=的图象上，顶点D 在x 轴的负半轴上．若平行四边形OBAD 的面积是5，则k 的值是（）A ．2B ．1C ．1-D ．2-【答案】D ．【解析】解：设B点坐标为3,mmæöç÷èø，则A3,3kmmæöç÷èø，因为平行四边形OBAD的面积是5，所以353kmmmæö-×=ç÷èø，解得k=-2【方法二】解：如图，连接OA，设AB交y轴于点C，∵四边形OBAD是平行四边形，平行四边形OBAD的面积是5，∴1522AOB OBADS S==V Y，AB∥OD，∴AB⊥y轴，∵点B在反比例函数3yx=的图象上，顶点A在反比例函数kyx=的图象上，∴3,22 COB COAkS S==-V V，∴35222 AOB COB COAkS S S=+=-=V V V，解得：2k=-．故选：D．6.（2022•湖北黄石中考真题）如图，反比例函数kyx=的图象经过矩形ABCD对角线的交点E和点A，点B、C在x轴上，OCE△的面积为6，则k=______________．【答案】8．【解析】设C （m ，0），由题意知E 为AC 中点，因为△OCE 面积为6，所以E 点纵坐标为12m，所以E 12,12km m æöç÷èø，A 24,6km m m æö-ç÷èø，又A 在反比例函数图像上所以246km m k mæö-×=ç÷èø解得k =8【方法二】解：如图作EF ⊥BC ，则12EF AB =，设E 点坐标为（a ，b ），则A 点的纵坐标为2b ，则可设A 点坐标为（c ，2b ），∵点A ，E 在反比例函数k y x=上，∴ab =k =2bc ，解得：a =2c ，故BF =FC =2c -c =c ，∴OC =3c ，故113622OEC S OC EF c b =´´=´´=V ，解得：bc =4，∴k =2bc =8，故答案为：8．7.（2022•贵州六盘水中考真题）如图，正比例函数与反比例函数的图象交于，两点．y x =4y x=A B(1)求，两点的坐标；(2)将直线向下平移个单位长度，与反比例函数在第一象限的图象交于点，与轴交于点，与轴交于点，若，求的值．【答案】(1)；(2)【解析】（1）解：联立与，解得，；（2）【方法一】解：如图，过点作轴于点，A B y x =a C x D y E 13CD DE =a ()()2,2,2,2A B --3a =y x =4y x=121222,22x x y y ==-ììíí==-îî()()2,2,2,2A B \--C CF y ^F，，，直线向下平移个单位长度得到，根据图象可知,令，得，令，得，，，，，与反比例函数在第一象限的图象交于点，，将代入，得，解得或（舍去）．【方法二】CF OD \∥Q 13CD DE =13OF CD OE DE \==Q y x =a y x a =-0a >0x =y a =-0y =x a =()0,E a \-(),0D a 10,3F a æö\ç÷èø13c y a \=Q y x a =-4y x=C 41213c x aa \==121,3C a a æöç÷èøy x a =-1123a a a=-3a =3a =-如图，连接OC ，过C 作CE ⊥x 轴，因为CD ：DE =1:3，CE ∥OE则△CDE ∽△EDO ，相似比为1:3，面积比为1:9，易知△ODE 面积为212a ，△OCE 的面积为12k =2，所以△OCD 的面积为2-2118a ，又△OCD 与△ODE 的面积比为1:3，所以2-2118a =21132a ´，解得：a =3或a =-3（舍）8.（2022•安徽中考真题）如图，平行四边形OABC 的顶点O 是坐标原点，A 在x 轴的正半轴上，B ，C 在第一象限，反比例函数1y x =的图象经过点C ，()0k y k x=¹的图象经过点B ．若OC AC =，则k =________．【答案】3．【解析】【方法一】设C 1,m m æöç÷èø，因为OC =AC所以A ()2,0m ，又OABC 为平行四边形所以B 13,m m æöç÷èø因为B 点在k y x =上，所以k =133m m ×=【方法二】解：过点C 作CD ⊥OA 于D ，过点B 作BE ⊥x 轴于E ，∴CD ∥BE ，∵四边形ABCO 为平行四边形，∴CB OA ∥ ，即CB DE ∥，OC =AB ，∴四边形CDEB 为平行四边形，∵CD ⊥OA ，∴四边形CDEB 为矩形，∴CD =BE ，∴在Rt △COD 和Rt △BAE 中，OC AB CD EB =ìí=î，∴Rt △COD ≌Rt △BAE （HL ），∴S △OCD =S △ABE ，∵OC =AC ，CD ⊥OA ，∴OD =AD ，∵反比例函数1yx=的图象经过点C，∴S△OCD=S△CAD=12，∴S平行四边形OCBA=4S△OCD=2，∴S△OBA=11 2OCBAS=平行四边形，∴S△OBE=S△OBA+S△ABE=13122+=，∴3232k=´=．故答案为3．。

01坐标系(含经典例题+答案)

坐标系一、极坐标系与极坐标在平面内取一个定点O ，由O 点出发的一条射线Ox 、一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向)，合称为一个极坐标系．O 点称为极点，Ox 称为极轴．平面上任一点M 的位置可以由线段OM 的长度ρ和从Ox 到OM 的角度θ来刻画(如图所示)．这两个数组成的有序数对(ρ，θ)称为点M 的极坐标．ρ称为极径，θ称为极角．二、点的极坐标和直角坐标的互化设M 是平面内任意一点，它的直角坐标是(x ，y)，极坐标是(ρ，θ)，可以得出它们之间的关系：x ＝ρcos θ，y ＝ρsin θ.又可得到关系式：ρ2＝x 2＋y 2，tan θ＝yx(x ≠0)．这就是极坐标与直角坐标的互化公式．三、常见曲线的极坐标方程曲线图形极坐标方程圆心在极点，半径为r 的圆ρ＝r (0≤θ＜2π)圆心为(r,0)，半径为r 的圆ρ＝2rcos θ (0≤θ＜2π)圆心为(r ，π2)，半径为r 的圆ρ＝2rsin θ (0≤θ＜2π)过极点，倾斜角为α的直线θ＝α(ρ∈R) 或θ＝π＋α(ρ∈R)过点(a,0)，与极轴垂直的直线ρcosθ＝a (－π2＜θ＜π2)过点(a ，π2)，与极轴平行的直线ρsinθ＝a (0＜θ＜π)例1：在极坐标系中，求经过点P 24,3π⎛⎫- ⎪⎝⎭且与极轴所在直线垂直的直线方程．解：∵x ＝ρcos θ＝4cos 23π⎛⎫- ⎪⎝⎭＝－2，y ＝ρsin θ＝4sin 23π⎛⎫- ⎪⎝⎭＝－23，∴点P 的直角坐标为()－2，－23.∴过点P 且与x 轴垂直的直线方程为x ＝－2，即极坐标方程为ρcos θ＝－2.例2：求圆心为C 3,6⎛⎫⎪⎝⎭，半径为3的圆的极坐标方程．解：如图，设圆上任一点为P (ρ，θ)，则|OP |＝ρ，∠POA ＝θ－π6，|OA |＝2×3＝6，在Rt △OAP 中，|OP |＝|OA |×cos ∠POA ，∴ρ＝6cos 6πθ⎛⎫- ⎪⎝⎭.∴圆的极坐标方程为ρ＝6cos 6πθ⎛⎫- ⎪⎝⎭.例3：已知直线l 的参数方程为：⎩⎪⎨⎪⎧x ＝2t ，y ＝1＋4t (t 为参数)，圆C 的极坐标方程为ρ＝22sin θ，试判断直线l 与解：将直线⎩⎪⎨⎪⎧x ＝2ty ＝1＋4t 化为普通方程得y ＝1＋2x ，圆ρ＝22sin θ的直角坐标方程为x 2＋(y －2)2＝2，圆心(0，2)到直线y ＝1＋2x 的距离为2－15，小于圆的半径，所以直线与圆相交．与极坐标(ρ，θ)(ρ≠0)建立一一对应关系．2．由极坐标系上点的对称性可得到极坐标方程ρ＝ρ(θ)的图形的对称性：若ρ(θ)＝ρ(－θ)，则相应图形关于极轴对称；若ρ(θ)＝ρ(π－θ)，则图形关于射线θ＝π2所在的直线对称；若ρ(θ)＝ρ(π＋θ)，则图形关于极点Ο对称．例4：在同一平面直角坐标系中，求一个伸缩变换，使得圆x 2＋y 2＝1变换为椭圆x 29＋y 24＝1.解：将变换后的椭圆的方程x 29＋y 24＝1改写为x ′29＋y ′24＝1，设伸缩变换为⎩⎪⎨⎪⎧x ′＝λx (λ>0)，y ′＝μy (μ>0)，代入上式得λ2x 29＋μ2y 24＝1，即23λ⎛⎫ ⎪⎝⎭x 2＋22μ⎛⎫ ⎪⎝⎭y 2＝1.与x 2＋y 2＝1比较系数，得221312λμ⎧⎛⎫=⎪ ⎪⎪⎝⎭⎨⎛⎫⎪= ⎪⎪⎝⎭⎩故⎩⎪⎨⎪⎧ λ＝3，μ＝2，所以伸缩变换为⎩⎪⎨⎪⎧x ′＝3x y ′＝2y ，即先使圆x 2＋y 2＝1上的点的纵坐标不变，将圆上的点的横坐标伸长到原来的3倍，得到椭圆x 29＋y 2＝1，再将该椭圆的点的横坐标不变，纵坐标伸长到原来的2倍，得到椭圆x 29＋y 24＝1.本例条件变为“求圆x 2＋y 2＝1经过伸缩变换⎪⎨⎪⎧x ′＝2x 后的图形”解：由⎩⎪⎨⎪⎧x ′＝2xy ′＝3y ∴⎩⎨⎧x ＝12x ′y ＝13y ′代入x 2＋y 2＝1，得x ′24＋y ′29＝1.∴经过伸缩变换⎩⎪⎨⎪⎧x ′＝2x y ′＝3y 后圆x 2＋y 2＝1变为椭圆例5：设平面上的伸缩变换的坐标表达式为⎩⎪⎨⎪⎧x ′＝12x ，y ′＝3y ，则在这一坐标变换下正弦曲线y ＝sin x 的方程变为例6：通过平面直角坐标系中的平移变换与伸缩变换，可以把椭圆(x ＋1)29＋(y －1)24＝1变为中心在原点的单1．平移变换：在平面直角坐标系中，设图形F 上任意一点P 的坐标为(x ，y )，向量a ＝(h ，k )，平移后的对应点为P ′(x ′，y ′)，则有(x ，y )＋(h ，k )＝(x ′，y ′)，或表示成⎩⎪⎨⎪⎧x ＋h ＝x ′，y ＋k ＝y ′.2．伸缩变换：一般地，由⎩⎪⎨⎪⎧kx ＝x ′，y ＝y ′k >0所确定的伸缩变换，是按伸缩系数为k 向着y 轴的伸缩变换(当k＞1时，表示伸长；当0<k ＜1时，表示压缩)，即曲线上所有点的纵坐标不变，横坐标变为原来的k 倍(这里，P (x ，y )是变换前的点，P ′(x ′，y ′)是变换后的点).例7：进行直角坐标方程与极坐标方程的互化：(1)y 2＝4x ；(2)x 2＋y 2－2x －1＝0；(3)ρ＝1cos θ.x 轴正半轴为极轴建立极坐标系，则点P 的极坐标可以是________．解：ρ＝x 2＋y 2＝2，tan θ＝－31＝－3，θ＝－π3＋2k π.例9:在极坐标系下，已知圆O ：ρ＝cos θ＋sin θ和直线l ：ρsin(θ－π4)＝22. (1)求圆O 和直线l 的直角坐标方1.将点的直角坐标(x ，y )化为极坐标(ρ，θ)时，运用公式ρ＝x 2＋y 2，tan θ＝yx(x ≠0)即可．在[0,2π)范围内，由tan θ＝yx(x ≠0)求θ时，要根据直角坐标的符号特征判断出点所在的象限．如果允许θ∈R ，再根据终边相同的角的意义，表示为θ＋2k π(k ∈Z)即可．2．极坐标与直角坐标的互化，常用方法有代入法、平方法等，还经常会用到同乘(或除以)ρ等技巧.例10：(1)(设点A 的极坐标为2,6π⎛⎫⎪⎝⎭，直线l 过点A 且与极轴所成的角为π3，则直线l 的极坐标方程为_____________．（2）在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝cos α，y ＝1＋sin α(α为参数)．在极坐标系(与直角坐标系xOy 取相同的长度单位，且以原点O 为极点，以x 轴正半轴为极轴)中，曲线C 2的方程为ρ(cos θ例11：在极坐标系中，曲线C 1：ρ＝2cos θ，曲线C 2：θ＝π4，若曲线C 1与C 2交于A 、B 两点，求线段AB 的例12：已知直线l 的参数方程是⎩⎨⎧x ＝1＋12t ，y ＝32t(t 为参数)，以原点O 为极点，x 轴正半轴为极轴建立极坐例13：在极坐标系中，直线l 的方程为ρsin θ＝3，求点2,6⎛⎫⎪到直线l 的距离．例14：已知直线l 经过点P 1,12⎛⎫ ⎪⎝⎭，倾斜角α＝π6，圆C 的极坐标方程为ρ＝2cos 4θ⎛⎫- ⎪⎝⎭(1)写出直线l 的参数方程，并把圆C 的方程化为直角坐标方程；(2)设l 与圆C 相交于两点A ，B ，求点P 到A ，B 两点的距离之积．例15：已知直线l 的参数方程为⎩⎨⎧x ＝12t ，y ＝22＋32t(t 为参数)，若以直角坐标系xOy 的O 点为极点，Ox 方向为极轴，选择相同的长度单位建立极坐标系，得曲线C 的极坐标方程为ρ＝2cos(θ－π4)．标系的单位长度相同，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－1＋t cos α，y ＝1＋t sin α(t 为参数)，曲线C 的极坐标方程为ρ＝4cos θ.(1)若直线l 的斜率为－1，求直线l 与曲线C 交点的极坐标；(2)若直线l 与曲线C 相交弦长为23，例17：在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝2＋2sin α，(α为参数)，M 是C 1上的动点，P 点满足OP ＝2OM ，P 点的轨迹为曲线C 2·(1)求C 2的方程；(2)在以O 为极点，x 轴的正半轴为极轴的极坐标系中，射线θ＝π3与C 1的异于极点的交点为A ，与C 2的异于极点的交点为B ，求|AB |.解：(1)设P (x ，y )，则由条件知M ,22x y ⎛⎫⎪⎝⎭.由于M 点在C 1上，所以⎩⎨⎧x2＝2cos α，y 2＝2＋2sin α.即⎩⎪⎨⎪⎧x ＝4cos α，y ＝4＋4sin α. 从而C 2的参数方程为⎩⎪⎨⎪⎧x ＝4cos α，y ＝4＋4sin α.(α为参数)．(2)曲线C 1的极坐标方程为ρ＝4sin θ，曲线C 2的极坐标方程为ρ＝8sin θ.射线θ＝π3与C 1的交点A 的极径为ρ1＝4sin π3，射线θ＝π3与C 2的交点B 的极径为ρ2＝8sin π3.所以|AB |＝|ρ2－ρ1|＝2 3.12(1)将两圆的极坐标方程化为直角坐标方程；(2)若两圆的圆心距为5，求a 的值．解：(1)由ρ＝2cos θ，得ρ2＝2ρcos θ.所以⊙O 1的直角坐标方程为x 2＋y 2＝2x ，即(x －1)2＋y 2＝1.由ρ＝2a sin θ，得ρ2＝2aρsin θ.所以⊙O 2的直角坐标方程为x 2＋y 2＝2ay ，即x 2＋(y －a )2＝a 2. (2)⊙O 1与⊙O 2的圆心距为12＋a 2＝5，解得a ＝±2.例19：极点O 引定圆ρ＝2cos θ的弦OP ，延长OP 到Q 使OP PQ ＝23，求点Q 的轨迹方程，并说明所求轨迹是解：设Q (ρ，θ)，P (ρ0，θ0)则θ＝θ0，ρ0ρ－ρ0＝23，∴ρ0＝25ρ.∵ρ0＝2cos θ0.∴25ρ＝2cos θ.即ρ＝5cos θ它表示一个圆．例20：已知双曲线的极坐标方程为ρ＝31－2cos θ，过极点作直线与它交于A 、B 两点，且|AB |＝6.解：设直线AB 的极坐标方程为θ＝θ1.A (ρ1，θ1)，B (ρ2，θ1＋π)，ρ1＝31－2cos θ1，ρ2＝31－2cos θ1＋π＝31＋2cos θ1.|AB |＝|ρ1＋ρ2|＝⎪⎪⎪⎪31－2cos θ1＋31＋2cos θ1＝⎪⎪⎪⎪61－4cos 2θ1，∴11－4cos 2θ1＝±1，∴cos θ1＝0或cos θ1＝±22 故直线AB 的极坐标方程为θ＝π2，θ＝π4或θ＝3π4.。

2024年中考化学答题技巧与模板构建专题01 质量守恒定律的应用(解析版)

专题01质量守恒定律的应用｜｜｜一、关于密闭容器中化学反应的数据分析二、有关质量守恒定律的微观反应示意图步骤具体方法①观察反应前后是否有相同的分子，若有则消除相同数目的同种分子；若无则省去此步②根据图注分别写出反应前后各物质的化学式，并配平方程式(如图注没给出原子的图示符号，可直接用物质的图示符号配平)③根据书写的化学方程式进行逐项判断正误三、运用质量守恒定律推断化学式或元素组成步骤具体方法①观察反应方程式，锁定“未知”物质X②推断化学式根据质量守恒定律，反应前后元素的种类、原子的数目均不改变，由此确定出未知物质的组成(或化学式)。

确定元素组成根据已知的反应物和生成物的质量进行计算③根据推断或计算进行逐项正误判断｜｜｜1.质量守恒定律只适用于化学变化，而不适用于物理变化。

2.质量守恒是物质的“质量”守恒，而非“体积”守恒。

3.“质量总和”是把各种状态的反应物与生成物都计算在内。

4.“参加”是指实际参加化学反应的反应物，不包括剩余的反应物和杂质。

5.在探究质量守恒定律时，尽量选用没有气体参加或生成的反应,若选用有气体参加或生成的反应,需在密闭容器中进行。

题型一密闭容器中化学反应的数据分析【例1】（2023·湖南郴州·中考真题）一定条件下，在密闭容器中发生某化学反应，测得反应过程中各物质的质量数据如下表：物质甲乙丙丁反应前的质量/g101602反应中的质量/g78a2反应后的质量/g b022c下列选项正确的是A．a=11B．丁一定是催化剂C．该反应为分解反应D．b=3模板应用步骤具体方法过程①确定待测质量“a”的值：根据反应前物质的质量总和=反应后物质的质量总和（或反应前各种物质的质量减少=反应后各种物质的质量增加）10g+16g+0g+2g=7g+8g+ag+2g=bg+0g+22g+cga=11可判断A正确b+c=6丁的质量随着反应的进行，没有发生改变，故c=2，b=6-2=4可判断D错误②判断反应物和生成物：计算表格中反应前后各物质质量变化(反应后－反应前)，(结果负值为反应物；结果正值为生成物；结果为0可能是催化剂，也可能是与反应无关的物质或杂质)甲：质量减少了10g-4g=6g，故甲是反应物，乙：质量减少了16g-0g=16g，故乙是反应物丙：质量增加了22g-0g=22g，故丙是生成物丁：质量随着反应的进行，没有发生改变，故丁可能是该反应的催化剂，也可能没有参与反应可判断B错误③写出反应的符号表达式，确定反应类型甲＋乙→丙化合反应可判断C错误【答案】A【解析】由于该反应在密闭容器内进行，根据质量守恒定律，则有10g+16g+0g+2g=7g+8g+ag+2g=bg+0g+22g+cg，解得a=11，b+c=6，由表中数据可知，丁的质量随着反应的进行，没有发生改变，所以丁可能是该反应的催化剂，也可能没有参与反应，故c=2，所以b=6-2=4。

中考数学复习考点知识归类讲解与练习01 平面直角坐标系与函数基本概念

中考数学复习考点知识归类讲解与练习专题01 平面直角坐标系与函数基本概念知识对接考点一、平面直角坐标系1．相关概念（1）平面直角坐标系（2）象限（3）点的坐标2.各象限内点的坐标的符号特征3.特殊位置点的坐标（1）坐标轴上的点（2）一三或二四象限角平分线上的点的坐标（3）平行于坐标轴的直线上的点的坐标（4）关于x轴、y轴、原点对称的点的坐标4.距离（1）平面上一点到x轴、y轴、原点的距离（2）坐标轴或平行于坐标轴的直线上两点间的距离（3）平面上任意两点间的距离5.坐标方法的简单应用（1）利用坐标表示地理位置（2）利用坐标表示平移1 / 27要点补充：点P(x,y)到坐标轴及原点的距离：（1）点P(x,y)到x 轴的距离等于；（2）点P(x,y)到y 轴的距离等于；（3）点P(x,y)到原点的距离等于.考点二、函数及其图象1.变量与常量2.函数的概念3.函数的自变量的取值范围4.函数值5.函数的表示方法（解析法、列表法、图象法）6.函数图象要点补充：由函数解析式画其图像的一般步骤：（1）列表：列表给出自变量与函数的一些对应值；（2）描点：以表中每对对应值为坐标，在坐标平面内描出相应的点；（3）连线：按照自变量由小到大的顺序，把所描各点用平滑的曲线连接起来.专项训练一、单选题1．已知点P （a ，a+3）在第二象限，且点P 到x 轴的距离为2，则a 的值为（）A ．1-B ．5-C ．2-D ．2y x 22y x +【答案】A【分析】先判断a的取值，进而根据点P到x轴的距离为2得到a+3=2，解得即可．【详解】解：∵点P（a，a+3）在第二象限，∴30aa<⎧⎨+>⎩，∴-3＜a＜0，∵点P到x轴的距离为2，∴|a+3|=2，∴a+3=2，∴a=-1，故选：A．【点睛】本题考查了各象限内点的坐标的符号特征以及解不等式，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．2．在平面直角坐标系中，点P（3，4）关于y轴对称点的坐标为（）A．（﹣3，4）B．（3，4）C．（﹣3，﹣4）D．（4，﹣3）【答案】A【分析】根据关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变可得答案．【详解】3 / 27解：点P （3，4）关于y 轴对称点的坐标为（－3，4），故选：A ．【点睛】此题主要考查了关于y 轴对称点的坐标，关键是掌握点的坐标的变化规律．3．如图，一个机器人从点O 出发，向正西方向走2m 到达点1A ；再向正北方向走4m 到达点2A ，再向正东方向走6m 到达点3A ，再向正南方向走8m 到达点4A ，再向正西方向走10m 到达点5A ，…按如此规律走下去，当机器人走到点20A 时，点20A 的坐标为（）A ．(20,20)-B ．(20,20)C ．(22,20)--D ．(22,22)-【答案】A【分析】先求出A 1，A 2，A 3，…A 8，发现规律，根据规律求出A 20的坐标即可．【详解】解：∵一个机器人从点O 出发，向正西方向走2m 到达点1A ，点A 1在x 轴的负半轴上，∴A 1（-2,0）从点A 2开始，由点1A 再向正北方向走4m 到达点2A ，A 2（-2,4），由点2A 再向正东方向走6m 到达点3A ，A 3（6-2，4）即（4，4），由点3A 再向正南方向走8m 到达点4A ，A 4（4，4-8）即（4，-4），由点A 4再向正西方向走10m 到达点5A ，A 5（4-10，-4）即（-6，-4），由点A 5再向正北方向走12m 到达点A 6，A 6（-6，12-4）即（-6，8），5 / 27由点A 6再向再向正东方向走14m 到达点A 7，A 7（14-6，8）即（8，8），由点A 7再向正南方向走16m 到达点8A ，A 8（8，8-16）即（8，-8），观察图象可知，下标为偶数时在二四象限，下标为奇数时（除1外）在一三象限，下标被4整除在第四象限．且横坐标与下标相同，因为2054=⨯，所以20A 在第四象限，坐标为(20,20)-．故选择A ．【点睛】本题考查平面直角坐标系点的坐标规律问题，掌握求点的坐标方法与过程，利用下标与坐标的关系找出规律是解题关键．4．小娜驾车从哈尔滨到大庆．设她出发第x min 时的速度为y km/h ，图中的折线表示她在整个驾车过程中y 与x 之间的函数关系式．下列说法：（1）在77≤x ≤88时，小娜在休息；（2）小娜驾车的最高速度是120km/h ；（3）小娜出发第16.5min 时的速度为48km/h ；（4）如果汽车每行驶100km 耗油10升，那么小娜驾车在33≤x ≤66时耗油6.6升．其中正确的个数是（）A ．1个B ．2个C ．3个D ．4个【答案】C【分析】根据函数图象对每个选项进行分析判断，最后得出结论．①观察图象在77≤x ≤88时，小娜在以时速96千米在行驶；②观察图象小娜的最高时速为120千米；③用待定系数法求出11≤x ≤22时的函数关系式，可求小娜出发第16.5min 时的速度；④小娜驾车在33≤x ≤66时时速为120千米/小时，依次求出小娜驾车在33≤x ≤66时行驶的路程，从而耗油量可求．【详解】解：①观察图象在77≤x ≤88时，小娜在以时速96千米在行驶；故①错误； ②观察图象小娜的最高时速为120千米，故②正确；③在11≤x ≤22时，设y ＝kx +b ．将（11，24）和（22，72）代入上式：11242272k b k b +=⎧⎨+=⎩，解得：481124k b ⎧=⎪⎨⎪=-⎩． ∴482411y x =-．当x ＝16.5min 时，y ＝48．∴小娜出发第16.5min 时的速度为48km /h ．故③正确；④由图象可知：小娜驾车在33≤x ≤66时时速为120千米/小时，∴车在33≤x ≤66时小娜行驶了66331206660-⨯=（千米）． ∴耗油为：66×10100＝6.6（升）．7 / 27故④正确；综上，正确的有②③④共三个．故选：C ．【点睛】本题主要考查了一次函数的应用．理解函数图象上的点的实际意义是解题的关键．另外待定系数法是确定函数解析式的重要方法．5．下列不能表示y 是x 的函数的是（）A ．B ．21y x =+C ．D ．【答案】C【分析】根据函数的定义（给定一个x 值都有唯一确定的y 值与它对应），对选项逐个判断即可．【详解】解：根据函数的定义（给定一个x 值都有唯一确定的y 值与它对应），对选项逐个判断， A ：观察列表数据发现，符合函数的定义，不符合题意；B ：观察x 与y 的等式发现，符合函数的定义，不符合题意；C ：观察函数图像发现，不符合函数的定义，符合题意；D ：观察函数图像发现，符合函数的定义，不符合题意；故选：C ．【点睛】此题主要考查了函数的定义，涉及到了函数的表示方法（解析法，图像法和列表法），熟练掌握函数的基础知识是解题的关键．x的函数的是（）6．下列各图象中，y不是．．A．B．C．D．【答案】B【分析】对于自变量x的每一个确定的值y都有唯一的确定值与其对应，则y是x的函数，根据函数的定义解答即可.【详解】根据函数的定义，选项A、C、D图象表示y是x的函数，B图象中对于x的一个值y有两个值对应，故B中y不是x的函数，故选：B.【点睛】此题考查函数的定义，函数图象，结合函数图象正确理解函数的定义是解题的关键.9 / 277．如图，在平面直角坐标系中，//AB DC ，AC BC ⊥，5CD AD ==，6AC =，将四边形ABCD向左平移m 个单位后，点B 恰好和原点O 重合，则m 的值是（）A ．11.4B ．11.6C ．12.4D ．12.6【答案】A【分析】由题意可得，m 的值就是线段OB 的长度，过点D 作DE AC ⊥，过点C 作CF OB ⊥，根据勾股定理求得DE 的长度，再根据三角形相似求得BF ，矩形的性质得到OF ，即可求解．【详解】解：由题意可得，m 的值就是线段OB 的长度，过点D 作DE AC ⊥，过点C 作CF OB ⊥，如下图：∵5CD AD ==，DE AC ⊥ ∴132CE AC ==，90DEC ∠=︒由勾股定理得4DE =∵//AB DC∴DCE BAC ∠=∠，90ODC BOD ∠=∠=︒又∵AC BC⊥∴90 ACB CED∠=∠=︒∴DEC BCA△∽△∴DE CE CDBC AC AB==，即4356BC AB==解得8BC=，10AB=∵CF OB⊥∴90 ACB BFC∠=∠=︒∴BCF BAC∽△△∴BC BFAB BC=，即8108BF=解得 6.4BF=由题意可知四边形OFCD为矩形，∴5OF CD==11.4OB BF OF=+=故选A【点睛】此题考查了相似三角形的判定与性质，图形的平移，矩形的判定与性质，勾股定理等，熟练掌握相关基本性质是解题的关键．8．在平面直角坐标系中，已知点A(0，0)、B(2，2)、C(3，0)，若以点A、B、C、D为顶点的四边形是平行四边形，则点D的坐标不可能为（）A．(﹣1，2) B．(5，2) C．(1，﹣2) D．(2，﹣2)【答案】D【分析】分三种情况：①BC为对角线时，②AB为对角线时，③AC为对角线时；由平行四边形的11 / 27性质容易得出点D 的坐标．【详解】解：分三种情况：①BC 为对角线时，点D 的坐标为（5，2） ②AB 为对角线时，点D 的坐标为（﹣1，2）， ③AC 为对角线时，点D 的坐标为（1，﹣2），综上所述，点D 的坐标可能是（5，2）或（﹣1，2）或（1，﹣2）．故选：D ．【点睛】本题考查了平行四边形的性质、坐标与图形的性质；熟练掌握平行四边形的性质是解决问题的关键．9．半径是R 的圆的周长C 2R π=，下列说法正确的是（） A ．C ，π，R 是变量，2是常量 B ．C 是变量，2，π，R 是常量 C ．R 是变量，2，π，C 是常量 D ．C ，R 是变量，2π是常量【答案】D 【分析】根据变量和常量的概念解答即可．【详解】解：在半径是R 的圆的周长2C R π=中，C ，R 是变量，2π是常量．故选D ．【点睛】本题主要考查了变量和常量，在一个变化的过程中，数值发生变化的量称为变量；数值始终不变的量称为常量．10．关于变量x ，y 有如下关系：①6-=x y ；②24y x =；③2y x =；④3y x =．其中y 是x 函数的是（） A ．①③ B ．①②③④ C ．①③④ D ．①②③【答案】C 【分析】根据函数的定义可知，满足对于x 的每一个取值，y 都有唯一确定的值与之对应关系，据此即可确定函数的个数．【详解】解：y 是x 函数的是①x -y =6；③y =2|x |；④3y x =； ∵x =1时，y =±2，∴对于y 2=4x ，y 不是x 的函数；故选：C ．【点睛】本题考查了函数的定义，函数的定义：在一个变化过程中，有两个变量x ，y ，对于x 的每一个取值，y 都有唯一确定的值与之对应，则y 是x 的函数，x 叫自变量．二、填空题11．若点()25,4P a a --到两坐标轴的距离相等，则点P 的坐标是______．【答案】()1,1或()3,3-；【分析】根据题意可得关于a 的绝对值方程，解方程可得a 的值，进一步即得答案. 【详解】解：∵P (2a -5，4-a )到两坐标轴的距离相等， ∴254a a -=-.13 / 27∴254a a -=-或25(4)a a -=--，解得3a =或1a =，当3a =时，P 点坐标为（1，1）；当1a =时，P 点坐标为（-3，3）．故答案为：（1，1）或（-3，3）．【点睛】本题考查了直角坐标系中点的坐标特征，根据题意列出方程是解题的关键.12．在平行四边形ABCD 中，点A 的坐标是（﹣1，0），点B 的坐标是（2，3），点D 的坐标是（3，1），则点C 的坐标是___．【答案】（6，4）．【分析】根据四边形ABCD 是平行四边形，可得AB∥DC ，且AB =DC ，根据坐标间关系可得2-（-1）=x C -3，3-0=y C -1，解得x C =6，y C =4即可．【详解】解：∵四边形ABCD 是平行四边形， ∴AB∥DC ，且AB =DC ， ∴2-（-1）=x C -3，3-0=y C -1， ∴x C =6，y C =4，点C （6，4）故答案为（6，4）．【点睛】本题考查平行四边形的性质，点的坐标关系建构方程，掌握平行四边形的性质，点的坐标关系建构方程．13．函数y＝182xx+-的自变量的取值范围是______．【答案】x≠4【分析】当表达式的分母中含有自变量时，自变量取值要使分母不为零，据此可得结论．【详解】解：由题可得，8﹣2x为分母，8﹣2x≠0，解得x≠4，∴函数182xyx+=-的自变量的取值范围是x≠4，故答案为：x≠4．【点睛】本题考查的是自变量的取值范围，由于此题表达式为分式，根据分式有意义的条件，分母不为零，得到自变量的取值范围．14．若一个函数图象经过点A（1，3），B（3，1），则关于此函数的说法：①该函数可能是一次函数；②点P（2，2.5），Q（2，3.5）不可能同时在该函数图象上；15 / 27③函数值y 一定随自变量x 的增大而减小；④可能存在自变量x 的某个取值范围，在这个范围内函数值y 随自变量x 增大而增大．所有正确结论的序号是 ___．【答案】①②④ 【分析】根据函数的定义，一次函数的图象及函数的性质一一分析即可求解．【详解】解：①因为一次函数的图象是一条直线，由两点确定一条直线，故该函数可能是一次函数，故正确；②由函数的定义：在一个变化过程中，有两个变量x ，y ，对于x 的每一个取值，y 都有唯一确定的值与之对应，则y 是x 的函数，x 叫自变量，所以点P （2，2.5），Q （2，3.5）不可能同时在该函数图象上，故正确；③因为函数关系不确定，所以函数值y 不一定一直随自变量x 的增大而减小，故错误； ④可能存在自变量x 的某个取值范围，在这个范围内函数值y 随自变量x 增大而增大，故正确；故答案为①②④．【点睛】本题主要考查函数的定义及一次函数的图象与性质，熟练掌握函数的定义及一次函数的图象与性质是解题的关键．15．在圆周长公式2C r π=中，常量是__________．【答案】2π 【分析】根据常量的定义即可解答．【详解】解：圆周长公式2C r π=中，常量是2π，故答案为：2π．【点睛】本题考查了常量的定义，正确理解定义是关键．16．如图，平面直角坐标系中O 是原点，等边△OAB 的顶点A 的坐标是（2，0），点P 以每秒1个单位长度的速度，沿O →A →B →O →A …的路线作循环运动，点P 的坐标是__________________．【答案】12⎛ ⎝⎭【分析】计算前面7秒结束时的各点坐标，得出规律，再按规律进行解答便可．【详解】解：由题意得，第1秒结束时P 点运动到了线段OA 的中点C 的位置，所以P 1的坐标为P 1（1，0）；第2秒结束时P 点运动到了点A 的位置，所以P 2的坐标为P 2（2，0）；第3秒结束时P 点运动到了线段AB 的中点D 的位置，如下图所示，过D点作x轴的垂线交于x2处，∵△OAB是等边三角形，且OA=2，∴在Rt△AD x2中，∠DA x2=60°，AD=1，∴21 2Ax=，2Dx=故D点的坐标为32⎛⎝⎭，即P332⎛⎝⎭;第4秒结束时P点运动到了点B的位置，同理过B点向x轴作垂线恰好交于点C，在Rt△OBC中，∠BOC =60°，2OB=，1OC=,BC故B点的坐标为（1，即P4（1；第5秒结束时P点运动到了线段OB的中点E的位置，根据点D即可得出E点的坐标为12⎛⎝⎭，即 P512⎛⎝⎭；第6秒结束时运动到了点O的位置，所以P6的坐标为P6（0，0）；第7秒结束时P点的坐标为P7（1，0），与P1相同；……17 / 27由上可知，P 点的坐标按每6秒进行循环， ∵2021÷8＝336……5，∴第2021秒结束后，点P 的坐标与P 5相同为12⎛ ⎝⎭，故答案为：12⎛ ⎝⎭．【点睛】本题主要考查了点的坐标特征，等边三角形的性质，数字规律，关键是求出前面几个点坐标，得出规律．17．平面直角坐标系中，点()5,3A -，()0,3B ，()5,0C -，在y 轴左侧一点(),P a b （0b ≠且点P 不在直线AB 上）．若40APO ∠=︒，BAP ∠与COP ∠的角平分线所在直线交于D 点．则ADO ∠的度数为______°．【答案】110或70 【分析】分两种情况，①点P 在AO 下方，设AP 与CO 交于点N ，过点N 作//NM AD ，先证明NM 平分PNO ∠，根据“三角形两内角平分线的夹角与第三个角的关系”，可以得出1902NMO P ∠=+∠，即可求解；②点P 在AO 上方，设PO 与AB 交于点M，过点M 作//NM OD ，先证明NM 平分PNA ∠，根据“三角形两内角平分线的夹角与第三个角的关系”，可以得出1902NMA P ∠=+∠，即可求解．【详解】19 / 27解：分两种情况， ①点P 在AO 下方时，设AP 与CO 交于点N ，过点N 作//NM AD ，PAD PNM ∴∠=∠， //AB NO ， BAN ONP ∴∠=∠，AD 平分BAN ∠，12PAD BAN ∴∠=∠，12PNM ONP ∴∠=∠，NM∴平分ONP ∠，OM 平分NOP ∠，111(180)70222MNO NOM ONP PON NPO ∴∠+∠=∠+∠=-∠=︒，110NMO ∴∠=︒， //NM AD ，110ADO NMO ∴∠=∠=︒；①点P 在AO 上方时，设AB 与PO 交于点N ，过点N 作//NM OD ，POD PNM ∴∠=∠，//AB CO ，PNA POC ∴∠=∠，DO 平分POC ∠，12POD POC ∴∠=∠，12PNM PNA ∴∠=∠，NM∴平分ANP ∠，直线CD 平分NAP ∠，111(180)70222MNA NAM PNA PAN NPA ∴∠+∠=∠+∠=-∠=︒，110NMA ∴∠=︒， //NM AD ，18070ADO NMO ∴∠=-∠=， 70ADO ∴∠=︒或110︒．故答案为：70或110．【点睛】本题主要考查了三角形双内角平分线模型，平行线的性质，解题的关键是找基本模型． 18．一个三角形的底边长是3，高x 可以任意伸缩，面积为y ，y 随x 的变化变化，则其中的常量为________，y 随x 变化的解析式为______________．【答案】3 32y x = 【分析】先根据变量与常量的定义，得到3为常量，x 和y 为变量，再根据三角形面积公式得到21 / 27y =12×3×x =32x （x ＞0），【详解】解：数值发生变化的量为变量，数值始终不变的量为常量，因此常量为底边长3，由三角形的面积公式得y 随x 变化的解析式为32y x =．故答案为：3；32y x =. 【点睛】本题考查主要函数关系式中的变量与常量和列函数关系式解决本题的关键是要理解函数关系中常量和变量．三、解答题19．已知一个圆柱的底面半径是3cm ，当圆柱的高(cm)h 变化时，圆柱的体积()3cm V 也随之变化．（1）在这个变化过程变量h 、V 中，自变量是______，因变量是______；（2）在这个变化过程中，写出圆柱的体积V 与高h 之间的关系式；（3）当圆柱的高h 由3cm 变化到6cm 时，圆柱的体积V 由______变化到______．【答案】（1）h ，V ；（2）9V h π=；（3）327cm π，354cm π 【分析】（1）利用函数的概念进行回答；（2）利用圆柱的体积公式求解；（3）分别计算出h ＝3和6对应的函数值可得到V 的变化情况．【详解】解：（1）在这个变化过程中，自变量是h ，因变量是V ；故答案为h ，V ；（2）V ＝π•32•h ＝9πh ；（3）当h ＝3cm 时，V ＝27πcm 3；当h ＝6cm 时，V ＝54πcm 3；所以当h 由3cm 变化到6cm 时，V 是由27πcm 3变化到54πcm 3．故答案为：27πcm3；54πcm3．【点睛】本题考查了函数关系式：用来表示函数关系的等式叫做函数解析式，也称为函数关系式．函数解析式是等式．解决此题的关键是圆柱的体积公式．20．一辆大客车和一辆小轿车同时从甲地出发去乙地，匀速而行，大客车到达乙地后停止，小轿车到达乙地后停留4小时，再按照原速从乙地出发返回甲地，小轿车返回甲地后停止，已知两车距甲地的路程s千米与所用的时间t小时的关系如图所示，请结合图象解答下列问题：（1）在上述变化过程中，自变量是________；因变量是________；（2）小轿车的速度是________km/h，大客车的速度是________ km/h；（3）两车出发多少小时后两车相遇，两车相遇时，距离甲地的路程是多少？【答案】（1）t，s；（2）50，30；（3）15小时，450km【分析】（1）根据函数图像可得；（2）根据函数图象中的数据，可以计算出小轿车和大客车的速度；（3）设两车出发xh时，两车相遇，根据题意列出方程，解之可得x，再乘以大客车的速度可得到甲地的距离．【详解】解：（1）自变量是时间t；因变量是路程s；（2）由图象可得，小轿车的速度为：500÷10=50（km/h），大客车的速度为：500÷503=30（km/h），故答案为：50，30；（3）设两车出发x小时，两车相遇，30x+50（x-14）=500，解得，x=15，30x=30×15=450，即两车出发15h后两车相遇，两车相遇时，距离甲地的路程是450km，故答案为：15，450．【点睛】本题考查了从函数图像获取信息，一元一次方程的应用，解答本题的关键是明确题意，结合函数图像得到必要信息．21．在平面直角坐标系中，O为坐标原点，C（4，0），A（a，3），B（a＋4，3）（1）求ΔOAC的面积；（2）若aOABC是菱形．【答案】（1）6；（2）见解析【分析】（1）过点A（a，3）作AE⊥x轴于点E，根据A（a，3），C（4，0）求出AE和OC的长度，23 / 27然后根据三角形面积公式求解即可；（2）首先根据点A 和点B 的纵坐标相同得到//AB OC ，然后结合AB OC =得到四边形OABC 是平行四边形，然后根据勾股定理求出OA 的长度，得到OA =OB ，根据菱形的判定定理即可证明．【详解】解：（1）如图所示，过点A （a ，3）作AE ⊥x 轴于点E ，则AE =3，又∵C （4，0）， ∴OC =4，∴S △OAC =11=43622OC AE ⨯⨯⨯⨯=．（2）若a =)A ，)43B ，， ∵A B y y =， ∴//AB OC ， ∵44AB OC ==，， ∴AB OC =．∴四边形OABC 是平行四边形，过点A 作AE ⊥x 轴，则90AEO ∠=︒，3AE OE ==，∴4OA =，∴OA AB=，∴四边形OABC是菱形．【点睛】此题考查了三角形面积的求法，菱形的判定，解题的关键是根据题意找到坐标和线段的关系．22．定义：平面直角坐标系中，点M（a，b）和点N（m，n）的距离为MN，例如：点（3，2）和（4，0（1）在平面直角坐标系中，点（2，5-）和点（2，1）的距离是，点（72，3）和点（12，1-）的距离是；（2）在平面直角坐标系中，已知点M（2-，4）和N（6，3-），将线段MN平移到M ′ N′，点M的对应点是M′，点N的对应点是N′，若M′的坐标是（8-，m），且MM′=10，求点N′的坐标；（3）在平面直角坐标系中，已知点A在x轴上，点B在y轴上，点C的坐标是（12，5），若BC=13，且△ABC的面积是20，直接写出点A的坐标．【答案】（1）6，5；（2）当M′（-8，12）时，N′（0，5），当M′（-8，-4）时，N′（0，-11）；（3）（8，0）或（-8，0）或（16，0）或（32，0）【分析】（1）分别利用两点间距离公式求解即可．（2）构建方程求出m的值，可得结论．（3）设(0,)B t，构建方程求出t的值，可得结论．【详解】解：（1）点(2,5)-和点(2,1)的距离6，25 / 27点7(2，3)和点1(2，1)-的距离5=，故答案为：6，5．（2）由题意，10MM '=，∴10=，12m =∴或4-，(8,12)M ∴'-或(8,4)--，当(8,12)M '-时，(0,5)N '，当(8,4)M '--时，(0,11)N '-．（3）设(0,)B t ，(12,5)C ，13BC =，∴13，解得0t =或10，(0,0)B ∴或(0,10)，当(0,0)B 时，20ABC S ∆=，∴15202OA ⨯⨯=， 8OA ∴=，(8,0)A ∴或(8,0)-．当(0,10)B 时，20ABC BOC AOC AOB S S S S ∆∆∆∆=+-=或20ABC AOC AOB BOC S S S S ∆∆∆∆=--=，∴111101*********OA OA ⨯⨯+⨯⨯-⨯⨯=或111101012520222OA OA ⨯⨯-⨯⨯-⨯⨯=，16OA ∴=或32，∴或(32,0)，A(16,0)综上所述，满足条件的点A的坐标为(8,0)或(8,0)-或(16,0)或(32,0)．【点睛】本题属于三角形综合题，考查了两点间距离公式，三角形的面积等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．27 / 27。

压轴题每周一练1(答案)

专题01压轴题每周一练1．已知直线l 与曲线()xf x e =和()lng x x =分别相切于点()11,A x y ，()22,B x y .有以下命题：①90AOB ∠>︒（O 为原点）；②()11,1x ∈-；③当10x <时，)2121x x ->，则正确命题的个数为（）A ．0B ．1C ．2D ．3【答案】C【思路引导】根据AB 为公切线可得1x 满足的方程，根据该方程及12,x x 的关系可以判断②③正确与否，再由OA OB u u u r u u u rg 的符号可判断90AOB ∠>︒是否成立.【解析】因为AB 为公切线，故11221221ln 1x x e x e x x x x ⎧=⎪⎪⎨-⎪=⎪-⎩，故21ln x x =-，所以11111x x x e x e x e -+=-，整理得到11111x x e x +=-. 因为11110,01x x e x +>∴>-，故11x >或11x <-，故②错误. 又1211x x x ex --=-，当1x <-时，令()12111xx x g x e e x x +=-=----，则()()2201xg x e x '=+>-，故()g x 在(),1-∞-上为增函数，而()21203g e --=-<,323125g e -⎛⎫-=- ⎪⎝⎭，因为2.5 2.8e <<，故315.62521.952e <<，故325e <，故325e <即3215e->，故302g ⎛⎫-> ⎪⎝⎭，所以1322x -<<-，令()3,2,2xh x ex x -⎛⎫=-∈-- ⎪⎝⎭，则()10x h x e -'=--<，所以()h x 在32,2⎛⎫-- ⎪⎝⎭为单调减函数，所以()3233352222h x h e ⎛⎫>-=+>+> ⎪⎝⎭，故③成立.又()1111221ln x x x OA OB x x e x x e e -=+=-u u u r u u u r g ，如果11x <-，则0OA OB <u u u r u u u r g ；若11x >，则0OA OB <u u u r u u u rg ，所以90AOB ∠>︒，所以①成立，综上，①③成立，故选：C.2.已知双曲线C ：22221(0,0)x y a b a b-=>>，过其右焦点F 作渐近线的垂线，垂足为B ，交y 轴于点C ，交另一条渐近线于点A ，并且点C 位于点A ，B 之间.已知O 为原点，且53OA a =，则||||FA FC =（） A ．54B ．43C ．32D【答案】B【思路引导】设出右焦点F 的坐标和渐近线,OA OB 的方程，由点到直线的距离公式求得BF ，结合直角三角形勾股定理和三角函数的定义、两直线的夹角公式，求得,a b 的关系，由此求得,FA FC 的长，进而求得||||FA FC 【解析】双曲线22221x y a b-=的右焦点(),0F c ，渐近线OB 的方程为b y x a =，即0bx ay -=，渐近线OA 的方程为by x a=-，即0bx ay +=.所以bc BF b c ===，OB a ==，43a AB ==. 所以4tan 3AB AOB OB ∠==，而()tan tan tan tan 1tan tan AOF BOF AOB AOF BOF AOF BOF∠-∠∠=∠-∠=+∠⋅∠22431b ba ab a--===-，解得2b a =或12b a =-（舍去）.所以44102333a a aAF b a =+=+=.在Rt COF ∆中，由射影定理得2OF BF FC =⋅，所以222225522OFc a b a a FC BF b b a +=====，所以10||435||32aFA a FC ==.故选：B3.在如图所示的平面四边形ABCD 中，4AB =，30CAB ∠=o ，AC CB ⊥，120ADC ∠=o ，则22DA DC +的最小值为（）A ．4B ．8C ．D ．【答案】B 【思路引导】在ABC V 中由三角函数求出AC ，在ADC V 中由余弦定理得2212DA DC DA DC =++⋅，再由基本不等式可得222DA DC DA DC ≥+⋅即可求出22DA DC +的最小值.【解析】在ABC V 中，因为30CAB ∠=︒，AC CB ⊥，所以cos ACBAC AB∠=cos 4AC AB BAC ∴=⋅∠==在ADC V 中，因为120ADC =∠︒，所以由余弦定理得2222cos AC DA DC DA DC ADC =+-⋅⋅∠，即2212DA DC DA DC =++⋅，又由不等式的性质可知222DA DC DA DC ≥+⋅，即得222DA DC DA DC +⋅≤，所以()22223122DA DC DA DC DA DC =++⋅≤+，从而228DA DC ≥+，当且仅当2DA DC ==时等号成立.故选：B .4.已知椭圆2211612x y C +=：的左、右焦点分别为F 1，F 2，点P 在椭圆上且异于长轴端点．点M ，N 在△PF 1F 2所围区域之外，且始终满足10MP MF ⋅=u u u r u u u u r ，20NP NF ⋅=u u u r u u u u r，则|MN |的最大值为（） A ．6 B ．8 C ．12D ．14【答案】A 【思路引导】设1PF ，2PF 的中点分别为C ，D ，则M ，N 在分别以C ，D 为圆心的圆上，直线CD 与两圆的交点(△12PF F 所围区域之外）分别为M ，N 时，||MN 的最大，可得||MN 的最大值为122PF PF CD a c ++=+即可．【解析】设1PF ，2PF 的中点分别为C ，D ，Q 10MP MF =u u u r u u u u r g ，20NP NF =u u u r u u u u rg ，则M ，N 在分别以C ，D 为圆心的圆上，∴直线CD 与两圆的交点(△12PF F 所围区域之外）分别为M ，N 时，||MN 最大， ∴||MN 的最大值为124262PF PF CD a c ++=+=+=，故选：A ．5.四面体ABCD 中， 2,BC CD BD AB AD AC ======ABCD 外接球的表面积为__________. 【答案】12π【思路引导】根据题中提供的数据可以得出ABC ∆和ADC ∆为直角三角形，取AC 的中点为E ，可以得出BE DE ==AE CE ==【解析】取AC 的中点为E ，在ABC ∆中， 2,BC AB AC ===故222 BC AB AC +=，所以ABC ∆为直角三角形，同理可得ADC ∆为直角三角形，则能得到 BE DE ==同时AC =E 为中点，所以AE CE ==所以E ABCD 外接球的表面积为2412ππ=. 故答案为：12π6.已知点P 为双曲线()2222:10x y C a b a b-=>>右支上一点，双曲线C 的左，右焦点分别为1211,,60F F F PF ∠=o且12F PF ∠的角平分线与x 轴的交点为Q ，满足121233PQ PF PF =+u u u r u u u r u u u u r，则双曲线C 的离心率为__________．【思路引导】化简121233PQ PF PF =+u u u r u u u r u u u u r,得到得122FQ QF =，故122PF Q PF Q S S =V V ，结合三角形面积公式和双曲线的定义、余弦定理可以求出离心率. 【解析】由121233PQ PF PF =+u u u r u u u r u u u u r，得122FQ QF =，故122PF Q PF Q S S =V V ，再由12111sin 30,22PF Q PF Q S PF PQ S =⋅⋅=o V V 2sin30PF PQ o g g ，故122PF PF =，再根据双曲线定义知122PF PF a -=，即212,4PF a PF a ==，在12PF F △中，由余弦定理知222224164812c a a a a =+-=,故223c a =，即e =.7.已知抛物线2:2(0)C y mx m =>，焦点为(0,1)F ，定点(0,2)P -.若点M ，N 是抛物线C 上的两相异动点，M ，N 不关于y 轴对称，且满足0PM PN k k +=,则直线MN 恒过的定点的坐标为_________. 【答案】(0,2)【分析】利用抛物线的焦点坐标，求得抛物线方程，设出,M N 两点的坐标，根据0PM PN k k +=列方程，化简求得128x x =-.写出直线MN 的方程，进而判断直线过定点()0,2 【解析】抛物线C 的标准方程为22y x m =，焦点为10,8m ⎛⎫ ⎪⎝⎭，所以111,88m m ==，所以24x y =.设(221212,,,44x x M x N x ⎛⎫⎫ ⎪⎪⎝⎭⎭，则2212PM PN 1222440x x k k x x +++=+=，整理得()()121280x x x x ++=，由于,M N 不关于y 轴对称，所以恒有128x x =-，直线MN 的方程为()221121211124444x x x x x x x x y x x x ++-=-=+-，即121244x x x x y x +=-，即1224x xy x +=+即所以过定点(0,2). 故答案为：()0,28.在平行四边形ABCD 中，0AB BD ⋅=u u u r u u u r，沿BD 将四边形折起成直二面角A BD C --，且|2BD +=u u r u u u r，则三棱锥A BCD -的外接球的表面积为________________.【答案】4π 【思路引导】由0AB BD ⋅=u u u r u u u r得AB BD ⊥，结合直二面角A BD C --，可证AB ⊥平面BCD ，从而有AB BC ⊥，因此AC 中点O 就是外接球球心．由此可求得表面积．【解析】由0AB BD ⋅=u u u r u u u r得AB BD ⊥，又平面ABD ⊥平面BCD ，∴AB ⊥平面BDC ，∴AB BC ⊥，同理CD AD ⊥，取AC 中点O ，则O 到四顶点的距离相等，即为三棱锥A BCD -的外接球的球心．222222222AC CD AD CD BD AB AB BD =+=++=+，∵||2BD +=u u r u u u r ，∴222|2BD AB BD BD +=+⋅+u u r u u u r u u u r u u r u u u r u u u r 2224AB BD =+=，∴24AC =，2AC =，∴224()42S ππ=⨯=．故答案为：4π．9.设抛物线Γ的方程为22y px =，其中常数0p >，F 是抛物线Γ的焦点.（1）设A 是点F 关于顶点O 的对称点，P 是抛物线Γ上的动点，求||||PA PF 的最大值；（2）设2p =，1l ，2l 是两条互相垂直，且均经过点F 的直线，1l 与抛物线Γ交于点A ，B ，2l 与抛物线Γ交于点C ，D ，若点G 满足4FG FA FB FC FD =+++u u u r u u u r u u u r u u u r u u u r，求点G 的轨迹方程. 【思路引导】（1）求得A 的坐标，设出过A 的直线为y ＝k （x 2p+），k ＝tanα，联立抛物线方程，运用判别式为0，求得倾斜角，可得所求最大值；（2）求得F （1，0），设A （x 1，y 1），B （x 2，y 2），C （x 3，y 3），D （x 4，y 4），G （x ，y ），设l 1：y ＝k （x ﹣1），联立抛物线方程，运用韦达定理，以及两直线垂直的条件：斜率之积为﹣1，结合向量的坐标表示，以及消元，可得所求轨迹方程．【解析】（1）A 是点(,0)2p F 关于顶点O 的对称点，可得(,0)2pA -，设过A 的直线为()2py k x =+，tan k α=，联立抛物线方程可得22222(2)04k p k x k p p x +-+=，由直线和抛物线相切可得2242(2)0k p p k p ∆=--=，解得1k =±，可取1k =，可得切线的倾斜角为45°，由抛物线的定义可得||11||sin(90)cos PA PF αα︒==-，而α的最小值为45°， ||||PA PF ；（2）由24y x =，可得(1,0)F ，设11(,)A x y ，22(,)B x y ，33(,)C x y ，44(,)D x y ，()G x y ,，设1:(1)l y k x =-，联立抛物线24y x =，可得2222(24)0k x k x k -++=，即有12242x x k +=+，12124()2y y k x x k k +=+-=，由两直线垂直的条件，可将k 换为1k-，可得23424x x k +=+，344y y k +=-，点G 满足4FG FA FB FC FD =+++u u u r u u u r u u u r u u u r u u u r，可得123412344(1,)(4,)x y x x x x y y y y -=+++-+++，即为2123424444x x x x x k k =+++=++，1234444y y y y y k k=+++=-+，可得222211()23y k k x k k=-=+-=-，则G 的轨迹方程为23y x =-.10,设函数()2cos 2x f x x x =+-.（1）讨论()f x 在[],ππ-上的单调性；（2）证明：()f x 在R 上有三个零点. 【思路引导】（1）利用导数的正负可求函数的单调区间.（2）结合函数的单调性和零点存在定理可证明()f x 在[],ππ-上有3个零点，再构建新函数可证明()f x 在()(),,ππ-∞-+∞U 上没有零点. 【解析】（1）()sin sin 2f x x x x x x ⎛⎫'=+-=- ⎪ ⎪⎝⎭，由()0f x '=及[],x ππ∈-，得0x =或4π或34π. 当x 变化时，()f x '和()f x 的变化情况如下表：所以()f x 的单调递减区间为[),0π-，3,44ππ⎛⎫⎪⎝⎭；()f x 的单调递增区间为0,4π⎛⎫ ⎪⎝⎭，3,4ππ⎛⎤ ⎥⎝⎦.（2）当[],x ππ∈-时，由（1）得，()f x 的极小值分别为()00f =，230428f f πππ⎛⎫⎛⎫<=<⎪ ⎪⎝⎭⎝⎭；极大值()004f f π⎛⎫>= ⎪⎝⎭.又()202f ππ=>，所以()f x 在[],0π-上仅有一个零点0；在30,4π⎛⎫ ⎪⎝⎭，3,4ππ⎛⎤⎥⎝⎦上各有一个零点.当x π<-时，()22xf x x ≥-，令()22x g x x =-，则()g x x x '=，显然3,2x ππ⎛⎫∈-- ⎪⎝⎭时，()g x '单调递增，()()0g x g ππ''<-=<；当3,2x π⎛⎤∈-∞-⎥⎝⎦时，()302g x π'≤-+<，从而x π<-时，()0g x '<，()g x 单调递减，因此()()202g x g ππ>-=>，即()()0f x g x ≥>，所以()f x 在(),π-∞-上没有零点.当x π>时，()22x f x x ≥-，令()22xh x x =，则()h x x x '=，显然3,2x ππ⎛⎫∈ ⎪⎝⎭时，0x >，()0h x '>；当3,2x π⎡⎫∈+∞⎪⎢⎣⎭时，()302h x π'≥->，从而x π>时，()0h x '>，()h x 单调递增，因此()()202h x h ππ>=>，即()()0f x h x ≥>，所以()f x 在(),π+∞上没有零点.故()f x 在R 上仅有三个零点.11.已知椭圆2222:1(0)x y E a b a b +=>>过椭圆E 的左焦点1F 且与x 轴垂直的直线与椭圆E 相交于的P ，Q 两点，O 为坐标原点，OPQ △（1）求椭圆E 的方程；（2）点M ，N 为椭圆E 上不同两点，若22OM ON b k k a⋅=-，求证：OMN V的面积为定值. 【思路引导】（1）离心率提供一个等式2c a =，PQ是椭圆的通径，通径长为22b a ，这样OPQ ∆的面积又提供一个等式2122b c a ⨯⨯=222a b c =+，可求得,a b 得椭圆标准方程．（2）设()()1122,,,M x y N x y ，由2214OM ONb k k a ⋅=-=-得12124x x y y =-，当直线MN 的斜率存在时，设直线MN 的方程为,(0)y kx m m =+≠，代入椭圆方程并整理，得()222148440kxkmx m +++-=.应用韦达定理得1212,x x x x +，代入12124x x y y =-可得,k m 的关系，注意>0∆，然后由圆锥曲线中的弦长公式计算弦长MN ，求出O 到直线MN 的距离，求得OMN ∆的面积，化简可得为定值，同样直线MN 的不斜率存在时，也求得OMN ∆的面积和刚才一样，即得结论．【解析】（1）设椭圆的半焦距为c，则c a =过椭圆左焦点1F 且与x 轴垂直的直线方程为x c =-，与椭圆方程联立解得2by a=±，所以22||b PQ a =，所以21222b c a ⨯⨯=② 把①代入②，解得21b =又2222234c a b a a -==，解得24a = 所以E 的方程为：2214x y +=（2）设()()1122,,,M x y N x y ，因为24a =，21b =，所以2214OM ONb k k a ⋅=-=-，即121214y y x x ⋅=-，即12124x x y y =-（i ）当直线MN 的斜率存在时，设直线MN 的方程为,(0)y kx m m =+≠，代入椭圆方程并整理，得()222148440k xkmx m +++-=.则122814km x x k +=-+，21224414m x x k-=+ ()()()22222(8)414441614km k m k m ∆=-+-=+-③()()()2222121212122414k m y y kx m kx m k x x km x x m k -+=++=+++=+ 所以2222244441414m k m k k--+=-⨯++，整理得22142k m +=，代入③，2160m ∆=>||MN == O 到直线MN 的距离d =所以OMN 1||||2S MN d m ∆=⋅==22||||||12m m m m m==⋅=，即OMN V 的面积为定值1 （ii ）当直线MN 的斜率不存在时，不妨设OM 的斜率为12且点M 在第一象限，此时OM 的方程为12yx =，代入椭圆方程，解得M ⎭，此时OMN V的面积为1212⎛= ⎝⎭. 综上可知，OMN V 的面积为定值1. 12.已知函数()()()4ln 1,12x a f x ax g x a R x=-+=-∈ (1)讨论函数()f x 的单调性;(2)设0a >,当函数()f x 与()g x 的图象有三个不同的交点时,求实数a 的取值范围.【思路引导】(1)对函数()f x 求导,根据a 的不同取值,结合不等式,可以判断出函数的单调性;(2)由题意可知：()()f x g x =,得4ln112x a ax x -+=-.得4ln 02x a ax x -+=, 设()4ln 2x a h x ax x=-+,则()()f x g x =有三个不同的根等价于函数()h x 存在三个不同的零点.对函数()h x 进行求导,然后判断出其单调性,结合零点存在原理,最后求出实数a 的取值范围.【解析】(1)()ln 12x f x x a =-+的定义域是()0,∞+,()2111'2ax f x a a x x x-=-=-=g , 当0a ≤时.()0.f x >两数()f x 在(0. )+∞上单调递增;当0a >时,令()'0f x >,得10x a <<;令()'0f x <,得1x a>. 故函数()f x 在10,a ⎛⎫ ⎪⎝⎭上单调递增,在1,a ⎛⎫+∞⎪⎝⎭上单洞递破. (2)由()()f x g x =，得4ln112x a ax x -+=-.得4ln 02x a ax x -+=, 设()4ln 2x a h x ax x=-+，则()()f x g x =有三个不同的根等价于函数()h x 存在三个不同的零点. ()()222144'0a ax x a h x a x x x x-+-=--=>, 当21 160.a =-≤V 即14a ≥时,()'0h x ≤，()h x 单调递减,不可能有三个不同的零点, 当21 160.a =->V 即104a <<，()24k x ax x a =-+-有两个零点10x =>, 20x =>, 又()24k x ax x a =-+-开口向下，当10x x <<时,()0,'(0)k x h x <<,函数()h x 在()10,x 上单调递诫:当12x x x <<时.()()0,'0.k x h x >>函数()h x 在()12x x +上单调递增:当2x x >时.()()0,'0k x h x <<,函数()h x 在2(,)x +∞上单调递减.因为()242ln 2022a h a =-+=，又124x x =，有122x x <<, 所以()()()1220.h x x h h <=<2222211141ln ln 2412a h a a a a a a a a ⎛⎫=-+=--+ ⎪⎝⎭g , 令()221124m a a a a =--+.则()222222411221' 12122a a a m a a a a a a -+=-++==. 令()412 21n a a a =-+.则()2'482n a a --单调递增.由()2'4820n a a =-=,求得14n a =>, 当104a <<时，()n a 单调递减，()3121140641n a n >=⎛⎫ ⨯⎪⎭+⎝->.，显然在()22113ln 2401416h m a m a ⎛⎫===-+< ⎪⎝⎭⎛⎫ ⎪⎝⎭上单调递增，故()22113ln 2401416h m a m a ⎛⎫==-+< ⎪⎝⎭⎛⎫< ⎪⎝⎭. 由零点存在性定理知()h x 在区间21,x a ⎛⎫ ⎪⎝⎭上有一个根.设为0x , 又()0040h x h x ⎛⎫+= ⎪⎝⎭.得040h x ⎛⎫= ⎪⎝⎭.所以1040x x <<.所以04x 是()h x 的另一个零点, 故当104a <<时,()h x 存在三个不同的零点004,2,x x . 故实数a 的取值范围是10,4⎛⎫ ⎪⎝⎭.。

专题01 选择压轴题-备战2022年中考数学满分真题模拟题分类汇编(扬州专用)(原卷版)

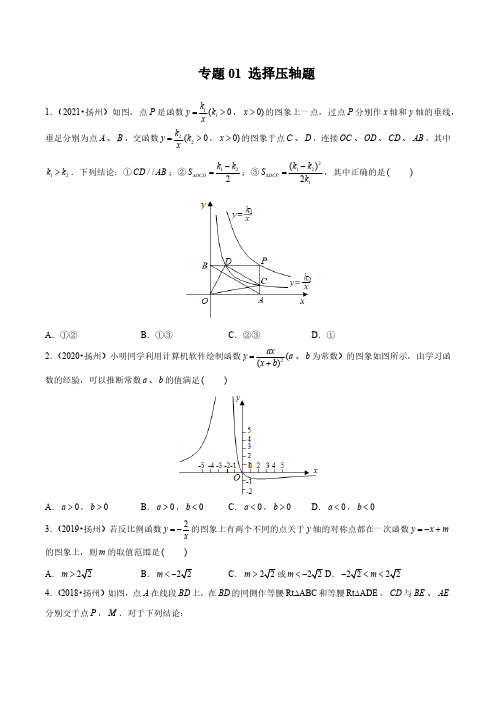
专题01 选择压轴题1．（2021•扬州）如图，点P 是函数11(0k y k x =>，0)x >的图象上一点，过点P 分别作x 轴和y 轴的垂线，垂足分别为点A 、B ，交函数22(0k y k x=>，0)x >的图象于点C 、D ，连接OC 、OD 、CD 、AB ，其中12k k >．下列结论：①//CD AB ；②122OCD k k S D -=；③2121()2DCP k k S k D -=，其中正确的是( )A ．①②B ．①③C ．②③D ．①2．（2020•扬州）小明同学利用计算机软件绘制函数2(()ax y a x b =+、b 为常数）的图象如图所示，由学习函数的经验，可以推断常数a 、b 的值满足( )A ．0a >，0b >B ．0a >，0b <C ．0a <，0b >D ．0a <，0b <3．（2019•扬州）若反比例函数2y x=-的图象上有两个不同的点关于y 轴的对称点都在一次函数y x m =-+的图象上，则m 的取值范围是( )A．m >B．m <-C．m >或m <-D．m -<<4．（2018•扬州）如图，点A 在线段BD 上，在BD 的同侧作等腰Rt ABC D 和等腰Rt ADE D ，CD 与BE 、AE 分别交于点P ，M．对于下列结论：①BAE CAD D D ∽；②MP MD MA ME =g g ；③22CB CP CM =g ．其中正确的是( )A ．①②③B ．①C ．①②D ．②③5．（2017•扬州）如图，已知ABC D 的顶点坐标分别为(0,2)A 、(1,0)B 、(2,1)C ，若二次函数21y x bx =++的图象与阴影部分（含边界）一定有公共点，则实数b 的取值范围是( )A ．2b -…B ．2b <-C ．2b -…D ．2b >-6．（2021•宝应县一模）把二次函数2(0)y ax bxc a =++>的图象作关于x 轴的对称变换，所得图象的解析式为2(1)2y a x a =--+，若(1)0m a b c -++…，则m 的最大值是( )A ．0B ．1C ．2D ．47．（2021•江都区模拟）关于x 的一元二次方程220(x x t t --=为实数）有且只有一个根在23x -<<的范围内，则t 的取值范围是( )A ．38t <…B ．18t -<…C ．38t <…或1t =-D ．13t -<<8．（2021•江都区模拟）如图所示，平行四边形OABC 的顶点C 在x 轴的正半轴上，O 为坐标原点，以OA 为斜边构造等腰Rt AOD D ，反比例函数(0)k y x x=>的图象经过点A ，交BC 于点E ，连接DE ．若cos AOC Ð=//DE x 轴，DE =，则k 的值为( )A ．12B ．16C ．18D ．249．（2021•江都区一模）如图，ABCD Y 的顶点B 在y 轴上，横坐标相等的顶点A 、C 分别在1k y x =与2k y x=图象上，则ABCD Y 的面积为( )A ．121()2k k +B ．12k k +C ．121()2k k -D ．12k k -10．（2021•邗江区二模）如图，已知点D 是ABC D 的边AC 的中点，点O 为ABC D 内部上的一点，已知90AOB Ð=°，1OD =，5BC =，则AB 的最小值为( )A ．2.5B ．3C ．3.5D ．411．（2021•宝应县二模）在平面直角坐标系中，长为3的线段CD （点D 在点C 右侧）在x 轴上移动，(0,2)A ，(0,4)B ，连接AC ，BD ，则AC BD +的最小值为( )A ．B ．C ．D ．12．（2021•高邮市模拟）如图，90AOB Ð=°，2OC =，D 为OC 中点，长为1的线段EF （点F 在点E 的下方）在直线OB 上移动，连接DE ，CF ，则DE CF +的最小值为( )A B C ．D ．13．（2021•仪征市二模）已知点(P m 、)n 在直线2y x =-+上，双曲线21(k y k x+=为常数）图象经过点P ，则222202*********m n k -+的值是( )A ．4040B ．2020C ．1-D ．114．（2021•江都区二模）如图，在平行四边形ABCD 中，120C Ð=°，4AD =，2AB =，点H 、G 分别是边CD 、BC 上的动点．连接AH 、HG ，点E 为AH 的中点，点F 为GH 的中点，连接EF ．则EF 的最大值与最小值的差为( )A ．1B 1-CD ．215．（2020•邗江区校级一模）在平面直角坐标系xOy 中，过点(5,0)A -作垂直于x 轴的直线AB ，直线y x b =+与双曲线4y x=-相交于点1(P x ，1)y 、2(Q x ，2)y ，与直线AB 相交于点3(R x ，3)y ．若123y y y >>时，则b 的取值范围是( )A ．4b >B ．4b >或4b <-C ．2945b -<<-或4b >D ．2945b <<或4b <-16．（2020•吴江区三模）如图，正方形ABCD 中，内部有4个全等的正方形，小正方形的顶点E 、F 、G 、H 分别在边AB 、BC 、CD 、AD 上，则tan (AEH Ð= )A ．13B ．25C ．27D ．1417．（2020•广陵区校级一模）我们知道，任意一个正整数n 都可以进行这样的分解：(n p q p =´，q 是正整数，且)p q …，在n 的所有这种分解中，如果p ，q 两因数之差的绝对值最小，我们就称p q ´是n 的最佳分解，并规定：()p F n q=．例如：12可以分解成112´，26´或34´，因为1216243->->-，所以34´是12的最佳分解，所以3(12)4F =．如果一个两位正整数t ，10(19t x y x y =+………，x ，y 为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数t 为“吉祥数”．根据以上新定义，下列说法正确的有：（1）3(48)4F =；（2）如果一个正整数m 是另外一个正整数n 的平方，我们称正整数m 是完全平方数，则对任意一个完全平方数m ，总有()1F m =；（3）15和26是“吉祥数”；（4）“吉祥数”中，()F t 的最大值为34．( )A ．1个B ．2个C ．3个D ．4个18．（2020•广陵区二模）两块等腰直角三角形纸片AOB 和COD 按图1所示放置，直角顶点重合在点O 处，其中AB =6CD =．保持纸片AOB 不动，将纸片COD 绕点O 逆时针旋转(090)a a °<<°，如图2所示．当BD 与CD 在同一直线上（如图3)时，tan a 的值等于( )A B ．12C ．13D 19．（2020•高邮市一模）如图，已知菱形ABCD 的顶点A 的坐标为(1,0)，顶点B 的坐标为(4,4)，若将菱形ABCD 绕原点O 逆时针旋转45°称为1次变换，则经过2020次变换后点C 的坐标为( )A ．(9,4)B ．(4,9)-C ．(9,4)--D ．(4,9)--20．（2020•广陵区校级一模）如图，矩形ABCD 的顶点A 和对称中心均在反比例函数(0,0)k y k x x=¹>上，若矩形ABCD 的面积为12，则k 的值为( )A ．12B ．6C ．4D ．321．（2020•江都区二模）如图，在平面直角坐标系中，已知点A 坐标(0,3)，点B 坐标(4,0)，将点O 沿直线34y x b =-+对折，点O 恰好落在OAB Ð的平分线上的O ¢处，则b 的值为( )A ．12B ．65C ．98D ．151622．（2020•邗江区校级三模）如图，O e 的半径为3，Rt ABC D 的顶点A 、B 在O e 上，90B Ð=°，点C 在O e 内，且3tan 4A =．当点A 在圆上运动时，OC 的最小值为( )A B ．32C D ．5323．（2020•宁蒗县模拟）如图，菱形ABCD 的的边长为6，60ABC Ð=°，对角线BD 上有两个动点E 、F （点E 在点F 的左侧），若2EF =，则AE CF +的最小值为( )A ．B ．C ．6D ．824．（2020•江都区三模）如图，OAC D 和BAD D 都是等腰直角三角形，90ACO ADB Ð=Ð=°，反比例函数k y x=在第二象限的图象经过点B ，且228OA AB -=，则k 的值( )A ．4B ．8C ．4-D ．8-25．（2020•宝应县二模）当1x =或3-时，代数式2ax bx c ++与mx n +的值相等，则函数2()y ax b m x c n =+-+-与x 轴的交点为( )A ．(1,0)和(3,0)-B ．(1,0)-C ．(3,0)D ．(1,0)-和(3,0)26．（2020•瑞安市一模）已知二次函数222y x x =-+（其中x 是自变量），当0x a ……时，y 的最大值为2，y 的最小值为1．则a 的值为( )A ．1a =B ．12a <…C ．12a <…D ．12a ……27．（2020•广陵区校级二模）如图，点1P 、2P 在反比例函数6(0)y x x=>的图象上，过点1P 作y 轴的平行线，过点2P 作x 轴的平行线，两直线相交于点Q ，若点Q 恰好在反比例函数2(0)y x x =>的图象上，则12PQ P Q ×的值为( )A ．3B ．4C ．6D ．828．（2020•仪征市模拟）如果二次函数22y x x t =++与一次函数y x =的图象两个交点的横坐标分别为m 、n ，且1m n <<，则t 的取值范围是( )A ．2t >-B ．2t <-C ．14t >D ．14t <29．（2020•邗江区校级二模）已知抛物线2231(0)y ax ax a a =-++¹图象上有两点1(A x ，1)y 、2(B x ，2)y ，121x x <<-时，有12y y <；当112x -……时，1y 最小值是6．则a 的值为( )A ．1-B ．5-C ．1或5-D ．1-或5-30．（2020•宝应县三模）已知关于x 的二次函数24y x x m =-+在13x -……的取值范围内最大值7，则该二次函数的最小值是( )A ．2-B ．1-C ．0D ．1。

高中生物7大题型解题思路汇总,高分必看!

题型一曲线类01解题步骤1、识标：弄清纵、横坐标的含义及它们之间的联系，这是解答此类题的基础。

2、明点：明确坐标图上曲线的特殊点的含义。

3、析线：根据纵、横坐标的含义可以得出，在一定范围内（或超过一定范围时），随“横坐标量”的变化，“纵坐标量”会有怎样的变化，从而揭示出各段曲线的变化趋势及其含义。

若为多重变化曲线坐标图，则可先分析每一条曲线的变化规律，再分析不同曲线变化的因果关系、先后关系，分别揭示其变化趋势，然后对比分析，找出符合题意的曲线、结论或者是教材中的结论性语言。

02例题下图表示生长素浓度对植物生长发育的影响。

下列叙述正确的是( )A．在茎的向光性实验中，若测得茎向光一侧的生长素浓度为b点浓度，则背光一侧的浓度一定在de之间。

B．若c点表示某植物顶芽的生长素浓度，则ce段可表示最靠近顶芽的侧芽中的生长素浓度。

C．在利用生长素作用原理来培育无子番茄时，所用生长素浓度应低于e点浓度。

D．若c点表示促进茎生长的最适宜浓度，则a、d点分别表示促进根、芽生长的最适宜浓度。

解析：茎背光一侧生长素浓度高于向光侧，且促进生长较向光侧快，若向光侧浓度是b ，则背光侧浓度应在bc之间；最靠近顶芽的侧芽生长素浓度高于顶芽，且侧芽处的生长素浓度对芽具有抑制作用，所以最靠近顶芽的侧芽的生长素浓度大于e；芽的最适宜浓度比茎的小，而d大于c。

答案：C题型二表格信息类01解题步骤1、仔细阅读并理解表格材料，明确该表格反映的是什么信息。

2、对表格材料进行综合分析，并能准确把握表格与题干间的内在联系。

3、将材料中的问题与教材知识有机结合起来加以论证。

02例题下表是缺碘与不缺碘的两类人群中，血液内与甲状腺活动密切相关的两种激素含量状况。

(1)表中A是________，B应________。

甲状腺激素对垂体分泌激素A起________作用。

在甲状腺激素的分泌调节中，控制枢纽是________。

(2)长期缺碘，成年人会表现出：①喜热、畏寒等体温偏低现象；②少言寡语、反应迟钝及嗜睡等现象。

(人教版)2020年高考化学一轮复习酸碱中和滴定曲线大全专题01 强碱滴定二元弱酸曲线练习

专题01 强碱滴定二元弱酸曲线1．常温下，向20 mL 0.2 mol·L－1 H2A溶液中滴加0.2 mol·L－1NaOH溶液。

有关微粒物质的量变化如下图(其中Ⅰ代表H2A，Ⅱ代表HA－，Ⅲ代表A2－)。

根据图示判断，下列说法正确的是( )A. H 2A在水中的电离方程式是：H2A===H＋＋HA－、HA－H＋＋A2－B. 等体积等浓度的NaOH溶液与H2A溶液混合后溶液显碱性C. 当V(NaOH)＝20 mL时，溶液中存在以下关系：c(H＋)＋c(H2A)＝c(A2－)＋c(OH－)D. 当V(NaOH)＝30 mL时，溶液中各粒子浓度的大小顺序为：c(Na＋)>c(HA－)>c(A2－)>c(H ＋)>c(OH－)【答案】C2．已知：pK a= -lgK a，25℃时，H2SO3的pK a1=1.85，pK a2=7.19。

常温下，用0.1mol/LNaOH 溶液滴定20mL 0．1mol/L H2SO3溶液的滴定曲线如图所示。

下列说法不正确的是A. A点所得溶液中：V o等于lOmLB. B点所得溶液中：C. C点所得溶液中：D. D点所得溶液中水解平衡常数【答案】A【解析】分析：A．A点溶液中pH=1.85，则溶液中c（H+）=10-1.85mol/L，结合亚硫酸的电离平衡常数分析；B．B点加入NaOH溶液的体积为20mL，此时反应恰好产生NaHSO3，根据溶液中电荷守恒分析；C．根据亚硫酸的电离平衡常数结合电荷守恒分析；D．D点为加入NaOH溶液40mL，此时溶液中恰好生成亚硫酸钠，根据水解常数与电离常数的关系计算。

详解：A．A点溶液中pH=1.85，则溶液中c（H+）=10-1.85mol/L，H2SO3的一级电离平衡常数为K a1=c(H+)c(HSO3−)/c(H2SO3)=10-1.85mol/L，所以c（H+）=K a1，表明溶液中c（NaHSO3）=c（H2SO3），若恰好是10mLNaOH，由于此时溶液显酸性，则所得溶液中c（H2SO3）＜c（NaHSO3），因此所加NaOH体积需＜10mL，才能使溶液中c（NaHSO3）=c（H2SO3），即V0＜10mL，A错误；B．B点加入NaOH溶液的体积为20mL，此时反应恰好产生NaHSO3，为第一个滴定终点，溶液中存在电荷守恒，c（Na+）+c（H+）=c(HSO3−)+2c（SO32-）+c（OH-），B正确；C．H2SO3的二级电离平衡常数为K a2=c(H+)c（SO32-）/c(HSO3−)=10-7.19mol/L，C点溶液的pH=7.19，即溶液中c（H+）=10-7.19mol/L，则c（H+）=K a2，表明溶液中c（SO32-）=c(HSO3−)，溶液中存在电荷守恒，c（Na+）+c（H+）=c(HSO3−)+2c（SO32-）+c（OH-），溶液显碱性，则溶液中c（Na+）＞3c(HSO3−)，C正确；D．D点为加入NaOH溶液40mL，此时溶液中恰好生成亚硫酸钠，为第二个滴定终点，此时亚硫酸钠水解使溶液显碱性，则K h1＝K w/K a2＝10−14/10−7.19＝10-6.81，D正确。

专题曲线运动和运动的合成分解高一物理 (人教版2019)(解析版)

专题01曲线运动和运动的合成分解一、曲线运动的特点和条件1．下列说法正确的是（）A．物体在恒力作用下一定做直线运动B．物体在变力作用下一定做曲线运动C．曲线运动一定是变速运动D．物体做圆周运动时，其所受合外力的方向一定指向圆心【答案】C【解析】AB．物体做直线运动还是曲线运动取决于合外力方向与运动方向的关系，共线则为直线，不共线则为曲线运动，故AB错误；C．曲线运动的速度方向一直在发生变化，所以曲线运动一定是变速运动，故C正确；D．物体做匀速圆周运动时，合外力提供向心力，但在变速圆周运动中，合外力即提供向心力，也给了物体一个切线方向的加速度，故此时合外力不指向圆心，故D错误。

故选C。

2．共享单车曾风靡一时，一同学骑单车在一路段做曲线运动，单车速率逐渐减小。

关于单车在运动过程中经过P点时的速度v和加速度a的方向，下列图中可能正确的是（）A．B．C．D．【答案】C【解析】速度的方向是曲线的切线方向，加速度的方向要指向轨迹弯曲的内侧，由于单车速率逐渐减小，加速度方向与速度方向成钝角，故选项C 正确，ABD 错误；故选C 。

二、蜡块的运动3．如图所示，竖直放置两端封闭的玻璃管内注满清水和一个用红蜡做成的圆柱体，甲图玻璃管倒置静止时圆柱体能匀速运动。

乙图是玻璃管倒置后水平向右匀速运动，圆柱体运动的速度大小为6cm/s ，与水平方向成θ=30︒，则（）A ．玻璃管水平方向运动的速度为6cm/sB ．玻璃管水平方向运动的速度为4cm/sC ．玻璃管倒置静止时红蜡块竖直向上运动速度为3cm/sD ．玻璃管倒置静止时红蜡块竖直向上运动速度为2cm/s【答案】C【解析】AB ．圆柱体运动的速度大小为6cm/s ，与水平方向成θ=30︒，玻璃管水平方向运动的速度为cos3033cm/s x v v =︒=故AB 错误；CD ．玻璃管倒置静止时红蜡块竖直向上运动速度为sin 303cm/s y v v =︒=故C 正确D 错误。

(必考题)高中数学高中数学选修4-4第一章《坐标系》检测题(答案解析)

一、选择题1．（理）在极坐标系中,圆2cos ρθ=的垂直于极轴的两条切线方程分别为（） A ．0()R θρ=∈ 和cos 2ρθ= B ．()2R πθρ=∈和cos 2ρθ=C ．()2R πθρ=∈和cos 1ρθ= D ．0()R θρ=∈和cos 1ρθ=2．已知曲线C 的极坐标方程为222123cos 4sin ρθθ=+，以极点为原点，极轴为x 轴非负半轴建立平面直角坐标系，则曲线C经过伸缩变换123x x y y ⎧=⎪⎪⎨=''⎪⎪⎩后，得到的曲线是（）A ．直线B ．椭圆C ．圆D ．双曲线3．已知圆C 与直线l 的极坐标方程分别为6cos ρθ=，sin 4πρθ⎛⎫+= ⎪⎝⎭C 到直线l 的距离是（） A ．1B ．2CD．24．在极坐标系中，点(),ρθ与(),ρπθ--的位置关系为（） A ．关于极轴所在直线对称 B ．关于极点对称 C ．重合D ．关于直线()2R πθρ=∈对称5．在极坐标系中，由三条直线0θ=，3πθ=，cos sin 1ρθρθ+=围成的图形的面积为（） A ．14BCD ．136．在极坐标系中，曲线1C 的极坐标方程为2sin ρθ=，曲线2C的极坐标方程为ρθ=，若曲线1C 与2C 交于A 、B 两点，则AB 等于（）A ．1BC ．2D．7．221x y +=经过伸缩变换23x xy y ''=⎧⎨=⎩后所得图形的焦距（）A．B．C ．4D ．68．将2216x y +=的横坐标压缩为原来的12，纵坐标伸长为原来的2倍，则曲线的方程变为（）A ．22134x y +=B ．22213x y +=C ．222112x y +=D ．222134x y +=9．已知曲线C 与曲线5ρ=3cos?5sin?θθ-关于极轴对称，则曲线C 的方程为( )A ．10cos ρ=-π-6θ⎛⎫ ⎪⎝⎭ B ．10cos ρ=π-6θ⎛⎫ ⎪⎝⎭ C ．10cos ρ=-π6θ⎛⎫+⎪⎝⎭D ．10cos ρ=π6θ⎛⎫+⎪⎝⎭10．在直角坐标系xOy 中，曲线C 的方程为22162x y+=，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为cos()36πρθ+=，射线M 的极坐标方程为(0)θαρ=≥.设射线m 与曲线C 、直线l 分别交于A 、B 两点，则2211OAOB+的最大值为（） A ．34B ．25C ．23D ．1311．极坐标方程cos ρθ=与1cos 2ρθ=的图形是（） A ． B ． C ． D ．12．在同一平面直角坐标系中，将曲线1cos 23y x =按伸缩变换23x x y y ''=⎧⎨=⎩后为（）A ．cos y x ''=B ．13cos 2y x ''= C ．12cos3y x ''= D ．1cos32y x ''=二、填空题13．在极坐标系中，曲线C 的方程为28cos 10sin 320ρρθρθ--+=，直线l 的方程为0()R θθρ=∈，0tan 2θ=，若l 与C 交于A ，B 两点，O 为极点，则||||OA OB +=________．14．在极坐标系中，直线sin 24πρθ⎛⎫-= ⎪⎝⎭4ρ=截得的弦长为______.15．（理）在极坐标系中，曲线sin 2ρθ=+与sin 2ρθ=的公共点到极点的距离为_________．16．已知在平面直角坐标系xOy 中，圆C 的参数方程为：2cos 22sin x y ϕϕ=⎧⎨=+⎩（ϕ为参数），以Ox 为极轴建立极坐标系，直线l 30cos sin θθ-=，则圆C截直线l 所得弦长为___________． 17．两条直线sin 20164πρθ⎛⎫+= ⎪⎝⎭，sin 20174πρθ⎛⎫-= ⎪⎝⎭的位置关系是_______ 18．点C 的极坐标是(2,)4π,则点C 的直角坐标为______________ 19．在极坐标系中0,02,ρθπ>≤<，曲线cos 1ρθ=-与曲线=2sin ρθ的交点的极坐标为_______________。

坐标曲线的解题方法

详细描述
指数函数曲线和对数函数曲线在平面坐标系中呈现出不同的变化趋势。指数函数曲线随着$x$的增大而快速上升，而对数函数曲线则随着$x$的增大而逐渐趋于平缓。在解决指数函数曲线和对数函数曲线问题时，需要掌握指数函数和对数函数的性质，如增减性、值域等，并能够运用换底公式、对数运算法则等知识点进行求解。在实际应用中，指数函数和对数函数曲线常用于描述人口增长、放射性物质的衰变等现象。
在坐标曲线问题中，常常需要求解曲线上点的坐标，代数法通过设置方程组来求解这些坐标。
代数法适用于解决一些比较简单的问题，但对于一些复杂的问题，可能需要使用其他方法。
几何法
几何法是一种通过几何图形来直观地解决坐标曲线问题的方法。
通过画图，可以直观地观察曲线的形状和特点，从而找到解决问
题的线索。
坐标曲线的重要性
实际应用
坐标曲线在各个领域都有广泛的应用，如物理学、工程学、经济
学等。
数学基础
坐标曲线是解析几何的重要组成部分，是学习高等数学和工程学科的基础。
培养逻辑思维
通过解决坐标曲线相关问题，可以培养人的逻辑思维和空间想象力。
坐标曲线的基本概念
点
坐标平面上的一个点用(x, y)表示，其中x和y是实数。
03
坐标曲线解题技巧
观察法
总结词
通过观察坐标曲线的基本形态，可以初步判断曲线的类型和性质。
详细描述
观察曲线的形状、趋势、对称性等特点，有助于确定曲线的方程或参数范围。
代数变换法
总结词
通过代数变换，将复杂的坐标曲线转化为简单的标准形式，便于分析。
详细描述
利用代数方程的变换技巧，如变量替换、平方、开方等，将曲线方程化简为标准形式，如圆、椭圆、直线等。

讲座图表曲线类题目的解题技巧

【解析】本题以红豆杉种群密度的调查为背景，考查学生绘制柱状图的能力。解题步骤为：第一步，先将数据如下处理；
等级
a级
b级
c级
d级
e级
数量（株） 120
62
32
16
6
第二步，建立平面直角坐标系。并用长方条表示各级数量多少。第三步，注明纵坐标：株高数量（株）；横坐标：高度等级， a级、b级等。
①因果关系：同一个坐标系中（或不同坐标系间）曲
线间的变化，有因果关系。即一个曲线的变化影响着另一曲线的变化。
解题技巧：一理二析法
&具体操作：
“二析”: ②并列关系：同一个坐标系中（或不同坐标系间）曲线的变化，无因果关系，是各自独立的。第二步：对曲线进行分析。第三步：得出结论。
【例2】甲、乙两图分别表示大草履虫和双小核草履虫单独培养（甲）和混合培养（乙）时种群的增长速率。从下图所示的结果可以推断乙
1
【解析】本题以大麦幼苗对矿质元素的吸收
2
为载体，考查学生绘制曲线图的能力。
解题方法为：
3
建立坐标系，标注两轴的含义并注明单位；
4
标出0、10、20、30、40、50、60、70
点相应的纵坐标点；
5
以能穿过最多点的直线或光滑的曲线连结各
6
在图下标出“大麦根尖各区域32P累积量”
点；
文字。
答案：大麦根尖区域32P的累积量
光照后的重量变化（mg）*
+3.5
+3
+2.5
+2
*均与暗处理前的重量进行比较，“-”表示减少的重量值，“+”表示增加的重量值
则在哪一温度条件下每小时叶片光合作用产生的氧气量最多

专题01 一次函数压轴题(十大题型)(原卷版)

(1)OC 的长为______，OD 的长为______；(2)如图，点()1,M a -是线段CD 上一点，连接OM ，作ON 并判断MON △的形状；(3)如备用图，若点()1,E b 为直线AB 上的点，点P 为y 轴上的点，是以点E 为直角顶点的等腰直角三角形，若存在，请求出此时(1)求直线CD 的函数表达式和点D 的坐标；(2)点P 为线段DE 上的一个动点，连接BP ．①若直线BP 将ACD 的面积分为7:9两部分，试求点②点P 是否存在某个位置，将BPD △沿着直线BP 翻折，使得点在，请直接写出点P 的坐标；若不存在，请说明理由．题型2：取值范围问题(1)求点A 的坐标；(2)若点C 在第二象限，ACD ①求点C 的坐标；②直接写出不等式组4x kx +>③将CAD 沿x 轴平移，点C(1)求点C 的坐标及直线BC 的表达式；(2)在点E 运动的过程中，若△DEF 的面积为5，求此时点(3)设点E 的坐标为（0，m ）；①用m 表示点F 的坐标；②在点E 运动的过程中，若△DEF 始终在△ABC 的内部（包括边界）题型3：最值问题5．已知一次函数()134502y kx k k =++≠．的坐标为(),a a ，求CM MP +的最小值．6．如图1，在平面直角坐标系xoy 中，直线1:1l y x =+与x 轴交于点A ，直线2:33l y x =-与x 轴交于点B ，与1l 相交于C 点，过x 轴上动点(),0E t 作直线3l x ⊥轴分别与直线1l 、2l 交于P 、Q 两点．(1)①请直接写出点A ，点B ，点C 的坐标：A ______，B ______，C ______．②若2PQ =，求t 的值；(2)如图2，若E 为线段AB 上动点，过点P 作直线PF PQ ⊥交直线2l 于点F ，求当t 为何值时，PQ PF -最大，并求这个最大值．题型4：旋转问题7．如图1，在平面直角坐标系中，一次函数()0y kx b k =+≠的图象交y 轴于点()0,1A -，交x 轴交于点B ，且2OB OC OA ==，过点C 作y 轴的垂线，交直线AB 于点D ．(1)求点D 的坐标；(2)点E 是线段CD 上一动点，直线BE 与y 轴交于点F ．①若BDF V 的面积为8，求点F 的坐标；②如图2，当点F 在y 轴正半轴上时，将直线BF 绕点B 顺时针旋转45︒后的直线与线段CD 交于点M ，连接FM ，若1OF MF =+，求线段MF 的长．备用图(1)求直线1l 的表达式；(2)过M 作y 轴的平行线，分别交直线1l ，直线2l 于点D ，E ，连接DE ，①当3m =时，求DE 的长；(1)求n 的值及直线2l 的表达式；(2)在直线2l 上是否存在点E ，使BO ABE A S S =△△若存在，则求出点(3)如图2，点P 为线段AD 上的一个动点，一动点H(1)求直线AB 的表达式；(2)由图象直接写出关于x 的不等式102x kx b <<+的解集；(3)如图②所示，P 为x 轴上A 点右侧任意一点，以BP 为边作等腰Rt BPM 直线MA 交y 轴于点Q ．当点P 在x 轴上运动时，线段OQ 的长度是否发生变化？若不变，求出线段长度；若变化，求线段OQ 的取值范围．题型6：定值问题11．如图1所示，直线l ：10y mx m =+与x 轴负半轴、y 轴正半轴分别交于(1)若点D坐标为(12，3)．①求直线BC的函数关系式；②若Q为RS中点，求点P坐标．(2)在点P运动的过程中，PQCR的值是否变化？若不变，求出该值；若变化，请说明理由．题型7：新定义题型13．函数图象是研究函数的重要工具，类比一次函数的学习，表是探究过程中的部分信息：x…2-1-01232y x=-…4a2-14(1)a的值为______；(2)在图中画出该函数的图象；(3)结合函数的图象，解决下列问题：①下列说法正确的是：______．（填所有正确选项）A．函数图像关于x轴对称x=时，函数有最小值，最小值为B．当0x>时，y随x的增大而增大C．当0③若12x -≤≤，则y 的取值范围为【拓展提升】18．对于两个不同的函数，通过加法运算可以得到一个新函数，我们把这个新函数称为两个函数的数”．例如：对于函数12y x =和231y x =-，则函数1y ，2y 的“和函数”3y =(1)已知函数1y x =和2=y ①写出3y 的表达式，并求出当②函数1y ，2y 的图象如图①所示，则．．．．(2)已知函数4y x =和5y =，这两个函数的“和函数”记为6y ．按照上图的速度步行前往学校，记录下小东10天到达学校所用的时间，如表．上学日期4号5号6号7号8号11号到达学校所用时间（单位：min）2524.825.324.925.124.8某天早上7：20，小东按照上表的速度步行上学．t（0＜t≤10）分钟后，小明骑自行车以从小区出发，沿着相同的路线上学．骑行7分钟后，自行车因零件损坏无法继续骑行，小明只好将自行车停在路边非机动车停靠点（停车时间忽略不计），改用步行前往学校．为了赶时间，小明的步行速度不小于。

专题01 函数的基本性质学霸必刷100题(原卷版)

专题01 函数的基本性质100题1．已知函数()f x （x ∈R ）满足()()4f x f x -=-，若函数21x y x+=与()y f x =图像的交点为()11,x y ，()22,x y ，…，(),m m x y ，则()1mi i i x y =+=∑（）A ．0B ．mC ．2mD ．4m2．已知函数2(2)2()log xf x ax +=+，若对任意(1,3]t ∈-，任意x ∈R ，不等式()()1f x f x kt +-≥+恒成立，则k 的最大值为 A ．1-B ．1C ．13-D ．133．已知函数()()f x g x ，的图象分别如图1，2所示，方程()()()()1f g x g f x ＝，＝－1，1(())2g g x =-的实根个数分别为a 、b 、c ，则（）A ．a b c +=B ．b c a ＋＝C ．b a c ＝D ．ab c ＝4．已知函数()f x 是定义在R 上的增函数，且其图象关于点()2,0-对称，则关于x 的不等式()()23120f x f x -+-≥的解集为（）A ．[)4,-+∞B ．[]4,2-C ．[]2,4-D ．(],2-∞5．已知定义域为()0,∞+的函数()f x 满足：（1）对任意()0,x ∈+∞，恒有()()22f x f x =成立；（2）当(]1,2x ∈时，()2f x x =-.给出如下结论：①对任意m Z ∈，有()20mf =；②函数()f x 的值域为[)0,+∞；③若函数()f x 在区间(),a b 上单调递减，则存在k Z ∈，使得()()1,2,2kk a b +⊆.其中所正确结论的序号是（）A ．①②B ．①③C ．②③D ．①②③6．已知定义域为R 的函数()f x 满足(1)(1)f x f x -=-+，且函数()f x 在区间()1,+∞上单调递增，如果121x x ，且122x x +>，则()()12f x f x +的值（）A ．恒小于0B ．恒大于0C ．可能为0D ．可正可负函数7．已知函数(1)2y f x =+-是奇函数，21()1x g x x -=-，且()f x 与()g x 的图像的交点为11(,)x y ，22(,)x y ，，66(,)x y ，则126126x x x y y y +++++++=( )A ．0B ．6C ．12D ．188．已知函数()|lg |f x x =,若0a b <<,且()()f a f b =,则2a b -的取值范围是( ) A ．(0,)+∞B ．[1,)-+∞C ．(,1)-∞-D ．(,0)-∞9．设函数()f x 是定义在R 上的偶函数，()()4f x f x =-，当02x ≤≤时，52x f x，函数112g xx ，则()()()F x f x g x =-零点个数为( ) A ．7B ．6C ．5D ．410．给出定义：若11(,]22x m m ∈-+（其中m 为整数），则m 叫做与实数x ”亲密的整数”记作{x }＝m ，在此基础上给出下列关于函数()|{}|f x x x =-的四个说法： ①函数()y f x =在(0,1)是增函数； ②函数()y f x =的图象关于直线()2kx k Z =∈对称； ③函数()y f x =在1(,)()2k k k Z +∈上单调递增④当(0,2)x ∈时，函数21()()22g x f x x =--有两个零点，其中说法正确的序号是（） A ．①②③B ．②③④C ．①②④D ．①③④11．已知函数()()2ln 122xxf x x -=-++，则使不等式()()12f x f x +<成立的x 的取值范围是（）A ．()(),11,-∞-+∞B ．()2,1--C ．()1,1,3⎛⎫-∞-+∞ ⎪⎝⎭D ．()(),21,-∞-⋃+∞12．已知()f x 是定义在()0,∞+上的单调函数，满足()()2ln 21xf f x ex e --+=-，则函数()f x 的零点所在区间为（） A ．210,e ⎛⎫ ⎪⎝⎭B ．211,e e ⎛⎫⎪⎝⎭ C ．1,1e ⎛⎫⎪⎝⎭D ．()1,e13．在平面直角坐标系xOy 中，已知n A ，n B 是圆222x y n +=上两个动点，且满足22n n nOA OB ⋅=-（*N n ∈），设n A ，n B到直线(1)0x n n +++=的距离之和的最大值为n a ，若数列1{}na 的前n 项和n S m <恒成立，则实数m 的取值范围是（）A ．3(,)4+∞B ．3[,)4+∞C ．3(,)2+∞D ．3[,)2+∞14．已知()f x 是定义在R 上的奇函数，对任意两个不相等的正数1x ，2x 都有()()2112120x f x x f x x x ->-，记:()0.20.24.14.1f a =，()2.12.10.40.4f b =，()0.24.10.2log4.1logf c =，则（）A ．a c b <<B ．a b c <<C ．c b a <<D ．b c a <<15．设函数()2f x ax bx c =++(,,a b c ∈R ，且0a >)，则（） A ．若02b f a ⎛⎫-< ⎪⎝⎭，则()()f f x 一定有零点 B ．若02b f f a ⎛⎫⎛⎫-> ⎪ ⎪⎝⎭⎝⎭，则()()f f x 无零点 C ．若02b f f a ⎛⎫⎛⎫-> ⎪ ⎪⎝⎭⎝⎭，且02b f a ⎛⎫-< ⎪⎝⎭，则()()f f x 一定有零点 D ．若02b f f a ⎛⎫⎛⎫-< ⎪ ⎪⎝⎭⎝⎭，则()()f f x 有两个零点16．对于函数()f x 和()g x ，设(){|0}x f x α∈=，(){|0}x g x β∈=，若存在α，β，使得1αβ-，则称()f x 与()g x 互为“零点相邻函数”．若函数()12x f x e x -=+-与()23g x x ax a =--+互为“零点相邻函数”，则实数a 的取值范围为（）A ．[]2,4B ．72,3⎡⎤⎢⎥⎣⎦C ．7,33⎡⎤⎢⎥⎣⎦D ．[]2,317．设函数()()()1122()sin sin sin n n f x a x a a x a a x a =++++⋅⋅⋅++，其中,i a j a （1,2,,i n =⋅⋅⋅，*n N ∈，2n ≥）为已知实常数，x ∈R ，下列关于函数()f x 的性质判断正确的个数是（）①若(0)02f f π⎛⎫==⎪⎝⎭，则()0f x =对任意实数x 恒成立；②若(0)0f =，则函数()f x 为奇函数；③若02f π⎛⎫= ⎪⎝⎭，则函数()f x 为偶函数；④当22(0)02f f π⎛⎫+≠ ⎪⎝⎭时，若()()120f x f x ==，则12()x x k k Z π-=∈；A ．4B ．3C ．2D ．118．函数()f x 的定义域为D ，若满足如下两个条件：（1）()f x 在D 内是单调函数；（2）存在,22m n D ⎡⎤⊆⎢⎥⎣⎦，使得()f x 在,22m n ⎡⎤⎢⎥⎣⎦上的值域为[],m n ，那么就称函数()f x 为“希望函数”，若函数()()()log 0,1x a f x a t a a =+>≠是“希望函数”，则t 的取值范围是（）A ．1,04⎛⎫-⎪⎝⎭B ．1,04⎡⎤-⎢⎥⎣⎦C ．1,02⎛⎫-⎪⎝⎭D ．1,02⎡⎤-⎢⎥⎣⎦19．定义在R 上的偶函数()f x 满足：对任意的()()1212,,0x x x x ∈-∞≠，有()()21210f x f x x x -<-，且()20f =，则不等式()()205f x f x x+-<解集是（）A ．()(),22-∞-+∞B ．()(),20,2-∞-C ．()()2,02-+∞D ．()()2,00,2-20．已知,0,22m R ππαβπ-≤≤≤≤∈,如果有33sin 0,cos 02m m πααββ⎛⎫++=-++= ⎪⎝⎭,则cos()αβ+的值为（）A ．1-B ．0C ．0.5D ．121．设函数()y f x =，()y g x =的定义域、值域均为R ，以下四个命题：①若()y f x =，()y g x =都是奇函数，则(())y f g x =是偶函数；②若()y f x =，()y g x =都是R 上递减函数，则(())y f g x =是R 上递减函数；③若(())y f g x =是周期函数，则()y f x =，()y g x =都是周期函数；④若(())y f g x =存在反函数，则()y f x =，()y g x =都存在反函数其中真命题的个数是（） A ．0B ．1C ．2D ．322．狄利克雷函数为F (x )()10x x R x ⎧=∈⎨⎩，为有理数时，，为无理数时，.有下列四个命题：①此函数为偶函数，且有无数条对称轴；②此函数的值域是[]0,1；③此函数为周期函数，但没有最小正周期；④存在三点()()()()()(),,,,,A a F a B b F b C c F c ，使得△ABC 是等腰直角三角形，以上命题正确的是（）A ．①②B ．①③C ．③④D ．②④23．符合以下性质的函数称为“S 函数”：①定义域为R ，②()f x 是奇函数，③()f x a <（常数0a >），④()f x 在0,上单调递增，⑤对任意一个小于a 的正数d ，至少存在一个自变量0x ，使()0f x d >.下列四个函数中()12arctan af x x π=，()221ax x f x x =+，()310001a x x f x x a x x ⎧->⎪⎪==⎨⎪⎪--<⎩，()42121x x f x a ⎛⎫-=⋅ ⎪+⎝⎭中“S 函数”的个数为（） A ．1个B ．2个C ．3个D ．4个24．如果一个函数()y f x =的图像是一个中心对称图形，关于点()P m n ,对称，那么将()y f x =的图像向左平移m 个单位再向下平移n 的单位后得到一个关于原点对称的函数图像.即函数()y f x m n =+-为奇函数.那么下列命题中真命题的个数是（）①二次函数2y ax bx c =++（0a ≠）的图像肯定不是一个中心对称图形；②三次函数32y ax bx cx d =+++（0a ≠）的图像肯定是一个中心对称图形； ③函数1xby c a =++（0a >且1a ≠）的图像肯定是一个中心对称图形. A ．0个 B ．1个C ．2个D ．3个25．定义域为R 的函数()f x 满足()()f x f x -=，且对()12,0,x x ∈+∞恒有1212()()0f x f x x x ->-，且305f ⎛⎫= ⎪⎝⎭，则不等式()0f x x<的解集是（） A ．30,5⎛⎫ ⎪⎝⎭B ．3,5⎛⎫+∞ ⎪⎝⎭C ．33,0,55⎛⎫⎛⎫-+∞ ⎪⎪⎝⎭⎝⎭D ．33,0,55⎛⎫⎛⎫-∞- ⎪⎪⎝⎭⎝⎭26．对于函数()f x ,若存在区间[,]A m n =,使得{|(),}y y f x x A A =∈=,则称函数()f x 为“可等域函数”,区间A 为函数的一个“可等域区间”.给出下列四个函数:①()||f x x =;②2()21f x x =-;③()|12|x f x =-;④2()log (22)f x x =-.其中存在唯一“可等域区间”的“可等域函数”的个数是( )A ．1B ．2C ．3D ．427．已知偶函数()2f x π+，当(,)22x ππ∈-时，13()sin f x x x =+．设(1)a f =，(2)b f =，(3)c f =，则（） A ．a b c <<B ．b c a <<C ．c b a <<D ．c a b <<28．定义在R 上的函数()f x 满足(2)2()f x f x +=，且当[2,4]x ∈时，224,23,()2,34,x x x f x x x x⎧-+≤≤⎪=⎨+<≤⎪⎩()1g x ax =+，对1[2,0]x ∀∈-，2[2,1]x ∃∈-，使得21()()g x f x =，则实数a 的取值范围为（） A ．11(,)[,)88-∞-+∞ B ．11[,0)(0,]48-C ．(0,8]D ．11(,][,)48-∞-+∞29．已知函数()()11332cos 1x x x f x --+=+--，则（）A ．()()0.5231log 9log 0.52f f f -⎛⎫>> ⎪⎝⎭B ．()()0.52310.5log 9log2f f f -⎛⎫>> ⎪⎝⎭ C ．()()0.53210.5loglog 92f f f -⎛⎫>> ⎪⎝⎭D ．()()0.5231log 90.5log2f f f -⎛⎫>> ⎪⎝⎭30．若在直角坐标平面内,A B 两点满足条件：①点,A B 分别在函数()y f x =，()y g x =的图象上；②点,A B 关于原点对称，则称,A B 为函数()y f x =和()y g x =的一个“黄金点对”．那么函数2()22(0)f x x x x =+-<和1()(0)g x x x=>的“黄金点对”的个数是（） A ．0个B ．1个C ．2个D ．3个31．对于函数()y f x =，若存在区间[],a b ，当[],x a b ∈时的值域为[](),0ka kb k >，则称()y f x =为k 倍值函数.若()2xf x e x =+是k 倍值函数，则实数k 的取值范围是（）A ．()1,e ++∞B ．()2,e ++∞C ．1,e e ⎛⎫++∞ ⎪⎝⎭D ．,e e 2⎛⎫++∞ ⎪⎝⎭32．定义在R 上的函数()f x 满足()()2=-+f x f x ，()()2f x f x =-，且当[]0,1x ∈时，()2f x x =，则方程()12f x x =-在[]8,10-上所有根的和为（） A ．0B ．8C ．16D ．3233．定义：若整数m 满足：1122m x m -<≤+，称m 为离实数x 最近的整数，记作{}x m =．给出函数(){}f x x x =-的四个命题：①函数()f x 的定义域为R ，值域为11,22⎛⎫- ⎪⎝⎭；②函数()f x 是周期函数，最小正周期为1；③函数()f x 在11,22⎛⎫- ⎪⎝⎭上是增函数；④函数()f x 的图象关于直线()2kx k Z =∈对称. 其中所有的正确命题的序号为（） A ．①③B ．②③C ．①②④D ．①②③34．设函数11,(,2)(){1(2),[2,)2x x f x f x x --∈-∞=-∈+∞，则函数()()1F x xf x =-的零点的个数为( )A ．4B ．5C ．6D ．735．设()g x 是定义在R 上，以1为周期的函数，若函数()()f x x g x =+在区间[]3,4上的值域为[]2,5-，则()f x 在区间[]10,10-上的值域为（）A ．[]16,12-B ．[]12,10-C ．[]15,11-D ．[]18,14-36．已知函数4()()f x x a a R x=+-∈，2()43g x x x =-++，在同一平面直角坐标系里，函数()f x 与()g x 的图像在y 轴右侧有两个交点，则实数a 的取值范围是（） A ．{}3a a <-B ．{}3a a >-C ．{}3a a =-D ．{}34a a -<<37．已知()f x 是定义在R 上的偶函数，且()()+2f x f x =对x R ∈恒成立，当[]0,1x ∈时，()2xf x =，则92f ⎛⎫-= ⎪⎝⎭A ．12BC ．2D ．138．对于函数()f x ，若存在区间[],A m n =，使得(){}|,y y f x x A A =∈=，则称函数()f x 为“可等域函数”，区间A 为函数()f x 的一个“可等域区间”．给出下列4个函数： ①()sin 2f x x π⎛⎫=⎪⎝⎭；②()221f x x =-； ③()12x f x =-； ④()()2log 22f x x =-．其中存在唯一“可等域区间”的“可等域函数”为（） A ．①②③B ．②③C ．①③D ．②③④39．若函数()y f x =在区间I 上是增函数，且函数()f x y x=在区间I 上是减函数，则称函数()f x 是区间I 上的“H 函数”．对于命题：①函数()f x x =-+()0,1上的“H 函数”； ②函数()221xg x x=-是()0,1上的“H 函数”．下列判断正确的是（） A ．①和②均为真命题 B ．①和②均为假命题 C ．①为假命题, ②为真命题D ．①为真命题, ②为假命题40．已知函数()14216x x f x +-+=，()()20g x ax a =->.若[]120,log 3x ∀∈，[]21,2x ∃∈，()()12f x g x =，则a 的取值范围是（）A ．21,3⎡⎤⎢⎥⎣⎦B ．2,23⎡⎤-⎢⎥⎣⎦C ．4,23⎡⎤⎢⎥⎣⎦D ．4,3⎡⎫+∞⎪⎢⎣⎭41．已知函数()|f x =，给出下列四个判断：①函数()f x 的值域是[0,2]；②函数()f x 的图像时轴对称图形；③函数()f x 的图像时中心对称图形；④方程3[()]2f f x =有实数解.其中正确的判断有（） A ．1个B ．2个C ．3个D ．4个42．定义在R 上的函数()f x ，满足()()cos22f x f x x +-=+，2()()sin g x f x x =+，若g()x 在R 上的最大值为M ，最小值为m ，则M m +值为（） A ．0B ．1C ．2D ．343．已知定义在R 上的函数()f x 满足()()22f x f x -=+，当2x ≤时，()xf x xe =．若关于x 的方程()()22f x k x =-+有三个不相等的实数根，则实数k 的取值范围是（）A ．()()1,00,1-B ．()()1,01,-⋃+∞C ．()(),00,e e -D ．()(),0,e e -+∞44．已知定义在R 上的函数()()522222x x x x f x --=----，则不等式()()2324f x f x ++-≥-的解集为（） A ．()0,1 B ．(]0,1 C ．(],1-∞ D ．[)1,+∞45．已知函数31()2sin 331xf x x x =-++在区间[2,2]-的值域为[,]m n ，则m n +=（） A ．2-B ．1-C ．0D ．146．设函数()f x 的定义域为R ，满足()()22f x f x +=，且当(]0,2x ∈时，()194f x x x =+-．若对任意(],x m ∈-∞，都有()23f x ≥-，则m 的取值范围是（） A ．215⎛⎤-∞ ⎥⎝⎦，B ．163⎛⎤-∞ ⎥⎝⎦，C ．184⎛⎤-∞ ⎥⎝⎦，D ．194⎛⎤-∞ ⎥⎝⎦，47．已知函数210()(1)0x x f x f x x -⎧-+≤=⎨->⎩,则下列命题中正确命题的个数是（）①函数()f x 在[1,)-+∞上为周期函数②函数()f x 在区间(),1m m +,()m N +∈上单调递增③函数()f x 在1x m =-（m N ∈）取到最大值0,且无最小值④若方程()log (2)a f x x =+（01a <<）有且仅有两个不同的实根,则11[,)32a ∈ A ．1个 B ．2个C ．3个D ．4个48．记表示不超过的最大整数，如，设函数，若方程有且仅有个实数根，则正实数的取值范围为（）A ．B ．C ．D ．49．已知定义在()0,∞+上的函数()f x 满足：对任意正实数,a b ，都有()()()2f ab f a f b =+-，且当1x >时恒有()2f x <，则下列结论正确的是（）A ．()f x 在()0,∞+上是减函数B ．()f x 在()0,∞+上是增函数C ．()f x 在()0,1上是减函数，在()1,+∞上是增函数D ．()f x 在()0,1上是增函数，在()1,+∞上是减函数50．已知函数()f x 是定义在R 上的奇函数，()1y f x =+为偶函数，且()11f =，则()()20182019(f f += )A ．2B ．1C ．0D ．1-51．设函数()f x 的定义域为R ，满足()()12f x f x +=，且当(]0,1x ∈时，()()1f x x x =-.若存在(],x m ∈-∞，使得()89f x ≥，则m 的最小值是（）A ．94B ．52C ．73D ．8352．已知函数()x a x a f x e e --+=+，若33log ab c ==，则（）A ．()()()f a f b f c <<B ．()()()f b f c f a <<C ．()()()f a f c f b <<D ．()()()f c f b f a <<53．函数()f x x =，2()3g x x x =-+.若存在129,,...,[0,]2n x x x ∈，使得1()f x +2()...f x ++1()n f x -+()n g x =1()g x +2()...g x ++1()n g x -+()n f x ，则n 的最大值为（）A ．5B ．6C ．7D ．854．已知定义在()(),00,-∞⋃+∞上的函数()f x ，且(1)1f =，函数(1)f x +的图象关于点(1,0)-中心对称，对于任意()1212,0,,x x x x ∈+∞≠，都有20192019112212()()0x f x x f x x x ->-成立. 则20191()f x x≤的解集为（） A ．[]1,1- B ．(][),11,-∞-+∞C ．(](],10,1-∞- D ．()2019,2019-55．对于定义在R 上的函数()f x ，若存在正常数a 、b ，使得()()f x a f x b +≤+对一切x ∈R 均成立，则称()f x 是“控制增长函数”.在以下四个函数中：①()21f x x x =++；②()f x =()()2sin f x x =；④()sin f x x x =⋅.是“控制增长函数”的有（）个A ．1B ．2C ．3D ．456．定义：{}min ,a b 表示a ，b 两数中较小的数．例如{}min 2,42=.已知{}2()min ,2f x x x =---，()2()x g x x m m =++∈R ，若对任意1[2,0]x ∈-，存在2[1,2]x ∈，都有()()12f x g x ≤成立，则m 的取值范围为（） A ．[4,)-+∞ B ．[6,)-+∞ C ．[7,)-+∞D ．[10,)-+∞57．定义在R 上的函数()f x 若满足：①对任意1x ，2x 且12x x ≠，都有()()()21210x x f x f x --<⎡⎤⎣⎦；②对任意x ，都有()()2f a x f a x b ++-=，则称函数()f x 为“中心捺函数”，其中点(),a b 称为函数()f x 的中心.已知函数()1y f x =-是以()1,0为中心的“中心捺函数”，若满足不等式()()2222f m n f n m +≤---，当1,12m ⎡⎤∈⎢⎥⎣⎦时，m m n +的最小值为（）A ．2B ．18C ．14D ．1258．给定函数()f x 和()g x ，令()max{(),()}h x f x g x =，对以下三个论断：（1）若()f x 和()g x 都是奇函数，则()h x 也是奇函数；（2）若()f x 和()g x 都是非奇非偶函数，则()h x 也是非奇非偶函数：（3）()f x 和()g x 之一与()h x 有相同的奇偶性；其中正确论断的个数为（） A ．0个B ．1个C ．2个D ．3个59．设函数的定义域是(0,1)，且满足：（1）对于任意的(0,1)x ∈，()0f x >；（2）对于任意的12,(0,1)x x ∈，恒有1122()(1)2()(1)f x f x f x f x -+≤-.则下列结论：①对于任意的(0,1)x ∈，()(1)f x f x >-；②()f x y x x=+在(0,1)上单调递减；③()f x 的图象关于直线12x =对称，其中正确结论的个数是（） A ．0B ．1C ．2D ．360．已知函数()f x 满足对于任意实数m ，n ，总有()()()f m n f m f n +=，其中()0f x ≠，()38f =，且当0x >时()1f x >，()()()31111f xg x f x -+=-+，若()()223g x g x ≥-+，则实数x 的取值范围为( ) A ．1x ≥B ．2x ≥C ．3x ≥D ．4x ≥61．设函数()12...( 201812...20)18f x x x x x x x x R =+++++++-+-++-∈，下列四个命题中真命题的序号是（）(1)()f x 是偶函数；(2)当且仅当0x =时，()f x 有最小值；(3)()f x 在(0,)+∞上是增函数；(4)方程()()255 2f a a f a -+=-有无数个实根.A ．()()14B ．()() 12C ．()() 12()3D ．()()()23462．若直角坐标平面内的两点,P Q 满足条件：①,P Q 都在函数()y f x =的图象上；②,P Q 关于原点对称．则称点对[],P Q 是函数()y f x =的一对“友好点对”(点对[],P Q 与[]，Q P 看作同一对“友好点对”)．已知函数()log 3a x f x x ⎧=⎨+⎩()()040>-≤<x x ()01a a >≠且，若此函数的“友好点对”有且只有一对，则a 的取值范围是( )A ．()()011+，，∞ B ．()111+4，，⎛⎫∞ ⎪⎝⎭C ．114，⎛⎫⎪⎝⎭D ．()01，63．狄利克雷函数是高等数学中的一个典型函数，若1,()0,R x Qf x x C Q∈⎧=⎨∈⎩，则称()f x 为狄利克雷函数．对于狄利克雷函数()f x ，给出下面4个命题：①对任意x ∈R ，都有[()]1f f x =；②对任意x ∈R ，都有()()0f x f x ；③对任意1x R ∈，都有2x ∈Q ，121()()f x x f x +=；④对任意,(,0)a b ∈-∞，都有{|()}{|()}x f x a x f x b >=>．其中所有真命题的序号是（）A ．①④B ．②③C ．①②③D ．①③④64．已知偶函数()f x 满足(4)(4)f x f x +=-，且当(]0,4x ∈时，ln(2)()x f x x=，关于x 的不等式2()()0f x af x +>在区间[]200,200-上有且只有300个整数解，则实数a 的取值范围是（）A ．1(ln 2,ln 6)3--B ．1(ln 2,ln 6]3--C ．13ln 2(ln 6,)34--D ．13ln 2(ln 6,]34-- 65．已知函数()()y f x x =∈R ，给出下列命题：①若()f x 既是奇函数又是偶函数，则()0f x =；②若()f x 是奇函数，且()()11f f -=，则()f x 至少有三个零点； ③若()f x 在R 上不是单调函数，则()f x 不存在反函数；④若()f x 的最大值和最小值分别为M 、()m m M <，则()f x 的值域为[],m M 则其中正确的命题个数是（） A ．1B ．2C ．3D ．466．若曲线C 在顶点为O 的角α内部，A 、B 分别是曲线C 上任意两点，且AOB α≥∠，我们把满足条件的最小角α叫做曲线C 相对点O 的“确界角”，已知O 是坐标原点，曲线C的方程为020x y x ≥=<⎪⎩，那么它相对点O 的“确界角”等于（）A ．3πB ．512πC ．712π D ．23π67．函数()f x 对于任意的x ∈R 都有()()1f x f x <+，给出以下命题: ①()f x 在R 上是增函数；②可能存在0M >，使得对任意的()x R f x M ∈≤，恒成立；③可能存在0x ，使得00(2)1f f x x ⎛⎫=+ ⎪⎝⎭成立； ④()f x 没有最大值和最小值. 则正确的命题的个数为（）. A ．1个B ．2个C ．3个D ．4个68．已知定义在R 上的函数()f x ，满足()00f =，当0x ≠ 时，()ln f x x =，设函数()()g x f x m =-（m 为常数）的零点个数为n ，则n 的所有可能取值构成的集合为（） A ．{}2,4B ．{}3,4C ．{}0,2,4D ．{}0,3,469．函数()f x 在[,]a b 上有定义,若对任意12,[,]x x a b ∈,有12121()[()()]22x x f f x f x +≤+ 则称()f x 在[,]a b 上具有性质P .设()f x 在[1,3]上具有性质P ,现给出如下题:①()f x 在[1,3]上的图像是连续不断的; ②()f x 在[1,3]上具有性质P ;③若()f x 在2x =处取得最大值1,则()1,[1,3]f x x =∈;④对任意1234,,,[1,3]x x x x ∈,有123412341()[()()()()]44x x x x f f x f x f x f x +++≤+++其中真命题的序号（） A ．①② B ．①③C ．②④D ．②③④70．设函数给出下列四个命题：①c = 0时，是奇函数； ②时，方程只有一个实根；③的图象关于点(0 , c)对称； ④方程至多3个实根.其中正确的命题个数是（） A ．1 B ．2 C ．3 D ．4 71．在研究函数22()41240f x x x x +-+的性质时，某同学受两点间距离公式启发将()f x 变形为，2222()(0)(02)(6)(02)f x x x =-+--+-，并给出关于函数()f x 以下五个描述：①函数()f x 的图像是中心对称图形；②函数()f x 的图像是轴对称图形； ③函数()f x 在[0,6]上是增函数；④函数()f x 没有最大值也没有最小值； ⑤无论m 为何实数，关于x 的方程()0f x m -=都有实数根.其中描述正确的是__________.72．已知函数()2f x x =，()g x 为偶函数，且当0x ≥时，()24g x x x =-.记{},max ,,a a ba b b a b≥⎧=⎨<⎩.给出下列关于函数()()(){}()max ,F x f x g x x R =∈的说法：①当6x ≥时，()24F x xx =-；②函数()F x 为奇函数；③函数()F x 在[]22-,上为增函数；④函数()F x 的最小值为0，无最大值.其中正确的是______.73．若函数()f x 同时满足：①对于定义域上的任意x ，恒有()()0f x f x +-=；②对于定义域上的任意12,x x ，当12x x ≠时，恒有()()12120f x f x x x -<-，则称函数()f x 为“理想函数”．给出下列四个函数中：①1()f x x x =+； ②()13f x x =； ③()11x x e f x e -=+； ④ ()22,0,0x x f x x x ⎧-≥=⎨<⎩，能被称为“理想函数”的有_____（请将所有正确命题的序号都填上）．74．已知定义在R 上的函数()f x ，若函数()1f x +为偶函数，函数()2f x +为奇函数，则()20191i f i =∑＝_____.75．已知()()ln 0f x a x x a =+>对于区间11,43⎡⎤⎢⎥⎣⎦内的任意两个相异实数1x ,2x ,恒有()()121211f x f x x x -<-成立,则实数a 的取值范围是______. 76．已知定义在[)1,+∞的函数()f x tx x=+，对满足121x x -≤的任意实数1x ，2x ，都有()()121f x f x -≤，则实数t 的取值范围为__________.77．定义函数()f x 如下:对于实数x ,如果存在整数m ,使得1||2x m -<,则()f x m =.则下列结论:①()f x 是实数R 上的递增函数;②()f x 是周期为1的函数;③()f x 是奇函数;④函数()f x 的图像与直线y x =有且仅有一个交点.则正确结论的序号是______.78．已知函数11()12x k f x x -++=-+,若对任意的实数123,,x x x ,不等式123()()()f x f x f x +≥恒成立,则实数k 的取值范围是________.79．已知，若定义域为[]0,1的函数()f x 同时满足以下三条：①对任意的[]0,1x ∈，总有()0f x ≥；②()11f =；③当10x ≥，20x ≥，121x x +≤时，()()()1212f x x f x f x +≥+成立，则称函数()f x 为Z函数.以下说法：（1）若函数()f x 为Z 函数，则()00f =；（2）函数()[]()210,1xg x x =-∈是一个Z 函数；（3）若函数()f x 为Z 函数，则函数在区间[]0,1上单调递增；（4）若函数()f x 、()g x 均为Z 函数，则函数()()mf x ng x +（0m >，0n >，且1m n +=）必为Z 函数，正确的有__________（填写序号）. 80．关于函数()1x f x x =-，给出以下四个命题，其中真命题的序号是_______.①0x >时，()y f x =单调递减且没有最值； ②方程()()0f x kx b k =+≠一定有解；③如果方程()f x k =有解，则解的个数一定是偶数； ④()y f x =是偶函数且有最小值. 81．方程||||1169x x y y +=-的曲线即为函数()y f x =的图象，对于函数()y f x =，有如下结论：①()f x 在(),-∞+∞上单调递减；②函数()4()3F x f x x =+存在零点；③函数()f x 的值域是R ；④若函数()g x 和()f x 的图象关于原点对称，则函数()y g x =的图象就是||||1169x x y y +=确定的曲线其中所有正确的命题序号是________.82．定义：如果函数()y f x =在定义域内给定区间[],a b 上存在()00x a x b <<，满足()()()0f b f a f x b a-=-，则称函数()y f x =是[],a b 上的“平均值函数”，0x 是它的一个均值点，例如2y x 是[]1,1-上的平均值函数，0就是它的均值点.现有函数()3f x x mx =+是[]1,1-上的平均值函数，则实数m 的取值范围是________.83．已知()f x x x =，若()()()220f x m m f x m -≤>对任意1x ≥恒成立，则实数m 的取值范围为____________.84．已知函数f （x ）的定义域为R ，当x ＞0时满足：①f （x ）﹣2f （﹣x ）＝0；②对任意x 1＞0，x 2＞0，x 1≠x 2有（x 1﹣x 2）（f （x 1）﹣f （x 2））＞0恒成立：③f （4）＝2f （2）＝2，则不等式x [f （x ）﹣1]＞0的解集为_____（用区间表示）85．若定义在[,](0)m m m ->上的函数()42cos (0,1)1x xa f x x x a a a ⋅+=+>≠+的最大值和最小值分别是M 、N ，则M N +=_________．86．已知函数()()131log 312xf x abx =++为偶函数，()22x x a b g x +=+为奇函数，其中a 、b 为常数，则()()()()2233100100a b a bab a b ++++++⋅⋅⋅++=___________87．已知定义在R 上的函数()f x 满足(2)(2)f x f x +=-，且当(2,2]x ∈-时，2111,02()22,20x x x f x x x x x x ⎧⎛⎫+--<≤⎪ ⎪=⎨⎝⎭⎪---<≤⎩，若函数()()log a g x f x x =-，(1)a 在(0,5)x ∈上有四个零点，则实数a 的取值范围为_____________.88．已知函数()f x ，对任意的[0,)x ∈+∞，恒有(2)()f x f x +=成立，且当[0,2)x ∈时，()2f x x =-.则方程1()f x x n=在区间[0,2)n （其中*n N ∈）上所有根的和为______. 89．已知函数f (x )=(12)|x |,若函数g (x )=f (x ﹣1)+a (e x ﹣1+e ﹣x +1)存在最大值M ,则实数a 的取值范围为_____90．已知函数()f x x =，()2252g x x mx m =-+-（m R ∈），对于任意的[]12,2x ∈-，总存在[]22,2x ∈-，使得()()12f x g x =成立，则实数m 的取值范围是______．91．若函数()f x 对其定义域内的任意1x ，2x ，当()()12f x f x =时总有12x x =，则称()f x 为紧密函数，例如函数()ln (0)f x x x =>是紧密函数，下列命题：①紧密函数必是单调函数；②函数()22(0)x x a f x x x++=>在0a <时是紧密函数；③函数()3log ,22,2x x f x x x ≥⎧=⎨-<⎩是紧密函数；④若函数()f x 为定义域内的紧密函数，12x x ≠，则()()12f x f x ≠；⑤若函数()f x 是紧密函数且在定义域内存在导数，则其导函数()'f x 在定义域内的值一定不为零．其中的真命题是______．92．已知函数(2)(2)f x f x +=-，且(]1,3x ∈-时，(](]1,1(),12,1,3x f x x x ∈-=--∈⎪⎩若方程()mf x x =恰有5个实数解（其中0m >），则m 的取值范围为______________. 93．已知()f x 是定义在[4,4]-上的奇函数，1()(2)3g x f x =-+．当[)2,0,2]0(x ∈-⋃时，||1()21x g x =-，(0)0g =则方程12()log (1)g x x =+的解的个数为_________．94．某同学在研究函数 f （x ）=1xx+（x ∈R ）时，分别给出下面几个结论：①等式f （-x ）=-f （x ）在x ∈R 时恒成立； ②函数f （x ）的值域为（-1，1）； ③若x 1≠x 2，则一定有f （x 1）≠f （x 2）； ④方程f （x ）=x 在R 上有三个根．其中正确结论的序号有______．（请将你认为正确的结论的序号都填上）95．已知()y f x =是定义在R 上的增函数，且()y f x =的图像关于点(6,0)对称．若实数,x y 满足不等式22(6)(836)0f x x f y y -+-+≤，则22x y +的取值范围是_____．96．已知函数()f x k =的定义域和值域都是[],a b ，则实数k 的取值范围是_________.97．对于具有相同定义域D 的函数()f x 和()g x ，若存在函数()h x kx b =+(k ，b 为常数)，对任给的正数m ，存在相应的0x D ∈，使得当x D ∈且0x x >时，总有0()()0()()f x h x mh x g x m<-<⎧⎨<-<⎩，则称直线:l y kx b =+为曲线()y f x =和()y g x =的“分渐近线”．给出定义域均为{|1}D x x =>的四组函数如下： ①()2f x x =，()g x =②()102xf x -=+，()23x g x x-=； ③21()x f x x+=,ln 1()ln x x g x x +=；④22()1x f x x =+,()()21xg x x e -=-- 其中，曲线()y f x =和()y g x =存在“分渐近线”的是________．98．对于函数()y f x =，若存在定义域D 内某个区间[,]a b ，使得()y f x =在[,]a b 上的值域也是[,]a b ，则称函数()y f x =在定义域D 上封闭.如果函数()(0)1||kxf x k x =≠+在R 上封闭，那么实数k 的取值范围是______.99．定义域为R 的函数()f x 同时满足以下两条性质： ①存在0x ∈R ,使得()00f x ≠； ②对于任意x ∈R ，有(1)2()f x f x +=.根据以下条件，分别写出满足上述性质的一个函数. （i ）若()f x 是增函数，则()f x =_______ ；（ⅱ）若()f x 不是单调函数，则()f x =_______ .100．太极图是由黑白两个鱼形纹组成的图案，俗称阴阳鱼，太极图展现了一种相互转化，相对统一的和谐美，定义：能够将圆O 的周长和面积同时等分成两个部分的函数称为圆O 的一个“太极函数”，则下列有关说法中：①对于圆22:1O x y +=的所有非常数函数的太极函数中，都不能为偶函数；②函数()sin 1f x x =+是圆()22:11O x y +-=的一个太极函数；③直线()()12110m x m y +-+-=所对应的函数一定是圆()()()222:210O x y R R -+-=>的太极函数；④若函数()()3f x kx kx k R =-∈是圆22:1O x y +=的太极函数，则()2,2.k ∈-所有正确的是__________．101．定义在实数集R 上的偶函数()f x 满足2(1)12()()f x f x f x +=-，则2019()2f =________. 102．设函数()xxxf x a b c =+-，其中0,0c a c b >>>>，若a 、b 、c 是ABC 的三条边长，则下列结论：①对于一切(),1x ∈-∞都有()0f x >；②存在0x >使x xa 、x b 、x c 不能构成一个三角形的三边长；③ABC 为钝角三角形，存在()1,2x ∈，使()0f x =，其中正确的个数为______个 A ．3 B ．2C ．1D ．0103．若1122m x m -<≤+（其中m 为整数），则称m 是离实数x 最近的整数，记作{}x m =.下列关于函数(){}||f x x x =-的命题中，正确命题的序号是__________．①函数()y f x =的定义域为R ，值域为1[0,]2； ②函数()y f x =是奇函数； ③函数()y f x =的图象关于直线2kx =（k Z ∈）对称； ④函数()y f x =是周期函数，最小正周期为1； ⑤函数()y f x =在区间11[,]22-上是增函数.104．某学校为了加强学生数学核心素养的培养，锻炼学生自主探究学习的能力，他们以教材第82页第8题的函数1()lg1xf x x-=+为基本素材，研究该函数的相关性质，取得部分研究成果如下： ①同学甲发现：函数()f x 的定义域为(1,1)-；②同学乙发现：函数()f x 是偶函数； ③同学丙发现：对于任意的(1,1)x ∈-都有22()2()1xf f x x =+； ④同学丁发现：对于任意的,(1,1)a b ∈-，都有()()()1a bf a f b f ab++=+； ⑤同学戊发现：对于函数()f x 定义域中任意的两个不同实数12,x x ，总满足1212()()0f x f x x x ->-.其中所有正确研究成果的序号是__________．105．已知函数()3241f x x ax x =-+++在(]0,2上是增函数，函数()ln 2ln g x x a x =--，若312,,x x e e ⎡⎤∀∈⎣⎦（e 为自然对数的底数）时，不等式()()125g x g x -≤恒成立，则实数a 的取值范围是______.。

01坐标系训练题(含经典例题+答案)

坐标系训练题一．选择题（共15小题）1．在极坐标方程中，曲线C的方程是ρ=4sinθ，过点（4，）作曲线C的切线，则切线长为（）A．4 B．C．2D．22．在极坐标系中，点（2，﹣）到圆ρ=﹣2cosθ的圆心的距离为（）A．2 B．C．D．3．在极坐标系中，圆ρ=2被直线ρsinθ=1截得的弦长为（）A．B．2 C．2D．34．在极坐标系中，圆ρ=2cosθ的半径为（）A．B．1 C．2 D．45．在极坐标系中，曲线C：ρ=2sinθ上的两点A，B对应的极角分别为，则弦长|AB|等于（）A．1 B．C．D．26．在极坐标系中，曲线ρ2﹣6ρcosθ﹣2ρsinθ+6=0与极轴交于A，B两点，则A，B两点间的距离等于（）A．B． C．D．47．在极坐标系中，曲线ρ=2cosθ是（）A．过极点的直线 B．半径为2 的圆C．关于极点对称的图形D．关于极轴对称的图形8．过点（2，）且平行于极轴的直线的坐标方程为（）A．ρsinθ=B．ρcosθ=C．ρsinθ=2 D．ρcosθ=29．在极坐标方程中，曲线C的方程是ρ=4sinθ，过点（4，）作曲线C的切线，切线长为（）A．4 B．7 C．2D．3 210．极坐标系中，点P，Q分别是曲线C1：ρ=1与曲线C2：ρ=2上任意两点，则|PQ|的最小值为（）A．1 B．C．D．211．已知点P的极坐标是，则过点P且垂直于极轴的直线的极坐标方程是（）A．ρ=1 B．ρ=cosθC． D．12．在极坐标系中，关于曲线C：ρ=4sin（θ﹣），下列判断中正确的是（）A．曲线C关于直线θ=对称B．曲线C关于直线θ=对称C．曲线C关于点（2，）对称D．曲线C关于点（0，0）对称13．在极坐标系中，直线l的方程为，则点到直线l的距离为（）A．B．C．D．14．已知点M的极坐标为，那么将点M的极坐标化成直角坐标为（）A．B．C．D．15．极坐标方程ρcosθ=2sin2θ表示的曲线为（）A．一条射线和一个圆 B．一条直线和一个圆C．两条直线D．一个圆二．解答题（共15小题）16．（2015•河北）在直角坐标系xOy中，直线C1：x=﹣2，圆C2：（x﹣1）2+（y﹣2）2=1，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．（Ⅰ）求C1，C2的极坐标方程；（Ⅱ）若直线C3的极坐标方程为θ=（ρ∈R），设C2与C3的交点为M，N，求△C2MN的面积．17．（2015•江苏）已知圆C的极坐标方程为ρ2+2ρsin（θ﹣）﹣4=0，求圆C的半径．18．（2015•新课标II）在直角坐标系xOy中，曲线C1：（t为参数，t≠0，0≤α＜π）在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，曲线C3：ρ=2co sθ．（1）求C2与C3交点的直角坐标（2）若C2与C1相交于点A，C1与C3相交于点B，求|AB|的最大值．19．（2015•陕西）在直角坐标系xOy中，直线l的参数方程为（t为参数），以原点为极点，x轴正半轴为极轴建立极坐标系，⊙C的极坐标方程为ρ=2sinθ．（Ⅰ）写出⊙C的直角坐标方程；（Ⅱ）P为直线l上一动点，当P到圆心C的距离最小时，求P的直角坐标．20．已知曲线C1的极坐标方程为ρ=6cosθ，曲线C2的极坐标方程为θ=（p∈R），曲线C1，C2相交于A，B两点．（Ⅰ）把曲线C1，C2的极坐标方程转化为直角坐标方程；（Ⅱ）求弦AB的长度．21．在直角坐标系xOy中，l是过定点P（4，2）且倾斜角为α的直线；在极坐标系（以坐标原点O为极点，以x轴非负半轴为极轴，取相同单位长度）中，曲线C的极坐标方程为ρ=4cosθ（Ⅰ）写出直线l的参数方程，并将曲线C的方程化为直角坐标方程；（Ⅱ）若曲线C与直线相交于不同的两点M、N，求|PM|+|PN|的取值范围．22．在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．已知曲线C1的极坐标方程为ρ2=，直线l的极坐标方程为ρ=．（Ⅰ）写出曲线C1与直线l的直角坐标方程；（Ⅱ）设Q为曲线C1上一动点，求Q点到直线l距离的最小值．23．已知极坐标系的极点与直角坐标系的原点重合，极轴与x轴的正半轴重合．若直线的极坐标方程为ρsin （）=3．（1）把直线的极坐标方程化为直角坐标系方程；（2）已知P为椭圆C：上一点，求P到直线的距离的最大值．24．在直角坐标系xOy中，以原点O为极点，以x轴正半轴为极轴，圆C的极坐标方程为（Ⅰ）将圆C的极坐标方程化为直角坐标方程；（Ⅱ）过点P（2，0）作斜率为1直线l与圆C交于A，B两点，试求的值．25．在极坐标系Ox中，直线C1的极坐标方程为ρsinθ=2，M是C1上任意一点，点P在射线OM上，且满足|OP|•|OM|=4，记点P的轨迹为C2．（Ⅰ）求曲线C2的极坐标方程；（Ⅱ）求曲线C2上的点到直线ρcos（θ+）=距离的最大值．26．在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，已知某圆的极坐标方程为：p2﹣4pcosθ+2=0（1）将极坐标方程化为普通方程（2）若点P（x，y）在该圆上，求x+y的最大值和最小值．27．在直角坐标平面内，直线l过点P（1，1），且倾斜角α=以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知圆C的极坐标方程为ρ=4sinθ（Ⅰ）求圆C的直角坐标方程；（Ⅱ）设直线l与圆C 交于A、B两点，求|PA|•|PB|的值．28．在极坐标系中，设圆C1：ρ=4cosθ 与直线l：θ=（ρ∈R）交于A，B两点．（Ⅰ）求以AB为直径的圆C2的极坐标方程；（Ⅱ）在圆C1任取一点M，在圆C2上任取一点N，求|MN|的最大值．29．在极坐标系中，曲线C：ρ=2acosθ（a＞0），l：ρcos（θ﹣）=，C与l有且仅有一个公共点．（Ⅰ）求a；（Ⅱ）O为极点，A，B为C上的两点，且∠AOB=，求|OA|+|OB|的最大值．30．在平面直角坐标xOy中，已知圆，圆．（1）在以O为极点，x轴正半轴为极轴的极坐标系中，分别求圆C1，C2的极坐标方程及这两个圆的交点的极坐标；（2）求圆C1与C2的公共弦的参数方程．一．选择题（共15小题）1．C；2．D；3．C；4．B；5．C；6．B；7．D；8．A；9．C；10．A； 11．D；12．A； 13．B； 14．D； 15．B；二．解答题（共15小题）16.解：（Ⅰ）由于x=ρcosθ，y=ρsinθ，∴C1：x=﹣2 的极坐标方程为ρcosθ=﹣2，故C2：（x﹣1）2+（y﹣2）2=1的极坐标方程为：（ρcosθ﹣1）2+（ρsinθ﹣2）2=1，化简可得ρ2﹣（2ρcosθ+4ρsinθ）+4=0．（Ⅱ）把直线C3的极坐标方程θ=（ρ∈R）代入ρ2﹣（2ρcosθ+4ρsinθ）+4=0，求得ρ1=2，ρ2=，∴|MN|=ρ1﹣ρ2=，由于圆C2的半径为1，∴C2M⊥C2N，△C2MN的面积为•C2M•C2N=．17．解：圆的极坐标方程为ρ2+2ρsin（θ﹣）﹣4=0，可得ρ2﹣2ρcosθ+2ρsinθ﹣4=0，化为直角坐标方程为x2+y2﹣2x+2y﹣4=0，化为标准方程为（x﹣1）2+（y+1）2=6，圆的半径r=．18．解：（1）曲线C2：ρ=2sinθ化为ρ2=2ρsinθ，∴x2+y2=2y．曲线C3：ρ=2cosθ化为ρ2=2ρcosθ，x2+y2=2x．联立，解得或．∴C2与C3交点的直角坐标为（0，0）和（，）；（2）曲线C1的极坐标方程为θ=α（ρ∈R，ρ≠0），其中0≤α＜π．因此A的极坐标为（2sinα，α），B的极坐标为（2cosα，α），所以|AB|=|2sin cosα|=4|sin（α﹣）|，当α=时，|AB|取得最大值，最大值为4．19．解：（I）由⊙C的极坐标方程为ρ=2sinθ．∴ρ2=2，化为x2+y2=，配方为=3．（II）设P，又C．∴|PC|==≥2，因此当t=0时，|PC|取得最小值2．此时P（3，0）．20．解：（Ⅰ）曲线C2：（p∈R）表示直线y=x，曲线C1：ρ=6cosθ，即ρ2=6ρcosθ所以x2+y2=6x即（x﹣3）2+y2=9（Ⅱ）∵圆心（3，0）到直线的距离，r=3所以弦长AB==．∴弦AB的长度．21．解：（I）直线l的参数方程为（t为参数）．曲线C的极坐标方程ρ=4cosθ可化为ρ2=4ρcosθ．把x=ρcosθ，y=ρsinθ代入曲线C的极坐标方程可得x2+y2=4x，即（x﹣2）2+y2=4．（II）把直线l的参数方程为（t为参数）代入圆的方程可得：t2+4（sinα+cosα）t+4=0．∵曲线C与直线相交于不同的两点M、N，∴△=16（sinα+cosα）2﹣16＞0，∴sinαcosα＞0，又α∈[0，π），∴．又t1+t2=﹣4（sinα+cosα），t1t2=4．∴|PM|+|PN|=|t1|+|t2|=|t1+t2|=4|sinα+cosα|=，∵，，∴．∴|PM|+|PN|的取值范围是．22．（Ⅰ）以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，曲线C1的极坐标方程为ρ2=，直线l的极坐标方程为ρ=，根据ρ2=x2+y2，x=ρcosθ，y=ρsinθ，则C1的直角坐标方程为x2+2y2=2，直线l的直角坐标方程为．（Ⅱ）设Q，则点Q到直线l的距离为=，当且仅当，即（k∈Z）时取等号．∴Q点到直线l距离的最小值为．23．解：（1）把直线的极坐标方程为ρsin（）=3展开得，化为ρsinθ﹣ρcosθ=6，得到直角坐标方程x﹣y+6=0．（2）∵P为椭圆C：上一点，∴可设P（4cosα，3sinα），利用点到直线的距离公式得d===．当且仅当sin（α﹣φ）=﹣1时取等号．∴P到直线的距离的最大值是．24．解：（Ⅰ）由x，可得ρ=4cosθ﹣4sinθ，∴ρ2=4ρcosθ﹣4ρsinθ，∴x2+y2=4x﹣4y，即（x﹣2）2+（y+2）2=8；（Ⅱ）过点P（2，0）作斜率为1直线l的参数方程为代入（x﹣2）2+（y+2）2=8得t2+2t﹣4=0，A，B对应的参数为t1、t2，则t1+t2=﹣2，t1t2=﹣4，由t的意义可得=+==．25．解：（Ⅰ）设P（ρ1，θ），M（ρ2，θ），由|OP|•|OM|=4，得ρ1ρ2=4，即．∵M是C1上任意一点，∴ρ2sinθ=2，即，ρ1=2sinθ．∴曲线C2的极坐标方程为ρ=2sinθ；（Ⅱ）由ρ=2sinθ，得ρ2=2ρsinθ，即x2+y2﹣2y=0．化为标准方程x2+（y﹣1）2=1．则圆心坐标为（0，1），半径为1．由直线ρcos（θ+）=，得：．即：x﹣y=2．圆心（0，1）到直线x﹣y=2的距离为d=．∴曲线C2上的点到直线ρcos （θ+）=距离的最大值为．26．解：（1）ρ2﹣4ρcosθ+2=0，化为直角直角坐标方程：x2+y2﹣4x+2=0；（2）由x2+y2﹣4x+2=0化为（x﹣2）2+y2=2，令x﹣2=cosα，y=sinα，α∈[0，2π）．则x+y=+2+=2+2，∵∈[﹣1，1]，∴（x+y）∈[0，4]．其最大值、最小值分别为4，0．27．解：（Ⅰ）由圆C的极坐标ρ=4sinθ，即ρ2=4ρsinθ，可得直角坐标方程为x2+（y﹣2）2=4，表示以（0，2）为圆心、半径等于2的圆．（Ⅱ）由直线l过点P（1，1），且倾斜角α=，可得直线的方程为．把直线方程代入曲线方程化简可得+﹣4（1+t），解得t1=，t2=﹣，∴|PA|•|PB|=|t1|•|t2|=2．28．解：（Ⅰ）以极点为坐标原点，极轴为x轴的正半轴，建立直角坐标系，则由题意得圆C1：ρ=4cosθ 化为ρ2=4ρcosθ，∴圆C1的直角坐标方程x2+y2﹣4x=0．直线l的直角坐标方程y=x．由，解得或．∴A（0，0），B（2，2）．从而圆C2的直角坐标方程为（x﹣1）2+（y﹣1）2=2，即x2+y2=2x+2y．将其化为极坐标方程为：ρ2=2ρcosθ+2ρsinθ．（Ⅱ）∵，∴|MN|max=|C1C2|+r1+r2=+2+=2+2．29．解：（Ⅰ）曲线C：ρ=2acosθ（a＞0），变形ρ2=2ρacosθ，化为x2+y2=2ax，即（x﹣a）2+y2=a2．∴曲线C是以（a，0）为圆心，以a为半径的圆；由l：ρcos（θ﹣）=，展开为，∴l的直角坐标方程为x+y﹣3=0．由直线l与圆C相切可得=a，解得a=1．（Ⅱ）不妨设A的极角为θ，B的极角为θ+，则|OA|+|OB|=2cosθ+2cos（θ+）=3cosθ﹣sinθ=2cos （θ+），当θ=﹣时，|OA|+|OB|取得最大值2．30．解：（1）圆C1的极坐标方程为ρ=2，圆C2的极坐标方程为ρ=4cosθ，由得，故圆C1，C2交点坐标为圆．（2）由（1）得，圆C1，C2交点直角坐标为，故圆C1与C2的公共弦的参数方程为。

初中化学坐标曲线题解题对策

初中化学坐标曲线题解题对策钱华萍(云南省曲靖市民族中学云南曲靖655000)【中图分类号】G633.8【文献标识码】B【文章编号】2095-3089(2016)16-0182-03化学坐标曲线题是近年来中考的热点题之一,常出现在选择题最后一题,且有一定难度,常属控制满分类题,也是考试过程中学生容易丢分的题。

这类题的特点是给出具体的文字叙述,并利用直角坐标系来描述有关化学量之间的函数关系,要求学生选出能正确对应或不能正确对应的选项。

通过对近两年全国各地的中考试题中坐标曲线选择题的分析,我们会发现常考查的坐标曲线选择题分以下几类:PH 变化曲线、化学反应中物质质量的变化曲线、溶液中相关量的变化曲线、电解水生成气体体积曲线等。

针对学生在考试过程中坐标曲线题容易丢分的这一问题,笔者将自己教学中对解答坐标曲线图像题的一些方法进行归纳整理,希望对提高学生对这类题解答有很大的帮助作用。

一、pH 变化曲线1.溶液稀释的pH 变化曲线图1图2(1)碱性溶液稀释时,由于碱性溶液的pH>7,而水的pH=7,随着水的质量的增加,pH 不断减小,但不会小于或等于7,变化曲线如图1。

(2)酸性溶液稀释时,由于酸性溶液的pH<7,而水的pH=7,随着水的质量的增加,pH 不断增大,但不会大于或等于7,变化曲线如图2。

学生做题时只要明确,酸加水稀释依然是酸,pH<7;碱加水稀释依然是碱,pH>7,所以随着水的不断加入,曲线只会不断的接近7,但不会跃过7。

2.化学反应过程中溶液的pH 曲线图3图4图5(1)向酸性溶液中(如稀盐酸)加入碱性溶液(如NaOH 溶液或碳酸钠溶液),在0点时溶液呈酸性,溶液的pH<7;当恰好完全反应时,溶液呈中性,溶液的pH=7;随着碱性溶液的继续加入,溶液呈碱性,溶液的pH>7,变化曲线如图3。

(2)向碱性溶液中加入酸性溶液时,在0点时溶液呈碱性,溶液的pH>7;当酸、碱恰好完全反应时,溶液呈中性,溶液的pH=7;随着酸性溶液的继续加入,溶液呈酸性,溶液的pH<7,变化曲线如图4。

江苏专版2020中考化学复习方案题型突破01图表类试题试题

题型突破(一) 图表类试题类型一坐标曲线类|针对训练|1.[2017·淮安]下列四个图像中,能正确反映对应变化关系的是 ( )A.用CuFe2O4-x作催化剂,光分解水生成氢气与氧气B.向氯化钠的饱和溶液中加入硝酸钾C.向混有少量硫酸的硫酸铜溶液中加入氢氧化钠溶液D.向一定质量的碳酸钠溶液中加水2.向一定量硝酸银和硝酸亚铁的混合溶液中加入锌粉,充分反应后所得溶液的质量与加入锌粉的质量关系如图T1-3所示。

下列说法正确的是( )图T1-3A.a点所得固体为银和铁B.b点所得溶液中的溶质为硝酸银、硝酸亚铁和硝酸锌C.c点所得溶液中的溶质为硝酸亚铁和硝酸锌D.d点所得固体为银、铁和锌3.[2018·河北]图T1-4所示的四个图像,分别对应四种过程,其中正确的是( )图T1-4A.①分别向等质量Mg和Cu中加入足量等质量、等浓度的稀硫酸B.②分别向等质量且足量的Zn中加入等质量、不同浓度的稀硫酸C.③分别向等质量且足量的Mg和Zn中,加入等质量、等浓度的稀硫酸D.④分别向等质量的Mg和Zn中加入等质量、等浓度且足量的稀硫酸4.[2019·湘潭]下列图像能正确反映其对应变化关系的是( )图T1-5A.某温度下,将一定量饱和氯化钠溶液恒温蒸发B.相同质量的等质量分数的盐酸分别与足量的固体反应C.向一定量氯化铜和稀盐酸的混合溶液中逐滴加入氢氧化钠溶液D.往盛有硫酸铜溶液的烧杯中加入铁粉至过量5.[2018·重庆A]常温下向一定质量的稀盐酸中逐渐加入镁条,充分反应(忽略挥发)。

下列图像(如图T1-6所示)正确的是 ( )图T1-6A. ①②B. ②③C. ①④D. ②④6.[2017·镇江](双选)向一定质量的Ba(OH)2溶液中先后滴加CuSO4、H2SO4溶液,过程中加入溶液的质量与产生沉淀的质量关系如图T1-7所示。

下列说法正确的是 ( )图T1-7A.a点对应溶液pH>7B.b点对应溶液中溶质有2种C.m=3.31D.取c点对应溶液,滴加NaOH溶液,立刻产生沉淀7.[2018·徐州节选]某化学兴趣小组借助氧气传感器探究微粒的运动,数据处理软件可实时绘出氧气体积分数随时间变化的曲线(如图T1-8甲)。