材料力学知识点总结.doc
材料力学知识点总结

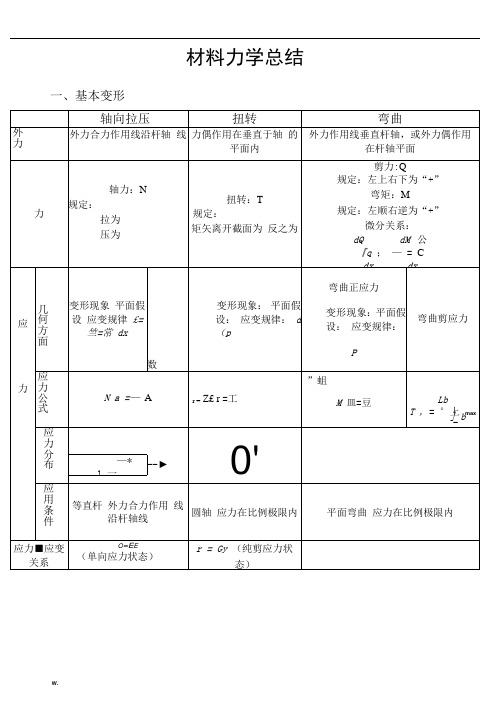
材料力学总结一、基本变形轴向拉压扭转弯曲外力外力合力作用线沿杆轴线力偶作用在垂直于轴的平面内外力作用线垂直杆轴,或外力偶作用在杆轴平面内力轴力:N规定:拉为“+”压为“-”扭转:T规定:矩矢离开截面为“+”反之为“-”剪力:Q规定:左上右下为“+”弯矩:M规定:左顺右逆为“+”微分关系:qdxdQ;QdxdM应力几何方面变形现象:平面假设:应变规律:dxld常数变形现象:平面假设:应变规律:dxd弯曲正应力弯曲剪应力变形现象:平面假设:应变规律:y应力公式ANPITtWTmaxZIM yZWMmaxbIQSbIQSzzzmaxmax*应力分布应用条件等直杆外力合力作用线沿杆轴线圆轴应力在比例极限内平面弯曲应力在比例极限内应力-应变关系E(单向应力状态)G(纯剪应力状态)强度条件nANumaxmax塑材:su脆材:bumaxmaxtWT弯曲正应力1.ctmax2.ctccmactt max弯曲剪应力bISQzmaxmaxmax轴向拉压扭转弯曲刚度条件max180PGIT注意:单位统一yy maxmax变形EAN dxl d ;EANL LEA —抗拉压刚度ZGIT dx d PGITL GI p —抗扭刚度EIx M x )()(1EIx M y)(''EI —抗弯刚度应用条件应力在比例极限圆截面杆,应力在比例极限小变形,应力在比例极限矩形A=bh 6;1223bh W bhI ZZ实心圆A=42d 16;3234dW dI tP32;6434dW dI ZZ空心圆)1(422DA)1(16)1(324344dW d I tP)1(6444dI Z )1(3243dW Z其它公式(1)'(2))1(2E G剪切(1)强度条件:AQ A —剪切面积(2)挤压条件:bsJbsbsA P A j —挤压面积矩形:A Q23max圆形:A Q 34max环形:AQ 2maxmax均发生在中性轴上二、还有:(1)外力偶矩:)(9549m N n N m N —千瓦;n —转/分(2)薄壁圆管扭转剪应力:tr T 22(3)矩形截面杆扭转剪应力:hb G T hb T32max;三、截面几何性质(1)平行移轴公式:;2A a I I ZCZ abAI I cc Y Z YZ(2)组合截面:1.形心:ni ini ci i cA y A y 11;ni ini cii cA z A z 112.静矩:ci i Zy A S ;cii y z A S 3. 惯性矩:iZ ZI I )(;iy yI I )(四、应力分析:(1)二向应力状态(解析法、图解法)a .解析法:b.应力圆::拉为“+”,压为“-”:使单元体顺时针转动为“+”:从x 轴逆时针转到截面的法线为“+”2sin 2cos 22xyx y x 2cos 2sin 2xyxyxxtg 2222minmax22xy x y xc :适用条件:平衡状态(2)三向应力圆:1m a x;3min ;231maxxyxnD'DAcB(3)广义虎克定律:)(13211E )(1zy xxE )(11322E )(1xz y y E )(12133E)(1yx z z E*适用条件:各向同性材料;材料服从虎克定律(4)常用的二向应力状态1.纯剪切应力状态:1,02,32.一种常见的二向应力状态:2231222234r 2243r 五、强度理论破坏形式脆性断裂塑性断裂强度理论第一强度理论(最大拉应力理论)莫尔强度理论第三强度理论(最大剪应力理论)第四强度理论(形状改变比能理论)破坏主要因素单元体内的最大拉应力单元体内的最大剪应力单元体内的改变比能破坏条件b1smaxfsfuu 强度条件131适用条件脆性材料脆性材料塑性材料塑性材料*相当应力:r11r ,313r ,][212132322214r 13x六、材料的力学性质脆性材料<5%塑性材料≥5%低碳钢四阶段:(1)弹性阶段(2)屈服阶段(3)强化阶段(4)局部收缩阶段强度指标bs,塑性指标,Etg拉压扭低碳钢断口垂直轴线剪断s b铸铁拉断断口垂直轴线b剪断拉断断口与轴夹角45o b七.组合变形类型斜弯曲拉(压)弯弯扭弯扭拉(压)简图公式)sincos(yZ IzIyMWMAP][4223r][3224r][4)(223NMr][3)(224NMr强度条件)sincos(maxmaxyZ WWM][WMAP maxmaxmax][圆截面][223ZWTMr][75.0224ZWTMr22)(4)(3tZ WTANWMr][22)(4)(4tZ WTANWMr][中性轴tgIIZytgyZyZyZeiAeIy2*bsαe4545o中性轴ZαMp滑移线与轴线45,剪断只有s,无b八、压杆稳定欧拉公式:2min2)(l EI P cr,22Ecr,应用范围:线弹性范围,cr <p ,>p柔度:iul ;E;ba s,柔度是一个与杆件长度、约束、截面尺寸、形状有关的数据,λ↑P cr ↓σcr ↓>p ——大柔度杆:22Ecro <<p ——中柔度杆:cr=a-b <0——小柔度杆:cr =s稳定校核:安全系数法:w Icr n P P n ,折减系数法:][AP 提高杆件稳定性的措施有:1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度;断裂特征:断裂前无显著塑性变形;断口特征:断口成光滑区和粗糙区。
材料力学知识点归纳总结(完整版)

材料力学知识点归纳总结(完整版)1.材料力学:研究构件(杆件)在外力作用下内力、变形、以及破坏或失效一般规律的科学,为合理设计构件提供有关强度、刚度、稳定性等分析的基本理论和方法。
2.理论力学:研究物体(刚体)受力和机械运动一般规律的科学。
3.构件的承载能力:为保证构件正常工作,构件应具有足够的能力负担所承受的载荷。
构4.件应当满足以下要求:强度要求、刚度要求、稳定性要求5.变形固体的基本假设:材料力学所研究的构件,由各种材料所制成,材料的物质结构和性质虽然各不相同,但都为固体。
任何固体在外力作用下都会发生形状和尺寸的改变——即变形。
因此,这些材料统称为变形固体。
第二章:内力、截面法和应力概念1.内力的概念:材料力学的研究对象是构件,对于所取的研究对象来说,周围的其他物体作用于其上的力均为外力,这些外力包括荷载、约束力、重力等。
按照外力作用方式的不同,外力又可分为分布力和集中力。
2.截面法:截面法是材料力学中求内力的基本方法,是已知构件外力确定内力的普遍方法。
已知杆件在外力作用下处于平衡,求m-m截面上的内力,即求m-m截面左、右两部分的相互作用力。
首先假想地用一截面m-m截面处把杆件裁成两部分,然后取任一部分为研究对象,另一部分对它的作用力,即为m-m截面上的内力N。
因为整个杆件是平衡的,所以每一部分也都平衡,那么,m-m截面上的内力必和相应部分上的外力平衡。
由平衡条件就可以确定内力。
例如在左段杆上由平衡方程1 N -F =0 可得N=F 3.综上所述,截面法可归纳为以下三个步骤:1、假想截开、假想截开 在需求内力的截面处,假想用一截面把构件截成两部分。
在需求内力的截面处,假想用一截面把构件截成两部分。
2、任意留取、任意留取 任取一部分为究研对象,将弃去部分对留下部分的作用以截面上的内力N 来代替。
来代替。
3、平衡求力、平衡求力 对留下部分建立平衡方程,求解内力。
对留下部分建立平衡方程,求解内力。
材料力学知识点总结

材料力学知识点总结材料力学是研究材料在各种外力作用下产生的应变、应力、强度、刚度和稳定性的学科。
它是工程力学的一个重要分支,对于机械、土木、航空航天等工程领域的设计和分析具有重要意义。
以下是对材料力学主要知识点的总结。
一、基本概念1、外力与内力外力是指物体受到的来自外部的作用力,包括集中力、分布力等。
内力则是物体内部各部分之间的相互作用力,当物体受到外力作用时,内力会随之产生以抵抗外力。
2、应力与应变应力是单位面积上的内力,它反映了材料内部受力的强弱程度。
应变是物体在受力作用下形状和尺寸的相对变化,分为线应变和切应变。
3、杆件的基本变形杆件在受力作用下主要有四种基本变形形式:拉伸(压缩)、剪切、扭转和弯曲。
二、拉伸与压缩1、轴力与轴力图轴力是指杆件沿轴线方向的内力。
通过绘制轴力图,可以直观地表示出轴力沿杆件轴线的变化情况。
2、横截面上的应力在拉伸(压缩)情况下,横截面上的应力均匀分布,其大小等于轴力除以横截面面积。
3、材料在拉伸与压缩时的力学性能通过拉伸试验,可以得到材料的强度指标(屈服强度、抗拉强度)和塑性指标(伸长率、断面收缩率)。
不同材料具有不同的力学性能,如低碳钢的屈服和强化阶段,铸铁的脆性等。
4、胡克定律在弹性范围内,应力与应变成正比,即σ =Eε ,其中 E 为弹性模量。
5、拉伸(压缩)时的变形计算根据胡克定律,可以计算杆件在拉伸(压缩)时的变形量。
三、剪切1、剪切内力与剪切应力剪切内力通常用剪力表示,剪切应力则是单位面积上的剪力。
2、剪切实用计算在工程中,通常采用实用计算方法来确定剪切面上的平均应力。
四、扭转1、扭矩与扭矩图扭矩是指杆件在扭转时横截面上的内力偶矩。
扭矩图用于表示扭矩沿杆件轴线的变化。
2、圆轴扭转时的应力与变形圆轴扭转时,横截面上的应力分布呈线性规律,其最大应力发生在圆周处。
扭转角的计算与材料的剪切模量、扭矩和轴的长度等因素有关。
五、弯曲1、剪力与弯矩弯曲内力包括剪力和弯矩,它们的计算和绘制剪力图、弯矩图是弯曲分析的重要内容。
材料力学知识点总结

材料力学知识点总结在材料科学领域,材料力学是一个重要的分支,它研究材料的力学性质,包括材料的强度、刚度、韧性等方面。
材料力学的研究可以帮助我们理解和预测材料在不同应力条件下的行为,并为材料的设计和应用提供依据。
本文将对材料力学的一些重要知识点进行总结。
1. 弹性模量弹性模量是材料应力和应变之间的比例系数,描述材料在受力时的变形能力。
其计算公式为:E = σ / ε其中,E表示弹性模量,σ表示应力,ε表示应变。
弹性模量越大,材料的刚度越高,即材料越不容易发生形变。
常见的材料弹性模量有杨氏模量、剪切模量等。
2. 屈服强度屈服强度是材料在拉伸过程中发生塑性变形的最大应力。
当材料受到超过屈服强度的应力时,将产生塑性变形。
屈服强度是材料强度的重要指标之一,对于材料的选择和设计具有重要意义。
3. 断裂强度断裂强度是材料在拉伸过程中发生断裂的最大应力。
材料的断裂强度是其极限强度,表示材料能够承受的最大应力。
对于工程结构和材料的可靠性分析,断裂强度是一个关键参数。
4. 韧性韧性是材料抵抗断裂的能力,描述了材料在发生破坏前吸收的能量。
韧性与断裂强度密切相关,通常情况下,韧性较高的材料在承受冲击和动态载荷时表现更好。
韧性可以通过材料的断裂延伸率来评估。
5. 硬度硬度是材料抵抗划痕和压痕的能力,常用来评估材料的耐磨性和耐腐蚀性。
硬度测试可以通过洛氏硬度、巴氏硬度等方法进行测量。
硬度与材料的结晶度、晶粒尺寸、相变和合金化等因素有关。
6. 断裂韧性断裂韧性是材料在发生断裂时的能量吸收能力,同时考虑了材料的强度和韧性。
断裂韧性通常用断裂韧性指标(例如KIC)来评估,该指标描述了材料在存在裂纹的情况下抵抗断裂的能力。
7. 塑性变形塑性变形是材料在应力作用下发生永久性变形的能力。
与弹性变形不同,塑性变形发生后材料不能恢复其原始形状。
塑性变形通常发生在材料的屈服点之后。
8. 蠕变蠕变是材料在长时间暴露于高温和恒定应力下发生的塑性变形。
材料力学知识点总结

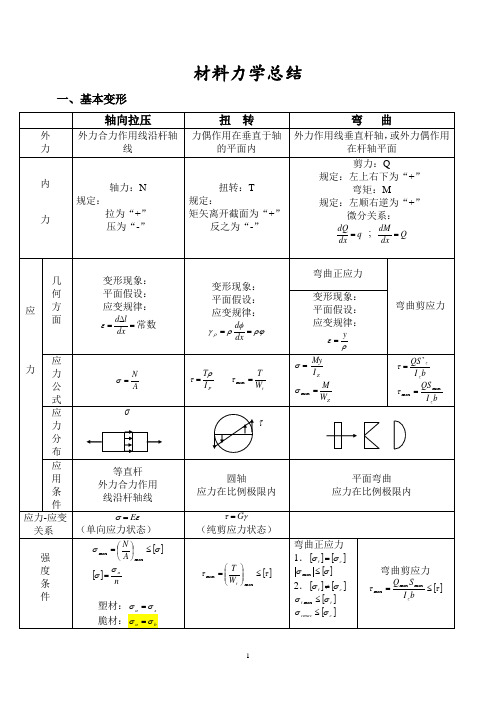
材料力学总结一、基本变形二、还有:(1)外力偶矩:)(9549m N nNm ∙= N —千瓦;n —转/分 (2)薄壁圆管扭转剪应力:tr T22πτ=(3)矩形截面杆扭转剪应力:hb G Th b T 32max ;βϕατ==三、截面几何性质(1)平行移轴公式:;2A a I I ZC Z += abA I I c c Y Z YZ += (2)组合截面: 1.形 心:∑∑===n i i ni ci i c A y A y 11 ; ∑∑===ni i ni ci i c A z A z 112.静 矩:∑=ci i Z y A S ; ∑=ci i y z A S 3. 惯性矩:∑=i Z Z I I )( ;∑=i y y I I )(四、应力分析:(1)二向应力状态(解析法、图解法)a . 解析法: b.应力圆:σ:拉为“+”,压为“-”τ:使单元体顺时针转动为“+”α:从x 轴逆时针转到截面的 法线为“+”ατασσσσσα2sin 2cos 22x yx yx --++=ατασστα2cos 2sin 2x yx +-=yx xtg σστα--=220 22minmax 22x y x yx τσσσσσ+⎪⎪⎭⎫⎝⎛-±+=c :适用条件:平衡状态(2)三向应力圆:1m a x σσ=; 3min σσ=;231max σστ-=x(3)广义虎克定律:[])(13211σσνσε+-=E [])(1z y x x E σσνσε+-=[])(11322σσνσε+-=E [])(1x z y y E σσνσε+-=[])(12133σσνσε+-=E [])(1y x z z E σσνσε+-=*适用条件:各向同性材料;材料服从虎克定律(4)常用的二向应力状态 1.纯剪切应力状态:τσ=1 ,02=σ,τσ-=32.一种常见的二向应力状态:223122τσσσ+⎪⎭⎫⎝⎛±=2234τσσ+=r2243τσσ+=r五、强度理论*相当应力:r σ11σσ=r ,313σσσ-=r ,()()()][212132322214σσσσσσσ-+-+-=r xσ六、材料的力学性质脆性材料 δ<5% 塑性材料 δ≥5%低碳钢四阶段: (1)弹性阶段(2)屈服阶段 (3)强化阶段 (4)局部收缩阶段 强度指标 σσb s ,塑性指标 δψ,E tg ==σα七.组合变形ε八、压杆稳定欧拉公式:2min 2)(l EI P cr μπ=,22λπσE cr =,应用范围:线弹性范围,σcr <σp ,λ>λp柔度:i ul =λ;ρρσπλE=;ba s σλ-=0, 柔度是一个与杆件长度、约束、截面尺寸、形状有关的数据,λ↑P cr ↓σcr ↓λ>λp ——大柔度杆:22λπσE cr =λo <λ<λp ——中柔度杆:σcr=a-b λλ<λ0——小柔度杆:σcr =σs稳定校核:安全系数法:w Icr n P P n ≥=,折减系数法:][σϕσ≤=A P提高杆件稳定性的措施有:1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度; 断裂特征:断裂前无显著塑性变形; 断口特征:断口成光滑区和粗糙区。
材料力学知识点总结

材料力学知识点总结材料力学是工程学科中的重要基础学科,它研究材料在外力作用下的力学性能和变形规律。
在工程实践中,对材料力学知识的掌握对于设计和制造具有重要意义的工程结构和材料具有重要的指导作用。
本文将对材料力学的一些重要知识点进行总结,以便于工程技术人员更好地掌握这一学科的核心内容。
1.应力和应变。
在材料力学中,应力和应变是两个最基本的概念。
应力是单位面积上的力,它描述了材料受力情况的强度。
而应变则是材料在受力作用下的形变程度,是长度、面积或体积的变化与原始长度、面积或体积的比值。
应力和应变是描述材料受力行为的重要物理量,对于材料的选取和设计具有重要的指导意义。
2.弹性力学。
弹性力学是研究材料在外力作用下的弹性变形规律的学科。
在弹性力学中,材料在受到外力作用后会发生弹性变形,而当外力消失时,材料会恢复到原始状态。
弹性力学研究材料的弹性模量、泊松比等重要参数,这些参数对于材料的选取和设计具有重要的指导作用。
3.塑性力学。
与弹性力学相对应的是塑性力学,它研究材料在受到外力作用后发生的塑性变形规律。
塑性变形是指材料在受到外力作用后发生的不可逆变形,这种变形会导致材料的形状和尺寸发生永久性的改变。
塑性力学研究材料的屈服强度、抗拉强度等重要参数,这些参数对于材料的加工和成形具有重要的指导作用。
4.断裂力学。
断裂力学是研究材料在受到外力作用下发生断裂的规律的学科。
材料的断裂是由于外力作用超过了其承受能力而导致的,断裂力学研究材料的断裂韧性、断裂强度等重要参数,这些参数对于材料的安全设计和使用具有重要的指导作用。
5.疲劳力学。
疲劳力学是研究材料在受到交变载荷作用下发生疲劳破坏的规律的学科。
在实际工程中,材料往往要经受交变载荷的作用,如果这种载荷作用时间足够长,就会导致材料的疲劳破坏。
疲劳力学研究材料的疲劳寿命、疲劳极限等重要参数,这些参数对于材料的使用寿命和安全具有重要的指导作用。
总之,材料力学是工程学科中的重要基础学科,它研究材料在外力作用下的力学性能和变形规律。
材料力学性能知识要点

1、低碳钢拉伸试验的过程可以分为 弹性变形 、 塑性变形 和 断裂 三个阶段。
2、材料常规力学性能的五大指标为: 屈服强度 、 抗拉强度 、 延伸率断面收缩率 、 冲击功 。
3、陶瓷材料增韧的主要途径有 相变增韧 、 微裂纹增韧 、 表面残余应力增韧 、 晶须或纤维增韧 显微结构增韧以及复合增韧六种。
4、常用测定硬度的方法有 布氏硬度 、 洛氏硬度 和 维氏硬度 测试法。
1、聚合物的弹性模量对 结构 非常敏感,它的粘弹性表现为滞后环、应力松弛和 蠕变 ,这种现象与温度、时间密切有关。
2、影响屈服强度的内在因素有: 结构健 、 组织 、 结构 、 原子本性 ;外在因素有: 温度 、 应变速率 、 应力状态 。
3、缺口对材料的力学性能的影响归结为四个方面: (1)产生应力集中 、(2)引起三相应力状态,使材料脆化 、 (3)由应力集中带来应变集中 、(4)使缺口附近的应变速率增高 。
4、低碳钢拉伸试验的过程可以分为 弹性变形 、 塑性变形 和 断裂 三个阶段。
5、材料常规力学性能的五大指标为: 屈服强度 、 抗拉强度 、 延伸率 断面收缩率 、 冲击功 。
6、陶瓷材料增韧的主要途径有 相变增韧 、 微裂纹增韧 、 表面残余应力增韧 、 晶须或纤维增韧 显微结构增韧以及复合增韧六种。
请说明下面公式各符号的名称以及其物理意义7、c IC c a Y K /=σσc :断裂应力,表示金属受拉伸离开平衡位置后,位移越大需克服的引力越大,σc 表示引力的最大值;K 1C :平面应变的断裂韧性,它反映了材料组织裂纹扩展的能力;Y :几何形状因子a c : 裂纹长度 8、对公式m K c dNda )(∆=进行解释,并说明各符号的名称及其物理意义(5分) 答:表示疲劳裂纹扩展速率与裂纹尖端的应力强度因子幅度之间的关系。
dNda :裂纹扩展速率(随周次); c 与m :与材料有关的常数;K ∆:裂纹尖端的应力强度因子幅度9、εss-蠕变速率,反映材料在一定的应力作用下,发生蠕变的快慢;n为应力指数,n并非完全是材料常数,随着温度的升高,n略有降低;A为常数;σ为蠕变应力。
材料力学知识点总结

材料力学知识点总结材料力学是研究材料在各种外力作用下产生的应变、应力、强度、刚度和稳定性等问题的一门学科。
它是工程力学的重要组成部分,对于机械、土木、航空航天等工程领域都有着至关重要的作用。
以下是对材料力学主要知识点的总结。
一、拉伸与压缩在拉伸和压缩的情况下,我们主要关注杆件的内力、应力和变形。
内力是指杆件在外力作用下,其内部各部分之间相互作用的力。
通过截面法可以求出内力。
应力则是单位面积上的内力。
正应力计算公式为σ = N / A ,其中 N 为轴力,A 为横截面面积。
对于拉伸和压缩变形,其变形量Δl 可以通过公式Δl = Nl / EA 计算,其中 E 为材料的弹性模量,l 为杆件长度。
二、剪切与挤压剪切是指在一对相距很近、大小相同、指向相反的横向外力作用下,杆件的横截面发生相对错动的变形。
剪切应力τ = Q / A ,其中 Q 为剪力,A 为剪切面面积。
挤压是连接件在接触面上相互压紧的现象,挤压应力σbs = Fbs /Abs ,Fbs 为挤压力,Abs 为挤压面面积。
三、扭转当杆件受到绕轴线的外力偶作用时,会发生扭转。
扭矩 T 可以通过外力偶矩计算得到。
圆轴扭转时的切应力分布规律是沿半径线性分布,最大切应力在圆轴表面。
扭转角φ 可以通过公式φ = Tl / GIp 计算,G 为材料的切变模量,Ip 为极惯性矩。
四、弯曲弯曲是指杆件在垂直于轴线的横向力或作用于轴线平面内的力偶作用下,轴线由直线变为曲线的变形。
弯矩是弯曲内力的一种,通过截面法可以求出。
弯曲应力的分布与截面形状有关,对于矩形截面,最大正应力在截面边缘。
挠度和转角是弯曲变形的两个重要参数,可以通过积分等方法求解。
五、应力状态与强度理论一点的应力状态可以用应力单元体来表示。
常用的强度理论有第一强度理论(最大拉应力理论)、第二强度理论(最大伸长线应变理论)、第三强度理论(最大切应力理论)和第四强度理论(形状改变比能理论)。
强度理论用于判断材料在复杂应力状态下是否发生破坏。
材料力学知识点总结
材料力学总结一、基本变形二、 还有:(1) 外力偶矩:川= 9549兰(N •小) N 一千瓦;n —转/分n (2) 薄壁圆管扭转剪应力:r = —2nr z t(3) 矩形截面杆扭转剪应力:M X =-2L ;0=—Z —cdrh Gpbh三、 截面几何性质(1) 平行移轴公式:,z=,zc+〃崩;/也4 (2) 组合截面: 1. 形心:y r =— ---------- ;“ n■-I2. 静矩:Sz=£/V“・;3. 惯性矩:; /,=£(/,),b .应力圆:a :拉为“ + ”,压为T :使单元体顺时针转动为“ + ” a :从x 轴逆时针转到截面的法线为“+"+ cr y a x - %,■】=X A四、应力分析:(1)二向应力状态(解析法、图解法) a.解析法:<r a = —--- + —----- cos 2a一r v sin2a a 2 2 *a x -a rT a = —---- sin la + cos 2aa 2tg2a。
= 一五、强度理论破坏形式脆性断裂塑性断裂强度理论第一强度理论(最大拉应力理论)莫尔强度理论第三强度理论(最大剪应力理论)第四强度理论(形状改变比能理论)(2)三向应力圆:max% 一气-nin = I ;f =—寸(3)广乂虎克定律:(司=手匠一仇—+/)]\ 旦==[b2 -讥/+/)]E“3=§&3_仇,+<72)]Z1+%)]*适用条件:各向同性材料;材料服从虎克定律(4)常用的二向应力状态1.纯剪切应力状态:c:适用条件:平衡状态2. 一种常见的二向应力状态:b,4 =W +3r2破坏主要 因素 单元体内的最大拉应力单元体内的最大 剪应力单元体内的改变比 能破坏条件g = Lu f =u fa 强度条件适用条件 脆性材料 脆性材料 塑性材料 塑性材料*相当应力:5’ $3=%-七,a f4 = '-[(cr, -cr 2)2 +(a 2 -a.)2 +(cr 3 -a.)2]六、材料的力学性质(1) 弹性阶段 (2) 屈服阶段 (3) 强化阶段 (4) 局部收缩阶段七. 组合变形脆性材料5<5% 塑性材料8>5% 低碳钢四阶段:强度指标低碳钢////// a h 剪断公式ycos。
材料力学知识点

材料力学 一、基本概念: 理论力学——研究刚体,研究力与运动的关系。 材料力学——研究变形体,研究力与变形的关系。 1、构件:工程结构或机械的每一组成部分。 (例如:行车结构中的横梁、吊索等) 2、变形:在外力作用下,固体内各点相对位置的改变。(宏观上看就是物体尺寸和形状的改 变) 弹性变形——随外力解除而消失 塑性变形(残余变形)—外力解除后不能消失 3、内力:构件内由于发生变形而产生的相互作用力。 (内力随外力的增大而增大) 4、应力:截面某一点单位面积上的内力称为应力。同截面垂直的称为正应力或法向应力, 同截面相切的称为剪应力或切应力。 5、刚度:在载荷作用下,构件抵抗变形的能力。 6、强度:在载荷作用下,构件抵抗破坏的能力。 7、稳定性:在载荷作用下,构件保持原有平衡状态的能力。 强度、刚度、稳定性是衡量构件承载能力的三个方面,材料力学就是研究构件承载能力的一 门科学。 材料力学的任务就是在满足强度、刚度和稳定性的要求下,为设计既经济又安全的构件,提 供必要的理论基础和计算方法。研究构件的强度、刚度和稳定性,还需要了解材料的力学性 能。因此在进行理论分析的基础上,实验研究是完成材料力学的任务所必需的途径和手段。 二、变形固体的基本假设 1、连续性假设:认为整个物体体积内毫无空隙地充满物质 2、均匀性假设:认为物体内的任何部分,其力学性能相同 3、各向同性假设:认为在物体内各个不同方向的力学性能相同 (沿不同方向力学性能不同的材料称为各向异性材料。如木材、胶合板、纤维增强材料等) 3、各向同性假设:认为在物体内各个不同方向的力学性能相同 (沿不同方向力学性能不同的材料称为各向异性材料。如木材、胶合板、纤维增强材料等) 4、小变形与线弹性范围:认为构件的变形极其微小,比构件本身尺寸要小得多。 三、外力及其分类 外力:来自构件外部的力(载荷、约束反力) 按外力作用的方式分类: 1、 体积力:连续分布于物体内部各点的力。如重力和惯性力 2、 表面力:1)分布力:连续分布于物体表面上的力。如油缸内壁的压力,水坝受到的水 压力等均为分布力 2)集中力:若外力作用面积远小于物体表面的尺寸,可作为作用于 一点的集中力。如火车轮对钢轨的压力等 按外力与时间的关系分类 1、 静载:载荷缓慢地由零增加到某一定值后,就保持不变或变动很不显著,称为静载。 2、 动载:载荷随时间而变化。如交变载荷和冲击载荷 四、变形与应变 1、变形:物体内任意两点的相对位置发生变化。 取一微正六面体 两种基本变形: 1) 线变形——线段长度的变化 2) 角变形——线段间夹角的变化
(完整版)材料力学知识点总结
材料力学总结一、基本变形二、还有:(1)外力偶矩:)(9549m N nNm •= N —千瓦;n —转/分 (2)薄壁圆管扭转剪应力:tr T22πτ=(3)矩形截面杆扭转剪应力:hb G Th b T 32max ;βϕατ==三、截面几何性质(1)平行移轴公式:;2A a I I ZC Z += abA I I c c Y Z YZ += (2)组合截面: 1.形 心:∑∑===ni ini cii c AyA y 11; ∑∑===ni ini cii c AzA z 112.静 矩:∑=ci i Z y A S ; ∑=ci i y z A S 3. 惯性矩:∑=i Z Z I I )( ;∑=i y y I I )(四、应力分析:(1)二向应力状态(解析法、图解法)a . 解析法: b.应力圆:σ:拉为“+”,压为“-” τ:使单元体顺时针转动为“+”α:从x 轴逆时针转到截面的 法线为“+”ατασσσσσα2sin 2cos 22x yx yx --++=ατασστα2cos 2sin 2x yx +-=yx xtg σστα--=220 22minmax 22x y x yx τσσσσσ+⎪⎪⎭⎫⎝⎛-±+=c :适用条件:平衡状态(2)三向应力圆:1max σσ=; 3min σσ=;231max σστ-=x(3)广义虎克定律:[])(13211σσνσε+-=E [])(1z y x x E σσνσε+-=[])(11322σσνσε+-=E [])(1x z y y E σσνσε+-=[])(12133σσνσε+-=E [])(1y x z z E σσνσε+-=*适用条件:各向同性材料;材料服从虎克定律(4)常用的二向应力状态 1.纯剪切应力状态:τσ=1 ,02=σ,τσ-=32.一种常见的二向应力状态:223122τσσσ+⎪⎭⎫⎝⎛±=2234τσσ+=r2243τσσ+=r五、强度理论*相当应力:r σ11σσ=r ,313σσσ-=r ,()()()][212132322214σσσσσσσ-+-+-=r σxσ六、材料的力学性质脆性材料 δ<5% 塑性材料 δ≥5%低碳钢四阶段: (1)弹性阶段(2)屈服阶段 (3)强化阶段 (4)局部收缩阶段 强度指标 σσb s ,塑性指标 δψ,E tg ==σα七.组合变形ε八、压杆稳定欧拉公式:2min2)(l EI P cr μπ=,22λπσE cr =,应用范围:线弹性范围,σcr <σp ,λ>λp柔度:iul =λ;ρρσπλE=;ba s σλ-=0,柔度是一个与杆件长度、约束、截面尺寸、 形状有关的数据,λ↑P cr ↓σcr ↓λ>λp ——大柔度杆:22λπσE cr =λo <λ<λp ——中柔度杆:σcr=a-b λλ<λ0——小柔度杆:σcr =σs稳定校核:安全系数法:w I cr n P P n ≥=,折减系数法:][σϕσ≤=AP提高杆件稳定性的措施有:1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度; 断裂特征:断裂前无显著塑性变形; 断口特征:断口成光滑区和粗糙区。
(完整版)材料力学必备知识点

材料力学必备知识点1、 材料力学的任务:满足强度、刚度和稳定性要求的前提下,为设计既经济又安全的构件,提供必要的理论基础和计算方法。
2、 变形固体的基本假设:连续性假设、均匀性假设、各向同性假设。
3、 杆件变形的基本形式:拉伸或压缩、剪切、扭转、弯曲。
4、 低碳钢:含碳量在0.3%以下的碳素钢。
5、 低碳钢拉伸时的力学性能:弹性阶段、屈服阶段、强化阶段、局部变形阶段 极限:比例极限、弹性极限、屈服极限、强化极限6、 名义(条件)屈服极限:将产生0.2%塑性应变时的应力作为屈服指标7、 延伸率δ是衡量材料的塑性指标塑性材料 随外力解除而消失的变形叫弹性变形;外力解除后不能消失的变形叫塑性变形。
>5%的材料称为塑性材料: <5%的材料称为脆性材料8、 失效:断裂和出现塑性变形统称为失效9、 应变能:弹性固体在外力作用下,因变形而储存的能量10、应力集中:因杆件外形突然变化而引起的局部应力急剧增大的现象11、扭转变形:在杆件的两端各作用一个力偶,其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线,致使杆件的任意两个横截面都发生绕轴线的相对转动。
12、翘曲:变形后杆的横截面已不再保持为平面;自由扭转:等直杆两端受扭转力偶作用且翘曲不受任何限制;约束扭转:横截面上除切应力外还有正应力13、三种形式的梁:简支梁、外伸梁、悬臂梁14、组合变形:由两种或两种以上基本变形组合的变形15、截面核心:对每一个截面,环绕形心都有一个封闭区域,当压力作用于这一封闭区域内时,截面上只有压应力。
16、根据强度条件 可以进行(强度校核、设计截面、确定许可载荷)三方面的强度计算。
17、低碳钢材料由于冷作硬化,会使(比例极限)提高,而使(塑性)降低。
18、积分法求梁的挠曲线方程时,通常用到边界条件和连续性条件;因杆件外形突然变化引起的局部应力急剧增大的现象称为应力集中;轴向受压直杆丧失其直线平衡形态的现象称为失稳19、圆杆扭转时,根据(切应力互等定理),其纵向截面上也存在切应力。
材料力学复习总结知识点

……
δn1X1 + δn2X2 +…+ δnnXn+ ΔnF = fn
4. 莫尔积分,图乘法,求系数δij,ΔiF 5. 求力法方程 6. 画内力图
六、动荷问题
1. 构件做等加速直线运动和等速转动
三、组合变形
1. 斜弯曲(平面弯曲组合) 2. 弯曲与拉(压) 3. 偏心拉(压)
4. 弯扭(拉扭):
r 3 2 42 , r4 2 32
r3M W 2 T 2, r4M 2 W 0 .7T 5 2
四、压杆稳定
1. 欧拉公式:
Fcr
2EI (l)2
动静法 能量法
变形比较法步骤: 1. 静不定次数 2. 建立相当系统 3. 补充方程
平衡方程(建立) 几何方程(补充) 物理方程(沟通) 4. 求解
等效载荷法步骤: 1. 能量守恒 2. 动荷因数 3. 等效载荷 4. 力学响应
三、不作重点要求内容
2.4.4 2.8
3
4.3.1 4.7 4.8 4.9 4.10
扭转
弯曲
外力
变 形
纵向 , E
E
横向 '
, G
G
当 p有
l FN l EA
当 P有
Tl G IP
纯弯曲:
1M EI
横力弯曲: 1 M(x)
(x) EI
位
EA 为拉压刚度。
GIp 为扭转刚度。
EI 为弯曲刚度。
移 静不定问题(三方面): 平衡关系 (受力图); 变形关系 (变形图);
材料力学知识点总结

一 强度问题
1. 静载荷强度
基本思路
简单模型
组合变形
基本程序
外力分析
内力分析
应力分析
应力状态分析
强度条件
变形几何 静不定
静荷载强度
基本技能
建立力学模型
画受力图
掌握基本变形应力分布规律
掌握应力状态分析
掌握强度条件
画内力图
掌握叠加原理和方法
q
a
2a
A
B
C
六. 14分 重量为P的重物从高度为H处自由下落,冲击到外伸梁的A端,试求梁的最大动应力,EI、W为已知量,
2a
a
A
P
H
B
七.简答题 每小题4分,共16分
b
h
z
y
一. 15分 矩形截面梁受到移动载荷作用,P=30kN, 材料的许用应力 =10MPa, =2MPa,h/b=1.5, 试确定梁截面尺寸b、h,
两个条件
1m
F
h
b
问题:F位于何处 σ ,τ 取最大值 也就是F 位于何处 M,FS 取最大值
1m
F
x
M
F(1-x)x
FS
Fx
F(1-x)
注意: FSmax ,Mmax可能位于不同截面, 它们取极值时 F可能位于不同位置,
Mmax= F/4
FSmax= F
M
Pa
2. 求△st ,st
M
a
2a/3
2a/3
P
2a
a
A
P
H
B
2分
1. 动荷因数
3. 最大静应力
完整版)材料力学知识点总结

完整版)材料力学知识点总结Summary of Material MechanicsI。
Basic nsAxial n and n: External forces act along the axis of the rod。
and internal XXX nal plane.n: XXX to the axis of the rod.Bending: Axial force N is defined as positive for XXX to the axis of the rod or in a plane containing the axis of the rod.Shear: Q is defined as positive for a XXX.Twisting: XXX.XXX: dQ/dx=q。
dM/dx=QII。
XXXXXX:XXX: ε=dΔl/dx=constantXXX:XXX: γ=ρdφ/dx=ρφXXX:XXX: ε=My/IzXXX: σ=Mz/WyShear stress: τ=QS*/IbNormal stress: σ=N/APlastic material: σu=σsXXX: σu=σbCircular shaft: XXX limitτ=GγXXX bending: XXX limit Normal bending stress:1.[σt]≤[σc]σmax≤[σ]2.[σt]≠[σc]σtmax≤[σt]。
σcmac≤[σc]Shear bending stress: τmax=Q/Iz b Elastic modulus:XXX: εmax≤[ε]n: φmax≤[φ]Bending: ymax≤[y]。
θmax≤[θ]Note: Units are XXX.N: XXXL: LengthE: Elastic modulusA: nal aread: DiameterI: Moment of inertiaP: Perimeterh: Heightb: WidthW: n modulusZ: Polar moment of inertia剪切公式:tau=\dfrac{Q}{A}\leq [\tau]$ A$—剪切面积挤压公式:sigma_{bs}=\dfrac{P}{A_j}\leq [\sigma_{bs}]$ A_j$—挤压面积圆形:tau_{max}=\dfrac{3Q}{2A}$矩形:tau_{max}=\dfrac{Q}{2A}$以上两式均发生在中性轴上截面几何性质:平行移轴公式:I_Z=I_{ZC}+a^2A$I_{YZ}=I_{ZC}+abA$组合截面:形心:bar{y}=\dfrac{\sum\limits_{i=1}^nA_iy_{ci}}{\sum\limits_ {i=1}^nA_i}$bar{z}=\dfrac{\sum\limits_{i=1}^nA_iz_{ci}}{\sum\limits_{ i=1}^nA_i}$静矩:S_Z=\sum\limits_{i=1}^nA_iy_{ci}$S_Y=\sum\limits_{i=1}^nA_iz_{ci}$惯性矩:I_Z=\sum\limits_{i=1}^n(I_Z)_i$I_Y=\sum\limits_{i=1}^n(I_Y)_i$应力分析:二向应力状态(解析法、图解法)解析法:sigma_y=\dfrac{\sigma_x+\sigma_y}{2}+\dfrac{\sigma_x-\sigma_y}{2}\cos 2\alpha-\tau_x\sin 2\alpha$tau_{xy}=\dfrac{\sigma_x-\sigma_y}{2}\sin2\alpha+\tau_x\cos 2\alpha$tau_{max}=\sqrt{\left(\dfrac{\sigma_x-\sigma_y}{2}\right)^2+\tau_x^2}$三向应力圆:sigma_{max}=\sigma_1$sigma_{min}=\sigma_1-\sigma_3$tau_{max}=\dfrac{\sigma_2}{3}$应力圆:sigma$: 拉为“+”,压为“-”tau$: 使单元体顺时针转动为“+”alpha$: 从$x$轴逆时针转到截面的法线为“+”广义虎克定律:dfrac{\epsilon_1}{E_1}=\dfrac{\epsilon_2}{E_2}=。
(完整版)材料力学知识点总结

以家为家,以乡为乡,以国为国,以天下为天下。——《管子·牧民》
六、材料的力学性质
脆性材料 <5%
塑性材料 ≥5% 低碳钢四阶段: (1)弹性阶段
(2) 屈服阶段 (3) 强化阶段 (4) 局部收缩阶段
强度指标 s , b
e
塑性指标 ,
拉
压
α
s
tg
b
E 扭
45
低
碳
钢
滑移线与轴线 45,剪
只有s,无b
( l)2
cr
2
cr p
p
柔度:
ul
;
i
E
;
0
a s b
,
柔度是一个与杆件长度、约束、截面尺寸、形 状有关的数据,λ↑Pcr↓σcr↓
>p——大柔度杆:
cr
2E
2
临界应力
o<<p——中柔度杆:cr=a-b
cr cr=s o
cr=a-b
2E
cr
2
P
<0——小柔度杆:cr=s
P 稳定校核:安全系数法: n cr n ,折减系数法:
材料疲劳极限:材料经无限次应力循环而不发生疲劳破坏的应力极限值——N=107:
1
条件疲劳极限:(有色金属)无水平渐近线:N=(5-7)107 对应的
1
构件疲劳极限:考虑各种因素 0
;
1
0 1
1 k
1 k
6
谋事在人,成事在天!——《增广贤文》
我尽一杯,与君发三愿:一愿世清平,二愿身强健,三愿临老头,数与君相见。——《白居易》
P
[]
P
w
A
I
提高杆件稳定性的措施有:
第六版材料力学知识点总结

第六版材料力学知识点总结第一章引言本章主要介绍了力学在材料科学与工程中的地位和作用。
力学是分析物体受力情况和相应变形的学科,这在材料科学与工程中具有重要意义。
本章的内容对整本教材的学习打下了基础。
第二章应力在本章中,主要介绍了材料在受到外力作用时所产生的应力的概念。
力的作用有拉伸作用、压缩作用和剪切作用三种,这些力对应的应力分别是拉应力、压应力和剪应力。
材料受力会导致应力在材料内部的分布,通过一些基本方程来描述材料受力的情况。
第三章应变这一章主要介绍了材料在受到外力作用时所产生的应变的概念。
应变是指材料在外部力作用下所产生的形变。
介绍了应变的三种基本形式:线性应变、剪切应变和体积变形。
第四章弹性模量本章介绍了材料的弹性行为及其数学描述。
材料在受力时会发生形变,而且形变是可逆的,这种性质称为弹性。
对材料的弹性行为进行了分析,并引入了弹性模量这一概念,分别是杨氏模量、剪切模量和泊松比。
这些弹性模量对于描述材料的弹性行为有着重要的意义。
第五章弯曲这一章介绍了材料在受力时进行弯曲变形的物理过程和数学描述。
利用梁的理论分析了材料受弯曲力时的受力和应变情况。
并引入了一些相关参数,并给出了一些实际应用问题的数学解析。
第六章扭转这一章详细介绍了材料在受扭转力作用下的受力和应变情况。
对材料进行了基本的力学分析,并引入了剪切弹性模量,这对于描述材料的扭转弹性行为具有重要意义。
第七章变形与尺寸稳定性本章主要介绍了材料在受力后的变形与尺寸稳定性。
材料在受力时会发生变形,而变形又分为弹性变形和塑性变形,并且介绍了材料的屈曲现象和相应的数学分析,这在实际工程中具有重要的意义。
第八章断裂这一章详细介绍了材料在受到过大外力作用时的断裂过程。
材料的断裂可以分为塑性断裂和脆性断裂,分析了断裂的过程及其影响因素,并引入了一些与断裂相关的参数。
第九章强度理论这一章主要介绍了材料的强度理论。
介绍了强度概念以及与强度相关的一些理论模型,如最大正应力理论、最大剪应力理论等。
材料力学知识点总结

、基本变形材料力学总结轴向拉压外力合力作用线沿杆轴线力偶作用在垂直于轴的平面内规定:轴力:N拉为“ +” 压为“-”扭转:T规定:矩矢离开截面为“ +”反之为“-”外力作用线垂直杆轴,或外力偶作用在杆轴平面剪力: Q规定:左上右下为“ +”弯矩:M规定:左顺右逆为“ +”微分关系:dQ dM 小一q ; 一Qdx dx几何方面变形现象平面假设应变规律dx常数变形现象平面假设应变规律ddx弯曲正应力变形现象平面假设应变规律y弯曲剪应力应力公式maxTW tmaxMyI ZMW ZQS*zI z bI z bmax应力分布应用条件应力-应变关系强度条件等直杆外力合力作用线沿杆轴线E(单向应力状态)maxmax塑材:脆材:圆轴应力在比例极限内平面弯曲应力在比例极限内G(纯剪应力状态)弯曲正应力1.maxTW tmaxmax2.t maxcmac c弯曲剪应力maxmaxSmaxI z b、还有:(1)外力偶矩:m 9549N(N?m) N —千瓦;n—转/分n(2)薄壁圆管扭转剪应力: T2 r2t(3)矩形截面杆扭转剪应力: Tb2hT G b3h三、截面几何性质(1 )平行移轴公式:I Z (2)组合截面:nA i y ci1 .形 心: y cAi 12 .静矩:S Z A i y c3•惯性矩:I z (l z )i ;四、应力分析:(1)二向应力状态(解析法、图解法)b.应力圆::拉为“ + ”,压为“-” :使单元体顺时针转动为“ +” :从x 轴逆时针转到截面的 法线为“ +”maxminc :适用条件:平衡状态⑵三向应力圆:..13max1;min3; maxtg2 0 x ysin 22ycos2 cos 2x sin 22I ZC a A ; I YZ I Z c Y cabAZ cnA i zcii 1nAi 1S yA i Z ciy (I y )ia .解析法:nx2适用条件:各向同性材料;材料服从虎克定律(4)常用的二向应力状态2.—种常见的二向应力状态:五、强度理论破坏形式脆性断裂塑性断裂强度理论第一强度理论(取大拉应力理论)莫尔强度理论第三强度理论(最大剪应力理论)第四强度理论(形状改变比能理论)破坏主要因素单兀体内的最大拉应力单元体内的最大剪应力单元体内的改变比能破坏条件1 b max su f u fs强度条件1 1 3适用条件脆性材料脆性材料塑性材料塑性材料相当应力:1 3r4(3)广义虎克定律:1E13)1)2)xyzz)x)y)1 •纯剪切应力状态:r1xr423六、材料的力学性质七.组合变形八、压杆稳定提高杆件稳定性的措施有:1减少长度 2、选择合理截面 3、加强约束九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度; 断裂特征:断裂前无显著塑性变形; 断口特征:断口成光滑区和粗糙区。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、基本变形轴向拉压材料力学总结扭转弯曲外外力合力作用线沿杆轴力线内轴力: N规定:力拉为“ +”压为“-”几变形现象:何平面假设:应方应变规律:面 d l常数dx力应力N公 A式力偶作用在垂直于轴的平面内扭转: T规定:矩矢离开截面为“ +”反之为“ - ”变形现象:平面假设:应变规律:ddxT TI PmaxW t外力作用线垂直杆轴,或外力偶作用在杆轴平面剪力: Q规定:左上右下为“ +”弯矩: M规定:左顺右逆为“ +”微分关系:dQ ; dMq Qdx dx弯曲正应力变形现象:平面假设:弯曲剪应力应变规律:yMy QS*zI Z I z bM QS maxmax maxW Z I z b应力分布应等直杆用外力合力作用条线沿杆轴线件应力-应 E变(单向应力状态)关系强Nmax 度Amax u条n件塑材:u s脆材:ub圆轴平面弯曲应力在比例极限内应力在比例极限内G(纯剪应力状态)弯曲正应力T 1.t cmax弯曲剪应力W t maxmax2.t c Q max S maxmaxI z bt max tcmac c轴向拉压扭转弯曲刚度T 180 0 ymax y maxGI P条注意:单位统一max件d l N; L NL d T 1 M ( x) EA变dx EA dx GI Z ( x) EITL y '' M (x)GI P EI EA—抗拉压刚度GI p—抗扭刚度EI —抗弯刚度应用形条件矩形实心圆空心圆其它公式应力在比例极限A=bh2A=d4A D 2 (1 2 )4(1)'E(2)G2(1)圆截面杆,应力在比例极限d 4 d 3I P ;W t32 16I Pd 4(1 4 )32W t d 3 (1 4 )16剪切(1)强度条件:QA —剪切面积A(2)挤压条件:P bsbs bsA JA j—挤压面积小变形,应力在比例极限bh 3 bh2I Z ; W Z12 6d 4 d 3I Z ; W Z64 32I Zd 4 4)(1643W Zd(1 4 )32矩形:max3Q2A圆形:max4Q3A环形:max 2QAmax 均发生在中性轴上二、还有:(1)外力偶矩:m 9549N(N ? m) N —千瓦; n—转 / 分n(2)薄壁圆管扭转剪应力:T2 r 2 t (3)矩形截面杆扭转剪应力:max T;T 2 3h b h G b三、截面几何性质(1)平行移轴公式:I Z I ZC a 2 A; IYZ I Z Y abAc c (2)组合截面:n nA i y ci A i z cii 1;z c i 1 1.形心:y c n nA i A ii 1 i 1 2.静矩:S Z A i y ci ;S y A i z ci3. 惯性矩:I Z (I Z ) i ;I y (I y )i四、应力分析:(1)二向应力状态(解析法、图解法)a.解析法: b.ynxxx y x ycos2 x sin 22 2x y sin 2 x cos 22tg 2 02 xx y2x y x y 2 max2 2 xminc:适用条件:平衡状态(2)三向应力圆:应力圆::拉为“ +”,压为“ - ”:使单元体顺时针转动为“+”:从 x 轴逆时针转到截面的法线为“ +”DBcAD 'max1 ;min 3 ; 1 3max2(3)广义虎克定律:111(23)xE1 (1)223yE1 (2)3 31zE1E1E1Ex y z(((y z )z x )x y)* 适用条件:各向同性材料;材料服从虎克定律(4)常用的二向应力状态31.纯剪切应力状态:1,20 ,x312.一种常见的二向应力状态:1 322r 32r 42432 22 2五、强度理论破坏形式脆性断裂塑性断裂第一强度理论第三强度理论莫尔强度理第四强度理论(形状强度理论(最大拉应力理(最大剪应力理论改变比能理论)论)论)破坏主要 单元体内的最大拉单元体内的最大单元体内的改变比因素应力剪应力能破坏条件 1 bmax su f u fs强度条件 11 3适用条件脆性材料 脆性材料 塑性材料 塑性材料* 相当应力:rr 11,r 313,r 41[122 23 2 312]2六、材料的力学性质脆性材料< 5%塑性材料≥ 5%低碳钢四阶段:(1)弹性阶段 (2)屈服阶段(3)强化阶段(4)局部收缩阶段强度指标s ,b塑性指标,拉低45碳 钢滑移线与轴线45 ,剪铸铁拉断断口垂直轴线besαtg E压扭断口垂直轴线剪断只有s,无bsb拉断 45ob剪断断口与轴夹角 45ob七.组合变形类斜弯曲拉(压)弯型简α 中性轴M图Zp公y cos zsin P M r3 M ( )A W式I Z I yr 4 强度max M max ( cos sinPmaxMmax W Z) maxW W y A条[ ] [ ]件r 3 中r4i Z2性y I Z tg y *I ZtgI y Ae y e yZ轴弯扭弯扭拉(压)24 2 [ ]( M N )24 2 [ ]r 323 2 [ ]( M N )23 2 [ ]r 4圆截面r3(MN )2 4(T)2M2T2 W Z A W t[ ] [ ]W ZM N T2 22 ) 2M 0.75T r 4 ( ) 4([ ] W Z A W t W Z [ ]八、压杆稳定2 EImin ,cr 2 E ,应用范围:线弹性范围,cr <p,> p欧拉公式: P cr2 2( l )柔度:ul ;E;0 abs ,i crcr =cr= a-b柔度是一个与杆件长度、约束、截面尺寸、2Ecr形状有关的数据,λ↑ P cr↓σcr↓ 2> p——大柔度杆:cr 2 E 2临界应力o < < p——中柔度杆:cr= a-b o P < 0——小柔度杆:cr =s稳定校核:安全系数法:P crn w,折减系数法:Pn [ ] P I A提高杆件稳定性的措施有:1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度;断裂特征:断裂前无显著塑性变形;断口特征:断口成光滑区和粗糙区。
循环特征平均应力应力幅度r min ;maxmax min;m 2max min2材料疲劳极限:材料经无限次应力循环而不发生疲劳破坏的应力极限值——N=107: 1 条件疲劳极限:(有色金属)无水平渐近线:N=(5-7 )107对应的 1构件疲劳极限:考虑各种因素0 1 ;11 1k k影响构件疲劳极限因素:应力集中;尺寸;表面质量。
影响材料疲劳极限因素:循环特性;变形形式;材料。
提高构件疲劳强度的主要措施:减缓应力集中;提高表面光洁度;增强表面强度。
