对称平板波导的模式计算
对称波导模式计算

目录摘要 (2)Abstract (3)绪论 (4)1平板波导.............................................................................. 错误!未定义书签。
1.1平板波导简介................................................................. 错误!未定义书签。
1.2平板波导基本结构与模式............................................. 错误!未定义书签。
1.3对称平板波导.............................................................. 错误!未定义书签。
1.4 光纤光栅谱.................................................................... 错误!未定义书签。
1.5 对称平板波导的应用.................................................... 错误!未定义书签。
2 Beamprop介绍 (7)3光谱仿真 (8)3.1 BeamProp参数设置步骤 (8)3.2 检查指数资料 (10)3.3 分析建立 (11)3.4 仿真 (11)3.5 在波长上的扫描 (12)4 心得体会.................................................................................. 错误!未定义书签。
参考文献...................................................................................... 错误!未定义书签。
第三章 波导中的光波2010(2)

W
2 n2 n ( γ a = − (κ a) tan(κ a) W = − n 2 U tan U TM奇) 1 n
W
π/2
π
3π/2
2π
π/2
π
3π/2
2π
U
U
TE偶模 TE偶模
TE奇模 TE奇模
3.2 平面介质光波导
传播常数图解
W
TE0 TE2 TE3 TE4
V=4
V=3 V=2 V=1
π/2
γ a = −(κ a ) cot(κ a )
2 n2 γ a = − 2 (κ a) tan(κ a) n1
波导材料和尺寸 确定,光频给定 时,可求解β。
超越方程,近似解。 波导层横向归一化传播常数: U = κ a = n12 k02 − β 2 a
2 波导层纵向归一化传播常数:W = γ a = β 2 − n2 k02 a 2 V = k0 a n12 − n2
E y =Ccos(κ x), x ≤ a −γ ( x − a ) , x ≥a E y =Ccos(κ a)e
γ a = (κ a) tan(κ a) γ a = −(κ a) cot(κ a)
TE偶模模式方程 TE奇模模式方程
x
3.2 平面介质光波导
z
模式方程
TM: TM:
令q =0,a / 3 < x < a / 2,波导层内。 2 q ≥ 1,5a / 3 < x < 3a / 2, 波导层外。
Hale Waihona Puke TE1:qπ = a, q = 0,1, 2..... U π / 2 < U < π , qa < x < 2qa x = 令q = 0, 则x=0,恰好处于波导中心。 q ≥ 1,x在波导层外。
集成光波导

Pin/2
23
Multiport splitters can be constructed by cascading 2-port couplers as indicated schematically below:
1 x 8 Coupler
24
4.6.2 有源器件
▪ 有源器件按其功能可分为两类:
21
For the ideal coupler, the coupling to port 4 (the isolated port) is zero. Thus,
10 log P4/P1 = 10 log 0 = -
22
An integrated optic power splitter is constructed with the waveguide pattern indicated below:
图4.5 对称平板波导的
模
式
图
1
4.5.1 波导色散
▪ 随波长的变化,有效折射率neff与折射率n一样会导致脉冲展
宽。在通常情况下,材料是色散的,因此波导色散与材料色 散会同时存在。
图4.5 对称平板波 导的模式图 (n1=3.6,n2=3.5 5)
2
4.5.1 波导色散
▪ 由波导色散所引起的脉冲展宽幅度与材料色散所导致的脉冲
图4.24 电光开关
26
As in the passive coupler, the power distribution is given by:
P2/P1 = cos2 (pL/2Lc) P3/P1 = sin2 (pL/2Lc) L is the interaction length and Lc is the coupling length.
多层平板波导[wsg]
![多层平板波导[wsg]](https://img.taocdn.com/s3/m/76dd6d6327d3240c8447efaa.png)
特征方程:
2 K 2d
五层平板波导
x2 n2 n1 n0 n-1 n-2 d+ 2a d-
x1 x0 x-1 x-2
各区场解为(中心层为振荡区,其余各层为指数解):
+ 2= A+ 0 cos + 0
1= 0= 0= 1=
2a x 2a 2d
exp[ p 3 ( x 2 a 2 d )]
p3 p4 K2 2 K 1 a m arctan C 14 + arctan C 12 tan arctan C 23 K1 K1 K2
(TE 模)
C ij ( n i /n j )
(TM 模)
由 (TE模)或n-2 (TM模)的连续条件可得模式方程
2 K 0 a m arctan[ C 01 arctan[ C 0 1 p 1 K0 p 1 K0 tanh( ar tanh C 12 p2 p 1 p 1 d 1 )] p 1 d 1 )]
A 0 cos K 0 ( x a ) 0 A 0 cos 0 A 0 cos 0
A+ 0 cos K 0 ( x a ) 0
cosh[ p 1 ( x x 1 ) 1 ] cosh 1 cosh[ p 1 d 1 1 ] cosh 1 exp[ p 2 ( x x 2 )]
2y E y 0 H x dE y j 0 H z dx dH z j E y j H x dx
方程组2: (TM模) = H
第1章--波导的模式

12.什么是本征模?本征模的作用是什么?
在一定的电磁场边界条件下求解波导的横向亥姆霍兹方程,可得到其一系列特解:场函数 和传播常数 ,这些特解称为本征模。
16.平板波导TM模的电磁场分量的表达式为
试阐述它们之间的相互关系。
由上面公式可知,TM模电磁场的6个分量中有3个分量为零,另外3个分量不为零,即Hx0(x) = 0,Hz0(x) = 0,Ey0(x) = 0,Hy0(x)0,Ex0(x)0,Ez0(x)0。还可看出,只要知道Hy0(x)的表达式,Ex0(x)、Ez0(x)的表达式都可以用Hy0(x)表示出来。因此对于TM模我们只要求出Hy0(x)的表达式,则Ex0(x)、Ez0(x)的表达式亦可求出。
25.对称型三层平板波导中导模的有效折射率随波导芯厚度的变化曲线如图所示,试阐述其变化规律。
(25题图)对称型三层平板波导中TE(实线)和TM(虚线)导模的有效折射率N随波导芯厚度b的变化曲线
图中可以看出,有效折射率N随波导芯厚度b的增大而增大,随模阶数m的增大而减小,其中0阶导模的传播常数为最大。当波导芯厚度给定后,传播常数取分立值,并组成分立谱。在此算例中芯层与上下包层的折射率差较小,模阶数相同的TE和TM导模的传播常数趋于相同而接近简并,相应的TE和TM导模的传输曲线近于重合。所谓简并,是指同一个有效折射率的值对应两个或两个以上的模式。如果芯层与上下包层的折射率差增加到足够大,这种简并将会被消除,相应的TE和TM导模的传输曲线将会分离。当导模的有效折射率N等于包层的折射率n2时, 变为零,此时导模不再存在,辐射模产生,称为导模截止,图中传输曲线与横轴的交点称为导模的截止点,这些截止点等间距分布。图中可以看出,0阶导模的传输曲线通过坐标原点,即0阶导模的截至芯厚度等于0,这意味着对于任何芯厚度的对称型平板波导,TE0和TM0基模总能在其中传输,永不截止。
1.2-介质板波导

k k0 n2
应有K 2 k0 2 n2 2 2 0, 令 2 2 k0 2 n2 2
D ( x d ) e i D x ( x d ) ( )e x
12
(3) 边界条件和特征方程式
当x d 时, 应有E y1 E y 2 , H z1 H z 2 A(1 K
1.2 介质平板波导
1
主要内容
1.
基本波动方程和波导方程式
2.
3.
对称介质平板波导的传输模式
介质板波导中的多模群时延
2
1、波动方程和波导方程式
1)波动方程:由麦克斯韦方程组推导出
B E t E ( B ) t D 2 ( E ) E ( ) t t D ( E ) E E 0 E E
准备2
i E z H z Ex 2 ( ) K x y i H z E z Hx ( ) 2 K x y i E z H z E y 2 ( ) K y x i H z E z Hy ( ) 2 K y x K 2 k 2 2 2 2
两个平面波的传输方向与介质板的法线夹角
tan
K
在介质板上,两个平面波满足内部全反射条件, 它们对介质板入射角度是由模式传输矢量的分量β、K所决定。
21 结论:模式截止的情况与以临界角入射到介质板上的平面波相对应
3)TM模式(以TE分析类似) 3.介质板波导中的多模群时延
d dL dH K 2 k0 2 n12 2 f 0
得 令
2-平板波导的电磁理论
ε =ε = k0 ω = ε 0 µ0 2π / λ 0n ,
2
j = 1, 2,3
TE波的波动方程:
E ( x, z , t ) E ( x) exp[i (z t )] H ( x, z , t ) H ( x) exp[i (z t )]
2 3 2 2
NTE
1 2 2 n2 n3 (Vc arctan 2 2 ) n n 1 2 int
N total NTE NTM
小结:波动光学方法
• 波动理论是一种比几何光学方法更为严 格的分析方法,其严格性在于:(1)从光波的 本质特性──电磁波出发,通过求解电磁波 所遵从的麦克斯韦方程,导出电磁场的场 分布,具有理论上的严谨性;(2) 未作任何 前提近似,因此适用于各种折射率分布的 单模光和多模光波导。
光波导技术的广阔应用领域光波导技术有源无源器件光纤通信干线光交换接入网aondwdmoadmotdmfttcboh位移振动温度压力应变应力电流电压电场磁场流量浓度可以测量70多个物理化学量广告显示牌激光手术刀仪表照明工艺装饰电力输送光纤面板医用内窥镜潜望镜光子集成光电子集成集成光路光收发模块光接入模块光开关模块光放大模块信息获取信息传输信息处理其它应用作业
1. 波导的有效折射率 N
定义: 由于: 所以:
N / k0 k0 n2 k0 n1
n2 N n1
k0 n2
N n2
波导中导模截止条件: 指数衰减场
2. 波导的归一化频率V
2 1/2 V k0 h(n12 n2 )
V ( , h, n)的物理意义?
广告显示牌 激光手术刀 仪表照明 工艺装饰 电力输送 光纤面板 医用内窥镜 潜望镜
脊波导的几种计算方法.

论述脊型光波导的分析方法及其模场分布的计算摘要:本文主要介绍了如何通过有效折射率法计算脊型光波导的模场分布以及如何通过有限元法来数值求解脊波导的模场分布其次我们介绍了脊波导的工作特性和制作方法,最后我们列举了脊波导在激光器,调制器等信息光电子器件中的应用。
关键词:脊波导有效折射率模场分布有限元法1引言:脊波导与相同尺寸的矩形波导比较主要优点是:主模H10波的截止波长较长,对于相同的工作波长,波导尺寸可以缩小;H10模和其它高次模截止波长相隔较远,因此单模工作频带较宽,可以达到数个倍频程;等效阻抗较低,因此易与低阻抗的同轴线及微带线匹配。
但脊波导承受功率比同尺寸的矩形波导低。
脊形波导在集成光学中有广泛的应用,它是薄膜激光器、藕合器、调制器、开关等许多光电器件的基础。
由于脊形波导边界复杂,精确地分析其光学特性十分困难,若考虑介质的吸收作用,则难度就更大。
其次要能够设计出性能优良的光波导,那么必须首先能够在理论上对光波导进行计算。
对于脊型光波导而言由于其结构复杂没有严格的解析解,应采用数值方法或近似法进行分析。
光波导分析方法常用的有:转移矩阵法、模耦合理论、有效折射率法、有限元法、时域有限差分法和束传播法等。
在本文中采用的计算方法是有效折射率法对脊型光波导进行分析计算,还介绍了一种利用有限元差分算法对脊波导的模式进行数值计算。
最后介绍了脊型光波导在信息光电子学中的应用。
2脊型光波导的理论模型分析2.1脊波导的有效折射率法脊波导的横截面如图一所示,图中,分别为芯区,下包层和上包层的折射率,a为脊宽,h为脊高,b为脊下的芯厚度,则b-h为脊两边的芯厚度,此时光功率主要限制在脊下波导的芯中传播。
有效折射率法是把这种波导等效为x方向厚度为a的对称三层平板波导,如图二所示。
在脊波导中主要存在两种形式的模,模和模,前者以为主,同时为0,后者以为主,同时为0。
我们以导模为例来说明这一等效平板波导的折射率分布是如何确定的。
对称平板波导的模式计算

课程设计任务书学生姓名:许文军专业班级:电子0901班指导教师:葛华工作单位:信息工程学院题目:初始条件:计算机、beamprop软件要求完成的主要任务:1、课程设计工作量:2周2、技术要求:(1)学习beamprop软件。
(2)设计对称平板波导的模式计算。
(3)对对称平板波导的模式计算进行beamprop软件仿真工作。
3、查阅至少5篇参考文献。
按《武汉理工大学课程设计工作规范》要求撰写设计报告书。
全文用A4纸打印,图纸应符合绘图规范。
时间安排:2012.6.25做课设具体实施安排和课设报告格式要求说明。
2012.6.25-6.28学习beamprop软件,查阅相关资料,复习所设计内容的基本理论知识。
2012.6.29-7.5对对称平板波导的模式计算进行设计仿真工作,完成课设报告的撰写。
2012.7.6 提交课程设计报告,进行答辩。
指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要 (I)Abstract (II)1 绪论 (1)2原理分析 (2)2.1 均匀介质薄膜波导 (2)2.2 平面光波导 (3)2.3 平板波导的波动理论 (5)3 BeamPROP软件 (7)3.1软件简介 (7)3.2 对称平面波导的BeamPROP仿真设置 (7)4 平面波导仿真图 (13)4.1 波导结构观察 (13)4.2 波导传输仿真 (13)4.3 不同模式仿真图 (14)5 总结 (17)参考文献 (18)摘要平面光波导,英文缩写PLC是英文Planar Lightwave Circuit的缩写,翻译成中文为:平面光波导(技术)。
所谓平面光波导,也就是说光波导位于一个平面内。
正如大家所熟悉的单层电路板,所有电路都位于基板的一个平面内一样。
本文从理论上推导了对称平板波导的模式计算,利用BeamPROP软件仿真,探究了对称平板波导的模式分类及各自特点,得到了其仿真特性和一些仿真图,验证了相关理论,并且加深了对对称平板波导的模式的理解。
光波导平面

B
y
-d
全反射相移
• 费涅尔定律:TE/TM波振幅反射系数
rTE = rTM =
2 2 n1 cosq n 2 n sin q j 1 2 2 n1 cosq n 2 n sin q j 1 2 2 n j cosq n1 n 2 n sin q j 1 2 2 n j cosq n1 n 2 n sin q j 1
2 1/ 2
)
2 2 1/ 2 2 0
2
n k
2 2 1/ 2 0 0
) )
2 归一化频率:V = k0 d n12 n2
本征值方程
Df=fD-f12-f10=2mp
TE : W2 1 W0 U = tg tg mp U U U (W2 W0 ) tgU = 2 U W0W2
本征值与模式分析(I)
• 基模:m=0, 2n1k0dcosq=f12q)f10q) • 本征值:曲线交点对应的q ; • 波导截止条件:
2 2 TE 1 n n 2 2 1 2 0 k0 d n1 n2 = tg A 2 ,A= 2 2 ( n / n ) TM n n 1 0 1 2
模式场分布
• • • • • Exmn模:Ex(x,y)=E1sin(xmp2a) sin(ynp2d) Ex11模:Ex(x,y)=E1sin(xp2a) sin(yp2d) Ex21模:Ex(x,y)=E1sin(xpa) sin(yp2d) Ex12模:Ex(x,y)=E1sin(xp2a) sin(ypd) Ex22模:Ex(x,y)=E1sin(xpa) sin(ypd) (0<x<2a; 0<y<2d)
1.1平板波导几何光学分析1102

1 1
1 1
导模
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
波导的n1、n2界面的全反射临界角 波导的n1、n3界面的全反射临界角 因为 n2 n3,所以 C12 C13
C 12 arcsin
C 13 arcsin
n2 n1
n3 n1
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
X 覆盖层 薄膜层 衬底层
Z
n3 n1 n2
Y
平板波导
Z-光波传输方向
从物理量随着指标变化来看,平板波导只与X、Z两 个指标波导。又可称平板波导为二维波导。
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
设n1 > n2 n3
n2= n3-对称平板波导; n2 n3-非对称平板波导;
sin 1 sin C 12 sin C 13
将
sin C 12
n2 n1
代入
n1sin 1 n2
n2 sin1 n1
k0n1sin 1 k0n2
而传播常数
k1z k0 n1 sin 1
n2 k0
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
1、导模 (1)传播常数 因为是导模,所以 1 > C12 C13, 定义:传播常数-薄膜层中,沿Z方向的波数。
k1z k0 n1 sin 1
n1k0
1
Z
=k1z =n1k0 sin1
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
覆盖层中,
平板波导理论

P
c
T
漏泄光线
z
zp1
3
3.1 均匀介质薄膜波导中光线的传播 方程
n0
d
n1
n2
❖ 厚度d很薄,约为数微米; ❖ 芯层折射率(n1)大于衬底折射率(n2)和敷层折
射率(n3); ❖ y方向比x方向尺度大得多。
4
3.1.1 光线的传播路径及光线的分类
t
n3
i r
z
n1
d d s
n
(
x
)
dx d s
d n1( x ) dx
d d s
n
(
x
)
dz ds
0
x
ds dx
z(x) dz
z(0) z
积分上面第二式得
n ( x ) d z const ds
由几何关系得
dz ds
cos
z
故
n(x) dz ds
n 1 ( x ) cos
z ( x ) n 1 ( 0 ) cos
)
0
所以
A
n
2 1
(
x
x tp )
cos
2 2 z ( x tp
)
2
即
dx dz
n
2 1
(
x
)
2
1/2
再次积分得
z(x)
x 0
n
2 1
(
x
)
2
1/2 d x
即 x 0时 , z 0的前提下 ,
给定 n1 ( x ) 和 z ( 0 ), 即可确定传播路径
14
3.2.2 传播时延及时延差 n2
左右手材料对称光波导的导波模式研究

73
左右 手 材 料 对 称 光 波导 的导 波 模 式 研 究 木
许 江 勇 ,周 丽 萍 ,谭 福 奎 ,李 珏
(兴义 民族师范学院 物理与工程技术学 院 ,贵州 兴义 562400)
摘 要: 利用传输矩 阵方法,研 究左右手材料 对称 光波导的导波模 式特性 。结果表 明 :导波层为右手材料时 ,模 系数 m 、m:、 m 、t/z4分 别有 4、3、2、1个导模 ,有 l、2、3、4个 电场振 荡,模 系数 为奇数 的电场振 荡呈轴对称 ,模 系数为偶数 的电场振 荡呈 中心 对称 ;导波层为左手材料 时,模 系数 m 、m m 、m 分别有 1、3、2、1个导模 ,有 0、1、2、3个 电场振 荡,模 系数 为奇数 的电场振 荡 呈中心对称 ,模 系数 为偶数 的电场振 荡呈轴对称 ;两种 导波层 的电场振 荡程 度都 随着模 系数从 m 至 m 逐渐增加 而加剧 ,包 裹层 的 电 场都 呈现 完 全 的 消 逝 现 象 。 关 键 词 : 左 右 手 材 料 ,对 称 光 波 导 ,导 波模 式 ,模 系数 ,电 场 分 布 中图分类号 :0411.3 文献标识码 :A 文章编号 :1003—6563(2018)02-0073-05
Guided m odes of sym m etric optical waveguides of left-handed and right—handed m aterials
XU Jiangyong,ZHOU Liping,TAN Fukui,LI Jue
(College of Physics and Engineering Technology,Xingyi Normal University for Nationalities,Xingyi 562400,China)
平板波导

H y ( x)
H 然后,根据边界条件,x=a,-a处, y , Ez 分量连续
n2 q f tan(ha ) 2 ns h n2 p f tan(ha ) 2 nc h
n2 q n2 p f f 2ha m arctan( 2 ) arctan( 2 ) ns h nc h 这就是TM模的特征方程
D 0 B 0 B t D H t E
B 0 H 0 H 0e i ( k r t ) D E E0e i ( k r t )
E -i0 H H i E
E z E y i0 H x y z Ex E z i0 H y z x E y E x i0 H z x y
Why free electrons will oscillate with the light wave excitation?
Hy 是SPP的本征模式. 然而, Ey 并不存在于表面等离子波 中. 所以只用讨论Hy 模式 如图所示,Hy Ex k 三者满足右手定则,Ex的正负半轴 激起金属中自由电子的震荡。
E y
z E x E z i0 H y z x E y i0 H z x
假设:
E E(x, y)e -iz H H ( x , y ) e i z
Ey E y x
0 Hx
Hy
Ex
i0 H z H z iE y x
As e
q ( x a )
, x a
根据边界条件,在x=a,-a处,有 E y , H z连续(E y 和它的偏导数)
q h p t an(ha ) h t an( ha )
《波导光学》1-2

n2
t • Et
z
将(1)代入 消去折射分量
n2 (Ei Er ) cost
Ht 折射光
TE波
(n1 cosi n2 cost )Ei (n1 cosi n2 cost )Er
12
菲涅耳(Fresnel)公式
得到TE波的反射系数
10
TM波: 横磁波
光波的偏振态
10、横磁波(TM波, P波):E矢量 入射面,H矢量 入射面
20、横电波(TE波, S波) : E矢量 入射面,H矢量 入射面
x
入射光 Ei
Er 反射光
Hi • i r • Hr
n1 n2
TM波
t • Ht
Et z 折射光
x
入射光
Ei
Er
Hi • i r •
3
沿空间任意方向传播的平面波
在均匀介质中光沿直线传播。
(在非均匀介质中,光线向折射率大的方向弯曲)
x
p(x,y,z)
k
r a
γ
z
β
y
4
单色平面波的复数表达式
E(r ,t) E0 exp{i[k • r t) 0 ]}
时空分离
E
(r,
t
)
E
0
exp
i
k•
r
exp
it
E
r
exp
it
其中
n2
反射光线位于入射光线和法线 n1 所决定的平面内,反射光线和 入射光线处于法线的两侧,且
t i r
i r , n1 sini n2 sint
菲涅耳(Fresnel)公式
1.2平板波导电磁场分析1102

2011年 §1.2 平板波导电磁场分析 2011年2月
第一章 平板波导
∂2 ∂ 2 i ( ωt − β Z ) ∇ 2 E y = 2 [ E y 0 ( x )]e i (ωt − βZ ) + E y 0 ( x ) 2 e ∂x ∂z ∂2 = 2 [ E y 0 ( x )]e i (ωt − βZ ) − β 2 [ E y 0 ( x )e i (ωt − βZ ) ] ∂x
2011年 §1.2 平板波导电磁场分析 2011年2月
第一章 平板波导
(三)平板波导波动方程 平板波导: 平板波导: (1)介质是非磁、无源、各向同性 (2)考虑解的时间部分为简谐振动 (3) Y方向无限制
∂ =0 ∂y
(4)介质是均匀的 ∇ε = 0
2011年 §1.2 平板波导电磁场分析 2011年2月
2 + (n 2 k 0 − β 2 ) E y ( x ) = 0 j
j = 1,2,3代表薄膜、衬底、覆盖层。坐标如图所 , , 示 。 导模 n1k0>β > n2k0≥ n3k0 j =3
2 2 E ′′( x ) + ( n3 k0 − β 2 ) E y ( x ) = 0 y 2 2 E ′′( x ) = [± ( β 2 − n3 k0 )1 / 2 ]2 E y ( x ) y
2011年 §1.2 平板波导电磁场分析 2011年2月
第一章 平板波导
一般把振幅(场随着x的分布) Ey0(x)写出Ey(x), 又称为不考虑时间和纵向的横向场分布。 所以, TE模 Ey满足
∂2Ey ∂x 2 + (k 2 − β 2 ) E y = 0 , 或 ∂2Ey ∂x 2 + ( n 2 k02 − β 2 ) E y = 0
光波导-1.2平板波导电磁场分析1102(精)

考虑到:解为时谐形式
i ( t k r ) H H0e
i ( t k r ) E E0e
i , t
2 2 t 2
§1.2 平板波导电磁场分析 2011年2月
第一章 平板波导
波动方程可以写为
2 E 2 H
E 2 0 2 t 2 H 2 0 t 2
2
再利用:
0 k n k
2 2 2
2 0
(下页证明)
得到波动方程
2 E k E 0 2 2 H k E 0 或 2 2 2 H n k 0 H 0
2 k n k 0 0 2 0 ﹟ 0
2 2 2 0
§1.2 平板波导电磁场分析 2011年2月
第一章 平板波导
(2) 可以证明,对于平板波导仅存在 横电—TE模,只有Ey、Hx、Hz分量,只需求Ey 横磁—TM模 只有Hy、Ex、Ez分量,只需求Hy 其余场分量可以由Ey或Hy推导得到。 注意: Ey或Hy的下标y表示是场分量的方向。
第一章 平板波导
§1.2 平板波导电磁场分析
一、波动方程
D H J ; t
(一)Maxwell 方程 —
E
H
B E ; B 0; D t 电场强度矢量; — 电位移矢量; D
— 磁场强度矢量; B
2
§1.2
平板波导电磁场分析
2011年2月
第一章 平板波导
并可以得到分量方程
E z E y i 0 H x y z
H z H y i E x y z
平板波导

i H x
i H y Ez x E i E x z i0 H y x
亥姆赫兹方程:
先研究TE模
2 ( x, y, z ) k 2 ( x, y, z ) 0 2 2 2 x 2 y 2 z 2
2
Ey Ey e
每一模式对应的锯齿光路和横向光场分布
6
对于特征方程中的 12 10 是上下界面处全反射所引起的相移,那 么具体可根据菲涅尔公式求出。
n cos1 n2 cos 2 rs rTE 1 n1 cos1 n2 cos 2 rp rTM n2 cos1 n1 cos 2 n2 cos1 n1 cos 2
E y
z E x E z i0 H y z x E y i0 H z x
假设:
E E(x, y)e -iz H H ( x , y ) e i z
Ey E y x
0 Hx
Hy
Ex
i0 H z H z iE y x
2h 212 210
5
如果相干相长,即满足谐振条件,则此入射角对应的光 线(模式)可以被导波所接受
2h 212 210 2m
物理意义:在波导厚度h确定的情况下,平板波导所能 维持的导模模式数量是有限的,此时m只能取有限个整 数值,这个方程也称作平板波导的本征方程
在x=a处利用
1 dH y ( x) dx
连续的边界条件
t an( 1a)
2 1 1 1 2 T
1 1a m arctan( ) T
17
surface plasmon polariton
表面等离子体是传播于介质与金属(银)界面上的电磁激 发,在垂直于界面的方向上呈指数衰减。金属中的自由电 子在外界电磁场的作用下相对于金属中的正离子发生相对 位移,带来电子密度的重新分布,从而在金属表面的两边 产生电场
光线通信课后题解答

1.6 RG-19/U is used at 100 MHz with an input power of 10 mW. The receiver sensitivity is 1 μm . Compute the maximum length of the communications link. Repeat the computation for the case in which a fiber with a loss of 5 dB/km replaces the coaxial cable. The fiber system’s input power and receiver sensitivity are the same as those of the coaxial cable system.(如果RG-19/U同轴电缆系统的工作频率在100MHz附近,假设其输入功率是100mW。
接收机的灵敏度是1 μW。
试计算通信线路的最大长度。
用损耗为5dB/km的光纤代替此同轴电缆,重复上面的计算。
假设光纤系统的输入功率和接收机的灵敏度与同轴电缆系统相同。
)1.29Suppose a fiber system operates at a wavelength of 1.55 μm. The system can handle digital information at a data rate equal to one-hundredth of one percent of the optical frequency. How many HDTV compressed video channels can be multiplexed onto this fiber system?(假设一个光纤系统的工作波长为1.55μm。
该系统可以传送的数字信息速率等于光频率的百分之一的百分之一。
试问,有多少个HDTV压缩图像信道可以复用到这个光纤系统)上?2.8 Compute the divergence angle of a Gaussian beam of wavelength 0.8 µm and spot size 1 mm. If this beam is aimed at the moon, what is its spot size on the moon’s surface?(The distance between the earth and the moon is3.8*108 m .) What is its spot size at distances of 1 km and 10 km?(假设高斯光束的波长为0.8µm,光斑尺寸为1mm,计算其发散角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计任务书学生姓名:专业班级:指导教师:工作单位:题目:初始条件:计算机、beamprop软件要求完成的主要任务:1、课程设计工作量:2周2、技术要求:(1)学习beamprop软件。
(2)设计对称平板波导的模式计算。
(3)对对称平板波导的模式计算进行beamprop软件仿真工作。
3、查阅至少5篇参考文献。
按《武汉理工大学课程设计工作规范》要求撰写设计报告书。
全文用A4纸打印,图纸应符合绘图规范。
时间安排:2012.6.25做课设具体实施安排和课设报告格式要求说明。
2012.6.25-6.28学习beamprop软件,查阅相关资料,复习所设计内容的基本理论知识。
2012.6.29-7.5对对称平板波导的模式计算进行设计仿真工作,完成课设报告的撰写。
2012.7.6 提交课程设计报告,进行答辩。
指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要 (I)Abstract (II)1 绪论 (1)2原理分析 (2)2.1 均匀介质薄膜波导 (2)2.2 平面光波导 (3)2.3 平板波导的波动理论 (5)3 BeamPROP软件 (7)3.1软件简介 (7)3.2 对称平面波导的BeamPROP仿真设置 (7)4 平面波导仿真图 (13)4.1 波导结构观察 (13)4.2 波导传输仿真 (13)4.3 不同模式仿真图 (14)5 总结 (17)参考文献 (18)摘要平面光波导,英文缩写PLC是英文Planar Lightwave Circuit的缩写,翻译成中文为:平面光波导(技术)。
所谓平面光波导,也就是说光波导位于一个平面内。
正如大家所熟悉的单层电路板,所有电路都位于基板的一个平面内一样。
本文从理论上推导了对称平板波导的模式计算,利用BeamPROP软件仿真,探究了对称平板波导的模式分类及各自特点,得到了其仿真特性和一些仿真图,验证了相关理论,并且加深了对对称平板波导的模式的理解。
关键词:对称平板波导的模式计算,beampropAbstractPlanar waveguide, abbreviations PLC is the abbreviation of English Planar Lightwave Circuit, translated into Chinese for: Planar waveguide (technology). The so-called planar waveguide, that is optical waveguide is located in a plane within. Just as we are familiar with the single circuit board, all circuit are located in base board of a plane within. This paper theoretically symmetry planar wave-guide model calculation, the use BeamPROP software simulation, explores the symmetric planar wave-guide pattern classification and characteristics, obtain the simulation characteristics and some simulation diagram, verify the related theory, and deepened to the symmetry of planar wave-guide the understanding of mode.Keywords: symmetrical planar wave-guide model calculation, beamprop1 绪论平面光波导,英文缩写PLC是英文Planar Lightwave Circuit的缩写,翻译成中文为:平面光波导(技术)。
所谓平面光波导,也就是说光波导位于一个平面内。
正如大家所熟悉的单层电路板,所有电路都位于基板的一个平面内一样。
因此,PLC是一种技术,它不是泛指某类产品,更不是分路器!我们最常见的PLC分路器是用二氧化硅(SiO2)做的,其实PLC技术所涉及的材料非常广泛,如玻璃/二氧化硅(Quartz/Silica/SiO2)、铌酸锂(LiNbO3)、III-V族半导体化合物(如InP, GaAs等)、绝缘体上的硅(Silicon-on-Insulator, SOI/SIMOX)、氮氧化硅(SiON)、高分子聚合物(Polymer)等。
基于平面光波导技术解决方案的器件包括:分路器(Splitter)、星形耦合器(Star coupler)、可调光衰减器(Variable Optical Attenuator, VOA)、光开关(Optical switch)、光梳(Interleaver)和阵列波导光栅(Array Waveguide Grating, AWG)等。
根据不同应用场合的需求(如响应时间、环境温度等),这些器件可以选择不同的材料体系以及加工工艺制作而成。
值得一提的是,这些器件都是光无源器件,并且是独立的。
他们之间可以相互组合,或者和其他有源器件相互组合,能构成各种不同功能的高端器件。
2原理分析2.1 均匀介质薄膜波导薄膜波导是最简单的光波导类型,对薄膜波导的分析,在光波导领域具有典型意义。
另一方面,薄膜波导又是集成光学的技术基础。
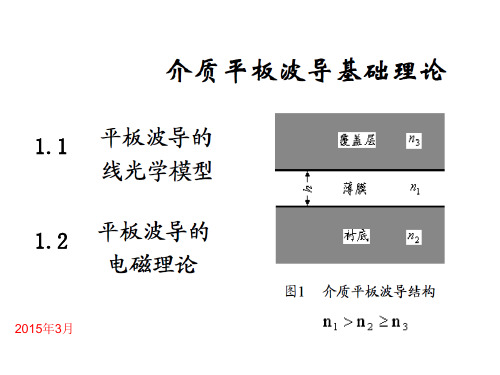
⑴波导结构薄膜波导也称平面介质波导,其结构如图2.1所示,是由两层低折射率介质膜和中间夹有的一层高折射率介质膜所组成的三层结构。
中间一层称为芯层,折射率为n 1,是光波传播的通道,下面一层称为衬底,折射率为n 2,上面一层称覆盖层,折射率n 3。
上下两层都是限制光线的阻挡层。
为了保证光线在芯层的传播,必须要求n 1大于n 2 和n 3,一般设定n 1>n 2 >n 3。
⑵波导光线均匀介质波导的芯层光线沿直线传播,经与上下界面的反射和折射,形成锯齿形光线。
光线可分为两种,满足全反射条件的光线,始终被束缚在芯层内,称为束缚光线或导波光线,未满足全反射条件的光线称为折射光线或辐射光线,这种光线可穿过界面进入衬底或覆盖层。
⑶导波条件假定芯层的锯齿形光线向z 方向传播,但是局部光线的指向却有上倾和下倾两种可能,即波矢量K不是唯一确定的,其x 方向分量α±=cos K n K 01x 1具有双值不确定性。
然而K的z 分量α=sin K n K 01z 1却是唯一确定的,而且在一条光线的传播过程中始终保持不变以,这是一个重要的不变量,以β表示,称zαθn 3 复盖层n 1 芯层n 2 衬底图2.1 薄膜波导示意图x为传播常数。
因而θ=α=βcos K n sin K n 0101 (2.1)因为导波光线必须满足界面反射条件,即αsin >12n /n ,所以传播常数β必须满足以下条件01K n >β>02K n (2.2)(2.2)式被称为导波条件,适用于多种类型的波导。
有的文献定义参数0K /β=β为有效折射率(或用eff n 表示),因而导波条件也可表示为1n >β>2n (2.3)均匀介质波导的缺点是存在多模色散问题,即不同光线之间存在传播时间差。
锯齿形光线的传播时间为,其中z 为传播距离,θ为光线与z 轴的夹角,因为受到全反射条件的限制,12n /n <θcos <1,所以导波光线之间的最大时间差可表示为(2.4)其中,为折射率相对偏差。
为了克服这种多模色散问题,出现了特殊设计的非均匀介质波导。
2.2 平面光波导按几何光学概念,凡是满足的光线均可在波导中 低损耗传输。
情况并非如此,只有某些分离的角的光线才能建起真正的有效传播。
其模式将由光波导参数方程及电磁场方程及边界条件导出。
这里可以从平面波简单理论得到相同的结果。
如图2.2所示:190<<θθc z cn )1n n(c z n t 1211∆=-=∆图2.2 平面波导传输示意图对平面波BB',CC 同相位,可见由B 到C ,由B'到C'所经历的相位差为2p 的整数倍.从 B'—C' 没有反射,位相变化为 k0n1B'C' 从 B —C 经过上下两次的反射,其附加位相为2f2,2f3 故相位差为:对TE 波,TM 波是不同的。
将BC,B'C'用d 与θ表示出来,产生的相位差为故 即 从而得到TM 波,与TE 波的相位差取值。
321022ϕϕ--BC n k 321022)(ϕϕ--''-=∆C B C B n k 32,ϕϕ111111cos sin )1(sin θθθθθθθd BC tg tg d C B C B tg ddtg C B =-='=''-='πϕϕθm d n k 222cos 232110=--11221212cos sin θθϕn n n tg IE -=1cos 2θd C B BC =''-对于对称平面光波导n1=n3。
m=0时为最低模,m=1,m=2其模式结构如图2.3所示。
图2.3 m 取不同值时波导结构2.3 平板波导的波动理论对于非对称三层介质光波导,假设光沿z 方向传输,在x.y 方向上不受限制,那么它的电磁场表示成:把它代入麦克斯韦方程:得到电磁场的分量方程:112212212221cos sin θθϕn n n n n tg TM-=()()(,)(,)j wt z j wt z E E x y e H H x y e ββ--==020=-=H E t EH n t με∂∇⨯∂∂∇⨯∂假设电磁场在y 方向上不随坐标y 变化,即 ,把这个关系代入方程,就可以得到电磁场的两种模式: TE 模:TM 模:波动方程:TE 模:把电场垂直于光的传输方向(也就是z 轴),这种电磁场分布称为横电模。
TM 模:把磁场垂直于光的传输方向(也就是z 轴),这种电磁场分布称为横磁模。
000zy x z x yy xx E j E j H yEj E j H xE E j H x yβωμβωμωμ∂+=-∂∂--=-∂∂∂-=-∂∂202020zy xzx yy zH j H j n E yH j H j n E xH Hxj n E x yβωεβωεωε∂+=∂∂--=∂∂∂-=∂∂00222220()0x yyz xx z y y y H EdE j H dE E E H d E k n E dxβωμωμβ=-====+-=2020222201()()0x y yz y x z y y E H ndH jE n dxE H H dH d k H dx n dx nβωεωεβ==-===+-=0y∂=∂3 BeamPROP软件3.1软件简介RSoft是一款非常实用的光波导仿真软件。
