理论力学第七章

合集下载

理论力学第7章

理论力学第7章
（3）机构传动，传动特点是在一个刚体上存在一个不变的接触点，相对于另一个刚体运动。例如：导杆滑块机构 —— 滑块为动点，
动系固结于导杆；凸轮挺杆机构 —— 杆上与凸轮接触点为动点，
动系固结于凸轮；摇杆滑道机构 —— 滑道中的点为动点，
摇杆为动系。（4）特殊问题，特点是相接触两个物体的接触点位置都随时间变化，此时，这两个物体的接触点都不宜选为动点，应选择满足前述的选择原则的非接触点为动点。
r
r
y x si n y co r s 1 co v s tsi ω n rt sivn c tω ost
理论力学r 第 7章
r
§ 7-2 点的速度合成定理
例：小球在金属丝上的运动
z
O x
绝对运动
M'
M2 v a
相对运动vrFra bibliotekveM1
M
y
牵连点的运动
理论力学第7章
点的速度合成定理动点在某瞬时的绝对速度等于它在该瞬时的牵连速度与相对速度的矢量和
第七章点的合成运动71相对运动牵连运动绝对运动72点的速度合成定理73牵连运动是平移时点的加速度合成定理74牵连运动是定轴转动时点的加速度合成定理科氏加速度理解相对运动绝对运动和牵连运动及相应三种速度和三种加速度的定义恰当选择动点动系熟练应用点的速度合成定理牵连运动为平动时点的加速度合成定理牵连运动为转动时点的加速度合成定理
1.动点、动系和定系必须分别属于三个不同的物体。否则，绝对、相对和牵连运动中就缺少一种运动，不能成为合成运动；
2. 动点相对动系的相对运动轨迹要易于直观判断。
（1）两个不相关的动点，求二者的相对速度。根据题意，选择其中之一为动点，动系为固结于另一点的坐标系。

理论力学第七篇_复合运动

例：刨床急回机构。曲柄长OA r , 两轴间
距杆的oo角1 速度l 。w求1 。当曲柄在水平位置时摇
wo
w1
o1
步骤:
运
速
动
度
分
分
析
析
va ve vr
wo
y 解：动点：滑块A；
va B
动系：固连在摇杆O1B上；
vr
ve A
绝对运动：圆周运动；
相对运动：直线运动；
牵连运动：转动。
va ve vr
t0 t
t0 t
t0 t
aa
lim
t 0
va ' va t
ar
lim vr
t 0
' vr1 t
ae
lim
t 0
ve1 ve t
lim vr ' vr lim vr ' vr1 vr1 vr
t0 t
t 0
t
ar
lim vr1 vr t0 t
ar w vr
lim ve ' ve lim ve ' ve1 ve1 ve
牵连运动：平动
aa ae ar
arn
vr2 R
vr
ve
sin
v
sin
arn
1 R
v2
sin2
aa ae ar arn
vr
va
ve
aa sin ae cos arn
aa
1
sin
a
cos
v2
R sin2
actg
v2
R sin3
例2 已知曲柄转动的匀角速度为w, OAr,
OO1 =l, 求当OA处于水平时摇杆O1B的加速度

理论力学第七章

12
例题
点的复合运动
例题 7-1
3. 速度分析。
绝对速度va：va＝OA · ＝r ω ，方 ω 向垂直于OA，沿铅垂
方向向上。
牵连速度ve：ve为所要求的未知量，方向垂直于O1B 。相对速度vr：大小未知，方向沿摇杆 O1B 。应用速度合成定理
va ve vr
13
例题
点的复合运动
2. 运动分析。绝对运动－以O为圆心的圆周运动。相对运动－沿杆BC直线运动。牵连运动－平动。
24
ω0
O
30
C
例题
点的复合运动
例题 8-10
3. 速度分析。
α
ω
60

绝对速度va：va = ω0 r，垂直于OA向下。
D A E 牵连速度ve： ve= vB，垂直于BD向右下。
B
vr vB v a
a
a
n ae sin 30 cos 30
2 3o l r 3l
所以杆BD的角加速度
t ae l
2 3 o r (l r )
3l 2
27
例题
点的复合运动
习题课
28
第七章
一、基本概念
点的合成运动习题课
1.一个动点，两个坐标系，三种运动 2.速度合成定理
v2 B
v1
30
vr 与 va 的夹角 ve
60

M
β
ve sin 60 46 12 arcsin vr
va
vr
18
§7-３点的加速度合成定理
先分析 k’ 对时间的导数。
' drA rA rO k vA e rA dt ' ' drO dk e (rO k ) dt dt 因为 v drO r O e O dt

理论力学第七章摩擦课件

>>摩擦力与摩擦角
当物体A保持静止并且临界状态为先滑动时，只要保证所有主动
外力的合力与公法线的夹角小于等于摩擦角m，则无论外力多大，
全约束反力总可以与其形成平衡，而不会滑动。这种现象称为自锁现象。如果主动力合力的作用线位于摩擦锥以外，则无论力多小，物体都不能保持平衡。
7.2 考虑摩擦时物体系统的平衡
F
F4
b cos h sin a cos
W 2
1m cos20 2m sin20 200 kN
1.8m cos30
2
104 .2kN
综合以上四个结果，可得系统保持平衡时，拉力F的取值范围为
40.2 kN F1 F F4 104 .2 kN
>> 考虑摩擦时物体系统的平衡
例7-4 等厚均质矩形体A和B，如图7.14 所示。A重20kN，A与铅垂墙间是光滑的，A与B和B与水平固定面间的摩擦系数均为fs。试求系统平衡时fs至少应为多大？B的重量W2至少应为多少？
(2) 当物体处于向上滑动的临界状态时，摩擦力方向与图（b）所示的摩擦力方向相反。
F
F2
sin cos
f f
cos sin
W
sin 20 0.2 cos 20 200 kN cos30 0.2 sin 30
109 .7 kN
(3) 当物体处于绕O点翻倒的临界状态时，此时有：x=0
Fy 0 FNB W 0 (c)
求解可得：
FNB
W cos 2 s in
Fs
W cos 2 s in
>> 考虑摩擦时物体系统的平衡
（2）这属于平衡的临界状态。首先
求角度的最小值，此时梯子的受力

理论力学第七章梁的应力

WZ

IZ y max
圆截面
IZ

d 4 64
d 3 W Z 32
空心圆截面
IZ
D4
64
(14)
WZ
D3
32
(14)
矩形截面
IZ

bh 3 12
WZ

bh 2 6
空心矩形截面
IZ

b0h03 12
bh3 12
WZ(b1 0h023b13h2)/(h0/2)
q=40kN/m
横力弯曲时，梁的横截面上既有正应力又有切应力.切应力使横截面发生翘曲，横向力引起与中性层平行的纵截面的挤压应力，纯弯曲时所作的平面假设和单向受力假设都不成立.
虽然横力弯曲与纯弯曲存在这些差异，但进一步的分析表明，工程中常用的梁，纯弯曲时的正应力计算公式，可以精确的计算横力弯曲时横截面上的正应力.
k
d
o
k'
o'
y
最大切应力发生在中性轴上
maxFISzSb*z
4FS 3A
式中 A πd 2 为圆截面的面积. 4
4.圆环形截面梁
z
k
图示为一段薄壁环形截面梁.环壁厚度为
，环的平均半径为r0，由于 «r0 故可假设
z （a）横截面上切应力的大小沿壁厚无变化；
d
o
k'
o'
y
（b）切应力的方向与圆周相切.
A
C
FAY
1.5m l = 3m
解：
B
x
FBY
FS 90kN
x
90kN 1. 绘制内力图
x

M

理论力学第七章

dLC dt
7-2 惯性力系的简化
7-2-2 刚体惯性力系的简化 1.平面运动 ①一般情形
FIR maC , M I C dLC dt (LC J xz i J yz j J z k )
②主平面情形(如质量对称面)
LC J C ω , M IC J C α
e
Fi FI i 0
质点系达朗贝尔原理
即作用在质点系的全部外力与惯性力构成平衡力系。
7-1 质点系的达朗贝尔原理
7-1-2 质点系的达朗贝尔原理
可列6个独立投影方程
7-1 质点系的达朗贝尔原理
7-1-2 质点系的达朗贝尔原理问题已知 m,l,θ,ω, AB h, 求A，B处动约束力。加惯性力，受力如图。由动平衡
FA
A
M 0,有
ml sin2
2 2
ml sin
l
2
mg
l
2
FA FB
O

h
ml sin

mg
B
FB
考虑斜杆质量时，结果如何?
7-1 质点系的达朗贝尔原理
7-2 惯性力系的简化
7-2-1 惯性力系的主矢和主矩 7-2-2 刚体惯性力系的简化
第七章达朗贝尔原理
7-2-1 惯性力系的主矢和主矩 1.主矢:
FIR FIi mi ai m aC
与质点系运动形式无关 2.主矩: ①对固定点O
M O FI i M O F
e
且 M F
e O
dLO dt
故 M I O M O FI i
dLO dt
与质点系的分布及运动形式相关同理 M I C

理论力学第7章(点的合成运动)

（已知绝对运动和牵连运动求解相对运动的问题除外）
点的速度合成定理是瞬时矢量式，共包括大小‚方向
六个元素，已知任意四个元素，就能求出其他两个。二、应用举例
[例] 桥式吊车已知：小
车水平运行，速度为v平，物块A相对小车垂直上升的速度为v。求物块A的运行速度。
解：选取动点: 物块A 动系: 小车静系: 地面相对运动: 直线; 相对速度vr =v 方向牵连运动: 平动; 牵连速度ve=v平方向绝对运动: 曲线; 绝对速度va 的大小, 方向待求。
由速度合成定理 va= vr+ ve ，作出速度平行四边形如图示。
v a v e tg 30 0 2 3 e 3 v AB 2 3 e ( ) 3
动点：AB杆上的A点动系：偏心轮
绝对运动：直线相对运动：圆周（曲线）牵连运动：定轴转动
铰接四边形O1A=O2B=100mm， O1O2=AB，杆 O1A以等角速度 ω =2rad/s绕轴O1转动。 AB杆上有一套筒C，此套筒与杆CD相铰接，机构的各部件都在同一铅垂平面内。
）
[例3] 圆盘凸轮机构已知：OC＝e , R 3e , （匀角速度）图示瞬时, OCCA 且 O、A、B三点共线。求：从动杆AB的速度。
解：动点取直杆上A点，动系固结于圆盘，静系固结于基座。绝对速度 va = ? 待求，方向//AB 相对速度 vr = ? 未知，方向CA 牵连速度 ve =OA=2e , 方向 OA
y
O C
x
x
合成运动：相对某一参考体的运动可由相对于其它参考体的几个运动组合而成，称这种运动为合成运动
动点：要研究的点
两个参考系：一般把固定在地球上的坐标系称为静参考系；用 Oxyz表示；固定在相对地球运动的参考体上的坐标系称为动参考系；用 Oxyz 表示。

理论力学第七章

确定性系统中的内在随机性
●在一个确定性的系统中，由于其本身的非线性性质所产生的运动随机性称为确定性系统的内在随机性。
例如，上述非线性单摆的运动。 ★支配整个系统运动的因素是严格确定的（具有确定的运动方程），系统完全不存在随机力的作用。 ★然而经过时间的演化，在这种确定性系统中出现了随机行为，产生出完全不可预测的、极为复杂的结果来，最后得到一条完全随机的运动轨道。
趋行及半，小奚扑，束断书崩，啼未即起。理书就束，而前门已牡下矣。予爽然思渡者言近道。天下之以躁急自败，穷暮而无所归宿者，其犹是也夫？其犹是也夫！（选自《清代五十家文选》周容）
0= 0，02
4g l
则其解为
0
cos
2
进行运动分析：
在最高点 = ， = 0， d 0
dt
A
O
l
m
N
最高点位非稳定平衡点，可能出现三种运动情况：
A
a. 停留在该顶点，尔后径直下落；
b. 调头沿原路返回； c. 越过该顶点继续向前运动。
O
l
m
N
最高点( = )，非稳平衡，运动非唯一性。
结论：对于一个非线性系统，在确定的初始条件下，其解可能具有不可预测的随机性。
& 相轨线
&
2
2n
2(n 1)
三维相空间
&
相轨线
2n
环形相空间
★通过分析相轨线在庞加莱截面上的交点的分布
规律，就可了解到在长时间周期性的演变过程
中系统的运动规律。
时间序列相图
阻尼运动周期运动多周期运动混沌运动
讨论：
●单周期振动，每隔2运动状态复原，即

第七章---理论力学

= −kv ,
v t =0 = v0 ,
求: x=x(t)
C LY
系列一
活塞作直线运动，取坐标轴Ox如图解：1 活塞作直线运动，取坐标轴如图
2
由
dv = −kv a= dt
dυ
υ
= − kdt
得
dv = − k t dt ∫v0 v ∫0
v
v = −kt, v = v0e −kt ln v0
3
由
dx = = −v0 e− kt v dt
v0 ( −kt ) x = x0 + 1 − e k
C LY
系列一
§7-5 自然法
以点的轨迹作为一条曲线形式的坐标轴来确定动点位置的方以点的轨迹作为一条曲线形式的坐标轴来确定动点位置的方轨迹作为一条曲线形式的坐标轴来确定动点法叫自然坐标法自然坐标法。法叫自然坐标法。一、弧坐标,自然轴系弧坐标,
C LY
系列一
点都作直线运动，轴如图所示。解：A，B点都作直线运动，取ox轴如图所示。点都作直线运动轴如图所示运动方程
xA = b + rsin ϕ = b + rsin ω +θ) ( t
xB = r sin ϕ = r sin ω +θ) ( t
B点的速度和加速度点的速度和加速度
知 O C C t 已： C = AC = B = l, M = a,ϕ =ω
求：① M 点的运动方程 ② 轨迹 ③ 速度 ④ 加速度
C LY
系列一
已知：已知： C = AC = B = l, M = a,ϕ =ωt O C C 求：x=x(t)， y=y(t)。作曲线运动，解：点M作曲线运动，取坐标系作曲线运动取坐标系xoy 运动方程

理论力学第7章答案

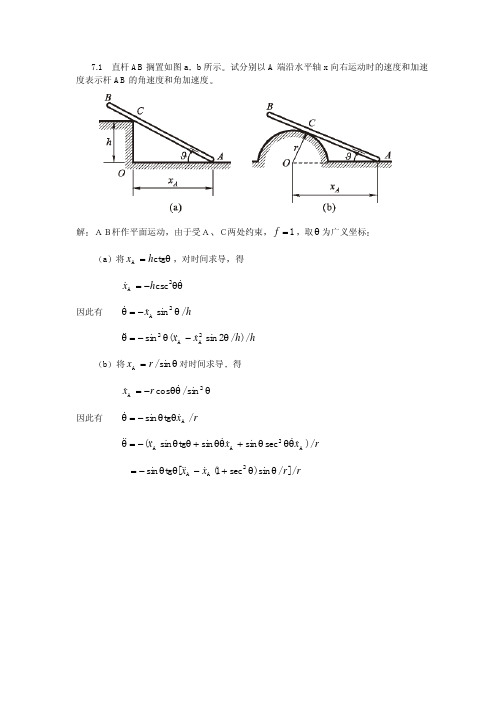
7.1 直杆AB 搁置如图a b 所示试分别以A 端沿水平轴x 向右运动时的速度和加速度表示杆AB 的角速度和角加速度解杆作平面运动由于受两处约束1=f 取θ为广义坐标a 将θ=ctg A h x 对时间求导得θθ−=&&2A csc h x因此有h x /sin 2A θ−=θ&&hh x x /)/2sin (sin 2A A 2θ−θ−=θ&&&&&b 将θ=sin /A r x 对时间求导得θθθ−=2A sin /cos &&r x因此有r x /tg sin A &&θθ−=θr x x x/)sec sin sin tg sin (A 2A A &&&&&&&&θθθ+θθ+θθ−=θr r x x/]/sin )sec 1([tg sin 2A A θθ+−θθ−=&&&7.2 试证明直杆AB 搁置如图a b 所示杆AB 运动时杆上点C 的速度沿杆AB其大小等于θcos A v解基点CA A C v v v +=a x ′0sin sinA CA A x C =θ+θ=−θ=′&&CA xv v v y ′θ=′cos A y C v v 证毕b x ′0sin sinA CA A x C =θ+θ=+θ=′&&CA x v v v y ′θ=′cos A y C v v 证毕7.3 滚压机构的滚子沿水平面作纯滚动如图示曲柄OA 长r 连杆AB 长l 滚子半径为R 若曲柄以匀角速度ω绕固定轴O 转动试求任意时刻θ=∠AOB 连杆AB和滚子的角速度解本机构自由度14233=×−×=f 除θ外取多余坐标ϕ两者间有约束方程ϕ=θsin sin l r 1矢量法基点BA A B v v v +=)(A r v ω=)sin()sin()sin(B 2A 2BA ϕ+θ=ϕ−=θ−ππv v v ϕθ=cos cos A BA v v ϕθω==ωcos cos BA AB l r l vϕϕ+θ=cos )sin(A B v v ϕϕ+θω==ωcos )sin(B B R r R v分析法将式1对时间求导得ϕθω=ϕθθ=ϕcos cos cos cos l r r &&对ϕ+θ=cos cos B l r x 对时间求导得ϕϕ+θω−=ϕϕ−θθ−=)sin(sin sin B r l r x&&&因此ϕϕ+θω=−=ωcos )sin(/B B R r R x&7.4 一放大机构中ABCD 为一平行四边形B 为OC 的中点D 为CE 的中点设图示位置点A 的速度如图示求点E 的速度解平行四边形机构在任意时有BC//ADAB//CD 因此1AD BC ωωω==2CD AB ωωω==A 基点ABB A v v v +=基点ECC E v v v +=Q OB OC 2=BACE 2=∴B11C 22v v =×=×=OB OC ωωAB22EC 22v v =×=×=BA CE ωω可导出AE 2v v =7.5 一自动卸货大卡车的升降机构如图示图中BFBE =l AC =在此瞬时活塞在处于水平的液压缸中的速度为v 求车厢转动的角速度解利用速度投影定理杆vv =o 60cosF vv 2F =v v v 2F E ==杆v v v ==o 60cosE D 因此lv AD v 2D ==ω7.6 画出图示机构中作平面运动的杆件在图示位置的速度瞬心7.7 图示拱桥上受到1F 和2F 两力作用若给出的三拱桥的支座C 若突然坍塌试求此瞬时GBJ 和ICJ 两部分的速度瞬心解GBI 构件瞬心为ICJ 构件瞬心在无穷远7.8 杆AB 可在作定轴转动的套筒O ′内滑动如图示其A 端与曲柄OA 铰接已知r O O OA =′=求杆的动瞬心轨迹和定瞬心轨迹解AB 杆作平面运动杆上与O 相重合之点速度O ′v 沿杆方向A v 垂直于OA 杆因此瞬心为C 不难看出C 点相对AB 杆和定系的位置可分别以),2(ϕr 和)2,(ϕr 表示则动定瞬心迹线分别是半径为r 2和r 的圆7.9 图示反平行四边形机构中a CD AB 2==c BD AC 2==c a >求杆BD的动瞬心轨迹和定瞬心轨迹解BD 杆的瞬心为AB 与CD 的交点P 容易证明三角形APC和DPB 全等因此瞬心P 点相对BD 杆和定系的位置均可用),(ϕρ表示在三角形APC 中有DPAP ==ρ 0sin )2(sin =ψρ−−ϕρa ca 2cos )2(cos =ψρ−+ϕρ上二式中消去ψ得222)2()cos 2()sin (ρ−=ϕρ−+ϕρa c 可导出如下椭圆方程]cos )/(1[]/)[(22ϕ−−=ρa c a c a 因此动定瞬心迹线均为椭圆7.11 三根连杆AB BC 和CD 用铰链相连组成一四连杆机构AD 可视作固定不动的连杆已知a BC AB ==a CD 2=杆AD 以匀角速度ω转动求图示两位置杆CD的角速度和角加速度解a 杆作瞬时平动0BC =ωBC v v =∴2/2/C CD ω==ωa v 基点ττ+=+CBn B n C C a a a a∴0C =τa 0CD =αb 杆速度瞬心在点0=C v ∴ω==ωa v /B BC 0CD =ω基点nCBCB n B C a a a a ++=ττx ′n CBn B c cos a a a −−=θτQ 4/7sin cos =ϕ=θaa 2n B ω=aa 2n CB ω=∴7/82C a a ω−=τ7/742/2C CD ω−==ατa a7.12 平面机构如图示已知CD//EG B 为杆DG 的中点O A B C D E G 均为铰链cm 20==EG CD cm 50=DG cm 40=OA 在图示位置杆CD 铅垂OA//CD cm/s20A =v 水平向左B 的加速度沿水平方向的分量2Bx cm/s10=a3.0tan =θ试用平面运动基点法求此瞬时 1杆CD 和杆OA 的角速度2B 的加速度沿铅垂方向的分量3杆OA 的角加速度解杆做瞬时平动AB =ωBA v v = rad/s 5.0/A OA ==ωOA v22OA nA cm/s10=ω=OA a 某点ττ++=+ABBy Bx A n A a a a a ax ′θ−θ=θ−θτsin cos cos sinBy Bx A nA a a a a 2By n A Bx A cm/s 1tg )(−=θ++−=τa a a a 2A OA rad/s )40/1(/−==ατOA a7.13 滚压机构的滚子沿水平面作纯滚动如图示曲柄OA 长r 连杆AB 长l 滚子半径为R 若曲柄以匀角速度ω绕固定轴O 转动计算连杆AB 和滚子的角加速度解矢量法基点nBABA n A B a a a a ++=τyϕ+ϕ−θ−=τsin cos sin 0n BA BA n A a a aϕω−ϕ=ϕθω−ϕϕ=τtg )(cos /)sin sin (2222BA &&l r l a x ′nBAn A B )cos(cos a a a +ϕ+θ=ϕϕϕ+ϕ+θω=cos /])cos([22B &l r a ∴ϕω−ϕ==ατtg )(/22BA AB &l a ϕϕ+ϕ+θω==αcos /])cos([/22B B R l r R a &分析法ϕω−ϕ=ϕϕθω+ϕθω−=ϕ=αtg )(cos /sin cos cos /sin 2222AB &&&l r l r ϕϕϕϕ+θω+ϕϕ+ωϕ+θω=ω=α2B B cos /sin )sin(cos /))(cos(R r R r &&&ϕϕ+ϕ+θω=cos /])cos([22R l r &7.14 半径为r 的圆盘在水平面上作直线纯滚子如图示其中心O 的速度O v 常量杆AB 长l 其B 端用铰链与圆盘边缘相连接求在水平面上运动的A 端的速度和加速度以转角ϕ表示之解本机构自由度1=f θ和ϕ有约束方程)cos 1(sin ϕ−=θr l )1(矢量法圆盘的瞬心为点杆的瞬心为点因此)2/sin(2)/(O O B ϕ==v BP r v v θϕϕ==ωcos /)2/cos()2/sin(2/O l v CB v B AB θϕ=cos /sin O l v ]2cos /)2/sin()[cos /sin (O ϕϕ+θθϕ=ω=l l v CA v AB A )2/sin()2/sin(2)cos /(O ϕϕ+θθ=v ]cos /)cos(1[O θϕ+θ−=v 基点nBO BO O B a a a a ++=τO =a τBOa基点nAB ABB A a a a a ++=τx ′nABB A )2cos(cos a a a +θ−ϕ−π=θ∴θϕ+θϕ+θ=3222A cos sin cos )sin(l v r v a O O 分析法将式1对时间求导得θϕ=θcos /sin Ol v &因为θ−ϕ−=cos sin O A l r x x 对时间求导得)cos /sin (sin cos O O O A A θϕθ+ϕ−==l v l v v xv &]cos /)cos(1[O θϕ+θ−=v θθθϕ+θ−θϕ+θϕ+θ==2O A A cos /sin )cos(cos /))(sin(&&&&v va θϕ+θϕ+θ=322O 2O cos sin cos )sin(l v r v7.15 半径为10cm 的轮B 由曲柄OA 和连杆AB 带动在半径为40cm 的固定轮上作纯滚动设OA 长10cm AB 长40cm OA 匀角速转动角速度rad/s 10=ω求在图示位置轮B 滚动的角速度和角加速度解矢量法杆作瞬时平动AB =ωω==r v v A Brad/s10/B B =ω==ωr v cmr 10=基点ττ+=+BA n A n B Ba a a ax ′α−=β−βτsin sin cos nA nB B a a a ∴75/154tg )5/(2222B ω−=βω−ω−=τr r r r a 2rad/s 7.2075/154/2B B −=ω−==ατr a 分析法设的坐标分别为A x A y BxB y 此瞬时0A =x r y =A rx 15B =0B =y 则有22A B 2A B )4()()(r y y x x =−+−将上式求导得0))(())((A B A B A B A B =−−+−−y y y y x xx x &&&&0))(()())(()(A B A B 2A B A B A B 2A B =−−+−+−−+−y y y y y y x x x x x x &&&&&&&&&&&&将0B A ==y y&&2A ω−=r y&&r x y 5/2B B &&&−=及0A =x&&等代入上二式得ω−==r x xB A &&75/1542B ω=r x&&因此导出rad/s 10/B B =−=ωr x &2B B rad/s 7.20/−=−=αr x&&7.16 半径为r 的两轮用长l 杆A O 2相连如图示前轮1O 匀速滚动轮心的速度为v求在图示位置后轮2O 滚动的角加速度解矢量法1O 轮纯滚动vv v 221O A ==A O 2杆瞬时平动v v v 2A O 2==0A O 2=ω2O 轮纯滚动rv r v /2/22O O ==ω基点1O n AOAOO A1a a a a ++=τ1O =a 0AO =τa2O 基点n AO A O AO 221a a a a ++=τx ′ϕ−=ϕsin cosA O2a a rv a /tg 2O 2ϕ−=222O O //22r l r v r a −−==α分析法A O 2杆长l ,故22O A 2O A )()(22l y y x x =−+−则有0))(())((2222O A O A O A O A =−−+−−y y y y x xx x &&&&0))(()())(()(222222O A O A 2O A O A O A 2O A =−−+−+−−+−y y y y y y x x x x x x &&&&&&&&&&&&将0B A ==y y&&r v y/2A −=&&02O =y&&0A =x&&代入上二式得v x x2A O2==&&222O /2r l v x−−=&&于是导出r v r x /2/22O O ==ω&222O O //22r l r v r x −−==α&&7.17 圆柱体C 在固定的半圆柱D 上纯滚动一杆AB 一端与圆柱体中心铰接另一端与滑块A 铰接在图示瞬时滑块A 的速度m/s3=v 加速度2m/s2=a 求此瞬时圆柱体C 的角速度和角加速度解B基点ABAA B v v v +=o o o 105sin 15sin 60sin ABA B v v v ==m/s 70.2B =v m/s80.0BA =v∴rad/s8.15.1/B C ==ωvrad/s1.08/BA AB ==ωv nBABA AnBBa a a a a ++=+ττ5.4/2B v 82AB ⋅ωx ′n BA A n B B 30cos 15sin 15cos a a a a +=−τo o o2B m/s 31.2=τa 2B C rad/s 54.15.1/==ατa7.18 一杆AB 一端与小齿轮中心A 铰接另一端与圆盘D 的边缘B 点铰接如图示若圆盘D 以匀角速度ω转动杆AB 长m5.0求此瞬时小齿轮在齿圈上滚动的角速度和角加速度解杆的速度瞬心即齿圈的圆心因此ω=−=ω)3/4()25.3/(B AB vω=ω=)3/16(4B A v ω==ω3.51/A A &v基点nABABnBnA Aa a a a a ++=+ττ4/2A v 22⋅ωABAB ωx ′n AB n B n A A45cos cos sin a a a a +=β+β−τo 在三角形中AB)45sin(5.1sin 445sin β+=β=o o 解得o377.15=β)m 10(92.41−=AB 于是有2A 45.12ω−=τa 2A45.121/ω−==ατa A7.19 直杆CD 在C 点处与齿轮B 铰接在图示瞬时杆CD 的速度为0=v 加速度2mm/s 600=a 求此瞬时齿条A 的加速度解(1)令齿轮轮心O, 以C 为基点有τOC C O a a a += 0Ox =a 0Oy =a 所以0O =a (2)τPOP a a =2CP m/s 8.0==OP OCa a 齿条加速度 )/(8.02P s m a a ==7.20 上题中若速度改为mm/s75=v 加速度不变求齿条A 的加速度解轮心O 为速度瞬心rad/s 1C==OCv ωnOCOC C O a a a a ++=τ2C rad/s 875600/===OC a αnPOPO O P a a a a ++=τ2O τPO Px m/s 725.0075.08.0=−=−=a a a 所以2Px A m/s725.0==a a7.21 图示动齿轮O ′由曲柄O O ′带动在定齿轮O 上滚动已知曲柄的角速度为ω计算齿轮相对曲柄的角速度解方法一ω−=′)(21O r r v ω−==ω′)1/(/212O r r r v a齿轮O ′动系O O ′杆er a ωωω+=ω=ω−−ω=ω)/()(21a r r r 方法二齿轮O ′瞬心位于O ′连线外侧因此因此r ω必与ω=ωe 反向由e r /ωω=′O C CO 得ω=ω)/(21r r r7.22 图示行星齿轮系中轮I 固定轮II 由曲柄AB 带动轮III 又由轮II 带动已知曲柄的角速度为ω角加速度为零求轮III 相对曲柄AB 的角速度和角加速度设轮II 轮III 半径相同解设轮半径为r 则rAB 2=ω=r v B 2ω==ω2/B 2r vω=ω=r r v 422P ω==ω4/P 3r v轮动系杆er a ωωω+=∴ω=ω−ω=ω34r 03=ω=ω=α&&r r7.23 图示传速器由以下齿轮组成半径cm 401=r 的定齿轮半径各为cm 202=r 和cm 303=r 的相连的行星齿轮以及半径cm 904=r 的内啮合齿轮主动轴转速min /r 18001=n 带动行星齿轮在定齿轮上滚动并通过内啮合齿轮使从动轴转动试求从动轴每分钟的转速2n 解A 点作圆周运动a21A )(n r r v +=齿轮2在定齿轮1上纯滚动r v A /2=ω齿轮3与齿轮2有相同角速度23ω=ω基点BAA B v v v +=b 4n r 33ωr a232133A B )/1)((n r r r r r v v ++=ω+=∴rpm3000/)/1)((/4a 23214b =++==r n r r r r r v n B rpm 转数分e r杆OA 作顺时针纯滚动圆盘半径为r 3r =OP 求圆盘中心B 的速度解方法一因r ω与e ω反向圆盘的瞬心在连线外侧由e r //ωω=CP CO 可得rCP =圆盘动系杆e r a ω+ω=ωω=ω3a∴ω=ω=r r v 232a B 方法二基点BPP B v v v +=Q ω=ω=r r v 33e P ω=ω=r r v 3a BP∴ω=+=r v v v 23)(2/12BP 2P B 方法三动系杆er a v v v +=Q ω=ω=r r v 4r r ω=ω=r r v 1010e e∴ω=β−+=r v v v v v 23)cos 2(2/1e r 2e 2r ae r杆OA 作顺时针纯滚动圆盘半径为r 3r =OP 试求圆盘与杆OA 的接触点P 的加速度解圆盘上动系杆kr n e e P a a a a a +++=τe r α323e r ω2rr ωQ 0=r v x ′2n e x P 3ω−=−=′r a ay ′222r e y P 13)4(3ω=ω+ω−=+=τ′r r r a a a7.27 图中直杆AB 表示齿条圆轮O 表示齿轮当齿条的一端运动时带动半径为cm 5的齿轮绕轴O 转动今设A 端以cm/s 30的速度向右匀速运动求图示位置齿条AB 及齿轮O 的角速度和角加速度解AB 杆瞬心为点rad/s3/AB ==ωPA v AABC ω=PC vrad/s3/AB C O =ω==ωCO v 矢量法圆盘动系杆ABr O ωωω+=rad/s6r =ωAB r O ααα+=ABO r α+α=α圆盘上动系杆ke r O a a a a ++=杆上O ′基点nOAOA A e a a a a ++=τ由于0O =a 0A =a 由以上二式得k n OA OA r =+++τa a a ar αr AB αOA 2AB ωOA r AB 2v ωrr ω=r v x ′060cos 30cos k n OA OA =−+−τa a a o o 2AB rad/s 39−=αy ′060sin 30sin n OA OA =−−τo o a a a r 2O rad/s 39=α分析法设ϕ为广义坐标)2/(ctg ϕ=r x A 将上式求导得2/)2/(csc 2ϕϕ−=&r v A可导出rad/s 3|/)2/(sin 2602A −=ϕ−=ϕ=ϕo &r v 260A rad/s 39|/sin =ϕϕ−=ϕ=ϕo &&&r v 因为为杆瞬心ϕ==cos /A A C v PA PC v v则有rad/s3|/cos /60A C O =ϕ==ω=ϕo r v r v 260A O rad/s 39|/sin =ϕϕ−=α=ϕo &r v7.28 一机构在图示位置时OB OA ⊥点C 位于AB 的中点已知rOA =r AB 4=求当杆OA 以匀角速度ω转动时杆CD 的速度和加速度解杆瞬时平动A C v v =′0AB =ω基点nBA BA n A B a a a a ++=τ0n BA =ay β+−=τcos 0BA n A a a 15/4/2BA AB ω==ατr a杆上动系杆e r a v v v +=15/CD ωr v = k e r a a a a a ++=0k =a杆上C ′基点nCA CA n A e a a a a ++=τ0n CA =a导出τ++=CAn A r a a a a a x ′τββCAn A a a a −=cos cos CD 15AB /r r r a 22CD 7cos /2ωαεω=−=7.29 套筒C 上装有一销轴可在半径为1m 的圆槽内滑动当滑块A 以匀速m/s 5.0=v 向右上方运动而杆DA 以匀角速度2rad/s =θ&转动时求图示瞬时套筒C 在杆AD 上滑动的速度和加速度图示位置o90=θ解动系杆e r a v v v += 1k e r n a a a a a a a ++=+τ 2杆C ′点基点CA A e v v v += 3nCA CA a e a a a a ++=τ 4由13得CA A r a v v v v ++=θ=&AC CA v m/s 8=a v m/s4r =v由24得kn CA r n a a a a a a a ++=+τ1/2a v 2θAC r2v θ&y oo o 30sin 30cos 30cos k n CA r n a a a a a −−−=−∴m/s6.5330tg 30cos /k n CA n r =−−=o o a a a a a7.30 图示一机构在某瞬时的位置此时ω=ωOA 0OA =αω=l v CD 0CD =a求杆AB 的角速度和角加速度解动系杆e r a v v v += 1k e r a a a a a ++=0a =a 2杆上P 点基点A P A e v v v +=3nPA PA na e a a a a ++=τ4由13得PAe r a v v v v ++=CD v OA ωl AB 2ωl x ′PAA a 45cos 45cos v v v +=−o o ω−=+ω−==ωl v l l v 2/)(2/CD OA PA AB y ′o o 45cos 45cos A r a v v v −=ω=l v 2r由24得0k nPA PA nA r =++++τa a a a a 2OA ωl AB 2αl 2AB 2ωl r AB 2v ω x ′045cosk PA nA =−+τa a a o 222PA AB 5.222/2/ω−=ω−ω−==ατl l l l a7.31 两个半径为cm 20=r 中心距离保持不变的圆盘在地面作纯滚动在其边缘B D 处铰接的连杆BD 上安装一滑块C 杆AC 一端与滑块铰接另一端与一圆盘的中心A 铰接若A 以cm/s 60A =v 匀速水平向左运动求图示位置杆AC 的角速度和滑块C 相对BD 的速度以及杆AC 的角加速度解矢量法圆盘rad/s3/A A ==ωrv 0/A A ==εra基点BAA B v v v +=1n BA BA A B a a a a ++=τ0A =a 0BA =τa2C基点CAA C v v v +=3n CACA A C a a a a ++=τ0A =a4C 动系BD e r C v v v +=B e v v=5e r C a a a +=B e a a=6由135得CA A BA A r v v v v v +=++ yo o 30cos 30sin CA BA v v=rad/s 13/CA AC ==ωr vxo o 30sin 30cos CA BA r v v -v −=cm/s 320r =v 由246得n CA CA n BA r a a a a +=+τy oo o 30sin 30cos 30cos n CA CA BA a a a n −=−τ2CA AC rad/s 3/383/−==ατr a 分析法取θϕ为坐标存在约束方程θ=ϕcos sin 3r r 高丽营对上式连续求导得θθ−=ϕϕ&&sin cos 3θθ−θθ−=ϕϕ−ϕϕ&&&&&&sin cos sin 3cos 322将o 30=ϕ=θrad/s 3/A−=−=θr v &0=θ&&代入得rad/s 1=ϕ&2rad/s 3/38−=ϕ&&令BC =ρ则有θ−ϕ=ρsin cos 3r r 因此cm/s 320|)cos sin 3(30r =θθ+ϕϕ−=ρ==ϕ=θo&&&r v7.32 图示机构中已知杆AB 相对杆OA 的角速度ω=ωr 杆AB 相对杆OA 的角加速度0r =α杆AB 长为l 2l OC =求图示位置杆AB 上点B 的速度和加速度解矢量法杆动系杆OA r AB ω+ω=ωOA r AB ααα+=0r =α动系套筒AB C ω=ωABC αα=e r a v v v +=ea 30cos v v =oω=ω2OA ω=ω=ω3AB Clv v a ω==32/r k n e e r n a a a a a a a a +++=+ττOA 3αl 2OA 3ωl C αl 2C ωl r C 2v ωx ′k e n a a 30sin 30cos a a a a −−=−−ττo o 2OA C 38ω=α=αy ′n e r n a a 30cos 30sin a a a a −−=−τo o 2r 15ω=a动系套筒er a v v v ′+′=′Q r r v v =′e e v v −=′iv l a ω−=′32kn e e r a a a a a a ′+++′=′′τ′其中r r a a =′ττ′−=e e a a n e n e a a −=′kk a a =′xl a a a a a 2e k n e r ax 1530cos )(30sin )(ω−=−′++′−=′τ′′o oy l a a a a a 2e k n e r ay 31130sin )(30cos )(ω−=−′−+′−=′τ′′o o 分析法本题一自由度取θϕ为坐标存在如下约束)sin(sin 3=ϕ+θ−θ对上式连续求导有0))(cos(cos 3=ϕ+θϕ+θ−θθ&&&0))(sin())(cos(cos 3sin ))(cos()sin (cos 322=ϕ+θϕ+θ+ϕ+θϕ+θ−θθ+ϕ+θϕ+θ−θθ−θθ&&&&&&&&&&&&o 30=ϕ=θ时ω=ω=θr &0=α=θr&&代入以上二式得ω=ϕ2&238ω=ϕ&&取为原点点坐标为)cos(2cos 3ϕ+θ+ϕ−=l l x B )sin(2sin 3ϕ+θ+ϕ−=l l y B 对上二式连续求导并代入具体数值解出l l l xB ω−=ϕ+θϕ+θ−ϕϕ=32))(sin(2sin 3&&&&0))(cos(2cos 3=ϕ+θϕ+θ+ϕϕ−=&&&&l l y B )cos (sin 32ϕϕ+ϕϕ=&&&&&l xB l l 2215]))(cos())([sin(2ω−=ϕ+θϕ+θ+ϕ+θϕ+θ−&&&&&&)sin (cos 32ϕϕ−ϕϕ−=&&&&&l y B l l 22311]))(sin())([cos(2ω−=ϕ+θϕ+θ−ϕ+θϕ+θ+&&&&&&。

哈尔滨工业大学第七版理论力学第7章课后习题答案

得
tan θ =
r sin ϕ h − r cos ϕ
sin ω 0 t h − cos ω 0 t r ]
图 7-5
注意到 ϕ = ω 0 t ，得
θ = tan −1 [
（2）
自 B 作直线 BD 垂直相交 CO 于 D，则
tan θ =
r sin ω 0 t BD = DO h − r cos ω 0 t
80
理论力学（第七版）课后题答案哈工大.高等教育出版社
7-6 如图 7-6 所示，摩擦传动机构的主动轴 I 的转速为 n = 600 r/min 。轴 I 的轮盘与轴Ⅱ的轮盘接触，接触点按箭头 A 所示的方向移动。距离 d 的变化规律为 d = 100 − 5t ，其中 d 以 mm 计， t 以 s 计。已知 r = 50 mm ， R = 150 mm 。求：（1）以距离 d 表示轴 II 的角加速度；（2）当 d = r 时，轮 B 边缘上 1 点的全加速度。解（1）两轮接触点的速度以及切向加速度相同
∠CBO =
π ， x B = 2 R cos ϕ 2 & B = 2 R + vt （↓） x B (0) = 2 R ， x
(2 R) 2 − x B
2
vt vt 1 2 − 2 2 − ( )2 R R 2R 2 v v ， vC = 2 Rω = − ω =− 2 R sin ϕ sin ϕ sin ϕ = =
两边对时间 t 求导：
vt l
& sec 2 ϕ = ， ϕ & = cos 2 ϕ ， ϕ && = − ϕ
当ϕ =
v l
v l
2v & cos ϕ sin ϕ ⋅ ϕ l

理论力学第七章

运动学
点的合成运动
牵连点分析
31
运动学
点的合成运动
牵连点分析
32
运动学
点的合成运动
牵连点分析
33
运动学
点的合成运动
牵连点分析
34
运动学
点的合成运动
牵连点分析
35
运动学练习
点的合成运动
牵连点分析
已知 , ，小球的相对速度u，OM=l。求：牵连速度和牵连加速度
53
例题
点的合成运动
解：由坐标变换关系
例题 7-2
已知点在平面内运动，其绝对运动方程为
x 5t 2 2t cos 4t 6t 2 sin 4t
y 3t 2t sin 4t 6t 2 cos 4t
点 M 相对于动坐标系 O’x’y’ 的相对运动方程为
x xo x cos y sin y yo x sin y cos
vt x x cos y sin r 1 cos r cos t r sin vt y x sin y cos r 1 cos sin t r sin r
vt sin t r vt cos t r
绝对运动：动点相对于定系的运动。相对运动：动点相对于动系的运动。牵连运动：动系相对于定系的运动。
刚体的运动
5
}
点的运动
绝对轨迹
绝对速度
绝对加速度
va aa
相对轨迹相对速度
相对加速度
vr ar
动点的选择原则：一般选择主动件与从动件的连接点，它是对两个坐标系都有运动的点。

理论力学经典课件第七章达朗贝尔原理

•
又
d
dt
di ωi ωj dt
F1
aC C
F2
rC
Fi
A
M IA y
dj ωj ωi d k 0 x
m aC
dt
dt
故 M IA ( J x α z J y ω z 2 ) i ( J y α z J x ω z 2 ) j J z α k
7-4-3 轴承动约束力
• 设动约束力如图。
z
r
m
r
m
r
m
r
2r
2m
r
m
(a)
(b)
静,动
静
(c)
静,动
mr m
rm
(d)
静
7-4-4 动约束力效应及消除方法
1. C 0 Wc=0。
由 TTv W
R
1mvc211m2R22
C
2
23
m g ( 2 R 2 R c o s) + m g R ( 1 c o s) l
而 VC 2R ，
• 1)静约束力——与主动力平衡
2)动约束力——与惯性力平衡
2.求解: 1)动量定理与动量矩定理
2)动静法形式不同，本质相同。
7-4-2 惯性力系的简化
• 如图已知ω 、α AB， l 向A点简化，且A-xyz
z
与刚体固结。
B
主矢主矩
FIRmaC
MIA
d LA dt
而 L AJxω ziJyω zjJzω k
由 Mx 0
B
F BlyJx z Jyz 20 F B x
F By
F1
FByJxzlJyz2

理论力学第七章

rM rO r '
r ' xi ' yj 'zk '
rM rM
M ' 为牵连点
18
vr
dr ' dt
xi
'
yj '
zk
'
导数上加“～”表示相对导数。
ve
drM dt
rO xi ' yj ' zk '
va
drM dt
rO xi ' yj ' zk ' xi ' yj ' zk '
2r,
ve 1 3v 3v
2r 2r 3 6r
（）
33
例题
点的复合运动
例题2
刨床的急回机构如图所示，曲柄OA的一端A与滑块用铰链连接，当曲柄OA以匀角速度ω绕固定轴O 转动时，滑块在摇杆 O1B 上滑动，并带动摇杆O1B绕固定轴O1摆动，设曲柄长OA=r，两间距离OO1= l，求当曲柄在水平位置时摇杆的角速度ω1。
29
动点、动系和静系的选择原则 1、动点、动系和静系必须分别属于三个不同的物体，否则绝对、相对和牵连运动中就缺少一种运动，不能成为合成运动 2、动点相对动系的相对运动轨迹易于直观判断（已知绝对运动和牵连运动求解相对运动的问题除外）。
30
动点几种情况：
1、两个互不相关的物体（或点）的运动——动点任取，动系固结在另一物体上。
小环M的牵连速度为 ve OM ω 2R ω cos
小环M的绝对速度为
va
ve
cos
2Rω
小环M的相对速度为 vr ve cot 2R ωsin 2R ωsinωt

哈尔滨工业大学第七版理论力学第7章课后习题答案

解
设轮缘上任 1 点 M 的全加速度为 a，切向加速度 a t = rα ，法向加速度 a n = ω r ，如图
2
7-11b 所示。
tan θ =
把
α=
dω ， θ = 60° 代入上式，得 dt
at α = 2 an ω
dω tan 60° = dt2
ω
分离变量后，两边积分：
∫ω
得
ω
0
dω
ω
2
=∫
⎤ ⎡ ⎥ ⎢ sin ω t 0 θ = tan −1 ⎢ ⎥ ⎢ h − cos ω 0 t ⎥ ⎥ ⎢ ⎦ ⎣r
故
50 π ⋅ 600 100π r ω1 = rad/s ⋅ = 100 − 5t 30 10 − 0.5t d dω 5 000 π d ⎛ 1 000π ⎞ α2 = 2 = ⎜ ⎟= dt dt ⎝ 100 − 5t ⎠ (100 − 5π )2
故得
h1 =
h4 = 2 mm 6
图 7-7
7-8 如图 7-8 所示，纸盘由厚度为 a 的纸条卷成，令纸盘的中心不动，而以等速 v 拉纸条。求纸盘的角加速度（以半径 r 的函数表示）。解纸盘作定轴转动，当纸盘转过 2π rad 时半径减小 a。设纸盘转过 dθ 角时半径增加 dr ，则
dθ =
y
B
t aB
α j
O
vA x
ω
(a) 图 7-12
aC
(b)
i 45° A n
C
t aC
解
由图 7-12b 得出
84
理论力学（第七版）课后题答案哈工大.高等教育出版社
v A = 0.2 j m/s ， v A = ω × Ri ， ω × 0.1i = 0.200 j ， ω = 2k ，

第七章理论力学

y dy
d2 j dt 2 dj
z dz
d 2k
dt 2
)
dk
)
(x
d
2i
y
d
2
j
z
d
2k
)
dt 2
dt 2
dt 2
dt dt dt dt dt dt
dt 2
dt 2
dt 2
ar
dvr dt
d 2r dt 2
d
(
dx
i
dy
j
dz
k )
dt dt
(
d 2x dt 2
dj dt
dz dt
dk ) dt
ae
又∵
dx di dy dj dz dk
vdxt(v(dvrtxii)dvtvy yjd(t
4、速度分析（略）；
D
5、加速度合成定理：
ae
ω
A
aa ae ar
O
φaa ar
B
C
大小 rω2 ? ?
方向 √ √ √
E
6、求解：ae aa cos r 2 cos
aDE ae r 2 cos
例7-4
已知：如图所示平面机构中，曲柄OA=r，以匀角速度ωO 转动。套筒A沿BC杆滑动。BC=DE，且BD=CE=l。
即：
aa ae ar ac ,
ac
2e
vr
证明：
设动系 ห้องสมุดไป่ตู้oy 作定轴转
动，转轴为通过坐标原点 o
的定轴 z ，动系的转动角速
度矢量为
．
∵
v
dr
dt
r
z

理论力学第七章点的运动学

2
2 当t 0时,S 0,sin 2 2

2sin

| | 1于是 2
2sin sin d 1 2 2 lபைடு நூலகம்m | | lim lim ( ) S S dS t 0 S t 0 t 0
§7–5 自然坐标轴系
§7–6 速度与加速的自然坐标表示法
§7.1 运动学的基本概念
一. 运动学：运动学是从几何的角度研究物体运动的科学。（即只研究物体运动的几何性质，不涉及改变运动的原因）二．参考系：参考系就是固定在参考体上的坐标系。
如:静参考系（定系）就是固定在地球上或相对地球静止的物
体上的坐标系。
r 得 cos 1 ( ) 2 sin 2 l
r 2 2 于是B的运动方程为 x r cos l 1 ( ) sin l
r 2 于是B的运动方程为 x r cos l 1 ( ) sin 2 l
为使计算方便,令
r 2 2 1 r 2 2 cos 1 ( ) sin 1 ( ) sin l 2 l 1 r 2 1 r 2 1 ( ) ( ) cos 2 4 l 4 l
x = x(t) 点的运动方程为： y = y(t) z = z(t)
轨迹为F(x,y)=0
P
k j iO
r
a
y
x
三矢径法选取空间选一点O为原点，动点的位置由矢径r表示 z
矢端曲线
P
P´ P
y
r r (t )
r r´ r
O
为点的矢径运动方程，且有
r xi y j z k
弧O1M R 2t

理论力学第7章分析解析

解： 1.运动分析：
动点：滑块A ；
动系:固连于杆BC上；
绝对运动：以O为圆心的圆周运动；相对运动：滑块A在杆BC上的直线运动；
牵连运动：BC的平移。
2.速度分析
va ve vr
？ √ √
大小：rωO ？方向：√
vr ve va rO
BD
ve rO BD l
ωt
绝对运动方程： vt vt x x cos y sin r 1 cos cos ωt r sin sin ωt r r
vt vt y x sin y cos r 1 cos sin ωt r sin cos ωt r r
§ 7-2 点的速度合成定理
例：小球在金属丝上的运动
绝对运动
M'
相对运动
M2
va ve
M1
牵连点的运动
z
vr
M y
x
O
点的速度合成定理
动点在某瞬时的绝对速度等于它在该瞬时的牵连速度与相对速度的矢量和
va ve vr
例7-3 已知：刨床的急回机构如图所示。曲柄OA的一端A与滑块用铰链连接。当曲柄OA以匀角速度ω绕固定轴O转动时，滑块在摇杆O1B上滑动，并带动杆O1B绕定轴O1摆动。设曲柄长为OA=r，两轴间距离OO1=l。求：曲柄在水平位置时摇杆的角速度 1 。
（3）机构传动，传动特点是在一个刚体上存在一个不变的接触点，相对于另一个刚体运动。例如：导杆滑块机构 —— 滑块为动点，动系固结于导杆；凸轮挺杆机构 —— 杆上与凸轮接触点为动点，动系固结于凸轮；摇杆滑道机构 —— 滑道中的点为动点，摇杆为动系。（4）特殊问题，特点是相接触两个物体的接触点位置都随时间变化，此时，这两个物体的接触点都不宜选为动点，应选择满足前述的选择原则的非接触点为动点。

理论力学第七章摩擦

补充方程：Fmax fs FN
再求F1的最小值。物体的受力如图（b）所示。
F1 sin W cos 0 FN sin f s cos fs FN F1min W 补充方程： Fmax cos f s sin
y
F F
x
0 0
0 F1 cos W sin Fmax
第七章摩擦
7.1 摩擦力与摩擦角一、摩擦力与摩擦角本章主要分析刚体在考虑摩擦时的力学行为。
>>摩擦力与摩擦角
d
MO cos FR
Fx 0, F Fx 0
Fx F FN W
Fx F arctan F W N
Fy 0, W FN 0
态。在此情形下，摩擦力Fs沿斜面向下，并达到最大值Fmax。物体共受4个力作用，如图（a）所示。列平衡方程
>> 考虑摩擦时物体系统的平衡
F F
x y
0 0
F1 cos W sin Fmax 0 FN F1 sin W cos 0
sin f s cos F1max W cos f s sin
还可以看出，即使不增加外力F的大小，只要增加hf，d的数值
也可以增加，也有可能达到，进而可以使物体运动（翻倒）。
>>摩擦力与摩擦角
和d一样，角度也随着外力F的大小增加而增大。自然地，随着外力F增大，物体达到滑动临界状态时，全约束反力与公切面的法线夹角也将达到最大值 m，该角度称为物体与接触面之间的摩擦角。
(c)
求解可得：
FNB W cos 2 sin W cos Fs 2 sin

理论力学 第七章

理论力学第7章

理论力学第七篇_复合运动

理论力学第七章

理论力学第七章摩擦课件

理论力学第七章梁的应力

理论力学第七章

理论力学第7章(点的合成运动)

理论力学第七章

第七章---理论力学

理论力学第7章答案

哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

理论力学第七章

理论力学经典课件第七章达朗贝尔原理

理论力学第七章

哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

第七章理论力学

理论力学 第七章 点的运动学

理论力学第7章分析解析

理论力学第七章 摩擦

理论力学第七章

哈尔滨工业大学第七版理论力学第7章课后习题答案

哈尔滨工业大学第七版理论力学第7章课后习题答案

理论力学第七章点的运动学

理论力学第七章摩擦