2017年中考数学试题分类汇编(三角形全等)0001
2017安徽省中考数学试题及解答0001

2017年安徽省初中学业水平考试(试题卷)注意事项:1•你拿到的试卷满分为150分,考试时间为2. 本试卷包括“试题卷”和“答题卷”两部分,3. 请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4. 考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共每小题都给出A、11 .丄的相反数是(21A .23 22 .计算a3的结果是120分钟。
“试题卷”共4页,“答题卷”共6页。
10小题,每小题4分,共40分)C、D四个选项,其中只有一个是正确的B、C. 2; D . -2C.a5;3•如图,一个放置在水平试验台上的锥形瓶,它的俯视图为(54.截止2016年底,国家开发银行对“一带一路”其中1600亿用科学计数法表示为()沿线国家累计发放贷款超过1600亿美元,A . 16 1010;B . 1.6 1010;111.6 10 ;12D. 0.16 10 ;5•不等式4 2x 0的解集在数轴上表示为(B.0 1 c.i I ■・J- 匚-2 -1 0 1 16.直角三角板和直尺如图放置,若A. 60 ;B. 50 ;1 20,则2的度数为()C. 40 ;D. 3010.如图,在矩形ABCD中,AB=5 , AD=3,动点P满足S V PAB13 S矩形ABCD,则点P到B两点距离之和PA+PB的最小值为(7•为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是()A . 280;B . 240;C . 300;D . 2608 一种药品原价每盒25元,经过两次降价后每盒16元,设两次降价的百分率都为X,则X 满足()2 2A. 16 1 2x 25 ;B. 25 1 2x 16 ;C. 16 1 x 25 ;D. 25 1 x 162b9.已知抛物线y ax bx c与反比例函数y 的图像在第一象限有一个公共点,其横x坐标为1,则一次函数y bx ac的图像可能是()A . B.);C.二、填空题(本大题共4小题,每小题5分,满分20分)11. _________________________ 27的立方根是.212. 因式分解:a b 4ab 4b =____________________ .13. 如图,已知等边VABC的边长为6,以AB为直径的e O与边AC,BC分别交于D,E两点,则劣弧DE的长为 _____________ .14. 在三角形纸片ABC中,A 90,C 30,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD (如图1 ),剪去VCDE后得到双层VBDE (如图2),再沿着过VBDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为__________ cm。
2017中考数学真题汇编----相似三角形的性质(选择、填空题)
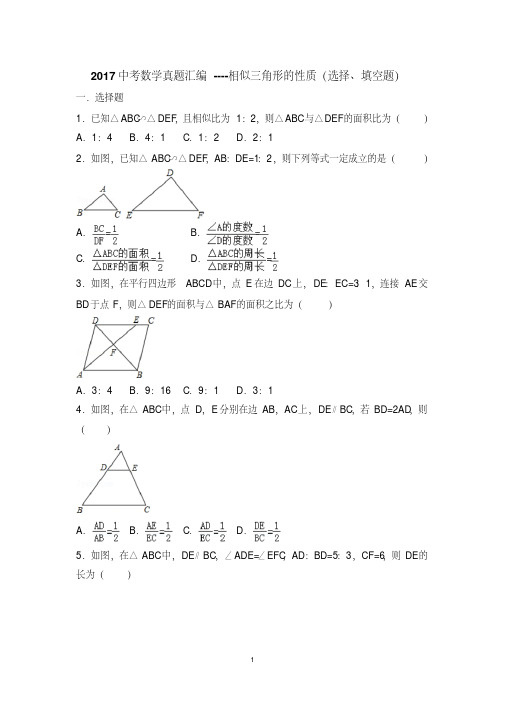
在 AB 边上移动时, DE始终与 AB 垂直, 若△ CEF与△ DEF相似,则 AD=
.
39.在平行四边形 ABCD的边 AB 和 AD 上分别取点 E 和 F,使
,
,
连接 EF交对角线 AC于 G,则 的值是
.
40.如图,点 A1,A2, A3,A4,…,An 在射线 OA 上,点 B1,B2, B3,…,Bn﹣1
A.2 B.3 C.4 D.5 19.如图,在等边△ ABC中, D 为 AC边上的一点,连接 BD,M 为 BD 上一点, 且∠ AMD=6°0 ,AM 交 BC于 E.当 M 为 BD 中点时, 的值为( )
A. B.
C. D.
20.将一张边长分别为 a, b( a> b)的矩形纸片 ABCD折叠,使点 C 与点 A 重
13.如图,在△ ABC中, D、 E 分别为 AB、 AC边上的点, DE∥ BC,点 F 为 BC边
上一点,连接 AF 交 DE于点 G,则下列结论中一定正确的是(
)
A. = B. = C. = D. =
14.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,
问井深几何? ”这是我国古代数学《九章算术》中的 “井深几何 ”问题,它的题意
DE⊥BC于点 E,连结 AE,则△ ABE的面积等于
.
8
29.如图,⊙ O 为等腰△ ABC的外接圆,直径 AB=12,P 为弧 上任意一点(不
与 B,C 重合),直线 CP交 AB 延长线于点 Q,⊙ O 在点 P 处切线 PD交 BQ 于点
D,下列结论正确的是
.(写出所有正确结论的序号)
①若∠ PAB=30°,则弧 的长为 π;②若 PD∥BC,则 AP平分∠ CAB;
专题18 三角形及全等三角形(40题)(原卷版)--2024年中考数学真题分类汇编
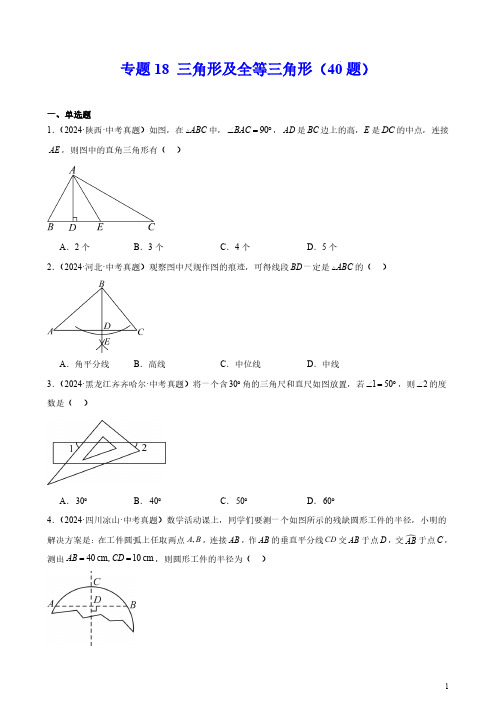
专题18三角形及全等三角形(40题)一、单选题1.(2024·陕西·中考真题)如图,在ABC 中,90BAC ∠=︒,AD 是BC 边上的高,E 是DC 的中点,连接AE ,则图中的直角三角形有()A .2个B .3个C .4个D .5个2.(2024·河北·中考真题)观察图中尺规作图的痕迹,可得线段BD 一定是ABC 的()A .角平分线B .高线C .中位线D .中线3.(2024·黑龙江齐齐哈尔·中考真题)将一个含30︒角的三角尺和直尺如图放置,若150∠=︒,则2∠的度数是()A .30︒B .40︒C .50︒D .60︒4.(2024·四川凉山·中考真题)数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是:在工件圆弧上任取两点,A B ,连接AB ,作AB 的垂直平分线CD 交AB 于点D ,交 AB 于点C ,测出40cm 10cm AB CD ==,,则圆形工件的半径为()A .50cmB .35cmC .25cmD .20cm5.(2024·云南·中考真题)已知AF 是等腰ABC 底边BC 上的高,若点F 到直线AB 的距离为3,则点F 到直线AC 的距离为()A .32B .2C .3D .726.(2024·四川凉山·中考真题)如图,在Rt ABC △中,90ACB DE ∠=, 垂直平分AB 交BC 于点D ,若ACD 的周长为50cm ,则AC BC +=()A .25cmB .45cmC .50cmD .55cm7.(2024·四川眉山·中考真题)如图,在ABC 中,6AB AC ==,4BC =,分别以点A ,点B 为圆心,大于12AB 的长为半径作弧,两弧交于点E ,F ,过点E ,F 作直线交AC 于点D ,连接BD ,则BCD △的周长为()A .7B .8C .10D .128.(2024·湖北·中考真题)平面坐标系xOy 中,点A 的坐标为()4,6-,将线段OA 绕点O 顺时针旋转90︒,则点A 的对应点A '的坐标为()A .()4,6B .()6,4C .()4,6--D .()6,4--9.(2024·北京·中考真题)下面是“作一个角使其等于AOB ∠”的尺规作图方法.(1)如图,以点O 为圆心,任意长为半径画弧,分别交OA ,OB 于点C ,D ;(2)作射线O A '',以点O '为圆心,OC 长为半径画弧,交O A ''于点C ';以点C '为圆心,CD 长为半径画弧,两弧交于点D ¢;(3)过点D ¢作射线O B '',则A O B AOB '''∠=∠.上述方法通过判定C O D COD '''△≌△得到A O B AOB '''∠=∠,其中判定C O D COD '''△≌△的依据是()A .三边分别相等的两个三角形全等B .两边及其夹角分别相等的两个三角形全等C .两角及其夹边分别相等的两个三角形全等D .两角分别相等且其中一组等角的对边相等的两个三角形全等10.(2024·广东广州·中考真题)下列图案中,点O 为正方形的中心,阴影部分的两个三角形全等,则阴影部分的两个三角形关于点O 对称的是()A .B .C .D .11.(2024·青海·中考真题)如图,OC 平分AOB ∠,点P 在OC 上,PD OB ⊥,2PD =,则点P 到OA 的距离是()A .4B .3C .2D .112.(2024·四川凉山·中考真题)一副直角三角板按如图所示的方式摆放,点E 在AB 的延长线上,当DF AB 时,EDB ∠的度数为()A .10︒B .15︒C .30︒D .45︒13.(2024·天津·中考真题)如图,Rt ABC △中,90,40C B ∠=︒∠=︒,以点A 为圆心,适当长为半径画弧,交AB 于点E ,交AC 于点F ;再分别以点,E F 为圆心,大于12EF 的长为半径画弧,两弧(所在圆的半径相等)在BAC ∠的内部相交于点P ;画射线AP ,与BC 相交于点D ,则ADC ∠的大小为()A .60B .65C .70D .7514.(2024·四川宜宾·中考真题)如图,在ABC 中,2AB AC ==,以BC 为边作Rt BCD ,BC BD =,点D 与点A 在BC 的两侧,则AD 的最大值为()A .2+B .6+C .5D .815.(2024·山东烟台·中考真题)某班开展“用直尺和圆规作角平分线”的探究活动,各组展示作图痕迹如下,其中射线OP 为AOB ∠的平分线的有()A .1个B .2个C .3个D .4个16.(2024·安徽·中考真题)在凸五边形ABCDE 中,AB AE =,BC DE =,F 是CD 的中点.下列条件中,不能推出AF 与CD 一定垂直的是()A .ABC AED∠=∠B .BAF EAF ∠=∠C .BCF EDF ∠=∠D .ABD AEC∠=∠17.(2024·浙江·中考真题)如图,正方形ABCD 由四个全等的直角三角形(,,,)ABE BCF CDG DAH △△△△和中间一个小正方形EFGH 组成,连接DE .若4,3AE BE ==,则DE =()A .5B .26C 17D .418.(2024·内蒙古赤峰·中考真题)等腰三角形的两边长分别是方程210210x x -+=的两个根,则这个三角形的周长为()A .17或13B .13或21C .17D .13二、填空题19.(2024·四川成都·中考真题)如图,ABC CDE △≌△,若35D ∠=︒,45ACB ∠=︒,则DCE ∠的度数为.20.(2024·甘肃临夏·中考真题)如图,在ABC 中,点A 的坐标为()0,1,点B 的坐标为()4,1,点C 的坐标为()3,4,点D 在第一象限(不与点C 重合),且ABD △与ABC 全等,点D 的坐标是.21.(2024·黑龙江牡丹江·中考真题)如图,ABC 中,D 是AB 上一点,CF AB ∥,D 、E 、F 三点共线,请添加一个条件,使得AE CE =.(只添一种情况即可)22.(2024·四川凉山·中考真题)如图,ABC 中,3080BCD ACB CD ∠∠=︒=︒,,是边AB 上的高,AE 是CAB ∠的平分线,则AEB ∠的度数是.23.(2024·江苏连云港·中考真题)如图,直线a b ,直线l a ⊥,1120∠=︒,则2∠=︒.24.(2024·黑龙江绥化·中考真题)如图,AB CD ∥,33C ∠=︒,OC OE =.则A ∠=︒.25.(2024·黑龙江绥化·中考真题)如图,已知50AOB ∠=︒,点P 为AOB ∠内部一点,点M 为射线OA 、点N 为射线OB 上的两个动点,当PMN 的周长最小时,则MPN ∠=.26.(2024·四川广元·中考真题)点F 是正五边形ABCDE 边DE 的中点,连接BF 并延长与CD 延长线交于点G ,则BGC ∠的度数为.27.(2024·湖南·中考真题)如图,在锐角三角形ABC 中,AD 是边BC 上的高,在BA ,BC 上分别截取线段BE ,BF ,使BE BF =;分别以点E ,F 为圆心,大于12EF 的长为半径画弧,在ABC ∠内,两弧交于点P ,作射线BP ,交AD 于点M ,过点M 作MN AB ⊥于点N .若2MN =,4AD MD =,则AM =.28.(2024·重庆·中考真题)如图,在ABC 中,延长AC 至点D ,使CD CA =,过点D 作DE CB ∥,且DE DC =,连接AE 交BC 于点F .若CAB CFA ∠=∠,1CF =,则BF =.29.(2024·陕西·中考真题)如图,在ABC 中,AB AC =,E 是边AB 上一点,连接CE ,在BC 右侧作BF AC ∥,且BF AE =,连接CF .若13AC =,10BC =,则四边形EBFC 的面积为.30.(2024·黑龙江齐齐哈尔·中考真题)如图,在平面直角坐标系中,以点O 为圆心,适当长为半径画弧,交x 轴正半轴于点M ,交y 轴正半轴于点N ,再分别以点M ,N 为圆心,大于12MN 的长为半径画弧,两弧在第一象限交于点H ,画射线OH ,若()21,1H a a -+,则=a .31.(2024·四川内江·中考真题)如图,在ABC 中,40DCE ∠=︒,AE AC =,BC BD =,则ACB ∠的度数为;三、解答题32.(2024·四川乐山·中考真题)知:如图,AB 平分CAD ∠,AC AD =.求证:C D ∠=∠.33.(2024·四川内江·中考真题)如图,点A 、D 、B 、E 在同一条直线上,AD BE =,AC DF =,BC EF=(1)求证:ABC DEF ≌△△;(2)若55A ∠=︒,45E ∠=︒,求F ∠的度数.34.(2024·江苏盐城·中考真题)已知:如图,点A 、B 、C 、D 在同一条直线上,AE BF ∥,AE BF =.若________,则AB CD =.请从①CE DF ∥;②CE DF =;③E F ∠=∠这3个选项中选择一个作为条件(写序号),使结论成立,并说明理由.35.(2024·广西·中考真题)如图,在ABC 中,45A ∠=︒,AC BC >.(1)尺规作图:作线段AB 的垂直平分线l ,分别交AB ,AC 于点D ,E :(要求:保留作图痕迹,不写作法,标明字母)(2)在(1)所作的图中,连接BE ,若8AB =,求BE 的长.36.(2024·四川南充·中考真题)如图,在ABC 中,点D 为BC 边的中点,过点B 作BE AC ∥交AD 的延长线于点E .(1)求证:BDE CDA ≌ .(2)若AD BC ⊥,求证:BA BE=37.(2024·云南·中考真题)如图,在ABC 和AED △中,AB AE =,BAE CAD ∠=∠,AC AD =.求证:ABC AED ≌△△.38.(2024·江苏苏州·中考真题)如图,ABC 中,AB AC =,分别以B ,C 为圆心,大于12BC 长为半径画弧,两弧交于点D ,连接BD ,CD ,AD ,AD 与BC 交于点E .(1)求证:ABD ACD △≌△;(2)若2BD =,120BDC ∠=︒,求BC 的长.39.(2024·黑龙江绥化·中考真题)已知:ABC .(1)尺规作图:画出ABC 的重心G .(保留作图痕迹,不要求写作法和证明)(2)在(1)的条件下,连接AG ,BG .已知ABG 的面积等于25cm ,则ABC 的面积是______2cm .40.(2024·福建·中考真题)如图,已知直线1l 2l .(1)在12,l l 所在的平面内求作直线l ,使得l 1l 2l ,且l 与1l 间的距离恰好等于l 与2l 间的距离;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的条件下,若1l 与2l 间的距离为2,点,,A B C 分别在12,,l l l 上,且ABC 为等腰直角三角形,求ABC 的面积.。
2017年浙江中考数学真题分类汇编解直角三角形(解析版)
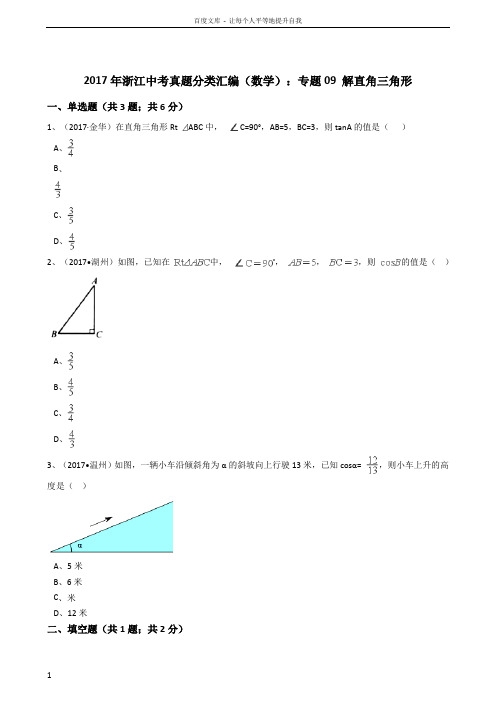
2017年浙江中考真题分类汇编(数学):专题09 解直角三角形一、单选题(共3题;共6分)1、(2017·金华)在直角三角形Rt ABC中,C=90°,AB=5,BC=3,则tanA的值是()A、B、C、D、2、(2017•湖州)如图,已知在中,,,,则的值是()A、B、C、D、3、(2017•温州)如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα= ,则小车上升的高度是()A、5米B、6米C、米D、12米二、填空题(共1题;共2分)4、(2017·嘉兴)如图,把个边长为1的正方形拼接成一排,求得,,,计算________,……按此规律,写出________(用含的代数式表示).三、解答题(共6题;共40分)5、(2017·衢州)计算:6、(2017·金华)(本题6分)计算:2cos60°+(−1)2017+|−3|−(2−1)0.7、(2017·台州)如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧与墙MN平行且距离为米,已知小汽车车门宽AO为米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由。
(参考数据:sin40°≈,cos40°≈,tan40°≈)8、(2017•绍兴)如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.(结果精确到。
参考数据:tan20°≈,tan18°≈)(1)求∠BCD的度数.(2)求教学楼的高BD9、(2017·嘉兴)如图是小强洗漱时的侧面示意图,洗漱台(矩形)靠墙摆放,高,宽,小强身高,下半身,洗漱时下半身与地面成(),身体前倾成(),脚与洗漱台距离(点,,,在同一直线上).(1)此时小强头部点与地面相距多少?(2)小强希望他的头部恰好在洗漱盆的中点的正上方,他应向前或后退多少?(,,,结果精确到)10、(2017·丽水)如图是某小区的一个健向器材,已知BC=,AB=,∠BOD=70°,求端点A到地面CD的距离(精确到).(参考数据:sin70°≈,cos70°≈,tan70°≈)答案解析部分一、单选题1、【答案】A【考点】勾股定理,锐角三角函数的定义【解析】【解答】解:在△ABC中,∵∠C=90°,AB=5,BC=3,∴AC===4,∴tanA==;故答案为A。
2017年中考真题分类解析 全等三角形

二、填空题1.(2017年贵州省黔东南州,12,4分)如图,点B,F,C,E在一条直线上,已知FB=CE,AC//DF,请你添加一个适当的条件使得△ABC≌△DEF.答案:答案不唯一,例如AC=FD,∠B=∠E,解析:证明三角形全等的方法有多种,选择合适的即可.所添条件,可以直接证全等也可间接得出结论证明全等.2.(2017陕西,14,3分)四边形ABCD中,AD=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为.DBAC答案:18,解析:过点A作AE⊥AC交CD的延长线于点E,有题意易证△AED≌△ACB,故四边形ABCD 的面积等于△ACE的面积,即四边形ABCD的面积=12AC×AE=12×6×6=18.3.15.(2017湖南怀化,4分)如图,AC=DC,BC=EC,请你添加一个适当的条件:,使得△ABC≌△DEC.答案第14题图EBDAC组边对应相等,利用SSS即可判定两三角形全等了.4.(2017湖南娄底,14,3分)如图5,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使△ABC≌△DCB.你添加的条件是__________.DB CA答案:AB=CD或AC=DB或∠ABC=∠DCB或∠ACB=∠DBC,解析:已知一斜边和一直角,要使两三角形全等,可考虑“HL”“AAS”.三、解答题1. (2017四川泸州,18,6分)如图,点A,F,C,D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF.求证:AB=DE.思路分析:根据AF=DC推导AC=DF,根据BC∥EF推导∠ACB=∠DFE,根据ASA判断△ABC≌△DEF 说明结论.证明:∵BC∥EF,∴∠ACB=∠DFE,又∵AF=DC,∴AF+FC=DC+FC,即:AC=DF.在△ABC与△DEF中,(第15题图)⎩⎪⎨⎪⎧∠A=∠D ,AC=DE ,∠ACB=∠DFE ,∴△ABC ≌△DEF (ASA ), ∴AB =DE .2. (2017重庆,24,10分)(本小题满分10分)在∆ABM 中,∠ABM =45゜,AM ⊥BM ,垂足为M .点C 是BM 延长线上一点,连接A C .(1)如图1,若AB =23,BC =5,求AC 的长;(2)如图2,点D 是线段AM 上一点,MD =MC ,点E 是∆ABC 外一点,EC =AC ,连接ED 并延长交BC 于点F ,且点F 是线段BC 的中点,求证:∠BDF =∠CEF .思路分析:(1)由AM ⊥BM ,易知∠AMB =∠AMC =90゜,利用三角形内角和定理可求得∠ABM =∠BAM ,由“等角对等边”可得AM =BM ,利用特殊角三角函数计算出AM =BM =3,又因BC =5,可得MC 的长度,最后在Rt∆AMC 中利用勾股定理即可求解出AC 的长度;(2)见中点易联想到做辅助线:延长EF 到点G ,使得FG =EF ,连接BG ,分别利用SAS 判定出∆BMD ≌∆AMC ,∆BFG ≌∆CFE ,从而将∠E 、线段CE 转化到∆BDG 中,由等腰三角形性质可证得∠BDG =∠G ,问题便可获得解决.解:(1)∵AM ⊥BM ,∴∠AMB =∠AMC =90゜,∵∠ABM =45゜,∴∠ABM =∠BAM =45゜,∴AM =BM ,∵AB =23,∴AM =BM =3,∵BC =5,∴MC =2,∴AC =133222=+;(2)延长EF 到点G ,使得FG =EF ,连接BG .由DM =MC ,∠BMD =∠AMC =90゜,BM =AM ,∴∆BMD ≌∆AMC ,故AC =BD ; 又CE =AC ,因此BD =CE ,∵点F 是线段BC 的中点,∴BF =FC ,由BF =FC ,∠BFG =∠EFC ,FG =FE ,∴∆BFG ≌∆CFE ,故BG =CE ,∠G =∠E ,所以BD =CE =BG ,∴∠BDG =∠G ,∴∠BDG =∠E .(2017年四川南充,19,8分)如图7,DE ⊥AB ,CF ⊥AB ,垂足分别是E ,F ,DE =CF ,AE =BF .求证:AC BD .思路分析:欲证AC ∥BD ,需证∠A =∠B ,即需证△AFC ≌△BED .这可利用“边角边”证得. 证明:∵AE =BF ,∴AE +EF =BF +EF , AF =BE .DE ⊥AB ,CF ⊥AB ,∴∠AFC =∠BED =90°. 在△AFC 和△BED 中,,,,AF BE AFC BED CF DE =∠=∠=∴△AFC ≌△BED (SAS). ∴∠A =∠B .∴AC ∥BD . 4. 18.(2017浙江温州,18, 8分)如图,在五边形ABCDE 中, ∠BCD =∠EDC =90°,BC =ED ,AC =A D .(1)求证:△ABC ≌△AE D. (2)当∠B =140°时,求∠BAE 的度数.EABCF图7第18题EDCB思路分析:(1)根据边角边判定△ABC 与△AED 三角形全等;(2)由三角形全等的性质得∠B =∠E =140°,五边形内角和为(5-2)×180°=540°,再求∠BAE 的度数.解:(1)∵AC =AD∴∠ACD =∠ADC又∵∠BCD =∠EDC =90°∴∠BCD -∠ACD =∠EDC -∠ADC 即∠BCA =∠ADE 在△ABC 和△AED 中 BC =ED∠BCA =∠ADE AC =AD∴△ABC ≌△AED (SAS ).(2) 由△ABC ≌△AED 得∠B =∠E =140°,五边形内角和为(5-2)×180°=540° ∴∠BAE =540°-2×140°-2×90°=80°.5. (2017江苏苏州,24,8分)如图,∠A=∠B ,AE =BE ,点D 在AC 边上,∠1=∠2,AE 和BD 相交于点O . (1)求证:△AEC ≌△BED ; (2)若∠1=42°,求∠BDE 的度数.思路分析:(1)用ASA 证明两三角形全等;(2)利用全等三角形的性质得出EC =ED ,∠C=∠BDE ,再利用等腰三角形性质:等边对等角,即可求出底角∠BDE =69°.解:(1)证明:∵AE 和BD 相交于点O ,AOD BOE ∴∠=∠.在AOD ∆和BOE ∆中,,2A B BEO ∠=∠∴∠=∠.又12,1,BEO AEC BED ∠=∠∴∠=∠∴∠=∠Q .在AEC ∆和BED ∆中,(),A B AE BEAEC BED ASA AEC BED ∠=∠⎧⎪=∴∆≅∆⎨⎪∠=∠⎩. (2),,AEC BED EC ED C BDE ∆≅∆∴=∠=∠Q . 在oo6.∠7. .AEDCB思路分析:利用同一三角形中等角对等边说明AB=AC,再利用中点的性质说明BD=CE,进而判断△BDC和△CEB全等,然后利用全等三角形的性质说明BE=CD.证明:∵∠ABC=∠ACB,∴AB=AC,∵点D,E分别为边AB,AC的中点,∴BD=CE,在△BDC和△CEB中,BD=CE,∠ABC=∠ACB,BC=CB,∴△BDC≌△CEB,∴BE=CD.8. (2017江苏常州,23,8分)如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC =∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.【解析】(1)证明:∵∠BCE=∠ACD=90°,∴∠BCA=∠ECD.在△BCA和△ECD中,BCA ECDBAC DBC CE∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCA≌△ECD,∴AC=CD;(2)∵AC=AE,∴∠AEC=∠ACE.又∵∠ACD=90°,AC=CD,∴△ACD是等腰直角三角形,∴∠DAC=45°,∴∠AEC=12(180°-∠DAC)=12(180°-45°),∴∠DEC=180°-∠AEC=180°-12(180°-45°)=112.5°.9. 18.(2017广东广州)(本小题满分9分)如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.思路分析:根据SAS证明两个三角形全等.证明:∵AE=BF,∴AE+EF=BF+EF,即AF =BE .在△ADF 和△BCE 中,AD BC A B AF BE =⎧⎪∠=∠⎨⎪=⎩,,, ∴△ADF ≌△BCE (SAS ).10. 18.(2017湖北恩施中考·分)如图7,△ABC,△CDE 均为等边三角形,连接BD ,AE 交于点O ,BC 与AE 交于点P .求证:∠AOB=600.思路分析:先由等边三角形的性质得到相等的线段和相等的角,进而证得△ACE ≌△BCE,得出∠CAE=∠CBD,再由180=∠AOB °-BAO ABD ∠-∠不难得出60=∠AOB ˚. 18.证明:在中中和BCD ACE ∆∆,⎪⎩⎪⎨⎧=∠=∠=.,,CD CE BCD ACE BC AC∴△ACE ≌△BCE,∴∠CAE=∠CBD,∴∠AOB=1800-∠BAO-∠ABO=1800-∠BAO-∠ABC-∠CBD=1800-∠ABC-∠BAO-∠CAE=1800-600-600=600.11. 18.(2017年武汉,18,8分)(本题8分)如图,点C 、F 、E 、B 在一条直线上,∠CFD =∠BEA ,CE =BF ,DF =AE ,写出CD 与AB 之间的关系,并证明你的结论.第18题图EBD F AC思路分析:判断两条线段的关系,一般包括数量关系与位置关系,这里根据已知条件,证明两个三角形全等即可,需要注意的是CE =BF 不是对应边相等,需转化. 解:CD 与AB 之间的关系为:CD =AB ,且CD ∥AB . 证明:∵CE =BF ,∴CF =BE .在△CDF 和△BAE 中 CF BE CFD BEA DF AE =⎧⎪∠=∠⎨⎪=⎩,∴△CDF ≌△BAE . ∴CD =BA , ∠C =∠B . ∴CD ∥BA18. (2017吉林,5分)如图,点E ,F 在BC 上,BE =CF ,AB =DC ,∠B =∠C . 求证:∠A =∠D .思路分析:证明两个三角形中的两个角相等,可以考虑这两个三角形全等,利用全等的性质证得. 解析:∵BE =CF ,∴BE +EF =CF +EF ,即BF =CE ,在△ABC 和△DCE 中,∵AB =DC ,∠B =∠C ,BF =CE ,∴△ABC ≌△DCE , ∴∠A =∠D .(2017福建,18,8分)(本小题满分8分)如图,点B ,E ,C ,F 在一条直线上,AB =DE ,AC =DF ,BE =CF .求证:∠A =∠D .思路分析:由BE =CF ,可得BC =EF ,进而利用全等三角形的判定条件“SSS ”可证△ABC ≌△DEF ,即得∠A =∠D .证明:∵BE =CF ,∴BE +EC =CF +EC ,即BC =EF .ABCFDE在△ABC和△DEF中,⎪⎩⎪⎨⎧===,,,EFBCDFACDEAB∴△ABC≌△DEF,∴∠A=∠D.14.((2017云南,15,6分))如图,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠ABC=∠DEF.思路分析:根据BE=CF,利用等式的性质可得BC=EF,又有条件AB=DE和AC=DF这三个条件得到三角形全等,再根据全等三角形的对应角相等得即可求证.证明:∵CF=BE,∴BE+EC=CF+EC,即BC=EF,在△AEB和△CFD中,⎪⎩⎪⎨⎧===DEABDFACEFBC,∴△ABC≌△DEF (SSS),∴∠ABC=∠DEF.。
2017年中考数学专题复习资料--全等三角形含答案(共11页)

A 12
F
C D E B
4 已知: AD 平分∠ BAC , AC=AB+BD ,求证:: AC 平分∠ BAD , CE⊥ AB ,∠ B+ ∠ D=180°,求证: AE=AD+BE
6 如图,四边形 ABCD 中,AB ∥ DC ,BE 、CE 分别平分∠ ABC 、∠ BCD ,且点 E 在 AD 上。求证:BC=AB+DC 。
P D A
C E
B
11 如图,△ ABC 中, AD 是∠ CAB 的平分线,且 AB=AC+CD ,求证:∠ C=2∠B A
C
D
B
12 如图: AE、 BC交于点 M, F 点在 AM上, BE∥ CF,BE=CF。 求证: AM是△ ABC的中线。
A
F
B
M
C
E
13 已知:如图, AB=AC,BD AC, CE AB,垂足分别为 D、 E,BD、 CE 相交于点 F 。 求证: BE=CD. C D
7 已知: AB=CD ,∠ A= ∠D ,求证:∠ B= ∠ C
A
D
B
C
8.P 是∠ BAC 平分线 AD 上一点, AC>AB ,求证: PC-PB<AC-AB C
A
P
D
B
9 已知, E 是 AB 中点, AF=BD , BD=5 ,AC=7 ,求 DC D
F
C
A
E
B
10.如图,已知 AD∥ BC,∠ PAB 的平分线与∠ CBA 的平分线相交于 E,CE 的连线交 AP 于 D .求证: AD +BC = AB.
17.如图 9 所示,△ ABC 是等腰直角三角形,∠ ACB = 90°, AD 是 BC 边上的中线,过 C 作 AD 的垂 线,交 AB 于点 E,交 AD 于点 F,求证:∠ ADC =∠ BDE .
2017全国中考数学真题 全等三角形(填空题+解答题)解析版

2017全国中考数学真题分类知识点28全等三角形(填空题+解答题)解析版一、填空题1. (2017年贵州省黔东南州,12,4分)如图,点B ,F ,C ,E 在一条直线上,已知FB =CE ,AC //DF ,请你添加一个适当的条件 使得△ABC ≌△DEF .答案:答案不唯一,例如AC =FD ,∠B =∠E ,解析:证明三角形全等的方法有多种,选择合适的即可.所添条件,可以直接证全等也可间接得出结论证明全等.2. (2017陕西,14,3分)四边形ABCD 中,AD =AD ,∠BAD =∠BCD =90°,连接AC .若AC =6,则四边形ABCD的面积为 .DAC答案:18,解析:过点A 作AE ⊥AC 交CD 的延长线于点E ,有题意易证△AED ≌△ACB ,故四边形ABCD 的面积等于△ACE 的面积,即四边形ABCD 的面积=12AC ×AE =12×6×6=18. 3. 15.(2017湖南怀化,4分)如图,AC =DC ,BC =EC ,请你添加一个适当的条件: ,使得△ABC ≌△DEC .答案:AB =DE .本题答案不唯一.解析:本题要判定△ABC ≌△DEC ,已知AC =DC ,BC =EC ,具备了两组边答案第14题图BDA (第15题图)对应相等,利用SSS 即可判定两三角形全等了.二、解答题1. (2017四川泸州,18,6分)如图,点A ,F ,C ,D 在同一条直线上,已知AF =DC ,∠A =∠D ,BC ∥EF . 求证:AB =DE .思路分析:根据AF =DC 推导AC =DF ,根据BC ∥EF 推导∠ACB =∠DFE ,根据ASA 判断△ABC ≌△DEF 说明结论.证明:∵BC ∥EF , ∴∠ACB =∠DFE , 又∵AF =DC , ∴AF +FC =DC +FC , 即:AC =DF .在△ABC 与△DEF 中,⎩⎪⎨⎪⎧∠A=∠D ,AC=DE ,∠ACB=∠DFE ,∴△ABC ≌△DEF (ASA ), ∴AB =DE .2. (2017重庆,24,10分)(本小题满分10分)在∆ABM 中,∠ABM =45゜,AM ⊥BM ,垂足为M .点C 是BM 延长线上一点,连接A C .(1)如图1,若AB =23,BC =5,求AC 的长;(2)如图2,点D 是线段AM 上一点,MD =MC ,点E 是∆ABC 外一点,EC =AC ,连接ED 并延长交BC 于点F ,且点F 是线段BC 的中点,求证:∠BDF =∠CEF .思路分析:(1)由AM ⊥BM ,易知∠AMB =∠AMC =90゜,利用三角形内角和定理可求得∠ABM =∠BAM ,由“等角对等边”可得AM =BM ,利用特殊角三角函数计算出AM =BM =3,又因BC =5,可得MC 的长度,最后在Rt ∆AMC 中利用勾股定理即可求解出AC 的长度;(2)见中点易联想到做辅助线:延长EF 到点G ,使得FG =EF ,连接BG ,分别利用SAS 判定出∆BMD ≌∆AMC ,∆BFG ≌∆CFE ,从而将∠E 、线段CE 转化到∆BDG 中,由等腰三角形性质可证得∠BDG =∠G ,问题便可获得解决.解:(1)∵AM ⊥BM ,∴∠AMB =∠AMC =90゜,∵∠ABM =45゜,∴∠ABM =∠BAM =45゜,∴AM =BM ,∵AB =23,∴AM =BM =3,∵BC =5,∴MC =2,∴AC =133222=+;(2)延长EF 到点G ,使得FG =EF ,连接BG .由DM =MC ,∠BMD =∠AMC =90゜,BM =AM ,∴∆BMD ≌∆AMC ,故AC =BD ; 又CE =AC ,因此BD =CE ,∵点F 是线段BC 的中点,∴BF =FC ,由BF =FC ,∠BFG =∠EFC ,FG =FE ,∴∆BFG ≌∆CFE ,故BG =CE ,∠G =∠E ,所以BD =CE =BG ,∴∠BDG =∠G ,∴∠BDG =∠E .3. (2017年四川南充,19,8分)如图7,DE ⊥AB ,CF ⊥AB ,垂足分别是E ,F ,DE =CF ,AE =BF .求证:AC ∥BD .思路分析:欲证AC ∥BD ,需证∠A =∠B ,即需证△AFC ≌△BED .这可利用“边角边”证得. 证明:∵AE =BF ,∴AE +EF =BF +EF , 即AF =BE .∵DE ⊥AB ,CF ⊥AB ,∴∠AFC =∠BED =90°. 在△AFC 和△BED 中,EDABCF图7,,,AF BE AFC BED CF DE =⎧⎪∠=∠⎨⎪=⎩∴△AFC ≌△BED (SAS). ∴∠A =∠B .∴AC ∥BD . 4. 18.(2017浙江温州,18, 8分)如图,在五边形ABCDE 中, ∠BCD =∠EDC =90°,BC =ED ,AC =A D .(1)求证:△ABC ≌△AE D.(2)当∠B =140°时,求∠BAE 的度数.第18题EDB思路分析:(1)根据边角边判定△ABC 与△AED 三角形全等;(2)由三角形全等的性质得∠B =∠E =140°,五边形内角和为(5-2)×180°=540°,再求∠BAE 的度数.解:(1)∵AC =AD∴∠ACD =∠ADC又∵∠BCD =∠EDC =90°∴∠BCD -∠ACD =∠EDC -∠ADC 即∠BCA =∠ADE 在△ABC 和△AED 中 BC =ED∠BCA =∠ADE AC =AD∴△ABC ≌△AED (SAS ).(2) 由△ABC ≌△AED 得∠B =∠E =140°,五边形内角和为(5-2)×180°=540° ∴∠BAE =540°-2×140°-2×90°=80°.5. (2017江苏苏州,24,8分)如图,∠A=∠B ,AE =BE ,点D 在AC 边上,∠1=∠2,AE 和BD 相交于点O . (1)求证:△AEC ≌△BED ; (2)若∠1=42°,求∠BDE 的度数.思路分析:(1)用ASA 证明两三角形全等;(2)利用全等三角形的性质得出EC =ED ,∠C=∠BDE ,再利用等腰三角形性质:等边对等角,即可求出底角∠BDE =69°.解:(1)证明:∵AE 和BD 相交于点O ,AOD BOE ∴∠=∠.在AOD ∆和BOE ∆中,,2A B BEO ∠=∠∴∠=∠.又12,1,BEO AEC BED ∠=∠∴∠=∠∴∠=∠.在AEC ∆和BED ∆中,(),A B AE BEAEC BED ASA AEC BED ∠=∠⎧⎪=∴∆≅∆⎨⎪∠=∠⎩. (2),,AEC BED EC ED C BDE ∆≅∆∴=∠=∠.在EDC ∆中,,142,69EC ED C EDC =∠=∴∠=∠=,69BDE C ∴∠=∠=.6. (2017湖北黄冈,16,6分)(本小题满分6分)已知:如图,∠BAC =∠DAM ,AB =AN ,AD =AM .求证:∠B =∠ANM .思路分析:要证明∠B =∠ANM ,根据条件只需证明△ABD ≌△ANM ,而证明△ABD ≌△ANM 的三个条件中∠BAD =∠NAM 没有直接给出,所以要先交代.证明:∵∠BAC =∠DAM ,∴∠BAC -∠DAC =∠DAM -∠DAC .即∠BAD =∠NAM . 在△ABD 和△ANM 中, ,,,AB AN BAD NAM AD AM =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△ANM (SAS ) ∴∠B =∠ANM .7. (2017湖南郴州,19,6分).已知△ABC 中,∠ABC =∠ACB ,点D ,E 分别为边AB ,AC 的中点,求证:BE =CD .思路分析:利用同一三角形中等角对等边说明AB =AC ,再利用中点的性质说明BD =CE ,进而判断△BDC 和△CEB 全等,然后利用全等三角形的性质说明BE =CD . 证明:∵∠ABC =∠ACB ,∴AB=AC ,∵点D ,E 分别为边AB ,AC 的中点,∴BD =CE , 在△BDC 和△CEB 中,BD =CE ,∠ABC =∠ACB ,BC=CB , ∴△BDC ≌△CEB ,∴BE =CD .8. (2017江苏常州,23,8分)如图,已知在四边形ABCD 中,点E 在AD 上,∠BCE =∠ACD =90°,∠BAC =∠D ,BC =CE .(1)求证:AC =CD;(2)若AC =AE ,求∠DEC 的度数.【解析】(1)证明:∵∠BCE =∠ACD =90°,∴∠BCA =∠ECD . 在△BCA 和△ECD 中,BCA ECD BAC D BC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCA ≌△ECD ,∴AC =CD;(2)∵AC =AE ,∴∠AEC =∠ACE .又∵∠ACD =90°,AC =CD ,∴△ACD 是等腰直角三角形,∴∠DAC =45°, ∴∠AEC =12(180°-∠DAC)=12(180°-45°), ∴∠DEC =180°-∠AEC =180°-12(180°-45°)=112.5°.9. 18.(2017广东广州)(本小题满分9分)如图,点E ,F 在AB 上,AD =BC ,∠A =∠B ,AE =BF . 求证:△ADF ≌△BCE .AEDCB思路分析:根据SAS 证明两个三角形全等.证明:∵AE =BF , ∴AE +EF =BF +EF , 即AF =BE .在△ADF 和△BCE 中,AD BC A B AF BE =⎧⎪∠=∠⎨⎪=⎩,,, ∴△ADF ≌△BCE (SAS ).10. 18.(2017湖北恩施中考·分)如图7,△ABC,△CDE 均为等边三角形,连接BD ,AE 交于点O ,BC 与AE 交于点P .求证:∠AOB=600.思路分析:先由等边三角形的性质得到相等的线段和相等的角,进而证得△ACE ≌△BCE,得出∠CAE=∠CBD,再由180=∠AOB °-BAO ABD ∠-∠不难得出60=∠AOB ˚. 18.证明:在中中和BCD ACE ∆∆,⎪⎩⎪⎨⎧=∠=∠=.,,CD CE BCD ACE BC AC∴△ACE ≌△BCE,∴∠CAE=∠CBD,∴∠AOB=1800-∠BAO-∠ABO=1800-∠BAO-∠ABC-∠CBD=1800-∠ABC-∠BAO-∠CAE=1800-600-600=600.11. 18.(2017年武汉,18,8分)(本题8分)如图,点C 、F 、E 、B 在一条直线上,∠CFD =∠BEA ,CE =BF ,DF =AE ,写出CD 与AB 之间的关系,并证明你的结论.第18题图EBD F AC思路分析:判断两条线段的关系,一般包括数量关系与位置关系,这里根据已知条件,证明两个三角形全等即可,需要注意的是CE =BF 不是对应边相等,需转化. 解:CD 与AB 之间的关系为:CD =AB ,且CD ∥AB . 证明:∵CE =BF ,∴CF =BE .在△CDF 和△BAE 中 CF BE CFD BEA DF AE =⎧⎪∠=∠⎨⎪=⎩,∴△CDF ≌△BAE . ∴CD =BA , ∠C =∠B . ∴CD ∥BA。
2017届云南中考数学题型专项(二)全等三角形的判定与性质(含答案)

最大最全最精的教育资源网题型专项 ( 二)全等三角形的判断与性质三角形的相关证明与计算是云南省考题中必考的基础,常常以解答题的形式出现,一般都是直接考察全等三角形的性质与判断,证明三角形全等时,只要仔细察看图形即可从已知条件中找寻出证明三角形全等的条件,但需注意解题格式,平常要增强训练.1. ( 2016·云南考试说明) 如图,已知点 E, C在线段 BF 上, BE= CF,AB∥ DE,∠ ACB=∠ F,求证:△ ABC≌△DEF.证明:∵ AB∥ DE,∴∠ B=∠ DEF.∵BE=CF,∴ BC= EF.∵∠ ACB=∠ F,∴△ ABC≌△ DEF.2.(2015 ·红河模拟 ) 已知:如图,E、 F 在 AC上, AD∥ CB且 AD= CB,∠ D=∠ B. 求证: AE= CF.证明:∵ AD∥ CB,∴∠ A=∠ C.在△ ADF和△ CBE中,∠ A=∠ C,AD= CB,∠ D=∠ B,∴△ ADF≌△ CBE(ASA).∴AF=CE.∴AF+EF= CE+EF,即 AE= CF.3.(2016 ·云南模拟 ) 在△ ABC中, AB= AC,点 E, F 分别在 AB, AC上, AE= AF, BF 与 CE订交于点 P. 求证:△EBC ≌△ FCB.证明:∵ AB= AC, AE= AF,∴∠ ABC=∠ ACB, AB- AE= AC- AF,即 BE= CF.在△ EBC和△ FCB中,BE= CF,∠ABC=∠ ACB,BC= CB,∴△ EBC≌△ FCB(SAS).全国中小学教育资源门户网站|天量课件、教学设计、试卷、教案免费下载|最大最全最精的教育资源网4.已知四边形ABCD是正方形.(1)如图, G是 BC边上随意一点 ( 不与 B,C 两点重合 ) ,连结 AG,作 BF⊥ AG于点 F,DE⊥ AG于点 E. 求证:△ABF≌△ DAE;(2) 在 (1) 中,线段EF 与 AF, BF 的等量关系是EF= AF- BF. ( 直接写出结论即可,不需要证明)证明:在正方形ABCD中, AB= AD,∠ BAD=90°,∴∠ BAF+∠ DAE= 90° .在 Rt△ ABF中,∠BAF+∠ ABF=90°,∴∠ ABF=∠DAE.∠ABF=∠ DAE,在△ ABF和△ DAE中,∠ AFB=∠ DEA=90°,AB= DA,∴△ ABF≌△ DAE.5.如图,已知AB∥ DE, AB= DE, AF= DC,请问图中有哪几对全等三角形?并任选此中一对赐予证明.解:此图中有 3 对全等三角形,它们分别是△ABF≌△ DEC,△ ABC≌△ DEF,△ BCF≌△ EFC.证明:∵ AB∥ DE,∴∠ A=∠ D.又∵ AB= DE, AF= DC,∴△ ABF≌△ DEC.同理,可证△ABC≌△ DEF或△ BCF≌△ EFC.6.(2016 ·昆明市校际中学模拟) 已知:如图,菱形ABCD中, E、 F 分别是 CB、 CD上的点,且BE= DF.求证:(1)△ ABE≌△ ADF;(2)∠ AEF=∠ AFE.证明: (1) ∵四边形ABCD是菱形,∴AB=AD,∠ B=∠ D.又∵ BE= DF,∴△ ABE≌△ ADF.(2) ∵△ ABE≌△ ADF,全国中小学教育资源门户网站|天量课件、教学设计、试卷、教案免费下载|最大最全最精的教育资源网∴AE=AF.∴∠ AEF=∠ AFE.7.(2014 ·曲靖 ) 如图,∠ ACB=90°, AC= BC, AD⊥ CE于点 D, BE⊥CE于点 E.(1)求证:△ ACD≌△ CBE;(2)已知 AD= 4, DE= 1,求 EF 的长.解: (1) 证明:∵ AD⊥ CE,∴∠ DCA+∠ DAC= 90° .又∵∠ BCE+∠ DCA= 90°,∴ ∠ BCE=∠ DAC.又∵ BE⊥ CE, AD⊥ CE,∴∠ E=∠ ADC=90° .∠ADC=∠ E,在△ ACD和△ CBE中,∠DAC=∠ ECB,AC= CB,∴△ ACD≌△ CBE.(2)∵△ ACD≌ △CBE,∴ AD=CE= 4.∴CD=BE= CE-DE= 4- 1= 3.∵∠ E=∠ ADF,∠ BFE=∠ AFD,BE EF∴△ BEF∽△ ADF.∴=.AD DF设 EF= x,则 DF=1- x.3x 3∴4=1-x. 解得 x=7.3∴EF= .78.(2016 ·云南考试说明 ) 如图 1,在△ ABC中, AB= AC, D 是 BC边上一点 ( 不与 B, C 两点重合 ) ,以 AD 为一边在AD的右边作△ ADE,使 AD= AE,∠ DAE=∠ BAC,连结 CE.(1)已知∠ BAC=90°,则∠ BCE= 90°;(2)如图 2,设∠ BAC=α ,∠ BCE=β,当点 D 在线段 BC上挪动时,α与β之间有如何的数目关系?请说明理由.解:α+β= 180° .原因:∵∠ DAE=∠ BAC,∴∠ BAC-∠ DAC=∠ DAE-∠ DAC,即∠ BAD=∠ CAE.全国中小学教育资源门户网站|天量课件、教学设计、试卷、教案免费下载|最大最全最精的教育资源网又∵ AB= AC, AD= AE,∴△ ABD≌△ ACE.∴∠ B=∠ ACE.∴∠ B+∠ ACB=∠ ACE+∠ ACB.∴∠ B+∠ ACB=β .∵ α+∠ B+∠ ACB= 180°,∴ α+β = 180° .全国中小学教育资源门户网站|天量课件、教学设计、试卷、教案免费下载|。
2017年中考数学试题 三角形分项版解析汇编(原卷+解析卷)

专题09 三角形一、选择题1.(2017重庆A卷第8题)若△ABC~△DEF,相似比为3:2,则对应高的比为()A.3:2 B.3:5 C.9:4 D.4:9【答案】A.【解析】试题解析:∵△ABC~△DEF,相似比为3:2,∴对应高的比为:3:2.故选A.考点:相似三角形的性质.2. (2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为()(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).A.5.1米B.6.3米C.7.1米D.9.2米【答案】A.【解析】试题解析:如图,延长DE交AB延长线于点P,作CQ⊥AP于点Q,∵CE∥AP,∴DP⊥AP,∴四边形CEPQ为矩形,∴CE=PQ=2,CQ=PE,∵i=140.753 CQBQ==,∴设CQ=4x、BQ=3x,由BQ2+CQ2=BC2可得(4x)2+(3x)2=102,解得:x=2或x=﹣2(舍),则CQ=PE=8,BQ=6,∴DP=DE+PE=11,在Rt△ADP中,∵AP=11tan tan40DPA=∠︒≈13.1,∴AB=AP﹣BQ﹣PQ=13.1﹣6﹣2=5.1,故选A.考点:解直角三角形的应用.3.(2017甘肃庆阳第6题)将一把直尺与一块三角板如图放置,若∠1=45°,则∠2为()A.115°B.120°C.135°D.145°【答案】C.【解析】试题解析:如图,由三角形的外角性质得,∠3=90°+∠1=90°+45°=135°,∵直尺的两边互相平行,∴∠2=∠3=135°.故选C .考点:平行线的性质;余角和补角.4. (2017甘肃庆阳第8题) 已知a ,b ,c 是△ABC 的三条边长,化简|a+b-c|-|c-a-b|的结果为( )A .2a+2b-2cB .2a+2bC .2cD .0【答案】D【解析】试题解析:∵a 、b 、c 为△ABC 的三条边长,∴a+b-c >0,c-a-b <0,∴原式=a+b-c+(c-a-b )=0.故选D .考点:三角形三边关系.5.(2017广西贵港第11题)如图,在Rt ABC ∆中,90ACB ∠= ,将ABC ∆绕顶点C 逆时针旋转得到'',A B C M ∆是BC 的中点,P 是''A B 的中点,连接PM ,若230BC BAC =∠= ,,则线段PM 的最大值是 ( )A .4B .3 C.2 D .1【答案】B【解析】试题解析:如图连接PC .在Rt △ABC 中,∵∠A=30°,BC=2,∴AB=4,根据旋转不变性可知,A′B′=AB=4,∴A′P=PB′,∴PC=12A′B′=2, ∵CM=BM=1,又∵PM ≤PC+CM ,即PM ≤3,∴PM 的最大值为3(此时P 、C 、M 共线).故选B .考点:旋转的性质.6.(2017湖北武汉第10题)如图,在Rt ABC ∆中,90C ∠=,以ABC ∆的一边为边画等腰三角形,使得它的第三个顶点在ABC ∆的其他边上,则可以画出的不同的等腰三角形的个数最多为( )A .4B .5C . 6D .7【答案】C【解析】试题解析:①以B 为圆心,BC 长为半径画弧,交AB 于点D ,△BCD 就是等腰三角形;②以A 为圆心,AC 长为半径画弧,交AB 于点E ,△ACE 就是等腰三角形;③以C 为圆心,BC 长为半径画弧,交AC 于点F ,△BCF 就是等腰三角形;④作AC 的垂直平分线交AB 于点H ,△ACH 就是等腰三角形;⑤作AB 的垂直平分线交AC 于G ,则△AGB 是等腰三角形;⑥作BC 的垂直平分线交AB 于I ,则△BCI 是等腰三角形.故选C.考点:画等腰三角形.7.(2017江苏无锡第10题)如图,△ABC 中,∠BAC=90°,AB=3,AC=4,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AED ,连CE ,则线段CE 的长等于( )A .2B .54C .53D .75 【答案】D .【解析】试题解析:如图连接BE 交AD 于O ,作AH ⊥BC 于H .在Rt △ABC 中,∵AC=4,AB=3,∴BC=2234 =5,∵CD=DB ,∴AD=DC=DB=52, ∵12•BC•AH=12•AB•AC, ∴AH=125, ∵AE=AB ,DE=DB=DC ,∴AD 垂直平分线段BE ,△BCE 是直角三角形, ∵12•AD•BO=12•BD•AH, ∴OB=125, ∴BE=2OB=245, 在Rt △BCE 中,EC=22222475()55BC BE -=-= . 故选D . 考点:1.翻折变换(折叠问题);2.直角三角形斜边上的中线;3.勾股定理.8.(2017甘肃兰州第3题)如图,一个斜坡长130m ,坡顶离水平地面的距离为50m ,那么这个斜坡与水平地面夹角的正切值等于( )A.513B.1213C.512D.1312【答案】C .【解析】试题解析:如图,在Rt △ABC 中,∵∠ACB=90°,AB=130m ,BC=50m ,∴AC=222213050AB BC -=-=120m ,∴tan∠BAC=50512012 BCAC==.故选C.考点:解直角三角形的应用﹣坡度坡角问题.9. (2017甘肃兰州第13题)如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(0.5DE BC==米,,,A B C三点共线),把一面镜子水平放置在平台上的点G处,测得15CG=米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得3CG=米,小明身高 1.6EF=米,则凉亭的高度AB约为( )A.8.5米B.9米C.9.5米D.10米【答案】A.【解析】试题解析:由题意∠AGC=∠FGE,∵∠ACG=∠FEG=90°,∴△ACG∽△FEG,∴AC CG EF GD=∴15 1.53 AC=∴AC=8,∴AB=AC+BC=8+0.5=8.5米.故选A.点:相似三角形的应用.10.(2017贵州黔东南州第2题)如图,∠ACD=120°,∠B=20°,则∠A的度数是()A .120°B .90°C .100°D .30°【答案】C .【解析】 试题解析:∠A=∠ACD ﹣∠B=120°﹣20°=100°,故选:C .考点:三角形的外角性质.11.(2017山东烟台第12题)如图,数学实践活动小组要测量学校附近楼房CD 的高度,在水平底面A 处安置侧倾器得楼房CD 顶部点D 的仰角为045,向前走20米到达'A 处,测得点D 的仰角为05.67.已知侧倾器AB 的高度为1.6米,则楼房CD 的高度约为( )(结果精确到0.1米,414.12 )A .14.34米B .1.34米 C.7.35米 D .74.35米【答案】C .【解析】试题解析:过B 作BF ⊥CD 于F ,∴AB=A′B′=CF=1.6米,在Rt △DFB′中,B′F=tan 67.5DF︒,在Rt △DFB 中,BF=DF , ∵BB′=AA′=20,∴BF ﹣B′F=DF﹣tan 67.5DF︒=20,∴DF ≈34.1米,∴CD=DF+CF=35.7米,答:楼房CD 的高度约为35.7米,故选C .考点:解直角三角形的应用﹣仰角俯角问题.12.(2017四川泸州第10题)已知三角形的三边长分别为a 、b 、c ,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron ,约公元50年)给出求其面积的海伦公式S=()()()p p a p b p c ---,其中p=2a b c++;我国南宋时期数学家秦九韶(约1202-1261)曾提出利用三角形的三边求其面积的秦九韶公式S=2222221()22a b c a b +--,若一个三角形的三边长分别为2,3,4,则其面积是( ) A.3158 B. 3154 C. 3152 D. 152【答案】B.考点:二次根式的应用.13.(2017浙江嘉兴第2题)长度分别为2,7,x 的三条线段能组成一个三角形,x 的值可以是( )A.4B.5C.6D.9【答案】C.【解析】试题解析:由三角形三边关系定理得7-2<x<7+2,即5<x<9.因此,本题的第三边应满足5<x<9,把各项代入不等式符合的即为答案.4,5,9都不符合不等式5<x<9,只有6符合不等式,故选C.考点:三角形的三边关系.二、填空题1.(2017浙江宁波第16题)如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知500AB=米,则这名滑雪运动员的高度下降了米.(参考数据:sin340.56°≈,cos340.83°≈,tan340.67°≈)【答案】280.【解析】试题分析:在RtΔABC中,sin34°=AC AB∴AC=AB×sin34°=500×0.56=280米.考点:解直角三角形的应用.2.(2017甘肃庆阳第16题)如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠:使点A与点B重合,那么折痕长等于 cm.【答案】154cm . 【解析】试题解析:如图,折痕为GH ,由勾股定理得:AB=226+8=10cm ,由折叠得:AG=BG=12AB=12×10=5cm ,GH ⊥AB , ∴∠AGH=90°,∵∠A=∠A ,∠AGH=∠C=90°,∴△ACB ∽△AGH , ∴AC BC AG GH=, ∴865GH=, ∴GH=154cm . 考点:翻折变换3.(2017广西贵港第16题)如图,点P 在等边ABC ∆的内部,且6,8,10PC PA PB ===,将线段PC 绕点C 顺时针旋转60得到'P C ,连接'AP ,则sin 'PAP ∠的值为 .【答案】35【解析】试题解析:连接PP′,如图,∵线段PC 绕点C 顺时针旋转60°得到P'C ,∴CP=CP′=6,∠PCP′=60°,∴△CPP′为等边三角形,∴PP′=PC=6,∵△ABC 为等边三角形,∴CB=CA ,∠ACB=60°,∴∠PCB=∠P′CA,在△PCB 和△P′CA 中PC P C PCB P CA CB CA '⎧=⎪'∠=∠⎨⎪=⎩∴△PCB ≌△P′CA,∴PB=P′A=10,∵62+82=102,∴PP′2+AP 2=P′A 2,∴△APP′为直角三角形,∠APP′=90°,∴sin ∠PAP′=63105PP P A '=='. 考点:旋转的性质;等边三角形的性质;解直角三角形.4.(2017贵州安顺第13题)三角形三边长分别为3,4,5,那么最长边上的中线长等于 .【答案】2.5【解析】试题解析:∵32+42=25=52,∴该三角形是直角三角形, ∴12×5=2.5. 考点:勾股定理的逆定理;直角三角形斜边上的中线.5.(2017湖北武汉第15题)如图△ABC 中,AB=AC ,∠BAC=120°,∠D AE=60°,BD=5,CE=8,则DE 的长为 .【答案】7.【解析】试题解析:∵AB=AC,∴可把△AEC 绕点A 顺时针旋转120°得到△AE′B,如图,∴BE′=EC=8,AE′=AE,∠E′AB=∠EAC,∵∠BAC=120°,∠DAE=60°,∴∠BAD+∠EAC=60°,∴∠E′AD=∠E′AB+∠BAD=60°,在△E′AD 和△EAD 中AE =AE E AD =EAD AD =AD ⎧'∠'∠⎪⎨⎪⎩∴△E′AD≌△EAD(SAS ),∴E′D=ED,过E′作EF⊥BD 于点F ,∵AB=AC,∠BAC=120°,∴∠ABC=∠C=∠E′BA=30°,∴∠E′BF=60°,∴∠BE′F=30°,∴BF=12BE′=4,E′F=43,∵BD=5,∴FD=BD-BF=1,在Rt△E′FD中,由勾股定理可得E′D=22(43)+1=7,∴DE=7.考点:1.含30度角的直角三角形;2.等腰三角形的性质.6.(2017湖南怀化第15题)如图,AC DC=,BC EC=,请你添加一个适当的条件:,使得ABC DEC△≌△.【答案】CE=BC.本题答案不唯一.【解析】试题解析:添加条件是:CE=BC,在△ABC与△DEC中,AC DC BC EC CE BC⎧=⎪=⎨⎪=⎩,∴△ABC≌△DEC.故答案为:CE=BC.本题答案不唯一.点:全等三角形的判定.7.(2017江苏无锡第18题)在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D 都在格点处,AB与CD相交于O,则tan∠BOD的值等于.【答案】3.【解析】试题解析:平移CD 到C′D′交AB 于O′,如图所示,则∠BO′D′=∠BOD ,∴tan ∠BOD=tan ∠BO′D′,设每个小正方形的边长为a ,则O′B=22(2)5a a a +=,O′D′=22(2a)(2)22a a +=,BD′=3a,作BE ⊥O′D′于点E ,则BE=3a 232222BD O F a a O D a''=='' , ∴O′E=2222322(5)()22a a O B BE a '-=-=, ∴tanBO′E=32a2322BE O E a==', ∴tan ∠BOD=3.考点:解直角三角形.8.(2017江苏盐城第12题)在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1= °.【答案】120°.【解析】试题解析:由三角形的外角的性质可知,∠1=90°+30°=120°. 考点:三角形的外角性质;三角形内角和定理.9.(2017甘肃兰州第17题)如图,四边形ABCD与四边形EFGH相似,位似中心点是O,3 5OE OA =,则FGBC=.【答案】3 5【解析】试题解析:如图所示:∵四边形ABCD与四边形EFGH位似,∴△OEF∽△OAB,△OFG∽△OBC,∴35 OE OFOA OB==,∴35 FG OFBC OB==.考点:位似变换.10.(2017贵州黔东南州第12题)如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件使得△ABC≌△DEF.【答案】∠A=∠D .【解析】试题解析:添加∠A=∠D .理由如下:∵FB=CE ,∴BC=EF .又∵AC ∥DF ,∴∠ACB=∠DFE .∴在△ABC 与△DEF 中,A D ACB DFEBC EF ⎧∠=∠⎪∠=∠⎨⎪=⎩ ,∴△ABC ≌△DEF (AAS ).考点:全等三角形的判定.11.(2017山东烟台第14题)在ABC Rt ∆中,090=∠C ,2=AB ,3=BC ,则=2sin A . 【答案】12. 【解析】试题解析:∵sinA=32BC AB =, ∴∠A=60°,∴sin 2A =sin30°=12. 考点:特殊角的三角函数值.12. (2017山东烟台第16题)如图,在平面直角坐标系中,每个小方格的边长均为1.AOB ∆与''OB A ∆是以原点O 为位似中心的位似图形,且相似比为2:3,点B A ,都在格点上,则点'B 的坐标是.【答案】(﹣2,43) 【解析】试题解析:由题意得:△A′OB′与△AOB 的相似比为2:3,又∵B (3,﹣2)∴B′的坐标是[3×2()3-,﹣2×2()3-],即B′的坐标是(﹣2,43) 考点:位似变换;坐标与图形性质.13.(2017四川泸州第16题)在△ABC 中,已知BD 和CE 分别是边AC 、AB 上的中线,且BD ⊥CE ,垂足为O .若OD=2cm ,OE=4cm ,则线段AO 的长度为 cm .【答案】45.【解析】试题解析:连接AO 并延长,交BC 于H ,由勾股定理得,DE=22=25OE OD +,∵BD 和CE 分别是边AC 、AB 上的中线,∴BC=2DE=45,O 是△ABC 的重心,∴AH是中线,又BD⊥CE,∴OH=12BC=25,∵O是△ABC的重心,∴AO=2OH=45.考点:1.三角形的重心;2.勾股定理.14.(2017四川自贡第14题)在△ABC中,MN∥BC 分别交AB,AC于点M,N;若AM=1,MB=2,BC=3,则MN 的长为.【答案】1.【解析】试题解析:∵MN∥BC,∴△AMN∽△ABC,∴AM MNAB BC=,即1123WN=+,∴MN=1.考点:相似三角形的判定与性质.15.(2017新疆建设兵团第15题)如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:①∠ABC=∠ADC;②AC与BD相互平分;③AC,BD分别平分四边形ABCD的两组对角;④四边形ABCD的面积S=12 AC•BD.正确的是(填写所有正确结论的序号)【答案】①④【解析】试题解析:①在△ABC和△ADC中,∵AB AD BC CD AC AC⎧=⎪=⎨⎪=⎩,∴△ABC≌△ADC(SSS),∴∠ABC=∠ADC,故①结论正确;③由②可知:AC平分四边形ABCD的∠BAD、∠BCD,而AB与BC不一定相等,所以BD不一定平分四边形ABCD的对角;故③结论不正确;④∵AC⊥BD,∴四边形ABCD的面积S=S△ABD+S△BCD=12BD•AO+12BD•CO=12BD•(AO+CO)=12AC•BD.故④结论正确;所以正确的有:①④考点:全等三角形的判定与性质;线段垂直平分线的性质.16.(2017江苏徐州第13题)ABC ∆中,点,D E 分别是,AB AC 的中点,7DE =,则BC = .【答案】14.【解析】试题解析:∵D ,E 分别是△ABC 的边AC 和AC 的中点,∴DE 是△ABC 的中位线,∵DE=7,∴BC=2DE=14.考点:三角形中位线定理.17. (2017江苏徐州第18题)如图,已知1OB =,以OB 为直角边作等腰直角三角形1A BO .再以1OA 为直角边作等腰直角三角形21A AO ,如此下去,则线段n OA 的长度为 .【答案】2n .【解析】试题解析:∵△OBA 1为等腰直角三角形,OB=1,∴AA 1=OA=1,OA 1=2OB=2;∵△OA 1A 2为等腰直角三角形,∴A 1A 2=OA 1=2,OA 2=2OA 1=2;∵△OA 2A 3为等腰直角三角形,∴A 2A 3=OA 2=2,OA 3=2OA 2=22;∵△OA 3A 4为等腰直角三角形,∴A 3A 4=OA 3=22,OA 4=2OA 3=4.∵△OA 4A 5为等腰直角三角形,∴A 4A 5=OA 4=4,OA 5=2OA 4=42,∵△OA 5A 6为等腰直角三角形,∴A 5A 6=OA 5=42,OA 6=2OA 5=8.∴OA n 的长度为2n .考点:等腰直角三角形.18.(2017浙江嘉兴第15题)如图,把n 个边长为1的正方形拼接成一排,求得1tan 1BAC ∠=,21tan 3BA C ∠=,31tan 7BA C ∠=,计算4tan BA C ∠= ,……按此规律,写出tan n BA C ∠= (用含n 的代数式表示).【答案】113,211n n -+. 【解析】试题解析:作CH⊥BA 4于H ,由勾股定理得,BA 4=22471=1+,A 4C=10,△BA 4C 的面积=4-2-32=12, ∴12×17×CH=12, 解得,CH=1717,则A 4H=223A C CH -=131717, ∴tan∠BA 4C=4CH A H =113, 1=12-1+1,3=22-2+1,7=32-3+1,∴tan∠BA n C=211n n -+.考点:1.解直角三角形;2.勾股定理;3.正方形的性质.三、解答题1.(2017浙江衢州第23题)问题背景如图1,在正方形A BCD 的内部,作∠DAE=∠ABF=∠BCG=∠CDH ,根据三角形全等的条件,易得△DAE ≌△ABF ≌△BCG ≌△CDH ,从而得到四边形EFGH 是正方形。
中考数学专题复习试题分类汇编三等腰三角形和直角三角形

中考数学专题复习试题分类汇编三等腰三角形和直角三角形学校:___________姓名:___________班级:___________考号:___________评卷人得分一、单选题1.已知线段AB,按如下步骤作图:①作射线AC,使AC AB⊥;①作BAC∠的平分线AD;①以点A为圆心,AB长为半径作弧,交AD于点E;①过点E作EP AB⊥于点P,则:AP AB=()A.1:5B.1:2C.1:3D.1:22.如图,在ABC中,45,60,B C AD BC∠=︒∠=︒⊥于点D,3BD=.若E,F分别为AB,BC的中点,则EF的长为()A.33B.32C.1D.623.如图,在Rt ABC△纸片中,90,4,3ACB AC BC∠=︒==,点,D E分别在,AB AC 上,连结DE,将ADE沿DE翻折,使点A的对应点F落在BC的延长线上,若FD 平分EFB∠,则AD的长为()252515204.如图,正三角形ABC的边长为3,将①ABC绕它的外心O逆时针旋转60°得到①A'B'C',则它们重叠部分的面积是()A.23B.334C.332D.35.如图,在Rt①ABC中,①ACB=90°,CD为中线,延长CB至点E,使BE=BC,连结DE,F为DE中点,连结BF.若AC=8,BC=6,则BF的长为()A.2B.2.5C.3D.46.①BDE和①FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道()A.①ABC的周长B.①AFH的周长C.四边形FBGH的周长D.四边形ADEC的周长7.如图,等腰直角三角形ABC中,①ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连结CP,过点A作AH①CP交CP的延长线于点H,连结AP,则①P AH的度数()B.随着θ的增大而减小C.不变D.随着θ的增大,先增大后减小8.已知直线m n,将一块含45︒角的直角三角板ABC按如图方式放置,其中斜边BC 与直线n交于点D.若125∠=︒,则2∠的度数为()A.60︒B.65︒C.70︒D.75︒9.“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC CD DE==,点D,E可在槽中滑动,若75BDE∠=︒,则CDE∠的度数是()A.60°B.65°C.75°D.80°10.在ABC中,若一个内角等于另外两个角的差,则()A.必有一个角等于30B.必有一个角等于45︒C.必有一个角等于60︒D.必有一个角等于90︒评卷人得分二、填空题11.如图,在①ABC中,①ACB=90°,AC<BC.分别以点A,B为圆心,大于12AB的长为半径画弧,两弧交于D,E两点,直线DE交BC于点F,连接AF.以点A为圆心,AF为半径画弧,交BC延长线于点H,连接AH.若BC=3,则①AFH的周长为_____.12.如图,在ABC中,AB AC=,70B∠=︒,以点C为圆心,CA长为半径作弧,交直线BC于点P,连结AP,则BAP∠的度数是_______.13.如图,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是_____ .评卷人得分三、解答题14.如图,在四边形ABCD中,AB=AD=20,BC=DC=102(1)求证:①ABC①①ADC;(2)当①BCA=45°时,求①BAD的度数.15.问题:如图,在①ABD中,BA=BD.在BD的延长线上取点E,C,作①AEC,使EA=EC,若①BAE=90°,①B=45°,求①DAC的度数.答案:①DAC=45°思考:(1)如果把以上“问题”中的条件“①B=45°”去掉,其余条件不变,那么①DAC的度数会改变吗?说明理由;(2)如果把以上“问题”中的条件“①B=45°”去掉,再将“①BAE=90°”改为“①BAE=n°”,其余条件不变,求①DAC的度数.16.如图,在△ABC和△DCE中,AC=DE,①B=①DCE=90°,点A,C,D依次在同一直线上,且AB①DE.(1)求证:△ABC①①DCE;(2)连结AE,当BC=5,AC=12时,求AE的长.17.如图1是实验室中的一种摆动装置,BC 在地面上,支架ABC 是底边为BC 的等腰直角三角形,摆动臂长AD 可绕点A 旋转,摆动臂DM 可绕点D 旋转,30AD =,10DM =.(1)在旋转过程中:①当,,A D M 三点在同一直线上时,求AM 的长;②当,,A D M 三点在同一直角三角形的顶点时,求AM 的长.(2)若摆动臂AD 顺时针旋转90︒,点D 的位置由ABC 外的点1D 转到其内的点2D 处,连结12D D ,如图2,此时2135AD C ∠=︒,260CD =,求2BD 的长.18.如图,在76⨯的方格中,ABC 的顶点均在格点上,试按要求画出线段EF (E ,F 均为格点),各画出一条即可.19.如图,在ABC中,AC AB BC.①已知线段AB的垂直平分线与BC边交于点P,连结AP,求证:2APC B;①以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若B,求B的度数.3AQC参考答案:1.D【解析】【分析】由题意易得①BAD =45°,AB =AE ,进而可得①APE 是等腰直角三角形,然后根据等腰直角三角形的性质可求解.【详解】解:①AC AB ⊥,①90CAB ∠=︒,①AD 平分BAC ∠,①①BAD =45°,①EP AB ⊥,①①APE 是等腰直角三角形,①AP =PE ,①222AE AP PE AP =+=,①AB =AE ,①2AB AP =,①:1:2AP AB =;故选D .【点睛】本题主要考查等腰直角三角形的性质与判定、勾股定理及角平分线的定义,熟练掌握等腰直角三角形的性质与判定、勾股定理及角平分线的定义是解题的关键.2.C【解析】【分析】根据条件可知①ABD 为等腰直角三角形,则BD =AD ,①ADC 是30°、60°的直角三角形,可求出AC 长,再根据中位线定理可知EF =2AC 。
2017年中考数学试题分类汇编(三角形全等)

已知a, b , c是厶ABC的三条边长,化简|a+b-c|-|c-a-b| 的结果为(【答案】D【答案】C.4. (2017湖南长沙第5题)一个三角形三个内角的度数之比为1: 2: 3,则这个三角形一定是A.锐角三角形B •直角三角形C •钝角三角形 D •等腰直角三角形【答案】B5. (2017 山东滨州第8题)如图,在厶ABC中,AB= AC D为BC上一点,且DA= DC BD= BA,则/ B的大小为(、选择题专题09三角形A. 2a+2b-2c B . 2a+2b C. 2c D. 01. (2017甘肃庆阳第8题)2. (2017浙江嘉兴第2题)长度分别为勺,3,目的三条线段能组成一个三角形,叫的值可以是()A. B. C. D.3. (2017天津第11题)如图,在叵]中,I最小值的是(IW 是的两条中线, 是叵上一个动点,C.B. 36°C. 80°D. 25°【答案】B.6. (2017山东滨州第11题)如图,点P为定角/ AOB的平分线上的一个定点,且/ MPN WZ AOB互补.若/ MPN在绕点P旋转的过程中,其两边分别与OA OB相交于M N两点,则以下结论:(1)PM= PN恒成立,(2)OW ON的值不变,(3)四边形PMO的面积不变,(4)MN的长不变,其中正确的个数为(A. 4B. 3C. 2D. 1【答案】B.A. 40°【答案】B.【薛析】如虱过点P作PC#£ A0于点G FD垂直B0于点D根1S角平分线的性质可得POPD,因N AOB ^ZMPN互补,可得ZMPN=ZCFD,gp可得ZMPC=ZDPN f即可判^CMP^NDP,所以PM=PN J(1)正确』由“CMP旦卫NDP可得CM-CN,所0M-0X=20C, (2)正确」四边形PMON的面积等于四边形P8D 的面积,(3)正确!连结CD, HPMD J PKI-PN, ZXIPN-ZCPD, PM>PC;可得CD^XIN;所以(4)错误,故选B.7. (2017山东荷泽第5题)如图,将WI绕直角顶点E顺时针旋转凶,得到WZI ,连接回,若上1则—J的度数是()A.冈B . 3 C. □ D . 38. (2017浙江金华第3题)下列各组数中,不可能成为一个三角形三边长的是()A. 1 z | B I 乂1 C I >■ I D . I 些I【答案】C.9. (2017浙江省台州市)如图,点P是/ AOB平分线OC上一点,PD丄OB垂足为D,若PD=2,则点P到边OA的距离是()ABC AB=AC 若以点B 为圆心,BC 长为半径画弧,交腰 AC 于点Rt △ ABC 中,Z C=90,以顶点 A 为圆心,适当长为半径画弧,分别交AC, AB大于t MN 的长为半径画弧,两弧交于点P,作射线AP 交边BC 于点D,若CD=4ABC 中, AB > AC, / CAD ^^ ABC 的外角,观察图中尺规作图的痕迹,则下列结论错A. 2B. 3c.D. 4【答案】A.E ,则下列结论一定正确的是( A. AE=EC B. AE=BE C.D.Z EBC=z ABE【答案】C.AB=15,则厶ABD 的面积是( A. 15 B. 30CC.【答案】B误的是( ) A.Z DAE 玄 B B ./ EAC=/ CD.Z DAE=/ EAC【答案】D. 13 . (2017湖北省襄阳市) 如图,在△ ABC 中,Z ACB=90 , Z A=30° ,BC=4以点 C 为圆心,CB 长为半径作弧,交AB 于点D;再分别以点 B 和点D 为圆心,大于』BD 的长为半径作弧,两弧相交于点E ,作射线 CE 交AB 于点F ,则AF 的长为( )10.(2017浙江省台州市)如图,已知等腰三角形 11. (2017山东省枣庄市)如图,在于点M N,再分别以点 M N 为圆心,12. (2017广西四市)如图,△A. 5B. 6【答案】B.【答案】B.150°14. (2017湖南株洲第5题)如图,15. (2017郴州第8题)小明把一副则H 等于叵]A. B.( )【解析】C.在厶ABC 中,/ BAC=X,/ B=2x°C. 155°,/ C=3x°,则/ BA D=( )D. 160°的直角三角板如图摆放,其中试题分析:T/a =Z 1 + Z D,Z3 =/ 4+Z F,/•/a +/3 =/ 1 + / D+/ 4+/ F=/ 2+/ D+/ 3+/ F=/ 2+/B.16. (2017河池第9题)三角形的下列线段中, 能将三角形分成面积相等的两部分是()A.中线.角平分线 C. 高 D .中位线【答案】A.、填空题1. (2017湖南怀化第15题)如图,』| , I-」,请你添加一个适当的条件:_____________________________ ,使得I .2. (2017江苏盐城第12题)在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则【答案】120°3. (2017贵州黔东南州第12题)如图,点B、F、C E在一条直线上,已知FB=CE AC// DF,请你添加一个适当的条件_______ 使得△ ABC^^ DEF【答案】/ A=Z D.4. (2017新疆建设兵团第15题)如图,在四边形ABCD中, AB=AD CB=CD对角线AC, BD相交于点O,下列结论中:①/ ABC d ADC②AC与BD相互平分;③AC BD分别平分四边形ABCD的两组对角;④四边形ABCD的面积S= * AC?BD正确的是_________ (填写所有正确结论的序号)5. _________________________________________________________________________________________________ (2017四川省达州市)△ ABC中,AB=5, AC=3 AD是厶ABC的中线,设AD长为m则m的取值范围是 _______________________【答案】1< m< 4.6. (2017黑龙江绥化第20题)在等腰耳 中, W] 交直线 耳 于点凶|,若 | x | ,则 EI 的顶角的度数为 _____________ . 【答案】30°或150°或90°.. 【解析】 试题分析:①BC 为腰,•/ ADL BC 于点 D, AD=^BC, /-Z ACD=30 , 如图1,人。
中考数学真题分类汇编第二期专题21全等三角形试题含解析

全等三角形一. 选择题1.(2018?遂宁?4分)以下说法正确的选项是()A.有两条边和一个角对应相等的两个三角形全等B.正方形既是轴对称图形又是中心对称图形C.矩形的对角线互相垂直均分D.六边形的内角和是540°【分析】直接利用全等三角形的判断以及矩形、菱形的性质和多边形内角和定理.【解答】解: A. 有两条边和一个角对应相等的两个三角形全等、错误、必定是两边及其夹角分别对应相等的两个三角形全等;B.正方形既是轴对称图形又是中心对称图形、正确;C.矩形的对角线相等且互相均分、故此选项错误;D.六边形的内角和是720°、故此选项错误.应选: B.【议论】此题主要观察了全等三角形的判断以及矩形、菱形的性质和多边形内角和定理、正确掌握相关性质是解题要点.2.(2018?贵州安顺?3分)如图、点、分别在线段、上、与订交于点、已知、现增加以下哪个条件仍不能够判断().....A. B. C. D.【答案】 D【分析】分析:欲使△ABE≌△ ACD、已知 AB=AC、可依照全等三角形判判定理AAS、 SAS、 ASA增加条件、逐一证明即可.详解:∵ AB=AC、∠ A 为公共角、A. 如增加∠ B=∠ C、利用 ASA即可证明△ ABE≌△ ACD;B. 如添 AD=AE、利用 SAS即可证明△ ABE≌△ ACD;C.如添 BD=CE、等量关系可得AD=AE、利用 SAS即可证明△ ABE≌△ ACD;D.如添 BE=CD、因为 SSA、不能够证明△ABE≌△ ACD、所以此选项不能够作为增加的条件.应选 D.点睛:此题主要观察学生对全等三角形判判定理的理解和掌握、此类增加条件题、要修业生应熟练掌握全等三角形的判判定理.3. ( 2018·黑龙江龙东地区· 3 分)如图、四边形 ABCD中、 AB=AD、AC=5、∠ DAB=∠DCB=90°、则四边形ABCD的面积为()A. 15B.12.5 C .14.5 D .17【分析】过 A 作 AE⊥ AC、交 CB的延长线于E、判断△ ACD≌△ AEB、即可获取△ ACE是等腰直角三角形、四边形 ABCD的面积与△ ACE的面积相等、依照S△ACE=×5× 、即可得出结论.【解答】解:如图、过 A 作 AE⊥ AC、交 CB的延长线于E、∵∠ DAB=∠DCB=90°、∴∠ D+∠ABC=180°=∠ ABE+∠ABC、∴∠ D=∠ ABE、又∵∠ DAB=∠CAE=90°、∴∠ CAD=∠EAB、又∵ AD=AB、∴△ ACD≌△ AEB、∴A C=AE、即△ ACE是等腰直角三角形、∴四边形 ABCD的面积与△ ACE的面积相等、∵S△ACE= ×5×5=12.5 、∴四边形ABCD的面积为12.5 、应选: B.【议论】此题主要观察了全等三角形的判断与性质、全等三角形的判断是结合全等三角形的性质证明线段和角相等的重要工具.在判断三角形全等时、要点是选择合适的判断条件.在应用全等三角形的判准时、要注意三角形间的公共边和公共角、必要时增加合适辅助线构造三角形.4. (2018?贵州黔西南州 ?4分)以下各图中 A.B.c 为三角形的边长、则甲、乙、丙三个三角形和左侧△ABC全等的是()A.甲和乙B.乙和丙C.甲和丙D.只有丙【分析】依照三角形全等的判断方法得出乙和丙与△ABC全等、甲与△ ABC不全等.【解答】解:乙和△ ABC全等;原由以下:在△ ABC和图乙的三角形中、满足三角形全等的判断方法:SAS、所以乙和△ ABC全等;在△ ABC和图丙的三角形中、满足三角形全等的判断方法:AAS、所以丙和△ ABC全等;不能够判断甲与△ABC全等;应选: B.【议论】此题观察了三角形全等的判断方法、判断两个三角形全等的一般方法有:SSS、SAS、、HL.注意: AAA.SSA 不能够判断两个三角形全等、判断两个三角形全等时、必定有边的参加、若有两边一角对应相等时、角必定是两边的夹角.5.( 2018 年湖南省娄底市)如图、△ ABC中、AB=AC、AD⊥ BC于D点、DE⊥AB于点E、BF⊥ AC于点F、DE=3cm、则 BF= 6 cm.【分析】先利用HL 证明 Rt △ ADB≌ Rt △ ADC、得出 S△ABC=2S△ABD=2×AB?DE=AB?DE=3AB、又 S△ABC=AC?BF、将AC=AB代入即可求出BF.【解答】解:在Rt △ ADB与 Rt△ ADC中、、∴R t △ ADB≌Rt △ ADC、∴S△ABC=2S△ABD=2×AB?DE=AB?DE=3AB、∵S△ABC=AC?BF、∴AC?BF=3AB、∴BF=3、∴B F=6.故答案为 6.【议论】此题观察了全等三角形的判断与性质、等腰三角形的性质、三角形的面积、利用面积公式得出等式是解题的要点.6.(2018?遂宁?4分)以下说法正确的选项是()A.有两条边和一个角对应相等的两个三角形全等B.正方形既是轴对称图形又是中心对称图形C.矩形的对角线互相垂直均分D.六边形的内角和是540°【分析】直接利用全等三角形的判断以及矩形、菱形的性质和多边形内角和定理.【解答】解: A. 有两条边和一个角对应相等的两个三角形全等、错误、必定是两边及其夹角分别对应相等的两个三角形全等;B.正方形既是轴对称图形又是中心对称图形、正确;C.矩形的对角线相等且互相均分、故此选项错误;D.六边形的内角和是720°、故此选项错误.应选: B.【议论】此题主要观察了全等三角形的判断以及矩形、菱形的性质和多边形内角和定理、正确掌握相关性质是解题要点.二. 填空题1.(2018?江苏宿迁? 3分)如图、在平面直角坐标系中、反比率函数(x>0)与正比率函数y=kx 、(k> 1)的图象分别交于点、若∠ AOB=45°、则△ AOB的面积是 ________.【答案】 2【分析】作BD⊥x轴、 AC⊥y轴、 OH⊥AB(如图)、设 A( x1、y1)、 B( x2、y2)、依照反比率函数k 的几何意义得 x1y1=x 2y2=2;将反比率函数分别与y=kx 、y= 联立、解得 x1=、x2=、进而得x1x2=2、所以y1=x2、y2=x1、依照 SAS得△ ACO≌△ BDO、由全等三角形性质得AO=BO、∠ AOC=∠BOD、由垂直定义和已知条件得∠AOC=∠BOD=∠AOH=∠°、依照AAS得△ ACO≌△ BDO≌△ AHO≌△ BHO、依照三角形面积公式得S△ABO=S△AHO+S△BHO=S△ACO+S△BDO= x1y1+ x2y2=×2+×2=2.【详解】如图:作BD⊥x轴、 AC⊥y轴、 OH⊥AB、设 A( x1、 y1)、 B( x2、y2)、∵A. B 在反比率函数上、∴x1y1=x2y2=2、∵、解得: x1= 、又∵、解得: x2=、∴x1x2=×=2、∴y1=x 2、 y 2=x1、即 OC=OD、 AC=BD、∵BD⊥x轴、 AC⊥y轴、∴∠ ACO=∠BDO=90°、∴△ ACO≌△ BDO(SAS)、∴AO=BO、∠ AOC=∠BOD、又∵∠ AOB=45°、 OH⊥AB、∴∠ AOC=∠BOD=∠AOH=∠°、∴△ ACO≌△ BDO≌△ AHO≌△ BHO、∴S△ABO=S△AHO+S△BHO=S△ACO+S△BDO= x1y1+x2y2=×2+×2=2、故答案为: 2.【点睛】此题观察了反比率函数系数k 的几何意义、反比率函数与一次函数的交点问题、全等三角形的判断与性质等、正确增加辅助线是解题的要点.2.( 2018?达州 ?3 分)如图、 Rt △ ABC中、∠ C=90°、 AC=2、 BC=5、点 D 是 BC 边上一点且 CD=1、点 P 是线段 DB上一动点、连接 AP、以 AP为斜边在 AP的下方作等腰 Rt△ AOP.当 P 从点 D 出发运动至点 B 停止时、点O的运动路径长为.【分析】过 O点作 OE⊥ CA于 E、 OF⊥ BC于 F、连接 CO、如图、易得四边形 OECF为矩形、由△ AOP为等腰直角三角形获取 OA=OP、∠ AOP=90°、则可证明△ OAE≌△ OPF、所以 AE=PF、OE=OF、依照角均分线的性质定理的逆定理获取 CO均分∠ ACP、进而可判断当 P 从点 D出发运动至点 B 停止时、点 O的运动路径为一条线段、接着证明CE=(AC+CP)、尔后分别计算P 点在 D 点和 B 点时 OC的长、进而计算它们的差即可获取P 从点 D【解答】解:过O点作 OE⊥ CA于 E、 OF⊥ BC于 F、连接 CO、如图、∵△ AOP为等腰直角三角形、∴OA=OP、∠ AOP=90°、易得四边形OECF为矩形、∴∠ EOF=90°、 CE=CF、∴∠ AOE=∠POF、∴△ OAE≌△ OPF、∴A E=PF、 OE=OF、∴C O均分∠ ACP、∴当 P 从点 D 出发运动至点 B 停止时、点 O的运动路径为一条线段、∵AE=PF、即 AC﹣ CE=CF﹣CP、而 CE=CF、∴C E= (AC+CP)、∴OC= CE=(AC+CP)、当 AC=2、 CP=CD=1时、 OC=×(2+1)=、当 AC=2、 CP=CB=5时、 OC=×(2+5)=、∴当 P 从点 D 出发运动至点 B 停止时、点O的运动路径长=﹣=2.故答案为2.【议论】此题观察了轨迹:灵便运用几何性质确定图形运动过程中不变的几何量、进而判断轨迹的几何特色、尔后进行几何计算.也观察了全等三角形的判断与性质.3.( 2018?湖州?4 分)在每个小正方形的边长为1 的网格图形中、每个小正方形的极点称为格点.以极点都是格点的正方形ABCD的边为斜边、向内作四个全等的直角三角形、使四个直角极点E、 F、 G、 H 都是格点、且四边形EFGH为正方形、我们把这样的图形称为格点弦图.比方、在如图1所示的格点弦图中、正方形ABCD 的边长为、此时正方形EFGH的而积为 5.问:当格点弦图中的正方形ABCD的边长为时、正方形EFGH 的面积的所有可能值是13 或 49(不包括5).【分析】当 DG=、CG=2222、可得正方形 EFGH的面积为 13.当 DG=8、时、满足 DG+CG=CD、此时 HG=222EFGH的面积为 49.CG=1时、满足 DG+CG=CD、此时 HG=7、可得正方形【解答】解:当 DG=、 CG=2时、满足222、可得正方形EFGH的面积为 13.DG+CG=CD、此时 HG=当 DG=8、 CG=1时、满足222DG+CG=CD、此时 HG=7、可得正方形 EFGH的面积为 49.故答案为13 或 49.【议论】此题观察作图﹣应用与设计、全等三角形的判断、勾股定理等知识、解题的要点是学会利用数形结合的思想解决问题、属于中考填空题中的压轴题.4.(2018?金华、丽水? 4分)如图、△ABC的两条高 AD 、 BE 订交于点 F、请增加一个条件、使得△ADC ≌△ BEC(不增加其他字母及辅助线)、你增加的条件是________.【分析】【解答】从题中不难得出∠ADC=∠BEC=90°、而且∠ACD=∠ BCE(公共角)、则只需要加一个对应边相等的条件即可、所以从“ CA=CB、CE=CD、BE=AD”中添加一个即可。
专题09 三角形-2017年中考数学试题分项版解析汇编(解析版)

专题9:三角形一、选择题1.(2017天津第2题)060cos 的值等于( )A 3B .1C .22D .21 【答案】D.2.(2017天津第9题)如图,将ABC ∆绕点B 顺时针旋转060得DBE ∆,点C 的对应点E 恰好落在AB 延长线上,连接AD .下列结论一定正确的是( )A .E ABD ∠=∠B .C CBE ∠=∠ C. BC AD // D .BC AD = 【答案】C.3. (2017天津第11题)如图,在ABC ∆中,AC AB =,CE AD ,是ABC ∆的两条中线,P 是AD 上一个动点,则下列线段的长度等于EP BP +最小值的是( )A .BCB .CE C. AD D .AC 【答案】B. 【解析】试题分析:在ABC ∆中,AC AB =,AD 是ABC ∆的中线,可得点B 和点D 关于直线AD 对称,连结CE ,交AD 于点P ,此时EP BP +最小,为EC 的长,故选B.4. (2017湖南长沙第5题)一个三角形三个内角的度数之比为1:2:3,则这个三角形一定是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰直角三角形 【答案】B 【解析】试题分析:根据三角形的内角和为180°,可知最大角为90°,因式这个三角形是直角三角形. 故选:B. 考点:直角三角形5.(2017山东滨州第7题)如图,在△ABC 中,AC ⊥BC ,∠ABC =30°,点D 是CB 延长线上的一点,且BD =BA ,则tan ∠DAC 的值为( ) A .2+3B .23C .3+3D .33【答案】A.6.(2017山东滨州第8题)如图,在△ABC 中,AB =AC ,D 为BC 上一点,且DA =DC ,BD =BA ,则∠B 的大小为( )A .40°B .36°C .80°D .25°【答案】B.【解析】设∠B=x ,因AB=AC,根据等腰三角形的性质可得∠B=∠C=x ,因AD=CD ,根据等腰三角形的性质可得∠DAC=∠C=x ,因BD=BA ,根据等腰三角形的性质和三角形外角的性质可得∠BAD=∠ADB=2x ,在△ABD 中,根据三角形的内角和定理可得x+2x+2x=180°,解得x=36°,即∠B=36°,故选B.8. (2017山东滨州第11题)如图,点P 为定角∠AOB 的平分线上的一个定点,且∠MPN 与∠AOB 互补.若∠MPN 在绕点P 旋转的过程中,其两边分别与OA ,OB 相交于M 、N 两点,则以下结论:(1)PM =PN 恒成立,(2)OM +ON 的值不变,(3)四边形PMON 的面积不变,(4)MN 的长不变,其中正确的个数AB CD为()A.4 B.3 C.2 D.1PAONBM【答案】B.9. (2017山东日照第4题)在Rt△ABC中,∠C=90°,AB=13,AC=5,则sinA的值为()A.B.C.D.【答案】B.试题分析:在Rt△ABC中,根据勾股定理求得BC=12,所以sinA=1213BCAB=,故选B.考点:锐角三角函数的定义.10.(2017江苏宿迁第8题)如图,在Rt C∆AB中,C90∠=,C6A=cm,C2B=cm.点P在边CA 上,从点A向点C移动,点Q在边C B上,从点C向点B移动,若点P、Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接QP,则线段QP的最小值是A.20cm B.18cm C.25cm D.32cm【答案】C.11. (2017山东菏泽第5题)如图,将t ABC ∆R 绕直角顶点C 顺时针旋转90,得到''A B C ∆,连接'AA ,若125∠=,则'BAA ∠的度数是( )A .55B .60 C.65 D .70 【答案】C. 【解析】试题分析:根据旋转的性质可得∠BAC=∠B 'A 'C,AC=CA ', ∠A 'CA=90°,即可得△ACA '是等腰直角三角形,∴所以∠BAC=∠B 'A 'C=45°-25°,即可得'BAA ∠=65,故选C.12. (2017浙江金华第3题)下列各组数中,不可能成为一个三角形三边长的是( ) A .2,3,4 B .5,7,7 C .5,6,12 D .10,8,6 【答案】C. 【解析】试题分析:根据三角形的三边关系:三角形任意两边的和大于第三边,可得:选项A ,2+3>4,能组成三角形;选项B ,5+7>7,能组成三角形;选项C ,5+6<12,不能组成三角形;选项D ,6+8>10,能组成三角形,故选C.13. (2017浙江湖州第3题)如图,已知在Rt C ∆AB 中,C 90∠=,5AB =,C 3B =,则cos B 的值是( ) A .35 B .45 C .34 D .43【答案】A 【解析】试题分析:根据根据余弦的意义cosB=B ∠的邻边斜边,可得conB=BC AB =35.故选:A 考点:余弦14. (2017浙江舟山第2题)长度分别为2,7,x 的三条线段能组成一个三角形,x 的值可以是( ) A .4 B .5 C .6 D .9 【答案】C. 【解析】试题分析:根据三角形的两边之大于第三边,两边这差小于第三边,可得7-2<x<2+7,即5<x<9,所以x 可以取6.故选C.考点:三角形的三边关系.15. (2017浙江金华第4题)在t ABC ∆R 中,90,5,3C AB BC ∠===,则tan A 的值是( ) A .34 B .43 C.35 D .45【答案】A. 【解析】试题分析:在△ABC 中,∠C=90°,AB=5,BC=3, 根据勾股定理可求得AC=4, 所以tanA=34BC AC =,故选A.16. (2017浙江台州第5题)如图,点P 是AOB ∠平分线OC 上一点,PD OB ⊥,垂足为D .若2PD =,则点P 到边OA 的距离是 ( )A .1B . 2 C. 3 D .4 【答案】B 【解析】试题分析:过P 作PE ⊥OA 于点E ,根据角平分线上的点到角两边的距离相等即可得到PE=PD.从而得出点P 到OA 的距离是2cm. 故选:B.学科网 考点:角平分线的性质17. (2017浙江湖州第6题)如图,已知在Rt C ∆AB 中,C 90∠=,C C A =B ,6AB =,点P 是Rt C ∆AB 的重心,则点P 到AB 所在直线的距离等于( ) A .1 B .2 C.32D .2【答案】A考点:1、三角形的重心,2、等腰直角三角形,3、相似三角形的判定与性质18. (2017浙江台州第8题)如图,已知等腰三角形,ABC AB AC =,若以点B 为圆心,BC 长为半径画弧,交腰AC 于点E ,则下列结论一定正确的是( )A .AE EC =B .AE BE = C. EBC BAC ∠=∠D .EBC ABE ∠=∠ 【答案】C 【解析】试题分析:根据AB=AC,BE=BC ,可以得出∠ABC=∠C,∠BEC=∠C,从而得出∠ABC=∠BEC,∠A=∠EBC. 故选:C.考点:1、三角形的外角性质,2、等腰三角形的性质19. (2017浙江湖州第9题)七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那副图是( )【答案】C 【解析】试题分析:根据勾股定理,可判断边长之间的关系,可知构不成C 图案,能构成A 、B 、D 图案.故选:C 考点:勾股定理二、填空题1.(2017北京第13题)如图,在ABC ∆中,M N 、分别为,AC BC 的中点.若1CMN S ∆=,则ABNM S =四边形 .【答案】3.考点:相似三角形的性质.2.(2017福建第12题)如图,ABC ∆中,,D E 分别是,AB AC 的中点,连线DE ,若3DE =,则线段BC 的长等于 .【答案】6【解析】∵E 、F 分别是AB 、AC 的中点,∴BC=2EF=6.3.(2017河南第15题)如图,在Rt ABC ∆中,90A ∠=︒,AB AC =,21BC =+,点M ,N 分别是边BC ,AB 上的动点,沿MN 所在的直线折叠B ∠,使点B 的对应点'B 始终落在边AC 上.若'MBC ∆为直角三角形,则BM 的长为 .【答案】1或212+. 【解析】试题分析:在Rt ABC ∆中,90A ∠=︒,AB AC =,可得∠B=∠C=45°,由折叠可知,BM='MB ,若使'MBC ∆为直角三角形,分两种情况:①0'90MB C ∠=,由∠C=45°可得'MB ='CB ,设BM=x ,则'MB ='CB =x ,MC=2x ,所以x+2x =21BC =+,解得x=1,即BM=1;②0'90B MC ∠=,此时点B 和点C 重合,BM=12122BC +=.所以BM 的长为1或212+. 考点:折叠(翻折变换).4.(2017广东广州第14题)如图7,Rt ABC ∆中,01590,15,tan 8C BC A ∠===,则AB = .【答案】17 【解析】试题分析:因为1515,tan 8BC BC A AC ===,所以,AC =8,由勾股定理,得:AB =17. 考点: 正切的定义.5.(2017山东临沂第16题)已知AB CD ∥,AD 与BC 相交于点O .若23BO OC =,10AD =,则AO = .【答案】4 【解析】试题分析:根据平行线分线段成比例定理,由AB ∥CD 可得BO OAOC OD=,然后根据AD=10,可知OD=10-OA ,代入可得2103BO OA OC OA ==-,解得OA=4. 故答案为:4考点:平行线分线段成比例定理6.(2017四川泸州第16题)在ABC ∆中,已知BD 和CE 分别是边,AC AB 上的中线,且BD CE ⊥,垂足为O ,若2,4OD cm OE cm ==,则线段AO 的长为 cm . 【答案】45. 【解析】试题分析:如图,由BD 和CE 分别是边,AC AB 上的中线,可得DE ∥BC ,且12DE OD OE BC OB OC === , 因BD CE ⊥,2,4OD cm OE cm ==,根据勾股定理可得DE=25 ,又因12DE OD OE BC OB OC ===,可得BC=45,连结AO 并延长AO 交BC 于点M ,由BD 和CE 分别是边,AC AB 上的中线交于点M ,可知AM 也是△ABC 的边BC 上的中线,在Rt △BOC 中,根据斜边的中线等于斜边的一半可得OM= 12BC=25,最后根据三角形重心的性质可得AO=2OM=45.7. (2017江苏宿迁第12题)如图,在C ∆AB 中,C 90∠A B =,点D 、E 、F 分别是AB 、C B 、C A 的中点.若CD 2=,则线段F E 的长是 .【答案】2. 【解析】试题分析:因在C ∆AB 中,C 90∠A B =,点D 是AB 的中点,CD 2=,根据直角三角形中斜边的中线等于斜边的一半可得AB=4,又因,点E 、F 分别是C B 、C A 的中点,根据三角形的中位线定理可得EF=12AB=2. 8. (2017江苏苏州第17题)如图,在一笔直的沿湖道路l 上有A 、B 两个游船码头,观光岛屿C 在码头A 北偏东60的方向,在码头B 北偏西45的方向,C 4A =km .游客小张准备从观光岛屿C 乘船沿C A 回到码头A 或沿C B 回到码头B ,设开往码头A 、B 的游船速度分别为1v 、2v ,若回到A 、B 所用时间相等,则12v v = (结果保留根号).【答案】2 . 【解析】试题分析:作CD AB ⊥ ,垂足为D6302AC CAB CD =∠=︒∴=,,在Rt BCD ∆ 中,45CBD ∠=︒ ,22BC ∴=开往码头A 、B 的游船速度分别为1v 、2v ,若回到A 、B 所用时间相等,∴12v v =4222=D.考点:特殊角三角函数的应用 .9. (2017浙江湖州第14题)如图,已知在C ∆AB 中,C AB =A .以AB 为直径作半圆O ,交C B 于点D .若C 40∠B A =,则D A 的度数是 度.【答案】140考点:圆周角定理10. (2017湖南湘潭第14题)如图,在ABC ∆中,D E 、分别是边AB AC 、的中点,则ADE ∆与ABC ∆的面积比:ADE ABC S S ∆∆= .【答案】41 【解析】试题分析:已知D E 、分别是边AB AC 、的中点,即可得DE 是三角形的中位线,所以DE ∥BC,即可判定ADE ∆∽ABC ∆,根据相似三角形的性质可得:ADE ABCS S ∆∆=412122=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛AB AD .11. (2017湖南湘潭第15题)如图,在Rt ABC ∆中,90C ∠=°,BD 平分ABC ∠交AC 于点D ,DE 垂直平分AB ,垂足为E 点,请任意写出一组相等的线段 .【答案】BC=BE 或DC=DE 【解析】试题分析:已知90C ∠=°,BD 平分ABC ∠,DE 垂直平分AB ,利用角平分线性质定理可知DC=DE ;根据已知条件易证BCD ∆≌BED ∆,根据全等三角形的性质可得BC=BE.12. (2017浙江舟山第16题)一副含030和045的三角板ABC 和DEF 叠合在一起,边BC 与EF 重合,cm EF BC 12==(如图1),点G 为边)(EF BC 的中点,边FD 与AB 相交于点H ,现将三角板DEF 绕点G 按顺时针方向旋转(如图2),在CGF ∠从00到060的变化过程中,观察点H 的位置变化,点H 相应移动的路径长为 (结果保留根号).【答案】123-18. 【解析】试题分析:如图2和图3,在 ∠ C G F 从 0 ° 到 60 ° 的变化过程中,点H 先向AB 方向移,在往BA 方向移,直到H 与F 重合(下面证明此时∠CGF=60度),此时BH 的值最大,如图3,当F 与H 重合时,连接CF ,因为BG=CG=GF ,所以∠BFC=90度,∵∠B=30度,∴∠BFC=60度,由CG=GF 可得∠CGF=60度.∵BC=12cm ,所以BF=32BC=63;如图2,当GH ⊥DF 时,GH 有最小值,则BH 有最小值,且GF//AB ,连接DG ,交AB 于点K ,则DG ⊥AB ,∵DG=FG ,∴∠DGH=45度,则KG=KH=22GH=22×(12×62)=3,BK=3KG=33,则BH=BK+KH=33+3则点H运动的总路程为63-(33+3)+[12(3-1)-(33+3)]=123-18(cm ).考点:旋转的性质.三、解答题1.(2017北京第19题)如图,在ABC ∆中,0,36AB AC A =∠=,BD 平分ABC ∠交AC 于点D . 求证:AD BC =.【答案】见解析. 【解析】考点:等腰三角形性质.2. (2017北京第28题)在等腰直角ABC ∆中,090ACB ∠=,P 是线段BC 上一动点(与点B C 、不重合),连接AP ,延长BC 至点Q ,使得CQ CP =,过点Q 作QH AP ⊥于点H ,交AB 于点M . (1)若PAC α∠=,求AMQ ∠的大小(用含α的式子表示). (2)用等式表示线段MB 与PQ 之间的数量关系,并证明.【答案】(1)【解析】分析:(1)由直角三角形性质,两锐角互余,可得∠AMQ=180°-∠AHM-∠PAM ,解得∠AMQ=45°+α.(2)由题意得AP=AQ=QM,再证RT △APC ≌RT △QME,.全等三角形对应边相等得出PC=ME ,得出△MEB 为等腰直角三角形,则PQ=2BM. 本题解析:(1) ∠AMQ=45°+α.理由如下:∵∠PAC=α,△ACB 是等腰直角三角形, ∴∠PAB =45°-α,∠AHM=90°,∴∠AMQ=180°-∠AHM-∠PAM =45°+α .(2)线段MB 与PQ 之间的数量关系:PQ=2 MB. 理由如下:连接AQ ,过点M 做ME ⊥QB ,∵AC ⊥QP,CQ=CP, ∴∠QAC=∠PAC=α,∴∠QAM=α+45°=∠AMQ, ∴AP=AQ=QM,在RT △APC 和RT △QME中,MQE PAC ACP QEM AP QM∠=⎧⎪∠=∠⎨⎪=⎩∴RT △APC ≌RT △QME, ∴PC=ME, ∴△MEB 是等腰直角三角形,∴1222PQ MB =, ∴PQ=2 MB.考点:全等三角形判定,等腰三角形性质 .3. (2017天津第22题)如图,一艘海轮位于灯塔P 的北偏东064方向,距离灯塔120海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东045方向上的B 处,求BP 和BA 的长(结果取整数). 参考数据:05.264tan ,44.064cos ,90.064sin 0≈≈≈,2取414.1.【答案】BP=153;BA=161. 【解析】试题分析:如图,过点P 作PC ⊥AB ,垂足为C ,由题意可知,∠A=64°,∠B=45°,PA=120,在Rt △APC 中,求得PC 、AC 的长;在Rt △BPC 中,求得BP 、BC 的长,即可得BA 的长. 试题解析:如图,过点P 作PCAB ,垂足为C , 由题意可知,∠A=64°,∠B=45°,PA=120, 在Rt △APC 中,sin ∠A=,cos PC ACA PA PA=, ∴PC=PA ·sin ∠A=120×sin64°, AC=PA ×cos ∠A=120×cos64°,在Rt △BPC 中,sin ∠B=,tan PC PCB BP BC=, ∴BP=00120sin 641200.90153sin sin 4522PC B ⨯⨯=≈≈ BC=120sin 64tan tan 45PC PC PC B ===⨯ ∴BA=BC+AC=120×sin64°+120×cos64°≈120×0.90+120×0.44≈161. 答:BP 的长约有153海里,BA 的长约有161海里.4. (2017福建第18题)如图,点,,,B E C F 在一条直线上,,,AB DE AC DF BE CF ===.求证:A D ∠=∠.【答案】证明见解析. 【解析】试题分析:利用SSS 证明△ABC 与△DEF 全等即可得.试题解析:∵BE=CF ,∴BE+EC=CF+EC ,即BC=EF ,在△ABC 和△DEF 中AB DEAC DF BC EF =⎧⎪=⎨⎪=⎩,∴△ABC≌△DEF(SSS ),∴∠A=∠D .5. (2017福建第19题)如图,ABC ∆中,90,BAC AD BC ∠=⊥o,垂足为D .求作ABC ∠的平分线,分别交,AD AD 于P ,Q 两点;并证明AP AQ =.(要求:尺规作图,保留作图痕迹,不写作法)【答案】作图见解析;证明见解析. 【解析】6. (2017河南第19题)如图所示,我国两艘海监船A ,B 在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C .此时,B 船在A 船的正南方向5海里处,A 船测得渔船C 在其南偏东45︒方向,B 船测得渔船C 在其南偏东53︒方向.已知A 船的航速为30海里/小时,B 船的航速为25海里/小时,问C 船至少要等待多长时间才能得到救援?(参考数据:4sin 535︒≈,3cos535︒≈,4tan 533︒≈,2 1.41≈)【答案】C 船至少要等待0.94小时才能得到救援.【解析】试题分析:过点C 作CD AB ⊥交AB 的延长线于点D ,可得∠CDA=90°,根据题意可知∠CDA=45°,设CD=x ,则AD=CD=x ,在Rt △BDC 中,根据三角函数求得CD 、BC 的长,在Rt △ADC 中,求得AC 的长,再分别计算出B 船到达C 船处约需时间和A 船到达C 船处约需时间,比较即可求解. 试题解析:过点C 作CD AB ⊥交AB 的延长线于点D ,则∠CDA=90° 已知∠CDA=45°,设CD=x ,则AD=CD=x ∴BD=AD-AB=x-5在Rt △BDC 中,CD=BD ·tan53°,即x=(x-5)·tan53°∴0455tan 533204tan 53113x ⨯=≈=-- ∴BC=0042025sin 53sin 535CD x =≈÷=∴B 船到达C 船处约需时间:25÷25=1(小时) 在Rt △ADC 中,AC=2x ≈1.41×20=28.2∴A 船到达C 船处约需时间:28.2÷30=0.94(小时) 而0.94<1,所以C 船至少要等待0.94小时才能得到救援. 考点:解直角三角形的应用.7. (2017河南第22题)如图1,在R t A B C ∆中,90A ∠=︒,AB AC =,点D ,E 分别在边AB ,AC 上,AD AE =,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想图1中,线段PM 与PN 的数量关系是 ,位置关系是 ; (2)探究证明把ADE ∆绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断PMN ∆的形状,并说明理由;(3)拓展延伸把ADE ∆绕点A 在平面内自由旋转,若4AD =,10AB =,请直接写出PMN ∆面积的最大值. 【答案】(1)PM=PN ,PM PN ⊥;(2)等腰直角三角形,理由详见解析;(3)492. 【解析】试题分析:(1)已知 点M ,P ,N 分别为DE ,DC ,BC 的中点,根据三角形的中位线定理可得11,22PM EC PN BD ==,//PM EC ,//PN BD ,根据平行线的性质可得∠DPM=∠DCE ,∠NPD=∠ADC ,在Rt ABC ∆中,90A ∠=︒,AB AC =,AD AE =,可得BD=EC ,∠DCE+∠ADC=90°,即可得PM=PN ,∠DPM+∠NPD=90°,即PM PN ⊥;(2)PMN ∆是等腰直角三角形,根据旋转的性质易证△BAD ≌△CAE ,即可得BD=CE ,∠ABD=∠ACE ,根据三角形的中位线定理及平行线的性质(方法可类比(1)的方法)可得PM=PN, ∠MPD=∠ECD ,∠PNC=∠DBC ,所以∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD ,∠DPN=∠PNC+∠PCN =∠DBC+∠PCN ,即可得∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°,即△PMN 为等腰直角三角形;(3)把ADE ∆绕点A 旋转到如图的位置,此时PN=12(AD+AB)=7, PM=12(AE+AC)=7,且PN 、PM 的值最长,由(2)可知PM=PN ,PM PN ⊥,所以PMN ∆面积的最大值为1497722⨯⨯= .试题解析:(1)PM=PN ,PM PN ⊥; (2)等腰直角三角形,理由如下: 由旋转可得∠BAD=∠CAE , 又AB=AC,AD=AE ∴△BAD ≌△CAE∴BD=CE ,∠ABD=∠ACE ,∵点M ,P 分别为DE ,DC 的中点 ∴PM 是△DCE 的中位线∴PM=12CE ,且//PM CE , 同理可证PN=12BD ,且//PN BD∴PM=PN, ∠MPD=∠ECD ,∠PNC=∠DBC , ∴∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD , ∠DPN=∠PNC+∠PCN =∠DBC+∠PCN ,∴∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°, 即△PMN 为等腰直角三角形. (3)492. 考点: 旋转和三角形的综合题.8. (2017广东广州第18题)如图10,点,E F 在AB 上,,,AD BC A B AE BF =∠=∠=. 求证:ADF BCE ∆≅∆.【答案】详见解析 【解析】试题分析:先将AE BF =转化为AF =BE ,再利用SAS 证明两个三角形全等 试题解析:证明:因为AE =BF ,所以,AE +EF =BF +EF ,即AF =BE , 在△ADF 和△BCE 中,AD BC A B AF BE =⎧⎪∠=∠⎨⎪=⎩所以,ADF BCE ∆≅∆考点:用SAS 证明两三角形全等9. (2017广东广州第20题) 如图12,在Rt ABC ∆中,0090,30,23B A AC ∠=∠==.(1)利用尺规作线段AC 的垂直平分线DE ,垂足为E ,交AB 于点D ;(保留作图痕迹,不写作法) (2)若ADE ∆的周长为a ,先化简()()211T a a a =+--,再求T 的值. 【答案】(1)详见解析;(2)3310+ 【解析】试题分析:(1)尺规作图——作线段的垂直平分线;(2)化简求值,利用三角函数求其余两边的长度。
2017年中考数学试卷两套合集四附答案解析

2017年中考数学试卷两套合集四附答案解析中考数学试卷一.仔细选一选(本题有10小题,每题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确答案.1.是一个()A.整数 B.分数 C.有理数D.无理数2.下列计算正确的是()A.的平方根为±8 B.的算术平方根为8C.的立方根为2 D.的立方根为±23.小明想用图形1通过作图变换得到图形2,下列这些变化中不可行的是()A.轴对称变换B.平移变换 C.旋转变换 D.中心对称变换4.下列各式计算正确的有()A.(p5q4)÷(2p3q)=2p2q3B.(﹣a+5)(﹣a﹣5)=﹣a2﹣25C.D.5.如果圆内接四边形ABCD的对角线交点恰好是该圆的圆心,则四边形ABCD一定是()A.平行四边形B.矩形 C.菱形 D.正方形6.已知a﹣b=1,则a2﹣b2﹣2b的值为()A.1 B.2 C.3 D.47.某种数码产品原价每只400元,经过连续两次降价后,现在每只售价为256元,则平均每次降价的百分率为()A.20% B.80% C.180% D.20%或180%8.为了有效保护环境,某居委会倡议居民将生活垃圾进行可回收的、不可回收的和有害的分类投放,一天,小林把垃圾分装在三个袋中,则他任意投放垃圾,把三个袋子都放错位的概率是()A.B.C.D.9.一个多边形的内角中,锐角的个数最多有()A.3个B.4个C.5个D.6个10.已知抛物线y=a(x﹣m)2+n的顶点为A,与y轴的交点为B,若直线AB的解析式为y=﹣2x+b,点A,B关于原点的对称点分别为A′,B′,且四边形ABA′B′为矩形,则下列关于m,n,b的关系式正确的是()A.5m=4b B.4m=5b C.5n=3b D.3n=5b二、认真填一填(本题有6个小题,每小题4分,共24分)11.数据1,5,2,1,5,4的中位数是,方差为.12.把代数式4a2b﹣3b2(4a﹣3b)进行因式分解得:.13.函数y=x2﹣2x﹣3,当y<0时,x的取值范围为;当﹣1<x<2时,y的取值范围为.14.已知弦AB与CD交于点E,弧的度数比弧的度数大20°,若∠CEB=m°,则∠CAB= (用关于m的代数式表示).15.正方形ABCD的边长为acm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是 cm2.16.如图,△ABC中,∠ACB=90°,BC=6cm,AC=8cm,动点P从A出发,以2cm/s的速度沿△ABC 的边按A→B→C→A的顺序运动一周,则点P出发s时,△BCP为等腰三角形.三、全面答一答(本题有7小题,共66分,)解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17.先化简,再求值:÷(x+2﹣),其中x满足x(x2﹣4)=0.18.为了深化我省义务教育课程改革,某校积极开展本校课程建设,计划成立“科普观察”、“架子鼓”、“足球”、“摄影”等多个社团,要求每个学生都自主选择其中一个社团.为此,随机调查了本校七、八、九年级部分学生选择社团的意向,并将调查结果绘制成如图统计表(不完整):某校被调查学生选择社团意向统计表架子鼓科普观察足球摄影其他选择意向所占30% a b 10% c百分比根据统计图表中的信息,解答下列问题:(1)求架子鼓和摄影社团的人数及a,b的值;(2)将条形统计图补充完整;(3)若该校共有1200名学生,试估计全校选择“科普观察”社团的学生人数.Array19.某政府大力扶持大学生创业,李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯,物价部门规定,这种护眼台灯的销售单价不得高于32元.销售过程中发现,月销售量y(件)与销售单价x(元)之间的关系可看作一次函数:y=﹣10x+n.(1)当销售单价x定为25元时,李明每月获得利润w为1250元,求n的值;(2)当销售单价定为多少元时,每月可获得最大利润?并求最大利润是多少?20.如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx﹣2的图象经过点A、C,并与y轴交于点E,反比例函数y=的图象经过点A.(1)点E的坐标是;(2)求反比例函数的解析式;(3)求当一次函数的值小于反比例函数的值时,x的取值范围.21.如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=.(1)求证:CD∥BF;(2)求⊙O的半径;(3)求弦CD的长.22.如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.(1)当AC的长度为多少时,△AMC和△BOD相似;(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;(3)连结BC.当S△AMC=S△BOC时,求AC的长.23.关于x的函数y=2mx2+(1﹣m)x﹣1﹣m(m是实数),探索发现了以下四条结论:①函数图象与坐标轴总有三个不同的交点;②当m=﹣3时,函数图象的顶点坐标是(,);③当m>0时,函数图象截x轴所得的线段长度大于;④当m≠0时,函数图象总经过两个定点.请你判断四条结论的真假,并说明理由.参考答案与试题解析一.仔细选一选(本题有10小题,每题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确答案.1.是一个()A.整数 B.分数 C.有理数D.无理数【考点】无理数.【分析】根据无理数的定义即可作答.【解答】解:∵是一个无限不循环小数,∴是一个无理数.故选D.【点评】本题考查了无理数的定义:无限不循环小数为无理数.初中范围内学习的无理数有三类:①π类,如2π,等;②开方开不尽的数,如,等;③虽有规律但是无限不循环的数,如0.1010010001…,等.2.下列计算正确的是()A.的平方根为±8 B.的算术平方根为8C.的立方根为2 D.的立方根为±2【考点】立方根;平方根;算术平方根.【分析】依据平方根、算术平方根、立方根的性质求解即可.【解答】解:A、=8,8的平方根为±2,故A错误;B、=8,8的算术平方根为2,故B错误;C、=8,8的立方根为2,故C正确;D、=8,8的立方根为2,故D错误.故选:C.【点评】本题主要考查的是立方根、平方根、算术平方根的性质,熟练掌握相关知识是解题的关键.3.小明想用图形1通过作图变换得到图形2,下列这些变化中不可行的是()A.轴对称变换B.平移变换 C.旋转变换 D.中心对称变换【考点】几何变换的类型.【分析】根据轴对称变换、平移变换、旋转变换和中心对称变换的概念进行判断即可.【解答】解:连接AB,作线段AB的垂直平分线,垂足为O,∴图形1以直线l为对称轴通过轴对称变换得到图形2,A可行;图形1以O为旋转中心,旋转180°得到图形2,C、D可行;故选:B.【点评】本题考查的是几何变换的类型,掌握轴对称变换、平移变换、旋转变换和中心对称变换的概念是解题的关键.4.下列各式计算正确的有()A.(p5q4)÷(2p3q)=2p2q3B.(﹣a+5)(﹣a﹣5)=﹣a2﹣25C.D.【考点】分式的加减法;平方差公式;整式的除法.【分析】根据单项式的除法、平方差公式以及分式的加减法进行计算即可.【解答】解:A、(p5q4)÷(2p3q)=p2q3,故错误;B、(﹣a+5)(﹣a﹣5)=a2﹣25,故错误;C、+=,故错误;D、正确;故选D.【点评】本题考查了分式的加减、平方差公式以及分式的加减,掌握运算法则是解题的关键.5.如果圆内接四边形ABCD的对角线交点恰好是该圆的圆心,则四边形ABCD一定是()A.平行四边形B.矩形 C.菱形 D.正方形【考点】圆内接四边形的性质.【分析】由圆内接四边形ABCD的对角线交点恰好是该圆的圆心,根据直径所对的圆周角是直角,可求得四边形ABCD的四个内角都是直角,即可判定四边形ABCD一定是矩形.【解答】解:∵圆内接四边形ABCD的对角线交点恰好是该圆的圆心,∴∠A=∠B=∠C=∠D=90°,∴四边形ABCD一定是矩形.故选B.【点评】此题考查了矩形的判定以及圆的内接四边形的性质.注意直径所对的圆周角是直角定理的应用是解此题的关键.6.已知a﹣b=1,则a2﹣b2﹣2b的值为()A.1 B.2 C.3 D.4【考点】完全平方公式.【分析】由已知得a=b+1,代入所求代数式,利用完全平方公式计算.【解答】解:∵a﹣b=1,∴a=b+1,∴a2﹣b2﹣2b=(b+1)2﹣b2﹣2b=b2+2b+1﹣b2﹣2b=1.故选:A.【点评】本题考查了完全平方公式的运用.关键是利用换元法消去所求代数式中的a.7.某种数码产品原价每只400元,经过连续两次降价后,现在每只售价为256元,则平均每次降价的百分率为()A.20% B.80% C.180% D.20%或180%【考点】一元二次方程的应用.【分析】可先表示出第一次降价后的价格,那么第一次降价后的价格×(1﹣降低的百分率)=256,把相应数值代入即可求解.【解答】解:设平均每次降价的百分率为x,根据题意得:400(1﹣x)2=256解得:x=20%或x=1.8(舍去),故选A.【点评】考查求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.8.为了有效保护环境,某居委会倡议居民将生活垃圾进行可回收的、不可回收的和有害的分类投放,一天,小林把垃圾分装在三个袋中,则他任意投放垃圾,把三个袋子都放错位的概率是()A.B.C.D.【考点】列表法与树状图法.【专题】计算题.【分析】(装可回收的、不可回收的和有害的垃圾的三个袋分别用A、B、C表示,陈放可回收的、不可回收的和有害的垃圾的地方分别为a、b、c)画树状图展示所用6种等可能的结果数,再找出把三个袋子都放错位的结果数,然后根据概率公式求解.【解答】解:(装可回收的、不可回收的和有害的垃圾的三个袋分别用A、B、C表示,陈放可回收的、不可回收的和有害的垃圾的地方分别为a、b、c)画树状图:共有6种等可能的结果数,其中他任意投放垃圾,把三个袋子都放错位的结果数为2,所以他任意投放垃圾,把三个袋子都放错位的概率==.故选C.【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.9.一个多边形的内角中,锐角的个数最多有()A.3个B.4个C.5个D.6个【考点】多边形内角与外角.【分析】利用多边形的外角和是360度即可求出答案.【解答】解:因为多边形的外角和是360度,在外角中最多有三个钝角,如果超过三个则和一定大于360度,多边形的内角与相邻的外角互为邻补角,则外角中最多有三个钝角时,内角中就最多有3个锐角.故选A.【点评】本题考查了多边形的内角问题.由于内角和不是定值,不容易考虑,而外角和是360度不变,因而内角的问题可以转化为外角的问题进行考虑.10.已知抛物线y=a(x﹣m)2+n的顶点为A,与y轴的交点为B,若直线AB的解析式为y=﹣2x+b,点A,B关于原点的对称点分别为A′,B′,且四边形ABA′B′为矩形,则下列关于m,n,b的关系式正确的是()A.5m=4b B.4m=5b C.5n=3b D.3n=5b【考点】二次函数的性质;一次函数图象上点的坐标特征.【分析】根据题意可知:A(m,n),B(0,b),所以B′的坐标为(0,﹣b),由题意可知:四边形ABA′B′为矩形,所以对角线AA′=BB′.【解答】解:由题意可知:A(m,n),B(0,b),∵点A,B关于原点的对称点分别为A′,B′,∴BB′=|2b|,∵四边形ABA′B′为矩形,∴AA′=BB′,∵OA2=m2+n2,∵AA′2=4OA2=4(m2+n2),∴4(m2+n2)=4b2,把(m,n)代入y=﹣2x+b,∴n=﹣2m+b,∴b2=m2+(﹣2m+b)2,化简可得:5m=4b,故选(A)【点评】本题考查了二次函数的性质,涉及矩形的性质,二次函数的性质,完全平方差公式,综合程度较高.二、认真填一填(本题有6个小题,每小题4分,共24分)11.数据1,5,2,1,5,4的中位数是 3 ,方差为 3 .【考点】方差;中位数.【专题】推理填空题.【分析】首先将这组数据按照从小到大的顺序排列,则中间两个数据的平均数就是这组数据的中位数;然后根据方差的含义和求法,求出数据1,5,2,1,5,4的方差是多少即可.【解答】解:∵数据1,5,2,1,5,4按照从小到大的顺序排列是:1,1,2,4,5,5,∴数据1,5,2,1,5,4的中位数是:(2+4)÷2=6÷2=3∵数据1,5,2,1,5,4的平均数是:(1+5+2+1+5+4)÷6=18÷6=3∴数据1,5,2,1,5,4的方差是:×[(1﹣3)2+(5﹣3)2+(2﹣3)2+(1﹣3)2+(5﹣3)2+(4﹣3)2]=×[4+4+1+4+4+1]=×18=3故答案为:3,3.【点评】此题主要考查了中位数、方差的含义和求法,要熟练掌握.12.把代数式4a2b﹣3b2(4a﹣3b)进行因式分解得:b(2a﹣3b)2.【考点】提公因式法与公式法的综合运用.【专题】计算题;因式分解.【分析】原式去括号整理后,提取b,再利用完全平方公式分解即可.【解答】解:原式=4a2b﹣12ab2+9b3=b(4a2﹣12ab+9b2)=b(2a﹣3b)2,故答案为:b(2a﹣3b)2【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.13.函数y=x2﹣2x﹣3,当y<0时,x的取值范围为﹣1<x<3 ;当﹣1<x<2时,y的取值范围为﹣4<y<0 .【考点】抛物线与x轴的交点.【分析】根据函数解析式可以确定图象与x轴的交点是(﹣1,0),(3,0),又当y<0时,图象在x轴的下方,由此可以确定x的取值范围,结合函数解析式求出y的取值范围.【解答】解:当y=0时,即x2﹣2x﹣3=0,∴x1=﹣1,x2=3,∴图象与x轴的交点是(﹣1,0),(3,0),当y<0时,图象在x轴的下方,此时﹣1<x<3.当﹣1<x<2时,y的取值范围为:﹣4<y<0,故答案为:﹣1<x<3,﹣4<y<0.【点评】本题主要考查了抛物线与x轴的交点问题,解答此题的关键是求出图象与x轴的交点,然后由图象找出当y<0时,自变量x的范围,锻炼了学生数形结合的思想方法.14.已知弦AB与CD交于点E,弧的度数比弧的度数大20°,若∠CEB=m°,则∠CAB=(用关于m的代数式表示).【考点】圆心角、弧、弦的关系.【分析】由弧BC与AD的度数之差为20°,根据圆周角定理,可得∠CAB﹣∠C=×20°=10°,又由∠CEB=60°,可得∠CAB+∠C=60°,继而求得答案.【解答】解:∵弧BC与AD的度数之差为20°,∴∠CAB﹣∠C=×20°=10°,∵∠CEB=∠CAB+∠C=m°,∴∠CAB=.故答案为:.【点评】此题考查了圆周角定理以及三角形外角的性质.此题难度不大,注意掌握方程思想与数形结合思想的应用.15.正方形ABCD的边长为acm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是 cm2.【考点】正方形的性质.【专题】几何图形问题.【分析】连接BD,可看出阴影部分的面积等于正方形的面积+一个三角形的面积,用相似求出三角形的面积,阴影部分的面积可证.【解答】解:连接BD,EF.∵阴影部分的面积=△ABD的面积+△BDG的面积(G为BF与DE的交点),∴△ABD的面积=正方形ABCD的面积=a2.∵△BCD中EF为中位线,∴EF∥BD,EF=BD,∴△GEF∽△GBD,∴DG=2GE,∴△BDE的面积=△BCD的面积.∴△BDG的面积=△BDE的面积=△BCD的面积=•a2=a2.∴阴影部分的面积=a2+a2=a2.故答案为: a2.【点评】本题考查正方形的性质,正方形的四个边长相等,关键是连接BD,把阴影部分分成两部分计算.16.如图,△ABC中,∠ACB=90°,BC=6cm,AC=8cm,动点P从A出发,以2cm/s的速度沿△ABC 的边按A→B→C→A的顺序运动一周,则点P出发2或2.5或11或1.4 s时,△BCP为等腰三角形.【考点】勾股定理;等腰三角形的判定.【专题】动点型.【分析】根据∠ACB=90°,BC=6cm,AC=8cm,利用勾股定理求出AB的长,①当点P在AB边上时;②当点P在BC边上时,不存在△BCP;③点P在AC边上时;利用P点的运动速度求出时间即可,注意分类讨论.【解答】解;∵△ABC中,∠ACB=90°,BC=6cm,AC=8cm,∴AB===10(cm),①当点P在AB边上时,当BP=BC=6cm时,∴AP=AB﹣BP=10﹣6=4,∵动点P从A出发,以2cm/s的速度沿AB移动,4÷2=2,∴点P出发2s时,△BCP为等腰三角形;当PC=PB时,P为斜边AB的中点,此时AP=BP=PC=5cm,5÷2=2.5,∴点P出发2.5s时,△BCP为等腰三角形;当BC=PC时,过点C作CD⊥AB于点D,如图1所示:则△BCD∽△BAC,∴=,即,解得:BD=3.6,∴BP=2BD=7.2,∴AP=10﹣7.2=2.8,2.8÷2=1.4,∴点P出发1.4s时,△BCP为等腰三角形;②当点P在BC边上时,不存在△BCP;③点P在AC边上时,CP=CB=6,AB+BC+CP=10+6+6=22,22×2=11,∴点P出发11s时,△BCP为等腰三角形.综上所述:点P出发2s或2.5s或11s或1.4s时,△BCP为等腰三角形;故答案为:2或2.5或11或1.4.【点评】此题主要考查勾股定理和等腰三角形的判定,解答此题的关键是首先根据勾股定理求出AB 的长,然后再利用等腰三角形的性质去判定.三、全面答一答(本题有7小题,共66分,)解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17.先化简,再求值:÷(x+2﹣),其中x满足x(x2﹣4)=0.【考点】分式的化简求值.【专题】计算题.【分析】先把括号内通分和把除法运算化为乘法运算,再把分子分母因式分解,约分得到原式,接着解x(x2﹣4)=0,然后利用分式有意义的条件确定x的值,再把x的值代入计算即可.【解答】解:原式=÷=•==,解x(x2﹣4)=0得x=0或x=2或x=﹣2,因为x≠0且x≠2,所以x=﹣2,当x=﹣2时,原式==﹣.【点评】本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.18.为了深化我省义务教育课程改革,某校积极开展本校课程建设,计划成立“科普观察”、“架子鼓”、“足球”、“摄影”等多个社团,要求每个学生都自主选择其中一个社团.为此,随机调查了本校七、八、九年级部分学生选择社团的意向,并将调查结果绘制成如图统计表(不完整):某校被调查学生选择社团意向统计表架子鼓科普观察足球摄影其他选择意向所占30% a b 10% c百分比根据统计图表中的信息,解答下列问题:(1)求架子鼓和摄影社团的人数及a,b的值;(2)将条形统计图补充完整;(3)若该校共有1200名学生,试估计全校选择“科普观察”社团的学生人数.【考点】条形统计图;用样本估计总体;统计表.【分析】(1)根据统计图和表格中的数据可以求得本次抽查的人数,从而可以解答本题;(2)根据(1)中求得的架子鼓和摄影社团的人数,可以将条形统计图补充完整;(3)根据统计图和表格中的数据可以估计全校选择“科普观察”社团的学生人数.【解答】解:(1)由图可得,本次抽查的学生有:(70+40+10)÷(1﹣30%﹣10%)=120÷60%=200(人),∴架子鼓的人数为:200×30%=60,摄影社团的人数为:200×10%=20,a=,b=,即架子鼓的人数为60,摄影社团的人数为20,a的值是35%,b的值是20%;(2)由(1)知架子鼓的人数为60,摄影社团的人数为20,故补全的条形统计图如右图所示;(3)由题意可得,1200×35%=420(人),即全校选择“科普观察”社团的学生人数是420.【点评】本题考查条形统计图、统计表、用样本股及总体,解题的关键是明确题意,利用数形结合的思想解答.19.某政府大力扶持大学生创业,李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯,物价部门规定,这种护眼台灯的销售单价不得高于32元.销售过程中发现,月销售量y(件)与销售单价x(元)之间的关系可看作一次函数:y=﹣10x+n.(1)当销售单价x定为25元时,李明每月获得利润w为1250元,求n的值;(2)当销售单价定为多少元时,每月可获得最大利润?并求最大利润是多少?【考点】二次函数的应用;一元二次方程的应用.【分析】(1)根据题意可以列出相应的方程,得到n的值,本题得以解决;(2)根据题意可以得到w与x的函数关系式,然后化为顶点式即可解答本题.【解答】解:(1)由题意可得,(25﹣20)(﹣10×25+n)=1250,解得,n=500,即n的值是500;(2)w=(x﹣20)(﹣10x+500)=﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250,∴x=35时,w取得最大值,此时w=2250,即当销售单价定为35元时,每月可获得最大利润,最大利润是2250元.【点评】本题考查二次函数的应用、一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.20.如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx﹣2的图象经过点A、C,并与y轴交于点E,反比例函数y=的图象经过点A.(1)点E的坐标是(0,﹣2);(2)求反比例函数的解析式;(3)求当一次函数的值小于反比例函数的值时,x的取值范围.【考点】反比例函数与一次函数的交点问题.【分析】(1)一次函数y=kx﹣2中代入x=0求得y的值,即可求得点E的坐标;(2)利用△ACD∽△CEO求得点A的坐标后代入反比例函数的解析式,即可求得反比例函数的解析式;(3)首先确定两个函数的交点坐标,然后结合图象确定x的取值范围即可.【解答】解:(1)一次函数y=kx﹣2中令x=0得y=﹣2,所以E(0,﹣2);(2)∵∠OCE=∠ACB,∴Rt△OCE∽Rt△BCA,∴=,即=,解得OC=4,∴C点坐标为(4,0);(2)把C(4,0)代入y=kx﹣2得4k﹣2=0,解得k=,∴一次函数解析式为y=x﹣2;∵OC=4,∴A点坐标为(6,1),把A(6,1)代入y=得m=6×1=6,∴反比例函数解析式为y=;(3)令解得,∴另一个交点(﹣2,﹣3),∴观察图象得:当x<﹣2或 0<x<6时次函数的值小于反比例函数的值.【点评】本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.21.如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=.(1)求证:CD∥BF;(2)求⊙O的半径;(3)求弦CD的长.【考点】切线的性质;勾股定理;垂径定理;圆周角定理;解直角三角形.【专题】证明题.【分析】(1)由BF是⊙O的切线得到AB⊥BF,而AB⊥CD,由此即可证明CD∥BF;(2)连接BD,由AB是直径得到∠ADB=90°,而∠BCD=∠BAD,cos∠BCD=,所以cos∠BAD=,然后利用三角函数即可求出⊙O的半径;(3)由于cos∠DAE=,而AD=3,由此求出AE,接着利用勾股定理可以求出ED,也就求出了CD.【解答】(1)证明:∵BF是⊙O的切线,∴AB⊥BF,∵AB⊥CD,∴CD∥BF;(2)解:连接BD,∵AB是直径,∴∠ADB=90°,∵∠BCD=∠BAD,cos∠BCD=,∴cos∠BAD=,又∵AD=3,∴AB=4,∴⊙O的半径为2;(3)解:∵∠BCD=∠DAE,∴cos∠BCD=cos∠DAE=,AD=3,∴AE=ADcos∠DAE=3×=,∴ED=,∴CD=2ED=.【点评】本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.22.如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.(1)当AC的长度为多少时,△AMC和△BOD相似;(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;(3)连结BC.当S△AMC=S△BOC时,求AC的长.【考点】相似三角形的判定与性质.【分析】(1)由于∠MCA=∠BDO=Rt∠,所以△AMC和△BOD相似时分两种情况:①△AMC∽△BOD;②△AMC∽△OBD.则两种情况都可以根据相似三角形对应边的比相等及tan∠EOF=2列出关于AC的方程,解方程即可求出AC的长度;(2)先由MC∥BD,得出△AMC∽△ABD,根据相似三角形对应边的比相等及三角形中位线的性质求出BD=2MC=8,OD=4,CD=8,AC=CD=8,再利用SAS证明△AMC≌△BOD,得到∠CAM=∠DBO,根据平行线的性质及三角形内角和定理求出∠ABO=90°,进而得出△ABO为直角三角形;(3)设OD=a,根据tan∠EOF=2得出BD=2a,由三角形的面积公式求出S△AMC=2AC,S△BOC=12a,根据S=S△BOC,得到AC=6a.由△AMC∽△ABD,根据相似三角形对应边的比相等列出关于a的方程,解方△AMC程求出a的值,进而得出AC的长.【解答】解:(1)∵∠MCA=∠BDO=Rt∠,∴△AMC和△BOD中,C与D是对应点,∴△AMC和△BOD相似时分两种情况:①当△AMC∽△BOD时, =tan∠EOF=2,∵MC=4,∴=2,解得AC=8;②当△AMC∽△OBD时, =tan∠EOF=2,∵MC=4,∴=2,解得AC=2.故当AC的长度为2或8时,△AMC和△BOD相似;(2)△ABO为直角三角形.理由如下:∵MC∥BD,∴△AMC∽△ABD,∴,∠AMC=∠ABD,∵M为AB中点,∴C为AD中点,BD=2MC=8.∵tan∠EOF=2,∴OD=4,∴CD=OC﹣OD=8,∴AC=CD=8.在△AMC与△BOD中,,∴△AMC≌△BOD(SAS),∴∠CAM=∠DBO,∴∠ABO=∠ABD+∠DBO=∠AMC+∠CAM=90°,∴△ABO为直角三角形;(3)连结BC,设OD=a,则BD=2a.∵S△AMC=S△BOC,S△AMC=•AC•MC=2AC,S△BOC=•OC•BD=12a,∴2AC=12a,∴AC=6a.∵△AMC∽△ABD,∴,即,解得a1=3,a2=﹣(舍去),∴AC=6×3=18.【点评】本题主要考查了相似三角形的判定与性质,锐角三角函数的定义,三角形的面积,三角形中位线定理,综合性较强,有一定难度.进行分类讨论是解决第一问的关键.23.关于x的函数y=2mx2+(1﹣m)x﹣1﹣m(m是实数),探索发现了以下四条结论:①函数图象与坐标轴总有三个不同的交点;②当m=﹣3时,函数图象的顶点坐标是(,);③当m>0时,函数图象截x轴所得的线段长度大于;④当m≠0时,函数图象总经过两个定点.请你判断四条结论的真假,并说明理由.【考点】二次函数的性质;抛物线与x轴的交点.【分析】①通过反例即可判断;②把m=﹣3代入,然后化成顶点式即可判断;③求得与x轴的交点,进而求得|x1﹣x2|的值,即可判断;④由y=2mx2+(1﹣m)x﹣1﹣m=(2x2﹣x﹣1)m+x﹣1,可知当2x2﹣x﹣1=0时,y的值与m无关,此时x1=1,x2=﹣,当x1=1,y=0;当x2=﹣时,y2=﹣,从而判定函数图象总经过两个定点(1,0),(﹣,﹣).【解答】解:①假命题;当m=0时,y=x﹣1为一次函数与坐标轴只有两个交点,②真命题;当m=﹣3时,y=﹣6x2+4x+2=﹣6(x﹣)2+,∴顶点坐标是(,),③真命题;当m>0时,由y=0得:△=(1﹣m)2﹣4×2m(﹣1﹣m)=(3m+1)2,∴x=,∴x1=1,x2=﹣﹣,∴|x1﹣x2|=+>,∴函数图象截x轴所得的线段长度大于;④真命题;当m≠0时,y=2mx2+(1﹣m)x﹣1﹣m=(2x2﹣x﹣1)m+x﹣1,当2x2﹣x﹣1=0时,y的值与m无关此时x1=1,x2=﹣,当x1=1,y=0;当x2=﹣时,y2=﹣,∴函数图象总经过两个定点(1,0),(﹣,﹣).【点评】本题考查了二次函数的性质,抛物线与二次函数的交点,熟练掌握二次函数的性质是解题的关键.中考数学试卷一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中.只有一项符合题目要求.1.在数﹣3,2,0,3中,大小在﹣1和2之间的数是()A.﹣3 B.2 C.0 D.32.已知一个单项式的系数是2,次数是3,则这个单项式可以是()A.﹣2xy2B.3x2C.2xy3D.2x33.的算术平方根是()A.2 B.±2 C.D.±4.下面四个几何体中,俯视图为四边形的是()A.B.C.D.5.不等式组的解集在数轴上表示正确的是()A.B.C.D.6.为了考察一批电视机的使用寿命,从中任意抽取了10台进行实验,在这个问题中样本是()A.抽取的10台电视机B.这一批电视机的使用寿命C.10D.抽取的10台电视机的使用寿命7.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是()A.B.C.D.8.下列运算正确的是()A.()﹣1=﹣ B.6×107=6000000C.(2a)2=2a2D.a3•a2=a59.如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是()A.60° B.90° C.100°D.120°10.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是()A.B.C.D.二、填空题:本大题共5小题,每小题3分,共l5分.11.分解因式:2a2﹣4a+2= .12.设x1、x2是一元二次方程x2﹣5x﹣1=0的两实数根,则x12+x22的值为.13.在函数y=+中,自变量x的取值范围是.14.若m1,m2,…,m2016是从0,1,2这三个数中取值的一列数,若m1+m2+…+m2016=1526(m1﹣1)2+(m2﹣1)2+…+(m2016﹣1)2=1510,则在m1,m2,…,m2016中,取值为2的个数为.15.如图,一次函数的图象与x轴、y轴分别相交于点A、B,将△AOB沿直线AB翻折,得△ACB.若C(,),则该一次函数的解析式为.。
近五年(2017-2021)年浙江中考数学真题分类汇编之图形的性质(含解析)

2017-2021年浙江中考数学真题分类汇编之图形的性质一.选择题(共14小题)1.(2021•杭州)如图,设点P是直线l外一点,PQ⊥l,垂足为点Q,点T是直线l上的一个动点,连结PT,则()A.PT≥2PQ B.PT≤2PQ C.PT≥PQ D.PT≤PQ 2.(2021•衢州)已知扇形的半径为6,圆心角为150°,则它的面积是()A.πB.3πC.5πD.15π3.(2020•宁波)如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE中点,连接BF.若AC=8,BC=6,则BF的长为()A.2B.2.5C.3D.4 4.(2021•衢州)如图,在△ABC中,AB=4,AC=5,BC=6,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为()A.6B.9C.12D.15 5.(2021•台州)小光准备从A地去往B地,打开导航、显示两地距离为37.7km,但导航提供的三条可选路线长却分别为45km,50km,51km(如图).能解释这一现象的数学知识是()A.两点之间,线段最短B.垂线段最短C.三角形两边之和大于第三边D.两点确定一条直线6.(2020•温州)如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA 的延长线于点D.若⊙O的半径为1,则BD的长为()A.1B.2C.D.7.(2021•绍兴)数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形纵向排列放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是()A.用3个相同的菱形放置,最多能得到6个菱形B.用4个相同的菱形放置,最多能得到16个菱形C.用5个相同的菱形放置,最多能得到27个菱形D.用6个相同的菱形放置,最多能得到41个菱形8.(2020•金华)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连接EG,BD相交于点O,BD与HC相交于点P.若GO=GP,则的值是()A.1+B.2+C.5﹣D.9.(2020•温州)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD 为边作▱BCDE,则∠E的度数为()A.40°B.50°C.60°D.70°10.(2020•衢州)过直线l外一点P作直线l的平行线,下列尺规作图中错误的是()A.B.C.D.11.(2020•湖州)如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是()A.DC=DT B.AD=DT C.BD=BO D.2OC=5AC 12.(2020•嘉兴)如图,在等腰△ABC中,AB=AC=2,BC=8,按下列步骤作图:①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于EF的长为半径作弧相交于点H,作射线AH;②分别以点A,B为圆心,大于AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;③以点O为圆心,线段OA长为半径作圆.则⊙O的半径为()A.2B.10C.4D.5 13.(2021•宁波)如图是一个由5张纸片拼成的平行四边形ABCD,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张矩形纸片EFGH的面积为S3,FH与GE相交于点O.当△AEO,△BFO,△CGO,△DHO的面积相等时,下列结论一定成立的是()A.S1=S2B.S1=S3C.AB=AD D.EH=GH14.(2021•金华)如图,在Rt△ABC中,∠ACB=90°,以该三角形的三条边为边向外作正方形,正方形的顶点E,F,G,H,M,N都在同一个圆上.记该圆面积为S1,△ABC 面积为S2,则的值是()A.B.3πC.5πD.二.填空题(共6小题)15.(2020•台州)如图,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是.16.(2020•绍兴)如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为.17.(2020•绍兴)将两条邻边长分别为,1的矩形纸片剪成四个等腰三角形纸片(无余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的(填序号).①,②1,③﹣1,④,⑤.18.(2020•衢州)图1是由七根连杆链接而成的机械装置,图2是其示意图.已知O,P两点固定,连杆P A=PC=140cm,AB=BC=CQ=QA=60cm,OQ=50cm,O,P两点间距与OQ长度相等.当OQ绕点O转动时,点A,B,C的位置随之改变,点B恰好在线段MN上来回运动.当点B运动至点M或N时,点A,C重合,点P,Q,A,B在同一直线上(如图3).(1)点P到MN的距离为cm.(2)当点P,O,A在同一直线上时,点Q到MN的距离为cm.19.(2019•绍兴)把边长为2的正方形纸片ABCD分割成如图的四块,其中点O为正方形的中心,点E,F分别为AB,AD的中点.用这四块纸片拼成与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠无缝隙),则四边形MNPQ的周长是.20.(2019•湖州)七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”.由边长为4的正方形ABCD可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型(其中点Q、R分别与图2中的点E、G重合,点P 在边EH上),则“拼搏兔”所在正方形EFGH的边长是.三.解答题(共2小题)21.(2020•台州)如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M.E是线段CM上的点,连接BE.F是△BDE的外接圆与AD的另一个交点,连接EF,BF.(1)求证:△BEF是直角三角形;(2)求证:△BEF∽△BCA;(3)当AB=6,BC=m时,在线段CM上存在点E,使得EF和AB互相平分,求m的值.22.(2020•衢州)【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.(1)判断△AFG的形状并说明理由.(2)求证:BF=2OG.【迁移应用】(3)记△DGO的面积为S1,△DBF的面积为S2,当=时,求的值.【拓展延伸】(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连接EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.2017-2021年浙江中考数学真题分类汇编之图形的性质参考答案与试题解析一.选择题(共14小题)1.(2021•杭州)如图,设点P是直线l外一点,PQ⊥l,垂足为点Q,点T是直线l上的一个动点,连结PT,则()A.PT≥2PQ B.PT≤2PQ C.PT≥PQ D.PT≤PQ【考点】垂线段最短.【专题】线段、角、相交线与平行线;推理能力.【分析】根据垂线的性质“垂线段最短”即可得到结论.【解答】解:∵PQ⊥l,点T是直线l上的一个动点,连结PT,∴PT≥PQ,故选:C.【点评】本题考查了垂线段最短,熟练掌握垂线的性质是解题的关键.2.(2021•衢州)已知扇形的半径为6,圆心角为150°,则它的面积是()A.πB.3πC.5πD.15π【考点】扇形面积的计算.【专题】常规题型;运算能力.【分析】把已知数据代入扇形面积公式计算,即可得到答案.【解答】解:扇形面积=,故选:D.【点评】本题考查的是扇形面积计算,掌握扇形面积公式:是解决本题的关键.3.(2020•宁波)如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE中点,连接BF.若AC=8,BC=6,则BF的长为()A.2B.2.5C.3D.4【考点】三角形中位线定理;直角三角形斜边上的中线;勾股定理.【专题】转化思想;等腰三角形与直角三角形;推理能力.【分析】利用勾股定理求得AB=10;然后由直角三角形斜边上的中线等于斜边的一半求得CD的长度;结合题意知线段BF是△CDE的中位线,则BF=CD.【解答】解:∵在Rt△ABC中,∠ACB=90°,AC=8,BC=6,∴AB===10.又∵CD为中线,∴CD=AB=5.∵F为DE中点,BE=BC即点B是EC的中点,∴BF是△CDE的中位线,则BF=CD=2.5.故选:B.【点评】本题主要考查了勾股定理,三角形中位线定理,直角三角形斜边上的中线,此题的突破口是推知线段CD的长度和线段BF是△CDE的中位线.4.(2021•衢州)如图,在△ABC中,AB=4,AC=5,BC=6,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为()A.6B.9C.12D.15【考点】三角形中位线定理.【专题】三角形;推理能力.【分析】根据三角形中位线定理、线段中点的概念分别求出AD、DE、EF、AF,根据四边形的周长公式计算即可.【解答】解:∵点D,E,F分别是AB,BC,CA的中点,∴DE=AC=2.5,AF=AC=2.5,EF=AB=2,AD=AB=2,∴四边形ADEF的周长=AD+DE+EF+AF=9,故选:B.【点评】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.5.(2021•台州)小光准备从A地去往B地,打开导航、显示两地距离为37.7km,但导航提供的三条可选路线长却分别为45km,50km,51km(如图).能解释这一现象的数学知识是()A.两点之间,线段最短B.垂线段最短C.三角形两边之和大于第三边D.两点确定一条直线【考点】线段的性质:两点之间线段最短;垂线段最短;直线的性质:两点确定一条直线.【专题】线段、角、相交线与平行线;几何直观.【分析】根据线段的性质,可得答案.【解答】解:从A地去往B地,打开导航、显示两地距离为37.7km,理由是两点之间线段最短,故选:A.【点评】本题考查了线段的性质,熟记线段的性质并应用是解题的关键.6.(2020•温州)如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA 的延长线于点D.若⊙O的半径为1,则BD的长为()A.1B.2C.D.【考点】切线的性质;菱形的性质;圆周角定理.【专题】与圆有关的位置关系;推理能力.【分析】连接OB,根据菱形的性质得到OA=AB,求得∠AOB=60°,根据切线的性质得到∠DBO=90°,解直角三角形即可得到结论.【解答】解:连接OB,∵四边形OABC是菱形,∴OA=AB,∵OA=OB,∴OA=AB=OB,∴∠AOB=60°,∵BD是⊙O的切线,∴∠DBO=90°,∵OB=1,∴BD=OB=,故选:D.【点评】本题考查了切线的性质,菱形的性质,等边三角形的判定和性质,解直角三角形,熟练正确切线的性质定理是解题的关键.7.(2021•绍兴)数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形纵向排列放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是()A.用3个相同的菱形放置,最多能得到6个菱形B.用4个相同的菱形放置,最多能得到16个菱形C.用5个相同的菱形放置,最多能得到27个菱形D.用6个相同的菱形放置,最多能得到41个菱形【考点】菱形的判定与性质.【专题】矩形菱形正方形;几何直观.【分析】根据题意画出图形,从图形中找到出现的菱形的个数即可.【解答】解:如图所示,用2个相同的菱形放置,最多能得到3个菱形;用3个相同的菱形放置,最多能得到8个菱形,用4个相同的菱形放置,最多能得到16个菱形,用5个相同的菱形放置,最多能得到29个菱形,用6个相同的菱形放置,最多能得到47个菱形.故选:B.【点评】本题主要考查菱形在实际生活中的应用,解题的关键是根据题意画出图形并熟练掌握菱形的判定.8.(2020•金华)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连接EG,BD相交于点O,BD与HC相交于点P.若GO=GP,则的值是()A.1+B.2+C.5﹣D.【考点】勾股定理的证明.【专题】计算题;等腰三角形与直角三角形;运算能力;推理能力.【分析】证明△BPG≌△BCG(ASA),得出PG=CG.设OG=PG=CG=x,则EG=2x,FG=x,由勾股定理得出BC2=(4+2)x2,则可得出答案.【解答】解:∵四边形EFGH为正方形,∴∠EGH=45°,∠FGH=90°,∵OG=GP,∴∠GOP=∠OPG=67.5°,∴∠PBG=22.5°,又∵∠DBC=45°,∴∠GBC=22.5°,∴∠PBG=∠GBC,∵∠BGP=∠BGC=90°,BG=BG,∴△BPG≌△BCG(ASA),∴PG=CG.设OG=PG=CG=x,∵O为EG,BD的交点,∴EG=2x,FG=x,∵四个全等的直角三角形拼成“赵爽弦图”,∴BF=CG=x,∴BG=x+x,∴BC2=BG2+CG2==,∴=.故选:B.【点评】本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,直角三角形的性质等知识,熟练掌握勾股定理的应用是解题的关键.9.(2020•温州)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD 为边作▱BCDE,则∠E的度数为()A.40°B.50°C.60°D.70°【考点】平行四边形的性质;等腰三角形的性质.【专题】等腰三角形与直角三角形;多边形与平行四边形;几何直观.【分析】根据等腰三角形的性质可求∠C,再根据平行四边形的性质可求∠E.【解答】解:∵在△ABC中,∠A=40°,AB=AC,∴∠C=(180°﹣40°)÷2=70°,∵四边形BCDE是平行四边形,∴∠E=70°.故选:D.【点评】考查了平行四边形的性质,等腰三角形的性质,关键是求出∠C的度数.10.(2020•衢州)过直线l外一点P作直线l的平行线,下列尺规作图中错误的是()A.B.C.D.【考点】作图—复杂作图;平行线的判定.【专题】线段、角、相交线与平行线;应用意识.【分析】根据平行线的判定方法一一判断即可.【解答】解:A、本选项作了角的平分线与等腰三角形,能得到一组内错角相等,从而可证两直线平行,故本选项不符合题意.B、本选项作了一个角等于已知角,根据同位角相等两直线平行,能判断是过点P且与直线l的平行直线,本选项不符合题意.C、由作图可知,垂直于同一条直线的两条直线平行,本选项不符合题意.D、作图只截取了两条线段相等,而无法保证两直线平行的位置关系,本选项符合题意.故选:D.【点评】本题考查作图﹣复杂作图,平行线的判定等知识,解题的关键是读懂图象信息,属于中考常考题型.11.(2020•湖州)如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是()A.DC=DT B.AD=DT C.BD=BO D.2OC=5AC【考点】全等三角形的判定与性质;等腰直角三角形;切线的性质.【专题】圆的有关概念及性质;应用意识.【分析】如图,连接OD.想办法证明选项A,B,C正确即可解决问题.【解答】解:如图,连接OD.∵OT是半径,OT⊥AB,∴DT是⊙O的切线,∵DC是⊙O的切线,∴DC=DT,故选项A正确,∵OA=OB,∠AOB=90°,∴∠A=∠B=45°,∵DC是切线,∴CD⊥OC,∴∠ACD=90°,∴∠A=∠ADC=45°,∴AC=CD=DT,∴AC=CD=DT,故选项B正确,∵OD=OD,OC=OT,DC=DT,∴△DOC≌△DOT(SSS),∴∠DOC=∠DOT,∵OA=OB,OT⊥AB,∠AOB=90°,∴∠AOT=∠BOT=45°,∴∠DOT=∠DOC=22.5°,∴∠BOD=∠ODB=67.5°,∴BO=BD,故选项C正确,根据筛选法,故选:D.【点评】本题考查切线的判定和性质,等腰直角三角形的判定和性质,全等三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.12.(2020•嘉兴)如图,在等腰△ABC中,AB=AC=2,BC=8,按下列步骤作图:①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于EF的长为半径作弧相交于点H,作射线AH;②分别以点A,B为圆心,大于AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;③以点O为圆心,线段OA长为半径作圆.则⊙O的半径为()A.2B.10C.4D.5【考点】作图—复杂作图;等腰三角形的性质;垂径定理.【专题】作图题;应用意识.【分析】如图,设OA交BC于T.解直角三角形求出AT,再在Rt△OCT中,利用勾股定理构建方程即可解决问题.【解答】解:如图,设OA交BC于T.半径为r,∵AB=AC=2,AO平分∠BAC,∴AO⊥BC,BT=TC=4,∴AT===2,在Rt△OCT中,则有r2=(r﹣2)2+42,解得r=5,故选:D.【点评】本题考查作图﹣复杂作图,等腰三角形的性质,垂径定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.13.(2021•宁波)如图是一个由5张纸片拼成的平行四边形ABCD,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张矩形纸片EFGH的面积为S3,FH与GE相交于点O.当△AEO,△BFO,△CGO,△DHO的面积相等时,下列结论一定成立的是()A.S1=S2B.S1=S3C.AB=AD D.EH=GH【考点】矩形的性质;全等三角形的判定与性质;等腰直角三角形;平行四边形的性质.【专题】图形的全等;多边形与平行四边形;矩形菱形正方形;推理能力.【分析】如图,连接DG,AH,过点O作OJ⊥DE于J.证明S△DGH=S△AEH,S△DGC=S,可得结论.△ADH【解答】解:如图,连接DG,AH,过点O作OJ⊥DE于J.∵四边形EFGH是矩形,∴OH=OF,EF=GH,∠HEF=90°,∵OJ⊥DE,∴∠OJH=∠HEF=90°,∴OJ∥EF,∵HO=OF,∴HJ=JE,∴EF=GH=2OJ,∵S△DHO=•DH•OJ,S△DHG=•DH•GH,∴S△DGH=2S△DHO,同法可证S△AEH=2S△AEO,∵S△DHO=S△AEO,∴S△DGH=S△AEH,∵S△DGC=•CG•DH,S△ADH=•DH•AE,CG=AE,∴S△DGC=S△ADH,∴S△DHC=S△ADE,∴S1=S2,故A选项符合题意;S3=HE•EF≠S1,故B选项不符合题意;AB=AD,EH=GH均不成立,故C选项,D选项不符合题意,故选:A.【点评】本题考查矩形的性质,全等三角形的判定和性质,等腰直角三角形的性质,平行四边形的性质,矩形的性质等知识,解题的关键是证明S△DGH=S△AEH,S△DGC=S△ADH.14.(2021•金华)如图,在Rt△ABC中,∠ACB=90°,以该三角形的三条边为边向外作正方形,正方形的顶点E,F,G,H,M,N都在同一个圆上.记该圆面积为S1,△ABC 面积为S2,则的值是()A.B.3πC.5πD.【考点】勾股定理;垂径定理.【专题】与圆有关的计算;推理能力.【分析】先设Rt△ABC的三边长为a,b,c,其中c为斜边,设⊙O的半径为r,根据图形找出a,b,c,r的关系,用含c的式子表示S1和S2,即可求出比值.【解答】解:如图,取AB的中点为O,AC的中点为D,连接OE,OG,OD,OC,设AB=c,AC=b,BC=a,则a2+b2=c2,①取AB的中点为O,∵△ABC是直角三角形,∴OA=OB=OC,∵圆心在MN和HG的垂直平分线上,∴O为圆心,连接OC,OG,OE,作OD⊥AC,则OG,OE为半径,由勾股定理得:,②由①②得a=b,∴,∴,,∴,故选:C.【点评】本题主要考查勾股定理的应用,关键在找到圆心,依据的知识点是直角三角形斜边上的中点等于斜边的一半,即斜边的中点为圆心,用字母表示多条边,然后找它们的关系是中考经常考的类型,平时要多加练习此类题型.二.填空题(共6小题)15.(2020•台州)如图,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是6.【考点】等边三角形的判定与性质;平行线的性质.【专题】等腰三角形与直角三角形;几何直观.【分析】根据三等分点的定义可求EF的长,再根据等边三角形的判定与性质即可求解.【解答】解:∵等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点,∴EF=2,∵△ABC是等边三角形,∴∠B=∠C=60°,又∵DE∥AB,DF∥AC,∴∠DEF=∠B=60°,∠DFE=∠C=60°,∴△DEF是等边三角形,∴剪下的△DEF的周长是2×3=6.故答案为:6.【点评】考查了等边三角形的性质,平行线的性质,关键是证明△DEF是等边三角形.16.(2020•绍兴)如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为4.【考点】正方形的性质.【专题】矩形菱形正方形;运算能力;推理能力.【分析】根据题意和图形,可以得到直角三角形的一条直角边的长和斜边的长,从而可以得到直角三角形的另一条直角边长,再根据图形,可知阴影部分的面积是四个直角三角形的面积,然后代入数据计算即可.【解答】解:由题意可得,直角三角形的斜边长为3,一条直角边长为2,故直角三角形的另一条直角边长为:=,故阴影部分的面积是:=4,故答案为:4.【点评】本题考查正方形的性质、勾股定理、三角形的面积,解答本题的关键是明确题意,利用数形结合的思想解答.17.(2020•绍兴)将两条邻边长分别为,1的矩形纸片剪成四个等腰三角形纸片(无余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的①②③④(填序号).①,②1,③﹣1,④,⑤.【考点】矩形的性质;三角形三边关系;等腰三角形的性质.【专题】矩形菱形正方形;几何直观.【分析】首先作出图形,再根据矩形的性质和等腰三角形的判定即可求解.【解答】解:如图所示:则其中一个等腰三角形的腰长可以是①,②1,③﹣1,④,不可以是.故答案为:①②③④.【点评】考查了矩形的性质,等腰三角形的判定与性质,根据题意作出图形是解题的关键.18.(2020•衢州)图1是由七根连杆链接而成的机械装置,图2是其示意图.已知O,P两点固定,连杆P A=PC=140cm,AB=BC=CQ=QA=60cm,OQ=50cm,O,P两点间距与OQ长度相等.当OQ绕点O转动时,点A,B,C的位置随之改变,点B恰好在线段MN上来回运动.当点B运动至点M或N时,点A,C重合,点P,Q,A,B在同一直线上(如图3).(1)点P到MN的距离为160cm.(2)当点P,O,A在同一直线上时,点Q到MN的距离为cm.【考点】勾股定理的应用;菱形的性质;轨迹;等腰三角形的性质.【专题】矩形菱形正方形;解直角三角形及其应用;应用意识.【分析】(1)如图3中,延长PO交MN于T,过点O作OH⊥PQ于H.解直角三角形求出PT即可.(2)如图4中,当O,P,A共线时,过Q作QH⊥PT于H.设HA=xcm.解直角三角形求出HT即可.【解答】解:(1)如图3中,延长PO交MN于T,过点O作OH⊥PQ于H.由题意:OP=OQ=50cm,PQ=P A﹣AQ=140﹣60=80(cm),PM=P A+BC=140+60=200(cm),PT⊥MN,∵OH⊥PQ,∴PH=HQ=40(cm),∵cos∠P==,∴=,∴PT=160(cm),∴点P到MN的距离为160cm,故答案为160.(2)如图4中,当O,P,A共线时,过Q作QH⊥PT于H.设HA=xcm.由题意AT=PT﹣P A=160﹣140=20(cm),OA=P A﹣OP=140﹣50=90(cm),OQ=50cm,AQ=60cm,∵QH⊥OA,∴QH2=AQ2﹣AH2=OQ2﹣OH2,∴602﹣x2=502﹣(90﹣x)2,解得x=,∴HT=AH+AT=(cm),∴点Q到MN的距离为cm.故答案为.【点评】本题考查解直角三角形的应用,等腰三角形的性质,菱形的性质等知识,解题的关键是理解题意,学会添加常用辅助线,构造直角三角形解决问题,学会利用参数构建方程解决问题.19.(2019•绍兴)把边长为2的正方形纸片ABCD分割成如图的四块,其中点O为正方形的中心,点E,F分别为AB,AD的中点.用这四块纸片拼成与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠无缝隙),则四边形MNPQ的周长是6+2或10或8+2.【考点】平面镶嵌(密铺);整式的加减.【专题】整式.【分析】先根据题意画出图形,再根据周长的定义即可求解.【解答】解:如图所示:图1的周长为1+2+3+2=6+2;图2的周长为1+4+1+4=10;图3的周长为3+5++=8+2.故四边形MNPQ的周长是6+2或10或8+2.故答案为:6+2或10或8+2.【点评】考查了平面镶嵌(密铺),关键是得到与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠无缝隙)的各种情况.20.(2019•湖州)七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”.由边长为4的正方形ABCD可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型(其中点Q、R分别与图2中的点E、G重合,点P 在边EH上),则“拼搏兔”所在正方形EFGH的边长是4.【考点】七巧板.【专题】图表型;矩形菱形正方形.【分析】如图2中,连接EG,GM⊥EN交EN的延长线于M,利用勾股定理解决问题即可.【解答】解:如图2中,连接EG,作GM⊥EN交EN的延长线于M.在Rt△EMG中,∵GM=4,EM=2+2+4+4=12,∴EG===4,∴EH==4,解法二:如图,连接EG交MN于点O.由题意,EN=MN=4,GM=8,∵∠EON=∠GOM,∠N=∠M=90°,∴△EON∽△GOM,∴==,∴ON=MN=,∴OE==,OG=2OE=,∴GF=EG=(OE+OG)=4.故答案为4.【点评】本题考查正方形的性质,七巧板,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.三.解答题(共2小题)21.(2020•台州)如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M.E是线段CM上的点,连接BE.F是△BDE的外接圆与AD的另一个交点,连接EF,BF.(1)求证:△BEF是直角三角形;(2)求证:△BEF∽△BCA;(3)当AB=6,BC=m时,在线段CM上存在点E,使得EF和AB互相平分,求m的值.【考点】圆的综合题.【专题】几何综合题;应用意识.【分析】(1)想办法证明∠BEF=90°即可解决问题(也可以利用圆内接四边形的性质直接证明).(2)根据两角对应相等两三角形相似证明.(3)证明四边形AFBE是平行四边形,推出FJ=BD=,EF=m,由△ABC∽△CBM,可得BM=,由△BEJ∽△BME,可得BE=,由△BEF∽△BCA,推出=,由此构建方程求解即可.【解答】(1)证明:∵∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,∴∠ADB=∠ACB=90°,∵∠EFB=∠EDB,∠EBF=∠EDF,∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,∴∠BEF=90°,∴△BEF是直角三角形.(2)证明:∵BC=BD,∴∠BDC=∠BCD,∵∠EFB=∠EDB,∴∠EFB=∠BCD,∵AC=AD,BC=BD,∴AB⊥CD,∴∠AMC=90°,∵∠BCD+∠ACD=∠ACD+∠CAB=90°,∴∠BCD=∠CAB,∴∠BFE=∠CAB,∵∠ACB=∠FEB=90°,∴△BEF∽△BCA.(3)解:设EF交AB于J.连接AE.∵EF与AB互相平分,∴四边形AFBE是平行四边形,∴∠EF A=∠FEB=90°,即EF⊥AD,∵BD⊥AD,∴EF∥BD,∵AJ=JB,∴AF=DF,∴FJ=BD=,∴EF=m,∵△ABC∽△CBM,∴BC:MB=AB:BC,∴BM=,∵△BEJ∽△BME,∴BE:BM=BJ:BE,∴BE=,∵△BEF∽△BCA,∴=,即=,解得m=2(负根已经舍弃).【点评】本题属于圆综合题,考查了圆周角定理,相似三角形的判定和性质平行四边形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考压轴题.22.(2020•衢州)【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.(1)判断△AFG的形状并说明理由.(2)求证:BF=2OG.【迁移应用】(3)记△DGO的面积为S1,△DBF的面积为S2,当=时,求的值.【拓展延伸】(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连接EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.【考点】四边形综合题.【专题】几何综合题;应用意识.【分析】(1)如图1中,△AFG是等腰三角形.利用全等三角形的性质证明即可.(2)如图2中,过点O作OL∥AB交DF于L,则∠AFG=∠OLG.首先证明OG=OL,再证明BF=2OL即可解决问题.(3)如图3中,过点D作DK⊥AC于K,则∠DKA=∠CDA=90°,利用相似三角形的性质解决问题即可.(4)设OG=a,AG=k.分两种情形:①如图4中,连接EF,当点F在线段AB上时,点G在OA上.②如图5中,当点F在AB的延长线上时,点G在线段OC上,连接EF.分别求解即可解决问题.【解答】(1)解:如图1中,△AFG是等腰三角形.理由:∵AE平分∠BAC,∴∠1=∠2,∵DF⊥AE,∴∠AHF=∠AHG=90°,∵AH=AH,∴△AHF≌△AHG(ASA),∴AF=AG,∴△AFG是等腰三角形.(2)证明:如图2中,过点O作OL∥AB交DF于L,则∠AFG=∠OLG.∵AF=AG,∴∠AFG=∠AGF,∵∠AGF=∠OGL,∴∠OGL=∠OLG,∴OG=OL,∵OL∥AB,∴△DLO∽△DFB,∴=,∵四边形ABCD是矩形,∴BD=2OD,∴BF=2OL,∴BF=2OG.(3)解:如图3中,过点D作DK⊥AC于K,则∠DKA=∠CDA=90°,∵∠DAK=∠CAD,∴△ADK∽△ACD,∴=,∵S1=•OG•DK,S2=•BF•AD,又∵BF=2OG,=,∴==,设CD=2x,AC=3x,则AD=x,∴==.(4)解:设OG=a,AG=k.①如图4中,连接EF,当点F在线段AB上时,点G在OA上.∵AF=AG,BF=2OG,∴AF=AG=k,BF=2a,∴AB=k+2a,AC=2(k+a),∴AD2=AC2﹣CD2=[2(k+a)]2﹣(k+2a)2=3k2+4ka,∵∠ABE=∠DAF=90°,∠BAE=∠ADF,∴△ABE∽△DAF,∴=,即=,∴=,∴BE=,由题意:10××2a×=AD•(k+2a),∴AD2=10ka,即10ka=3k2+4ka,∴k=2a,∴AD=2a,∴BE==a,AB=4a,∴tan∠BAE==.②如图5中,当点F在AB的延长线上时,点G在线段OC上,连接EF.∵AF=AG,BF=2OG,∴AF=AG=k,BF=2a,∴AB=k﹣2a,AC=2(k﹣a),∴AD2=AC2﹣CD2=[2(k﹣a)]2﹣(k﹣2a)2=3k2﹣4ka,∵∠ABE=∠DAF=90°,∠BAE=∠ADF,∴△ABE∽△DAF,∴=,即=,∴=,∴BE=,由题意:10××2a×=AD•(k﹣2a),∴AD2=10ka,即10ka=3k2﹣4ka,∴k=a,∴AD=a,∴BE==a,AB=a,∴tan∠BAE==,综上所述,tan∠BAE的值为或.【点评】本题属于四边形综合题,考查了矩形的性质,全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知a, b, c是厶ABC的三条边长,化简|a+b-c|-|c-a-b| 的结果为(【答案】D【答案】C.4. (2017湖南长沙第5题)一个三角形三个内角的度数之比为1: 2:A.锐角三角形B •直角三角形C •钝角三角形 D •等腰直角三角形【答案】B5.(2017 山东滨州第8题)如图,在厶ABC中,AB= AC D为BC上一点,且DA= DC BD= BA,则/ B的大小为(、选择题专题09三角形A. 2a+2b-2c B . 2a+2b C. 2c D.1. (2017甘肃庆阳第8题)2. (2017浙江嘉兴第2题)长度分别为7 , x的三条线段能组成一个三角形,x的值可以是()A. 4B. 5C.D.3. (2017天津第11题)如图,在ABC中, AB AC , AD,CE 是ABC的两条中线,P是AD上一个动点,AC3,则这个三角形- —定是B. 36°C. 80°D. 25°【答案】B.6. (2017山东滨州第11题)如图,点P为定角/ AOB的平分线上的一个定点,且/ MPN WZ AOB互补.若/ MPN在绕点P旋转的过程中,其两边分别与OA OB相交于M N两点,则以下结论:(1)PM= PN恒成立,(2)OW ON的值不变,(3)四边形PMO的面积不变,(4)MN的长不变,其中正确的个数为(A. 4B. 3C. 2D. 1【答案】B.EP最小值的是(C. AD DA. 40°M【答案】B.【薛析】如虱过点p作PC #£ AO于点G FD垂直BO于点D根IS角平分线的性质可得POPD,因N AOB ^ZMPN互补,可得Z'lPWZCPD即可得ZMPC=ZDPN,即可判走^CMP^NDP,所以PM=PN J(1)正确』由iCMP^iNDP可得CM-CN,所OM-OX=2OC, (2)正确」四边形PMON的面积等于四边形?COD 的面积,(3)正确!连待CD,ElPCXPD,PKI-PNj ZMPN-ZCPD, PM>PC;可得CD^XIX;所以(4)错误,故选B.Ur* 11 ■阳J7. (2017山东荷泽第5题)如图,将Rt ABC绕直角顶点C顺时针旋转90°,得到A'B'C,连接AA',若1 25°, 则BAA'的度数是()A. 55°B . 60° C. 65°D . 70°8. (2017浙江金华第3题)下列各组数中,不可能成为一个三角形三边长的是()A. 2,3, 4 B . 5,7,7 C . 5,6,12 D . 6,8,10【答案】C.9. (2017浙江省台州市)如图,点P是/ AOB平分线OC上一点,PD丄OB垂足为D,若PD=2,则点P到边OA的距离是()ABC AB=AC 若以点B 为圆心,BC 长为半径画弧,交腰 AC 于点Rt △ ABC 中,Z C=90,以顶点 A 为圆心,适当长为半径画弧,分别交AC, AB大于IM N 的长为半径画弧,两弧交于点P,作射线AP 交边BC 于点D,若CD=42ABC 中, AB > AC, / CAD ^^ ABC 的外角,观察图中尺规作图的痕迹,则下列结论错1B 和点D 为圆心,大于 丄BD 的长为半径作弧,两弧相交于点2A. 2B. 3 D. 4【答案】A.E ,则下列结论一定正确的是( / EBC=z BACA. AE=ECB. AE=BEC.D.Z EBC=z ABE【答案】C.AB=15,则厶ABD 的面积是( A. 15 B. 30CC.【答案】B误的是( ) A.Z DAE 玄 B B ./ EAC=/ CD.Z DAE=/ EAC【答案】D. 13 . (2017湖北省襄阳市)如图,在△ ABC 中,Z ACB=90 , Z A=30° , BC=4以点 C 为圆心,CB 长为半径作弧,则AF 的长为()10.(2017浙江省台州市)如图,已知等腰三角形11. (2017山东省枣庄市)如图,在于点M N,再分别以点 M N 为圆心,12. (2017广西四市)如图,△交AB 于点D;再分别以点E ,作射线 CE 交AB 于点F ,45°,30°的直角三角板如图摆放, 其中 C F 900, A 45°, D 30°,等于()试题分析:T/a =Z 1 + Z D,Z3 =/ 4+Z F ,.・./a +Z3 =Z 1 + / D+Z 4+Z F=Z 2+Z D+Z 3+Z F=Z 2+Z3+30° +90° =210°,故选 B.16. (2017河池第9题)三角形的下列线段中,能将三角形分成面积相等的两部分是()A.中线 B.角平分线C. 高 D .中位线【答案】A.A. 5B. 6 【答案】B. 【答案】B.150°14. ( 2017湖南株洲第5题)如图, C. 在厶ABC 中,/ BAC=x ,/ B=2x°,Z C=3x°,则/ BAD=( C. 155° D. 160°15. (2017郴州第8题)小明把一副A. 1800B . 2100C .360°D. 2700【解析】二、填空题1. (2017湖南怀化第15题)如图,AC=DC , BC=EC,请你添加一个适当的条件:_________________________________ ,使得△ ABC ◎△ DEC .【答案】CE=BC本题答案不唯一.2. (2017江苏盐城第12题)在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则【答案】120°3. (2017贵州黔东南州第12题)如图,点B、F、C E在一条直线上,已知FB=CE AC// DF,请你添加一个适当的条件________使得△ ABC^^ DEF【答案】/ A=Z D.4. (2017新疆建设兵团第15题)如图,在四边形ABCD中, AB=AD CB=CD对角线AC, BD相交于点O,下列结论中:①/ ABC d ADC②AC与BD相互平分;③AC BD分别平分四边形ABCD的两组对角;④四边形ABCD的面积1S=—AC?BD正确的是__________ (填写所有正确结论的序号)5._________________________________________________________________________________________________ (2017四川省达州市)△ ABC中,AB=5, AC=3 AD是厶ABC的中线,设AD长为m则m的取值范围是 _______________________【答案】1< m< 4.顶角的度数为【答案】30°或150°或90°..【解析】试题分析:①BC为腰,1•/ AD L BC于点D, AD=—BC, ACD=30 ,2如图1,人。
在厶ABC内部时,顶角/ C=30 , 如图2,人。
在厶ABC外部时,顶角/ ACB=180 - 30° =150°②BC为底,如图3,1•/ ADL BC 于点D, AD=—BC, • AD=BD=CD「./ B=Z BAD,2CD与AB之间的关系,并证明你的结论.2. (2017四川泸州第18题)如图,点A F、C、D在同一条直线上,已知AF=DC / A=/ D, BC// EF,求证:AB=DE3. (2017四川宜宾第18题)如图,已知点B E、C、F在同一条直线上,AB=DE / A=/ D, AC// DF.求证:BE=CF6. (2017黑龙江绥化第20题)在等腰ABC中,AD1BC交直线BC于点D,若AD - BC,贝V ABC的2/ C=Z CAD BAD/ CAD= 1X 180° =90°,21. 18题)如图,点C,F,E,B在一条直线上, CFD BEA, CE BF,DF AE •写出•••顶角/BAC=90 ,(2017湖北武汉第S3(2)用等式表示线段 MB 与PQ 之间的数量关系,并证明【答案】(1)【解析】分析: ⑴由直角三角形性质,两锐角互余,可得/ AMQ=18° -Z AHM - / PAM,解得/ AMQ=4° + .(2)由题意得AP=AQ=QM 再证RT ^AP 笑RT ^QME ,全等三角形对应边相等得出 PC=ME 得出△ MEB 为等腰直角三角形,贝U PQ= 2 BM. 本题解析:(1) Z AMQ=4° +.理由如下:4. (2017北京第19题)如图,在 ABC 中,AB AC,A 36° , BD 平分 ABC 交AC 于点D .求证:AD BC .2. (2017北京第28题)在等腰直角 ABC 中,ACB 900,P 是线段BC 上一动点(与点B 、C 不重合),连接 AP ,延长BC 至点Q ,使得CQ CP ,过点Q 作QHAP 于点H ,交AB 于点M .(1)若 PAC ,求 AMQ 的大小(用含的式子表示)•••/ PAC= , △ ACB是等腰直角三角形,•••/ PAB= 45°—,/ AHM=90 , A / AMQ=18°0 -Z AHM- / PAM= 45° +⑵线段MB与PQ之间的数量关系:PQ= 2 MB.理由如下:连接AQ过点M做ME I QB•/ ACLQP,CQ=CP/-Z QAC Z P AC= , •/ QAM= +45° =Z AMQ, • AP=AQ=QM; RT A APC和RT A QME MQE PAC中,ACP QEM •- RT A APC^ RT A QME, • PC=ME,「.A MEB 是等腰直角三角形,• 1PQ2MB,2 2AP QM• PQ= 2 MB.考点:全等三角形判定,等腰三角形性质5. (2017福建第19题)如图,ABC中,BAC 90o, AD BC,垂足为D •求作ABC的平分线,分别交AD.AC于P , Q两点;并证明AP AQ •(要求:尺规作图,保留作图痕迹,不写作法)【解析】试题分析;按作圉方法作出角平分线BQ,然后通过制用互为余角叹及等角的余角相等得到上肝沪么峻F, 从而证得AP=AQ.试题解析二作團如下,BQ就罡所求作的ZABC的平分线,Px Q就是所求作的点"证明如下:丁心丄BC, .\ZADB=90c, .\Z3FD+ZFBD=90P」/Z0AC=9O°, .\ZAQP+ZAEQ=90°, _._Z求证:ADF BCE .B, AE BF .【答案】作图见解析;证明见解析AE(i=ZPBD,二ZBPD二:ZEPD=Z:APQ, .'-ZAPO=Z AQP, ;.AP=AQ.和 D 相交于点 • (1)求证:C 也D ;(2)若 1 42°,求D 的度数.【答案】(1详见解析;(2) BDE 69°试题分析:先将AE BF 转化为AF = BE 再利用SAS 证明两个三角形全等试题解析:证明:因为 AE = BF ,所以,AE + EF = BF + EF ,即卩 AF = BEAD BCABAF BE所以, ADFBCE14. (2017四川泸州第18题)如图,点A,F,C,D 在同一直线上,已知 AF DC, A D,BC//EF ,.求证:AB DE .20.24题)(本题满分8分)如图,,点D 在 C 边上,1【解析】在厶ADF 和厶BCE 中,(2017江苏苏州第09 三角形【解析】试题分析:(1)用ASA证明两三角形全等;(2)利用全等三角形的性质得出EC ED, C BDE,再利用等边对等角求解即可•试题解析:⑴证明:Q AE和BD相交于点O, AOD BOE .在AOD和BOE中,A B, BEO 2.又Q 1 2, 1 BEO, AEC BED .在AEC和BED 中,A BAE BE , AEC BED ASA .AEC BED(2)Q AEC BED, EC ED, C BDE .在EDC 中,Q EC ED, 1 42°, C EDC 69°,BDE C 69°.考点:全等三角形的判定与性质43. (2017四川省南充市)如图,DE I AB CF丄AB 垂足分别是点E、F, DE=CF AE=BF求证:AC// BD58. (2017广东省)如图,在△ ABC中,/ A>Z B.(1)作边AB的垂直平分线DE,与AB, BC分别相交于点D, E (用尺规作图,保留作图痕迹,不要求写作法)(2)在(1)的条件下,连接AE若/ B=50°,求/ AEC的度数.【答案】(1)作图见见解析;(2)100°.【解析】试题分析:(1)根据题意作出图形即可;(2)由于DE是AB的垂直平分线,得到AE=BE根据等腰三角形的性质得到/ EAB2 B=50°,由三角形的外角的性质即可得到结论.09 三角形试题解析:(1)如图所示;(2)T DE是AB 的垂直平分线,••• AE=BE「・/ EAB2 B=50°,二/ AEC d EAB+Z B=100°5考点:1 •作图一基本作图;2 •线段垂直平分线的性质.63. (2017江苏省连云港市)如图,已知等腰三角形ABC中,AB=AC点D E分别在边AB. AC上,且AD=AE连接BE、CD交于点F.(1)判断/ ABE与/ ACD的数量关系,并说明理由;(2)求证:过点A F的直线垂直平分线段【答案】(1)Z ABE Z ACD (2)证明见解析.【解析】试题分析:(1)证得△ ABE^A ACD后利用全等三角形的对应角相等即可证得结论;(2)利用垂直平分线段的性质即可证得结论.试题解析:(1)Z ABE Z ACD在厶ABE 和厶ACD 中,T AB=AC Z A=Z A, AE=AD「.A ABE^A ACD •/ ABE Z ACDA、F均在(2)T AB=AC^Z ABC Z ACB 由(1)可知/ ABE Z ACD •/ FBC Z FCB • FB=FC T AB=AC •点线段BC的垂直平分线上,即直线AF垂直平分线段BC.考点:1.等腰三角形的性质;2.线段垂直平分线的性质; 3 .探究型.3. (2017郴州第19题)已知ABC中,ABC ACB ,点D, E分别为边AB, AC的中点,求证: BE CD .【答案】详见解析【解析】试题分析:由/ ABC d ACB可得AB=AC又点D E分别是AB AC的中点.得到AD=AE通过△ ABE^A ACD即可得到结果.证明! '.'Z ABC^Z ACB,T点臥E分别是皿AC的中点...AD=AE7在△血旺^A ACD中J=10 = ALjdC = AS/.AAaE^AACD,.'.BE=CD.考点:全等三角形的判定及性质•9. (2017哈尔滨第24题)已知:△ ACB和厶DCE都是等腰直角三角形,Z ACB = Z DCE =90°,连接AE , BD交于点O , AE与DC交于点M , BD与AC交于点N •(1)如图1,求证:AE= BD ;⑵如图2,若AC = DC,在不添加任何辅助线的情况下,请直接写出图【答案】(1)证明见解析;(2)A ACB^A DCE( SAS, △ EMC^A BCN( ASA), △ AON^A DO( AAS, △ AOB^A DOE2中四对全等的直角三角形(HL )【解析】试题分析:(1)根抿全等三角形的判定(SAS)证明"236 从而可扣AEFR(2)根据条件判断出圉中的全等直角三角形8卩可i试题解析:(i> '-'Aflca 和△DCE 都是等腰直吊三角形,Z ACS =Z DCE =90° , ;.AC =BC J DC =EG/. Z ACE +Z ACD = Z DCE 十 Z MD 八:Z BCD =Z ACI ,rAC = BC在厶 ACE ^AECD 中,£ACE~ ZB CD , .'.AACE^ABCD (SAS); .'.AE=BD ;CE^CDk.⑵ 二曲H 片EOCB F A ACB ^A DCE 〔弘S ”宙(I > 可知:Z AEC =Z BDC , Z EA ^Z DB C J /^Z DOH ^O * ,'.■ Z AEC =Z CAE = Z CBD , .\A EMC ^A ECN 辄站力/.CM=CN ;「•珊AA J ON^ADOM <MS ); \'DE=AB ? A0=D0』.\A^OB^ADOE <HL )考点:1.全等三角形的判定与性质;2.等腰直角三角形.10.(2017黑龙江齐齐哈尔第 23题)如图,在 ABC 中,AD BC 于D , BD AD , DG DC , E , F 分10,求EF 的长.【答案】(1)证明见解析;⑵EF=5.2别是BG ,AC 的中点.DF ;(2)连接EF ,若AC【解析】试题分析二(1)证明△⑪倉ZUDC.丰Rfe全等三角形的性质、直角三角形的性质证明;(2)根据直角三甬形的性J厉分别松tDE、D眄根据勾股定理计算P卩可.'BD二AD试题解析二(1) '/AD丄BC…:乂心氏厶血2=00冬;在△耽空和AADC中」ABDG = ZADC r\DG=DC/.A BDG^A ADC,.\BG^AC?Z EGD=Z C^■/ZAL0=ZWK=9O4J E, F 分别杲EG* 忆的中点/.DE=|D G^EG J DF^ - AC=AF,土£,'.DE=DF;ZErG=ZEGD, NlTA 乙理S ;.ZEDG+Zm=9O0,二DE丄DD⑵'/AC^O, .■-DE=D^5?由勾股是理得,E吐磁)尸十劝S专血.考点:1.全等三角形的判定与性质; 2.勾股定理.11. (2017湖北孝感第18题)如图,已知AB CD,AE BD,CF BD ,垂足分别为E,F,BF DE.求证AB PCD.【答案】证明见解析【解析】试题分析:根据全等三角形的判定与性质,可得/ B=Z D,根据平行线的判定,可得答案.试题解析:••• AE± BD CF丄BD •••/AEB2 CFD=90 ,•/ BF=DE「・BF+EF=DE+EF「. BE=DF亠AB CD在Rt△ AFB 和Rt△ CFD 中,,• Rt △AFB^ Rt △CFD( HL), •/ B=Z D,「. AB// CDBE DF考点:全等三角形的判定与性质。
