盘点几何中的著名定理
几何常用定理

1. 勾股定理(毕达哥拉斯定理)2. 射影定理(欧几里得定理)在Rt △ABC 中,∠ACB=90°,CD 是斜边AB 上的高,则有射影定理如下:①CD 2=AD ·DB;②BC 2=BD ·BA;③AC 2=AD ·AB;④AC ·BC=AB ·CD (等积式,可用面积来证明)。
3. 三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分。
4. 四边形两边中点的连线和两条对角线中点的连线交于一点。
5. 间隔的连接六边形的边的中点所做出的两个三角形的重心是重合的。
6. 三角形各边的垂直平分线交于一点。
三角形五心重心定义:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍。
该点叫做三角形的重心。
外心定义:三角形的三边的垂直平分线交于一点。
该点叫做三角形的外心。
垂心定义:三角形的三条高交于一点。
该点叫做三角形的垂心。
内心定义:三角形的三内角平分线交于一点。
该点叫做三角形的内心。
旁心定义:三角形一内角平分线和另外两顶点处的外角平分线交于一点。
该点叫做三角形的旁心。
三角形有三个旁心。
三角形的内心和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外接三角形。
三角形的三条内角平分线有一个且只有一个交点,这个交点到三角形三边的距离相等,就是三角形的内心 三角形有且只有一个内切圆。
内切圆的半径公式: ()()()s a s b s c r s−−−=(s 为三角形周长的一半)三角形的外心经过三角形各顶点的圆叫做三角形的外接圆.外接圆的圆心叫做三角形的外心,这个三角形叫做这个圆的内接三角形。
三角形三边的垂直平分线有一个且只有一个交点,这个交点到三角形三个顶点的距离相等,就是三角形的外心三角形有且只有一个外接圆。
设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL。
数学著名定理完整版

数学著名定理1、几何中的着名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)ss为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
盘点几何中的著名定理

盘点几何中的著名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:$r=sqrt{[(s-a)(s-b)(s-c)]/s}$s为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有$AB^2+AC^2=2(AP^2+BP^2)$16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有$nxxAB^2+mxxAC^2=(m+n)AP^2+(mn)/(m+n)BC^2$17、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD 18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n (值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有$ABxxCD+ADxxBC=ACxxBD$,推广对于一般的四边形ABCD,则有$ABxxCD+ADxxBC=ACxxBD$20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
一些有名的几何定理

取材自维基百科-中文版. 没事的时候大家可以证着玩! 答案在这里.1. 阿基M德中点定理说明:圆上有两点A,B,M为弧AB的中点,随意选圆上的一点C,D为AC上的点使得MD垂直AC。
若M、C在弦AB异侧,则AD=DC+BC;若M、C在弦AB同侧,则AD=DC-CB。
b5E2RGbCAP2. 婆罗摩笈多定理指出:若圆内接四边形的对角线相互垂直,则垂直于一边且过对角线交点的直线将平分对边。
婆罗摩笈多是印度数学家。
p1EanqFDPw3. 凡·奥贝尔定理<van Aubel's theorem)说明:给定一个四边形,在其边外侧构造一个正方形。
将相对的正方形的中心连起,得出两条线段。
线段的长度相等且垂直。
DXDiTa9E3d4. 芬斯勒–哈德维格尔定理<Finsler-Hadwiger Theorem)说明:若两个正方形ABCD和AB'C'D'拥有同一个顶点A。
B'D的中点、BD'的中点、ABCD的中心和AB'C'D'的中心将组成一个正方形。
RTCrpUDGiT5. 莫雷角三分线定理<Morley's theorem)说明对所有的三角形,其三个内角作角三分线,靠近公共边三分线的三个交点,是一个等边三角形。
此定理由法兰克·莫雷在1899年发现。
对外角作外角三分线,也会有类似的性质,可以再作出4个等边三角形。
5PCzVD7HxA此定理有趣的地方是我们没办法用尺规作图作出其等边三角形,因为已经证明出尺规做图无法做出三等分角。
6. 拿破仑定理,是拿破仑发现的平面几何学定理:“以三角形各边为边分别向外侧作等边三角形,则他们的中心构成一个等边三角形。
”该等边三角形称为拿破仑三角形。
如果向内作三角形,结论同样成立。
jLBHrnAILg同时拿破仑留下这样的名言:''一个国家只有数学蓬勃发展,才能表现他的国力强大。
几何中的著名定理大全
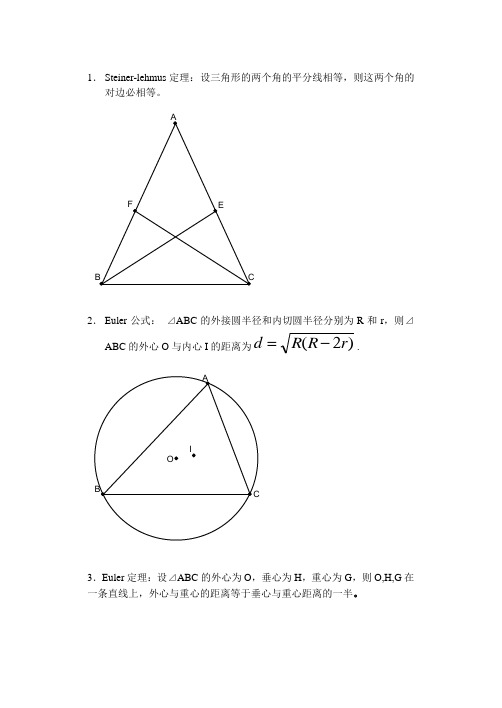
1.Steiner-lehmus定理:设三角形的两个角的平分线相等,则这两个角的对边必相等。
2.Euler公式:⊿ABC的外接圆半径和内切圆半径分别为R和r,则⊿ABC的外心O与内心I的距离为)2(rRRd-=.3.Euler定理:设⊿ABC的外心为O,垂心为H,重心为G,则O,H,G在一条直线上,外心与重心的距离等于垂心与重心距离的一半。
4.九点圆(Euler圆Feuerbach圆)定理:在⊿ABC中,三边的中点,从三顶点向三边做垂线所得垂足,三个顶点与垂心连线的中点,这九个点共圆。
4.已知非等腰锐角三角形ABC的外心、内心和垂心分别是O、I、H,∠A,若三角形ABC的三条高线分别是AD、BE、CF,则三角60=形OIH 的外接圆半径与三角形DEF 的外接圆半径之比为 .5. Euler 定理2:四边形ABCD 两对角线AC,BD 的中点分别是M,N,则22222224MN BD AC DA CD BC AB ++=+++6.Carnot 定理:设G 为⊿ABC 的重心,P 为⊿ABC 所在平面上任意一点,则)(313322222222222c b a PG PG GC GB GA PC PB PA +++=+++=++,其中后一等式为Leibnitz 公式。
6. 张角公式:已知⊿ABC 之BC 边上一点D ,设∠BAD=α,∠DAC=β,则.ABAC AD βαβαsin sin )sin(+=+7.Newton定理:设⊙O的外切四边形ABCD的对角线AC,BD的中点分别为E,F,则E,O,F共线。
8.Newton线定理:任意四边形的两条对角线的中点,两组对边延长线交点所构成的线段的中点,这三点在一条直线上。
BH10.Ptolemy 定理:圆内接四边形ABCD 的两组对边乘积的和等于他对角线的乘积。
BD AC BC AD CD AB⋅=⋅+⋅11.Morley 定理:⊿ABC 的各角的三等分线交点做成⊿DEF,则⊿DEF 是正三角形.AC12.Stewart 定理:⊿ABC 的边BC 上任取一点D,若BD=u,DC=v,AD=t,则uv av c u b t -+=222.D13.Ceva 定理:在⊿ABC 内任取一点P,直线AP,BP,CP 分别与边BC,CA,AB 相交于D,E,F,则1=⋅⋅FBAFEA CE DC BD ,其中点P 称为⊿ABC 的西瓦点. Ceva -1定理:在⊿ABC 的边BC,CA,AB 上分别取点D,E,F,如果1=⋅⋅FBAFEA CE DC BD ,那么直线AD,BE,CF 相交于一点.D14.Menelaus 定理:一直线与⊿ABC 的三边BC,CA,AB 或延长线分别交于X,Y ,Z,则1=⋅⋅YACYXC BX ZB AZ ,其中直线XYZ 称为⊿ABC 的Menelaus 线. Menelaus -1定理:X,Y,Z 分别是⊿ABC 的三边BC,CA,AB 上或其延长线上的三点,如果1=⋅⋅YACYXC BX ZB AZ ,那么X,Y,Z 三点共线. C15.Desargues 定理:在⊿ABC 和⊿A ’B ’C ’中若AA ’,BB ’,CC ’相交于一点S,则BC 与B ’C ’,CA 与C ’A ’,AB 与A ’B ’的交点D,E,F 三点共线.16.Pascal 定理:设圆内接六边形ABCDEF 的对边的延长线相交于三点X,Y ,Z,则这三点在一条直线上.17.Pappus 定理:有相异两直线l,m,若在l 上依次有A,E,C 三点,在m 上依次有D,B,F 三点,且AB 和DE 的交点为P;BC 和EF 的交点为Q;CD 和FA 的交点为R,则P,Q,R 三点共线.18.Simson 定理:从一点向三角形的各边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上.此直线称为此点关于三角形的.Simson 线.19.清宫定理:设P,Q,为三角形ABC 外接圆上异于A,B,C 的两点,P 点关于三边BC,CA,AB 的对称点分别为U,V ,W,若QU,QV ,QW 和边BC,CA,AB 或其延长线的交点分别为D,E,F,则D,E,F 三点在同一直线上.F20.欧拉Euler 关于垂足三角形的面积公式:P 是⊿ABC 所在平面上任意一点,过P 向⊿ABC 的三边做垂线,垂足分别是A 1,B 1,C 1,若OP=d,则ABC C B A S Rd R S 2221114-=,其中O 是⊿ABC 的外心,R 为其半径.21.Opiel 奥倍儿定理:通过三角形ABC 的顶点A,B,C 引三条互相平行的直线,设他们和三角形ABC 的外接圆的交点分别为A1,B1,C1,在三角形ABC 的外接圆周上取一点P,设PA1,PB1,PC1与三角形的三边BC,CA,AB 或其延长线的交点分别为D,E,F,则D,E,F22.Steiner (斯坦纳)定理:设三角形为P,则P 关于三角形ABC A 1CEP23 Steiner(斯坦纳)定理2:若P为三角形ABC内任意一点,作PD垂直于BC,交BC于D,PE垂直于CA,交CA于E,PF垂直于AB,交AB于F,则AF2+BD2+CE2=AE2+CD2+BF2.24.Weitzenbock外森皮克不等式:⊿ABC的三边分别为a,b,c,面积为S,则22c24.+≥S3a+b25.Finsler-Hadwiger定理:⊿ABC的三边分别为a,b,c,面积为S,则22)22224--a---+≥S3+b-a)()(c(abcbc26.Monge(蒙日)定理:三个圆每两个的根轴或平行或交于一点。
几何中的著名定理大全

几何中的著名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)ss为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E 的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB 分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
著名的几何定理

著名的几何定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心和各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)ss 为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
平面几何的60条著名定理

平面几何的60条著名定理一些平面几何的著名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、三角形的三条高线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s,s为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD ×BC=AC×BD20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和△DEF都是正三角形,则由线段AD、BE、CF的中心构成的三角形也是正三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
盘点几何中的著名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:$r=sqrt{[(s-a)(s-b)(s-c)]/s}$s为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有$AB^2+AC^2=2(AP^2+BP^2)$16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有$nxxAB^2+mxxAC^2=(m+n)AP^2+(mn)/(m+n)BC^2$17、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD 18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n (值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有$ABxxCD+ADxxBC=ACxxBD$,推广对于一般的四边形ABCD,则有$ABxxCD+ADxxBC=ACxxBD$20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
22、爱尔可斯定理2:若△ABC、△DEF、△GHI都是正三角形,则由三角形△ADG、△BEH、△CFI的重心构成的三角形是正三角形。
23、梅涅劳斯定理:设△ABC的三边BC、CA、AB或其延长线和一条不经过它们任一顶点的直线的交点分别为P、Q、R则有$(BP)/(PC)xx(CQ)/(QA)xx(AR)/(RB)=1$24、梅涅劳斯定理的逆定理:(略)25、梅涅劳斯定理的应用定理1:设△ABC的∠A的外角平分线交边CA于Q、∠C的平分线交边AB于R,、∠B的平分线交边CA于Q,则P、Q、R三点共线。
26、梅涅劳斯定理的应用定理2:过任意△ABC的三个顶点A、B、C作它的外接圆的切线,分别和BC、CA、AB的延长线交于点P、Q、R,则P、Q、R三点共线27、塞瓦定理:设△ABC的三个顶点A、B、C的不在三角形的边或它们的延长线上的一点S连接面成的三条直线,分别与边BC、CA、AB或它们的延长线交于点P、Q、R,则$(BP)/(PC)xx(CQ)/(QA)xx(AR)/RB()=1$.28、塞瓦定理的应用定理:设平行于△ABC的边BC的直线与两边AB、AC的交点分别是D、E,又设BE和CD交于S,则AS一定过边BC的中心M29、塞瓦定理的逆定理:(略)30、塞瓦定理的逆定理的应用定理1:三角形的三条中线交于一点31、塞瓦定理的逆定理的应用定理2:设△ABC的内切圆和边BC、CA、AB分别相切于点R、S、T,则AR、BS、CT交于一点。
32、西摩松定理:从△ABC的外接圆上任意一点P向三边BC、CA、AB或其延长线作垂线,设其垂足分别是D、E、R,则D、E、R共线,(这条直线叫西摩松线)33、西摩松定理的逆定理:(略)34、史坦纳定理:设△ABC的垂心为H,其外接圆的任意点P,这时关于△ABC的点P的西摩松线通过线段PH的中心。
35、史坦纳定理的应用定理:△ABC的外接圆上的一点P的关于边BC、CA、AB的对称点和△ABC的垂心H同在一条(与西摩松线平行的)直线上。
这条直线被叫做点P关于△ABC 的镜象线。
36、波朗杰、腾下定理:设△ABC的外接圆上的三点为P、Q、R,则P、Q、R关于△ABC的西摩松线交于一点的充要条件是:弧AP+弧BQ+弧CR$=_$0(mod2Π).37、波朗杰、腾下定理推论1:设P、Q、R为△ABC的外接圆上的三点,若P、Q、R关于△ABC的西摩松线交于一点,则A、B、C三点关于△PQR的的西摩松线交于与前相同的一点38、波朗杰、腾下定理推论2:在推论1中,三条西摩松线的交点是A、B、C、P、Q、R六点任取三点所作的三角形的垂心和其余三点所作的三角形的垂心的连线段的中点。
39、波朗杰、腾下定理推论3:考查△ABC的外接圆上的一点P的关于△ABC的西摩松线,如设QR为垂直于这条西摩松线该外接圆珠笔的弦,则三点P、Q、R的关于△ABC的西摩松线交于一点40、波朗杰、腾下定理推论4:从△ABC的顶点向边BC、CA、AB引垂线,设垂足分别是D、E、F,且设边BC、CA、AB的中点分别是L、M、N,则D、E、F、L、M、N六点在同一个圆上,这时L、M、N点关于关于△ABC的西摩松线交于一点。
41、关于西摩松线的定理1:△ABC的外接圆的两个端点P、Q关于该三角形的西摩松线互相垂直,其交点在九点圆上。
42、关于西摩松线的定理2(安宁定理):在一个圆周上有4点,以其中任三点作三角形,再作其余一点的关于该三角形的西摩松线,这些西摩松线交于一点。
43、卡诺定理:通过△ABC的外接圆的一点P,引与△ABC的三边BC、CA、AB分别成同向的等角的直线PD、PE、PF,与三边的交点分别是D、E、F,则D、E、F三点共线。
44、奥倍尔定理:通过△ABC的三个顶点引互相平行的三条直线,设它们与△ABC的外接圆的交点分别是L、M、N,在△ABC的外接圆取一点P,则PL、PM、PN与△ABC的三边BC、CA、AB或其延长线的交点分别是D、E、F,则D、E、F三点共线45、清宫定理:设P、Q为△ABC的外接圆的异于A、B、C的两点,P点的关于三边BC、CA、AB的对称点分别是U、V、W,这时,QU、QV、QW和边BC、CA、AB或其延长线的交点分别是D、E、F,则D、E、F三点共线46、他拿定理:设P、Q为关于△ABC的外接圆的一对反点,点P的关于三边BC、CA、AB的对称点分别是U、V、W,这时,如果QU、QV、QW与边BC、CA、AB或其延长线的交点分别为ED、E、F,则D、E、F三点共线。
(反点:P、Q分别为圆O 的半径OC和其延长线的两点,如果$OC^2=OQxxOP$则称P、Q 两点关于圆O互为反点)47、朗古来定理:在同一圆同上有$A_1B_1C_1D_1$4点,以其中任三点作三角形,在圆周取一点P,作P点的关于这4个三角形的西摩松线,再从P向这4条西摩松线引垂线,则四个垂足在同一条直线上。
48、从三角形各边的中点,向这条边所对的顶点处的外接圆的切线引垂线,这些垂线交于该三角形的九点圆的圆心。
49、一个圆周上有n个点,从其中任意n-1个点的重心,向该圆周的在其余一点处的切线所引的垂线都交于一点。
50、康托尔定理1:一个圆周上有n个点,从其中任意n-2个点的重心向余下两点的连线所引的垂线共点。
51、康托尔定理2:一个圆周上有A、B、C、D四点及M、N 两点,则M和N点关于四个三角形△BCD、△CDA、△DAB、△ABC中的每一个的两条西摩松的交点在同一直线上。
这条直线叫做M、N两点关于四边形ABCD的康托尔线。
52、康托尔定理3:一个圆周上有A、B、C、D四点及M、N、L三点,则M、N两点的关于四边形ABCD的康托尔线、L、N 两点的关于四边形ABCD的康托尔线、M、L两点的关于四边形ABCD的康托尔线交于一点。
这个点叫做M、N、L三点关于四边形ABCD的康托尔点。
53、康托尔定理4:一个圆周上有A、B、C、D、E五点及M、N、L三点,则M、N、L三点关于四边形BCDE、CDEA、DEAB、EABC中的每一个康托尔点在一条直线上。
这条直线叫做M、N、L三点关于五边形A、B、C、D、E的康托尔线。
54、费尔巴赫定理:三角形的九点圆与内切圆和旁切圆相切。
55、莫利定理:将三角形的三个内角三等分,靠近某边的两条三分角线相得到一个交点,则这样的三个交点可以构成一个正三角形。
这个三角形常被称作莫利正三角形。
56、牛顿定理1:四边形两条对边的延长线的交点所连线段的中点和两条对角线的中点,三点共线。
这条直线叫做这个四边形的牛顿线。
57、牛顿定理2:圆外切四边形的两条对角线的中点,及该圆的圆心,三点共线。
58、笛沙格定理1:平面上有两个三角形△ABC、△DEF,设它们的对应顶点(A和D、B和E、C和F)的连线交于一点,这时如果对应边或其延长线相交,则这三个交点共线。
59、笛沙格定理2:相异平面上有两个三角形△ABC、△DEF,设它们的对应顶点(A和D、B和E、C和F)的连线交于一点,这时如果对应边或其延长线相交,则这三个交点共线。
60、布利安松定理:连结外切于圆的六边形ABCDEF相对的顶点A和D、B和E、C和F,则这三线共点。
60、巴斯加定理:圆内接六边形ABCDEF相对的边AB和DE、BC和EF、CD和FA的(或延长线的)交点共线(。
