指数与指数幂的运算练习题
高一数学上册第二章--指数函数知识点及练习题(含答案)

课时 4 指数函数一 . 指数与指数幂的运算( 1)根式的观点①假如xna, a R, x R, n 1,且 nN ,那么 x 叫做 a 的 n 次方根. 当 n 是奇数时, a 的 n 次方根用符号 na 表示;当 n 是偶数时,正数 a 的正的 n 次方根用符号na 表示,负的 n 次方根用符号na表示; 0 的 n 次方根是 0;负数 a 没有 n 次方根.②式子 n a 叫做根式,这里 n 叫做根指数, a 叫做被开方数.当n 为奇数时, a 为随意实数;当 n 为偶数时, a.③根式的性质: (na )n a ;当 n 为奇数时, n a n a ;当 n 为偶数时, n a n | a |a (a 0) .a (a 0)( 2)分数指数幂的观点mna m (a①正数的正分数指数幂的意义是:a n 0, m,n N , 且 n 1) .0 的正分数指数幂等于0.②m(1m1 ) m( a正数的负分数指数幂的意义是:a n)n n (0, m, n N , 且 n1) .0 的负分数指aa数幂没存心义. 注意口诀: 底数取倒数,指数取相反数.( 3)分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质( 4)指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域(0,+ ∞)过定点 图象过定点(0,1 ),即当 x=0 时, y=1.奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y > 1(x > 0), y=1(x=0), 0< y < 1(x < 0)y > 1(x < 0), y=1(x=0), 0< y < 1(x > 0)变化状况a 变化对在第一象限内, a 越大图象越高,越凑近 y 轴; 在第一象限内, a 越小图象越高,越凑近 y 轴; 图象影响在第二象限内,a 越大图象越低,越凑近x 轴.在第二象限内,a 越小图象越低,越凑近x 轴.三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析: A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析: 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= [ f(x) ] nD.f [ (xy) n ] =[ f(x) ] n [ f(y) ] n (n ∈ N * )分析: 易知 A 、 B 、 C 都正确 .对于 D,f [(xy)n] =a (xy)n , 而[ f(x) ] n ·[f(y) ] n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析: a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析: 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析: 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. [ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析: 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ] ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析: 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈[ -1,1]时 ,函数 f(x)=3 x-2 的值域为 _______[ -5,1 ] ___________.3分析: f(x) 在[ -1,1 ]上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析: (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩[ 2,+ ∞]=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈[ -3,2]的最大值和最小值 .解: 设 2-x=t, 由 x ∈[ -3,2 ]得 t ∈[ 1,8 ] , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解: ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. [ 1,2]B.[ 2,3]C.(-∞ ,2]D.[ 2,+∞ )分析: 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈[ 2,+ ∞ ) 上递加 , 故所求的递加区间为[ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. [ -1,+∞ )B. [ -1,63)C.[ 0,+∞ )D.(0,63 ]分析: 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= [ f(x)-1 ]2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈[ 1,9 ].2.1 指数函数练习1.以下各式中建立的一项A . ( n)71n 7 m 7B .12 ( 3)433m3C . 4 x 3y 3( x y) 4D .393321111 1 52.化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D . 9a 2 A . 6aB . aC . 9a3.设指数函数 f ( x)a x ( a 0, a1) ,则以下等式中不正确的选项是f (x) A . f(x+y)=f(x) ·f(y)B . f ( x y )f ( y)C . f (nx)[ f ( x)]n (nQ )D . f ( xy) n [ f ( x)] n ·[f ( y)] n1 4.函数 y (x5) 0 ( x 2)2A . { x | x 5, x 2}B . { x | x 2}C . { x | x 5}D . { x | 2 x 5或 x 5}()()()(n N )( )5.若指数函数 y a x 在 [- 1,1]上的最大值与最小值的差是1,则底数 a 等于 ()A .15 B .1 5 C .15D .5 122 226.当 a0 时,函数 y axb 和 yb ax 的图象只可能是()7.函数 f ( x)2 |x| 的值域是()A . (0,1]B . (0,1)C . (0, )D . R8.函数 f ( x)2 x 1, x 0,知足 f ( x)1的 x 的取值范围1x 2 , x()A . ( 1,1)B . ( 1, )C . { x | x 0或 x2}D . { x | x 1或 x1}9.函数 y(1) x 2x2得单一递加区间是2()A .[ 1,1]B . ( , 1]C .[2,)D .[ 1,2]2exe x210.已知 f ( x)()2 ,则以下正确的选项是A .奇函数,在 R 上为增函数B .偶函数,在 R 上为增函数C .奇函数,在 R 上为减函数D .偶函数,在 R 上为减函数11.已知函数 f (x)的定义域是(1, 2),则函数 f (2 x ) 的定义域是.12.当 a >0 且 a ≠1 时,函数 f (x)=a x -2- 3 必过定点.三、解答题:13.求函数 y1的定义域 .x5 x 1114.若 a >0, b > 0,且 a+b=c ,求证: (1) 当r >1时, a r +b r < c r ; (2) 当r < 1时, a r +b r > c r .a x 1 15.已知函数 f ( x)(a >1) .a x1( 1)判断函数 f (x) 的奇偶性;( 2)证明 f (x)在 (-∞, +∞ )上是增函数 .xa16.函数 f(x) = a (a>0 ,且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2,求 a 的值.参照答案一、 DCDDD AADDA二、 11. (0,1);12. (2,- 2) ;三、 13. 解:要使函数存心义一定:x 1 0x 1x0 x 0x 1∴ 定义域为 : x xR 且 x0, x 1a rrrb r此中a1,0b114. 解:ba,c rcccc.r >1 ,a rb ra b 1,r r r当因此+b< c ;时c c c crrrrr当 r < 1 时, aba b1, 因此 a +b >c .ccc c15. 解 :(1)是奇函数 .(2) 设x <x ,则 f (x 1 )ax11 ax21 。
指数与指数幂的运算 习题(含答案)

【方法点晴】本题考查指数函数的变换,形如 的图象的作法:先做出 的图象,再将 轴下方的图象翻折到 轴上方. 的图象 的图象向下平移一个单位,再将 轴下方的图象翻折到 轴上方得到,由于底数 不确定,故应分 和 两种情况分别作图,结合图形可得最后结果.
23.4
【解析】原式 ,故答案为4.
试题解析:
(1) 原式=
(2)
.
27.(1) (2)
【解析】试题分析:
(1)根据分数指数幂的运算法则和对数的运算求解.(2)根据 求得 ,解方程组求出 后再求解.
试题解析:
(1)原式=3﹣3+(4﹣2)× = .
(2)∵sinα+cosα= ,①
∴ 1+2sinαcosα= ,
∴2sinαcosα=﹣ .
指数与指数幂的运算习题(含答案)
一、单选题
1.已知x,y为正实数,则
A.2lnx+lny=2lnx+2lnyB.2ln(x+y)=2lnx•2lny
C.2lnx•lny=2lnx+2lnyD.2ln(xy)=2lnx•2lny
2.化简 的结果为
A.−9B.7
C.−10D.9
3.若 ,且 , 为整数,则下列各式中正确的是
【解析】
【分析】
利用根式的运算法则运算即可.
【详解】
(1) ;
1) 中实数 的取值由 的奇偶性确定,只要 有意义,其值恒等于 ,即 ;
(2) 是一个恒有意义的式子,不受 的奇偶性限制, ,但 的值受 的奇偶性影响.
29.(1)89;(2) .
【解析】试题分析:指数幂运算要严格按照幂运算定义和法则运算,法则包括同底数幂相乘,底数不变,指数相加;同底数幂相除,底数不变指数相减;幂的乘方,底数不变指数相乘;积的乘方等于把积中每个因数乘方,再把所得的幂相乘;对数运算要注意利用对数运算法则,包括积、商、幂的对数运算法则,这些公式既要学会正用,还要学会反着用.
(完整版)指数与指数幂的运算习题(含答案),推荐文档

2 2 2 ⎝ ⎝ ⎭⎭指数与指数幂的运算 习题(含答案)一、单选题1.已知 x ,y 为正实数,则 A . 2lnx+lny =2lnx +2lny B . 2ln (x+y )=2lnx •2lny C . 2lnx•lny =2lnx +2lnyD . 2ln (xy )=2lnx •2lny12.化简[( ‒ 2)6]2 ‒ ( ‒ 1)0的结果为A . −9B . 7C . −10D . 93. 若 > 0,且 , 为整数,则下列各式中正确的是A . a m ÷ a n = anB . a m ⋅ a n = a mnC . () =+D . 1 ÷ a n = a 0 ‒ n4. 若 a >1,b >0,且 a b +a -b =2,则 a b -a -b 的值为( )A .B . 2 或-2C . -2D . 25.3‒ 27的值为(). A.9B. ‒ 9C.‒ 3D.3a 3x + a ‒ 3x26.若 = A . 2 ‒ 1 C . 2 + 1‒ 1,则 a x + a ‒ x 等于B . 2 ‒ 2 D . + 1log 3x , x > 0 ⎛ ⎛ 1 ⎫⎫7.已知函数 f (x )= { 2x , x ≤ 0,则 f f 9 ⎪⎪ 等于( )A . 4B . - 1 41C . -4D . 4 18.设 a = log 3,b = 20.3, c = log 2 ,则( )3A . a > b > cB . a > c > bC . c > a > b (1)9.设 y 1=40.9,y 2=80.48,y 3= 2 -1.5,则( ) A . y 3>y 1>y 2 B . y 2>y 1>y 3 C . y 1>y 2>y 3 D . y 1>y 3>y 2 10.有下列各式:D . b > a > c2 2n a n 3 x4+ y 36 (-5)2m ‒ 2n4 163 x3 x 227 - - ① = a ;②若 a ∈R ,则(a 2-a +1)0=1;4③ = x 3+ y ;④ 35 = .其中正确的个数是( ) A . 0 B . 1 C . 2D .311.化简(a 2-2+a -2)÷(a 2-a -2)的结果为( ) A . 1B . -1C .a 2 -1a 2 +1a 2 +1D .a 2 -112. 下列各式计算正确的是( )A . (-1)0=1B . 21a 2·a 2=a2 1 1 C . 43=8D . a 3÷ a - 3= a 313. 已知a m =4,a n =3,则 的值为( )2A.33B. 6 C . 2D . 2二、填空题化简 ⋅(x > 0) 的结果是.14.x ⋅ 15. 设函数 f (x ) = a x + (k -1)a -x + k 2 ( a > 0, a ≠ 1 )是定义域为 R 的奇函数.(1) 求 k 值;(2) 若 f (1) > 0 ,求使不等式 f (x 2 + x ) + f (t - 2x ) > 0 恒成立的t 的取值范围;(3)若 f (1) = 3 ,设 g (x ) = a 2x + a -2x - 2mf (x ) , g (x ) 在[1, +∞) 上的最小值为-1,2求m 的值.12⎛ 1 ⎫ - 16.计算: 83 ÷ ⎪ = .⎝ 4 ⎭ ⎛ 8 ⎫- 13 - ⎛ - 3 ⎫0+ =17. log 3 +⎝ 125 ⎪⎭ .⎝ 5 ⎪⎭2 518. (2a -3b 3 ) ⋅ (-3a -1b ) ÷ (4a -4b 3)(a > 0, b > 0) =.19.若2x + 2-x = 5 ,则8x + 8-x =.6 x23 a - 33 b- ⎛ 8 9 2 ( ‒ 8) (3) ;20. 0.064 13- - 1 ⎫0 + ⎡(-2)3 ⎤- 34 +16 ⎪ ⎣ ⎦⎝ ⎭- 34 + 0.0112 =⎛ 1 ⎫0 21. 计算: lg4 + lg25 + - ⎪ ⎝ ⎭=.22. 直线y = 2a 与函数 y = a x -1 (a > 0且a ≠ 1)的图象有且仅有两个公共点,则实数 a 的取值范围是.1 + log 12 - (0.7)0+ 0.25-1 =。
《幂的运算》练习题及答案

《幂的运算》练习题及答案幂的运算是数学中一个重要的概念,经常在代数和数论等领域出现。
本文将提供一些幂的练习题,并附上详细的答案,帮助读者加深对幂的运算规则的理解。
一、练习题1. 计算以下幂的结果:a) 2^3b) 5^2c) (-3)^4d) 10^0e) 1^1002. 化简以下幂的表达式:a) (2^3)^2b) 4^0c) (-2)^4d) (3^2)^3e) 5^13. 计算以下幂的结果,并写成最简形式:a) 2^(1/2)b) 10^(2/3)c) 8^(3/2)d) 27^(2/3)e) 16^(-1/2)二、答案解析1. 计算以下幂的结果:a) 2^3 = 2 * 2 * 2 = 8b) 5^2 = 5 * 5 = 25c) (-3)^4 = (-3) * (-3) * (-3) * (-3) = 81d) 10^0 = 1 (任何数的0次幂都等于1)e) 1^100 = 1 (任何数的1次幂都等于自身)2. 化简以下幂的表达式:a) (2^3)^2 = 2^(3*2) = 2^6 = 64b) 4^0 = 1 (任何非零数的0次幂均等于1)c) (-2)^4 = 2^4 = 16d) (3^2)^3 = 3^(2*3) = 3^6e) 5^1 = 5 (任何数的1次幂都等于自身)3. 计算以下幂的结果,并写成最简形式:a) 2^(1/2) = √2b) 10^(2/3) ≈ 4.641 (保留三位小数)c) 8^(3/2) = (√8)^3 = 2^3 = 8d) 27^(2/3) = (∛27)^2 = 3^2 = 9e) 16^(-1/2) = 1/√16 = 1/4上述练习题和答案介绍了幂的运算规则,包括幂的计算、幂的化简和带分数指数的幂运算等内容。
通过对这些问题的分析和解答,读者可以更好地理解幂的性质和规律。
总结:幂的运算是数学中一个重要的概念,掌握幂的运算规则对于数学学习和解题非常重要。
指数与指数幂运算的练习题

指数与指数幂运算的练习题1. 计算下列指数的值:(a) 2^3(b) 4^2(c) 10^0(d) 5^-22. 化简下列表达式:(a) (2^3)^2(b) 5^3 / 5^2(c) (3^2) * (3^4)(d) 2^4 * 2^2 / 2^33. 计算下列混合指数的值:(a) 2^3 * 4^2(b) (2^3)^2 * (5^2)^3(c) 3^5 / (3^2 * 3^2)(d) (2^3 * 4^2)^-14. 计算下列指数幂的值:(a) (3^4)^2(b) (6^3)^-2(c) (10^2)^0(d) (4^-2)^35. 填写下列空格:(a) 2^4 = ____(b) 5^0 = ____(c) 1^2 = ____(d) 10^-3 = ____6. 解决下列问题:(a) 如果一个投资每年增长15%,在5年后,该投资的总增长是多少?(b) 假设一个人每天使用1升水,经过30天该人使用的水总量是多少立方米?(c) 如果一个房屋的基价为100,000元,每年以5%的速度增加,每年增加的金额是多少?7. 写出下列指数的平方和立方:(a) 2^2 = ____, 2^3 = ____(b) 3^2 = ____, 3^3 = ____(c) 4^2 = ____, 4^3 = ____(d) 5^2 = ____, 5^3 = ____8. 计算下列指数幂的值并判断其是否为奇数或偶数:(a) 2^3(b) 6^4(c) 10^6(d) 3^59. 解决下列问题:(a) 如果一辆车以每小时60千米的速度行驶,10小时后的总行程是多少千米?(b) 如果一台机器每分钟生产30个产品,8小时后的总生产数量是多少个?(c) 如果一件商品原价为200元,以每年10%的折扣出售,10年后其售价是多少?10. 解决下列问题:(a) 如果一件商品原价为500元,并以每年10%的速度增长,经过5年后该商品的价值是多少?(b) 假设某公司的市场份额从30%增长到40%,增长率是多少?(c) 如果一个房屋的价值为100万,以每年5%的速度增长,10年后该房屋的价值是多少?Note: The document consists of practice problems related to indices and exponentiation in the Chinese language. Each question involves either calculating the value of an exponent, simplifying an expression, or solving a problem related to various real-life scenarios.。
幂运算练习题大全

幂运算练习题大全幂运算,是数学领域中一种常见的运算方式。
它用于表示一个数的某个指数次幂,例如2的3次幂就是2×2×2,通常表示为2^3。
幂运算在数学、物理、计算机科学等领域有着重要的应用。
在本文中,我们将提供一系列幂运算的练习题,帮助读者更好地掌握幂运算的概念和运用。
1. 简化以下幂运算:a) 2^4b) 3^2c) 5^3d) 10^02. 计算以下幂运算的结果:a) 2^5b) 4^3c) 6^2d) 8^43. 给定以下幂运算,求未知数的值:a) 2^x = 16b) 3^x = 27c) 4^x = 256d) 5^x = 6254. 简化以下幂运算的结果,使用负指数:a) 2^-3b) 3^-2c) 5^-4d) 10^-15. 简化以下幂运算的结果,使用幂与根相互抵消的关系:a) √(4^3)b) ∛(8^2)c) ∜(16^2)d) ⁵√(32^3)6. 简化以下幂运算的结果,使用幂运算的运算法则:a) (2^3) × (2^4)b) (3^2) ÷ (3^5)c) (5^6)^2d) (10^4)^07. 计算以下复合幂运算的结果:a) (2^3)^2b) (4^2)^3c) (6^4)^2d) (8^5)^08. 解决以下问题,应用幂运算的概念:a) 一台计算机每秒钟可以执行10^9次运算,那么1分钟内可以执行多少次运算?b) 一辆汽车每小时行驶80公里,那么2小时内可以行驶多远?c) 一块土地的面积为5^2平方米,如果将其分割成边长为1米的小方块,可以得到多少个小方块?9. 解决以下问题,应用幂运算的运算法则:a) 简化表达式:(2^3 × 2^4) ÷ 2^2b) 简化表达式:(3^5)^2 ÷ (3^2)c) 简化表达式:(5^3 ÷ 5^2) × 5^4d) 简化表达式:(10^6)^2 ÷ 10^3通过以上的练习题,可以帮助读者巩固幂运算的知识点和运用技巧。
高一数学上册 指数函数知识点及练习题含答案
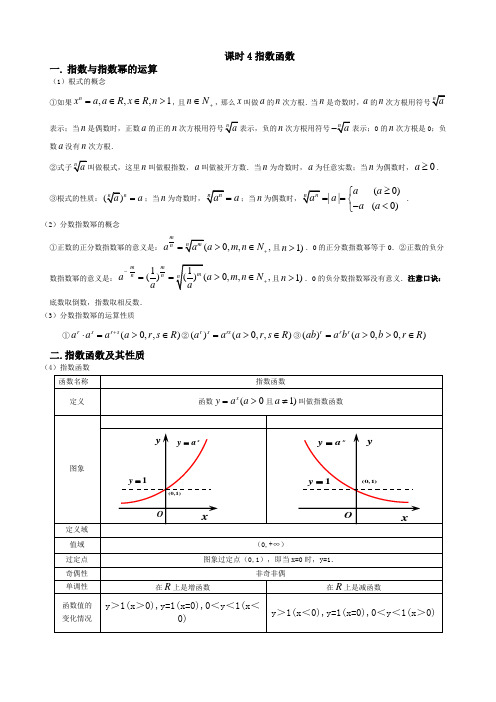
课时4指数函数一. 指数与指数幂的运算(1)根式的概念 ①如果,,,1nxa a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n表示;当n 是偶数时,正数a 的正的nn次方根用符号0的n 次方根是0;负数a 没有n 次方根.n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:n a =;当na =;当n(0)|| (0)a a a a a ≥⎧==⎨-<⎩.(2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m naa m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义.注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈二.指数函数及其性质(4)指数函数a 变化对图象影响在第一象限内,a 越大图象越高,越靠近y 轴; 在第二象限内,a 越大图象越低,越靠近x 轴. 在第一象限内,a 越小图象越高,越靠近y 轴; 在第二象限内,a 越小图象越低,越靠近x 轴.三.例题分析1.设a 、b 满足0<a<b<1,下列不等式中正确的是(C) A.a a <a b B.b a <b b C.a a <b a D.b b <a b解析:A 、B 不符合底数在(0,1)之间的单调性;C 、D 指数相同,底小值小.故选C. 2.若0<a<1,则函数y=a x 与y=(a-1)x 2的图象可能是(D)解析:当0<a<1时,y=a x为减函数,a-1<0,所以y=(a-1)x 2开口向下,故选D.3.设指数函数f(x)=a x (a>0且a ≠1),则下列等式中不正确的是(D) A.f(x+y)=f(x)f(y)B.f(x-y)=)()(y f x f C.f(nx)=[f(x)]n D.f [(xy)n ]=[f(x)]n [f(y)]n (n ∈N *) 解析:易知A 、B 、C 都正确. 对于D,f [(xy)n]=a(xy)n,而[f(x)]n·[f(y)]n=(a x )n·(a y)n=anx+ny,一般情况下D 不成立.4.设a=31)43(-,b=41)34(-,c=43)23(-,则a 、b 、c 的大小关系是(B)A.c<a<bB.c<b<aC.b<a<cD.b<c<a解析:a=413131)34()34()43(>=-=b,b=434141)23()278()34(-=>=c.∴a>b>c.5.设f(x)=4x -2x+1,则f -1(0)=______1____________. 解析:令f -1(0)=a,则f(a)=0即有4a-2·2a=0.2a·(2a-2)=0,而2a>0,∴2a=2得a=1.6.函数y=a x-3+4(a>0且a ≠1)的反函数的图象恒过定点______(5,3)____________.解析:因y=a x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a x-3+4的图象,易知恒过定点(3,5).故其反函数过定点(5,3).7.已知函数f(x)=xx xx --+-10101010.证明f(x)在R 上是增函数.证明:∵f(x)=1101101010101022+-=+---x x xx x x , 设x 1<x 2∈R ,则f(x 1)-f(x 2)=)110)(110()1010(21101101101101010101010101010212122112222111122222222++-=+--+-=+--+-----x x x x x x x x x x x x x x x x . ∵y=10x 是增函数, ∴21221010x x -<0. 而1210x +1>0,2210x +1>0, 故当x 1<x 2时,f(x 1)-f(x 2)<0, 即f(x 1)<f(x 2). 所以f(x)是增函数.8.若定义运算a ⊗b=⎩⎨⎧<≥,,,,b a a b a b 则函数f(x)=3x ⊗3-x 的值域为(A)A.(0,1]B.[1,+∞)C.(0,+∞)D.(-∞,+∞)解析:当3x ≥3-x ,即x ≥0时,f(x)=3-x ∈(0,1];当3x<3-x,即x<0时,f(x)=3x∈(0,1).∴f(x)=⎩⎨⎧<≥-,0,3,0,3x x x x 值域为(0,1).9.函数y=a x 与y=-a -x (a>0,a ≠1)的图象(C) A.关于x 轴对称B.关于y 轴对称 C.关于原点对称D.关于直线y=-x 对称解析:可利用函数图象的对称性来判断两图象的关系.10.当x ∈[-1,1]时,函数f(x)=3x -2的值域为_______[-35,1]___________. 解析:f(x)在[-1,1]上单调递增.11.设有两个命题:(1)关于x 的不等式x 2+2ax+4>0对一切x ∈R 恒成立;(2)函数f(x)=-(5-2a)x 是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a 的取值范围是_______(-∞,-2)__________.解析:(1)为真命题⇔Δ=(2a)2-16<0⇔-2<a<2.(2)为真命题⇔5-2a>1⇔a<2.若(1)假(2)真,则a ∈(-∞,-2].若(1)真(2)假,则a ∈(-2,2)∩[2,+∞]=∅. 故a 的取值范围为(-∞,-2).12.求函数y=4-x -2-x +1,x ∈[-3,2]的最大值和最小值. 解:设2-x =t,由x ∈[-3,2]得t ∈[41,8],于是y=t 2-t+1=(t-21)2+43.当t=21时,y 有最小值43.这时x=1.当t=8时,y 有最大值57.这时x=-3. 13.已知关于x 的方程2a 2x-2-7a x-1+3=0有一个根是2,求a 的值和方程其余的根. 解:∵2是方程2a 2x-2-9a x-1+4=0的根,将x=2代入方程解得a=21或a=4. (1)当a=21时,原方程化为2·(21)2x-2-9(21)x-1+4=0.① 令y=(21)x-1,方程①变为2y 2-9y+4=0, 解得y 1=4,y 2=21.∴(21)x-1=4⇒x=-1,(21)x-1=21⇒x=2. (2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0.② 令t=4x-1,则方程②变为2t 2-9t+4=0.解得t 1=4,t 2=21. ∴4x-1=4⇒x=2, 4x-1=21⇒x=-21. 故方程另外两根是当a=21时,x=-1; 当a=4时,x=-21. 14.函数y=243)31(x x -+-的单调递增区间是(D) A.[1,2]B.[2,3]C.(-∞,2]D.[2,+∞)解析:因为y=3x2-4x+3,又y=3t 单调递增,t=x 2-4x+3在x∈[2,+∞)上递增,故所求的递增区间为[2,+∞).15.已知f(x)=3x-b (2≤x ≤4,b 为常数)的图象经过点(2,1),则F(x)=f 2(x)-2f(x)的值域为(B) A.[-1,+∞)B.[-1,63) C.[0,+∞)D.(0,63]解析:由f(2)=1,得32-b =1,b=2,f(x)=3x-2. ∴F(x)=[f(x)-1]2-1=(3x-2-1)2-1. 令t=3x-2,2≤x≤4.∴g(t)=(t -1)2-1,t∈[1,9]. ∴所求值域为[-1,63].2.1指数函数练习1.下列各式中成立的一项()A .7177)(m n mn= B .31243)3(-=-C .43433)(y x y x +=+D .3339=2.化简)31()3)((656131212132b a b a b a ÷-的结果()A .a 6B .a -C .a 9-D .29a3.设指数函数)1,0()(≠>=a a a x f x ,则下列等式中不正确的是() A .f (x +y )=f(x )·f (y ) B .)()(y f x f y x f =-)( C .)()]([)(Q n x f nx f n∈=D .)()]([·)]([)(+∈=N n y f x f xy f n n n4.函数21)2()5(--+-=x x y()A .}2,5|{≠≠x x xB .}2|{>x xC .}5|{>x xD .}552|{><<x x x 或5.若指数函数x a y =在[-1,1]上的最大值与最小值的差是1,则底数a 等于 ()A .251+B .251+- C .251± D .215± 6.当a ≠0时,函数y ax b =+和y b ax =的图象只可能是 ()7.函数||2)(x x f -=的值域是()A .]1,0(B .)1,0(C .),0(+∞D .R8.函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ,满足1)(>x f 的x 的取值范围 ()A .)1,1(-B .),1(+∞-C .}20|{-<>x x x 或D .}11|{-<>x x x 或9.函数22)21(++-=x x y 得单调递增区间是 ()A .]21,1[-B .]1,(--∞C .),2[+∞D .]2,21[10.已知2)(xx e e x f --=,则下列正确的是 ()A .奇函数,在R 上为增函数B .偶函数,在R 上为增函数C .奇函数,在R 上为减函数D .偶函数,在R 上为减函数 11.已知函数f (x )的定义域是(1,2),则函数)2(x f 的定义域是. 12.当a >0且a ≠1时,函数f (x )=a x -2-3必过定点. 三、解答题:13.求函数y x x =--1511的定义域.14.若a >0,b >0,且a +b =c ,求证:(1)当r >1时,a r +b r <c r ;(2)当r <1时,a r +b r >c r .15.已知函数11)(+-=x x a a x f (a >1).(1)判断函数f (x )的奇偶性;(2)证明f (x )在(-∞,+∞)上是增函数.16.函数f(x)=a x(a>0,且a ≠1)在区间[1,2]上的最大值比最小值大,求a 的值.参考答案一、DCDDDAADDA二、11.(0,1);12.(2,-2); 三、13.解:要使函数有意义必须:∴定义域为:{}x x R x x ∈≠≠且01,14.解:rrrrr c b c a c b a ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+,其中10,10<<<<cbc a . 当r >1时,1=+<⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr,所以a r +b r <c r; 当r <1时,1=+>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr ,所以a r +b r >c r . 15.解:(1)是奇函数.(2)设x 1<x 2,则1111)()(221121+--+-=-x x x x a a a a x f x f 。
高一数学指数函数知识点及练习题(含答案)

+⎩ + 指数函数2.1.1 指数与指数幂的运算〔1〕根式的概念 ①如果 xn= a , a ∈ R , x ∈ R , n > 1,且 n ∈ N ,那么 x 叫做 a 的 n 次方根.当 n 是奇数时,a 的 n 次 方根用符号 n a 表示;当 n 是偶数时,正数 a 的正的 n 次方根用符号 n a 表示,负的 n 次方根用符号 - na表示;0 的 n 次方根是 0;负数 a 没有 n 次方根.②式子 n a 叫做根式,这里 n 叫做根指数, a 叫做被开方数.当 n 为奇数时, a 为任意实数;当 n 为偶数时, a ≥ 0 .nnn n⎧a (a ≥ 0)③根式的性质:( a ) = a ;当 n 为奇数时, a = a ;当 n 为偶数时,=| a |= ⎨-a .(a < 0)〔2〕分数指数幂的概念m①正数的正分数指数幂的意义是: a n= n a m(a > 0, m , n ∈ N , 且 n > 1) .0 的正分数指数幂等于 0.②- m1 m1正数的负分数指数幂的意义是: an= ( ) n = n ( )m (a > 0, m , n ∈ N + , 且 n > 1) .0 的负分数指a a数幂没有意义. 注意口诀:底数取倒数,指数取相反数. 〔3〕分数指数幂的运算性质①a r ⋅ a s = a r +s (a > 0,r , s ∈ R )②(a r )s = a rs (a > 0, r , s ∈ R )③(ab )r = a r b r (a > 0, b > 0, r ∈ R )2.1.2 指数函数及其性质〔4〕指数函数 函数名称 指数函数定义函数 y = a(a > 0 且 a ≠ 1)叫做指数函数图象a > 10 < a < 1y = 1 yOy = ax(0, 1)xy = a xy = 1Oy( 0 , 1 )x定义域 R值域 〔0,+∞〕过定点 图象过定点〔0,1〕,即当 x=0 时,y=1.奇偶性 非奇非偶单调性在 R 上是增函数在 R 上是减函数函数值的变化情况y >1(x >0), y=1(x=0), 0<y <1(x <0)y >1(x <0), y=1(x=0), 0<y <1(x >0)a 变化对图象影响在第一象限内, a 越大图象越高,越靠近 y 轴; 在第二象限内, a 越大图象越低,越靠近 x 轴.在第一象限内, a 越小图象越高,越靠近 y 轴; 在第二象限内, a 越小图象越低,越靠近 x 轴.n a n39 1 + 5 1 ± 5 12.1 指数函数练习1.以下各式中成立的一项〔〕A . ( n )7 = n 7m 7mB . 12(-3)4 =C . 4x 3+ y 33(x + y )4D .=2 11 1 1 1 52.化简(a 3 b 2)(-3a 2 b 3) ÷ ( 3a 6b 6 )的结果〔〕A . 6aB . - aC . - 9aD . 9a23.设指数函数 f (x ) = a x(a > 0, a ≠ 1) ,那么以下等式中不正确的选项是〔 〕A .f (x +y )=f(x )·f (y )B . f 〔x - y 〕=f (x )f ( y )C . f (nx ) = [ f (x )]n(n ∈ Q )- 1D . f (xy )n= [ f (x )]n·[ f ( y )]n(n ∈ N + )4.函数 y = (x - 5)0+ (x - 2)2A .{x | x ≠ 5, x ≠ 2} C .{x | x > 5}〔〕B .{x | x > 2}D .{x | 2 < x < 5或x > 5}5.假设指数函数 y = a x在[-1,1]上的最大值与最小值的差是1,那么底数a 等于 〔〕A .B . 2 2C .D .2 26.当 a ≠ 0 时,函数 y = ax + b 和 y = b ax的图象只可能是〔〕7.函数 f (x ) = 2-|x |的值域是〔 〕A . (0,1]B . (0,1)⎧⎪2- x- 1, x ≤ 0 C . (0,+∞)D .R8.函数 f (x ) = ⎨ 1 ,满足 f (x ) > 1的 x 的取值范围⎪⎩x 2 , x > 0〔 〕A . (-1,1)B . (-1,+∞)C .{x | x > 0或x < -2}D .{x | x > 1或x < -1}9.函数 y = ( 1 ) 2- x 2 + x +2 得单调递增区间是〔 〕11A . [-1, ]2B . (-∞,-1]C . [2,+∞)D . [ 2,2]3 - 33 3- 1 + 5 5 ± 1⎩ x e x - e - x10. f (x ) =,那么以下正确的选项是 〔 〕2A .奇函数,在 R 上为增函数B .偶函数,在 R 上为增函数C .奇函数,在 R 上为减函数D .偶函数,在 R 上为减函数11.函数 f (x )的定义域是〔1,2〕,那么函数 f (2 x) 的定义域是 .12.当 a >0 且 a ≠1 时,函数 f (x )=a x -2-3 必过定点 .三、解答题:13.求函数 y = 1的定义域.5 x -1 - 114.假设a >0,b >0,且a +b =c ,求证:(1)当r >1时,a r +b r <c r ;(2)当r <1时,a r +b r >c r .15.函数 f (x ) =a x - 1 a x + 1(a >1).〔1〕判断函数f (x )的奇偶性;〔2〕证明f (x )在(-∞,+∞)上是增函数.16.函数 f(x)=a x (a>0,且 a ≠1)在区间[1,2]上的最大值比最小值大 a,求 a 的值. 2参考答案一、DCDDDAAD D A二、11.(0,1);12.(2,-2);三、13. 解:要使函数有意义必须:⎧x - 1 ≠ 0⎧x ≠ 1⎪x ⇒⎨ ≠ 0 ⎩ x - 1⎨x ≠ 0∴定义域为: {x x ∈ R 且x ≠ 0, x ≠ 1}⎪1 a +1 a +12 14. 解: a r + br⎛ a ⎫r⎛ b ⎫r,其中 0 < a < 1,0 < b < 1.= ⎪ c rc + ⎪c ⎝ ⎭ ⎝ ⎭ 当r >1时,⎛ a ⎫ r ⎛ b ⎫r a b ,所以a r+b r <c r ;⎪ + ⎪ < + = 1⎝ c ⎭ ⎝ c ⎭ c c当 r <1 时,⎛ a ⎫r⎛ b ⎫ra b,所以 a r +b r >c r . ⎪ + ⎪ > + = 1 ⎝ c ⎭ ⎝ c ⎭ c c15.解:(1)是奇函数.(2) x <x ,a x 1 -1 a x2 -1 。
分数指数幂练习题

分数指数幂练习题分数、指数和幂是数学中非常重要的概念,它们在各个领域中都有广泛的应用。
本文将通过一系列练习题来帮助读者巩固和加深对分数、指数和幂的理解。
1. 简化下列分数:(1/2)^3解析:(1/2)^3 = 1/2 * 1/2 * 1/2 = 1/82. 计算下列指数:2^4解析:2^4 = 2 * 2 * 2 * 2 = 163. 计算下列幂:(-3)^2解析:(-3)^2 = (-3) * (-3) = 94. 简化下列分数:(3/4)^2解析:(3/4)^2 = 3/4 * 3/4 = 9/165. 计算下列指数:5^0解析:任何非零数的0次方都等于1,所以5^0 = 16. 计算下列幂:(-2)^3解析:(-2)^3 = (-2) * (-2) * (-2) = -8通过以上的练习题,我们可以看到分数、指数和幂的运算规律。
在分数的指数运算中,分子和分母都会被指数影响,而在指数和幂的运算中,底数会被指数影响。
接下来,我们将继续探索一些更加复杂的练习题。
7. 简化下列分数:(2/3)^-2解析:分母的指数为负数时,可以将其转化为分子的指数为正数,即(2/3)^-2= (3/2)^2 = 9/48. 计算下列指数:(-1/2)^3解析:(-1/2)^3 = -1/2 * -1/2 * -1/2 = -1/89. 计算下列幂:(4/5)^-1解析:分母的指数为负数时,可以将其转化为分子的指数为正数,即(4/5)^-1= (5/4)^1 = 5/410. 简化下列分数:(1/2)^0解析:任何非零数的0次方都等于1,所以(1/2)^0 = 111. 计算下列指数:(-3)^4解析:(-3)^4 = (-3) * (-3) * (-3) * (-3) = 8112. 计算下列幂:(-4/5)^2解析:(-4/5)^2 = (-4/5) * (-4/5) = 16/25通过以上的练习题,我们可以进一步巩固对分数、指数和幂的运算规律的理解。
指数幂运算-练习题

解:(A)不正确的. , 的4次方根是 .
(B)不正确,要对 分奇偶讨论.
(C)不正确, 的 次方根可能有一个值,可能有两个值,而 只表示一个确定的值.
(D)正确,根据根式运算的依据,当 为奇数时, 是正确的,当 为偶数时,因为 ,则有 .综上,当 时,无论 为何值均有 成立.
2.答案:
(1) ;(2) ;(3) .
3.分析:依照分数指数幂的运算法则,并结合概念来完成运算.
解:(1)原式 ;
(2)原式
4. 分析:这种类型的题目属于混合运算,运算的关键是顺序,先乘方,再乘除,最后做加减.
解:原式
5. 分析:一般根式的运算都化成分数指数幂的运算会比较方便.
解:原式 ,
当 时,原式 .
指数幂运算
课后练习
1.下列说法中正确的是( ).
(A) 的四次方根是 (B)正数的 次方根有两个
(C) 的 次方根就是 (D)
2.求值:
(1)
(2)
(3)
3.求下列各式的值:
(1) ;
(2ห้องสมุดไป่ตู้ .
4.计算: .
5.已知 , ,求 的值.
【答案】
1. 分析:从 次方根和 次根式的概念入手,认清各概念与各符号之间的关系.
2.1.1指数与指数幂的运算(二)(用)

1. 整数指数幂的运算性质:
(m, n Z ) n n n (ab) a b (n Z ).
(a ) a
m n mn
a a a
m n
m n
(m, n Z ),
2. 根式的运算性质: ① 当n为奇数时, n
当n为偶数时, n
a ( a 0) a | a | a(a 0). ② 当n为任意正整数时,( n a ) n a .
a a
n
m n
m
(a>0, m, n∈N*, 且n>1).
规定:
(1)
a
m n
1 a
m n
(a>0, m, n∈N*, 且n>1).
(2) 0的正分数指数幂等于0;
(3) 0的负分数指数幂无意义.
阅读P52页 无理数指数幂
有理指数幂的运算性质:
(a ) a
m n
n n
a a a
n
a a;
n
问题2 当生物死亡后,它机体内原有的碳14会按确定的 规律衰减,大约每经过5730年衰减为原来的一半,这 个时间称为“半衰期”.根据此规律,人们获得了生物 体内碳14含量P与死亡年数t之间的关系
1 P( ) 2
提问:
t 5730
.
100000 5730
1 ( ) 2
6000 5730
m n
m n
mn
n
(ab) a b
R (m, n Q), Z R ((m,,n Q), m, n Z )
nZ R (n Q).
例1 求值:
(1) 8 ,
2 3
2 3
(2)25 , (3)( ) , (4)( ) .
指数运算复习练习题

指数运算复习练习题2.1.1 指数与指数幂的运算练题1、有理数指数幂的分类:1)正整数指数幂 $a^n=a \cdot a \cdot a \cdot。
\cdota$ $(n$ 个 $a)$;2)零指数幂 $a^0=1$ $(a \neq 0)$;3)负整数指数幂 $a^{-n}=\dfrac{1}{a^n}$ $(n \in N^*)$;4)正分数指数幂$a^{\frac{m}{n}}=\sqrt[n]{a^m}$ $(a>0,m,n \in Q)$,等于$0$ 的正分数指数幂为 $0$,$0$ 的负分数指数幂没有意义。
2、有理数指数幂的性质:1)$a^m \cdot a^n=a^{m+n}$ $(a>0,m,n \in Q)$;2)$(a^m)^n=a^{mn}$ $(a>0,m,n \in Q)$;3)$(ab)^m=a^m \cdot b^m$ $(a>0,b>0,m \in Q)$。
知能点2:无理数指数幂若 $a>0$,$P$ 是一个无理数,则 $a^P$ 表示一个确定的实数,上述有理指数幂的运算性质,对于无理数指数幂都适用。
知能点3:根式1、根式的定义:一般地,如果 $x=\sqrt[n]{a}$,那么$x$ 叫做 $a$ 的 $n$ 次方根,其中 $n>1$,$n \in N$,$a$ 叫被开方数。
2、对于根式记号 $\sqrt[n]{a}$,要注意以下几点:1)$n \in N$,且 $n>1$;2)当$n$ 是奇数,则$\sqrt[n]{a^n}=a$;当$n$ 是偶数,则 $\sqrt[n]{a^n}=|a|$;3)负数没有偶次方根;4)零的任何次方根都是零。
3、我们规定:1)$\sqrt[n]{a^m}=a^{\frac{m}{n}}$ $(a>0,m,n \in N,n>1)$;2)$a^{-\frac{m}{n}}=\dfrac{1}{a^{\frac{m}{n}}}$ $ (a>0,m,n \inN^*,n>1)$。
指数与指数幂的运算--根式

a的n次方根的定义:
一般地,如果xn a,那么x叫做a的n次方根, 其中n 1,且n N.
试根据n次方根的定义分别求出下列各数的n
次方根.
(1)25的平方根是___±__5__; (2)27的3次方根是___3__; (3)-32的5次方根是__-2__; (4)16的4次方根是___±_2_; (5)a6的3次方根是____a_2 ; (6)0的7次方根是____0__.
例2.化简 : ( a 1)2 (1 a)2 3 (1 a)3
迁移运用:
例3.设 3 x 3, 求 x2 2x 1 x2 6x 9的值.
小结:
1.n次方根的定义:
一般地,如果xn a,那么x叫做a的n次方根,
其中n 1且n N.
2.根式的简单性质:
1) 当n 1, n N*时,总有 (n a )n a. 2) 当n为奇数时, n an a;
an
|
a
|
a
a
(a 0); (a 0).
例1.求下列各式的值
(1) 3 (8)3 ;
(2) (10)2 ;
(3) 4 (3 )4 ;
(4) (a b)2 (a b).
解: (1) 3 83 = -8; (2) 102 | 10 | =10; (3) 4 3 4 | 3 | 3; (4) a b2 | a b | a b a b.
注意:负数没有偶次方 根. 0的任何次方根都是 0.
叫做 根指数
na
叫做 根式
叫做被 开方数
探究2.根式的性质: 思考: (n a )n a成立吗 ?
结论1: 当n 1, n N*时,总有 (n a )n a.
指数幂运算练习题

指数幂运算练习题指数幂运算练习题指数幂运算是数学中的一个重要概念,它在各个领域都有广泛的应用。
本文将通过一些练习题来帮助读者巩固和加深对指数幂运算的理解。
1. 计算下列指数幂:a) 2^3 = 2 × 2 × 2 = 8b) 5^2 = 5 × 5 = 25c) (-3)^4 = (-3) × (-3) × (-3) × (-3) = 81d) 10^0 = 1 (任何数的0次方都等于1)2. 化简下列指数表达式:a) 2^3 × 2^4 = 2^(3+4) = 2^7 = 128b) 3^2 ÷ 3^5 = 3^(2-5) = 3^(-3) = 1/27c) (4^2)^3 = 4^(2×3) = 4^6 = 4096d) (2^3)^-2 = 2^(3×-2) = 2^(-6) = 1/643. 求解下列方程:a) 2^x = 16解:可以将16写成2的幂的形式,即16 = 2^4,所以2^x = 2^4。
根据指数幂的性质,当底数相等时,指数也相等,所以x = 4。
b) 5^(2x+1) = 125解:可以将125写成5的幂的形式,即125 = 5^3,所以5^(2x+1) = 5^3。
根据指数幂的性质,当底数相等时,指数也相等,所以2x+1 = 3,解得x = 1。
c) (3^2)^x = 81解:可以将81写成3的幂的形式,即81 = 3^4,所以(3^2)^x = 3^4。
根据指数幂的性质,当底数相等时,指数也相等,所以2x = 4,解得x = 2。
4. 求解下列指数方程:a) 2^x = 8解:可以将8写成2的幂的形式,即8 = 2^3,所以2^x = 2^3。
根据指数幂的性质,当底数相等时,指数也相等,所以x = 3。
b) 4^(2x+1) = 64解:可以将64写成4的幂的形式,即64 = 4^3,所以4^(2x+1) = 4^3。
指数及指数幂的运算--计算题训练

2.1.1指数与指数幂的运算--计算题训练一.填空题〔共3小题〕1.〔〕﹣×〔﹣〕0+8×﹣=.2.+lg4﹣lg=.3.〔0.027〕﹣〔﹣〕﹣2+〔2〕﹣〔〕0=.二.解答题〔共20小题〕4.计算:〔1〕〔2〕a+a=3,求值:a+a﹣1.5.计算〔字母为正数〕〔1〕〔4a2b〕〔﹣2a b〕÷〔﹣b〕;〔2〕﹣﹣〔﹣1〕0+〔﹣1〕2016+2﹣1.〔1〕〔1〕0﹣〔1﹣0.5﹣2〕÷〔〕7.计算:〔1〕•〔﹣3〕÷〔〕〔2〕﹣〔﹣〕0++.8.计算〔1〕〔2a b〕〔﹣6a b〕÷〔2〕.9.求以下各式的值〔1〕〔2〕0.5+0.1﹣2+〔2〕﹣3π0+;〔2〕〔﹣3〕+〔0.002〕﹣10〔﹣2〕﹣1+〔﹣〕0.11.〔1〕化简9×64÷30〔2〕化简〔〕×36÷3﹣3〔2〕化简〔a>0〕〔1〕;〔2〕.13.〔1〕计算〔2〕化简.14.〔1〕〔2a b〕〔﹣6a b〕÷〔﹣3a b〕;〔2〕〔×〕6+〔〕﹣×80.25﹣〔﹣2005〕0.15.不用计算器化简计算:〔1〕;〔2〕.16.计算以下各式:〔1〕〔2〕0.5+0.1﹣2+〔2〕+〔2〕〔a﹣2b﹣3〕〔﹣4a﹣1b〕÷〔12a﹣4b﹣2c〕17.计算:化简:.18.化简以下各式:〔1〕.〔2〕.19.计算:〔1〕+〔0.008〕﹣〔0.25〕×〔〕﹣4〔2〕〔×〕6+〔〕﹣4〔〕﹣×80.25﹣〔﹣2009〕0.20.化简:〔1〕〔〕﹣2+〔1﹣〕0﹣〔3〕+;〔2〕a b﹣2•〔﹣3a b﹣1〕÷〔4a b﹣3〕.21.〔1〕计算4x〔﹣3x y〕÷[﹣6〔x y〕];〔2〕.22.〔1〕[125+〔〕+49];〔2〕〔×〕6+〔〕﹣4〔〕﹣×80.25﹣〔﹣2005〕0.23.〔1〕化简:〔〕;〔2〕假设a>0,b>0,化简:.2.1.1指数与指数幂的运算--计算题训练参考答案与试题解析一.填空题〔共3小题〕1.〔2017春•启东市校级期中〕〔〕﹣×〔﹣〕0+8×﹣=.【解答】解:〔〕﹣×〔﹣〕0+8×﹣=+×﹣=2﹣=.故答案为:.2.〔2016秋•期末〕+lg4﹣lg= 2 .【解答】解:+lg4﹣lg=[〔34〕﹣0.25+]+lg2+lg5=〔+〕+1=2;故答案为:2.3.〔2016秋•荆州校级月考〕〔0.027〕﹣〔﹣〕﹣2+〔2〕﹣〔〕0= ﹣45 .【解答】解:0.027﹣﹣〔〕﹣2+〔2〕﹣〔﹣1〕0=0.027﹣49﹣1=﹣1=﹣45,故答案为:﹣45二.解答题〔共20小题〕4.〔2016春•昌邑区校级期中〕计算:〔1〕〔2〕a+a=3,求值:a+a﹣1.【解答】解:〔1〕原式=2=2×3=6.〔2〕∵a+a=3,两边平方可得:a+a﹣1+2=9,∴a+a﹣1=7.5.〔2016秋•秀屿区校级期中〕计算〔字母为正数〕〔1〕〔4a2b〕〔﹣2a b〕÷〔﹣b〕;〔2〕﹣﹣〔﹣1〕0+〔﹣1〕2016+2﹣1.【解答】解:〔1〕〔4a2b〕〔﹣2a b〕÷〔﹣b〕==.〔2〕﹣﹣〔﹣1〕0+〔﹣1〕2016+2﹣1===.6.〔2016秋•灵宝市校级期中〕计算与化简〔1〕〔1〕0﹣〔1﹣0.5﹣2〕÷〔〕〔2〕.【解答】解:〔1〕解析:原式=1﹣〔1﹣22〕÷=1﹣〔﹣3〕÷=1+3×=1+=.〔2〕原式===.7.〔2016秋•崇礼县校级期中〕计算:〔1〕•〔﹣3〕÷〔〕〔2〕﹣〔﹣〕0++.【解答】解:〔1〕•〔﹣3〕÷〔〕==;〔2〕﹣〔﹣〕0++.==.8.〔2016秋•鸠江区校级期中〕计算〔1〕〔2a b〕〔﹣6a b〕÷〔2〕.【解答】解:〔1〕〔2a b〕〔﹣6a b〕÷=4=4a.〔2〕=m2n﹣3.9.〔2016秋•区校级期中〕求以下各式的值〔1〕〔2〕0.5+0.1﹣2+〔2〕﹣3π0+;〔2〕〔﹣3〕+〔0.002〕﹣10〔﹣2〕﹣1+〔﹣〕0.【解答】解:〔1〕原式=+100+﹣3+=+100+﹣3+=100.〔2〕原式=+﹣+1=+10﹣10﹣20+1=﹣.10.〔2016秋•镜湖区校级期中〕计算:0.0081+〔4〕2+〔〕﹣16﹣0.75+2.【解答】解:原式=++﹣24×〔﹣0.75〕+5=0.3++﹣+5=5.5511.〔2016秋•金安区校级期中〕〔1〕化简9×64÷30〔2〕化简〔〕×36÷3﹣3〔2〕化简〔a>0〕【解答】解:〔1〕原式=×÷1=27×2=54,〔2〕原式=×÷=××27=,〔3〕原式==12.〔2016秋•郊区校级月考〕计算以下各式的值:〔1〕;〔2〕.【解答】解:〔1〕=〔〕﹣2+[〔〕3]﹣〔lg4+lg25〕+1=16+﹣2+1=.〔2〕=•=.13.〔2016秋•宜城市校级月考〕〔1〕计算〔2〕化简.【解答】解:〔1〕原式=+10﹣1×〔﹣2〕+﹣3+ =;〔2〕原式===a0b0=1;14.〔2016秋•肥城市校级月考〕〔1〕〔2a b〕〔﹣6a b〕÷〔﹣3a b〕;〔2〕〔×〕6+〔〕﹣×80.25﹣〔﹣2005〕0.【解答】〔此题总分值12分〕解:〔1〕〔2a b〕〔﹣6a b〕÷〔﹣3a b〕=[2×〔﹣6〕÷〔﹣3〕]=4.〔2〕〔×〕6+〔〕﹣×80.25﹣〔﹣2005〕0=+〔〕﹣=22×33+2﹣7﹣2﹣1=100.15.〔2016秋•阳春市校级月考〕不用计算器化简计算:〔1〕;〔2〕.【解答】解:〔1〕=.〔2〕==.16.〔2016秋•潜山县校级月考〕计算以下各式:〔1〕〔2〕0.5+0.1﹣2+〔2〕+〔2〕〔a﹣2b﹣3〕〔﹣4a﹣1b〕÷〔12a﹣4b﹣2c〕【解答】解:〔1〕〔1〕〔2〕0.5+0.1﹣2+〔2〕+ =〔〕++〔〕﹣+=+100++=103.〔2〕〔a﹣2b﹣3〕〔﹣4a﹣1b〕÷〔12a﹣4b﹣2c〕=﹣a﹣2﹣1﹣〔﹣4〕b﹣3+1﹣〔﹣2〕c﹣1=﹣ac﹣1=﹣.17.〔2016秋•沾益县校级月考〕计算:化简:.【解答】解:=4+3﹣1=6.==.18.〔2016秋•殷都区校级月考〕化简以下各式:〔1〕.〔2〕.【解答】解:〔1〕=2×〔﹣6〕÷〔﹣3〕=4a.〔2〕=〔﹣〕÷=﹣=.19.〔2016秋•汇川区校级月考〕计算:〔1〕+〔0.008〕﹣〔0.25〕×〔〕﹣4〔2〕〔×〕6+〔〕﹣4〔〕﹣×80.25﹣〔﹣2009〕0.【解答】解:〔1〕+〔0.008〕﹣〔0.25〕×〔〕﹣4=π﹣3+0.2﹣0.5×4=π﹣3+0.2﹣2=π﹣4.8.〔2〕〔×〕6+〔〕﹣4〔〕﹣×80.25﹣〔﹣2009〕0=4×27+〔2〕﹣7﹣16﹣1=108+2﹣7﹣2﹣1=100.20.〔2016秋•**区校级月考〕化简:〔1〕〔〕﹣2+〔1﹣〕0﹣〔3〕+;〔2〕a b﹣2•〔﹣3a b﹣1〕÷〔4a b﹣3〕.【解答】解:〔1〕〔1〕〔〕﹣2+〔1﹣〕0﹣〔3〕+==π﹣2.〔2〕a b﹣2•〔﹣3a b﹣1〕÷〔4a b﹣3〕=﹣=.21.〔2015秋•长安区校级期中〕〔1〕计算4x〔﹣3x y〕÷[﹣6〔x y〕];〔2〕.【解答】解:〔1〕4x〔﹣3x y〕÷[﹣6〔x y〕]=4×〔﹣3〕÷〔﹣6〕=;〔2〕==.22.〔2015秋•濉溪县校级期中〕〔1〕[125+〔〕+49];〔2〕〔×〕6+〔〕﹣4〔〕﹣×80.25﹣〔﹣2005〕0.【解答】解:〔1〕原式=〔5++7〕=〔〕=[〔〕2]=〔〕==;〔2〕原式=〔2×3〕6+〔〕﹣4×[〔〕2]﹣﹣2×3﹣1=23×32+2﹣7﹣3=108+2﹣7﹣3=100.23.〔2015秋•青州市期中〕〔1〕化简:〔〕;〔2〕假设a>0,b>0,化简:.【解答】解:〔1〕原式==﹣.〔2〕原式=﹣〔4a﹣1〕=4a﹣〔4a﹣1〕=1.。
(完整word版)指数与指数幂的运算练习题整理

2.1.1指数与指数幂的运算练习题高一( )班 座号: 姓名:知能点1:有理数指数幂及运算性质 1、有理数指数幂的分类(1)正整数指数幂()n na a a a a n N *=⋅⋅⋅⋅∈64748L 个; (2)零指数幂)0(10≠=a a ;(3)负整数指数幂()10,n n a a n N a-*=≠∈(4)0的正分数指数幂等于0, 0的负分数指数幂没有意义。
2、有理数指数幂的性质(1)()0,,mn m naa aa m n Q ==>∈ (2)()()0,,nm mn a a a m n Q =>∈(3)()()0,0,m m mab a b a b m Q =>>∈知能点2:无理数指数幂若a >0,P 是一个无理数,则pa 表示一个确定的实数,上述有理指数幂的运算性质,对于无理数指数幂都适用。
知能点3:根式1、根式的定义:一般地,如果a x n=,那么x 叫做a 的n 次方根,其中()*∈>N n n ,1,na 叫做根式,n 叫做根指数,a 叫被开方数。
2(1)n N ∈,且1n >; (2)当n 是奇数,则a a n n =;当n 是偶数,则⎩⎨⎧<-≥==00a aa a a a n n ;(3)负数没有偶次方根; (4)零的任何次方根都是零。
3、我们规定:(1))0,,,1m naa m n N n *=>∈>; (2))10,,,1m nm naa m n N n a-*==>∈>1、用根式的形式表示下列各式)0(>a (1)51a = (2)34a = (3)35a -= (4)32a-=2、用分数指数幂的形式表示下列各式:(1)34y x = (2))0(2>=m mm (3)85-⎝⎭=(4= (5= ; (6)a a a = ;(7) =•a a 2(8)=•323a a (9)=a a (10) =356q p 3、求下列各式的值(1)238= ;(2)12100-= ; (3)31()4-= ;(4)3416()81-=(5)3227= ;(6)23)4936(= ;(7)23)425(-= ;(8)2325=(9)122[(]-= (10)(1221⎡⎤⎢⎥⎣⎦= (11)=32644.化简(1)=••1274331a a a (2)=÷•654323a a a (3)=÷-•a a a 9)(34323(4)322a a a •= (5)3163)278(--b a = (6)⎪⎪⎭⎫ ⎝⎛---3231312212x x x = (7)()0,05354215658≠≠÷⋅⎪⎪⎭⎫ ⎝⎛--b a b a ba =(8))3()6)(2(656131212132b a b a b a -÷-= 5.计算(1)43512525÷-(2) (3)210319)41()2(4)21(----+-⋅- (4)()5.0212001.04122432-⎪⎭⎫⎝⎛⋅+⎪⎭⎫ ⎝⎛--(5)48373271021.097203225.0+-⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛--π (6)24130.753323(3)0.04[(2)]168----++-+(7)()14323112325671027.0-+-+⎪⎭⎫⎝⎛----- (8)5.00312603.1232366141+--+-⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛--(9)()()[]2175.034303101.016287064.0-++-+⎪⎭⎫ ⎝⎛----(10)()3263425.0031323228765.1⎪⎭⎫ ⎝⎛--⨯+⨯+⎪⎭⎫⎝⎛-⨯-6.解下列方程 (1)1318x - = (2)151243=-x (3)422240x x --= (4)2233800x x +---= (5)1321(0.5)4x x --=7.(1).已知11223a a -+=,求下列各式的值(1)1a a -+= ;(2)22a a -+=(2)若11225x x -+=,则21x x+的值是 (3).若13a a -+=,求下列各式的值:(1)1122a a -+= ;(2)22a a -+= ;一.填空题1.若0>a ,则43a 和53-a用根式形式表示分别为 和 ,56b a 和mm 3用分数指数幂形式表示分别为 和 。
高一数学指、对与幂基本运算(重点突破)练习题含答案

高一数学指、对与幂基本运算练习题【重难点知识点网络】:【重难点题型突破】: 一、指数运算 1、 根式与分数指数幂(1)、性质:(na )n=a (a 使na 有意义);当n 为奇数时,n a n =a ,当n 为偶数时,na n =|a |=⎩⎪⎨⎪⎧a ,a ≥0,-a ,a <0.(2)、规定:正数的正分数指数幂的意义是a m n =na m (a >0,m ,n ∈N *,且n >1);正数的负分数指数幂的意义是a -mn =1n a m(a >0,m ,n ∈N *,且n >1);0的正分数指数幂等于0;0的负分数指数幂没有意义.(3)、有理指数幂的运算性质:a r a s =a r +s ;(a r )s =a rs ;(ab )r =a r b r ,其中a >0,b >0,r ,s ∈Q. 例1、(1)、(2022·山东枣庄·高一期中)下列根式与分数指数幂的互化,正确的是( ) A.21()x =- B12y =C.310)x x -=≠ D .1432](0)x x =>(2)、(2022·湖南·长沙市同升湖高级中学有限公司高一期中))A .2B .532 C .562D .762(3)、(2022·黑龙江省饶河县高级中学高一阶段练习)已知16a a -+=,则1122a a --的值为( ) A .2B .-2 C.±D .±2【变式训练1-1】、(2022·湖北·恩施市第一中学高一阶段练习) ) A .25a - B .56a -C .56()a -D .56()a --【变式训练1-2】、(2022·上海·高一专题练习)已知11224x x -+=,则1x x -+=_______.【变式训练1-3】、(2022·上海市松江二中高一期中)0)a >化成有理数指数幂的形式为______.例2.(2022·江苏·常州市正行中学高一阶段练习)(1)计算:()1020.52312220.0154--⎛⎫⎛⎫+⨯- ⎪⎪⎝⎭⎝⎭;(20)a >.【变式训练2-1】、(2022·四川省眉山第一中学高一阶段练习)(1)求值:()1233127863125-⎛⎫⨯++-+⎪⎝⎭(2) 已知 1a a -+= 求44a a -+的值.二、对数运算 1、对数的概念如果a x =N (a >0,且a ≠1),那么x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数.2、对数的性质、换底公式与运算性质(1)对数的性质:①a log a N =N ;②log a a b =b (a >0,且a ≠1). (2)对数的运算法则如果a >0且a ≠1,M >0,N >0,那么①、log a (MN )=log a M +log a N ; ②、log a MN =log a M -log a N ;③、log a M n =n log a M (n ∈R); ④、log a m M n =nmlog a M (m ,n ∈R ,且m ≠0).(3)换底公式:log b N =log a Nlog a b(a ,b 均大于零且不等于1).例3、(1)、(2022·陕西·永寿县中学高一阶段练习)237log 7log 8log 3⋅⋅=______.(2)、(2022·广西·南宁二中高一阶段练习)计算:()1205122log 54⎛⎫--+= ⎪⎝⎭___________.(3)、(2022·陕西渭南·高一期末)已知0a >,且1a ≠,则下列各式恒成立的是( ) A .()2log 2log a a x x = B .2log 2log a a x x =C .log log log a a a x y x y ⋅=⋅D .()log log log a a a x y x y +=+【变式训练3-1】、(2022·江西·南昌市第一中学高一阶段练习))21lg12log 421221(lg 5)lg 2lg 504⎛⎫-+++⋅=⎪⎝⎭______.【变式训练3-2】、(2022·福建·莆田一中高一阶段练习)已知非零实数,,a b c 满足3624a b c ==,则,,a b c 之间的关系是( ) A .111b a c=+ B .312b a c =+ C .123b a c =+D .321b a c=+【变式训练3-3】、(2022·江苏徐州·高三学业考试)化简15932log 3-+的值为( )A .0B .1C .52D .32【变式训练3-4】、(2022·河北·21032128log 16(πe)25-+-++=__________.三、混合运算例4、(2022·浙江·高一期中)(1)01430.75337(0.064)(2)168---⎛⎫⎡⎤--+-+ ⎪⎣⎦⎝⎭.(2)3121log 24lg 539--⎛⎫- ⎪⎝⎭.【变式训练4-1】、(2021·陕西省米脂中学高一期中)计算: (1)33lg1000log 42log 14+-;(2)()0.51.500.5162536 1.5494-⎛⎫⎛⎫---- ⎪⎪⎝⎭⎝⎭【变式训练4-2】、(2022·湖北·武汉市第六中学高一阶段练习)计算下列各式的值:(1)1132(0.027)2-+ (2)22ln 2225lg 5lg 2lg 2lg 25log 5log 8e ++⋅+⋅+指、对与幂基本运算参考答案【重难点知识点网络】:【重难点题型突破】: 一、指数运算 1、 根式与分数指数幂(1)、性质:(na )n=a (a 使na 有意义);当n 为奇数时,na n=a ,当n 为偶数时,na n=|a |=⎩⎪⎨⎪⎧a ,a ≥0,-a ,a <0.(2)、规定:正数的正分数指数幂的意义是a mn =na m (a >0,m ,n ∈N *,且n >1);正数的负分数指数幂的意义是a -mn =1n a m(a >0,m ,n ∈N *,且n >1);0的正分数指数幂等于0;0的负分数指数幂没有意义.(3)、有理指数幂的运算性质:a r a s =a r +s ;(a r )s =a rs ;(ab )r =a r b r ,其中a >0,b >0,r ,s ∈Q. 例1、(1)、(2022·山东枣庄·高一期中)下列根式与分数指数幂的互化,正确的是( )A .21()x =- B 12y =C .310)xx -=≠ D .1432](0)x x =>(2)、(2022·湖南·长沙市同升湖高级中学有限公司高一期中))A .2B .532 C .562D .762(3)、(2022·黑龙江省饶河县高级中学高一阶段练习)已知16a a -+=,则1122a a --的值为( ) A .2 B .-2 C .±D .±2【变式训练1-1】、(2022·湖北·恩施市第一中学高一阶段练习) ) A .25a - B .56a -C .56()a -D .56()a --【变式训练1-2】、(2022·上海·高一专题练习)已知11224x x -+=,则1x x -+=_______. 【答案】14【变式训练1-3】、(2022·上海市松江二中高一期中)0)a >化成有理数指数幂的形式为______.例3.(2022·江苏·常州市正行中学高一阶段练习)(1)计算:()1020.52312220.0154--⎛⎫⎛⎫+⨯- ⎪ ⎪⎝⎭⎝⎭;(20)a >.【变式训练3-1】、(2022·四川省眉山第一中学高一阶段练习)(1)求值:()12303127863125-⎛⎫⨯++-+ ⎪⎝⎭(2) 已知 1a a -+= 求44a a -+的值.二、对数运算 1、对数的概念如果a x =N (a >0,且a ≠1),那么x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数.2、对数的性质、换底公式与运算性质(1)对数的性质:①a log a N =N ;②log a a b =b (a >0,且a ≠1). (2)对数的运算法则如果a >0且a ≠1,M >0,N >0,那么①、log a (MN )=log a M +log a N ; ②、log a MN =log a M -log a N ;③、log a M n =n log a M (n ∈R); ④、log a m M n =nmlog a M (m ,n ∈R ,且m ≠0).(3)换底公式:log b N =log a Nlog a b(a ,b 均大于零且不等于1).例3、(1)、(2022·陕西·永寿县中学高一阶段练习)237log 7log 8log 3⋅⋅=______.(2)、(2022·广西·南宁二中高一阶段练习)计算:()125122log 54⎛⎫--+= ⎪⎝⎭___________.【答案】32##1.5(3)、(2022·陕西渭南·高一期末)已知0a >,且1a ≠,则下列各式恒成立的是( ) A .()2log 2log a a x x = B .2log 2log a a x x =C .log log log a a a x y x y ⋅=⋅D .()log log log a a a x y x y +=+【变式训练3-1】、(2022·江西·南昌市第一中学高一阶段练习))21lg12log 421221(lg 5)lg 2lg 504⎛⎫-+++⋅=⎪⎝⎭______. 【答案】92##4.5【变式训练3-2】、(2022·福建·莆田一中高一阶段练习)已知非零实数,,a b c 满足3624a b c ==,则,,a b c 之间的关系是( ) A .111b a c=+ B .312b a c =+ C .123b a c =+D .321b a c=+【变式训练3-3】、(2022·江苏徐州·高三学业考试)化简15932log 3-+的值为( )A .0B .1C .52D .32【变式训练3-4】、(2022·河北·21032128log 16(πe)25-+-++=__________.【答案】15-##0.2-2132128log 16πe25252311241555故答案为:15-三、混合运算例4、(2022·浙江·高一期中)(1)01430.75337(0.064)(2)168---⎛⎫⎡⎤--+-+ ⎪⎣⎦⎝⎭. (2)3121log 24lg 539--⎛⎫- ⎪⎝⎭.【变式训练4-1】、(2021·陕西省米脂中学高一期中)计算: (1)33lg1000log 42log 14+-;(2)()0.51.500.5162536 1.5494-⎛⎫⎛⎫---- ⎪⎪⎝⎭⎝⎭【变式训练4-2】、(2022·湖北·武汉市第六中学高一阶段练习)计算下列各式的值: (1)1132(0.027)2-+ (2)22ln 2225lg 5lg 2lg 2lg 25log 5log8e ++⋅+⋅+。
指数幂运算练习题

指数幂运算练习题1. 计算以下指数幂:a) 3^4b) 5^3c) 2^6d) 10^22. 计算以下带有指数幂的表达式:a) 2^3 * 2^4b) 4^2 / 4^3c) 9^2 * 9^0d) (2^3)^23. 化简以下指数幂:a) (5^2)^3b) (6^3)^0c) (8^4)^(1/2)d) (10^2)^(-1)4. 计算以下指数幂的结果,并用科学记数法表示:a) 5^6b) 7^4c) 9^5d) 2^105. 填入适当的数值,使以下等式成立:a) 4^x = 64b) 3^(2x-3) = 27c) 10^(x/2) = 100d) (5^3)^x = 1256. 解决以下指数幂方程:a) 2^(x+3) = 16b) 6^(2x+1) = 36c) (4^2x+1) = 256d) 10^x = 10007. 通过变换指数幂中的底数,将以下表达式改写成指数形式:a) 16 = 2^4b) 81 = 3^4c) 64 = 4^3d) 625 = 5^48. 通过求根运算,将以下指数幂转化成普通数:a) 9^(1/2)b) 16^(1/4)c) 27^(1/3)d) 64^(1/6)9. 解决以下指数幂方程组:a) {2^x = 4, 2^y = 8}b) {2^(x+2) = 32, 4^y = 16}c) {3^(x+1) = 27, 9^(2y) = 1}d) {5^(3x) = 125, 3^(2y) = 9}10. 通过特定指数幂的性质,计算以下表达式:a) (3^2)^4b) 8^0c) 2^5 * 2^(-2)d) (7^3)^2 / (7^(-2))这些练习题旨在帮助你熟练掌握指数幂运算的计算和化简。
通过解决这些练习,你将能提高自己在这一领域的技能,并为将来的数学应用问题做好准备。
在解答时,请注意运算的顺序和所需的数学规则,并在需要时使用科学记数法表示结果,以方便计算。
高一数学指、对与幂基本运算练习题含答案

高一数学 指、对与幂基本运算练习题考试时间:90分钟 满分:100分A 组 基础巩固(60分)一、单选题:本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.1.(2022·山东·聊城颐中外国语学校高一期中)设集合{}12A x Z x =∈-≤≤,{}22B x x =<,则A B =( )A .{}1,0,1-B .{}0C .{}1,0-D .{}1,0,1,2-2.(2022·山东·聊城颐中外国语学校高一期中)函数231()x f x x-=的图象可能是( )A .B .C .D .3.(2020·山东聊城一中高一期中)已知421333111,,2325a b c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则( ) A .a b c << B .c<a<b C .a b c >> D .b<c<a4.(2021·山西·太原市外国语学校高一期中)已知0.932,9,3a b c ===,则,,a b c 的大小关系是( ) A .c b a << B .a c b << C .c a b <<D .a b c <<5.(2022·湖南·溆浦县第一中学高一期中)已知命题:p “0x ∃>,使得220x x -->”,则命题p 的否定是( ) A .0x ∀≤,总有220x x -->B .0x ∀>,总有220x x --≤C .0x ∃>,使得220x x --≤D .0x ∃≤,使得220x x -->6.(2022·山东省淄博实验中学高一期中)已知函数()3log 1,022,0x x x f x x +>⎧=⎨+≤⎩,则()()0f f =( )A .1B .2C .3D .47.(2022·广东·汕头市潮阳区棉城中学高一期中)已知()2f x ax bx =+是定义在[]1,2a a -上的偶函数,那么b a a +的值是( )A .43B .13C .12D .12-8.(2022·广东·汕头市潮阳区棉城中学高一期中)某汽车运输公司购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润y (单位:10万元)与营运年数()*N x x ∈为二次函数关系(如图所示),则每辆客车营运( )年时,其营运的年平均利润yx最大.A .3B .4C .5D .6二、多选题:本大题共2小题,每个小题5分,共10分.在每小题给出的选项中,只有一项或者多项是符合题目要求的.9.(2020·山东聊城一中高一期中)下列四组函数中,表示同一函数的有( ) A .2111x y y x x -==+-,B .2,0()(),0x x f x g v v x x ≥⎧=⎨-<⎩,C .3()20)()20)f x x x g x x x x =-≤=--≤,D .0()()1f x x g x ==,10.(2022·江西·鹰潭市余江区城北学校高一期中)设0a >,m ,n 是正整数,且1n >,则下列各式中,正确的是( ) A .mn m n a a =B .01a = C .-=-mn m n a a D n n a a =三、填空题:本大题共2小题,每小题5分,共10分.把答案填在答题卡中的横线上.11.(2022·浙江·杭州四中高一期中)计算:1623415log log 9lg 2lg 2(2)22⎡⎤⨯+++-=⎣⎦____________. 12.(2022·四川·太平中学高一期中)计算:12031820222-⎛⎫++= ⎪⎝⎭_________.B 组 能力提升(40分)四、解答题:本大题共4小题,共40分.解答应写出必要的文字说明、证明过程或演算步骤. 13.(2021·山西·太原市外国语学校高一期中)计算:(1)14116-⎛⎫ ⎪⎝⎭;(2)化简:(-0,0a b >>).14.(2022·江西·鹰潭市余江区城北学校高一期中)(1)计算:2021321168100481--⎛⎫⎛⎫⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭;(20)a ≥(用分数指数幂表示).15.(2022·山东·滨州高新高级中学有限公司高一期中)计算求值.(1)32log 70lg42lg5π3+++-(2)3log 169log log 273+ (3)1120370.02721)9-⎛⎫-- ⎪⎝⎭(4)232log 9log 42lne log 4⨯++16.(2022·黑龙江实验中学高一期中)计算(1)7111log 242238111()log 4[()]71643-+⋅+-+; (2)2215log 5log 4(lg5)lg 2(lg51)⨯++⨯+指、对与幂基本运算练习题参考答案考试时间:90分钟 满分:100分A 组 基础巩固(60分)一、单选题:本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.1.(2022·山东·聊城颐中外国语学校高一期中)设集合{}12A x Z x =∈-≤≤,{}22B x x =<,则A B =( )A .{}1,0,1-B .{}0C .{}1,0-D .{}1,0,1,2-【答案】A【分析】先解不等式化简集合,A B ,再由交集的概念,即可得出结果. 【详解】因为集合{}{}121,0,1,2A x Z x =∈-≤≤=-, {}{}2222B x x x x =<=-<<,因此{}1,0,1A B =-. 故选:A.2.(2022·山东·聊城颐中外国语学校高一期中)函数231()x f x x-=的图象可能是( )A .B .C .D .【答案】A3.(2020·山东聊城一中高一期中)已知421333111,,2325a b c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则( ) A .a b c << B .c<a<b C .a b c >> D .b<c<a4.(2021·山西·太原市外国语学校高一期中)已知0.92,3a b c ===,则,,a b c 的大小关系是( ) A .c b a << B .a c b << C .c a b << D .a b c <<故a b c <<. 故选:D5.(2022·湖南·溆浦县第一中学高一期中)已知命题:p “0x ∃>,使得220x x -->”,则命题p 的否定是( ) A .0x ∀≤,总有220x x --> B .0x ∀>,总有220x x --≤ C .0x ∃>,使得220x x --≤ D .0x ∃≤,使得220x x -->【答案】B【分析】考察特称命题的否定,先将存在量词改为全称量词,再否定结论即可【详解】因为命题p 为特称命题,所以命题p 的否定为全称命题,即命题p 的否定为:“0x ∀>,总有220x x --≤”,故选:B .6.(2022·山东省淄博实验中学高一期中)已知函数()3log 1,022,0x x x f x x +>⎧=⎨+≤⎩,则()()0f f =( )A .1B .2C .3D .4【答案】B【分析】根据题意,由函数的解析式求出()0f 的值,进而计算可得答案.【详解】根据题意,函数()3log 1,022,0x x x f x x +>⎧=⎨+≤⎩,则()00223f =+=,则()()()303log 312f f f ==+=,故选:B .7.(2022·广东·汕头市潮阳区棉城中学高一期中)已知()2f x ax bx =+是定义在[]1,2a a -上的偶函数,那么b a a +的值是( )A .43B .13C .12D .12-从而43ba a +=. 故选:A .8.(2022·广东·汕头市潮阳区棉城中学高一期中)某汽车运输公司购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润y (单位:10万元)与营运年数()*N x x ∈为二次函数关系(如图所示),则每辆客车营运( )年时,其营运的年平均利润yx最大.A .3B .4C .5D .6【答案】C【分析】先根据题意求出总利润y (单位:10万元)与营运年数()*N x x ∈为二次函数关系式,从而可得y x,化简后利用基本不等式可求得其最大值.【详解】根据二次函数的图象设二次函数为2(6)11y a x =-+, 因为图象过(4,7),所以27(46)11a =-+,解得1a =-,所以22(6)111225y x x x =--+=-+-(*N x ∈), 所以212252512y x x x x x x -+-==--+ 2512x x ⎛⎫=-++ ⎪⎝⎭252122x x≤-⋅+=,当且仅当25x x =,即=5x 时取等号,所以每辆客车营运5年时,其营运的年平均利润yx最大,故选:C.二、多选题:本大题共2小题,每个小题5分,共10分.在每小题给出的选项中,只有一项或者多项是符合题目要求的.9.(2020·山东聊城一中高一期中)下列四组函数中,表示同一函数的有( )A .2111x y y x x -==+-,B .,0()(),0x x f x g v x x ≥⎧=⎨-<⎩,C .()0)()0)f x x g x x =≤=-≤,D .0()()1f x x g x ==,10.(2022·江西·鹰潭市余江区城北学校高一期中)设0a >,m ,n 是正整数,且1n >,则下列各式中,正确的是( ) A .mn a =B .01a =C .-=mn a D a =三、填空题:本大题共2小题,每小题5分,共10分.把答案填在答题卡中的横线上.11.(2022·浙江·杭州四中高一期中)计算:1623415log log 9lg 2lg 2(2)22⎡⎤⨯+++-=⎣⎦____________. 【答案】812.(2022·四川·太平中学高一期中)计算:12031820222-⎛⎫++= ⎪⎝⎭_________.【答案】7【分析】根据指数的运算法则计算即可. 【详解】原式2417=++=. 故答案为:7.B 组 能力提升(40分)四、解答题:本大题共4小题,共40分.解答应写出必要的文字说明、证明过程或演算步骤. 13.(2021·山西·太原市外国语学校高一期中)计算:(1)14116-⎛⎫ ⎪⎝⎭;(2)化简:(-0,0a b >>).14.(2022·江西·鹰潭市余江区城北学校高一期中)(1)计算:221321168100481--⎛⎫⎛⎫⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭;(20)a ≥(用分数指数幂表示).15.(2022·山东·滨州高新高级中学有限公司高一期中)计算求值.(1)32log 70lg42lg5π3+++-(2)3log 169log log 273+(3)112370.02721)9-⎛⎫-- ⎪⎝⎭ (4)232log 9log 42lne log 4⨯++16.(2022·黑龙江实验中学高一期中)计算(1)7log 242238111()log 4[()]71643-+⋅+-+; (2)2215log 5log 4(lg5)lg 2(lg51)⨯++⨯+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、有理数指数幂的分类
(1)正整数指数幂()n n
a a a a a n N *=⋅⋅⋅⋅∈个
; (2)零指数幂)0(10
≠=a a ;
(3)负整数指数幂()10,n
n
a a n N a -*=≠∈
(4)0的正分数指数幂等于0, 0的负分数指数幂没有意义。
2、有理数指数幂的性质 (1)()0,,m
n
m n
a a a a m n Q ==>∈
(2)()()0,,n
m mn a a a m n Q =>∈
(3)()()0,0,m m m ab a b a b m Q =>>∈ 知能点2:无理数指数幂
若a >0,P 是一个无理数,则p a 表示一个确定的实数,上述有理指数幂的运算性质,对于无理数指数幂都适用。
知能点3:根式
1、根式的定义:一般地,如果a x n
=,那么x 叫做a 的n 次方根,其中()*
∈>N n n ,1,n
a 叫做根式,n 叫做根指数,a 叫被开方数。
2
(1)n N ∈,且
1n >;
(2)当n 是奇数,则a a
n
n
=;当n 是偶数,则
⎩⎨
⎧<-≥==0
0a a
a a
a a n
n
; (3)负数没有偶次方根;
(4)零的任何次方根都是零。
3、我们规定: (1))
0,,,1m n
a a m n N n *=>∈>;
(2))10,,,1m n
m n
a
a m n N n a
-*=
=
>∈>
一、填空
1、用根式的形式表示下列各式)0(>a
(1)51
a = (2)34a = (3)35
a -
= (4)32
a -
=
2、用分数指数幂的形式表示下列各式:
(1)3
4y x = (2))0(2
>=
m m
m (3
= ; (4)a
a a = ;
(5) =•a a 2 (6)=•3
2
3a a
(7)=a a
(8) =3
5
6q p 3、求下列各式的值
(1)2
38= ;(2)12
100-
= ; (3)3
1()4
-= ;
(4)3416()81-
= ;(5)3227= ; (6)23
)49
36(= ;
(7)23)4
25(-= ;(8)2325= ;(9
)1
2
2[(]-= ; (10)=3
264
4.化简 (1)=••12
74
33
1a
a a
(2)=֥6
54
32
3a a a
(3)=÷-•a a a
9)(34
32
3 (4)
3
2
2
a
a a •=
(5)3
163)278(--b a = (6)⎪⎪⎭
⎫ ⎝⎛---32
31312212x x x = (7)()0,053542
15
65
8
≠≠÷⋅⎪⎪⎭
⎫ ⎝
⎛
-
-b a b a b
a
=
(8))3()6)(2(6
56
13
12
12
13
2b a b a b a -÷-=
5.计算 (1)43
512525÷-
(2) (3)2
1031
9
)4
1
()2(4)2
1(----+-⋅- (4)()
5
.02
1
2001.04122432-⎪⎭
⎫
⎝⎛⋅+⎪
⎭⎫
⎝⎛-
-
6.已知112
2
3a a -+=,求下列各式的值(1)1
a a -+= ;(2)2
2
a a -+=
7.若0>a ,则43a 和5
3-
a 用根式形式表示分别为 和 ,
5
6b a 和
m
m
3
用分数指数幂形式表示分别为 和 。
8.使式子34
(12)x --有意义的x 的取值范围是 _.
9.若32a =,135b -=,则323a b
-的值= . 10.已知103,102m n
==,则32
10m n -的值为 . 二.选择题.
1、 R a ∈,下列各式一定有意义的是( )
A.2
-a B. 41a C. 3
2a D. 0
a
2、 R a ∈,下列各式一定有意义的是( )
A. a
)2(- B.2
-a C. 32
a D. 2
3a 3、 下列各式计算正确的是 ( )
A. 1)1(0
=- B.a a a =⋅2
2
1 C.8432= D. 2113
33
a a a -
÷= 4、若0a >,且,m n 为整数,则下列各式中正确的是 ( )
A 、m m n
n
a a a ÷= B 、n m n m a a a ⨯=⋅ C 、()n
m m n
a a += D 、01n n
a a -÷=
5、下列运算结果中,正确的是( )
A .6
32a a a =⋅ B .()()2
332a a -=- C .()110
=-a D .()6
3
2a a -=-
6.下列各式中成立的是( )
A .7
1
77m n m n =⎪⎭
⎫ ⎝⎛ B .()312433-=- C .()43
433y x y x +=+
D .3
3
39=
7.下列各式成立的是( )
A.()3
23
2
2
n m n m +=+ B.5
51
5
b a a b =⎪⎭⎫ ⎝⎛ C.()()31
6233-=-
D.
3
13
2
4=
8.将2
35写为根式,则正确的是( )
A .
3
2
5 B .
3
5 C .5
2
3 D .
3
5
9、化简()4
33
2
5⎥⎦
⎤⎢⎣⎡-的结果为( ) A .5 B .5 C .5-
D .-5
11.与a
a 1
-的值相等是( )
A.
a B. a - C. a - D. a --
12、已知31=+a
a ,则21
2
1
-+a a 等于(
)
A .2
B .5
C .5-
D .5±
13、化简
x
x 3-的结果是( )
A .x --
B .x
C .x -
D .x -
14、下列各式正确的是( ) A.35
a -=
B.
2
33
2
x
x =
C.111111()8
248
2
4
a
a a
a
-
⨯⨯-⋅⋅= D.1
1
23
33142(2)12x x x x
---=-
15、根式
a
a 11(式中0>a )的分数指数幂形式为( )
A.3
4
-a B.3
4a C.4
3-a D.4
3a。
