高一数学下期末试题及答案

合集下载

2022-2023学年广东省梅州市高一(下)期末数学试卷【答案版】

2022-2023学年广东省梅州市高一（下）期末数学试卷一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．复数z ＝（1+m ）+（2﹣m ）i （m ∈R ，i 为虚数单位）对应的点在第二象限内，则实数m 的取值范围是（） A ．﹣1＜m ＜2B ．m ＜﹣1C ．m ＞2D ．m ＜﹣1或m ＞22．已知|a →|=2，|b →|=3，且a →⊥b →，则|b →−a →|=（） A ．1B ．√5C ．√13D ．53．某水果店老板为了了解葡萄的日销售情况，记录了过去10天葡萄的日销售量（单位：kg ），结果如下：43，35，52，65，40，54，49，38，62，57．一次进货太多，水果会变得不新鲜；进货太少，又不能满足顾客的需求，店长希望每天的葡萄尽量新鲜，又能60%地满足顾客的需求（在100天中，大约有60天可以满足顾客的需求），每天大约应进（）千克葡萄． A ．49B ．51C ．53D ．554．已知a ，b ，c 是三条不同的直线，α，β是两个不同的平面，下列结论正确的是（） A ．若a ⊥b ，a ⊥c ，则b ∥c B ．a ∥α，b ∥α，则a ∥bC ．若a ∥α，b ⊥a ，则b ⊥αD ．若a ⊂α，α∥β，则a ∥β5．十字测天仪广泛应用于欧洲中世纪晚期的航海领域，主要用于测量太阳等星体的方位，便于船员确定位置，如图1所示，十字测天仪由杆AB 和横档CD 构成，并且E 是CD 的中点，横档与杆垂直并且可在杆上滑动，十字测天仪的使用方法如下：如图2，手持十字测天仪，使得眼睛可以从A 点观察，滑动横档CD 使得A ，C 在同一水平面上，并且眼睛恰好能观察到太阳，此时视线恰好经过点D ，DE 的影子恰好是AE ．然后，通过测量AE 的长度，可计算出视线和水平面的夹角∠CAD （称为太阳高度角），最后通过查阅地图来确定船员所在的位置．若在一次测量中，AE ＝60，横档CD 的长度为30，则太阳高度角的正弦值为（） A ．417B ．817C ．1317D ．15176．在直角坐标系xOy 中，已知a →=(1，3)，b →=(3，1)，若∀t ∈R ，|a →−λb →|≤|a →−tb →|恒成立，则λ＝（）A ．13B ．23C ．25D ．357．如图，三棱台ABC ﹣A 1B 1C 1中，底面ABC 是边长为6的正三角形，且AA 1＝A 1C 1＝C 1C ＝3，平面AA 1C 1C ⊥平面ABC ，则棱BB 1＝（）A ．3√62B ．3√3C ．3D ．3√28．在锐角△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，b ＝2，C =π3，则c 的取值范围为（） A ．(2，2√3)B ．(2√3，+∞)C ．(√3，2√3)D ．（2，+∞）二、选择题：本题共4小题，每小题5分，共20分。

【新结构】2023-2024学年广东省东莞市高一下学期期末教学质量检查数学试题+答案解析

【新结构】2023-2024学年广东省东莞市高一下学期期末教学质量检查数学试题❖一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知向量，，若，则()A.2B.C.D.2.为了解学生每日参加体育锻炼的情况，学校用比例分配的分层随机抽样方法从高一、高二、高三年级所有学生中抽取部分学生做抽样调查，已知该学校高一、高二、高三年级学生人数的比例如图所示，若抽取的样本中高三年级的学生有36人，则抽取的样本容量为()A.90B.100C.120D.1603.棱长为a的正方体的顶点都在球面上，则球的表面积为()A. B. C. D.4.若，则()A. B.2 C. D.5.已知m，n为两条不同的直线，，为两个不同的平面，则下列命题正确的是()A.若，，则B.若，，且，则C.若，，则D.若，，则6.已知向量，，且，任意点M关于点A的对称点为S，点S关于点B的对称点为N，则()A. B.6 C. D.37.已知三棱锥，平面ABC ，，，则异面直线PB 与AC 所成角的余弦值为()A. B. C. D.8.一枚质地均匀的正方体骰子，其六个面分别刻有1，2，3，4，5，6六个数字，投掷这枚骰子两次，设事件“第一次朝上面的数字是奇数”，则下列事件中与M 相互独立的是()A.第一次朝上面的数字是偶数B.第一次朝上面的数字是1C.两次朝上面的数字之和是8D.两次朝上面的数字之和是7二、多选题：本题共3小题，共18分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得6分，部分选对的得2分，有选错的得0分。

9.已知某地一周每天的最高温度单位：分别为：31、27、26、28、27、30、27，则下列关于这组数据的结论中正确的是()A.众数是27 B.极差是4C.中位数是28D.平均数是2810.已知的半径为2，为其内接三角形，则下列结论中正确的是()A.若，则B.若，则周长的最大值为C.若，则D.若，则面积的最大值为11.如图，在棱长为1的正方体中，点E，F分别为AB，的中点，平面经过点C，E，F，且与交于点G，则下列结论正确的是()A.平面B.平面平面C. D.二面角的正切值为三、填空题：本题共3小题，每小题5分，共15分。

高一下期末数学试卷含答案解析

则0≤α＜π，且tanα= ，故α=60°，
故选B．
3．在正项等比数列{an}中，若a2=2，a4﹣a3=4，则公比为（）
A．2B．1C． D．
【考点】等比数列的通项公式．
【分析】利用等比数列的通项公式及其性质即可得出，
【解答】解：设正项等比数列{an}的公比为q＞0，
∵a2=2，a4﹣a3=4，∴ =2q2﹣2q=4，
22．已知A（﹣1，0），B（1，0），圆C：x2﹣2kx+y2+2y﹣3k2+15=0．
（Ⅰ）若过B点至少能作一条直线与圆C相切，求k的取值范围．
（Ⅱ）当k= 时，圆C上存在两点P1，P2满足∠APiB=90°（i=1，2），求|P1P2|的长．
-学年河北省沧州市高一（下）期末数学试卷
参考答案与试题解析
化为q2﹣q﹣2=0，解得q=2．
故选；A．
4．若a＞b，则下列不等式成立的是（）
A．a2＞b2B． C．lga＞lgbD．
【考点】不等关系与不等式．
【分析】利用不等式的性质和指数函数的单调性就看得出．
【解答】解：∵a＞b，∴2a＞2b＞0，∴ ，
故D正确．
故选D．
5．若直线l∥平面α，直线m⊂α，则l与m的位置关系是（）
A． B． C． D．3
【考点】由三视图求面积、体积．
【分析】由三视图知该几何体是一个长方体截去一个三棱锥所得的组合体，由三视图求出几何元素的长度，由柱体、锥体的体积公式求出几何体的体积．
【解答】解：由三视图知几何体是一个长方体截去一个三棱锥所得的组合体，
且长方体长、宽、高分别是1、1、3，
三棱锥的底面是等腰直角三角形、直角边是1，三棱锥的高是1，
A．2B．1C． D．

2023-2024学年北京市朝阳区高一下学期期末考试数学试卷+答案解析

2023-2024学年北京市朝阳区高一下学期期末考试数学试卷一、单选题：本题共10小题，每小题5分，共50分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.若复数z满足，则()A. B. C. D.2.已知向量，，则()A. B. C.3 D.53.如图，八面体的每个面都是正三角形，并且4个顶点A，B，C，D在同一平面内，若四边形ABCD是边长为2的正方形，则这个八面体的表面积为()A.8B.16C.D.4.已知m，n是平面外的两条不同的直线，若，则“”是“”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.在中，，，，则()A. B. C. D.6.李华统计了他爸爸2024年5月的手机通话明细清单，发现他爸爸该月共通话60次，他按每次通话时间长短进行分组每组为左闭右开的区间，画出了如图所示的频率分布直方图．则每次通话时长不低于5分钟且小于15分钟的次数为()A.18B.21C.24D.277.已知向量，不共线，，，若与同向，则实数t的值为()A. B. C.3 D.或38.近年来，我国国民经济运行总体稳定，延续回升向好态势．下图是我国2023年4月到2023年12月规模以上工业增加值同比增长速度以下简称增速统计图．注：规模以上工业指年主营业务收入2000万元及以上的工业企业．下列说法正确的是()A.4月，5月，6月这三个月增速的方差比4月，5月，6月，7月这四个月增速的方差大B.4月，5月，6月这三个月增速的平均数比4月，5月，6月，7月这四个月增速的平均数小C.连续三个月增速的方差最大的是9月，10月，11月这三个月D.连续三个月增速的平均数最大的是9月，10月，11月这三个月9.在梯形ABCD中，，，，，，则与夹角的余弦值为()A. B. C. D.10.已知，，若动点P，Q与点A，M共面，且满足，，则的最大值为()A.0B.C.1D.2二、填空题：本题共6小题，每小题5分，共30分。

2023-2024学年安徽省六安一中高一(下)期末数学试卷+答案解析

2023-2024学年安徽省六安一中高一（下）期末数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.若复数为纯虚数，则复数z的共轭复数为()A. B.2024i C. D.2025i2.已知向量，若，则()A. B. C.1 D.23.已知，，是不共面的三个向量，则能构成空间的一个基底的一组向量是()A.，，B.，，C.，，D.，，4.某不透明的袋中有3个红球，2个白球，它们除颜色不同，质地和大小都完全相同.甲、乙两同学先后从中各取一个球，先取的球不放回，则他们取到不同颜色球的概率为()A. B. C. D.5.已知样本数据，，，…，的平均数为x，方差为，若样本数据，，，…，的平均数为，方差为，则平均数()A.1B.C.2D.6.已知，，，则M到直线AB的距离为()A. B. C.1 D.7.PA，PB，PC是从点P出发的三条射线，每两条射线的夹角均为，那么直线PC与平面PAB所成角的正弦值是()A. B. C. D.8.中国古代数学瑰宝《九章算术》中记载了一种称为“曲池”的几何体，该几何体为上、下底面均为扇环形的柱体扇环是指圆环被扇形截得的部分现有一个如图所示的曲池，其中底面ABCD，底面扇环所对的圆心角为，扇环对应的两个圆的半径之比为1：2，，，E是的中点，则异面直线BE与所成角的余弦值为()A. B. C. D.二、多选题：本题共3小题，共18分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得6分，部分选对的得2分，有选错的得0分。

9.2021年11月10日，中国和美国在联合国气候变化格拉斯哥大会期间发布《中美关于在21世纪20年代强化气候行动的格拉斯哥联合宣言》以下简称《宣言》承诺继续共同努力，并与各方一道，加强《巴黎协定》的实施，双方同意建立“21世纪20年代强化气候行动工作组”，推动两国气候变化合作和多边进程．为响应《宣言》要求，某地区统计了2020年该地区一次能源消费结构比例，并规划了2030年一次能源消费结构比例，如图所示：经测算，预估该地区2030年一次能源消费量将增长为2020年的倍，预计该地区()A.2030年煤的消费量相对2020年减少了B.2030年天然气的消费量是2020年的5倍C.2030年石油的消费量相对2020年不变D.2030年水、核、风能的消费量是2020年的倍10.下列对各事件发生的概率判断正确的是()A.某学生在上学的路，上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是，那么该生在上学路上到第3个路口首次遇到红灯的概率为B.三人独立地破译一份密码，他们能单独译出的概率分别为，，，假设他们破译密码是彼此独立的，则此密码被破译的概率为C.从1，2，3，4中任取2个不同的数，则取出的2个数之差的绝对值为2的概率是D.设两个独立事件A和B都不发生的概率为，A发生B不发生的概率与B发生A不发生的概率相同，则事件A发生的概率是11.如图，已知正方体的棱长为1，P为底面ABCD内包括边界的动点，则下列结论正确的是()A.不存在点P，使平面B.三棱锥的体积为定值C.若，则P点在正方形底面ABCD内的运动轨迹长为D.若点P是AD的中点，点Q是的中点，过P，Q作平面平面，则平面截正方体的截面面积为三、填空题：本题共3小题，每小题5分，共15分。

浙江宁波市九校2024年高一下学期期末联考数学试题+答案

宁波市2023学年第二学期期末九校联考高一数学试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．四棱锥至多有几个面是直角三角形？ A ．2B ．3C ．4D ．52．已知点()2,3A ，()3,1−B ，若直线l 过点()0,1P 且与线段AB 相交，则直线I 的斜率k 的取值范围是（） A ．23≤−k 或1≥k B ．23≤−k 或01≤≤k C ．203−≤≤k 或1≥kD ．213−≤≤k 3．若平面向量,,a b c 两两的夹角相等，且1= a ，1= b ，2= c ，则++=a b c （） A ．1B ．4C ．1或4D ．1或24．已知m ，n 为两条不同的直线，αβ为两个不同的平面，若α⊥m ，β⊂n ，则“⊥m n ”是“αβ∥”的（） A ．充要条件 B ．必要不充分条件 C ．充分不必要条件D ．既不充分也不必要条件5．逢山开路，遇水搭桥，我国摘取了一系列高速公路“世界之最”，锻造出中国路、中国桥等一张张闪亮的“中国名片”。

如图，一辆汽车在一条水平的高速公路上直线行驶，在A ，B ，C 三处测得道路一侧山顶的仰角依次为30°，45°，60°，若=AB a ，()03=<<BC b a b ，则此山的高度为（）ABCD6．已知复数11=+z i 是关于x 的方程2)0(,++=∈x px q p q R 的一个根，若复数z 满足1−=−z z p q ，复数z 在复平面内对应的点Z 的集合为图形M ，则M 围成的面积为（） A ．πB ．4πC ．16πD ．25π7．慢走是一种简单又优良的锻炼方式，它不仅可以帮助减肥，还可以增强心肺功能、血管弹性、肌肉力量等小温从小到大记录了近6周的慢走里程（单位：公里）：11，12，m ，n ，20，27，其中这6周的慢走里程的中位数为16，若要使这6周的周慢走里程的标准差最小，则=m （） A ．14B ．15C ．16D ．178．在锐角三角形ABC 中，角A ，B ，C 的对边分别为a ，b ，c ．若2222sin −+=b c B c a ，且2=a ，则tan tan tan AB C的最大值为（）A 2−B ．3−C D 二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．9．下列描述正确的是（）A ．若事件A ，B 相互独立，()0.6=P A ，()0.3=P B ，则()0.54= P AB AB B ．若三个事件A ，B ，C 两两独立，则满足()()()()=P ABC P A P B P CC ．若()0>P A ，()0>P B ，则事件A ，B 相互独立与A ，B 互斥一定不能同时成立D ．必然事件和不可能事件与任意事件相互独立10．已知复数12=−+z ，则下列说法正确的是A ．zB ．12=−z z C ．复平面内1+z z对应的点位于第二象限 D ．2024=z z11．如图，已知四面体ABCD 的各条棱长均等于2，E ，F 分别是棱AD ，BC 的中点．G 为平面ABD 上的一动点，则下列说法中正确的有（）A ．三棱锥E -AFCB ．线段+CG GFC ．当G 落在直线BD 上时，异面直线EF 与AG D ．垂直于EF 的一个面α，截该四面体截得的截面面积最大为1第Ⅱ卷三、填空题：本题共3小题，每小题5分，共15分，12．已知直线1:40+−=l ax y 23:202+++=l x a y 平行，则实数=a _______． 13．已知圆O 的直径AB 把圆分成上下两个半圆，点C ，D 分别在上、下半圆上（都不与A ，B 点重合）若2=AC ，1=AD ，则⋅=AB DC _______．14．已知三棱锥P -ABC 的四个面是全等的等腰三角形，且=PA ，==PB AB ，点D 为三棱锥P -ABC 的外接球球面上一动点，=PD 时，动点D 的轨迹长度为_______．四、解答题：本题共5小题，共77分，解答应写出文字说明、证明过程或演算步骤15．（13分）如图，在等腰梯形ABCD 中，2222====ADDC CB AB a ，E ，F 分别为AB ，AD 的中点，BF 与DE 交于点M ．（1）用 AD ，AE 表示 BF ；（2）求线段AM 的长．16．（15分）已知直线l ：()()1231−=−+a y a x ．（1）求证：直线l 过定点；（2）若直线l 不经过第二象限，求实数a 的取值范围；（3）若直线l 与两坐标轴的正半轴围成的三角形面积最小，求l 的方程17．（15分）“数学好玩”是国际著名数学家陈省身赠送给少年数学爱好者们的一句话某校为了更好地培养学生创新精神和实践能力，激发学生钻研数学的兴趣和热情，特举办数学节活动．在活动中，共有20道数学问题，满分100分在所有的答卷中随机抽取100份作为样本，将样本的成绩分成六段：[)40,50，[)50,60，……，[]90,100，得到如图所示的频率分布直方图．（1）求频率分布直方图中a 的值，并估计该校全体学生这次数学成绩的中位数；（2）活动中，甲、乙、丙三位同学独立参加竞赛，已知甲同学答对了12道，乙同学答对了8道，丙同学答对了n 道，假设每道数学问题难度相当，被答对的可能性都相同．（i ）任选一道数学问题，求甲、乙两位同学恰有一人答对的概率；（ii ）任选一道数学问题，若甲、乙、丙三个人中至少有一个人答对的概率为2225，求n 的值． 18．（17分）如图1，有一个边长为4的正六边形ABCDEF ，将四边形ADEF 沿着AD 翻折到四边形ADGH 的位置，连接BH ，CG ，形成的多面体ABCDGH 如图2所示．（1）求证：AD ⊥CG ：（2）若AH ⊥CD ，试求直线CH 与平面ABCD 所成角的正弦值：（3）若二面角H -AD -B M 是线段CG 上的一个动点（M 与C ，G 不重合），试问四棱锥M -ABCD 与四棱锥M -ADGH 的体积之和是否为定值？若是，求出这个定值，若不是，请说明理由19．（17分）矩形ABCD 中，P ，Q 为边AB 的两个三等分点，满足===AP PQ QB BC ，R 点从点A 出发．沿着折线段AD -DC -CB 向点B 运动（不包含A ，B 两点），记α∠=ARP ，β∠=BRQ ．（1）当△APR 是等腰三角形时，求sin α；（2）当R 在线段AD （不包含A ，D 两点）。

湖北省武汉2023-2024学年高一下学期期末考试数学试卷含答案

武汉2023-2024学年度下学期期末考试高一数学试卷（答案在最后）命题教师：考试时间：2024年7月1日考试时长：120分钟试卷满分：150分一、选择题：本题共8小题，每题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若复数z 满足(2i)3i z +=-，则z =（）A.1i +B.1i- C.1i-+ D.1i--【答案】A 【解析】【分析】先利用复数的除法运算法则化简得到复数z ，再根据共轭复数的概念即可求解.【详解】因为(2i)3i z +=-，所以3i (3i)(2i)1i 2i 41z ---===-++，所以1i z =+.故选：A2.△ABC 中，60A =︒，BC =AC =C 的大小为（）A.75︒B.45︒C.135︒D.45︒或135︒【答案】A 【解析】【分析】利用正弦定理可得sin B =45B = ，由三角形内角和即可求解.【详解】由正弦定理可得sin sin BC AC A B=,故32sin 2B ==,由于60A =︒，故0120B ︒︒<<,故45B = ，18075C A B =--= ,故选：A3.已知数据1x ，2x ，L ，9x 的方差为25，则数据131x +，231x +，L ，931x +的标准差为（）A.25B.75C.15D.【答案】C 【解析】【分析】根据方差的性质求出新数据的方差，进而计算标准差即可.【详解】因为数据1x ，2x ，L ，9x 的方差为25，所以另一组数据131x +，231x +，L ，931x +的方差为2325225⨯=，15=.故选：C4.在正方形ABCD 中，M 是BC 的中点．若AC AM BD λμ=+，则λμ+的值为（）A.43B.53C.158D.2【答案】B 【解析】【分析】建立平面直角坐标系，利用向量的坐标运算求解作答.【详解】在正方形ABCD 中，以点A 为原点，直线AB ，AD 分别为x ，y 轴建立平面直角坐标系，如图，令||2AB =，则(2,0),(2,2),(0,2),(2,1)B C D M ，(2,2),(2,1),(2,2)AC AM BD ===-，(22,2)AM BD λμλμλμ+=-+ ，因AC AM BD λμ=+ ，于是得22222λμλμ-=⎧⎨+=⎩，解得41,33λμ==，53λμ+=所以λμ+的值为53.故选：B5.正三棱柱111ABC A B C -的底面边长为2D 为BC 中点，则三棱锥11A B DC -的体积为A.3B.32C.1D.32【答案】C 【解析】【详解】试题分析：如下图所示，连接AD ，因为ABC ∆是正三角形，且D 为BC 中点，则AD BC ⊥，又因为1BB ⊥面ABC ，故1BB AD ⊥，且1BB BC B ⋂=，所以AD ⊥面11BCC B ，所以AD 是三棱锥11A B DC -的高，所以11111133133A B DC B DC V S AD -∆=⋅==．考点：1、直线和平面垂直的判断和性质；2、三棱锥体积．6.在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若cos cos sin sin()sin B C AA C b c C ⎛⎫++= ⎪⎝⎭，3B π=，则a c +的取值范围是（）A.332⎛⎝ B.332⎛⎝ C.332⎣ D.332⎡⎢⎣【答案】A 【解析】【分析】利用三角恒等变换及正弦定理将cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭进行化简，可求出b 的值，再利用边化角将a c +化成角，然后利用辅助角公式及角的范围即可得到答案.【详解】由题知cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭，3B π=∴cos cos sin sin sin B C AB bc C ⎛⎫+=⎪⎝⎭即cos cos 3sin B C Ab c C+=由正弦定理化简得∴sin cos cos 3sin 3A cB bC C ⋅+⋅==∴23sin sin cos cos sin 3AC B C B +=∴23sin sin()sin 3AB C A +==∴2b =3B π=∴1sin sin sin a b cA B C===∴23sin sin sin sin()sin cos )3226a c A C A A A A A ππ+=+=+-=+=+ 203A π<<∴5666A πππ<+<∴)26A π<+≤即2a c <+≤故选：A .【点睛】方法点睛：边角互化的方法（1）边化角：利用正弦定理2sin sin sin a b cr A B C===（r 为ABC 外接圆半径）得2sin a r A =，2sin b r B =，2sin c r C =；（2）角化边：①利用正弦定理：sin 2aA r=，sin 2b B r =，sin 2c C r=②利用余弦定理：222cos 2b c a A bc+-=7.设O 为△ABC 的外心，若2AO AB AC =+，则sin BAC ∠的值为（）A.4B.4C.4-D.4【答案】D 【解析】【分析】设ABC 的外接圆半径为R ，由已知条件可得,2AC BO = ，所以12AC R =，且//AC BO ，取AC的中点M ，连接OM 可得π2BOM ∠=，计算cos sin BOC MOC ∠=-∠的值，再由余弦定理求出BC ，在ABC 中，由正弦定理即可求解.【详解】设ABC 的外接圆半径为R ，因为2AO AB AC =+ ,2AC AO AB BO =-=，所以1122AC BO R ==，且//AC BO ，取AC 的中点M ，连接OM ，则OM AC ⊥，因为//AC BO ，所以OM BO ⊥，即π2BOM ∠=，所以11π124cos cos sin 24AC RMC BOC MOC MOC OC OB R ⎛⎫∠=+∠=-∠=-=-=-=- ⎪⎝⎭,在BOC中由余弦定理可得：2BC R ===，在ABC中，由正弦定理得：2sin 224RBCBAC RR ∠===.故选：D8.高为8的圆台内有一个半径为2的球1O ，球心1O 在圆台的轴上，球1O 与圆台的上底面、侧面都相切.圆台内可再放入一个半径为3的球2O ，使得球2O 与球1O 、圆台的下底面及侧面都只有一个公共点.除球2O ，圆台内最多还能放入半径为3的球的个数是（）A.1 B.2C.3D.4【答案】B 【解析】【详解】作过2O 的圆台的轴截面，如图1.再作过2O 与圆台的轴垂直的截面，过截面与圆台的轴交于圆O .由图1.易求得24OO =.图1这个问题等价于：在以O 为圆心、4为半径的圆上，除2O 外最多还可放几个点，使以这些点及2O 为圆心、3为半径的圆彼此至多有一个公共点.由图2，3sin45sin sin604θ︒<=︒，有4560θ︒<<︒.图2所以，最多还可以放入36013122θ︒⎡⎤-=-=⎢⎣⎦个点，满足上述要求.因此，圆台内最多还可以放入半径为3的球2个.二、多项选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.已知某地区有小学生120000人，初中生75000人，高中生55000人，当地教育部门为了了解本地区中小学生的近视率，按小学生、初中生、高中生进行分层抽样，抽取一个容量为2000的样本，得到小学生，初中生，高中生的近视率分别为30%，70%，80%.下列说法中正确的有（）A.从高中生中抽取了460人B.每名学生被抽到的概率为1125C.估计该地区中小学生总体的平均近视率为60%D.估计高中学生的近视人数约为44000【答案】BD 【解析】【分析】根据分层抽样、古典概型、频率公式等知识对选项进行分析，从而确定正确选项.【详解】高中生抽取5500020004401200007500055000⨯=++人，A 选项错误.每名学生被抽到的概率为200011200007500055000125=++，B 选项正确.学生总人数为1200007500055000250000++=，估计该地区中小学生总体的平均近视率为1200007500055000132.50.30.70.80.53250000250000250000250⨯+⨯+⨯==，C 选项错误.高中学生近视人数约为550000.844000⨯=人，D 选项正确.故选：BD10.G 是ABC 的重心，2,4,120,AB AC CAB P ∠=== 是ABC 所在平面内的一点，则下列结论正确的是（）A.0GA GB GC ++= B.AB 在AC上的投影向量等于12- AC .C.3AG =D.()AP BP CP ⋅+ 的最小值为32-【答案】ACD 【解析】【分析】根据向量的线性运算，并结合重心的性质，即可判断A ，根据投影向量的定义，判断B ；根据向量数量积公式，以及重心的性质，判断C ；根据向量数量积的运算率，结合图形转化，即可判断D.【详解】A.以,GB GC 为邻边作平行四边形GBDC ，,GD BC 交于点O ，O 是BC 的中点，因为G 是ABC 的重心，所以,,A G O 三点共线，且2AG GO =，所以2GB GC GD GO +== ，2GA AG GO =-=- ，所以0GA GB GC ++=，故A 正确；B.AB 在AC 上的投影向量等于1cos1204AC AB AC AC ⨯=-，故B 错误；C.如图，因为()12AO AB AC =+ ，所以()222124AO AB AC AB AC =++⋅,即211416224342AO ⎛⎫=+-⨯⨯⨯= ⎪⎝⎭，即3AO = 因为点G 是ABC 的重心，22333AG AO ==，故C 正确；D.取BC 的中点O ，连结,PO PA ，取AO 中点M ，则2PA PO PM += ，()12AO AB AC =+，()()2221124816344AO AB AB AC AC =+⋅+=⨯-+= ,则()()()()221224AP BP CP PA PB PC PA PO PA PO PA PO ⎡⎤⋅+=⋅+=⋅=⨯+--⎢⎥⎣⎦，222132222PM OA PM =-=- ,显然当,P M 重合时，20PM = ，()AP BP CP ⋅+ 取最小值32-，故D 正确.故选：ACD【点睛】关键点点睛：本题的关键是对于重心性质的应用，以及向量的转化.11.如图，在棱长为2的正方体1111ABCD A B C D -中，O 为正方体的中心，M 为1DD 的中点，F 为侧面正方形11AA D D 内一动点，且满足1B F ∥平面1BC M ，则（）A.三棱锥1D DCB -的外接球表面积为12πB.动点F 的轨迹的线段为22C.三棱锥1F BC M -的体积为43D.若过A ，M ，1C 三点作正方体的截面Ω，Q 为截面Ω上一点，则线段1AQ 长度的取值范围为45,225⎡⎢⎣⎦【答案】AC 【解析】【分析】选项A ：三棱锥1D DCB -的外接球即为正方体的外接球，结合正方体的外接球分析；选项B ：分别取1AA ，11A D 的中点H ，G ，连接1B G ，GH ，1HB ，1AD ；证明平面1B GH ∥平面1BC M ，从而得到点F 的轨迹为线段GH ；选项C ：根据选项B 可得出GH ∥平面1BC M ，从而得到点F 到平面1BC M 的距离为H 到平面1BC M 的距离，再结合线面垂直及等体积法，利用四棱锥的体积求解所求三棱锥的体积；选项D ：设N 为1BB 的中点，从而根据面面平行的性质定理可得到截面Ω即为面1AMC N ，从而线段1AQ 长度的最大值为线段11A C 的长，最小值为四棱锥11A AMC N -以1A 为顶点的高.【详解】对于A ：由题意可知：三棱锥1D DCB -的外接球即为正方体的外接球，可知正方体的外接球的半径3R =所以三棱锥1D DCB -的外接球表面积为24π12πR =，故A 正确；对于B ：如图分别取1AA ，11A D 的中点H ，G ，连接1B G ，GH ，1HB ，1AD ．由正方体的性质可得11B H C M ∥，且1B H ⊂平面1B GH ，1C M ⊄平面1B GH ，所以1C M //平面1B GH ，同理可得：1BC //平面1B GH ，且111BC C M C ⋂=，11,BC C M ⊂平面1BC M ，所以平面1B GH ∥平面1BC M ，而1B F ∥平面1BC M ，所以1B F ⊂平面1B GH ，所以点F 的轨迹为线段GH ，其长度为12222⨯=，故B 错误；对于C ：由选项B 可知，点F 的轨迹为线段GH ，因为GH ∥平面1BC M ，则点F 到平面1BC M 的距离为H 到平面1BC M 的距离，过点B 作1BP B H ⊥，因为11B C ⊥平面11ABB A ，BP ⊂平面11ABB A ，所以11B C BP ⊥，又1111⋂=B C B H B ，111,B C B H ⊂平面11B C MH ，所以BP ⊥平面11B C MH ，所以1111111111114252232335F BC M H BC M B C MH B B C MH B C MHV V V V S BP ----====⨯=⨯⨯⨯⨯，故C 正确；对于D ：如图，设平面Ω与平面11AA B B 交于AN ，N 在1BB 上，因为截面Ω⋂平面11AA D D AM =，平面11AA D D ∥平面11BB C C ，所以1AM C N ∥，同理可证1AN C M ∥，所以截面1AMC N 为平行四边形，所以点N 为1BB 的中点，在四棱锥11A AMC N -中，侧棱11A C 最长，且11A C =设棱锥11A AMC N -的高为h ，因为1AM C M ==1AMC N 为菱形，所以1AMC 的边1AC ，又1AC =则112AMC S =⨯=△1111111142223323C AA M AA M V SD C -=⋅=⨯⨯⨯⨯=△，所以1111114333A AMC AMC C AA M V S h V --=⋅===△，解得3h =.综上，可知1AQ 长度的取值范围是,3⎡⎢⎣，故D 错误.故选：AC【点睛】关键点睛：由面面平行的性质得到动点的轨迹，再由锥体的体积公式即可判断C ，D 选项关键是找到临界点，求出临界值.三、填空题：本小题共3小题，每小题5分，共15分.12.已知复数()221i i()z m m m =-++⋅∈R 表示纯虚数，则m =________．【答案】1-【解析】【分析】根据2i 1=-和复数的分类要求得出参数值；【详解】因为复数()()2221ii=11i()z m m mm m =-++⋅-+-⋅∈R 表示纯虚数，所以210,10,m m ⎧-=⎨-≠⎩解得1m =-，故答案为：1-.13.定义集合(){},02024,03,,Z |A x y x y x y =≤≤≤≤∈，则从A 中任选一个元素()00,x y ，它满足00124x y -+-<的概率是________．【答案】42025【解析】【分析】利用列举法求解符合条件的()00,x y ，即可利用古典概型的概率公式求解.【详解】当0y =时，02024,Z x x ≤≤∈，有2025种选择，当1,2,3y =时，02024,Z x x ≤≤∈，分别有2025种选择，因此从A 中任选一个元素()00,x y ，共有202548100⨯=种选择，若00y =，则022y -=，此时由00124x y -+-<得012x -<，此时0x 可取0，1，2，若01y =或3，则021y -=，此时由00124x y -+-<得013x -<，此时0x 可取0，1，2，3，若02y =，则020y -=，此时由00124x y -+-<得014x -<，此时0x 可取0，1，2，3，4，综上可得满足00124x y -+-<的共有342516+⨯+=种情况，故概率为16481002025=故答案为：4202514.在ABC 和AEF △中，B 是EF的中点，1,6,AB EF BC CA ====，若2AB AE AC AF ⋅+⋅= ，则EF 与BC的夹角的余弦值等于__________.【答案】23【解析】【分析】【详解】由题意有：()()2AB AE AC AF AB AB BE AC AB BF ⋅+⋅=⋅++⋅+=,即22AB AB BE AC AB AC BF +⋅+⋅+⋅= ，而21AB =，据此可得：11,AC AB BE BF ⋅=⨯-=- ，即()112,2BF AC AB BF BC +⋅--=∴⋅= ，设EF 与BC 的夹角为θ，则2cos 2,cos 3BF BC θθ⨯⨯=∴= .四、解答题：本小题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.某学校为了解本校历史、物理方向学生的学业水平模拟测试数学成绩情况，分别从物理方向的学生中随机抽取60人的成绩得到样本甲，从历史方向的学生中随机抽取n 人的成绩得到样本乙，根据两个样本数据分别得到如下直方图：已知乙样本中数据在[70,80)的有10个．（1）求n 和乙样本直方图中a 的值；（2）试估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的第75百位数（同一组中的数据用该组区间中点值为代表）；（3）采用分层抽样的方法从甲样本数据中分数在[60,70)和[70,80)的学生中抽取6人，并从这6人中任取2人，求这两人分数都在[70,80)中的概率．【答案】（1）50n =，0.018a =；（2）物理方向的学生本次模拟测试数学成绩的平均值为81.5，历史方向的学生本次模拟测试数学成绩的第75百位数为88.25；（3）25【解析】【分析】（1）由频率分布直方图得乙样本中数据在[70,80)的频率为0.2，这个组学生有10人，由此能求出n ，由乙样本数据直方图能求出a ；（2）利用甲、乙样本数据频率分布直方图能估计估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的第75百位数；（3）由频率分布直方图可知从分数在[60,70)和[70,80)的学生中分别抽取2人和4人，将从分数在[60,70)中抽取的2名学生分别记为1A ，2A ，从分数在[70,80)中抽取的4名学生分别记为1b ，2b ，3b ，4b ，利用列举法能求出这两人分数都在[70,80)中的概率．【小问1详解】解：由直方图可知，乙样本中数据在[70,80)的频率为0.020100.20⨯=，则100.20n=，解得50n =；由乙样本数据直方图可知，(0.0060.0160.0200.040)101a ++++⨯=，解得0.018a =；【小问2详解】解：甲样本数据的平均值估计值为(550.005650.010750.020850.045950.020)1081.5⨯+⨯+⨯+⨯+⨯⨯=，乙样本数据直方图中前3组的频率之和为(0.0060.0160.02)100.420.75++⨯=<，前4组的频率之和为(0.0060.0160.020.04)100.820.75+++⨯=>，所以乙样本数据的第75百位数在第4组，设第75百位数为x ，(80)0.040.420.75x -⨯+=，解得88.25x =，所以乙样本数据的第75百位数为88.25，即物理方向的学生本次模拟测试数学成绩的平均值为81.5，历史方向的学生本次模拟测试数学成绩的第75百位数为88.25；【小问3详解】解：由频率分布直方图可知从分数在[60,70)和[70,80)的学生中分别抽取2人和4人，将从分数在[60,70)中抽取的2名学生分别记为1A ，2A ，从分数在[70,80)中抽取的4名学生分别记为1b ，2b ，3b ，4b ，则从这6人中随机抽取2人的基本事件有：12(,)A A ，11(,)A b ，12(,)A b ，13(,)A b ，14(,)A b ，21(,)A b ，22(,)A b ，23(,)A b ，24(,)A b ，12()b b ,，13(,)b b ，14(,)b b ，23(,)b b ，24(,)b b ，34(,)b b 共15个，所抽取的两人分数都在[70,80)中的基本事件有6个，即这两人分数都在[70,80)中的概率为62155=．16.（建立空间直角坐标系答题不得分）如图，在四棱锥11A BCC B -中，平面ABC ⊥平面11BCC B ，△ABC 是正三角形，四边形11BCC B 是正方形，D 是AC 的中点．（1）求证：1//AB 平面1BDC ；（2）求直线BC 和平面1BDC 所成角的正弦值的大小．【答案】（1）证明见解析（2）55【解析】【分析】（1）连接1B C ，交1BC 于点O ，连接OD ，由中位线的性质，可知1//OD AB ，再由线面平行的判定定理，得证；（2）过点C 作1CE C D ⊥于点E ，连接BE ，可证CE ⊥平面1BDC ，从而知CBE ∠即为所求，再结合等面积法与三角函数的定义，得解．【小问1详解】连接1B C ，交1BC 于点O ，连接OD ，则O 为1B C 的中点，因为D 是AC 的中点，所以1//OD AB ，又OD ⊂平面1BDC ，1AB ⊄平面1BDC ，所以1AB ∥平面1BDC ．【小问2详解】过点C 作1CE C D ⊥于点E ，连接BE ，因为四边形11BCC B 是正方形，所以1BC CC ⊥，又平面ABC⊥平面11BCC B ，1CC ⊂平面11BCC B ，平面ABC ⋂平面11BCC B BC =，所以1CC ⊥平面ABC ，因为BD ⊂平面ABC ，所以1CC BD ⊥，因为ABC 是正三角形，且D 是AC 的中点，所以BD AC ⊥，又1CC AC C =I ，1,⊂CC AC 平面1ACC ，所以BD ⊥平面1ACC ，因为CE ⊂平面1ACC ，所以BD CE ⊥，又1C D BD D =I ，1,C D BD ⊂平面1BDC ，所以CE ⊥平面1BDC ，所以CBE ∠就是直线BC 和平面1BDC 所成角，设2BC =，在1Rt DCC 中，11CE DC CD CC ⋅=⋅，所以5CE ==，在Rt BCE 中，5sin 25CE CBE BC ∠===.17.甲、乙两人进行乒乓球对抗赛，每局依次轮流发球，连续赢2个球者获胜，且比赛结束，通过分析甲、乙过去比赛的数据知，甲发球甲赢的概率为23，乙发球甲赢的概率为25，不同球的结果互不影响，已知某局甲先发球.（1）求该局打4个球甲赢的概率；（2）求该局打5个球结束的概率.【答案】（1）875（2）44675【解析】【分析】（1）先设甲发球甲赢为事件A ，乙发球甲赢为事件B ，然后分析这4个球的发球者及输赢者，即可得到所求事件的构成，利用相互独立事件的概率计算公式即可求解；（2）先将所求事件分成甲赢与乙赢这两个互斥事件，再分析各事件的构成，利用互斥事件和相互独立事件的概率计算公式即可求得概率.【小问1详解】设甲发球甲赢为事件A ，乙发球甲赢为事件B ，该局打4个球甲赢为事件C ，由题知，2()3P A =，2()5P B =，则C ABAB =，所以23228()()()(()()353575P C P ABAB P A P B P A P B ===⨯⨯⨯=，所以该局打4个球甲赢的概率为875.【小问2详解】设该局打5个球结束时甲赢为事件D ，乙赢为事件E ，打5个球结束为事件F ，易知D ，E 为互斥事件，D ABABA =，E ABABA =，F D E =⋃，所以()()()()()()()P D P ABABA P A P B P A P B P A ==2222281135353675⎛⎫⎛⎫=-⨯⨯-⨯⨯= ⎪ ⎪⎝⎭⎝⎭，()()()()()()()P E P ABABA P A P B P A P B P A ==2222241113535375⎛⎫⎛⎫⎛⎫=⨯-⨯⨯-⨯-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以8444()()()()67575675P F P D E P D P E =⋃=+=+=，所以该局打5个球结束的概率为44675.18.在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，22cos a c b C -=.（1）求B ；（2）若点D 为边BC 的中点，点E ，F 分别在边AB ，AC （包括顶点）上，π6EDF ∠=，2b c ==.设BDE α∠=，将DEF 的面积S 表示为α的函数，并求S 的取值范围.【答案】（1）π3（2）3ππ,π328sin 23S αα=≤≤⎛⎫- ⎪⎝⎭，3,84S ⎡∈⎢⎣⎦【解析】【分析】（1）由题干及余弦定理可得222a c b ac +-=，再根据余弦定理即可求解；（2）由题可得ABC 为等边三角形，ππ32α≤≤，在BDE 与CDF 中，分别由正弦定理求出DE ，DF ，根据三角形面积公式可得3ππ,2ππ3216sin sin 36S ααα=≤≤⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，由三角恒等变换及正弦函数的图象与性质即可求解.【小问1详解】因为22cos a c b C -=，所以222222222a b c a b c a c b ab a +-+--=⋅=，即222a cb ac +-=，所以2221cos 222a cb ac B ac ac +-===.因为()0,πB ∈，所以π3B =.【小问2详解】由π3B=及2b c==可知ABC为等边三角形.又因为π6EDF∠=，BDEα∠=，所以ππ32α≤≤.在BDE中，2π3BEDα∠=-，由正弦定理可得sin sinDE BDB BED∠=，即32π2sin3DEα=⎛⎫-⎪⎝⎭.在CDF中，π6CFDα∠=-，由正弦定理可得sin sinDF CDC CFD∠=，即π2sin6DFα=⎛⎫-⎪⎝⎭.所以31π3ππsin,2ππ2ππ8632 sin sin16sin sin3636Sααααα=⨯⨯=≤≤⎛⎫⎛⎫⎛⎫⎛⎫----⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.因为2ππ11sin sin cos sin sin cos362222αααααα⎛⎫⎛⎫⎛⎫⎛⎫--=+-⎪⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭2213313sin cos cos sin sin2cos224444αααααα=-+=-1πsin223α⎛⎫=-⎪⎝⎭，因为ππ32α≤≤，所以ππ2π2,333α⎡⎤-∈⎢⎥⎣⎦，所以π3sin2,132α⎤⎛⎫-∈⎥⎪⎝⎭⎣⎦，所以1π1sin2,2342α⎤⎛⎫-∈⎥⎪⎝⎭⎣⎦.所以2ππ16sin sin36αα⎛⎫⎛⎫⎡⎤--∈⎪ ⎪⎣⎦⎝⎭⎝⎭，所以33,2ππ8416sin sin36αα⎡∈⎢⎛⎫⎛⎫⎣⎦--⎪ ⎪⎝⎭⎝⎭，所以333,2ππ8416sin sin36Sαα⎡=∈⎢⎛⎫⎛⎫⎣⎦--⎪ ⎪⎝⎭⎝⎭.所以S 的取值范围为3,84⎡⎢⎣⎦.19.（建立空间直角坐标系答题不得分）如图，在三棱柱ADP BCQ -中，侧面ABCD 为矩形．（1）若PD⊥面ABCD ，22PD AD CD ==，2NC PN =，求证：DN BN ⊥；（2）若二面角Q BC D --的大小为θ，π2π,43θ⎡⎤∈⎢⎥⎣⎦，且2cos 2AD AB θ=⋅，设直线BD 和平面QCB 所成角为α，求sin α的最大值．【答案】（1）证明见解析（2）12-【解析】【分析】（1）问题转化为证明DN⊥平面BCP ，即证明ND BC ⊥和DN PC ⊥，ND BC ⊥转化为证明BC ⊥平面PQCD ，而ND BC ⊥则只需证明PDN PCD△△（2）作出二面角Q BC D --的平面角以及直线BD 与平面QCB 所成的角，列出sin α的表达式，最后把问题转化为函数最值问题.【小问1详解】因为PD⊥平面ABCD ，BC ⊂平面ABCD ，所以PD BC ⊥，又CD BC ⊥，PD CD D ⋂=，,PD CD ⊂平面PCD ，所以BC ⊥平面PQCD ，又ND ⊂平面PQCD ，所以ND BC ⊥，在Rt PCD 中，2PD ==，则CD =3PC =，所以2NC =，1PN =，由PN PDND PC=，DPN CPD ∠=∠，所以PDN PCD △△，所以DN PC ⊥，又因为ND BC ⊥，PC BC C ⋂=，,PC BC ⊂平面BCP ，所以DN⊥平面BCP ，又因为BN ⊂平面BCP ，所以DN BN ⊥.【小问2详解】在平面QBC 中，过点C 作CF BC ⊥，因为ABCD 为矩形，所以BC CD ⊥，所以DCF ∠为二面角Q BC D --的平面角，且DCF θ∠=，又⋂=CF CD C ，,CD CF ⊂平面CDF ，所以BC ⊥平面CDF ，在平面CDF 中，过点D 作DG FC ⊥，垂足为G ，连接BG ，因为BC ⊥平面CDF ，DG ⊂平面CDF ，所以DG BC ⊥，又BC FC C ⋂=，,BC FC ⊂平面BCQ ，所以DG ⊥平面BCQ ，所以DBG ∠为直线BD 与平面QCB 所成的角，即DBG α∠=，sin DG DC θ=，又因为2cos 2AD AB θ=⋅，所以222sin 32cos 14cos 2DGBDAB AD αθθ===+++π2π,43θ⎡⎤∈⎢⎥⎣⎦可得12cos ,22θ⎡∈-⎢⎣⎦，21cos 0,2θ⎡⎤∈⎢⎥⎣⎦，设32cos t θ=+，2,32t ⎤∈+⎥⎦，则23cos 2t θ-=，()2223sin 1cos 14t θθ-=-=-，所以()2222563125651sin 14222t t t t α⎛⎫-++ ⎪--+⎝⎭=-=≤=，当且仅当25t =时等号，所以sin α51-.【点睛】关键点点睛：本题的关键是作出二面角Q BC D --的平面角以及直线BD 与平面QCB 所成的角，然后写出sin α的表达式，最后求函数最值问题利用了换元法和基本不等式.。

上海市高一下学期期末考试数学试卷含答案

上海市高一数学下学期期末考试试卷考试范围：必修二；总分：150分；考试时间：120分钟学校:___________姓名：___________班级：___________考号：___________注意事项：1．本试卷共4页，21道试题，满分150分，考试时间120分钟．2．本试卷分设试卷和答题纸．试卷包括试题与答题要求．作答必须涂（选择题）或写（非选择题）在答题纸上，在试卷上作答一律不得分．3．答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号码等相关信息． 4．测试范围：高二下+高三全部内容 5．考试结束后，将本试卷和答题卡一并交回。

一、填空题（本大题共有12题，满分54分，第1-6题每题4分，第7-12题每题5分）考生应在答题纸的相应位置直接填写结果．1．如图，在平面直角坐标系xOy 中，角α与β角均以Ox 为始边，终边分别是射线OA 和射线OB ，射线OA ，OC 与单位圆的交点分别为34,55A ⎛⎫⎪⎝⎭，(1,0)C -．若6BOC π∠=，则cos()βα-的值是_________．2．化简sin sin()tan(3)23cos sin()2παπαπαπαα⎛⎫+++ ⎪⎝⎭=⎛⎫+- ⎪⎝⎭________． 3．复数112z i =-+，21z i =-，332z i =-，它们所对应的点分别为A 、B 、C ，若(),OC xOA yOB x y R =+∈，则yx=________. 4．设z ＝1－i ，则复数22()z z+·z ＝________． 5．已知向量()()1,3,3,3a b ==-，则a 与b 的夹角大小为___________.6．已知向量()()()2,1,0,1,4,3a b c ===，若λ为实数，且()a b c λ+⊥，则λ=___________.7．若函数()cos f x x =,[]2π,2πx ∈-,则不等式()0xf x >的解集为______. 8．若1sin 33πα⎛⎫-=-⎪⎝⎭，则cos 6πα⎛⎫+= ⎪⎝⎭___________.9．已知1sin 64x π⎛⎫+= ⎪⎝⎭，则25sin sin 63x x ππ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭_______.10．已知函数()3sin 4cos f x x x =+，[]12,0,x x ∈π，则()()12f x f x -的最大值是________． 11．若函数()2sin 21()6f x x a a R π⎛⎫=++-∈ ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上有两个不同的零点12,x x ，则12x x a +-的取值范围是______________.12．已知将函数()sin()(06,)22f x x ππωθωθ=+<<-<<的图象向右平移3π个单位长度得到画()g x 的图象，若()f x 和()g x 的图象都关于4x π=对称，则ωθ⋅=________.二、选择题（本大题共有4题，满分20分，每题5分）每题有且只有一个正确选项，考生应在答题纸的相应位置，将代表正确选项的小方格涂黑．13．把复数z 1与z 2对应的向量OAOB ，分别按逆时针方向旋转4π和53π后，重合于向量OM 且模相等，已知21z =-，则复数1z 的代数式和它的辐角主值分别是（）A ．，34π B ．3,4πC ．,4πD ．,4π14．已知两非零向量b 与a 的夹角为120︒，且2243a a b =-=，，则b =（） A ．8B ．6C ．4D ．215．关于函数()sin |||sin |f x x x =+有下述四个结论正确的是（） A ．()f x 是周期函数B ．()f x 在区间,2ππ⎛⎫⎪⎝⎭单调递减 C ．()f x 在[,]-ππ有4个零点D ．()f x 的值域为[2,2]-16．在ABC 中，已知2b =，45B =︒，c =C 为（） A ．60︒B ．150︒C ．60︒或120︒D ．120︒三、解答题（本大题共有5题，满分76分）解答下列各题必须在答题纸的相应位置写出必要的步骤． 17．若不等式m 2－(m 2－3m )i <(m 2－4m ＋3)i ＋10成立，求实数m 的值.18．已知向量33cos,sin ,cos ,sin 2222x x a x x b ⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭，且0,2x π⎡⎤∈⎢⎥⎣⎦，求：（1）a b ⋅及||a b +；（2）若()2||f x a b a b λ=⋅-+的最小值为32-，求实数λ的值．19．已知函数21())sin ()(02)632f x x x ππωωω=+++-<<，且()04f π=．（1）求()f x 的解析式;（2）先将函数()y f x =图象上所有的点向右平移6π个单位长度，再将所得各点的纵坐标伸长到原来的2倍，横坐标不变，得到函数()y g x =的图象．若()g x 在区间,44ππαα⎛⎫-+⎪⎝⎭有且只有一个0x ，使得0()g x 取得最大值，求α的取值范围．20．在①sinsin sin A b cB C b a+=--；②c a =③2S CB =⋅，这三个条件中任选一个，补充在下面的横线上，并加以解答．在ABC 中，角A ，B ，C 的对边分别是a ，b ，C ，S 为ABC 的面积，若__________（填条件序号）（1）求角C 的大小；（2）若边长2c =，求ABC 的周长的最大值．21．ABC 的内角A ，B ，C 所对的边分别是a ，b ，c ．已知222(2sin )4sin sin A B C B =-．（1）求角C 的大小；（2）若1,b c ==，求cos()B C -的值．高一数学下学期期末答案解析考试范围：必修二；总分：150分；考试时间：120分钟学校:___________姓名：___________班级：___________考号：___________注意事项：5．本试卷共4页，21道试题，满分150分，考试时间120分钟．6．本试卷分设试卷和答题纸．试卷包括试题与答题要求．作答必须涂（选择题）或写（非选择题）在答题纸上，在试卷上作答一律不得分．7．答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号码等相关信息． 8．测试范围：高二下+高三全部内容 5．考试结束后，将本试卷和答题卡一并交回。

潍坊市高一数学下学期期末考试试题含解析

因为， ,所以点P到x轴的距离的最大值为6，故C不正确；
当时， ,此时，点，，故D正确，
故选:AD．
【点睛】本题考查的是有关函数的应用问题，涉及到的知识点有数学建模，将实际问题转化为函数问题来解决，结合三角函数的相应的性质求得结果,属于中档题。
三、填空题：本题共4小题，每小题5分，共20分。
【答案】(1）；（2）。
【解析】
【分析】
（1）用三角函数的定义；
（2)先求正切值，再把弦化切.
【详解】(1)由题意知，，
因为，
所以。
解得，
所以 .
(2）当时，，
所以。
【点睛】本题为基础题，考查三角函数的定义及同角三角函数的关系。
18。某广场设置了一些多面体形或球形的石凳供市民休息.如图(1)的多面体石凳是由图(2）的正方体石块截去八个相同的四面体得到,且该石凳的体积是 .
【详解】由题意，某扇形的半径为 ,圆心角为 ,
根据扇形的面积公式，可得
所以此扇形的面积为。
故选:B。
【点睛】本题主要考查了扇形的面积公式及其应用，其中解答中熟记扇形的面积公式是解答的关键,着重考查推理与运算能力。
4。在中，点满足，则（ )
A。 B.
C. D。
【答案】A
【解析】
【分析】
由已知条件可得，然后由向量的加减法法则进行运算可得答案.
对于C，因为平面与平面的位置关系有：相交或平面，因为 , 是空间两个不同的平面,而 ,所以平面与相交，即，必相交于一条直线，故C正确；
对于D，当直线与平面相交，且垂直于平面内的无数条直线,若这些直线中没有相交直线，则不一定垂直平面 ,故D 不正确，

2022-2023学年山东省济南市高一(下)期末数学试卷【答案版】

2022-2023学年山东省济南市高一（下）期末数学试卷一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．在复平面内，复数z =11+2i对应的点位于（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．《2023年五一出游数据报告》显示，济南凭借超强周边吸引力，荣登“五一”最强周边游“吸金力”前十名榜单．其中，济南天下第一泉风景区接待游客100万人次，济南动物园接待游客30万人次，千佛山景区接待游客20万人次．现采用按比例分层抽样的方法对三个景区的游客共抽取1500人进行济南旅游满意度的调研，则济南天下第一泉风景区抽取游客（） A ．1000人B ．300人C ．200人D ．100人3．设α，β为两个平面，则α⊥β的充要条件是（） A ．α过β的一条垂线B ．α，β垂直于同一平面C ．α内有一条直线垂直于α与β的交线D ．α内有两条相交直线分别与β内两条直线垂直 4．袋子中有5个大小质地完全相同的球，其中3个红球，2个黄球，从中不放回地依次随机摸出2个球，则第二次摸到红球的概率为（） A ．110B ．15C ．25D ．355．已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，B =π4，b =1，c =√62，则角C 的值为（）A ．π3B ．2π3C ．π3或2π3D ．无解6．如果三棱锥S ﹣ABC 底面不是等边三角形，侧棱SA ，SB ，SC 与底面ABC 所成的角都相等，SO ⊥平面ABC ，垂足为O ，则O 是△ABC 的（） A ．垂心B ．重心C ．内心D ．外心7．已知锐角△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，B =π3，c =2，则△ABC 的周长的取值范围为（）A ．(3+√3，2+2√3)B ．(3+√3，4+2√3)C ．(3+√3，6+2√3)D ．(3+√3，+∞)8．在四棱锥P ﹣ABCD 中，P A ⊥底面ABCD ，底面ABCD 为正方形，P A ＝AB ＝1．点E ，F ，G 分别为平面P AB ，平面P AD 和平面ABCD 内的动点，点Q 为棱PC 上的动点，则QE 2+QF 2+QG 2的最小值为（） A ．12B ．23C ．34D ．1二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 9．已知复数ω=−12+√32i ，则下列说法中正确的是（）A ．|ω|＝1B ．ω3＝﹣1C ．ω2＝ωD ．ω2+ω+1＝010．先后抛掷质地均匀的硬币两次，则下列说法正确的是（） A ．事件“恰有一次正面向上”与事件“恰有一次反面向上”相等B ．事件“至少一次正面向上”与事件“至少一次反面向上”互斥C ．事件“两次正面向上”与事件“两次反面向上”互为对立事件D ．事件“第一次正面向上”与事件“第二次反面向上”相互独立11．某学校为了调查高一年级学生每天体育活动时间情况，随机选取了100名学生，绘制了如图所示频率分布直方图，则下列说法正确的是（）A ．平均数的估计值为30B ．众数的估计值为35C ．第60百分位数估计值是32D ．随机选取这100名学生中有25名学生体育活动时间不低于40分钟12．如图，已知三棱锥D ﹣ABC 可绕AB 在空间中任意旋转，△ABC 为等边三角形，AB 在平面α内，AB ⊥CD ，AB ＝2，CD =√6，cos∠CBD =14，则下列说法正确的是（）A ．二面角D ﹣AB ﹣C 为π2B ．三棱锥D ﹣ABC 的外接球表面积为20π3C ．点C 与点D 到平面α的距离之和的最大值为2 D ．点C 在平面α内的射影为点M ，线段DM 的最大值为√15+√32三、填空题：本题共4小题，每小题5分，共20分． 13．一组数据1，2，4，5，8的第75百分位数为．14．在正方体ABCD ﹣A 1B 1C 1D 1中，直线BC 1与直线CD 1夹角的余弦值为． 15．在圆C 中，已知弦AB ＝2，则AB →⋅AC →的值为．16．已知△ABC 的重心为G ，面积为1，且AB ＝2AC ，则3AG 2+BC 2的最小值为．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10分）已知e →1，e →2是两个单位向量，夹角为π3，设a→=e →1+2e →2，b→=te →1−3e →2．（1）求|a →|；（2）若a →⊥b →，求t 的值．18．（12分）已知正三棱柱ABC ﹣A 1B 1C 1的棱长均为2，M 为A 1C 1的中点．（1）求证：BC 1∥平面AB 1M ；（2）求点B 到平面AB 1M 的距离d ．19．（12分）独立事件是一个非常基础但又十分重要的概念，对于理解和应用概率论和统计学至关重要．它的概念最早可以追溯到17世纪的布莱兹•帕斯卡和皮埃尔•德•费马，当时被定义为彼此不相关的事件．19世纪初期，皮埃尔•西蒙•拉普拉斯在他的《概率的分析理论》中给出了相互独立事件的概率乘法公式．对任意两个事件A 与B ，如果P （AB ）＝P （A ）P （B ）成立，则称事件A 与事件B 相互独立，简称为独立．（1）若事件A 与事件B 相互独立，证明：A 与B 相互独立；（2）甲、乙两人参加数学节的答题活动，每轮活动由甲、乙各答一题，已知甲每轮答对的概率为35，乙每轮答对的概率为23．在每轮活动中，甲和乙答对与否互不影响，各轮结果也互不影响，求甲乙两人在两轮活动中答对3道题的概率．20．（12分）某社区工作人员采用分层抽样的方法分别在甲乙两个小区各抽取了8户家庭，统计了每户家庭近7天用于垃圾分类的总时间（单位：分钟），其中甲小区的统计表如下，设x i ，y i 分别为甲，乙小区抽取的第i 户家庭近7天用于垃圾分类的总时间，s x 2，s y 2分别为甲，乙小区所抽取样本的方差，已知x =18∑ 8i=1x i =200，s x 2=18∑ 8i=1(x i −x)2=200，y =195，s y 2=210，其中i ＝1，2，⋯，8．（1）若a ≤b ，求a 和b 的值；（2）甲小区物业为提高垃圾分类效率，优先试行新措施，每天由部分物业员工协助垃圾分类工作，经统计，甲小区住户每户每天用于垃圾分类的时间减少了5分钟．利用样本估计总体，计算甲小区试行新措施之后，甲乙两个小区的所有住户近7天用于垃圾分类的总时间的平均值z 和方差s z 2．参考公式：若总体划为2层，通过分层随机抽样，各层抽取的样本量、样本平均数和样本方差分别为：m ，x 1，s 12；n ，x 2，s 22，总的样本平均数为ω，样本方差为s 2，则s 2=m m+n [s 12+(x 1−ω)2]+n m+n[s 22+(x 2−ω)2]．21．（12分）如图1，在等腰△ABC 中，AC ＝4，A =π2，O ，D 分别为BC 、AB 的中点，过D 作DE ⊥BC 于E ．如图2，沿DE 将△BDE 翻折，连接BA ，BC 得到四棱锥B ﹣ACED ，F 为AB 中点．（1）证明：DF ⊥平面AOB ；（2）当OB =√2时，求直线BF 与平面BCD 所成的角的正弦值．22．（12分）射影几何学中，中心投影是指光从一点向四周散射而形成的投影，如图，O 为透视中心，平面内四个点E ，F ，G ，H 经过中心投影之后的投影点分别为A ，B ，C ，D ．对于四个有序点A ，B ，C ，D ，定义比值x =CACBDA DB叫做这四个有序点的交比，记作（ABCD ）．（1）证明：（EFGH ）＝（ABCD ）；（2）已知（EFGH）=32，点B为线段AD的中点，AC=√3OB=3，sin∠ACOsin∠AOB=32，求cos A．2022-2023学年山东省济南市高一（下）期末数学试卷参考答案与试题解析一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．在复平面内，复数z=11+2i对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限解：z=11+2i=1−2i(1+2i)(1−2i)=15−25i，它在复平面内对应点为（15，−25），在第四象限．故选：D．2．《2023年五一出游数据报告》显示，济南凭借超强周边吸引力，荣登“五一”最强周边游“吸金力”前十名榜单．其中，济南天下第一泉风景区接待游客100万人次，济南动物园接待游客30万人次，千佛山景区接待游客20万人次．现采用按比例分层抽样的方法对三个景区的游客共抽取1500人进行济南旅游满意度的调研，则济南天下第一泉风景区抽取游客（）A．1000人B．300人C．200人D．100人解：依题意济南天下第一泉风景区应抽取游客1500×100100+30+20=1000(人)．故选：A．3．设α，β为两个平面，则α⊥β的充要条件是（）A．α过β的一条垂线B．α，β垂直于同一平面C．α内有一条直线垂直于α与β的交线D．α内有两条相交直线分别与β内两条直线垂直解：由α⊥β可得α经过β的一条垂线，反之若α经过β的一条垂线，由面面垂直的判定定理可得α⊥β，故A正确；α，β垂直于同一个平面，可得α，β平行或相交，故B错误；α内有一条直线垂直于α与β的交线，可得α，β不一定垂直，故C 错误； α内有两条相交直线分别与β内两条直线垂直，可得α，β平行或相交，故D 错误．故选：A ．4．袋子中有5个大小质地完全相同的球，其中3个红球，2个黄球，从中不放回地依次随机摸出2个球，则第二次摸到红球的概率为（） A ．110B ．15C ．25D ．35解：袋子中有5个大小质地完全相同的球，其中3个红球，2个黄球，从中不放回地依次随机摸出2个球，第二次摸到红球的情况有两种：①第一次摸到红球，第二次摸到红球，概率为：P 1=35×24=310， ②第一次摸到黄球，第二次摸到红球，概率为：P 2=25×34=310，则第二次摸到红球的概率为P ＝P 1+P 2=310+310=35．故选：D ．5．已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，B =π4，b =1，c =√62，则角C 的值为（） A ．π3B ．2π3C ．π3或2π3D ．无解解：∵B =π4，b ＝1，c =√62，由正弦定理有：bsinB=c sinC，∴sinC =csinB b =√62×√221=√32，∵c ＞b ，∴C ＞B ，∴C ∈(π4，π)，∴C =π3或2π3．故选：C ．6．如果三棱锥S ﹣ABC 底面不是等边三角形，侧棱SA ，SB ，SC 与底面ABC 所成的角都相等，SO ⊥平面ABC ，垂足为O ，则O 是△ABC 的（） A ．垂心 B ．重心C ．内心D ．外心解：如图所示：因为SO ⊥平面ABC ，侧棱SA ，SB ，SC 与底面ABC 所成的角都相等，则∠SAO ＝∠SBO ＝∠SCO ，AO =SO tan∠SAO ，BO =SO tan∠SBO ，CO =SOtan∠SCO，故AO ＝BO ＝CO ，故O 是△ABC 的外心．故选：D ．7．已知锐角△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，B =π3，c =2，则△ABC 的周长的取值范围为（）A ．(3+√3，2+2√3)B ．(3+√3，4+2√3)C ．(3+√3，6+2√3)D ．(3+√3，+∞)解：∵B =π3，c ＝2， ∴由正弦定理得asinA=b sinπ3=2sinC，∴b =√3sinC ，a =2sinA sinC =2sin(π3+C)sinC =√3cosC+sinCsinC， ∴a +b =√3sinC+√3cosC+sinCsinC=√3(cosC+1)sinC+1=2√3cos 2C 22sin C 2cos C 2+1=√3tan C 2+1，在锐角△ABC 中，{0＜C ＜π20＜2π3−C ＜π2，解得π6＜C ＜π2， ∴π12＜C 2＜π4，即tanπ12＜tan C2＜1，又tan π6=2tanπ121−tan 2π12=√33，解得tan π12=2−√3或tan π12=−2−√3（不合题意，舍去）， ∴2−√3＜tan C2＜1，∴1＜1tan C 212−3=2+√3，∴√3+1＜√3tan C 2+1＜4+2√3，即√3+1＜a +b ＜4+2√3，∴√3+3＜a +b +c ＜6+2√3，故△ABC 的周长的取值范围为（√3+3，6+2√3）．故选：C ．8．在四棱锥P ﹣ABCD 中，P A ⊥底面ABCD ，底面ABCD 为正方形，P A ＝AB ＝1．点E ，F ，G 分别为平面P AB ，平面P AD 和平面ABCD 内的动点，点Q 为棱PC 上的动点，则QE 2+QF 2+QG 2的最小值为（） A ．12B ．23C ．34D ．1解：由题意得QE ，QF ，QG 均最小时，平方和最小，过点Q 分别作平面P AB ，平面P AD ，平面ABCD 的垂线，垂足分别为E ，F ，G ，连接AQ ，因为P A ⊥面ABCD ，BC ⊂平面ABCD ，所以P A ⊥BC ，因为底面ABCD 为正方形，所以AB ⊥BC ，又因为P A ∩AB ＝A ，P A ，AB ⊂平面P AB ，所以BC ⊥面P AB ，因为QE ⊥平面P AB ，则QE ∥BC ，又因为点Q 在PC 上，则点E 应在PB 上，同理可证F ，G 分别位于PD ，AC 上，从而补出长方体EQFJ ﹣HGIA ，则AQ 是以QE ，QF ，QG 为共点的长方体的对角线，则AQ ²＝QE ²+QF ²+QG ²，则题目转化为求AQ 的最小值，显然当AQ ⊥PC 时，AQ 的最小值，因为四边形ABCD 为正方形，且P A ＝AB ＝1，则AC =√2，因为P A ⊥面ABCD ，AC ⊂面ABCD ，所以P A ⊥AC ，所以PC =√PA 2+AC 2=√3，则直角三角形P AC 斜边AC 的高AQ =1×√2√3=√63，此时AQ 2=23，则QE ²+QF ²+QG ²的最小值为23，故选：B ．二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 9．已知复数ω=−12+√32i ，则下列说法中正确的是（）A ．|ω|＝1B ．ω3＝﹣1C ．ω2＝ωD ．ω2+ω+1＝0解：ω=−12+√32i ，则ω2=(−12+√32i)=−12−√32i ，ω2≠ω，故C 错误； |ω|=√(−12)2+(√32)2=1，故A 正确；ω3＝ω2•ω=(−12−√32i)(−12+√32i)=1，故B 错误； ω2+ω+1=−12−√32i −12+√32i +1=0，故D 正确．故选：AD．10．先后抛掷质地均匀的硬币两次，则下列说法正确的是（）A．事件“恰有一次正面向上”与事件“恰有一次反面向上”相等B．事件“至少一次正面向上”与事件“至少一次反面向上”互斥C．事件“两次正面向上”与事件“两次反面向上”互为对立事件D．事件“第一次正面向上”与事件“第二次反面向上”相互独立解：根据题意，依次分析选项：对于A，事件“恰有一次正面向上”即“一次正面向上、一次反面向上”，同样，事件“恰有一次反面向上”也是“一次正面向上、一次反面向上”，两个事件相等，A正确；对于B，事件“至少一次正面向上”，即“一次正面向上、一次反面向上”和“两次都是正面向上”，事件“至少一次反面向上”，即“一次正面向上、一次反面向上”和“两次都是反面向上”，两个事件不互斥，B错误；对于C，事件“两次正面向上”与事件“两次反面向上”不是对立事件，还有一种情况“一次正面向上、一次反面向上”，C错误；对于D，由相互独立事件的定义，事件“第一次正面向上”与事件“第二次反面向上”相互独立，D正确．故选：AD．11．某学校为了调查高一年级学生每天体育活动时间情况，随机选取了100名学生，绘制了如图所示频率分布直方图，则下列说法正确的是（）A．平均数的估计值为30B．众数的估计值为35C．第60百分位数估计值是32D．随机选取这100名学生中有25名学生体育活动时间不低于40分钟解：对于A，由频率分布直方图可知平均数的估计值为：5×0.1+15×0.18+25×0.22+35×0.25+45×0.2+55×0.05＝29.2，故A 错误；对于B ，由频率分布直方图可知[30，40）的频率最大，因此众数的估计值为35，故B 正确；对于C ，由频率分布直方图得从第一组到第六组的频率依次是0.1，0.18，0.22，0.25，0.2，0.05，所以第60百分位数估计值m 在[30，40）内，所以0.1+0.18+0.22+（m ﹣30）×0.025＝0.6，解得m ＝34，故C 错误；对于D ，随机选取这100名学生中体育活动时间不低于40分钟的人数为100×（0.2+0.05）＝25，故D 正确．故选：BD ．12．如图，已知三棱锥D ﹣ABC 可绕AB 在空间中任意旋转，△ABC 为等边三角形，AB 在平面α内，AB ⊥CD ，AB ＝2，CD =√6，cos∠CBD =14，则下列说法正确的是（）A ．二面角D ﹣AB ﹣C 为π2B ．三棱锥D ﹣ABC 的外接球表面积为20π3C ．点C 与点D 到平面α的距离之和的最大值为2 D ．点C 在平面α内的射影为点M ，线段DM 的最大值为√15+√32解：对于A 选项，在△BCD 中，BC =AB =2，CD =√6，cos∠CBD =14，由余弦定理可得CD 2＝BC 2+BD 2﹣2BC •BD cos ∠CBD ，即4+BD 2−4BD ×14=6，即BD 2﹣BD ﹣2＝0，因为BD ＞0，解得BD ＝2，取AB 的中点E ，连接CE 、DE ，如下图所示：因为△ABC 为等边三角形，E 为AB 的中点，所以，CE ⊥AB ，又因为CD ⊥AB ，CD ∩CE ＝C ，CD ，CE ⊂平面CDE ，所以，AB ⊥平面CDE ，因为DE ⊂平面CDE ，所以，DE ⊥AB ，所以，二面角D ﹣AB ﹣C 的平面角为∠CED ，因为E 为AB 的中点，所以，AD ＝BD ＝2，故△ABD 也是边长为2的等边三角形，所以DE =√AD 2−AE 2=√4−1=√3，CE =√AC 2−AE 2=√4−1=√3，又因为CD =√6，所以，CE 2+DE 2＝CD 2，则CE ⊥DE ，故二面角D ﹣AB ﹣C 为π2，A 对；对于B 选项，设△ABC 、△ABD 的中心分别为点G 、H ，分别过点G 、H 作GO ∥DE 、HO ∥CE ，设GO ∩HO ＝O ，因为CE ⊥DE ，CE ⊥AB ，AB ∩DE ＝E ，AB 、DE ⊂平面ABD ，所以，CE ⊥平面ABD ，因为HO ∥CE ，则OH ⊥平面ABD ，同理，OG ⊥平面ABC ，所以，O 为三棱锥D ﹣ABC 的外接球球心，由等边三角形的几何性质可知，HE =13DE =√33，同理，GE =13CE =√33，因为OH ∥GE ，OG ∥EH ，HE =GE =√33，GE ⊥HE ，所以，四边形OHEG 为正方形，且OH =GE =√33，又因为DH =DE −HE =√3−√33=2√33，因为CE ⊥DE ，OH ∥CE ，则OH ⊥DE ，则OD =√OH 2+DH 2=√(33)2+(233)2=√153，所以，三棱锥D ﹣ABC 的外接球半径为√153，因此，三棱锥D ﹣ABC 的外接球的表面积为4π⋅OD 2=4π×(√153)2=20π3，B 对；对于C 选项，设点D 在平面α内的射影点为N ，连接MN ，因为CM ⊥a ，DN ⊥a ，则CM ∥DN ，故点C 、D 、N 、M 四点共面，因为AB ⊂α，则AB ⊥CM ，又因为CD ⊥AB ，CD ∩CM ＝C ，CD 、CM ⊂平面CDNM ，则AB ⊥平面CDNM ，又因为AB ⊥平面CDE ，故平面CDE 与平面CDNM 重合，又因为E ∈α，M ，N ∈α，故E ∈MN ，设∠CEM ＝θ，其中0≤θ≤π2，又因为∠CED =π2，则∠DEN =π−∠CED −∠CEM =π−π2−θ=π2−θ，所以，CM =CEsin ∠CEM =√3sinθ，DN =DEsin ∠DEN =√3sin(π2−θ)=√3cosθ，所以，点C 与点D 到平面α的距离之和CM +DN =√3sinθ+√3cosθ=√6sin(θ+π4)，因为0≤θ≤π2，则π4≤θ+π4≤3π4，故当θ+π4=π2时，即当θ=π4时，CM +DN 取最大值√6，C 错；对于D 选项，ME =CEcosθ=√3cosθ，∠DEM =∠CED +∠CEM =π2+θ，由余弦定理可得DM =√DE 2+EM 2−2DE ⋅EMcos(π2+θ) =√3+3cos 2θ+2√3⋅√3cosθsinθ=√3+3×1+cos2θ2+3sin2θ =√3sin2θ+3cos2θ2+92=√352sin(2θ+φ)+92，其中φ为锐角，且tanφ=12，因为0≤θ≤π2，则φ≤2θ+φ≤π+φ，故当2θ+φ=π2时，DM 取得最大值，且(DM)max =√9+352=√18+654=√15+√32，D 对．故选：ABD ．三、填空题：本题共4小题，每小题5分，共20分． 13．一组数据1，2，4，5，8的第75百分位数为 5 ．解：5×75%＝3.75，故一组数据1，2，4，5，8的第75百分位数为5．故答案为：5．14．在正方体ABCD ﹣A 1B 1C 1D 1中，直线BC 1与直线CD 1夹角的余弦值为 12．解：如图，连接A 1C 1，A 1B ，在正方体ABCD ﹣A 1B 1C 1D 1中，有A 1D 1∥B 1C 1∥BC ，A 1D 1＝B 1C 1＝BC ，所以四边形A 1D 1CB 为平行四边形，所以A 1B ∥CD 1，所以∠A 1BC 1为直线BC 1与直线CD 1夹角或其补角，设正方体ABCD ﹣A 1B 1C 1D 1棱长为a ，则A 1B =BC 1=A 1C 1=√2a ，所以△A 1BC 1为等边三角形，所以∠A 1BC 1=π3，故直线BC 1与直线CD 1夹角的余弦值为cos ∠A 1BC 1=cos π3=12．故答案为：12．15．在圆C 中，已知弦AB ＝2，则AB →⋅AC →的值为 2 ．解：∵在圆C 中，已知一条弦AB ＝2，∴根据圆的几何性质得出：|AC |cos ∠CAB =12|AB |=12×2=1， ∵AB →•AC →=|AB →•|AC →|cos ∠CAB ＝2×1＝2．故答案为：2．16．已知△ABC 的重心为G ，面积为1，且AB ＝2AC ，则3AG 2+BC 2的最小值为4√213．解：由题意c ＝2b ，S △ABC =12bc sin A ＝1，即b 2sin A ＝1；连接AG 并延长交BC 于D ，则D 为BC 的中点，可得AD →=12（AB →+AC →），又因为G 为三角形的重心，则AG →=23AD →，可得AG →=13（AB →+AC →），BC →=AC →−AB →，所以AG 2=AG →2=19（AB →2+AC →2+2AB →•AC →）=19（c 2+b 2+2bc cos A ）=19（5b 2+4b 2cos A ）， BC 2=BC →2=AC →2+AB →2﹣2AB →•AC →=b 2+c 2﹣2bc cos A ＝5b 2﹣4b 2cos A ，所以3AG 2+BC 2=53b 2+4b 23cos A +5b 2﹣4b 2cos A =203b 2−83b 2cos A =203sinA −8cosA 3sinA，令t =203sinA −8cosA 3sinA＞0，则3t sin A +8cos A ＝20，即sin （A +φ）=20√9t +64≤1，当且仅当A +φ=π2时取等号，tan φ=82t ，可得9t 2+64≥400，解得t ≥4√213或t ≤−4√213（舍），即t 的最小值为：4√213．故答案为：4√213．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10分）已知e →1，e →2是两个单位向量，夹角为π3，设a→=e →1+2e →2，b→=te →1−3e →2．（1）求|a →|；（2）若a →⊥b →，求t 的值．解：（1）∵|e 1→|=|e 2→|=1，＜e 1→，e 2→＞=π3， ∴e 1→⋅e 2→=12，∴|a →|=√e 1→2+4e 2→2+4e 1→⋅e 2→=√1+4+2=√7；（2）∵a →⊥b →，∴a →⋅b →=(e 1→+2e 2→)⋅(te 1→−3e 2→)=te 1→2−6e 2→2+(2t −3)e 1→⋅e 2→=t −6+12(2t −3)=0，解得t =154． 18．（12分）已知正三棱柱ABC ﹣A 1B 1C 1的棱长均为2，M 为A 1C 1的中点．（1）求证：BC 1∥平面AB 1M ；（2）求点B 到平面AB 1M 的距离d ．证明：（1）连接A 1B 交AB 1于点N ，连接MN ，则正三棱柱中A 1B 1BA 是平行四边形，所以N 为A 1B 的中点，又M 为A 1C 1的中点，所以MN ∥BC 1，BC 1⊄平面AB 1M ，MN ⊂平面AB 1M ，所以BC 1∥平面AB 1M ．解：（2）过M 作MH ⊥A 1B 1，垂足为H ，由题意可得B 1M =√3，AM =√5，AB 1=2√2，所以B 1M 2+AM 2=AB 12，所以B 1M ⊥AM ，所以△AB 1M 的面积S △AB 1M =12×√3×√5=√152，因为正三棱柱中平面A 1B 1C 1⊥平面A 1B 1BA ，又平面A 1B 1C 1∩平面A 1B 1BA ＝A 1B 1，MH ⊂平面A 1B 1C 1，且MH ⊥A 1B 1，所以MH ⊥平面A 1B 1BA ，即M 到平面A 1B 1BA 的距离为MH =MA 1sin π3=√32，又△ABB 1的面积S △ABB 1=12AB ⋅BB 1=2，所以V M−ABB 1=13MH ⋅S △ABB 1=13×√32×2=√33，又V M−ABB 1=V B−MAB 1，所以13S △AB 1M ⋅d =√33，解得d =2√55，所以点B 到平面AB 1M 的距离为2√55． 19．（12分）独立事件是一个非常基础但又十分重要的概念，对于理解和应用概率论和统计学至关重要．它的概念最早可以追溯到17世纪的布莱兹•帕斯卡和皮埃尔•德•费马，当时被定义为彼此不相关的事件．19世纪初期，皮埃尔•西蒙•拉普拉斯在他的《概率的分析理论》中给出了相互独立事件的概率乘法公式．对任意两个事件A 与B ，如果P （AB ）＝P （A ）P （B ）成立，则称事件A 与事件B 相互独立，简称为独立．（1）若事件A 与事件B 相互独立，证明：A 与B 相互独立；（2）甲、乙两人参加数学节的答题活动，每轮活动由甲、乙各答一题，已知甲每轮答对的概率为35，乙每轮答对的概率为23．在每轮活动中，甲和乙答对与否互不影响，各轮结果也互不影响，求甲乙两人在两轮活动中答对3道题的概率．解：（1）证明：事件A 与事件B 相互独立，则P （AB ）＝P （A ）P （B ），又由B =A B +AB ，事件A B 和AB 互斥，则有P （B ）＝P （A B +AB ）＝P （AB ）+P （A B ）＝P （A ）P （B ）+P （A B ），变形可得：P （A B ）＝P （B ）﹣P （A ）P （B ）＝[1﹣P （A ）]P （B ）＝P （A ）P （B ），故事件A 与B 相互独立；（2）根据题意，设事件A 1、A 2分别表示甲答对1道、2道题目，事件B 1、B 2分别表示乙答对1道、2道题目，则P （A 1）＝2×35×（1−35）=1225，P （A 2）=35×35=925， P （B 1）＝2×23×（1−23）=49，P （B 2）=23×23=49，若甲乙两人在两轮活动中答对3道题，即A 2B 1+A 1B 2，则甲乙两人在两轮活动中答对3道题的概率P ＝P （A 2B 1+A 1B 2）＝P （A 2B 1）+P （A 1B 2）=925×49+1225×49=2875． 20．（12分）某社区工作人员采用分层抽样的方法分别在甲乙两个小区各抽取了8户家庭，统计了每户家庭近7天用于垃圾分类的总时间（单位：分钟），其中甲小区的统计表如下，设x i，y i分别为甲，乙小区抽取的第i户家庭近7天用于垃圾分类的总时间，s x2，s y2分别为甲，乙小区所抽取样本的方差，已知x=18∑8i=1x i=200，s x2=18∑8i=1(x i−x)2=200，y=195，s y2=210，其中i＝1，2，⋯，8．（1）若a≤b，求a和b的值；（2）甲小区物业为提高垃圾分类效率，优先试行新措施，每天由部分物业员工协助垃圾分类工作，经统计，甲小区住户每户每天用于垃圾分类的时间减少了5分钟．利用样本估计总体，计算甲小区试行新措施之后，甲乙两个小区的所有住户近7天用于垃圾分类的总时间的平均值z和方差s z2．参考公式：若总体划为2层，通过分层随机抽样，各层抽取的样本量、样本平均数和样本方差分别为：m，x1，s12；n，x2，s22，总的样本平均数为ω，样本方差为s2，则s2=mm+n [s12+(x1−ω)2]+nm+n[s22+(x2−ω)2]．解：（1）已知x=18∑8i=1x i=18(200+220+200+180+200+a+b+220)=200，整理得a+b＝380，①又s x2=18∑8i=1(x i−x)2=8[3×（200﹣200）2+2×（220﹣200）2+（180﹣200）2+（a﹣200）2+（b﹣200）2]＝200，整理得（a﹣200）2+（b﹣200）2＝400，②联立①②，解得a＝180，b＝200或a＝200，b＝180，因为a≤b，所以a＝180，b＝200；（2）设甲小区试行新措施之后，甲小区抽取的第i户家庭近7天用于垃圾分类的总时间为m i，此时m i＝x i﹣35，则m i=x−35＝165，s m2=s x2=200，所以z=116（8m+8y）=12（165+195）＝180，s z2=88+8[s m2+（m−z）2]+88+8[s y2+（y−z）]=12[200+（165﹣180）2]+12[210+（195﹣180）2]＝430．21．（12分）如图1，在等腰△ABC中，AC＝4，A=π2，O，D分别为BC、AB的中点，过D作DE⊥BC于E ．如图2，沿DE 将△BDE 翻折，连接BA ，BC 得到四棱锥B ﹣ACED ，F 为AB 中点．（1）证明：DF ⊥平面AOB ；（2）当OB =√2时，求直线BF 与平面BCD 所成的角的正弦值．（1）证明：因为DE ⊥BE ，DE ⊥OE ，且BE ∩OE ＝E ，BE 、OE ⊂平面BCE ，所以DE ⊥平面BCE ，又OA ∥DE ，所以OA ⊥平面BCE ，设点P 是翻折前点B 所在的位置，则D 为AP 的中点，因为F 为AB 的中点，所以DF ∥PB ，因为PB ⊂平面BCE ，所以OA ⊥PB ，所以OA ⊥DF ，由题意知，DA ＝DB ，因为F 为AB 的中点，所以DF ⊥AB ，又OA ∩AB ＝A ，OA 、AB ⊂平面AOB ，所以DF ⊥平面AOB ．（2）解：以O 为坐标原点，建立如图所示的空间直角坐标系，则A （0，0，2√2），P （2√2，0，0），C （﹣2√2，0，0），D （√2，0，√2），由（1）知，DF ⊥平面AOB ，因为DF ∥PB ，所以PB ⊥平面AOB ，所以PB ⊥OB ，又OB =√2=12OP ，所以∠POB ＝60°，所以B （√22，√62，0），F （√24，√64，√2），所以BF →=（−√24，−√64，√2），CD →=（3√2，0，√2），CB →=（5√22，√62，0），设平面BCD 的法向量为n →=（x ，y ，z ），则{n →⋅CD →=0n →⋅CB →=0，即{3√2x +√2z =05√22x +√62y =0，令x ＝1，则y =53，z ＝﹣3，所以n →=（1，53，﹣3），设直线BF 与平面BCD 所成的角为θ，则sin θ＝|cos ＜BF →，n →＞|=|BF →⋅n →||BF →|⋅|n →|=|−√24+√64×5√3−3√2|(24)+(64)√1+(5√3)=4√3355，故直线BF 与平面BCD 所成的角的正弦值为4√3355． 22．（12分）射影几何学中，中心投影是指光从一点向四周散射而形成的投影，如图，O 为透视中心，平面内四个点E ，F ，G ，H 经过中心投影之后的投影点分别为A ，B ，C ，D ．对于四个有序点A ，B ，C ，D ，定义比值x =CACBDA DB叫做这四个有序点的交比，记作（ABCD ）．（1）证明：（EFGH ）＝（ABCD ）；（2）已知（EFGH ）=32，点B 为线段AD 的中点，AC =√3OB =3，sin∠ACOsin∠AOB =32，求cos A ．解：（1）证明：在△AOC 、△AOD 、△BOC 、△BOD 中，CA CB =S △AOC S △BOC =12OA⋅OCsin∠AOC 12OB⋅OCsin∠BOC =OAsin∠AOC OBsin∠BOC，DA DB=S △AOD S △BOD=12OA⋅ODsin∠AOD 12OB⋅ODsin∠BOD =OAsin∠AOD OBsin∠BOD，所以(ABCD)=CA CB DA DB=OAsin∠AOC OBsin∠BOC OAsin∠AOD OBsin∠BOD=sin∠AOC⋅sin∠BODsin∠BOC⋅sin∠AOD，又在△EOG 、△EOH 、△FOG 、△FOH 中，GE GF =S △EOG S △FOG =12OE⋅OGsin∠EOG 12OF⋅OGsin∠FOG =OEsin∠EOG OFsin∠FOG，HE HF=S △EOH S △FOH=12OE⋅OHsin∠EOH 12OF⋅OHsin∠FOH =OEsin∠EOH OFsin∠FOH，所以(EFGH)=GE GF HE HF=OEsin∠EOG OFsin∠FOG OEsin∠EOH OFsin∠FOH=sin∠EOG⋅sin∠FOHsin∠FOG⋅sin∠EOH ，又∠EOG ＝∠AOC ，∠FOH ＝∠BOD ，∠FOG ＝∠BOC ，∠EOH ＝∠AOD ，所以sin∠AOC⋅sin∠BOD sin∠BOC⋅sin∠AOD=sin∠EOG⋅sin∠FOH sin∠FOG⋅sin∠EOH，所以（EFGH ）＝（ABCD ）．（2）由题意可得(EFGH)=32，所以(ABCD)=32，即CACB DA DB=32，所以CA CB ⋅DBDA=32，又点B 为线段AD 的中点，即DB DA=12，所以CACB=3，又AC ＝3，则AB ＝2，BC ＝1，设OA ＝x ，OC ＝y 且OB =√3，由∠ABO ＝π﹣∠CBO ，所以cos ∠ABO +cos ∠CBO ＝0，即2√3)222×2×√3+2√3)222×1×√3=0，解得x 2+2y 2＝15，①在△AOB 中，由正弦定理可得AB sin∠AOB =x sin∠ABO，②在△COB 中，由正弦定理可得OB sin∠BCO=y sin∠CBO，③且sin ∠ABO ＝sin ∠CBO ，②③得，x y=AB sin∠AOB⋅sin∠BCO OB=32×√3=√3，即x =√3y ，④由①④解得x =3，y =√3（负值舍去），即AO =3，OC =√3所以cosA =AO 2+AB 2−OB 22AO⋅AB =32+22−(√3)22×3×2=56．。

2023-2024学年北京市海淀区高一下学期7月期末考试数学试题+答案解析

2023-2024学年北京市海淀区高一下学期7月期末考试数学试题一、单选题：本题共10小题，每小题5分，共50分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.若复数z满足，则z的虚部为()A. B.2 C. D.i2.已知向量，则()A.0B.C.D.3.函数的部分图象如图所示，则其解析式为()A. B.C. D.4.若，且，则()A. B. C. D.75.在中，点D满足，若，则()A. B. C.3 D.6.已知，则下列直线中，是函数对称轴的为()A. B. C. D.7.在平面直角坐标系xOy中，点，点，其中若，则()A. B. C. D.8.在中，已知则下列说法正确的是()A.当时，是锐角三角形B.当时，是直角三角形C.当时，是钝角三角形D.当时，是等腰三角形9.已知是非零向量，则“”是“对于任意的，都有成立”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件10.定义域为、的函数的图象的两个端点分别为点是的图象上的任意一点，其中，点N满足向量，点O为坐标原点．若不等式恒成立，则称函数在上为k函数．已知函数在上为k函数，则实数k的取值范围是()A. B. C. D.二、填空题：本题共5小题，每小题5分，共25分。

11.知复数z满足，则__________，__________.12.在中，，P满足，则__________.13.在中，若，则k的一个取值为__________；当时，__________.14.一名学生想测算某风景区山顶上古塔的塔尖距离地面的高度，由于山崖下河流的阻碍，他只能在河岸边制定如下测算方案：他在河岸边设置了共线的三个观测点A，B，如图，相邻两观测点之间的距离为200m，并用测角仪器测得各观测点与塔尖的仰角分别为，，，根据以上数据，该学生得到塔尖距离地面的高度为___________________15.已知函数，给出下列四个结论：①对任意的，函数是周期函数；②存在，使得函数在上单调递减；③存在，使得函数的图象既是轴对称图形，又是中心对称图形；④对任意的，记函数的最大值为，则其中所有正确结论的序号是__________.三、解答题：本题共4小题，共48分。

高一下学期数学期末试卷含答案(共5套)

高一下学期期末考试数学试题第Ⅰ卷选择题一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}A |2,x x x R =≤∈，集合B 为函数y lg(1)x =-的定义域，则B A I （） A ．(1,2) B ．[1,2] C ．[1,2) D ．(1,2]2.已知20.5log a =，0.52b =，20.5c =，则a ，b ，c 的大小关系为（）A ．a b c <<B ．c b a <<C ．a c b <<D ．c b a <<3.一个单位有职工800人，其中高级职称160人，中级职称300人，初级职称240人，其余人员100人，为了解职工收入情况，现采取分层抽样的方法抽取容量为40的样本，则从上述各层中依次抽取的人数分别为（）A ．15,24,15,19B ．9,12,12,7C ．8,15,12,5D ．8,16,10,6 4.已知某程序框图如图所示，若输入实数x 为3，则输出的实数x 为（）A ．15B ．31 C.42 D ．63 5.为了得到函数4sin(2)5y x π=+，x R ∈的图像，只需把函数2sin()5y x π=+，x R ∈的图像上所有的点（）A ．横坐标伸长到原来的2倍，纵坐标伸长到原来的2倍．B ．纵坐标缩短到原来的12倍，横坐标伸长到原来的2倍．C ．纵坐标缩短到原来的12倍，横坐标缩短到原来的12倍． D ．横坐标缩短到原来的12倍，纵坐标伸长到原来的2倍．6.函数()1ln f x x x=-的零点所在的区间是（）A ．(0,1)B ．(1,2) C.(2,3) D ．(3,4)7.下面茎叶图记录了在某项体育比赛中，九位裁判为一名选手打出的分数情况，则去掉一个最高分和最低分后，所剩数据的方差为（）A ．327 B ．5 C.307D ．4 8.已知函数()222cos 2sin 1f x x x =-+，则（）A ．()f x 的最正周期为2π，最大值为3．B ．()f x 的最正周期为2π，最大值为1． C.()f x 的最正周期为π，最大值为3． D ．()f x 的最正周期为π，最大值为1．9.平面向量a r 与b r 的夹角为23π，(3,0)a =r ，||2b =r ，则|2|a b +=r r （）A C.7 D ．3 10.已知函数2log (),0()(5),0x x f x f x x -<⎧=⎨-≥⎩，则()2018f 等于（）A ．1-B ．2 C.()f x D ．111.设点E 、F 分别为直角ABC ∆的斜边BC 上的三等分点，已知3AB =，6AC =，则AE AF ⋅u u u r u u u r（）A ．10B ．9 C. 8 D ．712.气象学院用32万元买了一台天文观测仪，已知这台观测仪从启动的第一天连续使用，第n 天的维修保养费为446(n )n N *+∈元，使用它直至“报废最合算”（所谓“报废最合算”是指使用的这台仪器的平均每天耗资最少）为止，一共使用了（）A ．300天B ．400天 C.600天 D ．800天第Ⅱ卷非选择题二、填空题（本大题共4小题，每题5分，满分20分，将答案填在答题纸上） 13.已知θ为锐角且4tan 3θ=，则sin()2πθ-= ． 14.A 是圆上固定的一点，在圆上其他位置任取一点B ，连接A 、B 两点，它是一条弦，它的长度不小于半径的概率为．15.若变量x ，y 满足2425()00x y x y f x x y +≤⎧⎪+≤⎪=⎨≥⎪⎪≥⎩，则32z x y =+的最大值是．16.关于x 的不等式232x ax >+（a为实数）的解集为，则乘积ab 的值为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. 在ABC ∆中，角A ，B C ，所对应的边分别为a ，b ，c ，且5a =，3A π=，cos B =（1）求b 的值；（2）求sin C 的值．18. 已知数列{}n a 中，前n 项和和n S 满足22n S n n =+，n N *∈．（1）求数列{}n a 的通项公式；（2）设12n n n b a a +=，求数列{}n b 的前n 项和n T ． 19. 如图，在ABC ∆中，点P 在BC 边上，AC AP >，60PAC ∠=︒，PC =10AP AC +=．（1）求sin ACP ∠的值；（2）若APB ∆的面积是，求AB 的长．20. 已知等差数列{}n a 的首项13a =，公差0d >．且1a 、2a 、3a 分别是等比数列{}n b 的第2、3、4项．（1）求数列{}n a 与{}n b 的通项公式；（2）设数列{}n c 满足2 (n 1)(n 2)n n na c ab =⎧=⎨⋅≥⎩，求122018c c c +++L 的值（结果保留指数形式）．21.为响应党中央“扶贫攻坚”的号召，某单位知道一贫困村通过种植紫甘薯来提高经济收入．紫甘薯对环境温度要求较高，根据以往的经验，随着温度的升高，其死亡株数成增长的趋势．下表给出了2018年种植的一批试验紫甘薯在不同温度时6组死亡株数：经计算：615705i i i x y ==∑，6214140ii x ==∑，62110464i i y ==∑≈0.00174．其中i x ，i y 分别为试验数据中的温度和死亡株数，1,2,3,4,5,6.i =（1）y 与x 是否有较强的线性相关性？请计算相关系数r （精确到0.01）说明．（2）求y 与x 的回归方程ˆˆˆ+a y bx =（ˆb 和ˆa 都精确到0.01）；（3）用（2）中的线性回归模型预测温度为35C ︒时该批紫甘薯死亡株数（结果取整数）．附：对于一组数据11(,v )u ，22(,v )u ，L L ，(,v )n n u ，①线性相关系数ni i u v nu vr -=∑，通常情况下当|r |大于0.8时，认为两个变量具有很强的线性相关性．②其回归直线ˆˆv u αβ=+的斜率和截距的最小二乘估计分别为： 1221ˆni i i nii u v nu vunu β==-=-∑∑，ˆˆˆav u β=-；22.已知函数()2lg(a)1f x x =+-，a R ∈．（1）若函数()f x 是奇函数，求实数a 的值；（2）在在（1）的条件下，判断函数()y f x =与函数lg(2)xy =的图像公共点各数，并说明理由；（3）当[1,2)x ∈时，函数lg(2)x y =的图像始终在函数lg(42)xy =-的图象上方，求实数a 的取值范围．答案一、选择题答案9. 【解析】方法1： (1,b =-,2(1,a b +=±,|2|13a b +=。

北京高一下学期期末数学试卷含答案(共5套)

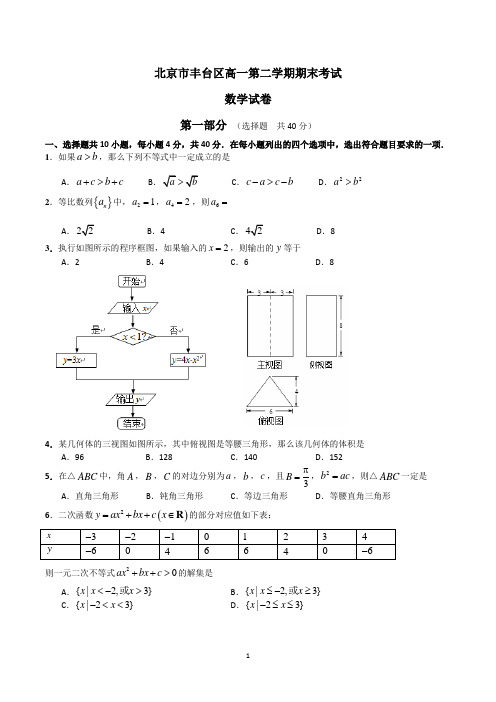
北京市丰台区高一第二学期期末考试数学试卷第一部分（选择题共40分）一、选择题共10小题，每小题4分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．如果a b >，那么下列不等式中一定成立的是A ．a c b c +>+B ．a b >C ．c a c b ->-D ．22a b >2．等比数列{}n a 中，21a =，42a =，则6a =A ．22B ．4C ．42D ．8 3．执行如图所示的程序框图，如果输入的2x =，则输出的y 等于A ．2B ．4C ．6D ．84．某几何体的三视图如图所示，其中俯视图是等腰三角形，那么该几何体的体积是A ．96B ．128C ．140D ．152 5．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且3B π=，2b ac =，则△ABC 一定是 A ．直角三角形B ．钝角三角形C ．等边三角形D ．等腰直角三角形6．二次函数()2y ax bx c x =++∈R 的部分对应值如下表：x3- 2- 1- 0 1 2 3 4 y6- 04 6 6 4 0 6-则一元二次不等式20ax bx c ++>的解集是A ．{|2,3}x x x <->或B ．{|2,3}x x x ≤-≥或C ．{|23}x x -<<D ．{|23}x x -≤≤7．在数列{}n a 中，12n n a a +=+，且11a =，则1223349101111a a a a a a a a ++++= A ．919B ．1819C ．1021D ．20218．已知各项均为正数的等比数列{}n a 中，如果21a =，那么这个数列前3项的和3S 的取值范围是A ．(],1-∞-B ．[)1,+∞C ．[)2,+∞D ．[)3,+∞ 9．已知n 次多项式1110()n n n n n f x a x a x a x a --=++++，在求0()n f x 值的时候，不同的算法需要进行的运算次数是不同的．例如计算0kx （k ＝2，3，4，…，n ）的值需要 k －1次乘法运算，按这种算法进行计算30()f x 的值共需要9次运算（6次乘法运算，3次加法运算）．现按右图所示的框图进行运算，计算0()n f x 的值共需要次运算． A ．2nB ．2nC ．(1)2n n + D ．+1n10．如图，在正方体1111ABCD A B C D -中，点P 在正方体表面运动，如果11ABD PBD S S ∆∆=，那么这样的点P 共有 A ．2个 B ．4个 C ．6个 D ．无数个D 11B 1A D第二部分（非选择题共60分）二、填空题共6小题，每小题4分，共24分．11．从某企业生产的某种产品中抽取100件样本，测量这些样本的一项质量指标值，由测量结果得如下频数分布表：质量指标值分组 [75，85)[85，95) [95，105)[105，115)[115，125]频数62638228则样本的该项质量指标值落在[105，125]上的频率为_____． 12．函数()(2)(02)f x x x x =-<<的最大值是_____．13．如图，样本数为9的三组数据，它们的平均数都是5，频率条形图如下，则标准差最大的一组是．14．已知两条不重合的直线,a b 和两个不重合的平面α,β，给出下列命题：①如果a α∥，b α⊂，那么a b ∥；②如果αβ∥，b α⊂，那么b β∥； ③如果a α⊥，b α⊂，那么a b ⊥；④如果αβ⊥，b α⊂，那么b β⊥．上述结论中，正确结论．．．．的序号是（写出所有正确结论的序号）． 15．如图，为了测量河对岸,A B 两点之间的距离．观察者找到了一个点C ，从C 可以观察到点,A B ；找到了一个点D ，从D 可以观察到点,A C ；找到了一个点E ，从E 可以观察到点,B C ．并测量得到图中一些数据，其中23CD =，4CE =，60ACB ∠=，90ACD BCE ∠=∠=，60ADC ∠=，45BEC ∠=，则AB = ．16．数列{}n a 满足11a =，112n n n a a -+⋅=，其前n 项和为n S ，则（1）5a = ；（2）2n S = ．三、解答题共4小题，共36分．解答应写出文字说明，演算步骤或证明过程． 17.（本小题共9分）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且sin 6sin A C =，3c =．（Ⅰ）求a 的值；（Ⅱ）如果3cos 3A =，求b 的值及△ABC 的面积．18.（本小题共9分）某校在“普及环保知识节”后，为了进一步增强环保意识，从本校学生中随机抽取了一批学生参加环保基础知识测试．经统计，这批学生测试的分数全部介于75至100之间．将数据分成以下5组：第1组[)80,75，第2组[)85,80，第3组[)90,85，第4组[)95,90，第5组[]100,95，得到如图所示的频率分布直方图．（Ⅰ）求a 的值；（Ⅱ）现采用分层抽样的方法，从第3，4，5组中随机抽取6名学生座谈，求每组抽取的学生人数；（Ⅲ）假设同一组中的每个数据可用该组区间的中点值代替，试估计随机抽取学生所得测试分数的平均值在第几组（只需写出结论）．19.（本小题共9分）如图，在四棱锥P ABCD -中，底面ABCD 为正方形，点E 是棱PA 的中点，PB PD =，平面BDE ⊥平面ABCD ．（Ⅰ）求证：PC //平面BDE ；（Ⅱ）求证：PC ⊥平面ABCD ；(Ⅲ) 设AB PC λ=,试判断平面PAD ⊥平面PAB 能否成立；若成立，写出λ的一个值（只需写出结论）．20.（本小题共9分）设数列{}n a 满足12a =，12nn n a a +-=；数列{}n b 的前n 项和为n S ，且21(3)2n S n n =-．（Ⅰ）求数列{}n a 和{}n b 的通项公式；（Ⅱ）把数列{}n a 和{}n b 的公．共项．．从小到大排成新数列{}n c ,试写出1c ，2c ，并证明{}n c 为等比数列．（考生务必将答案答在答题卡上，在试卷上作答无效）丰台区第二学期期末高一数学参考答案一、选择题（本题共10小题，共40分）二、填空题（本题共6小题，共24分）11．0.3 12．1 13．第三组14．②③ 15．16．（1）4；（2）122n +-（第16题第一空2分，第二空2分）三、解答题（本题共4小题，共36分） 17. （本小题9分）解：（Ⅰ）因为sin sin a cA C=以及sin A C =， …………2分所以a =，因为c =……………3分所以a = ……………4分（Ⅱ）因为2222cos a b c bc A =+-以及cos 3A =……………5分所以22150b b --=，因为0b >， ……………6分所以5b = ……………7分因为cos 3A =，0π<<A ，所以sin A =……………8分所以1sin 22ABC S bc A ∆==. ……………9分 18．（本小题9分）解：（1）因为各组的频率之和为1，(0.010.020.060.07)51a ⨯++++⨯=，解得0.04a = …………3分（2）由频率分布直方图知，第3，4，5组的学生人数之比为3:2:1． …………4分所以，每组抽取的人数分别为：第3组：3636⨯=；第4组：2626⨯=；第5组：1616⨯=．所以从3，4，5组应依次抽取3名学生，2名学生，1名学生． …………7分（3）第3组 …………9分19．（本小题9分）证明：（Ⅰ）证明：设AC BD O =，连接OE ，因为底面ABCD 为正方形，所以O 是AC 的中点，又点E 是棱PA 的中点，所以EO 是的PAC ∆中位线，所以EO // PC …………………1分因为EO ⊂平面BDE ，PC ⊄平面BDE ，所以PC //平面BDE ； …………………3分（Ⅱ）证明：(法一）在PAB ∆和PAD ∆中，因为AB AD =，PB PD =，PA PA =，所以PAB ∆≌PAD ∆，又点E 是棱PA 的中点，所以EB ED =， ………………5分所以EO BD ⊥，因为平面BDE ⊥平面ABCD ，平面BDE 平面ABCD BD =，EO ⊂平面BDE所以EO ⊥平面ABCD ， ………………7分所以EO ⊥AC ,EO ⊥BD , 因为EO //PC所以PC ⊥AC ,PC ⊥BD ,又AC ∩BD=O所以PC ⊥平面ABCD ． …………………8分（法二）连接PO因为底面ABCD 是正方形，所以O 是BD 的中点，BD ⊥AC ,又PB=PD ,所以PO ⊥BD ,又PO ∩AC =O ,PO ⊂平面PAC ,AC ⊂平面PAC 所以BD ⊥平面PAC又OE ⊂平面PAC , 所以BD ⊥OE ， …………………5分因为平面BDE ⊥平面ABCD ，平面BDE 平面ABCD BD =， EO ⊂平面BDE所以EO ⊥平面ABCD ， …………………7分所以EO ⊥AC ,EO ⊥BD , 因为OE ∥PC,所以PC ⊥AC ,PC ⊥BD ,又AC ∩BD=O所以所以PC ⊥平面ABCD ． …………………8分 (Ⅲ) 不能成立 …………………9分20．（本小题9分）解：（Ⅰ）由已知，当2n ≥时，112211[()()()]n n n n n a a a a a a a a ---=-+-++-+12(222)2n n --=++++2n =． …………………2分又因为12a =，所以数列{}n a 的通项公式为2n n a =．因为21(3)2n S n n =-，所以，211[3(1)(1)](2)2n S n n n -=---≥ 两式做差可得32n b n =-，且111b S ==也满足此式，所以32n b n =-. …………………4分（Ⅱ）由2nn a =，32n b n =-，可得1224c a b ===，24616c a b ===.…………………5分假设2kn m k c b a ===,则32=2k m -.所以112222(32)3(21)1k kk a m m ++==⋅=-=--,不是数列{}n b 中的项；2+2=2424(32)k k k a m +=⋅=-=3(42)2m --，是数列{}n b 中的第42m -项.所以+142=n m c b -=222k k a ++=，从而2+1242k n k n c c +==.所以{}n c 是首项为4,公比为4的等比数列. …………………9分（若用其他方法解题，请酌情给分）北京市东城区高一年级下学期期末考试数学试卷本试卷共100分，考试时长120分钟。

2023北京大兴区高一(下)期末数学试题及答案

2023北京大兴高一（下）期末数学2023.07考生须知1．本试卷共4页，共两部分，21道小题.满分150分.考试时间120分钟.2．在试卷和答题卡上准确填写学校名称、班级、姓名和准考证号.3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效.4．在答题卡上，选择题用2B 铅笔作答，其他题用黑色字迹签字笔作答.第一部分（选择题共40分）一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1.复数()21i +=（）A.0B.2C.2iD.2i-2.已知向量()1,2a =-r 与()2,b m = ，且2b a =，则m =（）A.4- B.1- C.1D.43.某学校现有小学和初中学生共2000人，为了解学生的体质健康合格情况，决定采用分层抽样的方法从全校学生中抽取一个容量为400的样本，其中被抽到的初中学生人数为180，那么这所学校的初中学生人数为（）A.800B.900C.1000D.11004.已知在复平面内复数z 对应的点的坐标为()3,4-，则z =（）A.3B.4C.5D.5.已知平面α，β，直线l ⊂α，则“//l β”是“//αβ”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6.设a ，b 为非零向量，且满足a b a b +=- ，则a b ⋅= （）A.0B.－1C.1D.27.在ABC中，3a =，2b c -=，1cos 2B =-，则b =（）A.B. C.5D.78.某校举办知识竞赛，将100人的成绩整理后画出的频率分布直方图如下．则根据频率分布直方图，下列结论正确的是（）A.中位数估计为75B.众数估计为70C.平均数估计为68.5D.第85百分位数估计为859.已知边长为3的正方形ABCD ，点E 是边BC 上动点，则AE DE ⋅的最大值是（）A.274B.9C.43D.1010.已知点P 在棱长为2的正方体1111ABCD A B C D -表面运动，且1PB PD =，则线段AP 的长的取值范围是（）A.[0,23]B.[1,3]C.23]D.2,3]2第二部分（非选择题共110分）二、填空题共5小题，每小题5分，共25分.11.复数z 满足1z +为纯虚数，则z 的实部为___________．12.对于一组数据2，3，3，4，6，6，8，8，则第50百分位数是___________．13.已知向量a ，b 在正方形网格中的位置如图所示，则a ，b的夹角的余弦为___________．14.一个铁制的底面半径为4，侧面积为16π3的实心圆柱的体积为___________，将这个实心圆柱熔化后铸成一个实心球体，则这个铁球的半径为___________．15.如图，已知菱形ABCD 中，2AB =，120BAD ∠=︒，E 为边BC 的中点，将ABE 沿AE 翻折成1AB E △（点1B 位于平面ABCD 上方），连接1B C 和1B D ，F 为1B D 的中点，则在翻折过程中，给出下列四个结论：①平面1⊥AB E 平面1B EC ；②1AB 与CF 的夹角为定值π3；③三棱锥1B AED -体积最大值为233；④点F 的轨迹的长度为π2；其中所有正确结论的序号是___________．三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.16.已知向量a ，b满足10a = ，()3,4b = ．（1）求b；（2）若//a b r r，求a 的坐标；（3）若a b ⊥，求a b - ．17.已知tan 2α=．（1）求πtan 4α⎛⎫+ ⎪⎝⎭的值；（2）求2sin 2cos 1cos 2ααα-+的值．18.如图，在三棱柱111ABC A B C -中，侧面11BCC B 为正方形，平面11BCC B ⊥平面11ABB A ，M ，N 分别为11A B ，AC 的中点．（1）求证：MN //平面11BCC B ；（2）再从条件①、条件②这两个条件中选择一个作为已知，求证：1AB BB ⊥．条件①：AB MN ⊥；条件②：,AB BC BM MN ==．注：如果选择条件①和条件②分别解答，按第一个解答计分．19.某工厂生产某款产品，该产品市场平级规定：评分在10分及以上的为一等品，低于10分的为二等品．下面是检验员从一批产品中随机抽样的10件产品的评分：9.610.19.79.810.09.710.09.810.110.2经计算得1021198.04810i i x ==∑，其中i x 为抽取的第i 件产品的评分，1,2,3,,10i =⋅⋅⋅．（1）求这组样本平均数和方差；（2）若厂家改进生产线，使得生产出的每件产品评分均提高0.2．根据以上随机抽取的10件产品改进后的评分，估计改进后该厂生产的产品评分的平均数和方差；（3）在第（2）问前提下，再从改进后生产的产品中随机抽取10件产品，估计这10件产品的平均等级是否为一等品？说明理由．20.在ABC 中，222a c b ac +-=，D 是AC 边上的点，1CD =，3AD BD ==．（1）求B 的大小；（2）求tan A 的值；（3）求BCD △的面积．21.如图，从长、宽，高分别为a ，b ，c 的长方体AEBF GCHD -中截去部分几何体后，所得几何体为三棱锥A BCD -．（1）求三棱锥A BCD -的体积；（2）证明：三棱锥A BCD -的每个面都是锐角三角形；（3）直接写出一组a ，b ，c 的值，使得二面角D AB C --是直二面角．参考答案第一部分（选择题共40分）一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.题号12345678910答案CABCBADCBD第二部分（非选择题共110分）二、填空题共5小题，每小题5分，共25分.11.1-12.513.35.14.32π3；215.①②④.（全选对5分，漏选1个3分，漏选2个2分，不选或选错0分）三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.16.（I）因为()3,4b =，所以5b== ；……………4分（II ）设(),a x y = ，由10a = ，//a b r r，得10430x y =-=⎪⎩，解得68x y =-⎧⎨=-⎩或68x y =⎧⎨=⎩，所以a的坐标为()6,8--或()6,8；（III ）若a b⊥ ，则0a b ⋅=，故a b -=.……………5分17.（I）因为tan 2α=，所以πtan tanπ214tan 3π41211tan tan 4ααα++⎛⎫+===- ⎪-⨯⎝⎭-.……………7分（II ）2222sin 2cos 2sin cos cos cos (2sin cos )1cos 212cos 12cos ααααααααααα---==++-.2sin cos 2cos ααα-=1tan 2α=-13222=-=……………7分18.（I）取BC 的中点P ，连接,PM PC ，因为M ，P 分别为11A B ，11B C 的中点，所以11//PM A C 且1112PM A C =，因为四边形11ACC A 为平行四边形，且N 为AC 的中点，所以11//CN A C 且1112CN A C =，所以//PM CN 且PM CN =，所以四边形PMNC 是平行四边形，所以//MN PC ，又MN ⊄平面11BCC B ，PC ⊂平面11BCC B ，所以MN //平面11BCC B ；……………6分（II ）因为平面11BCC B ⊥为正方形，所以1BC BB ⊥又因为平面11BCC B ⊥平面11ABB A ，且平面11BCC B 平面111ABB A BB =，所以BC ⊥平面11ABB A 所以BC AB⊥选①，因为AB MN ⊥，所以1AB PB ⊥，又11,,PB BC P PB BC ⋂=⊂平面11BCC B ，所以AB ⊥平面11BCC B ，又1BB ⊂平面11BCC B ，所以1AB BB ⊥.选②，取AB 的中点Q ，连接,MQ NQ ，因为M ，N 分别为11A B ，AC 的中点，所以//NQ BC 且12NQ BC =，1//QM BB ，因为BC ⊥平面11ABB A ，所以NQ ⊥平面11ABB A ，又MQ Ì平面11ABB A ，所以NQ MQ ⊥，即90MQN ∠=︒，因为AB BC =，所以12NQ AB BQ ==，又,MN MB MQ MQ ==，所以MBQ MNQ ≅ ，所以90MQB MQN ∠=∠=︒，所以MQ AB ⊥，又1//QM BB ，所以1AB BB ⊥ (8)分19.（I）样本平均值为9.610.19.79.810.09.710.09.810.110.29.910x +++++++++==，样本方差为()101022222111198.0489.90.0381010i ii i s x x x x ===-=-=-=∑∑，……………5分（II ）因为改进后随机抽取的10件产品是改进前抽取的10件产品每个提高0.2分，所以估计改进后生产的产品评分的平均数0.210.1X x =+=，方差为220.038S s ==，……………6分（III ）可以认为是一等品，因为改进后该厂生产的产品评分由样本数据估计平均数为10.110>，所以可以认为这10件产品平均等级为一等品，不一定是一等品，因为样本数据具有随机性，所以新样本平均值不一定达到10分以上，所以新样本平均等级不一定是一等品.……………3分20.（I）因为222a c b ac +-=，由余弦定理2221cos 22a cb B ac +-==，又()0,πB ∈，所以π3B =.……………4分（II ）如图，令A α∠=，因为3AD BD ==，所以ABD A α∠=∠=，所以π3DBC α∠=-，2π3C α∠=-，2BDC α∠=，在BCD △中，由正弦定理得sin sin BD CDBCD DBC=∠∠，即312ππsin sin 33αα=⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，所以2ππsin 3sin 33αα⎛⎫⎛⎫-=-⎪ ⎪⎝⎭⎝⎭，即2π2πππsin cos cos sin3sin cos cos sin 3333αααα⎛⎫-=-⎪⎝⎭，所以3131cos sin3cos sin2222αααα⎛⎫+=-⎪⎪⎝⎭，解得tan2α=，即3tan2A=.（III ）由2222sin cos2tan43sin sin2sin cos tan17BDCααααααα∠====++，所以114363sin132277BCDS BD CD BDC=⋅∠=⨯⨯⨯=.……………5分21.（I）在长方体AEBF GCHD-中，三棱锥11113326A GCD GCDV AG S c a b abc-=⋅=⨯⨯⨯=，同理可得16C ABED ABF C BHDV V V abc---===，所以AEBF GCHDV abc-=，所以114634AEBF GCHDA BCD A GCDV V abc abc abcV----==-⨯=.……………5分（II）由已知易得三棱锥A BCD-的每个面的三角形的三条边均为不妨设a b c≥≥为最大边，各面的最大角为θ，则2222222cos0b c c a a bθ+++-+=，又()0,πθ∈，所以各面的最大角为θ为锐角，所以三棱锥A BCD-的每个面都是锐角三角形.（III）a b==1c=，（满足a b==或2222220a cbc a b+-=均可）（答案不唯一），连接EF 交AB 于点O ，连接OC 、OD ，则AD BD AC BC ====O 为AB 的中点，所以OC AB ⊥，OD AB ⊥，所以COD ∠为二面角D AB C --的平面角，又112OE OF EF ====，2DC ==，OC OD ===，所以222OC OD DC +=，所以OC OD ⊥，即90COD ∠=︒，所以二面角D AB C --是直二面角.。

2023年高一下学期期末数学试卷(附答案)

高一下学期数学期末试卷(试卷总分:100分,考试时间:100分钟)考生注意：请将正确答案填写在答题卷上规定的位置，在本试卷上作答一律无效！一、选择题（本大题共18小题，每小题3分，共54分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

在答题卷上的相应题目的答题区域内作答。

1.下列命题为真命题的是（）.A. 平行于同一平面的两条直线平行；B.与某一平面成等角的两条直线平行；C.垂直于同一平面的两条直线平行；D.垂直于同一直线的两条直线平行 2．已知数列{}n a 的通项公式是n a=1(2)2n n +，则220是这个数列的（）. A ．第20项 B ．第19项 C ．第21项 D ．第22项3.右图的正方体ABCD-A ’B ’C ’D ’中,异面直线AA ’与BC 所成的角是（）. A. 300 B.450 C. 600 D. 9004.右图的正方体ABCD- A ’B ’C ’D ’中，二面角D ’-AB-D 的大小是（）. A. 300 B.450 C. 600 D. 905. 在△ABC 中，若a = 2 ,23b =,030A = , 则B 等于( ).A ．60B ．60或 120C ．30D ．30或1506.已知一个算法，其流程图如右图所示，则输出的结果是（）. A. 3 B. 9 C.27 D.81 7．直线5x-2y-10=0在x 轴上的截距为a,在y 轴上的截距为b,则（）A.a=2,b=5;B.a=2,b=-5C.a=-2,b=5;D.a=-2,b=-58.直线2x-y=7与直线3x+2y-7=0的交点是（）.A (3,-1)B (-1,3)C (-3,-1)D (3,1) 9. 在△ABC 中，已知ab c b a 2222+=+，则C=( ).A .300 B. 1500 C. 450 D. 135A BD A ’ B ’ D ’C ’ C图1乙甲751873624795436853432110.计算机中常用十六进制是逢16进1的计数制，采用数字0～9和字母A ～F 共16个计数符号，这些符号与十进制的数的对应关系如下表：16进制10 1 2 3 4 5 6 7 8 9 A B C D E F 10进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 那么十六进制下的 1AF 转化为十进制为（）. A. 431 B.321 C.248 D. 250 11. 等差数列{}n a 中，73,10,d a =-=，则1a 等于（）. A ．-39 B ．28 C ．39 D ．3212．圆x 2+y 2-4x-2y-5=0的圆心坐标是：（）.A.(-2,-1);B.(2,1);C.(2,-1);D.(1,-2).13.直线3x+4y-13=0与圆1)3()2(22=-+-y x 的位置关系是：（）. A. 相离; B. 相交; C. 相切; D. 无法判定14.已知等差数列{}n a 中，22a =，46a =，则前4项的和4S 等于（）. A.12 B.10 C.8 D.1415.当输入a 的值为2，b 的值为3-时，右边程序运行的结果是( )..2A - .1B - .1C .2D16．10名工人某天生产同一个零件的件数是15，17，14，10，15，17，17，16，14，12，设其平均数为a ，中位数为b ，众数为c ，则有（）A ．c b a >>B ．a c b >>C ．b a c >>D ．a b c >>17．抛掷一枚质地均匀的硬币，如果连续抛掷1000次，那么第999次出现正面朝上的概率是（）.A ．9991 B ．10001C ．1000999D ．2118.如图是某赛甲、乙两名篮球运动员每场比赛得分的茎叶图，则甲、乙两人这几场比赛得分的中位数之和是（）. A ．62 B. 63 C ．64 D ．65二、填空题：本大题共4小题，每小题4分，共16分。

河南省郑州市2023-2024学年高一下学期7月期末考试数学含答案

2024学年郑州市高一年级（下）期末考试数学（答案在最后）注意事项：1.答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚.2.每道选择题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.在试题卷上作答无效.3.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效.4.考试结束后，请将本试卷和答题卡一并交回.一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.命题p ：0x ∃>，0y >，使得不等式(5x y λ+>++成立，则命题p 成立的一个充分不必要条件可以是（）A.52λλ⎧⎪≥⎨⎪⎪⎩⎭B.53λλ⎧⎪≥⎨⎪⎪⎩⎭C.54λλ⎧⎪>⎨⎪⎪⎩⎭D.55λλ⎧⎪>⎨⎪⎪⎩⎭2.已知 1.30.920.9, 1.3,log 3a b c ===，则（）A.a c b <<B.c a b <<C .a b c<< D.c b a<<3.将函数()πcos 23f x x ⎛⎫=+⎪⎝⎭的图象向右平移π6个单位长度，得到函数()g x 的图象，则函数()()242h x g x x x =-+-的零点个数为（）A.1B.2C.3D.44.甲、乙、丙三人参加“社会主义核心价值观”演讲比赛，若甲、乙、丙三人能荣获一等奖的概率分别为123,,234且三人是否获得一等奖相互独立，则这三人中至少有两人获得一等奖的概率为（）A.14B.724C.1124D.17245.华罗庚是享誉世界的数学大师，国际上以华氏命名的数学科研成果有“华氏定理”“华氏不等式”“华氏算子”“华—王方法”等，其斐然成绩早为世人所推崇．他曾说：“数缺形时少直观，形缺数时难入微”，告知我们把“数”与“形”，“式”与“图”结合起来是解决数学问题的有效途径．在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来分析函数图象的特征．已知函数()y f x =的图象如图所示，则()f x 的解析式可能是（）A.sin ()2xf x = B.cos ()2xf x = C.()sin 12xf x ⎛⎫= ⎪⎝⎭D.()cos 12xf x ⎛⎫= ⎪⎝⎭6.在ABC 中，D 为BC 上一点，且3BD DC =，ABC CAD ∠=∠，2π3BAD ∠=，则tan ABC ∠=（）A.3913B.133C.33D.357.已知π02α<<，()2ππ1sin 2sin 2cos cos 2714αα+=，则α=（）A.3π14B.5π28C.π7D.π148.已知z 是复数，z 是其共轭复数，则下列命题中正确的是（）A.22z z= B.若1z =，则1i z --1+C.若()212i z =-，则复平面内z 对应的点位于第一象限D.若13i -是关于x 的方程20(R)x px q p q ++=∈,的一个根，则8q =-二、多项选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，有选错的得0分，若只有2个正确选项，每选对1个得3分；若只有3个正确选项，每选对1个得2分.9.已知函数()()()sin 0,0,π2πf x A x A ωϕωϕ=+>><<的部分图象如图所示，其图象上最高点的纵坐标为2，且图象经过点()π0,1,,13⎛⎫-⎪⎝⎭，则（）A.11π6ϕ=B.3ω=C.()f x 在π2π,23⎡⎤⎢⎥⎣⎦上单调递减D.方程()()21f x a a =-<<-在0,π]［内恰有4个互不相等的实根10.已知a ，b ，c是平面上三个非零向量，下列说法正确的是（）A.一定存在实数x ，y 使得a xb yc =+成立B.若a b a c ⋅=⋅，那么一定有()a b c⊥- C.若()()a c b c -⊥-，那么2a b a b c-=+- D .若()()a b c a b c ⋅⋅=⋅⋅ ，那么a ，b ，c 一定相互平行11.已知函数2()2sin cos 23cos f x x x x =-，则下列结论中正确的有（）A.函数()f x 的最小正周期为πB.()f x 的对称轴为ππ32k x =+，k ∈Z C.()f x 的对称中心为ππ(0)3,2k +，k ∈ZD.()f x 的单调递增区间为π5π[π,π]1212k k -++，k ∈Z 三、填空题：本大题共3个小题，每小题5分，共15分.12.已知142x y >->-，，且21x y +=，则19214x y +++的最小值为_________.13.球面被平面所截得的一部分叫做球冠，截得的圆叫做球冠的底，垂直于截面的直径被截得的一段叫做球冠的高.球被平面截下的一部分叫做球缺，截面叫做球缺的底面，垂直于截面的直径被截下的线段长叫做球缺的高，球缺是旋转体，可以看做是球冠和其底所在的圆面所围成的几何体.如图1，一个球面的半径为R ，球冠的高是h ，球冠的表面积公式是2πS Rh =，如图2，已知,C D 是以AB 为直径的圆上的两点，π,6π3COD AOC BOD S ∠=∠==扇形，则扇形COD 绕直线AB 旋转一周形成的几何体的表面积为__________.14.已知点O 是ABC 的外心，60BAC ∠=︒，设AO mAB nAC =+，且实数m ，n 满足42m n +=，则mn 的值是___________.四、解答题：本大题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.已知,a b R ∈且0a >，函数4()4x xbf x a+=-是奇函数.（1）求a ，b 的值；（2）对任意(0,)x ∈+∞，不等式()02x mf x f ⎛⎫-> ⎪⎝⎭恒成立，求实数m 的取值范围.16.本学期初，某校对全校高二学生进行数学测试（满分100），并从中随机抽取了100名学生的成绩，以此为样本，分成[50,60),[60,70),[70,80),[80,90),[90,100]，得到如图所示频率分布直方图.（1）估计该校高二学生数学成绩的平均数和85%分位数；（2）为进一步了解学困生的学习情况，从数学成绩低于70分的学生中，分层抽样6人，再从6人中任取2人，求此2人分数都在[)60,70的概率.17.已知ABC 的面积为9，点D 在BC 边上，2CD DB =．（1）若4cos 5BAC ∠=，AD DC =，①证明：sin 2sin ABD BAD ∠=∠；②求AC ；（2）若AB BC =，求AD 的最小值．18.如图，在四棱柱1111ABCD A B C D -中，已知侧面11CDD C 为矩形，60BAD ABC ∠=∠=︒，3AB =，2AD =，1BC =，1AA =，12AE EA =uu u r uuu r，2AFFB =.（1）求证：平面DEF 平面1A BC ；（2）求证：平面11ADD A ⊥平面ABCD ；（3）若三棱锥1E A BC -的体积为33，求平面1A BC 与平面ABCD 的夹角的余弦值.19.已知),cos2a x x =，()2cos ,1b x =- ，记()()R f x a b x =⋅∈（1）求函数()y f x =的值域；（2）求函数()y f x =，[]0,πx ∈的单调减区间；（3）若()π24F x f x m ⎛⎫=+- ⎪⎝⎭，π0,3x ⎛⎤∈ ⎥⎝⎦恰有2个零点12,x x ，求实数m 的取值范围和12x x +的值．2024学年郑州市高一年级（下）期末考试数学注意事项：1.答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚.2.每道选择题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.在试题卷上作答无效.3.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

高一数学下期末试题及答案

2022-2023学年广东省梅州市高一(下)期末数学试卷【答案版】

【新结构】2023-2024学年广东省东莞市高一下学期期末教学质量检查数学试题+答案解析

高一下期末数学试卷含答案解析

2023-2024学年北京市朝阳区高一下学期期末考试数学试卷+答案解析

2023-2024学年安徽省六安一中高一(下)期末数学试卷+答案解析

浙江宁波市九校2024年高一下学期期末联考数学试题+答案

湖北省武汉2023-2024学年高一下学期期末考试数学试卷含答案

上海市高一下学期期末考试数学试卷含答案

最新人教版高一下册数学期末考试含答案

潍坊市高一数学下学期期末考试试题含解析

2022-2023学年山东省济南市高一(下)期末数学试卷【答案版】

2023-2024学年北京市海淀区高一下学期7月期末考试数学试题+答案解析

高一下学期数学期末试卷含答案(共5套)

北京高一下学期期末数学试卷含答案(共5套)

2023北京大兴区高一(下)期末数学试题及答案

2023年高一下学期期末数学试卷(附答案)

河南省郑州市2023-2024学年高一下学期7月期末考试 数学含答案

河南省郑州市2023-2024学年高一下学期7月期末考试数学含答案