(word完整版)初二数学动点问题归类复习(含例题、练习及答案)
初二数学动点问题练习含答案word文档良心出品
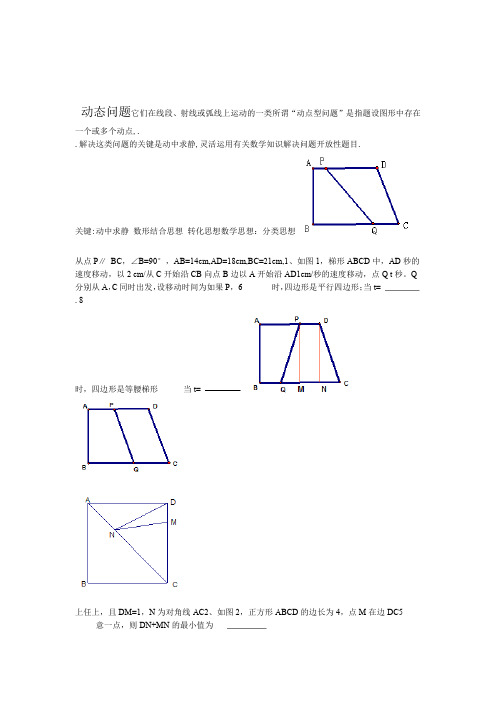
动态问题它们在线段、射线或弧线上运动的一类所谓“动点型问题”是指题设图形中存在一个或多个动点,..解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题开放性题目.关键:动中求静数形结合思想转化思想数学思想:分类思想从点P∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,1、如图1,梯形ABCD中,AD秒的速度移动,以2 cm/从C开始沿CB向点B边以A开始沿AD1cm/秒的速度移动,点Q t秒。
Q 分别从A,C同时出发,设移动时间为如果P,6 时,四边形是平行四边形;当t=. 8时,四边形是等腰梯形当t=上任上,且DM=1,N为对角线AC2、如图2,正方形ABCD的边长为4,点M在边DC5 意一点,则DN+MN的最小值为°90?ACB?AC?60°BC?2O Rt△ABC,?B中,.点、如图,在,是的中点,过3COOlACDAB作重合的位置开始,绕点.从与作逆时针旋转,交过点点边于点的直线?lABl ∥CEE于点的旋转角为,设直线交直线.??EDBCAD;的长为1()①当度时,四边形是等腰梯形,此时??EDBCAD;度时,四边形是直角梯形,此时的长为②当l?EDBC90°?)当(2是否为菱形,并说明理由.时,判断四边形CEO ;;②解:(1)①30,160,1.5?0 .是菱形时,四边形EDBC)当∠(2α=90BA 0DAB, 是平行四边形∴四边形EDBC∵∠α=∠ACB=90//,∴BCED. ∵CE// 000.在Rt△ABC,∠B=60,BC=2, ∴∠中,∠ACB=90A=30C1AC O3320=2.,∴=30中,∠. =2∴AOA=AD= .在Rt△AOD=4,∴ABACB A 又∵四边形EDBC是平行四边形,. BD∴=2. ∴BD=BC(备用图)EDBC是菱形∴四边形E.D于,BE⊥MN于ADMNACB=90°4、在△ABC中,∠,AC=BC,直线经过点C,且⊥MN M M M C D C C E N D EA B B B A AD E图1N 图3N 图21;DE=AD+BE绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②(1)当直线MN ;的位置时,求证:DE=AD-BE绕点(2)当直线MNC旋转到图2具有怎样的等量关系?请写出这个等量BEAD、当直线MN绕点C旋转到图3的位置时,试问DE、(3). 关系,并加以证明∠ACD=90°CAD+∠ACD=90°∴∠BCE+∠解:(1)①∵∠ACD=ACB=90°∴∠CEB ADC≌△CAD=∠BCE ∵AC=BC ∴△∴∠DE=CE+CD=AD+BE ∴CE=AD,CD=BE ∴②∵△ADC≌△CEBAC=BC ∴∠ACD=∠CBE 又∵(2) ∵∠ADC=∠CEB=∠ACB=90°DE=CE-CD=AD-BE∴∴CE=AD,CD=BE ∴△ACD≌△CBE) ,3的位置时,DE=BE-AD(或AD=BE-DEBE=AD+DE等(3) 当MN旋转到图∠CBE,又∵AC=BC,∵∠ADC=∠CEB=∠ACB=90°∴∠ACD= DE=CD-CE=BE-AD. CD=BE,∴∴△ACD≌△CBE,∴AD=CE,90??AEF BCABCDE,5、数学课上,张老师出示了问题:如图1,四边形是边是正方形,点的中点.DCG?EFCFEFFAE 交正方形外角=,求证:的平行线.且于点ECABMMEAM,易证,连接经过思考,小明展示了一种正确的解题思路:取=的中点,则ECF△AME≌△EFAE?,所以.在此基础上,同学们作了进一步的研究:CEBCEBCB外)的任意是边上(除的中点”改为“点,(1)小颖提出:如图2,如果把“点是边EFAE”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明一点”,其它条件不变,那么结论“= 过程;如果不正确,请说明理由;EFAEEBCC”是“的延长线上(除=点外)的任意一点,其他条件不变,结论(2)小华提出:如图3,点仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.D )正确.解:(1A EC?AMMEABM D ,连接证明:在,使上取一点.A F135???AME??BME?45BE??BM..,°°F M 135ECF?CF??DCF?45??,.是外角平分线,°°B C E G ECF????AME.B 1 图C E G90?AEB??CEFAEB??BAE??90?,,°°D A ?BAE??CEF?△AME≌△BCFEF??AE?(ASA...) F (2)正确.NAN?CENEBA..使的延长线上取一点证明:在,连接B E C G?BN?BE??N??PCE?45N ..°FF2图ABCDBE?AD D .是正方形,四边形∥A D ACEF????NAEBEA??DAE??..ECF≌△?△ANE)ASA(.EF??AE.B E C G B E C G 3图沿射线M从3,动点P且MB外一点,AB=5A到射线MB的距离为是射线射线6、如图, MB 上,MB=9,A 的运动时间为t. 秒的速度移动,设MB方向以1个单位/P 值;PAB为直角三角形的t)△t)△1 PAB为等腰三角形的值;(2 求(值为直角三角形的ABM=45 AB=5 3()若且∠°,其他条件不变,直接写出△PABt2BC∥ADCDABCDBCEF∥EABE于点,交中,是作7、如图1,在等腰梯形的中点,过点6BC?AB?4,BC60?∠B?EF到)求点的距离;求:.(,1.ADCBCMN∥ABPEFPM?PMMEF交折线过过作于点作,(2)点交为线段上的一个动点,PNxEP?N.,连结于点,设PMNP△NMN△AD的周长;若的形状是否发生改变?若不变,求出2)①当点在线段,上时(如图改变,请说明理由;PMN△NDCP为等腰三角形?若存在,请求出所有),是否存在点②当点在线段,使上时(如图3x满足要求的的值;若不存在,请说明理由N A A A D D DN PPF F F EE EBBBC C CM M3图1 图2图(第25题)AD A DF EF EBC BC5图(备用)图4(备用)1.?BE?2AB.GEG?BC2EEAB于点∵∴为11解()如图,过点的中点,作122.2EG1?BGBE?,??1?3.Rt△30?60,?∠BEG??B∠EBG2∴在中,∴3.3BC A D E即点到的距离为PMN△NAD的形状不发生改变.2)①当点上运动时,在线段(F E.∥EG?EGEF,PMPM?EF,∴∵.?3PM?EG.GM4?MNAB?EPEF∥BC,?同理,∴∵ BCG ,∥ABPH?MNMNPH如图2,过点于作,∵1图NA D 31.?PH?PM.??60?,∠PMH?30∠NMC?∠B∴∴22PFE533.???MN?MH?4MH?PM cos30??.NH∴则H222 BCMG?22.7?PN?NH?PH??PNH△Rt在中,????2图??22????.4PM?PN?MN?3?7?PMN△的周长∴=MNCNDC△PMN△在线段的形状发生改变,但上运动时,恒为等边三角形.②当点.?MNMR?NRPM?PNPRR于时,如图3当,作,则3?.MR.3MN?3.MN?2MR?△MNCMC?类似①,∵是等边三角形,∴∴2.?6?1?3?2?x?EPGM?BC?BG?MC此时,A DA D A DN P PP)F(EF EFE N RNBCBCBCGMGM GM 图54图3图x?EP?GM?6?1?3.?3?5?3.MPMC?MN?MNMP?此时,,这时时,如图当4NP?NM∠NPM?∠PMN?30?.∠MNC?60?,∠PMN?120?,则5,当又时,如图∠PNM?∠MNC?180?.△PMCPF为直角三角形.∴与重合,因此点MC?PM tan30??1.x?EP?GM?6?1?1?4.此时,∴??3?5PMN△x?2或时,或4综上所述,当为等腰三角形.8BC??△ABCAB?AC10ABD厘米,点为厘米,8、如图,已知中,的中点.点A点向上由在线段点点运动,点向的速度由上以在线段如果点(1)PBC3cm/sBC同时,QCAC 运动4△CQP BPD△是否全等,请说明理由;与的运动速度与点P的运动速度相等,经过1秒后,①若点Q△CQP BPD△与能够使P的运动速度不相等,当点Q的运动速度为多少时,②若点Q 的运动速度与点全等?△ABC都逆时针沿以原来的运动速度从点B同时出发,以②中的运动速度从点C出发,点P (2)若点Q△ABC的哪条边上相遇?第一次在三边运动,求经过多长时间点P与点Q A3??1BP?CQ?31?t)①∵∴厘米,秒,解:(15BD?AB?10ABD厘米.厘米,点∵为∴的中点DQBD?5PC?BC?8PC?8?3?PCBC?BP,厘米,又∵厘米,∴∴BCPCQP△BPD≌△C?B??AB?AC.∴又∵,∴,vv?5?CQ?BDBPCQP?PC?4,?BPCQ△BPD≌△C?B??QP,,,∴则②∵,,又∵155CQ?v??4BP Q4t4??t Q333P秒。
(完整word版)初中数学动点问题专题复习及答案

初中数学动点问题练习题1、佇夏回族自治区)已知:等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B 时运动终止),过点M、N分别作AB边的垂线,与△ ABC的其它边交于P、Q两点,线段MN运动的时间为t秒.1、线段MN在运动的过程中,t为何值时,四边形MNQP恰为矩形?并求出该矩形的面积;(2)线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t .求四边形MNQP的面C积S随运动时间t变化的函数关系式,并写岀自变量t的取值范围.QPAM N B2、如图,在梯形ABCD中,AD // BC,AD 3,DC 5,AB 4. 2,Z B 45 .动点M 从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD 以每秒1个单位长度的速度向终点D运动•设运动的时间为t秒.(1)求BC的长.(2)当MN // AB时,求t的值.(3)试探究:t为何值时,△ MNC为等腰三角形.3、如图,在平面直角坐标系中,四边形OABC是梯形,OA// BC,点A的坐标为(6,0),点B 的坐标为(4,3),点C在y轴的正半轴上.动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒).(1)求线段AB的长;当t为何值时,MN // OC?⑵设△ CMN的面积为S,求S与t之间的函数解析式, 并指出自变量t的取值范围;S是否有最小值?若有最小值,最小值是多少?x(3)连接AC,那么是否存在这样的 t ,使MN 与AC 互相垂直? 若存在,求出这时的t 值;若不存在,请说明理由.4、(河北卷)如图,在 Rt A ABC 中,/ C = 90°, AC = 12, BC = 16,动点P 从点A 出发沿 AC 边向点C 以每秒3个单位长的速度运动,动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动.P, Q 分别从点A , C 同时出发,当其中一点到达端点时,另一点也随之 停止运动.在运动过程中,△ PCQ 关于直线PQ 对称的图形是△ PDQ.设运动时间为t (秒). (1 )设四边形PCQD 的面积为y ,求y 与t 的函数关系式; (2) t 为何值时,四边形 PQBA 是梯形?(3) 是否存在时刻t ,使得PD // AB ?若存在,求出t 的值;若不存在,请说明理由; (4) 通过观察、画图或折纸等方法,猜想是否存在时刻t ,使得PD 丄AB ?若存在,请估计t 的值在括号中的哪个时间段内( O W t < 1 ; 1 v t w 2 ; 2v t w 3; 3 v t < 4);若不存在,请简要说明理由.5、(山东济宁)如图, A 、B 分别为x 轴和y 轴正半轴上的点。
初中数学动点问题及练习题附参考答案(K12教育文档)

初中数学动点问题及练习题附参考答案(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初中数学动点问题及练习题附参考答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为初中数学动点问题及练习题附参考答案(word版可编辑修改)的全部内容。
初中数学动点问题及练习题所谓“动点型问题"是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目。
解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题。
关键:动中求静.数学思想:分类思想函数思想方程思想数形结合思想转化思想注重对几何图形运动变化能力的考查。
从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,通过“对称、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理.选择基本的几何图形,让学生经历探索的过程,以能力立意,考查学生的自主探究能力,促进培养学生解决问题的能力.图形在动点的运动过程中观察图形的变化情况,需要理解图形在不同位置的情况,才能做好计算推理的过程.在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
这些压轴题题型繁多、题意创新,目的是考察学生的分析问题、解决问题的能力,内容包括空间观念、应用意识、推理能力等.从数学思想的层面上讲:(1)运动观点;(2)方程思想;(3)数形结合思想;(4)分类思想;(5)转化思想等.研究历年来各区的压轴性试题,就能找到今年中考数学试题的热点的形成和命题的动向,它有利于我们教师在教学中研究对策,把握方向.只的这样,才能更好的培养学生解题素养,在素质教育的背景下更明确地体现课程标准的导向.本文拟就压轴题的题型背景和区分度测量点的存在性和区分度小题处理手法提出自己的观点.专题一:建立动点问题的函数解析式函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容。
八年级数学专题复习:“动点”问题专题解析汇编(,含解析、点评和练习).doc

八年级数学专题复习:“动点”问题专题解析汇编八年级数学下册中的“动点”题型主要集中在《勾股定理》、《平行四边形》和《一次函数》三个章节,常常是这三个章节综合起来的题型比较多.动点问题的题型一直统考和中考的热点题型,但由于动点变化较大,所以也是学生感到比较头疼的一类题型;下面我精选了一部分含动点的典型题进行分析、解答、点评并附有少量追踪练习,希望同学们能从屮悟出一些道理,总结破题的思路,同时感受到这类题型所蕴含的数学魅力.、在动点中求最小值例1.如图,在正方形ABCD中,E为A3上的一点,BE = 2,P是AC上一动点,则PB + PE的最小值是多少?分析:如分析图所示,过B作关于4C的对称点,根据正方形的性质其对称点恰好在D点处, 连结ED交AC于点P,根据轴对称的性质、三角形三边之间的关系以及连接D、E两点之间线段最短,可以知道此时的PB+PK值最小.(这里有个“将军饮马”的故事与同学们分享.)略解:过B作关于AC的对称点,根据正方形的性质其对称点恰好在D点处,连结仞交AC于点连接PW•/ BE = 2, AE = 3BE :. AE = 6 :. AB = 8•根据正方形的性质的性质可知:= = 8, ZDAB = 9(T ・在RtZ\DAE中勾股定理易求ED 二yJAE2 +AD2 = ^62 +82 =10.・・・B和D关于AC对称,根据轴对称的性质可知:P'B = P'D,DAE:.P'B+P'E = P'D+P'E=DE=10.变式:正方形ABCD的边长为4, ZDAC的平分线交DC于点E,若P、0分别是AD和AE上的动点,则DQ+PQ的最小值是 .分析:本题和刚才的例题相比是两个动点,难度增加了不少.英实我们可以假设P先是定点, 作出D 关于AE的对称点如图根据角平分线的定义、轴对称的性质和全等三角形(即图中的△4DF9ZX4Z/F)可以知道D关于AE 的对称点D恰好落在正方形的对角线AC上;但问题是我们是把P假设为定点,实际上P为动点,那么P应该运动到什么位置上才使D到AD最短距离最短呢?显然根据垂线段最短,我们过D作的垂线段DP即可找到P、0能使DQ + P Q有最小值的位置(见图中P\ 0的位置),此时DP'最小;根据轴对称的性质可知・•・= = 根据正方形的性质可以得出ZDAC=45°,在RtA AP'D1中,ZAD'P' = 90° -45° =45° , A ZDAC = ZAD,P, A P'D'^P'A V A ADF A AD*F ・•・AD'=AD = 4在RtA4P'D r 中容易算出DPjgxQ =^8 = 2^2 .故应填2逅.例2.如图,在直角坐标系xOy中,点M(x,0)可在x轴上移动,且它到点P(5,5), 0(2, /)两点的距离分别为MP和M0, 若MP + MQ有最小值时:(1)•请作图找岀满足MP + MQ最小值的M点的位置.(保留作图痕迹,不写作法)(2).求此时点M的坐标.分析:本题的⑴问和例1的道理是一样的.;据轴对称的性质、三角形三边之间的关系以及连接P、0'两点之间线段最短,M点的位置就满足MP + MQ的值最小.木题的⑵问可以利用轴对称的性质求出Q'的坐标,在你利用待定 系数法求出P 、0两点所在直线的解析式,进而求出M 的坐标. 略解:(1).过Q 作关于x 轴的对称点0,连接P0交x 轴于M 点,连接Q'M ,此时MP + MQ 的值最小.⑵.根据轴对称的性质求出0的坐标^(2,-7) 设P0所在的直线的解析式为y= kx + b,因为P(5,5), 0(2,-7)7 、故点M 的坐标为-,0 .丿点评:在一直线上求作一点,使其到直线同一侧的两定点的距离之和最小,往往要通过作其 屮一个点关于此直线的对称点,把两定点转化到直线的两侧,连接对称点和另一定点就可以 找到这个动点的使其有最小值的位置,根据的是“两点之间,线段最短”、“垂线段最最短”. 在动点中求最小值容易和多个知识点串联以来,能较好的考查的数学的基本功和数学素养.追踪练习:1、 正方形ABCD 的面积为64, DE = gcE,P 为AC 上的一动点;求PD+PE 的最小值?2、 菱形ABCD 的对角线分别为12和16, M 、N 分別为BC 、CD 的屮点,P 是对角线BD 上的一动点,贝ij PM+PN 的最小值为 ____所以5k + b = 5 2k + b = -I 贝 ij y = 3x-73、如图,在矩形ABCD 中,AB = 4, AD = 6t E 是AB 边的中点,F 是线段BC 边上的动点,将分析: (1) .由角平分线的的定义和平行线的性质容易推出上1 = Z5,Z3二Z6 ,贝WE = OC.OF = OC ; 等量代换后0E 二OF. (2) . CO 是AECF 的EF 的中线,根据题中的提供的数据,无非△ ECF 是特殊三角形才能求出 CO ;4 EBF 沿EF 所在直线折叠得到4 EB F ,连接皮D,则30的附值是A. 2/10-2B. 6C. 2^73-2 ED. 44、如图,直线y = kx-6经过点A(4,0),直线y = -3x + 3与x 轴交 于B点,口两直线交于点C.(1).求k 的值; (2) .求△ABC 的面积;⑶•若点P 是坐标轴上的一个动点,当PB+PC 的值最小时,求P 点的坐标.• • • •二、在动点中来探究四边形的形状B F例1・如图,△ABC 中,点0是AC 边上的一个动点,过点0作直线MN 〃BC, 设MN 交ZBCA若AECF是直角三角形,一切问题解决了;根据题中交ZBCA的平分线于点E,交ZBCA的外角平分线于点F,可以证得ZECF = 90° .而点0在4C的位置是发生变化的.要证四边形AECF是矩形,已经知道ZECF = 90。
初二动点问题(含标准答案)

初二动点问题(含答案)作者:日期: 2动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目•解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题•关键:动中求静•数学思想:分类思想数形结合思想转化思想1、如图1,梯形ABCD 中,AD // BC,/ B=90 ° , AB=14cm,AD=18cm,BC=21cm,点P 从A开始沿AD边以1cm/秒的速度移动,点Q从C开始沿CB向点B以2 cm/秒的速度移动,如果P, Q分别从A , C同时出发,设移动时间为t秒。
当t= _____ 时,四边形是平行四边形;6当t= _____ 时,四边形是等腰梯形• 82、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1 , N为对角线AC上任意一点,则DN+MN的最小值为_________ 53、如图,在只也ABC中,ACB 90°, B 60°, BC 2•点°是AC的中点,过点°的直线l从与AC重合的位置开始,绕点°作逆时针旋转,交AB边于点D •过点C作2CE // AB 交直线I 于点E ,设直线I 的旋转角为(1)①当度时,四边形EDBC 是等腰梯形,此时AD 的长为②当度时,四边形EDBC 是直角梯形,此时 AD 的长为(2)当 90°时,判断四边形 EDBC 是否为菱形,并说明理由.解:(1 [① 30, 1 :② 60, 1.5;(2)当/% =900时,四边形 EDBC 是菱形•v/a =/ACB=90°,「. BC//ED. T CE//AB,二四边形 EDBC 是平行四边形 在 Rt △ABC 中,/ ACB=900,/ B=60°,BC=2, /./ A=30°.137AC3••• AB=4,AC=2 '3. ••• A°= 2 = 3 •在 Rt △ AOD 中,/ A=30,二 AD=2.B• BD=2. • BD=BC. 又•••四边形 EDBC 是平行四边形, •四边形EDBC 是菱形 4、C ,A(1) 当直线 MN 绕点C 旋转到图1的位置时,求证:①△ ADC ◎△ CEB •,②DE=AD + BE ;⑵当直线 MN 绕点C 旋转到图2的位置时,求证: DE=AD-BE ;⑶当直线MN 绕点C 旋转到图3的位置时,试问 DE 、AD 、BE 具有怎样的等量关系?请写出这个等量 关系,并加以证明•解:(1 [① •••/ ACD= / ACB=90 •••/ CAD+ / ACD=90 /-Z BCE+ / ACD=90•••/ CAD= Z BCE •/ AC=BCADC ◎△ CEB② •/△ ADC ◎△ CEB • CE=AD , CD=BE • DE=CE+CD=AD+BE(2) T Z ADC= Z CEB= Z ACB=90°ACD= Z CBE又 ■: AC=BCACD ◎△ CBE • CE=AD , CD=BE • DE=CE-CD=AD-BE(3) 当 MN 旋转至U 图 3 的位置时,DE=BE-AD(或 AD=BE-DE , BE=AD+DE 等)•/Z ADC= Z CEB= Z ACB=90° /Z ACD= Z CBE , 又 ■: AC=BC ,ACD ◎△ CBE ,• AD=CE , CD=BE ,• DE=CD-CE=BE-AD.5、数学课上,张老师出示了问题: 如图1,四边形ABCD 是正方形,点E 是边BC 的中点. AEF 90°,且EF 交正方形外角 DCG 的平行线CF 于点F ,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB 的中点 M 连接 ME 则 AM =EC,易证△ AME ECF ,所以 AE EF .在此基础上,同学们作了进一步的研究:(1 )小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点 E 是边BC 上(除B, C 外)的任意 一点”,其它条件不变,那么结论“ AE=EF'仍然成立,你认为小颖的观点正确吗?如果正确,写出证明 过程;如果不正确,请说明理由;(3) 若AB=5且Z ABM=45 °,其他条件不变,直接写出△ PAB 为直角三角形的t 值(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE=EF' 仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程; 解:(1)正确. 证明:在 AB 上取一点M ,使AM45°DCFBM BE . BME QCF 是外角平分线,AMEQ AEBBAE(2)正确.证明:在BA 的延长线上取一点 NBN BE . N PCEQ 四边形ABCD 是正方形, ADAE BEA . NAE △ ANEECF (ASA ). AE EF .ECF . BAE 90°, CEF . AEB△6、如图,射线MB 上,MB=9,A 是射线 MB 方向以1个单位/秒的速度移动,设 求(PAB 为等腰三角形的t 值;MB 外一点,AB=5且A 到射线 P 的运动时间为t.(2)△ PAB 为直角三角形的t 值; 如果不正确,请说明理由. MB 的距离为3,动点P 从图沿射线2 >过P 作PG 丄IVIN 于G VMN/7AB^NM=NP过N 作NR 丄MP^R 则有:RM=0.5FM= V宀 忑 J :Rt ANMRM^RM- y MN=」CMV3 再A — {5・X j ■亍:、x=43。
初二数学动点问题练习含答案

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,敏捷运用有关数学学问解决问题.关键:动中求静.数学思想:分类思想 数形结合思想 转化思想1、如图1,梯形ABCD 中,AD ∥ BC ,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P 从A 开场沿AD 边以1cm/秒的速度挪动,点Q 从C 开场沿CB 向点B 以2 cm/秒的速度挪动,假如P ,Q 分别从A ,C 同时动身,设挪动时间为t 秒。
当t= 时,四边形是平行四边形;6 当t= 时,四边形是等腰梯形. 82、如图2,正方形ABCD 的边长为4,点M 在边DC 上,且DM=1,N 为对角线AC 上随意一点,则DN+MN 的最小值为 53、如图,在Rt ABC △中,9060ACB B ∠=∠=°,°,2BC =.点O 是AC的中点,过点O 的直线l 从与AC 重合的位置开场,绕点O 作逆时针旋转,交AB 边于点D .过点C 作CE AB ∥交直线l 于点E ,设直线l 的旋转角为α. (1)①当α= 度时,四边形EDBC 是等腰梯形,此时AD 的长为 ;②当α= 度时,四边形EDBC 是直角梯形,此时AD 的长为 ;(2)当90α=°时,推断四边形EDBC 是否为菱形,并说明O ECDα lOC理由.解:(1)①30,1;②60,1.5;(2)当∠α=900时,四边形EDBC 是菱形.∵∠α=∠ACB=900,∴BC //ED . ∵CE //AB , ∴四边形EDBC 是平行四边形 在Rt △ABC 中,∠ACB =900,∠B =600,BC =2, ∴∠A =300. ∴AB =4,AC. ∴AO =12AC.在Rt △AOD 中,∠A =300,∴AD =2.∴BD =2. ∴BD =BC . 又∵四边形EDBC 是平行四边形, ∴四边形EDBC 是菱形4、在△ABC 中,∠ACB =90°,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE=AD +BE ; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE=AD-BE ; (3)当直线MN 绕点C 旋转到图3的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.解:(1)① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90°∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB② ∵△ADC ≌△CEB ∴CE=AD ,CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ,CD=BE ∴DE=CE-CD=AD-BEC B AE D图1 N M A B CDEM N图2 A C B ED N M 图3(3) 当MN 旋转到图3的位置时,DE=BE-AD(或AD=BE-DE ,BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE , 又∵AC=BC , ∴△ACD ≌△CBE , ∴AD=CE ,CD=BE , ∴DE=CD-CE=BE-AD.5、数学课上,张教师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .经过思索,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此根底上,同学们作了进一步的讨论:(1)小颖提出:如图2,假如把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的随意一点”,其它条件不变,那么结论“AE =EF ”仍旧成立,你认为小颖的观点正确吗?假如正确,写出证明过程;假如不正确,请说明理由;(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的随意一点,其他条件不变,结论“AE =EF ”仍旧成立.你认为小华的观点正确吗?假如正确,写出证明过程;假如不正确,请说明理由. 解:(1)正确.证明:在AB 上取一点M ,使AM EC =,连接ME . CF 是外角平分线,45DCF ∴∠=°,135ECF ∴∠=°.90AEB BAE ∠+∠=°,90AEB CEF ∠+∠=°,∴BAE CEF ∠=∠. AME BCF ∴△≌△(ASA ). AE EF ∴=. (2)正确.A DFCGE B 图1A DFC GE B图2A DF CGE BM证明:在BA 的延长线上取一点N .使AN CE =,连接NE .BN BE ∴=. 45N PCE ∴∠=∠=°.四边形ABCD 是正方形, AD BE ∴∥. ANE ECF ∴△≌△(ASA ). 6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的间隔 为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度挪动,设P 的运动时间为t.求(1)△ PAB 为等腰三角形的t 值;(2)△ PAB 为直角三角形的t 值; (3) 若AB=5且∠ABM=45 °,其他条件不变,干脆写出△ PAB 为直角三角形的t 值7、如图1,在等腰梯形ABCD 中,AD BC ∥,E 是AB 的中点,过点E 作EF BC∥交CD 于点F .46AB BC ==,,60B =︒∠.求:(1)求点E 到BC 的间隔 ; (2)点P 为线段EF 上的一个动点,过P 作PM EF ⊥交BC 于点M ,过M 作MN AB ∥交折线ADC 于点N ,连结PN ,设EP x =.①当点N 在线段AD 上时(如图2),PMN △的形态是否发生变更?若不变,求出PMN △的周长;若变更,请说明理由;②当点N 在线段DC 上时(如图3),是否存在点P ,使PMN △为等腰三角形?若存在,恳求出全部满意要求的x 的值;若不存在,请说明理由A D FC GE B图3A D FC GE BN解(1)如图1,过点E作EG BC⊥于点G . ∵E为AB的中点,∴122BE AB ==.在Rt EBG △中,60B =︒∠, ∴30BEG =︒∠.∴112BG BE EG ====,即点E 到BC 的间隔(2)①当点N 在线段AD 上运动时,PMN △的形态不发生变更.∵EF BC ∥, ∴EP GM =,PM EG ==同理4MN AB ==.如图2,过点P 作PH MN ⊥于H ,∵MN AB ∥, ∴6030NMC B PMH ==︒=︒∠∠,∠.∴122PH PM == ∴3cos302MH PM =︒=. 则35422NH MN MH =-=-=.在Rt PNH △中,PN === ∴PMN △的周长=4PM PN MN ++=.②当点N 在线段DC 上运动时,PMN △的形态发生变更,但MNC △恒为等图1A D EB F CG图2A DE BF CPN MG HA D E BFC图4(备AD EBF C图5(备A D E BF C 图图A DE BF C P N M图A DEBFC P N M(第25边三角形.当PM PN =时,如图3,作PR MN ⊥于R ,则MR NR =.类似①,32MR =.∴23MN MR ==. ∵MNC △是等边三角形,∴3MC MN ==.此时,6132x EP GM BC BG MC ===--=--=.当MP MN=时,如图4,这时MC MN MP ===此时,615x EP GM ===-=-当NP NM =时,如图5,30NPM PMN ==︒∠∠. 则120PMN =︒∠,又60MNC =︒∠, ∴180PNM MNC +=︒∠∠. 因此点P 与F 重合,PMC △为直角三角形. ∴tan301MC PM =︒=. 此时,6114x EP GM ===--=. 综上所述,当2x =或4或(5时,PMN △为等腰三角形.8、如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点. (1)假如点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,可以使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 动身,点P 以原来的运动速度从点B 同时动身,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第图3A DE B FCPN M图4A D E BFCP M N 图5A D E BF CMN GGR G一次在ABC △的哪条边上相遇?解:(1)①∵1t =秒, ∴313BP CQ ==⨯=厘米, ∵10AB =厘米,点D 为AB 的中点, ∴5BD =厘米.又∵8PC BC BP BC =-=,厘米, ∴835PC =-=厘米, ∴PC BD =.又∵AB AC =, ∴B C ∠=∠, ∴BPD CQP △≌△. ②∵P Qv v ≠, ∴BP CQ≠, 又∵BPD CQP△≌△,B C ∠=∠,则45BP PC CQ BD ====,,∴点P ,点Q 运动的时间433BP t ==秒, ∴515443Q CQ v t===厘米/秒。
[终稿]初中数学动点问题及练习题附参考答案.docx
![[终稿]初中数学动点问题及练习题附参考答案.docx](https://img.taocdn.com/s3/m/c60b285784868762cbaed557.png)
例1.如图,已知在矩形ABCD 中,A£)=8, CD=4,点E 从点小I ]发,沿线段D4以每秒1 个单位长的速度向点A 方向移动,同吋点尸从点C 出发,沿射线CQ 方向以每秒2个单位 长的速度移动,当B, E, F 三点共线时,两点同时停止运动.设点E 移动的时间为/(秒).(1) 求当r 为何值时,两点同时停止运动;(2) 设四边形BCFE 的面积为S,求S 与/之间的函数关系式,并写岀r 的取值范围;(3) 求当t 为何值时,以E, F, C 三点为顶点的三介形是等腰三用形;例2•正方形ABCD 边长为4,、N 分别是BC 、CD 上的两个动点,当M 点在BC 上运动时,保持AM 和MN 垂直, (1) 证明:Rt/XABM s RM\MCN ;(2) 设B M =x,梯形ABCN 的而积为y,求歹与兀之间的函数关系式;当M 点运动到 什么位置吋,四边形ABCN 而积最大,并求出最大而积;(3)当M 点运动到什么位置时Rt/XABM ^Rt/\AMN ,求此时x 的值.例 3.如图,在梯形 ABCD 中,AD // BC, AP = 3, DC = 5, AB = 4^2, ZB = 45。
.动 点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同吋从C 点 出发沿线段CD 以每秒1个单位长度的速度向终点Q 运动.设运动的时间为/秒.(09年济南中考) (1)求BC 的长。
(2) 当MN // AB 时,求f 的值.(3) 试探究:f 为何值时,HMNC 为等腰三角形.(4)求当f 为何值时,ZBEC 二ZBFC.由题意可知:ED=t, BC=8, FD= 2/-4, FC= It.FD ED•: ED//BC,4FEDs/\FBC.:・——=——・FC BC2—4 t・・・一解得/=4.2t 8.・・当匸4时,两点同时停止运动;(3分)1 1 9(2)•:ED=t, CF=2t, :.S=S^BC^- S^BCF= - X8X4+ - X2rXr= 16+ z2.2 2即S=16+f. (0 W/ W4);.......................................................................... (6 分) (3)①若EF=EC时,则点F只能在CD的延长线上,VEF2=(2r-4)2+r2 =5r2-16r + 16,EC2=42 + z2 = z2 +16 , 5z2— 16f +16 = z2 +16 . f=4 ^=0 (^i);4 L②若EC=FC W,VEC2=42+r2 =r2 + 16, FC2=4r, A r+ 16=4r.:・t = -』3 ;3③若EF=FC时,*:EF2=⑵一4尸 + 尸=5厂 _ 16/ +16 , FC2=4/2,5t2—I6t +16 =4r2. .'.Z|=16+8A/3 (舍去),t2= 16 —8A/3.・•・当/的值为4, -V3, 16-8^3时,以E, F, C三点为顶点的三角形是等腰三3角形; ............................................................. (9分)Be CF(4)在RtA^CF 和RtAC££> 中,•/ ZBCD=ZCDE=90° ,——=——=2 ,CD ED:.RtABCF^RtACEP・:.ZBFC=ZCED. (10 分)•:AD//BC、:.ZBCE=ZCED.若ZBEC=ZBFC,则ZBEC=ZBCE.即BE=BC.*.* BE 2=t~ —16/ + 80 , /. t~ — 16/ + 80 =64./.Z J =16 + 8A /3 (舍去),t2= 16 — 8A /3 .・・・当匸16-朋 时,ZBEC=ZBFC. ......................................................... (12分) 例2.解:(1)在正方形ABCD 中,AB = BC = CD = 4, ZB = ZC = 90°, •・• AM 丄MN ,.•・ ZAMN =90\ZCMN + ZAMB = 90° f在 RtAABM 中,ZMAB + ZAMB = 90°, :.ZCMN =AM AB ,RtAABM s Rt/\MCN ,(2) ••• Rt/\ABM s RtAMCTV ,AB BM 4 x• _ — __ • ___ — _•• MC_ CN …4_x_ CN '当x = 2吋,歹取最大值,最大值为10.(3) v ZB = ZAW=90°,AM AR .••要使厶ABM s^AMN ,必须有—— =— MN BM•••当点M 运动到BC 的中点时,s ZMN ,此时x = 2. 例3.解:(1)如图①,过4、D 分别作4K 丄BC 于K , DH 丄BC 于H ,则四边形ADHK 是矩形 ・・.KH = AD = 3.在RtZ\ABK 中,AK = AB sin45° = 4^2.—= 4 2••• CN = -X 2 + 4x _4-U^^ + 4〕・4 二丄i i 9 2J + 2X + 8 = --(X -2)+10 由(1)知如MN AB~M CBK = AB cos 45° = 4迈—=42在RtACPH中,由勾股定理得,HC = V52 -42 = 3・•・ BC = BK + KH + HC = 4 + 3 + 3 = 10(图①)(图②)(2)如图②,过D作DG// AB交BC于G点,则四边形ADGB是平行四边形・・・MN // AB:.MN // DG:.BG = AD = 3:.GC = 10 — 3 = 7由题意知,当M、N运动到f秒时,CN=t, CM =10-2r.•・・ DG // MN:.ZNMC = ZDGC乂zc=zc・・・ ZXMNC s'GDC.CN CM9~CD~~CG10-2/7解得,(3)分三种情况讨论:①当NC = MC时,如图③,即/二10-2/10(图③)(图④)② 当MN = NC 时,如图④,过N 作NE 丄MC 于E VZC = ZC,乙DHC =乙NEC = 90°・•・ 'NEC s HDHC.NC EC^~DC~~HC 即[=□5 3•,兰8③ 当MN=MC 时,如图⑤,过M 作MF 丄CN 于F 点.FC=-NC = -t 2 2 VZC = ZC,乙MFC = ZDHC = 90° ・•・HMFCs'DHC ・ FC MC"~HC~~DC1即二Si3 5・ 60 • ■ t = -- 17综上所述,当/=巴、 3 &业好文档精心整理欢迎下载 2兰或2聖 8 17时,HMNC 九等腰三和形 (图⑤)。
(完整版)初二数学动点问题练习(含答案)

eandr动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想数形结合思想转化思想1、如图1,梯形ABCD中,AD∥ BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动,点Q从C开始沿CB向点B以2 cm/秒的速度移动,如果P,Q分别从A,C同时出发,设移动时间为t秒。
当t= 时,四边形是平行四边形;6当t= 时,四边形是等腰梯形. 82、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1,N为对角线AC上任意一点,则DN+MN的最小值为53、如图,在Rt ABC△中,9060ACB B∠=∠=°,°,2BC=.点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D.过点C作CE AB∥交直线l于点E,设直线l的旋转角为α.(1)①当α=度时,四边形EDBC是等腰梯形,此时AD的长为;②当α=度时,四边形EDBC是直角梯形,此时AD的长为;(2)当90α=°时,判断四边形EDBC是否为菱形,并说明理由.解:(1)①30,1;②60,1.5;(2)当∠α=900时,四边形EDBC是菱形.∵∠α=∠ACB=900,∴BC//ED. ∵CE//AB, ∴四边形EDBC是平行四边形在Rt△ABC中,∠ACB=900,∠B=600,BC=2, ∴∠A=300.∴AB=4,AC∴AO=12AC.在Rt△AOD中,∠A=300,∴AD=2.∴BD=2. ∴BD=BC. 又∵四边形EDBC是平行四边形,∴四边形EDBC是菱形4、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等AA(备用图)CBAED图1NMA BCDEMN图2ACBEDNM图3量关系,并加以证明.解:(1)① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB② ∵△ADC ≌△CEB ∴CE=AD ,CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ,CD=BE ∴DE=CE-CD=AD-BE(3) 当MN 旋转到图3的位置时,DE=BE-AD(或AD=BE-DE ,BE=AD+DE 等)∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE , 又∵AC=BC ,∴△ACD ≌△CBE , ∴AD=CE ,CD=BE , ∴DE=CD-CE=BE-AD.5、数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠= ,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.解:(1)正确.证明:在AB 上取一点M ,使AM EC =,连接ME .BM BE ∴=.45BME ∴∠=°,135AME ∴∠=°.CF 是外角平分线,45DCF ∴∠=°,135ECF ∴∠=°. AME ECF ∴∠=∠.90AEB BAE ∠+∠= °,90AEB CEF ∠+∠=°,∴BAE CEF ∠=∠. AME BCF ∴△≌△(ASA ). AE EF ∴=.(2)正确.证明:在BA 的延长线上取一点N .使AN CE =,连接NE .BN BE ∴=. 45N PCE ∴∠=∠=°.四边形ABCD 是正方形, AD BE ∴∥.DAE BEA ∴∠=∠. NAE CEF ∴∠=∠.ANE ECF ∴△≌△(ASA ).AE EF ∴=.6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动,设P 的运动时间为t.求(1)△ PAB 为等腰三角形的t 值;(2)△ PAB 为直角三角形的t 值;(3) 若AB=5且∠ABM=45 °,其他条件不变,直接写出△ PAB 为直角三角形的t 值AD F C GB图1ADFC GEB图3A DFC GB 图2AD FC GE B MADFGE BNAllthisinth7、如图1,在等腰梯形ABCD中,AD BC∥,E是AB的中点,过点E作EF BC∥交CD于点F.46AB BC==,,60B=︒∠.求:(1)求点E到BC的距离;(2)点P为线段EF上的一个动点,过P作PM EF⊥交BC于点M,过M作MN AB∥交折线ADC于点N,连结PN,设EP x=.①当点N在线段AD上时(如图2),PMN△的形状是否发生改变?若不变,求出PMN△的周长;若改变,请说明理由;②当点N在线段DC上时(如图3),是否存在点P,使PMN△为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由解(1)如图1,过点E作EG BC⊥于点G.∵E为AB的中点,∴122BE AB==.在Rt EBG△中,60B=︒∠,∴30BEG=︒∠.∴112BG BE EG====,.即点E到BCA DA DEBFC图4(备用)A DEBFC图5(备用)A DEBFC图1图2A DEBFCPNM图3A DEBFCPNM(第25题)si(2)①当点N在线段AD上运动时,PMN△的形状不发生改变.∵PM EF EG EF⊥⊥,,∴PM EG∥.∵EF BC∥,∴EP GM=,PM EG==同理4MN AB==.如图2,过点P作PH MN⊥于H,∵MN AB∥,∴6030NMC B PMH==︒=︒∠∠,∠.∴12PH PM==∴3cos302MH PM=︒=A.则35422NH MN MH=-=-=.在Rt PNH△中,PN===∴PMN△的周长=4PM PN MN++=++.②当点N在线段DC上运动时,PMN△的形状发生改变,但MNC△恒为等边三角形.当PM PN=时,如图3,作PR MN⊥于R,则MR NR=.类似①,32MR=∴23MN MR==.∵MNC△是等边三角形,∴3MC MN==.此时,6132x EP GM BC BG MC===--=--=.当MP MN=时,如图4,这时MC MN MP===此时,615x EP GM===--=当NP NM=时,如图5,30NPM PMN==︒∠∠.则120PMN=︒∠,又60MNC=︒∠,∴180PNM MNC+=︒∠∠.因此点P与F重合,PMC△为直角三角形.∴tan301MC PM=︒=A.此时,6114x EP GM===--=.综上所述,当2x=或4或(5时,PMN△为等腰三角形.8、如图,已知ABC△中,10AB AC==厘米,8BC=厘米,点D为AB的中点.(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动①若点Q的运动速度与点P的运动速度相等,经过1秒后,BPD△与CQP△是否全等,请说明理由;图3A DEBFCPNM图4A DEBFCPMN图5A DEBF(PCMNGGRG图2A DEBFCPNMGH②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?解:(1)①∵1t =秒, ∴313BP CQ ==⨯=厘米,∵10AB =厘米,点D 为AB 的中点, ∴5BD =厘米.又∵8PC BC BP BC =-=,厘米, ∴835PC =-=厘米, ∴PC BD =.又∵AB AC =, ∴B C ∠=∠, ∴BPD CQP △≌△.②∵P Qv v ≠,∴BP CQ ≠, 又∵BPD CQP △≌△,B C ∠=∠,则45BP PC CQ BD ====,,∴点P ,点Q 运动的时间433BP t ==秒, ∴515443Q CQ v t===厘米/秒。
初二动点问题(含答案)

动态问题一、所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题. 关键:动中求静.数学思想:分类思想 数形结合思想 转化思想 类型:1.利用图形想到三角形全等,相似及三角函数2.分析题目,了解有几个动点,动点的路程,速度(动点怎么动)3.结合图形和题目,得出已知或能间接求出的数据4.分情况讨论,把每种可能情况列出来,不要漏5.动点一般在中考都是压轴题,步骤不重要,重要的是思路6.动点类题目一般都有好几问,前一问大都是后一问的提示,就像几何探究类题一样,如果后面的题难了,可以反过去看看前面问题的结论二、例题:1、如图1,梯形ABCD 中,AD ∥ BC ,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P 从A 开始沿AD 边以1cm/秒的速度移动,点Q 从C 开始沿CB 向点B 以2 cm/秒的速度移动,如果P ,Q 分别从A ,C 同时出发,设移动时间为t 秒。
当t= 时,四边形是平行四边形; 当t= 时,四边形是等腰梯形.2、如图2,正方形ABCD 的边长为4,点M 在边DC 上,且DM=1,N 为对角线AC 上任意一点,则DN+MN 的最小值为3、如图,在Rt ABC △中,9060ACB B ∠=∠=°,°,2BC =.点O 是AC 的中点,过点O 的直线l 从与AC 重合的位置开始,绕点O 作逆时针旋转,交AB 边于点D .过点C 作CE AB ∥交直线l 于点E ,设直线l 的旋转角为α.(1)①当α= 度时,四边形EDBC 是等腰梯形,此时AD 的长为 ;②当α= 度时,四边形EDBC 是直角梯形,此时AD 的长为 ;(2)当90α=°时,判断四边形EDBC 是否为菱形,并说明理由.4、在△ABC 中,∠ACB=90°,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE=AD +BE ; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE=AD-BE ;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.5、数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .OE CDα lC B ED 图1 N M A B C DE M N 图2A CB E D N M 图3经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动,设P 的运动时间为t. 求(1)△ PAB 为等腰三角形的t 值;(2)△ PAB 为直角三角形的t 值;(3) 若AB=5且∠ABM=45 °,其他条件不变,直接写出△ PAB 为直角三角形的t 值8、如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点.(1)如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动A D F C G EB 图1 AD FG E B 图3A D FC G E B 图2①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?。
初二动点问题(含答案解析)

动态问题动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点所谓“动点型问题”是指题设图形中存在一个或多个动点,,它们在线段、射线或弧线上运动的一类开放性题目开放性题目..解决这类问题的关键是动中求静解决这类问题的关键是动中求静,,灵活运用有关数学知识解决问题灵活运用有关数学知识解决问题. .关键关键::动中求静动中求静. .数学思想:分类思想数学思想:分类思想 数形结合思想数形结合思想数形结合思想 转化思想转化思想1、如图1,梯形ABCD 中,AD ∥ BC ,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P 从A 开始沿AD 边以1cm/秒的速度移动,秒的速度移动,点点Q 从C 开始沿CB 向点B 以2 cm/秒的速度移动,秒的速度移动,如果P ,Q 分别从A ,C 同时出发,设移动时间为t 秒。
秒。
当t= 时,四边形是平行四边形;6 当t= 时,四边形是等腰梯形. 8 2、如图2,正方形ABCD 的边长为4,点M 在边DC 上,且DM=1,N 为对角线AC 上任意一点,则DN+MN 的最小值为的最小值为 5 3、如图,在Rt ABC △中,9060ACB B Ð=Ð=°,°,2BC =.点O 是AC 的中点,过点O 的直线l 从与AC 重合的位置开始,绕点O 作逆时针旋转,交AB 边于点D .过点C 作CE AB ∥交直线l 于点E ,设直线l 的旋转角为a .(1)①当a = 度时,四边形EDBC 是等腰梯形,此时AD 的长为的长为 ;②当a = 度时,四边形EDBC 是直角梯形,此时AD 的长为的长为 ; (2)当90a =°时,判断四边形EDBC 是否为菱形,并说明理由.是否为菱形,并说明理由. 解:(1)①30,1;②60,1.5;(2)当∠α=900时,四边形EDBC 是菱形. ∵∠α=∠ACB=900,∴BC //ED . ∵CE //AB , ∴四边形EDBC 是平行四边形是平行四边形 在Rt △ABC 中,∠ACB =900,∠B =600,BC =2, ∴∠A =300.∴AB =4,AC =23. ∴AO =12AC=3 .在Rt △AOD 中,∠A =300,∴AD =2. ∴BD =2. ∴BD =BC . 又∵四边形EDBC 是平行四边形,是平行四边形, ∴四边形EDBC 是菱形是菱形4、在△ABC 中,∠ACB=90°,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E. O E CB DAal OCB A(备用图)(备用图) C B AE D N M A B C D E M A C B E D M(1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE=AD +BE ; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE=AD-BE ;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明. 解:(1)①)① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB ② ∵△ADC ≌△CEB ∴CE=AD ,CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ,CD=BE ∴DE=CE-CD=AD-BE (3) 当MN 旋转到图3的位置时,DE=BE-AD(或AD=BE-DE ,BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE , 又∵AC=BC , ∴△ACD ≌△CBE , ∴AD=CE ,CD=BE , ∴DE=CD-CE=BE-AD. 5、数学课上,数学课上,张老师出示了问题:张老师出示了问题:张老师出示了问题:如图如图1,四边形ABCD 是正方形,是正方形,点点E 是边BC 的中点.90AEF Ð=,且EF 交正方形外角DCG Ð的平行线CF 于点F ,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;过程;如果不正确,请说明理由;((2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由. 解:(1)正确.)正确. 证明:在AB 上取一点M ,使AM EC =,连接ME . BM BE \=.45BME \Ð=°,135AME \Ð=°. CF 是外角平分线,45DCF \Ð=°,135ECF \Ð=°. AME ECF \Ð=Ð. 90AEB BAE Ð+Ð=°,90AEB CEF Ð+Ð=°, \BAE CEF Ð=Ð. AME BCF \△≌△(ASA ASA)). AE EF \=. (2)正确.)正确.证明:在BA 的延长线上取一点N .使AN CE =,连接NE .BN BE \=. 45N PCE \Ð=Ð=°. 四边形ABCD 是正方形,是正方形, AD BE \∥. DAE BEA \Ð=Ð. NAE CEF \Ð=Ð.ANE ECF \△≌△(ASA ASA)). AE EF \=.6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动,设P 的运动时间为t. 求(1)△)△ P AB 为等腰三角形的t 值;(2)△)△ P AB 为直角三角形的t 值;值; (3) 若AB=5且∠ABM=45 °,其他条件不变,直接写出△°,其他条件不变,直接写出△ P AB 为直角三角形的t 值A D F C G E B 图1 A D F C G E B 图3 A D F C G E B 图2 A D F C G E B M A D F C G E B N 7、在等腰梯形ABCD中,AD‖BC,E为AB的中点,过点E作EF‖BC交CD于点F.AB=4,BC=6, ∠B=60°。
初二数学动点问题练习(含答案)

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想数形结合思想转化思想1、如图1,梯形ABCD中,AD∥ BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动,点Q从C开始沿CB向点B以2 cm/秒的速度移动,如果P,Q分别从A,C同时出发,设移动时间为t秒。
当t= 时,四边形是平行四边形;6当t= 时,四边形是等腰梯形. 82、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1,N为对角线AC上任意一点,则DN+MN的最小值为 53、如图,在中,,.点是的中点,过点的直线从与重合的位置开始,绕点作逆时针旋转,交边于点.过点作交直线于点,设直线的旋转角为.(1)①当度时,四边形是等腰梯形,此时的长为;②当 度时,四边形是直角梯形,此时的长为 ; (2)当时,判断四边形是否为菱形,并说明理由. 解:(1)①30,1;②60,1.5;(2)当∠α=900时,四边形EDBC 是菱形.∵∠α=∠ACB=900,∴BC//ED. ∵CE//AB, ∴四边形EDBC 是平行四边形 在Rt△ABC 中,∠ACB=900,∠B=600,BC=2, ∴∠A=300. ∴AB=4,AC=2. ∴AO== .在Rt△AOD 中,∠A=300,∴AD=2. ∴BD=2. ∴BD=BC. 又∵四边形EDBC 是平行四边形, ∴四边形EDBC 是菱形4、在△ABC 中,∠ACB=90°,AC=BC ,直线MN 经过点C ,且AD⊥MN 于D ,BE⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD +BE ;(2)当直线MN 绕点C 旋转到图2的位置时,求证:DE=AD-BE ;CBAE D图1NM(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.解:(1)① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90°∴∠BCE+∠ACD=90°∴∠CAD=∠BCE ∵AC=BC ∴△ADC≌△CEB② ∵△ADC≌△CEB ∴CE=AD,CD=BE ∴DE=CE+CD=AD+BE(2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC∴△ACD≌△CBE ∴CE=AD,CD=BE ∴DE=CE-CD=AD-BE(3) 当MN旋转到图3的位置时,DE=BE-AD(或AD=BE-DE,BE=AD+DE等)∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE,又∵AC=BC,∴△ACD≌△CBE,∴AD=CE,CD=BE,∴DE=CD-CE=BE-AD.5、数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E 是边BC的中点.,且EF交正方形外角的平行线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证,所以.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.解:(1)正确.证明:在上取一点,使,连接..,.是外角平分线,,..,,.(ASA)..(2)正确.证明:在的延长线上取一点.使,连接...四边形是正方形,...(ASA)..6、如图, 射线MB上,MB=9,A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P从M沿射线MB方向以1个单位/秒的速度移动,设P的运动时间为t.求(1)△ PAB为等腰三角形的t值;(2)△ PAB为直角三角形的t值;(3)若AB=5且∠ABM=45 °,其他条件不变,直接写出△ PAB为直角三角形的t值7、如图1,在等腰梯形中,,是的中点,过点作交于点.,.求:(1)求点到的距离;(2)点为线段上的一个动点,过作交于点,过作交折线于点,连结,设.①当点在线段上时(如图2),的形状是否发生改变?若不变,求出的周长;若改变,请说明理由;②当点在线段上时(如图3),是否存在点,使为等腰三角形?若存在,请求出所有满足要求的的值;若不存在,请说明理由解(1)如图1,过点作于点 ∵为的中点, ∴ 在中, ∴ ∴ 即点到的距离为(2)①当点在线段上运动时,的形状不发生改变. ∵ ∴ ∵ ∴, 同理 如图2,过点作于,∵A D E BF C图4(备用)AD EBF C 图5(备用)A D E BFC图1 图2A D EBFC PNM图3A D E BF C PN M (第25题)∴ ∴ ∴ 则 在中, ∴的周长=②当点在线段上运动时,的形状发生改变,但恒为等边三角形. 当时,如图3,作于,则类似①, ∴ ∵是等边三角形,∴ 此时,当时,如图4,这时 此时, 当时,如图5, 则又∴ 因此点与重合,为直角三角形. ∴ 此时,图3A D E BFCPN M 图4A D EBF CP MN 图5A DEBF (P ) CM NGGRG综上所述,当或4或时,为等腰三角形.8、如图,已知中,厘米,厘米,点为的中点.(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?解:(1)①∵秒,∴厘米,∵厘米,点为的中点,∴厘米.又∵厘米,∴厘米,∴.又∵,∴,∴.②∵,∴,又∵,,则,∴点,点运动的时间秒,∴厘米/秒。
初二数学期末复习一次函数的应用动点问题附练习及答案

课题一次函数的应用——动点问题教学目的1.学会结合几何图形的性质,在平面直角坐标系中列函数关系式。
2.通过对几何图形的探究活动和对例题的分析,感悟探究动点问题列函数关系式的方法,进步解决问题的实力。
重点、难点理解在平面直角坐标系中,动点问题列函数关系式的方法。
小结:1用函数学问求解动点问题,须要将问题给合几何图形的性质,建立函数模型求解,解要符合题意,要留意数及形结合。
2.以一次函数为背景的问题,要充分运用方程、转化、函数以及数形结合等思想来探讨解决,留意自变量的取值范围例题1:如图,直线1l的解析表达式为33y x=-+,且1l及x轴交于点D,直线2l经过点A B,,直线1l,2l交于点C.〔1〕求点D的坐标;〔2〕求直线2l的解析表达式;〔3〕求ADC△的面积;〔4〕在直线2l上存在异于点C的另一点P,使得ADP△及ADC△的面积相等,请干脆..写出点P的坐标.例题2:如图,在平面直角坐标系内,点A〔0,6〕、点B〔8,0〕,动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O挪动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A挪动,设点P、Q挪动的时间为t秒.(1) 求直线AB的解析式;(2) 当t为何值时,△APQ的面积为524个平方单位?当堂稳固:如图,直线6y kx=+及x轴、y轴分别交于点E、F,点E的坐标为〔-8,0〕,点A的坐标为〔-6,0〕。
〔1〕求k 的值;〔2〕假设点P 〔x ,y 〕是第二象限内的直线上的一个动点,在点P 的运动过程中,试写出△OPA 的面积S 及x 的函数关系式,并写出自变量x 的取值范围;〔3〕探究:当点P 运动到什么位置时,△OPA 的面积为278,并说明理由。
课后检测:1、假如一次函数y=-x+1的图象及x 轴、y 轴分别交于点A 点、B 点,点M 在x 轴上,并且使以点A 、B 、M 为顶点的三角形是等腰三角形,那么这样的点M 有〔 〕。
初二数学期末复习《一次函数的应用—动点问题》(附练习及答案)

课 题一次函数的应用——动点问题教学目标1.学会结合几何图形的性质,在平面直角坐标系中列函数关系式。
2.通过对几何图形的探究活动和对例题的分析,感悟探究动点问题列函数关系式的方法,提高解决问题的能力。
重点、难点理解在平面直角坐标系中,动点问题列函数关系式的方法。
小结:1用函数知识求解动点问题,需要将问题给合几何图形的性质,建立函数模型求解,解要符合题意,要注意数与形结合。
2.以一次函数为背景的问题,要充分运用方程、转化、函数以及数形结合等思想来研究解决,注意自变量的取值范围例题1:如图,直线1l 的解析表达式为33y x =-+,且1l 与x 轴交于点D ,直线2l 经过点A B ,,直线1l ,2l 交于点C .(1)求点D 的坐标;(2)求直线2l 的解析表达式;(3)求ADC △的面积;(4)在直线2l 上存在异于点C 的另一点P ,使得ADP △与ADC △的面积相等,请直接..写出点P 的坐标.例题2:如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒.(1) 求直线AB 的解析式;(2) 当t 为何值时,△APQ 的面积为524个平方单位?当堂巩固:如图,直线6y kx =+与x 轴、y 轴分别交于点E 、F ,点E 的坐标为(-8,0),点A 的坐标为(-6,0)。
(1)求k 的值;(2)若点P (x ,y )是第二象限内的直线上的一个动点,在点P 的运动过程中,试写出△OPA 的面积S 与x 的函数关系式,并写出自变量x 的取值范围;(3)探究:当点P 运动到什么位置时,△OPA 的面积为278,并说明理由。
课后检测: 1、如果一次函数y=-x+1的图象与x 轴、y 轴分别交于点A 点、B 点,点M 在x 轴上,并且使以点A 、B 、M 为顶点的三角形是等腰三角形,那么这样的点M 有( )。
初二数学动点问题练习(含答案)

初⼆数学动点问题练习(含答案)动态问题所谓“动点型问题”是指题设图形中存在⼀个或多个动点,它们在线段、射线或弧线上运动的⼀类开放性题⽬.解决这类问题的关键是动中求静,灵活运⽤有关数学知识解决问题.关键:动中求静.数学思想:分类思想数形结合思想转化思想1、如图1,梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动,点Q从C开始沿CB向点B以2 cm/秒的速度移动,如果P,Q分别从A,C同时出发,设移动时间为t秒。
当t= 时,四边形是平⾏四边形;6当t= 时,四边形是等腰梯形. 82、如图2,正⽅形ABCD的边长为4,点M在边DC上,且DM=1,N为对⾓线AC上任意⼀点,则DN+MN的最⼩值为 53、如图,在Rt ABC△中,9060ACB B∠=∠=°,°,2BC=.点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D.过点C作CE AB∥交直线l于点E,设直线l的旋转⾓为α.(1)①当α=度时,四边形EDBC是等腰梯形,此时AD的长为;②当α=度时,四边形EDBC是直⾓梯形,此时AD的长为;(2)当90α=°时,判断四边形EDBC是否为菱形,并说明理由.解:(1)①30,1;②60,1.5;(2)当∠α=900时,四边形EDBC是菱形.∵∠α=∠ACB=900,∴BC//ED. ∵CE//AB, ∴四边形EDBC是平⾏四边形在Rt△ABC中,∠ACB=900,∠B=600,BC=2, ∴∠A=300.∴AB=4,AC=23. ∴AO=12AC=3.在Rt△AOD中,∠A=300,∴AD=2.∴BD=2. ∴BD=BC. ⼜∵四边形EDBC是平⾏四边形,∴四边形EDBC是菱形4、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明. OE CDAαlOCA(备⽤图)CBAED图1NMA BCDEMACBEDNM解:(1)①∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB②∵△ADC ≌△CEB ∴CE=AD ,CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE ⼜∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ,CD=BE ∴DE=CE-CD=AD-BE(3) 当MN 旋转到图3的位置时,DE=BE-AD(或AD=BE-DE ,BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE ,⼜∵AC=BC ,∴△ACD ≌△CBE ,∴AD=CE ,CD=BE ,∴DE=CD-CE=BE-AD.5、数学课上,张⽼师出⽰了问题:如图1,四边形ABCD 是正⽅形,点E 是边BC 的中点.90AEF ∠=o,且EF 交正⽅形外⾓DCG ∠的平⾏线CF 于点F ,求证:AE =EF .经过思考,⼩明展⽰了⼀种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进⼀步的研究:(1)⼩颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意⼀点”,其它条件不变,那么结论“AE =EF ”仍然成⽴,你认为⼩颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)⼩华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意⼀点,其他条件不变,结论“AE =EF ”仍然成⽴.你认为⼩华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.解:(1)正确.证明:在AB 上取⼀点M ,使AM EC =,连接ME . BM BE ∴=.45BME ∴∠=°,135AME ∴∠=°. CF Q 是外⾓平分线,45DCF ∴∠=°,135ECF ∴∠=°.AME ECF ∴∠=∠. 90AEB BAE ∠+∠=Q °,90AEB CEF ∠+∠=°,∴BAE CEF ∠=∠. AME BCF ∴△≌△(ASA ). AE EF ∴=.(2)正确.证明:在BA 的延长线上取⼀点N .使AN CE =,连接NE .BN BE ∴=. 45N PCE ∴∠=∠=°. Q 四边形ABCD 是正⽅形, AD BE ∴∥. DAE BEA ∴∠=∠. NAE CEF ∴∠=∠.ANE ECF ∴△≌△(ASA ). AE EF ∴=. 6、如图, 射线MB 上,MB=9,A 是射线MB 外⼀点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB ⽅向以1个单位/秒的速度移动,设P 的运动时间为t. 求(1)△ PAB 为等腰三⾓形的t 值;(2)△ PAB 为直⾓三⾓形的t 值;(3)若AB=5且∠ABM=45 °,其他条件不变,直接写出△ PAB 为直⾓三⾓形的t 值AD FGB 图1 A D FC G B 图3A D FGB 图2A D F C GE B M A D FG B N7、如图1,在等腰梯形ABCD 中,AD BC ∥,E 是AB 的中点,过点E 作EF BC ∥交CD 于点F .46AB BC ==,,60B =?∠.求:(1)求点E 到BC 的距离;(2)点P 为线段EF 上的⼀个动点,过P 作PM EF ⊥交BC 于点M ,过M 作MN AB ∥交折线ADC 于点N ,连结PN ,设EP x =.①当点N 在线段AD 上时(如图2),PMN △的形状是否发⽣改变?若不变,求出PMN △的周长;若改变,请说明理由;②当点N 在线段DC 上时(如图3),是否存在点P ,使PMN △为等腰三⾓形?若存在,请求出所有满⾜要求的x 的值;若不存在,请说明理由解(1)如图1,过点E 作EG BC ⊥于点G .∵E 为AB 的中点,∴122BE AB ==.在Rt EBG△中,60B =?∠,∴30BEG =?∠.∴112BG BE EG =即点E 到BC(2)①当点N 在线段AD 上运动时,PMN △的形状不发⽣改变.∵PM EF EG EF ⊥⊥,,∴PM EG ∥.∵EF BC ∥,∴EP GM =,PM EG ==同理4MN AB ==.如图2,过点P 作PH MN ⊥于H ,∵MN AB ∥,∴6030NMC B PMH ==?=?∠∠,∠.∴12PH PM == ∴3cos302MH PM =?=g .则35422NH MN MH =-=-=.图1 A D E BF CGA D E BFCPNMG HA D E BF C图4(备⽤)AD EBF C 图5(备⽤)A D E BF CA D E BF C PNM图3A D EBFCPNM(第25题)在Rt PNH △中,PN === ∴PMN △的周长=4PM PN MN ++=.②当点N 在线段DC 上运动时,PMN △的形状发⽣改变,但MNC △恒为等边三⾓形.当PM PN =时,如图3,作PR MN ⊥于R ,则MR NR =.类似①,32MR =.∴23MN MR ==.∵MNC △是等边三⾓形,∴3MC MN ==.此时,6132x EP GM BC BG MC ===--=--=.当MP MN=时,如图4,这时MC MN MP ===此时,615x EP GM ===--= 当NP NM =时,如图5,30NPM PMN ==?∠∠.则120PMN =?∠,⼜60MNC =?∠,∴180PNM MNC +=?∠∠.因此点P 与F 重合,PMC △为直⾓三⾓形.∴tan301MC PM =?=g .此时,6114x EP GM ===--=.综上所述,当2x =或4或(5-时,PMN △为等腰三⾓形.8、如图,已知ABC △中,10AB AC ==厘⽶,8BC =厘⽶,点D 为AB 的中点.(1)如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第⼀次在ABC △的哪条边上相遇?解:(1)①∵1t =秒,∴313BP CQ ==?=厘⽶,∵10AB =厘⽶,点D 为AB 的中点,∴5BD =厘⽶.图3A D E BFCPN M图4A D EBF CP MN 图5A DEBF (P ) CM NGGRG⼜∵8PC BC BP BC =-=,厘⽶,∴835PC =-=厘⽶,∴PC BD =.⼜∵AB AC =,∴B C ∠=∠,∴BPD CQP △≌△.②∵P Qv v ≠,∴BP CQ ≠,⼜∵BPD CQP △≌△,B C ∠=∠,则45BP PC CQ BD ====,,∴点P ,点Q 运动的时间433BP t ==秒,∴515443Q CQ v t===厘⽶/秒。
(完整word版)初二数学动点问题归类复习(含例题、练习及答案)

初二数学动点问题归类复习(含例题、练习及答案)所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想数形结合思想转化思想本文将初一至二学习过的有关知识,结合动点问题进行归类复习,希望对同学们能有所帮助。
一、等腰三角形类:因动点产生的等腰三角形问题例1:(2013年上海市虹口区中考模拟第25题)如图1,在Rt△ABC中,∠A=90°,AB=6,AC =8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC 上的一动点,且∠PDQ=90°.(1)求ED、EC的长;(2)若BP=2,求CQ的长;(3)记线段PQ与线段DE的交点为F,若△PDF为等腰三角形,求BP的长.图1 备用图思路点拨1.第(2)题BP=2分两种情况.2.解第(2)题时,画准确的示意图有利于理解题意,观察线段之间的和差关系.3.第(3)题探求等腰三角形PDF时,根据相似三角形的传递性,转化为探求等腰三角形CDQ.解答:(1)在Rt△ABC中,AB=6,AC=8,所以BC=10.在Rt△CDE中,CD=5,所以315tan544ED CD C=⋅∠=⨯=,254EC=.(2)如图2,过点D作DM⊥AB,DN⊥AC,垂足分别为M、N,那么DM、DN是△ABC的两条中位线,DM=4,DN=3.由∠PDQ=90°,∠MDN=90°,可得∠PDM=∠QDN.因此△PDM∽△QDN.所以43PM DMQN DN==.所以34QN PM=,43PM QN=.图2 图3 图4 ①如图3,当BP=2,P在BM上时,PM=1.此时3344QN PM==.所以319444CQ CN QN=+=+=.②如图4,当BP=2,P在MB的延长线上时,PM=5.此时31544QN PM ==.所以1531444CQ CN QN =+=+=. (3)如图5,如图2,在Rt △PDQ 中,3tan 4QD DN QPD PD DM ∠===.在Rt △ABC 中,3tan 4BA C CA ∠==.所以∠QPD =∠C .由∠PDQ =90°,∠CDE =90°,可得∠PDF =∠CDQ . 因此△PDF ∽△CDQ .当△PDF 是等腰三角形时,△CDQ 也是等腰三角形.①如图5,当CQ =CD =5时,QN =CQ -CN =5-4=1(如图3所示). 此时4433PM QN ==.所以45333BP BM PM =-=-=. ②如图6,当QC =QD 时,由cos CHC CQ =,可得5425258CQ =÷=. 所以QN =CN -CQ =257488-=(如图2所示). 此时4736PM QN ==.所以725366BP BM PM =+=+=. ③不存在DP =DF 的情况.这是因为∠DFP ≥∠DQP >∠DPQ (如图5,图6所示).图5 图6考点伸展:如图6,当△CDQ 是等腰三角形时,根据等角的余角相等,可以得到△BDP 也是等腰三角形,PB =PD .在△BDP 中可以直接求解256BP =. 二、直角三角形:因动点产生的直角三角形问题 例2:(2008年河南省中考第23题)如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0).(1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S . ① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.图1思路点拨:1.第(1)题说明△ABC 是等腰三角形,暗示了两个动点M 、N 同时出发,同时到达终点. 2.不论M 在AO 上还是在OB 上,用含有t 的式子表示OM 边上的高都是相同的,用含有t 的式子表示OM 要分类讨论.3.将S =4代入对应的函数解析式,解关于t 的方程.4.分类讨论△MON 为直角三角形,不存在∠ONM =90°的可能. 解答:(1)直线434+-=x y 与x 轴的交点为B (3,0)、与y 轴的交点C (0,4). Rt △BOC 中,OB =3,OC =4,所以BC =5.点A 的坐标是(-2,0),所以BA =5. 因此BC =BA ,所以△ABC 是等腰三角形.(2)①如图2,图3,过点N 作NH ⊥AB ,垂足为H .在Rt △BNH 中,BN =t ,4sin 5B =,所以45NH t =. 如图2,当M 在AO 上时,OM =2-t ,此时211424(2)22555S OM NH t t t t =⋅⋅=-⨯=-+.定义域为0<t ≤2.如图3,当M 在OB 上时,OM =t -2,此时211424(2)22555S OM NH t t t t =⋅⋅=-⨯=-.定义域为2<t ≤5.图2 图3②把S =4代入22455S t t =-,得224455t t -=. 解得1211t =,2211t =.因此,当点M 在线段OB 上运动时,存在S =4的情形,此时211t = ③如图4,当∠OMN =90°时,在Rt △BNM 中,BN =t ,BM 5t =-,3cos 5B =,所以535tt-=.解得258t=.如图5,当∠OMN=90°时,N与C重合,5t=.不存在∠ONM=90°的可能.所以,当258t=或者5t=时,△MON为直角三角形.图4 图5考点伸展:在本题情景下,如果△MON的边与AC平行,求t的值.如图6,当ON//AC时,t=3;如图7,当MN//AC时,t=2.5.图6 图7三、平行四边形问题:因动点产生的平行四边形问题例3:(2010年山西省中考第26题)在直角梯形OABC中,CB//OA,∠COA=90°,CB=3,OA=6,BA=35.分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.图1 图2思路点拨:1.第(1)题和第(2)题蕴含了OB与DF垂直的结论,为第(3)题讨论菱形提供了计算基础.2.讨论菱形要进行两次(两级)分类,先按照DO为边和对角线分类,再进行二级分类,DO与DM、DO与DN为邻边.解答:(1)如图2,作BH⊥x轴,垂足为H,那么四边形BCOH为矩形,OH=CB=3.在Rt△ABH中,AH=3,BA=35,所以BH=6.因此点B的坐标为(3,6).(2) 因为OE=2EB,所以223E Bx x==,243E By y==,E(2,4).设直线DE的解析式为y=kx+b,代入D(0,5),E(2,4),得5,2 4.bk b=⎧⎨+=⎩解得12k=-,5b=.所以直线DE的解析式为152y x=-+.(3) 由152y x=-+,知直线DE与x轴交于点F(10,0),OF=10,DF=55.①如图3,当DO为菱形的对角线时,MN与DO互相垂直平分,点M是DF的中点.此时点M的坐标为(5,52),点N的坐标为(-5,52).②如图4,当DO、DN为菱形的邻边时,点N与点O关于点E对称,此时点N的坐标为(4,8).③如图5,当DO、DM为菱形的邻边时,NO=5,延长MN交x轴于P.由△NPO∽△DOF,得NP PO NODO OF DF==,即51055NP PO==.解得5NP=,25PO=.此时点N的坐标为(25,5)-.图3 图4考点伸展如果第(3)题没有限定点N在x轴上方的平面内,那么菱形还有如图6的情形.图5 图6四、相似三角形:因动点产生的相似三角形问题例4:(2013年苏州中考28题)如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E、F、G运动的时间为t(单位:s).(1)当t=s时,四边形EBFB′为正方形;(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;(3)是否存在实数t,使得点B′与点O重合?若存在,求出t的值;若不存在,请说明理由.思路点拨:(1)利用正方形的性质,得到BE=BF,列一元一次方程求解即可;(2)△EBF与△FCG 相似,分两种情况,需要分类讨论,逐一分析计算;(3)本问为存在型问题.假设存在,则可以分别求出在不同条件下的t值,它们互相矛盾,所以不存在.解答:(1)若四边形EBFB′为正方形,则BE=BF,即:10﹣t=3t,解得t=2.5;(2)分两种情况,讨论如下:①若△EBF∽△FCG,则有,即,解得:t=2.8;②若△EBF∽△GCF,则有,即,解得:t=﹣14﹣2(不合题意,舍去)或t=﹣14+2.∴当t=2.8s或t=(﹣14+2)s时,以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似.(3)假设存在实数t,使得点B′与点O重合.如图,过点O作OM⊥BC于点M,则在Rt△OFM中,OF=BF=3t,FM=BC﹣BF=6﹣3t,OM=5,由勾股定理得:OM2+FM2=OF2,即:52+(6﹣3t)2=(3t)2解得:t=;过点O作ON⊥AB于点N,则在Rt△OEN中,OE=BE=10﹣t,EN=BE﹣BN=10﹣t﹣5=5﹣t,ON=6,由勾股定理得:ON 2+EN 2=OE 2,即:62+(5﹣t )2=(10﹣t )2解得:t =3.9.∵≠3.9,∴不存在实数t ,使得点B ′与点O 重合.考点伸展:本题为运动型综合题,考查了矩形性质、轴对称、相似三角形的判定性质、勾股定理、解方程等知识点.题目并不复杂,但需要仔细分析题意,认真作答.第(2)问中,需要分类讨论,避免漏解;第(3)问是存在型问题,可以先假设存在,然后通过推导出互相矛盾的结论,从而判定不存在. 拓展练习:1、如图1,梯形ABCD 中,AD ∥ BC ,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P 从A 开始沿AD 边以1cm/秒的速度移动,点Q 从C 开始沿CB 向点B 以2 cm/秒的速度移动,如果P ,Q 分别从A ,C 同时出发,设移动时间为t 秒。
初二数学动点问题练习(含答案)

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想数形结合思想转化思想1、如图1,梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动,点Q从C开始沿CB向点B以2cm/秒的速度移动,如果P,Q分别从A,C同时出发,设移动时间为t秒。
当t= 时,四边形是平行四边形;6当t= 时,四边形是等腰梯形.82、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1,N为对角线AC上任意一点,则DN+MN的最小值为53、如图,在Rt ABC△中,9060ACB B∠=∠=°,°,2BC=.点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D.过点C作CE AB∥交直线l于点E,设直线l的旋转角为α.(1)①当α=度时,四边形EDBC是等腰梯形,此时AD的长为;②当α=度时,四边形EDBC是直角梯形,此时AD的长为;(2)当90α=°时,判断四边形EDBC是否为菱形,并说明理由.解:(1)①30,1;②60,1.5;(2)当∠α=900时,四边形EDBC是菱形.∵∠α=∠ACB=900,∴BC//ED.∵CE//AB,∴四边形EDBC是平行四边形在Rt△ABC中,∠ACB=900,∠B=600,BC=2,∴∠A=300.∴AB=4,AC=23. ∴AO=12AC=3.在Rt△AOD中,∠A=300,∴AD=2.∴BD=2.∴BD=BC.又∵四边形EDBC是平行四边形,∴四边形EDBC是菱形4、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.OE CDAαlOCA(备用图)CBAEDNMA BCDMACBEM(1)当直线MN 绕点C 旋转到图1的位置时,求证:①△AD C≌△CEB;②DE=AD+B E; (2)当直线MN 绕点C旋转到图2的位置时,求证:DE=AD-BE;(3)当直线MN 绕点C 旋转到图3的位置时,试问D E、AD 、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.解:(1)① ∵∠ACD=∠AC B=90° ∴∠CA D+∠ACD=90° ∴∠BC E+∠A CD =90° ∴∠CAD=∠BCE ∵A C=BC ∴△ADC ≌△CEB② ∵△A DC ≌△CEB ∴CE=A D,CD=B E ∴DE=CE +CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠AC D=∠CBE 又∵A C=BC ∴△ACD ≌△CBE ∴CE=A D,CD=BE ∴D E=CE -CD =AD -B E (3) 当M N旋转到图3的位置时,DE=B E-AD(或AD =BE-D E,BE =AD +DE 等) ∵∠ADC =∠CEB=∠ACB=90° ∴∠ACD=∠C BE , 又∵A C=BC,∴△A CD ≌△CB E, ∴AD =CE ,C D=B E, ∴DE=C D-CE=BE-AD .5、数学课上,张老师出示了问题:如图1,四边形AB CD 是正方形,点E 是边B C的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接M E,则A M=EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC 的中点”改为“点E 是边B C上(除B,C 外)的任意一点”,其它条件不变,那么结论“A E=EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由; (2)小华提出:如图3,点E 是BC 的延长线上(除C点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由. 解:(1)正确. 证明:在AB 上取一点M ,使AM EC =,连接ME . BM BE ∴=.45BME ∴∠=°,135AME ∴∠=°. CF 是外角平分线,45DCF ∴∠=°,135ECF ∴∠=°. AME ECF ∴∠=∠. 90AEB BAE ∠+∠=°,90AEB CEF ∠+∠=°, ∴BAE CEF ∠=∠. AME BCF ∴△≌△(ASA). AE EF ∴=.(2)正确.证明:在BA 的延长线上取一点N .使AN CE =,连接NE .BN BE ∴=. 45N PCE ∴∠=∠=°. 四边形ABCD 是正方形, AD BE ∴∥. DAE BEA ∴∠=∠. NAE CEF ∴∠=∠.ANE ECF ∴△≌△(ASA ). AE EF ∴=.6、如图, 射线MB 上,MB =9,A 是射线MB外一点,AB=5且A 到射线M B的距离为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动,设P 的运动时间为t.求(1)△ PAB 为等腰三角形的t 值;(2)△ PAB 为直角三角形的t 值;AD FC G B 图1 AD FC G B 图3A D FC GB 图2A D F C G EB M A D FG E B N(3)若AB=5且∠ABM=45°,其他条件不变,直接写出△PAB为直角三角形的t值7、如图1,在等腰梯形ABCD中,AD BC∥,E是AB的中点,过点E作EF BC∥交CD于点F.46AB BC==,,60B=︒∠.求:(1)求点E到BC的距离;(2)点P为线段EF上的一个动点,过P作PM EF⊥交BC于点M,过M作MN AB∥交折线ADC于点N,连结PN,设EP x=.①当点N在线段AD上时(如图2),PMN△的形状是否发生改变?若不变,求出PMN△的周长;若改变,请说明理由;②当点N在线段DC上时(如图3),是否存在点P,使PMN△为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由解(1)如图1,过点E作EG BC⊥于点G.∵E为AB的中点,∴122BE AB==.在Rt EBG△中,60B=︒∠,∴30BEG=︒∠.∴22112132BG BE EG===-=,.A DEBFC图4(备用)A DEBFC图5(备用)A DEBFC图1 图2A DEBFCPNM图3A DEBFCPNM(第25题)即点E 到BC(2)①当点N 在线段AD 上运动时,PMN △的形状不发生改变. ∵PM EF EG EF ⊥⊥,, ∴PM EG ∥. ∵EF BC ∥, ∴EP GM =,PM EG == 同理4MN AB ==. 如图2,过点P 作PH MN ⊥于H ,∵MN AB ∥,∴6030NMC B PMH ==︒=︒∠∠,∠.∴12PH PM == ∴3cos302MH PM =︒=. 则35422NH MN MH =-=-=.在Rt PNH △中,PN === ∴PMN △的周长=4PM PN MN ++=.②当点N 在线段DC 上运动时,PMN △的形状发生改变,但MNC △恒为等边三角形. 当PM PN =时,如图3,作PR MN ⊥于R ,则MR NR =.类似①,32MR =.∴23MN MR ==. ∵MNC △是等边三角形,∴3MC MN ==.此时,6132x EP GM BC BG MC ===--=--=.当MP MN =时,如图4,这时MC MN MP ===此时,615x EP GM ===-=- 当NP NM =时,如图5,30NPM PMN ==︒∠∠. 则120PMN =︒∠,又60MNC =︒∠, ∴180PNM MNC +=︒∠∠. 因此点P 与F 重合,PMC △为直角三角形. ∴tan301MC PM =︒=. 此时,6114x EP GM ===--=. 综上所述,当2x =或4或(5-时,PMN △为等腰三角形.8、如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点.(1)如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动,同时,点Q在线段CA 上由C 点向A点运动图3A D E BFCPN M 图4A D EBF CP MN 图5A DEBF (P ) CM NGGRG图1 A D EBF CG图2A D E BFCPNMG H①若点Q的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由; ②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q第一次在ABC △的哪条边上相遇? 解:(1)①∵1t =秒, ∴313BP CQ ==⨯=厘米, ∵10AB =厘米,点D 为AB 的中点, ∴5BD =厘米.又∵8PC BC BP BC =-=,厘米, ∴835PC =-=厘米, ∴PC BD =. 又∵AB AC =, ∴B C ∠=∠, ∴BPD CQP △≌△. ②∵P Qv v ≠, ∴BP CQ ≠, 又∵BPD CQP △≌△,B C ∠=∠,则45BP PC CQ BD ====,,∴点P ,点Q 运动的时间433BP t ==秒, ∴515443Q CQ v t===厘米/秒。
初二数学动点问题练习(含答案)

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想数形结合思想转化思想1、如图1,梯形ABCD中,AD∥ BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动,点Q从C开始沿CB向点B以2 cm/秒的速度移动,如果P,Q分别从A,C同时出发,设移动时间为t秒。
当t= 时,四边形是平行四边形;6当t= 时,四边形是等腰梯形. 82、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1,N为对角线AC上任意一点,则DN+MN的最小值为 53、如图,在中,,.点是的中点,过点的直线从与重合的位置开始,绕点作逆时针旋转,交边于点.过点作交直线于点,设直线的旋转角为.(1)①当度时,四边形是等腰梯形,此时的长为;②当 度时,四边形是直角梯形,此时的长为 ; (2)当时,判断四边形是否为菱形,并说明理由. 解:(1)①30,1;②60,1.5;(2)当∠α=900时,四边形EDBC 是菱形.∵∠α=∠ACB=900,∴BC//ED. ∵CE//AB, ∴四边形EDBC 是平行四边形 在Rt△ABC 中,∠ACB=900,∠B=600,BC=2, ∴∠A=300. ∴AB=4,AC=2. ∴AO== .在Rt△AOD 中,∠A=300,∴AD=2. ∴BD=2. ∴BD=BC. 又∵四边形EDBC 是平行四边形, ∴四边形EDBC 是菱形4、在△ABC 中,∠ACB=90°,AC=BC ,直线MN 经过点C ,且AD⊥MN 于D ,BE⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD +BE ;(2)当直线MN 绕点C 旋转到图2的位置时,求证:DE=AD-BE ;CBAE D图1NM(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.解:(1)① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90°∴∠BCE+∠ACD=90°∴∠CAD=∠BCE ∵AC=BC ∴△ADC≌△CEB② ∵△ADC≌△CEB ∴CE=AD,CD=BE ∴DE=CE+CD=AD+BE(2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC∴△ACD≌△CBE ∴CE=AD,CD=BE ∴DE=CE-CD=AD-BE(3) 当MN旋转到图3的位置时,DE=BE-AD(或AD=BE-DE,BE=AD+DE等)∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE,又∵AC=BC,∴△ACD≌△CBE,∴AD=CE,CD=BE,∴DE=CD-CE=BE-AD.5、数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E 是边BC的中点.,且EF交正方形外角的平行线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证,所以.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.解:(1)正确.证明:在上取一点,使,连接..,.是外角平分线,,..,,.(ASA)..(2)正确.证明:在的延长线上取一点.使,连接...四边形是正方形,...(ASA)..6、如图, 射线MB上,MB=9,A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P从M沿射线MB方向以1个单位/秒的速度移动,设P的运动时间为t.求(1)△ PAB为等腰三角形的t值;(2)△ PAB为直角三角形的t值;(3)若AB=5且∠ABM=45 °,其他条件不变,直接写出△ PAB为直角三角形的t值7、如图1,在等腰梯形中,,是的中点,过点作交于点.,.求:(1)求点到的距离;(2)点为线段上的一个动点,过作交于点,过作交折线于点,连结,设.①当点在线段上时(如图2),的形状是否发生改变?若不变,求出的周长;若改变,请说明理由;②当点在线段上时(如图3),是否存在点,使为等腰三角形?若存在,请求出所有满足要求的的值;若不存在,请说明理由解(1)如图1,过点作于点 ∵为的中点, ∴ 在中, ∴ ∴ 即点到的距离为(2)①当点在线段上运动时,的形状不发生改变. ∵ ∴ ∵ ∴, 同理 如图2,过点作于,∵A D E BF C图4(备用)AD EBF C 图5(备用)A D E BFC图1 图2A D EBFC PNM图3A D E BF C PN M (第25题)∴ ∴ ∴ 则 在中, ∴的周长=②当点在线段上运动时,的形状发生改变,但恒为等边三角形. 当时,如图3,作于,则类似①, ∴ ∵是等边三角形,∴ 此时,当时,如图4,这时 此时, 当时,如图5, 则又∴ 因此点与重合,为直角三角形. ∴ 此时,图3A D E BFCPN M 图4A D EBF CP MN 图5A DEBF (P ) CM NGGRG综上所述,当或4或时,为等腰三角形.8、如图,已知中,厘米,厘米,点为的中点.(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?解:(1)①∵秒,∴厘米,∵厘米,点为的中点,∴厘米.又∵厘米,∴厘米,∴.又∵,∴,∴.②∵,∴,又∵,,则,∴点,点运动的时间秒,∴厘米/秒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二数学动点问题归类复习(含例题、练习及答案)所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想数形结合思想转化思想本文将初一至二学习过的有关知识,结合动点问题进行归类复习,希望对同学们能有所帮助。
一、等腰三角形类:因动点产生的等腰三角形问题例1:(2013年上海市虹口区中考模拟第25题)如图1,在Rt△ABC中,∠A=90°,AB=6,AC =8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC 上的一动点,且∠PDQ=90°.(1)求ED、EC的长;(2)若BP=2,求CQ的长;(3)记线段PQ与线段DE的交点为F,若△PDF为等腰三角形,求BP的长.图1 备用图思路点拨1.第(2)题BP=2分两种情况.2.解第(2)题时,画准确的示意图有利于理解题意,观察线段之间的和差关系.3.第(3)题探求等腰三角形PDF时,根据相似三角形的传递性,转化为探求等腰三角形CDQ.解答:(1)在Rt△ABC中,AB=6,AC=8,所以BC=10.在Rt△CDE中,CD=5,所以315tan544ED CD C=⋅∠=⨯=,254EC=.(2)如图2,过点D作DM⊥AB,DN⊥AC,垂足分别为M、N,那么DM、DN是△ABC的两条中位线,DM=4,DN=3.由∠PDQ=90°,∠MDN=90°,可得∠PDM=∠QDN.因此△PDM∽△QDN.所以43PM DMQN DN==.所以34QN PM=,43PM QN=.图2 图3 图4①如图3,当BP=2,P在BM上时,PM=1.此时3344QN PM==.所以319444CQ CN QN=+=+=.②如图4,当BP=2,P在MB的延长线上时,PM=5.此时31544QN PM ==.所以1531444CQ CN QN =+=+=. (3)如图5,如图2,在Rt △PDQ 中,3tan 4QD DN QPD PD DM ∠===.在Rt △ABC 中,3tan 4BA C CA ∠==.所以∠QPD =∠C .由∠PDQ =90°,∠CDE =90°,可得∠PDF =∠CDQ . 因此△PDF ∽△CDQ .当△PDF 是等腰三角形时,△CDQ 也是等腰三角形.①如图5,当CQ =CD =5时,QN =CQ -CN =5-4=1(如图3所示). 此时4433PM QN ==.所以45333BP BM PM =-=-=. ②如图6,当QC =QD 时,由cos CHC CQ =,可得5425258CQ =÷=. 所以QN =CN -CQ =257488-=(如图2所示). 此时4736PM QN ==.所以725366BP BM PM =+=+=. ③不存在DP =DF 的情况.这是因为∠DFP ≥∠DQP >∠DPQ (如图5,图6所示).图5 图6考点伸展:如图6,当△CDQ 是等腰三角形时,根据等角的余角相等,可以得到△BDP 也是等腰三角形,PB =PD .在△BDP 中可以直接求解256BP =. 二、直角三角形:因动点产生的直角三角形问题 例2:(2008年河南省中考第23题)如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0).(1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S . ① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.图1思路点拨:1.第(1)题说明△ABC 是等腰三角形,暗示了两个动点M 、N 同时出发,同时到达终点. 2.不论M 在AO 上还是在OB 上,用含有t 的式子表示OM 边上的高都是相同的,用含有t 的式子表示OM 要分类讨论.3.将S =4代入对应的函数解析式,解关于t 的方程.4.分类讨论△MON 为直角三角形,不存在∠ONM =90°的可能. 解答:(1)直线434+-=x y 与x 轴的交点为B (3,0)、与y 轴的交点C (0,4). Rt △BOC 中,OB =3,OC =4,所以BC =5.点A 的坐标是(-2,0),所以BA =5. 因此BC =BA ,所以△ABC 是等腰三角形.(2)①如图2,图3,过点N 作NH ⊥AB ,垂足为H .在Rt △BNH 中,BN =t ,4sin 5B =,所以45NH t =. 如图2,当M 在AO 上时,OM =2-t ,此时211424(2)22555S OM NH t t t t =⋅⋅=-⨯=-+.定义域为0<t ≤2.如图3,当M 在OB 上时,OM =t -2,此时211424(2)22555S OM NH t t t t =⋅⋅=-⨯=-.定义域为2<t ≤5.图2 图3②把S =4代入22455S t t =-,得224455t t -=. 解得1211t =,2211t =.因此,当点M 在线段OB 上运动时,存在S =4的情形,此时211t = ③如图4,当∠OMN =90°时,在Rt △BNM 中,BN =t ,BM 5t =-,3cos 5B =,所以535tt-=.解得258t=.如图5,当∠OMN=90°时,N与C重合,5t=.不存在∠ONM=90°的可能.所以,当258t=或者5t=时,△MON为直角三角形.图4 图5考点伸展:在本题情景下,如果△MON的边与AC平行,求t的值.如图6,当ON//AC时,t=3;如图7,当MN//AC时,t=2.5.图6 图7三、平行四边形问题:因动点产生的平行四边形问题例3:(2010年山西省中考第26题)在直角梯形OABC中,CB//OA,∠COA=90°,CB=3,OA=6,BA=35.分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.图1 图2思路点拨:1.第(1)题和第(2)题蕴含了OB与DF垂直的结论,为第(3)题讨论菱形提供了计算基础.2.讨论菱形要进行两次(两级)分类,先按照DO为边和对角线分类,再进行二级分类,DO与DM、DO与DN为邻边.解答:(1)如图2,作BH⊥x轴,垂足为H,那么四边形BCOH为矩形,OH=CB=3.在Rt△ABH中,AH=3,BA=35,所以BH=6.因此点B的坐标为(3,6).(2) 因为OE=2EB,所以223E Bx x==,243E By y==,E(2,4).设直线DE的解析式为y=kx+b,代入D(0,5),E(2,4),得5,2 4.bk b=⎧⎨+=⎩解得12k=-,5b=.所以直线DE的解析式为152y x=-+.(3) 由152y x=-+,知直线DE与x轴交于点F(10,0),OF=10,DF=55.①如图3,当DO为菱形的对角线时,MN与DO互相垂直平分,点M是DF的中点.此时点M的坐标为(5,52),点N的坐标为(-5,52).②如图4,当DO、DN为菱形的邻边时,点N与点O关于点E对称,此时点N的坐标为(4,8).③如图5,当DO、DM为菱形的邻边时,NO=5,延长MN交x轴于P.由△NPO∽△DOF,得NP PO NODO OF DF==,即551055NP PO==.解得5NP=,25PO=.此时点N的坐标为(25,5)-.图3 图4考点伸展如果第(3)题没有限定点N在x轴上方的平面内,那么菱形还有如图6的情形.图5 图6四、相似三角形:因动点产生的相似三角形问题例4:(2013年苏州中考28题)如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E、F、G运动的时间为t(单位:s).(1)当t=s时,四边形EBFB′为正方形;(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;(3)是否存在实数t,使得点B′与点O重合?若存在,求出t的值;若不存在,请说明理由.思路点拨:(1)利用正方形的性质,得到BE=BF,列一元一次方程求解即可;(2)△EBF与△FCG 相似,分两种情况,需要分类讨论,逐一分析计算;(3)本问为存在型问题.假设存在,则可以分别求出在不同条件下的t值,它们互相矛盾,所以不存在.解答:(1)若四边形EBFB′为正方形,则BE=BF,即:10﹣t=3t,解得t=2.5;(2)分两种情况,讨论如下:①若△EBF∽△FCG,则有,即,解得:t=2.8;②若△EBF∽△GCF,则有,即,解得:t=﹣14﹣2(不合题意,舍去)或t=﹣14+2.∴当t=2.8s或t=(﹣14+2)s时,以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似.(3)假设存在实数t,使得点B′与点O重合.如图,过点O作OM⊥BC于点M,则在Rt△OFM中,OF=BF=3t,FM=BC﹣BF=6﹣3t,OM=5,由勾股定理得:OM2+FM2=OF2,即:52+(6﹣3t)2=(3t)2解得:t=;过点O作ON⊥AB于点N,则在Rt△OEN中,OE=BE=10﹣t,EN=BE﹣BN=10﹣t﹣5=5﹣t,ON=6,由勾股定理得:ON 2+EN 2=OE 2,即:62+(5﹣t )2=(10﹣t )2解得:t =3.9.∵≠3.9,∴不存在实数t ,使得点B ′与点O 重合.考点伸展:本题为运动型综合题,考查了矩形性质、轴对称、相似三角形的判定性质、勾股定理、解方程等知识点.题目并不复杂,但需要仔细分析题意,认真作答.第(2)问中,需要分类讨论,避免漏解;第(3)问是存在型问题,可以先假设存在,然后通过推导出互相矛盾的结论,从而判定不存在. 拓展练习:1、如图1,梯形ABCD 中,AD ∥ BC ,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P 从A 开始沿AD 边以1cm/秒的速度移动,点Q 从C 开始沿CB 向点B 以2 cm/秒的速度移动,如果P ,Q 分别从A ,C 同时出发,设移动时间为t 秒。
