行星齿轮减速器PPT幻灯片课件
合集下载
行星齿轮机构的传动原理和结构ppt课件

图3-6齿圈输入,太阳轮制动,行星架输出传动图与结构简图
16
行星齿轮变速装置
2)传动比计算 ①用运动方程计算传动比
该行星齿轮机构运动方程n1+αn2-(1+α)n3=0中,由于 太阳轮制动n1 =0,该方程变为αn2-(1+α)n3=0得n2/n3= (1+α)/α即传动比i=n2/n3 =(1+α)/α>1 即该单排行 星齿轮机构转向相同,减速增矩。
②用矢量图法计算传动比
右 动 似图,三为齿角行 圈 形CR星输原1 架出理输矢,n入量可3 ,图以太。计CR阳根算1轮据出n制相传n32 α α 动比i= n3/n2
=α/(1+α)<1 即该单排
行 减星矩齿。轮S机构n转1向相同S、增速
R n2 1 n3 C α
S
R
1
C n3 α
S
21
Байду номын сангаас
行星齿轮变速装置
行星轮即可绕行星轴自 转,又可绕太阳轮公转。 太阳轮与行星轮是外啮合, 二者旋转方向相反;行星 轮与齿圈是内啮合,二者 旋转方向相同。行星齿轮 系统的齿轮均采用斜齿常 啮合状态
5
行星齿轮变速装置 单排单级行星齿轮机构运动
6
行星齿轮变速装置 单排单级行星齿轮机构组成
7
行星齿轮变速装置 单排单级行星齿轮机构实物运动
行星齿轮变速装置
2)传动比计算 ①用运动方程计算传动比
该行星齿轮机构运动方程n1+αn2-(1+α)n3=0中,由于 太阳轮制动n1=0,该方程变为αn2-(1+α)n3=0 得 n3/n2=α/(1+α)传动比i= n3/n2=α/(1+α)<1 即该单排 行星齿轮机构转向相同、增速减矩。
行星齿轮变速器 ppt课件

PPT课件
26
片式制动器工作过程
PPT课件
27
(2)带式制动器
它由制动带、油缸、活塞 和调整件组成。外弹簧为 活塞的回位弹簧。内弹簧 为旋转鼓反作用力的缓冲 弹簧,防止活塞振动。调 整点多在带的支撑端,可 在体外调整或拆下油底调 整。拧动调整螺栓来调整 (旋紧再松2~3圈),调 好后再用锁紧螺母锁紧。
活塞 活塞杆
制动鼓 制动带
优点:结构简单易于安装, 带式制动器轴向尺寸小可 缩短变速器的长度。
工作油路
缺点:使变速器壳体上产 生局部的高应力区;制动 带磨损后需要调整间隙; 工作的平顺性差,控制油 路中多配有缓冲阀。
PPT课件
调整螺钉
28
点击播放
PPT课件
29
带式制动器
PPT课件
30
(三)单向离合器
基本组成:离合器鼓、离合器活塞、回位弹簧、离合器片(钢 片、摩擦片)、花键毂
摩擦片与旋转的花键毂的齿键连接,可轴向移动,为输入端, 片上有钢基粉末冶金层或合成纤维层。
从动钢片与转动鼓的内花键连接也可轴向移动,可输出扭矩。
活塞为环状,另外活主塞动上盘有密封圈、回位弹簧。
壳体
卡环
活塞
压盘
PPT课件
18
(一)离合器
(1)作用 自动变速器中的湿式 多片离合器是用来连接输 入轴或输出轴和某个基本 元件,或将行星齿轮机构 中某两个基本元件连接在 一起实现转矩的传递。
PPT课件
点击播放
19
离合器片
PPT课件
20
离合器
PPT课件
21
(2)构造:一般为多片摩擦式,是液压控制的执行元件。
PPT课件
自动变速器行星齿轮机构ppt课件
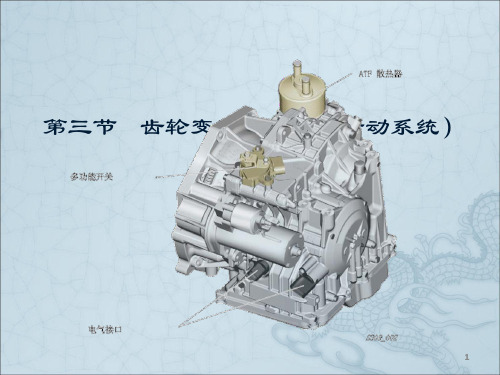
第三节 齿轮变速器(机械传动系统)
1
第三节 齿轮变速器
作用:具备普通手动变速器所有的作用。 (1)改变传动比; (2)实现到车行驶; (3)中断动力传递。
结构组成:变速齿轮机构和换档执行机构。
典型的齿轮变速机构的形式:平行轴式(或称定轴式、 普通齿轮式)和行星齿轮式(包括有辛普森式、拉维 娜式、串联式等)。
片式制动器
• 9-弹簧 • 10-活塞 • 11-内外O形密
封圈 • 12-壳体 • 13-滚针轴承 • 14-推力轴承 • 15-密封环52
制动器 53
带式制动器的结构与工作原理
制动器间隙由调 整螺钉调整。
54
带式制动器
伺服机构的形式有: 直杆式、杠杆式、钳形式等。
55
3、单向离合器
作用:利用单向锁止的原理实现对单排元 件的固定或者是单排中两个元件的锁止或 者前后两个单排元件的连接。
8
一、单排行星齿轮机构分析
传动方案:有8种。
9
一、单排行星齿轮机构分析
档位设置: 行星齿轮架作从动件---------1档或2档 两元件连接后带另一元件-----3档 行星齿轮架作主动件---------O/D档 行星齿轮架固定-------------倒档。
10
二、行星排的组合
现代轿车自动变速器所采用的行星齿轮机构包括复合 式行星齿轮机构和串联式行星机构。
23
三、行星排的表达方式
捷豹JX波箱
24
三、行星排的表达方式
4HP20
25
三、行星排的表达方式
09G变速器结构
26
三、行星排的表达方式
09G变速器结构
27
三、行星排的表达方式
1
第三节 齿轮变速器
作用:具备普通手动变速器所有的作用。 (1)改变传动比; (2)实现到车行驶; (3)中断动力传递。
结构组成:变速齿轮机构和换档执行机构。
典型的齿轮变速机构的形式:平行轴式(或称定轴式、 普通齿轮式)和行星齿轮式(包括有辛普森式、拉维 娜式、串联式等)。
片式制动器
• 9-弹簧 • 10-活塞 • 11-内外O形密
封圈 • 12-壳体 • 13-滚针轴承 • 14-推力轴承 • 15-密封环52
制动器 53
带式制动器的结构与工作原理
制动器间隙由调 整螺钉调整。
54
带式制动器
伺服机构的形式有: 直杆式、杠杆式、钳形式等。
55
3、单向离合器
作用:利用单向锁止的原理实现对单排元 件的固定或者是单排中两个元件的锁止或 者前后两个单排元件的连接。
8
一、单排行星齿轮机构分析
传动方案:有8种。
9
一、单排行星齿轮机构分析
档位设置: 行星齿轮架作从动件---------1档或2档 两元件连接后带另一元件-----3档 行星齿轮架作主动件---------O/D档 行星齿轮架固定-------------倒档。
10
二、行星排的组合
现代轿车自动变速器所采用的行星齿轮机构包括复合 式行星齿轮机构和串联式行星机构。
23
三、行星排的表达方式
捷豹JX波箱
24
三、行星排的表达方式
4HP20
25
三、行星排的表达方式
09G变速器结构
26
三、行星排的表达方式
09G变速器结构
27
三、行星排的表达方式
行星齿轮PPT

(2)齿圈固定,行星齿轮架带太阳轮 Z1 i2=----- < 1 (增速同向) (动画) ZC (3)太阳轮固定,齿圈带动行星齿轮架 ZC i3=----- > 1 (减速同向) (动画) Z2
九江职业技术学院
行星齿轮变速原理
(4)太阳轮固定,行星齿轮架带动齿圈 Z2 i4=----- < 1 (增速同向)(动画) ZC (5)行星齿轮架固定,太阳轮带动齿圈 Z2 i5=----- > 1 (减速反向) (动画) Z1
九江职业技术学院
行星齿轮变速原理
2.特点: 三元件同轴, 行星齿轮既有公转又有自转, 采用斜齿常啮合,结构紧凑, 改变各元件的运动状态,可获得多个传动比。 3.传动比 太阳轮的齿数为Z1,齿圈的齿数为Z2 , 将行星齿轮架视作一个齿轮, 则其齿数ZC= Z1 + Z2, 称作行星齿轮架的当量齿数。
九江职业技术学院
辛普森式齿轮传动原理 轿车自动变速器所采用的行星齿轮机构的类型 主要有两类: 1.辛普森式(大部分车使用) 2.拉维萘赫式行星齿轮机构。
九江职业技术学院
辛普森式齿轮传动原理
辛普森行星齿轮机构实物图
九江职各零件之间的关系。 以丰田A340E自动变速器为例(视频)
任两个连成一体 即无任一元件制动又无任二元件连 成一体
九江职业技术学院
行星轮系 一.换档执行元件 1.离合器
(1) 作用:传递.连接。 (2) 类型: 湿式多片式离合器。 (3) 结构: 主动部分:离合器鼓.钢片等 从动部分:离合器毂.摩擦片等, 压紧机构:油缸.活塞等, 分离机构:回位弹簧等。
九江职业技术学院
行星轮系
离合器片为钢片材料,外缘有凸耳,与鼓相连。 离合器盘为摩擦材料,内缘有凸耳与离合器毂相连。
九江职业技术学院
行星齿轮变速原理
(4)太阳轮固定,行星齿轮架带动齿圈 Z2 i4=----- < 1 (增速同向)(动画) ZC (5)行星齿轮架固定,太阳轮带动齿圈 Z2 i5=----- > 1 (减速反向) (动画) Z1
九江职业技术学院
行星齿轮变速原理
2.特点: 三元件同轴, 行星齿轮既有公转又有自转, 采用斜齿常啮合,结构紧凑, 改变各元件的运动状态,可获得多个传动比。 3.传动比 太阳轮的齿数为Z1,齿圈的齿数为Z2 , 将行星齿轮架视作一个齿轮, 则其齿数ZC= Z1 + Z2, 称作行星齿轮架的当量齿数。
九江职业技术学院
辛普森式齿轮传动原理 轿车自动变速器所采用的行星齿轮机构的类型 主要有两类: 1.辛普森式(大部分车使用) 2.拉维萘赫式行星齿轮机构。
九江职业技术学院
辛普森式齿轮传动原理
辛普森行星齿轮机构实物图
九江职各零件之间的关系。 以丰田A340E自动变速器为例(视频)
任两个连成一体 即无任一元件制动又无任二元件连 成一体
九江职业技术学院
行星轮系 一.换档执行元件 1.离合器
(1) 作用:传递.连接。 (2) 类型: 湿式多片式离合器。 (3) 结构: 主动部分:离合器鼓.钢片等 从动部分:离合器毂.摩擦片等, 压紧机构:油缸.活塞等, 分离机构:回位弹簧等。
九江职业技术学院
行星轮系
离合器片为钢片材料,外缘有凸耳,与鼓相连。 离合器盘为摩擦材料,内缘有凸耳与离合器毂相连。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表达式齿数比前的正负号表示的含义是: “+”表示转化轮系中首末两轮转向相 同,“-”表示首末两轮转向相反。它 影响着各构件角速度之间的数量关系。
式中各角速度均表示代数值。计算时要 带符号运算。
18
示例:
如图所示轮系中, 已 知 z1=100, z2=101, z3=100,z4=99, 求iH1
24
3.满足安装条件:
为了平衡轮系中的离心惯性力,减少行星架 的支承反力,减轻轮齿上的载荷,一般采用 多个行星轮均布在两个中心轮之间。因此行 星轮的数目与各轮齿数之间必须满足一定的
关系。即: z1 z3 N k
式中的k为行星轮的个数,N为整数。含义是 两个中心轮的齿数和应为行星轮个数的整数 倍。
2
一、周转轮系的组成
3
1.定义:
周转轮系:
轮系中如果至少有一个齿轮的轴线绕另一个齿轮
的轴线转动,这个轮系则为周转轮系。
行星轮:
既绕自身轴线旋转又绕公共轴线旋转的齿轮称为 行星轮。
中心轮K:
齿轮的中心线固定并与主轴线重合,且与行星齿 轮相啮合的齿轮称为中心轮。
行星架H(系杆):
支承行星轮的构件称为行星架或系杆。
i1H3
n1 nH n3 nH
n1 nH nH
i1H
1
z3 z1
i1H=1+z3/z1 ∴ z3/z1=i1H-1
23
2.满足同心条件:
要保证两个中心 轮与行星架的回 转轴线重合。 dd21==mmzz21,, d3=mz3 且 d3/2=d2+d1/2 ∴ z3=z1+2z2
1
z2 z4 z1z3
20
示例解答(2):
i1H
1
z2 z4 z1z3
1 101 99 100 100
1 10000
iH 1 10000
21
四、行星轮系中各轮齿数的确定
设计行星轮系时,行星轮系中各轮 齿数的选配要满足以下四个条件:
22
1.满足传动比条件:
因为轮系中有:
n1 nH Z2 Zk
nk nH
Z1 Zk1
16
3.周转轮系传动比计算公式推导(2): 转化轮系传动比的计算公式为:
i1Hk
1 H k H
n1 nH Z2 Zk
nk nH
Z1 Zk1
17
3.使用转化轮系传动比公式注意事项:
只适合于转化轮系中首末两轮轴线平行 的情况。
30
行星轮图例(1):
31
行星轮图例(2):
32
行星轮图例(3):
行星齿轮传动及 行星齿轮减速器
1
引言:
机器人设计时要求其驱动装置及其传动 装置质量轻,并具有较大的功率质量比。 为此机器人所使用的传动机构要求质量 轻且输出功率大。
行星齿轮传动是一种具有动轴线的齿轮 传动,可用于减速、增速和差动装置。 行星齿轮传动和圆柱齿轮传动相比具有 质量轻、体积小、传动比大、效率高等 优点。缺点是结构复杂,精度要求较高。
4
周转轮系图例:
a)中心轮均不 固定—差动轮系
主要构成:
b)一个中心轮固 定——行星轮系
1、3—中心轮 2—行星轮 H—系杆
5
2.周转轮系的构成:
周转轮系由行星轮、中心轮K、行星架H 和机架构成。周转轮系中凡是轴线与主 轴轴线重合,并承受外力矩的构件称为 基本构件。如:中心轮、系杆等。
6
二、周转轮系的分类
14
3.周转轮系传动比计算公式推导(1):
如图所示的周转轮系中,各构件在原机构和转
化机构中的角速度如下表所示:
构件 周转轮系中角速度 转化轮系中角速度
1
ω1
ω1H=ω1-ωH
2
ω2
ω2H=ω2-ωH3 Nhomakorabeaω3
ω3H=ω3-ωH
H
ωH
ωHH=ωH-ωH=0
15
转化轮系公式推导图例:
i1Hk
1 H k H
11
三、周转轮系传动比的计算
12
1.定轴轮系传动比的计算:
所有齿轮中心 线是固定的。
运动输入
i n1
15 n5
z2 z3 z4 z5 z1z2 z3 z4
运动输出
13
2.周转轮系传动比计算基本思想:
由于周转轮系中有行星轮,故其传动 比不能直接用定轴轮系传动比的公式 进行计算。但是如果把轮系中的行星 架相对固定,即将周转轮系转化为定 轴轮系,就可以借助该转化机构按定 轴轮系的传动比公式进行周转轮系传 动比的计算。这种方法称为反转法或 机构转化法。
25
满足安装条件图例:
26
4.满足邻接条件:
多个行星轮装入两个中心轮之间,应 保证相邻两行星轮之间不发生干涉。 应满足:
(z1+z2)sin(180°/k)>z2+2ha※
27
五、太阳轮、行星轮、行星架常见结构
28
1.太阳轮结构:
当太阳轮不浮动时,可简支安装或 悬臂安装
29
2.行星轮结构:
2K-H型周转轮系:
轮系中有两个中心轮。
3K型周转轮系:
轮系中有三个中心轮,行星架只是起支承 行星轮的作用。
K-H-V行星轮系:
轮系中只有一个中心轮,其运动是通过等 角速机构由V轴输出。
9
周转轮系分类图例(1):
2K-H型周转轮系
10
周转轮系分类图例(2):
3K型行星轮
K-H-V型行星轮
19
示例解答(1):
从图中可以看出,只有一个独立的主运 动中心轮,因而是行星轮系。且n4=0。
运用转化机构公式进行计算:
∵
i1H4
n1 nH n4 nH
z2 z4 z1z3
有:
i1H4
n1 nH n4 nH
n1 nH nH
n1 nH
1 i1H
7
1.按周转轮系的自由度分:
差动轮系:
若周转轮系的自由度为2,则称其为差动轮系。 亦即该轮系有两个独立运动的主动件。
行星轮系:
若周转轮系的自由度为1,则为行星轮系。这种 轮系只有一个独立运动的主动件。
附:机构的自由度:
指机构中各构件相对于机架所具有的独立运动 的数目。
8
2.按基本构件的组成分:
中、低速行星齿轮传动:常用的行星轮结 构如图。常采用滚动轴承支承。
当传动比较大,行星轮的直径较大时:轴 承可安装在行星轮孔内。这样可以减小传
动的轴向尺寸,并使装配结构简化。在行
星孔内装两个轴承时,应尽量使轴承之间 的距离增大。 当行星轮内装轴承的尺寸不够时:可将轴
承装在行星架上。 高速重载的行星传动:可采用滑动轴承。
式中各角速度均表示代数值。计算时要 带符号运算。
18
示例:
如图所示轮系中, 已 知 z1=100, z2=101, z3=100,z4=99, 求iH1
24
3.满足安装条件:
为了平衡轮系中的离心惯性力,减少行星架 的支承反力,减轻轮齿上的载荷,一般采用 多个行星轮均布在两个中心轮之间。因此行 星轮的数目与各轮齿数之间必须满足一定的
关系。即: z1 z3 N k
式中的k为行星轮的个数,N为整数。含义是 两个中心轮的齿数和应为行星轮个数的整数 倍。
2
一、周转轮系的组成
3
1.定义:
周转轮系:
轮系中如果至少有一个齿轮的轴线绕另一个齿轮
的轴线转动,这个轮系则为周转轮系。
行星轮:
既绕自身轴线旋转又绕公共轴线旋转的齿轮称为 行星轮。
中心轮K:
齿轮的中心线固定并与主轴线重合,且与行星齿 轮相啮合的齿轮称为中心轮。
行星架H(系杆):
支承行星轮的构件称为行星架或系杆。
i1H3
n1 nH n3 nH
n1 nH nH
i1H
1
z3 z1
i1H=1+z3/z1 ∴ z3/z1=i1H-1
23
2.满足同心条件:
要保证两个中心 轮与行星架的回 转轴线重合。 dd21==mmzz21,, d3=mz3 且 d3/2=d2+d1/2 ∴ z3=z1+2z2
1
z2 z4 z1z3
20
示例解答(2):
i1H
1
z2 z4 z1z3
1 101 99 100 100
1 10000
iH 1 10000
21
四、行星轮系中各轮齿数的确定
设计行星轮系时,行星轮系中各轮 齿数的选配要满足以下四个条件:
22
1.满足传动比条件:
因为轮系中有:
n1 nH Z2 Zk
nk nH
Z1 Zk1
16
3.周转轮系传动比计算公式推导(2): 转化轮系传动比的计算公式为:
i1Hk
1 H k H
n1 nH Z2 Zk
nk nH
Z1 Zk1
17
3.使用转化轮系传动比公式注意事项:
只适合于转化轮系中首末两轮轴线平行 的情况。
30
行星轮图例(1):
31
行星轮图例(2):
32
行星轮图例(3):
行星齿轮传动及 行星齿轮减速器
1
引言:
机器人设计时要求其驱动装置及其传动 装置质量轻,并具有较大的功率质量比。 为此机器人所使用的传动机构要求质量 轻且输出功率大。
行星齿轮传动是一种具有动轴线的齿轮 传动,可用于减速、增速和差动装置。 行星齿轮传动和圆柱齿轮传动相比具有 质量轻、体积小、传动比大、效率高等 优点。缺点是结构复杂,精度要求较高。
4
周转轮系图例:
a)中心轮均不 固定—差动轮系
主要构成:
b)一个中心轮固 定——行星轮系
1、3—中心轮 2—行星轮 H—系杆
5
2.周转轮系的构成:
周转轮系由行星轮、中心轮K、行星架H 和机架构成。周转轮系中凡是轴线与主 轴轴线重合,并承受外力矩的构件称为 基本构件。如:中心轮、系杆等。
6
二、周转轮系的分类
14
3.周转轮系传动比计算公式推导(1):
如图所示的周转轮系中,各构件在原机构和转
化机构中的角速度如下表所示:
构件 周转轮系中角速度 转化轮系中角速度
1
ω1
ω1H=ω1-ωH
2
ω2
ω2H=ω2-ωH3 Nhomakorabeaω3
ω3H=ω3-ωH
H
ωH
ωHH=ωH-ωH=0
15
转化轮系公式推导图例:
i1Hk
1 H k H
11
三、周转轮系传动比的计算
12
1.定轴轮系传动比的计算:
所有齿轮中心 线是固定的。
运动输入
i n1
15 n5
z2 z3 z4 z5 z1z2 z3 z4
运动输出
13
2.周转轮系传动比计算基本思想:
由于周转轮系中有行星轮,故其传动 比不能直接用定轴轮系传动比的公式 进行计算。但是如果把轮系中的行星 架相对固定,即将周转轮系转化为定 轴轮系,就可以借助该转化机构按定 轴轮系的传动比公式进行周转轮系传 动比的计算。这种方法称为反转法或 机构转化法。
25
满足安装条件图例:
26
4.满足邻接条件:
多个行星轮装入两个中心轮之间,应 保证相邻两行星轮之间不发生干涉。 应满足:
(z1+z2)sin(180°/k)>z2+2ha※
27
五、太阳轮、行星轮、行星架常见结构
28
1.太阳轮结构:
当太阳轮不浮动时,可简支安装或 悬臂安装
29
2.行星轮结构:
2K-H型周转轮系:
轮系中有两个中心轮。
3K型周转轮系:
轮系中有三个中心轮,行星架只是起支承 行星轮的作用。
K-H-V行星轮系:
轮系中只有一个中心轮,其运动是通过等 角速机构由V轴输出。
9
周转轮系分类图例(1):
2K-H型周转轮系
10
周转轮系分类图例(2):
3K型行星轮
K-H-V型行星轮
19
示例解答(1):
从图中可以看出,只有一个独立的主运 动中心轮,因而是行星轮系。且n4=0。
运用转化机构公式进行计算:
∵
i1H4
n1 nH n4 nH
z2 z4 z1z3
有:
i1H4
n1 nH n4 nH
n1 nH nH
n1 nH
1 i1H
7
1.按周转轮系的自由度分:
差动轮系:
若周转轮系的自由度为2,则称其为差动轮系。 亦即该轮系有两个独立运动的主动件。
行星轮系:
若周转轮系的自由度为1,则为行星轮系。这种 轮系只有一个独立运动的主动件。
附:机构的自由度:
指机构中各构件相对于机架所具有的独立运动 的数目。
8
2.按基本构件的组成分:
中、低速行星齿轮传动:常用的行星轮结 构如图。常采用滚动轴承支承。
当传动比较大,行星轮的直径较大时:轴 承可安装在行星轮孔内。这样可以减小传
动的轴向尺寸,并使装配结构简化。在行
星孔内装两个轴承时,应尽量使轴承之间 的距离增大。 当行星轮内装轴承的尺寸不够时:可将轴
承装在行星架上。 高速重载的行星传动:可采用滑动轴承。
