几种常见的统计图表
几种常见的统计图表

第十二章数据的描述12.1 几种常见的统计图表[教学目标]1.知识与能力:认识条形图、扇形图、折线图、直方图,能够从统计图中获取相关信息.2.过程与方法:从问题的解决过程中体会各个统计图的优点和缺点,感受统计图的作用.3.情感、态度与价值观:培养学生运用统计图的能力以及用数据说话的习惯.[重点难点]1.教学重点:能够利用条形图、扇形图、折线图、直方图描述数据,能够从统计图中获取相关信息.2.教学难点:读图、识图、获取信息.[教学方法]创设情境——主体探究——合作交流——应用提高.[教学过程]一、创设情境,激发学生兴趣,认识条形图和扇形图问题 1:展示空气质量图(课本 54 页),2002 年 1 月 1 日,这 31 个城市中,空气质量为一级,二级,…,五级的城市各有多少个?各占百分之几?学生活动设计:学生分组合作、共同解决问题.按空气质量级别对这 31 个数据分组,数出每一组的城市个数,再计算它们所占的百分比,列出下表:级别划记频数(城市个数)频率(频数/31)百分比一级一 1 0.032 3.2% 二级正8 0.258 25.8% 三级正正正19 0.613 61.3%四级 2 0.065 6.5%五级一 1 0.032 3.2%合计31 31 1 100% 从表中可以看出空气质量为各级的城市个数及其所占百分比.如空气质量为二级的有8 个城市,占 25.8%.教师活动设计:教师在学生解决问题的基础上作以下归纳:落在不同小组中的数据个数为该组的频数,频数与数据总数的比为频率.在此过程中,注重学生参与活动的程度.问题 2:对于上述数据我们可以怎样描述呢?学生活动设计:学生根据所学知识,想到可以利用条形图和扇形图来描述数据.为了清楚地描述空气质量为各个级别的城市的个数,可以用条形图[如图(1)]来描述;为了清楚地看出各个空气质量级别的城市个数占总城市数(31 个)的百分比,可以用扇形图[如图(2)]来描述.图(1)图(2)学生独立完成上述统计图的制作,在制作过程中,让学生体会上述两种图形的制作方法,最后引导学生对两种图形的优缺点进行分析.条形图:(1)能够显示每组中的具体数据;(2)易于比较数据之间的差别.扇形图:(1)用扇形的面积表示部分在总体中所占的百分比;(2)易于清楚地看出各个项目占总数的百分比,但不能看出各个项目的频数以及数据总数.二、小组合作,认识折线图问题 3:出示图片(课本第 58 页:两会漫笔)分析上面报纸中的数据(文中提到 1993 年,当年的国内生产总值为 34 561 亿元),用什么样的统计图可以很好地描述我国 GDP (国内生产总值)的变化趋势?你能制作相应的统计图吗?学生活动设计:学生独立思考,发现可以用折线图来描述数据的变化趋势,然后小组合作,制作折线图,如图(3).年份1986 1991 1993 1997 1999 2001 GDP/万亿元 1.02 2.17 3.46 7.31 8.04 9.59图(3)在学生解决问题后,引导学生归纳折线图的特点:易于显示数据的变化趋势.三、主体探究,认识直方图问题 4:为了研究 800 米赛跑后学生心率的分布情况,体育老师统计了全班同学一分时间脉搏的次数,并整理成下面的表格. 根据下列表格,你能用统计图描述表中的数据吗?脉搏次数x(次/分)频数(学生人数)130≤x<135 1135≤x<140 2140≤x<145 4145≤x<150 6150≤x<155 9155≤x<160 14160≤x<165 11165≤x<170 2学生活动设计:学生小组讨论,发现可以用类似条形图的方法进行描述,如图(4).图(4)通过上述统计图可以发现:(1)脉搏次数x在 155≤x<160 范围的学生最多,有 14 个;(2)脉搏次数x在 135≤x<140 范围的学生有 2 个;(3)脉搏次数x在 150≤x<155 范围的学生比在 160≤x<165 范围的学生少 2 个;(4)全班一共有 49 个学生.教师活动设计:引导学生作以下归纳:体育老师把全班学生的脉搏次数按范围分成成 8 组,每一组的两个端点的差都是 5. 我们把分成的组的个数称为组数,每一组两个端点的差称为组距,上述这样的表格称为频数分布表,利用频数分布表画出的统计图叫做直方图.归纳直方图的特点:(1)能够显示各组频数分布的情况;(2)易于显示各组之间频数的差别.四、应用提高、拓展创新问题 5:随着我国对外开放程度的不断扩大,我国对外贸易迅速发展.下表是我国近几年的进出口额数据.你能用统计图来描述这两组数据,从而对它们进行比较吗?年份1985 1990 1995 1998 2000 2002 出口额(亿美元)274 621 1 488 1 837 2 492 3 256进口额(亿美元)423 534 1 321 1 402 2 251 2 952 师生活动设计:教师引导学生利用折线图和复合条形图来描述这两组数据,如图(5)(6).图(5)图(6)五、归纳小结、布置作业小结:描述数据的方法——几种常见的统计图.作业:习题 12.1.。
讲解Excel的16种图表类型的“含义”,知道该怎么画图了!
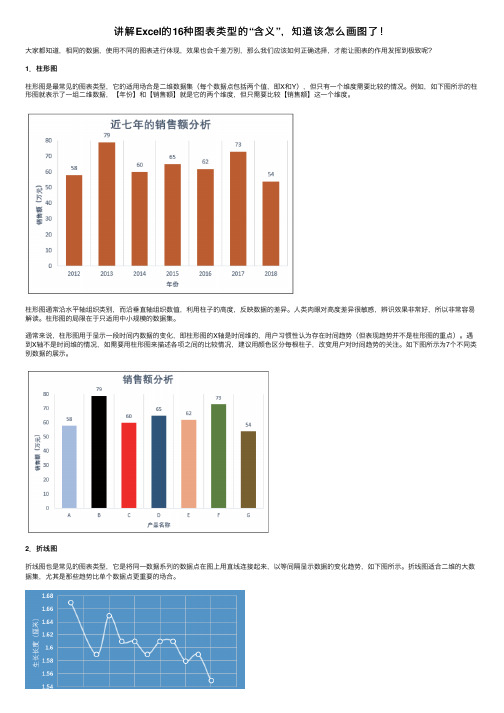
讲解Excel的16种图表类型的“含义”,知道该怎么画图了!⼤家都知道,相同的数据,使⽤不同的图表进⾏体现,效果也会千差万别,那么我们应该如何正确选择,才能让图表的作⽤发挥到极致呢?1.柱形图柱形图是最常见的图表类型,它的适⽤场合是⼆维数据集(每个数据点包括两个值,即X和Y),但只有⼀个维度需要⽐较的情况。
例如,如下图所⽰的柱形图就表⽰了⼀组⼆维数据,【年份】和【销售额】就是它的两个维度,但只需要⽐较【销售额】这⼀个维度。
柱形图通常沿⽔平轴组织类别,⽽沿垂直轴组织数值,利⽤柱⼦的⾼度,反映数据的差异。
⼈类⾁眼对⾼度差异很敏感,辨识效果⾮常好,所以⾮常容易解读。
柱形图的局限在于只适⽤中⼩规模的数据集。
通常来说,柱形图⽤于显⽰⼀段时间内数据的变化,即柱形图的X轴是时间维的,⽤户习惯性认为存在时间趋势(但表现趋势并不是柱形图的重点)。
遇到X轴不是时间维的情况,如需要⽤柱形图来描述各项之间的⽐较情况,建议⽤颜⾊区分每根柱⼦,改变⽤户对时间趋势的关注。
如下图所⽰为7个不同类别数据的展⽰。
2.折线图折线图也是常见的图表类型,它是将同⼀数据系列的数据点在图上⽤直线连接起来,以等间隔显⽰数据的变化趋势,如下图所⽰。
折线图适合⼆维的⼤数据集,尤其是那些趋势⽐单个数据点更重要的场合。
折线图可以显⽰随时间⽽变化的连续数据(根据常⽤⽐例设置),它强调的是数据的时间性和变动率,因此⾮常适⽤于显⽰在相等时间间隔下数据的变化趋势。
在折线图中,类别数据沿⽔平轴均匀分布,所有的值数据沿垂直轴均匀分布。
折线图也适合多个⼆维数据集的⽐较,如下图所⽰为两个产品在同⼀时间内的销售情况⽐较。
不管是⽤于表现⼀组或多组数据的⼤⼩变化趋势,在折线图中数据的顺序都⾮常重要,通常数据之间有时间变化关系才会使⽤折线图。
3.饼图饼图虽然也是常⽤的图表类型,但在实际应⽤中应尽量避免使⽤饼图,因为⾁眼对⾯积的⼤⼩不敏感。
例如,对同⼀组数据使⽤饼图和柱形图来显⽰,效果如下图所⽰。
常见的六种图表类型

常见的六种图表类型1、柱形图,又称长条图、柱状统计图,是一种以长方形的长度为变量的统计图表。
作为我们最常用的图表之一,通常是为了表现数据大小的对比。
柱形图经久不衰,正是因为它的可读性与简洁性。
2、饼图,或称饼状图,是一个划分为几个扇形的圆形统计图表,用于描述数量、频率或百分比之间的相对关系。
在饼图中,每个扇区的弧长(以及圆心角和面积)大小为其所表示的数量的比例。
这些扇区合在一起刚好是一个完全的圆形。
3、环形图是由两个及两个以上大小不一的饼图叠在一起,挖去中间的部分所构成的图形,主要是为了区分或表明某种关系。
环形图与饼图类似,但又有区别。
环形图中间有一个“空洞”,每个样本用一个环来表示,样本中的每一部分数据用环中的一段表示。
因此环形图可显示多个样本各部分所占的相应比例,从而有利于构成的比较研究。
4、气泡图,即以气泡形状为主,绘制展示信息的图。
它可以直接做散状气泡,可以与坐标系结合,也可以在它们之间用各种连接线表达关系。
气泡图因为它外观简洁直观、可视化数据信息;种类多,应用领域广;帮助整理思维,启发思维和想象等优点,越来越受到职场人的追捧和学习。
5、对比图就是将两个或两个以上的主体,通过一张图来进行多维度同步分析的一种分析方法。
这种图形我们日常在分析不同产品型号、竞品分析、产品功能分析中常见。
6、甘特图又称为横道图、条状图,其通过条状图来显示项目,进度,和其他时间相关的系统进展。
该图表以提出者亨利·劳伦斯·甘特(Henry Laurence Gantt)先生的名字命名。
甘特图横轴是时间线,纵轴是项目名称。
可以看出每个项目需要多少时间,在所有项目中某个特定项目开始和结束的时间点,发现有多少项目正在同时进行、哪些项目快到期,明确项目紧急性,从而及时做出调整。
几种常见的统计图表

R
W
扇形图(sector diagram)
概念:以一个圆面积为100%,用圆内 各扇形面积所占的百分比来表示各 部分所占的构成比例 适用资料:构成比资料 绘制要点: ①每3.6o为1%,用3.6乘以百分数即为 请问:如何表示 所占扇形的度数。用量角器画出. 扇形内各部分所 ②从相当于时钟12点或9点的位置开始 顺时针方向绘图. ③每部分用不同线条或颜色表示,并在 图上标出百分比,下附图例说明. ④当比较不同资料的百分构成时,可以 画两个相等大小的圆,在每个圆的 下面写明标题,并用相同的图例表 示同一个构成部分. 应用:描述各部分的百分构成.
展变化或一种现象随另一种现象变迁的情况 2、适用资料:连续性资料。 3、绘制要点: ①坐标轴:横轴表示时间或组段,纵轴表示频数或频率。 纵轴坐标可以不从0开始,因此在看图时要注意纵轴的 起点坐标。 ②数据点画在组段中间位置。相邻的点用直线连接,不要 用平滑的曲线连接。无数据的组段用虚线连接。直线 不能任意外延。 ③同一张折线图上不要画太多条曲线,否则不易分清。当 有两条或两条以上曲线在同一张折线图上时,须用不 同颜色或不同的图形形式加以区分,并附图例加以说 明。 4、应用:反映事物的连续的动态变化规律。
190 180 170 160 150 40 45 50 ©Û ¤ 55 Ç ª± (cm)
ì ß É µ (cm)
Í 10.Ä ³ 20Ë Ä Ç Ä É µ · Ç Û ± Ä ¶ Ï ¼ ± Ø ê Ð ê ì ß Í ©ª¤³ Ø ³
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 5 10 15 20 25 30
9% 18% 43%
ô · « ² È Ï ä Æ
ü ³ ° ¡ Î Ï ¼ ° ¾ ¡ È ° ë Ô ° ¡ Ì Ð ¼ ° ü Ë
高中地理常考图表10 ——人口统计图的判读
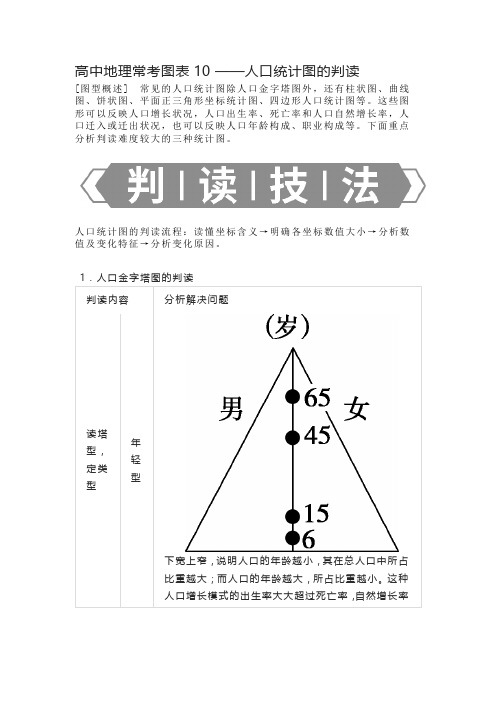
高中地理常考图表10 ——人口统计图的判读[图型概述] 常见的人口统计图除人口金字塔图外,还有柱状图、曲线图、饼状图、平面正三角形坐标统计图、四边形人口统计图等。
这些图形可以反映人口增长状况,人口出生率、死亡率和人口自然增长率,人口迁入或迁出状况,也可以反映人口年龄构成、职业构成等。
下面重点分析判读难度较大的三种统计图。
人口统计图的判读流程:读懂坐标含义→明确各坐标数值大小→分析数下宽上窄,说明人口的年龄越小,其在总人口中所占比重越大;而人口的年龄越大,所占比重越小。
这种人口增长模式的出生率大大超过死亡率,自然增长率底部与中部的宽窄相近,儿童、青少年所占比重趋于减少,中老年人口所占比重有所增加,人口增长速度减缓,总人口继续增长。
属于传统型的后期阶段,一般属于发展中国家形中的已知点(如图中的P点)分析三组年龄人口的构成情况,具体操作方法:过已知点分别作三角形三边的平行线,这样每个轴上可得到两个交点,其中靠近原点的那个点对应的数值,就是已知点在相应的坐标轴上的数值。
如图所示,P点0~14岁人口比重为A点的数值,15~64岁3.四边形统计图的判读四边形统计图中有两边分别表示两个变量(一般是人口出生率和人口死亡率),另外两边表示一个变量(通常是人口自然增长率)。
对于人口出生率和人口死亡率,根据一般直角坐标图的判断即可得出数据,而人口自然增长率的读取,我们一般以第三个变量作四边形的一条对角线,读数时下图为1982年和2009年我国人口年龄结构统计图。
读图,回答(1)~(2)题。
(1)图中信息反映出( )A.1982-2009年人口出生率呈上升趋势B.1982年的人口平均年龄比2009年的低C.1982年的40岁及以上人口比重比2009年的高D.1982年的20~24岁年龄组人口数量比2009年的多(2)与1982年相比,2009年我国人口年龄结构的变化( )A.显示人口的增长速度加快B.意味着社会养老负担加重C.不影响劳动人口的职业构成D.表明25~59岁劳动力资源数量下降【判读流程】图表信息获取【尝试解答】(1)B (2)B下图中a、b、c分别对应0~14岁、15~64岁、65岁及以上三个年龄段人口所占总人口的比重。
第32讲 常见的统计图

【点拨】(1)由 C 类的人数及其百分比可得总人数,总人数乘 B 类的百分比即可得 B 类的人数;(2)根据百分比之和为 1,求得 A 类的百分比,再乘 360° 和总人数可分别求得; (3)总人数乘样本 中 A, B, C 三类的百分比之和可得答案. 解:(1)本次调查的市民有 200÷ 25%= 800(人 ), ∴B 类的人数为 800× 30%= 240(人 ). 故答案为 800, 240;
4.频数分布直方图的绘制步骤 (1)计算最大值与最小值的差; (2)决定组距与组数; (3)确定分点,常使分点比数据多一位小数,并且把第一组的 起点稍微减小一点; (4)列频数分布表; (5)用横轴表示各分段数据,纵轴表示各分段数据的频数,小 长方形的高表示频数,绘制频数分布直方图.
5. 条形图和直方图的区别 (1)条形图是用条形的高度表示频数的大小,而直方图实际上 是用长方形的面积表示频数; (2)条形图中,横轴上的数据是孤立的,是一个具体的数据, 而直方图中,横轴上的数据是连续的,是一个范围; (3)条形图中,各长方形之间有空隙,而直方图中,各长方形 是靠在一起的.
第32讲
常见的统计图
考点一
几种常见的统计图
1.条形统计图 用长方形的高来表示数据的图形. 它的特点:(1)能够显示每组中的 具体数据 ;(2)易于比较各 组数据之间的差别. 2.折线统计图 用几条线段连成的折线来表示数据的图形. 它的特点:易于显示数据的 变化趋势 .
3.扇形统计图 (1)用一个圆代表总体,圆中的各个扇形分别代表总体中的不 同部分,扇形的大小反映部分在总体中所占 百分比 的大小,这 样的统计图叫做扇形统计图; (2)百分比的意义:在扇形统计图中,每部分占总体的百分比 等于该部分所对扇形的圆心角的度数与 360° 的比; (3)扇形的圆心角= 360° × 该部分占总体的百分比 .
人口统计图表判读专题-PPT

可能原因: a.就业人口大量迁入; b.升学人口大量迁入。
六.人口金字塔图的判读方法:
异常变化——三种情况
③处(男女比例的明显失调)
可能原因: a.战争导致大量男 性死亡; b.钢铁厂、纺织厂
图1中,青壮年人口性别比例是男多女少,原因可能 是由于大量的青壮年男性人口迁入所造成的。而图2 中,青壮年人口性别比例是男少女多,原因可能是 由于近期发生过战争,夺去了大量的青壮年男性的 生命所致。
2、图甲所示城市人口自然增长状况最接近图乙中的( )
A、I阶段
B、Ⅱ阶段
C、Ⅲ阶段
D、Ⅳ阶段
19
六.人口金字塔图的判读方法:
异常变化——三种情况 ①处(某年龄段男女比例突然变小)
可能原因: a.计划生育导致出 生率突然降低; b.重大灾害导致死 亡率上升; c.人口大量外迁。
六.人口金字塔图的判读方法:
23
结构类图(包括扇形图、饼状图等):
七.饼状图:
圆形图(包括扇形图、 饼状图等),是以几 何图形——圆形的面 积大小,表示地理数 据资料的统计图表。 这种图表在反映总体 内部结构时更为清晰。
24
八.扇形图
1964~2000年中国 各年龄段人口占总 人口比重变化图
25
学以致用
(随学随练,轻松夺冠)
8
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
9
学以致用
(随学随练,轻松夺冠)
甲市2008年户籍人口出生9.67万人,出生率为0.699%;死亡 10.7万人,死亡率为0.773%。甲市户籍人口这种自然增长态势 已持续14年。图上显示四个地区的人口出生率和死亡率。据此 完成1-2题。
华师大版-数学-八年级上册-华师 几种常见的统计图表 教案

【同步教育信息】一. 本周教学内容:华师七上第五章几种常见的统计图表教案二. 教学目标1、理解数据的频数、频率及频率分布的意义,会就一组数据列出频数分布表和画出频数分布直方图,频数折线图。
2、了解不同统计图的特征,能根据具体问题选择合适的统计图来清晰地描述数据。
三. 教学重点和难点重点:理解条形、折线、扇形、直方统计图的特点,并会制作统计图。
难点:能根据不同的问题,选择不同的统计图。
[教学过程]知识点归纳:知识点1 频数和频率的概念在调查中每个对象所出现的次数称为频数。
一般我们称落在不同小组中的数据个数为该组的频数。
频数与数据总数的比为频率。
频率反映了各组频数的大小在总数中所占的分量,频率 100%就是百分比。
知识点2 数据的表示方法(1)条形图用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,再把这些直条按照一定的顺序排列起来,这样的统计图叫做条形统计图。
条形统计图能清楚地表示出每个项目的具体数字,即根据条形统计图可以直接看被统计对象的准确数据。
例如:某校八年级学生共300人,到学校上学的方式有骑自行车的,有步行的,有坐车的,还有其它方式的,这四种方式的人数可用条形统计图表示出来。
知识点3 数据的表示方法(2)扇形图利用圆和扇形来表示总体和部分的关系,圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形统计图能清楚地表示出每个部分在总体中所占的百分比,即根据统计图可看出被统计对象所占比例。
例如:上面用条形图表示的某校八年级学生到校上学方式的情况,可用扇形统计图形表示。
知识点4 数据的表示方法(3)折线图用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来,所得的统计图叫做折线统计图。
折线统计图能清楚地反映事物的变化情况。
即根据折线统计图能清楚地看出事物变化的趋势。
年龄(岁) 5 10 15 20 25身高(cm)92 140 178 183 185该同学的生长情况,可用折线统计图表示出来,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中的具体数据
级别
想一想:能用什么样的统计图来描述各个
空气质量级别的城市个数在计图
6% 3% 3% 26% Ò º ¶ þ È ý Ë Ä Î å ¶ » ¶ » ¶ » ¶ » ¶ »
62%
你能归纳出条形图和扇形图的特点吗?
能表示出每个项目 的具体数目
能表示出各部分在总体中 所占的百分比
62%
1
级别
优点: 中的具体数据
(1)用扇形的面积表示部 思考: 用条形统计图和扇形统计图来 (1)能够显示每组 优点:分在总体中所占的百分比; (2)易于比较各组 数据之间的差别
描述数据各有什么优、缺点? (2)易于显示每组数据
相对于总数的大小。
无法直接显示每组 缺点:难以直接看出每组数据 缺点:
Ò ú × à é ö ³ Æ » Î ¸ µ ¿ Ç ¾ Í » Í 4% 2% 20% 39%
34%
1%
û × · µ °µ Ô × Ö × À µ À × Ä µ Ó × ½ µ º ¨Ó × ¼ Í Ã µ
试一试,你能从这两个统计图中获得哪些信息?
± © ½ ¼ É ÷ Î ª » Ö À ¼ Õ Ë £ · ¨ ¼ Ó ¹ Ï Ä ¼ É « ¶ × Ö ë Ç Æ Ô Ï Ä Ê · à Ë
落在不同小组中的数据的个数叫做该组的频数 频数与数据总数的比叫做频率
频率反映了各组频数的大小在总数中所占的份量, 频率 100%就是百分比.
想一想:能用什么样的统计图来描述空气质量为
一、二、三、四、五级的城市的个数呢?
条形统计图
频数
20 15 10 5 0 º¶ Ò» þ¶ ¶» ý¶ È» Ķ Ë» å¶ Î» 1 8 2 1 19
大气污染既危害人体健康,又影响动植物的生长,破坏经济资源。 严重时可改变大气的性质。 1.对人体健康的危害。受污染的大气进入人体,可导致呼吸、 心血管、神经等系统疾病和其他疾病。①化学性物质污染。主要来 自煤和石油的燃烧、冶金、火力发电、石油化工和焦化等工业生产 过程排入大气的有害物质最多。一般通过呼吸道进入人体,也有少 数经消化道或皮肤进入人体。对居民主要产生慢性中毒,城市大气 污染是慢性支气管炎、肺气肿和支气管哮喘等疾病的直接原因或诱 因。世界上闻名的重大污染事件有比利时的马斯河谷事件,美国的 多诺拉事件。墨西哥的帕沙利卡事件,英国的伦敦事件等。②放射 性物质污染。主要来自核爆炸产物。放射性矿物的开采和加工、放 射性物质的生产和应用,也能造成空气污染。污染大气起主要作用 的是半衰期较长的放射性元素。③生物物质污染。一种空气应变源, 主要有花粉和一些霉菌孢子,能在个别人身上起过敏反应,可诱发 鼻炎、气喘、过敏性肺部病变。城市居民受大气污染是综合性的, 一般是先污染蔬菜、鱼贝类,经食物链进入人体。
2.对动植物危害。动物往往由于食用或饮用积累了大 气污染的植物和水,发生中毒或死亡。大气污染物浓 度超过植物的忍耐程度,会使植物的细胞和组织器官 受到伤害,生理功能和生长发育受阻,产量下降,产 品品质变坏,群落组成发生变化, 甚至造成植物个体 死亡,种群消失。急性伤害导致细胞死亡,常在短时 间里显示出来。 3.对材料的危害。如腐蚀金属、侵蚀建筑材料、使橡 胶制品脆裂、损坏艺术品、使有色金属褪色等。 4.对大气的影响。能改变大气的性质和气候的形式。 二氧化碳吸收地面幅射,颗粒物散射阳光,可使地面 温度上升或降低。细微颗粒物可降低见光度,增加云 量和降水量,雾的出现频率也增加并延长持续时间。
条形统计图
扇形统计图
“权”的意义
思考:在制作扇形统计图时,需要 注意哪些问题?
填上标题
填写名称
计算各个部分 圆心角度数
填写百分比
2013-12-23
思考:在制作条形统计图时,需要注意哪 些问题? 表示 频数
200 150 131 182
100
50
98
68 39 A B C D D
条形图是 用宽度相 同的条形 的高度或 长短来表 示数据变 动的统计 图。
条形之间是 分开的,而 且间距相等
表示级别或类别
思考练习
奥科学校八(4)班参加兴趣小组人数统计图如右图:
1) 2) 3)
该班共有多少人参加? 哪小组人最多?哪小组人少? 哪小组占总人数的百分比最多?
微机 15%
绘画 31%
20 18 小提琴 16 10% 14 12 10 围棋 8 24% 6 4 2 0
几种常见的统计图表
条形图与扇形图
活动1
人数(千万)
10 8 6 4 2 0
观察下面的两个统计图,回答问题:
2000Ä È ¸ È ¾ Æ ² ² ²Ê ½ Í » Í ê«úËÚÕé¾Öýݳƻ ±© ½ ¼÷ ÉÎ ªÖ »À Õ ¼Ë £¨ ·¼ ÓÏ ¹Ä ¼« ɶ ×ë ÖÇ 省市 Ô Ä ÆÏ Êà ·Ë
18 14 6 小提琴 围棋 书法 绘画 微机 12 9
书法 20%
小结
1.在描述数据时如何选用 条形图和扇形图?
条形统计图 频数
20 15 10 5 0 º¶ Ò» þ¶ ¶» ý¶ È» Ķ Ë» å¶ Î» 1 8 2 19
扇形统计图 3% 3%
6% 26% º Ò þ ¶ ý È Ä Ë å Î ¶ » ¶ » ¶ » ¶ » ¶ »
