机器人运动学PPT课件
合集下载
第二章 机器人运动学PPT课件

系的位置矢量 AP、BP具有如下变换关系
APB ARBPAPBO
(2-1-12)
15
ZA {A}
OA XA
ZB
ZC {C}
{B}
AP
BP YB
OB(OC)
YC
P A
BO XC YA
XB
图2.1.4 平移加旋转变换 注:坐标系{C}为过渡坐标系
16
2.齐次变换
一般情况下,刚体的运动是转动和平移的复合运 动,为了用同一矩阵既表示转动又表示平移,因此引 入齐次坐标变换矩阵。
28
X
偏转
Z
横滚
O船
Y
俯仰
偏转
X
Z
横滚
O
夹手
Y
俯仰
(a)
(b)
图2.1.11 RPY角的定义
29
§2.2 操作臂运动学
一、机械手位置和姿态的表示
图2.2.1所示为机器人的一个机械手。 描述机械手方位的坐标系置于手指尖的 中 位心置,可其以用原矢点量由矢p在量固p表定示坐。标机系械的手坐的标 表示为
H
0
1
0
b
称为平移的齐次变换矩阵,又可表示为
0 0 1 c
0
0
0
1
HTraa,b n,c)s。(矩阵中的第四列为平移参考矢量的齐次坐标。
19
Z
V
U
P
O
Y
X 图2.1.5 平移的齐次变换
20
例平2移.1,求向平量移U 后i得3到j的5k向沿量向V量 。P 3i7jk
解:
1 0 0 3 1 4
系,首先需要用两个参数对每个连杆进行描述。 如图2.2.2所示,对于任意一个两端带有关节i和
电机拖动技术基础第三章机器人的运动学PPT课件

第三章 机器人的运动学
►3.1 刚体的位姿描述 ►3.2 坐标变换 ►3.3 齐次坐标和齐次变换 ►3.4 变换方程和欧拉角 ►3.5 机器人运动学的正问题和逆问题
3.1 刚体的位姿描述
一、位姿的定义
刚体参考点的位置(坐标系的位置)和刚体的姿态统称为刚体的位姿。
(为描述机器人本身的各个连杆之间.机器人和环境之间的运动关系,将
n
n o a
手爪的方位由旋转矩阵R规定。
R n
o
a
手爪的位置由位置矢量 p
规定。
代表手p 爪坐标系的原点。
则手爪的位姿可由四个矢量
来 来描述。
noa p
记为:
T n o a p
3.2 坐标变换
定义:由于空间中任意点P在不同坐标系中的描述不同,所以需要 研究从一个坐标系的描述到另一个坐标系的描述之间的变换关,通 常称为坐标变换。
{S}代表工作站(操作台)坐标系(工作站框)
{G}代表目标坐标系(目标框) 它们之间的位姿关系用相应的齐次变换来描述。图3-6 机器人与环境坐标系
B S
T描述工作站框{S}相对于基座{B}的位姿,
S G
T描述目标框{G}相对于工作站{S}的位姿。
对物体进行操作时(搬运或装配机器人),工具框{T}相对目标框{G} 的位姿 直接GT T 影响操作效果。 是机GT T器人控制和轨迹规划的对象。
=
相对于固定坐标系运动 相对于活动坐标系运动
2.变换过程的可逆性
齐次坐标变换过程是可逆的. 若有 ,则逆变换
。
所以有 I44BATABT A B0R BP 1AO BA0R AP 1BO
A BR0BAR
A BRAPB1OBPAO
►3.1 刚体的位姿描述 ►3.2 坐标变换 ►3.3 齐次坐标和齐次变换 ►3.4 变换方程和欧拉角 ►3.5 机器人运动学的正问题和逆问题
3.1 刚体的位姿描述
一、位姿的定义
刚体参考点的位置(坐标系的位置)和刚体的姿态统称为刚体的位姿。
(为描述机器人本身的各个连杆之间.机器人和环境之间的运动关系,将
n
n o a
手爪的方位由旋转矩阵R规定。
R n
o
a
手爪的位置由位置矢量 p
规定。
代表手p 爪坐标系的原点。
则手爪的位姿可由四个矢量
来 来描述。
noa p
记为:
T n o a p
3.2 坐标变换
定义:由于空间中任意点P在不同坐标系中的描述不同,所以需要 研究从一个坐标系的描述到另一个坐标系的描述之间的变换关,通 常称为坐标变换。
{S}代表工作站(操作台)坐标系(工作站框)
{G}代表目标坐标系(目标框) 它们之间的位姿关系用相应的齐次变换来描述。图3-6 机器人与环境坐标系
B S
T描述工作站框{S}相对于基座{B}的位姿,
S G
T描述目标框{G}相对于工作站{S}的位姿。
对物体进行操作时(搬运或装配机器人),工具框{T}相对目标框{G} 的位姿 直接GT T 影响操作效果。 是机GT T器人控制和轨迹规划的对象。
=
相对于固定坐标系运动 相对于活动坐标系运动
2.变换过程的可逆性
齐次坐标变换过程是可逆的. 若有 ,则逆变换
。
所以有 I44BATABT A B0R BP 1AO BA0R AP 1BO
A BR0BAR
A BRAPB1OBPAO
机器人学导论--ppt课件可编辑全文

关节变量
ppt课件
2
1.2 描述:位置、姿态和坐标系
位置描述
一旦建立坐标系,就能用一
个3*1的位置矢量对世界坐标 系中的任何点进行定位。因 为在世界坐标系中经常还要 定义许多坐标系,因此在位 置矢量上附加一信息,标明 是在哪一坐标系中被定义的。
例如:AP表示矢量P在A坐标系中的表示。
BP 表示矢量P在B坐标系中的表示。
c os90
c os120 c os30 c os90
XB XA
X
B
YA
X B Z A
c os90 c os90 cos0
]
YB X A YB YA YB Z A
ZB XA
ZB
YA
ZB Z A
ppt课件
5
坐标系的变换
完整描述上图中操作手位姿所需的信息为位置和姿态。机器人学中
在从多重解中选择解时,应根据具体情况,在避免碰撞的前 提下通常按“最短行程”准则来选择。同时还应当兼顾“多 移动小关节,少移动大关节”的原则。
ppt课件
23
4 PUMA560机器人运动学反解-反变换法
❖ 由于z4 , z5, z6 交于一点W,点W在基础坐标系中的位置仅与 1,2,3
有关。据此,可先解出 1,2,3 ,再分离出 4 ,5,6 ,并逐
PUMA560变换矩阵
ppt课件
21
将各个连杆变换矩阵相乘便得到PUMA560手臂变换矩阵
06T 01T (1)21T (2 )23T (3 )34T (4 )45T (5 )56T (6 )
什么是机器人运动学正解? 什么是机器人运动学反解?
ppt课件
22
操作臂运动学反解的方法可以分为两类:封闭解和数值解、 在进行反解时总是力求得到封闭解。因为封闭解的计算速度 快,效率高,便于实时控制。而数值法不具有些特点为。 操作臂的运动学反解封闭解可通过两种途径得到:代数解和 几何解。 一般而言,非零连杆参数越多,到达某一目标的方式也越多, 即运动学反解的数目也越多。
机器人运动学ppt
2章 ロボットの運動学
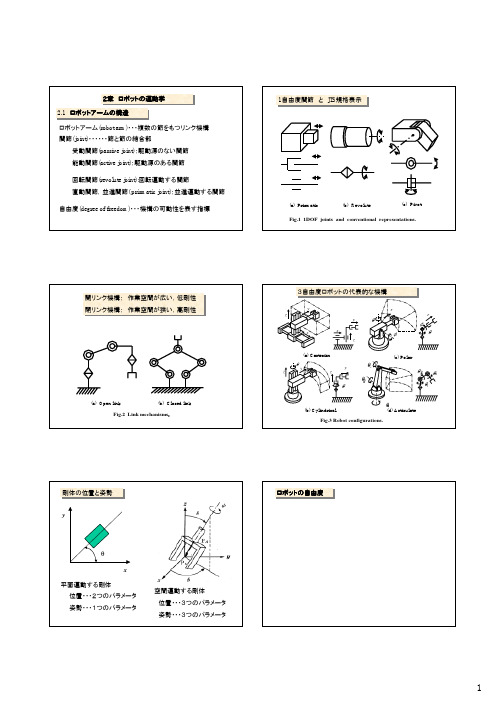
2章 ロボットの運動学2.1 ロボットアームの構造ロボットアームの構造
2.1 ロボットアームの構造ロボットアームの構造ロボットアーム(robot arm)・・・複数の節をもつリンク機構1自由度関節 と JIS 規格表示
1自由度関節 と JIS 規格表示開リンク機構: 作業空間が広い,低剛性閉リンク機構: 作業空間が狭い,高剛性
開リンク機構: 作業空間が広い,低剛性閉リンク機構: 作業空間が狭い,高剛性r
y
3自由度ロボットの代表的な機構
3自由度ロボットの代表的な機構剛体の位置と姿勢剛体の位置と姿勢ロボットの自由度
ロボットの自由度
空間リンク機構(ロボット)の可動度(mobility)
空間リンク機構(ロボット)の可動度(mobility)平面運動機構の自由度と可動度の例
平面運動機構の自由度と可動度の例パラレルリンク機構の自由度と可動度
パラレルリンク機構の自由度と可動度ロボットの座標系(coordinate system)
ロボットの座標系(coordinate system)座標系の平行移動
座標系の平行移動座標系の回転移動
座標系の回転移動
座標系の平行移動と回転移動座標系の平行移動と回転移動
z A
姿勢表現・・・zyzオイラー角
姿勢表現・・・zyzオイラー角
姿勢表現・・・ロール・ピッチ・ヨウ角(zyxオイラー角)姿勢表現・・・ロール・ピッチ・ヨウ角(zyxオイラー角)
z。
第七章 机器人运动学ppt课件

Ai Ai-1
编辑版pppt
8
➢ 杆件参数的定义—— 、li 、 i 和di i
由运动学的观点来看,杆件保持其两端关节间的形态
不变,这种形态由两个参数决定:杆件长度 li 和杆件扭
转角 i 。杆件的相对位置关系,由另外两个参数决定:
杆件的距离 di 和杆件的回转角 i 。
li — 关节 Ai 轴和 Ai+1 轴线公法线的长度。
li
i zi
yi
xi oi
绕 xi 轴转 i 角度,两
坐标系完全重合.
li 1
di
zi1 oi1
yi1
i
xi1
i 1 A i R ( z i 1 ,i ) T r a n s ( z i 1 , d 编i ) 辑T 版pr ppa t n s ( x i , l i ) R ( x i ,i )
机器人技术及空间应用
第七章 机器人运动学
机器人运动学主要是把机器人相对于固定参考 系的运动作为时间的函数进行分析研究,而不 考虑引起这些运动的力和力矩 将机器人的空间位移解析地表示为时间的函数, 特别是研究机器人关节变量空间和机器人末端 执行器位置和姿态之间的关系 本章将讨论机器人运动学几个具有实际意义的 基本问题。
• 并联机器人:刚性好,负载大,误差不积累,工作空间 小,姿态范围不大。
• 本章讲解以串联机器人为主。
编辑版pppt
3
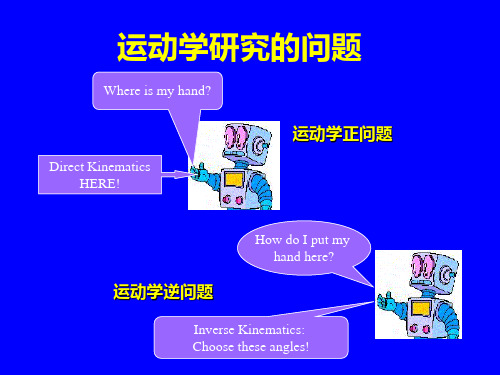
§7.1.2 运动学研究的问题
Where is my hand?
Direct Kinematics HERE!
运动学正问题
运动学逆问题
How do I put my hand here?
ny
z
n0x
编辑版pppt
8
➢ 杆件参数的定义—— 、li 、 i 和di i
由运动学的观点来看,杆件保持其两端关节间的形态
不变,这种形态由两个参数决定:杆件长度 li 和杆件扭
转角 i 。杆件的相对位置关系,由另外两个参数决定:
杆件的距离 di 和杆件的回转角 i 。
li — 关节 Ai 轴和 Ai+1 轴线公法线的长度。
li
i zi
yi
xi oi
绕 xi 轴转 i 角度,两
坐标系完全重合.
li 1
di
zi1 oi1
yi1
i
xi1
i 1 A i R ( z i 1 ,i ) T r a n s ( z i 1 , d 编i ) 辑T 版pr ppa t n s ( x i , l i ) R ( x i ,i )
机器人技术及空间应用
第七章 机器人运动学
机器人运动学主要是把机器人相对于固定参考 系的运动作为时间的函数进行分析研究,而不 考虑引起这些运动的力和力矩 将机器人的空间位移解析地表示为时间的函数, 特别是研究机器人关节变量空间和机器人末端 执行器位置和姿态之间的关系 本章将讨论机器人运动学几个具有实际意义的 基本问题。
• 并联机器人:刚性好,负载大,误差不积累,工作空间 小,姿态范围不大。
• 本章讲解以串联机器人为主。
编辑版pppt
3
§7.1.2 运动学研究的问题
Where is my hand?
Direct Kinematics HERE!
运动学正问题
运动学逆问题
How do I put my hand here?
ny
z
n0x
机器人技术基础课件第三章 机器人运动学

T = f(qi) 其中,T为机器人末端执行器的位姿,qi为机器人各个关 节变量。若给定qi,要求确定相应的T,称为正运动学问题 。
30
3.2.1 机器人正运动学方程
如图所示是个三自由度的机器人, 三个关节皆为旋 转关节,第3关节轴线垂直于1、2关节轴线所在的平 面,各个关节的旋转方向如图所示,用D-H方法建立 各连杆坐标系,求出该机器人的运动学方程。
刚体的姿态可由动坐标系的坐
标的轴刚 位方置体向可Q在来用固表齐定示次坐。坐标令标系n形、O式oX、的YZa一中分
别为X′、y ′、z ′坐标轴的 个(4×1)列阵表示为: 单位方向矢量,每个单位方向 矢量在固定坐标系上的分量为 动坐标系各坐标轴的方向余弦, 用齐次坐标形式的(4×1)列阵 分别表示为:
y L1 sin1 L2 sin(1 2 )
通常的矢量形式:
r f ( )
29
3.2.1 机器人正运动学方程
机器人正运动学将关节变量作为自变量,研究机器人末 端执行器位姿与基座之间的函数关系。总体思想是:
(1)给每个连杆指定坐标系; (2)确定从一个连杆到下一连杆变换(即相邻参考系 之间的变化); (3)结合所有变换,确定末端连杆与基座间的总变换 ; (4)建立运动学方程求解。 机器人运动学的一般模型为:
03T 01T12T 23T
如此类推,对于六连杆机器人,有下列矩阵:
06T 01T12T 23T 34T 45T 56T
3.2 3.2 机械手运动学方程
26
0 6
T
3.1.4 连杆变换矩阵及其乘积
06T 01T12T23T34T 45T56T
机器人运动学方程
此式右边表示了从固定参考系到手部坐标系的各连杆
30
3.2.1 机器人正运动学方程
如图所示是个三自由度的机器人, 三个关节皆为旋 转关节,第3关节轴线垂直于1、2关节轴线所在的平 面,各个关节的旋转方向如图所示,用D-H方法建立 各连杆坐标系,求出该机器人的运动学方程。
刚体的姿态可由动坐标系的坐
标的轴刚 位方置体向可Q在来用固表齐定示次坐。坐标令标系n形、O式oX、的YZa一中分
别为X′、y ′、z ′坐标轴的 个(4×1)列阵表示为: 单位方向矢量,每个单位方向 矢量在固定坐标系上的分量为 动坐标系各坐标轴的方向余弦, 用齐次坐标形式的(4×1)列阵 分别表示为:
y L1 sin1 L2 sin(1 2 )
通常的矢量形式:
r f ( )
29
3.2.1 机器人正运动学方程
机器人正运动学将关节变量作为自变量,研究机器人末 端执行器位姿与基座之间的函数关系。总体思想是:
(1)给每个连杆指定坐标系; (2)确定从一个连杆到下一连杆变换(即相邻参考系 之间的变化); (3)结合所有变换,确定末端连杆与基座间的总变换 ; (4)建立运动学方程求解。 机器人运动学的一般模型为:
03T 01T12T 23T
如此类推,对于六连杆机器人,有下列矩阵:
06T 01T12T 23T 34T 45T 56T
3.2 3.2 机械手运动学方程
26
0 6
T
3.1.4 连杆变换矩阵及其乘积
06T 01T12T23T34T 45T56T
机器人运动学方程
此式右边表示了从固定参考系到手部坐标系的各连杆
工业机器人第二章 工业机器人运动学PPT课件

0T 0T 6A 1A 2A 3A 4A 5A 6
Z0 Z2
Z1
Z2 Z1 Z0
Z4 Z3
Z6 Z5
反向运动学
❖ 反向求解
——在已知手部要达到的目标位姿的情况下求 出各关节变量,以驱动各关节马达,使手部位 姿得到满足。
❖ 机器人运动学逆解问题求解存在若干问题:
解可能不存在; 存在多重解; 求解方法的多样性—分离变量法/直接求解法。
Z2 c2 0 0s2 01 0Y3 0
Z1
s2
0
0
0 1 0
00c2
0
X3
0
0Z2
d2 X2 1
0
1
Y2
A2
A3
A6 Rot (Zz3 5 ,6 )TranZs4 (0,0, H
Z6
X4
Y4
Z3
Z5
Z4
A4
c6
s5Rco6tX3(
s6
Yc3 5s6
z3 ,csZ654 4s)6
Xb
XP-Lcαcβ
Yb = YP-L(sαcγ +cαsβsγ)
(5)
Zb
ZP-L(sαsγ -cαsβcγ)
分析该机构特点,得Xa≡L, Yb≡L, Zc≡L,可建立该机构的位姿约束方程:
XP-Lsβ-L = 0
YP-L(sαcγ +cαsβsγ) -L= 0
(6)
ZP-L(cαsγ +sαsβcγ) -L= 0
A3
s
3
0
c 3 0
0
0
0
1
0
0
1 00 0 1 0
0
0
0
1
0
0
Z0 Z2
Z1
Z2 Z1 Z0
Z4 Z3
Z6 Z5
反向运动学
❖ 反向求解
——在已知手部要达到的目标位姿的情况下求 出各关节变量,以驱动各关节马达,使手部位 姿得到满足。
❖ 机器人运动学逆解问题求解存在若干问题:
解可能不存在; 存在多重解; 求解方法的多样性—分离变量法/直接求解法。
Z2 c2 0 0s2 01 0Y3 0
Z1
s2
0
0
0 1 0
00c2
0
X3
0
0Z2
d2 X2 1
0
1
Y2
A2
A3
A6 Rot (Zz3 5 ,6 )TranZs4 (0,0, H
Z6
X4
Y4
Z3
Z5
Z4
A4
c6
s5Rco6tX3(
s6
Yc3 5s6
z3 ,csZ654 4s)6
Xb
XP-Lcαcβ
Yb = YP-L(sαcγ +cαsβsγ)
(5)
Zb
ZP-L(sαsγ -cαsβcγ)
分析该机构特点,得Xa≡L, Yb≡L, Zc≡L,可建立该机构的位姿约束方程:
XP-Lsβ-L = 0
YP-L(sαcγ +cαsβsγ) -L= 0
(6)
ZP-L(cαsγ +sαsβcγ) -L= 0
A3
s
3
0
c 3 0
0
0
0
1
0
0
1 00 0 1 0
0
0
0
1
0
0
《机器人运动学》课件

机器人正向运动学建模
正向运动学
根据机器人关节参数,计算机器人末端执行器在笛卡尔坐标 系中的位置和姿态的过程。
正向运动学模型
描述机器人末端执行器位置和姿态与关节参数之间关系的数 学模型。
机器人逆向运动学建模
逆向运动学
已知机器人末端执行器在笛卡尔坐标系中的位置和姿态,求解机器人关节参数 的过程。
逆向运动学模型
02
它主要关注机器人在三维空间中 的位置和姿态,以及如何通过关 节运动来实现这些位置和姿态的 变化。
机器人运动学的研究内容
机器人位姿表示
研究如何用数学表达式表示机 器人在三维空间中的位置和姿
态。
运动学方程
建立机器人末端执行器位姿与 关节状态之间的数学关系,即 运动学方程。
运动学逆解与正解
研究如何通过给定的位姿求解 关节状态(逆解),以及如何 通过给定的关节状态求解位姿 (正解)。
关节坐标系
基于机器人关节建立的坐标系,常用于描述机器 人的关节运动状态。
工作坐标系
基于机器人工作需求建立的坐标系,常用于描述 机器人末端执行器的位置和姿态。
CHAPTER 03
机器人运动学建模
齐次变换与坐标变换
齐次变换
描述空间中物体位置和方向变化的数 学工具,包括平移和旋转。
坐标变换
将一个坐标系中的位置和方向信息转 换到另一个坐标系中的过程,涉及到 齐次变换的应用。
关节空间的轨迹规划
定义
关节空间是指机器人的各个关节角度 构成的坐标系,关节空间的轨迹规划 是指通过控制机器人的关节角度来实 现机器人的运动。
方法
常用的方法包括多项式插值、样条曲 线插值等,通过设定起始和目标位置 的关节角度,计算出一条平滑的关节 角度路径。
第三章机器人运动学PPT课件
用一组关节变量(di或i)来描述。这组变量通常称为关节矢量或关节坐标,
由这些矢量描述的空间称为关节空间。
• 正向运动学:关节空间末端笛卡儿空间,单射 • 逆向运动学:末端笛卡儿空间关节空间,复射
不同的关节空间,相同的 末端笛卡儿空间
关节空间与末端笛卡儿空 间映射关系
第三章 机器人的运动学
3.1 工业机器人运动学
,它的齐
次坐标就是
,即满足Px=ωPx/ω,Py=ωPy/ω,
Pz=ωPz/ω(ω是非零整数)。可以看出,在三维直角坐标系中,
由于ω取值的不同,一个点的齐次坐标的表达不唯一。
齐次坐标不仅可以规定点的位置(ω为非零整数),还可以
用来规定矢量的方向(第四个元素为零时)。列向量
(
)表示空间的无穷远点,a,b和c称为它的方向
单位主矢量相对于坐标系{A}的方向余弦组成:
xB
yB
zB
xA
yA
zA
其中:co scoxB s ,xA ()
既表示了刚体F在{A}系中的方位,也描述了{B}系在{A}系中的 姿态。
3.1.2.2 坐标变换
一、坐标平移
如图3-5,坐标系{B}与{A} 方向相同,但原点不重合。
图3-5 坐标平移
此式称为平移方程。其中 是B系中的原点在A系中的表示。
0
0
0
1
1
1
给定坐标系{A},{B}和{C},已知{B}相对{A}的描述为 ,
{C}相对{B}的描述为
AP A BTBP BPC BTCP APC ATCP
,则有
APA BTC BTCP
CATABTCBT
从而定义复合变换
。
同理得出:
由这些矢量描述的空间称为关节空间。
• 正向运动学:关节空间末端笛卡儿空间,单射 • 逆向运动学:末端笛卡儿空间关节空间,复射
不同的关节空间,相同的 末端笛卡儿空间
关节空间与末端笛卡儿空 间映射关系
第三章 机器人的运动学
3.1 工业机器人运动学
,它的齐
次坐标就是
,即满足Px=ωPx/ω,Py=ωPy/ω,
Pz=ωPz/ω(ω是非零整数)。可以看出,在三维直角坐标系中,
由于ω取值的不同,一个点的齐次坐标的表达不唯一。
齐次坐标不仅可以规定点的位置(ω为非零整数),还可以
用来规定矢量的方向(第四个元素为零时)。列向量
(
)表示空间的无穷远点,a,b和c称为它的方向
单位主矢量相对于坐标系{A}的方向余弦组成:
xB
yB
zB
xA
yA
zA
其中:co scoxB s ,xA ()
既表示了刚体F在{A}系中的方位,也描述了{B}系在{A}系中的 姿态。
3.1.2.2 坐标变换
一、坐标平移
如图3-5,坐标系{B}与{A} 方向相同,但原点不重合。
图3-5 坐标平移
此式称为平移方程。其中 是B系中的原点在A系中的表示。
0
0
0
1
1
1
给定坐标系{A},{B}和{C},已知{B}相对{A}的描述为 ,
{C}相对{B}的描述为
AP A BTBP BPC BTCP APC ATCP
,则有
APA BTC BTCP
CATABTCBT
从而定义复合变换
。
同理得出:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cosθ - sinθ 0 0
Tz,θ = sinθ cosθ 0 0 Ttran =
0
0 10
0
0 01
1 0 0 dx 0 1 0 dy
0 0 1 dz
0 001
Pxyz = T Puvw
.
16
课前提问:
(1)什么是机器人运动学的正问题和逆问题? (2)机器人的坐标变换矩阵的一般形式是什
么? (3)连续的变换矩阵,什么情况下依次左乘、
= 旋转矩阵3×3 位置矢量3×1
O1×3
1
.
15
若三维空间的位置矢量P表示成齐次坐标,即
P = px py pz 1 T ,
10
00
cosβ 0 sinβ 0
Tx,α = 0 cosα - sinα 0 0 sinα cosα 0
Ty,β = 0
1 00
- sinβ 0 cosβ 0
00
01
0 0 01
什么情况下依次右乘? (4)什么是齐次坐标和齐次变换?
.
17
§2.3 机器人运动学正问题
(The Forward Kinematic Problem)
Denavit – Hartenberg ( D - H )表示法
.
18
1.坐标系的建立:
n关节机器人需建立n+1个坐标系,其中参
考(机座) 坐标系为O0x0y0z0,,机械手末端的坐 标系为Onxnynzn
.
12
例题:求表示绕Oy轴转φ角,然后绕Ow 轴转θ角,再绕Ou轴转α角的合成旋转 矩阵。
R Ry, Rw, Ru,
c 0 s c s 01 0 0
0
1
0 s
c
00
c
s
s0 0 c 0 0 10 s c
cc
s
sc
ss csc cc
ssc cs
css sc
cs
cc sss
.
2
§2.1 引 言(The Introduction)
➢ 机器人运动学 正问题:定义 逆问题:定义
➢ 机器人动力学
.
3
基本概念(The Basic Concepts)
自由度:物体能够对坐标系进行独立运动的
数目称为自由度(DOF, degree of freedom)。
刚体具有6个自由度
➢ 三个旋转自由度 R1, R2, R3 ➢ 三个平移自由度T1, T2, T3
.
13
例题:坐标系{B}的初始位姿与参考坐
标系{A}相同,坐标系{B} 相对于{A}的 zA轴旋转30,再沿{A}的xA轴移动12,沿 {A}的yA轴移动6。求旋转矩阵。
解:
c30 s30 0 0.866 0.5 0
R
R(z,
30
)
s30
c30
0
0.5
0.866 0
0
0 1 0
0 1
将上式写成矩阵形式:
Px = ix ˙iu ix ˙jv ix ˙kw Pu Py = iy˙iu iy ˙jv iy ˙kw Pv Pz = iz˙iu iz ˙jv iz ˙kw Pw
Pxyz=R Puvw
同样,也有Puvw=QPxyz, Q=R-1 =RT
.
9
如果Ouvw坐标系统绕Ox轴转动α角,变换矩阵Rx, α称为 绕Ox轴转动α角的旋转矩阵,此时ix=iu ,
.
14
二、齐次坐标和变换矩阵
齐次坐标是用n +l 维坐标来描述n维空间中的位置,其 第n+1个分量(元素) ω称为比例因子。
P=(ωPx, ωPy , ωPz , ω)T
在机器人学的应用中,一般将比例因子取为1。
机器人系统运动分析中,齐次变换矩阵写成以下形式:
T=
R3×3 P3×1 O1×3 I1×1
创新设计作业:
设计一种类人教学机器人。要求机器人具有类似人的四肢, 单片机控制。给出总体的设计方案、机械结构和传动方案、 选择合适的传感器、控制方案。
.
1
第2章 机器人运动学 (Kinematics of Robots)
➢ 引言 ➢ 机器人位置与姿态的描述 ➢ 机器人运动学正问题 ➢ 机器人运动学逆问题 ➢ 机器人的雅可比矩阵
.
7
一、机器人坐标系变换(Coordinate Transformation)
Ouvw :Puvw=(Pu , Pv , Pw)T Oxyz :Pxyz=(Px , Py , Pz)T
当Ouvw坐标系绕一轴线转动后,
均可通过一个3x3旋转矩阵R
将原坐标Puvw变换到Oxyz系中 的坐标Pxyz ,
即: Pxyz=R Puvw
.
8
由矢量分量的定义有:Puvw= pu iu + pv jv + pw kw
pu、pv、pw分别表示P沿Ou、Ov、Ow 轴的分量
Px = ix˙P = ix ˙iu pu+ ix ˙jv pv+ix ˙kw pw Py = iy˙P = iy˙iu pu+˙iu pu+ iz ˙jv pv+iz ˙kw pw
Z R3
T3
T2
Y
T1
R2
X R1
.
4
机动度:Degree of Mobility
关节:Joint
连杆:Link
自由度由机动度构成,
23 4
机动度不一定是自由度. 1
5
5个机动度,2个自由度
.
5
§2.2 机器人位置与姿态的描述 (The Description of Position and Posture)
ix ˙iu ix ˙jv ix ˙kw 1 0 0
Rx, α = iy˙iu iy ˙jv iy ˙kw = 0 cosα - sinα
iz˙iu iz ˙jv iz ˙kw
0 sinα cosα
向量点乘:a· b=|a|·|b| · cos(a)
.
10
类似地,绕Oy 轴转动φ角和绕Oz 轴转θ角的3×3旋转矩阵分别为,
cosφ 0 sinφ
Ry, φ = 0
10
- sinφ 0 cosφ
cosθ -sinθ 0
Rz, θ = sinθ cosθ 0
0
01
矩阵Rx, α、Ry, φ和Rz, φ称为基本旋转矩阵。
任何旋转变换可以由有限个基本旋转变换合成得到。
.
11
依次左乘(如果uvw对xyz旋转)
依次右乘(如果uvw绕自己的坐标轴旋转) R=Rz,θRy,φRx,α
z
0
Z 0Tn
y
E
B
•
x
G
一个物体与机械手
.
6
位置与姿态的表示
位置描述:位置矢量(position vector)
直角坐标系{A}, 位置矢量Ap
矩阵表示
px
zA p
A
p
py
Ap
pz
oA
yA
矢量和表示
xA
A p pxi py j pzk
矢量的模 p px2 py2 pz2 ,单位矢量
