等腰三角形的性质优质课课件
等腰三角形的性质(八下优质课件)

等边对等角 三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底 边上的高和中线才有这一性 质.而腰上高和中线与底角 的平分线不具有这一性质.
∵AB=AC, ∠1=∠2(已知),
12
∴BD=CD,AD⊥BC(等腰三角形三线合一). B D C
∵AB=AC, BD=CD (已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一).
∵AB=AC, AD⊥BC(已知), ∴BD=CD, ∠1=∠2(等腰三角形三线合一).
典例精析
例1 如图,在△ABC中 ,AB=AC,点D在AC上, 且BD=BC=AD,求△ABC各角的度数.
角∠BAC的角平分线、底边BC上的高线 .
总结归纳
定理:等腰三角形的两个底角相等(等边对等角).
如图,在△ABC中, ∵AB=AC(已知), ∴∠B=∠C(等边对等角).
A
B
C
推论:等腰三角形顶角的平分线、底边上的中线及 底边上的高线互相重合(三线合一).
证明后的结论,以后可以直接运用.
A 综上可得:如图,在△ABC中,
(1)若AD=AE,求证:BD=CE;
(2)若BD=CE,F为DE的中点,如图②,求证:
AF⊥BC.
A
A
B
D GE
B C
DF E
C
图①
图②
解析:(1)过A作AG⊥BC于G,根据等腰三角形的性质
得出BG=CG,DG=EG即可证明;(2)先证BF=CF,
再根据等腰三角形的性质证明.
A
A
B
D GE
B C
1.两点确定一条直线;
2.两点之间线段最短; 3.同一平面内,过一点有且只有一条直线与已知直线
等腰三角形全国优质课一等奖完美PPT课件

直角三角形相关知识回顾
直角三角形的定义
有一个内角为90°的三角形 称为直角三角形。
2024/1/28
直角三角形的性质
直角三角形的两个锐角互 余,斜边是直角三角形的 最长边,且满足勾股定理 。
直角三角形的判定
若一个三角形满足有一个 内角为90°或满足勾股定理 ,则该三角形为直角三角 形。
21
相似三角形相关知识拓展
02
若一个三角形中有一个角为90度 ,且这个三角形的两条直角边相 等,则这个三角形是等腰直角三 角形。
13
其他特殊情况下判定方法
若一个三角形的三条边满足勾股定理, 即其中两条边的平方和等于第三条边的 平方,则这个三角形是直角三角形。若 此时直角边相等,则为等腰直角三角形
。
2024/1/28
若一个三角形的三条边满足 a:b:c=1:1:√2的关系(a、b为直角边, c为斜边),则这个三角形是等腰直角
顶角与底角的关系
顶角的度数是底角度数的两倍,即顶角 = 2 × 底 角。
3
高、中线与角平分线的关系
在等腰三角形中,高、中线和顶角的角平分线互 相重合。
2024/1/28
9
等腰三角形性质总结
对称性
等腰三角形是Hale Waihona Puke 对称图形,对 称轴是底边的垂直平分线。
2024/1/28
边角关系
在等腰三角形中,两底角相等 ,且顶角的度数是底角度数的 两倍。
3
课程背景与意义
三角形是初中数学的重要内容 ,等腰三角形作为特殊三角形 ,具有独特的性质和广泛的应 用。
2024/1/28
学习等腰三角形有助于学生理 解三角形的基本性质,掌握证 明方法,提高几何推理能力。
等腰三角形课件ppt

边与角的相互影响
边长变化对角度的影响
当等边的长度增加或减少时,底角α的大小会发生变化。这是因为角度α与基边的长度成 反比。
角度变化对边长的影响
当底角α的大小发生变化时,基边的长度也会相应地增加或减少。这是因为角度的变化会 影响到三角形的周长,从而影响基边的长度。
Part
03
等腰三角形的判定与证明
04
等腰三角形的面积与周长
面积的计算
1 2
面积公式
等腰三角形的面积可以通过底边长度和对应的高 来计算,公式为 (S = frac{1}{2} times text{底边 长度} times text{高})。
面积与底边和高
等腰三角形的面积与底边长度和高有关,当底边 长度和高发生变化时,面积也会相应地变化。
等腰三角形与勾股定理
总结词
勾股定理是几何学中的重要定理之一 ,它可以应用于等腰三角形,特别是 等腰直角三角形。
详细描述
勾股定理表明在一个直角三角形中, 直角边的平方和等于斜边的平方。对 于等腰直角三角形,两条直角边长度 相等,因此它们的平方和等于斜边的 平方。
详细描述
等腰三角形是两边相等的三角形,根据等腰三角形的性质,两个底角相等,并且 三角形的内角和为180度,因此每个底角的大小为(180度 - 顶角度数)/ 2。
等腰三角形的外角和定理
总结词
等腰三角形的外角和定理表明等腰三角形的一个外角等于它 不相邻的两个内角之和。
详细描述
根据三角形外角定理,一个三角形的外角等于它不相邻的两 个内角之和,对于等腰三角形来说,由于两个底角相等,所 以一个底角的外角等于另一个底角。
等腰三角形课件
• 等腰三角形的定义与性质 • 等腰三角形的边与角 • 等腰三角形的判定与证明 • 等腰三角形的面积与周长 • 等腰三角形的拓展知识
13. 等腰三角形的性质 PPT课件(华师大版)

等腰三角 形的顶角平分线AD,然
后证明△ABD≌ △ACD.
证明:画∠ABC的平分线AD. 在 △ABD和 △ACD中, ∵ AB=AC (已知), ∠ 1 = ∠ 2(角平分线的定义), AD =AD (公共边), ∴ △ABD≌ △ACD(S.A.S.). ∴ ∠B=∠C(全等三角形的对应角相等)•
2.等腰三角形“三线合一”的性质常常可以用来证明角相 等、线段相等和线段垂直.在遇到等腰三角形的问题 时, 尝试作这条辅助线,常常会有意想不到的效果.
例4 如图 13.3.4,在△ABC中, AB=AC ,D是BC 边上的中点, ∠B =30°.求 :
(1)∠ADC的大小; (2)∠1的大小. 解: (1)∵ AB=AC ,BD=DC (已知),
3 (中考·丹东)如图,在△ABC中,AB=AC,∠A=30° ,E为BC的延长线上一点,∠ABC与∠ACE的平 分线交于点D,则∠D的度数为( ) A.15° B.17.5° C.20° D.22.5°
知识点 2 等腰三角形的轴对称性:三线合一
探索
由前面的“做一做”,你还可以发现什么结论?请 写 出你的发现:
例2 已知:在△ABC中, AB=AC , ∠B =80°.求 ∠C和∠A的大小.
解: ∵ AB=AC (已知), ∴ ∠C=∠B = 80°(等边对等角). 又∵ ∠A + ∠B + ∠C = 180°(三角形的内角和 等于 180 °), ∴ ∠A = 180 °- ∠B - ∠C (等式的性质) = 180°- 80°- 80°= 20°.
做
一
做
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角 形的大小和形状可以不一样,如图13.3.2,把纸片对折,让
人教版数学等腰三角形的性质公开课PPT课件
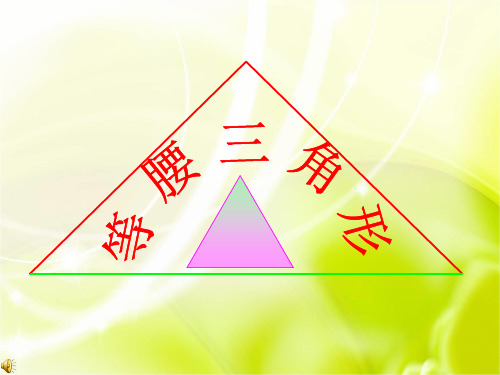
性质2 等腰三角形的顶角平分线与底边上的中线, 底边上的高互相重合. (简写成“三线合一” )
几何语言:
A
(1)∵ AB=AC, AD⊥BC,
∴∠ 1 = ∠ 2 , BD = CD .
12
(2) ∵ AB=AC, BD=CD,
∴ AD ⊥ BC ,∠ 1 =∠ 2 .
∟
(3) ∵ AB=AC, ∠1= ∠ 2,
谢 谢 指 导!
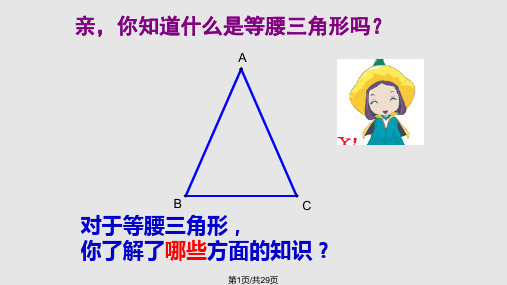
如图,AOB是一钢架,且∠AOB=10°,为使钢
架更加坚固,需在其内部添一些钢管EF、FG、 GH……,添加的钢管长度都与OE相等,则∠M
HA = 50 °,最多能添加这样的钢管8 根。
B
G
M
40° 60°
60°808°0°
E
20° 40°
20°
10°
10° 30°
30° 50° 50°70°70°90°
13.3.1 等腰三角形(第1课时)
如图所示,把一张长方形的纸按图中虚线对折,然 后画出一条裁剪线,并剪去阴影部分,再把它展开,得 到的△ABC 有什么特点?
底角 腰
B
A
D
底 边
顶角
C
腰
底角
定义:有两边相等的三角形,叫做等腰三角形.ຫໍສະໝຸດ 在△ABC 中,AB=AC
把剪出的等腰三角形ABC 沿折痕对折,找出其中相等
体验了什么数学思想? 分类思想 方程思想
想进一步研究的问题是
A
.................
B
C
等边三角形
如图,点B,D,E,C在同一直线上,AB=AC , AD=AE. 求证:BD=CE.
A
方法:求有关等腰三角 形的问题,作顶角平分 线、底边中线,底边的 高是常用的辅助线
等腰三角形性质PPT课件
M
7A
E
2
10°
1
3
6
4
5
8
O
F
H
B
老师,这个题我明白了,会做了!
第27页/共29页
(1)本节课里你学到了什么???
有两边相等的三角形 概念
腰、底、顶角、底角 等腰三角形
性质 等边对等角 三线合一
(2)等腰三角形中常作的辅助线: 作顶角的平分线、底边上的高或底边上的中线
第28页/共29页
感谢您的观看!
所以这个三角形的边为4 ,4 ,2
第25页/共29页
5.如图,AOB是一钢架,且∠AOB=10°, 为使钢架更加坚固,需在其内部添一些钢管EF、FM、 MH……,添加的 钢管长度都与OE相等, 添加这样的钢管4根时,则∠AHB 的度数为___5_0_°_
M
A
E
10°
O
F
H
B
第26页/共29页
如图,AOB是一钢架,且∠AOB=10°, 为使钢架更加坚固,需在其内部添一些钢管EF、FM、 MH……,添加的 钢管长度都与OE相等, 添加这样的钢管4根时,则∠AHB的度数为__5_0_°__
如图,在下列等腰三角形中, 分别求出其它两个角的度数。
A
A
36°
120°
B
30°
72° 72°
B
C
30°
C
第21页/共29页
1.填空题 巩固练习
(1)如果等腰三角形的一个底角为500,则其余 两个角为_8_0_0_和_5_0_0_.
(2)如果等腰三角形的顶角为800,则它的一个 底角为_5_0_0_. (3)如果等腰三角形的一个角为800,则其余两 个角为__8_0_0和__2_0_0___或_5_0_0_和__5_0_0. (4)如果等腰三角形的一个角为1000,则其余两 个角为__4_0_0和__4_0_0_.
等腰三角形的性质PPT授课课件

HK版 八年级上
第三章 声的世界
第2节 声音的特性
第2课时 噪声的防治
习题链接
提示:点击 进入习题
1 噪声;空气 4 dB;不能
答案呈现
7 人耳 10 见习题
2D
5D
8C
3C
6 声源;传播过程 9 B
基础巩固练
8.[中考·山东潍坊]将教室的门窗关闭,室内同学听到的 室外噪声减弱。对该现象说法正确的是( C ) A.室外噪声不再产生 B.噪声音调大幅降低 C.在传播过程中减弱了噪声 D.噪声在室内的传播速度大幅减小
AB=AC,
∵
BD=CD,
AD=AD,
∴△BAD ≌△CAD (SSS).
∠B=∠C.
这样,我们就证明了性质1
感悟新知
归纳
知1-讲
我们可以发现等腰三角形的性质: 性质1 等腰三角形的两个底角相等(简写成“等边 对顶角”.
感悟新知
例 1 如图,在△ABC中,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数.
16 B
答案呈现
17 B 18 见习题 19 见习题
基础巩固练
1.某市已经明令禁止在城区内燃放烟花爆竹,因为燃放 烟花爆竹除了会造成空气污染外,燃放烟花爆竹时的 巨大声音还是一种___噪__声___(填“乐音”或“噪声”),爆 竹的巨大声音是__空__气____的振动产生的。
基础巩固练
7.[安徽霍邱月考]如图所示,在女子10 m气手枪比赛中,射 击时,很多运动员在耳朵里放一个耳塞或戴上耳罩,这 主要是在___人__耳___处减弱噪声。
能力提升练
解:(1)据题可知,“控制音量”是在声源处减弱噪声, 控制的是噪声的响度。
《等腰三角形的性质》优秀课件

全等识别
若两个三角形三边及三角分别相等,则这两个三角形全等。在等腰三角形中, 若两个等腰三角形的底边和腰长分别相等,则这两个等腰三角形全等。
2024/1/26
21
对后续知识点(如圆、三角函数)的铺垫作用
对圆的知识点铺垫
等腰三角形的性质与圆的性质有密切联系。例如,在等腰三角形中,底边上的中垂线同时也是底边所 在圆的直径;此外,在等腰三角形中引入外接圆和内切圆的概念,可以进一步探讨三角形的性质。
SAS全等判定
若两个三角形两边和夹角分别相等,则这两个三 角形全等。
3
HL全等判定(直角三角形)
在直角三角形中,若斜边和一条直角边分别相等 ,则这两个三角形全等。
2024/1/26
5
与其他特殊三角形关系
与等边三角形的关系
等边三角形是特殊的等腰三角形,三 边都相等。
与相似三角形的关系
若两个等腰三角形的顶角和底角分别 相等,则这两个三角形相似。
8
边角关系
等腰三角形中,两个等腰边所 对的两个底角相等,即等边对 等角。
2024/1/26
等腰三角形的顶角平分线、底 边上的中线、底边上的高相互 重合,即“三线合一”。
等腰三角形中,若有一个角是 60度,则这个三角形是等边三 角形。
9
面积计算公式
等腰三角形的面积可以通过以下公式计算
面积 = (底边长度 × 高) / 2。其中,底边长度是两个等腰边所夹的底边的长度, 高是从顶点到底边的垂直距离。
《等腰三角形的性质》 优秀课件
2024/1/26
1
目录
2024/1/26
• 等腰三角形基本概念 • 等腰三角形性质探究 • 等腰三角形在生活中的应用 • 等腰三角形相关定理证明 • 等腰三角形在几何变换中的地位和作用 • 典型例题解析与课堂互动环节
等腰三角形的性质定理ppt课件

为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
例3已知:如图,AD平分∠BAC,∠ADB=∠ADC 求证:AD⊥BC
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
已知:如图,房屋的顶角∠BAC=100 º, 过屋顶A的 立柱AD BC , 屋椽AB=AC. 求顶架上∠B、∠C、 ∠BAD、∠CAD的度数.
A
B
D
C
等腰三角形的性质定理2 等腰三角形的顶角平分线、底边上
的中线和高线互相重合,简称等腰三
角形三线合一
等腰三角形顶角的平分线平分底边并且 垂直于底边.
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
定理解析
定理解析
等腰三角形三线合一
用符号语言表示为: A
在△ABC中
12
(1)∵1 AB=A2C,ABDD⊥BCCD,
∴∠___=∠___,____=____;
(2)∵1 AB=2AC,AADD是中BC线, B ∴∠_=∠_,____⊥____;
D
C
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____.
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
《等腰三角形的性质》优秀课件pptx

定义及特点定义有两边相等的三角形叫做等腰三角形,相等的两边叫做腰,另一边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角。
特点等腰三角形是轴对称图形,有一条对称轴,即底边的垂直平分线;两腰相等,两底角相等。
与等边三角形关系区别等边三角形的三边都相等,三个角都是60度;而等腰三角形只有两边相等,两底角相等,顶角可以是任意角度(小于180度)。
联系等边三角形可以看作是特殊的等腰三角形,即当等腰三角形的顶角为60度时,它就变成了等边三角形。
03在建筑设计中,等腰三角形常被用于构建具有对称美的结构,如尖顶房屋、桥梁的支撑结构等。
建筑学在机械设计和制造中,等腰三角形的稳定性被广泛应用,如三脚架、起重机的支撑结构等。
工程学在解决一些实际问题时,等腰三角形可以作为数学模型,帮助我们理解和解决问题,如测量高度、计算角度等。
数学建模实际应用举例01等腰三角形定义有两边相等的三角形称为等腰三角形。
02两边相等定理内容等腰三角形的两个底角相等。
03定理证明方法通过构造中线或高,利用全等三角形或相似三角形的性质进行证明。
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合,简称“三线合一”。
两角相等定理内容定理证明方法推论通过构造角平分线或中线,利用全等三角形或相似三角形的性质进行证明。
在等腰三角形中,若有一个角是60°,则这个三角形是等边三角形。
030201等腰三角形是轴对称图形,对称轴是底边的垂直平分线。
对称性在等腰三角形中,若两条边相等,则对应的两个角也相等。
对称性推论1在等腰三角形中,若一个角是另一个角的两倍,则这个三角形是直角三角形,且直角在顶角处。
对称性推论2在等腰三角形中,若底边两端点到对称轴的距离相等,则这两个点是底边的两个三等分点。
对称性推论3对称性及其推论两条边相等根据等腰三角形的定义,若一个三角形有两条边长度相等,则该三角形为等腰三角形。
两个角相等等腰三角形的两个底角相等,因此若一个三角形有两个角相等,则可根据此性质判定该三角形为等腰三角形。
等腰三角形的性质教学课件-2024鲜版

在等腰三角形中,有时会出现一些特殊情况,如等边三 角形、直角三角形等。在解题时,要注意这些特殊情况 的处理方法,避免出错。
22
06 解题实例与解析
2024/3/28
23
实例一:利用等腰三角形性质求角度
问题描述:已知等腰三角形的一个底角为30°,求顶角的 度数。
解题步骤
解题思路:根据等腰三角形的性质,两个底角相等,因 此另一个底角也为30°。三角形内角和为180°,因此顶角 度数为180° - 30° - 30° = 120°。
1. 识别等腰三角形,确定底角和顶角的位置。
2. 利用等腰三角形性质,求出另一个底角的度数。 2024/3/28
2024/3/28
证明角相等
等腰三角形的两个底角相 等,这一性质可用于证明 角相等的问题。
辅助线应用
在等腰三角形中,常通过 作高、中线或角平分线等 辅助线,将复杂问题简化 为基本问题。
16
设计中 有着广泛应用,如等腰三 角形的屋顶设计,既美观 又实用。
2024/3/28
等腰三角形的两底角的平分线 相等(两条腰上的中线相等,
两条腰上的高相等)。
等腰三角形底边上的垂直平分 线到两条腰的距离相等。
2024/3/28
9
等腰三角形的对称性
等腰三角形是轴对称图形,对称轴是底边的垂直平分线(或顶角的平分线、底边上 的中线所在的直线)。
对于轴对称图形,如果沿对称轴将它对折,那么两部分就完全重合。因此,在等腰 三角形中,如果沿底边的垂直平分线将它对折,那么两部分就完全重合。
计算机科学
在计算机图形学中,等腰三角形可用 于生成三维模型的基本形状,提高渲 染效率。
国家级优质课 等腰三角形的性质 课件

通过与其他三角形进行比较,让学生 更深入地理解等腰三角形的性质,例 如将等腰三角形与等边三角形进行比 较,找出它们的异同点。
实例教学
通过具体的实例,让学生在实际操作 中掌握等腰三角形的性质,例如让学 生自己制作等腰三角形,观察并总结 其性质。
教学评价与反馈
01
课堂互动评价
通过观察学生在课堂上的表现,评价他们对等腰三角形性质的理解程度
04
等腰三角形与其他三角形的 关系
等腰三角形与直角三角形的关系
总结词
等腰三角形可以转化为直角三角 形
详细描述
在等腰三角形中,作底边上的高 ,将等腰三角形分成两个直角三 角形。利用直角三角形的性质, 可以推导出等腰三角形的性质。
等腰三角形与等边三角形的关系
总结词
等边三角形是特殊的等腰三角形
详细描述
等边三角形的三边相等,每个角都是60度,因此它满足等腰三角形的性质,即两边相等,两底角相等 。
等腰三角形与等角三角形的关系
总结词
等腰三角形不一定是等角三角形
详细描述
等腰三角形只要求两边相等,并不要 求角相等。而等角三角形要求所有角 都相等。因此,不是所有等腰三角形 都是等角三角形。
05
教学方法与技巧
等腰钝角三角形的两条等腰边相等
等腰钝角三角形的两条等腰边长度相等,这是等腰钝角三角形的基本性质。
等腰钝角三角形的钝角对应的边最长
在等腰钝角三角形中,钝角对应的边是最长的,这是由于钝角三角形中的角度和边长关系 所决定的。
等腰钝角三角形的两个锐角都小于90度
在等腰钝角三角形中,除了一个钝角外,还有两个锐角,这两个锐角都小于90度,这是 由于钝角三角形中的角度和边长关系所决定的。
等腰三角形的性质优质课市公开课一等奖省优质课获奖课件
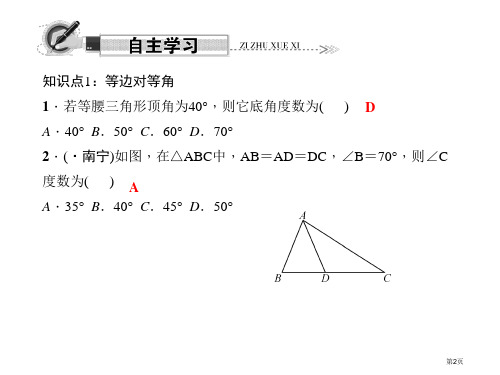
BD=CE.另两种选法可由证三角形全等而得
第10页
16.如图,在等腰三角形ABC中,AB=AC,点D在BC上,且AD=AE. (1)若∠BAC=90°,∠BAD=30°,求∠EDC度数; (2)若∠BAC=α(α>30°),∠BAD=30°,求∠EDC度数; (3)猜测∠EDC与∠BAD数量关系.(无须证实)
第11页
解:(1)∵∠BAC=90°,AB=AC,∴∠B=∠C=12(180°-∠BAC)=45 °,∴∠DAC=∠BAC-∠BAD=90°-30°=60°,∵AD=AE,∴∠
ADE=∠AED=12(180°-∠DAC)=60°,又∵∠ADC=∠B+∠BAD= 45°+30°=75°,∴∠EDC=∠ADC-∠ADE=75°-60°=15°,∴ ∠EDC 的度数是 15°
知识点1:等边对等角 1.若等腰三角形顶角为40°,则它底角度数为( ) D A.40° B.50° C.60° D.70° 2.(·南宁)如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C 度数为( ) A A.35° B.40° C.45° D.50°
第2页
3.如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB= AC,若∠1=20°,则∠2度数为( ) B A.25° B.65° C.70° D.75°
利用等腰三角形性质解题时,考虑不全方面而漏解.
第13页
第4页
知识点2:三线合一
6.等腰三角形是轴对称图形,它对称轴是( C)
A.过顶点直线
B.底边垂线
等腰三角形的性质 课件 公开课一等奖课件

C
底边上的中线,底边上的高互相重合 A 在△ABC中,AB =AC, 点 D在BC上
1、∵AD ⊥ BC 1 2 BD DC 。 ∴∠ 1 = ∠ ,____= 2、∵AD是中线, 1 1 2 2 AD BC 1 2 ∴ ⊥ ,∠ =∠ 。 3、∵AD是角平分线, B BD AD DC BC ∴ ⊥ , = 。 D 等腰三角形是轴对称图形.对称轴是底边上的 中线(顶角平分线,底边上的高)所在直线
• 活动2:探索等腰三角形性质
• 上面剪出的等腰三角形是轴对称图形吗? • 把剪出的等腰三角形ABC沿折痕AD对折,找出其中相等的线 段和角,填入下表
B
重合的线段
A C D
重合的角
AB 和 AC
∠B和 ∠C
和
和
和
和
你能发现等腰三角形有什么性质吗?说一
说你的猜想.
性质1:等腰三角形的 两底角相等。(简写成 “等边对等角” )
C
活动3:等腰三角形性质定理的证明
证明性质1:等腰三角形的两个底角相等 (等边对等角) 。
提问:这性质的条件和结论是什么?用数学符号如何 表达条件和结论?
已知:△ABC中,AB=AC 求证:∠B=C 分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形? 证明:在△ABC中,AB=AC,作底边 BC的中线AD, 在 △ BAD 与△ CAD 中 ∵ AB=___ AC CD BD=___ AD AD=___ B ∴ △ BAD ≌△ CAD( SSS ) ∠C ∠B= ___
青 春 风 采
高考总分:
692分(含20分加分) 语文131分 数学145分 英语141分 文综255分
毕业学校:北京二中 报考高校: 北京大学光华管理学 院 北京市文科状元 阳光女孩--何旋
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A C
D
C
如图,是西安半坡博物馆屋顶的截面图, 如图,是西安半坡博物馆屋顶的截面图,已经知道它 的两边AB AC是相等的 AB和 是相等的. 的两边AB和AC是相等的.建筑工人师傅对这个建筑物 做出了两个判断: 做出了两个判断: 工人师傅在测量了∠ 37°以后,并没有测量∠ ①工人师傅在测量了∠B为37°以后,并没有测量∠C , 就说∠ 的度数也是37 37° 就说∠C 的度数也是37°. 工人师傅要加固屋顶,他们通过测量找到了横梁BC ②工人师傅要加固屋顶,他们通过测量找到了横梁BC 的中点D 然后在AD两点之间钉上一根木桩, AD两点之间钉上一根木桩 的中点D,然后在AD两点之间钉上一根木桩,他们认 为木桩是垂直横梁的. 为木桩是垂直横梁的.
A
1 2 1 2 B C D
思考:
(1)等腰三角形的对称轴怎样回答? 等腰三角形的对称轴怎样回答? 等腰三角形的对称轴怎样回答 等腰三角形是轴对称图形.对称轴是底边上 等腰三角形是轴对称图形 对称轴是底边上 的中线(顶角平分线 底边上的高)所在直线 顶角平分线,底边上的高 的中线 顶角平分线 底边上的高 所在直线 (2)等腰三角形底角的平分线与它所对边上的 等腰三角形底角的平分线与它所对边上的 中线和高线重合么? 中线和高线重合么?
下课了!
等腰三角形的有关概念
A
顶 角
腰
腰
B
C
返回
A 的中线AD 证明: 作△ABC 的中线
则有 BD= CD = 在△ABD和△ACD中 和 AB= AB=AC C B D BD=CD = AD=AD (公共边) = 公共边) ∴ △ABD≌ △ACD (SSS) ≌ ) ∴ ∠B=∠C 全等三角形对应角相等) = (全等三角形对应角相等)
A 的高线AD 证明: 作△ABC 的高线
例1、如图,在△ABC中 ,AB=AC,点D在AC上,且 、如图, 中 , 在 上 BD=BC=AD,求△ABC各角的度数。 各角的度数。 , 各角的度数
A
解:∵AB=AC,BD=BC=AD, AB=AC,BD=BC=AD, ∴∠ABC=∠ ∠ ∴∠ABC=∠C=∠BDC,∠A=∠ABD ABC= , ∠ 等边对等角) (等边对等角 设∠A=x,则∠BDC= ∠A+ ∠ABD=2x, 则 从而∠ 从而∠ABC= ∠C= ∠BDC=2x,
等 腰 三 角 形 的 性 质
心灵手巧
如图:把一张长方形纸片按图中的虚线对折 如图:把一张长方形纸片按图中的虚线对折, 并剪去红线下方的部分,再把它展 并剪去红线下方的部分 再把它展 开,得△ABC 得
B
A C
D
观察
AC和AB有什么关系 这个三角形有什么特点 和 有什么关系 这个三角形有什么特点? 有什么关系?这个三角形有什么特点
C
2x B
⌒ ⌒ ⌒ ⌒ x D 2x
于是在△ 于是在△ABC中,有 中 ∠A+∠ABC+∠C=x+2x+2x=180°, ∠ ∠ ° 解得x=36°, ° 解得
在△ABC中, ∠A=36°,∠ABC=∠C=72° 中 ° ∠ °
4 :△ ABC是等腰直角三角形 是等腰直角三角形 (AB=AC, ∠ BAC=90°), 是底 , °),AD是底 上的高, 边BC上的高,标出∠ B, ∠ C, 上的高 标出∠ , , 的度数? ∠ BAD, ∠ DAC的度数? , 的度数 B 答: ∠ B= ∠ C= ∠ BAD= ∠ DAC=45° ° 5:在△ ABC中,AB=AD=DC, : 中 , ∠BAD=16°,求∠ B和∠ C的度数 ° 和 的度数 答:∠ B= 82° ,∠ C =41° ° ° B A D
∠1=∠2=55 等式性质)。 ∴ ∠1=∠2=550(等式性质)。 ∵AB=AC(已知) (2)在△ABC ∵AB=AC(已知) AD是 ABC的中线 已知) 的中线( 又∵AD是△ABC的中线(已知) AD⊥BC(等腰三角形底边上的中线垂直底边)。 ∴ AD⊥BC(等腰三角形底边上的中线垂直底边)。 ∵AB=AC(已知) (1)解:在△ABC ∵AB=AC(已知)
C
归纳结论
性质2:
等腰三角形的顶角平分线与底边上的中线,底边上 等腰三角形的顶角平分线与底边上的中线,底边上 顶角平分线 上的中线 的高互相重合 的高互相重合 (等腰三角形三线合一) 用符号语言表示为: 用符号语言表示为:
在△ABC中,AB =AC, 点 D在BC上 中 在 上 1、∵AD ⊥ BC 、 BD = CD 。 ∴∠ 1 = ∠ 2 , 2、∵AD是中线, 是中线, 、 是中线 ∴ AD⊥ BC ,∠ 1 =∠ 2 。 ∠ 3、∵AD是角平分线, 是角平分线, 、 是角平分线 。 ∴ AD ⊥ BC , BD= CD
则有 ∠ADB=∠ADC =90º = 在Rt△ABD和Rt△ACD中 △ 和 △ AB= AB=AC 公共边) (公共边)B AD=AD =
D
C
∴ Rt△ABD≌Rt△ACD (HL) △ ≌ △ ) ∴ ∠B=∠C 全等三角形对应角相等) = (全等三角形对应角相等)
归纳结论
性质1
等腰三角形的两个底角相等。 等腰三角形的两个底角相等。 (等边对等角) 用符号语言表示为: 用符号语言表示为:
C
一题多解 如图, 的边BC上 如图,点D、E在△ABC的边 上, 、 在 的边 且AB=AC,AD=AE,此时 与CE有 , ,此时BD与 有 何关系?请说明理由。 何关系?请说明理由。
谈谈你的收获! 谈谈你的收获!
轴对称图形
性质一:两个底角相等(等边对角) 等边对角) 性质一:
性质二:顶角平分线、底边上的中线、 性质二:顶角平分线、底边上的中线、 互相重合( 和底边上的高互相重合(三线合 一)
ABC是等腰三角形 AC=AB, △ABC是等腰三角形
(1)什么是等腰三角形?
有两条边相等的三角形叫做等腰三角形. 有两条边相等的三角形叫做等腰三角形
(2)等腰三角形的有关概念 (3)三角形中学过哪些重要线段?
三角形的中线、 三角形的中线、角平分线和高线 如图:中线 角平分线AE,高AF 如图:中线AD,角平分线 角平分线 高
B D C
大胆猜想
等腰三角形除了两腰相等以外, 等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗? 你还能发现它的其他性质吗?
猜想与论证
猜想
等腰三角形的两个底角相等。 等腰三角形的两个底角相等。 已知:△ABC中,AB=AC
A
求证:∠B=∠C
分析: 如何证明两个角相等 如何证明两个角相等? 分析:1.如何证明两个角相等? 2.如何构造两个全等的 2.如何构造两个全等的 三角形? 三角形?
A
在△ABC中, 中 ∵ AC=AB(已知) (已知) 等边对等角) ∴ ∠B=∠C (等边对等角) ∠
C
B
看谁算得快 如图,在下列等腰三角形中, 如图,在下列等腰三角形中,分别求 出它们的底角的度数。 出它们的底角的度数。 A A
36° ° 120° °
B B C
C
巩固练习(1)
⒈等腰三角形一个底角为75°,它的另外两个 等腰三角形一个底角为75° 75 75°, __; 角为_____ 角为_____ 30° ; __ ⒉等腰三角形一个角为70°,它的另外两个角 等腰三角形一个角为70° 70 70°,40°或55°,55° 为___________________; ___________________; ⒊等腰三角形一个角为110°,它的另外两个角 等腰三角形一个角为110° 110 35°,35° __。 为______ __。
等腰三角形是轴对称图形吗? 等腰三角形是轴对称图形吗?
把剪出的等腰三角形ABC沿折痕对折, 沿折痕对折, 把剪出的等腰三角形 沿折痕对折 找出其中重合的线段和角. 找出其中重合的线段和角
重合的线段
重合的角
A
AB=AC = BD=CD = AD=AD =
∠B = ∠C.
∠BAD = ∠CAD ∠ADB = ∠ADC
论证猜想
作顶角的平分线AD, 证明: 作顶角的平分线 ,
则有∠ = 则有∠1= ∠2
A 12
在△ABD和△ACD中 和 AB= AB=AC B D ∠1=∠2 = AD=AD (公共边) = 公共边) ∴ △ABD≌ △ACD (SAS) ≌ ) ° ∴ BD=CD ∠ADB =∠ADC= 90° =
B D
C
A 作顶角的平分线AD, 证明: 作顶角的平分线 ,
则有∠ = 则有∠1= ∠2
12
在△ABD和△ACD中 和 AB= AB=AC C B D ∠1=∠2 = AD=AD (公共边) = 公共边) ∴ △ABD≌ △ACD (SAS) ≌ ) ∴ ∠B=∠C 全等三角形对应角相等) = (全等三角形对应角相等)
请同学们想想,工人师傅的说法对吗?请说明理由. 请同学们想想,工人师傅的说法对吗?请说明理由.A(学以致用)B
D
C
我思,我进步 我思 我进步1
如图,已知AB=AC, AD是 ABC的中 如图,已知AB=AC,∠BAC=1100,AD是△ABC的中 AB=AC 线。 A 的度数; (1)求∠1和∠2的度数; 1 2 AD⊥BC吗 为什么? (2)AD⊥BC吗?为什么? B D 又∵AD是△ABC的中线(已知) AD是 ABC的中线(已知) 的中线 1 ∠1=∠2= ∠BAC(等腰三角形底边上的中线平分顶角) ∴ ∠1=∠2= ∠BAC(等腰三角形底边上的中线平分顶角) 2 ∠BAC=110 已知) ∵ ∠BAC=1100(已知)
想一想: 想一想:
刚才的证明除了能得到∠ = 刚才的证明除了能得到∠B=∠C 你 还能发现什么? 还能发现什么
重合的线段 AB=AC = BD=CD = AD=AD = 重合的角
