第六章狭义相对论
第6章-狭义相对论

第6章-狭义相对论第六章狭义相对论1、证明牛顿定律在伽利略交换下是协变的,麦克斯韦方程在伽利略变换下不是协变的。
证明:根据题意,不妨分别取固着于两参考系的直角坐标系,且令t =0时,两坐标系对应轴重合,计时开始后,'∑系沿∑系的x 轴以速度v 作直线运动,根据伽利略变换有:'x x vt =-,'y y =,'z z =,'t t =I 、牛顿定律在伽利略变换下是协变的,以牛顿第二定律22d d xF m t=r r 为例。
在Σ系下,22d d xF m t=r r 在Σ系下,'x x vt =-,'y y =,'z z =,'t t =于是,22222222d 'd [',',']d [,,]d 'd d 'd d x x vt y z x y z xF m m m m F t t t t+=====r r r r II 、麦克斯韦方程在伽利略变换下不是协变的,以真空中的麦氏方程BE t=-?rr 为例。
设有一正电荷q 位于O 点并随'∑系运动。
在'∑系中q 是静止的故: 20'4'r qE e r πε=r r ,'0B =r ;于是方程''0B E t '=-=?rr 成立在∑中有:3332222222222220{}4[()][()][()]x y z q x vt y zE e e e x vt y z x vt y z x vt y z πε-=++-++-++-++r r r r于是方程3222203[()()()]4[()]x y z q E y z e z x vt e x vt y e x vt y z πε??=--+-++---++rr r r不一定为02、设有两根互相平行的尺,在各自静止的参考系中的长度均为,它们以相同速率v 相对于某一参考系运动,但运动方向相反,且平行于尺子。
第六章狭义相对论

2
l
l0
l0
u 1 2 c
运动长度 l l0
★ 注意:长度收缩只发生在速度方向
例4(4357)在O参照系中,有一个静止的正方
形,其面积为100cm2。观测者O’以0.8C的
匀速度沿正方形的对角线运动求O’所测得
的该图形的面积。 解:在O参照系中A、B间对角线长度
在O’参照系中A、B间长 度 ★ O’所测得的该图形的面积
u
例5(4370)在K惯性系中,相距 的两个地方发生两事件,时间间隔 而在相对于K系沿正 方向匀速运动的K’系中 观测到这两事件却是同时发生的。试计算:在 K’系中发生这两事件的地点间的距离是多少? 解1 :
解2 :
作业:P339~340 6.1 6.3
6.4
6.5 6.6
练习(5616)一列高速火车以速度 驶过车站时, 固定在站台上的两只机械手在车厢上同时划 出两个痕迹,静止在站台上的观察者同时测 出两痕迹之间的距离为1m,则车厢上的观察 者应测出这两个痕迹之间的距离为多少? 解:车上观察者测的两痕迹之间的距离 =原长 l0 静止在站台上的观察者同时测出两痕迹之间 的距离 =运动长 l
5 4 u2 1 2 c
0
(2)乙测得这两个事件发生的地点的距离
例2(4167) 子是一种基本粒子,在相对于它静 止的坐标系中测得其寿命为 ,如 果 子相对于地球的速度为 ( 为真空中光速),则在地球坐标系中测 出的 子的寿命 解:设:相对于 子静止的参照系为 S’
★ 在地球坐标系中测出的 子的寿命
两个事件的空间间隔 事件二:测量尺子(棒) 右端坐标
长度 右端坐标 — 左端坐标
★
在相对于尺子(棒)运动的参照系中要 条件: 同时记录尺子(棒)两端的坐标。 (如:相对于尺子(棒)运动的参照系是S’ 系 则: t1’ ) t2’ l x’ x ’
第六章 狭义相对论(revised2)

y ∑ 0 z
y’ ∑’ 0’ z’
v
P x, x’
x 2 + y 2 + z 2 − c 2 t 2 = x′ 2 + y′ 2 + z′ 2 − c 2 t ′ 2 = 0
另外, 因为时间和空间是均匀的,而且空间是各向同性的, P 这就意味着∑系和∑’ 系之间的时空变换必须是线性的。 ( x, y, z,t )
x = x ′ + vt ′ r ′ = r − v t y = y′ t ′ = t 伽利略变换 z = z′ 速度变换: u ′ = u − v t = t ′
3、迈克尔逊—莫雷(Michelson-Morley)实验 、迈克尔逊 莫雷 莫雷( 实验
由于在伽利略变换下,Maxwell’s equations不能保持其形 式不变,这是因为从Maxwell’s equations得到电磁波在真空 中的传播速度为 c 的结论。如果Maxwell’s equations在伽利 略变换下保持不变,则在任何惯性系中电磁波在真空中的 各个方向速率都应该等于c,那么在另一个与它有相对运动 的惯性系中,该电磁波的传播速度不可能各向都是 c。 由此可见,在不同的惯性系中,电动力学的规律并不相同。 ----- 电磁规律形式发生变化, 相对性原理不成立。 如果确实如此,从牛顿绝对时空观出发,电磁波只能够 对一个特定参考系的传播速度为c,进而Maxwell’s equations也就只能对该特殊参考系成立。
x 2 + y 2 + z 2 = c 2t 2 x 2 + y 2 + z 2 − c 2t 2 = 0
0 z
0’
x, x’
z’ 而在∑’ 系观察者看来,因为光脉冲也是在∑’ 系的原点 0’ 发出,P点收到光信号的时刻 t’, P 点的空间坐标为 (x’, y’, z’) 根据光速不变原理: r ′ 2 = c ′ 2 t ′ 2 或者
大学物理上册课件:第6章 狭义相对论

例题6-8 带电π介子静止时的平均寿命为2.6×10 – 8 s,某加 速器射出的带电π介子的速率为2.4×10 8 m/s,试求1)在实验室 中测得这种粒子的平均寿命;2)这种π介子衰变前飞行的平均 距离。
解 1) 由于u = 2.4×10 8m/s=0.8c,故在实验室中测得
这种π介子的平均寿命为:
1 2
Δx Δx uΔt
1 2
Δt uΔx / c 2 Δt
1 2
1、不同地事件的同时性是相对的。
Δx Δx uΔt
1 2
Δt Δt uΔx / c2
1 2
Δx uΔt Δx
1 2
Δt uΔx / c2 Δt
1 2
即x 0, t 0时 ,t ux / c2
二、洛仑兹变换
惯性系S、S ′,在 t = t ′= 0时,原点重合,S ′以u 相对 S 系沿
x 轴正向匀速运动。某事件P,在 S 和S ′系中的时空坐标分别为:
y
y
S : P(x , y , z ,t ) S : P( x', y', z', t' )
S
S
u •P(x, y, z, t)
(x, y, z, t)
解 取速度为- 0.9c 的飞船
为S 系,地面为S ′系。
u = 0.9 c v′ x = 0.9 c
y S
y 0.9c
Sx
O
0.9c x
vx
vx u 1 uvx / c2
0.9c 0.9c 1 0.9 0.9
0.994c
说明 洛仑兹变换中 vx 0.994c,这和伽利略变换的结果
vx v'x u是不1同.8的c 。
大学物理曲晓波-第6章 狭义相对论

x
x u t 1 u2 /c2
洛 仑
y
y
兹 z z
逆 变 换
t
t
ux c2
1 u2 /c2
洛伦兹逆变换只是把洛伦兹变换中的u→ - u,x与x’,
y与y’,z与z’交换位置。
说明:
①洛伦兹变换表示同一事件在不同惯性系中时空坐标的变换关系。 规定每个惯性系使用对该系统为静止的时钟和尺进行量度。
在所有惯性系中,物理定律的表达形式都相同。这就是爱因 斯坦相对性原理,即相对性原理。
此原理说明所有惯性系对于描述物理规律都是等价的,不存 在特殊的惯性系。可以看出,爱因斯坦相对性原理是力学相对 性原理的推广。
由此可得出,在任何惯性系中进行物理实验,其结果都是一 样的,运动的描述只有相对意义,而绝对静止的参考系是不存 在的。因此不论设计力学实验,还是电磁学实验,去寻找某惯 性系的绝对速度是没有意义的。
S 系v 中 x d d x t,v y d d y t,v z d d z t
v
x
vx 1
u
uvx c2
速 度 变 换
v
y
vy
1 u2 /c2
1
uvx c2
v
z
vz
1 u2 /c2
1
uvx c2
vx
v
x
1
u
u v x c2
速 度 逆 变 换
v
y
v
y
1 u2 /c2Biblioteka 1u v x c2
vz
v
z
1 u2 /c2
1
u v x c2
讨论:
①当u,v(vx,vy,vz)远小于光速c时,相对论速度变换式退化
狭义相对论

坐标位置无关,时间间隔与时空位置无关.
2.间隔不变性:
事件p1和p2:在 :(x1, y1, z1,t1), (x2 , y2 , z2 ,t2 )
: (x1, y1, z1,t1), (x2, y2 , z2 ,t2)
两朵小乌云: 迈克耳逊——莫雷“以太漂移”实验
黑体辐射实验
狭义相对论 量子力学
近代物理学的两大 支柱,逐步建立了 新的物理理论。
强调:
近代物理不是对经典理论的补充,是全新的理论。
近代物理不是对经典理论的简单否定。
§6.1相对论的实验基础
一.伽利略的相对性原理
1.伽利略变换:
设以v相对于运动,t=0时,两坐标系原点重合
2.光速不变原理:真空中的光速在任意惯性系中沿各
个方向均为c,与光源运动无关.
• 说明: • ⑴它否定了经典速度公式,即否定伽利略变换。 • ⑵光的速度大小与参照系无关,但方向在不同参照系中
可以不同。 • ⑶光速数值不变,则不同参照系中时间、空间、尺度关系
不同。
狭义相对论原理与经典时空的不同:
'
按照二事件间隔将相对论时空划分为三个区域. (1)类时区域(类时间隔):
s2 0,即c2t2 x2
x 2
二事件可用小于光速的信号联系,信号速度 u
c
t
(2)类空区域: s2 0,即c2t2 x2 ,u c,这种讯号不存在
(3)类光区域:s2 0, u c
类空
类时 类空
类时
系中静止。 • 在以太中静止的物体为绝对静止,相对以太运动的物体为
绝对运动。
二.相对论实验基础:
第6章狭义相对论

1. 物理规律对所有惯性系都是一样的。
这后来被称为爱因斯坦相对性原理。
2. 任何惯性系中,真空中光的速率都为 c 。
这一规律称为光速不变原理。 光速不变原理与伽利略变换是彼此矛盾的, 若保持光速不变原理,就必须抛弃伽利略变换, 也就是必须抛弃绝对时空观。
力学相对性原理的另一种表述: 在一个惯性系内部 所作的任何力学的实验都不能区分这一惯性系本身 是在静止状态还是在作匀速直线运动状态。
6
2. 经典力学的绝对时空观
(1)同时性是绝对的。
S系:两事件同时发生,S 系:也是同时发生。 (2)时间间隔是绝对的。
t1 t 2 t1 或写为 t t t2
8
—— 常量
根据伽利略变换,光在不同惯性系中速度不同。
那么在哪个参考系中才是标准光速? 经典理论中认为光在以太中传播,于是以太可以 被视为“绝对静止参考系”。也即通过光学实验, 可以区分惯性系的运动状态。
9
于是必然导致以下结论之一: 一、麦克斯韦方程组不正确。
二、麦克斯韦方程组在伽利略变换下不满足力 ? 学相对性原理。
ux 22 ) t 2 (t 2 c ux1 2 ) t1 ( t1 c
23
ux 22 ) t 2 (t 2 c ux1 2 ) t1 ( t1 c t t u2 1 2 c
ux t ( t 2 ) c ( x 0 )
u 1 2 c
2
1
2
19
1 u 1 2 c
2
1 1
2
如果u≥c,则 就变为无穷大或有虚数值,这显然 是没有物理意义的。 因而得出推论:任何物体相对于另一物体的速 度不可能等于或大于真空中的光速。即真空中的光 速c是一切物体运动速度的极限。 这一推论与实验符合,也符合因果律的要求。
第六章 狭义相对论

二、爱因斯坦相对性原理和光速不变原理 (Einsteins principle of relativity and principle of constant speed of light)
1905年爱因斯坦在《论动体的电动力学》一书中提 出如下两条基本原理: 1. 物理规律对所有惯性系都是一样的。 这后来被称为爱因斯坦相对性原理。 2. 任何惯性系中,真空中光的速率都为 c 。
21
22
23
t — 原时(proper time) 原时:同一地点两事件的时间间隔
u t t 1 2 t, c
2
∴ 原时最短 。
一个运动的钟C 和一系列静止的钟C1、C2… 比较,运动的钟C 变慢了。 一个运动时钟的“1秒”比一系列静止时钟的
“1秒”长,这称为运动时钟的“时间延缓”。 时间延缓完全是一种相对效应。
两朵令人不安的乌云,----”
2
这两朵乌云是指什么呢? 迈克尔逊莫雷实验
热辐射实验
后来的事实证明,正是这两朵乌 云掀起了一场物理界的革命风暴,乌 云落地化为一场春雨,浇灌着两朵鲜 花。
3
量子力学诞生
爱因斯坦的相对论问世
经典 力学
高速领域 微观领域
相对论 量子力学
4
相对论由爱因斯坦(Albert Einstein)创立, 它包括了两大部分: 狭义相对论(Special Relativity)(1905)
当 u << c 时t = t ,这就回到绝对时间了。
26
结论:
1)运动的钟变慢:
t
0
1 u / c
2 2
2)运动参照系中所有物理过程的节奏都变慢了。
27
第6章 狭义相对论课件
2mc M 0c M 0 2m
2 2
五、相对论的能量、动量关系
由 m
m0 v 1 2 c
2
两边 平方
2 2
m (c v ) m c
2 2 2 2 0 2 2 2 0 2
2
m (c v ) c m c c
2 2 2 2 2
2
(mc ) m v c (m0c )
2 16
27
12
1kg这种核燃料所释放的能量为:
E 2.79910 14 3.3510 J/kg 27 m1 m2 8.348610
这相当于同质量的优质煤燃烧所释放热量的1千多万倍!
12
大亚湾核电站夜景
例
两全同粒子以相同的速率相向运动,碰后复合
解:设复合粒子质量为M ,速度为 V v1 v2 m1 m2 V 0 碰撞过程,动量守恒 m1v1 m2v2 MV
四、相对论能量 质能关系
动能 总能量
静止能量
2
EK mc m0c
2
除动能以外的能量
1.静能
当物体静止时,尽管EK=0,仍有能量 2 E0 m0c m0c2,称为物体的静能量E0(分子间势 能、分子热运动能量等)。
虽然静止物体不存在整体运动,动能EK=0,但在其内部 仍有很大的能量m0c2 。例m0=1Kg的任何物体,它的静止 能量E0=1×(3 × 108)2=9 × 1016(J) ,直到目前为止,人 们还无法把这么巨大的静止能量全部释放出来,为人类 服务。
S系
u v
x
§6
狭义相对论动力学基础
高速运动时动力学概念如何? 基本出发点: 基本规律在洛仑兹变换下形式不变;
第六章狭义相对论

第六章狭义相对论6.1相对论的基本原理和时空理论认为时空和质量的测量有绝对意义,与观测者所处的参考系⽆关,这种绝对时空和绝对质量观念是经典⼒学的“公理”基础,其集中反映便是伽俐略变换.但从19世纪末年起,⼈们发现这种观念与电磁现象和⾼速运动的实验事实不符.在迈克尔孙等⼈光速测量实验的基础上,爱恩斯坦于1905年创⽴了狭义相对论.这⼀理论的两个基本假设是:相对性原理——物理定律在所有惯性系都有相同的形式;光速不变原理——真空中的光速在所有惯性系沿任何⽅向都是常数c,与光源的运动⽆关.间隔不变性间隔不变性是相对性原理与光速不变原理的数学表述.设惯性系中,任意两事件的空时坐标为和,定义两事件的间隔为(6.1)在另⼀惯性系中,这两事件的空时坐标为,,间隔为(6.2)惯性系概念要求空时坐标变换必须是线性变换,即,,⽽当两个惯性系的相对速度时,这两个惯性系将等同于⼀个惯性系.因⽽对任何两个惯性系,应当有(6.3)洛伦兹变换设惯性系以速度沿惯性系的x轴正向运动,两参考系相应坐标轴平⾏,时两参考系的原点重合(⼀个事件),由(6.3)式,可导出任⼀事件的空时坐标从系到系的变换——洛伦兹变换,,, (6.4)其中 , (6.5)将(6.4)式中的换为,可得逆变换.当, (6.4)过渡到伽俐略变换.因果律与相互作⽤的最⼤传播速度洛伦兹变换表明,时空的测量有相对意义,即测量结果与观测者所处的参考系有关,这是相对论时空观的⼀个⽅⾯.另⼀⽅⾯,是认为事物发展变化的因果关系有绝对意义,即因果关系不因参考系的变换⽽改变,从时间次序来说,就是在⼀个惯性系中,作为结果的事件必定发⽣在作为原因的事件之后,变换到任何其它惯性系,都必须保持这⼀时间次序.从这⼀要求出发,由间隔不变性或洛伦兹变换,可得出推论——真空中的光速c是⾃然界⼀切相互作⽤传播速度的极限.间隔分类在任何⼀个惯性系中,任何两事件的间隔只能属于如下三种分类之⼀:类时间隔;类光间隔;类空间隔.在⼀个惯性系中有因果关系的两事件,两者之间必定存在某种相互作⽤,其传播速度只能⼩于c或等于c,因⽽有因果关系的两事件之间隔必定类时或类光,变换到任何其它惯性系,绝对保持因果关系,相互作⽤的传播速度仍然⼩于c或等于c,即间隔仍然类时或类光.在⼀个惯性系中⽆因果关系的两事件,间隔必定类空,变换到任何其它惯性系,绝对保持⾮因果关系,间隔仍然类空.同时相对性在某个惯性系中,如果两事件于不同地点同时发⽣,即这两事件⽆因果关系,由洛伦兹变换可推知,在其它惯性系看来,这两事件的发⽣不同时.这意味着,在某个惯性系不同地点对准的时钟,在其它惯性系看来没有对准.时钟延缓效应在物体静⽌的参考系中,测得任⼀过程进⾏的时间,称为这过程的“固有时”.由洛伦兹变换,在其它惯性系中,测得这过程进⾏的时间变慢了:(6.6)这效应对于两个惯性系来说是相对的,即在系上看系的时钟变慢,在系上看系的时钟也变慢.但是在有加速运动的情形,时间延缓效应是绝对效应.尺度缩短效应当物体以速度相对于惯性系运动,若在平⾏于运动⽅向上这物体的静⽌长度为,由洛伦兹变换,在系中测得这长度缩短为(6.7)这效应对于两个惯性系来说,也是相对的.但在垂直于运动的⽅向,这⼀效应不会发⽣.时钟延缓与尺度缩短效应,是在不同参考系中观察物质运动在时空关系上的客观反映,是统⼀时空的两个基本属性,与具体过程和物质的具体结构⽆关.速度变换由洛伦兹变换(6.4),可导出物体速度从惯性系到之间的变换, ,(6.8)将换为-,可得逆变换.可以证明,若在⼀个参考系中物体的速度,变换到任何其它参考系仍有.仅当,(6.8)式才过渡到经典速度变换.6.2 洛伦兹变换的四维形式四维协变量相对论认为时空是统⼀的.为此将三维空间与第四维虚数坐标统⼀为四维复空间(6.9)于是当系以速度沿系的轴正向运动时,洛伦兹变换(6.4)可表为, (6.10)重复指标(上式中右⽅的)意味着要对它从1⾄4求和.变换系数构成的矩阵为(6.11)由于洛伦兹变换(6.10)满⾜间隔不变性(6.3),亦即不变量 (6.12)因此,洛伦兹变换是四维时空中的正交变换,即变换矩阵满⾜(6.13)(6.10)的逆变换为(6.14)在洛伦兹变换下,按物理量的变换性质分类为:标量(零阶张量,不变量) (6.15)四维⽮量(⼀阶张量) (6.16)四维⼆阶张量 (6.17)例如,间隔和固有时就是洛伦兹不变量.可以证明,每⼀类四维协变量的平⽅都是洛伦兹变换下的不变量.利⽤这⼀普遍规律,可将物体的速度和光速,能量和动量,电荷密度和电流密度,标势和⽮势,电场和磁场等物理量统⼀为四维协变量,由此可以清楚地显⽰出被统⼀起来的物理量之间的内在联系,并将描写物理定律的⽅程式表⽰成相对性原理所要求的协变形式.6.3 相对论⼒学相对论⼒学⽅程在低速运动情形下,经典⼒学⽅程在伽利略变换下满⾜协变性.为使⾼速运动情况下⼒学⽅程也满⾜协变性,构造四维速度 (6.18)四维动量 (6.19)四维⼒ (6.20) (四维加速度 ),其中是三维速度,是三维⼒,是⼒的功率,是四维⼒的空间分量.由于固有时和静⽌质量是洛伦兹不变量,因此、和都是按(6.16)⽅式变换的四维协变⽮量,于是相对论⼒学⽅程(6.21)在洛伦兹变换下满⾜协变性.由,这⽅程包含的两个⽅程为(6.22)(6.23)相对论质量、动量和能量由⽅程(6.22)和(6.23)可知,⾼速运动情形下物体的质量、动量和能量分别为(6.24)(6.25)(6.26)质速关系(6.24)表明,物体的质量随其运动速度的增⼤⽽增加,即质量测量与时空测量⼀样,存在相对论效应.仅当,才有,此时相对论动量(6.25)过渡到经典动量.质能关系(6.26)中,是运动物体或粒⼦的总能量,是其静⽌能量,是其相对论动能.仅当物体或粒⼦的速度,才有,即⾮相对论动能.质能关系的重要意义在于它表明,⼀定的质量来源于⼀定的相互作⽤能量.由可推知,静⽌质量的粒⼦,必定有静⽌能量,因⽽应当存在某种深层次的内部结构,物体或粒⼦的静⽌质量,来源于其内部存在的相互作⽤能量.由多粒⼦组成的复合物之所以出现质量亏损,便是这复合物内部的粒⼦存在⼀定相互作⽤能(结合能)的反映.(6.19)式表⽰的四维动量,是将相对论动量和能量统⼀起来的协变⽮量:(6.27)在物体或粒⼦静⽌的参考系中,其动量,能量,在任⼀惯性系中,设其动量为,能量为,由的平⽅是洛伦兹变换下的不变量,可得能量、动量和质量的普遍关系式(6.28)由(6.26)和(6.28),可得粒⼦静⽌质量的⼀种表达式(6.29)即通过测量粒⼦的动量和动能,可计算其静⽌质量.光⼦的能量和动量由质能关系(6.26)可推知,以速度运动的粒⼦,例如光⼦,其静⽌质量应当为零,即这类粒⼦应当没有内部结构.由波粒⼆象性,光⼦能量为,其中为⾓频率,,为普朗克常数.因光⼦,由(6.28)式,其动量为,为波⽮量,表⽰光⼦运动⽅向的单位⽮量.6.4 电动⼒学的相对论协变性相对论电动⼒学⽅程定义四维算符(6.30)(6.31)是协变⽮量算符,是标量算符.电流是电荷的运动效应,⽽电荷电流是电磁势和电磁场的激发源.因此,有理由将电荷密度与电流密度,标势与⽮势 ,电场E与磁场B ,统⼀为四维协变量.四维电流密度 (6.32)四维势 (6.33)其中,带电体静⽌时的电荷密度是洛伦兹标量,和均按(6.16)变换.由,构造电磁场张量(6.34)它按(6.17)变换.这是⼀个反对称张量,其矩阵形式为(6.35)构造四维洛伦兹⼒密度(6.36)它按(6.16)变换,其中是三维洛伦兹⼒密度,是电场对电荷作的功率密度.于是,电动⼒学的基本⽅程电荷守恒定律 (6.37)洛伦兹规范 (6.38)达朗贝尔⽅程 (6.39)麦克斯韦⽅程(6.40)能量动量守恒定律 (6.41)都满⾜相对论协变性.(6.41)式中,是将电磁场的能量密度,能流密度S,动量密度g和动量流密度统⼀起来的协变张量:(6.42)矩阵形式为(6.43)势和场的相对论变换在参考系变换下,电荷与电流存在相对性,电磁势和电磁场必然也存在相对性.当惯性系以速度沿系x 1轴的正向运动时,电磁势按变换,即, , , (6.44)电磁场按变换,即,, (6.45)其中下标∥表⽰与运动⽅向平⾏的分量,⊥表⽰垂直分量.将(6.44)式和(6.45)式中的改为-,即得逆变换.在参考系变换下,电磁波的相位是不变量.构造四维波⽮量(6.46)它与四维时空的乘积反映了相位不变性.因此,四维波⽮量必定按变换.当光源沿系x 1轴的正向以速度运动时,便有, , , (6.47)由此可得相对论多普勒效应与光⾏差的表达式, (6.48)其中,为光源静⽌参考系系中的辐射频率,是波⽮即辐射⽅向与x 1轴正向的夹⾓;是在系中观测到的频率,是这参考系中辐射⽅向与光源运动⽅向的夹⾓.6.5电磁场中带电粒⼦的拉格朗⽇量和哈密顿量静⽌质量为,电荷为e的带电粒⼦在电磁场中以速度相对于系运动时,粒⼦的相对论运动⽅程为(6.49)为粒⼦的动量.由, ,可导出粒⼦的拉⽒量(6.50)⽽和作⽤量S都是洛伦兹变换下的不变量:(6.51)(6.52)由⼴义动量的定义 ,可得粒⼦的正则动量和哈密顿量H:(6.53)(6.54)于是拉格朗⽇⽅程(6.55)和正则运动⽅程, (6.56)均与⽅程(6.49)等价.哈密顿量(6.54)第⼀项是粒⼦的相对论能量,故可构造四维正则动量(6.57)由此可得相对论正则运动⽅程, (6.58)。
6狭义相对论基础

系无关。质量的测量与运动无关。
牛顿力学的回答: 对于任何惯性参照系 , 牛顿力学的规律都具有
相同的形式 . 这就是经典力学的相对性原理 .
或 牛顿力学规律在伽利略变换下形式不变 或 牛顿力学规律是伽利略不变式
三.伽利略变换的困难
对于不同的惯性系,电磁现象基本规律的形式 是一样的吗 ?
真空中的光速
y
s
x1
o 12
9
3
6
12
9
3
6
d
x2
12 x
93
6
t (t' ux')
c2
x' 0
t t2 t1 t'
t t'
1 2
固有时间 :同一地点发生的两事件的时间间隔 .
t t' t0 固有时间
时间延缓 :运动的钟走得慢 .
注意 1)时间延缓是一种相对效应 .
2)时间的流逝不是绝对的,运动将改变 时间的进程.(例如新陈代谢、放射性的衰变、 寿命等 . )
c
d
v
t1 t2
结果:观察者先看到投出后的球,后看到投出前的球.
900 多年前(公元1054年5月)一次著名的超新星 爆发, 这次爆发的残骸形成了著名的金牛星座的蟹状 星云。北宋天文学家记载从公元 1054年 ~ 1056年均能 用肉眼观察, 特别是开始的 23 天, 白天也能看见 .
当一颗恒星在发生超新星爆发时, 它的外围物质向 四面八方飞散, 即有些抛射物向着地球运动, 现研究超 新星爆发过程中光线传播引起的疑问 .
*
(x', y', z'
x'
x
ma'
第06章 狭义相对论

t2
M2 2l
G
30 30
M2
M1
s
T
G
T
s
G M1
M2
N
2Δ
v
v
2
v 2l 2 c
4
l 10m, 500 nm, v 3 10 m/s
N 0.4
实验结果
仪器可测量精度
N 0.01
N 0
31
未观察到地球相对于“以太”的运动.
以后又有许多人在不同季节、时刻、 方向上反复重做迈克尔孙-莫雷实验.近年 来,利用激光使这个实验的精度大为提高, 但结论却没有任何变化. 迈克尔孙-莫雷实验测 到以太漂移速度为零,对以 太理论是一个沉重的打击, 被人们称为是笼罩在9世纪 物理学上空的一朵乌云.
大学物理3
10
热力学和经典统计力学—热力学第一、第二 及第三定律及分子运动论
成功地解释了热现象。 经典电磁理论—麦克斯韦电磁理论 成功地解释了波动光学及许多电磁现象
大学物理3
11 11
•
有一个故事很可以说明在人们心目中,古 典物理学的完善程度。 德国著名的物理学家普朗克年轻时曾向他的 老师表示要献身于理论物理学,老师劝他说: “年轻人,物理学是一门已经完成了的科学, 不会再有多大的发展了,将一生献给这门学科, 太可惜了!”
凭直觉,爱因斯坦给出的答案是:
爱因斯坦说: “只有大胆的思辨而不是经验的堆积,才能 使我们进步。”
36
二、爱因斯坦的两个重要假设
⑴ 物理规律对所有惯性系都是一样的,不存在任 何一个特殊的(例如“绝对静止”的)惯性系
——爱因斯坦相对性原理
⑵ 在任何惯性系中,光在真空中的速率都相等
高一物理章节内容课件 第六章狭义相对论

在地球坐标系中测出的 子的寿命
解:
例3(4378)火箭相对于地面以V=0.6C (C
为真空中光速)的匀速度飞离地球。在
火箭发射
秒钟后(火箭上的
钟),该火箭向地面发射一导弹,其速
度相对于地面为V1=0.3C,问火箭发射 后多长时间,导弹到达地球?(地球上
的钟)计算中假设地面不动。
解:火箭飞离地球到发射 导弹经历的时间间隔
中,两个事件同地发生)
4. 长度收缩(条件:在相对棒运动的参照 系中,要同时纪录棒两端的 坐标)
5. 相对论质量 6. 相对论能量 7. 相对论动量 8. 质点系动量守恒
9. 核反应的总能量守恒、释放的能量、质量 亏损
10 .相对论动量与能量的关系
例一(4604)设快速运动的介子的能量约为
E=3000MeV,而这种介子在静止时的
的速率V沿隧道长度方向通过隧道,若 从列车上观测:
(1)隧道的尺寸如何? (2)设列车的长度为 ,它全部通过隧
道的时间?
1.(4720)解答 (1) 从列车上观察,隧道的长度缩短, 其他尺寸不变。隧道长度为
(2)列车全部通过隧道的时间为
2.(4373)静止的 子的平均寿命约
为
,今在8Km的高空,由于
能量为E0=100MeV。若这种介子的固有
寿命是
,求它运动的
距离。
例二(4733)已知一静止质量为m0的粒子, 其固有寿命为实验室测量到的寿命的
1/n,则此粒子的动能是多少?
例一(4604)解答
例二(4733)解答
例三(4735)已知 子的静止能量为
105.7MeV ,平均寿命为
。
试求动能为150MeV的子的速度是多少?
第6章狭义相对论

绝对时空观念只适用于低速运动; 绝对时空观念只适用于低速运动;而在 低速运动 高速运动中,它的缺陷就明显表现出来了。 高速运动中,它的缺陷就明显表现出来了 四 . 伽利略变换的困难 电磁现象总结出来的麦克斯韦方程组,给出电磁 电磁现象总结出来的麦克斯韦方程组, 波(光) 以恒定速度 在真空中传播 光 以恒定速度c在真空中传播
2. 经典力学的绝对时空观 (1)同时性是绝对的。 同时性是绝对的。 同时性是绝对的 S系:两事件同时发生, 两事件同时发生, S′ 系:两事件也是同时 发生的。 发生的。 (2)时间间隔是绝对的。 时间间隔是绝对的。 时间间隔是绝对的
x′ = x ut
y′ = y z′ = z t′ = t
S′
x′ = γ ( x ut )
逆 y = y′ 变 z = z′ 换 t = γ ( t′ + ux′ ) 2
c
x = γ ( x′ + ut′ )
γ=
1 u 1 2 c
2
18
(1) 当u<<c时,洛仑兹 时 洛仑兹 变换式就变成伽利略变 换式: 换式:
S′
S
x′ = γ ( x ut )
ux t′ = γ ( t 2 ) c
S
′ ′ t2 t1 = t2 t1
或写为
t′ = t
7
(3)空间间隔 距离 是绝对的。 空间间隔(距离 是绝对的。 空间间隔 距离)是绝对的
d′ = ( x′ ) + ( y′ ) + ( z′ )
2 2
y′ = y z′ = z 2 2 2 = ( x ) + ( y ) + ( z ) = d t′ = t
2
x′ = x ut
电动力学-第六章-狭义相对论
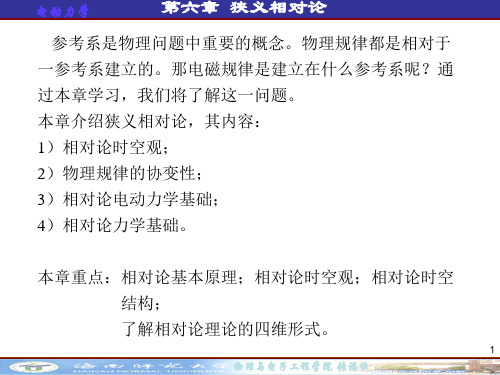
2.相互作用最大传播速度
既然同时是相对的,那因果关系是否会发生颠倒呢?当 然,这种因果关系是不能发生颠倒的!即因果关系是绝对 的。这就对相对论提出了要求。 由洛伦兹变换:
t2 t1
t2 t1 x2 x1 / c 2
1 2 / c2
若两事件有因果关系,即若t2 - t1 0,则必有t2 - t1 0。
x1 x, x2 y, x3 z , x4 ict
另外:
/c
1 1 2
18
物理与电子工程学院 张福恒
电动力学
第六章 狭义相对论
2.物理量按空间变换性质分类
变换规律:
所有物理量称为张量:
1)零阶张量称为标量,经坐标变换后保持不变的量;
2)一阶张量称为矢量; 3)二阶张量称为二阶张量;等等。
24
物理与电子工程学院 张福恒
电动力学
第六章 狭义相对论
3.电磁场张量
25
物理与电子工程学院 张福恒
电动力学
第六章 狭义相对论
4.电磁场的不变量
26
物理与电子工程学院 张福恒
电动力学
第六章 狭义相对论 §6 相对论力学
1.能量-动量四维矢量
27
物理与电子工程学院 张福恒
电动力学
第六章 狭义相对论
4.运动的尺子缩短了
在系中有一位于x轴的尺子,测得其长度为l0(静 止长度)。由洛伦兹变换得:
x2 x1
即:
x2 x1 t2 t1 / c 2 1 2 / c2
l 1 2 / c2
l l0 1 2 / c2
即有:
l l0
第六章狭义相对论

第六章狭义相对论§6.1 狭义相对论的基本原理1905年,爱因斯坦根据下列两个基本原理建立了狭义相对论。
1.相对性原理在每个惯性系里,自然现象所遵循的物理规律都相同。
2.光速不变性原理在每个惯性系里,光在真空中的速率都相同(即都是c)。
§6.2 洛伦兹变换由两个基本原理,可以得出彼此相对运动的两个惯性坐标系之间的变换关系,这种变换关系通常叫做洛伦兹变换。
1.特殊洛伦兹变换设两个笛卡儿坐标系∑和'∑的坐标轴互相平行,其中x 轴相重合。
'∑系沿x正轴方向以匀速)0,0,(x v v =相对于∑系运动。
在0'==t t 时刻,两个坐标系的原点重合。
则洛伦兹变换为)4.2.6()()3.2.6()2.2.6()1.2.6()(2''''x c v t t z z y y vt x x -===-=γγ 式中c 是真空中的光速, 2211c v -=γ (6.2.5)逆变换只需将速度改变符号即可。
2.一般洛伦兹变换如图1-5-1所示,两个笛卡儿坐标系∑和'∑的坐标轴保持平行,'∑系的原点'o 以匀速),,(z y x v v v v =相对于∑系做匀速直线运动。
这时洛伦兹变换为t v z v v v y v v v x v v x x y x y x xγγγγ--+-+⎥⎦⎤⎢⎣⎡-+=2222')1()1()1(1(6.2.6) t v z v v v y v v x v v v y zy y z y γγγγγ--+⎥⎥⎦⎤⎢⎢⎣⎡-++-=2222')1()1(1)1( (6.2.7)t v z v v y v v v x v v v z z z y z x z γγγγ-⎥⎦⎤⎢⎣⎡-++-+-=2222')1(1)1()1((6.2.8) t z cv y c v x c v t z y x γγγγ+---=222' (6.2.9)§6.3 相对论的时空理论1.同时性概念的相对性根据洛伦兹变换,再同一个惯性系里的各个地方,有共同的同时性;而在两个做相对运动的惯性系里,则没有共同的同时性。
第六章-狭义相对论基础

c
1 2
1 2
得
l l 12
(5)
空间间隔(或称物体长度)是相对的,和 物体一起运动的惯性系中测得的长度最长,而 与物体相对运动的惯性系中测得的长度就短 些,即运动物体沿其运动方向的长度变短了。
尺缩效应动画
6.4 洛仑兹变换 相对论时空观的再讨论
6.4.1 洛仑兹变换 两个惯性系
S 和 S′,因二者只 沿 x 方向有相对
(3)长度缩短(尺缩效应)
t2 t1 2lc (3) •
l
入射段:
o
图1
lVt1ct1
t1
l c V
V t1
••
o o
l
图2
反射段:
lV t2ct2
t2
l c V
V(t1t2)
•
•
o
o
l
图3
M
V
M
M
tt1t2c lVc lV12 lc2
由 (2)式 ,得
t t
1 2
(4)
于是有
2l
2l
c
物体的速度不能超过真 空中的光速。
6.4.2 相对论时空观的再讨论
(1)同时的相对性
S S V
a l •
O (x1,t1) O
( x1 , t1 )
M l b
•
•
x (x2,t2 )
x ( x2 , t2 )
在S'系看
t2 t1
x2x1 2l
在S系看,由洛仑兹变换
t1
t1 Vx1 1V 2
c2 c2
由洛仑兹变换
xa
xa Vta
1 2
b(xb ,tb ) x
第六章 狭义相对论
12
R
例8(
V
)解答
o
B A
(转台+二人)对转轴 角动量守恒
2V
台
1 2 L台 mR 0 2
1 1 LA rA ( m )VA地 mR 20 2 2
1 1 1 2 LB rB ( m )VB 地 m( R ) 0 2 2 2
13
走动前
成的摩擦阻力矩)
4
解:
(1)子弹击中圆盘后,圆盘 所获得的角速度
R
v0
m
子弹和圆盘在碰撞前后角动量守恒
1 mv0 R ( MR 2 mR 2 ) 2
mv0 1 ( 2 M m)R
5
(2)经过多少时间后,圆盘停止转动 解一:据定轴转动定律 根
d M J J dt
27
1887 年 , 体 现 上 面 思 想 的 迈 克 耳 孙 — 莫 雷 (Michelson-Morlay)实验却得到了“零”结 果! 地球就是“绝对静止”的参考系? 用各种企图保持绝对参考系的假说来解 释该实验结果,均遭到失败。典型的有: 发射说:光速要叠加上光源的速度。 双星观测否定了发 c + u1 双 射说,即实际上观测 地球 星 u2 不到双星位置的扭曲, 不能同时 c u2 m2 到达地球 28 而是符合力学规律。 应观察到双星位置的扭曲
7
例7( )一匀质细棒长为2L,质量 为m。以与棒长方向相垂直 的速度 V0在光滑水平面内平动时与前方一 固定的光滑支点O发生完全非弹性 A 碰撞。碰撞点位于棒 L 2 o 中心的一方L/2处, L 2 如图所示。 L 求棒在碰撞后的瞬时绕 O点转动时的角速度 B V0
8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
′ = αλν αµσTνσ 二阶张量: Tλµ
对称张量: Tµν = Tνµ ,有10个独立分量(四维) 例如三维空间中对称张量:电四极矩张量Qij;转动惯量 张量I;材料力学中的应力张量 ;Maxwell应力张量;电 磁场动量流密度张量Tij等等。
Tµν = −Tνµ 只有6个独立分量,因为 Tµ µ=0 反对称张量:
三阶张量有43=64个分量:Tµνλ
三阶全反对称张量:Tµνλ ,若对每两个脚标都是反对称的 称之为三阶全反对称张量。即有二个及二个以上脚标相同 时矩阵元为零,共40个0元素,24个非零元素。 24个非零元素中只有4个独立元素T234,T314,T412 和 T123. 它们可用一个4维矢量表示。
A′ µ = α µν A ν
同意味着求和。
约定脚标希腊字母从1取到4,英文字母从1取到3,脚标相 这种约定求和的脚标如上式中ν称为“哑标”,对不参加求和 的脚标,如上式中的μ称为“自由脚标”。 等式两边的自由脚标必须对应。 由于哑标只表示对该脚标从1到4求和的一个约定,所以哑 脚标的字母可以更换,如上式中 A′ µ = α µν A ν = α任意一个二阶张量总可以分解为一个二阶对称张量和一个 二阶反对称张量之和”。 证明:设Tµ σ 为任意一个二阶张量,
Tµ σ = Tµ σ + Tσµ 2 + Tµ σ − Tσµ 2 = Sµ σ + Aµ σ
式中 S µ σ = S σµ 是对称张量,
A µ σ = − A σ µ 是反对称张量,证毕。
三维空间中反对称张量是两矢量叉乘出来的,又叫赝矢 r r r r r r r r r r r υ = ω× r,L = r × F , J = r × p 量。例如 B = ∇ × A , r r r r B, ω, L, J 构成三维空间的二阶反对称张量,因只有三个独 立分量故可用一矢量表示,叫赝矢量。 在坐标变换时不能当矢量处理,否则会出错。 在四维空间二阶反对称张量有六个独立分量,比空间维数 多2,不能用4-矢量表示。 坐标变换时必须还物理量的本来面目。 顺便指出:在正交变换下,对称张量保持为对称;反对称张量 保持为反对称。
结论:一个矢量场的偏微商构成一个二阶张量场,依次类推。
如果 A νµ 是一个二阶张量场,其微商就构成一个三阶张量场。
将这普遍结论表述为定理如下:
定理:
一个r阶张量场对坐标 x µ 的偏微商是一个r+1阶的张量场 (证明略)。 注意:此定理只对笛卡尔张量场适用,因为对笛卡儿张量 场,坐标变换是线性变换:
x'µ = α µυ x ν
狭义相对论只涉及惯性系变换,都是笛卡儿坐标。 张量也是笛卡儿张量。 广义相对论则不然。
⑤特殊张量: 4维二阶单位张量:用Kronecker符号表示,
δ µυ
1 (υ = µ ) µ ,υ = 1, 2, 3,4 = 0 (υ ≠ µ )
δ 只有一个,不依赖于坐标系,在任意两个坐标系 xµ 和x'µ中, µυ 有
′ = δ µω δ µω
洛仑兹变换的正交性可如下表示:α λµ α λυ = α µλ α υλ = δµυ 4维三阶完全反对称张量用 ε αβλ(Levi-Civita符号) 表示。
第六章 狭义相对论
§6.4 张量分析初步
§6.4
张量分析初步
1.复四维空间张量的定义 2.张量代数运算规则 3. 张量场和张量分析初步 4. 四维张量方程的洛仑兹协变性
相对论要求惯性系之间变换时,时间和空间必须一起变。为 了方便,引进了闵氏空间,是一个赝欧氏空间。 在闵氏空间中,复洛仑兹变换代表四维坐标转动,是么正变换。 要求所有物理量表示成四维张量的形式,所有方程表示成四 维协变式,叫洛仑兹协变式。 这协变式在惯性系之间转换时保持不变,满足相对性原理的 要求。 体现一切惯性系是等价的。 所谓相对论电动力学以及相对论力学的任务就是把一切物理 量表示成闵氏空间中的4-维张量,一切动力学方程改写成洛 仑兹协变的形式。 所需要的数学工具就是张量的运算。
r r 例如 E , H 是三维矢量,不是四维空间的矢量。
③4—张量(二阶): 一个物理量 Tµν 有16个分量(µ,ν=1,2,3,4),当坐标转动时, 其变换规律与坐标乘积的变换规律相同,叫四维空间的 二阶张量,有42=16个分量
' ' x 坐标乘积: λ xµ = (α λν xν )(α µσ xσ ) = α λν α µσ xν xσ
2.张量代数运算规则
①两4维矢量外乘或外积(相当与三维叉乘): Aλ ,Bµ 的外积 为 A λ B µ ,是二阶反对称张量,符合二阶张量变换关系。 ②两4—矢量内乘(内积)(相当三维点乘):A λ 和 B µ ,其内积 为 A µ B µ 。脚标相同,内积是标量,在坐标转动变换下保持 不变。 两矢量内乘,张量阶数相减(1-1=0阶)。 两矢量外乘,张量阶数相加(1+1=2阶)。 ③张量的和与差:两个r阶张量的和与差等于其对应分量的和 与差,阶数不变。 例如 a µυ 和 b λσ,其和与差为 Cµυ = aµυ ± bµυ,也是二阶。
∂φ′ ∂φ ∂φ ∂xµ = = ∂ x′ ∂ x′ ∂ x µ ∂ x′ υ υ υ
∂x µ
∂x′ υ
?
−1 由 ∆x'υ = α υµ ∆xµ ,有 α υµ ∆x 'υ = ∆x µ ,即 ∆xµ = α µυ ∆x′ υ
∂x µ = α µυ 代入上式,得 于是有 ∂x′ υ
∂φ′ ∂φ ∂φ = α µυ = α υµ ∂ x′ ∂x µ ∂x µ υ
其定义:
ε αβλ
0 = 1 − 1
当α = β或β = λ或α = λ时 当αβλ 为1, 2, 3,4的偶数次交换排列时 当αβλ 为1, 2, 3,4的奇数次交换排列时
4维四阶完全反对称单位张量 ε αβλσ 只有一个,不依赖坐 标系 ε αχλυ
= ε′ στθϕ
,其定义与三阶类似。
④两张量外乘(外积) 两个张量(r阶和s阶)外积是一个r+s阶张量,其分量是这两 个张量各分量之积。是升阶运算:(r+s)阶。例 Aµν 和 Bλστ 之积是五阶张量,其分量:Cµυλστ = A µυ B λστ ⑤张量的缩阶 一个阶数r≥2的张量,使其分量的两个指标相同,并对这 重复的指标求和,这样的运算称为缩阶(降阶:r-2阶)。 例如 A µν 使υ=μ得到 A µµ =A11 +A22 +A33+A44 ,这正是矩 阵的迹。一个二阶张量经缩阶后就成为一个标量;
⑥两个张量的内乘(内积) 将它们的外积对两个分属于不同张量的分量的指标进行缩 阶。 例如两矢量 A µ 和 B ν,先求其外积 A µ B ν ,通过缩阶得到 内积:Aµ Bµ =A1B1+A2B2+A3B3+A4B4,正是两矢量标积或点 乘。 又例如两个二阶张量 A µν 和 Bλτ ,先求其外积 A µν B λτ , 分别进行缩阶运算。 可以有四种不同的内积如下:
又例如一个三阶张量 A µνλ 对前二个指标进行缩阶,得
Cλ = Aµµλ = A11λ + A22λ + A33λ + A44λ (λ=1,2,3,4共四个分量)
缩阶后变成一个矢量。
Aµνν ,其结果都成为一个 另外还有两种可能的缩阶:Aµνµ 、 矢量。
缩阶运算就是把任意两个指标变成一对哑标,对这哑标从1 到4求和。 r阶张量缩阶后得到一个(r-2)阶的张量(要r≥2)。 缩阶运算没有运算符号,一般不单独进行,而是与其它运算 一起运行。
r r
真标量和赝标量:当坐标反演时,其符号不变的标量叫真标 量,如三维空间电荷密度ρ等,要改变符号的标量叫赝标 r r r r 量,如极矢量 E 和轴矢量 B 的点积 E ⋅ B ,三个极矢量混合 r r r 积 A ⋅ (B × C) 等。 一般说,赝矢量和真矢量点乘出来的标量是赝标量。 真张量和赝张量:当坐标系反演时,张量的分量改变符号, 则是真张量;若分量不改变符号,则是赝张量如 ε αβλ 。 在乘积运算中按经验有如下结论:(a)两真张量或两赝张 量相乘之积是真张量;(b)一个真张量和一个赝张量相乘 之积是赝张量。
φ′(x′ µ ) = φ(x µ )
40=1,只有个分量。 ②4-矢量:一个物理量有四个分量(μ=1,2,3,4),当坐标 转动时其变换性质同坐标的变换性质相同叫四维(度)矢量也 叫一阶张量(分量的个数是41=4个)
x = α µν x ν
' µ
(坐标变换) α µν 是洛仑兹变换 (矢量变换)(μ,ν=1,2,3,4)
⑥赝张量: 坐标旋转时,坐标系类型保持不变,右手系仍是右手系。 当空间反演即三个坐标基矢同时变符号时,右手系改变为 左手系,左手系变为右手系。 真矢量和赝矢量:当坐标反演时,不改变方向的矢量称为 ;当坐标反演时,要改变方向的 r r r 矢量称为赝矢量(或轴矢量)。如力矩 L = r × F ,动量矩 r r r r r r r J = r × p ,线速度 υ = ω× r ,磁场 B 等。 一般说,两个矢量叉乘出来的矢量是赝矢量。 真矢量(或极矢量),如
A µν B λτ
使 µ = λ 并对其求和,得 A µν B µ τ = Dν τ 使 τ = µ 并对其求和,得 Aµν Bλµ = Dνλ 使 λ = ν 并对其求和,得 A µν B ν τ = D µ τ 使 τ = ν 并对其求和,得 A µν B λν = Dµλ 四种内积都是二阶张量。 两个二阶张量的内积仍是一个二阶张量. 对r阶和s阶张量求内积运算得到(r+s-2)阶张量。
本节是相对论的数学准备。 对于三维空间张量已经有一些概念,四维张量与三维张量 在数学上没有本质区别。 因此我们直接讲四维张量。
