2014年湖南省长沙市中考数学试卷解析版
长沙市历年中考数学试卷及答案

2014年长沙市初中毕业学业水平考试试卷数 学注意事项:1、答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2、必须在答题卡上答题,在草稿纸、试题卷上答题无效;3、答题时,请考生注意各大题题号后面的答题提示;4、请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;5、答题卡上不得使用涂改液、涂改胶和贴纸;6、本学科试卷共26个小题,考试时量120分钟,满分120分。
一、选择题(在下列各题的四个选项中,只有一项是符合题意的。
请在答题卡中填涂符合题意的选项。
本题共10个小题,每小题3分,共30分) 1.21的倒数是( ) A .2B .-2C .21 D .-21 2.下列几何体中主视图、左视图、俯视图完全相同的是( )A .圆锥B .六棱柱C .球D .四棱锥3.一组数据3,3,4,2,8的中位数和平均数分别是 ( )A . 3和3B . 3和4C . 4和3D . 4和4 4.平行四边形的对角线一定具有的性质是( )A .相等B .互相平分C . 互相垂直D .互相垂直且相等 5 .下列计算正确的是( )A .752=+ B .422)(ab ab = C .a a a 632=+ D .43a a a =⋅6 .如图,C 、D 是线段AB 上两点,D 是线段AC 的中点,若AB=10cm,BC=4cm,则AD 的长等于( )A . 2 cmB . 3 cmC . 4 cmD . 6 cm 7 .一个关于x 的一元一次不等式组在数轴上的解集如图所示,则此不等式组的解集是( )A . x >1B .x ≥1C .x >3D .x ≥3 8.如图,已知菱形ABCD 的边长等于2,∠DAB=60°, 则对角线BD 的长为 ( )A . 1 BC . 2D .A B DCAD B姓名 准考证号9.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后能与原图形完全重合的是( )10.函数a y x=与函数2y ax =(0a ≠)在同一坐标系中的图像可能是( )二、填空题:(本大题8个小题,每小题3分,共24分)在每小题中,请将答案直接填在答题卡中对应的横线上.11.如图,直线a ∥b,直线c 与a,b 相交,∠1=70°,则∠2= 度; 12.抛物线23(2)5y x =-+的顶点坐标为 ;13.如图,A 、B 、C 是⊙O 上的三点,∠AOB=100°,则∠ACB= 度;14.已知关于x 的 一元二次方程22340x kx -+=的一个根是1,则k= . 15.100件外观相同的产品中有5件不合格,从中任意抽出1件进行检测,则抽到不合格产品的概率为 . 16.如图,△ABC 中,DE ∥BC,23DE BC =,△ADE 的面积为8,则△ABC 的面积为 ;17.如图,B 、E 、C 、F 在同一直线上,AB ∥DE,AB=DE,BE=CF,AC=6,则DF= ; 18.如图,在平面直角坐标系中,A(2,3),B(-2,1),在x 轴上存在点P ,使P 到A,B 两点的距离之和最小,则P 的坐标为 ;三、解答题:(本大题2个小题,每小题6分,共12分)ab c 12第11题图 A BO C第13题图 AE D C 第16题图 C AFD E 第17题图19.计算:201411(1)()453--︒20.先化简,再求值:22121(1)24x x x x -++÷--,其中,x =3;四、解答题:(本大题2个小题,每小题8分,共16分)21.某数学兴趣小组在全校范围内随机抽取了50同学进行“舌尖上的长沙——我最喜欢的小吃”调查活动,将调查问卷整理后绘成如图所示的不完整条形统计图.请根据所给信息解答以下问题: (1) 请补全条形统计图; (2) 若全校有2000名学生,请估计全校同学中最喜欢“臭豆腐”的同学有多少人; (3) 在一个不透明的口袋中有四个完全相同的小球,把他们分别标号为四种小吃的序号A,B,C,D ,随机摸出一个小球然后放回,再随机摸出一个小球,请用列表或画树形图的方法,求两次都摸到“A ”的概率;小吃类别 口味人数臭豆唆螺 糖油粑22.如图,四边形ABCD 是矩形,把矩形沿对角线AC 折叠,点B 落在点E 处,CE 与AD 相交于点O,(1) 求证:△AEO ≌△CDO ;(2)若∠OCD=30°,,求△ACO 的面积;五、解答题:(本大题2个小题,每小题9分,共18分)23. 为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼的进行,某施工队准备购买甲、乙两种树苗共400棵,对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元。
长沙市历年中考数学试卷及答案

2014年长沙市初中毕业学业水平考试试卷数 学注意事项:1、答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2、必须在答题卡上答题,在草稿纸、试题卷上答题无效;3、答题时,请考生注意各大题题号后面的答题提示;4、请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;5、答题卡上不得使用涂改液、涂改胶和贴纸;6、本学科试卷共26个小题,考试时量120分钟,满分120分。
一、选择题(在下列各题的四个选项中,只有一项是符合题意的。
请在答题卡中填涂符合题意的选项。
本题共10个小题,每小题3分,共30分) 1.21的倒数是( ) A .2B .-2C .21 D .-21 2.下列几何体中主视图、左视图、俯视图完全相同的是( )A .圆锥B .六棱柱C .球D .四棱锥3.一组数据3,3,4,2,8的中位数和平均数分别是 ( )A . 3和3B . 3和4C . 4和3D . 4和4 4.平行四边形的对角线一定具有的性质是( )A .相等B .互相平分C . 互相垂直D .互相垂直且相等 5 .下列计算正确的是( )A .752=+ B .422)(ab ab = C .a a a 632=+ D .43a a a =⋅6 .如图,C 、D 是线段AB 上两点,D 是线段AC 的中点,若AB=10cm,BC=4cm,则AD 的长等于( )A . 2 cmB . 3 cmC . 4 cmD . 6 cm 7 .一个关于x 的一元一次不等式组在数轴上的解集如图所示,则此不等式组的解集是( )A . x >1B .x ≥1C .x >3D .x ≥3 8.如图,已知菱形ABCD 的边长等于2,∠DAB=60°, 则对角线BD 的长为 ( )A . 1 BC . 2D .A B DCAD B姓名 准考证号9.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后能与原图形完全重合的是( )10.函数a y x=与函数2y ax =(0a ≠)在同一坐标系中的图像可能是( )二、填空题:(本大题8个小题,每小题3分,共24分)在每小题中,请将答案直接填在答题卡中对应的横线上.11.如图,直线a ∥b,直线c 与a,b 相交,∠1=70°,则∠2= 度; 12.抛物线23(2)5y x =-+的顶点坐标为 ;13.如图,A 、B 、C 是⊙O 上的三点,∠AOB=100°,则∠ACB= 度;14.已知关于x 的 一元二次方程22340x kx -+=的一个根是1,则k= . 15.100件外观相同的产品中有5件不合格,从中任意抽出1件进行检测,则抽到不合格产品的概率为 . 16.如图,△ABC 中,DE ∥BC,23DE BC =,△ADE 的面积为8,则△ABC 的面积为 ;17.如图,B 、E 、C 、F 在同一直线上,AB ∥DE,AB=DE,BE=CF,AC=6,则DF= ; 18.如图,在平面直角坐标系中,A(2,3),B(-2,1),在x 轴上存在点P ,使P 到A,B 两点的距离之和最小,则P 的坐标为 ;三、解答题:(本大题2个小题,每小题6分,共12分)ab c 12第11题图 A BO C第13题图 AE D C 第16题图 C AFD E 第17题图19.计算:201411(1)()453--︒20.先化简,再求值:22121(1)24x x x x -++÷--,其中,x =3;四、解答题:(本大题2个小题,每小题8分,共16分)21.某数学兴趣小组在全校范围内随机抽取了50同学进行“舌尖上的长沙——我最喜欢的小吃”调查活动,将调查问卷整理后绘成如图所示的不完整条形统计图.请根据所给信息解答以下问题: (1) 请补全条形统计图; (2) 若全校有2000名学生,请估计全校同学中最喜欢“臭豆腐”的同学有多少人; (3) 在一个不透明的口袋中有四个完全相同的小球,把他们分别标号为四种小吃的序号A,B,C,D ,随机摸出一个小球然后放回,再随机摸出一个小球,请用列表或画树形图的方法,求两次都摸到“A ”的概率;小吃类别 口味人数臭豆唆螺 糖油粑22.如图,四边形ABCD 是矩形,把矩形沿对角线AC 折叠,点B 落在点E 处,CE 与AD 相交于点O,(1) 求证:△AEO ≌△CDO ;(2)若∠OCD=30°,,求△ACO 的面积;五、解答题:(本大题2个小题,每小题9分,共18分)23. 为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼的进行,某施工队准备购买甲、乙两种树苗共400棵,对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元。
(整理)湖南省长沙市中考数学试卷解析版

2014年湖南省长沙市中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.12的倒数是()A、2B、-2C、1D、-12.下列几何体中,主视图、左视图、俯视图完全相同的是()=4+=6.(3分)(2014•长沙)如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为()AC=43m7.(3分)(2014•长沙)一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是()8.(3分)(2014•长沙)如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是().9.(3分)(2014•长沙)下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转..==90=180=7210.(3分)(2014•长沙)函数y=与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是()..y=y=二、填空题(共8小题,每小题3分,共24分)11.(3分)(2014•长沙)如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2=110度.12.(3分)(2014•长沙)抛物线y=3(x﹣2)2+5的顶点坐标是(2,5).13.(3分)(2014•长沙)如图,A、B、C是⊙O上的三点,∠AOB=100°,则∠ACB=50度.ACB=∠AOB=×14.(3分)(2014•长沙)已知关于x的一元二次方程2x2﹣3kx+4=0的一个根是1,则k=2.15.(3分)(2014•长沙)100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是.件进行检测,抽到不合格产品的概率是:=故答案为:16.(3分)(2014•长沙)如图,在△ABC中,DE∥BC,=,△ADE的面积是8,则△ABC的面积为18.=(=17.(3分)(2014•长沙)如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=6.18.(3分)(2014•长沙)如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是(﹣1,0).的坐标代入得:.三、解答题(共2小题,每小题6分,共12分)19.(6分)(2014•长沙)计算:(﹣1)2014+﹣()﹣1+sin45°.20.(6分)(2014•长沙)先简化,再求值:(1+)+,其中x=3.••=.四、解答题(共2小题,每小题8分,共16分)21.(8分)(2014•长沙)某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:请根据所给信息解答以下问题:(1)请补全条形统计图;(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.××.22.(8分)(2014•长沙)如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E 处,CE与AD相交于点O.(1)求证:△AOE≌△COD;(2)若∠OCD=30°,AB=,求△AOC的面积.,÷=2=××=五、解答题(共2小题,每小题9分,共18分)23.(9分)(2014•长沙)为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼地进行,某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.(1)若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?(2)若购买甲种树苗的金额不少于购买一中树苗的金额,至少应购买甲种树苗多少棵?24.(9分)(2014•长沙)如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC 的中点D,过点D作⊙O的切线交AC于点E.(1)求证:DE⊥AC;(2)若AB=3DE,求tan∠ACB的值.x=ACB=六、解答题(共2小题,每小题10分,共20分)25.(10分)(2014•长沙)在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),(,),…都是“梦之点”,显然,这样的“梦之点”有无数个.(1)若点P(2,m)是反比例函数y=(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+,试求出t的取值范围.y=,,则(=42b+=.<,进而求出(y=≠x=,,时,,)k=,,(===.<>=,>26.(10分)(2014•长沙)如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).(1)求a,b,c的值;(2)求证:在点P运动的过程中,⊙P始终与x轴相交;(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.,进而与,±,x,,x r=r=>a PA=,PM=PN=PH=aAM=,,=时,=4a;=4(负数舍去)a2或2。
2014湖南省长沙市中考数学试卷

2014 中考数学试卷精编 word 版2014 年湖南省长沙市中考数学试卷(满分 120 分,考试时间 120 分钟)一、选择题(在下列各题的四个选项中,只有一项是符合题意的,请在答题卡中填涂符合题意的选项 . 本题共 10 个小题,每小题 3 分,共 30 分) 1、 1.( 2014 湖南省长沙市,第1 题, 3分)1的倒数是( )1 21A2B-2DC-22【答案】 A2. ( 2014 湖南省长沙市,第 2 题, 3 分) 下列几何体中,主视图、左视图、俯视图完全相同的是( ) A圆锥B六棱柱C球D四棱锥【答案】 C3. ( 2014 湖南省长沙市,第 3 题, 3 分) 一组数据 3, 3, 4, 2, 8 的中位数和平均数分别是( ) A 3和3 B 3和4C4和3 D 4和4【答案】 B4. ( 2014 湖南省长沙市,第 A 、相等B 、互相平分4 题, 3 分) 平行四边形的对角线一定具有的性质是(C 、互相垂直D 、互相垂直且相等)【答案】B5. ( 2014 湖南省长沙市,第 5 题, 3 分) 下列计算正确的是()A 257 B ab 224C 2a+3a=6aD a a 3a 4ab 【答案】 D 6.AC( 2014 湖南省长沙市,第 6 题, 3 分) 如图, C 、 D的中点,若 AB=10 cm,BC=4 cm, 则 AD 的长为()是线段AB上的两点,且D 是线段A 2 cmB 3 cmC 4 cmD 6 cm【答案】B2014 中考数学试卷精编 word 版7. ( 2014 湖南省长沙市,第 7 题, 3 分) 一个关于 x 的一元一次不等式组的解集在数轴上 的表示如图,则该不等式组的解集是( )A x > 1B x ≥1C x > 3Dx ≥3【答案】 C8. j ( 2014 湖南省长沙市, 第则对角线 BD 的长是()8 题,3 分)如图,已知菱形ABCD的边长为2,∠ DAB=60°,A 1B3C2D2 3【答案】 C9. j ( 2014 湖南省长沙市,第为旋转中心,顺时针旋转9 题, 3 分)下列四个图形图案中,分别以它们所在圆120°后,能与原图形完全重合的是()的圆 心AB C D【答案】 A10. ( 2014 湖南省长沙市,第 10 题, 3 分)函数 ya与y ax 2(a 0) 在同一平面直角坐x标系中的图象可能是()yyyyoooxoxxxA BCD2014 中考数学试卷精编word 版【答案】 D二、填空题(本题共8 个小题,每小题 3 分,共 24 分.)11. ( 2014 湖南省长沙市,第11题,3分)如图,直线a//b,直线 c 分别与 a, b 相交,∠ 1=70°则∠ 2=度 .eC1aOb2A B第11题图第 13题图【答案】 11012. ( 2014 湖南省长沙市,第12 题, 3 分)抛物线y 3 x 22.5 的顶点坐标是【答案】( 2, 5)13.( 2014 湖南省长沙市,第 13 题,3 分)如图,A,B,C是⊙O上的三点,∠AOB=100°则∠ ACB=度.【答案】 5014.(2014湖南省长沙市,第14题,3分)已知关于x的一元二次方程2x23kx 4 0 2x23kx 4 0 的一个根是1,则 k=.【答案】 215. ( 2014 湖南省长沙市,第15 题, 3 分)100件外观相同的产品中有中任意抽取 1 件进行检测,抽到不合格产品的概率是.5 件不合格,现从【答案】12016. ( 2014湖南省长沙市,第16 题,3分)如图,在DE2 ABC 中, DE//BC ,,ADEBC3的面积是8,则 ABC 的面积为.【答案】 182014 中考数学试卷精编 word 版17. j ( 2014 湖南省长沙市,第 17 题, 3 分)如图,点 AB=DE , BE=CF , AC=6 ,则 DF=.B ,E ,C , F 在一条直线上,AB//DE,【答案】618.jsc ( 2014 湖南省长沙市,第 18 题, 3 分) 如图在平面直角坐标系中,已知点 A ( 2, 3),点 B (- 2,1),在 x 轴上存在点 P 到 A ,B 两点的距离之和最小,则 P 点的坐标是 .【答案】(- 1, 0)yAAAD32EB1DOx123 –3 –2 –1–1BCECF–2B第 16题–3第 17题第 18题三、解答题(本题共 2 个小题,每小题 6 分,共12 分)20141 119. ( 2014 湖南省长沙市,第19 题,6 分)计算382 sin45013【答案】 解:原式 =1+2- 3+22= 1220. ( 2014 湖南省长沙市,第20 题, 61 x 22x 1,分) 先化简,再求值: 1x 24x 2其中 x = 3【答案】 解:原式 =x1 · (x2)( x 2) = x 2 x 2( x 1) 2 x 1当 x 3 时,原式= 32 = 53 12四、解答题(本题共2 个小题,每小题8 分,共 16 分)21. ( 2014 湖南省长沙市,第 21 题, 8 分)某数学兴趣小组在全校范围内随机抽取了 50 名同学进行 “舌尖上的长沙―――我最喜爱的长沙小吃” 调查活动, 将调查问卷整理后绘制成2014 中考数学试卷精编word 版如图所示的不完整条形统计图 .y252021调查问卷1514在下面四种长沙小吃中你最10喜爱的是()单选55A 臭豆腐B 口味虾C 田螺D 糖油粑粑0臭豆腐口味虾田螺糖油粑粑X请根据所给信息解答以下问题:(1)请补全条形统计图;(2)若全校有 2000 名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号 A ,B, C, D,随机地摸出一个小球然后放回,再随机地摸出一个小球. 请用列表或画树形图的方法,求出恰好两次都摸到“ A ”的概率 .【答案】解:( 1) 50-14- 21-5= 10(条形图略)( 2) 2000×14= 560(人)50∴估计全校同学中最喜爱“臭豆腐”的同学有560 人.( 3)A B C DA(A,A)(A,B)(A,C)(A,D)B(B,A)(B,B)(B,C)(B,D)C(C,A)(C,B)(C,C)(C,D)D(D,A)(D,B)(D,C)(D,D)共有 16 种等可能结果,其中两次都摸到A的有 1 种,∴P(两次都摸到A)=11622. j( 2014 湖南省长沙市,第22 题, 8 分)如图,四边形ABCD 是矩形,把矩形沿对角线AC 折叠,点 B 落在点 E 处, CE 与 AD 相交于点O.(1)求证:AOE ≌ COD ;(2) 若∠ OCD=30 °, AB= 3 ,求AOC 的面积。
湖南省长沙市2014年中考数学试题及答案

2014年湖南省长沙市中考数学试卷一、选择题(共10小题,每小题3分,共30分)1.12的倒数是()A.2 B.-2 C.12D.-122.下列几何体中,主视图、左视图、俯视图完全相同的是()A.圆锥B.六棱柱C.球D.四棱锥3.(3分)(2014·长沙)一组数据3,3,4,2,8的中位数和平均数分别是()A.3和3 B.3和4 C.4和3 D.4和44.(3分)(2014·长沙)平行四边形的对角线一定具有的性质是()A.相等B.互相平分C.互相垂直D.互相垂直且相等5.(3分)(2014·长沙)下列计算正确的是()AB.()224ab ab=C.236a a a+=D.34a a a⋅=6.(3分)(2014·长沙)如图,C、D是线段AB上的两点,且D是线段AC的中点,若10cmAB=,4cmBC=,则AD的长为()D C BAA.2cm B.3cm C.4cm D.6cm7.(3分)(2014·长沙)一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是()A.1x>B.1x≥C.3x>D.3x≥8.(3分)(2014·长沙)如图,已知菱形ABCD的边长为2,60DAB∠=︒,则对角线BD的长是()60°D CBAA.1B C.2D.9.(3分)(2014·长沙)下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是()D.C.B.A.10.(3分)(2014·长沙)函数ayx=与()20y ax a=≠在同一平面直角坐标系中的图象可能是()A. B. C. D.二、填空题(共8小题,每小题3分,共24分)11.(3分)(2014·长沙)如图,直线a b∥,直线c分别与a b,相交,若170∠=︒,则2∠=__________度.bac21312cab12.(3分)(201·长沙)抛物线()2325y x=-+的顶点坐标是__________.13.(3分)(2014·长沙)如图,A、B、C是O上的三点,100A B∠⋅=︒,则ACB∠=__________度.14.(3分)(2014·长沙)已知关于x的一元二次方程22340x kx-+=的一个根是1,则k=__________.15.(3分)(2014·长沙)100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是__________.16.(3分)(2014·长沙)如图,在ABC△中,DE BC∥,23DEBC=,ADE△的面积是8,则ABC△面积为__________.ED CBA17.(3分)(2014·长沙)如图,点B 、E 、C 、F 在一条直线上,AB DF ∥,AB DE =,BE CF =,6AC =,则DF =__________.FEDCB A18.(3分)(2014·长沙)如图,在平面直角坐标系中,已知点()23A ,,点()21B -,,在x 轴上存在点P 到A ,B 两点的距离之和最小,则P 点的坐标是__________.三、解答题(共2小题,每小题6分,共12分)19.(6分)(2014·长沙)计算:()1201411453-⎛⎫-++︒ ⎪⎝⎭.20.(6分)(2014·长沙)先简化,再求值:22121124x x x x -+⎛⎫++ ⎪--⎝⎭,其中3x =. 四、解答题(共2小题,每小题8分,共16分) 21.(8分)(2014·长沙)某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙-我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图: 请根据所给信息解答以下问题:在下面四种长沙小吃中,你最喜欢的是( )(单选)D.糖油粑粑C.唆螺B.口味虾A.臭豆腐调查问卷人数种类(1)请补全条形统计图;(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A 、B 、C 、D ,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A ”的概率. 22.(8分)(2014·长沙)如图,四边形ABCD 是矩形,把矩形沿对角线AC 折叠,点B 落在点E 处,CE 与AD 相交于点O .OEDCB A(1)求证:AOE COD △≌△;(2)若30OCD ∠=︒,AB AOC △的面积.五、解答题(共2小题,每小题9分,共18分) 23.(9分)(2014·长沙)为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼地进行,某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.(1)若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?(2)若购买甲种树苗的金额不少于购买一中树苗的金额,至少应购买甲种树苗多少棵? 24.(9分)(2014·长沙)如图,以ABC △的一边AB 为直径作O ,O 与BC 边的交点恰好为BC 的中点D ,过点D 作O 的切线交AC 于点E .(1)求证:DE AC ⊥;(2)若3AB DE =,求tan ACB ∠的值.六、解答题(共2小题,每小题10分,共20分) 25.(10分)(2014·长沙)在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(-1,-1),(0,0),,…都是“梦之点”,显然,这样的“梦之点”有无数个. (1)若点()2P m ,是反比例函数ny x=(n 为常数,0n ≠)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数31y kx s =+-(k ,s 是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;(3)若二次函数21y ax bx =++(a ,b 是常数,0a >)的图象上存在两个不同的“梦之点”()11A x x ,,()22B x x ,,且满足122x -<<,122x x -=,令2157248t b b =-+,试求出t 的取值范围. 26.(10分)(2014·长沙)如图,抛物线2y ax bx c =++(a ,b ,c 是常数,0a ≠)的对称轴为y 轴,且经过(0,0)和116⎫⎪⎭,两点,点P 在该抛物线上运动,以点P 为圆心的P 总经过定点()02A ,.(1)求a ,b ,c 的值;(2)求证:在点P 运动的过程中,P 始终与x 轴相交;(3)设P 与x 轴相交于()10M x ,,()20N x ,()12x x <两点,当AMN △为等腰三角形时,求圆心P 的纵坐标.2014年湖南省长沙市中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.A考点:倒数.分析:根据乘积为的1两个数倒数,可得一个数的倒数. 解答:解:12的倒数是2, 故选:A .点评:本题考查了倒数,分子分母交换位置是求一个数的倒数的关键. 2.C考点:简单几何体的三视图.分析:找到从物体正面、左面和上面看得到的图形全等的几何体即可.解答:解:A.圆锥的主视图、左视图、俯视图分别为等腰三角形,等腰三角形,圆及圆心,故A选项不符合题意;B.六棱柱的主视图、左视图、俯视图分别为四边形,四边形,六边形,故B选项不符合题意;C.球的主视图、左视图、俯视图分别为三个全等的圆,故C选项符合题意;D.四棱锥的主视图、左视图、俯视图分别为三角形,三角形,四边形,故D选项不符合题意;故选C.点评:考查三视图的有关知识,注意三视图都相同的常见的几何体有球和正方体.3.B考点:中位数;算术平均数.分析:根据中位数及平均数的定义求解即可.解答:解:将数据从小到大排列为:2,3,3,4,8,则中位数是3,平均数2334845++++==.故选B.点评:本题考查了平均数及中位数的知识,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.4.B考点:平行四边形的性质.分析:根据平行四边形的对角线互相平分可得答案.解答:解:平行四边形的对角线互相平分,故选:B.点评:此题主要考查了平行四边形的性质,关键是掌握平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.5.D考点:幂的乘方与积的乘方;实数的运算;合并同类项;同底数幂的乘法.分析:根据二次根式的加减,可判断A,根据积的乘方,可判断B,根据合并同类项,可判断C,根据同底数幂的乘法,可判断D.解答:解:A.被开方数不能相加,故A错误;B.积的乘方等于每个因式分别乘方,再把所得的幂相乘,故B错误;C.系数相加字母部分不变,故C错误;D.底数不变指数相加,故D正确;故选:D.点评:本题考查了积的乘方,积的乘方等于每个因式分别乘方,再把所得的幂相乘.6.B考点:两点间的距离.分析:由10cmAB=,4cmBC=,可求出6cmAC AB BC=-=,再由点D是AC的中点,则可求得AD 的长.解答:解:∵10cmAB=,4cmBC=,∴6cmAC AB BC=-=,又点D是AC的中点,∴143m2AD AC==,答:AD的长为3cm.故选:B.点评:本题考查了两点间的距离,利用线段差及中点性质是解题的关键.7.C考点:在数轴上表示不等式的解集.分析:根据不等式组的解集是大于大的,可得答案.解答:解:一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是3x>.故选:C.点评:本题考查了不等式组的解集,不等式组的解集是大于大的.8.C考点:菱形的性质.分析:利用菱形的性质以及等边三角形的判定方法得出DAB△是等边三角形,进而得出BD的长.解答:解:∵菱形ABCD的边长为2,∴2AD AB==,又∵60DAB∠=︒,∴DAB△是等边三角形,∴2AD BD AB===,则对角线BD的长是2.故选:C.点评:此题主要考查了菱形的性质以及等边三角形的判定,得出DAB△是等边三角形是解题关键.9.A考点:旋转对称图形.分析:求出各旋转对称图形的最小旋转角度,继而可作出判断.解答:解:A.最小旋转角度3601203==︒;B.最小旋转角度360904==︒;C.最小旋转角度3601802==︒;D.最小旋转角度360725==︒;综上可得:顺时针旋转120°后,能与原图形完全重合的是A.故选A.点评:本题考查了旋转对称图形的知识,求出各图形的最小旋转角度是解题关键.10.D考点:二次函数的图象;反比例函数的图象.分析:分0a>和0a<两种情况,根据二次函数图象和反比例函数图象作出判断即可得解.解答:解:0a>时,ayx=的函数图象位于第一三象限,2y ax=的函数图象位于第一二象限且经过原点,a<时,ayx=的函数图象位于第二四象限,2y ax=的函数图象位于第三四象限且经过原点,纵观各选项,只有D选项图形符合.故选D.点评:本题考查了二次函数图象,反比例函数图象,熟记反比例函数图象与二次函数图象的性质是解题的关键,难点在于分情况讨论.二、填空题(共8小题,每小题3分,共24分)11.110考点:平行线的性质;对顶角、邻补角.专题:计算题.分析:直线a b∥,直线c分别与a,b相交,根据平行线的性质,以及对顶角的定义可求出.解答:解:∵170∠=︒,∴3170∠=∠=︒,∵a b∥,∴23180∠+∠=︒,∴218070110∠=︒-︒=︒.故填110.点评:本题考查两直线平行,同位角相等及邻补角互补.12.(2,5)考点:二次函数的性质.分析:由于抛物线()2y a x h k=-+的顶点坐标为()h k,,由此即可求解.解答:解:∵抛物线()2325y x=-+,∴顶点坐标为:(2,5).故答案为:(2,5).点评:此题主要考查了二次函数的性质,解题的关键是熟练掌握抛物线()2y a x h k=-+的顶点坐标为()h k,.13.50考点:圆周角定理.分析:根据圆周角定理即可直接求解.解答:解:111005022ACB A B∠=∠⋅=⨯︒=︒.故答案是:50.点评:此题主要考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.14.2考点:一元二次方程的解.分析:把1x=代入已知方程列出关于k的一元一次方程,通过解方程求得k的值.解答:解:依题意,得2213140k⨯-⨯+=,即2340k-+=,解得,2k=.故答案是:2.点评:本题考查了一元二次方程的解的定义.此题是通过代入法列出关于k的新方程,通过解新方程可以求得k的值.15.1 20考点:概率公式.分析:由100件外观相同的产品中有5件不合格,直接利用概率公式求解即可求得答案.解答:解:∵100件外观相同的产品中有5件不合格,∴从中任意抽取1件进行检测,抽到不合格产品的概率是:5110020=. 故答案为:120. 点评: 此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比. 16.18考点: 相似三角形的判定与性质.分析: 根据相似三角形的判定,可得ADE ABC △∽△,根据相似三角形的性质,可得答案. 解答:解;∵在ABC △中,DE BC ∥, ∴ADE ABC △∽△. ∵23DE BC =, ∴222439ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭△△, 849ABCS =△, ∴18ABC S =△,故答案为:18.点评: 本题考查了相似三角形判定与性质,利用了相似三角形的判定与性质. 17.6考点: 全等三角形的判定与性质.分析: 根据题中条件由SAS 可得ABC DEF △≌△,根据全等三角形的性质可得6AC DF ==. 解答:证明:∵AB DE ∥, ∴B DEF ∠=∠ ∵BE CF =, ∴BC EF =,在ABC △和DEF △中, AB DE B DEF BC EF =⎧⎪∠=∠⎨⎪=⎩, ∴ABC DEF △≌△()SAS ,∴6AC DF ==. 故答案是:6.点评: 本题主要考查了全等三角形的判定及性质问题,应熟练掌握.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件. 18.(-1,0)考点: 轴对称-最短路线问题;坐标与图形性质.分析: 作A 关于x 轴的对称点C ,连接BC 交x 轴于P ,则此时AP BP +最小,求出C 的坐标,设直线BC 的解析式是y kx b =+,把B 、C 的坐标代入求出k 、b ,得出直线BC 的解析式,求出直线与x 轴的交点坐标即可.解答:解:作A 关于x 轴的对称点C ,连接BC 交x 轴于P ,则此时AP BP +最小, ∵A 点的坐标为(2,3),B 点的坐标为(-2,1), ∴C (2,-3),设直线BC 的解析式是:y kx b =+, 把B 、C 的坐标代入得:2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩.即直线BC 的解析式是1y x =--, 当0y =时,10x ---=,解得:1x =-,∴P 点的坐标是(-1,0). 故答案为:(-1,0).点评: 本题考查了一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,轴对称-最短路线问题的应用,关键是能找出P 点,题目具有一定的代表性,难度适中. 三、解答题(共2小题,每小题6分,共12分)19.考点:实数的运算;负整数指数幂;特殊角的三角函数值.分析: 本题涉及零指数幂、乘方、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果. 解答:解:原式=1+2-3+1=1.点评: 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算. 20.考点: 分式的化简求值. 专题: 计算题.分析: 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,将x 的值代入计算即可求出值. 解答:解:原式()()()2222121x x x x x +--+=⋅-- ()()()222121x x x x x +--=⋅--21x x +=-, 当3x =时,原式325312+==-. 点评: 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键. 四、解答题(共2小题,每小题8分,共16分)21.考点:条形统计图;用样本估计总体;列表法与树状图法. 专题: 计算题. 分析:(1)总人数以及条形统计图求出喜欢“唆螺”的人数,补全条形统计图即可; (2)求出喜欢“臭豆腐”的百分比,乘以2000即可得到结果;(3)列表得出所有等可能的情况数,找出恰好两次都摸到“A ”的情况数,即可求出所求的概率. 解答:解:(1)根据题意得:喜欢“唆螺”人数为:50-(14+21+5)=10(人), 补全统计图,如图所示:种类人数(2)根据题意得:2000×1450×100%=560(人),则估计全校同学中最喜爱“臭豆腐”的同学有560人; (3所有等可能的情况有16种,其中恰好两次都摸到“A ”的情况有1种,则116P =. 点评: 此题考查了条形统计图,用样本估计总体,以及列表法与树状图法,弄清题意是解本题的关键. 22.考点: 翻折变换(折叠问题). 分析:(1)根据矩形的对边相等可得AB CD =,90B D ∠=∠=︒,再根据翻折的性质可得AB AE =,B E ∠=∠,然后求出AE CD =,D E ∠=∠,再利用“角角边”证明即可;(2)根据全等三角形对应边相等可得AO CO =,解直角三角形求出CO ,然后利用三角形的面积公式列式计算即可得解. 解答:(1)证明:∵四边形ABCD 是矩形, ∴AB CD =,90B D ∠=∠=︒,∵矩形ABCD 沿对角线AC 折叠点B 落在点E 处, ∴AB AE =,B E ∠=∠, ∴AE CD =,D E ∠=∠, 在AOE △和COD △中, D E AOE COD AE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴AOE COD △≌△()AAS ; (2)解:∵AOE COD △≌△, ∴AO CO =,∵30OCD ∠=︒,AB =,∴cos302CO CD =÷︒==, ∴AOC △的面积11222AO CD =⋅=⨯点评: 本题考查了翻折变换的性质,全等三角形的判定与性质,矩形的性质,熟记各性质并确定出三角形全等的条件是解题的关键.五、解答题(共2小题,每小题9分,共18分)23.考点: 一元一次不等式的应用;二元一次方程组的应用. 分析:(1)设购买甲种树苗x 棵,则购买乙种树苗(400-x )棵,根据购买两种树苗的总金额为90000元建立方程求出其解即可;(2)设至少应购买甲种树苗a 棵,则购买乙种树苗(400-a )棵,根据购买甲种树苗的金额不少于购买一中树苗的金额建立不等式求出其解即可. 解答:解:(1)设购买甲种树苗x 棵,则购买乙种树苗(400-x )棵,由题意,得()20030040090000x x +-=,解得:300x =,∴购买乙种树苗400-300=100棵,答:购买甲种树苗300棵,则购买乙种树苗100棵;(2)设至少应购买甲种树苗a 棵,则购买乙种树苗(400-a )棵,由题意,得 ()200300400a a -≥,解得:240a ≥.答:至少应购买甲种树苗240棵.点评: 本题考查了列一元一次方程解实际问题的运用,一元一次不等式的解法的运用,解答时建立方程和不等式是关键. 24.考点: 切线的性质. 分析:(1)连接OD ,可以证得DE OD ⊥,然后证明OD AC ∥即可证明DE AC ⊥; (2)利用ADE CDE △∽△,求出DE 与CE 的比值即可. 解答:(1)证明:连接OD , ∵D 是BC 的中点,OA OB =, ∴OD 是ABC △的中位线,∴OD AC ∥,∵DE 是O 的切线, ∴OD DE ⊥, ∴DE AC ⊥;(2)解:连接AD , ∵AB 是O 的直径, ∴90ADB ∠=︒, ∵DE AC ⊥,∴90ADC DEC AED ∠=∠=∠=︒, ∴ADE DCE ∠=∠ 在ADE DCE =∠△, AED DECADE DCE ∠=∠⎧⎨∠=∠⎩∴CDE ADE △∽△,∴DE CEAE DE=, 设tan ACB x ∠=,CE a =,则DE ax =,3AC ax =,3AE ax a =-,∴3ax a ax a ax =-,整理得:2310x x -+=,解得:x ,∴tan ACB ∠=.点评: 本题主要考查了切线的性质的综合应用,解答本题的关键在于如何利用三角形相似求出线段DE 与CE 的比值.六、解答题(共2小题,每小题10分,共20分) 25.考点: 二次函数综合题.分析:(1)先由“梦之点”的定义得出2m =,再将点P 坐标代入ny x=,运用待定系数法即可求出反比例函数的解析式;(2)假设函数31y kx s =+-(k ,s 是常数)的图象上存在“梦之点”(x ,x ),则有31x kx s =+-,整理得()311k x s -=-,再分三种情况进行讨论即可;(3)先将()11A x x ,,()22B x x ,代入21y ax bx =++,得到()211110ax b x +-+=,()222110ax b x +-+=,根据方程的解的定义可知1x ,2x 是一元二次方程()2110ax b x +-+=的两个根,由根与系数的关系可得121b x x a -+=,121x x a⋅=,则()()222121212221444b b a x x x x x x a -+--=+-⋅==,整理得出()222212b b a -=+-,则()22157612214848t b b a =-+=++.再由122x -<<,122x x -=,得出244x -<<,1288x x -<⋅<,即188a -<<,又0a >,解不等式组得出18a >,进而求出t 的取值范围.解答:解:(1)∵点()2P m ,是“梦之点”,∴2m =,∵点()22P ,在反比例函数ny x=(n 为常数,0n ≠)的图象上, ∴224n =⨯=,∴反比例函数的解析式为4y x=; (2)假设函数31y kx s =+-(k ,s 是常数)的图象上存在“梦之点”(x ,x ), 则有31x kx s =+-, 整理,得()311k x s -=-,当310k -≠,即13k ≠时,解得131s x k -=-;当310k -=,10s -=,即13k =,1s =时,x 有无穷多解;当310k -=,10s -≠,即13k =,1s ≠时,x 无解;综上所述,当13k ≠时,“梦之点”的坐标为113131s s k k --⎛⎫ ⎪--⎝⎭,;当13k =,1s =时,“梦之点”有无数个;当13k =,1s ≠时,不存在“梦之点”;(3)∵二次函数21u ax bx =++(a ,b 是常数,0a >)的图象上存在两个不同的“梦之点”()11A x x ,,()22B x x ,,∴2211122211x ax bx x ax bx =++=++,, ∴()211110ax b x +-+=,()222110ax b x +-+=, ∴1x ,2x 是一元二次方程()2110ax b x +-+=的两个不等实根, ∴121b x x a -+=,121x x a⋅=,∴()()222212121221121444b b b x x x x x x a a a --+⎛⎫-=+-⋅=-⋅== ⎪⎝⎭, ∴()2222441212b b a a a -=+-=+-, ∴()()22215715761221221484848t b b a a =-+=+-+=++. ∵122x -<<,122x x -=, ∴240x -<<或204x <<, ∴244x -<<, ∴1288x x -<⋅<,∴188a-<<, ∵0a >, ∴18a >∴()261256117214816486a ++>+=, ∴176t >. 点评: 本题是二次函数的综合题,考查了运用待定系数法求反比例函数的解析式,形如ax b =的方程的解的情况,一元二次方程根与系数的关系,不等式的性质等知识,综合性较强,有一定难度. 26.考点:二次函数综合题. 分析:(1)根据题意得出二次函数一般形式进而将已知点代入求出a ,b ,c 的值即可; (2)设()P x y ,,表示出P 的半径r ,进而与214x 比较得出答案即可;(3)分别表示出AM ,AN 的长,进而分别利用当AM AN =时,当AM MN =时,当AN MN =时,求出a 的值,进而得出圆心P 的纵坐标即可.解答:解:(1)∵抛物线2y ax bx c =++(a ,b ,c 是常数,0a ≠)的对称轴为y 轴,且经过(0,0)和116⎫⎪⎭,两点,∴抛物线的一般式为:2y ax =,∴2116a =,解得:14a =±,∵图象开口向上,∴14a =, ∴抛物线解析式为:214y x =,故14a =,0b c ==;(2)设()P x y ,,P 的半径r ,又∵214y x =-,则r =化简得:214r x >, ∴点P 在运动过程中,P 始终与x 轴相交;(3)设214P a a ⎛⎫ ⎪⎝⎭,,∵PA =,作PH MN ⊥于H ,则PM PN =, 又∵214PH a =,则2MH NH ==,故4MN =,∴()20M a -,,()20N a +,,又∵()02A ,,∴AM =AN =当AM AN =解得:0a =,当AM MN =4,解得:2a =±,则2144a =+;当AN MN =4,解得:2a =-±,则2144a =-;综上所述,P 的纵坐标为0或4+4-点评:此题主要考查了二次函数综合以及等腰三角形的性质以及勾股定理等知识,根据题意利用数形结合以及分类讨论得出是解题关键.。
专题 压轴题--湖南省2014-2017年中考数学试题分项解析(解析版)

一、选择题1.(2014年,湖南省长沙市,3分)函数y=ax与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是()【考点】1.二次函数的图象;2.反比例函数的图象.2.(2014年湖南省株洲市,3分)在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是()A.(66,34)B.(67,33)C.(100,33)D.(99,34)3.(2016年湖南省娄底市,3分)如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值()A.不变B.增大C.减小D.先变大再变小【答案】C.考点:锐角三角函数的增减性.4.(2016年湖南省永州市,4分)我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:3根据上表规律,某同学写出了三个式子:①log 216=4,②log 525=5,③log 2=﹣1.其中正确的是( ) A .①② B .①③ C .②③ D .①②③ 【答案】B. 【解析】试题分析:根据表格中的规律可得:①因为24=16,此选项正确;②因为55=3125≠25,所以此选项错误;③因为2﹣1=21,所以此选项正确;故答案选B . 考点:实数的运算.5. (2016年湖南省岳阳市,3分)对于实数a ,b ,我们定义符号max{a ,b}的意义为:当a ≥b 时,max{a ,b}=a ;当a <b 时,max{a ,b]=b ;如:max{4,﹣2}=4,max{3,3}=3,若关于x 的函数为y=max{x+3,﹣x+1},则该函数的最小值是( ) A .0B .2C .3D .4【答案】B 【解析】考点:分段函数6.(2016年湖南省长沙市,3分)已知抛物线y=ax 2+bx+c (b >a >0)与x 轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y 轴左侧; ②关于x 的方程ax 2+bx+c+2=0无实数根; ③a ﹣b+c ≥0; ④的最小值为3.其中,正确结论的个数为( ) A .1个 B .2个 C .3个 D .4个 【答案】D .考点:二次函数的图象与系数的关系.1.(2014年,湖南省衡阳市,3分)如图,在平面直角坐标系xOy中,已知点M0的坐标为(1,0),将线段OM0绕原点O逆时针方向旋转45°,再将其延长到M1,使得M1M0⊥OM0,得到线段OM1;又将线段OM1绕原点O逆时针方向旋转45°,再将其延长到M2,使得M2M1⊥OM1,得到线段OM2;如此下去,得到线段OM3,OM4,OM5,…根据以上规律,请直接写出OM2014的长度为▲ .2.(2015·湖南常德)取一个自然数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1。
2014各地中考题北师大版九年级上册数学 湖南长沙

湖南省长沙市2014年中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.12的倒数是()A、2B、-2C、1D、-12.下列几何体中,主视图、左视图、俯视图完全相同的是()=4+=6.(3分)(2014•长沙)如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为()AC=43m7.(3分)(2014•长沙)一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是()8.(3分)(2014•长沙)如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是().9.(3分)(2014•长沙)下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转..==90=180=7210.(3分)(2014•长沙)函数y=与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是()..y=y=二、填空题(共8小题,每小题3分,共24分)11.(3分)(2014•长沙)如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2=110度.12.(3分)(2014•长沙)抛物线y=3(x﹣2)2+5的顶点坐标是(2,5).13.(3分)(2014•长沙)如图,A、B、C是⊙O上的三点,∠AOB=100°,则∠ACB=50度.ACB=∠AOB=×14.(3分)(2014•长沙)已知关于x的一元二次方程2x2﹣3kx+4=0的一个根是1,则k=2.15.(3分)(2014•长沙)100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是.件进行检测,抽到不合格产品的概率是:=故答案为:16.(3分)(2014•长沙)如图,在△ABC中,DE∥BC,=,△ADE的面积是8,则△ABC的面积为18.=(=17.(3分)(2014•长沙)如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=6.18.(3分)(2014•长沙)如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是(﹣1,0).的坐标代入得:.三、解答题(共2小题,每小题6分,共12分)19.(6分)(2014•长沙)计算:(﹣1)2014+﹣()﹣1+sin45°.20.(6分)(2014•长沙)先简化,再求值:(1+)+,其中x=3.••=.四、解答题(共2小题,每小题8分,共16分)21.(8分)(2014•长沙)某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:请根据所给信息解答以下问题:(1)请补全条形统计图;(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.××.22.(8分)(2014•长沙)如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E 处,CE与AD相交于点O.(1)求证:△AOE≌△COD;(2)若∠OCD=30°,AB=,求△AOC的面积.,÷=2=××=五、解答题(共2小题,每小题9分,共18分)23.(9分)(2014•长沙)为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼地进行,某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.(1)若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?(2)若购买甲种树苗的金额不少于购买一中树苗的金额,至少应购买甲种树苗多少棵?24.(9分)(2014•长沙)如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC 的中点D,过点D作⊙O的切线交AC于点E.(1)求证:DE⊥AC;(2)若AB=3DE,求tan∠ACB的值.x=ACB=六、解答题(共2小题,每小题10分,共20分)25.(10分)(2014•长沙)在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),(,),…都是“梦之点”,显然,这样的“梦之点”有无数个.(1)若点P(2,m)是反比例函数y=(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+,试求出t的取值范围.y=,,则(=42b+=.<,进而求出(y=≠x=,,时,,)k=,,(===.<>=,>26.(10分)(2014•长沙)如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).(1)求a,b,c的值;(2)求证:在点P运动的过程中,⊙P始终与x轴相交;(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.,进而与,±,x,,x r=r=>a PA=,PM=PN=PH=aAM=,,=时,=4a;=4(负数舍去)a2或2。
2014长沙市中考数学试卷及详细答案11

黄坝中心学校九年级第二次模拟考试一、选择题(本题共10个小题,每个小题4分 ,共40分) 1.21的倒数是( ) A .2B .-2C .21 D .-21 2.下列几何体中主视图、左视图、俯视图完全相同的是( )A .圆锥B .六棱柱C .球D .四棱锥3.一组数据3,3,4,2,8的中位数和平均数分别是 ( )A . 3和3B . 3和4C . 4和3D . 4和4 4.平行四边形的对角线一定具有的性质是( )A .相等B .互相平分C . 互相垂直D .互相垂直且相等 5 .下列计算正确的是( )A .752=+ B .422)(ab ab = C .a a a 632=+ D .43a a a =⋅6 .如图,C 、D 是线段AB 上两点,D 是线段AC 的中点,若AB=10cm,BC=4cm,则AD 的长等于( )A . 2 cmB . 3 cmC . 4 cmD . 6 cm7 .一个关于x 的一元一次不等式组在数轴上的解集如图所示,则此不等式组的解集是( )A . x >1B .x ≥1C .x >3D .x ≥38.如图,已知菱形ABCD 的边长等于2,∠DAB=60°, 则对角线BD 的长为 ( )A . 1 BC . 2D .9.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后能与原图形完全重合的是( )A B D CC10.函数ay x=与函数2y ax =(0a ≠)在同一坐标系中的图像可能是( ) 二、填空题:(本大题8个小题,每小题3分,共24分)在每小题中,请将答案直接填在答题卡中对应的横线上.11.如图,直线a ∥b,直线c 与a,b 相交,∠1=70°,则∠2= 度; 12.抛物线23(2)5y x =-+的顶点坐标为 ;13.如图,A 、B 、C 是⊙O 上的三点,∠AOB=100°,则∠ACB= 度;14.已知关于x 的 一元二次方程22340x kx -+=的一个根是1,则k= . 15.100件外观相同的产品中有5件不合格,从中任意抽出1件进行检测,则抽到不合格产品的概率为 . 16.如图,△ABC 中,DE ∥BC,23DE BC =,△ADE 的面积为8,则△ABC 的面积为 ;17.如图,B 、E 、C、F 在同一直线上,AB ∥DE,AB=DE,BE=CF,AC=6,则DF= ; 18.如图,在平面直角坐标系中,A(2,3),B(-2,1),在x 轴上存在点P ,使P 到A,B 两点的距离之和最小,则P 的坐标为 ;三、解答题:(本大题2个小题,每小题8分,共16分) 19.计算:201411(1)()453--+︒ab c 12第11题图 第13题图 AE D C 第16题图 C AFD E 第17题图20.先化简,再求值:22121(1)24x x x x -++÷--,其中,x =3;四、解答题:(本大题2个小题,每小题10分,共20分)21.某数学兴趣小组在全校范围内随机抽取了50同学进行“舌尖上的长沙——我最喜欢的小吃”调查活动,将调查问卷整理后绘成如图所示的不完整条形统计图.请根据所给信息解答以下问题: (1) 请补全条形统计图; (2) 若全校有2000名学生,请估计全校同学中最喜欢“臭豆腐”的同学有多少人; (3) 在一个不透明的口袋中有四个完全相同的小球,把他们分别标号为四种小吃的序号A,B,C,D ,随机摸出一个小球然后放回,再随机摸出一个小球,请用列表或画树形图的方法,求两次都摸到“A ”的概率;小吃类别 口味人数臭豆唆螺 糖油粑22.如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O,(1) 求证:△AEO≌△CDO;(2)若∠OCD=30°,求△ACO的面积;AEOCD第22题五、解答题:(本大题2个小题,每小题10分,共20分)23. 为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼的进行,某施工队准备购买甲、乙两种树苗共400棵,对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元。
湖南省长沙市2014年中考数学真题试题(含答案)
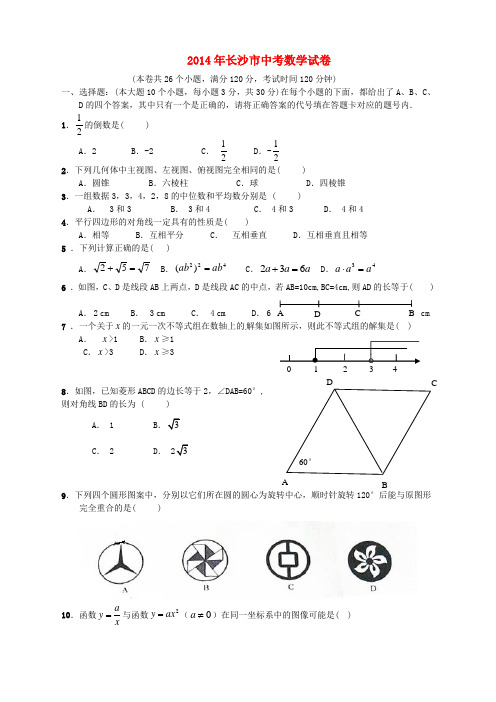
2014年长沙市中考数学试卷(本卷共26个小题,满分120分,考试时间120分钟)一、选择题:(本大题10个小题,每小题3分,共30分)在每个小题的下面,都给出了A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将正确答案的代号填在答题卡对应的题号内. 1.21的倒数是( ) A .2B .-2C .21 D .-21 2.下列几何体中主视图、左视图、俯视图完全相同的是( )A .圆锥B .六棱柱C .球D .四棱锥3.一组数据3,3,4,2,8的中位数和平均数分别是 ( )A . 3和3B . 3和4C . 4和3D . 4和4 4.平行四边形的对角线一定具有的性质是( )A .相等B .互相平分C . 互相垂直D .互相垂直且相等 5 .下列计算正确的是( )A .752=+ B .422)(ab ab = C .a a a 632=+ D .43a a a =⋅6 .如图,C 、D 是线段AB 上两点,D 是线段AC 的中点,若AB=10cm,BC=4cm,则AD 的长等于( )A . 2 cmB . 3 cmC . 4 cmD . 6 cm 7 .一个关于x 的一元一次不等式组在数轴上的解集如图所示,则此不等式组的解集是( )A . x >1B .x ≥1C .x >3D .x ≥3 8.如图,已知菱形ABCD 的边长等于2,∠DAB=60°, 则对角线BD 的长为 ( )A . 1 BC . 2D .9.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后能与原图形完全重合的是( )10.函数a y x=与函数2y ax =(0a ≠)在同一坐标系中的图像可能是( ) A B DCA D B二、填空题:(本大题8个小题,每小题3分,共24分)在每小题中,请将答案直接填在答题卡中对应的横线上.11.如图,直线a ∥b,直线c 与a,b 相交,∠1=70°,则∠2= 度; 12.抛物线23(2)5y x =-+的顶点坐标为 ;13.如图,A 、B 、C 是⊙O 上的三点,∠A OB=100°,则∠ACB= 度;14.已知关于x 的 一元二次方程22340x kx -+=的一个根是1,则k= . 15.100件外观相同的产品中有5件不合格,从中任意抽出1件进行检测,则抽到不合格产品的概率为 . 16.如图,△ABC 中,DE ∥BC,23DE BC =,△AD E 的面积为8,则△ABC 的面积为 ;17.如图,B 、E 、C、F 在同一直线上,AB ∥DE,AB=DE,BE=CF,AC=6,则DF= ;18.如图,在平面直角坐标系中,A(2,3),B(-2,1),在x 轴上存在点P ,使P 到A,B 两点的距离之和最小,则P 的坐标为 ;三、解答题:(本大题2个小题,每小题6分,共12分) 19.计算:201411(1)()453--+︒20.先化简,再求值:22121(1)24x x x x -++÷--,其中,x =3;四、解答题:(本大题2个小题,每小题8分,共16分)21.某数学兴趣小组在全校范围内随机抽取了50同学进行“舌尖上的长沙——我最喜欢的小吃”调查活动,将调查问卷整理后绘成如图所示的不完整条形统计图.a bc 12 第11题图 第13题图 AEDC第16题图 C AF DE 第17题图小吃类别口味人数臭豆唆螺 糖油粑请根据所给信息解答以下问题: (1) 请补全条形统计图;(2) 若全校有2000名学生,请估计全校同学中最喜欢“臭豆腐”的同学有多少人; (3) 在一个不透明的口袋中有四个完全相同的小球,把他们分别标号为四种小吃的序号A,B,C,D ,随机摸出一个小球然后放回,再随机摸出一个小球,请用列表或画树形图的方法,求两次都摸到“A ”的概率;22.如图,四边形ABCD 是矩形,把矩形沿对角线AC 折叠,点B 落在点E 处,CE 与AD 相交于点O, (1) 求证:△AEO ≌△CDO ;(2)若∠OCD=30°,求△ACO 的面积;五、解答题:(本大题2个小题,每小题9分,共18分)23. 为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼的进行,某施工队准备购买甲、乙两种树苗共400棵,对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元。
2014年湖南省长沙市中考数学试卷(含解析版)

2014年湖南省长沙市中考数学试卷一、选择题(共10小题,每小题3分,共30分)1.的倒数是()A、2B、-2C、D、-2.下列几何体中,主视图、左视图、俯视图完全相同的是()A.圆锥B.六棱柱C.球D.四棱锥3.(3分)(2014•长沙)一组数据3,3,4,2,8的中位数和平均数分别是()A.3和3 B.3和4 C.4和3 D.4和44.(3分)(2014•长沙)平行四边形的对角线一定具有的性质是()A.相等B.互相平分C.互相垂直D.互相垂直且相等5.(3分)(2014•长沙)下列计算正确的是()A.+= B.(ab2)2=ab4C.2a+3a=6a D.a•a3=a46.(3分)(2014•长沙)如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为()A.2cm B.3cm C.4cm D.6cm7.(3分)(2014•长沙)一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是()A.x>1 B.x≥1C.x>3 D.x≥38.(3分)(2014•长沙)如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是()A.1B.C.2 D.29.(3分)(2014•长沙)下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是()A.B.C.D.10.(3分)(2014•长沙)函数y=与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.D.二、填空题(共8小题,每小题3分,共24分)11.(3分)(2014•长沙)如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2=度.12.(3分)(2014•长沙)抛物线y=3(x﹣2)2+5的顶点坐标是.13.(3分)(2014•长沙)如图,A、B、C是⊙O上的三点,∠AOB=100°,则∠ACB=度.14.(3分)(2014•长沙)已知关于x的一元二次方程2x2﹣3kx+4=0的一个根是1,则k= .15.(3分)(2014•长沙)100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是.16.(3分)(2014•长沙)如图,在△ABC中,DE∥BC,=,△ADE的面积是8,则△ABC的面积为.17.(3分)(2014•长沙)如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF= .18.(3分)(2014•长沙)如图,在平面直角坐标系中,已知点A(2,3),点B (﹣2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是.三、解答题(共2小题,每小题6分,共12分)19.(6分)(2014•长沙)计算:(﹣1)2014+﹣()﹣1+sin45°.20.(6分)(2014•长沙)先简化,再求值:(1+)+,其中x=3.四、解答题(共2小题,每小题8分,共16分)21.(8分)(2014•长沙)某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:请根据所给信息解答以下问题:(1)请补全条形统计图;(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.22.(8分)(2014•长沙)如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.(1)求证:△AOE≌△COD;(2)若∠OCD=30°,AB=,求△AOC的面积.五、解答题(共2小题,每小题9分,共18分)23.(9分)(2014•长沙)为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼地进行,某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.(1)若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?(2)若购买甲种树苗的金额不少于购买一中树苗的金额,至少应购买甲种树苗多少棵?24.(9分)(2014•长沙)如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.(1)求证:DE⊥AC;(2)若AB=3DE,求tan∠ACB的值.六、解答题(共2小题,每小题10分,共20分)25.(10分)(2014•长沙)在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),(,),…都是“梦之点”,显然,这样的“梦之点”有无数个.(1)若点P(2,m)是反比例函数y=(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+,试求出t的取值范围.26.(10分)(2014•长沙)如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).(1)求a,b,c的值;(2)求证:在点P运动的过程中,⊙P始终与x轴相交;(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.2014年湖南省长沙市中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.的倒数是()A、2B、-2C、D、-倒数.考点:分根据乘积为的1两个数倒数,可得一个数的倒数.析:解:的倒数是2,解答:故选:A.本题考查了倒数,分子分母交换位置是求一个数的倒数的关键.点评:2.下列几何体中,主视图、左视图、俯视图完全相同的是()A.圆锥B.六棱柱C.球D.四棱锥简单几何体的三视图.考点:分析:找到从物体正面、左面和上面看得到的图形全等的几何体即可.解答:解:A、圆锥的主视图、左视图、俯视图分别为等腰三角形,等腰三角形,圆及圆心,故A选项不符合题意;B、六棱柱的主视图、左视图、俯视图分别为四边形,四边形,六边形,故B选项不符合题意;C、球的主视图、左视图、俯视图分别为三个全等的圆,故C选项符合题意;D、四棱锥的主视图、左视图、俯视图分别为三角形,三角形,四边形,故D选项不符合题意;故选C.点评:考查三视图的有关知识,注意三视图都相同的常见的几何体有球和正方体.3.(3分)(2014•长沙)一组数据3,3,4,2,8的中位数和平均数分别是()A.3和3 B.3和4 C.4和3 D.4和4考点:中位数;算术平均数.分析:根据中位数及平均数的定义求解即可.解答:解:将数据从小到大排列为:2,3,3,4,8,则中位数是3,平均数==4.故选B.点评:本题考查了平均数及中位数的知识,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.4.(3分)(2014•长沙)平行四边形的对角线一定具有的性质是()A.相等B.互相平分C.互相垂直D.互相垂直且相等考点:平行四边形的性质.分析:根据平行四边形的对角线互相平分可得答案.解答:解:平行四边形的对角线互相平分,故选:B.。
2014长沙中考数学试题(解析版)

湖南省长沙市2014年中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.12的倒数是()A、2B、-2C、1D、-1=4.+=AC=43m=120°;=90°;=180°;=72°;10.(3分)(2014•长沙)函数y=与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是()的函数图象位于第一三象限,y=解:∠ACB=∠AOB=×100°=50°.15.(3分)(2014•长沙)100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是.件进行检测,抽到不合格产品的概率是:=故答案为:16.(3分)(2014•长沙)如图,在△ABC中,DE∥BC,=,△ADE的面积是8,则△ABC的面积为18 .∵=∴(,的坐标代入得:解得19.(6分)(2014•长沙)计算:(﹣1)2014+﹣()﹣1+sin45°.20.(6分)(2014•长沙)先简化,再求值:(1+)+,其中x=3.====.四、解答题(共2小题,每小题8分,共16分)21.(8分)(2014•长沙)某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:请根据所给信息解答以下问题:(1)请补全条形统计图;(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸×100%=560(人).于点O.(1)求证:△AOE≌△COD;AB=∴CO=CD÷cos30°==2AO•CD=×2×=五、解答题(共2小题,每小题9分,共18分)23.(9分)(2014•长沙)为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼地进行,某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.(1)若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?D作⊙O的切线交AC于点E.(1)求证:DE⊥AC;∴∴x=∴tan∠ACB=25.(10分)(2014•长沙)在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),(,),…都是“梦之点”,显然,这样的“梦之点”有无数个.(1)若点P(2,m)是反比例函数y=(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+,试求出t的取值范围.,运用待定系数法即可求出反比例函数的,==2b+=.再由﹣<,进而求出y=(y=k≠x=k=k=k≠(,,,s≠1,=(﹣4•=4=2+.<∴a>>+=∴t>.26.(10分)(2014•长沙)如图,抛物线y=ax+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).(1)求a,b,c的值;(2)求证:在点P运动的过程中,⊙P始终与x轴相交;,进而与)和(,)∴(解得:a=±∵图象开口向上,∴a=,x,,又∵y=xr=>xa,∵PA=PM=PN=,又∵PH=aMH=NH=,∴AM=,,时,=,时,=4解得:a=2±2a;时,=4﹣2±2(负数舍去),则;4+2或.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年湖南省长沙市中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.12的倒数是()A、2B、-2C、12D、-12解:12的倒数是2,故选:A.2.下列几何体中,主视图、左视图、俯视图完全相同的是()A.圆锥B.六棱柱C.球D.四棱锥解:A、圆锥的主视图、左视图、俯视图分别为等腰三角形,等腰三角形,圆及圆心,故A 选项不符合题意;B、六棱柱的主视图、左视图、俯视图分别为四边形,四边形,六边形,故B选项不符合题意;C、球的主视图、左视图、俯视图分别为三个全等的圆,故C选项符合题意;D、四棱锥的主视图、左视图、俯视图分别为三角形,三角形,四边形,故D选项不符合题意;故选C.3.(3分)(2014•长沙)一组数据3,3,4,2,8的中位数和平均数分别是()A.3和3 B.3和4 C.4和3 D.4和4 解:将数据从小到大排列为:2,3,3,4,8,则中位数是3,平均数==4.故选B.4.(3分)(2014•长沙)平行四边形的对角线一定具有的性质是()A.相等B.互相平分C.互相垂直D.互相垂直且相等解:平行四边形的对角线互相平分,故选:B.5.(3分)(2014•长沙)下列计算正确的是()A.+=B.(ab2)2=ab4C.2a+3a=6a D.a•a3=a4解:A、被开方数不能相加,故A错误;B、积的乘方等于每个因式分别乘方,再把所得的幂相乘,故B错误;C、系数相加字母部分不变,故C错误;D、底数不变指数相加,故D正确;故选:D.6.(3分)(2014•长沙)如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为()A.2cm B.3cm C.4cm D.6cm解:∵AB=10cm,BC=4cm,∴AC=AB﹣BC=6cm,又点D是AC的中点,∴AD=AC=43m,答:AD的长为3cm.故选:B.7.(3分)(2014•长沙)一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是()A.x>1 B.x≥1C.x>3 D.x≥3解:一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是x>3.故选:C.8.(3分)(2014•长沙)如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是()A.1B.C.2D.2解:∵菱形ABCD的边长为2,∴AD=AB=2,又∵∠DAB=60°,∴△DAB是等边三角形,∴AD=BD=AB=2,则对角线BD的长是2.故选:C.9.(3分)(2014•长沙)下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是()A.B.C.D.解:A、最小旋转角度==120°;B、最小旋转角度==90°;C、最小旋转角度==180°;D、最小旋转角度==72°;综上可得:顺时针旋转120°后,能与原图形完全重合的是A.故选A.10.(3分)(2014•长沙)函数y=与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.D.解:a>0时,y=的函数图象位于第一三象限,y=ax2的函数图象位于第一二象限且经过原点,a<0时,y=的函数图象位于第二四象限,y=ax2的函数图象位于第三四象限且经过原点,纵观各选项,只有D选项图形符合.故选D.二、填空题(共8小题,每小题3分,共24分)11.(3分)(2014•长沙)如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2=110度.解:∵∠1=70°,∴∠3=∠1=70°,∵a∥b,∴∠2+∠3=180°,∴∠2=180°﹣70°=110°.故填110.12.(3分)(2014•长沙)抛物线y=3(x﹣2)2+5的顶点坐标是(2,5).解:∵抛物线y=3(x﹣2)2+5,∴顶点坐标为:(2,5).故答案为:(2,5).13.(3分)(2014•长沙)如图,A、B、C是⊙O上的三点,∠AOB=100°,则∠ACB=50度.解:∠ACB=∠AOB=×100°=50°.故答案是:50.14.(3分)(2014•长沙)已知关于x的一元二次方程2x2﹣3kx+4=0的一个根是1,则k=2.解:依题意,得2×12﹣3k×1+4=0,即2﹣3k+4=0,解得,k=2.故答案是:2.15.(3分)(2014•长沙)100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是.解:∵100件外观相同的产品中有5件不合格,∴从中任意抽取1件进行检测,抽到不合格产品的概率是:=.故答案为:.16.(3分)(2014•长沙)如图,在△ABC中,DE∥BC,=,△ADE的面积是8,则△ABC的面积为18.解;∵在△ABC中,DE∥BC,∴△ADE∽△ABC.∵=,∴=()2=,,∴S△ABC=18,故答案为:18.17.(3分)(2014•长沙)如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=6.证明:∵AB∥DE,∴∠B=∠DEF∵BE=CF,∴BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(SAS),∴AC=DF=6.故答案是:6.18.(3分)(2014•长沙)如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是(﹣1,0).解:作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,∵A点的坐标为(2,3),B点的坐标为(﹣2,1),∴C(2,﹣3),设直线BC的解析式是:y=kx+b,把B、C的坐标代入得:解得.即直线BC的解析式是y=﹣x﹣1,当y=0时,﹣x﹣﹣1=0,解得:x=﹣1,∴P点的坐标是(﹣1,0).故答案为:(﹣1,0).三、解答题(共2小题,每小题6分,共12分)19.(6分)(2014•长沙)计算:(﹣1)2014+﹣()﹣1+sin45°.解:原式=1+2﹣3+1=1.20.(6分)(2014•长沙)先简化,再求值:(1+)+,其中x=3.解:原式=•=•=,当x=3时,原式==.四、解答题(共2小题,每小题8分,共16分)21.(8分)(2014•长沙)某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:请根据所给信息解答以下问题:(1)请补全条形统计图;(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.解:(1)根据题意得:喜欢“唆螺”人数为:50﹣(14+21+5)=10(人),补全统计图,如图所示:(2)根据题意得:2000××100%=560(人),则估计全校同学中最喜爱“臭豆腐”的同学有560人;(3)列表如下:A B C DA (A,A)(B,A)(C,A)(D,A)B (A,B)(B,B)(C,B)(D,B)C (A,C)(B,C)(C,C)(D,C)D (A,D)(B,D)(C,D)(D,D)所有等可能的情况有16种,其中恰好两次都摸到“A”的情况有1种,则P=.22.(8分)(2014•长沙)如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.(1)求证:△AOE≌△COD;(2)若∠OCD=30°,AB=,求△AOC的面积.解答:(1)证明:∵四边形ABCD是矩形,∴AB=CD,∠B=∠D=90°,∵矩形ABCD沿对角线AC折叠点B落在点E处,∴AB=AE,∠B=∠E,∴AE=CD,∠D=∠E,在△AOE和△COD中,,∴△AOE≌△COD(AAS);(2)解:∵△AOE≌△COD,∴AO=CO,∵∠OCD=30°,AB=,∴CO=CD÷cos30°=÷=2,∴△AOC的面积=AO•CD=×2×=.五、解答题(共2小题,每小题9分,共18分)23.(9分)(2014•长沙)为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼地进行,某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.(1)若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?(2)若购买甲种树苗的金额不少于购买一中树苗的金额,至少应购买甲种树苗多少棵?解:(1)设购买甲种树苗x棵,则购买乙种树苗(400﹣x)棵,由题意,得200x+300(400﹣x)=90000,解得:x=300,∴购买乙种树苗400﹣300=100棵,答:购买甲种树苗300棵,则购买乙种树苗100棵;(2)设至少应购买甲种树苗a棵,则购买乙种树苗(400﹣a)棵,由题意,得200a≥300(400﹣a),解得:a≥240.答:至少应购买甲种树苗240棵.24.(9分)(2014•长沙)如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC 的中点D,过点D作⊙O的切线交AC于点E.(1)求证:DE⊥AC;(2)若AB=3DE,求tan∠ACB的值.解答:(1)证明:连接OD,∵D是BC的中点,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,∵DE是⊙O的切线,∴OD⊥DE,∴DE⊥AC;(2)解:连接AD,∵AB是⊙O的直径,∴∠ADB=90°,∵DE⊥AC,∴∠ADC=∠DEC=∠AED=90°,∴∠ADE=∠DCE在△ADE和△CDE中,∴△CDE∽△ADE,∴,设tan∠ACB=x,CE=a,则DE=ax,AC=3ax,AE=3ax﹣a,∴,整理得:x2﹣3x+1=0,解得:x=,∴tan∠ACB=.六、解答题(共2小题,每小题10分,共20分)25.(10分)(2014•长沙)在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),(,),…都是“梦之点”,显然,这样的“梦之点”有无数个.(1)若点P(2,m)是反比例函数y=(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+,试求出t的取值范围.解:(1)∵点P(2,m)是“梦之点”,∴m=2,∵点P(2,2)在反比例函数y=(n为常数,n≠0)的图象上,∴n=2×2=4,∴反比例函数的解析式为y=;(2)假设函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”(x,x),则有x=3kx+s﹣1,整理,得(3k﹣1)x=1﹣s,当3k﹣1≠0,即k≠时,解得x=;当3k﹣1=0,1﹣s=0,即k=,s=1时,x有无穷多解;当3k﹣1=0,1﹣s≠0,即k=,s≠1时,x无解;综上所述,当k≠时,“梦之点”的坐标为(,);当k=,s=1时,“梦之点”有无数个;当k=,s≠1时,不存在“梦之点”;(3)∵二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),∴x1=ax12+bx1+1,x2=ax22+bx2+1,∴ax12+(b﹣1)x1+1=0,ax22+(b﹣1)x2+1=0,∴x1,x2是一元二次方程ax2+(b﹣1)x+1=0的两个不等实根,∴x1+x2=,x1•x2=,∴(x1﹣x2)2=(x1+x2)2﹣4x1•x2=()2﹣4•==4,∴b2﹣2b=4a2+4a﹣1=(2a+1)2﹣2,∴t=b2﹣2b+=(2a+1)2﹣2+=(2a+1)2+.∵﹣2<x1<2,|x1﹣x2|=2,∴﹣4<x2<0或0<x2<4,∴﹣4<x2<4,∴﹣8<x1•x2<8,∴﹣8<<8,∵a>0,∴a>∴(2a+1)2+>+=,∴t>.26.(10分)(2014•长沙)如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).(1)求a,b,c的值;(2)求证:在点P运动的过程中,⊙P始终与x轴相交;(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.解:(1)∵抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,∴抛物线的一般式为:y=ax2,∴=a()2,解得:a=±,∵图象开口向上,∴a=,∴抛物线解析式为:y=x2,故a=,b=c=0;(2)设P(x,y),⊙P的半径r=,又∵y=x2,则r=,化简得:r=>x2,∴点P在运动过程中,⊙P始终与x轴相交;(3)设P(a,a2),∵PA=,作PH⊥MN于H,则PM=PN=,又∵PH=a2,则MH=NH==2,故MN=4,∴M(a﹣2,0),N(a+2,0),又∵A(0,2),∴AM=,AN=,当AM=AN时,=,解得:a=0,当AM=MN时,=4,解得:a=2±2(负数舍去),则a2=4+2;当AN=MN时,=4,解得:a=﹣2±2(负数舍去),则a2=4﹣2;综上所述,P的纵坐标为0或4+2或4﹣2.。
