8章习题解答03--
第8章-皮炎和湿疹-习题及答案

第八章皮炎和湿疹一填空题1.湿疹的四大特点是__、__、__、__。
2.特应性皮炎(又称异位性皮炎)在不同年龄阶段有不同的特点,通常可分为三个阶段__、__、__。
3.接触性皮炎属于__型变态反应。
4.接触性皮炎的发病机制一般分为__和__。
5.湿疹通常根据起病的缓急分为__、__、__三种。
二判断改错题1.诊断接触性皮炎最常做的皮肤试验是皮内试验。
2.对于急性期伴有渗出的皮炎湿疹类损害,应首选封包治疗。
3.急性湿疹面部红肿、糜烂、渗出时应给予3%硼酸溶液湿敷。
4.婴儿湿疹伴消化不良,应该纠正消化不良。
三选择题【A型题】1.夏季发生于双足背前端的接触性皮炎考虑其可能的接触物为__。
CA.袜子B.皮鞋C.拖鞋D.肥皂E.洗涤剂2.脂溢性皮炎的常见并发症有__。
BA.丹毒B.毛囊炎及疖C.念珠菌感染D.维生素缺乏E.糖尿病3.由原发性刺激引起的接触性皮炎,发病因素取决于__。
CA.是首次接触还是再次接触B.接触物有否抗原性C.接触物的刺激性或毒性D.机体对该物质是否过敏E.机体本身的抵抗力4.女性,30岁,双下肢反复发生多数小片状类圆形红斑,密集成簇的丘疱疹,境界清楚。
痒。
冬重夏轻。
应考虑__。
CA.郁积性皮炎B.干燥性湿疹C.钱币状湿疹D.体癣E.多形性红斑5.为寻找接触性皮炎的病因,对可疑致敏的接触物,常用何种方法以助确诊__。
EA.划破试验B.皮肤划痕试验C.皮内试验D.激发试验E.斑贴试验6.下列哪种是原发刺激物__。
AA.浓盐酸B.1:5000呋喃西林C.0.5%醋酸铅液D.氯霉素眼药水E.麻黄素滴鼻剂7.接触性皮炎致敏的抗原呈递细胞是__。
EA.角质形成细胞B.棘细胞C.颗粒细胞D.基底细胞E.朗格罕斯细胞8.成年患者,手足背、四肢伸侧有边缘清楚的红斑,表面群集小水疱、鳞屑和痂,诊断为以下哪种疾病的可能性大__。
BA.药疹B.钱币状湿疹C.体癣D.神经性皮炎E.玫瑰糠疹9.慢性湿疹最需与下列哪种疾病鉴别__。
初二物理第八章练习题含答案

初二物理第八章练习题含答案1. 选择题(1) 以下属于力的性质是:A. 大小B. 方向C. 作用点D. 面积答案:A、B、C(2) 能够使物体发生位移的只有:A. 摩擦力B. 重力C. 弹力和悬挂力D. 正确答案全部都对答案:C(3) 法拉第一定律指出的是:A. 外力作用于物体上时,物体一定保持静止或匀速直线运动B. 外力作用于物体上时,物体的速度将发生变化C. 物体受到的合力为零时,物体一定保持静止或匀速直线运动D. 物体受到的合力为零时,物体的速度将发生变化答案:C2. 填空题(1) 一个力从右往左作用于一个物体,这个物体产生的反作用力的方向是______。
答案:从左往右(2) 一个力从上往下作用于一个物体,这个物体产生的反作用力的方向是______。
答案:从下往上(3) 一个物体受到A力的作用产生加速度a,如果力A的大小不变,改变作用方向,则产生的加速度为______。
答案:-a3. 解答题(1) 什么是力?力的三要素是什么?解答:力是物体之间相互作用的结果,是导致物体发生变化的原因。
力的三要素包括大小、方向和作用点。
大小表示力的强弱程度,方向表示力作用的直线方向,作用点表示力作用的具体位置。
(2) 什么是合力?如何求合力?解答:合力是同时作用在物体上的多个力的共同效果。
求合力的方法是将所有作用在物体上的力按照大小和方向合成,可以通过向量法或图示法来求解。
(3) 描述牛顿第一定律,并用实例说明其应用。
解答:牛顿第一定律也称为惯性定律,指出在没有外力作用时,物体将保持静止或匀速直线运动的状态。
例如,当我们用力推动一张光滑的桌子上的书时,如果力的大小和方向适当,书就会保持匀速直线运动,直到受到其他力的作用。
这说明物体在没有外力干扰时具有惯性,保持原来的状态不发生变化。
总结:初二物理第八章练习题主要涉及力的性质和作用、法拉第一定律等内容。
通过选择题和填空题加深对知识点的理解,同时通过解答题展开思考和拓展。
氧化还原及电极电位

第八章氧化还原反应与电极电位首页难题解析学生自测题学生自测答案章后习题解答难题解析[TOP]例8-1写出并配平下列各电池的电极反应、电池反应,注明电极的种类。
(1)(-) Ag(s) | AgCl(s) | HCl(sln) | C12(100kp) | Pt (s) (+)(2)(-) Pb(s) | PbSO4(s) | K2SO4(sln) II KC1 (sin) | PbC12(s) | Pb(s) (+)(3)(-) Zn(s) | Zn2+(cl) llMnO4-(c2), Mn2+(c3), H+(c4) | Pt (s) (+)(4)(-) Ag(s) | Ag+ (cl) II Ag+(c2) | Ag(s) (+)分析将所给原电池拆分为两个电极。
负极发生氧化反应,正极发生还原反应,写出正、负极反应式,由正极反应和负极反应相加构成电池反应。
解(1)正极反应C12(g)+2e-〜2 Cl- (aq) 属于气体电极负极反应Ag(s)+Cl-(aq)〜AgCl(s)+e-属于金属-难溶盐-阴离子电极电池反应2Ag (s) + C12(g) ^2AgCl(s) n=2(2)正极反应PbC12(s)+2e --------- P b(s)+2C1- (aq)属于金属-难溶盐-阴离子电极负极反应Pb(s)+SO42-(aq) -*PbSO4(s)+2e- 属于金属-难溶盐-阴离子电极电池反应PbC12(s) +SO42- (aq)f PbSO4(s) +2Cl-(aq) n二2(3)正极反应Mn04-(aq) +8H+(aq)+5e- -Mn2+(aq)+ 4H20(l)属于氧化还原电极负极反应Zn(s) — Zn2+(aq)+2e- 属于金属-金属离子电极电池反应2MnO4~ (aq)+16H+(aq)+5Zn(s)f2Mn2+(aq)+8H20(l)+5Zn2+ (aq) n二10 (4)正极反应Ag+(c2) +e- - Ag(s) 属于金属-金属离子电极负极反应Ag(s) -* Ag+ (cl) + e- 属于金属-金属离子电极电池反应Ag+ (c2) f Ag+ (cl) n=l例8-2 25°C时测得电池(-)Ag(s) | AgCl(s) | HCl(c) | C12(100kp) | Pt(s) (+)的电动势为 1. 136V,已知(C12/C1-)二1.358V, ( Ag+/Ag)二0. 799 6V,求AgCl 的溶度积。
环境工程原理课后习题答案2-8章

课
后
答
案
网
ww w
.k
hd
3.4如图所示,有一水平通风管道,某处直径由400mm减缩至200mm。 为了粗略估计管道中的空气流量,在锥形接头两端各装一个U形管 压差计,现测得粗管端的表压为100mm水柱,细管端的表压为40mm 水柱,空气流过锥形管的能量损失可以忽略,管道中空气的密度为 1.2kg/m3,试求管道的空气流量 。
《第二章 质量衡算与能量衡算》
.c om
2.8 某河流的流量为3.0m3/s,有一条流量为0.05m3/s的
课
后
答
质量流量是多少?假设原河水和小溪中不含示踪剂。
案
网
出,溪水中示踪剂的最低浓度是多少?需加入示踪剂的
ww w
1.0mg/L。为了使河水和溪水完全混合后的示踪剂可以检
.k
hd
溪水中加入示踪剂。假设仪器检测示踪剂的浓度下限为
A1 19 19 1.12 19 15 Am 16.9 19 ln 15 A1 19 1.27 A2 15
1 0.002 1 0.00026 0.000176 458 45 3490 2.95 10 3 m 2 K / W
课
后
答
案
网
α1为管外流体 对流传热系数
rm1 3 28.47 mm 30 ln 27 30 43.28mm 60 ln 30 30 73.99mm 90 ln 60
rm 3
课
rm 2
后
答
案
网
解:设铝复合管、石棉、软木的对数平均半径分别为rm1、rm2、rm3
ww w
.k
hd
aw
.c om
脂类习题参考答案第03章

脂类习题参考答案第03章第三章脂类习题⼀、填空题:1、脂肪酸、醇类、脂肪酸、⽢油、脂肪酸、⾼级⼀元醇。
2、1:1:1。
3、越⼤。
4、因为油脂当中含有的⼩分⼦物质的挥发引起的。
5、⽆。
6、脂溶性维⽣素。
7、⽆。
8、越⾼。
9、⽢油和脂肪酸。
10、饱和脂肪酸、硬脂酸或软脂酸、不饱和脂肪酸、油酸、亚油酸、亚⿇酸、花⽣四烯酸。
11、乳化剂。
1.单脂类是由和构成的酯。
油脂是由与构成的酯。
蜡是由与构成的酯。
2.在油脂的营养中,重要的⼀点是要注意油脂中各种脂肪酸间要有良好的⽐例关系,⼀般推荐饱和脂肪酸、不饱和脂肪酸、多不饱和脂肪酸为。
3.油脂的营养质量可以⽤各种油脂的多不饱和脂肪酸与饱和脂肪酸的⽐(P/S)表⽰,P/S的脂肪酸的营养功能越好。
4.⾷⽤油脂的发烟是。
5.纯净的油脂是⾊的。
6.油脂的⾊泽来⾃。
7.纯净的油脂是味的。
8.三酰⽢油酯分⼦间内摩擦⼒越⼤,油脂的粘度就。
9.油脂在酸的作⽤下都会发⽣⽔解⽣成和。
10.卵磷脂分⼦中的R1脂肪酸是饱和脂肪酸,如硬脂酸或软脂酸;R2脂肪酸是不饱和脂肪酸,如油酸、亚油酸、亚⿇酸或花⽣四烯酸等。
卵辚脂是两亲物质,因此,是⾷品中常⽤的⼤⾖磷脂。
12、外源性胆固醇。
13、烃类、羟基脂肪酸、过氧化物、环状聚合物、⽢油酯的⼆聚物和多聚物。
11.12.从⾷物中获得的胆固醇称为外源性胆固醇。
13.⽼化油脂中的有毒物质主要有:烃类、羟基脂肪酸、过氧化物、以及环状聚合物、⽢油酯的⼆聚物、多聚物。
⼆、简答题:1.油脂在烹饪中的作⽤2.油脂的⽣理功⽤3.简述天然油脂中脂肪酸分布特点4.天然油脂中脂肪酸的种类5.天然油脂中脂肪酸的特点6.天然油脂中脂肪酸的表⽰⽅法7.必需脂肪酸8.必需脂肪酸的结构特点9.亚⿇酸是必需脂肪酸吗,为什么?10.n3或ω3系列脂肪酸的功能性质11.影响油脂熔点范围的主要因素12.油脂的熔点与⼈体消化吸收率之间的关系13.油脂的发烟点14.油烟中⼩分⼦物质的来源15.闪点16.燃点17.油脂为什么具有颜⾊?18.油脂的味的来源19.油脂的⾹⽓来源20.阈值:21.油性22.油脂的粘度23.影响油脂粘度的主要因素24.塑性脂肪的概念25.稠度26.塑性脂肪的性能27.油脂膨胀曲线28.油脂膨胀曲线的意义29.固体脂肪指数(SFI)30.SFI的意义31.同质多晶32.乳状液33.内相34.外相(分散介质、连续相)35.使乳状液稳定存在的⽅法36.乳化剂37.乳化剂的分⼦结构特点38.乳化剂的作⽤原理39.乳化剂的功能40.⾷品中常见的乳状液体系41.皂化反应42.皂化值43.测定⽅法44.皂化值的意义45.油脂的⽔解对其品质的影响46.碘价(碘值)47.碘值的意义48.油脂的⼲性49.油脂氢化的意义50.酯交换反应作⽤51.油脂的酸败52.油脂的酸败的原因53.影响油脂⾃动氧化的因素54.预防油脂的⾃动氧化应采取哪些措施55.导致油脂⽼化的原因56.⽼化油脂的品质变化57.导致油脂⽼化的主要反应类型58.影响油脂⽼化的因素59.类脂60.为什么说磷脂是天然乳化剂?61.卵磷脂为什么可以做抗氧化剂?62.烹调加⼯对胆固醇有何影响?三、判断题:1.油脂同其他化合物⼀样具有明确的熔点。
第03章(刚体力学)习题答案

内力做功,机械能守恒,动量守恒的条件为合外力为零,转轴不属于系统,转轴与盘之间有
作用力,动量不守恒。
3-2 如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑
O
固定轴 O 旋转,初始状态为静止悬挂.现有一个小球自左方水平打
击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆
与小球这一系统的哪种物理量守恒? 答:在碰撞时,小球重力过转轴,杆的重力也过轴,外力矩为
思考题 32 图
零,所以角动量守恒。因碰撞时转轴与杆之间有作用力,所以动量不守恒。碰撞是非弹性的,
所以机械能也不守恒。
3-3 一圆盘绕过盘心且与盘面垂直的光滑固定轴 O 以角速度w按图示方向转动.若如图
所示的情况那样,将两个大小相等方向相反但不在同一条直线的力
F 沿盘面同时作用到圆盘上,则圆盘的角速度w 如何变化?
解:此过程角动量守恒
Jw0
=
1 3
Jw
Þ
w
=
3w0
3-10 一轴承光滑的定滑轮,质量为 M=2.00 kg,半径为 R=0.100 m,
一根不能伸长的轻绳,一端固定在定滑轮上,另一端系有一质量为 m=5.00
kg 的物体,如图所示.已知定滑轮的转动惯量为 J= 1 MR 2 ,其初角速 2
w 0
R M
解:(1)设在任意时刻定滑轮的角速度为w,物体的速度大小为 v,则有 v=Rw.
则物体与定滑轮的总角动量为: L = Jw + mvR = Jw + mR2w
根据角动量定理,刚体系统所受的合外力矩等于系统角动量对时间的变化率:
M = dL ,该系统所受的合外力矩即物体的重力矩:M=mgR dt
所以: b
概率论与数理统计03-第三章作业及答案

概率论与数理统计03-第三章作业及答案习题3-1⽽且12{0}1P X X ==. 求1和2的联合分布律.解由12{0}1P X X ==知12{0}0P X X ≠=. 因此X 1和X 2的联合分布于是根据边缘概率密度和联合概率分布的关系有X 1和X 2的联合分布律(2) 注意到12{0,0}0P X X ===, ⽽121{0}{0}04P X P X =?==≠, 所以X 1和X 2不独⽴.2. 设随机变量(X ,Y )的概率密度为(,)(6),02,24,0,.f x y k x y x y =--<<<其它求: (1) 常数k ; (2) {1,3}P X Y <<; (3) { 1.5}P X <; (4) {4}P X Y +≤.解 (1) 由(,)d d 1f x y x y +∞+∞-∞, 得2424222204211d (6)d (6)d (10)82y k x y x k y x x y k y y k =--=--=-= , 所以 18k =. (2) 31201,31{1,3}d (6)d 8(,)d d x y P X Y y x y x f x y x y <<<<==--??1322011(6)d 82y x x y =--321113()d 828y y =-=?. (3) 1.51.5 { 1.5}d (,)d ()d X P X x f x y y f x x +∞-∞-∞-∞<==??4 1.521d (6)d 8y x y x --=22011(6)d 82y x x y =--?421633()d 882y y =-? 2732=. (4) 作直线4x y +=, 并记此直线下⽅区域与(,)0f x y ≠的矩形区域(0,2)(0,4)?的交集为G . 即:02,0G x y <<<≤4x -.见图3-8. 因此{P X Y +≤4}{(,)}P X Y G =∈(,)d d Gf x y x y =??44201d (6)d 8x y x y x -=--??4422011(6)d 82xy x x y -=--?42211[(6)(4)(4)]d 82y y y y =----? 42211[2(4)(4)]d 82y y y =-+-? 423211(4)(4)86y y =----?23=. 图3-8 第4题积分区域3. ⼆维随机变量(,)X Y 的概率密度为2(,),1,01,0,f x y kxy x y x =≤≤≤≤其它.试确定k , 并求2{(,)},:,01P X Y G G x y x x ∈≤≤≤≤. 解由2111401(,)d d d (1)d 26xk k f x y xdy x kxy y x x x +∞+∞-∞-∞====-??,解得6=k .因⽽ 2112401{(,)}d 6d 3()d 4x xP X Y G x xy y x x x x ∈==-=. 4. 设⼆维随机变量(X , Y )概率密度为4.8(2),01,0,(,)0,.y x x y x f x y -=??≤≤≤≤其它求关于X 和Y 边缘概率密度.解 (,)X Y 的概率密度(,)f x y 在区域:0G ≤x ≤1,0≤y ≤x 外取零值.因⽽, 有24.8(2)d ,01,()(,)d 0,2.4(2),01,0,x X y x y x f x f x y y x x x +∞-∞-<<==-<<=其它.其它. 124.8(2)d ,01,()(,)d 0,2.4(34),01,0,yY y x x y f y f x y x y y y y +∞-∞-<<==-+<<=其它.其它.5. 假设随机变量U 在区间[-2, 2]上服从均匀分布, 随机变量 1,1,1,1,U X U --=>-??若≤若 1,1,1, 1.U Y U -=>??若≤若试求:(1) X 和Y 的联合概率分布;(2){P X Y +≤1}.解 (1) 见本章第三节三(4).(2){P X Y +≤1}1{1}P X Y =-+>1{1,1}P X Y =-==13144=-=. 习题3-21. 设(X , Y )的分布律为求: (1) 在条件X =2下Y 的条件分布律;(2) {22}P X Y ≥≤.解 (1) 由于6.02.01.003.0}2{=+++==X P ,所以在条件X =2下Y 的条件分布律为216.03.0}2{}1,2{}2|1{========X P Y X P X Y P ,06.00}2{}2,2{}2|2{========X P Y X P X Y P ,616.01.0}2{}3,2{}2|3{========X P Y X P X Y P ,316.02.0}2{}4,2{}2|4{========X P Y X P X Y P ,{P Y ≤2}{1}{2}P Y P Y ==+==0.10.3000.20.6++++=. ⽽{2,2}{2,1}{2,2}{3,1}{3,2}P X Y P X Y P X Y P X Y P X Y ===+==+==+==≥≤0.3000.20.5=+++=.因此{2,2}{22}{2}P X Y P X Y P Y =≥≤≤≥≤0.550.66==. 2. 设⼆维随机变量(X , Y )的概率密度为(,)1,01,02,0,.f x y x y x =<<<其它求:(1) (X , Y )的边缘概率密度(),()X Y f x f y ;(2)11{}.22P Y X ≤≤ 解 (1) 当01x <<时,20()(,)d d 2xX f x f x y y y x +∞-∞===?;当x ≤0时或x ≥1时, ()0X f x =.故 2,01,()0,其它.X x x f x <<=??当02()(,)d d 12y Y y f y f x y x x +∞-∞===-;当y ≤0时或y ≥2时, ()0Y f y =.故 1,02,()20,.Y yy f y -<<=其它 (2) 当z ≤0时,()0Z F z =; 当z ≥2时,1)(=z F Z ;当0z f x y x y -=≤2x12202-2d 1d d 1d zxz x zx y x y =?+24z z =-.故 1,02,()20,.()其它Z zzz f z F z -<<'== (3) {}{}11311322161122442≤,≤≤≤≤P X Y P Y X P X ===. 3. 设G 是由直线y =x , y =3,x =1所围成的三⾓形区域, ⼆维随机变量(,)X Y 在G 上服从⼆维均匀分布.求: (1) (X , Y )的联合概率密度;(2) {1}P Y X -≤;(3) 关于X 的边缘概率密度.解 (1)由于三⾓形区域G 的⾯积等于2, 所以(,)X Y 的概率密度为∈=.),(,0,),(,21),(G y x G y x y x f (2)记区域x y y x D -=|),{(≤}1与G 的交集为0G ,则{1}P Y X -≤0011113d d (2)22224G G x y S ===-=??. 其中0G S 为G 0的⾯积.(3) X 的边缘概率密度()(,)d X f x f x y y +∞-∞=?. 所以,当]3,1[∈x 时, 311()d (3)22X xf x y x ==-?. 当1x 时, 0)(=x f X .因此∈-=.,0],3,1[),1(21)(其它x x x f X习题3-31. 设X 与Y 相互独⽴, 且分布律分别为下表:求⼆维随机变量(,)X Y 的分布律.解由于X 与Y 相互独⽴, 所以有}{}{},{j i j i y Y P x X P y Y x X P =?====,6,5,2,0;0,21,1=--=j i .因此可得⼆维随机变量(,)X Y 的联合分布律2. 设(X , Y )的分布律如下表:问,αβ为何值时X 与Y 相互独⽴? 解由于边缘分布满⾜23111,1i j i j p p ??====∑∑, ⼜X , Y 相互独⽴的等价条件为p ij = p i . p .j (i =1,2; j =1,2,3).故可得⽅程组 21,3111().939αβα++==?+解得29α=,19β=.经检验, 当29α=,19β=时, 对于所有的i =1,2; j =1,2,3均有p ij = p i .p .j 成⽴. 因此当29α=,19β=时, X 与Y 相互独⽴..3. 设随机变量X 与Y 的概率密度为()e (,)0,.,01,0,x y b f x y x y -+=?<<>?其它 (1) 试确定常数b .(2) 求边缘概率密度()X f x , ()Y f y . (3) 问X 与Y 是否相互独⽴?解 (1) 由11()101(,)d d e d d e d e d (1e )x y y x f x y x y b y x b y x b +∞+∞+∞+∞-+----∞-∞====-?,得 111e b -=-.(2) ()(,)d X f x f x y y ∞-∞=?1e ,01,1e 0,xx --<<=-??其它.()(,)d Y f y f x y x ∞-∞=?e ,0,0,y y ->=其它.(3) 由于(,)()()X Y f x y f x f y =?,所以X 与Y 相互独⽴.4. 设X 和Y 是两个相互独⽴的随机变量, X 在(0, 1)上服从均匀分布, Y 的概率密度为21e ,0,()20Y yy f y y ->=,≤0.(1) 求X 和Y 的联合概率密度.(2) 设关于a 的⼆次⽅程为220a Xa Y ++=, 试求a 有实根的概率.解 (1) 由题设知X 和Y 的概率密度分别为1,01,()0,X x f x <<=??其它, 21e ,0,()20,.yY y f y ->=其它因X 和Y 相互独⽴, 故(X , Y )的联合概率密度为21e ,01,(,)()()20,.yX Y x y f x y f x f y -<<>==其它 (2) ⽅程有实根的充要条件是判别式⼤于等于零. 即244X Y ?=-≥20X ?≥Y .因此事件{⽅程有实根}2{X =≥}Y .下⾯计算2211221(,)d d e d (1e)d 2yxx Df x y xdy x y x --===-2121ed 12[(1)(0)]0.1445xx πΦΦ-=-=--≈?.图3-3 第6题积分区域习题3-41. 设⼆维随机变量(X ,Y )的概率分布为YX 0 10 0.4 a 1 b 0.1若随机事件{X =0}与{X +Y =1}相互独⽴, 求常数a , b .解⾸先, 由题设知0.40.11a b +++=. 由此得0.5a b +=. 此外,{0}0.4P X a ==+,{1}{0,1}{1,0}0.5P X Y P X Y P X Y a b +====+===+=, {0,1}{0,1}P X X Y P X Y a =+=====. 根据题意有{0,1}{0}{1}P X X Y P X P X Y =+===+=,即(0.4)0.5a a =+?. 解得0.4,0.1a b ==.2. 设两个相互独⽴的随机变量X ,Y 的分布律分别为求随机变量Z = X + Y 的分布律.解随机变量Z = X + Y 的可能取值为7,5,3.Z 的分布律为18.06.0.03}2,1{}3{=?=====Y X P Z P , {5}{1,4}{3,2}0.30.4070.60.54P Z P X Y P X Y ====+===?+?=,28.04.07.0}4,3{}7{=?=====Y X P Z P ,或写为3. 设X 和Y 是两个相互独⽴的随机变量, 且X 服从正态分布N (µ, σ2 ), Y 服从均匀分布U (-a , a )( a >0), 试求随机变量和Z =X +Y 的概率密度.解已知X 和Y 的概率密度分别为22()2()x X f x µσ--=,),(+∞-∞∈x ;-?-∈=).,(,0),,(,21)(a a y a a y ay f Y .由于X 和Y 相互独⽴, 所以22()21()()()d d 2z y a Z X Y f z f z y f y y y a µσ---+∞=1[()()]2z µa z µa ΦΦa σσ-+---. 4. 设随机变量X 和Y 的联合分布是正⽅形G={(x,y )|1≤x ≤3, 1≤y ≤3}上的均匀分布, 试求随机变量U=|X -Y|的概率密度f (u ).解由题设知, X 和Y 的联合概率密度为111,3,3,(,)40,.x y f x y =≤≤≤≤其它记()F u 为U 的分布函数, 参见图3-7, 则有当u ≤0时,(){||F u P X Y =-≤u }=0; 当u ≥2时,()1F u =;当0< u <2时, 图3-7 第8题积分区域||(){}(,)d d x y uF u P U u f x y x y -==≤≤21[42(2)]412u =-?- 211(2)4u =--.故随机变量||U X Y =-的概率密度为1(2),02,()20,u u p u -<<=其它..总习题三1. 设随机变量(X , Y )的概率密度为<<<=.,0,10,||,1),(其它x x y y x f 求条件概率密度)|()|(||y x f x y f Y X X Y 和.解⾸先(,)其它X x x f x f x y dy +∞-∞<<==??1,01,()1,10,0,(,)≤其它.Y y y f y y y f x y dx +∞-∞-<<==+-图3-9第1题积分区域当01y <<时, |1,1,1(|)0,X Y y x y f x y x <<-=??取其它值.当1y -<≤0时, |1,1,1(|)0,X Y y x y f x y x -<<+=??取其它值.当10<,||,(|)20,Y X y x f y x x y <=取其它值.2. 设随机变量X 与Y 相互独⽴, 下表列出⼆维随机变量(,)X Y 的分布律及关于X 和关于Y 的边缘分布律中部分数值, 试将其余数值填⼊表中空⽩处 .解⾸先, 由于11121{}{,}{,}P Y y P X x Y y P X x Y y ====+==, 所以有24P X x Y y P Y y P X x Y y ====-===-=.在此基础上利⽤X 和Y 的独⽴性, 有11111{,}124{}1{}46P X x Y y P X x P Y y =======.于是 2113{}1{}144P X x P X x ==-==-=.再次, 利⽤X 和Y 的独⽴性, 有12211{,}18{}1{}24P X x Y y P Y y P X x =======. 于是 312111{}1{}{}1623P Y y P Y y P Y y ==-=-==--=.最后, 利⽤X 和Y 的独⽴性, 有2222313{,}{}{}428P X x Y y P X x P Y y ======?=; 2323311{,}{}{}434P X x Y y P X x P Y y ======?=; 1313111{,}{}{}43123.(34)e (,)0,.,0,0,x y k f x y x y -+=?>>??其它(1) 求常数k ;(2) 求(X ,Y )的分布函数;(3) 计算{01,02}P X Y <<≤≤; (4) 计算(),x f x ()y f y ;(5) 问随机变量X 与Y 是否相互独⽴?解 (1)由3401(,)d d e d e d 12xy kf x y x y k x y +∞+∞+∞+∞---∞-∞===,可得12=k .(2) (X ,Y )的分布函数(,)(,)d d x y F x y f u v x y -∞-∞=??.当x ≤0或y ≤0时,有 0),(=y x F ;当,0>>y x 时,34340(,)12e d e d (1e )(1e )x即 34(1e )(1e ),0,0,(,)0,.其它x y x y F x y --?-->>=??(3) {01,02}P X Y <<≤≤38(1,2)(0,0)(1e )(1e )F F --=-=--.(4) (34)012ed ,0,()(,)d 0,其它.x y X y x f x f x y y +∞-++∞-∞>==所以 33e ,0,()0,其它.x X x f x -?>=??类似地, 有44e ,0,()0,其它.y Y y f y -?>=?显然2),(),()(),(R y x y f x f y x f Y X ∈??=, 故X 与Y 相互独⽴. 4.解已知),(Y X 的分布律为注意到41260}1{}1{=++====Y P X P , ⽽0}1,1{===Y X P ,可见P{X=1, Y=1}≠P{X=1}P{Y=1}. 因此X与Y不相互独⽴.(2) Z X Y =+的可能取值为3, 4, 5, 6, 且316161}1,2{}2,1{}3{=+===+====Y X P Y X P Z P , }1,3{}2,2{}3,1{}4{==+==+====Y X P Y X P Y X P Z P 3 112161121=++=, 3(3) V =21}2,2{}1,2{}2,1{}2{===+==+====Y X P Y X P Y X P V P , 2 1}2{1}3{==-==V P V P . 即max(,)V X Y =的分布律为(4) min{U =}3,1{}2,1{}1{==+====Y X P Y X P U P}1,2{}1,3{==+==+Y X P Y X P 21=, 21}1{1}2{==-==U P U P .即min{,}U X Y =的分布律为(5) W U =+31}1,2{}2,1{}2,1{}3{===+=======Y X P Y X P V U P W P ,。
组织行为学第8-9章复习题

第8、9章复习题1.群体成员相互吸引和共同参与群体目标的程度是()。
A.群体内聚力B.社会促进C.群体思维D.群体压力答案:A2.期望理论中的奖赏的吸引力是指奖赏的()。
A.效价B.手段C.可及性D.期望答案:A3. 根据弗鲁姆的期望理论,以下公式中错误的是( )。
A.E高×V高=M高B.E高×V低=M高C.E低×V高=M低D.E低×V低=M低答案:A4. 在组织中,通过满足成员的社会需要而发挥着重要作用的群体是()。
A.正式群体B.任务群体C.命令群体D.非正式群体答案:D5. 群体决策有许多优势,包括()。
A.创造才智的融会B.激发管理层进行战略性思考C.促进员工队伍的多元化D.提供更全面的信息答案:D6. ()能够根据个体的教育背景、年龄、技能或经验而被非正式地授予。
A.地位B.规范C.群体内聚力D.角色答案:A7. 如果一个人具有高权力需要,那么他()。
A.左右其他人只能按照某种方式行为B.建立友好和亲密的人际关系,营造合作的氛围等C.不喜欢赌博,承担个人责任,回避那些他们觉得特别容易或者特别困难的工作任务D.具有强烈的成功驱动力,希望在某些事上比别人做得更好答案:A8. 群体成员共同接受、共同遵守、约定俗成的行为准则叫( ) 。
A.群体规范B.工作制度C.群体纪律D.群体压力答案:A9. ()向群体的生产率应至少等于每个群体成员生产率之和的观点提出了正面的挑战。
A.群体内聚力B.“搭便车效应”C.群体思维D.地位答案:B10.一个人的活动由于有他人同时参加或在场旁观,活动效率就会提高,这种现象叫()。
A.社会惰化效应B.群体促进作用C.协同效应D.从众效应答案:A11. 群体规模会对群体运行过程造成的影响是()。
A.群体规模越大,决策质量差B.小规模群体会产生“搭便车效应”C.大规模群体能提供更全面的信息和更多的备选方案D.对群体运行过程没有影响答案:C12. 对群体内聚集力和生产率之间的关系研究表明,当群体内聚力(),群体与组织目标一致性()时,群体的生产效率会明显提高。
信息论与编码第7-8章习题解答

相应的校验矩阵为
1 0 0 1 ' G 和 G 的差别仅是列的置换,所以 H 和 H ' 的差别也是同样的列置换,所以 1 1 0 1 1 0 1 1 0 1 1 1 1 0 H = 0 1 1 1 0 0 0 I 4×4 0 0 0 1 1 1 1
该码的校验矩阵任意二列线性独立,而第 1,2,3 列之和为零矢量,所以存在 着相关的三列,从而最小 Hamming 重量为 3。
wH (c 1 + c 2 ) = wH (c 1 ) + wH (c 2 ) − 2 wH (c 1 ⋅ c 2 ) 是偶数,其中 c1 ⋅ c 2 表示 c1 和 c 2 的交截。因此 c1 + c 2 ∈ E n ,所以 En 是一个线性码。
由于对称性, 在所有长度为 n 的二元矢量中, 奇数重量与偶数重量的矢量数相等, n −1 所以 En 中码字数为 2 , 从而 k = n − 1 ; 又 En 中最小非零码字的重量为 2, 所以 d = 2 , 于是 En 的参数为 ( n, n − 1,2) 。 7-4 设二元线性码 M 的生成矩阵为 1 0 0 1 1 G = 0 0 1 0 1 0 1 1 1 1 求 M 的最小距离。 [解] 由 G 生成的(5,3)码的八个码字为 (00000) , (10011 ) , (00101) , (01111) (10110) , (01010) , (11100) , (11001) 所以非零码字最小重量为 2,从而最小 Hamming 矩离 d min = 2 。 7-5 设二元线性码 M 的生成矩阵为 1 1 0 1 0 G = 0 1 0 1 0 , 建立码 M 的标准阵,并对码字 11111 和 10000 分别进行译码。 [解] 由 G 生成的(5,2)码 M 的标准阵列为 (00000) , (11010) , (01010) , (10000) (00001) , (11011) , (01011 ) , (10001) (00010) , (11000) , (01000) , (10010) (00100) , (11110) , (01110) , (10100) (00011 ) , (11001) , (01001) , (10011 ) (00101) , (11111) , (01111) , (10101) (01100) , (10110) , (00110) , (11100)
山东大学分子生物学章节习题及参考答案03DNA的生物合成(复制)

第三章 DNA的生物合成(复制)一、选择题1.F.Crik中心法则遗传信息的传递方式不包括A.RNA→蛋白质B.DNA→rRNAC.DNA→DNAD.RNA→DNAE.DNA→mRNA2.M.Meselson和F.W.Stahl用15NH4Cl 证明的机制是A. DNA混合式复制B. DNA转录为mRNAC. mRNA翻译为蛋白质D. DNA半保留复制E. DNA全保留复制3.不参与原核DNA复制的物质是A.dNTPB.Dna GC.Uvr BD.SSBE.NTP4.复制中维持DNA单链状态的蛋白质是A.Dna BB.UvrBC.SSBD.Rec AE.Lex A5.DNA复制时, 合成5'-TAGATCC-3'的互补序列是A.5'-GGATCTA-3'B.5'-CCTAGAT-3'C.5'-GGAUCUA-3'D.5'-GGAUAGA-3'E.5'-ATCTAGG-3'6.关于DNA-pol Ⅲ的叙述,错误的是A.有3'→5'外切酶活性B.有5'→3'外切酶活性C.复制延长中催化核苷酸聚合D.细胞中含量最少比活性最高E.有5'→3'聚合酶活性7.DNA复制保真性的叙述,错误的是A.DNA-polⅠ的即时校读功能B.DNA-pol 对碱基的选择性C.DNA-pol 对模板的依赖性D.DNA-pol对模板的高亲和性E.严格的碱基配对原则8.DNA拓扑异构酶的作用是A.解开DNA双螺旋间氢键B.复制时理顺DNA链C.使DNA异构为核小体D.辨认复制起始点E.稳定和保护单链DNA9.复制中,RNA引物的作用是A.活化SSBB.使冈崎片段延长<P%2@`���<NTEXT style="LINE-HEIGHT: 18pt; TEXT-INDENT:7.9pt">C.参与构成引发体D.协助解螺旋酶作用E.提供3'-OH末端供dNTP加入10.紫外线照射最常引起的碱基二聚体是A.C-CB.C-TC.T-TD.T-UE.U-C11.DNA切除修复时①DNA-polⅠ;②DNA连接酶;③Uvr A;④Uvr C、Uvr B 作用顺序是A.③、④、①、②B.①、②、③、④C.②、③、①、④D.③、②、④、①E.①、③、④、②12. 着色性干皮病的分子基础是A.Uvr类蛋白缺乏B.DNA-pol δ基因缺陷C.DNA-pol ε基因突变D.Lex A类蛋白缺乏E.XP类基因缺陷13. 关于逆转录酶的叙述,错误的是A.以单链RNA为模板B.以单链DNA为模板C.水解杂化双链中的RNAD.促使新合成DNA转入宿主细胞E.能生成cDNA双链14. 能直接以DNA为模板合成的物质是A.阻遏物B.hnRNAC.引物酶D.诱导剂E.辅阻遏物15. 参与DNA复制的物质不包括A.引物酶B.拓扑酶C.连接酶D.核酶E.SSB16. 关于端粒酶的叙述,错误的是A.以染色体DNA为模板B.是RNA-蛋白质复合物C.催化端粒DNA生成D.含有RNA模板E.有逆转录酶活性17.产生冈崎片段的原因是A.复制速度过快B.拓扑酶作用生成C.多个复制起始点D.复制与解链方向相反E.RNA引物过短18. 关于突变的叙述, 错误的是A.点突变导致错配B.缺失一定引起框移突变C.插入不一定引起框移突变D.插入可改变密码子阅读方式E.A取代G是突变19. 为真核生物DNA连接酶供能的物质是A.GTPB.ATPC.NAD+D.NADPHE.FAD20. 不需要DNA连接酶参与的过程是A.DNA复制B.切除修复C.SOS修复D.DNA复性E.DNA重组二、名词解释1. 中心法则(the central dogma)2. 基因和基因表达(gene and gene expression)3. 半保留复制(semiconservative replication)4. 端粒和端粒酶(telomere and telomerase)5.逆转录和逆转录酶(reverse transcription and reverse transcriptase)三、问答题1.DNA复制时是如何保证其保真性的?2.论述参与DNA复制的主要物质及各自的功能。
第八章德育课后习题及参考答案

第八章德育课后习题及参考答案作者:潘友刚发布时间:2011-03-31 17:11:44《教育学》第八章课后习题一、名次解释德育内容德育过程德育原则德育方法德育途径二、简答题1、简述马卡连柯的德育思想。
2、简述合作教育学的德育思想。
3、德育的途径有哪些?4、试列出集中主要的德育方法。
5、德育的主要原则《教育学》第八章课后习题答案一、名次解释德育内容:德育内容是用以形成受教育者品德的社会思想政治准则和法纪道德规范的总和。
德育过程:德育过程是教育者和受教育者双方借助于教育内容和方法,进行施教传道和受教修养的统一活动过程,是促使受教育者道德认识、道德情感、道德意志和道德行为发展的过程,是个体社会化与社会规范个体化的统一过程。
德育原则:德育原则是根据教育目的、德育目标和德育过程规律提出的指导德‘育工作的基本要求。
德育原则对制定德育大纲、确定德育内容、选择德育方法、运用德育组织形式等具有指导作用。
德育方法:德育方法是为达到德育目的,在德育过程中采用的教育者和受教育者相互作用的活动方式的总和。
它包括教育者的施教传道方式和受教育者的受教修养方式。
德育途径:德育途径是指德育的实施渠道或形式。
二、简答题1、马卡连柯的德育思想。
马卡连柯是苏联早期著名的教育实践和教育理论家。
他在长期从事流浪儿和违法少年的教育改造工作中,总结概括出以下很有特色和价值的德育思想理论:(1)尊重信任与严格要求相结合的德育原则。
(2)集体教育的思想。
(3)劳动教育的思想。
(4)纪律教育的思想。
2、简述合作教育学的德育思想。
“合作教育学”是前苏联80年代普通教育改革中出现的新的教育理论。
它是一批长期从事教育实验的教师和学者提出的。
其核心思想是强调教育的社会主义人道主义和个性民主化,主张教学、教育过程应建立在师生合作的新型关系之上。
3、德育的途径:德育途径是指德育的实施渠道或形式。
我国学校德育实施途径主要有:1.教学。
2.共青团、少先队、学生会组织的活动。
高频电路原理与分析-习题解答

3-9 已知高频功放工作在过压状态,现欲将它调整到临界状 态,可以改变哪些外界因素来实现,变化方向如何?在 此过程中集电极输出功率如何变化? 答3-9 可以通过采取以下措施 1. 2. 3. 4. 减小激励Ub,集电极电流Ic1和电压振幅UC基本不变,输 出功率和效率基本不变。 增大基极的负向偏置电压,集电极电流Ic1和电压振幅UC 基本不变,输出功率和效率基本不变。 减小负载电阻RL,集电极电流Ic1增大,IC0也增大,但电 压振幅UC减小不大,因此输出功率上升。 增大集电极电源电压,Ic1、IC0和UC增大,输出功率也随 之增大,效率基本不变。
有载品质因数为58.125,这时需要并 答:回路电感为0.586mH,有载品质因数为 回路电感为 有载品质因数为 这时需要并 的电阻。 联236.66k 的电阻。
2-2 图示为波段内调谐用的并联振荡回路,可变电容 C的变化 范围为 12~260 pF,Ct为微调电容,要求此回路的调谐 范围为 535~1605 kHz,求回路电感L和Ct的值,并要求 C的最大和最小值与波段的最低和最高频率对应。 解2-2:
根据已知条件,可以得出: 回路总电容为C∑ = C + Ct ,因此可以得到以下方程组 1 1 1605 ×103 = = 2π LCmin 2π L(12 × 10−12 + Ct ) 1 1 535 ×103 = = 2π LCmax 2π L(260 × 10−12 + Ct )
1-2 无线通信为什么要用高频信号?“高频”信号指的 是什么? 答: 高频信号指的是适合天线发射、传播和接收的射频信 号。 采用高频信号的原因主要是: (1)频率越高,可利用的频带宽度就越宽,信道容量就 越大,而且可以减小或避免频道间的干扰; (2)高频信号更适合电线辐射和接收,因为只有天线尺 寸大小可以与信号波长相比拟时,才有较高的辐射效率和接 收效率,这样,可以采用较小的信号功率,传播较远的距离, 也可获得较高的接收灵敏度。
流体输配管网第八章必考习题

第8章8-1.如图4所示流体输配管网图,各分支的阻抗为:S(1)=3.2,S(2)=3.3,S(3)=3.4,S(4)=0.2,S(5)=0.3,S(6)=0.4(单位:kg/m7)。
该管网图没有节点流量。
在分支③上设有机械动力,在其合理的工作流量范围,输出全压和流量的函数关系为: Pa。
试建立求解该管网的分支流量Q(Q1,Q2,…Q6)的方程组。
(1)写出基本关联矩阵B k,建立节点流量平衡方程组。
(2)选出管网图的最小阻抗生成树,写出独立回路矩阵C f,建立独立回路压力平衡方程组。
(3)将独立回路压力平衡方程组转化为只有余枝流量未知数的方程组。
(2分)解:(1)以节点4为参考节点,基本关联矩阵和节点流量平衡方程组为:;(2)最小阻抗生成树由分支4、5、6组成。
(3)首先将分支4、5、6的流量用分支1、2、3表示。
,代入独立回路压力平衡方程组即得。
8-2.如图为某流体输配管网图,所有分支的阻抗均已知。
各节点流量如下表。
(1)以节点V6为参考节点,写出该管网图的基本关联矩阵B k,和节点流量平衡方程组。
(2)以管段1、2为余枝,写出该管网图的独立回路矩阵Cf和独立回路压力平衡方程组。
解:以节点6为参考点的基本关联矩阵B k=节点流量平衡方程矩阵=(2)独立回路矩阵C f=节点压力平衡方程矩阵=写成方程的形式:将代入。
8-3.如下图所示的流体输配管网图,各管段的阻抗(单位:kg/m7)为:S(1)=5.2,S(2)=5.3,S(3)=1.2,S(4)=1.3,S(5)=1.4。
该管网图的1、4节点分别有节点流量,其大小方向如图示。
试建立求解管段流量Q(Q1,Q2, (5)的方程组。
(1)建立矩阵形式表示的节点流量平衡方程组。
(2)选出管网图的最小阻抗生成树,写出独立回路矩阵C f,建立矩阵形式的独立回路压力平衡方程组。
(3)将独立回路压力平衡方程组简化为只有余枝流量未知数的方程组。
解:(1)以节点4为参考节点,节点流量平衡方程组如下:(2)最小阻抗树由分支3、4、5组成。
电子科技大学中山学院-分析化学(科教版)-1-8章习题及答案

第 1 章 绪论
填空题 1.分析化学的任务是 , , 和 。试剂用量在效数字为
误差的规律性,总体平均值 表示样本测量值的 ,总体标准偏差 表示样
特性,在不存在系统误差的情况下,就是 本测量值的 特性, 越小, 越好。
11.有些辅助试剂与被测离子形成的配合物有较大的稳定性,这时空白实验并不能完全消 除其影响,要想消除其影响,做 实验,该值与 之差就是空白值。 属于常量分析; 在 之
0.1060、0.1036、0.1032、0.1018、0.1034。 (1)用 Q 检验法判断有无可疑值要舍弃(置信水平 90%)? (2)应以什么浓度值报出结果? (3)计算平均值在 95%置信度时的置信区间。 6.某试样中含有约 5%的 S,将 S 氧化为 SO4 ,然后沉淀为 BaSO4。若要求在一台分度 值为 0.1mg/分度的天平上称量 BaSO4 质量时,称量误差不超过 0.1%。问必须称取试样多 少克?(M BaSO4=233.4,Ms==32.07) 7.经过无数次分析(假定已消除了系统误差)测得某药物中阿司匹林的含量为 78.60% ,其 标准偏差 为 0.10%,试求测定值落在 78.40%~78.80%的概率为多少? 8.已知测定某元素的原子量时,经过无数次的测定得原子量为 10.82,标准偏差是 0.12。 若该结果分别是测定 1 次、4 次、9 次得出。计算置信度为 95%时的平均值的置信区间。上 述结果说明什么问题?(置信度为 95%时, u =1.96)
第8章 多元函数微分法及其应用 习题 9 (3)

(1) ∫∫∫ (x + y + z)dv , 其中 Ω 是由圆锥面 z = 1 − x2 + y2 与平面 z = 0 围成的闭 Ω
区域;
(2) ∫∫∫ z x2 + y2 dv , 其中 Ω 是由柱面 y = 2x − x2 与平面 z = 0 , z = 1 及 y = 0 Ω
围成的闭区域. 解 (1) Ω 可表示为 0 ≤ z ≤ 1 − ρ , 0 ≤ ρ ≤ 1, 0 ≤ θ ≤ 2π , 故
区域是圆域 x2 + y2 ≤ 1 , 于是 Ω 可用不等式表 示为:
z z = x2 + 2y2 = 2 − x2
O y
x 图 9.41
x2 + 2 y2 ≤ z ≤ 2 − x2 , − 1 − x2 ≤ y ≤ 1 − x2 , −1 ≤ x ≤ 1 ,
1
因此
∫∫∫ ∫ ∫ ∫ 1
1− x2
x, 0 ≤ x ≤
π }
,
故
2
∫∫∫ ∫ ∫ ∫ π y cos(x + z)dv = 2 dx
x
dy
π 2
−x
y
cos(x
+
z)dz
0
0
0
Ω
∫ ∫ ∫ π
= 2 dx
x ( y - y sin x)dy =
π 2
x(1 − sin
x) dx
=
π2
−
1
.
0
0
0
2
16 2
3
(5)
法1
不妨设 h > 0 ,
2 dρ
4−ρ2 f (ρ 2 + z2 )ρdz ,
微机原理与接口技术习题答案

第3章8086/8088指令系统与寻址方式习题3.3 8086系统中,设DS=1000H,ES=2000H,SS=1200H,BX=0300H,SI=0200H,BP=0100H,VAR的偏移量为0600H,请指出下列指令的目标操作数的寻址方式,若目标操作数为存储器操作数,计算它们的物理地址。
(1)MOV BX,12 ;目标操作数为寄存器寻址(2)MOV [BX],12 ;目标操作数为寄存器间址PA=10300H(3)MOV ES:[SI],AX ;目标操作数为寄存器间址PA=20200H(4)MOV VAR,8 ;目标操作数为存储器直接寻址PA=10600H(5)MOV [BX][SI],AX ;目标操作数为基址加变址寻址PA=10500H(6)MOV 6[BP][SI],AL ;目标操作数为相对的基址加变址寻址PA=12306H (7)MOV [1000H],DX ;目标操作数为存储器直接寻址PA=11000H(8)MOV 6[BX],CX ;目标操作数为寄存器相对寻址PA=10306H(9)MOV VAR+5,AX ;目标操作数为存储器直接寻址PA=10605H3.4 下面这些指令中哪些是正确的那些是错误的如果是错误的,请说明原因。
(1)XCHG CS,AX ;错,CS不能参与交换(2)MOV [BX],[1000] ;错,存储器之不能交换(3)XCHG BX,IP ;错,IP不能参与交换(4)PUSH CS(5)POP CS ;错,不能将数据弹到CS中(6)IN BX,DX ;输入/输出只能通过AL/AX(7)MOV BYTE[BX],1000 ;1000大于255,不能装入字节单元(8)MOV CS,[1000] ;CS不能作为目标寄存器(9)MOV BX,OFFSET VAR[SI] ;OFFSET只能取变量的偏移地址(10)MOV AX,[SI][DI] ;SI、DI不能成为基址加变址(11)MOV COUNT[BX][SI],ES:AX ;AX是寄存器,不能加段前缀3.7 设当前SS=2010H,SP=FE00H,BX=3457H,计算当前栈顶的地址为多少当执行PUSH BX 指令后,栈顶地址和栈顶2个字节的内容分别是什么当前栈顶的地址=2FF00H当执行PUSH BX 指令后,栈顶地址=2FEFEH(2FEFEH)=57H(2FEFFH)=34H3.8 设DX=78C5H,CL=5,CF=1,确定下列各条指令执行后,DX和CF中的值。
环境工程原理课后习题答案2-8章

课
后
答
案
网
ww w
.k
hd
3.4如图所示,有一水平通风管道,某处直径由400mm减缩至200mm。 为了粗略估计管道中的空气流量,在锥形接头两端各装一个U形管 压差计,现测得粗管端的表压为100mm水柱,细管端的表压为40mm 水柱,空气流过锥形管的能量损失可以忽略,管道中空气的密度为 1.2kg/m3,试求管道的空气流量 。
R 21rm1 b1 22 rm 2 b2 23rm3 b3
网
每米管段的冷损失量: Q T 5 105 46.85W / m
21rm1
答
(2)
案
R
3 30 30 2 45 28.47 2 0.04 43.28 2 0.15 73.99 3.189 K / W
aw
.c om
课
(2)管径增加一倍: um变为原来的1/4,μ和l不变,阻力损失变为原来的1/16
后
答
案
(1)管长增加一倍:阻力损失增加一倍
网
ww w
2 8uml 32uml l um p f 2 2 r0 d d 2
.k
hd
aw
3.6水在圆形直管中呈层流流动,若流量不变,说明在下列情况 下,因流动阻力而产生的能量损失的变化情况: (1)管长增加一倍 (2)管径增加一倍。
A1 19 19 1.12 19 15 Am 16.9 19 ln 15 A1 19 1.27 A2 15
1 0.002 1 0.00026 0.000176 458 45 3490 2.95 10 3 m 2 K / W
课
后
答
案
MRPⅡ-ERP原理与应用习题解答
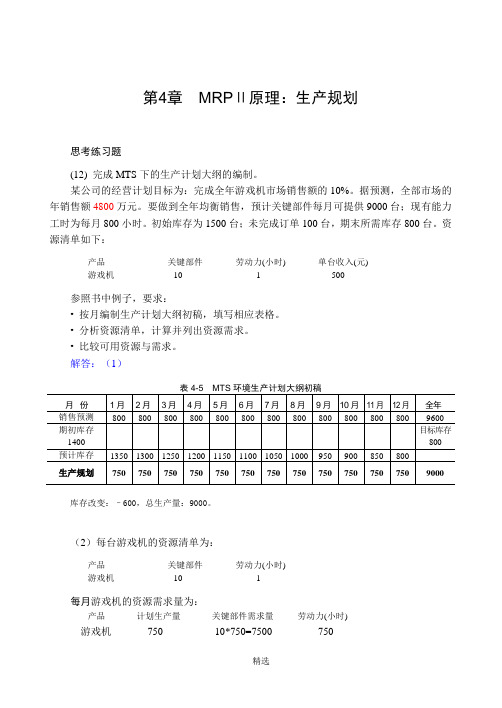
第4章MRPⅡ原理:生产规划思考练习题(12) 完成MTS下的生产计划大纲的编制。
某公司的经营计划目标为:完成全年游戏机市场销售额的10%。
据预测,全部市场的年销售额4800万元。
要做到全年均衡销售,预计关键部件每月可提供9000台;现有能力工时为每月800小时。
初始库存为1500台;未完成订单100台,期末所需库存800台。
资源清单如下:产品关键部件劳动力(小时) 单台收入(元)游戏机10 1 500参照书中例子,要求:•按月编制生产计划大纲初稿,填写相应表格。
•分析资源清单,计算并列出资源需求。
•比较可用资源与需求。
解答:(1)库存改变:–600,总生产量:9000。
(2)每台游戏机的资源清单为:产品关键部件劳动力(小时)游戏机10 1每月游戏机的资源需求量为:产品计划生产量关键部件需求量劳动力(小时)游戏机750 10*750=7500 750(3)可用资源为关键部件每月可提供9000台;现有能力工时为每月800小时,能够满足需求量。
(13) 完成MTO下的生产计划大纲的编制。
某公司的经营计划目标为:完成全年游戏机市场销售额的10%。
据预测,全部市场的年销售额4800万元。
要做到全年均衡销售,预计关键部件每月可提供9000台;现有能力工时为每月800小时。
期初未交货数量1400台,交货日期为:1月750台;2月400台;3月200台;4月50台;期末未交货数量:800台。
资源清单如下:产品关键部件劳动力(小时) 单台收入(元)游戏机10 1 500参照书中例子,要求:•按月编制生产计划大纲初稿,填写相应表格。
•分析资源清单,计算并列出资源需求。
•比较可用资源与需求。
解答:(1)未完成订单的改变:-600,总产量:10200。
(2)每台游戏机的资源清单为:产品关键部件劳动力(小时)游戏机10 1每月游戏机的资源需求量为:产品计划生产量关键部件需求量劳动力(小时)游戏机850 10*850=8500 850(3)可用资源为关键部件每月可提供9000台;现有能力工时为每月800小时,能力工时不能够满足需求量,出现资源短缺,故计划需要调整,或增添资源。
彭泽县八中七年级数学下册第八章二元一次方程组8.2消元__解二元一次方程组第3课时选择适当的方法解二

x+y=12, 解:(1)设成人人数为 x 人,学生人数为 y 人,则有35x+325y=350,
解得xy= =84, . ∴一共去了 8 个成人,4 个学生. (2)当按团体购票时共需 12×35×0.6=252 元,∵252<350,∴按团 体票最省钱.
14.(导学号 09124091)(2017·南召县期末)如下是按一定规律排列的方程
包寄往贫困地区,其中每包书的数目相等.第一次他们领来这批书的23, 结果打了 16 个包还多 40 本;第二次他们把剩下的书全部取来,连同 第一次打包剩下的书一起,刚好又打了 9 个包.那么这批书共有多少 本?
23y=16x+40, 解:设每包有 x 本书,这批书共有 y 本,则31y=9x-40, 解得
例2 甲、乙两商场以同样的价格出售同样的商
品,并且又各自要推使出购不物同花的优费惠最方少案,:在甲商 场收费累;计你到在购哪能乙买从些商10题信0场你元息目累后是计中?,怎购得超么买出想超1过0的0元5?0元的后部,分超按过90%50
元的部分按95%收费.顾客到哪家商场购物花 费少?
分析 在甲商场购物超过 100 元后享受优 惠,在乙商场购物超过 50 元后享受优 惠.因此,我们需要分三种情况讨论: (1)累计购物不超过 50 元;
购物款
在甲商场花费
不超过50元(0<x≤50)
x
超过50,但不超过100 元(50<x≤100)
x
超过100元(x>100) 100+0.9(x-100)
在乙商场花费 x
50+0.95(x-50) 50+0.95(x-50)
你能从表格中看出在哪 家商场花费少吗?
(a)当0<x≤50时,在两家商场花费一样,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-3.一定量的理想气体,其体积和压强依照V=a a 为已知常数。
试求: (1)气体从体积V 1膨胀到V 2所作的功;(2)体积为V 1时的温度T 1与体积为V 2时的温度T 2之比。
解:⎪⎪⎭⎫ ⎝⎛-===⎰⎰21222112121V V a dv v a pdv A v v v V (2)由状态方程 RT MmPV =得 21212222212111 ,V VT T RV a R V P T RV a R V p T =∴====8-4. 0.02kg 的氦气(视为理想气体),温度由17℃升为27℃,假设在升温过程中 (1)体积保持不变;(2)压强保持不变;(3)不与外界交换热量。
试分别求出气体内能的改变,吸收的热量,外界对气体所作的功。
解:氦气为单原子分子理想气体,i =3 (1)定容过程,V=常量,A=0 据Q=ΔE+ A 可知 J T T C ME Q V 623)(m12m =-==,∆ (2)定压过程,P=常量,J 1004.1)(m312m ⨯=-=T T C MQ P , ΔE 与(1)同417J A Q E =-∆=外界对气体所做的功为:A '=-A=-417J(3)Q=0,ΔE 与(1)同气体对外界做功:623J A E =-∆=- 外界对气体所做的功为:A’=-A=623J.8-5.如习题8-5图所示,C 是固定的绝热壁,D 是可动活塞,C ,D 将容器分成A ,B 两部分。
开始时A ,B 两室中各装入同种类的理想气体,它们的温度T ,体积V ,压强P 均相同,并与大气压强平衡。
现对A ,B 两部分气体缓慢的加热,当对A 和B 给予相等的热量Q 以后,A 室中气体的温度升高度数与B 室中气体温度升高度数之比为7:5。
试求:(1)该气体的定容摩尔热容C V ,m 和定压摩尔热容C P ,m 。
(2)B 室中气体吸收的热量中有百分之几用于对外作功。
习题8-5图解:(1)对A, B 两部分气体缓慢的加热,皆可看作准静态过程,两室内是同种气体 ,而且开始时两部分气体的P, V ,T 均相等,所以两室的摩尔数M/μ 也相同. A 室气体经历的是等容过程,B 室气体经历的是等压过程, 所以A, B 室气体吸收的热量分别为(),A V m A mQ C T T M =- (),B P m B mQ C T T M =-已知B A Q Q = ,由上两式得,,75P m A V mBC T C T γ∆===∆因为,P m C = ,V m C +R,代入上式得,,57,22V m P m C R C R ==(2) B 室气体作功为B m A P V R T M =∆=∆B 室中气体吸收的热量转化为功的百分比,,28.6%72BBP m P m B mR T A R R M m Q C C T R M ∆====∆8-6. 有一定量的理想气体,其压强按2C P V=的规律变化,C 是常量。
试求:(1) 将气体从体积V 1增加到V 2所作的功;(2) 该理想气体的温度是升高还是降低。
(1) 221121211VV V V CA PdV dV C V V V ⎛⎫===- ⎪⎝⎭⎰⎰(2)根据理想气体的状态方程有: PV RT ν=所以C PV RT V ν==C T RV ν=11C T RV ν=,22C T RV ν=因为:21V V > 所以:21T T <因此,理想气体的温度降低。
8-7. 1mol 单原子分子理想气体的循环过程如图8-7的T —V 图所示,其中c 点的温度为T c =600K ,试求:(1)ab 、bc 、ca 各个过程系统吸收的热量; (2)经一循环系统所做的净功;(3)循环的效率。
(注:循环效率=A /Q 1,A 为循环过程系统对外作的净功,Q 1为循环过程系统从外界吸收的热量,ln 2=0.693) 解:(1)由图可知,ab 过程中V 和T 成正比,因此为等压过程,bc为等容过程,ca 为等温过程。
根据图所示和理想气体的状态方程,可得各转折点的状态参量(P ,V ,T )分别为:a 点:2252831600210m 600K 249310Pa 210.,,.a a a RTV T P Vν--⨯=⨯====⨯⨯, b 点:225110m 300K 249310Pa ,,.a a b a V T P P -=⨯===⨯ c 点:225c 110m 600K 2498610Pa ,,.a c aV T P P -=⨯===⨯ 设在ab 、bc 、ca 三个过程中所吸收的热量分别为123,,Q Q Q()31583130062310J 2,..P m Q C T ν=∆=⨯⨯-=-⨯32383130037410J 2,..V m Q C T ν=∆=⨯⨯=⨯3a3c cln831600ln234610J ..V Q RT V ν==⨯⨯=⨯ (2)根据热力学第一定律,在整个循环过程中有312309710J .A Q Q Q Q ==++=⨯(3)次循环的效率为23=134+.%A A Q Q Q η==吸 8-8. 热容比=1.40的理想气体,进行如习题8-8图所示的ABCA 循环,状态A 的温度为300K 。
试求:(1)状态B 和C 的温度; (2)各过程中气体吸收的热量、气体所作的功和气体内能的增量。
解:根据题意和图有,对A 点:32m 400a T =300A A A V P P K ==,,,因此摩尔数为4002=032mol 831300..A A A P V RT ν⨯==⨯ 对B 点:310066m 100a T ===225032083..B B B PV V P P K R ν⨯==⨯,,习题8-7图习题8-8图对C 点:32m 100a T =T =75CC C C B BV V P P K V ==,, (2)AB 过程:2=14.i iγ+=,可得5i =, ()15=032183175500J 22..i E R T ν∆∆=⨯⨯⨯-=-,()1400+1004==1000J 2AB A S ⨯=下 1500J Q A E =+∆=BC 过程:()25=03218311501000J 22..i E R T ν∆∆=⨯⨯⨯-=-;2-=-1004=-400J BC A S =⨯下;222-1400J Q A E =+∆=CA 过程:35=03218312251500J 22..iE R T ν∆∆=⨯⨯⨯=;30A =; 3331500J Q A E =+∆=8-9. 某理想气体在P -V 图上等温线和绝热线相交于A 点,如习题8-9图所示,已知A 点的压强P 1=2×105Pa ,体积V 1=0.5×10-3m 3,而且A 点处等温线斜率与绝热线斜率之比为0.741。
现使气体从A 点绝热膨胀至B 点,其体积V 2=1×10-3m 3,试求B 点处的压强和在此过程中气体对外作功。
解:(1)等温线PV =C 得 V P dV dP T-=⎪⎭⎫⎝⎛绝热线 C PV =γ得V P dv dP Qγ-=⎪⎭⎫⎝⎛由题意知()()10.741V QdP dV P V dP dV P V γγ-===-故:11.350.741γ== 由绝热方程γγ2211V p V p = 可得习题8-9图412127.8510a V P P P V γ⎛⎫==⨯⎪⎝⎭(2) 221111122161.41V V V V V PV PV A PdV P dV J V γγ-⎛⎫==== ⎪-⎝⎭⎰⎰8-10. 习题8-10图中所示是一定量理想气体所经历的循环过程,其中a b 和c d 是等压过程。
bc 和da 为绝热过程。
已知b 点和c 点温度分别2T 和3T ,试求循环效率,并判断这个循环是否是卡诺循环。
解:a-b 吸热(),ab P m b a mQ C T T M=- a-b 放热(),dc P m d c mQ C T T M=-- 1ab dc c d ab b aQ Q T T Q T T η--==--又,绝热过程方程:1111,a a d d b b cc P T P T P T P T γγγγγγγγ--------== 上述两式相比得:b a dc T T T T =上式两边同减1:3211c d b a T T TT T T η-=-=--不是卡诺循环。
习题7-7图。
