2011年北京大学保送生考试数学试题
2011年普通高等学校招生全国统一考试北京文科数学和理科数学整编卷详细解析(精品回顾)

绝密★使用完毕前2011年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时间长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合P={x ︱x 2≤1},M={a }.若P ∪M=P,则a 的取值范围是(A )(-∞, -1] (B )[1, +∞) (C )[-1,1] (D )(-∞,-1] ∪[1,+∞) (2)复数212i i-=+(A )i(B )-i(C )(D )4355i--4355i -+(3)在极坐标系中,圆ρ=-2sin θ的圆心的极坐标系是(A)(B) (C) (1,0)(1,)2π(1,2π-(D)(1,)π(4)执行如图所示的程序框图,输出的s 值为(A )-3 (B )-12(C )13(D )2(5)如图,AD ,AE ,BC 分别与圆O 切于点D ,E ,F ,延长AF 与圆O 交于另一点G 。
给出下列三个结论:AD+AE=AB+BC+CA ;○1回归往日精品,再现今日辉煌AF·AG=AD·AE○2③△AFB ~△ADG 其中正确结论的序号是(A )①② (B )②③ (C )①③ (D )①②③(6)根据统计,一名工作组装第4件某产品所用的时间(单位:分钟)为(A ,C 为常数)。
已知工人组装第4件产品用时30分钟,组装第A 件产品用时15分钟,那么C 和A 的值分别是(A )75,25 (B )75,16 (C )60,25 (D )60,16 (7)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是(A) 8 (B) (C)10 (D) (8)设,,,.记为平行四边形()0,0A ()4,0B ()4,4C t +()(),4D t t R ∈()N t ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数的值域为()N t(A ) (B ) {}9,10,11{}9,10,12(C ) (D ) {}9,11,12{}10,11,12第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2011北大自主招生数学详解版

值为何? 解 由 a7 a3 4d 可得公差 d 4 , 从而 a1 21 . 令 21 4( x 1) 0 得 x 6.25 , 故 {an } 从第 7 项开 始为正, 所以 {S n } 的最小项为 S6 66 . 4. 在 ABC 中, a b 2c ,求证: C 60 . 证 根据正弦定理有 sin A sin B 2sin C , 从而有
2011 年北约等十三校联考自主招生数学试卷 厦门一中徐小平
1. 已知平行四边形的其中两条边长为 3 和 5,一条对角线长为 6,求另一条对角线长. 解一 (引理) 平行四边形的对角线平方和等于四边的平方和. 另一对角线长为
2(32 52 ) 62 4 2 . C B 解二 如图, 设 AB 3 , AD 5 , BD 6 , 则据余弦定理有 2 2 2 2 AB AD cos A AB AD BD 2 , 于是 AC 2 DC 2 AD 2 2 DC AD cos CDA D A 32 52 2 AB AD cos A 32 , 从而 AC 4 2 . 2 2 2. 求过抛物线 y 2 x 2 x 1 和 y 5 x 2 x 3 的交点的直线方程. 解 由上述两方程消去二次项可得 6 x 7 y 1 0 , 此即为过两抛物线交点的直线方程. 3. 在等差数列 {an } 中, a3 13, a7 3 ,数列 {an } 的前 n 项和为 S n ,求数列 {S n } 的最小项,并指出其
2011年北京大学等13所大学自主招生数学试题解答

4sin2Ccos2C =2sin C≤sin A+sin B=
的方程.
{y=2x2 -2x-1,
解法 2 联 立 方 程 组
消去 y=-5x2 +2x+3.
2 011×|x-2 0111|=|x-1|+(|x-21|+|x-21|)+
(|x-31|+|x-31|+|x-31|)+ … +
(|x-2 0111|+|x-2 0111|+ … +|x-2 0111|)=
(|x-1|+|x-201 11|)+(|x-21|+|x-2 0111|)+
(|x-21|+|x-2 0111|)+(|x-31|+|x-2 0111|)+
其2 个交点为A(x1 ,y1 )、B(x2 ,y2 ).代入点 A 的坐
标
得
烄y1 烅 烆y1
=2x12 -2x1 -1, =-5x21 +2x1 +3.
① ②
①×5+②×2 得 7y1 =-6x1 +1,即 6x1 +7y1 -1
=0.同理得 6x2 +7y2 -1=0.
所以,两交点 A、B 都在直线6x+7y-1=0 上,
(|x-31|+|x-2 0111|)+ …
(※)
其中共有(1+2+3+ … +2 011)÷2=503×2 011
解法2 设等差数列{an}的公差为d,则3=a7 = a3 +4d=-13+4d,解得d=4>0,则通项
an=a3 +(n-3)d=4n-25. 令 an =4n-25<0,得 正 整 数 n≤6,则
a1 <a2 <…<a5 <a6 <0<a7 <…, S1 >S2 >…>S5 >S6 <S7 <S8 <…. 所以,数列S1 ,S2 ,…中的第 6 项最小,最小值为
2011年普通高等学校招生全国统一考试数学试题(北京卷) 文 (精校版含答案)

2011年普通高等学校招生全国统一考试数学(文)(北京卷) 本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、 选择题共8小题,每小题5分,共40分。
在每小题列出四个选项中,选出符合题目要求的一项。
(1) 已知全集U=R ,集合{}21P x x =∣≤,那么U P =ð(A)(,1-∞-) (B)(1,+∞) (C)(-1,1) (D)()()11-∞,-,+∞(2)复数212i i-=+ (A)i (B )i - (C)4355i -- (D)4355i -+ (3)如果1122log log 0x y <<,那么(A )1y x << (B)1x y << (C)1x y << (D)1y x <<(4)若p 是真命题,q 是假命题,则(A )p q ∧是真命题 (B)p q ∨是假命题题 (C)p ⌝是真命题 (D)q ⌝是真命(5)某四棱锥的三视图如图所示,该四棱锥的表面积是 (A)32(B)16+(C)48(D)16+(6)执行如图所示的程序框图,若输入A 的值为2,则输出的P 值为(A)2(B)3(C)4(D)5(7)某车间分批生产某种产品,每批的生产准备费用为800元。
若每批生产x 件,则平均仓储时间为8x 天,且每件产品每天的仓储费用为1元。
为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品(A )60件 (B)80件 (C )100件 (D )120件(8)已知点()()0,2,2,0A B 。
若点C 在函数2y x =的图象上,则使得ABC 的面积为2的点C 的个数为(A )4 (B)3 (C)2 (D)1第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
(9)在ABC 中,若15,,sin 43b B A π=∠==,则a = . (10)已知双曲线2221(0)y x b b-=>的一条渐近线的方程为2y x =,则b = .(11)已知向量),(01),(a b c k ==-=2a b -与c ,共线,则k = .(12)在等比数列{}n a 中,若141,4,2a a ==则公比q = ; 12n a a a ++⋯+= .数 若关于x 的方程()f x k = 有两个不同的实(13)已知函根,则实数k 的取值范围是 . (14)设(0,0),(4,0),(4,3),(,3)(A B C t D t t +∈R )。
2011年高考北京市数学试卷-文科(含详细答案)

2011年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出四个选项中,选出符合题目要求的一项。
(1) 已知全集U=R ,集合{}21P x x =½£,那么U P =ð(A)(,1-¥-) (B)(1,+¥) (C)(-1,1) (D)()()11-¥,-,+¥【解析】:2111x x £Þ-££,U P =ð()()11-¥,-,+¥ ,故选D (2)复数212ii-=+(A)i (B )i - (C)4355i -- (D)4355i -+ 【解析】:22i 2(i 2)(12i)2242(1)2412i (12i)(12i)1414(1)i i i i i i i ---------+====++----,选A 。
(3)如果1122log log 0x y <<,那么,那么(A )1y x << (B)1x y << (C)1x y << (D)1y x << 【解析】:1122log log x y x y <Þ>,12log 01y y <Þ>,即1y x <<故选D(4)若p 是真命题,q 是假命题,则是假命题,则(A )p q Ù是真命题是真命题 (B)p q Ú是假命题是假命题 (C)p Ø是真命题是真命题 (D)q Ø是真命题是真命题 【解析】:或(Ú)一真必真,且(Ù)一假必假,非(Ø)真假相反,故选D(5)某四棱锥的三视图如图所示,该四棱锥的表面积是(A)32 (B)16+162 (C)48 (D)16322+【解析】:由三视图可知几何体为底面边长为4,高为2的正四棱锥,则四棱锥的斜高为22,表面积2142244161622´´´+=+故选B 。
2011年北京大学保送生考试数学试题赏析

G(
x 1 +x 2 +x 3 , 3
y 1 +y 2 +y 3 )= G( ) , 而 0, 0 3 ) , 故 B C 的外心 为 O( 0, 0 △A , 为正三角形 A B C △
0.
2 2 从而 4 x 4 x p -4 q)< 0, p - 1 =- ( 2 ≤- ( , 故x 4 x . q)< 0, 1 <0 2 <0 因此 , x x . p =- ( q =x 1 +x 2) 1 2 >0 > 0, , , 综合以上情况可得 : 问题得证 . p ≥ 0q ≥ 0 点评 此题研究的其实是复合方程问题 , 一 般解决的方法 是 代 数 法 , 此法对恒等变形的要求 还有数 形 结 合 的 思 想 方 法 也 是 解 决 这 类 题 较高 , 目的很好工具 , 有时更显 得 形 象 直 观 . 在历年的名 这种 题 型 出 现 比 较 多 , 以下两 校自主招生试题中 , 例供同学们参考 : ( 已知 1. 2 0 0 8年上海交通大学自主招生试题 ) ( ) , 函数 f( 且f( x) x2 + b x+ c a ≠0 x) =a =x 无 ]= x 是否有实数根 ? 实根 , 试判断 f[ 证明你 x) f(
2 a , ) , 设切线与 x 轴的交点为 Q , 则得 Q( 0 x 0 2 a c+ 2 F1Q x c x0 +a e x0 +a 0 ∴ = 2 = 2 = F2Q e x0 -a a c x0 -a c- x 0 P F1 , = P F2 又由三角形内角平分线定理逆定理知 , P Q平
2011年北大保送数学考试一道题目的简解

2011年北大保送数学考试一道题目的别解
宁夏固原市五原中学 马占山 田晨光 756000
文[1]证明了下面题目。
已知ABC ∆内有一点,且,ACO CBO CAO BAO ∠=∠=∠=∠求证: ABC ∆的三边成等比数列。
本文用角元素塞瓦定理(见文[2])给出一个
简证。
证明:由文[2]给出的角元素塞瓦定理得
1sin sin sin sin sin sin =∠∠∠∠∠∠BCO
ABO CAO ACO CBO BAO 1)2
sin()2sin 2sin 21sin 3=-⇔A C A B A A -()( )2sin()2sin(2sin 2A C A B A --=⇔ )cos()cos(cos 1A C B C B A -+--=-
)cos(1A C B -++A C B cos )cos(+-=
由于A A C B 2-=-+π,因此有
C B A sin sin sin 22=,即bc a =2
可见用角元素塞瓦定理证明这道题目十分简单。
参考文献
1. 范端喜.2011年北大保送生考试数学试题赏析。
数学通讯,2011,4 (下半月)。
2.李成章.《角元素塞瓦定理及其应用》《中等数学》2006,1
B。
2011年普通高等学校招生全国统一考试(北京卷)数学试题 (文科)(解析版)

本试卷共 5 页,150 分。考试时长 120 分钟。考生务必将答案答在答题卡上,在试卷上作答无 效。考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共 40 分)
一、选择题共 8 小题,每小题 5 分,共 40 分。在每小题列出四个选项中,选出符合题目要求的一项。
55
(D) 4 3 i 55
【解析】: i 2 1 2i
(i 2)(1 2i) (1 2i)(1 2i)
i 2i2 2 4i 1 4i2
i 2(1) 2 1 4(1)
4i
i
,选
A。
(3)如果 log 1 x log 1 y 0 ,那么 (
2
2
(A) y x 1 (B) x y 1
(6)执行如图所示的程序框图,若输入 A 的值为 2,则输出的 P 值为( )
(A)2
(B)3 (C)4 (D)5
【答案】C
第 1页 (共 7页)
【解析】执行三次循环,S 1 A 2 成立, p 11 2 ,S 1 1 1 1 3 ,S 3 A 2
P 22
2
成立, p 2 1 3 , S 3 1 3 1 11 , S 11 A 2 成立, p 3 1 4
y
2x ,则 b
.
【答案】2
第 2页 (共 7页)
【解析】:由
x2
y2 b2
1得渐近线的方程为 x2
y2 b2
0y
bx
即
y
bx ,由一条渐近线的方程
为 y 2x 得b 2
(11)已知向量 a ( 3,1),b (0 1), c (k, 3) 。若 a 2b 与 c ,共线,则 k =
2008-2011北京大学(北约)自主招生数学试题(全附答案)
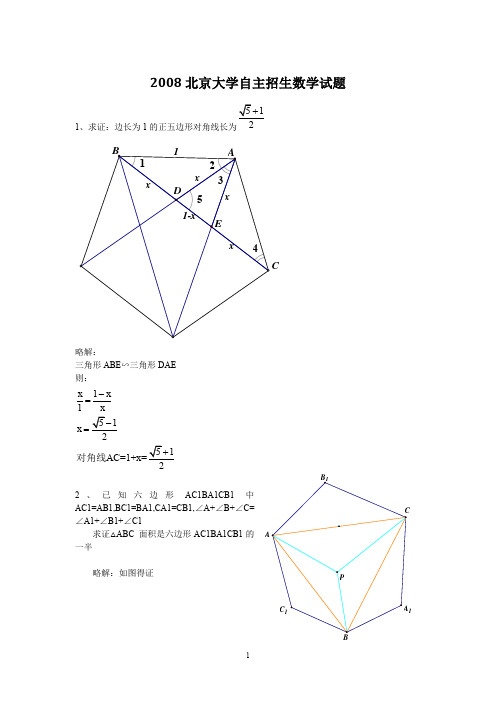
5
答案: 1、 不妨设角 ADC 为 a,那么角 ABC=π-a。 由余弦定理可得 AC=根号(9+16-24cosa)=根号(1+4+4cosa) 从而可解出 cosa=5/7.即有 sina=2(根号 6)/7. 代入 cosa=5/7,可得 AC=根号(55/7). 所以圆的半径就是 AC/2sina. 2、设 13=a1+md,25=a1+nd,41=a1+kd. 那么我们可得 a1+(m+499(k+m-2n))d=2009. 而实际上这道题是有漏洞的,因为 (m+499(k+m-2n))可能是负的,也就是当这是递减的等差数列的时候,那么 2009 就不在这个 数列中了。 3、 挺简单,设 a=tanx+(根 3),b=cotx+(根号 3),假设均为有理数。 那么由(a-(根号 3) ) (b-(根号 3) )=1 可得(a+b)根号 3=ab+2.若 a+b 非零,除过来就矛盾了。 所以必有 a+b=0,此时 ab+2 也是 0. 显然与 a,b 是有理数矛盾。 4、b=0 的时候可知得有|a|≤1.,此时 a+b≤1.下面考虑 b 不等于 0 的情况。 代入+1 和-1 后得出的式子可以化成|a|≤b+1.....(1)(必有 b≥-1) 对称轴的位置是 x=-a/4b.当对称轴在[-1,1]外的时候 那么 1≤|-a/4b|≤(b+1)/4|b|. 分类讨论后就可以得出 b≤1/3.此时 a+b≤b+1+b≤5/3. 若对称轴在[-1,1]内,则可得 a^2≤8(b-b^2)......(2) 这里注意到(b+1)^2-8(b-b^2)=(3b-1)^2≥0.故只需要(2)式成立,就必有 (1)式也成立。此时用柯西不等式 (a+b-1/2)^2≤(a^2+8(b-1/2)^2)(1+1/8)≤9/4 那么就有了 a+b≤2.等号成立的充要条件是 a=4/3,b=2/3,易验证这是成立的. 比较三种情况,显然 2 是 a+b 的最大值, 5、设优秀有 a 人,及格 b 人,不及格 c 人。 则 a+b+c=333 ① 6a+4b+0c≤1000(这里都取各层次里的最少人,故用小于等于) 即 6a+4b≤1000 即 3a+2b≤500 由①得 2a+2b=666-2c 即 a+666-2c≤500 即 a+166≤2c 若 a≥167 则这 167 人至少共解出 167*6=1002 道题,矛盾 故 a≤166 故 a+166≤166+166≤2c 即 c≥166 所以 c≥166≥a 即不及格得人数大于等于优秀的人数
北京大学保送生数学真题及答案

北京大学保送生数学真题及答案2012年北京大学保送生考试数学试题及参考答案1. 已知数列{}na 为正项等比数列,且34125a a a a +--=,求56aa +的最小值.解:设数列{}na 的公比为()0q q >,则231115a qa q a a q +--=,12351a q q q ∴=+--()251(1)q q =+-.由1a>知1q >.()454556111a a a q a q a q q ∴+=+=+()()44225511(1)1q q q q q q =⋅+=+--222211515122011qq q q ⎛⎫⎛⎫=++=-++≥ ⎪ ⎪--⎝⎭⎝⎭,当且仅当22111qq -=-即q =56aa +有最小值20.2.已知()f x 为二次函数,且()()()()()(),,,a f a f f a f f f a 成正项等比数列,求证:()f a a =.证法一:设()()20f x mx nx t m =++≠,数列()()()()()(),,,a f a f f a f f f a 的公比为()0q q >,则()()()()()()()()223,,f a aq f f a f aq aq f f f a f aq aq =====,2ma na t aq∴++=①22()m aq naq t aq ++=②2223()m aq naq t aq ++=③①-②得()()()22111ma q na q aq q ∴-+-=-, ②-③得()()()2222111ma q q naq q aq q ∴-+-=-.若1q =,则()f a a =; 若1q ≠,则()21ma q na aq++=与()21ma q q na aq++=矛盾.()f a a ∴=.证法二:由()()()()()(),,,a f a f f a f f f a 成等比数列得()()()()()()()()()f f f a f f a f a af a f f a ==,()()()()()()()()()()()()f f f a f f a f f a f a f a af f a f a --∴=--.∴三点()()()()()()()()()()()(),,,,,A a f a B f a f a C f a f a 满足ABBCkk =,,,A B C ∴三点共线,与,,A B C 三点在抛物线上矛盾,()f a a ∴=.3.称四个顶点都落在三角形三边上的正方形叫三角形的内接正方形.若锐角三角形ABC 的三边满足a b c >>,证明:这个三角形的内接正方形边长的最小值为sin sin ac B a c B+. 解:如图所示,设正方形MNPQ 的边长为x ,AE MNAD BC=,sin sin c B x x c B a -∴=,sin sin 2ac B abcx a c B Ra bc∴==++. 同理可得其它两用人才种情况下内接正方形边长为D Q EPNMCB A,22abc abcRb ac Rc ab++. ()()()2220Rb ac Ra bc b a R c +-+=--<,()()()2220Rc ab Ra bc c a R b +-+=--<,∴这个三角形的内接正方形边长的最小值为sin sin ac Ba c B+. 4.从O 点发出两条射线12,l l ,已知直线l 交12,l l 于,A B两点,且OABSc∆=(c 为定值),记AB 中点为X ,求证:X 的轨迹为双曲线.解:以12,l l 的角平分线所在直线为x 示的直角坐标系.设AOx BOx α∠=∠=,,OA a OB b ==,(),X x y , 则1sin 22OABS ab c α∆==,2sin 2c ab α=.()()cos ,sin ,cos ,sin A a a B b b αααα-,cos cos ,2sin sin ,2a b x a b y αααα+⎧=⎪⎪∴⎨-⎪=⎪⎩(1)cos 2(2)sin 2xa b y a b αα+⎧=⎪⎪∴⎨-⎪=⎪⎩22(1)(2)-得22222cos sin sin 2x y cab ααα-==,∴X 的轨迹为双曲线. 5.已知()1,2,,10ia i =满足1210121030,21a aa a a a +++=<,求证:()1,2,,10i a i ∃=,使1ia <.X证明:用反证法,假设()1,2,,10ia i ∀=, 1ia ≥.令()11,2,,10i i a b i =+=,则i b ≥,且121020b b b +++=.()()()12101210111a aa b b b ∴=+++121012231b b b b b b b =+++++++12232121b bb b =+++≥与121021a a a <矛盾,()1,2,,10ia i ∴∃=,使1ia <.。
2011年高考北京卷文科数学试题

2011年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时间长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知全集U=R,集合P={x ︱x 2≤1},那么(A )(-∞, -1] (B )[1, +∞) (C )[-1,1] (D )(-∞,-1] ∪[1,+∞)(2)复数212i i-=+ (A )i (B )-i (C )4355i -- (D )4355i -+ (3)如果,0log log 2121<<y x 那么(A )y< x<1 (B )x< y<1(C )1< x<y (D )1<y<x(4)若p 是真命题,q 是假命题,则(A )p ∧q 是真命题 (B )p ∨q 是假命题(C )﹁p 是真命题 (D )﹁q 是真命题(5)某四棱锥的三视图如图所示,该四棱锥的表面积是(A )32 (B )16+162(C )48(D )16+322(6)执行如图所示的程序框图,若输入A 的值为2,则输入的P 值为(A)2(B)3(C)4(D)5(7)某车间分批生产某种产品,每批的生产准备费用为800元。
若每批生产x 件,则平均仓储时间为8x 天,且没见产品每天的仓储费用为1元。
为使平均没见产品的生产准备费用与仓储费用之和最小,每批应生产产品(A )60件 (B )80件 (C )100件 (D )120件(8)已知点A(0,2),B(2,0). 若点C 在函数y = x 的图像上,则使得ΔABC 的面积为2的点C 的个数为(A )4 (B )3 (C )2 (D )1第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
北京大学保送生数学真题及答案

同理可得其它两用人才种情况下内接正方形边长为
abc
abc
,
.
B
2Rb ac 2Rc ab
2Rb ac 2Ra bc b a 2R c 0
M
E
N
Q
DP C
,
2Rc ab 2Ra bc c a 2R b 0,
这个三角形的内接正方形边长的最小值为
acsin B . a c sin B
4.从 O 点发出两条射线 l1, l2 ,已知直线 l 交 l1, l2 于 A, B 两点,且 S OAB c ( c 为定值),
21与 a1a2 a10 21 矛盾,
ai i 1,2, ,10 ,使 ai 1 .
ai i 1,2, ,10 ,使 ai 1.
证明:用反证法,假设 ai i 1,2, ,10 , ai 1.
令 ai 1 bi i 1,2, ,10 ,则 bi 0 ,且 b1 b2
b10 20 .
a1 a2 a10 1 b1 1 b2
1 b10
1 b1 b2
b10 b1b2 b2b3
21 b1b2 b2b3
X O
B l2
acos b co s
x
,
2
asi n b s i n
y
,
2
x ab
(1 )
co s
2
(1)2 (2) 2
得
y ab
(2)
si n
2
x2 cos2
y2 sin 2
2c
ab
,
sin 2
X 的轨迹为双曲线.
5 . 已 知 ai i 1 , 2 , , 满1 0足 a1 a2
a1 03 0 , a 1a 2 a 1 20,1 求 证 :
2011保送生考试各科内容

保送生考试回顾去年12月,我参加了北大的保送生考试,差不多一年过去了,很多东西都记不清了,整理了一下残存的记忆,记录如下。
关于考试内容考试分6部分,语文,数学,英语,物理,化学,面试。
每门100分,总分600分。
语文:试卷大概分了4个部分第一部分:10分单选一共十道。
都是一些文学常识的题目。
记忆中有一题是考错别字;有一个是关于形声字,象形字什么的;还有一个是对联,给出上联选最佳的下联;其余记不得了。
第二部分:25分文言文翻译文章忘了,但是我读过去感觉还可以,大致能翻译出来。
个人认为这是一个蛮重要的部分,因为我语文学习中花在文言文上的时间还是很多的,所以这25分中的大部分还是应该要拿下的,并且难度也不高。
第三部分:25分阅读理解时间仓促,貌似是一篇散文,然后后面有几道小题。
第四部分:40分作文给铁道部长的一封信。
应该网上都能找到,我就不赘述了。
数学:试卷共5道题,每题20分。
做过去感觉还是蛮基本的,就有一个卡住了,并且最后也没做出来,是一个解析几何题,后来问了一下,貌似要用到一个不知道什么定理,但是学过数学竞赛的孩纸应该都知道。
但是试卷难度每年都有变化,所以我也给不出什么建议,但是好好学习还是最重要的。
英语:单选1*20阅读2*20 5篇文章完型0.5*20改错1*10翻译20关于英语,我也说不出什么来,关键就是生词量很大,就全靠平时积累了,临考背单词不知道有没有用。
反正我是英语做到吐血,很多都是靠rp来瞎选了,但是大体上还是认真地把题目读过去并做题的(虽然有时候读了等于没读)。
当然,我英语分数必然很低了。
物理:总共7道大题,算是简单的竞赛题吧。
题目什么的不记得了,网上找找或许能找到题目。
其实物理考得我不是很舒服。
化学:总共10道大题。
我以一个没有搞过化学竞赛的学生的角度看,有些题目比较难,用到了我不知道的知识,但也有题目还是属于高考范围的,甚至有些题是平常练得比较多的。
在最后的总复习中多做做题,把基本的概念理清了,还是能把题意理解了并做出来的。
一道2011年北大保送生考试题的多种解法

C
图1
A B于 点D、E.
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
2 . 4
0<2< 3 2
在 Rt ACM P 中, CPM = 9 。 / 0
・ .
(J。 △AM E ∽ /EN , 3 ・ ’ _ k
.
一
‘sn/CM P - C P i
.
. 1= ZB A O .。 O AC = OC A , . . . ’
’ .
CS 一cs  ̄+2 ) O 2 o( 4
2
・ . .
AO = OC ,AE = O E , A AO E  ̄ / A CO ' , AC = 丽C O ( = ) A E
…
.
・
・
.
①
’ ・
Y 0 一 5 盖
函数关 系式 为 = 一2 +5 定义域为 1 0
,
解得 k =0舍去)k =8 l ( ,2 .
。 . .
・
.
.
综 卜所 述 :AP 的 长 为 2 2或 4 . 2
21 年第 9 01 期
数 学教 学
93 -9
《 s =s ( ) s (+ . = i 2 n i + ・i , )…⑤ n ny 由于s ( ) s ( ) i( ) i  ̄+ ・i  ̄+ =s  ̄+ ・ n n n s( i  ̄一3 ) i( ) s ( ̄+ = n 一 =s  ̄+ ・i 3 ) n n
一
发现这个问题有多种解法. 如图 1 已知 △ 中, ) , B (是三角形 内一点, = 满 足: BAO = C / AO = C BO = (, = ) 求证: △AB C三边成等比数列. 法一: 如图2 过点O作 C的平行线交B , 、
2008-2011北京大学(北约)自主招生数学试题(全附答案)

形
=
舞ACBABA慧CB麓AC =/缓二C
。,
。/
l/
Dk
:::.?日 \、E。.・。
\I,・’
,‘1
.。.
BA 。,
。
口2丁,62丁,
.al一口2
bI—b2
B A +£ A B C +£C .,二 C
即证{一(口I+口2+bI+62)一(口l+d2+口,+
a 口l a 口2
2丁+口,
2丁一口'
【百189】+1=13分,而北方最高分的最大值为6+n
万方数据
14
中’?善i:.7(200s年第2期・高中版)
南方球队内部比赛总得分CⅢ2
,12
・解题研究・
=136,
一l=11分<13分,
.・.
冠军在南方队
北方球队内部比赛总得分c2=28,
北方胜南方得分=30—28=2, 北方球队最高得分=7+2=9, 因为9×17=153<270, 所以南方球队中至少有一支得分超过9分. 冠军在南方球队中.综上所述,冠军是一支南方 球队. 点评这道试题要注意突破口的选择,也需要 耐心和比较强的推理、分析能力. 5.(理科)0一xyz坐标系内xoy平面系内0≤,,≤ 2一石2绕),轴旋转一周构成一个不透光立体在点 (1,0,1)设置一光源,在xoy平面内有一以原点为圆 心的圆c被光照到的长度为2霄,求曲线C上未被照 到的长度.
c:+。+n(肛+9)≥召,c:≤A,
即3n2—22n一36。<0.
‘.・
’B=9A,
.・.c:+9+n(,l+9)≥B=9A1>9c:,
(1)
,’2
又总分为乞Ⅲ有10I乞小钴厶(1)得厅=6或8.
