动态规划法回溯法分支限界法求解TSP问题实验报告
动态规划法,回溯法,分支限界法求解TSP问题实验报告

TSP问题算法实验报告指导教师:****名:***学号:**********提交日期:2015年11月目录总述 (2)动态规划法 (3)算法问题分析 (3)算法设计 (3)实现代码 (3)输入输出截图 (6)OJ提交截图 (6)算法优化分析 (6)回溯法 (6)算法问题分析 (6)算法设计 (7)实现代码 (7)输入输出截图 (9)OJ提交截图 (9)算法优化分析 (10)分支限界法 (10)算法问题分析 (10)算法设计 (10)实现代码 (10)输入输出截图 (15)OJ提交截图 (15)算法优化分析 (15)总结 (16)总述TSP问题又称为旅行商问题,是指一个旅行商要历经所有城市一次最后又回到原来的城市,求最短路程或最小花费,解决TSP可以用好多算法,比如蛮力法,动态规划法…具体的时间复杂的也各有差异,本次实验报告包含动态规划法,回溯法以及分支限界法。
动态规划法算法问题分析假设n个顶点分别用0~n-1的数字编号,顶点之间的代价存放在数组mp[n][n]中,下面考虑从顶点0出发求解TSP问题的填表形式。
首先,按个数为1、2、…、n-1的顺序生成1~n-1个元素的子集存放在数组x[2^n-1]中,例如当n=4时,x[1]={1},x[2]={2},x[3]={3},x[4]={1,2},x[5]={1,3},x[6]={2,3},x[7]={1,2,3}。
设数组dp[n][2^n-1]存放迭代结果,其中dp[i][j]表示从顶点i经过子集x[j]中的顶点一次且一次,最后回到出发点0的最短路径长度,动态规划法求解TSP问题的算法如下。
算法设计输入:图的代价矩阵mp[n][n]输出:从顶点0出发经过所有顶点一次且仅一次再回到顶点0的最短路径长度1.初始化第0列(动态规划的边界问题)for(i=1;i<n;i++)dp[i][0]=mp[i][0]2.依次处理每个子集数组x[2^n-1]for(i=1;i<n;i++)if(子集x[j]中不包含i)对x[j]中的每个元素k,计算d[i][j]=min{mp[i][k]+dp[k][j-1]};3.输出最短路径长度。
TSP问题求解实验报告

TSP问题求解(一)实验目的熟悉和掌握遗传算法的原理,流程和编码策略,并利用遗传求解函数优化问题,理解求解TSP问题的流程并测试主要参数对结果的影响。
(二)实验原理巡回旅行商问题给定一组n个城市和俩俩之间的直达距离,寻找一条闭合的旅程,使得每个城市刚好经过一次且总的旅行距离最短。
TSP问题也称为货郎担问题,是一个古老的问题。
最早可以追溯到1759年Euler提出的骑士旅行的问题。
1948年,由美国兰德公司推动,TSP成为近代组合优化领域的典型难题。
TSP是一个具有广泛的应用背景和重要理论价值的组合优化问题。
近年来,有很多解决该问题的较为有效的算法不断被推出,例如Hopfield神经网络方法,模拟退火方法以及遗传算法方法等。
TSP搜索空间随着城市数n的增加而增大,所有的旅程路线组合数为(n-1)!/2。
在如此庞大的搜索空间中寻求最优解,对于常规方法和现有的计算工具而言,存在着诸多计算困难。
借助遗传算法的搜索能力解决TSP问题,是很自然的想法。
基本遗传算法可定义为一个8元组:(SGA)=(C,E,P0,M,Φ,Г,Ψ,Τ)C ——个体的编码方法,SGA使用固定长度二进制符号串编码方法;E ——个体的适应度评价函数;P0——初始群体;M ——群体大小,一般取20—100;Ф——选择算子,SGA使用比例算子;Г——交叉算子,SGA使用单点交叉算子;Ψ——变异算子,SGA使用基本位变异算子;Т——算法终止条件,一般终止进化代数为100—500;问题的表示对于一个实际的待优化问题,首先需要将其表示为适合于遗传算法操作的形式。
用遗传算法解决TSP,一个旅程很自然的表示为n个城市的排列,但基于二进制编码的交叉和变异操作不能适用。
路径表示是表示旅程对应的基因编码的最自然,最简单的表示方法。
它在编码,解码,存储过程中相对容易理解和实现。
例如:旅程(5-1-7-8-9-4-6-2-3)可以直接表示为(5 1 7 8 9 4 6 2 3)(三)实验内容N>=8。
旅行商问题的求解方法动态规划法和贪心法;算法论文

旅行商问题的求解方法摘要旅行商问题(TSP问题)时是指旅行家要旅行n个城市然后回到出发城市,要求各个城市经历且仅经历一次,并要求所走的路程最短。
该问题又称为货郎担问题、邮递员问题、售货员问题,是图问题中最广为人知的问题。
本文主要介绍用蛮力法、动态规划法、贪心法和分支限界法求解TSP问题,其中重点讨论动态规划法和贪心法,并给出相应求解程序。
矚慫润厲钐瘗睞枥庑赖。
关键字:旅行商问题;动态规划法;贪心法;分支限界法1引言旅行商问题(TSP)是组合优化问题中典型的NP-完全问题,是许多领域内复杂工程优化问题的抽象形式。
研究TSP的求解方法对解决复杂工程优化问题具有重要的参考价值。
关于TSP的完全有效的算法目前尚未找到,这促使人们长期以来不断地探索并积累了大量的算法。
归纳起来,目前主要算法可分成传统优化算法和现代优化算法。
在传统优化算法中又可分为:最优解算法和近似方法。
最优解算法虽然可以得到精确解,但计算时间无法忍受,因此就产生了各种近似方法,这些近似算法虽然可以较快地求得接近最优解的可行解,但其接近最优解的程度不能令人满意。
但限于所学知识和时间限制,本文重点只讨论传统优化算法中的动态规划法、贪心法和分支限界法,并对蛮力法做简单介绍,用以比较。
聞創沟燴鐺險爱氇谴净。
2正文2.1蛮力法2.1.1蛮力法的设计思想蛮力法所依赖的基本技术是扫描技术,即采用一定的策略将待求解问题的所有元素一次处理一次,从而找出问题的解。
一次处理所有元素的是蛮力法的关键,为了避免陷入重复试探,应保证处理过的元素不再被处理。
在基本的数据结构中,一次处理每个元素的方法是遍历。
残骛楼諍锩瀨濟溆塹籟。
2.1.2算法讨论用蛮力法解决TSP问题,可以找出所有可能的旅行路线,从中选取路径长度最短的简单回路。
如对于图1,我们求解过程如下:酽锕极額閉镇桧猪訣锥。
(1)路径:1->2->3->4->1;路径长度:18;(2)路径:1->2->4->3->1;路径长度:11;(3)路径:1->3->2->4->1;路径长度:23;(4) 路径:1->3->4->2->1;路径长度:11;(5) 路径:1->4->2->3->1;路径长度:18;(6) 路径:1->4->3->2->1;路径长度:18;从中,我们可以知道,路径(2)和(4)路径长度最短。
实验报告4.回溯算法

算法设计与分析实验报告实验名称_____回溯算法_____学院________数学与计算机学院____ 班级_______信科00000___________ 学号_______6666666666__________ 姓名_____000000________________ 2016年月日{if(((a+b)==24)||((a-b)==24)||((a*b)==24)||(b!=0&&a%b==0&&a/b==24)){//如果经过上面的计算得到解while(!route.empty()){node now=route.front();printf("%d%c%d=%d\n",now.a,now.oper,now.b,now.sum);//依次输出前面的计算过程route.pop();}if((a+b)==24){if(b>a) swap(a,b);printf("%d+%d=%d\n",a,b,a+b);}if((a-b)==24) printf("%d-%d=%d\n",a,b,a-b);if((a*b)==24) {if(b>a) swap(a,b);printf("%d*%d=%d\n",a,b,a*b);}if(a%b==0&&b!=0&&(a/b)==24) printf("%d/%d=%d\n",a,b,a/b);//a/b比较特殊,要求结果必须是整数flag=true;//表示找到解,一旦找到任何一个解就退出}return ;}queue <node> temp=route;node x;x.a=a,x.b=b,x.sum=a+b,x.oper='+';if(b>a) swap(x.a,x.b);temp.push(x);dfs(cur+1,a+b,num[cur+1],temp);//(((a*b)*c)*d) 模型temp=route;x.a=a,x.b=b,x.sum=a*b,x.oper='*';if(b>a) swap(x.a,x.b);temp.push(x);dfs(cur+1,a*b,num[cur+1],temp);temp=route;x.a=a,x.b=b,x.sum=a-b,x.oper='-';temp.push(x);dfs(cur+1,a-b,num[cur+1],temp);if(b!=0&&a%b==0){//a/b需要验证合法性temp=route;x.a=a,x.b=b,x.sum=a/b,x.oper='/';temp.push(x);dfs(cur+1,a/b,num[cur+1],temp);}temp=route;x.a=b,x.b=num[cur+1],x.sum=b+num[cur+1],x.oper='+';if(x.b>x.a) swap(x.a,x.b);temp.push(x);dfs(cur+1,a,b+num[cur+1],temp);//a*((b*c)*d) 模型temp=route;x.a=b,x.b=num[cur+1],x.sum=b*num[cur+1],x.oper='*';if(x.b>x.a) swap(x.a,x.b);temp.push(x);dfs(cur+1,a,b*num[cur+1],temp);temp=route;x.a=b,x.b=num[cur+1],x.sum=b-num[cur+1],x.oper='-';temp.push(x);dfs(cur+1,a,b-num[cur+1],temp);if(num[cur+1]!=0&&b%num[cur+1]==0) {temp=route;x.a=b,x.b=num[cur+1],x.sum=b/num[cur+1],x.oper='/';temp.push(x);dfs(cur+1,a,b/num[cur+1],temp);}}int main(){//freopen("point24.in","r",stdin);//输入输出重定向//freopen("point24.out","w",stdout);queue <node> t;scanf("%d %d %d %d",&num[0],&num[1],&num[2],&num[3]);while(!flag){dfs(1,num[0],num[1],t);printf("%d %d %d %d\n",num[0],num[1],num[2],num[3]);if(!next_permutation(num,num+4)) break;}if(!flag) printf("No answer!\n");system("pause");return 0;}。
【VIP专享】回溯法求解TSP问题

人工智能实验报告实验名称:TSP问题姓名:xxx学号:xxxxx大学计算机学院2014年1月14日示与其相连的城市if (hasVis[tab[cityId][i].second] == false) {//当与cityID城市连接的城市没有被访问过hasVis[tab[cityId][i].second] = true;pre[tab[cityId][i].second] = cityId;Backtracking(tab[cityId][i].second, depth + 1, len + tab[cityId][i].first); //递归调用,直到走完5个节点pre[tab[cityId][i].second] = -1;//返回上一层hasVis[tab[cityId][i].second] = false; //false表示没有走过这个城市}}}2、把原问题需要的数据存放在了txt文件当中,通过读取文件来读取题目要求,使得操作更简单关键代码:void getTab() { //用户输入城市信息int u, //城市uv, //城市vw; //uv之间的距离//printf("Inputing ends up with -1 -1 -1\n");while (1) {fscanf(fp,"%d %d %d", &u, &v, &w);if (u == -1 && v == -1 && w == -1)break;tab[u].push_back(PII(w, v)); //对于城市u来说,uv之间的距离是wtab[v].push_back(PII(w, u)); //对于城市v来说也是一样}}3、使用了vector容器,更有利于存放子空间的解,避免了使用数组不当造成的相关问题。
typedef pair<int, int> PII;//定义<int,int>类型存放城市的相邻城市和它们之间的费用vector<PII> tab[10];tab[u].push_back(PII(w, v));tab[nodeId][i].first tab[nodeId][i].second6、实验心得1、重温了算法课程里面学过的回溯法,强化了这种编程思想。
动态规划法,回溯法,分支限界法求解TSP问题实验报告材料

TSP问题算法实验报告指导教师:季晓慧姓名:辛瑞乾学号: 1004131114 提交日期: 2015年11月目录总述 (2)动态规划法 (3)算法问题分析 (3)算法设计 (3)实现代码 (3)输入输出截图 (6)OJ提交截图 (6)算法优化分析 (6)回溯法 (6)算法问题分析 (6)算法设计 (7)实现代码 (7)输入输出截图 (9)OJ提交截图 (10)算法优化分析 (10)分支限界法 (10)算法问题分析 (10)算法设计 (10)实现代码 (11)输入输出截图 (15)OJ提交截图 (16)算法优化分析 (16)总结 (16)总述TSP问题又称为旅行商问题,是指一个旅行商要历经所有城市一次最后又回到原来的城市,求最短路程或最小花费,解决TSP可以用好多算法,比如蛮力法,动态规划法…具体的时间复杂的也各有差异,本次实验报告包含动态规划法,回溯法以及分支限界法。
动态规划法算法问题分析假设n个顶点分别用0~n-1的数字编号,顶点之间的代价存放在数组mp[n][n]中,下面考虑从顶点0出发求解TSP问题的填表形式。
首先,按个数为1、2、…、n-1的顺序生成1~n-1个元素的子集存放在数组x[2^n-1]中,例如当n=4时,x[1]={1},x[2]={2},x[3]={3},x[4]={1,2},x[5]={1,3},x[6]={2,3},x[7]={1,2,3}。
设数组dp[n][2^n-1]存放迭代结果,其中dp[i][j]表示从顶点i经过子集x[j]中的顶点一次且一次,最后回到出发点0的最短路径长度,动态规划法求解TSP问题的算法如下。
算法设计输入:图的代价矩阵mp[n][n]输出:从顶点0出发经过所有顶点一次且仅一次再回到顶点0的最短路径长度1.初始化第0列(动态规划的边界问题)for(i=1;i<n;i++)dp[i][0]=mp[i][0]2.依次处理每个子集数组x[2^n-1]for(i=1;i<n;i++)if(子集x[j]中不包含i)对x[j]中的每个元素k,计算d[i][j]=min{mp[i][k]+dp[k][j-1]};3.输出最短路径长度。
蛮力法、动态规划法、回溯法和分支限界法求解01背包问题【精选】

一、实验内容:分别用蛮力法、动态规划法、回溯法和分支限界法求解0/1背包问题。
注:0/1背包问题:给定种物品和一个容量为的背包,物品的重n C i 量是,其价值为,背包问题是如何使选择装入背包内的物品,使得装i w i v 入背包中的物品的总价值最大。
其中,每种物品只有全部装入背包或不装入背包两种选择。
二、所用算法的基本思想及复杂度分析:1.蛮力法求解0/1背包问题:1)基本思想:对于有n 种可选物品的0/1背包问题,其解空间由长度为n 的0-1向量组成,可用子集数表示。
在搜索解空间树时,深度优先遍历,搜索每一个结点,无论是否可能产生最优解,都遍历至叶子结点,记录每次得到的装入总价值,然后记录遍历过的最大价值。
2)代码:#include<iostream>#include<algorithm>using namespace std;#define N 100//最多可能物体数struct goods //物品结构体{int sign;//物品序号int w;//物品重量int p;//物品价值}a[N];bool m(goods a,goods b){return (a.p/a.w)>(b.p/b.w);}int max(int a,int b){return a<b?b:a;}int n,C,bestP=0,cp=0,cw=0;int X[N],cx[N];/*蛮力法求解0/1背包问题*/int Force(int i){if(i>n-1){if(bestP<cp&&cw+a[i].w<=C){for (int k=0;k<n;k++)X[k]=cx[k];//存储最优路径bestP=cp;}return bestP;}cw=cw+a[i].w;cp=cp+a[i].p;cx[i]=1;//装入背包Force(i+1);cw=cw-a[i].w;cp=cp-a[i].p;cx[i]=0;//不装入背包Force(i+1);return bestP;}int KnapSack1(int n,goods a[],int C,int x[]){Force(0);return bestP;}int main(){goods b[N];printf("物品种数n: ");scanf("%d",&n);//输入物品种数printf("背包容量C: ");scanf("%d",&C);//输入背包容量for (int i=0;i<n;i++)//输入物品i 的重量w 及其价值v {printf("物品%d 的重量w[%d]及其价值v[%d]:",i+1,i+1,i+1);scanf("%d%d",&a[i].w,&a[i].p);b[i]=a[i];}int sum1=KnapSack1(n,a,C,X);//调用蛮力法求0/1背包问题printf("蛮力法求解0/1背包问题:\nX=[ ");for(i=0;i<n;i++)cout<<X[i]<<" ";//输出所求X[n]矩阵printf("]装入总价值%d\n",sum1);bestP=0,cp=0,cw=0;//恢复初始化}3)复杂度分析:蛮力法求解0/1背包问题的时间复杂度为:。
Tsp问题的几种算法的分析

摘要本文分析比较了tsp问题的动态规划算法,分支界限法,近似等算法。
分析了旅行商问题的时间度特点,针对启发式算法求解旅行商问题中存在的一些问题提出了改进算法。
此算法将群体分为若干小子集,并用启发式交叉算子,以较好利用父代个体的有效信息,达到快速收敛的效果,实验表明此算法能提高寻优速度,解得质量也有所提高。
关键词:旅行商问题TSPAbstractthis paper analyzed the time complexity of traveling salesman problem,then put forward some imprivement towards the genetic algorithm for solving this problen: divding the population into some small parent individual well.so it can quickly get into convergence, the experimental result indicates the impwoved algorithm can accelerate the apeed of finding solution and improve the precision.Keywords traveling salesman problem; genetic algorithm; subset; henristic crossover operator目录1、摘要--------------------------------------------------------------12、Abstract---------------------------------------------------------13、Tsp问题的提法------------------------------------------------24、回溯法求Tsp问题--------------------------------------------35、分支限界法求Tsp问题--------------------------------------76、近似算法求解Tsp问题-------------------------------------107、动态规划算法解Tsp问题----------------------------------12引言tsp问题刚提出时,不少人都认为很简单。
TSP问题求解实验报告

TSP问题求解(一)实验目的熟悉和掌握遗传算法的原理,流程和编码策略,并利用遗传求解函数优化问题,理解求解TSP问题的流程并测试主要参数对结果的影响。
(二)实验原理巡回旅行商问题给定一组n个城市和俩俩之间的直达距离,寻找一条闭合的旅程,使得每个城市刚好经过一次且总的旅行距离最短。
TSP问题也称为货郎担问题,是一个古老的问题。
最早可以追溯到1759年Euler提出的骑士旅行的问题。
1948年,由美国兰德公司推动,TSP成为近代组合优化领域的典型难题。
TSP是一个具有广泛的应用背景和重要理论价值的组合优化问题。
近年来,有很多解决该问题的较为有效的算法不断被推出,例如Hopfield神经网络方法,模拟退火方法以及遗传算法方法等。
TSP搜索空间随着城市数n的增加而增大,所有的旅程路线组合数为(n-1)!/2。
在如此庞大的搜索空间中寻求最优解,对于常规方法和现有的计算工具而言,存在着诸多计算困难。
借助遗传算法的搜索能力解决TSP问题,是很自然的想法。
基本遗传算法可定义为一个8元组:(SGA)=(C,E,P0,M,Φ,Г,Ψ,Τ)C ——个体的编码方法,SGA使用固定长度二进制符号串编码方法;E ——个体的适应度评价函数;P0——初始群体;M ——群体大小,一般取20—100;Ф——选择算子,SGA使用比例算子;Г——交叉算子,SGA使用单点交叉算子;Ψ——变异算子,SGA使用基本位变异算子;Т——算法终止条件,一般终止进化代数为100—500;问题的表示对于一个实际的待优化问题,首先需要将其表示为适合于遗传算法操作的形式。
用遗传算法解决TSP,一个旅程很自然的表示为n个城市的排列,但基于二进制编码的交叉和变异操作不能适用。
路径表示是表示旅程对应的基因编码的最自然,最简单的表示方法。
它在编码,解码,存储过程中相对容易理解和实现。
例如:旅程(5-1-7-8-9-4-6-2-3)可以直接表示为(5 1 7 8 9 4 6 2 3)(三)实验内容N>=8。
动态规划解TSP问题

用动态规划方法编程求解下面的问题:某推销员要从城市v1 出发,访问其它城市v2,v3,…,v6 各一次且仅一次,最后返回v1。
D 为各城市间的距离矩阵。
问:该推销员应如何选择路线,才能使总的行程最短?⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=012201622561801011274516804323415105019232125301801250403020100654321v v v v v v D1、变量设定阶段k :已遍历过k 个结点,k=1,2…6,7。
K=1表示刚从V1出发,k=7表示已回到起点V1状态变量Xk=(i ,Sk):已遍历k 个结点,当前位于i 结点,还未遍历的结点集合为Sk 。
则X1=(1,{2,3,4,5,6}),X6=(i ,Φ),X7=(1,Φ)决策变量Uk=(i ,j):已遍历k 个结点,当前位于i 结点,下一个结点选择j 。
状态转移方程:X k+1 = T(Xk ,Uk) = (j ,Sk-{j}) 第k 阶段的指标函数Vk = D[i,j]。
最优指标函数Fk(Xk) = Fk(i ,Sk):已遍历k 个结点,当前从i 结点出发,访问Sk中的结点一次且仅一次,最后返回起点V1的最短距离。
则Fk(i ,Sk) = min{ D[i,j] + F k+1(j ,Sk-{j}) } 1≤k ≤6 F 7(X7) = F 7(1,Φ) = 02、分析:(1)k=6时,F6(i ,Φ) = min{D[i,1] + F7(X7)} = D[i,1] i=2,3,4,5,6(6)k=1时,F1(1,S1) = min{D[1,j] + F2(j,S2)}3、伪代码和时间复杂度为方便计算,结点编号改为0到5.(1)用一张二维表格F[][]表示F(i,Sk),行数是n,列数是2n-1。
(2)行号表示当前所在的结点i。
列号对应的五位二进制表示表示{V5,V4,V3,V2,V1}的一个子集,1表示在集合中,0表示不在集合中。
TSP问题——实验报告

TSP问题目录1实验目的 (1)2问题描述与分析 (1)3算法分析 (1)3.1回溯法 (1)3.2 动态规划 (1)3.3 模拟退火算法 (2)4程序设计 (2)4.1回溯法 (2)4.2动态规划算法 (3)4.3模拟退火算法 (4)5实验结果及分析 (5)6实验总结 (6)7源代码 (6)1实验目的1.使用搜索方法进行TSP问题的求解2.了解相关智能算法3.了解NP难问题的求解策略2问题描述与分析某售货员要到若干城市去推销商品,已知各城市之间的路程(或旅费)。
他要选定一条从驻地出发,经过每个城市一遍,最后回到驻地的路线,使总的路程(或旅费)最小。
分析:问题的本质是搜索问题,而且这个问题是NP完全问题,问题的复杂度指数增长,所以普通的搜索无法在有限的时间里完成搜索,尽管有各种优化的算法:启发式算法、深度优先搜索、动态规划、回溯等。
都无法改变复杂度。
实际上大多时候人们并不关心NP完全问题的最优解,只要得出一个近似的解就可以了,因此,人们发明了很多算法,例如粒子群算法、遗传算法、模拟退火算法,这一类算法被称为“智能算法”,但是,他们都无法求出最优解,仅能得到近似解,但这已经足够了。
在本次试验中,一共设计了三个算法:回溯法,动态规划,模拟退火算法。
3算法分析3.1回溯法回溯法采用深度优先方式系统地搜索问题的所有解,基本思路是:确定解空间的组织结构之后,从根结点出发,即第一个活结点和第一个扩展结点向纵深方向转移至一个新结点,这个结点成为新的活结点,并成为当前扩展结点。
如果在当前扩展结点处不能再向纵深方向转移,则当前扩展结点成为死结点。
此时,回溯到最近的活结点处,并使其成为当前扩展结点,回溯到以这种工作方式递归地在解空间中搜索,直到找到所求解空间中已经无活结点为止。
旅行商问题的解空间是一棵排列树.对于排列树的回溯搜索与生成1,2,……, n的所有排列的递归算法Perm类似,设开始时x=[ 1,2,… n ],则相应的排列树由x[ 1:n ]的所有排列构成.旅行商问题的回溯算法。
TSP问题分析动态规划-分支界限法-蛮力法教学文案

T S P问题分析动态规划-分支界限法-蛮力法算法综合实验报告学号: 1004111115 姓名:李宏强一、实验内容:分别用动态规划、贪心及分支限界法实现对TSP问题(无向图)的求解,并至少用两个测试用例对所完成的代码进行正确性及效率关系上的验证。
二、程序设计的基本思想、原理和算法描述:(包括程序的数据结构、函数组成、输入/输出设计、符号名说明等)1、动态规划法(1)数据结构:①利用二进制来表示集合,则集合S可由一个十进制数x相对应,此x所对应的二进制数为y,如果y的第k位为1,则表示k存在集合S中。
例如:集合S={0,1}(其子集合为{}{0}{1}{01}),我们用二进制数11(所对应十进制数为3)表示S,11中右手边第1个数为1表示0在集合S中,右手边第二个数为1表示1在集合S中,其他位为0表示其它数字不在集合S中;同理,集合S={0,2}(其子集合为{}{0}{2}{02}可用二进制数101(所对应十进制数为5)表示(右手边第1个数为1表示0在集合S中,右手边第二个数为0表示1不在集合S中,右手边第3个数为1表示2在集合S中,则说明0,2在集合中,1不在集合中。
②利用邻接矩阵表示任意两点之间的距离例如:mp[i][j]表示点i,j两点之间的距离。
(2)函数组成①输入函数in()②利用动态规划法算法实现的求解函数solve()③主函数main()(3)输入/输出设计本程序可以通过键盘进行输入、屏幕进行输出。
(根据实际程序情况,还可以选择随机产生输入数据、将输出数据输出到文件等其它方式)这里采用随机产生输入数据,将数据输出在屏幕上的方式。
(4)符号名说明① n 表示顶点个数。
② mp[i][j] 表示顶点i和顶点j之间的距离。
③ dp[i][j] 表示顶点i经过集合S(用二进制表示的数为j)后回到起始点的最短路径和。
(5)算法描述①某一个点i不经过任意点回到起始点的最短路径和为mp[i][0](默认初始点为0)dp[i][0] = mp[i][0]; (1<=i<n)②点i经过集合S(二进制表示的数为j)的最短路径和为从点i经过集合S中的某一点k后再从该点出发,经过集合S-{k}的最小值。
算法设计与分析---回溯+分支限界法实验报告

《算法设计与分析》作业作业四+五回溯法+分支限界法1. 二元最大连通块搜索因为下了场大雨,青蛙王子高兴坏了,它有机会重新划定自己的王国范围。
在下图中,空白区域表示积水的地方,青蛙王子需要找到一块最大的连续积水区域(上下或左右相连)作为自己的新领地。
2. 三元最大连通块搜索小明在玩一种消除游戏。
游戏中有一个长方形的区域,被RGB(红绿蓝)三种颜色的小球充满。
要求每次找出当前最大连通区域(上下左右相邻同种颜色即可算作连通),进行消除。
####.######.######.#####the ans is 712 8..#......##....#.#....#..###.#......#.....##.#...#....#..##..#.####..#......#......#......#.....the ans is 181.3 程序运行情况1.4 程序源码(含注释)#include"bits/stdc++.h"using namespace std;#define inf 999//代码下标从0始,输入时.为可走,#为不可走int n,m;//行、列int ans,now;//最大连通数,当前搜索时连通数char e[inf][inf];//地图int book[inf][inf];//标记地图int pos[4][2]={-1,0,1,0,0,1,0,-1};//方位,上下右左void read()//输入数据{printf("input the row and the column of the map:"); scanf("%d%d",&n,&m);printf("now input the map:\n");for(int i=0;i<n;i++)scanf("%s",e[i]);2.4 程序源码(含注释)#include"bits/stdc++.h"using namespace std;#define inf 999//代码下标从0始int n,m;//行、列int ans,now;//最大连通数,当前搜索时连通数int ans_x,ans_y;//最大连通对应的字符char e[inf][inf];//地图int book[inf][inf];//标记地图int pos[4][2]={-1,0,1,0,0,1,0,-1};//方位,上下右左void read()//输入数据{printf("input the row and the column of the map:");scanf("%d%d",&n,&m);printf("now input the map:\n");for(int i=0;i<n;i++)scanf("%s",e[i]);。
实验三:分支限界法
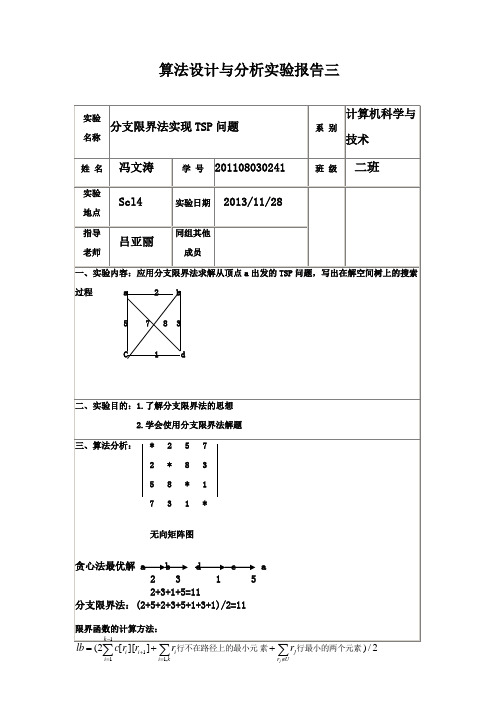
算法设计与分析实验报告三=∉=+k i U r j i i i i j ,111行最小的两个元素素行不在路径上的最小元五.实验程序:#include<iostream>#include<stack>#define N 200using namespace std;class HeapNode{public:double uprofit,profit,weight; int level,x[N];};stack<HeapNode> H;double w[N],p[N];double cw,cp,c;int n;double Bound(int i){double cleft=c-cw,b=cp;while(i<=n&&w[i]<=cleft){cleft-=w[i];b+=p[i];i++;}if(i<=n) b+=p[i]/w[i]*cleft;return b;}void AddLiveNode(double up,double cp,double cw,bool ch,int level)HeapNode nod;nod.uprofit=up;nod.profit=cp;nod.weight=cw;nod.level=level;if(level<=n) H.push(nod); }double Knap(){int i=1;cw=cp=0;double bestp=0,up=Bound(1); while(1){double wt=cw+w[i];if(wt<=c){if(cp+p[i]>bestp) bestp=cp+p[i];AddLiveNode(up,cp+p[i],cw+w[i],true,i+1); }up=Bound(i+1);if(up>=bestp)AddLiveNode(up,cp,cw,false,i+1);if(H.empty()) return bestp;HeapNode node=H.top();H.pop();cw=node.weight;cp=node.profit;up=node.uprofit;i=node.level;}}int main(){cout<<"请输入n和c:"; cin>>n>>c; cout<<"请输入w[i]"<<endl;for(int i=1;i<=n;i++) cin>>w[i];cout<<"请输入p[i]"<<endl;for(int j=1;j<=n;j++) cin>>p[j];cout<<"最优值是:"<<Knap()<<endl; return 0;}。
实验三:分支限界法

算法设计与分析实验报告三=∉=+k i U r j i i i i j ,111行最小的两个元素素行不在路径上的最小元五.实验程序:#include<iostream>#include<stack>#define N 200using namespace std;class HeapNode{public:double uprofit,profit,weight; int level,x[N];};stack<HeapNode> H;double w[N],p[N];double cw,cp,c;int n;double Bound(int i){double cleft=c-cw,b=cp;while(i<=n&&w[i]<=cleft){cleft-=w[i];b+=p[i];i++;}if(i<=n) b+=p[i]/w[i]*cleft;return b;}void AddLiveNode(double up,double cp,double cw,bool ch,int level)HeapNode nod;nod.uprofit=up;nod.profit=cp;nod.weight=cw;nod.level=level;if(level<=n) H.push(nod); }double Knap(){int i=1;cw=cp=0;double bestp=0,up=Bound(1); while(1){double wt=cw+w[i];if(wt<=c){if(cp+p[i]>bestp) bestp=cp+p[i];AddLiveNode(up,cp+p[i],cw+w[i],true,i+1); }up=Bound(i+1);if(up>=bestp)AddLiveNode(up,cp,cw,false,i+1);if(H.empty()) return bestp;HeapNode node=H.top();H.pop();cw=node.weight;cp=node.profit;up=node.uprofit;i=node.level;}}int main(){cout<<"请输入n和c:"; cin>>n>>c; cout<<"请输入w[i]"<<endl;for(int i=1;i<=n;i++) cin>>w[i];cout<<"请输入p[i]"<<endl;for(int j=1;j<=n;j++) cin>>p[j];cout<<"最优值是:"<<Knap()<<endl; return 0;}。
回溯法求解TSP问题

回溯法求解T S P问题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN人工智能实验报告实验名称:TSP问题姓名:xxx学号:xxxxx大学计算机学院2014年1月14日一.实验目的掌握递归回溯法的思想,能够求解TSP 问题,增强自己的编程能力.二.实验内容下图是5个城市的交通图,城市之间的连线权重表示城市之间路程的费用。
要求从A 城出发,经过其它城市一次且仅一次,最后回到A 城,找出一条费用最低的回路。
请用伪代码形式描述所设计的算法。
BDE三、回溯法思想: 回溯法(探索与回溯法)是一种选优搜索法,按选优条件向前搜索,以达到目标。
但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
若已有满足约束条件的部分解,不妨设为(x1,x2,x3,……xi ),I<n,则添加x(i+1)属于s(i+2),检查 (x1,x2,……,xi,x(i+1))是否满足条件,满足了就继续添加x(i+2)、s(i+2),若所有的x(i+1)属于s(i+1)都不能得到 部分解,就去掉xi ,回溯到(xi,x2,……x(i- 1)),添加那些未考察过的x1属于s1,看其是否满足约束条件,为此反复进行,直至得到解或证明无解。
四、算法流程:五、关键技术:1、使用了递归回溯法,通过递归调用,节省了代码量,使代码更简洁易懂。
关键代码:void Backtracking(int cityId, int depth, int len) { ize(); i++) { econd] == false) {econd] = true;pre[tab[cityId][i].second] = cityId;Backtracking(tab[cityId][i].second, depth + 1, len +tab[cityId][i].first); econd] = -1;econd] = false; ush_back(PII(w, v));ush_back(PII(w, u)); ush_back(PII(w, v));tab[nodeId][i].first tab[nodeId][i].second六、实验心得1、重温了算法课程里面学过的回溯法,强化了这种编程思想。
动态规划法-回溯法-分支限界法求解TSP问题实验报告

动态规划法-回溯法-分支限界法求解TSP问题实验报告TSP问题算法实验报告指导教师:季晓慧姓名:辛瑞乾学号: 1004131114 提交日期: 2015年11月目录总述 (4)动态规划法 (4)算法问题分析 (4)算法设计 (5)实现代码 (6)输入输出截图 (10)OJ提交截图 (10)算法优化分析 (10)回溯法 (11)算法问题分析 (11)算法设计 (11)实现代码 (12)输入输出截图 (17)OJ提交截图 (17)算法优化分析 (17)分支限界法 (18)算法问题分析 (18)算法设计 (19)实现代码 (20)输入输出截图 (29)OJ提交截图 (29)算法优化分析 (29)总结 (30)总述TSP问题又称为旅行商问题,是指一个旅行商要历经所有城市一次最后又回到原来的城市,求最短路程或最小花费,解决TSP可以用好多算法,比如蛮力法,动态规划法…具体的时间复杂的也各有差异,本次实验报告包含动态规划法,回溯法以及分支限界法。
动态规划法算法问题分析假设n个顶点分别用0~n-1的数字编号,顶点之间的代价存放在数组mp[n][n]中,下面考虑从顶点0出发求解TSP问题的填表形式。
首先,按个数为1、2、…、n-1的顺序生成1~n-1个元素的子集存放在数组x[2^n-1]中,例如当n=4时,x[1]={1},x[2]={2},x[3]={3},x[4]={1,2},x[5 ]={1,3},x[6]={2,3},x[7]={1,2,3}。
设数组dp[n][2^n-1]存放迭代结果,其中dp[i][j]表示从顶点i经过子集x[j]中的顶点一次且一次,最后回到出发点0的最短路径长度,动态规划法求解TSP问题的算法如下。
算法设计输入:图的代价矩阵mp[n][n]输出:从顶点0出发经过所有顶点一次且仅一次再回到顶点0的最短路径长度1.初始化第0列(动态规划的边界问题)for(i=1;i<n;i++)dp[i][0]=mp[i][0]2.依次处理每个子集数组x[2^n-1]for(i=1;i<n;i++)if(子集x[j]中不包含i)对x[j]中的每个元素k,计算d[i][j]=min{mp[i][k]+dp[k][j-1]};3.输出最短路径长度。
动态规划法,回溯法,分支限界法求解TSP问题实验报告

#define rson m + 1 , r , rt << 1 | 1
using namespace std;
int mp[20][20];
int x[30],vis[30];
int n,k,cur,ans;
void init()
{
for(int i=0;i<n;i++)
{
mp[i][j]=inf;
continue;
}
int tmp;
scanf("%d",&tmp);
mp[i][j]=tmp;
}
}
int mx=(1<<(n-1));
dp[0][0]=0;
for(int i=1; i<n; i++)
{
dp[i][0]=mp[i][0];
}
dp[0][mx-1]=inf;
实现代码
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
算法设计
输入:图的代价矩阵mp[n][n]
输出:从顶点0出发经过所有顶点一次且仅一次再回到顶点0的最短路径长度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
输入:无向图G=(V,E)
输出:哈密顿回路
1、将顶点数组x[n]初始化为0,标志数组vis[n]初始化为0;
2、从顶点0出发构造哈密顿回路:vis[0]=1;x[0]=1;k=1;
3、While(k>=1)
、x[k]=x[k]+1,搜索下一个顶点。
、若n个顶点没有被穷举完,则执行下列操作
∈E,转步骤;
#include <numeric>
#include <iomanip>
#include <bitset>
#include <sstream>
#include <fstream>
#define debug "output for debug\n"
#define pi (acos)
#define eps (1e-8)
Mp[i].clear();
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
if(i!=j)
{
scanf("%d",&mp[i][j]);
Mp[i].push_back(mp[i][j]);
}
else
mp[i][j]=inf;
}
sort(Mp[i].begin(),Mp[i].end());
scanf("%d",&mp[i][j]);
}
}
egin();
sum+=*it;
it++;
sum+=*it;
}
return sum/2;
}
int gao(node s)
{
int res=*2;
int t1=inf,t2=inf;
for(int i=1; i<=n; i++)
{
if(![i])
{
t1=min(t1,mp[i][]);
for(int j=1; j<(mx-1); j++)
{
for(int i=1; i<n; i++)
{
if((j&(1<<(i-1)))==0)
{
int x,y=inf;
for(int k=1; k<n; k++)
{
if((j&(1<<(k-1)))>0){
x=dp[k][(j-(1<<(k-1)))]+mp[i][k];
实现代码9
输入输出截图14
OJ提交截图14
算法优化分析14
总结15
总述
TSP问题又称为旅行商问题,是指一个旅行商要历经所有城市一次最后又回到原来的城市,求最短路程或最小花费,解决TSP可以用好多算法,比如蛮力法,动态规划法…具体的时间复杂的也各有差异,本次实验报告包含动态规划法,回溯法以及分支限界法。
printf("%d\n",ans);
}
return 0;
}
输入输出截图
OJ提交截图
算法优化分析
分支限界法的复杂度是根据数据的不同而不同,搜索的节点越少,复杂度越低,跟目标函数的选择有很大关系。目标函数值的计算也会需要一定时间,比如此文章中的目标函数值求解的复杂度是O(n^2)。当然此算法仍然有可以优化的地方,比如在记录该路径每个叶子结点的孩子结点时可以采用二进制的思想,从而使算法的时间复杂度在下降到当前T/n的数量级,解决COJ1814问题应该不成问题。
#include <algorithm>
#include <string>
#include <vector>
#include <deque>
#include <list>
#include <set>
#include <map>
#include <stack>
#include <queue>
#include <cctype>
}
}
int cnt=+mp[p][]+mp[][p];
node tmp=();
if(cnt<=
{
ans=min(ans,cnt);
return;
}
else
{
up=min(up,cnt);
ans=min(ans,cnt);
continue;
}
}
node tmp;
for(int i=1; i<=n; i++)
using namespace std;
int mp[20][20];
int x[30],vis[30];
int n,k,cur,ans;
void init()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
mp[i][j]=-1;
ans=-1;cur=0;
for(int i=1;i<=n;i++)x[i]=i;
{
if(![i])
{
=;
=+mp[][i];
=i;
=+1;
for(int j=1; j<=n; j++) [j]=[j];
[i]=1;
=gao(tmp);
if<=up)
(tmp);
}
}
}
}
int main()
{
while(~scanf("%d",&n))
{
for(int i=0; i<=n; i++)
#define debug "output for debug\n"
#define pi (acos)
#define eps (1e-8)
#define inf 0x3f3f3f3f
#define ll long long int
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
t2=min(t2,mp[][i]);
}
}
res+=t1;
res+=t2;
int tmp;
for(int i=1; i<=n; i++)
{
tmp=inf;
if(![i])
{
it=Mp[i].begin();
res+=*it;
for(int j=1; j<=n; j++)
tmp=min(tmp,mp[j][i]);
y=min(y,x);
}
}
dp[i][j]=y;
}
}
}
dp[0][mx-1]=inf;
for(int i=1;i<n;i++)
dp[0][mx-1]=min(dp[0][mx-1],mp[0][i]+dp[i][(mx-1)-(1<<(i-1))]);
printf("%d\n",dp[0][mx-1]);
}
return 0;
}
输入输出截图
OJ提交截图
算法优化分析
该算法需要对顶点集合{1,2,…,n-1}的每一个子集进行操作,因此时间复杂度为O(2^n)。和蛮力法相比,动态规划法求解TSP问题,把原来的时间复杂度是O(n!)的排列问题,转化为组合问题,从而降低了算法的时间复杂度,但仍需要指数时间。
回溯法
动态规划法
算法问题分析
假设n个顶点分别用0~n-1的数字编号,顶点之间的代价存放在数组mp[n][n]中,下面考虑从顶点0出发求解TSP问题的填表形式。首先,按个数为1、2、…、n-1的顺序生成1~n-1个元素的子集存放在数组x[2^n-1]中,例如当n=4时,x[1]={1},x[2]={2},x[3]={3},x[4]={1,2},x[5]={1,3},x[6]={2,3},x[7]={1,2,3}。设数组dp[n][2^n-1]存放迭代结果,其中dp[i][j]表示从顶点i经过子集x[j]中的顶点一次且一次,最后回到出发点0的最短路径长度,动态规划法求解TSP问题的算法如下。
、若数组x[n]已经形成哈密顿路径,则输出数组x[n],算法结束;
、若数组x[n]构成哈密顿路径的部分解,则k=k+1,转步骤3;
、否则,取消顶点x[k]的访问标志,重置x[k],k=k-1,转步骤3。
实现代码
#include <cstdio>
#include <cstdlib>
#include <cstring>
ans=cur+mp[x[n-1]][x[n]]+mp[x[n]][1];
}
}
else
{
for(int i=t;i<=n;i++)
{
if(mp[x[t-1]][x[i]]!=-1&&(cur+mp[x[t-1]][x[i]]<ans||ans==-1))
{
swap(x[t],x[i]);
cur+=mp[x[t-1]][x[t]];
