matlab优化的参数传递
matlab fmincon句柄 代入参数-概述说明以及解释

matlab fmincon句柄代入参数-概述说明以及解释1.引言概述部分的内容应该对整篇文章进行简要介绍,包括讨论的主题和目标。
以下是一个示例:1.1 概述在科学与工程领域,数学建模是解决复杂问题的重要手段之一。
而在数学建模过程中,确定问题的最优解往往是一个关键目标。
为了实现这个目标,需要运用数学优化方法进行问题求解。
本文将关注于一种常用的数学优化工具——Matlab中的fmincon函数及其句柄的应用。
fmincon函数是Matlab的优化工具箱中的一个功能强大的函数,广泛应用于各个领域的数学建模中。
它通过最小化或最大化目标函数来寻找约束条件下的最优解。
了解和掌握fmincon句柄的使用方法对于运用Matlab进行数学建模和优化具有重要意义。
通过使用fmincon句柄,我们可以灵活地对目标函数和约束条件进行修改,从而实现对问题的个性化求解,获得更加准确和适应的结果。
本文将首先介绍fmincon句柄的基本原理和使用方法,包括如何定义目标函数和约束条件。
接着,将详细讨论代入参数的实现方法,即在求解过程中动态地修改目标函数和约束条件的参数值,从而适应不同的实际问题。
通过深入讨论fmincon句柄的优势和代入参数的应用前景,我们将对该方法在实际问题中的潜力和可行性进行评估和展望。
最后,本文将总结fmincon句柄的优点和不足,并给出进一步研究和应用的建议。
通过本文的学习,读者将能够掌握使用fmincon句柄进行数学建模和优化的核心技巧,从而在实际问题中更好地应用和发展这一方法。
同时,文章还将为读者提供一个关于代入参数应用前景的新思路,帮助读者在解决复杂问题时找到更加有效和创新的解决方法。
文章结构部分的内容可以编写为:1.2 文章结构本文共分为三个主要部分:引言、正文和结论。
在引言部分,我们将对文章的主题进行一个简要的概述,介绍文章的目的和意义。
正文部分将分为三个小节。
首先,我们将详细介绍fmincon句柄的基本概念和功能,包括它是如何工作的,以及它在数值优化问题中的应用。
MATLAB敏感性分析与优化方法

MATLAB敏感性分析与优化方法引言在今天的科学和工程领域,数值模拟和优化问题的求解变得越来越重要。
MATLAB作为一种强大的工具和语言,在敏感性分析和优化问题的解决中发挥了重要作用。
本文将探讨MATLAB在敏感性分析和优化方法中的应用,介绍一些常用的技术和算法。
一、敏感性分析敏感性分析是指在给定系统模型和参数的情况下,研究系统输出对于参数的变化敏感程度的方法。
敏感性分析可以帮助我们理解系统的行为,优化系统设计并提高模型的准确性。
MATLAB提供了许多工具和函数来进行敏感性分析。
1. 参数敏感性分析参数敏感性分析是最常见和基础的敏感性分析方法之一。
MATLAB中,通过使用参数敏感性分析工具箱或编写自定义函数,可以计算模型输出对于参数变化的敏感度。
这些敏感度指标可以帮助我们确定哪些参数对于模型输出具有最大影响,从而指导我们在优化设计中的决策。
2. 系统敏感性分析与参数敏感性分析相比,系统敏感性分析考虑了系统模型本身的动态行为。
在MATLAB中,系统敏感性分析可以通过计算系统的传递函数或状态空间模型的特征值和特征向量来实现。
这些特征值和特征向量反映了系统对于参数变化的敏感性,可以帮助我们理解系统的稳定性和响应特性。
二、优化方法优化是指在给定的约束条件下,寻找使得目标函数达到最优的变量取值。
MATLAB提供了广泛的优化方法和算法,可以帮助我们解决各种复杂的优化问题。
1. 非线性优化在实际问题中,非线性优化是最常见的优化类型。
MATLAB中,我们可以使用fmincon函数来求解具有约束条件的非线性优化问题。
通过定义目标函数和约束条件函数,我们可以使用这个函数来寻找最优解。
2. 全局优化全局优化是指在整个搜索空间中寻找全局最优解的优化问题。
MATLAB中,我们可以使用全局优化工具箱来解决这类问题。
这个工具箱提供了一系列的全局优化算法,例如遗传算法、模拟退火算法和粒子群算法等,可以帮助我们在复杂的优化问题中找到全局最优解。
优化-二阶系统的MATLAB仿真设计

优化-二阶系统的MATLAB仿真设计随着科技的发展和应用的需求,优化控制在控制系统设计中扮演着越来越重要的角色。
在现代控制理论中,二阶系统是常见的一种模型。
本文将介绍如何利用MATLAB进行二阶系统的仿真设计,并优化其性能。
1. 二阶系统的基本原理二阶系统是指由二阶微分方程描述的动态系统。
它通常包含一个二阶传递函数,形式为:G(s) = K / (s^2 + 2ζωn s + ωn^2)其中,K是增益,ζ是阻尼比,ωn是自然频率。
2. MATLAB仿真设计MATLAB是一种功能强大的工具,可用于系统仿真与优化。
以下是使用MATLAB进行二阶系统仿真设计的基本步骤:2.1. 创建模型首先,我们需要在MATLAB中创建二阶系统的模型。
可以使用`tf`函数或`zpk`函数来定义系统的传递函数。
s = tf('s');G = K / (s^2 + 2*zeta*wn*s + wn^2);2.2. 仿真分析通过对系统进行仿真分析,可以获得系统的时域响应和频域特性。
可以使用`step`函数进行阶跃响应分析,使用`bode`函数进行频率响应分析。
step(G);bode(G);2.3. 控制器设计根据系统的性能要求,设计合适的控制器来优化系统的性能。
可以使用PID控制器等不同类型的控制器来调节系统。
2.4. 优化系统利用MATLAB提供的优化工具,对系统进行参数调节和优化。
可以使用`fmincon`函数等进行系统优化。
2.5. 仿真验证通过对优化后的系统进行仿真验证,评估其性能是否达到预期。
可以再次使用`step`函数或`bode`函数来分析系统。
3. 总结通过MATLAB进行二阶系统的仿真设计,可以帮助工程师优化系统的性能。
本文介绍了MATLAB仿真设计的基本步骤,包括模型创建、仿真分析、控制器设计、系统优化和仿真验证。
希望本文能对相关研究和工作提供一些参考和帮助。
matlab 传递函数

matlab 传递函数Matlab传递函数是一种Matlab语言中的基本概念,它把函数作为参数传递给其他函数,从而可以对函数进行更复杂的处理。
Matlab传递函数由三部分组成:函数名、函数参数和函数体。
函数名是函数的标识符,它可以是任意字母、数字或特殊符号的组合,但必须以字母开头,用于标识函数的名称,在Matlab中,函数名不区分大小写。
函数参数是函数调用时提供的参数,它们是函数在运行时需要使用的数据,函数参数可以是任意类型的数据,包括标量、向量、矩阵或其他Matlab变量类型。
函数体是函数执行的代码,它是Matlab语句的集合,描述函数要完成的功能。
事实上,函数体是函数实际工作的地方,函数体由一系列Matlab语句构成,它们按照一定的执行顺序执行,从而完成函数的功能。
Matlab传递函数的定义如下:函数名(参数1,参数2,...,参数N)语句1;语句2;...语句N;end上述定义中,函数名用于标识整个函数,参数列表用于指定函数的输入变量,函数体中的Matlab语句用于实现函数的功能,end表明函数定义的结束。
Matlab传递函数的最大优势在于它可以使函数之间形成复杂的调用关系。
这意味着,可以使用Matlab传递函数将一组函数组织成一个更大的函数,从而实现复杂的功能。
此外,Matlab传递函数还可以用于实现一些复杂的数据处理流程,例如,可以将一组函数用于处理大量数据,从而提高处理效率。
因此,Matlab传递函数是一种非常有用的概念,它可以帮助开发者更好地组织和管理函数。
通过使用Matlab传递函数,可以将一些复杂的功能实现为一个函数,从而使代码更加简洁和可读性更强。
matlab parameters的用法

matlab parameters的用法摘要:1.Matlab 参数概述2.Matlab 参数的定义与设置3.Matlab 参数的运算4.Matlab 参数的优化与调整5.Matlab 参数在实际应用中的案例分析正文:Matlab 是一款广泛应用于科学计算和数据分析的软件,其强大的数值计算和绘图功能深受广大用户的喜爱。
在Matlab 中,参数是用于定义和控制算法、函数、图形和其他各种工具的关键元素。
本文将为您详细介绍Matlab 参数的用法。
1.Matlab 参数概述在Matlab 中,参数可以是全局参数,也可以是局部参数。
全局参数在所有脚本和函数中都可以访问,局部参数则只能在定义它的函数或脚本范围内访问。
参数可以是数值、字符串、逻辑值、结构体、函数句柄等不同类型的数据。
2.Matlab 参数的定义与设置在Matlab 中,可以通过以下方式定义和设置参数:- 直接赋值:在Matlab 命令窗口中直接输入参数名和值,如`A = 3`;- 使用`assignin`函数:通过`assignin`函数可以将一个或多个参数传递给一个函数或脚本,例如`assignin("myScript", "A", 3)`;- 在脚本中使用`global`或`local`声明:使用`global`声明可以将全局变量声明为局部变量,使用`local`声明可以将全局变量声明为局部变量并赋予一个新的名字。
3.Matlab 参数的运算在Matlab 中,可以对参数进行各种数学运算,如加、减、乘、除等。
此外,Matlab 还提供了许多高级的数学运算功能,如矩阵运算、函数计算、优化算法等。
4.Matlab 参数的优化与调整Matlab 提供了一系列优化工具箱,可以帮助用户对参数进行优化和调整。
例如,可以使用`fmincon`函数进行一维优化,使用`fitness`函数进行多维优化等。
5.Matlab 参数在实际应用中的案例分析以下是一个使用Matlab 参数的简单示例:```matlab% 定义一个函数,该函数接受两个参数x 和yfunction z = myFunction(x, y)% 在函数内部定义局部参数A 和Blocal A = 2;local B = 3;% 使用参数A 和B 进行计算z = A * x + B * y;end% 调用函数,传递参数值x = 1;y = 2;z = myFunction(x, y);% 输出结果disp("z = ");disp(z);```通过以上案例,我们可以看到Matlab 参数在实际应用中的重要作用。
matlab参数传递

matlab参数传递(最新版)目录1.MATLAB 参数传递的概述2.MATLAB 参数传递的方式3.使用 MATLAB 参数传递的注意事项正文一、MATLAB 参数传递的概述MATLAB 是一种广泛应用于科学计算、数据分析、可视化等领域的编程语言。
在 MATLAB 中,函数之间通过参数传递数据,实现函数的功能。
参数传递是函数之间数据交流的一种方式,通过参数传递,我们可以实现函数的复杂功能,提高代码的复用性和可读性。
二、MATLAB 参数传递的方式MATLAB 参数传递的方式主要有以下两种:1.值传递值传递是 MATLAB 中最常用的参数传递方式。
当一个函数调用另一个函数时,会将实参的值传递给形参。
在值传递过程中,实参和形参是两个独立的变量,它们之间并不存在直接的联系。
因此,当函数执行完毕后,实参的值并不会发生改变。
2.引用传递引用传递是 MATLAB 中另一种参数传递方式。
当一个函数调用另一个函数时,会将实参的地址传递给形参。
在引用传递过程中,实参和形参共享同一个内存空间,因此,当函数执行完毕后,实参的值会发生改变。
三、使用 MATLAB 参数传递的注意事项在使用 MATLAB 参数传递时,需要注意以下几点:1.确定参数传递方式在使用参数传递时,需要根据实际需求确定使用值传递还是引用传递。
对于不需要修改实参值的情况,可以使用值传递;对于需要修改实参值的情况,可以使用引用传递。
2.避免参数名重复在编写函数时,应确保不同函数的参数名不同,避免出现参数名重复的情况。
如果出现参数名重复,可能导致函数调用失败。
3.注意参数的顺序在调用函数时,应确保参数的顺序与函数定义时的顺序一致。
如果参数顺序不一致,可能导致函数调用失败。
综上所述,MATLAB 参数传递是函数之间数据交流的一种方式,通过参数传递,我们可以实现函数的复杂功能,提高代码的复用性和可读性。
Matlab中的多目标优化算法实现指南

Matlab中的多目标优化算法实现指南简介:多目标优化是在现实问题中常见的一种情况,例如在工程设计、金融投资和决策支持等领域。
Matlab作为一种强大的数值计算和工程仿真软件,提供了多种多目标优化算法的工具箱,如NSGA-II、MOGA等。
本文将介绍如何使用Matlab实现多目标优化算法,并给出一些应用示例。
一、多目标优化问题多目标优化问题是指在存在多个冲突的目标函数的情况下,找到一组最优解,使得这些目标函数能够达到最优。
在现实问题中,通常会涉及到多个目标,例如在工程设计中同时考虑成本和性能,或者在金融投资中同时考虑风险和收益等。
二、Matlab的多目标优化工具箱Matlab提供了多种多目标优化算法的工具箱,如Global Optimization Toolbox、Optimization Toolbox等。
这些工具箱可以帮助用户快速实现多目标优化算法,并且提供了丰富的优化函数和评价指标。
三、NSGA-II算法实现NSGA-II(Non-dominated Sorting Genetic Algorithm II)是一种常用的多目标优化算法,它通过遗传算法的方式来搜索最优解。
在Matlab中,我们可以使用NSGA-II工具箱来实现该算法。
1. 确定目标函数首先,我们需要确定待优化的问题中具体的目标函数,例如最小化成本和最大化性能等。
在Matlab中,我们可以使用函数句柄来定义这些目标函数。
2. 设定决策变量决策变量是影响目标函数的参数,我们需要确定这些变量的取值范围。
在Matlab中,可以使用函数句柄或者向量来定义这些变量。
3. 设定其他参数除了目标函数和决策变量,NSGA-II算法还需要其他一些参数,例如种群大小、迭代次数等。
在Matlab中,我们可以使用结构体来存储这些参数。
4. 运行算法将目标函数、决策变量和其他参数传递给NSGA-II工具箱,然后运行算法。
Matlab会自动进行优化计算,并给出一组最优解。
MATLAB中的优化算法及其使用方法

MATLAB中的优化算法及其使用方法1. 引言在科学与工程领域,优化问题是一类常见且重要的问题。
它涉及到在给定约束条件下,寻找最优解或使目标函数达到最小或最大值的问题。
在解决这类问题时,MATLAB是一个非常强大且常用的工具,它提供了多种优化算法和函数。
本文将介绍MATLAB中的部分常见优化算法及其使用方法。
2. 优化问题的形式化表示在应用优化算法之前,首先需要将优化问题进行形式化表示。
假设我们要解决一个优化问题,其中有一个目标函数f(x)和一组约束条件h(x) = 0和g(x) ≤ 0。
这里,x是一个n维向量,表示我们要优化的参数。
3. 无约束优化算法无约束优化算法用于解决没有约束条件的优化问题。
MATLAB中提供了多个无约束优化算法,常用的有fminunc和fminsearch。
3.1 fminunc函数fminunc函数是MATLAB中用于寻找无约束优化问题最小值的函数。
它基于梯度下降算法,通过迭代优化来逼近最优解。
使用fminunc函数,我们需要提供目标函数和初始解作为输入参数,并指定其他可选参数,如最大迭代次数和精度要求。
3.2 fminsearch函数fminsearch函数也是用于无约束优化问题的函数,但与fminunc不同的是,它使用了模拟退火算法来搜索最优解。
使用fminsearch函数,我们需要提供目标函数和初始解作为输入参数,并指定其他可选参数,如最大迭代次数和收敛容忍度。
4. 约束优化算法约束优化算法用于解决带有约束条件的优化问题。
MATLAB中提供了多个约束优化算法,常用的有fmincon和ga。
4.1 fmincon函数fmincon函数是MATLAB中用于求解约束优化问题的函数。
它基于拉格朗日乘子法,并使用内点法等技术来求解约束优化问题。
使用fmincon函数,我们需要提供目标函数、约束条件、初始解和约束类型等作为输入参数,并指定其他可选参数,如最大迭代次数和精度要求。
Matlab调用DLL以及matlab指针参数传递

Matlab调用DLL本来想把算法写成一个DLL的形式,这样既可以在控制软件中方便调用,又可以在Matlab中通过调用外部DLL的形式对算法进行仿真分析,所以需要了解Matlab调用外部DLL的方法,但是后来发现Matlab调用DLL只支持用C语法写成的DLL,C++的一些关键特性如类、继承等都不支持,用起来的话局限性很大的,还不如单独再用M文件把算法再写一遍进行仿真呢。
这里把Matlab调用DLL 的过程记录一下吧,以后有用到的时候再说。
在Matlab的Help中搜索"Calling Functions in Shared Libraries"即可看到关于此内容的帮助文档。
下面以一个简单的小例子演示Matlab调用DLL的过程:1、编译器准备在Matlab的命令窗口输入:mex -setup选择你的编译器,我的是:[2] Microsoft Visual C++ 2008 SP1 in c:\Program Files\Microsoft Visual Studio 9.02、编写你自己的DLL在Visual Studio 2008中新建一个Win32的Dll工程,不妨设名字为MatlabDllTest,编辑MatlabDllTest.cpp:#include "MatlabDllTest.h"double add(double x, double y){return (x+y);}编辑MatlabDllTest.h:#ifndef MATLABDLLTEST_H#define MATLABDLLTEST_H#ifdef __cplusplusextern"C"{#endif__declspec(dllexport) double add(double x, double y);#ifdef __cplusplus}#endif#endif3、加载DLL:把编译连接之后产生的MatlabDllTest.dll和MatlabDllTest.h 文件拷贝到Matlab的当前工作目录下,输入loadlibrary('MatlabDllTest','MatlabDllTest.h');(一定要有这步,如果dll不成功,会显示错误原因)4、查看DLL中导出的函数libfunctions MatlabDllTest -full-full选项会列出导出函数的详细输入和输出参数,这是输出信息如下:Functions in library MatlabDllTest:double add(double, double)5、调用函数calllib('MatlabDllTest', 'add', 1.3, 4.6)此时就会输出正确的结果ans =5.9000总结:这个例子比较简单,只是为了演示整个过程,如果你是真的用到了Matlab来调用外部DLL的这种方式的话,就要注意你的DLL工程要符合Matlab 的要求啦,详细信息请自己查看Matlab的帮助文件,我就不罗嗦了。
用matlab求解优化问题

§8.1.1 线性规划问题的MATLAB 求解方法与一般线性规划理论一样,在MATLAB 中有线性规划的标准型。
在调用MATLAB 线性规划函数linprog 时,要遵循MATLAB 中对标准性的要求。
线性规划问题的MATLAB 标准形为:⎪⎪⎩⎪⎪⎨⎧≤≤=≤=ub x lb b x A b Ax t s x c f eq eq T .. min 在上述模型中,有一个需要极小化的目标函数f ,以及需要满足的约束条件假设x 为n 维设计变量,且线性规划问题具有不等式约束1m 个,等式约束2m 个,那么:x 、、lb c 、 和ub 均为n 维列向量,b 为1m 维列向量,eq b 为m 2维列向量,A 为n m ⨯1维矩阵,eq A 为n m ⨯2维矩阵需要注意的是:MATLAB 标准型是对目标函数求极小,如果遇到是对目标函数求极大的问题,在使用MATLAB 求解时,需要在函数前面加一个负号转化为对目标函数求极小的问题;MATLAB 标准型中的不等式约束形式为""≤,如果在线性规划问题中出现""≥形式的不等式约束,则我们需要在两边乘以(-1)使其转化为MATLAB 中的""≤形式。
如果在线性规划问题中出现了“<”或者“>”的约束形式,则我们需要通过添加松弛变量使得不等式约束变为等式约束之后,我们只需要将所有的约束(包括不等式约束和等式约束)转化为矩阵形式的即可。
例如,对于如下线性规划模型:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥=+=+-≥-+-≤+-+-=0,,7 32 8228 122 ..24 max 3212131321321321x x x x x x x x x x x x x t s x x x f 要转化为MATLAB 标准形,则要经过:(1)原问题是对目标函数求极大,故添加负号使目标变为:32124 m in x x x f -+-=;(2)原问题中存在“≥”的约束条件,故添加负号使其变为:8228321≤+-x x x用MATLAB 表达则为c=[-4; 2; -1]; %将目标函数转化为求极小A=[2 -1 1; 8 -2 2]; b=[12; -8]; %不等式约束系数矩阵Aeq=[-2 0 1; 1 1 0];beq=[3; 7]; %等式约束系数矩阵lb=[0; 0; 0];ub=[Inf; Inf; Inf] %对设计变量的边界约束MATLAB 优化工具箱中求解线性规划问题的命令为linprog ,其函数调用方法有多种形式如下所示:x = linprog(c,A,b)x = linprog(c,A,b,Aeq,beq)x = linprog(c,A,b,Aeq,beq,lb,ub)x = linprog(c,A,b,Aeq,beq,lb,ub,x0)x = linprog(c,A,b,Aeq,beq,lb,ub,x0,options)x = linprog(problem)[x,fval] = linprog(...)[x,fval,exitflag] = linprog(...)[x,fval,exitflag,output] = linprog(...)[x,fval,exitflag,output,lambda] = linprog(...)输入参数MATLAB工具箱中的linprog函数在求解线性规划问题时,提供的参数为:模型参数、初始解参数和算法控制参数。
matlab parameters的用法

matlab parameters的用法一、Matlab参数简介Matlab作为一种广泛应用于科学计算和工程领域的编程语言,其强大的功能离不开参数的使用。
Matlab参数是指在编写程序时,用于控制程序运行过程、调整程序性能的一些变量。
了解Matlab参数的用法,对于提高编程效率和程序性能具有重要意义。
二、Matlab参数的设置与使用方法1.设置参数在Matlab中,可以通过以下方法设置参数:- 使用`matlab.parse`函数进行语法解析,自动生成参数。
- 手动创建参数,使用`param`关键字声明。
例如:```matlabfunction f = my_function(x, params)% 参数设置params.a = 1;params.b = 2;% 函数主体部分f = x * params.a + params.b;end```2.调用参数在函数调用时,可以通过以下方式传递参数:- 直接传递参数,如`my_function(x, 1, 2)`。
- 使用数组传递参数,如`my_function(x, [1, 2])`。
3.修改参数在程序运行过程中,可以通过以下方法修改参数:- 使用`params.a = 3;`修改参数`a`的值。
- 使用`params([1, 3]);`修改参数`b`的值。
4.获取参数值获取参数值的方法如下:```matlabvalue = params.a;value = params([1, 2]);```三、Matlab参数的应用场景1.函数参数:在函数调用时,可以使用参数传递函数内部的变量,实现不同输入输出之间的转换。
2.对象属性:在创建对象时,可以使用参数设置对象的属性,如图像处理中的阈值、滤波器尺寸等。
3.回调函数:在Matlab中,许多内置函数(如`fmin`、`gui`等)都支持回调函数,通过回调函数对优化过程中的参数进行实时调整。
四、Matlab参数优化与调试1.参数优化方法:- 网格搜索:在指定区间内遍历所有可能的参数值,找到最优解。
如何使用matlab中signalconstraint模块优化PID参数详细版解读
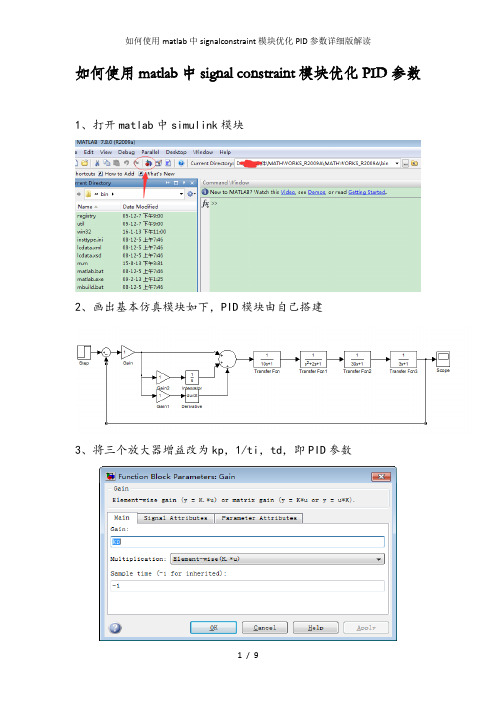
如何使用matlab中signal constraint模块优化PID参数1、打开matlab中simulink模块2、画出基本仿真模块如下,PID模块由自己搭建3、将三个放大器增益改为kp,1/ti,td,即PID参数4、进入simulink design optimization中找到signal constraint5、将signal constraint模块添加到仿真模型中6、右击signal constraint,点击explore7、进入后点击model workspace然后再点add,选择第一个matlab variable,创建三个matlab变量var,双击var改为kp、ti、td,分别对应PID的三个参数,初始值可都取1,然后apply8、回仿真界面双击signal constraint,出现如下对话框9、点击optimization,再点击tuned parameters10、点击add,将kp、ti、td逐一添加,完成后点击ok退出该界面11、用鼠标拖动黑线可改变动态指标要求,也可以进入goals/desired response中进行修改12、设好性能指标后点击上图中三角尖仿真按钮,发现系统运行时间较长而且没有得出满意结果,这是因为系统不稳定或者动态性能指标太高难以达到;13、此处为了方便删除两个环节之后再进行仿真,就得到了满意结果。
最后的结果并不是唯一的,因为有很多种kp、ti、td参数组合都可以达到这个动态性能指标。
有较多人直接使用而没有定义变量,所以最后添加变量的时候会出现找不到变量的情况。
以上仅为个人拙见,如有错误,请予以批评指正。
如何使用matlab中signalconstraint模块优化PID参数详细版解读读书的好处1、行万里路,读万卷书。
2、书山有路勤为径,学海无涯苦作舟。
3、读书破万卷,下笔如有神。
4、我所学到的任何有价值的知识都是由自学中得来的。
optimoptions函数

optimoptions函数optimoptions函数是MATLAB所提供的优化选项函数,它允许用户以一种简单而清晰的方式设置各种优化算法的选项。
这个函数在解决一些实际问题的过程中非常有用,其使用过程如下。
第一步是确定要使用的优化算法。
在MATLAB中,有各种不同的优化算法可供选择,每种算法都有其优点和缺点。
有些算法适用于寻找全局最优解,而另一些则适用于求解局部最优解。
用户需要了解不同算法的特点和适用范围,然后选择最合适的算法。
第二步是设置算法的参数。
每个优化算法都有一组参数,这些参数对算法的效率和准确度有着重要的影响。
用户需要了解每个参数的作用和取值范围,并根据具体问题调整这些参数的值。
设置这些参数需要使用optimoptions函数中的各种选项。
第三步是使用optimoptions函数来创建一个选项对象。
选项对象包含算法和参数的所有信息,可以传递给优化函数使用。
创建选项对象的代码如下:options = optimoptions(‘算法名称’,'选项参数1',值1,'选项参数2',值2,…);其中,‘算法名称’指定要使用的优化算法的名称,‘选项参数1’和‘选项参数2’是各种选项参数的名称,值1和值2是相应的选项值。
用户可以使用多个选项参数来设置不同的选项。
第四步是使用选项对象来调用优化函数。
选项对象通常作为优化函数的最后一个参数进行传递。
例如,要使用优化函数fminunc来求解一个无约束的优化问题,代码如下:[x,fval,exitflag,output] = fminunc(@(x)myfun(x),x0,options);其中,myfun是用户定义的目标函数,x0是初始点。
options是之前创建的选项对象。
总的来说,optimoptions函数是MATLAB中非常有用的一个函数。
合理设置优化算法的参数,可以让优化算法的执行效率更高、结果更准确。
同时,选项对象的创建和使用也非常简单和便捷,为MATLAB用户提供了很大的便利。
最优化方法的Matlab实现(公式(完整版))

第九章最优化方法的Matlab实现在生活和工作中,人们对于同一个问题往往会提出多个解决方案,并通过各方面的论证从中提取最佳方案。
最优化方法就是专门研究如何从多个方案中科学合理地提取出最佳方案的科学。
由于优化问题无所不在,目前最优化方法的应用和研究已经深入到了生产和科研的各个领域,如土木工程、机械工程、化学工程、运输调度、生产控制、经济规划、经济管理等,并取得了显著的经济效益和社会效益。
用最优化方法解决最优化问题的技术称为最优化技术,它包含两个方面的内容:1)建立数学模型即用数学语言来描述最优化问题。
模型中的数学关系式反映了最优化问题所要达到的目标和各种约束条件。
2)数学求解数学模型建好以后,选择合理的最优化方法进行求解。
最优化方法的发展很快,现在已经包含有多个分支,如线性规划、整数规划、非线性规划、动态规划、多目标规划等。
9.1 概述利用Matlab的优化工具箱,可以求解线性规划、非线性规划和多目标规划问题。
具体而言,包括线性、非线性最小化,最大最小化,二次规划,半无限问题,线性、非线性方程(组)的求解,线性、非线性的最小二乘问题。
另外,该工具箱还提供了线性、非线性最小化,方程求解,曲线拟合,二次规划等问题中大型课题的求解方法,为优化方法在工程中的实际应用提供了更方便快捷的途径。
9.1.1 优化工具箱中的函数优化工具箱中的函数包括下面几类:1.最小化函数表9-1 最小化函数表2.方程求解函数表9-2 方程求解函数表3.最小二乘(曲线拟合)函数表9-3 最小二乘函数表4.实用函数表9-4 实用函数表5.大型方法的演示函数表9-5 大型方法的演示函数表6.中型方法的演示函数表9-6 中型方法的演示函数表9.1.3 参数设置利用optimset函数,可以创建和编辑参数结构;利用optimget函数,可以获得o ptions优化参数。
● optimget函数功能:获得options优化参数。
语法:val = optimget(options,'param')val = optimget(options,'param',default)描述:val = optimget(options,'param') 返回优化参数options中指定的参数的值。
matlab 中 m 文件里面的参数-解释说明

matlab 中m 文件里面的参数-概述说明以及解释1.引言1.1 概述概述部分:参数在Matlab中的M文件中起着重要的作用,它们是用来传递数值、变量或是一些特定的设置给函数或脚本的。
通过使用参数,我们可以为M 文件提供灵活性和可重用性,使得代码更加可配置和可扩展。
在M文件中,参数通常用来控制特定的行为或计算过程。
通过在函数或脚本定义时声明参数,并在调用函数或执行脚本时提供相应的数值或变量,我们可以根据实际需求来调整程序的行为。
参数的设置可以灵活地改变程序的输出结果,提高了代码的可定制性和适用性。
在本文中,我们将详细介绍M文件中参数的定义和使用方法。
我们将探讨参数的常见用法和技巧,包括参数的类型、默认值的设定以及参数的传递方式等。
此外,我们还将探讨一些参数的优化与应用,以帮助读者理解参数在M文件中的重要性和使用价值。
通过对M文件中参数的深入研究,我们能够更好地理解和使用Matlab的函数和脚本。
参数的合理设置不仅能够提高代码的执行效率和准确性,也能够使代码更易读、易维护和易扩展。
因此,理解参数在M文件中的作用和用法对于编写高效、优质的Matlab代码至关重要。
在下一节中,我们将详细介绍M文件及其作用,以帮助读者更好地理解参数在M文件中的使用环境和背景。
请继续阅读下一节内容。
文章结构部分的内容如下:1.2 文章结构本篇文章主要围绕着matlab 中m 文件中的参数展开讨论。
文章分为引言、正文和结论三个部分。
在引言部分,我们首先对文章的主题进行了概述,说明了本文将要讨论的问题和目的。
接着介绍了文章的结构,明确了各个部分的内容和顺序。
最后,对整篇文章进行了总结,给出了一个简要的概括。
在正文部分,我们详细讨论了matlab 中的M 文件及其作用。
我们解释了M 文件的含义和作用,介绍了其在matlab 编程中的重要性。
然后,我们重点关注了M 文件中的参数定义,解释了参数的概念和用途。
接着我们详细阐述了在M 文件中参数的使用方法,包括如何定义参数、如何传递参数以及如何在程序中使用参数。
matlab参数传递

matlab参数传递在MATLAB中,参数传递主要有两种方式:通过函数输入输出变量(input-output)和全局变量(global)。
通过函数输入输出变量这是最常用的一种参数传递方式。
在MATLAB中,函数可以接收输入参数(input arguments),然后生成输出参数(output arguments)。
这些参数需要在函数声明和定义中进行明确。
例如:matlabfunction [y] = myFunction(x)y = x^2; % 计算x的平方end在这个例子中,x是输入参数,y是输出参数。
调用这个函数时,需要将参数传递给x:matlabresult = myFunction(5); % result将被赋值为25 全局变量全局变量可以在MATLAB的任何地方访问,包括函数和脚本。
要使一个变量成为全局变量,你需要在函数或脚本的开始处使用global关键字声明它。
例如:matlabglobal x;function y = myFunction()x = 5; % 修改全局变量x的值y = x^2; % 计算x的平方end在这个例子中,x是一个全局变量,可以在任何函数或脚本中访问和修改。
注意,使用全局变量可以简化代码,但也可能导致代码更难理解和维护。
因此,通常只在确实需要时才使用全局变量。
以下是两个MATLAB中参数传递的例子:例子1:传递数组假设我们有一个数组A,我们想通过函数来修改这个数组。
我们可以将这个数组作为输入参数传递给函数: matlabA = [1, 2, 3]; % 定义一个数组Afunction modifyArray(inputArray)inputArray(2) = 0; % 将数组的第二个元素设置为0endmodifyArray(A); % 调用函数,修改数组A在这个例子中,我们将数组A作为输入参数传递给modifyArray函数,然后函数修改了数组的第二个元素。
matlab参数传递的方法

Parameterizing Functions一.实现参数传递的方法实现参数传递的方法有两个,分别是Parameterizing Using Nested Functions(嵌套函数法)和Parameterizing Using Anonymous Functions(匿名函数法)。
一.Parameterizing Using Nested Functions(嵌套函数法)1.简介:使用完全包含在程序文件中的另一个函数中的嵌套函数进行参数传递。
2.具体做法:首先,创建一个m文件(findzero.m),包含母函数findzero和嵌套函数poly:function y = findzero(b,c,x0)y = fzero(@poly,x0);function y = poly(x)y = x^3 + b*x + c;EndEnd然后,在Command Window里面调用函数:x = findzero(2,3.5,0)x =-1.09453.原理:嵌套函数定义了具有一个输入变量x的三次多项式,母函数findzero接受参数b和c输入值。
母函数findzero的嵌套函数poly可以共享母函数的workspace。
因此,参数b和c 的值由母函数传递给了嵌套函数。
4.举例说明:function y = findzero(b,c,x0)y = fzero(@poly,x0);function y = poly(x)y =3*x^7+x^2+b*x+c;endend>> x = findzero(1,2,0)x =-0.9399三.Parameterizing Using Anonymous Functions(匿名函数法)1.简介:使用匿名函数进行参数传递。
匿名函数是在单个命令中定义的函数,而需要不创建单独的程序文件,可以使用当前woekspace中可用的任何变量。
2.具体做法:首先,创建一个描述三次多项式的匿名函数的句柄,并找到零:b = 2;c = 3.5;cubicpoly = @(x) x^3 + b*x + c;x = fzero(cubicpoly,0)然后,在Command Window里面调用函数:x =-1.09453.原理:函数cubicpoly是具有一个输入值x的匿名函数的函数句柄,输入的匿名函数将在符号@后面的括号中显示。
matlab 贝叶斯优化参数迭代曲线-定义说明解析

matlab 贝叶斯优化参数迭代曲线-概述说明以及解释1.引言1.1 概述引言部分的内容应该是对整篇文章的概述和背景介绍。
下面是关于文章引言部分的一个例子:引言贝叶斯优化是一种用于高效优化复杂黑盒函数的强大方法,近年来在各个领域都得到了广泛应用。
它结合了贝叶斯统计和优化算法,通过对目标函数的探索和利用历史观测结果来动态地调整参数取值,从而逐步逼近全局最优解。
在实际应用中,我们通常需要调整一系列参数来优化某个目标函数的性能。
然而,这个过程可能非常耗时和复杂,因为参数之间可能存在复杂的相互关系,且目标函数通常是一个黑盒函数,无法获得其解析表达式。
而贝叶斯优化通过自适应地选择下一次参数取值点,从而实现在有限的迭代次数内找到尽可能优秀的参数解。
本文主要介绍了MATLAB中的贝叶斯优化工具箱及其应用。
我们将深入探讨贝叶斯优化的基本原理和算法,并详细介绍MATLAB中如何使用该工具箱来优化参数。
同时,我们还将讨论参数迭代曲线在贝叶斯优化中的意义,以及在MATLAB中如何生成和分析参数迭代曲线。
通过本文的阅读,读者将能够理解贝叶斯优化的基本原理,掌握MATLAB中的贝叶斯优化工具箱的使用方法,并了解参数迭代曲线在贝叶斯优化中的重要性。
最后,我们将通过实验验证贝叶斯优化在不同问题上的有效性,并指出未来改进和扩展的方向。
总之,本文旨在为读者提供一个全面的了解贝叶斯优化以及在MATLAB中的应用的指南,以便能够更好地应用贝叶斯优化算法解决实际问题。
1.2 文章结构文章结构部分是对整篇文章的组织和章节安排进行介绍。
本文将按照以下章节结构展开:1. 引言:本节将对贝叶斯优化参数迭代曲线的研究意义和背景进行概述,介绍文章结构,并明确本文的研究目的。
2. 正文:本节将详细介绍贝叶斯优化的基本概念和原理,以及MATLAB中贝叶斯优化的实现方法。
然后,将重点讨论参数迭代曲线在贝叶斯优化中的意义与作用,并介绍MATLAB中如何生成和分析参数迭代曲线。
optimproblem在matlab中的用法

optimproblem在matlab中的用法OptimProblem在Matlab中的用法OptimProblem是Matlab中用于定义优化问题的一种数据类型。
它允许用户以数学公式的形式定义目标函数和约束条件,在求解优化问题时提供了很大的便利性。
以下是OptimProblem在Matlab中的一些常见用法的详细讲解。
创建优化问题用户可以通过OptimProblem类创建优化问题对象。
以下是创建优化问题的基本步骤: 1. 导入优化工具箱:首先,在Matlab中导入优化工具箱,以便使用OptimProblem类。
2. 定义目标函数:使用Matlab的符号计算功能,创建一个符号函数,表示优化问题的目标函数。
3. 定义约束条件:使用Matlab的符号计算功能,创建一个符号函数组成的向量,表示优化问题的约束条件。
4. 创建优化问题对象:使用OptimProblem类的构造函数,创建一个优化问题对象,并将目标函数和约束条件作为参数传递给构造函数。
设置优化问题的类型在创建优化问题对象后,用户可以通过设置问题的类型来定义问题的性质。
以下是一些常见的问题类型: - 最小化问题:用户可以设置目标函数的类型为最小化,以使得优化求解器能够找到目标函数的最小值。
- 最大化问题:用户可以设置目标函数的类型为最大化,以使得优化求解器能够找到目标函数的最大值。
- 等式约束问题:用户可以将所有约束条件分组为等式约束,以确定优化问题的可行解集。
- 不等式约束问题:用户可以将所有约束条件分组为不等式约束,以确定优化问题的可行解集。
添加变量优化问题通常涉及到一些变量,用户可以使用OptimProblem对象的addVariable方法来添加变量。
以下是一些添加变量的常用方式:- 添加连续变量:用户可以使用addVariable方法,将连续变量添加到优化问题中。
连续变量没有限制条件,可以取任意实数值。
- 添加离散变量:用户可以使用addVariable方法,并指定变量的取值范围和步长来添加离散变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 初学者最爱用但是最不提倡的方法:全局变量法
适用于MA TLAB7以及以前或者以后的版本
function withaddtionpara1
global b c
b = 2;
c = 3.5; x0 =0;
options = optimset('Display', 'off'); % Turn off Display
y = fsolve(@poly, x0, options)
function y = poly(x) % Compute the polynomial.
global b c
y = x^3 + b*x + c;
2. 直接传递法
适用于MA TLAB7以及以前或者以后的版本
根据:
X=FSOLVE(FUN,X0,OPTIONS,P1,P2,...) passes the problem-dependent parameters P1,P2,... directly to the function FUN: FUN(X,P1,P2,...). Pass an empty matrix for OPTIONS to use the default values.
如果options不需要设置,则用空矩阵('[]')占位
function withaddtionpara2
b = 2;
c = 3.5; x0 =0;
options = optimset('Display', 'off'); % Turn off Display
y = fsolve(@poly, x0, options,b,c)
function y = poly(x,b,c) % Compute the polynomial.
y = x^3 + b*x + c;
3. 采用evalin以及assignin函数法
适用于MA TLAB7以及以前或者以后的版本
function withaddtionpara3
b = 2;
c = 3.5; x0 =0;
assignin('base','b',b);
assignin('base','c',c);
options = optimset('Display', 'off'); % Turn off Display y = fsolve(@poly, x0, options)
function y = poly(x) % Compute the polynomial.
b = evalin('base','b');
c = evalin('base','c');
y = x^3 + b*x + c;
4. 匿名函数法(Anonymous function)
适用于MA TLAB7以及以后的版本
function withaddtionparas4
options = optimset('Display', 'off'); % Turn off Display b =2; c = 3.5; x0 =0;
y = fsolve(@(x)mypoly(x,b,c), x0, options)
function y = mypoly(x,b,c)
y = x^3 + b*x + c;
5. 嵌套函数法(nested function)
适用于MA TLAB7以及以后的版本
function withaddtionpara5
b =2;
c = 3.5; x0 =0;
options = optimset('Display', 'off'); % Turn off Display y = fsolve(@poly, x0, options)
function y = poly(x) % Compute the polynomial.
y = x^3 + b*x + c;
end
end
6. 采用文件传递(有些太笨拙了的办法)
适用于MA TLAB7以及以前或者以后的版本
function withaddtionpara6
b = 2;
c = 3.5; x0 =0;
save paras b c
options = optimset('Display', 'off'); % Turn off Display y = fsolve(@poly, x0, options)
function y = poly(x) % Compute the polynomial. load paras.mat
y = x^3 + b*x + c;。
