(完整版)行列式练习题(有答案).

第一章行列式习题及答案

第一章行列式习题1. n 阶行列式D 的值为c ，若将D 的第一列移到最后一列，其余各列依次保持原来的次序向左移动，则得到的行列式值为。

（1(1)n c --）2. n 阶行列式D 的值为c ，若将D 的所有元素改变符号，得到的行列式值为。

（(1)n c -）3. 2(1)(2,1,21,2,,1,)(21)0(23)0122k k N k k k k k k k k --+=-++-+++=+?。

4. 由行列式的定义计算行列式413331233626xx x x xx展开式中4x 和3x 的系数。

（3412, 12x x -）（分析：4x 的系数：四个元素中必须全都包含x 。

第一行只能取11a ，第三行只能取33a ，这样第二、四行只能取22a 和44a ，则此项为(1234)411223344(1)4312N a a a a x x x x x -=⋅⋅⋅=。

3x 的系数：(2134)(4231)3331221334441223314(1)(1)3912N N a a a a a a a a x x x -+-=--=-。

）5. 已知1703，3159，975，10959能被13整除，不直接计算行列式17033159097510959的值，证明他是13的倍数。

证明：12341701703170170341000131531593153159410021309709750979754103109510959109510959l c c l c c l c c l +⋅+⋅=⋅+⋅，能被13整除。

注意，以下两个行列式：170317037033159315915909759759751095910959959≠，所以一定要加到最后一列上。

6. 设行列式311252342011133--=--D ，求11213141243A A A A +--及2123242-++M M M 。

（0和-5）解：112131412112423424301011333A A A A -+--==----。

行列式课后练习及答案

0

0 0 0 0 0 0

0 解：Dn (1)
n ( n 1) 2

0 0 0
0 0

0 0
...............................

0

(1)
n ( n 1) 2

[ n ( 1) n 1 n ]
[ n 1 (1) n 1 n 1 ] (1)
2.若
(5 ) x1 2 x2 2 x3 0, 2 x1 (6 ) x2 0, 有非零解, 则 = 2或5或8 . 2 x1 (4 ) x3 0
5
x1 x2 x3 x4 5, x 2 x2 x3 4 x4 2, 3. 1 2 x 3x x3 5 x4 2, 的解是否唯一? 3x1 x 2 1 2 2 x3 11x4 0
答案：1.行列式概念的引进课后作业
a11
1. a21
a12 a22 a32 4 3 6 1 0 0 3 5
a13 a23 a11a22a33 a12a23a31 a13a21a32 a13a22a31 a12a21a33 a11a23a32 a33
a31 1 3 1 3
2. 5 2 1 80
(1 a) x1 x2 xn 0, 2 x (2 a)x 2x 0, 2 n 4.设齐次线性方程组为 1 (n 2) , 若其有非零解, nx1 nx2 (n a)xn 0.
则 a=
n(n 1) 或a 0 2
x1 2 x2 x3 1, 5.用克莱姆法则求解 2 x1 3x2 x3 0, 4 x 7 x 2 x 2. 2 3 1

线性代数习题册行列式-习题详解.doc

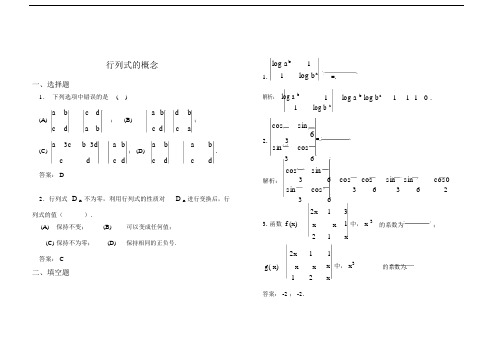
行列式的概念一、选择题1．下列选项中错误的是 ( )a b c d (B)a b d b (A)da b ； c dc ；caa 3cb 3d a b a ba b (C)cdc ； (D)c dc.dd答案： D2．行列式 D n 不为零，利用行列式的性质对 D n 进行变换后，行列式的值（）．(A) 保持不变； (B) 可以变成任何值；(C) 保持不为零； (D)保持相同的正负号．答案： C二、填空题1.log a b 1 =.1log b a解析： log ab1 log a b log b a1 1 1 0 .1 log b acos sin2.36=.sincos 3 6cos sin解析：3 6 cos cos sin sin cos0sin cos 3 63 6 23 62x 1 33. 函数 f (x)x x 1 中， x 3 的系数为；21 x2x 1 1g( x)x x x 中， x 3的系数为.12x答案： -2 ； -2.阶行列式 D n中的n最小值是.答案： 1.1 2 35.三阶行列式0 2 4 中第2行第1列元素的代数余子式3 1 1等于.答案： 5.6.若 2x 8 0 ，则x= .1 2答案： 2.7. 在n 阶行列式 D a ij 中，当 i<j 时，aij 0(i, j 1,2, L ,n) ，则D= .答案： a11 a22 a nn.a b 0b a 0 0.1 0 1a b 0( 1ab )解析： b a 0 ( a2 b2 ) 01 0 1b a故 a 0, b 0 .三、解答题1.用行列式的定义计算 .0 1 0 11 0 1 0(1)1 0；0 00 0 1 11 1 0 1 0 1 解：原式 =1 ( 1)1 20 0 0 1 ( 1)1 4 0 1 00 1 0 0 0 18. 设a, b 为实数，则当a=, b=时，0 0 1 0 1解：由对角线法则，得 D 111 2 , D 21 0 0 111 2a b 0 0 若 D 1 D 2 , 则于是1或 1.0 c d 0(2)四、证明题0 0 e.f1. （略）g h 0行列式的性质c d 0 0 d 0原式 = a 0 efb 0 ef一、选择题h 0 0g 0 0x 0 1 2 3 2e f0 f 0 f1．设行列式 D 10 x 1 0 , D 2 1 5 3 , 若 D 1 D 2 ,10 x3 1 1=a cdbdh g= adfhbdfg则 x 的取值为 ( ).(A)2 ，-1 ； (B)1 ， -1 ；(C)0 ，2；(D)0，1．0 1 3 1 1答案： B2. 设行列式 D 10 1 0 ,D 2 2 3 2 , 若 D 1 D 2 ,a 11 a 12 a 1311 5 32．若 Da 21a 22a233 ，求的值 .a31a32a332a11 5a13 a12 a13则 D1 2a21 5a23 a22 a23=（）．2a31 5a33 a32 a33(A)30；(B) -30 ；(C)6 ；(D)-6．答案： C二、填空题1．若三阶行列式 D 的第一行元素分别是1,2,0, 第三行元素的余子式分别是8，x，19，则 x =.解析： 1 8 2x 0 19 0, x 4 .2016 2018=.2．201620142016 2018 2 2 2 2 解析：2016 2014 2016 0 4 .2014 2a b c3. 行列式D b a c ，则 A11 A21 A31= .d b c1 b c解析： A11 A21 A31 1 a c 0 .1 b c5x 1 2 34. 行列式D42 1 x 3x x 2的展开式中， x 4的系数31 2 1 3x为； x3 的系数为.5x 1 2 3 5x 1 2 32 1 x3 x x 2 3解析： D 4x 2 3 2 1 x 3x1 2 1 3x 1 2 1 3x5x 1 2 30 x1 8 125 5 52 1 x 31 2 1 3x含 x4， x3的项仅有主对角线上元素之积项，故x 4， x3的系数分别为 15， -3.三、解答题1. 计算下列行列式 .1 2 3 42 3 4 1 (1)；3 4 1 2 4 1 2 3解：各行加到第一行，得10 10 10 10 1 1 1 1 2 3 4 1 2 3 4 1 原式 =4 1 2 104 1 2 3 3 41 2 3 4 1 2 31 1 1 1 1 1 1 10 1 2 1 0 1 2 1 = 101 2 1 100 4 160 .0 0 0 03210 041 1 1 1 11 234 52 2 22(2) 12 3 4 5 ；3 3 3 3 1 2 345 4444 1 234 5解：原式 =(5-4)(5-3)(5-2)(5-1)(4-3)(4-2)(4-1)(3-2)(3-1) =288.1 4 9 16 4 9 16 25 ；(3)16 25 3691625 36491 4 9 16 1 4 9 16 3 5 7 9 3 5 7 9 原式 =7 9 11 2 2 2 0 .5 2 7 9 11 132 2 2 20 y 0 xx 0 y 0；(4)x 0 yy 0 x 0x y 0 x 0 y 原式 = y 0 0 y x 0 x 0y x 0 y 0 x= y 2 xy x 2 x y ( x 2 y 2 ) 2 . y x y x1 x yz(5) 1 y zx ；1 z xy1 x yz原式 = 0 y x z( y x)0 z x y( z x)=1 z( y x)( z x) ( x y )( y z )( z) .y x11 0 1 0 00 2 1 0 0(6) 3 1 0 0 0 ；0 0 0 2 10 0 0 0 21 0 1 01 0 1 1 0 10 2 1 04 0 2 1 4 0 2 1原式 = 21 0 033 1 0 0 1 30 0 0 2=2 14 20 .1 31 x1 1 1 11 1 x2 1 1；(7)1 1 1 x3 11 1 1 1 x41 x1 x1 x1 x1解：原式 = 1 x2 0 0 1 0 x3 0 1 0 0 x41x1 x1 x1x1 x1 x1 x1x3x2 x4= 0 x2 0 00 0 x3 00 0 0 x4= x1 x2 x3 x4 x2 x3 x4 x1 x3 x4 x1 x2 x4 x1 x2 x3.1 5 1 31 1 3 4，计算 A41 A42 A43 A44的值.2. 设D1 2 312 23 4其中 A4 j ( j 1,2,3,4) 是 D 的代数余子式.1 5 1 3解： A41 A42A431 1 3 4A441 26 .1 31 1 1 13 5 2 13. 已知D1 1 0 1 M11M21M31M41.1 3 1, 求12 4 1 1解： M 11M21M31M41=1 M11( 1)M 21 1 M 31 ( 1)M 411 52 11 1 0 1=3 1=0.1 11 4 1 14. 计算下列n 阶行列式.2 1 1 1 1 1 1 (1) 1 2 1 ；y x y y解：原式 = x (n 1) y y y x y1 1 2n 1 1 1 1 1 1解：原式n 1 2 1 1 2 1 = = (n 1)n 1 1 2 1 1 21 1 1= (n 1) 0 1 0.n 1 0 0 1x y y yy x y y (2) y y x y ；y y y xy y y x1 1 1 10 x y 0 0= x (n 1) y 0 0 x y 00 0 0 x y= x (n 1) y ( x y) n 1.0 1 1 11 x1 0 0(3) 1 0 x2 0 ( x i 0,i 1,2, ,n) .1 0 0 x nn1111i 1 x i解：原式 =0 x 1 0 0 00 x 2 0x n=x 1 x 2x n (n1) .i 1x i四、证明题11 1= (b a)(c a)112ab a 2c 2ac a 2b= (b a)(c a)(c 2 b 2ac ab)= (b a)(ca)(c b)( a b c) =0,由于 a , b , c 是互异的实数，故要上式成立，当且仅当 a+b+c=0.abcd2. 证明a a+ba b c c a b c da 4a 2ab 3a 2b 4a 3b 2cd a3a b 6a 3b c 10a 6b 3c d1. 设 a , b , c 是互异的实数，证明a b c 0 的充分必要条 a bc da 3b 3c 3r 4r 30 a a ba b c件是 a+b+c=0.证明：左边r 3 r 2a2a b3a2bc11 1 1r 2r 10 a 3a b 6a 3b c证明： ab c a b a c a a bc d a bc da3b 3c 3a 3b 3 a 3c 3 a 3r 3 0 a a b a b c0 a a b a b cr 44r 3 r 21 0 0ar 4r 3a ab ac a2a b 0 2a b =a 3 c 3 a 30 0a3a b0 0ab 3=右边克莱姆法则一、选择题x1 x2 x3 1,1．方程组x1 x2 x3 1, ,有唯一解,则( ).x1 x2 x3 1(A) 1且 2 ；(B) 1 且 2 ；(C) 1且 2 ；(D) 1 且 2 ．1 1解析：由克莱姆法则，当 1 1 (2 )( 1) 2 0 ，即1 11且 2 ，选B.ax z 0,2. 当a （）时，方程组2x ax z 0, 只有零解.ax 2 y z 0(A) -1 ；(B) 0 ；(C) -2 ； (D) 2.解析：由克莱姆法则，a 0 1 0 0 1当 2 a 1 2 a a 1 2(a 2) 0a 2 1 0 2 1即a 2 ，选D.三、解答题1.用克莱姆法则下列解方程组 .x 2 y z 2,(1) x 2 y 2z 3,2x y z 3;1 2 1解： D 1 2 2 3 0 ，2 1 1由克莱姆法则知，此方程组有唯一解，22 1D13 2 2 3 ，31 11 2 1 1 2 2D 2 1 3 2 6 ， D 3 1 3 3 9 ，2 3 1 2 3 3因此方程组的解为D1 D 22 ， z D 33 .x 1, yDD Dx1 2 x2 x3 x4 1,2x1 3x2 x3 2x4 3, (2)3x2 2x3 x4 ..x1 2, 2x1 4x2 3x3 3x4 21 2 1 1解： D 2 3 1 24 01 32 12 43 3由克莱姆法则知，此方程组有唯一解，1 2 1 1 1 1 1 13 3 1 28 ， D 22 3 1 2D13 2 1 1 2 22 ,2 12 43 3 2 2 3 31 2 1 1 1 2 1 12 3 3 2D 42 3 1 32 .D33 22 ,1 32 21 12 4 23 24 3 2因此方程组的解为D12 , x2D 2 1 D 3 1 D 4 1x1D， x3D, x4D.D 2 2 22x1 2x2 x3 0,2. 判断线性方程组x1 2x2 4 x3 0, 是否有非零解5x1 8x2 2x3 02 2 1 1 2 4解：因为系数行列式 D 1 2 4 2 2 15 8 2 5 8 21 2 4 1 2 4= 0 6 9 0 6 9 30 0 ,0 18 22 0 0 5所以，方程组只有零解.x1 kx2 x3 0,3. 已知齐次线性方程组kx1 x2 x3 0, 有非零解，求k 的值.2x1 x2 x3 0解：因为齐次线性方程组有非零解，所以该方程组的系数行列式必为零，即1 k 1 1 k 1k 1 1 0 1 k 2 1 k2 1 1 0 1 2k 3= 3(1 k 2 ) (1 k)(1 2k)= (1 k)( 4 k ) 0解得， k=-1 或 k=4.2x1 4x2 ( 1) x3 0 4. 当取何值时，齐次线性方程组 ( 3) x1 x2 2x3 0 有非x1 (1 ) x2 x3 0 零解解：由齐次线性方程组有非零解的条件可知，2 4 13 1 2 0 ,解得0,2,3 .1 1 1第一章综合练习一、判断题1. n 阶行列式D n中的 n 最小为2.( ╳ )2. 在 n 阶行列式D a ij 中元素 a ij (i, j 1,2, L) 均为整数，则D必为整数 .( √ )a 11 0a 14a22a23a 14 a 23a 32 a 41 .(╳3.a32a33a 11a22 a 33 a44a410 0a44)二、选择题1. 若 D 13x 1 x 2x 11 1x 1， D 2x，则 D 1 与 D 2 的大12小关系是 ( ).(A) D 1D 2 ； (B) D 1 D 2 ； (C) D 1 D 2 ； (D) 随 x 值变化而变化 . 答案： Ca bcos20 sin 40 =.1.cos40sin 20解析：cos20 sin 40 cos20 cos40sin 20cos401cos60.2 2. 若 x 2y 2 x x , 则 x+y =. 1 1yy解析：由 x2y 2 xx ，得 x 2 y 21 1 y y即 ( xy) 2 0 ，从而 x+y =0.sin 20 sin 402xy2. 行列式 (a,b,c, d 1,1,2 ) 的所有可能值中，最大 c d的是 ( ).(A) 0 ； (B)2 ； (C)4 ； (D)6.答案： D3. 已知x2 0,x y 1，则 y = .1 1 11x 2 x y 解析：由1 10,1 , 得 x =2, x-y =1, 从而 y =11 1三、填空题13 54.若a2b2c2a2 A2b2 B2c2 C 2,则 C 2化简后的结果24 6等于.解析： C21 32 .2 42x x 1 25. 设f ( x) 1 x 1 14 的系数为； x3的3 2 x，则 x11 1 1 x系数为.解析：当 f ( x)的主对角线的 4 个元素相乘才能得出x 4，系数3为 2；含x的项只能是a12 , a21, a33 , a44的乘积，系数为-1.1 2 3 4 51 1 12 26. 设D 3 2 1 4 6 ,2 2 2 1 14 3 2 10则 (1) A31A32 A33= ； (2)A34A35 ；（ 3）A51 A52 A53 A54 A55 .解析： A31A32A33 2( A34 A35 ) 02(A31A32 A33 ) ( A34 A35 ) 0于是A31 A32 A33 0 ， A34 A35 0 .1 2 3 4 51 1 12 2A51A52A53A54A55 3 2 1 4 62 2 2 1 11 1 1 1 11 2 3 4 51 1 12 23 2 14 60 .3 3 3 3 31 1 1 1 1即 A51A52A53A54A550 .四、解答题1.计算下列行列式 .x1 y1 x1 y2 x1 y3 x1 y4(1) x2 y1 x2 y2 x2 y3 x2 y4 ；x3 y1 x3 y2 x3 y3 x3 y4x4 y1 x4 y2 x4 y3 x4 y4x1 y1 y2 y1 y3 y1 y4 y1x2 y1 y2 y1 y3 y1 y4 y1 解：原式 =x3 y1 y2 y1 y3 y1 y4 y1x4 y1 y2 y1 y3 y1 y4 y1x1 y1 y2 y1 y3 y1 y4 y1x2 x1 0 0 0 =x1 0 00 .x3 0x4 x1 0 0 01 x1 1 1 11 1 x2 1 1(2) ；1 1 1 x3 11 1 1 1 x41 x1 x1 x1 x11 x2 0 0解：原式 =0 x3 011 0 0 x41x1 x1 x1x1 x1 x1x1x3 x4x2= 0 x2 0 00 0 x3 00 0 0 x4= x1 x2 x3 x4 x2 x3 x4 x1 x3 x4 x1 x2 x4 x1 x2 x3.0 0 0 1 0 0 0 2 0 0(3)2005 0 0 .0 02006 0 0 0 00 0 0 0 20072006 2005解：原式 = 2007 ( 1) 2 2006! = 2007!1 2 3 4 52 2 2 1 12. 已知D 3 1 2 4 527 ,1 1 12 24 3 15 0求 (1) A41A42 A43；(2)A44A45.解： 1 A41 1 A42 1 A43 2( A44 A45 ) 272( A41 A42 A43 ) ( A44 A45 ) 0得 A41A42A439 , A44A4518 .3.计算下列 n 阶行列式.1 1 12 2 2 2n(1) D n 3 32 3n；n n 2 n n解：（利用范德蒙行列式计算）1 1 1D n D n T1 2 nn! 3 32 3n1 2n 1 n n 1n!(2 1)(3 1) ( n 1)(3 2)(4 2) (n 2) n ( n 1)n!(n 1)!( n 2)! 2! .2 1 1(2) 1 2 1 ；1 1 2n 1 1 1 1 1 1解：原式n 1 2 1 1 2 1 = = (n 1)n 1 1 2 1 1 21 1 1= (n 1) 0 1 0.n 1 0 0 1x1 m x2 x nx1 x2 m x n(3) D nx1 x2 x n m解：将第 2 列，L，第n列分别加到第一列，并提取第一列的公因子，得x1 x2 x n m x2 x nD nx1 x2 x n m x2 m x nx1 x2 x n m x2 x n m1 x2 x n( x1 x2 x n1 x2 m x nm)1 x2 x n m1 0 0( x1 x 2 x n1 m 0m)1 0 m( x1 x2 x n m)( m) n1b1 b2 b3 b n 1 b na1 a2 0 0 0 (4) D n 0 a2 a3 0 00 0 0 a n 1 a n（其中 a i 0,i 1,2, , n ）a1 a2 0 0 解： D n ( 1)1 n b n0 a2 0 00 0 0 an 1b1 b2 b n 2 b n 1a1 a2 0 0 a n 0 a2 0 00 0 a n 2 an 1a1 a2 a n b nanDn 1a na1 a2 nb i.a na ii 1三、证明题1. 试证：如果n次多项式f ( x) a0 a1 x a n x n对 n+1 个不同的 x 值都是零，则此多项式恒等于零.( 提示：用范德蒙行列式证明)。

(完整版)行列式习题1附答案.doc

⋯⋯_ ⋯_ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯：⋯号⋯学⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ 线_ 订_ _ 装_ _ ⋯_ _ ⋯_ _ ⋯_ ⋯：⋯名⋯姓⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯：⋯⋯⋯班⋯⋯⋯《线性代数》第一章练习题⋯⋯一、填空⋯⋯⋯1、(631254) _____________ 8⋯⋯⋯2、要使排列（3729m14n5）偶排列， m =___8____, n =____6_____⋯⋯x 1 13 , x 2 的系数分是⋯3、关于x的多式x x x中含 x -2,4⋯1 2 2x⋯⋯4、 A 3方， A 2， 3A* ____________ 108⋯⋯⋯5、四行列式det( a ij)的次角元素之（即a14a23a32a41）一的符号+⋯⋯1 2 1线1234 2346、求行列式的 (1) =__1000 ；（2）2 4 2 =_0___；封2469 469密10 14 13⋯⋯1 2000 2001 2002⋯0 1 0 2003⋯⋯(3)0 1=___2005____;⋯0 20040 0 0 2005⋯⋯1 2 3⋯中元素 0 的代数余子式的___2____⋯(4) 行列式2 1 0⋯3 4 2⋯⋯1 1 1 1⋯1 5 25⋯ 4 2 3 57、 1 7 49 = 6 ；= 1680⋯16 4 9 25⋯1 8 64⋯64 8 27 125⋯⋯矩方，且，，， A 1 1 。

⋯A 4⋯8、|A|=5 | A*| =__125 | 2A| =__80___ | |=50 1 10 1 2 22 2 2 09、 1 0 1 = 2 。

；3 0121 1 01 01 0 0 0bx ay010、若方程cx az b 有唯一解，abc≠0 cy bz a11、把行列式的某一列的元素乘以同一数后加到另一列的元素上，行列式12、行列式a11a12a13a14a21a22a23a24 的共有4! 24, 在a11a23 a14a42, a34a12a31a32a33a34a41a42a43a44a34a12a43 a21 是行列式的，符号是 + 。

《线性代数》第一章行列式精选习题及解答

(C)0, 2
(D)0,1
解按三阶行列式的对角线法则得 D1 = (λ + 1)(λ − 1)2 , D2 = 0 . 若 D1 = D2 ，则
(λ + 1)(λ −1)2 = 0 ，于是 λ = 1,−1，故正确答案为（B）．
例 1.5
方程组 ⎪⎨⎧λx1x1++λxx22
故逆序数为 1；于是这个排列的逆序数为 t=0+0+2+4+1=7，故正确答案为（B）．
例 1.2 下列排列中（）是偶排列.
(A)54312 (B)51432
(C) 45312
(D) 654321
解按照例 1 的方法计算知：排列 54312 的逆序数为 9；排列 51432 的逆序数为 7；排列
例17分析如果行列式的各行列数的和相同时一般首先采用的是将各列行加到第一列行提取第一列行的公因子简称列行加法这个行列式的特点是各列4个数的和为10于是各行加到第一行得10101010分析此类确定系数的题目首先是利用行列式的定义进行计算
第一章行列式
1.1 目的要求
1．会求 n 元排列的逆序数； 2．会用对角线法则计算 2 阶和 3 阶行列式； 3．深入领会行列式的定义； 4．掌握行列式的性质，并且会正确使用行列式的有关性质化简、计算行列式； 5．灵活掌握行列式按（列）展开； 6．理解代数余字式的定义及性质； 7．会用克拉默法则判定线性方程组解的存在性、唯一性及求出方程组的解．
（2） A34 + A35 = （）, （3） A51 + A52 + A53 + A54 + A55 = （）．
分析此类题目一般不宜算出表达式里每一项的值，而是注意观察要求的表达式的结构，

行列式练习题及答案

行列式练习题一、判断题1. 行列式的行数和列数可以相同也可以不同。

（）2. n 阶行列式共有2n 个元素，展开后共有n ！项。

（）3. n 阶行列式展开后的n ！项中，带正号的项和带负号的项各占一半。

（）4. 行列式D 中元素ij a 的余子式ij M 与其代数余子式ij A 符号相反。

（）5. 上（下）三角形行列式的值等于主对角线上元素的乘积。

（）6. 行列式与它的转置行列式符号相反。

（）7. 行列式中有一行的元素全部是零则行列式的值为零。

（）8. 行列式中有两行元素相同，行列式的值为零。

（）9. 行列式中有两行元素成比例，行列式的值为零。

（） 10．互换行列式的两行，行列式的值不变。

（） 11. 行列式中某一行的公因子k 可以提到行列式符号之外。

( ) 12. 行列式中若所有元素均相同，则行列式的值为零。

（） 13. 行列式的值等于它的任一行（列）的元素与其对应的代数余子式乘积。

（）14. 行列式某一行（列）的元素与另一行（列）的对应的元素的代数余子式乘积之和为零。

（） 15. 齐次线性方程组的系数行列式0D ≠，则它仅有零解。

（）二、填空题1.=______x yyx -。

2.sin cos =______cos sin θθθθ-。

3. 123246=______345。

4．2-20310=______450。

5．=______a x xx b x x x c。

6. 211123=0______49x x x =，则。

7.222031,005D =-已知111213=______M M M -+则。

8．=______x y x y y x y x x y x y+++。

9．100110=______011001a b c d---。

10．222=______a b c a b c b c c a a b+++。

11. 已知21341023,15211152D =-则1323432=______A A A ++。

行列式测试题(有答案)

第九讲队列式单元测试题评论一、填空题（每题2 分，满分 20 分）1．全体 3 阶摆列一共有 6 个，它们是 123,132,213,231,312,321；2. 奇摆列经过奇数次对调变成偶摆列，奇摆列经过偶数次对调变成奇摆列；3. 队列式 D 和它的转置队列式D 相关系式 DD ；4. 互换一个队列式的两行（或两列），队列式的值改变符号；5. 假如一个队列式有两行（或两列）的对应元素成比率，则这个队列式等于零；6. 一个队列式中某一行（列）全部元素的公因子能够提到队列式符号的外边；7. 把队列式的某一行（列）的元素乘以同一数后加到另一行（列）的对应元素上，队列式的值不变；8. 队列式的某一行（列）的元素与另一行（列）的对应元素的代数余子式的乘积之和等于零；a11a 12La 1n0 a22La2na 11a 22 K a nn ;9. MMMMLann10.当 k= 214kk2时，45。

2k二、判断题（每题 3 分，满分 24 分）1. 若(i1i2i n )k,则 (i 2 i1i 3 i n ) k 1（∨）a11a12a1n2.设D a21a22a2n , 则D的一般项 a ij a i j2ai j的符号1 12n nan1an2ann是( 1)( j1 j2j n ).（×）3.若 n(n>2)阶队列式 D=0,则 D 有两行（列）元素同样 . (×) 4．若 n 阶队列式 D 恰有 n 个元素非 0，则 D≠0.(×) 5.关于线性方程组，只需方程个数等于未知数个数，就能够直接使用克莱姆法例求解。

（×）6．若队列式 D 的同样元素多于n2n 个，则D=0.(× )a11a12a13a13a23a337.a21a22a23a12a22a23(× )a31a32a33a11a21a31阶队列式主对角线上元素乘积项带正号，副对角线上元素乘积项带负号。

高等代数《行列式》部分习题及解答

高等代数《行列式》部分习题及解答例1：决定以下9级排列的逆序数，从而决定它们的奇偶性： 1）.134782695；2）.217986354；3）.987654321. 答：1）. ()134782695=10τ，134782695是一个偶排列；2）. ()217986354=18τ，217986354是一个偶排列； 3）. ()987654321=36τ，987654321是一个偶排列. 例2：写出把排列12435变成排列25341的那些对换.答：()()()()()()()12154,312435214352543125341−−→−−→−−−→.例3：如果排列121...n n x x x x -的逆序数为k ，排列121...n n x x x x -的逆序数是多少？答：()112n n k --例4：按定义计算行列式： 000100201).0100000n n - 010000202).0001000n n -001002003).1000000n n-答：1）.原行列式()()()()1,1,,2,121!1!n n n n n n τ--=-=-2）.原行列式()11!.n n -=-3）.原行列式()()()1221!n n n --=-.例5：由行列式定义计算()212111321111x x x f x x x-=中4x 与3x 的系数，并说明理由. 答：()f x 的展开式中x 的4次项只有一项；2,x x x x ⋅⋅⋅故4x 的系数为2；x 的3次项也只有一项()()213411,x x x τ-⋅⋅⋅故3x 的系数为-1.例6：由111111=0111，证明：奇偶排列各半.证明：由于12n j j j 为奇排列时()()121n j j j τ- 为-1，而偶排列时为1,.设有k 个奇排列和l 个偶排列，则上述行列式()()()()12121212110.n n nnj j j j j j j j j j j j l k ττ=-+-=-=∑∑ 即奇偶排列各占一半.例7：证明1111111112222222222b cc a a b a b c b c c a a b a b c b c c a a b a b c ++++++=+++. 证明：111111111111111111122222222222222222222222.2b cc a a bac aa baa b a cab c b c c a a b a c a a b a a b a c a b c b c c a a b a c a a b a a b a c a b c +++-+++++++=-++=++=+++-++++ 例8：算出行列式：121401211).00210003-；1122).321014-的全部代数余子式. 答：111213142122232431323334414243441).6,0;12,6,0;15,6,3,0;7,0,1, 2.A A A A A A A A A A A A A A A A =-====-=====-=-=====-1112132122233132332).7,12,3;6,4,1;5,5, 5.A A A A A A A A A ==-====-=-== 例9：计算下面的行列式：111121131).12254321-；11112112132).1111321112---；01214201213).135123312121035-- 答：1111111111110115011501151).= 1.011400010012012300120001---------==-=-------原式132).12-3).483-. 例10：计算下列n 级行列式： 0000001).;000000x y x y x yyx1112121222122).n nn n n na b a b a b a b a b a b a b a b a b ---------122222223).;2232222n1231110004)..02200011n n n n-----答：()()110000000000000001).11.000000000000000n n n n xy xy yx y x xy x y x y x y x yy yxxxy++=+-=+-2）.当1n =时，为11a b -；当2n =时，为()()1212a a b b --；当3n ≥时，为零.()12221000222222223).22!223200102220002n n n -==-⋅--（利用第2行（列）的特点）()()11231110001!4).1.02200211n n nn n n---+=---- （从左起，依次将前一列加到后一列）例11：用克拉默法则解线性方程组1234123412341234232633325323334x x x x x x x x x x x x x x x x -++=⎧⎪-++=⎪⎨--+=⎪⎪-+-=⎩.答：2132333270031123131d --==-≠----，所以可以用克拉默法则求解.又因16132533270;31124131d --==-----22632353270;33123431d ==---32162335270;31323141d --==----42136333570;31133134d --==----所以此线性方程组有唯一解，解为1234 1.x x x x ====例12：求12121212111222,n nnnj j j j j j j j j nj nj nj a a a a a a a a a ∑这里12nj j j ∑是对所有n 级排列求和.答：对每个排列12n j j j ，都有：()()121212121111112122221222121.n n nnj j j n j j j j j j nn n nnnj nj nj a a a a a a a a a a a a a a a a a a τ=- 因为在全部n 级排列中，奇偶排列个数相同，各有!2n 个.所以121212121112220n n nnj j j j j j j j j nj nj nj a a a a a a a a a =∑.例13：计算n 级行列式：12222122221212111.nnn n n nnn n nx x x x x x x x x x x x ---答：作范德蒙德行列式：1212222121111111211211111.n n n n n n n n n n nnn nn n x x x x x x x x D x x x x x x x x ++----++=将这个行列式按最后一列展开，展开式中11n n x -+的系数的()11n n++-倍就是所求行列式D ，因为()111,ji i j n D xx ≤<≤+=-∏所以()()()()11111111.nnn nji k ji k k k i j n i j n D xx x xx x ++==≤<≤+≤<≤+=---=-∑∑∏∏。

(完整版)行列式习题答案

线性代数练习题第一章行列式系专业班姓名学号第一节 n 阶行列式一．选择题1．若行列式 = 0，则[ C ]x52231521-=x （A ）2 （B ）（C ）3（D ）2-3-2．线性方程组，则方程组的解=[ C ]⎩⎨⎧=+=+473322121x x x x ),(21x x （A ）（13，5）（B ）（，5）（C ）（13，）（D ）（）13-5-5,13--3．方程根的个数是[ C ]093142112=x x （A ）0 （B ）1 （C ）2 （D ）34．下列构成六阶行列式展开式的各项中，取“+”的有 [ A ]（A ）（B ） 665144322315a a a a a a 655344322611a a a a a a （C ）（D ）346542165321a a a a a a 266544133251a a a a a a 5．若是五阶行列式的一项，则的值及该项的符号为[ B ]55443211)541()1(a a a a a l k l k N -ij a l k ,（A ），符号为正；（B ），符号为负；3,2==l k 3,2==l k （C ），符号为正；（D ），符号为负2,3==l k 2,3==l k 6．下列n （n >2）阶行列式的值必为零的是 [ BD ](A) 行列式主对角线上的元素全为零 (B) 三角形行列式主对角线上有一个元素为零 (C) 行列式零的元素的个数多于n 个 (D) 行列式非零元素的个数小于n 个二、填空题1．行列式的充分必要条件是1221--k k 0≠3,1k k ≠≠-2．排列36715284的逆序数是133．已知排列为奇排列，则r =2,8,5s = 5,2,8，t = 8,5,2397461t s r4．在六阶行列式中，应取的符号为负。

ij a 623551461423a a a a a a 三、计算下列行列式：1．=181322133212．=5598413111３．yxyx x y x yyx y x +++332()x y =-+４．=10001100000100100５．000100002000010n n -1(1)!n n -=-６．0011,22111,111 n n nn a a a a a a --(1)212,11(1)n n n n n a a a --=-线性代数练习题第一章行列式系专业班姓名学号第二节行列式的性质一、选择题：1．如果，，则 [ C ]1333231232221131211==a a a a a a a a a D 3332313123222121131211111232423242324a a a a a a a a a a a a D ---==1D （A ）8（B ）（C ）（D ）2412-24-2．如果，，则 [ B ]3333231232221131211==a a a a a a a a a D 2323331322223212212131111352352352a a a a a a a a a a a a D ---==1D （A ）18（B ）（C ）（D ）18-9-27-3． = [ C ]2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a （A ）8 （B ）2（C ）0（D ）6-二、选择题：1．行列式 12246000 2. 行列式-3=30092280923621534215=11101101101101112．多项式的所有根是0211111)(321321321321=+++++=x a a a a x a a a a x a a a a x f 0,1,2--3．若方程= 0 ，则225143214343314321x x --1,x x =±=4．行列式 5==2100121001210012D 三、计算下列行列式：1．2605232112131412-21214150620.12325062r r +=2．xa a a x a a a x 1[(1)]().n x n a x a -=+--线性代数练习题第一章行列式系专业班姓名学号第三节行列式按行（列）展开一、选择题：1．若，则中x 的一次项系数是[D]111111111111101-------=x A A （A ）1（B ）（C ）（D ）1-44-2．4阶行列式的值等于 [D ]443322110000000a b a b b a b a （A ）（B ）43214321b b b b a a a a -))((43432121b b a a b b a a --（C ）（D ）43214321b b b b a a a a +))((41413232b b a a b b a a --3．如果，则方程组的解是 [B]122211211=a a a a ⎩⎨⎧=+-=+-0022221211212111b x a x a b x a x a （A ），（B ），2221211a b a b x =2211112b a b a x =2221211a b a b x -=2211112b a b a x =（C ），（D ），2221211a b a b x ----=2211112b a b a x ----=2221211a b a b x ----=2211112b a b a x -----=二、填空题：1．行列式中元素3的代数余子式是 -6122305403--2．设行列式，设分布是元素的余子式和代数余子式，4321630211118751=D j j A M 44,j a 4则 =，=-6644434241A A A A +++44434241M M M M +++3．已知四阶行列D 中第三列元素依次为，2，0，1，它们的余子式依次分布为1-5，3，4，则D = -15,7-三、计算行列式：1．321421431432432112341234134101131010141201311123031111310131160.311-==---=-=-2.12111111111na a a +++ ==121111011101110111n a a a+++121111100100100na a a---211112111110010010n c c a a a a a+--+111223211111100001000na a cc a a a a++-+11121101111000000ni ni iia a a c a c a=+++∑1211()(1)nn i i a a a a =+∑或121123113111111000000nn a r r a r r a r r a a a a+------211211212311111000000na a aa a a c c a a a a+++--11122313311111100000ni in nnaa a c c a a a c c a a a a=++++∑1122()(1)nn i ia a a a a =++∑或11221121121110111110111111111(1).n n n n nn i ia a a a a a D a a a a a a a --=++++=+=+=+∑线性代数练习题第一章行列式系专业班姓名学号综合练习一、选择题：1．如果，则 = [ C ]0333231232221131211≠==M a a a a a a a a a D 3332312322211312111222222222a a a a a a a a a D =（A ）2 M（B ）－2 M（C ）8 M（D ）－8 M2．若，则项的系数是[ A ]xxx x x x f 171341073221)(----=2x （A ）34 （B ）25 （C ）74 （D ）6二、选择题：1．若为五阶行列式带正号的一项，则 i = 2 j = 154435231a a a a a j i 2. 设行列式，则第三行各元素余子式之和的值为 8。

行列式习题1附答案

级班命题人或命题小组负责人签名: 教研室（系）主任签名：一、填空题«线性代数》第一章练习题1、（631254） ____________ 82、要使排列（3729m14n5为偶排列，则m =___8 __ , n = ____ 6 ____x 11 「入 3 23、关于x 的多项式x x X 中含x 3,x 2项的系数分别是-2,4122x4、 A 为3阶方阵，A 2，则3A* ________________ 1085、四阶行列式det （a j ）的次对角线元素之积（即aga 23a 32a 41）一项的符号为 +6、求行列式的值（1）1234 2469 234469=__1000__1 2 1⑵ 24 2 =010 14 131 0 2000 12001⑶0 12002 2003 =20052004 20051 2⑷行列式213 40中元素0的代数余子式的值为 27、 1 5 25 1 7 49 1 8 641 11 1 423 516 4925 64 827 125: ___ 1680 ________8、设矩阵A 为4阶方阵，且|A|=5,则|A*|=__125.1| 2A| =__80__，| A |=0 1 19、 1 0 1 =2;1 1 0bx ay 010、若方程组 cx az bcy bz a有唯一解，则abcM _______0 1 2 22 2 2 0 121 3 0 01 0 0 0O11、把行列式的某一列的元素乘以同一数后加到另一列的对应元素上行列式^不变 12、行列式a 12a 13 a 22a 23a 32 a 33a 42 a 43a 11 a 21a 31 a 41a 14 a 24 a 34a 44的项共有4! 24 项，在&11&23&14&42a 34 a 12a 43a 21中,X 2 X 3 013、当a 为1 1或2时，方程组x 12x 2 ax 3 0有非零解。

行列式练习题与答案资料讲解

行列式练习题与答案收集于网络，如有侵权请联系管理员删除第1章行列式 (作业1)一、填空题1．设自然数从小到大为标准次序，则排列1 3 … )12(-n 2 4 … )2(n 的逆序数为，排列1 3 … )12(-n )2(n )22(-n …2的逆序数为 . 2．在6阶行列式中，651456314223a a a a a a 这项的符号为 . 3．所有n 元排列中，奇排列的个数共个. 二、选择题1.由定义计算行列式nn 0000000010020001000 -= （）.（A ）!n （B ）!)1(2)1(n n n -- （C ）!)1(2)2)(1(n n n --- （D ）!)1()1(n n n --2．在函数xx x xx x f 21123232101)(=中，3x 的系数是（）.（A ）1 （B ）-1 （C ）2 （D ）33．四阶行列式的展开式中含有因子32a 的项，共有（）个. （A ）4；（B ）2；（C ）6；（D ）8.三、请按下列不同要求准确写出n 阶行列式)det(ij a D =定义式： 1．各项以行标为标准顺序排列；2．各项以列标为标准顺序排列；3．各项行列标均以任意顺序排列.四、若n阶行列式中，等于零的元素个数大于nn 2，则此行列式的值等于多少？说明理由.收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除第1章行列式 (作业2)一、填空题1．若D=._____324324324,13332313123222121131211111333231232221131211=---==a a a a a a a a a a a a D a a a a a a a a a 则2．方程229132513232213211x x --=0的根为___________ .二、计算题 1． 8171160451530169144312----- 2．dc b a100110011001---3．ab b babb b a D n=收集于网络，如有侵权请联系管理员删除4.111113213211211211211nn n n n a a a a x a a a a x a a a a xa a a a x D---+=5．计算n 阶行列式)2(212121222111≥+++++++++=n nx x x n x x x n x x x D n n n n 。

行列式习题答案

线性代数练习题第一章行列式系专业班学号第一节 n 阶行列式一．选择题1．若行列式x52231521- = 0，则=x [ C ] （A ）2 （B ）2- （C ）3 （D ）3- 2．线性方程组⎩⎨⎧=+=+473322121x x x x ，则方程组的解),(21x x = [ C ]（A ）（13，5）（B ）（13-，5）（C ）（13，5-）（D ）（5,13--）3．方程093142112=x x根的个数是 [ C ] （A ）0 （B ）1 （C ）2 （D ）34．下列构成六阶行列式展开式的各项中，取“+”的有 [ A ] （A ）665144322315a a a a a a （B ）655344322611a a a a a a （C ）346542165321a a a a a a （D ）266544133251a a a a a a 5．若55443211)541()1(a a a a a l k l k N -是五阶行列式ij a 的一项，则l k ,的值及该项的符号为[ B ]（A ）3,2==l k ，符号为正；（B ）3,2==l k ，符号为负；（C ）2,3==l k ，符号为正；（D ）2,3==l k ，符号为负6．下列n （n >2）阶行列式的值必为零的是 [ BD ] (A) 行列式主对角线上的元素全为零 (B) 三角形行列式主对角线上有一个元素为零 (C) 行列式零的元素的个数多于n 个 (D) 行列式非零元素的个数小于n 个二、填空题 1．行列式1221--k k 0≠的充分必要条件是 3,1k k ≠≠-2．排列36715284的逆序数是 133．已知排列397461t s r 为奇排列，则r = 2,8,5 s = 5,2,8 ，t = 8,5,24．在六阶行列式ij a 中，623551461423a a a a a a 应取的符号为负。

（完整版）行列式练习题及答案

（完整版）行列式练习题及答案一、填空题1．设自然数从小到大为标准次序，则排列1 3 … )12(-n 2 4 … )2(n 的逆序数为，排列1 3 … )12(-n )2(n )22(-n …2的逆序数为 . 2．在6阶行列式中，651456314223a a a a a a 这项的符号为 . 3．所有n 元排列中，奇排列的个数共个. 二、选择题1.由定义计算行列式nn 00000010020001000ΛΛΛΛΛΛΛΛΛΛ-= （）. （A ）!n（B ）!)1(2)1(n n n --（C ）!)1(2)2)(1(n n n --- （D ）!)1()1(n n n --2．在函数xx x x xx f 21123232101)(=中，3x 的系数是（）.（A ）1 （B ）-1 （C ）2 （D ）33．四阶行列式的展开式中含有因子32a 的项，共有（）个. （A ）4；（B ）2；（C ）6；（D ）8.三、请按下列不同要求准确写出n 阶行列式)det(ij a D =定义式：1．各项以行标为标准顺序排列；2．各项以列标为标准顺序排列；3．各项行列标均以任意顺序排列.四、若n 阶行列式中，等于零的元素个数大于n n -2，则此行列式的值等于多少？说明理由.一、填空题1．若D=._____324324324,13332313123222121131211111333231232221131211=---==a a a a a a a a a a a a D a a a a a a a a a 则2．方程229132513232213211x x --=0的根为___________ .二、计算题 1． 8171160451530169144312----- 2．dc b a100110011001---3．abbb a b b b a D n ΛΛΛΛΛΛΛ=4.111113213211211211211nn n n n a a a a x a a a a x a a a a x a a a a x D ΛΛΛΛΛΛΛΛΛΛΛ---+=5．计算n 阶行列式)2(212121222111≥+++++++++=n nx x x n x x x n x x x D n n n n ΛΛΛΛΛΛΛ。

行列式练习题与答案

.第1章行列式(作业1) 一、填空题1．设自然数从小到大为标准次序，则排列13 ⋯(2n1)24 ⋯(2n)的逆序数为，排列13⋯(2n1)(2n)(2n 2)⋯2的逆序数为.2．在6阶行列式中，a23a42a31a56a14a65这项的符号为. 3．所有n元排列中，奇排列的个数共个.二、选择题00010002001.由定义计算行列式=（）.n100000000n（A）n(n1)!（）(n1)(n2)（）n!（B）(1)2C (1)2n! D (1)n(n1)n!nx x102．在函数1x23中，x3的系数是（）. f(x)3x22112x（A）1 （B）-1 （C）2 （D）33．四阶行列式的展开式中含有因子a32的项，共有（）个. （A）4；（B）2；（C）6；（D）8.三、请按下列不同要求准确写出n阶行列式 D det(a ij)定义式：1．各项以行标为标准顺序排列；2．各项以列标为标准顺序排列；3．各项行列标均以任意顺序排列.四、若n阶行列式中，等于零的元素个数大于n2n，则此行列式的值等于多少？说明理由.......第1 章行列式 (作业2) 一、填空题a11 a12 a134a 11 2a 11 3a 12 a13 1．若D=a21 a22 a23 1,则D14a21 2a21 3a22 a23_____. a31 a32 a33 4a 312a 31 3a 32 a331 12 31 2 x 2 2 3的根为___________. 2．方程3 1 =0 2523 1 9 x 2二、计算题2 13 4a 1 0 0 4 1 9 161 b 1 01． 15 45 60 2．1 c 130 0 117 1 80 1 da b b b a b 3．Dnb ba.....x a1a2a1x a2a1a2x 4.D n1a1a2a3a1a2a3.an11a n11a n11x1a n1x11x12x1n x21x22x2n5．计算n阶行列式D n(n2)。

(完整版)行列式练习题及答案

一、填空题1．设自然数从小到大为标准次序，则排列1 3 … 2 4 … 的逆序数为)12(-n )2(n ，排列1 3 … …2的逆序数为 .)12(-n )2(n )22(-n 2．在6阶行列式中，这项的符号为 .651456314223a a a a a a 3．所有n 元排列中，奇排列的个数共个.二、选择题1.由定义计算行列式= （）.nn 0000000010020001000 -（A ）（B ）（C ）（D ）!n !)1(2)1(n n n --!)1(2)2)(1(n n n ---!)1()1(n n n --2．在函数中，的系数是（）.xx xx x x f 21123232101)(=3x （A ）1 （B ）-1 （C ）2 （D ）33．四阶行列式的展开式中含有因子的项，共有（）个.32a （A ）4；（B ）2；（C ）6；（D ）8.三、请按下列不同要求准确写出n 阶行列式定义式：)det(ij a D =1．各项以行标为标准顺序排列；2．各项以列标为标准顺序排列；3．各项行列标均以任意顺序排列.四、若n 阶行列式中，等于零的元素个数大于，则此行列式的值等于多少？说明理由.n n -2一、填空题1．若D=._____324324324,13332313123222121131211111333231232221131211=---==a a a a a a a a a a a a D a a a a a a a a a 中2．方程=0的根为___________ .229132513232213211x x --二、计算题1．2．8171160451530169144312-----dc b a10011001101---3．ab b ba b b b aD n =4.111113213211211211211n n n n n a a a a x a a a a x a a a a x a a a a x D ---+=5．计算n 阶行列式。