苏教版九年级数学圆复习学案
苏教版九年级数学圆复习学案
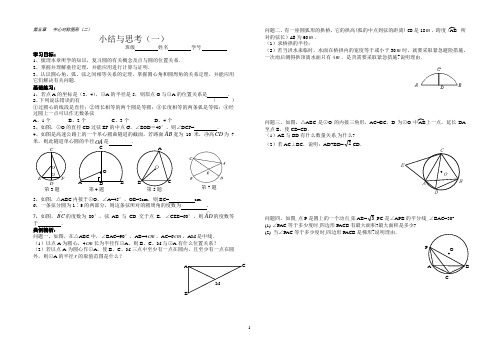
第4题 第五章 中心对称图形（二）小结与思考（一）班级 姓名 学号学习目标：1、梳理本章所学的知识，复习圆的有关概念及点与圆的位置关系．2、掌握并理解垂径定理，并能应用进行计算与证明．3、认识圆心角、弧、弦之间相等关系的定理，掌握圆心角和圆周角的关系定理，并能应用它们解决有关问题． 基础练习：1、若点A 的坐标是（3，4），⊙A 的半径是5，则原点O 与⊙A 的位置关系是 ．2、下列说法错误的有 （ ） ①过圆心的线段是直径；②周长相等的两个圆是等圆；③长度相等的两条弧是等弧；④经过圆上一点可以作无数条弦A 、1个B 、2个C 、3个D 、4个3、如图，⊙O 的直径CD 过弦EF 的中点G ，∠EOD ＝40°，则∠DCF= ．4、如图是高速公路上的一个单心圆曲隧道的截面，若路面AB 宽为10米，净高C D 为7米，则此隧道单心圆的半径O A 是 ．5、如图，△ABC 内接于⊙O ，∠A=45°，OB=2cm ，则BC= cm ．6、一条弦分圆为1∶5的两部分，则这条弦所对的圆周角的度数为 .7、如图，⋂BC 的度数为80°，弦AB 与CD 交于点E ，∠CEB=60°，则⋂AD 的度数等于 ． 典例精析：问题一、如图，在△ABC 中，∠BAC=90°，AB=4cm ，AC=6cm ，AM 是中线． （1）以点A 为圆心，4cm 长为半径作⊙A ，则B 、C 、M 与⊙A 有什么位置关系？（2）若以点A 为圆心作⊙A ，使B 、C 、M 三点中至少有一点在圆内，且至少有一点在圆外，则⊙A 的半径r 的取值范围是什么？问题二、有一座圆弧形的拱桥，它的拱高(弧的中点到弦的距离) CD 是18m ，跨度（ 所对的弦长）AB 为60m ． （1）求桥拱的半径；（2）若当洪水来临时，水面在桥拱内的宽度等于或小于30m 时，就要采取紧急避险措施，一次雨后测得拱顶离水面只有4m ．是否需要采取紧急措施?说明理由．问题三、如图，△ABC 是⊙O 的内接三角形，AC=BC ，D 为⊙O 上一点，延长DA 至点E ，使CE=CD ．（1）AE 与BD 有什么数量关系,为什么? （2）若AC ⊥BC ，说明：AD+BD=2CD ．问题四、如图,点P 是圆上的一个动点,弦AB=3,PC 是∠APB 的平分线, ∠BAC=30°. (1) ∠PAC 等于多少度时,四边形PACB 有最大面积?最大面积是多少? (2) 当∠PAC 等于多少度时,四边形PACB 是梯形?说明理由．A B CM第7题 C AB AB 第5题E F C DG O 第3题ＡA BC 图（a ） 图（b ） 图（c ）图3（d ） AAC D P课后作业：1、若小唐同学掷出的铅球在场地上砸出一个直径约为10 cm 、深约为2 cm 的小坑，则该铅球的直径约为 cm ．2、下列说法：①如图（a ），可以利用刻度尺和三角板测量圆形工件的直径；②如图（b ），可以利用直角曲尺检查工件是否为半圆形；③如图（c ），两次使用丁字尺（C D 所在直线垂直平分线段AB3、如上右图，⊙O 是△ABC 的内切圆，OD ⊥AB 于点D ，交⊙O 于点E ，∠C=60°，如果⊙O 的半径为2，则下列结论错误的是 （ ） A 、AD=DB B、 =C 、OD=1D 、AB=3 4、如图，⊙O 是A B C ∆的外接圆，点D 在⊙O 上，已知∠ACB=∠D ，BC=2,则AB 的长是__________． 5、如图，将半径为2cm 的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长为 ．6、如图，△ABC 内接于⊙O ，∠BAC =120°， AB =AC ，BD 为 ⊙O 的直径，AD =6，则BC ＝ .7、已知：如图，在⊙O 中,弦AB 、CD 交于点M 、AC 、DB 的延长线交于点N ，则图中相似三角形有________对8、如图,要把破残的圆片复制完整, 已知弧上的三点A 、B 、C ．（1）用尺规作图法，找出弧BC 所在圆的圆心O （保留作图痕迹，不写作法）； （2）设△ABC 是等腰三角形，底边BC = 10cm ，腰AB = 6 cm ，求圆片的半径R ．9、如图，已知PB 交⊙O 于点A ，PO 与⊙O 交于点C ，且PA=AB=6cm ，PO ＝12cm.． （1）求⊙O 的半径；（2）求△PBO 的面积．10、已知：如图等边A B C △内接于⊙O ，点P 是劣弧BC 上的一点（端点除外），延长B P 至D ，使B D A P =，连结C D ．（1）若AP 过圆心O ，如图①，请你判断PD C △是什么三角形？并说明理由． （2）若AP 不过圆心O ，如图②，PD C △又是什么三角形？为什么？11、如图1，半圆O 为△ABC 的外接半圆，AC 为直径，D 为 上的一动点． （1）问添加一个什么条件后，能使得B D B E B CB D=？请说明理由；（2）若AB ∥OD ，点D 所在的位置应满足什么条件？请说明理由；（3）如图，在 （1）和（2）的条件下，四边形AODB 是什么特殊的四边形？说明你的结论．第4题 第6题 N 第7题 图①D图②。
九年级数学苏科版上册 第二单元《单元复习》教学设计 教案
圆的复习课教师姓名年级九年级科目数学学生姓名上课时间课题第2章圆的复习课教学目标1.理解、掌握圆的有关性质、直线和圆的位置关系、圆和圆的位置关系、正多边形和圆的位置关系.2.探索、总结、归纳与圆有关的各种问题，进行知识梳理，构建圆的知识体系.3.渗透数形结合和分类的数学思想，并逐步学会用数学的眼光认识世界，学会有条理的表达、推理.教学重点和难点重点;与圆有关的知识点梳理.难点；会用圆的有关知识解决问题.1.圆有关的概念:圆的定义：到定点的距离等于定长的点的集合。
定义用来判断几点共圆，也可画出辅助圆解决问题.（1）圆心角：顶点在圆心的角叫做圆心角．（2）圆周角：顶点在圆上，并且两边都和圆相交的角叫做圆周角．（3）弧：圆上任意两点间的部分叫做圆弧，简称弧，大于半圆的弧称为优弧，小于半圆的弧称为劣弧．等弧是完全重合的弧，包括弧长和弧度（所对圆心角度数）,只能在同圆或等圆中.（4）弦：连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径．2.圆的有关的性质：（1）圆心角、弦和弧三者之间的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量分别相等.（2）垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧.（3）圆心角定理：圆心角的度数等于它所对弧的度数.（4）圆心角与圆周角的关系: 同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半．（5）圆周角定理：直径所对的圆周角是直角，反过来，90°的圆周角所对的弦是直径. （6）切线的判定：①经过半径的外端并且垂直于这条半径的直线是圆的切线；②圆心到直线的距离等于半径；③直线与圆只有唯一的公共点.方法：(无切点)作垂直，证半径;(有切点)连半径，证垂直.（7）切线的性质定理：圆的切线垂直于过切点的半径.（8）切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，这点与圆心的连线平分两切线的夹角；圆中常作的辅助线：已知切线，常过切点作半径；已知直径，常作直径所对的圆周角. 求解有关弦的问题，作弦心距，借助垂径定理和勾股定理解决；弧的中点常和圆心连结.B IAC圆中作辅助线的解题思路：利用垂径定理勾股定理、相似三角形，同弧所对的圆周角相等，以及圆周角与圆心角之间的关系.若题目中只配有一幅图，有时不代表就只有一解.要注意题目中的条件：比如动点，直线等等字眼.油的截面问题是有图一解，无图两解. 3．三角形的内心和外心(1)确定圆的条件：不在同一直线上的三个点确定一个圆． (2) ①外心：三边中垂线的交点.② 性质:(1)OA=OB=OC.（2）外心不一定在三角形的内部． ③ 应用:∠BOC=2∠A.(3) ①三角形的内心：三角形三条角平分线的交点.②性质（a ）到三边的距离相等；（b ）IA 、IB 、IC 分别平分∠BAC 、∠ABC 、∠ACB ； （c ）内心在三角形内部．③应用∠BIC=900+21∠A(三角形内角和角平分线得)；S ⊿ABC =21C ⊿ABC r 内切.任意多边形的内切圆的半径与面积和周长公式之间的关系：S=21CR ．(4)直角三角形中,∠C=90°, R 外接=21c, r 内切=21(a+b-c)=c b a ab++.(5)等边三角形中边长为a R 外接=33a ，r 内切=63a, h=23a, s=243a .4.点与圆的位置关系：点在圆外，点在圆上，点在圆内，设圆的半径为r ，点到圆心的距离为d ，则点在圆外⇔d ＞r ．点在圆上⇔d=r ．点在圆内⇔d ＜r ．5．直线和圆的位置关系有三种：相交、相切、相离． 设圆的半径为r ，圆心到直线的距离为d ，则直线与圆相交⇔d ＜r ，直线与圆相切⇔d=r ，直线与圆相离⇔d ＞r. 6.圆与圆的位置关系:设两圆的圆心距为d ，两圆的半径分别为R 和r ，则⑴ 两圆外离⇔d ＞R+r ； ⑵ 两圆外切⇔d=R ＋r ；⑶ 两圆相交⇔R －r ＜d ＜R+r （R ＞r ）; ⑷ 两圆内切⇔d=R －r （R ＞r ）;⑸ 两圆内含⇔d ＜R —r （R ＞r ）（R 与r 大小不定加绝对值）. 判断两圆位置关系：圆心距、两圆半径和、两圆半径差（绝对值）直线与圆是相离、相切、相交，圆与圆相离包含外离和内含，相切包括内切和外切n ︒r S180r n l π＝弧长2扇形R π360n S =lR21=7.圆有关的计算:(1)(2)360l rn •=圆锥侧面展开图（扇形）1、h 2+r 2=l 22、S 侧 =πrl3、l 即为R, 圆锥母线长是展开图扇形半径（大半径），r 是底面圆小半径，看清楚求的是扇形面积还是弧长，面积是360作分母，弧长是180作分母。
苏教版九年级数学圆复习学案
图2 O B Q A PRO RB Q A P 图1 第五章 中心对称图形（二）小结与思考（二）班级 姓名 学号 学习目标： 1、梳理本章所学的知识，复习直线和圆的位置关系． 2、了解切线的概念，会利用切线的性质与判定进行有关计算和证明，发展推理能力． 3、了解三角形的内切圆、切线长的概念，能利用切线长的性质解决有关问题． 基础练习: 1、⊙O 的半径为5㎝，点A 在直线l 上，如果OA=5㎝，那么直线l 与⊙O的位置关系() A 、相切 B 、相交 C 、相离 D 、相切或相交2、直角坐标系中，以P （2，1）为圆心，r 为半径的圆与坐标轴恰好有三个公共点，则r 的值为 ．3、下列说法正确的是 （ ）A 、垂直于圆的半径的直线是圆的切线B 、经过半径外端的直线是圆的切线C 、直线上一点到圆心的距离等于圆的半径的直线是圆的切线D、到圆心的距离等于圆的半径的直线是圆的切线4的直径，点D 在AB 的延长O 的切线，切点为C ，若∠______．5、为了测量一个圆铁环的半径，某同学用了如下方法，将铁环平放在水平桌面上，用有一个角为30°的直角三角板和刻度尺按如图所示的方法得到相关数据，进而求出铁环半径，若测得PA=5cm ，则铁环的半径是 cm ． 6、如图，⊙O 内切于ABC △，切点分别为D 、E 、F ．已知∠A=70°，连结DE 、DF 、BO 、CO ，，那么∠EDF = ；∠BOC= ． 典型例题: 问题一、在同一平面内,已知点O 到直线l 的距离为5．以O 为圆心,r 为半径画圆．探索、归纳： （1）当r = 时，⊙O 上有且只有1个点到直线l 的距离等于3； （2）当r = 时，⊙O 上有且只有3个点到直线l 的距离等于3；（3）随着r 的变化，⊙O 上到直线l 的距离等于3的点的个数有哪些变化？ 问题二、一位小朋友在粗糙不打滑的“Z ”字形平面轨道上滚动一个半径为10cm 的圆盘，如图所示，AB 与C D 是水平的，BC 与水平面的夹角为600，其中AB=60cm ，CD=40cm ，BC=40cm ，请你作出该小朋友将圆盘从A 点滚动到D 点其圆心所经过的路线的示意图，并求出此路线的长度． 问题三、有这样一道习题：如图1，已知OA 和OB 是⊙O 的半径，并且OA ⊥OB ，P 是OA 上任一点(不与O 、A 重合)，BP 的延长线交⊙O 于Q ，过Q 点作⊙O 的切线交OA 的延长线于R .说明：RP ＝RQ ． 请探究下列变化： 变化一：交换题设与结论. 已知：如图1，OA 和OB 是⊙O 的半径，并且OA ⊥OB ，P 是OA 上任一点(不与O 、A 重合)，BP 的延长线交⊙O 于Q ，R 是OA 的延长线上一点，且RP ＝RQ ．说明：RQ 为⊙O 的切线．变化二：运动探求. 1．如图2，若OA 向上平移，变化一中的结论还成立吗？(只需交待判断) 2．如图3，如果P 在OA 的延长线上时，BP 交⊙O 于Q ，过点Q 作⊙O 的切线交OA 的延长线于R ，原题中的结论还成立吗？为什么？3．若OA 所在的直线向上平移且与⊙O 无公共点，4，并判断结论是否) M 与x 轴M 的直径，过点C 的直，已知点M 的坐标为OB图3第4题第5题A P 60° 30°第2题ＡＢＯ第3题 图1 (0，直线CD 的函数解析式为y =-+（1）求点D 的坐标和BC 的长； （2）求点C 的坐标和⊙M 的半径； （3）说明：CD 是⊙M 的切线．课后作业：1、若边长为2的等边三角形ABC 内接于⊙Ｏ，外切于⊙I ，则⊙Ｏ的半径是_______，⊙I 的半径是_______．2、如图，PA 切 ⊙O 于点A,PO 交⊙Ｏ于B ，延长PO 交⊙Ｏ于C, OB=PB=1，OA 绕点O 逆时针方向旋转60°到OD ，则PD 的长为 ．3、如图，已知直线l 的解析式是434-=x y ，并且与x 轴、y 轴分别交于A 、B 两点．一个半径为1.5的⊙C,圆心C 从点（0，1.5）开始以每秒0.5个单位的速度沿着y 轴向下运动,当⊙C 与直线l 相切时,则该圆运动的时间为 ．4、如图，AC ⊥BC 于点C ，BC =a ，CA =b ，AB =c ，⊙O 与直线AB 、 BC 、CA 都相切，则⊙O 的半径等于 ．5、如图，在ABC △中，10AB =，8AC =，6BC =，经过点C 且与边AB 相切的动圆与CA CB ，分别相交于点P Q ，，则线段PQ 长度的最小值是 ．8、如图，A 是半径为12cm 的⊙O 上的定点，动点P 从A 出发，以2πcm/s 的速度沿圆周逆时针运动，当点P 回到A 点立即停止运动．（1）如果90POA ∠=，求点P 运动的时间； （2）如果点B 是OA 延长线上的一点，AB OA =，那么当点P 运动的时间为2s 时，判断直线BP 与⊙O 的位置关系，并说明理由．9、如图，在△ABC 中，AB=AC ，内切圆O 与边BC 、AC 、AB 分别切于D 、E 、F. （1）求证：BF=CE ；（2）若∠C=30°，CE =AC ．10、已知：如图，ABC △中，CA CB =，点D 为AC 的中点，以AD 为直径的⊙O 切BC 于点E ，2AD =． （1）求BE 的长；（2）过点D 作DF BC ∥交⊙O 于点F ，求DF 的长．11、已知如图，点D 是以AB 为直径的圆O 上任意一点，且不与点A 、B 重合，点C 是弧BD 的中点，过C 作CE ∥AB ，交AD 或其延长线于E ，连结BE 交AC 于G ．(1)求证：AE ＝CE ；(2)若过点C 作CM ⊥AD 交AD 的延长线于点M ， 试说明：MC 与⊙O 相切；(3)若CE ＝7，CD ＝6，求EG 的长．12、如图，在平面直角坐标系xoy 中，M 是x 轴正半轴上一点，⊙M 与x 轴的正半轴交于A B ，两点，A 在B 的左侧，且OA OB ，的长是方程212270x x -+=的两根，ON 是⊙M 的切线，N 为切点，N 在第四象限．（1）求⊙M 的直径；（2）求直线ON 的解析式； （3）在x 轴上是否存在一点T ，使O T N △是等腰三角形，若存在请在图2中标出T 点所在位置，并画出（要求尺规作图，保留作图痕迹，不第5题第4题。
苏科版九上 圆周角复习 教案
初三数学教学案执笔：汪荣跃审核：初三数学备课组课题：§5.3圆周角课型：复习时间：〖学习过程〗第一部分：复习相关知识1.顶点在_______，并且________都和圆相交的角叫做圆周角.2.在同圆或等圆中，同弧或等弧所对的圆周角_________，都等于该弧所对的圆心角的________.3.直径(或半圆)所对的圆周角是________，90°的圆周角所对的弦是_________。
第二部分：巩固练习一、填空题或选择题1.如图，△ABC的3个顶点都在⊙O上，∠ACB=40°，则∠AOB=_______，∠OAB=_____。
2.如图，点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，在这8个角中，有几对相等的角？请把它们分别表示出来：___________________________________________________.3.如图，AB是⊙O的直径，∠BOC=120°，CD⊥AB，则∠ABD＝___________。
4.如图，△ABC的3个顶点都在⊙O上，∠BAC的平分线交BC于点D，交⊙O于点E，则与△ABD相似的三角形有______________________。
5.已知，∠BOC=100°,∠BAC=( )A. 100°B. 130°C. 50°D. 80°6.如图，△ABC的顶点都在⊙O上，若∠BOC=120°，则∠BAC=( )A. 60°B. 90°C. 120°D. 150°7.如图，AB、AC是⊙O的弦，延长CA到点D，使AD=AB，若∠D＝20°，则∠BOC等于( )A. 20°B.40°C.80°D.120°8.如图，AB是半圆O的直径，∠BAC＝32°，D是AC的中点，∠DAC=________.9.已知⊙O的弦AB所对的圆心角∠AOB＝60°,该弦所对的圆心角大小为___________.10.在⊙O中，圆心角∠AOB＝56°，弦AB所对的圆心角等于( )A.28°B.112°C.28°或152°D.124°或56°11.在Rt△ABC中，∠C=90°，以AC为直径的⊙O与斜边AB相交于点D，若AC＝4cm，BC=3cm，则CD=________cm，O到AB的距离为___________cm。
2019-2020学年九年级数学上册 2.1 圆学案(1)(新版)苏科版.doc
2019-2020学年九年级数学上册 2.1 圆学案（1）（新版）苏科版学习目标：1．理解圆的定义（圆的描述概念和圆的集合概念）；2．掌握点和圆的三种位置关系；3．会利用点到圆心的距离和圆的半径之间的数量关系判定点和圆的位置关系；4．初步会运用圆的定义证明四个点在同一个圆上．学习重、难点：确定点和圆的三种位置关系以及圆的集合概念的理解；点和圆的三种位置关系的理解和应用．学习过程：一、问题导入圆的描述定义：把一条线段OP的一个端点O固定，线段OP绕点O在平面内旋转一周，另一个端点P所形成的图形叫做_______．其中，定点O叫_______，线段OP叫_______．以点O为圆心的圆，记作_______，读作_______．注：（1）确定一个圆的两个要素是_______和________；（2）以定点A为圆心作圆，能作_______个圆；（3）以定长r为半径作圆，能作_______个圆；（4）以定点A为圆心、定长r为半径作圆，能且只能作_______个圆；（5）圆心确定_______，半径确定_______．二、自学探究1．操作与思考：请你在圆上任取3个点，分别量出这三个点到圆心的距离，你发现了什么？小结：（1）圆上的点到圆心的距离都_______半径；到圆心的距离等于半径的点都在圆______．（2）满足上述两个条件，我们可以把圆看成是一个集合．即圆是__________________________________________________．(圆的集合定义)请你在圆内任取3个点，分别量出这三个点到圆心的距离，你发现了什么？小结：（1）圆内的点到圆心的距离都_______半径；到圆心的距离小于半径的点都在圆______．（2）圆的内部是到圆心的距离______半径的点的集合．请你在圆外任取3个点，分别量出这三个点到圆心的距离，你发现了什么？小结：（1）圆外的点到圆心的距离都_______半径；到圆心的距离大于半径的点都在圆______．（2）圆的外部是到圆心的距离______半径的点的集合．因此，我们得到如下结论：2．尝试交流：已操作：（1）画线段PQ，使PQ=2 cm；（2）画出下列图形：到点P的距离等于1 cm的点的集合；到点Q的距离等于1.5 cm的点的集合．（3）在所画图中，到点P的距离等于1 cm，且到点Q的距离等于1.5 cm的点有几个？请在图中将它们表示出来．（4）在所画图中，到点P的距离小于或等于1 cm，且到点Q的距离大于或等于1.5 cm的点的集合是怎样的图形？把它画出来．三、学以致用活动一：已知⊙O的半径为5cm，A为线段OP的中点，当OP满足下列条件时，分别指出点A和⊙O的位置关系：（1）OP＝6cm；（2）OP＝10cm；（3）OP＝14cm．活动二：已知RT△ABC，AC=3 cm，BC=4 cm，CD是斜边AB上的高．以点C为圆心，3 cm长度为半径画圆，判断点A、B、D与⊙C的位置关系．活动三：已知：如图，AC⊥BC，AD⊥BD．求证：点A、B、C、D在同一个圆上．四、当堂检测1．已知⊙O 的半径为4 cm ．如果点P 到圆心O 的距离为4.5 cm ，那么点P 与⊙O 有怎样的位置关系？如果点P 到圆心O 的距离分别为4 cm 、3 cm 呢？2．用图形表示到点A 的距离小于或等于2 cm 的点的集合．3．如图，已知矩形ABCD 的边AB =3 cm ，AD =4 cm （直接写出答案）（1）以点A 为圆心，3厘米为半径作圆A ，则点B 、C 、D 与圆A 的位置关系如何？（2）以点A 为圆心，4厘米为半径作圆A ，则点B 、C 、D 与圆A 的位置关系如何？（3）以点A 为圆心，5厘米为半径作圆A ，则点B 、C 、D 与圆A 的位置关系如何？4．已知矩形ABCD 的对角线AC 、BD 相交于点O ．点A 、B 、C 、D 是否在以点O 为圆心的同一个圆上？为什么？五、课后反馈A 组题：1．已知⊙O 的直径为6 cm ，且点P 在⊙O 内，线段PO 的长度范围是（） A ．小于6 cm B ．6 cm C ．3 cm D ．小于3 cm2．两圆的圆心都是O ，半径分别是1r 、2r （21r r <）．若21r op r <<，则（） A ．点P 在大圆外、小圆外B ．点P 在大圆内、小圆外C ．点P 在大圆外、小圆内D ．点P 在大圆内、小圆内3．在直径AB =5 cm 的圆上，到AB 的距离为2.5 cm 的点有（ ）A ．无数个B ．1个C ．2个D ．4个 B 组题： 4．在Rt △ABC 中，∠C =90°，AC =2 cm ，BC =4 cm ，若以C 为圆心，2 cm 为半径作圆，•则点A 在⊙C _______，点B 在⊙C ________．若以AB 为直径作⊙O ，则点C 在⊙O ________．5．有一张矩形的纸片，AB =3 cm ，AD =4 cm,若以A 为圆心作圆，并且要使点D 在⊙A 内，而点C 在⊙A 外，A CD⊙A的半径r的取值范围是_____________．6．设AB=5 cm，点C在边AB上，且AC=2 cm，分别画出具有下列性质的点的集合的图形：（1）和点C的距离为2 cm的点的集合；（2）和点A的距离为3 cm的点的集合；（3）和点B、C的距离都为2 cm的点的集合．C组题：7.（1）矩形ABCD的对角线AC、BD相交于点O.求证：点A、B、C、D在以点O为圆心的圆上．（2）如果E、F、G、H分别为OA、OB、OC、OD的中点，求证：点E、F、G、H在同一个圆上．。
苏科版九年级数学第二章圆期末复习(自主复习学案)
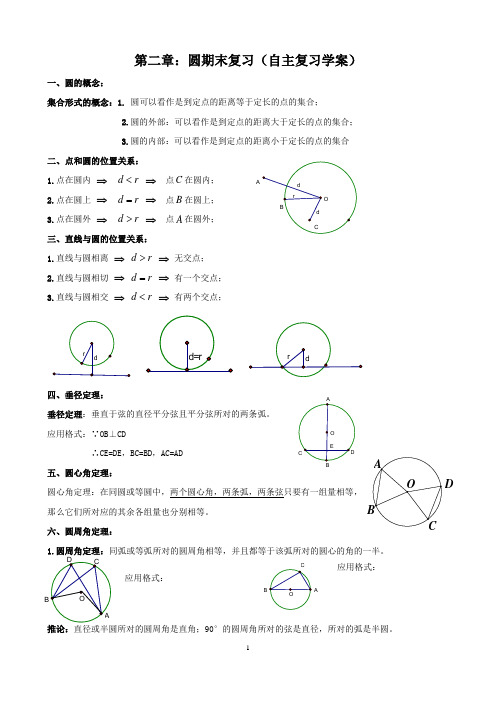
D第二章：圆期末复习（自主复习学案）一、圆的概念：集合形式的概念：1. 圆可以看作是到定点的距离等于定长的点的集合； 2.圆的外部：可以看作是到定点的距离大于定长的点的集合； 3.圆的内部：可以看作是到定点的距离小于定长的点的集合 二、点和圆的位置关系：1.点在圆内 ⇒ d r < ⇒ 点C 在圆内；2.点在圆上 ⇒ d r = ⇒ 点B 在圆上；3.点在圆外 ⇒ d r > ⇒ 点A 在圆外； 三、直线与圆的位置关系：1.直线与圆相离 ⇒ d r > ⇒ 无交点；2.直线与圆相切 ⇒ d r = ⇒ 有一个交点；3.直线与圆相交 ⇒ d r < ⇒ 有两个交点；四、垂径定理：垂径定理：垂直于弦的直径平分弦且平分弦所对的两条弧。
应用格式：∵OB ⊥CD∴CE=DE ，BC=BD ，AC=AD 五、圆心角定理：圆心角定理：在同圆或等圆中，两个圆心角，两条弧，两条弦只要有一组量相等， 那么它们所对应的其余各组量也分别相等。
六、圆周角定理：1.圆周角定理：同弧或等弧所对的圆周角相等，并且都等于该弧所对的圆心的角的一半。
推论：直径或半圆所对的圆周角是直角；90°的圆周角所对的弦是直径，所对的弧是半圆。
AB BA应用格式：应用格式：七、圆内接四边形：圆的内接四边形定理：圆的内接四边形的对角互补，外角等于它的内对角。
八、切线的性质与判定定理：（1）切线的判定定理：经过半径的外端并且垂直于半径的直线是圆的切线。
（2）性质定理：切线垂直于经过切点的半径。
（如上图）九、切线长定理切线长定理：从圆外一点画圆的两条切线，它们的切线长相等，并且这点与圆心的连线平分两条切线的夹角。
应用格式：∵PA 、PB 与⊙O 相切 ∴PA PB =，PO 平分BPA ∠ 十、三角形的三心（外心、内心、重心）：1.外心：外接圆的圆心，即各边垂直平分线的交点。
到各顶点的距离相等。
2.内心：内切圆的圆心，即各角平分线的交点。
九年级数学上册 圆(一)学案苏科版
中心对称图形（二）4.1圆(一)班级姓名学号学习目标1、理解、掌握圆的定义.2、经历探索点与圆的位置关系的过程，以及如何确定点和圆的三种位置关系.3、初步渗透数形结合和转化的数学思想，并逐步学会用数学的眼光和运动、集合的观点去认识世界、解决问题.学习重点：理解、掌握圆的概念.学习难点：会确定点和圆的位置关系.教学过程一、情境引入：思考：平面上的一个圆把平面上的点分成哪几部分？二、探究学习：1．尝试：量一量（1）利用圆规画一个⊙O，使⊙O的半径r=3cm.（2）在平面内任意取一点P，点与圆有哪几种位置关系？若⊙O的半径为r，点P到圆心O的距离为d，那么：①点P在圆 d r②点P在圆 d r③点P在圆 d2．概括总结．（1）圆是到定点距离定长的点的集合.（2）圆的内部是到的点的集合；（3）圆的外部是的点的集合。
3.典型例题：例1、已知点P、Q，且PQ=4cm，⑴画出下列图形：到点P的距离等于2cm的点的集合；到点Q的距离等于3cm的点的集合。
⑵在所画图中，到点P的距离等于2cm，且到点Q的距离等于3cm的点有几个？请在图中将它们表示出来。
⑶在所画图中，到点P的距离小于或等于2cm，且到点Q的距离大于或等于3cm的点的集合是怎样的图形？把它画出来。
例2．如图，在直角三角形ABCD中，角C为直角，AC=4，BC=3，E，F分别为AB，AC的中点。
⇔⇔⇔F CBAP Q以B为圆心，BC为半径画圆，试判断点A，C，E，F与圆B的位置关系。
4.巩固练习（1）⊙O的半径10cm，A、B、C三点到圆心的距离分别为8cm、10cm、12cm，则点A、B、C与⊙O的位置关系是：点A在；点B在；点C在。
（2）⊙O的半径6cm，当OP=6时，点A在；当OP 时点P在圆内；当OP 时，点P不在圆外。
（3）正方形ABCD的边长为2cm，以A为圆心2cm为半径作⊙A，则点B在⊙A ；点C在⊙A ；点D在⊙A 。
（4）已知AB为⊙O的直径P为⊙O 上任意一点，则点关于AB的对称点P′与⊙O的位置为( )(A)在⊙O内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定三、归纳总结：（1）圆的定义。
九年级数学上册 第2章 对称图形—圆复习导学案(新版)苏科版
第二章圆班级姓名一、学习目标1．理解、掌握圆的有关性质、点和圆直线和圆的位置关系，切线的判定和性质2．探索、总结、归纳与圆有关的各种问题，进行知识梳理，构建圆的知识体系.3．渗透数形结合和分类的数学思想，并逐步学会用数学的眼光认识世界、解决问题，学会有条理的表达、推理.二、学习重点：与圆有关的知识的梳理.三、学习难点：会用圆的有关知识解决问题.四、教学过程（一）、1、点与圆的位置关系2、直线与圆的位置关系例1. 在Rt△ ABC中，∠C=90°,BC=3cm,AC=4cm,D为AB的中点，E为AC的中点，以B为圆心，BC为半径作⊙B，问：（1）A、C、D、E与⊙B的位置关系如何？（2）AB、AC与⊙B的位置关系如何？（二）、1、过三点的圆及外接圆2、三角形的内切圆1.过______________可以确定一个圆2.锐角三角形的外心在三角形____，直角三角形的外心在三角形____，钝角三角形的外心在三角形____。
3.外心到___________________的距离相等，是________________________的交点；内心到______________________的距离相等,是_______________________的交点4. Rt△ ABC三边的长为a、b、c，则内切圆的半径是r=_______，外接圆的半径=_______5. 边长分别为3,4,5的三角形的内切圆半径与外接圆半径的比为( )A.1∶5B.2∶5C.3∶5D.4∶56.已知△ABC，AC=12，BC=5，AB=13。
则△ABC的外接圆半径为。
7. 正三角形的边长为a,它的内切圆和外接圆的半径分别是____, ____8．如图，直角坐标系中一条圆弧经过网格点A，B，C，其中B点坐标为（4，4），则该圆弧所在圆的圆心坐标为。
（三）、垂径定理（涉及半径、弦、弦心距、平行弦等）例2．如图4，⊙M 与x 轴相交于点A （2，0），B （8，0），与y 轴相切于点C ，则圆心M 的坐标是 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
D C B 第五章 中心对称图形（二）
小结与思考（二）
班级 姓
名 学号 学习目标：
1、梳理本章所学的知识，复习直线和圆的位置关系．
2、了解切线的概念，会利用切线的性质与判定进行有关计算和证明，发展推理能力．
3、了解三角形的内切圆、切线长的概念，能利用切线长的性质解决有关问题． 基础练习:
1、⊙O 的半径为5㎝，点A 在直线l 上，如果5㎝，那么直线l
位置
关
系
(
A 、相切
B 、相交
C 、相离
D 、相切或相交
2、直角坐标系中，以P （2，1）为圆心，r 为半径的圆与坐标轴恰好有三个公共点，则r 的值为 ．
3、下列说法正确的是 （ ）
A 、垂直于圆的半径的直线是圆的切线
B 、经过半径外端的直线是圆的切线
C 、直线上一点到圆心的距离等于圆的半径的直线是圆的切线
D 、到圆心的距离等于圆的半径的直线是圆的切线
4、如图，AB 是⊙O 的直径，点D 在AB 的延长线上，过点D 作⊙
O 的切线，切点为C ，若25A =∠，则D =∠．
5、为了测量一个圆铁环的半径，某同学用了如下方法，将铁环平放在水平桌面上，用有一个角为30°的直角三角板和刻度尺
A 第4第6题 第5题 A P 60° 30°
图2 O B Q A P R
O R B
Q A P 图1 按如图所示的方法得到相关数据，进而求出铁环半径，若测得5，则铁环的半径是 ．
6、如图，⊙O 内切于ABC △，切点分别为D 、E 、F ．已知∠70°，连结、、、，，那么∠ = ；∠ ． 典型例题:
问题一、在同一平面内,已知点O 到直线l 的距离为5．以O 为圆心,r 为半径画圆．探索、归纳：
（1）当r = 时，⊙O 上有且只有1个点到直线l 的距离等于3；
（2）当r = 时，⊙O 上有且只有3个点到直线l 的距离等于3；
（3）随着r 的变化，⊙O 上到直线l 的距离等于3的点的个数有哪些变化？
问题二、一位小朋友在粗糙不打滑的“Z ”字形平面轨道上滚动一个半径为10的圆盘，如图所示，与C D 是水平的，与水平面的夹角为600，其中60，40，40，请你作出该小朋友将圆盘从A 点滚动到D 点其圆心所经过的路线的示意图，并求出此路线的
长度．
问题三、有这样一道习题：如图1，已知和是⊙O 的半径，并且⊥，P 是上任一点(不与O 、A 重合)，的延长线交⊙O 于Q ，过
Q 点作⊙O 的切线交的延长线于R .说明：＝．
请探究下列变化： 变化一：交换题设与结论.
已知：如图1，和是⊙O 的半径，并且⊥，P 是上任一点(不与O 、
A 重合)，的延长线交⊙O 于Q ，R 是的延长线上一点，且＝．
说明：为⊙O 的切线．
O P B
Q A R 图3
• O
A
图4
第2题
第3题
A M
O B C D y x
变化二：运动探求.
1．如图2，若向上平移，变化一中的结论还成立吗？(只需交待判断)
2．如图3，如果P 在的延长线上时，交⊙O 于Q ，过点Q 作⊙
O 的切线交的延长线于R ，原题中的结论还成立吗？为什么？
3．若所在的直线向上平移且与⊙O 无公共点，请你根据原题中的条件完成图4，并判断结论是否还成立？ (只需交待判断)
问题四、如图，在平面直角坐标系中，⊙M 与x 轴交于A B ，两点，
AC 是⊙M 的直径，过点C 的直线交x 轴于点D ，连结BC ，已知点M 的坐标为(03)，，直线CD 的函数解析式为353y
x ． （1）求点D 的坐标和BC 的长；
（2）求点C 的坐标和⊙M 的半径；
（3）说明：CD 是⊙M 的切线．
课后作业：
1、若边长为2的等边三角形内接于⊙Ｏ，外切于⊙I ，则⊙Ｏ的半径是，⊙I 的半径是．
2、如图，切 ⊙O 于点交⊙Ｏ于B ，延长交⊙Ｏ于C, 1，绕点O 逆时针方向旋转60°到，则的长为 ．
3、如图，已知直线l 的解析式是43
4
-=
x y ，并且与x 轴、y 轴
分别交于A 、B 两点．一个半径为1.5的⊙C,圆心C 从点（0，1.5）开始以每秒0.5个单位的速度沿着y 轴向下运动,当⊙C 与直线l 相切时,则该圆运动的时间为 ．
4、如图，⊥于点C ，，，，⊙O 与直线、 、都相切，则⊙O 的半径等于 ．
5、如图，在ABC △中，10AB =，8AC =，6BC =，经过点C 且与边AB 相切的动圆与CA CB ，分别相交于点P Q ，，则线段PQ 长度的最小值是 ．
8、如图，A 是半径为12cm 的⊙O 上的定点，动点P 从A 出发，以
2πcm/s 的速度沿圆周逆时针运动，当点P 回到A 点立即停止运动．
第5题
A
B
C
Q
P
第4题
Ａ Ｐ Ｂ
Ｏ
（1）如果90POA ∠=，求点P 运动的时间；
（2）如果点B 是OA 延长线上的一点，AB OA =，那么当点P 运动的时间为2s 时，判断直线BP 与⊙O 的位置关系，并说明理由．
9、如图，在△中，，内切圆O 与边、、分别切于D 、E 、F. （1）求证：；
（2）若∠30°，3CE =
10、已知：如图，ABC △中，CA CB =，点D 为AC 的中点，以AD 为直径的⊙O 切BC 于点E ，2AD =． （1）求BE 的长；（2）过点D
作DF BC ∥交⊙O 于点F ，求DF 的长．
11、已知如图，点D 是以为直径的圆O 上任意一点，且不与点
A 、
B 重合，点
C 是弧的中点，过C 作∥，交或其延长线于E ，
连结交于G ． (1)求证：＝；
(2)若过点C 作⊥交的延长线于点M ， 试说明：与⊙O 相切； (3)若＝7，＝6，求的长．
12、如图，在平面直角坐标系xoy 中，M 是x 轴正半轴上一点，⊙M 与x 轴的正半轴交于A B ，两点，A 在B 的左侧，且OA OB ，的长是方程212270x x -+=的两根，ON 是⊙M 的切线，N 为切点，N 在第四象限．
（1）求⊙M 的直径；
（2）求直线ON 的解析式；
A B C E D
F O
G
M E C O
D
（3）在x轴上是否存在一点T，使OTN
△是等腰三角形，若存在
T OTN
△
图1
图2。