决策树例题分析及解答 1
决策树习题练习(答案)

决策树习题练习(答案)决策树习题练习答案1.某投资者预投资兴建一工厂,建设方案有两种:①大规模投资300万元;②小规模投资160万元。
两个方案的生产期均为10年,其每年的损益值及销售状态的规律见表15。
试用决策树法选择最优方案。
表1 各年损益值及销售状态销售状态概率损益值(万元/年)大规模投资小规模投资销路好 0.7100 60 销路差 0.3 -2020【解】(1)绘制决策树,见图1;100×10 -20×10 60×1020×10 销路好0.7 销路差(0.3)销路好0.7 销路差(0.3)大规模小规模 340 340 3202 31 图1 习题1决策树图(2)计算各状态点的期望收益值节点②:节点③:将各状态点的期望收益值标在圆圈上方。
(3)决策比较节点②与节点③的期望收益值可知,大规模投资方案优于小规模投资方案,故应选择大规模投资方案,用符号“//”在决策树上“剪去”被淘汰的方案。
2.某项目有两个备选方案A和B,两个方案的寿命期均为10年,生产的产品也完全相同,但投资额及年净收益均不相同。
A方案的投资额为500万元,其年净收益在产品销售好时为150万元,,销售差时为50万元;B方案的投资额为300万元,其年净收益在产品销路好时为100万元,销路差时为10万元,根据市场预测,在项目寿命期内,产品销路好时的可能性为70%,销路差的可能性为30%,试根据以上资料对方案进行比选。
已知标准折现率ic=10%。
【解】(1)首先画出决策树150 5010010 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -3002 31 图2 决策树结构图此题中有一个决策点,两个备用方案,每个方案又面临着两种状态,因此可以画出其决策树如图18。
(2)然后计算各个机会点的期望值机会点②的期望值=150(P/A,10%,10)×0.7+(-50)(P/A,10%,10)×0.3=533(万元) 机会点③的期望值=100(P/A,10%,10)×0.7+10(P/A,10%,10)×0.3=448.5(万元) 最后计算各个备选方案净现值的期望值。
决策树例题分析

• 建设小工厂投资280万元,如销路好,3年后扩建,扩建需要投资400万元, 可使用7年,每年赢利190万元。不扩建则每年赢利80万元。如销路不好则 每年赢利60万元。
• 试用决策树法选出合理的决策方案。 经过市场调查,市场销路好的概率为 0.7,销路不好的概率为0.3。
5
• 计算完毕后,开始对决策树进行剪枝,在每个决策结点删去除 了最高期望值以外的其他所有分枝,最后步步推进到第一个决 策结点,这时就找到了问题的最佳方案
• 方案的舍弃叫做修枝,被舍弃的方案用“≠”的记号来表示,最 后的决策点留下一条树枝,即为最优方案。
6
• A1、A2两方案投资分别为450万和240万,经营年限为5年,销 路好的概率为0.7,销路差的概率为0.3,A1方案销路好、差年 损益值分别为300万和负60万;A2方案分别为120万和30万。
1
例:设某茶厂计划创建精制茶厂,开始有两个方案,方案一是建年加工能力 为800担的小厂,方案二是建年加工能力为2000担的大厂。两个厂的使用期 均为10年,大厂投资25万元,小厂投资10万元。产品销路没有问题,原料来 源有两种可能(两种自然状态):一种为800担,另一种为2000担。两个方案每 年损益及两种自然状态的概率估计值见下表
自然状态
原料800担 原料2000担
概率 建大厂(投资25万元) 建小厂(投资10万元)
0.8
13.5
0.2
25.5
15.0 15.0
2
补充: 风险型决策方法——决策树方法
• 风险决策问题的直观表示方法的图示法。因为图的形状像树,所以被称为决 策树。
决策树决策表练习题与参考答案

1.某厂对一部分职工重新分配工作,分配原则是:
⑴年龄不满20岁,文化程度是小学者脱产学习,文化程度是中学者当电工;
⑵年龄满20岁但不足50岁,文化程度是小学或中学者,男性当钳工,女性当车工;文化程度是大专者,当技术员。
⑶年龄满50岁及50岁以上,文化程度是小学或中学者当材料员,文化程度是大专者当技术员。
优化后的决策表如下:
2、试画出某企业库存量监控处理的判断树。
若库存量≤0,按缺货处理;若库存量≤库存下限,按下限报警处理;若库存量>库存下限,而又≤储备定额,则按订货处理;若库存量>库存下限,而又>储备定额,则按正常处理;若库存量≥库存上限,又>储备定额,则按上限报警处理。
3某货运站收费标准如下:
若收件地点在本省,则快件6元/公斤,慢件4元/公斤;
若收件地点在外省,则在25公斤以内(包括25公斤),快件8元/公斤,慢件6元/公斤;而超过25公斤时,快件10元/公斤,慢件8元/公斤;
画出决策表和决策树:
决策表:
优化后的结果如下所示:决策树:
收费
本省
外省快件
慢件
快件
慢件
≤25斤
>25斤
≤25斤
>25斤
6元
4元
8元
10元
6元
8元
地点规格重量收费金额
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求。
决策树习题练习(答案)

决策树习题练习答案1.某投资者预投资兴建一工厂,建设方案有两种:①大规模投资300万元;②小规模投资160万元。
两个方案的生产期均为10年,其每年的损益值及销售状态的规律见表15。
试用决策树法选择最优方案。
【解】(1)绘制决策树,见图1;(2)计算各状态点的期望收益值节点②:[]10300340()⨯⨯⨯-=1000.7+(-20)0.3万元 节点③:[]10160320()⨯⨯⨯-=600.7+200.3万元 将各状态点的期望收益值标在圆圈上方。
(3)决策比较节点②与节点③的期望收益值可知,大规模投资方案优于小规模投资方案,故应选择大规模投资方案,用符号“//”在决策树上“剪去”被淘汰的方案。
表1 各年损益值及销售状态2.某项目有两个备选方案A和B,两个方案的寿命期均为10年,生产的产品也完全相同,但投资额及年净收益均不相同。
A方案的投资额为500万元,其年净收益在产品销售好时为150万元,,销售差时为50万元;B方案的投资额为300万元,其年净收益在产品销路好时为100万元,销路差时为10万元,根据市场预测,在项目寿命期内,产品销路好时的可能性为70%,销路差的可能性为30%,试根据以上资料对方案进行比选。
已知标准折现率i c=10%。
【解】(1)首先画出决策树此题中有一个决策点,两个备用方案,每个方案又面临着两种状态,因此可以画出其决策树如图18。
(2)然后计算各个机会点的期望值机会点②的期望值=150(P/A,10%,10)×0.7+(-50)(P/A,10%,10)×0.3=533(万元)机会点③的期望值=100(P/A,10%,10)×0.7+10(P/A,10%,10)×0.3=448.5(万元)最后计算各个备选方案净现值的期望值。
方案A的净现值的期望值=533-500=33(万元)方案B的净现值的期望值=448.5-300=148.5(万元)因此,应该优先选择方案B。
人工智能决策树例题经典案例

人工智能决策树例题经典案例一、经典案例:天气预测决策树在天气预测中有广泛应用,下面是一个关于是否适宜进行户外运动的示例:1. 数据收集:- 温度:高(>30℃)/中(20℃-30℃)/低(<20℃)- 降水:是/否- 风力:高/中/低- 天气状况:晴朗/多云/阴天/雨/暴雨- 应该户外运动:是/否2. 构建决策树:- 根据温度将数据分为三个分支:高温、中温、低温- 在每个分支中,继续根据降水、风力和天气状况进行划分,最终得到是否适宜户外运动的决策3. 决策树示例:温度/ / \高温中温低温/ | | \ |降水无降水风力适宜/ \ | | / \是否高中低| |不适宜适宜- 如果温度是高温且有降水,则不适宜户外运动- 如果温度是高温且无降水,则根据风力判断,如果风力是高,则不适宜户外运动,如果风力是中或低,则适宜户外运动 - 如果温度是中温,则不论降水和风力如何,都适宜户外运动- 如果温度是低温,则需要考虑风力,如果风力是高,则适宜户外运动,如果风力是中或低,则不适宜户外运动4. 参考内容:决策树的构建和应用:决策树通过对输入特征进行划分,构建了一棵树形结构,用于解决分类或回归问题。
构建决策树主要包括数据预处理、特征选择、划分策略和停止条件等步骤。
特征选择可以使用信息增益、基尼指数等算法,划分策略可以使用二叉划分或多叉划分,停止条件可以是叶子节点纯度达到一定阈值或达到预定的树深度。
决策树的应用包括数据分类、特征选择和预测等任务。
天气预测案例中的决策树:将天气预测问题转化为分类问题,通过构建决策树,可以得到识别是否适宜户外运动的规则。
决策树的决策路径可以用流程图或树状图表示,帮助理解和解释决策过程。
决策树的节点表示特征值,分支表示判断条件,叶子节点表示分类结果。
决策树的生成算法可以基于启发式规则或数学模型,如ID3、C4.5、CART等。
决策树的优缺点:决策树具有可解释性强、易于理解和实现、能处理非线性关系等优点。
决策树例题分析

决策树例题分析决策树是一种常见的机器学习算法,它通过树形结构对数据进行分类和预测。
本文将基于一个例题,详细分析决策树的构建和应用过程。
例题描述:某公司想要根据客户的特征来判断他们是否会购买某个产品。
为了实现这个目标,公司收集了以下一些数据:客户的年龄、年收入和婚姻状况,以及他们最终购买与否的情况。
现要用这些数据建立一个决策树模型来预测客户是否会购买产品。
数据集准备:首先,我们需要对数据集进行准备和清洗。
将数据集划分为训练集和测试集,其中训练集用于建立决策树模型,测试集用于评估模型的性能。
然后,对于缺失值或异常值,可以根据具体情况进行处理,例如使用均值填充或删除异常样本。
特征选择:在决策树算法中,需要选择最佳的特征来构建决策树。
一个好的特征应该能够很好地区分不同类别的样本。
在本例中,我们可以使用信息增益或基尼系数作为特征选择的标准。
根据特征选择的结果,选择最佳的特征作为根节点。
决策树构建:在选择了根节点特征后,我们需要对数据集进行划分,并递归地构建决策树。
在每个节点上,根据选择的分裂特征和划分标准,将数据集分为更小的子集。
直到满足终止条件,例如节点中只包含同一类别的样本或达到了预定深度。
在构建过程中,可以使用剪枝技术来防止过拟合。
决策树预测:构建完决策树模型后,就可以用它来进行预测了。
对于一个新的样本,从根节点开始,根据节点的特征判断样本应该往哪个分支走,直到到达叶节点。
叶节点对应的类别就是预测的结果。
可以使用预测准确率、精确率、召回率等指标来评估模型的性能。
模型评估和优化:在预测的过程中,我们可以使用测试集来评估模型的性能。
根据评估结果,可以选择调整模型参数或选择其他特征,并再次训练模型。
一般来说,更好的特征和更合适的模型参数可以提高决策树的性能。
总结:决策树是一种常见而强大的分类和预测算法。
通过选择最佳特征、构建决策树和预测样本,可以实现对数据集的分类和预测。
在实际应用中,需要根据不同问题的特点选择合适的特征和模型参数,以达到更好的性能。
【决策树习题练习(答案)】

【决策树习题练习(答案)】决策树习题练习答案 1.某投资者预投资兴建一工厂,建设方案有两种:①大规模投资300万元;②小规模投资160万元。
两个方案的生产期均为10年,其每年的损益值及销售状态的规律见表15。
试用决策树法选择最优方案。
表1 各年损益值及销售状态销售状态概率损益值(万元/年)大规模投资小规模投资销路好 0.7 100 60 销路差 0.3 -20 20 【解】(1)绘制决策树,见图1;100×10 -20×10 60×10 20×10 销路好0.7 销路差(0.3)销路好0.7 销路差(0.3)大规模小规模 340 340 320 2 3 1 图1 习题1决策树图(2)计算各状态点的期望收益值节点②:节点③:将各状态点的期望收益值标在圆圈上方。
(3)决策比较节点②与节点③的期望收益值可知,大规模投资方案优于小规模投资方案,故应选择大规模投资方案,用符号“//”在决策树上“剪去”被淘汰的方案。
2.某项目有两个备选方案A和B,两个方案的寿命期均为10年,生产的产品也完全相同,但投资额及年净收益均不相同。
A方案的投资额为500万元,其年净收益在产品销售好时为150万元,,销售差时为50万元;B方案的投资额为300万元,其年净收益在产品销路好时为100万元,销路差时为10万元,根据市场预测,在项目寿命期内,产品销路好时的可能性为70%,销路差的可能性为30%,试根据以上资料对方案进行比选。
已知标准折现率ic=10%。
【解】(1)首先画出决策树 150 50 100 10 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -300 2 3 1 图2 决策树结构图此题中有一个决策点,两个备用方案,每个方案又面临着两种状态,因此可以画出其决策树如图18。
(2)然后计算各个机会点的期望值机会点②的期望值=150(P/A,10%,10)×0.7+(-50)(P/A,10%,10)×0.3=533(万元) 机会点③的期望值=100(P/A,10%,10)×0.7+10(P/A,10%,10)×0.3=448.5(万元) 最后计算各个备选方案净现值的期望值。
决策树习题练习(答案)

决策树习题练习(答案)决策树习题练习答案1.某投资者预投资兴建一工厂,建设方案有两种:①大规模投资300万元;②小规模投资160万元。
两个方案的生产期均为10年,其每年的损益值及销售状态的规律见表15。
试用决策树法选择最优方案。
表1 各年损益值及销售状态销售状态概率损益值(万元/年)大规模投资小规模投资销路好 0.7100 60 销路差 0.3 -2020【解】(1)绘制决策树,见图1;100×10 -20×10 60×1020×10 销路好0.7 销路差(0.3)销路好0.7 销路差(0.3)大规模小规模 340 340 3202 31 图1 习题1决策树图(2)计算各状态点的期望收益值节点②:节点③:将各状态点的期望收益值标在圆圈上方。
(3)决策比较节点②与节点③的期望收益值可知,大规模投资方案优于小规模投资方案,故应选择大规模投资方案,用符号“//”在决策树上“剪去”被淘汰的方案。
2.某项目有两个备选方案A和B,两个方案的寿命期均为10年,生产的产品也完全相同,但投资额及年净收益均不相同。
A方案的投资额为500万元,其年净收益在产品销售好时为150万元,,销售差时为50万元;B方案的投资额为300万元,其年净收益在产品销路好时为100万元,销路差时为10万元,根据市场预测,在项目寿命期内,产品销路好时的可能性为70%,销路差的可能性为30%,试根据以上资料对方案进行比选。
已知标准折现率ic=10%。
【解】(1)首先画出决策树150 5010010 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -3002 31 图2 决策树结构图此题中有一个决策点,两个备用方案,每个方案又面临着两种状态,因此可以画出其决策树如图18。
(2)然后计算各个机会点的期望值机会点②的期望值=150(P/A,10%,10)×0.7+(-50)(P/A,10%,10)×0.3=533(万元) 机会点③的期望值=100(P/A,10%,10)×0.7+10(P/A,10%,10)×0.3=448.5(万元) 最后计算各个备选方案净现值的期望值。
决策树例题分析

计算各点的期望值: • 点②:0.7×200×10+0.3×(-40)×10-600(投资)
=680(万元) • 点⑤:1.0×190×7-400=930(万元) • 点⑥:1.0×80×7=560(万元) 比较决策点4的情况可以看到,由于点⑤(930万元)
与点⑥(560万元)相比,点⑤的期望利润值较大, 因此应采用扩建的方案,而舍弃不扩建的方案。 把点⑤的930万元移到点4来,可计算出点③的期望利 润值: • 点③:0.7×80×3+0.7×930+0.3×60×(3+7)-280 = 719(万元)
11
最后比较决策点1的情况: • 由于点③(719万元)与点②(680万元)
相比,点③的期望利润值较大,因此取 点③而舍点②。这样,相比之下,建设 大工厂的方案不是最优方案,合理的策 略应采用前3年建小工厂,如销路好,后 7年进行扩建的方案。
12
3
状态节点
2 方案分枝
1 决策结点
方案分枝
3
状态节点
概率分枝 4 结果节点
概率分枝 5 结果节点
概率分枝 6
结果节点
概率分枝 7
结果节点
4
• 应用决策树来作决策的过程,是从右向 左逐步后退进行分析。根据右端的损益 值和概率枝的概率,计算出期望值的大 小,确定方案的期望结果,然后根据不 同方案的期望结果作出选择。
9
680万元 2
建大厂
销路好(0.7) 销路差(0.3)
200万元 -40万元
1 719万元
扩建 5 销路好(1.0)
建小厂
930万元
销路好(0.7) 4 不扩建
930万元
6 销路好(1.0)
决策树习题练习(答案)

决策树习题练习(答案)决策树题练答案题目1:某投资者预计投资兴建一工厂,建设方案有两种:①大规模投资300万元;②小规模投资160万元。
两个方案的生产期均为10年,其每年的损益值及销售状态的规律见表15.试用决策树法选择最优方案。
解答:首先绘制决策树,如图1所示。
然后计算各状态点的期望收益值,并将其标在圆圈上方。
最后比较节点②与节点③的期望收益值,选择期望收益值更高的方案,即大规模投资方案。
题目2:某项目有两个备选方案A和B,两个方案的寿命期均为10年,生产的产品也完全相同,但投资额及年净收益均不相同。
A方案的投资额为500万元,其年净收益在产品销售好时为150万元,在销售差时为50万元;B方案的投资额为300万元,其年净收益在产品销路好时为100万元,在销路差时为10万元。
根据市场预测,在项目寿命期内,产品销路好时的可能性为70%,销路差的可能性为30%,试根据以上资料对方案进行比选。
已知标准折现率ic10%。
解答:首先画出决策树,如图2所示。
然后计算各个机会点的期望值,最后计算各个备选方案净现值的期望值,选择期望净现值更高的方案,即方案A。
根据计算,方案A的净现值期望值为33万元,方案B的净现值期望值为148.5万元。
因此,选择方案B为优先方案。
接着,投资者提出了第三个方案,先进行小规模投资160万元,生产3年后根据销售情况再决定是否进行大规模投资。
根据表2的销售概率表,绘制出决策树,计算各节点的期望收益值。
经过计算,节点④的期望收益值为616万元,节点⑤的期望收益值为-140万元,节点②的期望收益值为281.20万元,节点⑧的期望收益值为476万元,节点⑨的期望收益值为392万元,因此选择扩建方案。
节点⑥的期望损益值取扩建方案的期望损益值476万元。
节点⑦的期望收益值为140万元。
某建筑公司计划建一预制构件厂,方案一为建大厂,需投资300万元,每年可盈利100万元,若销路差则每年亏损20万元,使用期为10年;方案二为建小厂,需投资170万元,每年可盈利40万元,若销路差则每年盈利30万元。
回归问题的决策树题目和解答

回归问题的决策树题目和解答【最新版】目录1.决策树概念介绍2.回归问题的决策树构建方法3.决策树的应用实例4.决策树在回归问题中的优缺点正文一、决策树概念介绍决策树是一种常见的机器学习方法,它通过一系列的问题来对数据进行分类或者回归。
决策树可以看作是一个问题树,每个内部节点表示一个特征,每个分支代表一个决策规则,每个叶子节点代表一个分类或回归结果。
决策树在数据挖掘、机器学习等领域具有广泛的应用。
二、回归问题的决策树构建方法回归问题决策树的构建方法与分类问题类似,不过回归问题的决策树是用于预测连续值而非类别。
以下是回归问题决策树的构建步骤:1.特征选择:从训练数据集中选择一个最佳特征进行分裂。
通常使用信息增益、增益率或基尼指数作为特征选择标准。
2.特征分裂:根据选定的特征和阈值将数据集划分为不同的子集。
3.终止条件:当满足终止条件时,不再继续构建决策树。
常见的终止条件包括:所有样本属于同一类别、没有可选特征等。
4.返回叶子节点的值:对于回归问题,叶子节点的值即为预测结果。
三、决策树的应用实例决策树在回归问题中的应用非常广泛,例如房价预测、股票市场预测等。
这里我们以房价预测为例,展示如何使用决策树进行回归分析。
假设我们有一套房屋数据,包括房屋面积、卧室数量、距离市中心的距离等特征,以及对应的房价。
我们可以使用决策树来预测新房子的房价。
具体步骤如下:1.读取数据集,对数据进行预处理,如缺失值处理、异常值处理等。
2.选择一个特征作为决策树的根节点,例如“房屋面积”。
3.根据房屋面积将数据集划分为不同的子集,然后计算每个子集的平均房价。
4.更新决策树的叶子节点,将平均房价作为叶子节点的值。
5.重复步骤 3 和 4,直到满足终止条件。
6.使用训练好的决策树预测新房子的房价。
四、决策树在回归问题中的优缺点决策树在回归问题中具有以下优点:1.可以处理连续值问题,适用于回归预测。
2.容易理解和解释,因为决策树是一个问题树,每个内部节点表示一个特征,每个分支代表一个决策规则,每个叶子节点代表一个分类或回归结果。
决策树例题分析及解答分解课件

目录
CONTENTS
• 决策树与其他机器学习算法的比 • 决策树未来发展方向
01
决策树简 介
决策树的定义
决策树是一种监督学习算法,用于解决分类和回归问题。
它通过递归地将数据集划分成更纯的子集来构建决策树,每个内部节点表示一个 特征属性上的判断条件,每个分支代表一个可能的属性值,每个叶子节点表示一 个类别。
03
决策树例题分析
题目描述
题目
预测一个学生是否能够被大学录 取
数据集
包含学生的个人信息、成绩、活动 参与情况等
目标变量
是否被大学录取(0表示未录取,1 表示录取)
数据预处理
01
02
03
数据清洗
处理缺失值、异常值和重 复值
数据转换
将分类变量转换为虚拟变 量,将连续变量进行分箱 处理
数据归一化
将特征值缩放到0-1之间, 以便更好地进行模型训练
结果解读与优化建议
结果解读
根据模型输出的结果,分析决策树 的构建情况,理解各节点的划分依据。
优化建议
根据模型评估结果和业务需求,提出 针对性的优化建议,如调整特征选择、 调整模型参数等。
05
决策树与其他机器
学习算法的比 较
与逻辑回归的比较
总结词
逻辑回归适用于连续和二元分类问题,而决策树适用于多元分类问题。
建立决策树模型
选择合适的决策树算 法:ID3、C4.5、 CART等
构建决策树模型并进 行训练
确定决策树的深度和 分裂准则
模型评估与优化
使用准确率、召回率、F1分数等指标 评估模型性能
对模型进行优化:剪枝、调整参数等
进行交叉验证,评估模型的泛化能力
决策树例题分析

2
补充: 风险型决策方法——决策树方法
• 风险决策问题的直观表示方法的图示法。因为图的形状 像树,所以被称为决策树。
• 决策树的结构如下图所示。图中的方块代表决策节点, 从它引出的分枝叫方案分枝。每条分枝代表一个方案, 分枝数就是可能的相当方案数。圆圈代表方案的节点, 从它引出的概率分枝,每条概率分枝上标明了自然状态 及其发生的概率。概率分枝数反映了该方案面对的可能 的状态数。末端的三角形叫结果点,注有各方案在相应 状态下的结果值。
3
状态节点
概率分枝 4 概率分枝 5
结果节点
2
方案分枝
结果节点
1 方案分枝 决策结点 3 概率分枝 状态节点 7 结果节点 概率分枝 6 结果节点
4
• 应用决策树来作决策的过程,是从右向 左逐步后退进行分析。根据右端的损益 值和概率枝的概率,计算出期望值的大 小,确定方案的期望结果,然后根据不 同方案的期望结果作出选择。
9
销路好(0.7) 680万元 2 建大厂 销路差(0.3)
200万元
-40万元
1
719万元
扩建 建小厂 930万元 销路好(0.7) 4 不扩建 销路好(1.0) 6 930万元 3 719万元 前3年,第一次决策 560万元 销路差(0.3) 后7年,第二次决策
5ቤተ መጻሕፍቲ ባይዱ
销路好(1.0)
190万元
80万元
1
例:设某茶厂计划创建精制茶厂,开始有两个方案,方案 一是建年加工能力为 800担的小厂,方案二是建年加工能 力为 2000 担的大厂。两个厂的使用期均为 10 年,大厂投 资25万元,小厂投资10万元。产品销路没有问题,原料来 源有两种可能 ( 两种自然状态 ) :一种为 800 担,另一种为 2000担。两个方案每年损益及两种自然状态的概率估计值 见下表
决策树例题分析及解答_(1)
状
益损值 态
方案
需求 需求 量较 量一
高般
甲
600 400
乙
800 350
丙
350 220
丁
400 250
需求 量较
低
-150
-350
50
需求量 很低
max
min
-350 -700 -100
600 -350 800 -700 350 -100
a=0.7
315 350 215
90 -50 400 -50 265
自然状态 概率 建大厂(投资25 建小厂(投资10
万元)
万元)
原料800担 0.8 原料2000担 0.2
13.5 25.5
15.0 15.0
4
补充: 风险型决策方法——决策树方法
• 风险决策问题的直观表示方法的图示法。因为图的形状 像树,所以被称为决策树。
• 决策树的结构如下图所示。图中的方块代表决策节点, 从它引出的分枝叫方案分枝。每条分枝代表一个方案, 分枝数就是可能的相当方案数。圆圈代表方案的节点, 从它引出的概率分枝,每条概率分枝上标明了自然状态 及其发生的概率。概率分枝数反映了该方案面对的可能 的状态数。末端的三角形叫结果点,注有各方案在相应 状态下的结果值。
600×0.7+(--350 ×0.3)=315
28
决策准则小结
不同决策者甚至同一决策者在不同决 策环境下对同一个问题的决策可能截 然不同,并没有所谓的“正确答案” 。决策准则的选取主要取决于决策者 对于决策的性格和态度,以及制定决 策时的环境
所有的准则都不能保证所选择的方案 在实际情况发生时会成为最佳方案
• 试用决策树法选出合理的决策方案。 经过市场调查, 市场销路好的概率为0.7,销路不好的概率为0.3。
回归问题的决策树题目和解答

回归问题的决策树题目和解答摘要:一、回归问题的概念1.回归问题的定义2.回归问题的应用场景二、决策树的介绍1.决策树的基本概念2.决策树在回归问题中的应用三、回归问题的决策树题目及解答1.题目一:某公司想了解广告投入对销售收入的影响2.题目二:房价与房屋面积的关系3.题目三:空气质量指数与市民健康状况的关系4.题目四:教育投入与经济增长的关系四、决策树在回归问题中的优势与局限1.优势:易于理解和解释2.局限:容易受到噪声数据的影响正文:一、回归问题的概念回归问题是指在数据集中寻找两个或多个变量之间的关系。
这种关系可以用来预测一个变量的值,或者解释另一个变量的变化原因。
回归问题的应用场景广泛,例如经济学、市场营销、医学研究等领域。
二、决策树的介绍决策树是一种基于树结构的分类与回归模型。
它通过一系列的问题对数据进行递归划分,最终得到一个叶子节点,每个叶子节点代表一个分类或回归结果。
决策树在回归问题中的应用可以帮助我们快速找到变量之间的关系,从而进行预测或解释。
三、回归问题的决策树题目及解答1.题目一:某公司想了解广告投入对销售收入的影响解答:通过构建决策树,我们可以分析广告投入与销售收入之间的关系。
首先,将广告投入作为自变量,销售收入作为因变量。
然后,通过递归划分数据集,找到广告投入与销售收入之间的关系。
最后,根据决策树预测在不同广告投入下的销售收入。
2.题目二:房价与房屋面积的关系解答:同样地,我们可以通过构建决策树分析房价与房屋面积之间的关系。
首先,将房价作为因变量,房屋面积作为自变量。
然后,通过递归划分数据集,找到房价与房屋面积之间的关系。
最后,根据决策树预测在不同房屋面积下的房价。
3.题目三:空气质量指数与市民健康状况的关系解答:针对这个问题,我们可以构建一个决策树,以空气质量指数作为自变量,市民健康状况作为因变量。
通过递归划分数据集,找到空气质量指数与市民健康状况之间的关系。
最后,根据决策树预测在不同空气质量指数下的市民健康状况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
决策过程如下 :画图,即绘制决策树
? A1的净收益值=[300×0.7+(-60)× 0.3] ×5-450=510万
? A2的净收益值=(120×0.7+30×0.3)× 5-240=225万 ? 选择:因为A1大于A2,所以选择A1方案。 ? 剪枝:在A2方案枝上打杠,表明舍弃。
10
例题
? 为了适应市场的需要,某地提出了扩大电视机生产的两 个方案。一个方案是建设大工厂,第二个方案是建设小 工厂。
利润量 (元)
30000 9600 13200 52800
在生产出16.5万公顷玉米的前提下,将获得 5.28万元的利润,在忙劳动力资源尚剩余 680 个工日可用于其他产品生产。
3
例:设某茶厂计划创建精制茶厂,开始有两个方案,方案 一是建年加工能力为 800担的小厂,方案二是建年加工能 力为2000 担的大厂。两个厂的使用期均为 10年,大厂投 资25万元,小厂投资10万元。产品销路没有问题,原料来 源有两种可能 (两种自然状态 ):一种为 800 担,另一种为 2000担。两个方案每年损益及两种自然状态的概率估计值 见下表
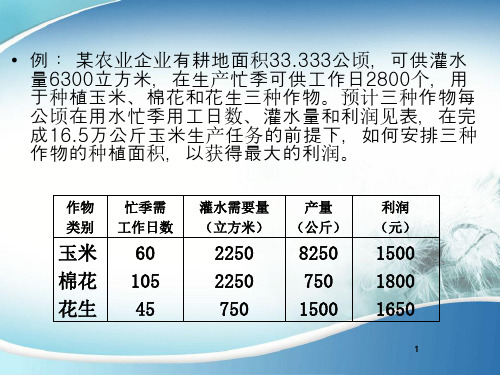
? 例: 某农业企业有耕地面积33.333公顷,可供灌水 量6300立方米,在生 产忙季可供工作日 2800个,用 于种植玉米、棉花和花生三 种作物。预计三种作物每 公顷在用水忙季用工日 数、灌水量和利 润见表,在完 成16.5万公斤玉米生 产任务的前提下,如何安排三 种 作物的种植面积,以获得最大的利 :0.7× 200× 10+0.3× (-40)× 10-600(投资)
=680(万元) ? 点⑤:1.0× 190× 7-400=930(万元) ? 点⑥:1.0× 80× 7=560(万元) ? 比较决策点4的情况可以看到,由于点⑤(930万元)
与点⑥(560万元)相比,点⑤的期望利润值较大, 因此应采用扩建的方案,而舍弃不扩建的方案。 ? 把点⑤的930万元移到点4来,可计算出点③的期望利 润值: ? 点③:0.7× 80× 3+0.7× 930+0.3× 60× (3+7)-280 = 719(万元)
自然状态 概率 建大厂(投资25 建小厂(投资10
万元)
万元)
原料800担 0.8 原料2000担 0.2
13.5 25.5
15.0 15.0
4
补充: 风险型决策方法——决策树方法
? 风险决策问题的直观表示方法的图示法。因为图的形状 像树,所以被称为决策树。
? 决策树的结构如下图所示。图中的方块代表决策节点, 从它引出的分枝叫方案分枝。每条分枝代表一个方案, 分枝数就是可能的相当方案数。圆圈代表方案的节点, 从它引出的概率分枝,每条概率分枝上标明了自然状态 及其发生的概率。概率分枝数反映了该方案面对的可能 的状态数。末端的三角形叫结果点,注有各方案在相应 状态下的结果值。
作物 类别
玉米 棉花 花生
忙季需 工作日数
60 105 45
灌水需要量 (立方米)
2250 2250 750
产量 (公斤)
8250 750 1500
利润 (元)
1500 1800 1650
1
解:玉米、棉花、花生和种植面积分别为X1,X2,X3公顷,依 题意列出线性规划模型。
目标函数:S=1500X1+1800X2+1650X3——极大值 约束条件:X1+X2+X3≤33.333 60X1+105X2+45X3≤2800 2250X1+2250X2+750X3≤63000 8250X1≤165000 X1,X2,X3≥0 采用单纯形法求出决策变量值: X1=20公顷 X2=5.333公顷 X3=8公顷
13
?最后比较决策点1的情况: ? 由于点③(719万元)与点②(680万元)
相比,点③的期望利润值较大,因此取点 ③而舍点②。这样,相比之下,建设大工 厂的方案不是最优方案,合理的策略应采 用前3年建小工厂,如销路好,后7年进行 扩建的方案。
2
决策方案评价
作物类别
玉米 棉花 花生 合计 资源供给量 资源余缺量
占用耕 忙季耗用 灌水用量 地面积 工日数 (立方米) (公顷)
20 5.333
1200 560
45000 12000
8
360
6000
33.333
2120
63000
33.333
2800
63000
0
680
0
总产量 (千瓦)
165000 40000 120000
7
? 计算完毕后,开始对决策树进行剪枝, 在每个决策结点删去除了最高期望值以 外的其他所有分枝,最后步步推进到第 一个决策结点,这时就找到了问题的最 佳方案
? 方案的舍弃叫做修枝,被舍弃的方案用“ ≠”的记号来表示,最后的决策点留下一 条树枝,即为最优方案。
8
? A1、A2两方案投资分别为450万和240万, 经营年限为5年,销路好的概率为0.7,销路 差的概率为0.3,A1方案销路好、差年损益 值分别为300万和负60万;A2方案分别为1 20万和30万。
? 建设大工厂需要投资600万元,可使用10年。销路好每 年赢利200万元,销路不好则亏损40万元。
? 建设小工厂投资280万元,如销路好,3年后扩建,扩 建需要投资400万元,可使用7年,每年赢利190万元。 不扩建则每年赢利80万元。如销路不好则每年赢利60 万元。
? 试用决策树法选出合理的决策方案。 经过市场调查, 市场销路好的概率为0.7,销路不好的概率为0.3。
5
状态节点
2 方案分枝
1 决策结点
方案分枝
3
状态节点
概率分枝 4 结果节点
概率分枝 5 结果节点
概率分枝 6
结果节点
概率分枝 7
结果节点
6
? 应用决策树来作决策的过程,是从右向 左逐步后退进行分析。根据右端的损益 值和概率枝的概率,计算出期望值的大 小,确定方案的期望结果,然后根据不 同方案的期望结果作出选择。
11
680万元 2
建大厂
销路好(0.7) 销路差(0.3)
200万元 -40万元
1 719万元
扩建 5 销路好(0.7)
建小厂
930万元
销路好(0.7) 4 不扩建
930万元 6 销路好(0.7)
3
560万元
719万元
销路差(0.3)
前3年,第一次决策
后7年,第二次决策
190万元
80万元 60万元
