统计学例题-动态趋势分析共23页
统计学原理试题 (1)

统计学原理试题(总分:99.98,做题时间:120分钟)一、单项选择题(每题1分,共15分)(总题数:15,分数:15.00)1.社会经济统计学是一门社会科学,它对社会经济现象的研究()(分数:1.00)A.是一种纯数量的研究B.是从定性认识开始,以定量认识为最终目的C.是在社会经济现象的质与量的密切联系中,研究其数量关系√D.是一种对经济现象做的定性研究解析:2.对某市科技人员进行调查,科技人员的职称和年龄()(分数:1.00)A.是品质标志B.是数量标志C.前者是数量标志,后者是品质标志D.前者是品质标志,后者是数量标志√解析:3.对企业职工按工种分组,在此基础上再按工资水平分组,这种分组属于()(分数:1.00)A.简单分组B.复合分组√C.品质标志分组D.数量标志分组解析:4.计算比较相对指标()(分数:1.00)A.只能是两个总量指标对比B.只能是两个相对指标对比C.只能是两个平均指标对比D.既可以是两个总量指标对比,也可以是两个相对指标或平均指标对比√解析:5.某地区工业增加值1995年比1994年增长6%,1996年比1995年增长4%,1997年比1996年增长8%。
则三年来该地区工业增加值平均每年增长速度的计算方法为()(分数:1.00)C.106%×104%×108% -100% √D.6%×4%×8%解析:6.某企业1997年比1996年产量增长了15%,产品单位成本下降了4%,1996年企业总成本支付了30万元,则1997年总成本比1996年多支付()(分数:1.00)A.3万元B.4.5万元C.3.12万元√D.1.38万元解析:7.调查误差包括登记误差和代表性误差,在抽样调查中()(分数:1.00)A.只有登记误差B.只有代表性误差C.两种误差都有√D.两种误差都没有解析:8.在简单随机抽样条件下,当极限误差范围Δ扩大一倍,则抽样单位数()(分数:1.00)A.只需原来的1/2B.只需原来的1/4 √C.是原来的1倍D.是原来的√2倍解析:9.加权调和平均数指数要成为综合指数的变形,其权数()(分数:1.00)A.必须用基期的价值量指标B.必须用报告期的价值量指标√C.必须用基期的数量指标D.必须用报告期的数量指标解析:10.配合回归直线的前提条件是()(分数:1.00)A.两个变量必须有明显的依存关系B.两个变量必须有函数关系C.两个变量存在一定的相关关系D.两个变量存在显著的线性相关关系√解析:11.在相关分析中,若变量X的值减少,变量Y的值也随之减少,则两个变量间的关系是()(分数:1.00)A.正相关√B.负相关C.复相关D.不相关解析:12.对某企业职工平均工资的变动进行分析时,若分析职工人员结构的变动对总平均工资的影响程度应采用()(分数:1.00)A.总平均工资可变构成指数B.总平均工资综合指数C.总平均工资固定构成指数D.总平均工资结构影响指数√解析:13.检验回归方程代表性大小的统计分析指标是()(分数:1.00)A.相关系数B.回归系数C.估计标准误√D.符号系数解析:14.对甲乙两企业工人劳动生产率的高低进行抽样调查,调查的工人数甲企业80人,乙企业150人,两企业工人劳动生成率的方差相同,则抽样平均误差()(分数:1.00)A.甲企业大√B.乙企业大C.两个企业一样大D.不能确定解析:15.在总体内部情况复杂,而且各单位之间差异程度大、单位数又多的情况下,宜采用()(分数:1.00)A.简单随机抽样B.等距抽样C.类型抽样√D.整群抽样解析:二、多项选择题(每题1分,共10分)(总题数:10,分数:10.00)16.总量指标的重要意义在于它是()(分数:1.00)A.对社会经济现象认识的起点√B.计算相对指标的基础√C.计算平均指标的基础√D.实行经营管理的依据√E.反映某些相关事物之间数量联系程度的综合指标解析:17.对某项资料进行统计分组时,其关键的问题是()(分数:1.00)A.划分数量标志和品质标志B.选择分组标志√C.选择分组体系D.区分简单分组与复合分组E.划分各组界限√解析:18.设P为价格,Q为销售量,则总指数∑P0Q1/∑P0Q0的意义是()(分数:1.00)A.综合反映多种商品的销售量的变动程度√B.综合反映商品价格和销售量的变动C.综合反映商品销售额的变动D.反映商品销售量的变动对销售额变动的影响程度√E.综合反映多种商品价格的变动程度解析:19.普查是一种()(分数:1.00)A.专门组织的调查√B.只调查时期现象C.不连续调查√D.全面调查√E.非全面调查解析:20.在直线回归方程中,回归系数()(分数:1.00)A.表明两变量之间的相关程度B.表明两变量之间的相关方向√C.表明两变量之间的密切程度D.表明两变量之间的量变关系√E.在数学上称为斜率√解析:21.时点指标所形成的时间数列中()(分数:1.00)A.指标的各个数值是可以相加的B.指标的各个数值是不能相加的√C.指标的各个数值相加起来没有实际意义√D.数列中各项指标数值的大小与时点间隔有直接关系E.数列中的资料通过连续登记取得解析:22.在一定的误差范围要求下()(分数:1.00)A.概率度大,要求可靠性低,抽样数目相应要多B.概率度大,要求可靠性高,抽样数目相应要多√C.概率度小,要求可靠性低,则抽样数目相应要少√D.概率度小,要求可靠性高,则抽样数目相应要少E.概率度小,要求可靠性低,抽样数目相应要多解析:23.定基增长速度等于()(分数:1.00)A.累积增长量除以基期发展水平√B.环比增长速度的连乘积C.环比发展速度的连乘积减去1√D.定基发展速度减1√E.逐期增长量除以基期水平解析:24.平均指标的特点是()(分数:1.00)A.将同一总体各单位标志值的差异抽象化√B.将总体统计指标值的差异抽象化C.将不同总体各单位标志值的差异抽象化D.将各总体的数量差异抽象化E.是总体数量特征的代表值√解析:25.下列属于时点指标的有()(分数:1.00)A.某地区某年人口增加数B.某地区某年乡镇企业总数√C.某地区某年招工录取率D.某地区某年商业网点数√E.某种原材料期初库存量√解析:三、填空题(每空1分,共15分)(总题数:8,分数:15.00)26.抽样调查是按照 1抽选调查单位进行调查的方法,其目的是 2。
动态趋势分析

8 12 991 36 2 8 204 362
603
10 220 336
30.42
a
统计学
动态趋势分析
一、时间序列的变动因素和现象的变动形态
1、变动因素: 偶然因素和基本因素 2、变动形态 1.长期趋势(T) 2.循环变动(C) 3.季节变动(S) 4.不规则变动(I)
动态趋势分析
二、长期趋势分析方法
1.时距扩大法
(1)时距扩大总数法
该法是将原时间数列中较短的时距适当地予以扩大,再将扩 大了的时距内的较短时距的若干个数据加以合并,得出一系列扩 大了的时距的数据,形成一个新的时间数列的方法。
5
170
148.33
143.00
143.57
6
165
161.67
148.00
145.71
7
150
153.33
158.00
148.57
8
145
151.67
152.00
154.29
9
160
148.33
149.00
157.86
10
140
150.00
158.00
—
11
150
161.67
—
—
12
195
—
—
—
动态趋势分析
【例5.17】 由某商品各月的销售量资料分别采用3项、5项和7项
移动平均所得的资料如表5.15所示。
表5.15 移动平均计算结果表
单位:吨
月份
销售量
3项移动平均 5项移动平均 7项移动平均
1
123
—
—
—
2
145
《统计学》案例——时间序列趋势分析

《统计学》案例——时间序列趋势分析囤积粮食可以创高价吗1、问题的提出某贸易公司是经营粮油副食品的批发公司,基于前4年当地的消费物价指数的变化,该公司认为今后两年内消费物价指数将有大幅度上涨,为此该公司计划囤积粮食至下一年(第6年)以创高价。
这个计划是否可行?2、方法的选择根据下表的数据,可采用时间序列的趋势分析方法和季节变动分析方法,进行相应的分析预测,以了解消费物价指数的发展趋势。
表23 122.434 139.373、消费物价指数的预测根据题意需预测出第6年各季的物价指数,若指数升幅较大,那么粮食价格将会提高,否则囤积货物只会增加保管成本而不可能得到高价。
在物价指数预测中,循环变动和不规则变动难以准确预测,故仅考虑长期趋势与季节变动的影响。
本案例分析应用EXCEL软件。
(1)计算移动平均数。
输出结果见下表和图:表3.(2)分离长期趋势T。
对于T×C,按照表8.14中时间顺序,用最小平方法建立长期趋势模型yc=111.498+1.173t ,据以计算各期趋势值T(见上表)。
(3)分离季节变动S。
首先剔除长期趋势的影响y/T×C,即T×C×S×I/T×C=S×I;然后根据S×I序列计算各期季节比率S。
计算结果为:1季度季节比率=0.9773,2季度季节比率=0.9874,3季度季节比率=1.0076,4季度季节比率=1.0277。
(4)预测第6年各季消费物价指数。
首先需要根据时间序列模型计算第6年各季的趋势值,即将t=19、20、21、22分别代入yc=111.498+1.173t计算得第6年各季度趋势值:1季的趋势值为133.792季趋势值为134.963季趋势值为136.144季趋势值为137.31然后分别乘以各自季节比率得到各季预测值,1季物价指数=133.79×0.9773=130.75%2季物价指数=134.96×0.9874=133.26%3季物价指数=136.14×1.0076=137.17%4季物价指数=137.31×1.0277=141.11%。
【统计课件】第11章 动态分析

=前期水平 100
八、平均发展速度和平均增长速度
反映环比发展速度一般水平的指标称为平均发 展速度。 有两种计算方法:几何平均法、方程式法。 反映环比增长速度一般水平的指标称为平均增 长速度。只有计算出平均发展速度的基础上才 可以计算平均增长速度,即: 平均增长速度=平均发展速度-1(或100%)
a
a
n
2.由间隔相等时点数列计算序时平均数
1 1 a1 a 2 a n 2 2 a n 1
例:
某企业1999年职工人数资料如下表,求该企业1999年 平均人数。
1月1日 208 4月1日 214 7月1日 222 10月1日 220 12月31日 217
时间 职 工 人 数 (人)
11.2 动态分析指标
一、发展水平(a)
最初水平 a0 和最末水平 an
a
1
a
2
………………
a
n 1
an
报告期水平和基期水平
二、平均发展水平(序时平均数)
绝对数时间序列的序时平均数 相对数时间数列的序时平均数 a 平均数时间数列的序时平均数
a
由绝对数动态数列计算序时平均数
1.由时期数列计算序时平均数
60 个人存款所 占比重(%) 全部存款额 (万元) 100
三、增长量
反映现象在一定时期增加或减少的绝对数量称 为增长量。 增长量=报告期水平-基期水平 根据比较的基期不同,可以分为逐期增长量和 累计增长量。 逐期增长量=报告期水平-前期水平 累计增长量=报告期水平 二者的关系 :一定时期逐期增长量之和等于该 段时期的累计增长量。
例:
某高校2004年在册学生统计数据如下表(2005 年1月初为3600人),求该年平均在册学生人 数。
统计学例题-集中趋势指标分析
该组平均数以下的人数
该组人数 该组组距
(平均数
-
该组下限)
上网时间大于平均数的人数比重为:
3 10 15 50 (20 18.1)
5
47%
100
练习题:
对某地区庭人口情况随机抽样调查,调查结果如 下表所示:
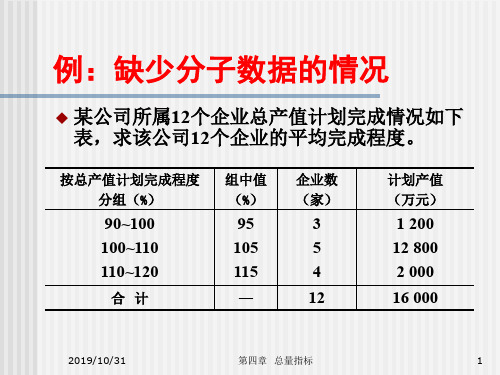
例:缺少分子数据的情况
某公司所属12个企业总产值计划完成情况如下 表,求该公司12个企业的平均完成程度。
按总产值计划完成程度 分组(%)
90~100 100~110 110~120
合计
组中值 (%)
95 105 115
—
企业数 (家)
3 5 4 12
计划产值 (万元)
1 200 12 800 2 000 16 000
2 1070
100 646.73元
2019/10/31
14
练习题:
从某校随机抽取了100名学生进行上网情况 调查,调查结果如下表所示:
(1)根据上述样本资料计算在校大学生上网时 间的众数和中位数。
(2)已知样本资料的平均数为18.10小时,试说 明样本资料的分布状态,计算每周上网时 间大于平均数的人数比重。
700
1070 510
100 = 645.63元
(1070 600) (1070 510)
2019/10/31
13
中位数的计算:
用下限公式:
3000 1000
M e 600
2 1070
100 646.73元
用上限公式:
3000 930
M e 700
【统计学概论】 动态趋势分析

二、移动平均法
从时间数列的第一项开始按一定的项数平 均,逐项移动逐项平均,从而计算出一系列移 动平均数,构成新的时间数列。由移动平均数 形成的新的时间序列对原时间数列的波动起到 修匀作用,从而呈现出现象发展的变动趋势。
移动项数为K(1< K < n)的移动平均数为:
ai
ai
ai1
aK i1 K
4.79
5.40
5.19
5.70
5.55
或例2 P172-P174 移动平均法中移动项数的选择 1、尽量选择奇数项移动平均。
偶数项移动平均后需要再进行一次2项移动平均。 2、如果现象的发展具有一定的周期性,应以周期长度作
为移动间隔的长度。
新时序项数 = 原时序项数 - 移动平均项数 + 1
三、趋势线配合法(数学模型法)
第一步:趋势线的选择:方法有两种
1、观察散点图 2、根据观察数据本身,按以下标准选择趋势线
一次差大体相同,配合直线 Yˆt a bt
二次差大体相同,配合二次曲线 Yˆt a bt ct 2
Yˆ ab 对数的一次差大体相同,配合指数曲线
t
t
一次差的环比值大体相同,配合修正指数曲线
2模型 乘法模型:Yi = Ti × Si × Ci × Ii 较常见 加法模型:Yi = Ti + Si + Ci + Ii
第二节时间数列的修匀方法
一、时距扩大法 对原来的时间数列按照一定的项数合计或平均,
得到一个新的时间数列,从而呈现出较明显的规律。 具体方法:
1、时距扩大总和法:适用于时期数列 2、时距扩大平均法:时期、时点均适用 例1 P171—P172
第三节曲线趋势的测定与分析
统计学计算题例题

统计学计算题例题(总20页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除第四章1. 某企业1982年12月工人工资的资料如下:要求:(1)计算平均工资;(79元)(2)用简捷法计算平均工资。
2. 某企业劳动生产率1995年比1990年增长7%,超额完成计划2%,试确定劳动生产率计划增长数。
7%-2%=5%3. 某厂按计划规定,第一季度的单位产品成本比去年同期降低8%。
实际执行结果,单位产品成本较去年同期降低4%。
问该厂第一季度产品单位成本计划的完成程度如何%( (1-4%)/(1-8%)*100%=96%/92%*100%=%结果表明:超额完成%(%-100%))4. 某公社农户年收入额的分组资料如下:要求:试确定其中位数及众数。
中位数为(元)众数为(元)求中位数:先求比例:(1500-720)/(1770-720)=分割中位数组的组距:(800-700)*=加下限700+=求众数:D1=1050-480=570D2=1050-600=450求比例:d1/(d1+d2)=570/(570+450)=分割众数组的组距:*(800-700)=加下限:700+=年某月份某企业按工人劳动生产率高底分组的生产班组数和产量资料如下:(55*300+65*200+75*140+85*60)/(300+200+140+60)6.某地区家庭按人均月收入水平分组资料如下:根据表中资料计算中位数和众数。
中位数为(元) 众数为(元) 求中位数:先求比例:(50-20)/(65-20)= 分割中位数组的组距:(800-600)*= 加下限:600+=7.某企业产值计划完成103%,比去年增长5%。
试问计划规定比去年增长 多少%(上年实际完成= 本年实际计划比上年增长 ()/==%)8.甲、乙两单位工人的生产资料如下:试分析:(1)哪个单位工人的生产水平高(2)哪个单位工人的生产水平整齐%3.33V %7.44V /8.1x /5.1x ====乙甲乙甲人)(件人)(件9.在计算平均数里,从每个标志变量中减去75个单位,然后将每个差数 缩小10倍,利用这个变形后的标志变量计算加权算术平均数,其中各个变量的权数扩大7倍,结果这个平均数等于个单位。
趋势预测法例题参考及作业 PPT课件

总和 0 3636 2092 60 3636 —— 32.934
aˆ 3636 404 bˆ 2092 34.87
9
60
第34页/共102页
• 所求直线预测模型为:
yˆt 404 34.87t
• 3、预测
•以
代入预测模型,则可预测2010年化纤零售量为:
t0 5
yˆ1987 404 34.87 5 578.35(万米)
第10页/共102页
2007 335 321 346 363 329 327 368 350 341 312 327 351 4070 339.2
❖ 首先,用下列公式估计出预测标准差。
式中: Sx
(xi x)2 n 1
Sx — —标准差 xi — —实际值 x — —预测值(平均数)
n — —观察期数
测中,主要是为求得回归方程或趋势方程,但在求得方程的参数时,就要用到上面的两条数学性质。
•
第17页/共102页
第18页/共102页
a , b 估计参数的确定
第19页/共102页
a , b 估计参数的确定
第20页/共102页
参见教材p233
第21页/共102页
第22页/共102页
直线模型预测法
例2 某市2001—2009年化纤零售量如表 所示,试预测2010年化纤零售量。
• 某市化纤零售量及其一阶差分 单位:万米
年份
2001 2002 2003 2004 2005 2006 2007 2008 2009
零售量 265 297 333 370 405 443 474 508 541
一阶差分 —— 32 36 37 35 38 31 34 33
统计学例题-动态趋势分析

某企业前3年A商品的销售额资料如下表所示:
第1年 第2年 第3年
第一季度 560
620
470
第二季度 142
170
150
第三季度 180
200
220
第四季度 401
390
430
要求:(1)用季平均法计算各季度的季节比率,并根据 计算结果进行简要分析;(2)假设已预测第4年全年的 销售额为1500万元,试预测第4年1季度的销售额。
147.70
146.65
113.84 97.34 114.36 110.09
108.91
108.13
计算修正系数
修正系数 400%
400%
Si 84.74% 61.52% 147.70% 108.91%
0.9929
修正后季节比率(%)= S × 修正系数
注:用分析修匀趋势剔除法不会在计算过程中缺失一部 分数据,因此其计算的季节比率更为精确。
yc a bt 80.23 5.32t 80.23 5.32 7 117.47
10/31/2019
19
方法二:
年 份 编号 t 粮食产量
t2
2004
-5
85.6
25
2005
-3
91.0
9
2006
-1
96.1
1
2007
1
101.2
1
2008
3
107.0第二季度 第三季度 第四季度
2006年
21 16 50 39
2007年
32 28 74 52
2008年
43 31 95 83
2009年
第9章动态趋势分析

• 根据季节模型预测各季销售量
一季度:27.5×124.4%=34.21(万公升) 二季度:27.5×90%=24.75(万公升) 三季度:27.5×77.5%=21.31(万公升) 四季度:27.5×108.1%=29.73(万公升)
直线趋势方程为:yt=a+bt,见P159书上例子
三、数 学 模 型 法
数学模型法是根据动态数列的资料配合一个 方程式,据以计算各期的趋势值。
直线趋势的测定方法
如果动态数列逐期增长量相对稳定,则采用直线 作为趋势线,来描述动态数列的趋势变化,并进 行预测。
直线趋势方程为: yc abt
公式中: yc 因变量,代表所研究现象的预测值
t 自变量,代表时间的序号
a、b为方程参数
用最小平方法求解方程参数 a、b:
bnn tty2 ( t t)2y
aybtybt nn 例题:教材P403表9-18
1990—2019年粮食产量资料
年份
时间代 粮食产
码t
量y
t2
ty Yc=80.23+5.23t
1990
1
85.6
曲线趋势的测定与分析(略)
• 时间数列的变动趋势有直线型和曲线型,在 建立方程之前先要确定趋势的形态,判断趋 势的形态的方法主要有:(1)画散点图(2)根据 动态分析指标分析.而直线型变动是曲线型 变动分析的基础.
根据散点图的分 布规律进行选择
直线型
o
抛物线型
o
指数曲线型
季节变动的测定与分析
• 季节变动及意义 • 季节变动是指某些现象由于受自然因素和
