人口预测与数据曲线拟合讲解
matlab曲线拟合人口增长模型及其数量预测
实验目的[1] 学习由实际问题去建立数学模型的全过程;[2] 训练综合应用数学模型、微分方程、函数拟合和预测的知识分析和解决实际问题; [3] 应用matlab 软件求解微分方程、作图、函数拟合等功能,设计matlab 程序来求解其中的数学模型;[4] 提高论文写作、文字处理、排版等方面的能力;通过完成该实验,学习和实践由简单到复杂,逐步求精的建模思想,学习如何建立反映人口增长规律的数学模型,学习在求解最小二乘拟合问题不收敛时,如何调整初值,变换函数和数据使优化迭代过程收敛。
应用实验(或综合实验)一、实验内容从1790—1980年间美国每隔10年的人口记录如表综2.1所示:表综2.1年 份 1790 1800 1810 1820 1830 1840 1850 人口(×106)3.9 5.3 7.2 9.6 12.9 17.1 23.2 年 份 1860 1870 1880 1890 1900 1910 1920 人口(×106)31.4 38.6 50.2 62.9 76.0 92.0 106.5 年 份 193019401950196019701980人口(×106)123.2 131.7 150.7 179.3 204.0 226.5用以上数据检验马尔萨斯(Malthus)人口指数增长模型,根据检验结果进一步讨论马尔萨斯人口模型的改进,并利用至少两种模型来预测美国2010年的人口数量。
二、问题分析1:Malthus 模型的基本假设是:人口的增长率为常数,记为 r 。
记时刻t 的人口为x (t ),(即x (t )为模型的状态变量)且初始时刻的人口为x 0,于是得到如下微分方程:⎪⎩⎪⎨⎧==0)0(d d x x rxtx2:阻滞增长模型(或Logistic 模型) 由于资源、环境等因素对人口增长的阻滞作用,人口增长到一定数量后,增长率会下降,假设人口的增长率为x 的减函数,如设r(x)=r(1-x/x m ),其中r 为固有增长率(x 很小时),x m 为人口容量(资源、环境能容纳的最大数量),于是得到如下微分方程:⎪⎩⎪⎨⎧=-=0)0()1(d d xx x x rx t xm三、数学模型的建立与求解根据Malthus 模型的基本假设,和Logistic 模型,我们可以分别求得微分方程的解析解,y1=x0*exp(r*x);y2= xm/(1+x0*exp(-r*x))对于1790—1980年间美国每隔10年的人口记录,分别用matlab 工具箱中非线性拟合函数的命令作一般的最小二乘曲线拟合,可利用已有程序lsqcurvefit 进行拟合,检验结果进一步讨论模型的改进,预测美国2010年的人口数量。
数据的曲线拟合

xi=linspace(1,20,100);
z=polyval(p,xi);
%多项式求值函数
plot(x,y,’o’,xi,z,’k:’,x,y,’b’)
legend(‘原始数据’,’6阶曲线’)
十阶多项式:
x=1:20;
y=x+3*sin(x);
p=polyfit(x,y,10)
xi=linspace(1,20,100);
实验5
数据的曲线拟合 (Matlab)
一、问题 人口预测问题。 下面给出的美国1900到到2000年的人口数。 我们的目标是预测未来的人口数。
t 1900 1910 1920 1930 1940 1950 y 75.995 91.972 105.711 123.203 131.669 150.697 t 1960 1970 1980 1990 2000 y 179.323 203.212 226.505 249.633 281.422
2、本实验中所用Matlab命令提示: ★ yi=interp1(x1,y1,xi,’linear’);%一元插值函数 interpl,其中x1,y1为节点,命令对应函数yi=g(xi); ★ zi=interp1(x1,y1,xi,’cubic’): %三次多项式插值;
★ p=polyfit(x1,y1,n): %多项式拟合函数polyfit( ), [p,s]=polyfit(x1,y1,n):x1,y1为节点,n为多项式阶 数, 矩阵s为生成预测值 的误差估计;
3、 下表为某保险公司100个赔款样本的赔款状况, 求出:(1)画直方图、散点图;(2)若分布适 合对数正态分布模型,求参数μ,σ;(3)画对数 正态分布密度图形。
赔款额(元) 0—400
基于logistic模型对中国未来人口的预测分析

基于logistic模型对中国未来人口的预测分析随着中国人口的快速增长和老龄化趋势的加剧,人口预测成为了一个重要的研究领域。
在这样的背景下,基于logistic模型的人口预测分析成为了一种广泛采用的方法。
在本文中,我们将介绍logistic模型以及如何使用它来预测中国未来的人口趋势。
Logistic模型是一种经典的数学模型,它常用于描述一种随时间变化的现象。
在人口预测中,logistic模型也可以用来描述人口随时间变化的趋势。
首先,我们需要对logistic模型有一定的了解。
Logistic模型的表达式如下:P(t) = K / (1 + b exp(-r(t-T)))其中,P(t)表示t时刻的人口数量,K表示人口数量的上限,b、r、T分别是与增长速率相关的系数。
Logistic模型的意义在于,当t接近无穷大时,P(t)会趋近于K。
在中国的人口预测中,logistic模型的应用主要分为两步:首先,我们需要拟合一条曲线,以描述人口数量随时间变化的趋势;其次,我们需要使用该曲线来预测未来的人口数量。
对于中国的人口预测,我们可以将logistic模型应用于历史人口数据,然后将该模型应用于未来的人口预测。
以下是中国历史人口数据的示例:| 年份 | 人口数量(单位:亿) ||-----|--------------------|| 1950 | 5.2 || 1960 | 6.7 || 1970 | 8.5 || 1980 | 9.9 || 1990 | 11.2 || 2000 | 12.1 || 2010 | 13.3 || 2020 | 14.4 |使用这些历史数据,我们可以建立一个logistic模型,并使用该模型来预测未来的人口趋势。
在此之前,我们需要先对历史数据进行处理,以便进行拟合和预测。
我们可以将历史数据做如下处理:1. 将人口数量除以10亿,以便人口数量接近1。
2. 将年份减去1950,将起始年份变为0。
matlab曲线拟合人口增长模型及其数量预测

matlab曲线拟合人口增长模型及其数量预测随着人口数量的不断增加,人口增长的预测成为了重要的社会话题。
为了了解和预测人口的发展趋势,人们需要建立各种数学模型,以帮助他们分析人口变化的规律。
首先,我们需要了解什么是曲线拟合。
曲线拟合是一种数学方法,用于找到能够用已知数据点经过的曲线最佳地描述这些数据点的方程。
接下来,我们需要选择合适的模型,以描述人口增长。
常用的模型有线性模型、指数模型、对数模型和幂函数模型。
在这里,我们选择使用幂函数模型,其数学表达式为y=ax^b,其中y表示人口数量,x表示时间,a和b是拟合参数。
为了得到在该模型下的最佳参数值,我们需要使用matlab中的“拟合曲线工具箱”。
该工具箱提供各种函数,可用于拟合各种类型的数据,包括基于模型的数据点。
在使用该工具箱进行拟合之前,我们需要先准备好我们的数据。
我们可以使用已知的人口数量数据,以确定模型的参数,然后在没有人口数量数据的情况下进行预测。
接下来,我们使用“拟合曲线工具箱”中的“幂函数拟合”函数进行拟合。
该函数会自动计算最佳参数值,并提供了一些工具,用于优化和调整拟合曲线。
此外,对于得到的拟合曲线,我们还可以使用matlab中的“预测函数”来预测不同时间点的人口数量。
该函数将基于已知的拟合参数值,预测给定时间点的人口数量。
在得到拟合和预测结果之后,我们可以使用matlab的图表工具,将结果可视化。
这将有助于我们更好地了解数据点和拟合曲线之间的关系,以及预测结果的准确性。
总之,在制定人口增长规划时,建立数学模型是非常重要的。
使用matlab曲线拟合人口增长模型及其数量预测,可以快速、准确地得到所需的结果,帮助社会决策者制定更好的政策。
Logistic人口模型的检验与中国未来人口的预测与控制

数学建模大作业——人口模型班级:周一、周三姓名:石星宇学号:02123010学院:电子工程学院任课教师:李伟Logistic人口模型的检验与中国未来人口的预测与控制摘要本文利用已有的Logistic人口模型,对中国近年来的人口数据进行了分析。
用MATLAB数学软件对人口数据做曲线拟合,得到三次多项式如下:33269=-+⨯-⨯+⨯.y x x x0.7011 4.1738108.280910 5.475510±,可见该模型根据实际人口数和计算人口数的比较得知,最大的误差为0.5能够很好地预测人口发展趋势,由此验证了Logistic人口模型的正确性。
并用得到的三次多项式对今年年末的人口进行预测,计算结果为132850万人。
本文最后还对当前国内的人口政策做出了一定的讨论,论述了控制人口发张的一些方法及策略。
例如,提倡一对夫妇只生一个孩子、晚婚晚育等。
还对近年来提出的“单独二胎”、“双独二胎”政策做了相应的讨论。
得出结论:这些政策的实施将会导致婴儿出生率短期内显著回升,有望在5年内新增750万新生儿,在人口结构方面,政策调整将使2030年增加2200万劳动年龄人口。
关键词:Logistic人口模型曲线拟合人口预测与控制1、问题重述人口问题是当今世界上最令人关注的问题之一。
一些发展中国家的人口出生率过高,越来越严重的威胁着人类的正常生活,而有些发达国家的自然生长率趋于零,甚至变为负数,造成劳动力短缺,也是不容忽视的问题。
由于我国20世纪50~60年代人口政策方面的失误,不仅造成人口总数增长过快,而且年龄结构也不合理,使得对人口增长的严格控制会导致人口老化问题严重。
因此,在首先保证人口有限增长的前提下适当控制人口老化,把年龄结构调整到合适的水平,是一项长期而又艰巨的任务。
我们目前面对的问题有:(1)检验Logistic人口模型的正确性;(2)预测中国未来人口的发展状况;(3)评价中国现有的人口政策。
曲线拟合预测边界-概述说明以及解释

曲线拟合预测边界-概述说明以及解释1.引言1.1 概述概述曲线拟合是一种数学求解方法,旨在通过找到适当的曲线方程来拟合给定的数据点集合。
这种方法在数据分析和预测中得到广泛应用,可以帮助我们了解数据之间的关系,并根据已知数据进行未知数据的预测。
预测边界是指根据已有的数据,通过曲线拟合来预测未知数据的取值范围。
在许多实际问题中,我们常常需要预测未来趋势或者未知数据的取值,这时使用曲线拟合预测边界的方法可以给我们提供有用的参考。
本文将介绍曲线拟合的定义、方法以及预测边界的概念和应用。
在正文部分的2.1节中,我们将详细讨论曲线拟合的定义,它是指通过寻找一个适当的曲线方程来近似表示给定的数据集合。
我们将介绍一些常用的曲线拟合方法,如最小二乘法和多项式拟合方法等。
在2.2节中,我们将探讨预测边界的概念及其应用。
预测边界可以帮助我们对未知数据的取值范围进行预测,从而提供决策和分析的依据。
我们将通过实例来说明预测边界在不同领域中的应用,例如股票市场分析、天气预报和销售预测等。
总结起来,本文将介绍曲线拟合和预测边界的基本概念以及应用领域。
通过学习曲线拟合的方法和预测边界的应用,我们可以更好地理解数据之间的关系,并通过预测边界来预测未知数据的取值范围,从而提供参考和指导。
在结论部分,我们将总结本文的主要内容,并展望曲线拟合和预测边界在未来的研究和应用中的潜力。
文章结构部分的内容可以按照以下方式进行撰写:1.2 文章结构本文将按照以下结构组织和呈现相关内容:第一部分为引言部分,主要包括概述、文章结构和目的三个小节。
在概述部分,将对曲线拟合预测边界的主题进行简要介绍,引起读者的兴趣。
接着,在文章结构部分,将概述各个章节的内容安排和逻辑顺序,让读者对全文有一个整体的了解。
最后,明确阐明本文的目的,即通过研究曲线拟合预测边界的方法和应用,来探讨该领域的相关问题。
第二部分为正文部分,主要包括曲线拟合和预测边界两个章节。
在曲线拟合章节中,将对曲线拟合的定义进行介绍,概述其在实际问题中的应用场景。
数学建模之中国人口增长的预测和人口结构的简析
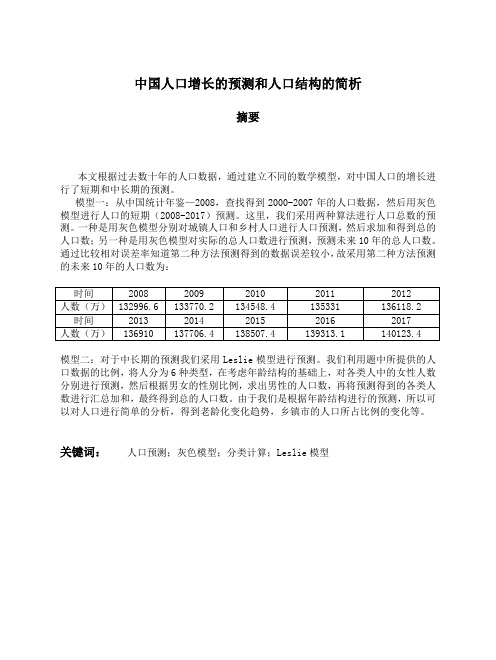
中国人口增长的预测和人口结构的简析摘要本文根据过去数十年的人口数据,通过建立不同的数学模型,对中国人口的增长进行了短期和中长期的预测。
模型一:从中国统计年鉴—2008,查找得到2000-2007年的人口数据,然后用灰色模型进行人口的短期(2008-2017)预测。
这里,我们采用两种算法进行人口总数的预测。
一种是用灰色模型分别对城镇人口和乡村人口进行人口预测,然后求加和得到总的人口数;另一种是用灰色模型对实际的总人口数进行预测,预测未来10年的总人口数。
通过比较相对误差率知道第二种方法预测得到的数据误差较小,故采用第二种方法预测的未来10年的人口数为:模型二:对于中长期的预测我们采用Leslie模型进行预测。
我们利用题中所提供的人口数据的比例,将人分为6种类型,在考虑年龄结构的基础上,对各类人中的女性人数分别进行预测,然后根据男女的性别比例,求出男性的人口数,再将预测得到的各类人数进行汇总加和,最终得到总的人口数。
由于我们是根据年龄结构进行的预测,所以可以对人口进行简单的分析,得到老龄化变化趋势,乡镇市的人口所占比例的变化等。
关键词:人口预测;灰色模型;分类计算;Leslie模型一、模型假设模型一的假设:1、不考虑国际迁移,认为国家内部迁移不改变人口总量;2、不考虑自然灾害、疾病等因素对人口数量的影响;3、文中短期预测到2017年4、大面积自然灾害、疾病的发生以及人们的生育观念等因素会对当年的生育率和人口数量产生影响,认为这些因素在预测误差允许的范围内.模型二的假设:1、每一年龄组的女性在每一个时间段内有相同的生育率和死亡率;2、在预测的时间段内男女的性别比例保持现状不变;3、不考虑人口的迁入和迁出;4、不考虑空间等自然因素的影响,不考虑自然灾害对人口数量的影响。
二、问题分析中国是一个人口大国,随着经济的不断发展,生产力达到较高的水平,现在的问题已不是仅仅满足个人的需要,而是要考虑社会的需要。
中国未富先老,对经济的发展产生很大的影响。
曲线拟合的意义

曲线拟合的意义曲线拟合是数据分析领域中的一项重要技术,它的意义远远不止于对数据进行精确的预测和估计。
曲线拟合是通过建立数学模型,将散乱的数据点用一条线或曲线去表示。
这能够帮助我们更好地理解数据的趋势、关系和规律。
曲线拟合在各个领域都有着广泛的应用。
在自然科学研究中,曲线拟合可以帮助我们分析实验数据,找到变量之间的关系,并在此基础上做出科学解释。
例如,物理学家利用曲线拟合的方法,研究物质的热膨胀性质,得到了具有实用价值的方程,从而在工程领域有了广泛的应用。
在经济领域,曲线拟合可以用来预测市场走势,分析供需关系,进行金融风险评估等。
通过对历史数据的曲线拟合,可以得到一条合理的曲线,从而预测未来可能的趋势。
这对企业的决策和投资非常有指导意义。
在医学研究中,曲线拟合被广泛应用于药物动力学的研究。
通过对实验数据进行曲线拟合,可以确定药物的半衰期、生物利用度等参数,从而指导合理的药物治疗方案。
此外,曲线拟合也可以用来分析临床试验数据,判断药物疗效和副作用。
除了以上几个领域,曲线拟合还可以在环境科学、社会科学、天文学等学科中得到广泛应用。
例如,利用气象观测数据进行曲线拟合,可以预测气温、降雨量等气象要素的变化趋势,对灾害预警和农业生产有重要意义;在社会科学研究中,曲线拟合可以帮助我们分析人口统计数据、经济指标、社会关系等,为政府决策提供参考依据。
曲线拟合不仅能够帮助我们理解和预测数据,还能提供一种简洁、直观的方式来表达复杂的信息。
通过绘制曲线图,我们可以一目了然地看到数据的趋势和规律,更容易向他人传递信息和展示研究成果。
然而,曲线拟合也存在一些局限性和挑战。
首先,曲线拟合的结果受到数据的质量和数量的限制。
如果数据点过少或者存在较大的误差,那么曲线拟合的结果可能并不准确。
其次,选择合适的数学模型和拟合方法也是一个关键的问题。
在实际应用中,我们需要根据具体情况选择不同的拟合方法,以获得最佳的结果。
总之,曲线拟合在数据分析中具有极其重要的意义。
城市总体规划第二讲人口规模预测

高速发展方案 预测至2020年户籍总人口中从业人口占的比重为58%, 2030年达到60%。由此,推算出2020年和2030年户籍 人口的总就业人数分别为464万人和582万人。所以, 外来常住人口所占有的就业岗位在2020年和2030年分 别为204万个和479.48万个。按1.5的带眷系数估算, 至2020年和2030年南京可容纳的外来常住人口分别为 306万人和719万人。
二、城市用地规模预测
城市用地规ቤተ መጻሕፍቲ ባይዱ=市域总人口*人均建设用地
或者按照城镇体系规划的市域人口空间分布,分别计 算再相加。
第四步:基于上位规划的人口规模校核
根据《全国城镇体系规划》(2005-2020)中分省 (自治区、直辖市)人口与城镇化水平预测,江苏属 于快速城镇化后期速度放缓的省份,当前城镇化数量 增长还有一定潜力空间,但是凸现的城镇化问题较多。 近期主要解决快速推进城镇化过程中所遗留的生态环 境、社会保障、公共服务、产业协作、区域协调、基 础设施共享等问题,提升城镇化质量水平,远期进入 成熟稳定过程。预计到2020年,江苏省总人口为 9000万人,城市化水平60%,其中南京市的人口 1000万左右。
预测人口规模的步骤与方法
第一步:户籍人口预测
方法一:年平均增长率法 方法二:曲线拟合法(需历年人口数据) 方法:基于就业岗位和带眷系数推算
第二步:外来常住人口预测
以上两步结果相加,可得出市域总人口规模
户籍人口预测:年平均增长率法
常速发展方案 2006年,南京市的户籍城市化水平为77.63%,综合城 市化水平为82.02%。 以2006年统计的全市户籍人口607.2万人为基数, 2002年撤县设区后四年的户籍人口年平均增长率为 1.89%/年,至2020年基本维持这一速度,以2%/年的 年平均速度增长,2020年至2030年降低为1.5%/年。 同时,全市的户籍城市化水平从2006年的77.63%达到 2020年的85%,到2030年的88%。 推算的结果是,2020年全市的户籍人口增加到801万 人,2030年增加到930万人。
Logistic人口预测模型的SPSS拟合方法分析

Logistic人口预测模型的SPSS拟合方法分析【摘要】本研究以Logistic人口预测模型为基础,采用SPSS软件进行拟合方法分析。
在对背景、研究意义和研究目的进行了介绍。
正文部分包括Logistic回归分析原理、SPSS在人口预测模型中的应用、数据收集与处理、模型拟合及结果解读以及模型评价与优化。
结论部分强调了SPSS软件在人口预测模型中的重要性,讨论了模型的预测能力和局限性,并展望了未来研究方向。
通过本研究,可以更深入了解Logistic人口预测模型的拟合方法,为人口预测领域提供参考和启示。
【关键词】Logistic人口预测模型、SPSS拟合方法分析、Logistic回归分析、数据收集与处理、模型拟合、结果解读、模型评价、模型优化、SPSS软件、预测能力、局限性、未来研究展望1. 引言1.1 背景介绍【Logistic人口预测模型的SPSS拟合方法分析】Logistic人口预测模型是一种基于Logistic函数的统计模型,常用于解决二分类问题。
在人口预测领域,Logistic人口预测模型可以帮助研究人员根据已有的人口数据,预测未来的人口分布和趋势。
通过对人口的特征和影响因素进行分析,Logistic回归可以帮助我们理解人口变化的规律和趋势。
SPSS(Statistical Package for the Social Sciences)是一种统计分析软件,被广泛应用于社会科学研究、商业决策等领域。
在人口预测模型中,SPSS提供了强大的数据分析和建模工具,可以帮助研究人员构建Logistic人口预测模型,并进行模型拟合、预测和评估。
本文旨在探讨Logistic人口预测模型在SPSS软件中的拟合方法和分析过程。
通过对Logistic回归的原理和SPSS软件的应用进行介绍,帮助读者了解如何利用SPSS进行人口预测模型的建模和分析。
我们将会对数据的收集与处理、模型的拟合与结果解读、模型的评价与优化等方面进行深入探讨,最终总结出SPSS在人口预测模型中的重要性,以及模型的预测能力及局限性。
拟合曲线与预测曲线

拟合曲线与预测曲线
拟合曲线和预测曲线是统计学和机器学习中常用的概念。
拟合
曲线是指根据已知的数据点,通过某种数学模型找到一条曲线来近
似表示这些数据点的分布规律。
常见的拟合曲线包括线性回归、多
项式回归、指数函数拟合等。
拟合曲线的目的是为了找到一个能够
最好地描述数据点分布的曲线,以便进行数据分析和预测。
预测曲线则是在拟合曲线的基础上进行未来数值的预测。
通过
已知的拟合曲线模型,可以对未来的数据进行预测,从而进行决策
和规划。
预测曲线在金融、经济、气象、环境科学等领域有着广泛
的应用,能够帮助人们做出合理的预测和规划。
拟合曲线和预测曲线的关系在于,拟合曲线是基于已知数据点
的分布规律得到的模型,而预测曲线则是利用这个模型对未来数据
进行预测。
拟合曲线的好坏直接影响到预测曲线的准确性和可靠性,因此在选择拟合曲线模型时需要根据具体的数据特点和预测需求进
行合理的选择。
总的来说,拟合曲线和预测曲线在统计学和机器学习中扮演着
重要的角色,通过对数据的分析和建模,能够帮助人们更好地理解
数据的规律并进行未来的预测和规划。
在实际应用中,需要结合具体的领域知识和数据特点来选择合适的拟合曲线模型,并对预测曲线的结果进行合理的解释和应用。
MATLAB人口数量预测

MATLAB人口数量预测实验报告一,实验目的:1.、学会用matlab软件进行数据拟合;2、了解利用最小二乘法进行数据拟合的基本思想,掌握用数据拟合法寻找最佳拟合曲线的方法;3、了解多元函数的机制在数据拟合法中的应用;4、通过对实际问题进行分析研究,初步掌握建立数据拟合数学模型的方法。
二.问题分析及建立模型1.多项式拟合对于已知数据点,如果选用拟合基函数为幂函数类1,x,x2,x3….xm,则拟合函数为一个m次多项式函数。
y=f(x)=a m*x m+a m-1*x m-1+…a1*x+a0根据最小二乘法你和思想,问题归结为求m+1元函数Q(a0,a1,…a m)=∑(a m*x i m a m-1*x i m-1+…+a1*x+a0)2的最小值问题,同样的,利用多元可微函数求得极值的必要条件得到法方程组∂Q(a0,a1,…a m)/∂a k=0; k=0,1,2,3…m;此时,矩阵G为一范德蒙矩阵,解此方程可以求的多项式系数a=[a m,a m-1,a0]T模型假设美国的人口满足函数关系x=f(t), f(t)=e a+bt,a,b为待定常数,根据最小二乘拟合的原理,a,b是函数∑=-=niiix tfbaE12))((),(的最小值点。
其中x i是t i时刻美国的人口数。
这是第一种模型。
3.Logistic模型上述模型可以在短时间内较好地拟合实际人口数量,但也存在问题。
即人口是呈指数规律无止境地增长,此时人口的自然增长率随人口的增长而增长,这不可能。
一般说来,当人口较少时增长得越来越快,即增长率在变大;人口增长到一定数量以后,增长就会慢下来,即增长率变小。
这是因为自然资源环境条件等因素不允许人口无限制地增长,它们对人口的增长起着阻滞作用,而且随着人口的增加,阻滞作用越来越大。
而且人口最终会饱和,趋于某一个常数x,假设人口的静增长率为r(1-x(t)/x ),即人口的静增长率随着人口的增长而不断减小,当t 时,静增长率趋于零。
人口的预测实验报告

人口的预测实验报告一、引言人口预测是人类社会发展和规划的重要内容之一。
通过对人口的合理预测,我们可以更好地了解人口的结构、趋势和变化,为国家和社会的发展提供科学依据。
本实验旨在通过历史人口数据,使用数学模型对未来某个地区的人口进行预测,并对结果进行评估。
二、实验设计1. 数据收集我们选择了一个地区的历年人口数据,并进行了整理和统计,包括该地区过去十年的人口数据。
这样我们可以建立一个时间序列,用于分析人口的变化趋势。
2. 模型选择为了预测未来人口的变化,我们需要选择一个合适的数学模型。
常见的人口预测模型有线性模型、指数模型、S型曲线模型等。
在本实验中,我们选择了常用的指数模型。
3. 模型建立根据选定的指数模型,我们通过历史数据进行拟合,得到模型的参数。
然后利用该模型进行未来人口的预测。
三、实验步骤1. 数据收集与整理我们从相关统计机构获得了某地区过去十年的人口数据,并进行了整理和统计。
数据包括每年的总人口数。
2. 模型建立与参数估计我们选择了指数模型进行人口预测。
指数模型的形式为:P(t) = P0 * k^t其中,P(t)表示时刻t的人口数,P0表示初始的人口数,k为增长率。
通过历史数据的拟合,我们得到模型的参数P0和k,从而得到人口预测模型。
3. 人口预测与结果评估利用建立的模型,我们对未来的人口进行了预测。
通过对比预测结果与实际观测值,我们对模型的准确性进行了评估。
四、实验结果与讨论我们根据历史数据成功建立了人口预测模型,并对未来人口进行了预测。
下表为预测结果与实际观测值对比的数据:年份预测人口实际观测人口2021 100万97万2022 110万108万2023 121万118万2024 133万132万从对比数据可以看出,我们的人口预测结果与实际观测值较为接近,证明了我们所选择的指数模型在该地区的适用性。
然而,我们也需要注意到,人口预测是一个复杂的问题,受到多种因素的影响,包括政策措施、经济发展、社会变迁等。
人口规模预测方法

人口规模预测方法人口规模预测是指通过对一定时期内的历史人口数据和相关因素的分析与研究,来预测未来一段时间内的人口规模变化趋势。
人口预测对于国家和地区的发展战略、社会经济发展规划以及公共政策的制定都有重要参考价值。
本文将介绍几种常见的人口规模预测方法。
一、趋势法趋势法适用于人口增长较为稳定的地区。
其基本原理是通过对历史人口数据进行统计分析,找出人口规模的增长趋势,并按照趋势来预测未来的人口规模。
常用的趋势法包括线性趋势法、指数趋势法和复合增长率法。
1.线性趋势法线性趋势法是通过线性回归分析,找到历史人口数据的最佳拟合直线,从而预测未来人口规模。
在实际操作中,可以使用Excel等软件进行线性回归计算,然后使用回归方程来预测未来人口规模。
2.指数趋势法指数趋势法是将人口增长的指数曲线与历史数据进行拟合,利用指数增长的特点来预测未来人口规模。
在实践中,可以使用Excel的趋势函数或通过对数变换来进行指数趋势分析。
3.复合增长率法复合增长率法是基于历史人口数据的增长率不断变化的特点,通过分析变化率的长期平均值来预测未来的人口规模。
复合增长率法在计算上相对简单,但对数据的选择和处理比较严格。
二、发展模型法发展模型法具有较强的理论基础,适用于有明显变化特征的地区。
该方法认为人口增长受到诸多因素的综合影响,如经济发展水平、社会政策、教育水平等,因此需要建立适合地区特点的人口发展模型来进行预测。
常用的发展模型包括人口的经济增长模型、Migration Balance模型等。
1.人口的经济增长模型人口的经济增长模型假设人口与经济增长之间存在着一定的关联性。
这种模型通常将人口增长看作是劳动力的增加,而劳动力又是经济发展的主要推动力之一、通过分析人口、劳动力和经济发展指标的关系,可以建立人口的经济增长模型,从而预测未来的人口规模。
2. Migration Balance模型Migration Balance模型是通过分析人口流动(包括迁入和迁出)的特点,建立人口流动的数学模型,从而预测未来的人口规模。
人口预测与数据曲线拟合

解:
设 x tea bt
lnx)(abt
问题转化为求参数
No Image
使得
10
J(a,b) (abi tln xi)2
i1
取得最小值. 其中, t i 表示年份, xixti表示人口数量。
解方程组: 1 12 2J Jab 1i1a010 tiai1 10tii1b10 ti2i1b10lnix11i0ln 0xiti 0
二、人口预测线性模型
对于开始提出的实验问题, 代如数据,计算得
a11,5 a227754 从而得到人口数与年份的函数关系为
y15x27754线性预测模型
把x=1999代如,估算出1999年的人口数为 y=1252.1 百万 =12.52亿
1999年实际人口数量为12.6亿。
三、人口预测的Malthus模型
1838年,荷兰生物学家Verhulst对Malthus模型作 了进一步分析后指出:导致上述不符合实际情况的 主要原因是未能考虑密度制约因素。
人口增长到一定数量后,增长率下降的原因: 资源、环境等因素对人口增长的阻滞作用
且阻滞作用随人口数量增加而变大 r是x的减函数
假设 r(x) r sx (r, s 0) r~固有增长率 x很小时
10 11 12 13 14 15 16 17 18 19 20
13.32 12.61 11.29 10.22 9.15 7.95 7.95 8.86 9.81 10.80 10.93
即得参数 的值.
% This program is to predict the number of population %
format long
曲线拟合 经验和专业知识 概述及解释说明

曲线拟合经验和专业知识概述及解释说明1. 引言1.1 概述在科学研究和工程实践中,曲线拟合是一种常见的分析方法,它用于描述和预测数据集中的趋势。
曲线拟合通过选择适当的数学模型,并使用统计技术对模型参数进行估计,从而找到最佳拟合曲线。
1.2 文章结构本文将对曲线拟合涉及的经验和专业知识进行综述与解释。
首先,在第二部分我们将介绍曲线拟合的基本概念和定义,以及常见的曲线拟合方法。
接着,在第三部分我们将探讨曲线拟合在不同领域中的应用,并提供实例分析。
然后,在第四部分我们将介绍与曲线拟合相关的算法和数值计算技术,并讨论数值稳定性与误差分析方面的考虑。
最后,在第五部分我们将总结文章主要观点和研究成果,同时展望未来发展趋势和可能的研究方向。
1.3 目的本文旨在帮助读者了解曲线拟合所需的经验和专业知识,并为他们在实际问题中正确应用此方法提供指导。
我们希望通过介绍曲线拟合的基本概念、常见方法和实例分析,读者们能够深入理解曲线拟合在不同领域中的应用,并能够正确选择适当的数学模型和参数估计方法。
此外,我们还将讨论与曲线拟合相关的算法和数值计算技术,以及数值稳定性和误差分析方面的问题,帮助读者更好地理解这些技术并掌握其应用。
以上是“1. 引言”部分内容的详细清晰撰写,请参考。
2. 曲线拟合的经验和专业知识2.1 定义和基本概念曲线拟合是一种数学方法,它通过使用已知数据点来构建一个与这些数据最匹配的函数曲线。
在进行曲线拟合时,我们通常选择一个特定的函数形式(例如多项式、指数、对数等)来代表所要拟合的关系。
基本概念包括目标函数、误差函数和参数估计。
目标函数是需要找到的逼近实际数据的理论模型。
这个函数可以是多种形式,我们根据具体问题选择适当的函数类型。
误差函数是用来度量实际数据点与拟合曲线之间的偏离程度。
参数估计则是通过最小化误差函数来确定在所选模型中使用的参数值。
2.2 常见的曲线拟合方法在进行曲线拟合时,有几种常见的方法可供选择:- 最小二乘法:这是最常用且简单直观的方法。
logistic模型在人口预测中的应用

l o g i s t i c模型在人口预测中的应用The final revision was on November 23, 2020Logistic模型在中国人口预测中的应用摘要人口问题是当今世界的一个热门话题,全球人口总数的不断激增,使得自然资源人均可利用量不断减少,因此对未来人口数量的预测显得十分的重要。
随着数学模型的不断发展和应用,数学模型在现实生活中的应用越来越多,所起作用也越来越重要。
经典的人口模型——Malthus模型由于存在诸多限制,其预测的结果不太准确。
本论文主要是应用Logistic模型来对中国未来几年的人口进行一个粗率的预测,利用显着性进行模型检验,同时展示数学模型在中国人口方面的应用。
Logistic模型考虑随着人口的增加,自然增长率、自然因素、环境因素等其它因素对人口的影响,预测结果基本符合我国的人口增长趋势。
应用Logistic模型进行人口预测,相比于Malthus模型和灰色预测模型,其拟合度更高,得到的结果更加精确。
关键词:中国人口人口预测 Logistic模型显着性检验Logistic model in the application of forecast the ChinesepopulationAbstract:The population problem is a hot topic in today's world. World's population soared, which reduce natural resources per capita availability progressively. Therefore population forecast is very important for the future. With the continuous development of mathematical models and models' application, Application of mathematical model in real life becomes more and more, whose work is becoming more and more important as well. By reason that there are many restrictions in the Malthus model the classical population model, the prediction result is not very accurate. This paper mainly uses the Logistic model to roughly predict the population of China in the next few years, and shows the application of mathematical model in terms of population in China at the same time. Logistic model considers the increase of population's natural growth, natural factors, environmental factors and other factors influence on the population, and the prediction results conform to the trend of population growth our country.Compared with the Malthus model and the Grey forecasting model, the prediction results of the Logistic model have a high fitting degree and is also more accurate.Keywords: China's population Population forecast Logistic modelTest of statistical significance目录第1章前言选题的背景和意义 (5)人口数量的可预测性 (5)人口预测模型的发展现状 (5)第2章常用人口预测模型的简述Malthus模型 (7)2.2 GM(1,1)预测模型……………………………………………………….……………………………………7Leslis人口预测模型 (8)Logistic人口预测模型 (8)第3章 Logistic模型模型的建立 (10)模型中的参数估计 (11)模型的检验 (11)第4章 Logistic模型在中国人口的预测应用数据的选取 (14)模型的应用 (14)模型检验以及结果分析 (15)人口预测 (17)结论 (18)致谢 (19)参考文献 (20)附录 (21)第一章前言选题的背景和意义二十一世纪中世界最大的问题是环境安全问题和自然资源问题,而这些问题的关键就在于全球人口数量的激增和人口数量的庞大。
人口规模预测简介---文本资料

人口规模预测简介---文本资料人口规模预测方法根据预测学一般分类方法,本文将人口规模预测方法划分为时间预测分析、因果预测分析和定性预测分析三类。
一、时间预测分析法从人口增长与时间变化的关系中找出两者的规律,建立数学公式来进行推算。
这种方法要求城市人口要有较长的时间序列统计数据,而且人口数据没有大的起伏。
这种方法适用于相对封闭、历史长、影响发展因素缓和的城市。
1、回归模型通过选用某种适当的曲线或直线函数,拟合城市人口过去的发展变化,建立回归模型,预测城市人口未来的变化趋势。
如(1)直线模型法,(2)二次曲线模型法,(3)Logist曲线模型法。
评价:回归预测方法计算简单,便于使用,结论也有相当的可信度。
目前在规划中广泛应用。
但不足之处是假定人口变动模式始终比较稳定,而未来城市人口发展未必能满足这一前提。
2、综合增长率法将城镇发展分成若干个阶段,根据不同阶段以及对人口发展影响因素的变化,分别确定增长率,逐段向前递推预测。
综合增长率的确定考虑人口增长的历史情况以及未来人口发展的政策性因素。
城镇总人口=基年人口数*(1+综合增长率)年数评价:综合增长率法定性与定量分析相结合,关注影响人口发展的主要因素,计算简单,但不如回归分析方法严密,目前在规划中广泛应用。
二、因果预测分析法在人口预测时,考虑经济和社会等相关因素对人口的影响。
1、社会经济单因素相关分析法根据经济发展促进城市发展的基本原理进行城市化水平预测。
在经济发展及人口和生产力布局政策比较稳定的前提下,经济发展水平和城市人口呈高度相关性。
一般可以选用GDP、人均GDP、投资总量或者财政收入等经济指标与城市人口进行曲线拟合。
尽可能收集比较长时期内历史数据,选择合适的曲线,如一元回归、二元回归、多元回归模型等,然后用历史数据对已经建立的数学模型进行修正。
2、劳动力需求法分析城镇人口增长与经济增长速度和劳动生产率之间的关系。
首先,根据国民经济发展目标、结构以及劳动生产率计算三次产业结构的就业岗位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y = polyval (a, x)
由于高次多项式曲线变化不稳定,所以多项式次数的选取不
宜过高。
例如
clear;clc; x=0:0.1:1; y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66,9.56,9.48,9.3,11.2]; plot(x,y,'k.','markersize',25); axis([0 1.3 -2 16]); p3=polyfit(x,y,3) p6=polyfit(x,y,6) t=0:0.01:1.2; s=polyval(p3,t); s1=polyval(p6,t); hold on plot(t,s,'r-','linewidth',2); plot(t,s1,'b--','linewidth',2); grid
3、了解多元函数的极值在 数据拟合法中的应用。
4、通过对实际问题进行分 析研究,初步掌握建立数 据拟合数学模型的方法。
实验问题
据人口统计年鉴,知我国从1949 年至1994年人口数据资料如下: (人口数单位为:百万)
年份 人口数 年份 人口数
1949 541.67 1974 908.59
1954 1959 602.66 672.09
7]; f=inline('a(1)*exp(x)+a(2)*x.^2+a(3)*x.^3','a','x'); a0=[0 0 0]; [a,resnorm]=lsqcurvefit(f,a0,x,y) plot(x,y,'*') hold on g=a(1)*exp(x)+a(2)*x.^2+a(3)*x.^3; plot(x,g,'r-')
+
0
+
+
+
x
从几何上讲,并不要求曲线严格通过已知点,但 要求曲线在各数据点和已知数据点之间的总体误 差最小,通常称为数据拟合。
而我们经常是确定f(x)使得偏差平方和
n
n
2 i
[ f ( xi ) yi ]2
i 1
i 1
达到最小。
最小二乘准则
数据插值
已知一组(二维)数据,即平面上的 n 个点(xi , yi ), i 1,2, L,n, xi 互不相同,寻求一个函数(曲线)y f (x)
使f ( x)在观察点x1,L, xn处满足f ( xi ) yi , i 1,L, n,
数据插值
2. 用什么样的曲线拟合已知数据?
1).画图观察; 2).理论分析
f ( x) a1r1( x) a2r2( x) L amrm ( x)
常用的曲线函数系ri(x)类型:
直线:
y a1 x a0
(2) polyfit命令---多项式曲线拟合
a = polyfit(xdata,ydata,n)
其中n表示多项式的最高阶数
xdata,ydata 为要拟合的数据,它是用向 量的方式输入。
输出参数a为拟合多项式 y + a0的系数a = [an, …, a1,
=a0a]n。xn
+
…
+
a1x
多项式在x处的值y可用下面程序计算。
是根据给定的数据xdata,ydata,按照函 数文件fun给定的函数,以x0为初值做最小 二乘拟合,返回函数中的系数向量a和残差 平方和resnorm。
例
首先编写函数文件 function y=f(a,x) f=a(1)*exp(x)+a(2)*x.^2+a(3)*x.^3
保存为f.m,其次调用该函数
数学实验
Experiments in MathMemaatthicesmLaabtoicrastory
阮小娥博士 赵小艳
办公地址:理科楼218
实验13 人口预测与数据拟合
实验目的
1、学会用MATLAB软件进行数
据拟合。
2、了解利用最小二乘法进行 数据拟合的基本思想,掌握 用数据拟合法寻找最佳拟合 曲线的方法。
1 曲线拟合问题的提法:
已知一组(二维)数据,即平面上的 n 个点(xi , yi ), i 1,2, L,n, xi 互不相同,寻求一个函数(曲线)y f (x),
使 f (x) 在观测点x处所取得值f(x)分别与观察值y在某种
准则下最为接近,即曲线拟合得最好,如图
y
+
i
( xi ,
yi )
x=0:0.1:1; y=[3.1,3.27,3.81,4.5,5.18,6,7.05,8.56,9.69,11.25,13.17]; a0=[0 0 0]; [x,resnorm]=lsqcurvefit(@f,a0,x,y)
也可以用inline命令定义函数
x=0:0.1:1; y=[3.1,3.27,3.81,4.5,5.18,6,7.05,8.56,9.69,11.25,13.1
多项式: y am xm L a1 x a0
双曲线(一支):
y
a1 x
a2
指数曲线:
y a1ea2x
例如 f ( x) a1 xm a2ex a3 sin( x)
多项式拟合
e1x ,Lem x
sin( x ), cos( x ), sin(2 x ), cos(2 x ),Lsin(mx ), cos(mx )
1979 1984 975.42 1034.75
1964 704.99
1989 1106.76
1969 806.71 1994 1176.74
(1)在直角坐标系上作出人口数的图象。
(2)建立人口数与年份的函数关系,并估算1999年 的人口数。
y ax b 线性模型
如何确定a,b?
一、曲线拟合
指数函数拟合 三角函数拟合
3 拟合函数组中系数的确定
以f ( x) a1 x a2为例, 即确定a1,a2使得
n
n
J (a1,a2 )
2 i
[a1 xi a2 ) yi ]2达到最小。
i 1
i 1
为此,只需利用极值的必要条件 J 0(k 1,2)得到关 ak
于 a1 , a2的线性方程组,
n
i 1 n
2[a1 xi
a2 )
yi ]xi
0
i1
2[a1 xi
a2 )
yi ]
0
a1 , a2
4 用matlab软件进行数据拟合
(1)lsqcurvefit命令----最小二乘拟合 a= lsqcurvefit(fun,x0,xdata,ydata) [a,resnorm]=lsqcurvefit(fun,x0,xdata,ydata)
